The Heterotic-Ricci Flow and Its Three-Dimensional Solitons

Abstract

We introduce a novel curvature flow, the Heterotic-Ricci flow, as the two-loop renormalization group flow of the Heterotic string common sector and study its three-dimensional compact solitons. The Heterotic-Ricci flow is a coupled curvature evolution flow, depending on a non-negative real parameter $\kappa$, for a complete Riemannian metric and a three-form H on a manifold M. Its most salient feature is that it involves several terms quadratic in the curvature tensor of a metric connection with skew-symmetric torsion H. When $\kappa = 0$ the Heterotic-Ricci flow reduces to the generalized Ricci flow and hence it can be understood as a modification of the latter via the second-order correction prescribed by Heterotic string theory, whereas when $H=0$ and $\kappa >0$ the Heterotic-Ricci flow reduces to a constrained version of the RG-2 flow and hence it can be understood as a generalization of the latter via the introduction of the three-form H. Solutions of Heterotic supergravity with trivial gauge bundle, which we call Heterotic solitons, define a particular class of three-dimensional solitons for the Heterotic-Ricci flow and constitute our main object of study. We prove a number of structural results for three-dimensional Heterotic solitons, obtaining, in particular, the complete classification of compact three-dimensional strong Heterotic solitons as hyperbolic three-manifolds or quotients of the Heisenberg group equipped with a left-invariant metric. Furthermore, we prove that all Einstein three-dimensional Heterotic solitons have constant dilaton and leave as open the construction of a Heterotic soliton with non-constant dilaton. In this direction, we prove that Einstein Heterotic solitons with constant dilaton are rigid and therefore cannot be deformed into a solution with non-constant dilaton. This is, to the best of our knowledge, the first rigidity result for compact supergravity solutions in the literature.

1 Introduction

1.1 Background and Motivation

The main purpose of this article is to introduce a novel curvature flow, namely the Heterotic-Ricci flow, and prove a number of structural results about the particular class of its three-dimensional solitons that can be interpreted as solutions of Heterotic supergravity [4, 5]. The Heterotic-Ricci flow and its associated solitons provide a general framework in which a number of notable curvature flows as well as their solitons, all inspired to some extent by some of the building blocks of Heterotic string theory, appear as natural particular cases, hence giving a conceptual understanding of these flows as limiting cases of a well-defined geometric construction determined by Heterotic supersymmetry. The Heterotic-Ricci flow, which we introduce in Definition 2.1 as the two-loop renormalization group flow of the Heterotic string common sector, involves a real parameter $\kappa$ and evolves a family of metrics $g_t$ and three-forms $H_t$ coupled via a system of equations that contains several quadratic terms in the curvature tensor of the unique metric connection $\nabla ^{g_t,H_t}$ with skew-torsion $-H_t$. In particular, the Heterotic-Ricci flow is related to other recent or more classical flows as follows [43, 44]:

• When $\kappa =0$ and $H_t = 0$, the Heterotic-Ricci flow is the classical Ricci-flow [30].

• When $H_t=0$, the Heterotic-Ricci flow reduces to the RG 2-flow [27] involving a quadratic constraint on the Riemann tensor that is inherited from the Bianchi identity of the system. To the best of our knowledge this constraint has not been studied in the RG 2-flow literature, and, based on previous experience with anomaly cancellation constraints, it may lead to a better-behaved RG 2-flow.

• When $\kappa = 0$, the Heterotic-Ricci flow reduces to the generalized Ricci flow [23, 42, 52].

• If we consider the Heterotic-Ricci flow on a complex manifold with the trivial canonical bundle and if, using the standard notation in the literature, we set $H_t = -\textrm{d}^c \omega _t$ for a family of Hermitian metrics $\omega _t$, then the Bianchi identity of the Heterotic-Ricci flow corresponds to the main equation of the Anomaly flow [44,45,46].

• In the set-up of the previous bullet point, if in addition, we assume $\kappa = 0$ then we obtain the generalized Kähler–Ricci flow [54], which in turn is naturally related to the pluriclosed flow [57, 59] as explained in [26, 58].

• The Heterotic-Ricci flow should be a particular case of the generalized Ricci flow on a string Courant algebroid as introduced in [20], although this remains to be checked explicitly. Clarifying the precise condition on the underlying Courant algebroid that reduces the flow of [20] to the Heterotic-Ricci flow would clarify the behavior of the latter under T-duality, see also [51, 53]?.

• Being the renormalization group flow of a string theory, the Heterotic-Ricci flow can be expected to be related to other curvature evolution flows inspired by string theory [13,14,15], although the precise relationship may not be straightforward and may require non-trivial string theory dualities.

Naturally, following the previous list, the solitons of the Heterotic-Ricci flow are similarly related to the solitons of the Ricci flow [9], RG-2 flow [25, 29], generalized Ricci flow [23, 55, 60], and Anomaly flow [44,45,46], respectively. In particular, solutions to the celebrated Hull–Strominger system [11, 12, 16,17,18,19, 24, 32, 62] or the coupled Hermite–Einstein equations, recently introduced in [21, 22], are automatically particular solutions of the Einstein equation of Heterotic supergravity and hence are intimately related to the solitons of the Heterotic-Ricci flow. Note that, whereas the Hull–Strominger system involves a single higher curvature term, which appears in its Bianchi identity, the soliton system of the Heterotic-Ricci flow will involve three different higher curvature terms, all of them quadratic in the curvature of a metric connection with skew torsion.

The Heterotic Ricci flow, although neatly packed in terms of curvature tensors with torsion, is a very complex curvature flow. As a first attempt to understand its main properties, we focus in this article on the three-dimensional solitons of the system, and in particular on those admitting an interpretation as solutions of three-dimensional Heterotic supergravity. This leads us to define the Heterotic system in Sect. 3 together with its strong version, which is obtained by exploiting the internal consistency of the system and which admits a natural higher-dimensional geometric interpretation in terms of the total space of the underlying frame bundle.

1.2 Main Results and Overview

• In Sect. 2 we propose and define the Heterotic-Ricci flow as the two-loop renormalization group flow of the Heterotic string common sector. We reformulate it in three dimensions and we study a particular class of Heterotic-Ricci flows, that we call homothety flows, for which the metric evolves only by homotheties. We find the explicit homothety flows and we perform a detailed numerical analysis in the most difficult cases where explicit expressions cannot be obtained. In the latter cases, we obtain explicit numerical examples of eternal and regular flows, showcasing that these flows can be better behaved than their counterparts in the generalized Ricci flow or the RG-2 flow.

• In Sect. 3 we introduce the Heterotic soliton system as the equations of motion of Heterotic supergravity with the trivial gauge bundle. Studying the consistency of the system we arrive at the notion of strong Heterotic soliton, which we interpret geometrically in terms of the total space of the frame bundle of the underlying Riemannian manifold.

• In Sect. 4 we study compact three-dimensional Heterotic solitons. In Theorem 4.11 we prove that all Einstein three-dimensional Heterotic solitons have constant dilaton. Furthermore, in Theorem 4.15 we prove that all three-dimensional compact strong Heterotic solitons have constant dilaton and are either hyperbolic manifolds or quotients of the Heisenberg group.

• In Sect. 5 we study the local deformations of Einstein Heterotic solitons. In particular, in Theorem 5.9 we prove that all three-dimensional compact Einstein Heterotic solitons are rigid and therefore cannot be deformed into Heterotic solitons with non-constant dilaton. To the best of our knowledge, this seems to be the first rigidity result for a compact solution of a supergravity theory.

It should be mentioned that being a new curvature flow, the most fundamental properties of the Heterotic-Ricci flow remain to be investigated, especially its weak parabolicity regime and short-time existence. The latter has been studied in [7, 28] for the case of the RG 2-flow, proving the short-time existence of the flow assuming a bound on the sectional curvature of the initial data. Similarly, the basic properties of the solitons of the Heterotic-Ricci flow remain to be studied, especially the construction of examples, their higher-categorical interpretation, and the study of the associated moduli and stability. In particular, it would be interesting to extend to the Heterotic-Ricci case the work of [25, 29] for solitons of the RG 2-flow. Particularly intriguing is the study of the solitons of the Heterotic-Ricci flow on a complex manifold, with an adapted Ansatz as proposed in [26, 55, 60, 61] for the solitons of the generalized Ricci flow, and their relation with the coupled Hermite–Einstein system of [21, 22]. Related to the existence of solitons for the flow, we have not been able to construct a three-dimensional Heterotic soliton with non-constant dilaton. Regarding this problem, we do not have enough evidence to make a conjecture in either sense, so constructing an example with non-trivial dilaton or proving that its non-existence constitutes the main open problem that can be derived from this article.

2 The Heterotic-Ricci Flow

In this section, we introduce the Heterotic-Ricci flow as the renormalization group flow of the Neveu-Schwarz sector of the Heterotic string at second order in the string-slope parameter $\kappa$. At first order in $\kappa$ this renormalization group flow corresponds to the generalized Ricci-flow [23, 42, 52], a fact that we use to propose the Heterotic-Ricci flow as a higher-order curvature correction to the latter.

2.1 Preliminaries

Let M be an oriented manifold M of dimension d equipped with a Riemannian metric g. We will denote by $\langle -, -\rangle _g$ the determinant inner product induced by g on the exterior algebra bundle of M, and by $\vert - \vert _g$ its associated norm. For every linear connection $\nabla$ on TM, we will denote by $\mathcal {R}^{\nabla }$ its curvature tensor, which in our conventions is defined by the following formula:

$$\begin{aligned} \mathcal {R}^{\nabla }_{u,v} w = \nabla _{u} \nabla _{v} w - \nabla _{v} \nabla _{u} w - \nabla _{[u,v]} w, \end{aligned}$$

for every vector fields $u,v,w\in \mathfrak {X}(M)$. In the following, we will exclusively consider metric-compatible connections on the given Riemannian manifold (M, g), and we will understand their curvature tensors $\mathcal {R}^{\nabla }$ as sections of $\wedge ^2 M\otimes \wedge ^2 M$, upon identification of skew-symmetric endomorphisms with two-forms, using the Riemannian metric. Therefore, in our conventions the norm of $\mathcal {R}^{\nabla }$ is explicitly given by:

$$\begin{aligned} \vert \mathcal {R}^{\nabla } \vert _g^2&: =&\langle \mathcal {R}^{\nabla }, \mathcal {R}^{\nabla } \rangle _g = \frac{1}{2} \sum _{i,j=1}^d \langle \mathcal {R}^{\nabla }_{e_i,e_j}, \mathcal {R}^{\nabla }_{e_i,e_j} \rangle _g \\= & {} \frac{1}{4}\sum _{i,j,k,l=1}^d \mathcal {R}^{\nabla }_{e_i,e_j}(e_k,e_l)\, \mathcal {R}^{\nabla }_{e_i,e_j}(e_k,e_l), \end{aligned}$$

in terms of any orthonormal frame $(e_i)$, where $\mathcal {R}^{\nabla }_{e_i,e_j} = e_j \lrcorner e_i\lrcorner \mathcal {R}^{\nabla }$ denotes evaluation of $e_i$ and $e_j$ in the first factor $\wedge ^2 M$ of $\mathcal {R}^{\nabla }$ and $\mathcal {R}^{\nabla }(e_i,e_j)$ denotes evaluation of $e_i$ and $e_j$ on the second factor $\wedge ^2\,M$ of $\mathcal {R}^{\nabla }$. For every three-form $H\in \Omega ^3(M)$, we define the symmetric bilinear form:

$$\begin{aligned} (H\circ _g H)(v_1,v_2):= & {} \langle v_1\lrcorner H, v_2\lrcorner H\rangle _g = \frac{1}{2} \sum _{i,j=1}^d H(v_1,e_i,e_j) H(v_2,e_i,e_j)\,, \\{} & {} \quad v_1, v_2 \in \mathfrak {X}(M). \end{aligned}$$

Similarly, we define another symmetric bilinear form associated to the curvature tensor of $\nabla$ by:

$$\begin{aligned} (\mathcal {R}^{\nabla }\circ _g \mathcal {R}^{\nabla })(v_1,v_2):= & {} \langle v_1\lrcorner \mathcal {R}^{\nabla }, v_2\lrcorner \mathcal {R}^{\nabla }\rangle _g \\= & {} \frac{1}{2}\sum _{i,j,k=1}^d \mathcal {R}^{\nabla }_{v_1 e_i}(e_j,e_k) \mathcal {R}^{\nabla }_{v_2 e_i}(e_j, e_k)\,, \quad v_1, v_2 \in \mathfrak {X}(M). \end{aligned}$$

Furthermore, associated to the curvature tensor of $\nabla$, we define the four-form:

$$\begin{aligned} \langle \mathcal {R}^{\nabla }\wedge \mathcal {R}^{\nabla }\rangle _g = \frac{1}{2} \sum _{i,j=1}^d \mathcal {R}^{\nabla }(e_i,e_j)\wedge \mathcal {R}^{\nabla }(e_i,e_j). \end{aligned}$$

Obtained by taking the wedge product on the first factor and the norm of the second factor of $\mathcal {R}^{\nabla }$ in $\wedge ^2 M\otimes \wedge ^2 M$. Given a three-form $H\in \Omega ^3(M)$ and vector field $u\in \mathfrak {X}(M)$ on (M, g), for ease of notation, we will occasionally denote by $H_u\in \Gamma (\textrm{End}(TM))$ the skew-symmetric endomorphism of TM defined by:

$$\begin{aligned} H_u(v) = H(u,v)^{\sharp _g}, \end{aligned}$$

Fwhere $\sharp _g:T^{*}M \rightarrow TM$ is the musical isomorphism induced by g. We will denote by the same symbol the extension of $H_u$ to all tensor bundles over M as derivation. In particular, if $\alpha$ is any p-form and $(e_i)$ some local orthonormal frame,

$$\begin{aligned} H_u(\alpha )=\sum _{i=1}^d H_u(e_i)\wedge e_i\lrcorner \alpha . \end{aligned}$$

Given $u, v \in \mathfrak {X}(M)$ the composition of $H_u$ and $H_v$ will be denoted by $H_u\circ H_v\in \Gamma (\textrm{End}(TM))$, whereas their commutator as endomorphisms will be denoted by $[H_u, H_v] \in \Gamma (\textrm{End}(TM))$. Similarly, given tensors $\tau _1, \tau _2 \in \Gamma (T^{*}M\otimes T^{*}M)$, their commutator as endomorphisms obtained via the underlying Riemannian metric will be denoted simply by $[\tau _1, \tau _2] \in \Gamma (\textrm{End}(TM))$. For every Riemannian metric g and three-form H on M we define the connection $\nabla ^{g,H}$ on the tangent bundle TM as the unique metric connection on (M, g) with totally skew-symmetric torsion equal to $- H$. The connection $\nabla ^{g,H}$ is explicitly given in terms of the Levi-Civita connection $\nabla ^g$ of g as follows:

$$\begin{aligned} \nabla _{u}^{g,H} v = \nabla _{u}^g v - \frac{1}{2} H_u(v) = \nabla _{u}^g v - \frac{1}{2} H(u,v)^{\sharp _g}, \qquad \forall \,\, u, v \in \mathfrak {X}(M). \end{aligned}$$

For ease of notation in the following the Riemannian curvature tensor of g will be denoted by $\mathcal {R}^g$, whereas the curvature tensor of a metric connection with skew-symmetric torsion $\nabla ^{g,H}$ will be denoted by $\mathcal {R}^{g,H}$. Recall the standard relation:

$$\begin{aligned} \mathcal {R}^{g,H}_{u\, v} = \mathcal {R}^g_{u\, v} - \frac{1}{2} (\nabla ^g_u H)(v) + \frac{1}{2} (\nabla ^g_v H)(u) + \frac{1}{4} [H_u, H_v], \end{aligned}$$

(2.1)

between the curvature tensor $\mathcal {R}^{g,H}$ of $\nabla ^{g,H}$ and the Riemann tensor of g. Taking the trace of $\mathcal {R}^{g,H}$ in the previous equation we obtain the Ricci tensor of $\nabla ^{g,H}$, given explicitly by:

$$\begin{aligned} \textrm{Ric}^{g,H} = \textrm{Ric}^{g} - \frac{1}{2} H\circ _{g_t} H + \frac{1}{2} \delta ^{g} H. \end{aligned}$$

This equation will be useful in Sect. 3 to understand the Heterotic soliton system.

2.2 The Bosonic String Action and the Generalized Ricci Flow

Let X be a compact and oriented real surface and let M be an oriented manifold of dimension d. Given a Riemannian metric g on M, a two-form $b\in \Omega ^2(M)$, and a function $\phi \in C^{\infty }(M)$, the bosonic string action determined by the triple $(g,b,\phi )$ on the pair (X, M) is the action functional:

$$\begin{aligned} \mathcal {S}:\textrm{Met}(X)\times C^{\infty }(X,M) \rightarrow \mathbb {R}, \end{aligned}$$

defined on the space of Riemannian metrics $\textrm{Met}(X)$ on X and the space of smooth maps $C^{\infty }(X,M)$ from X to M by the following action functional [48]:

$$\begin{aligned} \mathcal {S}[h,\Psi ] = - \frac{1}{\kappa } \int _{X} \left\{ \vert \textrm{d}\Psi \vert _{h,g}^2 + *_h (\Psi ^{*} b ) - \kappa \, \phi \circ \Psi \, \textrm{R}^h\right\} \,\nu _h, \end{aligned}$$

where $h\in \textrm{Met}(X)$, $\Psi \in C^{\infty }(X,M)$ and $\kappa$ is a positive real constant. Here $\textrm{R}^h$ denotes the scalar curvature of h, $\textrm{d}\Psi \in \Omega ^1 (X,TM^{\Psi })$ is the differential of $\Psi$ understood as a one-form on X taking values in the pull-back $TM^{\Psi }$ of TM by $\Psi$ and $\vert \textrm{d}\Psi \vert _{h,g}^2\in C^{\infty }(X)$ denotes the standard energy of the map $\Psi :X\rightarrow M$ computed with respect to the metrics h and g. Therefore, the configuration space of the bosonic string action consists of pairs $(h,\Psi )$ given by Riemannian metrics g on X and maps $\Psi :X\rightarrow M$. This configuration space admits a large automorphism group of transformations that preserves the action functional $\mathcal {S}$. In particular, $\mathcal {S}$ is invariant under Weyl transformations, namely conformal rescalings of h by a positive real function. These symmetries are particularly important for the physical interpretation of the bosonic string action, as we will remark below.

The triple $(g,b,\phi )$ that determines the action functional $\mathcal {S}$ is not dynamical and is instead interpreted in this framework as the couplings of the bosonic string action. Every such choice of data $(g,b,\phi )$ gives rise to a well-defined theory at the classical level, that is, at the level of the classical equations of motion that are obtained via the first-order extremization of the action functional $\mathcal {S}$. In contrast, not every triple $(g,b,\phi )$ leads to a bosonic string action admitting a consistent quantization. The quantization scheme of the bosonic string theory involves a regularization procedure that introduces an ultra-violet cutoff $\lambda$ [48]. Through this procedure, physical quantities, in particular, the couplings of the theory, normally acquire a dependence on the scale $\lambda$, in which case the theory is no longer conformally invariant, that is, it is not invariant under Weyl transformations. This implies that Weyl transformations are not guaranteed to be symmetries of the bosonic string at the quantum level, something that cannot be allowed because of the physical consistency of the theory as a theory of quantum gravity. The dependence of the couplings of $\mathcal {S}$ on the renormalization scale $\lambda$ is controlled through the renormalization group flow equations, which in the present case are given by:

$$\begin{aligned} \frac{\partial g_t}{\partial t} = - \beta _{g_t}\,, \qquad \frac{\partial b_t}{\partial t} = - \beta _{b_t}\,, \qquad \frac{\partial \phi _t}{\partial t} = - \beta _{\phi _t}, \end{aligned}$$

where $t\in \mathbb {R}$ is the logarithm of the renormalization scale, $(g_t,b_t,\phi _t)$ denotes a one-parameter family of Riemannian metrics, two-forms and functions on M and:

$$\begin{aligned} \beta _{g_t}\in \Gamma (T^{*}M\odot T^{*}M), \quad \beta _{b_t}\in \Omega ^2(M)\,,\quad \beta _{\phi _t}\in C^{\infty }(M), \end{aligned}$$

denote the beta functionals of $g_t$, $b_t$, and $\phi _t$, respectively, where the latter are being understood as families of coupling fields of the bosonic string action. For Weyl invariance to be preserved in the quantum theory we must have $\beta _g = \beta _b = \beta _{\phi } = 0$ possibly modulo a time-dependent diffeomorphism. Computing the beta functionals of the bosonic string is a complicated task that is usually performed perturbatively in the constant $\kappa$. Let $\textrm{Ric}^{g_t}$ denote the Ricci tensor of $g_t$. To the lowest order in $\kappa$ we have [42, 48]:

$$\begin{aligned}&\frac{\partial g_t}{\partial t} = - \kappa (\textrm{Ric}^{g_t} - \frac{1}{2} H_t\circ H_t) + o(\kappa ^2)\,, \\&\frac{\partial b_t}{\partial t} = - \frac{\kappa }{2} \, \delta ^{g_t} H_t + o(\kappa ^2), \quad \frac{\partial \phi _t}{\partial t} = c + \frac{\kappa }{4}\, \big (-\delta ^{g_t}\varphi _t + \vert H_t\vert _{g_t}^2 \big ) + o(\kappa ^2), \end{aligned}$$

where c is a constant that depends on the dimension of M and we have set $H_t:= \textrm{d}b_t$ and $\varphi _t:= \textrm{d}\phi _t$. Assuming $c=0$, which we will do freely in the following, the previous equations define a weakly parabolic flow whose self-similar solutions are solutions of the bosonic sector of NS–NS supergravity on M. By virtue of the evolution equation satisfied by $b_t$, we obtain the following evolution equation for $H_t$:

$$\begin{aligned} \frac{\partial H_t}{\partial t} = - \frac{\kappa }{2} \, \textrm{d}\delta ^{g_t} H_t + o(\kappa ^2). \end{aligned}$$

This equation is sometimes considered instead of the evolution equation for $b_t$ as part of the renormalization group flow equations of the NS–NS worldsheet at first order in $\kappa$. Note that the evolution equation for $\phi _t$ decouples and therefore can be considered separately. The generalized Ricci flow [23] can be introduced as the first-order renormalization group flow for $(g_t,H_t)$, which after an appropriate time rescaling by $\kappa /2$ is given by the following system of evolution equations:

$$\begin{aligned} \frac{\partial g_t}{\partial t} = - 2 \textrm{Ric}^{g_t} + \frac{1}{2} H_t\circ H_t, \quad \frac{\partial H_t}{\partial t} = - \textrm{d}\delta ^{g_t} H_t, \end{aligned}$$

for pairs $(g_t,H_t)$.

2.3 The Heterotic Extension of the Generalized Ricci Flow

The first-order renormalization group flow equations of the bosonic string receive higher-order corrections in $\kappa$ [3]. To compute these corrections, the bosonic string needs to be considered as a subsector of a particular string theory, which can be the bosonic string itself or any of the five superstring theories since all of them have the bosonic string as a common subsector. Considering the bosonic string as the NS–NS truncation of Heterotic string theory, a careful inspection of the effective action of Heterotic supergravity expanded perturbatively in the string slope parameter $\kappa$ together with the computation of the beta functionals of the Heterotic (1,0) worldsheet leads to the following renormalization group flow equations for $(g_t,H_t,\phi _t)$ at second-order in $\kappa$ [4, 5, 36, 37]:

$$\begin{aligned} \frac{\partial g_t}{\partial t}{} & {} = -\kappa \, (\textrm{Ric}^{g_t} - \frac{1}{2} H_t\,\,\circ _{g_t} H_t) - \kappa ^2\, \mathcal {R}^{g_t,H_t} \circ _{g_t}\mathcal {R}^{g_t,H_t} + o(\kappa ^3)\,, \\ \frac{\partial H_t}{\partial t}{} & {} = - \frac{\kappa }{2} \, \textrm{d}\delta ^{g_t} H_t + o(\kappa ^3)\,, \quad \frac{\partial \phi _t}{\partial t} = \frac{\kappa }{4}\, (\vert H_t\vert _{g_t}^2 -\delta ^{g_t}\textrm{d}\phi _t - \kappa \, |\mathcal {R}^{g_t,H_t}|^2_{g_t}) + o(\kappa ^3), \end{aligned}$$

together with the Bianchi identity for $H_t$:

$$\begin{aligned} \textrm{d}H_t + \kappa \, \langle \mathcal {R}^{g_t,H_t} \wedge \mathcal {R}^{g_t,H_t}\rangle _{g_t}=0. \end{aligned}$$

(2.2)

As in the case of the renormalization group flow equations at first order, the evolution equation for the dilaton $\phi _t$ decouples from the evolution equations of $(g_t,H_t)$ and therefore can be considered separately. Proceeding analogously to the generalized Ricci-flow case, we define the Heterotic-Ricci flow equations as the renormalization group flow equations of the NS–NS sector of the Heterotic string at second order in $\kappa$, that is:

Definition 2.1

The Heterotic-Ricci flow on M is the following differential system:

$$\begin{aligned}{} & {} \partial _t g_t = -2 \, (\textrm{Ric}^{g_t} - \frac{1}{2} H_t\,\,\circ _{g_t} H_t) - 2 \kappa \,\mathcal {R}^{g_t,H_t} \circ _{g_t} \mathcal {R}^{g_t,H_t} \,, \quad \partial _t H_t = - \textrm{d}\delta ^{g_t} H_t\,,\\{} & {} \textrm{d}H_t +\kappa \, \langle \mathcal {R}^{g_t,H_t} \wedge \mathcal {R}^{g_t,H_t}\rangle _{g_t} = 0, \end{aligned}$$

for families $(g_t,H_t)$ of Riemannian metrics and three forms on M.

We will refer to solutions to the Heterotic-Ricci flow simply as Heterotic-Ricci flows. Clearly, when $\kappa = 0$ we recover the generalized Ricci flow whereas when $H_t=0$ the Heterotic-Ricci flow reduces to the RG-2 flow [27] subject to the intriguing constraint:

$$\begin{aligned} \kappa \, \langle \mathcal {R}^{g_t,H_t} \wedge \mathcal {R}^{g_t,H_t}\rangle _{g_t}=0, \end{aligned}$$

which to the best of our knowledge has not been studied in the RG-2 flow literature. It would be interesting to investigate precisely how the previous equation constrains the RG 2-flow and how it affects its long-time behavior and existence. We will refer to solutions $(g_t,H_t)$ to the Heterotic-Ricci flow equations simply as Heterotic-Ricci flows. Note that a Heterotic-Ricci flow $(g_t,H_t)$ can be completed into a solution of the two-loop renormalization group flow equations of the NS–NS sector of the Heterotic string if and only if there exists a closed one-form $\varphi _0\in \Omega ^1(M)$ and a family of functions $\phi _t$ such that the following equation, to which we will refer as the dilaton flow equation, is satisfied:

$$\begin{aligned} \frac{\partial \phi _t}{\partial t} = \frac{1}{2}\, \bigg (\vert H_t\vert _{g_t}^2 -\delta ^{g_t}\varphi _t - \kappa \, |\mathcal {R}^{g_t,H_t}|^2_{g_t}\bigg ), \end{aligned}$$

(2.3)

where we have set $\varphi _t = \varphi _0 + \textrm{d}\phi _t$. Note that if $\kappa =0$ the previous equation reduces to the dilaton flow as defined in [56]. It would be very interesting to see if the dilaton flow with $\kappa \ne 0$ can have the same type of applications for the Heterotic-Ricci flow as it does when $\kappa = 0$ for the generalized Ricci flow, as explained in [56].

Definition 2.2

Let $(g_t,H_t)$ be a Heterotic-Ricci flow, and let $\sigma \in H^1(M,\mathbb {R})$ be a cohomology class. A dilaton for $(g_t,H_t)$ with Lee class $\sigma$ is a closed one-form $(\varphi _0)$ on M such that $\sigma = [\varphi _0]$ and a family of functions $(\phi _t)$ which solves the dilaton flow equation (2.3) for $\varphi _t:= \varphi _0 + \textrm{d}\phi _t$.

Note that the term $\mathcal {R}^{g_t,H_t} \circ _{g_t} \mathcal {R}^{g_t,H_t}$ involves quadratic terms in the Riemann tensor of $g_t$ as well as terms involving covariant derivatives of $H_t$ with respect to the Levi–Civita connection $\nabla ^{g_t}$. On the other hand, given a Heterotic-Ricci flow $(g_t,H_t)$ the dilaton evolution equation becomes an inhomogeneous linear heat equation for $\phi _t$ on M, and therefore standard theory applies regarding the existence and uniqueness of its solutions.

Proposition 2.3

Let $(g_t,H_t)$ be a Heterotic-Ricci flow on a compact manifold M and defined on the interval $\mathcal {I}$. Then, for each cohomology class $\sigma \in H^1(M,\mathbb {R})$ there exists a unique dilaton $\varphi _t$ with Lee class $\sigma$ associated to $(g_t,H_t)$.

Proof

Let $(g_t,H_t)$ be a Heterotic-Ricci flow. Given a cohomology class $\sigma \in H^1(M,\mathbb {R})$, fix a closed one-form $\varphi _0\in \Omega ^1(M)$ such that $\sigma = [\varphi _0]$ and write $\varphi _t = \varphi _0 + \textrm{d}\phi _t$ in terms of a family of functions $\phi _t$. Plugging $\varphi _t = \varphi _0 + \textrm{d}\phi _t$ in the dilaton equation (2.3) we obtain:

$$\begin{aligned} \frac{\partial \phi _t}{\partial t} = \frac{1}{2}\, \bigg ( - \Delta _{g_t}\phi _t + \vert H_t\vert _{g_t}^2 - \kappa \, |\mathcal {R}^{g_t,H_t}|^2_{g_t} - \delta ^{g_t}\varphi _0 \bigg ), \end{aligned}$$

where $(g_t,H_t)$ is considered as given data and $\Delta _{g_t} = (\textrm{d}\delta ^{g_t} + \delta ^{g_t}\textrm{d})$ denotes the Laplace-de-Rham operator. This is a linear parabolic equation for $(\phi _t)$ and by [1, Theorem 4.47] it admits a unique smooth solution on $\mathcal {I}$ such that $\phi _0 = 0$. $\square$

Remark 2.4

If $\varphi _t = \varphi _0 + \textrm{d}\phi _t$ and $\varphi _t^{\prime } = \varphi ^{\prime }_0 + \textrm{d}\phi ^{\prime }_t$ are two dilatons with the same Lee class and associated to the same Heterotic-Ricci flow on a compact manifold M, then $\phi _t^{\prime } = \phi _t + f$ for a function f on M unique modulo an additive constant.

By the previous proposition, we will not be concerned with the dilaton equation in the sequel.

Example 2.5

When M is two-dimensional we have $H_t=0$ identically and the Heterotic-Ricci flow equations reduce to the RG-2 flow equations [27]:

$$\begin{aligned}&\frac{\partial g_t}{\partial t} = -2 \, \textrm{Ric}^{g_t} - 2 \kappa \, \textrm{R}^{g_t} \circ _{g_t}\textrm{R}^{g_t}, \end{aligned}$$

where $\textrm{R}^{g_t}$ is the Riemann tensor of $g_t$. As explained in [41], in this dimension the RG-2 flow equations simplify to:

$$\begin{aligned} \frac{\partial g_t}{\partial t} = - \bigg (s_{g_t} + \frac{\kappa }{2}s_{g_t}^2\bigg ) \, g_t, \end{aligned}$$

where $s_{g_t}$ denotes the scalar curvature of $g_t$. We refer the reader to [41] for more details.

Remark 2.6

The proper gauge theoretic formulation of the Heterotic-Ricci flow in terms of the b-field instead of the three-form flux H requires understanding the Heterotic-Ricci flow as a system of differential equations either on a string algebroid, as a particular case of [20], or on a string structure on the frame bundle of M, see [34, 49, 63] and references therein for more details. This perspective is crucial to properly understand the groupoid of automorphisms of the flow equations as well as its moduli of solitons.

2.4 Heterotic-Ricci Flows on Three-Manifolds

As remarked in Example 2.5, in two dimensions the Heterotic-Ricci flow reduces to the RG-2 flow [27], a curvature flow that is well-known to arise through a second-order correction to the Ricci-flow as prescribed by the renormalization group flow of a metric non-linear sigma model. In three dimensions the Heterotic-Ricci flow equations reduce to:

$$\begin{aligned} \partial _t g_t = -2 \, \bigg (\textrm{Ric}^{g_t} - \frac{1}{4} H_t\circ H_t\bigg ) - 2 \kappa \, \mathcal {R}^{g_t,H_t} \circ _{g_t}\mathcal {R}^{g_t,H_t} \,, \quad \partial _t H_t = - \textrm{d}\delta ^{g_t} H_t, \end{aligned}$$

(2.4)

for families $(g_t,H_t)$ of Riemannian metrics and three-forms $H_t$ on M. In particular, $H_t$ is closed and the Bianchi identity (2.2) is automatically satisfied for dimensional reasons. Suppose that $H_t$ evolves within the de Rham cohomology class that it determines at $t_0$. We can write:

$$\begin{aligned} H_t = H_0 + \textrm{d}b_t. \end{aligned}$$

With this assumption Eq. (2.4) is equivalent to:

$$\begin{aligned} \frac{\partial b_t}{\partial t} = -\delta ^{g_t} H_t + \omega _t, \end{aligned}$$

for a family of closed two-forms $(\omega _t)$. Setting this spurious family $(\omega _t)$ of two forms to zero we obtain the following refined formulation of the Heterotic-Ricci flow:

$$\begin{aligned} \partial _t (g_t + b_t) = -2 \textrm{Ric}^{g_t,H_t} - 2 \kappa \, \mathcal {R}^{g_t,H_t} \circ _{g_t}\mathcal {R}^{g_t,H_t}, \end{aligned}$$

(2.5)

which now involves a family of Riemannian metrics $(g_t)$ and two-forms $(b_t)$. Indeed, every family $(g_t,b_t)$ solving the previous flow equations naturally yields a solution of equations (2.4), although the converse may not be true. This is related to the fact that the proper, gauge-theoretic, formulation of the Heterotic-Ricci flow involves the notion of b-field and occurs in terms of connections on a string structure, see Remark 2.6. This point of view requires the development of novel Riemannian tools on string structures and will be considered elsewhere. Here instead we will simplify equations (2.4) using the fact that the dual of a three-form is a function and the fact that the Riemann tensor is completely determined by the Ricci curvature. Given a pair $(g_t, H_t)$, we write $H_t= f_t \nu _{g_t}$ in terms of the unique family of functions $f_t = *_{g_t} H_t\in C^{\infty }(M)$, where $\nu _{g_t}$ denotes the Riemannian volume form associated $g_t$. Consequently, when M is three-dimensional we define the configuration space $\textrm{Conf}(M)$ of the Heterotic-Ricci flow system on M as the set of tuples $(g_t,f_t)$, where $g_t$ is a family of Riemannian metrics and $f_t$ is a family of functions. Similarly, we define the set of Heterotic-Ricci flows $\textrm{Sol}_{\kappa }(M)$ on M as the set of pairs $(g_t,f_t)\in \textrm{Conf}(M)$ such that $(g_t,H_t = *_{g_t} f_t)$ is a Heterotic-Ricci flow with parameter $\kappa \in \mathbb {R}$. Using Lemma A.1 in Appendix A we can write the three-dimensional Heterotic-Ricci flow as an evolution differential system for a family of metrics $g_t$ and a family of functions $f_t$ involving exclusively the Ricci tensor and scalar curvature of $g_t$ as the only curvature operators occurring in the system.

Proposition 2.7

A pair $(g_t, f_t)\in \textrm{Conf}(M)$ is a Heterotic-Ricci flow if and only if it satisfies the following evolution equations:

$$\begin{aligned} \partial _t g_t{} & {} = 2\kappa \, \textrm{Ric}^{g_t} \circ \textrm{Ric}^{g_t} - (2 + \kappa (2 s^{g_t} - f^2_t) ) \textrm{Ric}^{g_t}\nonumber \\{} & {} \quad +(f_t^2 + \kappa ((s^{g_t})^2 -2 \vert \textrm{Ric}^{g_t} \vert _{g_t}^2 - \frac{1}{2}\vert \textrm{d}f_t \vert _{g_t}^2 - \frac{1}{4} f^4_t) )g_t \nonumber \\{} & {} \quad - \kappa [*_{g_t}\textrm{d}f_t,\textrm{Ric}^{g_t}] - \frac{1}{2}\kappa \,\textrm{d}f_t \otimes \textrm{d}f_t, \end{aligned}$$

(2.6)

$$\begin{aligned}{} & {} \partial _t f_t + \frac{1}{2} \textrm{Tr}_{g_t}(\partial _t g_t) f_t + \Delta _{g_t} f_t = 0, \end{aligned}$$

(2.7)

where $f_t = *_{g_t} H_t$ and $\Delta _{g_t} = \delta ^{g_t}\textrm{d}:C^{\infty }(M) \rightarrow C^{\infty }(M)$ is the Laplace operator on functions.

Proof

By definition $(g_t, f_t)\in \textrm{Conf}(M)$ is a Heterotic-Ricci flow if and only if $(g_t,H_t = f_t \nu _{g_t})$ satisfies equations (2.4). Plugging Eq. (A.3) into the first equation in (2.4) and using the identity:

$$\begin{aligned} H_t\circ _{g_t} H_t(v_1,v_2) = g_t(v_1,v_2) f^2_t, \end{aligned}$$

it follows that the first equation in (2.4) is equivalent to Eq. (2.6). For the second equation in (2.4) we compute:

$$\begin{aligned} \partial _t H_t = \partial _t (f_t \nu _{g_t}) = (\partial _t f_t) \nu _{g_t} + \frac{1}{2} \textrm{Tr}_{g_t}(\partial _t g_t) f_t \nu _{g_t}, \end{aligned}$$

whence the second equation in (2.4) is equivalent to:

$$\begin{aligned} (\partial _t f_t) \nu _{g_t} + \frac{1}{2} \textrm{Tr}_{g_t}(\partial _t g_t) f_t \nu _{g_t} = \textrm{d}*_{g_t} \textrm{d}f_t. \end{aligned}$$

Taking the Hodge dual of this equation we obtain (2.7) and we conclude. $\square$

2.5 Homothety Flows

In this section, we consider a particular class of three-dimensional Heterotic Ricci flows for which the metric evolves by homotheties. Note that, in contrast with the standard Ricci flow, the Heterotic-Ricci flow is not scale-invariant unless the constant $\kappa$ is rescaled too. Doing this for time-dependent rescalings would introduce a time dependence in $\kappa$. This is a priori not allowed but can be a convenient mechanism to consider, see [8] for a detailed discussion of this issue in the context of the RG 2-flow. As a consequence, Heterotic-Ricci flows that evolve by homotheties can be non-trivial and may become remarkably complicated. Suppose then that $(g_t,f_t)$ satisfies:

$$\begin{aligned} g_t =\sigma _t g \,, \qquad \textrm{d}f_t = 0, \end{aligned}$$

where $(\sigma _t)$ is a family of constants and g is a Riemannian metric on M. We will call such pairs $(\sigma _t g, f_t)$ homothety flows. A direct computation by substitution yields the following characterization of the homothety flows that solve the Heterotic-Ricci flow equations.

Lemma 2.8

A homothety flow $(\sigma _t g, f_t)$ is a Heterotic-Ricci flow if and only if:

$$\begin{aligned} \frac{1}{2}\partial _t \sigma ^2_t\, g{} & {} = 2\kappa \,\sigma _t\, \textrm{Ric}^{g} \circ \textrm{Ric}^{g} - \left( 2 \sigma _t + \kappa \left( 2 s_{g} - \frac{\mu ^2}{\sigma ^2_t}\right) \right) \textrm{Ric}^{g} \nonumber \\{} & {} \quad + \left( \kappa \left( s_g^2 -2 \vert \textrm{Ric}^{g} \vert _{g}^2 - \frac{\mu ^4}{4 \sigma ^4_t}\right) + \frac{\mu ^2}{\sigma _t} \right) \, g, \end{aligned}$$

(2.8)

and $f_t = \mu \sigma _t^{-\frac{3}{2}}$ for a real constant $\mu \in \mathbb {R}$.

The initial point of a homothety flow cannot be arbitrary, as we are showing next. This is the Heterotic-Ricci flow analog of [27, Theorem 3] that was proven in Op. Cit. for the RG 2-flow.

Proposition 2.9

Let $(g_t=\sigma _t g, f_t = \mu \sigma _t^{-\frac{3}{2}})$ be a homothety flow solving the Heterotic-Ricci flow with non-constant $\sigma _t$. If $s_g^2+\mu ^2\ne 0$, then (M, g) is Einstein.

Proof

We can diagonalize $\textrm{Ric}^g$ in Eq. (2.8), obtaining:

$$\begin{aligned} \sigma _t\partial _t \sigma _t \! = \!2\kappa \,\sigma _t\, \lambda ^2_i - \left( 2 \sigma _t\! +\! \kappa \left( 2 s_{g} - \frac{\mu ^2}{\sigma ^2_t}\right) \right) \lambda _i \!+ \!\left( \kappa \left( s_g^2 \! -\!2 \vert \textrm{Ric}^{g} \vert _{g}^2 \! -\! \frac{\mu ^4}{4 \sigma ^4_t}\right) \! +\! \frac{\mu ^2}{\sigma _t} \right) , \end{aligned}$$

where $\lambda _i$, $i=1,2,3$, are principal Ricci curvatures of g. Subtracting the previous equations by pairs, we obtain:

$$\begin{aligned} (\lambda ^2_1 - \lambda ^2_2) = F_t (\lambda _1 - \lambda _2) \,, \quad (\lambda ^2_1 - \lambda ^2_3) = F_t (\lambda _1 - \lambda _3) \,,\quad (\lambda ^2_2 - \lambda ^2_3) = F_t (\lambda _2 - \lambda _3), \end{aligned}$$

where

$$\begin{aligned} F_t:= \frac{1}{\kappa } + \left( \frac{s_{g}}{\sigma _t} - \frac{\mu ^2}{2\sigma ^3_t}\right) . \end{aligned}$$

If either $s_g\ne 0$ or $\mu \ne 0$ then $F_t$ is not constant and we obtain $\lambda _1 = \lambda _2 = \lambda _3$. $\square$

Remark 2.10

Condition $s_g^2+\mu ^2 \ne 0$ in Proposition 2.9 is necessary. In fact, consider the Riemannian Lie group $(\textrm{SU}(2),g)$ for which the following the following left-invariant frame $\{e_1,e_2,e_3\}$ is orthonormal:

$$\begin{aligned}{}[e_2,e_3]=\frac{1}{2 \sqrt{\kappa }} e_1, \quad [e_3,e_1]=\frac{1}{2 \sqrt{\kappa }} e_2, \quad [e_1,e_2]=\frac{2}{\sqrt{\kappa }}e_3. \end{aligned}$$

Direct computation reveals that $\textrm{Ric}^g=-\kappa ^{-1} g+ 3 \kappa ^{-1} e_3 \otimes e_3$. Clearly, the eigenvalues of $\textrm{Ric}^g$ are $\lambda _1=\lambda _2=-\kappa ^{-1}$ and $\lambda _3=2\kappa ^{-1}$, so that $s_g=0$. If W is the Lambert W function, defined as the inverse of the function $p(x)=x e^x$ when restricted to the interval $x \in (-e^{-1},+\infty )$, it can be checked that:

$$\begin{aligned} \sigma _t=3+3 W\left( -\frac{2}{3} {\exp }\left[ \frac{2}{3} \left( 2t/\kappa -1\right) \right] \right) , \end{aligned}$$

solves Eq. (2.8) for $s_g=\mu =0$ and for the choice $(\textrm{SU}(2),g)$, which is not Einstein. Observe that this particular $\sigma _t$ is defined for $t \in (-\infty ,t_{\textrm{max}})$, where $t_{\textrm{max}}=\kappa /4(\log (27/8)-1)$.

Assuming that g is Einstein in Eq. (2.8) we obtain the following ordinary differential equation:

$$\begin{aligned} \frac{1}{2}\partial _t \sigma ^2_t = \left( \frac{2\kappa \, s_g}{3} - 2\right) \frac{s_g}{3} \sigma _t - \frac{\kappa \, s^2_g}{3} + \frac{\mu ^2}{\sigma _t} - \frac{\kappa \, s_g \,\mu ^2}{\sigma _t^2} - \frac{\kappa \,\mu ^4}{4 \sigma ^4_t}, \end{aligned}$$

(2.9)

controlling the evolution of $\sigma _t$. If we set $\kappa = 0$ and $\mu =0$ we recover the standard linear behavior of $\sigma _t$ that corresponds to the Ricci flow case. If we just set $\mu =0$ we obtain the differential equation that controls $\sigma _t$ according to the RG-2 flow, namely:

$$\begin{aligned} \frac{1}{2}\partial _t \sigma ^2_t = \left( \frac{2\kappa \, s_g}{3} - 2\right) \frac{s_g}{3} \sigma _t - \frac{\kappa \, s^2_g}{3}. \end{aligned}$$

Although the standard existence and uniqueness theorems for ordinary differential equations guarantee the existence of a solution to (2.9) in some short time interval, the equation is in the general case too complex to admit a solution by elementary functions. After possibly rescaling the metric g, we can set $s_g=1$, $s_g = 0$ or $s_g =-1$ obtaining respectively, the positive homothety flow:

$$\begin{aligned} \frac{1}{2}\partial _t \sigma ^2_t = 2\,\left( \frac{\kappa }{9} - \frac{1}{3}\right) \sigma _t - \frac{\kappa }{3} + \frac{\mu ^2}{\sigma _t} - \frac{\kappa \,\mu ^2}{\sigma _t^2} - \frac{\kappa \,\mu ^4}{4 \sigma ^4_t}. \end{aligned}$$

(2.10)

The flat homothety flow:

$$\begin{aligned} \frac{1}{2}\partial _t \sigma ^2_t = \frac{\mu ^2}{\sigma _t} - \frac{\kappa \,\mu ^4}{4\,\sigma ^4_t}, \end{aligned}$$

(2.11)

and the negative homothety flow:

$$\begin{aligned} \frac{1}{2}\partial _t \sigma ^2_t = 2\,\left( \frac{\kappa }{9} + \frac{1}{3}\right) \sigma _t - \frac{\kappa }{3} + \frac{\mu ^2}{\sigma _t} + \frac{\kappa \,\mu ^2}{\sigma _t^2} - \frac{\kappa \,\mu ^4}{4 \sigma ^4_t}. \end{aligned}$$

(2.12)

It is interesting to note that whereas in the flat case $s_g = 0$ both the Ricci flow and RG-2 flow produce trivial homothety flows, the homothety Heterotic-Ricci flow is non-trivial and is instead prescribed by Eq. (2.11). This equation perfectly illustrates a phenomenon that is a common theme of the Heterotic-Ricci flow, that is, a positive contribution corresponding to the term appearing in the generalized Ricci flow together with an opposite negative contribution corresponding to the higher-order correction introduced by the Heterotic-Ricci flow.

Remark 2.11

Although the terms positive and negative in the previous paragraph have no specific meaning, in the original Lorentzian formulation of the system theory, they can be traced back to the fact that the higher-order correction $\mathcal {R}^{g,H}\circ _g\mathcal {R}^{g,H}$ present in the Heterotic system gives a negative energy contribution that is of opposite sign to the contribution given by the other terms of the system.

Let us study separately the positive, flat and negative cases.

2.5.1 Positive Homothety Flows

Finding explicit solutions to Eq. (2.10) is quite challenging, but it is possible to examine some qualitative and numerical features of its solutions. The crucial object to study is the right-hand side of Eq. (2.10), which determines the derivative of $\sigma _t$:

$$\begin{aligned} F_p(\kappa ,\mu ,y)=2\,\left( \frac{\kappa }{9} - \frac{1}{3}\right) y - \frac{\kappa }{3} + \frac{\mu ^2}{y} - \frac{\kappa \,\mu ^2}{y^2} - \frac{\kappa \,\mu ^4}{4 y^4}. \end{aligned}$$

The first aspect to analyze is the existence of static solutions, i.e., $\sigma _t=1$ for every $t \in \mathbb {R}$. Setting $F_p(\kappa ,\mu ,1)=0$, we find a one-parameter family of values of $(\kappa ,\mu )$ satisfying such condition, which is given by:

$$\begin{aligned} \kappa (\mu )=\kappa _{\textrm{crit}}^p(\mu )=\frac{36 \mu ^2-24}{9\mu ^2(\mu ^2+4)+4}. \end{aligned}$$

Note that $\kappa _{\textrm{crit}}^p(\mu ) \ge 0$ if and only if $\mu ^2 \ge 2/3$. Whenever $\kappa \ne \kappa _{\textrm{crit}}^p(\mu )$, the solution is no longer static. We observe that:

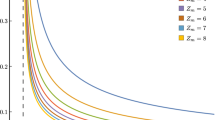
• When considering pairs $(\kappa ,\mu )$ such that $0<\kappa <\kappa _{\textrm{crit}}^p(\mu )$, it turns out that $F_p(\kappa ,\mu ,1)>0$. Sticking to these values of $(\kappa ,\mu )$, one notices that there exist $y_1 \in (0,1)$ and $y_2>1$ such that $F_p(\kappa ,\mu ,y_1)=F_p(\kappa ,\mu ,y_2)=0$. Since the vanishing of $F_p(\kappa ,\mu ,t)$ implies the vanishing of $\partial _t\sigma _t$, we conclude that all solutions $\sigma _t$ to Eq. (2.10) with $\kappa < \kappa _{\textrm{crit}}^p(\mu )$ are well-defined for all times $t \in \mathbb {R}$, satisfying that $1> \lim _{t \rightarrow -\infty } \sigma _t>0$ and $+\infty> \lim _{t \rightarrow +\infty } \sigma _t>1$. Therefore, they define eternal and regular (in the sense that they asymptote to finite values as $t \rightarrow \pm \infty$) flows, which do not exist for the Ricci flow case $\kappa =\mu =0$. Some solutions of this type are illustrated in Fig. 1 (left).

• For pairs $(\kappa ,\mu )$ such that $\kappa > \textrm{max}(0,\kappa _{\textrm{crit}}^p(\mu ))$, a more detailed examination is required:

  • If $\mu ^2$ is greater than the unique real and positive solution of the algebraic equation¹$27 x^3 +6 x^2-68 x-8=0$, then all solutions $\sigma _t$ are seen to collapse at finite time. This is due to the fact that $F_p(\kappa ,\mu ,1)<0$, while $F_p(\kappa ,\mu ,y)$ decreases as y goes to zero (so that $\sigma _t$ approaches zero at some finite time).

  • Otherwise, there is an interval $\kappa \in (\textrm{max}(0,\kappa _{\textrm{crit}}^p(\mu )),\kappa _0(\mu ))$ for which the solution is seen to exist for all times (diverging nonetheless as $t \rightarrow -\infty$, while remaining finite for $t\rightarrow +\infty$), thus yielding an eternal flow. The value $\kappa _0(\mu )$ can be found by solving the equations:

    $$\begin{aligned} F_p(\kappa _0(\mu ),\mu ,y_0)=0\,, \quad \partial _{y} F_p(\kappa _0(\mu ),\mu ,y_0)=0, \end{aligned}$$

    for $y_0 \in (0,1)$. If $\kappa >\kappa _0(\mu )$, then solutions collapse at finite time.

  Fig. 1

  

  Left: numerical solutions of the positive homothety flow defined by Eq. (2.10), for the specific values of $\kappa$ and $\mu$ indicated in the graph. Right: numerical solutions of the negative homothety flow defined by Eq. (2.12), for the specific values of $\kappa$ and $\mu$ indicated in the graph. In both cases, the solutions correspond to eternal and regular flows

  On the other hand, if $\mu =0$ and $\kappa >0$, the solution is seen to collapse at finite time, while for $\mu =\kappa =0$ we have that $\sigma _t=-2t/3+1$. Finally, for $\kappa =0$, if $\mu ^2<2/3$ we have that the flow is eternal, diverging as $t \rightarrow -\infty$ and remaining finite as $t \rightarrow +\infty$, while it collapses at finite time if $\mu ^2>2/3$ (the case $\mu ^2=2/3$ corresponds to the static one).

2.5.2 Flat Homothety Flows

In this case, it is possible to find an explicit solution to Eq. (2.11). Assuming $\mu \ne 0$ and defining $b=4/(\kappa \mu ^2)-1$, the solution can be seen to be:

$$\begin{aligned} \sigma _t=\left\{ \begin{matrix}\left( \frac{\kappa \mu ^2}{4}\right) ^{1/3} \left( 1+W\left( b \, e^{12 t/\kappa +b} \right) \right) ^{1/3} \,, &{} b \ne 0 \\ \\ 1 \,, \quad &{} b=0\end{matrix}, \right. \end{aligned}$$

(2.13)

where we have used the Lambert W function (introduced in Remark 2.10). It can be easily checked that for $b \ge 0$ the corresponding solution $\sigma _t$ exists for all times (for b strictly positive, it tends to $\left( \frac{\kappa \mu ^2}{4}\right) ^{1/3}$ as $t \rightarrow -\infty$ and grows indefinitely as $t \rightarrow +\infty$), while for $b<0$ the solution is only defined in the interval $(-\infty , t_*)$, where $t_*=-\kappa /12 (1+b+\log (-b))$. In this latter case, the solution also asymptotes to $\left( \frac{\kappa \mu ^2}{4}\right) ^{1/3}$ as $t \rightarrow -\infty$.

On the other hand, if $\mu =0$ the only solution corresponds to the static one, namely $\sigma _t=1$, whereas for $\kappa =0$ the solution reads $\sigma _t=(1+3t \mu ^2)^{1/3}$. The latter is defined for $t \in (-(3\mu ^2)^{-1}, +\infty )$.

2.5.3 Negative Homothety Flows

In analogy with the positive case, it is not possible to find explicit solutions for generic $(\kappa ,\mu )$, so we restrict ourselves to a qualitative and numerical study of the solutions of Eq. (2.12). We define:

$$\begin{aligned} F_n(\kappa ,\mu ,y)=2\,\left( \frac{\kappa }{9} + \frac{1}{3} \right) y - \frac{\kappa }{3} + \frac{\mu ^2}{y} + \frac{\kappa \,\mu ^2}{y^2} - \frac{\kappa \,\mu ^4}{4 y^4}. \end{aligned}$$

We start by examining the existence of static solutions. Demanding $F_n(\kappa ,\mu ,1)=0$, we find:

$$\begin{aligned} \kappa (\mu )=\kappa _{\textrm{crit}}^n(\mu )=\frac{36 \mu ^2+24}{9\mu ^2(\mu ^2-4)+4}. \end{aligned}$$

We note that for $\mu _-<\mu <\mu _+$, with $\mu _{\pm }^2=2/3(3\pm 2 \sqrt{2})$, there are no static solutions, since $\kappa _{\textrm{crit}}^n(\mu )$ would be negative. This suggests to split our study depending on the value of $\mu ^2$:

• If $\mu _-^2>\mu ^2>0$, there are two different subcases to consider:

  • If $\kappa <\kappa _{\textrm{crit}}^n(\mu )$, we have that $F_n(\kappa ,\mu ,1)>0$, with $F_n(\kappa ,\mu ,y)$ growing monotonically as we increase y and diverging as $y \rightarrow +\infty$. Also, we observe that there exists a value $y_0 \in (0,1)$ such that $F_n(\kappa ,\mu ,y_0)=0$. Therefore, solutions $\sigma _t$ in this case are eternal and tend to a finite and positive value as $t \rightarrow -\infty$ and diverge as $t \rightarrow +\infty$. The case $\kappa =\kappa _{\textrm{crit}}^n(\mu )$ corresponds to the static solution $\sigma _t=1$.

  • If $\kappa >\kappa _{\textrm{crit}}^n(\mu )$, then $F_n(\kappa ,\mu ,1)<0$. Furthermore, it is verified that there always exist $y_1 \in (0,1)$ and $y_2>1$ such that $F_n(\kappa ,\mu ,y_1)=F_n(\kappa ,\mu ,y_2)=0$. Consequently, these solutions are eternal and regular flows satisfying that $+\infty> \lim _{t \rightarrow -\infty } \sigma _t>1$ and $1> \lim _{t \rightarrow +\infty } \sigma _t>0$. We show some instances of these solutions in Fig. 1 (right).

• If $\mu _+^2\ge \mu ^2 \ge \mu _-^2$, regardless of the value of $\kappa$ we observe the same qualitative behaviour: the subsequent solution $\sigma _t$ exists for all times, asymptoting to a finite value as $t \rightarrow -\infty$ and diverging as $t\rightarrow +\infty$. This is due to $F_n(\kappa ,\mu ,y) >0$ for every $y\ge 1$ and to the existence of $y_0 \in (0,1)$ such that $F_n(\kappa ,\mu ,y_0)=0$.

• Finally, for $\mu ^2>\mu _+^2$, two subcases need to be addressed:

  • For $\kappa <\kappa _{\textrm{crit}}(\mu )$, we have that $F_n(\kappa ,\mu ,y)>0$ for $y \ge 1$, always existing $y_0 \in (0,1)$ such that $F_n(\kappa ,\mu ,y_0)=0$. Therefore, the subsequent solutions $\sigma _t$ are defined for all times, remaining finite as $t \rightarrow -\infty$ and diverging when $t \rightarrow +\infty$. The case $\kappa =\kappa _{\textrm{crit}}(\mu )$ corresponds to the static solution $\sigma _t=1$.

  • If $\kappa >\kappa _{\textrm{crit}}(\mu )$, it is easily verified that $F_n(\kappa ,\mu ,1)<0$. Since $F_n(\kappa _\mu ,y)$ decreases monotonically as y takes smaller values and diverges when $y \rightarrow 0^+$, we conclude that these solutions collapse at finite time.

For $\kappa =0$, the flow collapses at finite time regardless the value of $\mu \ne 0$ (if $\mu =0$, then $\sigma _t=2t/3+1$). Finally, if $\mu =0$, it is observed that the solution collapses at finite time if $\kappa >6$, it corresponds to the static one for $\kappa =6$ and it yields a solution that asymptotes to a finite and positive number for $t \rightarrow -\infty$ and diverges as $t \rightarrow +\infty$ for $\kappa <6$.

3 Heterotic Supergravity with Trivial Gauge Bundle

The notion of Heterotic soliton was introduced in [40] as a manifold equipped with a solution to the bosonic sector of Heterotic supergravity with trivial gauge bundle at first order in the string slope parameter, which we called the Heterotic soliton system. In the following, we revisit the Heterotic soliton system and discuss some of its basic geometric properties.

3.1 The Heterotic Soliton System

Heterotic solitons are expected to be solitons for the Heterotic-Ricci flow, an expectation that we will prove to be correct in the three-dimensional case considered in Sect. 4, and hence are expected to define a subclass of Heterotic-Ricci solitons for which there exists an interpretation within the context of supergravity.

Definition 3.1

Let $\kappa \ge 0$ be a non-negative real constant. The Heterotic soliton system on a manifold M is the following system of partial differential equations:

$$\begin{aligned} \textrm{Ric}^{g,H} + \nabla ^{g,H}\varphi + \kappa \, \mathcal {R}^{g,H} \circ _g\mathcal {R}^{g,H} = 0\,, \quad \delta ^g\varphi + |\varphi |^2_g - |H|^2_g + \kappa \, |\mathcal {R}^{g,H}|^2_{g} = 0,\nonumber \\ \end{aligned}$$

(3.1)

together with the Bianchi identity:

$$\begin{aligned} \textrm{d}H + \kappa \langle \mathcal {R}^{g,H}\wedge \mathcal {R}^{g,H}\rangle _g = 0, \end{aligned}$$

(3.2)

for triples $(g,\varphi ,H)$, where g is a Riemannian metric on M, $\varphi \in \Omega ^1(M)$ is a closed one-form and $H\in \Omega ^3(M)$ is a three-form. A Heterotic soliton is a triple $(g,\varphi ,H)$ satisfying the Heterotic soliton system.

Remark 3.2

Evidently, the Bianchi identity (3.2) is not an identity but an equation that needs to be solved. The terminology comes from the physics community and is nowadays pervasive also in the mathematics community.

We will denote the configuration space and solution space of the Heterotic soliton system by $\textrm{Conf}(M)$ and $\textrm{Sol}_{\kappa }(M)$, respectively. Given $(g,\varphi ,H)\in \textrm{Conf}(M)$, the cohomology class $[\varphi ]\in H^1(M,\mathbb {R})$ determined by $\varphi$ will be called the Lee class of the configuration. This terminology is inherited from [24] in the context of the twisted Hull–Strominger system, for which $\varphi$ is necessarily the Lee form of a Hermitian structure on a complex manifold. By the explicit form of Eqs. (3.1) and (3.2), which are completely determined by supersymmetry, it is clear that the Heterotic soliton system can be considered to be a natural differential system for Riemannian geometries with torsion.

Remark 3.3

The Heterotic soliton system corresponds to the equations of motion of bosonic Heterotic supergravity with trivial gauge bundle at first order in the string slope parameter $\kappa$ [4, 5]. The symmetric part of the first equation in (3.1) is usually referred to in the literature as the Einstein equation, whereas its skew-symmetric part is usually called the Maxwell equation. On the other hand, the second equation in (3.1) is commonly referred to in the literature as the dilaton equation.

A Heterotic soliton $(g,\varphi ,H)\in \textrm{Sol}_{\kappa }(M)$ for which both $\varphi$ and H vanish identically reduces to a Ricci-flat metric. Hence, we will refer to such Heterotic solitons as Ricci-flat. If g is, in addition, flat, we will say that such a soliton is trivial. A soliton $(g,\varphi ,H)\in \textrm{Sol}_{0}(M)$ with $\kappa =0$ is a particular instance of steady generalized Ricci soliton [23] which is Ricci-flat if and only if $\varphi$ is an exact one-form. Hence, non-Ricci-flat Heterotic solitons with $\kappa =0$ are particular cases of non-gradient steady generalized Ricci solitons. In the following, we will always assume that $\kappa >0$. For further reference, we introduce the following maps based on the defining equations of the Heterotic soliton system:

$$\begin{aligned}&\mathcal {E}_{\textrm{E}} :\textrm{Conf}(M) \rightarrow \Gamma (T^{*}M\otimes T^{*}M)\, ,\nonumber \\&\qquad \quad (g,\varphi ,H) \mapsto \textrm{Ric}^{g,H} + \nabla ^{g, H}\varphi + \kappa \, \mathcal {R}^{g,H} \circ _g\mathcal {R}^{g,H}\nonumber \\&\mathcal {E}_{\textrm{D}} :\textrm{Conf}(M) \rightarrow \mathcal {C}^{\infty }(M)\, ,\quad (g,\varphi ,H) \mapsto \nabla ^{g*}\varphi + |\varphi |^2_g - |H|^2_g + \kappa \, |\mathcal {R}^{g,H}|^2_{g} \nonumber \\&\mathcal {E}_{\textrm{B}} :\textrm{Conf}(M) \rightarrow \Omega ^4(M)\, , \quad (g,\varphi ,H) \mapsto \textrm{d}H + \kappa \langle \mathcal {R}^{g,H}\wedge \mathcal {R}^{g,H}\rangle _g, \end{aligned}$$

(3.3)

which we interpret as smooth maps of Fréchet manifolds. Clearly, the solution space $\textrm{Sol}_{\kappa }(M)$ of the system corresponds to the preimage of zero by $\mathcal {E}:= (\mathcal {E}_{\textrm{E}},\mathcal {E}_{\textrm{D}},\mathcal {E}_{\textrm{B}})$. We incidentally note that very little is known about the structure and properties $\textrm{Sol}_{\kappa }(M)$, our main conjecture being that it should be a finite-dimensional smooth manifold locally around an irreducible solution $(g,\varphi ,H)\in \textrm{Sol}_{\kappa }(M)$, namely a solution of the system with no automorphisms.

Remark 3.4

For every $(g,\varphi ,H)\in \textrm{Conf}(M)$ the symmetric and skew-symmetric projections $\mathcal {E}_{\textrm{E}}^s(g,\varphi ,H)\in \Gamma (T^{*}M^{\odot 2})$ and $\mathcal {E}_{\textrm{E}}^a(g,\varphi ,H)\in \Omega ^2(M)$ of $\mathcal {E}_{\textrm{E}}(g,\varphi ,H)$ are explicitly given by:

$$\begin{aligned} \mathcal {E}_{\textrm{E}}^s(g,\varphi ,H){} & {} = \textrm{Ric}^{g} + \nabla ^{g}\varphi - \frac{1}{2} H \circ _g H + \kappa \, \mathcal {R}^{g,H} \circ _g\mathcal {R}^{g,H}, \nonumber \\ \mathcal {E}_{\textrm{E}}^a(g,\varphi ,H){} & {} = \frac{1}{2}\delta ^{g} H + \frac{1}{2} H(\varphi ). \end{aligned}$$

These formulas can be very convenient to do explicit computations.

Due to the fact that we are studying an exact truncation of Heterotic supergravity at first order in the string slope parameter, the divergence of the Einstein equation $\mathcal {E}_{\textrm{E}}^s$ evaluated on an element $(g,\varphi ,H)$ satisfying the remaining equations of the system may not vanish identically, as we proceed to show below through a calculation that will naturally lead us to introduce the notion of strong Heterotic soliton, see Definition 3.8.

Lemma 3.5

The following identity holds:

$$\begin{aligned} \nabla ^{g*} (\mathcal {R}^{g,H}\circ _g \mathcal {R}^{g,H})(v){} & {} = \langle \nabla ^{g,H*}\mathcal {R}^{g,H},\mathcal {R}^{g,H}_v \rangle _g \nonumber \\{} & {} \quad - \frac{1}{2} v (\vert \mathcal {R}^{g,H}\vert ^2_g) - \frac{1}{2} \langle H, v\lrcorner \langle \mathcal {R}^{g,H}\wedge \mathcal {R}^{g,H}\rangle _g\rangle _g, \end{aligned}$$

for every $v\in \mathfrak {X}(M)$, where $\nabla ^{g,H*}:\Gamma (\wedge ^2\,M\otimes \wedge ^2\,M) \rightarrow \Gamma (\wedge ^1\,M\otimes \wedge ^2\,M)$ is the formal $L^2$ adjoint of $\textrm{d}^{\nabla ^{g,H}}:\Gamma (\wedge ^1\,M\otimes \wedge ^2\,M) \rightarrow \Gamma (\wedge ^2\,M\otimes \wedge ^2\,M)$ with respect to the determinant norm and $\nabla ^{g*}:\Gamma (T^{*}M\otimes T^{*}M) \rightarrow \Omega ^1(M)$ is the formal $L^2$ adjoint of $\nabla ^g:\Omega ^1(M) \rightarrow \Gamma (T^{*}M\otimes T^{*}M)$.

Proof

We choose an orthonormal frame $\left\{ e_i \right\}$ parallel with respect to $\nabla ^g$ at a given point $m\in M$. For every $v\in \mathfrak {X}(M)$ parallel with respect to $\nabla ^g$ at m we compute (using from now on Einstein’s summation convention on repeated indices):

$$\begin{aligned} \nabla ^{g*} (\mathcal {R}^{g,H}\circ _g \mathcal {R}^{g,H})(v)\!=\! & {} \!-\!\bigg (\nabla ^{g}_{e_i}(\mathcal {R}^{g,H}\circ _g \mathcal {R}^{g,H})\bigg )(e_i, v)\!=\!\!-\! \textrm{d}\big \langle \mathcal {R}^{g,H}_{e_i, e_j}, \mathcal {R}^{g,H}_{v,e_j}\big \rangle _g(e_i)\\&\! =\!&\big \langle \nabla ^{g,H*}\mathcal {R}^{g,H}, \mathcal {R}^{g,H}_v \big \rangle _g\! -\! \big \langle \mathcal {R}^{g,H}_{e_i,e_j}, (\nabla ^{g,H}_{e_i}\mathcal {R}^{g,H})_{v, e_j} \big \rangle _g\\= & {} \big \langle \nabla ^{g,H*}\mathcal {R}^{g,H}, \mathcal {R}^{g,H}_v \big \rangle _g - \frac{1}{2}\big \langle \mathcal {R}^{g,H}_{e_i, e_j}, \mathcal {C}(\nabla ^{g,H}_{e_i}\mathcal {R}^{g,H})_{v, e_j} \nonumber \\{} & {} \quad + (\nabla ^{g,H}_{v}\mathcal {R}^{g,H})_{e_i, e_j} \rangle _g \\= & {} \big \langle \nabla ^{g,H*}\mathcal {R}^{g,H}, \mathcal {R}^{g,H}_v \big \rangle _g - \frac{1}{2}\langle \mathcal {R}^{g,H}_{e_i, e_j}, \mathcal {C}(\nabla ^{g,H}_{e_i}\mathcal {R}^{g,H})_{v, e_j}\rangle _g \nonumber \\{} & {} \quad - \frac{1}{2} v\big (\vert \mathcal {R}^{g,H}\vert ^2_g\big ), \end{aligned}$$

where $\mathcal {C}$ denotes here the sum over all cyclic permutations of the set $(e_i,v,e_j)$. Using now the second Bianchi identity for connections with torsion we obtain after some tedious but straightforward computation:

$$\begin{aligned} \bigg \langle \mathcal {R}^{g,H}_{e_i, e_j}, \mathcal {C}(\nabla ^{g,H}_{e_i}\mathcal {R}^{g,H})_{v, e_j}\bigg \rangle _g = \bigg \langle H, v\lrcorner \bigg \langle \mathcal {R}^{g,H}\wedge \mathcal {R}^{g,H}\bigg \rangle _g\bigg \rangle _g, \end{aligned}$$

and we conclude. $\square$

We will also need the following:

Lemma 3.6

The following identity holds for every configuration $(g,\varphi ,H)\in \textrm{Conf}(M)$:

$$\begin{aligned} \nabla ^{g*}(H\circ _g H)(v){} & {} = - \frac{1}{2} v(\vert H\vert _g^2) - (H\circ _g H)(\varphi ,v) - \kappa \langle H, v\lrcorner \langle \mathcal {R}^{g,H}\wedge \mathcal {R}^{g,H}\rangle _g\rangle _g \\{} & {} \quad + 2 \langle \mathcal {E}^a_{\textrm{E}}(g,\varphi ,H), H(v)\rangle _g + \langle H, v\lrcorner \, \mathcal {E}_{\textrm{B}}(g,H)\rangle _g, \end{aligned}$$

where $v\in \mathfrak {X}(M)$ is a vector field.

Proof

We choose an orthonormal frame $\left\{ e_i \right\}$ adapted to $\nabla ^g$ at a given point $m\in M$ and compute.

$$\begin{aligned} -\nabla ^{g*}(H\circ _g H)(v){} & {} = (\nabla ^g_{e_i} (H\circ _g H))(e_i,v) = \textrm{d}\langle H(e_i), H(v)\rangle _g(e_i) = -\langle \nabla ^{g*}H, H(v)\rangle _g \\{} & {} \quad + \langle H(e_i), v\lrcorner \nabla ^g_{e_i}H\rangle _g = \langle H(\varphi ), H(v)\rangle _g - 2 \langle \mathcal {E}^a_E(g,\varphi ,H), H(v)\rangle _g \\{} & {} \quad - \langle H, v\lrcorner (e_i\wedge \nabla ^g_{e_i}H) \rangle _g + \langle H, \nabla ^g_v H \rangle _g \\{} & {} = \frac{1}{2} v(\vert H\vert _g^2) - 2 \langle \mathcal {E}^a_{\textrm{E}}(g,\varphi ,H), H(v)\rangle _g +\langle H(\varphi ),H(v)\rangle _g \nonumber \\{} & {} \quad + \kappa \langle H, v\lrcorner \langle \mathcal {R}^{g,H}\wedge \mathcal {R}^{g,H}\rangle _g\rangle _g - \langle H, v\lrcorner \mathcal {E}_{\textrm{B}}(g,H)\rangle _g, \end{aligned}$$

where $v\in \mathfrak {X}(M)$ is any vector field adapted to $\nabla ^g$ at $m\in M$. $\square$

Proposition 3.7

The following formula holds:

$$\begin{aligned}{} & {} v\lrcorner ( \nabla ^{g*}\mathcal {E}^s_{\textrm{E}}(g,\varphi ,H) + \varphi \lrcorner \mathcal {E}^s_{\textrm{E}}(g,\varphi ,H) + \frac{1}{2} \textrm{d}\textrm{Tr}_g(\mathcal {E}^s_{\textrm{E}}(g,\varphi ,H)) )\\{} & {} \quad = \kappa \langle \mathcal {R}^{g,H}_v , \nabla ^{g,H*}\mathcal {R}^{g,H} + \varphi \lrcorner \mathcal {R}^{g,H}\rangle _g\\{} & {} \qquad + \frac{1}{2} v\lrcorner \textrm{d}\mathcal {E}_{\textrm{D}}(g,\varphi ,H) - \langle \mathcal {E}^a_{\textrm{E}}(g,\varphi ,H), H(v)\rangle _g - \frac{1}{2} \langle H, v\lrcorner \, \mathcal {E}_{\textrm{B}}(g,H)\rangle _g, \end{aligned}$$

for every $(g,\varphi ,H)\in \textrm{Conf}(M)$ and $v \in \mathfrak {X}(M)$.

Proof

Let $(g,\varphi ,H)\in \textrm{Conf}(M)$. First, recall the standard identities:

$$\begin{aligned} \nabla ^{g*}\textrm{Ric}^g = -\frac{1}{2} \textrm{d}s_g\,, \quad \nabla ^{g*}\nabla ^g\varphi = \Delta _g\varphi - \textrm{Ric}^g(\varphi ). \end{aligned}$$

Using Lemmas 3.5 and 3.6 together with the previous standard identities we obtain:

$$\begin{aligned} v\lrcorner \nabla ^{g*}\mathcal {E}^s_{\textrm{E}}(g,\varphi ,H){} & {} = -\frac{1}{2} v (s_g) + \frac{1}{4}v\bigg (\vert H\vert ^2\bigg ) + \frac{1}{2} (H\circ _g H)(\varphi ,v) + \Delta _g\varphi (v) \\ {}{} & {} \quad - \textrm{Ric}^g(\varphi ,v) - \frac{\kappa }{2} v\bigg (\vert \mathcal {R}^{g,H}\vert _g^2\bigg )\\{} & {} \quad + \kappa \langle \mathcal {R}^{g,H}_v, \nabla ^{g,H*}\mathcal {R}^{g,H} \rangle _g - \langle \mathcal {E}^a_{\textrm{E}}(g,\varphi ,H), H(v)\rangle _g\\{} & {} \quad - \frac{1}{2} \langle H, v\lrcorner \, \mathcal {E}_{\textrm{B}}(g,H)\rangle _g, \end{aligned}$$

for every vector field $v\in \mathfrak {X}(M)$. On the other hand, a quick computation reveals that:

$$\begin{aligned} v\lrcorner \varphi \lrcorner \mathcal {E}^s_{\textrm{E}}\,(g,\varphi ,H)= & {} \textrm{Ric}^{g}(\varphi ,v) + \frac{1}{2} v\bigg (\vert \varphi \vert _g^2\bigg ) - \frac{1}{2} (H \circ _g H)(\varphi ,v) \\{} & {} + \kappa \, \bigg (\mathcal {R}^{g,H} \circ _g\mathcal {R}^{g,H}\bigg )(\varphi ,v), \end{aligned}$$

as well as:

$$\begin{aligned} \textrm{d}\textrm{Tr}_g(\mathcal {E}^s_{\textrm{E}}(g,\varphi ,H)) = \textrm{d}\bigg ( s_g - \frac{3}{2} \vert H\vert _g^2 - \delta ^g\varphi + 2 \kappa \vert \mathcal {R}^{g,H}\vert _g^2\bigg ). \end{aligned}$$

Hence:

$$\begin{aligned}{} & {} v\lrcorner (\nabla ^{g*}\mathcal {E}^s_{\textrm{E}}(g,\varphi ,H) + \varphi \lrcorner \, \mathcal {E}^s_{\textrm{E}}(g,\varphi ,H) + \frac{1}{2} \textrm{d}\textrm{Tr}_g(\mathcal {E}^s_{\textrm{E}}(g,\varphi ,H)) )\\ {}{} & {} \quad = \kappa \langle \mathcal {R}^{g,H}_v, \nabla ^{g,H*}\mathcal {R}^{g,H} \rangle _g + \kappa \, (\mathcal {R}^{g,H} \circ _g\mathcal {R}^{g,H})(\varphi ,v) + \frac{1}{2} \textrm{d}( \delta ^g\varphi + \vert \varphi \vert _g^2 \\ {}{} & {} \qquad - \vert H\vert _g^2 + \kappa \vert \mathcal {R}^{g,H}\vert _g^2)(v) - \langle \mathcal {E}^a_{\textrm{E}}(g,\varphi ,H), H(v)\rangle _g - \frac{1}{2} \langle H, v\lrcorner \, \mathcal {E}_{\textrm{B}}(g,H)\rangle _g \\ {}{} & {} \quad = \kappa \langle \mathcal {R}^{g,H}_v, \nabla ^{g,H*}\mathcal {R}^{g,H} \rangle _g + \kappa \langle \mathcal {R}^{g,H}_v, \mathcal {R}^{g,H}_{\varphi }\rangle _g + \frac{1}{2} v\lrcorner \textrm{d}\mathcal {E}_{\textrm{D}}(g,\varphi ,H) \\{} & {} \qquad - \langle \mathcal {E}^a_{\textrm{E}}(g,\varphi ,H), H(v)\rangle _g - \frac{1}{2} \langle H, v\lrcorner \, \mathcal {E}_{\textrm{B}}(g,H)\rangle _g, \end{aligned}$$

which gives the equation in the statement. $\square$

Clearly, by the previous proposition, every Heterotic soliton satisfies:

$$\begin{aligned} \langle \mathcal {R}^{g,H}_v, \nabla ^{g,H*}\mathcal {R}^{g,H} + \varphi \lrcorner \mathcal {R}^{g,H}\rangle _g = 0, \end{aligned}$$

for every vector field $v\in \mathfrak {X}(M)$. This motivates the following definition.

Definition 3.8

The strong Heterotic soliton system is the Heterotic soliton system for triples $(g,\varphi ,H)\in \textrm{Conf}(M)$ together with the strong condition:

$$\begin{aligned} \nabla ^{g,H*}\mathcal {R}^{g,H} + \varphi \lrcorner \mathcal {R}^{g,H} = 0. \end{aligned}$$

(3.4)

A strong Heterotic soliton is a solution of the strong Heterotic soliton system.

The strong Heterotic soliton system is an overdetermined system of partial differential equations. Despite being overdetermined, as we will see below it still has natural non-trivial solutions. This is a remarkable fact that can be traced back to the internal consistency and coherence of supersymmetric field theories and, in particular, Heterotic supergravity and its various truncations. Discussing the consistency of the perturbative expansion Heterotic supergravity and its consistent truncations is beyond the scope of this article. The interested reader is referred to [35] and its references for more details.

Remark 3.9

Note that every $(g,\varphi ,H)\in \textrm{Conf}(M)$ satisfying $\mathcal {E}^{a}_{\textrm{E}}(g,\varphi ,H)=0$, $\mathcal {E}_{\textrm{D}}(g,\varphi ,H)=0$ and $\mathcal {E}_{\textrm{B}}(g,\varphi ,H)=0$ together with the strong condition automatically satisfies:

$$\begin{aligned} \nabla ^{g*}\mathcal {E}_{\textrm{E}}(g,\varphi ,H) + \varphi \lrcorner \,\mathcal {E}_{\textrm{E}}(g,\varphi ,H) + \frac{1}{2} \textrm{d}\textrm{Tr}_g(\mathcal {E}_{\textrm{E}}(g,\varphi ,H)) = 0. \end{aligned}$$

Identities of this type, involving the divergence of the Einstein equation, are closely related to the existence of variational principles associated with the Heterotic soliton system. Studying the action functionals that can be associated with the Heterotic soliton system is a fundamental problem that is currently a work in progress and that we will consider elsewhere.

The strong condition is an equation in $\wedge ^1\,M\otimes \wedge ^2\,M$. Hence, by projecting to $\wedge ^3\,M$ we obtain an equation in $\wedge ^3 M$ that is satisfied by any strong Heterotic soliton and does not explicitly involve any curvature operators. On the other hand, by contraction we obtain an equation on $\wedge ^1\,M$.

Proposition 3.10

Let $(g,\varphi ,H)\in \textrm{Conf}(M)$ be a solution to the strong condition. Then, the following equations hold:

$$\begin{aligned} \nabla ^{g*}\nabla ^g H{} & {} + \frac{1}{2}\delta ^g \textrm{d}H - \frac{1}{2} (\delta ^g H)_{e_i}\wedge H_{e_i} + \frac{1}{2} H_{e_j}(e_i)\wedge (\nabla ^g_{e_j}H)_{e_i} + \frac{1}{2} H_{e_j}(\nabla ^g_{e_j} H) \nonumber \\{} & {} + \frac{1}{4} e_j \lrcorner \, H_{e_j}(\textrm{d}H) - \frac{1}{4} H_{e_j}(H_{e_j}(e_i)\wedge H_{e_i}) + \nabla ^g_{\varphi }H + \frac{1}{2}\varphi \lrcorner \textrm{d}H \nonumber \\{} & {} - \frac{1}{2} H_{\varphi }(e_i)\wedge H_{e_i} = 0, \end{aligned}$$

(3.5)

where $(e_i)$ is any local orthonormal frame.

Proof

Let v be any tangent vector. By (2.1) and the first Bianchi identity for $\mathcal {R}^g$, the totally skew-symmetric part of $\mathcal {R}^{g,H}_{v}$ is explicitly given by:

$$\begin{aligned} e_i\wedge \mathcal {R}^{g,H}_{v \, e_i}{} & {} = - \frac{1}{2} e_i \wedge (\nabla ^g_{v} H)(e_i) + \frac{1}{2} e_i\wedge (\nabla ^g_{e_i} H)(v) + \frac{1}{4} e_i\wedge [H_{v}, H_{e_i}] \\{} & {} = -\nabla ^g_{v} H - \frac{1}{2} v\lrcorner \, \textrm{d}H + \frac{1}{2} H_{v}(e_i)\wedge H_{e_i}. \end{aligned}$$

We choose the local orthonormal frame $(e_i)$ to be $\nabla ^g$-parallel at some point $m\in M$. Taking $v=e_j$ in the above formula, differentiating with respect to $e_j$ and summing over j, the skew-symmetric part of $\nabla ^{g,H*}\mathcal {R}^{g,H}$ at m can be computed as follows:

$$\begin{aligned} e_i\wedge (\nabla ^{g,H}_{e_j} \mathcal {R}^{g,H})_{e_j e_i}{} & {} = (\nabla ^g_{e_j} - \frac{1}{2} H_{e_j}) (-\nabla ^g_{e_j} H - \frac{1}{2} e_j \lrcorner \, \textrm{d}H + \frac{1}{2} H_{e_j}(e_i)\wedge H_{e_i})\\{} & {} =\nabla ^{g*}\nabla ^g H + \frac{1}{2}\delta ^g \textrm{d}H - \frac{1}{2} (\delta ^g H)_{e_i}\wedge H_{e_i} + \frac{1}{2} H_{e_j}(e_i)\wedge (\nabla ^g_{e_j}H)_{e_i}\\{} & {} \quad +\frac{1}{2} H_{e_j}(\nabla ^g_{e_j} H) + \frac{1}{4} e_j \lrcorner \, H_{e_j}(\textrm{d}H) - \frac{1}{4} H_{e_j}(H_{e_j}(e_i)\wedge H_{e_i}), \end{aligned}$$

where we have used that:

$$\begin{aligned} H_{e_j}(e_j \lrcorner \,\textrm{d}H) = e_j \lrcorner \, H_{e_j}(\textrm{d}H). \end{aligned}$$

Combining the previous equations together with the skew-symmetrization of (3.4), yields (3.5). $\square$

Remark 3.11

Equation (3.5) will be fundamental for the classification of the three-dimensional strong Heterotic solitons, considered in Sect. 4.3, where it becomes a scalar equation, see Lemma 4.13.

3.2 Lift to the Frame Bundle

We have introduced the Heterotic soliton system as a system of differential equations for a metric connection with skew-symmetric torsion that is determined by Heterotic supergravity and implicitly by the expected structure of the self-similar solutions to the Heterotic-Ricci flow. In the following, we show that the Heterotic soliton system, and especially its strong condition, can be naturally interpreted when lifted to the reference frame bundle of the underlying manifold M. For this, we will adapt the construction of [2, Proposition 7.1] to our case in which the gauge bundle is not an abstract bundle and the gauge connection is not an arbitrary connection but metric-compatible for each choice of Riemannian metric.

Given $(g,\varphi ,H)\in \textrm{Conf}(M)$, we denote by $\textrm{Fr}_g(M)$ the bundle of oriented frames of (M, g). Given any metric connection $\nabla$ on (M, g), in particular $\nabla ^{g,H}$, we denote by:

$$\begin{aligned} \textrm{CS}(\nabla ) \in \Omega ^3(\textrm{Fr}_g(M)), \end{aligned}$$

its Chern–Simons form, which defines a three-form on the total space of $\textrm{Fr}_g(M)$. There is a natural map:

$$\begin{aligned} \textrm{Conf}(M) \rightarrow \textrm{Met}(\textrm{Fr}_g(M))\,, \qquad (g,\varphi ,H)\mapsto {\bar{g}}_{\kappa }, \end{aligned}$$

from $\textrm{Conf}(M)$ into the Riemannian metrics over $\textrm{Fr}_g(M)$ that, to every $(g,\varphi ,H)$, associates the metric:

$$\begin{aligned}{} & {} {\bar{g}}_{\kappa }(X_1,X_2) = g_m(\textrm{d}\pi (X_1), \\{} & {} \quad \textrm{d}\pi (X_2)) - \kappa \, \textrm{Tr}(\mathcal {A}_{g,H}(X_1), \mathcal {A}_{g,H}(X_2)),\, X_1, X_2 \in T_p\textrm{Fr}_g(M), \end{aligned}$$

where $\mathcal {A}_{g,H}$ is the metric connection $\nabla ^{g,H}$, understood as a one-form in the total space of $\textrm{Fr}_g(M)$ with values in $\mathfrak {so}(n)$. In particular, for every $X\in T_p \textrm{Fr}_g(M)$ we have $\mathcal {A}_{g,H}(X)\in \mathfrak {so}(n)$. Note that the metric ${\bar{g}}_{\kappa }$ is invariant under the principal bundle action of $\textrm{Fr}_g(M)$.

Proposition 3.12

[2, Proposition 7.1] A triple $(g,\varphi ,H)\in \textrm{Conf}(M)$ is a strong Heterotic soliton with constant $\kappa$ if and only if the associated triple $({\bar{g}}_{\kappa },\bar{\varphi },{\bar{H}})$ satisfies:

$$\begin{aligned} \textrm{Ric}^{{\bar{g}}_{\kappa },{\bar{H}}_{\kappa }} + \nabla ^{{\bar{g}}_{\kappa },{\bar{H}}_{\kappa }}\bar{\varphi } = 0, \quad \delta ^{{\bar{g}}_{\kappa }}\bar{\varphi } + |\bar{\varphi }|^2_{{\bar{g}}_{\kappa }} - |{\bar{H}}_{\kappa }|^2_{{\bar{g}}_{\kappa }} = 0,\quad \textrm{d}{\bar{H}}_{\kappa }=0, \end{aligned}$$

(3.6)

where $\bar{\varphi } = \pi ^{*}\varphi$ and ${\bar{H}}_{\kappa } = H + \kappa \, \textrm{CS}(\mathcal {A}_{g,H})$.

Remark 3.13

The interest of the previous proposition is that equations (3.6) precisely correspond to the equations of motion of NS–NS supergravity for a pseudo-Riemannian metric of split signature and a three-form flux ${\bar{H}}_k$ belonging to a given string class [49] for each choice of metric. The fact that the signature of the metric ${\bar{g}}$ on the total space of $\textrm{Fr}_g(M)$ is of split signature is not accidental and can be traced back to the sign of the higher order curvature term $\mathcal {R}^{g,H}\circ _g \mathcal {R}^{g,H}$ in (3.1), see also Remark 2.11. Had this term appeared with the opposite sign (recall that $\kappa$ is assumed to be non-negative), then the corresponding ${\bar{g}}$ would be positive definite. This would be however inconsistent with the physical interpretation of the system.

4 Heterotic Solitons on Three-Manifolds

In this section, we consider the Heterotic soliton system on a compact three-manifold with the goal of obtaining a classification result for three-dimensional strong Heterotic solitons.

4.1 Three-Dimensional Reformulation

The Heterotic soliton system can be simplified in three dimensions using the fact that the Hodge dual of H is a function and the fact that the Riemann tensor is completely determined by the Ricci curvature. Given a triple $(g,\varphi ,H)$, we write $H= f \nu _g$ in terms of the unique function $f = *_g H\in C^{\infty }(M)$, where $\nu _g$ denotes the Riemannian volume form associated to g. Consequently, we define the configuration space $\textrm{Conf}(M)$ of the Heterotic soliton system on M as the set of triples $(g,\varphi ,f)$, where g is a Riemannian metric, $\varphi$ is a one-form and f is a function. Similarly, we define the set of Heterotic solitons $\textrm{Sol}_{\kappa }(M)$ on M as the set of triples $(g,\varphi ,f)\in \textrm{Conf}(M)$ such that $(g,\varphi ,H = *_g f)$ satisfies the Heterotic soliton system with parameter $\kappa \in \mathbb {R}$.

Using the Lemma A.1 in Appendix A we can write the Heterotic system in three dimensions as a system of differential equations for a metric g, a closed one-form $\varphi$ and a function f involving the Ricci tensor and scalar curvature of g as the only curvature operators.

Proposition 4.1

A triple $(g,\varphi , f)\in \textrm{Conf}(M)$ is a Heterotic soliton if and only if it satisfies the following system of equations:

$$\begin{aligned} - \kappa \, \textrm{Ric}^g \circ _g \textrm{Ric}^g{} & {} + (1 + \kappa s_g - \frac{\kappa }{2} f^2 )\textrm{Ric}^{g} + \left( \kappa \vert \textrm{Ric}^g \vert _g^2-\frac{\kappa }{2} s_g^2+\frac{\kappa }{4} \vert \textrm{d}f \vert _g^2 - \frac{1}{2} f^2+\frac{\kappa }{8}f^4\right) g \nonumber \\{} & {} + \frac{\kappa }{2}\, [*_g\textrm{d}f, \textrm{Ric}^g] + \frac{\kappa }{4} \textrm{d}f \otimes \textrm{d}f + \nabla ^{g}\varphi = 0, \end{aligned}$$

(4.1)

$$\begin{aligned}{} & {} f \varphi =\textrm{d}f\,, \quad s_g= 3\, \delta ^g \varphi +2 \vert \varphi \vert ^2 -\frac{1}{2} f^2, \end{aligned}$$

(4.2)

where $f = *_g H$.

Proof

Since in three dimensions the Bianchi equation (2.2) is automatically satisfied, a triple $(g,\varphi , f)\in \textrm{Conf}(M)$ is a Heterotic soliton if and only if $(g,\varphi , H = f \nu _g)$ satisfies equations (3.1). Plugging Eq. (A.3) into $\mathcal {E}_{\textrm{E}}^s(g,\varphi ,H) = 0$ and using the identity:

$$\begin{aligned} H\circ _g H(v_1,v_2) = g(v_1,v_2) f^2, \end{aligned}$$

it follows that Eq. (4.1) is equivalent to $\mathcal {E}_{\textrm{E}}^s(g,\varphi ,H) = 0$, namely it is equivalent to the symmetric part of the first equation in (3.1). For the skew-symmetric part $\mathcal {E}_{\textrm{E}}^a(g,\varphi ,H) = 0$ of $\mathcal {E}_{\textrm{E}}(g,\varphi ,H)=0$ we compute:

$$\begin{aligned} \delta ^g H + \iota _{\varphi } H =-*_g \textrm{d}*_g (f \nu _g) + f \iota _{\varphi } \nu _g = -*_g \textrm{d}f +f *_g\varphi , \end{aligned}$$

whence equation $\mathcal {E}_{\textrm{E}}^a(g,\varphi ,H)=0$ is equivalent to the first equation in (4.2). The second equation in (3.1) can be proven to be equivalent to the second equation in (4.2) by combining it appropriately to the trace of $\mathcal {E}_{\textrm{E}}(g,\varphi ,H)=0$. $\square$

Therefore, the Heterotic soliton system, as introduced in Definition 4.2, is equivalent in three dimensions to Eqs. (4.1) and (4.2) for tuples of the form $(g,\varphi ,f)\in \textrm{Conf}(M)$.

Definition 4.2

Let $\kappa >0$ be a positive real number. Equations (4.1) and (4.2) are the three-dimensional Heterotic soliton system on M. Solutions of this system are three-dimensional Heterotic solitons.

The following result is the key reason why solutions to the three-dimensional Heterotic system are relevant in relation to the three-dimensional Heterotic-Ricci flow: the former are, as their name suggests, self-similar solutions of the latter.

Proposition 4.3

Let $(g,\varphi ,f)\in \textrm{Sol}_{\kappa }(M)$ be a three-dimensional Heterotic soliton. Then, there exists a one-parameter family of diffeomorphisms $\left\{ \psi _t\right\} _{t\in \mathcal {I}}$ for some interval $\mathcal {I}$ such that:

$$\begin{aligned} (g_t,f_t) = (\psi ^{*}_t g, f\circ \psi _t), \end{aligned}$$

is a Heterotic-Ricci flow.

Proof

Suppose that $(g,\varphi ,f)\in \textrm{Sol}_{\kappa }(M)$ and define $\left\{ \psi _t\right\} _{t\in \mathcal {I}}$ the one-parameter family of diffeomorphisms defined by the flow of $\varphi$. Then:

$$\begin{aligned} \partial _t (\psi ^{*}_t g) = \psi ^{*}_t \mathcal {L}_{\varphi }g = 2\psi ^{*}_t \nabla ^{g}\varphi , \end{aligned}$$

where we have used that $\varphi$ is closed. Plugging this equation into (2.6) we directly obtain (4.1). Regarding (2.7), we compute:

$$\begin{aligned}{} & {} \partial _t (f\circ \psi _t ) + \frac{1}{2} \textrm{Tr}_{\psi ^{*}_t g}(\partial _t \psi ^{*}_t g) f\circ \psi _t + \Delta _{\psi ^{*}_t g} (f\circ \psi _t) = \psi _t^{*} (\textrm{d}f(\varphi ) + \textrm{Tr}_g(\nabla ^g\varphi ) f \\{} & {} \quad + \delta ^g\textrm{d}f) = 0. \end{aligned}$$

Here we have used that $\textrm{d}f = f\varphi$, which implies:

$$\begin{aligned} \delta ^g\textrm{d}f = -\textrm{d}f(\varphi ) + f \delta ^g\varphi , \end{aligned}$$

together with the identity $\textrm{Tr}_g(\nabla ^g\varphi ) = - \delta ^g\varphi$. Hence $(g_t,f_t) = (\psi ^{*}_t g, f\circ \psi _t)$ is a solution of the three-dimensional Heterotic-Ricci flow and consequently solutions of (4.1) and (4.2) are self-similar solutions of the Heterotic-Ricci flow. $\square$

Remark 4.4

We expect Heterotic solitons in all dimensions to be actual solitons for the Heterotic-Ricci flow. However, in dimensions larger than four, $H_t$ is in general not closed, and therefore obtaining the solitons of the flow requires a precise understanding of the symmetries of the system when formulated either on a string structure [34, 49, 63] or or on a transitive Courant algebroid [2, 20], see Remark 2.6. We plan to come back to this issue in the future.

The strong condition introduced in Definition 3.8 can, of course, be adapted to three dimensions, but in its generality, it reduces to an expression that is not particularly illuminating. We will come back to this point later, see Sect. 4.3.

4.2 General Properties

In this subsection, we will prove a number of structural results about three-dimensional Heterotic solitons.

Proposition 4.5

Let (M, g) be a closed Riemannian three-manifold. A three-dimensional Heterotic soliton is trivial if and only if $f=0$.

Proof

The only if direction holds by definition. Therefore, assume that $f=0$. The trace of Eq. (4.1) reduces to:

$$\begin{aligned} \delta ^{g}\varphi = 2\kappa \vert \textrm{Ric}^{g}_0\vert ^2_g +\frac{\kappa }{6} s_g^2 + s_g, \end{aligned}$$

where $\textrm{Ric}^{g}_0 = \textrm{Ric}^g - s_g\, g/3$ is the trace-free part of the Ricci tensor. On the other hand, the second equation in (4.1) reduces to:

$$\begin{aligned} s_g= 3\, \delta ^{g} \varphi +2 \vert \varphi \vert ^2_g. \end{aligned}$$

Combining the previous equations and integrating we obtain:

$$\begin{aligned} \int _M (2\kappa \vert \textrm{Ric}^{g}_0\vert ^2_g +\frac{\kappa }{6} s_g^2 + 2\vert \varphi \vert ^2) \nu _g = 0, \end{aligned}$$

where $\nu _g$ is the volume form of g. Hence $\varphi =s_g=\vert \textrm{Ric}^{g}_0\vert ^2_g=0$, so g is Ricci-flat. Since M is three-dimensional implies that g is in fact a flat Riemannian metric. $\square$

Lemma 4.6

Let $(g,\varphi ,f)$ be a non-trivial three-dimensional Heterotic soliton. Then, there exists a function $\phi \in C^{\infty }(M)$ such that $\varphi = \textrm{d}\phi$ and $f = c\, e^{\phi }$ for a non-zero constant $c\in \mathbb {R}^{*}$.

Proof

Let $(g,\varphi ,f)$ be a non-trivial three-dimensional Heterotic soliton. We first prove that f is nowhere vanishing. To do this, assume that $f(m) = 0$ for a given $m\in M$. For every smooth curve:

$$\begin{aligned} \gamma :\mathcal {I}\rightarrow M \,,\quad t\mapsto \gamma _t, \end{aligned}$$

where $\mathcal {I}$ is an interval containing 0 and $\gamma (0) = m$, the first equation in (4.2) implies:

$$\begin{aligned} \partial _t(f\circ \gamma _t) = (\gamma ^{*}\varphi )(\partial _t (f\circ \gamma _t)), \end{aligned}$$

which is a linear ordinary differential equation for $f\circ \gamma :\mathcal {I}\rightarrow \mathbb {R}$. Since $f(m)=0$, the existence and uniqueness of solutions to the previous ordinary differential equation imply that $f\circ \gamma _t = 0$ for all $t\in \mathcal {I}$. Since this holds for every such $\gamma :\mathcal {I}\rightarrow M$ and M is connected, we conclude that f vanishes identically, which is not allowed since (g, f) is by assumption a non-trivial Heterotic soliton, cf. Proposition 4.5. Hence f is nowhere vanishing, in which case the first equation in (4.2) is equivalent to $\varphi =\textrm{d}\phi$ and $f = c e^{\phi }$ for $\phi \in C^\infty (M)$ and for a non-zero constant $c\in \mathbb {R}^{*}$. $\square$

By the previous proposition, we will always assume from now on that $f= c e^{\phi }$ for any non-trivial three-dimensional Heterotic soliton $(g,\varphi ,f)\in \textrm{Sol}_{\kappa }(M)$. This allows us to denote three-dimensional Heterotic solitons simply as pairs $(g,f)\in \textrm{Sol}_{\kappa }(M)$. In particular, we will sometimes refer to f as the dilaton of the three-dimensional Heterotic soliton $(g,f)\in \textrm{Sol}_{\kappa }(M)$.

Proposition 4.7

Let $(g,f)\in \textrm{Sol}_{\kappa }(M)$ be a non-trivial Heterotic soliton. Then, the scalar curvature $s_g$ of g is strictly negative on some non-empty open set of M.

Proof

Let (g, f) be a Heterotic soliton and consider the second equation in (4.2), which can be equivalently rewritten as follows:

$$\begin{aligned} 2 f^2 s_g = - 6 f^2 \textrm{Tr}_g(\textrm{Hes}_g(\log (f))) + 4\vert \textrm{d}f\vert _g^2 -f^4, \end{aligned}$$

where $\textrm{Hes}_g(\log (f))$ denotes the Hessian of $\log (f)$ with respect to g. If f is constant then the previous equation reduces to $2 f^2 s_g = -f^4$, which immediately implies that $s_g$ is a strictly negative constant since f cannot be zero. If f is non-constant then evaluating the previous equation at an absolute minimum $m\in M$ of f we obtain:

$$\begin{aligned} 2 f_m^2 (s_g)_m = - 6 f^2 \textrm{Tr}_g(\textrm{Hes}_g(\log (f)))_m -f^4_m, \end{aligned}$$

where the subscript m denotes evaluation at $m\in M$. Since m is an absolute minimum and $f^2$ is strictly positive, we have $\textrm{Tr}_g(\textrm{Hes}_g(\log (f)))_m\ge 0$ and we conclude. $\square$

Remark 4.8

The previous proposition rules out the possibility of having three-dimensional Heterotic solitons with positive scalar curvature, which in dimension three is obstructed [33]. In contrast, any function on M that is negative on some open set is the scalar curvature of a metric on M.

Given the complexity of the Heterotic soliton system, it is natural to look for examples that satisfy natural curvature conditions. In the following result, we consider metrics whose Ricci tensor has constant principal curvatures, where the latter are defined as the eigenvalues of the Ricci endomorphism.

Proposition 4.9

A non-trivial three-dimensional Heterotic soliton $(g,f)\in \textrm{Sol}_{\kappa }(M)$ with constant dilaton f has constant principal Ricci curvatures $(\mu _1,\mu _2,\mu _3)$ which satisfy one of the following conditions:

• (1) $\kappa f^2 = 1$ and $\bigg (\mu _1 = \mu _2 = -\frac{1}{2\kappa }, \mu _3 = \frac{1}{2\kappa }\bigg )$.

• (2) $\kappa f^2 = 2$ and $\bigg (\mu _1 = \mu _2 =0, \mu _3 = -\frac{1}{\kappa }\bigg )$. In particular, the universal cover of M is isometric to either $\widetilde{\textrm{Sl}}(2,\mathbb {R})$ or $\textrm{E}(1,1)$ equipped with a left-invariant metric.

• (3) $\kappa f^2 = 3$ and $\bigg (\mu _1 = \mu _2 = \mu _3 = -\frac{1}{2\kappa }\bigg )$. In particular (M, g) is a hyperbolic three-manifold endowed with a metric of scalar curvature $-\frac{3}{2\kappa }$.

Proof

Assume that f is a constant, which by Proposition 4.5 must then be non-zero. With this assumption, Eqs. (4.1) and (4.2) reduce to:

$$\begin{aligned} - \kappa \, \textrm{Ric}^g \circ _g \textrm{Ric}^g + (1 - \kappa f^2 )\textrm{Ric}^{g} + \bigg ( \kappa \vert \textrm{Ric}^g \vert _g^2 - \frac{1}{2} f^2\bigg ) g = 0\,, \quad s_g= -\frac{1}{2} f^2. \end{aligned}$$

Taking the trace of the first equation and combining it with the second equation we find:

$$\begin{aligned} 2 \kappa \vert \textrm{Ric}^g \vert _g^2 = 2 f^2 - \frac{\kappa f^4}{2}, \end{aligned}$$

which plugged back into the previous equations yields:

$$\begin{aligned} - \kappa \, \textrm{Ric}^g \circ _g \textrm{Ric}^g + (1 - \kappa f^2 )\textrm{Ric}^{g} + \frac{1}{2} \left( f^2 - \frac{\kappa f^4}{2}\right) g = 0\,, \qquad s_g= -\frac{1}{2} f^2.\nonumber \\ \end{aligned}$$

(4.3)

The discriminant of the previous equation can be verified to be one, and by solving it we obtain the cases listed in the statement of the Proposition, similarly to [40, Proposition 4.6, Theorem 4.9], whose proof involves solving the same algebraic equation for the Ricci tensor. $\square$

Remark 4.10

In case (1) of the previous proposition, Reference [40] proves the existence of an associated Sasakian structure, possibly involving a different Riemannian metric, constructed out of the unit-norm eigenvector of $\textrm{Ric}^g$ with positive eigenvalue. Very little is currently known about the basic properties of this auxiliary Sasakian structure.

Ideally, we would like to construct or, at least, prove the existence of three-dimensional Heterotic solitons (g, f) with non-constant dilaton f. The following result excludes for this purpose the case of Heterotic solitons with Einstein metrics.

Theorem 4.11

All Einstein three-dimensional Heterotic solitons have constant dilaton.

Proof

If (M, g) is Einstein, so that $\textrm{Ric}^g=\frac{1}{3} s_g g$, the Einstein equation (4.1) becomes:

$$\begin{aligned} \left( \frac{1}{3} s_g-\frac{\kappa }{6}s_gf^2+\frac{\kappa }{18} s_g^2+\frac{\kappa }{4} \vert \textrm{d}f \vert _g^2 - \frac{1}{2} f^2+\frac{\kappa }{8}f^4\right) g + \frac{\kappa }{4} \textrm{d}f \otimes \textrm{d}f + \nabla ^{g}\varphi = 0.\nonumber \\ \end{aligned}$$

(4.4)

Taking the trace with respect to g in this equation yields:

$$\begin{aligned} s_g-\frac{\kappa }{2} s_g f^2+\frac{\kappa }{6} s_g^2+\kappa \vert \textrm{d}f \vert _g^2 - \frac{3}{2} f^2+\frac{3\kappa }{8}f^4 - \delta ^{g}\varphi = 0. \end{aligned}$$

(4.5)

Using now the dilaton equations (4.2) we readily obtain $\vert \textrm{d}f\vert _g^2=\alpha (f)$, for some explicit rational function $\alpha$ given by:

$$\begin{aligned} \alpha (t):= & {} \frac{-\frac{2}{3} s_g+\frac{\kappa }{2}s_gt^2-\frac{\kappa }{6} s_g^2 +\frac{5}{3} t^2-\frac{3\kappa }{8}t^4}{\kappa +\frac{2}{3t^2}}\\= & {} \frac{-2s_gt^2+\frac{3}{2} \kappa s_gt^4-\frac{1}{2}\kappa s_g^2t^2 +5 t^4-\frac{9\kappa }{8}t^6}{3\kappa t^2+2}. \end{aligned}$$

Applying then (4.4) to (the metric dual of) $\textrm{d}f$ and using that:

$$\begin{aligned} \nabla ^g_{\textrm{d}f}\varphi =\nabla ^g_{\textrm{d}f}\left( \frac{\textrm{d}f}{f}\right) =\frac{1}{2} \textrm{d}(\vert \textrm{d}f\vert _g^2)\frac{1}{f}-\frac{\vert \textrm{d}f\vert _g^2}{f^2}\textrm{d}f=\left( \frac{\alpha '(f)}{2f}-\frac{\alpha (f)}{f^2}\right) \textrm{d}f, \end{aligned}$$

we obtain:

$$\begin{aligned} \left( \frac{1}{3}s_g-\frac{\kappa }{6}s_gf^2+\frac{\kappa }{18} s_g^2+\frac{\kappa }{2} \alpha (f) - \frac{1}{2} f^2+\frac{\kappa }{8}f^4+\frac{\alpha '(f)}{2f}-\frac{\alpha (f)}{f^2}\right) \textrm{d}f= 0.\nonumber \\ \end{aligned}$$

(4.6)

Since $\alpha (t)\sim _{t\rightarrow +\infty }-\frac{3}{8}t^4$ and $\alpha '(t)\sim _{t\rightarrow +\infty } -\frac{3}{2} t^3$, we deduce from (4.6) that $P(f)\textrm{d}f=0$, where P is some (explicit) non-vanishing polynomial. This shows that the dilaton f is constant. $\square$

If we weaken the condition of having constant principal Ricci curvatures in order to construct Heterotic solitons with non-constant dilaton we can rapidly encounter important obstructions, as illustrated by the following result.

Proposition 4.12

Let $(g,f)\in \textrm{Sol}_{\kappa }(M)$ be a non-trivial three-dimensional Heterotic soliton such that $\textrm{d}f\ne 0$ and:

$$\begin{aligned} \textrm{d}s_g = 0\,, \qquad \textrm{d}\vert \textrm{Ric}^g\vert _g^2 = 0. \end{aligned}$$

Then M is diffeomorphic to the sphere $S^3$.

Proof

Suppose (g, f) is a Heterotic soliton with non-constant dilaton f. We evaluate Eqs. (4.1) and (4.2) at a critical point $m\in M$ of f whose critical value we denote by $f_c$. We obtain:

$$\begin{aligned} - \textrm{Hes}(\log f)_m{} & {} = - \kappa \, \textrm{Ric}^g_m \circ _g \textrm{Ric}^g_m +\bigg (1 + \kappa (s_g)_m - \frac{\kappa }{2} f^2_c \bigg )\textrm{Ric}^{g}_m \\ {}{} & {} \quad + \left( \kappa \vert \textrm{Ric}^g_m \vert _g^2-\frac{\kappa }{2} (s^2_g)_m- \frac{1}{2} f^2_c+\frac{\kappa }{8}f^4_c\right) g, \\ \textrm{Tr}_g(\textrm{Hes}(\log f)_m){} & {} = -\frac{(s_g)_m}{3} -\frac{1}{6} f^2_c. \end{aligned}$$

Taking the trace of the first equation and combining it with the second we obtain a quadratic equation for $f^2_c$ whose coefficients are constant due to the assumption $\textrm{d}s_g = 0$ and $\textrm{d}\vert \textrm{Ric}^g\vert _g^2 = 0$. Hence, the function f can have at most two critical values, implying that it is either constant, which is not allowed, or has exactly two critical points. The latter implies that M is diffeomorphic to the sphere [38, 50]. $\square$

We note that the existence of three-dimensional Heterotic solitons with non-constant dilaton is currently an open problem.

4.3 Classification of Three-Dimensional Strong Heterotic Solitons

In this subsection, we consider strong three-dimensional Heterotic solitons and provide their complete classification.

Lemma 4.13

A strong three-dimensional Heterotic soliton $(g,f)\in \textrm{Sol}_{\kappa }(M)$ has constant dilaton f.

Proof

Every strong Heterotic soliton satisfies by definition the strong condition (3.4) and therefore also satisfies its skew-symmetric projection (3.5). Plugging $H= f\nu _g$ into equation (3.5) and simplifying we obtain that it is equivalent to:

$$\begin{aligned} \nabla ^{g*} \nabla ^g H + \nabla ^g_{\varphi } H =0. \end{aligned}$$

Setting now $H = f \nu _g$ in the previous equation we obtain that it is equivalent to:

$$\begin{aligned} f\Delta _g f + \vert \textrm{d}f\vert _g^2 = 0. \end{aligned}$$

Integrating over M, this implies $\textrm{d}f=0$. $\square$

The previous lemma reduces the study of three-dimensional strong Heterotic solitons to the study of the strong condition given at Eq. (3.4) in the three possible classes of three-dimensional Heterotic solitons listed in Proposition 4.9. Since f is a non-zero constant, the system (4.1) and (4.2) is equivalent to (4.3) and the strong Eq. (3.4) becomes:

$$\begin{aligned} \nabla ^{g,H*}\mathcal {R}^{g,H}=0. \end{aligned}$$

(4.7)

We easily compute $\mathcal {R}^{g,H}_{v_1,v_2}=\mathcal {R}^g+\frac{1}{4}f^2v_1\wedge v_2$ for every tangent vectors $v_1,v_2$, therefore using the Bianchi identity $\nabla ^{g*}\mathcal {R}^{g}=\textrm{d}^{\nabla ^g}\textrm{Ric}^g$ we obtain after a straightforward computation that (4.7) is equivalent to:

$$\begin{aligned} \textrm{d}^{\nabla ^g}\textrm{Ric}^g(v)+\frac{3f}{2} \times (\textrm{Ric}^g_0(v)) =0,\qquad \forall v\in TM, \end{aligned}$$

(4.8)

where $\textrm{Ric}^g_0$ is the traceless Ricci tensor. If (M, g) is Einstein, this equation is clearly satisfied, so the solitons in case (3) of Proposition 4.9 satisfy automatically the strong condition. If (g, f) is of type (1) or (2) of Proposition 4.9, the Ricci tensor has one double eigenvalue $\mu _1$ and one simple eigenvalue $\mu _3$. Let $\xi$ denote a unit vector field on M satisfying $\textrm{Ric}^g(\xi )=\mu _3\xi$ (here we might have to replace M with a double cover in order for $\xi$ to be globally defined). We write:

$$\begin{aligned} \textrm{Ric}^g=\mu _1 g+(\mu _3-\mu _1)\xi \otimes \xi ,\qquad \textrm{Ric}^g_0=(\mu _3-\mu _1)\left( -\frac{1}{3}g+\xi \otimes \xi \right) , \end{aligned}$$

so $\textrm{d}^{\nabla ^g}\textrm{Ric}^g=(\mu _3-\mu _1)(\textrm{d}\xi \otimes \xi +(e_i\wedge \xi )\otimes \nabla ^g_{e_i}\xi )$. The strong equation (4.8) becomes:

$$\begin{aligned} g(v,\xi )\,\textrm{d}\xi +g(\nabla ^g_{e_i}\xi ,v)\,e_i\wedge \xi +\frac{3f}{2} \times \left( -\frac{1}{3}v+g(v,\xi )\,\xi \right) =0,\qquad \forall v\in TM. \end{aligned}$$

For $v=\xi$ this gives $\textrm{d}\xi =-f \times \xi$. Reinjecting in the above equation we obtain:

$$\begin{aligned} g(\nabla ^g_{e_i}\xi ,v)\,e_i\wedge \xi =\frac{f}{2} \times \left( v-g(v,\xi )\,\xi \right) ,\qquad \forall v\in TM. \end{aligned}$$

Taking the interior product with $\xi$ in this equation and using again $\textrm{d}\xi =-f \times \xi$ yields:

$$\begin{aligned} \frac{f}{2} \times (v\wedge \xi ){} & {} =g(\nabla ^g_\xi \xi ,v)\xi -g(\nabla ^g_{e_i}\xi ,v)\,e_i \\ {}{} & {} =\textrm{d}\xi (\xi ,v) \xi -g(\nabla ^g_v\xi ,e_i)\,e_i-\textrm{d}\xi (e_i,v)\,e_i \\ {}{} & {} =-\nabla ^g_v\xi -f \times (\xi \wedge v), \end{aligned}$$

showing that $\nabla _v\xi =-\frac{1}{2}f \times (\xi \wedge v)$ for every $v\in TM$. In particular, $\xi$ is Killing. The Bochner formula gives $2\textrm{Ric}^g(\xi ) =f^2\xi$ whence $2\mu _3=f^2=-2s_g=-2(2\mu _1+\mu _3)$, that is, $\mu _1+\mu _3=0$. We are thus in case (1) of Proposition 4.9. Reversing the order of the above calculations shows that, conversely, if the Ricci tensor of (M, g) satisfies the condition (1) in Proposition 4.9 and $\xi$ is a unit length vector field on M satisfying $\nabla \xi =-\frac{1}{2}f \times \xi$, then (M, g, f) is a strong three-dimensional soliton. It remains to characterize the manifolds satisfying these conditions.

Proposition 4.14

Let (M, g) be a complete simply connected three-dimensional Riemannian manifold such that there exists a positive constant f and a unit vector field $\xi$ with $\nabla ^g\xi =-\frac{1}{2}f \times \xi$ and $\textrm{Ric}^g=\frac{1}{2}f^2(-g+2\xi \otimes \xi )$. Then (M, g) is isometric to the Heisenberg group $\textrm{H}_3$, endowed with a left-invariant metric. Conversely, for every left-invariant metric on $\textrm{H}_3$ there exist f and $\xi$ with the above properties.

Proof

Consider the metric connection with torsion on (M, g) defined by

$$\begin{aligned} {\bar{\nabla }}_v:=\nabla ^g_v-\frac{1}{2}f \times v+fg(v,\xi ) \times \xi . \end{aligned}$$

We have

$$\begin{aligned} {\bar{\nabla }}_v\xi :=\nabla ^g_v\xi -\frac{1}{2}f \times v(\xi )=-\frac{1}{2}f \times \xi (v)-\frac{1}{2}f \times v(\xi )=0, \end{aligned}$$

so $\xi$ is ${\bar{\nabla }}$-parallel. A straightforward but tedious computation then shows that ${\bar{\nabla }}$ is flat. Consequently, there exists a ${\bar{\nabla }}$-parallel oriented orthonormal frame $\xi ,v,w$ on TM. We have:

$$\begin{aligned} 0= & {} {\bar{\nabla }}_vw-{\bar{\nabla }}_wv=[v,w]-f \times (v\wedge w)=[v,w]-f\xi \,,\\ 0= & {} {\bar{\nabla }}_v\xi -{\bar{\nabla }}_\xi v=[v,\xi ]-\frac{1}{2}f \times v(\xi )+\frac{1}{2}f \times \xi (v)-f \times \xi (v)=[v,\xi ], \end{aligned}$$

and similarly $[w,\xi ]=0$. This shows that the frame $(e_1,e_2,e_3):=(f\xi ,v,w)$ satisfies the commutator relations

$$\begin{aligned}{}[e_1,e_3]=[e_2,e_3]=0,\ [e_2,e_3]=e_1, \end{aligned}$$

of the Heisenberg Lie algebra $\mathfrak {h}_3$, and thus (M, g) is isometric to $\textrm{H}_3$ endowed with the left-invariant metric determined by the scalar product $f^2e^1\otimes e^1+e^2\otimes e^2+e^3\otimes e^3$.

Conversely, if f is a positive constant and (M, g) is the Heisenberg group endowed with the above left-invariant metric, the standard formulas of Riemannian Lie groups show that the unit left-invariant vector field $\xi$ induced by $\frac{1}{f}e_1$ satisfies $\nabla ^g\xi =-\frac{1}{2}f \times \xi$ and that $\textrm{Ric}^g=\frac{1}{2}f^2(-g+2\xi \otimes \xi )$. $\square$

Altogether, the previous discussion results in the following classification of compact strong Heterotic solitons in three dimensions.

Theorem 4.15

Every compact three-dimensional strong Heterotic soliton has constant dilaton and is either isometric to a compact quotient of the Heisenberg group equipped with a left-invariant metric or homothetic to a compact hyperbolic three-manifold.

5 Rigidity of Einstein Heterotic Solitons

All known Heterotic solitons on a compact three-manifold have constant principal Ricci curvatures and constant dilaton f. In this section, we study the local moduli of three-dimensional Heterotic solitons around an Einstein Heterotic soliton, which must be then either flat or of negative constant sectional curvature, in order to evaluate the possibility of deforming them to construct compact three-dimensional Heterotic solitons with non-constant dilaton. For definiteness, we will exclusively focus on the deformation of non-trivial Heterotic solitons with constant dilaton. The deformation problem of trivial Heterotic solitons can be easily studied by directly inspecting the Heterotic soliton system, from which the rigidity of trivial Heterotic solitons follows.

In three dimensions the Bianchi identity is automatically satisfied and, after solving the Maxwell equation as prescribed in Lemma 4.6 the maps introduced in (3.3) reduce to:

$$\begin{aligned} \mathcal {E}= (\mathcal {E}_{\textrm{E}}, \mathcal {E}_{\textrm{D}}) :\textrm{Conf}(M) \rightarrow \Gamma (T^{*}M\otimes T^{*}M)\times \mathcal {C}^{\infty }(M), \end{aligned}$$

namely to the maps defined by the Einstein and dilaton equations. The diffeomorphism group $\textrm{Diff}(M)$ acts naturally on $\textrm{Conf}(M)$. This action is smooth in the Fréchet category when we consider $\textrm{Conf}(M)$ as a Fréchet manifold and $\textrm{Diff}(M)$ as a Fréchet–Lie group. Furthermore, the map $\mathcal {E}$ is diffeomorphism-equivariant, namely:

$$\begin{aligned} \mathcal {E}(u^{*}g,f\circ u) =(u^{*}\mathcal {E}_{\textrm{E}}(g,f), \mathcal {E}_{\textrm{D}}(g,f)\circ u), \end{aligned}$$

for every $(g,f)\in \textrm{Conf}(M)$ and $u\in \textrm{Diff}(M)$. Hence, the action maps Heterotic solitons to Heterotic solitons. The moduli space of three-dimensional Heterotic solitons on a closed three-manifold M is then defined as follows:

$$\begin{aligned} \mathfrak {M}(M):= \mathcal {E}^{-1}(0)/\textrm{Diff}(M). \end{aligned}$$

It is equipped with the quotient topology of the subspace topology induced by the $\mathcal {C}^{\infty }$ topology of $\textrm{Conf}(M)$ corresponding to its Fréchet manifold structure. The main result that we need to understand the local structure of $\mathfrak {M}(M)$ is a slice theorem for the action of $\textrm{Diff}(M)$ on $\textrm{Conf}(M)$.

5.1 Local Slice in Configuration Space

The fact that we are studying Heterotic solitons in three dimensions together with the simplification given by Lemma 4.6, implies that the configuration space of the system reduces in this case to that of the classical Ricci solitons, namely pairs (g, f) as described above, although the equations that define our system are remarkably more complicated than the standard Ricci soliton system. Furthermore, for us f is a variable of the system whereas in the theory of Ricci solitons f is usually considered as being completely determined as an eigenvalue of a Schrödinger type of operator associated to the system. The moduli space of standard Ricci solitons together with a slice theorem for the corresponding action of the diffeomorphism group is proved in [47] by considering Sobolev completions of the spaces involved. Here we adopt a direct approach and we consider the smooth right action $\Psi :\textrm{Conf}(M)\times \textrm{Diff}(M)\rightarrow \textrm{Conf}(M)$ of $\textrm{Diff}(M)$ on $\textrm{Conf}(M)$ via pull-back. For every $(g,f)\in \textrm{Conf}(M)$ define:

$$\begin{aligned} \Psi _{g,f} :\textrm{Diff}(M) \rightarrow \textrm{Conf}(M)\,, \qquad u\mapsto (u^{*}g,f\circ u), \end{aligned}$$

to be the orbit map associated with (g, f). In particular, $\mathcal {O}_{g,f}:= \Im \textrm{m}(\Psi _{g,f})$ is the orbit of the action $\Psi$ passing through (g, f). The differential of $\Psi _{g,f} :\textrm{Diff}(M) \rightarrow \textrm{Conf}(M)$ at the identity $e\in \textrm{Diff}(M)$ reads:

$$\begin{aligned} \textrm{d}_e\Psi _{g,f} :\mathfrak {X}(M) \rightarrow T_{g,f}\textrm{Conf}(M), \qquad v \mapsto \mathcal {L}_v g \oplus \textrm{d}f(v), \end{aligned}$$

where the symbol $\mathcal {L}$ denotes the Lie derivative. Its $L^2$ adjoint is given by:

$$\begin{aligned} \textrm{d}^{*}_e\Psi _{g,f} :T_{g,f}\textrm{Conf}(M) \rightarrow \mathfrak {X}(M) \,, \qquad h\oplus \sigma \mapsto 2(\nabla ^{g*} h)^{\sharp _g} + \sigma \textrm{d}f^{\sharp _g}. \end{aligned}$$

Lemma 5.1

We have a $L^2$ orthogonal decomposition:

$$\begin{aligned} T_{g,f}\textrm{Conf}(M) = \Im \textrm{m}(\textrm{d}_e\Psi _{g,f}) \oplus \textrm{Ker}(\textrm{d}_e\Psi ^{*}_{g,f}), \end{aligned}$$

in terms of closed subspaces of $T_{g,f}\textrm{Conf}(M)$.

Proof

The result follows from the fact that the symbol of $\textrm{d}_e\Psi _{g,f} :\mathfrak {X}(M) \rightarrow T_{g,f}\textrm{Conf}(M)$ is injective. $\square$

Therefore, if (g, f) is a three-dimensional Einstein Heterotic soliton with constant dilaton, then the projection of $\textrm{d}_e\Psi _{g,f} :\mathfrak {X}(M) \rightarrow T_{g,f}\textrm{Conf}(M)$ to $C^{\infty }(M)$ is zero and the slice for the action of $\textrm{Diff}(M)$ around (g, f) can be characterized as follows.

Proposition 5.2

Let (g, f) be a three-dimensional Einstein Heterotic soliton with constant dilaton. Any smooth submanifold $\mathcal {S}_{g.f}\subset \textrm{Conf}(M)$ of the form:

$$\begin{aligned} \mathcal {S}_{g,f} = \mathcal {S}_g\times C^{\infty }(M), \end{aligned}$$

where $\mathcal {S}_g\subset \textrm{Met}(M)$ is a slice for the action of $\textrm{Diff}(M)$ on $\textrm{Met}(M)$ is a slice for the action of $\textrm{Diff}(M)$ on $\textrm{Conf}(M)$. In particular:

$$\begin{aligned} T_{g,f}\mathcal {S}_{g,f} = \textrm{Ker}(\nabla ^{g*}:\Gamma (T^{*}M\odot T^{*}M)\rightarrow \Omega ^1(M))\oplus C^{\infty }(M), \end{aligned}$$

is the tangent bundle of $\mathcal {S}_{g,f}$ at (g, f).

Remark 5.3

Thanks to recent developments in the theory of infinite dimensional groups and actions [10] we do not need to work in any Sobolev completion of $\textrm{Conf}(M)$ and we can remain in the category of Fréchet spaces and Fréchet Lie groups of smooth sections.

5.2 Essential Deformations

Let (g, f) be a non-trivial three-dimensional Einstein Heterotic soliton with constant dilaton. Recall that in this case, the Heterotic soliton system implies:

$$\begin{aligned} \textrm{Ric}^g= - \frac{f^2}{6} g\,, \qquad \kappa f^2 = 3. \end{aligned}$$

We will tacitly use these equations in the following. The existence of a natural slice for the action of the diffeomorphism group around every point $(g,f)\in \textrm{Conf}(M)$ immediately implies the following inclusion of vector spaces:

$$\begin{aligned} T_{g,f}\mathfrak {M}(M) \subset \textrm{Ker}(\textrm{d}_{g,f} \mathcal {E})\cap \textrm{Ker}(\textrm{d}_e\Psi ^{*}_{g,f}), \end{aligned}$$

where $T_{g,f}\mathfrak {M}(M)$ the tangent space of $\mathfrak {M}(M)$ at the class $[g,f]\in \mathfrak {M}$ determined by (g, f) and:

$$\begin{aligned} \textrm{d}_{g,f} \mathcal {E}:T_{g,f} \textrm{Conf}(M) \rightarrow T_{g,f} \textrm{Conf}(M), \end{aligned}$$

is the differential of $\mathcal {E}$ at (g, f). This motivates the following definition.

Definition 5.4

Let (g, f) be a non-trivial three-dimensional Einstein Heterotic soliton with constant dilaton. The vector space $\mathbb {E}_{g,f}$ of essential deformations of (g, f) is:

$$\begin{aligned} \mathbb {E}_{g,f} = \textrm{Ker}(\textrm{d}_{g,f} \mathcal {E})\cap \textrm{Ker}(\textrm{d}_e\Psi ^{*}_{g,f}). \end{aligned}$$

If $\mathbb {E}_{g,f} = 0$ then (g, f) is rigid.

Remark 5.5

By the existence of a slice around (g, f), the previous notion of rigidity corresponds to the intuitive one, namely, if (g, f) is rigid then there exists a neighborhood of (g, f) in $\mathcal {E}^{-1}(0)$ in which every element is diffeomorphic to (g, f).

Lemma 5.6

Let (g, f) be a non-trivial three-dimensional compact Einstein Heterotic soliton with constant dilaton. Then, the following equation holds:

$$\begin{aligned} \Delta _g\textrm{Tr}_g(h) = f^2 \textrm{Tr}_g(h)\,, \qquad \sigma = \frac{7f}{12}\textrm{Tr}_g(h), \end{aligned}$$

for every $(h,\sigma )\in \mathbb {E}_{g,f}$.

Proof

Let (g, f) be a three-dimensional Einstein Heterotic soliton with a constant dilaton and fix a pair $(h,\sigma )\in \textrm{Ker}(\textrm{d}_e\Psi ^{*}_{g,f})$. We have:

$$\begin{aligned} (\textrm{d}_g\textrm{Ric})(h){} & {} = \frac{1}{2} \nabla ^{g*}\nabla ^{g}h - \frac{f^2}{4} h + \frac{f^2}{12} \textrm{Tr}_g(h) g - \frac{1}{2} \nabla ^g\textrm{d}\textrm{Tr}_g(h), \\ (\textrm{d}_g s) (h){} & {} = \Delta _g \textrm{Tr}_g(h) + \frac{f^2}{6} \textrm{Tr}_g(h), \end{aligned}$$

which follow from the standard formulas for the linearization of the Ricci and scalar curvatures [6] and Eq. (A.1) in Appendix A. Note that the latter implies in particular:

$$\begin{aligned} \mathcal {R}^g_{v_1,v_2} = \frac{f^2}{12} v_1\wedge v_2 \qquad v_1,v_2 \in TM. \end{aligned}$$

Using the previous formulae we compute:

$$\begin{aligned} (\textrm{d}_g \vert \textrm{Ric} \vert _g^2) (h){} & {} = - 2 g(h, \textrm{Ric}^g\circ _g \textrm{Ric}^g) + 2 g(\textrm{d}_g\textrm{Ric}(h), \textrm{Ric}^g) \\ {}{} & {} \!=\!\! -\!\frac{f^4}{18} \textrm{Tr}_g(h)\! -\!\frac{f^2}{6} \textrm{Tr}_g(\nabla ^{g*}\nabla ^{g}h\! -\! \frac{f^2}{2} h \!+ \!\frac{f^2}{6} \textrm{Tr}_g(h) g \!- \!\nabla ^g\textrm{d}\textrm{Tr}_g(h))\\ {}{} & {} = -\frac{f^2}{3} (\Delta _g \textrm{Tr}_g(h) + \frac{f^2}{6} \textrm{Tr}_g(h)). \end{aligned}$$

In particular:

$$\begin{aligned} (\textrm{d}_g \vert \textrm{Ric} \vert _g^2) (h) = -\frac{f^2}{3} (\textrm{d}_g s)(h). \end{aligned}$$

Assuming now that $(h,\sigma )\in \mathbb {E}_{g,f}$ holds, the differential of the trace of the Einstein equation (4.1) at (g, f) gives:

$$\begin{aligned}{} & {} 2\kappa \, \textrm{d}_g\vert \textrm{Ric}^g \vert _g^2(h) - \frac{3}{2} \textrm{d}_g s(h) +\frac{3}{2} f \sigma -2 \textrm{d}_g s(h) + 3 \bigg (\frac{3}{2}f \sigma +\frac{3}{2} \textrm{d}_g s(h) - f \sigma \bigg ) \\{} & {} \quad -\frac{1}{f} \Delta _{g}\sigma = 3 f \sigma -\textrm{d}_g s(h) -\frac{1}{f} \Delta _{g}\sigma = 0. \end{aligned}$$

On the other hand, the differential of equation (4.2) at (g, f) immediately gives:

$$\begin{aligned} \textrm{d}_g s(h) = \frac{3}{f}\Delta _g \sigma - f\sigma . \end{aligned}$$

Combining the previous two equations we obtain:

$$\begin{aligned} \Delta _g \sigma = f^2 \sigma , \end{aligned}$$

and a quick computation reveals that:

$$\begin{aligned} \Delta _g \bigg (\textrm{Tr}_g(h) - \frac{12}{7f} \sigma \bigg ) = -\frac{f^2}{6} \bigg (\textrm{Tr}_g(h) - \frac{12}{7f} \sigma \bigg ), \end{aligned}$$

whence

$$\begin{aligned} \textrm{Tr}_g(h) = \frac{12}{7f} \sigma , \end{aligned}$$

and we conclude. $\square$

Remark 5.7

By the previous lemma, if $(h,\sigma )\in \mathbb {E}_{g,f}$ then:

$$\begin{aligned} (\textrm{d}_g s) (h) = \frac{7 f^2}{6} \textrm{Tr}_g(h)\,, \qquad \bigg (\textrm{d}_g \vert \textrm{Ric} \vert _g^2\bigg ) (h) = -\frac{7 f^4}{18}\textrm{Tr}_g(h). \end{aligned}$$

We will tacitly use these identities in the following.

Lemma 5.8

Let (g, f) be a non-trivial three-dimensional compact Einstein Heterotic soliton with constant dilaton. Then, the following equations hold:

$$\begin{aligned} \nabla ^{g*}\nabla ^g h = \frac{f^2}{6} h + f^2 \textrm{Tr}_g(h) g + \frac{13}{6} \nabla ^g \textrm{d}\textrm{Tr}_g(h)\,, \quad \Delta _g \textrm{Tr}_g(h) = f^2 \textrm{Tr}_g (h), \end{aligned}$$

for every $(h,\sigma )\in \mathbb {E}_{g,f}$.

Proof

Let (g, f) be a non-trivial three-dimensional Einstein Heterotic soliton with constant dilaton. Differentiating Eq. (4.1) at (g, f), manipulating and repeatedly using Lemma 5.6 we obtain:

$$\begin{aligned}{} & {} -\textrm{d}_g\textrm{Ric}(h) - \frac{f^2}{6}h + f\sigma g + \frac{1}{f} \nabla ^g \textrm{d}\sigma = -\frac{1}{2} \nabla ^{g*}\nabla ^{g}h + \frac{f^2}{12} h + \frac{f^2}{2} \textrm{Tr}_g(h) g \\{} & {} ]\quad + \frac{13}{12} \nabla ^g \textrm{d}\textrm{Tr}_g(h), \end{aligned}$$

and we conclude. $\square$

Theorem 5.9

Let (g, f) be a non-trivial three-dimensional compact Einstein Heterotic soliton with constant dilaton. Then $\mathbb {E}_{g,f}=0$.

Proof

Fix a non-trivial three-dimensional compact Einstein Heterotic soliton (g, f) with constant dilaton and a pair $(h,\sigma )\in \mathbb {E}_{g,f}$. Denote by $\textrm{d}^g :\Omega ^1(M,TM) \rightarrow \Omega ^2(M,TM)$ the exterior covariant derivative defined by the Levi-Civita connection of (M, g) on the bundle of one-forms taking values in TM. Denote by $\textrm{d}^{g*} :\Omega ^2(M,TM) \rightarrow \Omega ^1(M,TM)$ its formal adjoint. Our starting point is the celebrated Weitzenböck formula:

$$\begin{aligned} (\textrm{d}^g\textrm{d}^{g*} + \textrm{d}^{g*}\textrm{d}^{g})(\alpha \otimes v) = \nabla ^{g*}\nabla ^g(\alpha \otimes v) + q^g(\alpha \otimes v), \end{aligned}$$

where $\alpha \in \Omega ^1(M)$, $v\in \mathfrak {X}(M)$ and $q_g$ is the linear operator given explicitly by:

$$\begin{aligned} q^g(\alpha \otimes v) = \textrm{Ric}^g(\alpha )\otimes v + e_i\otimes \mathcal {R}^g_{\alpha ,e_i}v, \end{aligned}$$

in terms of an orthonormal basis $(e_i)$. We compute:

$$\begin{aligned} q^g(h) = q^g(h(e_k)\otimes e_k) = \textrm{Ric}^g(h(e_k)\otimes e_k + e_i\otimes \mathcal {R}^g_{e_k,e_i} h(e_k) = -\frac{f^2}{4} h_0, \end{aligned}$$

where $h_0$ is the trace-free part of h and we have used that:

$$\begin{aligned} \textrm{Ric}^g = -\frac{f^2}{6} g\,, \qquad \mathcal {R}^g_{v_1,v_2} = \frac{f^2}{12} v_1\wedge v_2\,, \quad v_1,v_2\in TM. \end{aligned}$$

We obtain:

$$\begin{aligned} \textrm{d}^{g*}\textrm{d}^g h = \nabla ^{g*}\nabla ^g h - \frac{f^2}{4} h_0 = -\frac{f^2}{12} h + \frac{13 f^2}{12} \textrm{Tr}_g(h) g + \frac{13}{6} \nabla ^g \textrm{d}\textrm{Tr}_g(h), \end{aligned}$$

upon use of Lemma 5.8. We apply now $\textrm{d}^{g*}:\Omega ^1(M,TM)\rightarrow \mathfrak {X}(M)$ to both sides of the previous equation. Observing that the result of applying $\textrm{d}^{g*}$ to each monomial in the previous equation is a constant times $\textrm{Tr}_g(h)$ and that the combination of all terms does not vanish we conclude:

$$\begin{aligned} \textrm{d}\textrm{Tr}_g(h) = 0, \end{aligned}$$

which in turn implies $\textrm{Tr}_g(h) = 0$ since $\Delta _g \textrm{Tr}_g(h) = f^2 \textrm{Tr}_g(h)$ and $f\ne 0$ by assumption. Hence, by Lemma 5.6 we also have $\sigma = 0$ and by Lemma 5.8 we finally end up with:

$$\begin{aligned} \textrm{d}^{g*}\textrm{d}^g h = -\frac{f^2}{12} h. \end{aligned}$$

This immediately implies $h=0$ since the differential operator of the left hand side of the equation is positive. $\square$

The existence of a slice for the action of the diffeomorphism group around (g, f) together with the previous theorem immediately implies the following result.

Corollary 5.10

Three-dimensional compact Einstein Heterotic solitons with constant dilaton are rigid.

Remark 5.11

We are not aware of any rigidity result for a compact solution of a supergravity theory, especially in the non-supersymmetric case.

Appendix A: Riemannian Curvature in Three Dimensions

Let (M, g) be a Riemannian three-manifold. The Riemannian tensor $\mathcal {R}^g$ of g can be written as follows in terms of its Ricci tensor $\textrm{Ric}^g$:

$$\begin{aligned} \mathcal {R}^g_{v_1,v_2} = \frac{s_g}{2} v_1\wedge v_2 + v_2\wedge \textrm{Ric}^g(v_1) + \textrm{Ric}^g(v_2)\wedge v_1, \qquad \forall v_1,v_2 \in TM, \end{aligned}$$

(A.1)

where $s_g$ is the scalar curvature of g. In particular, using the previous formula it is easy to show that the contraction $\mathcal {R}^g\circ _g \mathcal {R}^g$, is given by:

$$\begin{aligned} \mathcal {R}^g\circ _g \mathcal {R}^g = - \textrm{Ric}^g\circ \textrm{Ric}^g + s_g \textrm{Ric}^g + \bigg (\vert \textrm{Ric}^g\vert ^2_g - \frac{s_g^2}{2}\bigg ) g, \end{aligned}$$

(A.2)

where we have defined:

$$\begin{aligned} \textrm{Ric}^g\circ _g \textrm{Ric}^g(v_1,v_2):= g(\textrm{Ric}^g(v_1),\textrm{Ric}^g(v_2))\,, \qquad \forall v_1, v_2\in TM. \end{aligned}$$

In particular, the norm of $\textrm{R}^g$ is given by:

$$\begin{aligned} \vert \mathcal {R}^g \vert _g^2 = \frac{1}{2} \textrm{Tr}_g(\mathcal {R}^g\circ _g \mathcal {R}^g) = \vert \textrm{Ric}^g \vert _g^2 - \frac{1}{4} s_g^2. \end{aligned}$$

Using the previous formulae, we can obtain an explicit expression for $\mathcal {R}^{g,H} \circ _g\mathcal {R}^{g,H}$ in terms of standard curvature tensors of g and derivatives of $f = *_g H \in C^{\infty }(M)$.

Lemma A.1

Let g be a Riemannian metric on M and $H\in \Omega ^3(M)$. The following equation holds:

$$\begin{aligned} \mathcal {R}^{g,H} \circ _g \mathcal {R}^{g,H}{} & {} \!=\!\!-\! \textrm{Ric}^g \circ \textrm{Ric}^g \!+\! ( s_g \!-\! \frac{f^2}{2}) \textrm{Ric}^g\!+\!( \vert \textrm{Ric}^g \vert _g^2\!-\!\frac{s_g^2}{2} \!+ \!\frac{1}{4}\vert \textrm{d}f \vert _g^2 \!+\! \frac{1}{8} f^4) g \nonumber \\{} & {} \quad + \frac{1}{2}[*_g\textrm{d}f, \textrm{Ric}^g] +\frac{1}{4} \textrm{d}f \otimes \textrm{d}f, \end{aligned}$$

(A.3)

where we have set $f:= *_g H$.

Remark A.2

Here $[*_g\textrm{d}f, \textrm{Ric}^g] \in \Gamma (\textrm{End}(TM))$ denotes the standard commutator of endomorphisms, understanding both $*_g\textrm{d}f$ and $\textrm{Ric}^g$ as endomorphisms of TM by means of the musical isomorphisms determined by g.

Proof

Since $H=f \nu _g$, we have:

$$\begin{aligned} \nabla _{v_1}^{g,H} v_2=\nabla _{v_1}^g v_2-\frac{f}{2} *_g (v_1^\flat \wedge v_2^\flat )^{\sharp _g} \,, \qquad v_1,v_2 \in \mathfrak {X}(M). \end{aligned}$$

Using the previous formula we compute:

$$\begin{aligned} \mathcal {R}^{g,H}_{v_1,v_2} =\mathcal {R}^g_{v_1,v_2} -\frac{1}{2} (v_1(f) *_g v_2-v_2(f) *_g v_1) + \frac{f^2}{4}v_1\wedge v_2 \,, \qquad v_1,v_2 \in \mathfrak {X}(M). \end{aligned}$$

Substituting this expression into $\mathcal {R}^{g,H} \circ \mathcal {R}^{g,H}$ and expanding we obtain (A.3) and we conclude. $\square$

Using the previous lemma we can compute one-half of the trace of $\mathcal {R}^{g,H} \circ _g \mathcal {R}^{g,H}$, which corresponds to twice the norm of $\mathcal {R}^{g,H}$, obtaining:

$$\begin{aligned} \vert \mathcal {R}^{g,H}\vert ^2_{g} = \frac{1}{2} \textrm{Tr}_g (\mathcal {R}^{g,H} \circ _g \mathcal {R}^{g,H})= \vert \textrm{Ric}^g\vert ^2_g - \frac{1}{4} s_g^2 - \frac{1}{4} f^2 s_g + \frac{1}{2} \vert \textrm{d}f\vert ^2_g + \frac{3}{16} f^4. \end{aligned}$$

This formula is tacitly used in several computations throughout the paper.