Pair-approximation analyses of evolutionarily stable strategies for flowering time in clonal monocarpic plants

Abstract

Clonal plants can employ two distinct reproductive strategies, clonal and sexual reproduction. Bamboos are monocarpic clonal plants that flower after a long-term clonal reproduction, and then die after seed production. To explore the effect of spatial structure formed through clonal reproduction on the evolution of such long flowering intervals, we developed a model for population growth of clonal plants on a regular lattice. We applied the pair-approximation that enables us to obtain a closed form of the dynamics. We derived the condition that an infinitely long flowering interval (a pure clonal strategy) or annual flowering strategy became an evolutionarily stable strategy. We demonstrate that localized dispersal broadens the region in which finite flowering interval evolves. Our finding highlights the importance to take into account the spatial structure on the studies of life history strategy in clonal plants.

Appendix: Derivation of population dynamics by using pair-approximation

By using the definition of local density, Eq. 1 in the main text is written as follows:

$$\begin{aligned} {p}'_\mathrm{r} =\left\{ \begin{array}{ll} f_\mathrm{c} \left( {p_\mathrm{r} ,q_{r/r} } \right) = \left( {1-\delta } \right) p_\mathrm{r} +\delta p_{\mathrm{r,}} \left( 1-\exp \left[ -\alpha \left( {1-\delta } \right) q_{\mathrm{r}/\mathrm{r}} \right] \right) \\ \qquad \qquad \qquad \quad \quad +\left( {1-p_\mathrm{r} } \right) \left( 1-\exp \left[ {-\alpha \left( {1-\delta } \right) \frac{p_\mathrm{r} \left( {1-q_{\mathrm{r}/\mathrm{r}} } \right) }{1-p_\mathrm{r} }} \right] \right) &{}\quad {\hbox {if }t\hbox { mod } \tau _\mathrm{r} \ne \hbox {0}} \\ \qquad \qquad \qquad \quad \quad \left( {1-\delta } \right) p_\mathrm{r} \left( {1-\exp \left[ {-\beta \left( {\frac{4}{5}\left( {1-\delta } \right) q_{r/r} +\frac{1}{5}} \right) } \right] } \right) \\ f_\mathrm{s} \left( {p_\mathrm{r} ,q_{r/r} } \right) = +\delta p_\mathrm{r} \left( 1-\exp \left[ {-\frac{4}{5}\beta \left( {1-\delta } \right) q_{r/r} } \right] \right) &{}\quad {\hbox {otherwise}} \\ \qquad \qquad \qquad \quad \quad +\left( {1-p_\mathrm{r} } \right) \left( 1-\exp \left[ {-\frac{4}{5}\beta \left( {1-\delta } \right) \frac{p_\mathrm{r} \left( {1-q_{\mathrm{r}/\mathrm{r}} } \right) }{1-p_\mathrm{r} }} \right] \right) \end{array}\right. \end{aligned}$$

(36)

Note that we abbreviate the time t from the equation, because the time of every variable $(p_\mathrm{r} ,q_{\mathrm{r}/\mathrm{r}} )$ in the right-hand side of equality is always $t. {p}'_\mathrm{r}$ means the global density in year $t+1, p_{\mathrm{r,}t+1}$. We need to derive the dynamics of pair density for both clonal and sexual reproduction. When individuals undergo clonal reproduction $(\hbox {if }t\hbox { mod } \tau _\mathrm{r} \ne \hbox {0})$, the doublet density in the next year $({p}'_{\mathrm{rr}} =p_{\mathrm{rr,}t+1} )$ is written as follows;

$$\begin{aligned} {p}'_{\mathrm{rr}}= & {} p_{00} \left( {1-\exp \left[ {-\alpha \frac{3}{4}\left( {1-\delta } \right) q_{\mathrm{r}/00} } \right] } \right) ^{2} \nonumber \\&+\,2\delta p_{0\hbox {r}} \left( {1-\exp \left[ {-\alpha \frac{3}{4}\left( {1-\delta } \right) q_{\mathrm{r}/0\hbox {r}} } \right] } \right) \left( {1-\exp \left[ {-\alpha \frac{3}{4}\left( {1-\delta } \right) q_{\mathrm{r}/\mathrm{r0}} } \right] } \right) \nonumber \\&+\,2\left( {1-\delta } \right) p_{0\hbox {r}} \left( {1-\exp \left[ {-\alpha \left( {\frac{3}{4}\left( {1-\delta } \right) q_{\mathrm{r}/0\hbox {r}} +\frac{1}{4}} \right) } \right] } \right) \nonumber \\&+\,\delta ^{2}p_{\mathrm{rr}} \left( {1-\exp \left[ {-\alpha \frac{3}{4}\left( {1-\delta } \right) q_{\mathrm{r}/\mathrm{rr}} } \right] } \right) ^{2} \nonumber \\&+\,2\delta \left( {1-\delta } \right) p_{\mathrm{rr}} \left( {1-\exp \left[ {-\alpha \left( {\frac{3}{4}\left( {1-\delta } \right) q_{\mathrm{r}/\mathrm{rr}} +\frac{1}{4}} \right) } \right] } \right) \nonumber \\&+\,\left( {1-\delta } \right) ^{2}p_{\mathrm{rr}}. \end{aligned}$$

(37)

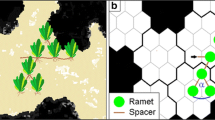
where $q_{\sigma _0 /\sigma _1 \sigma _2 } \{\sigma _0 ,\sigma _1 ,\sigma _2 =0\hbox { or r}\}$ is the conditional probability that the randomly chosen n.n. site of $\sigma _1$ site is $\sigma _0$ site, provided that another randomly chosen n.n. site of $\sigma _1$site is $\sigma _2$ site. We should proceed further to calculate the dynamics of theses conditional probabilities of a higher order by tracing the dynamics of triplet probabilities, but the dynamics would contain conditional probabilities of higher orders. Hence we adopt pair approximation to construct a closed dynamics of singlet and doublet densities by neglecting correlations beyond pairs (Matsuda et al. [12]; Harada and Iwasa [13]):

$$\begin{aligned} q_{\sigma _0 /\sigma _1 \sigma _2 } \cong q_{\sigma _0 /\sigma _1 }\quad \forall \sigma _0 ,\sigma _1 ,\sigma _2 \hbox { in }\left\{ {0,\hbox {r}} \right\} . \end{aligned}$$

(38)

Using pair approximation and the definition of conditional probability, Eq. 36 becomes:

$$\begin{aligned} {p}'_\mathrm{r} {q}'_{\mathrm{r}/\mathrm{r}}= & {} g_\mathrm{c} \left( {p_\mathrm{r} ,q_{\mathrm{r}/\mathrm{r}} } \right) =\left( {1-2p_\mathrm{r} +p_\mathrm{r} q_{\mathrm{r}/\mathrm{r}} } \right) \nonumber \\&\times \left( {1-\exp \left[ {-\alpha \frac{3}{4}\left( {1-\delta } \right) \frac{p_\mathrm{r} \left( {1-q_{\mathrm{r}/\mathrm{r}} } \right) }{1-p_\mathrm{r} }} \right] } \right) ^{2}\nonumber \\&+\,2\delta p_\mathrm{r} \left( {1-q_{\mathrm{r}/\mathrm{r}} } \right) \left( {1-\exp \left[ {-\alpha \frac{3}{4}\left( {1-\delta } \right) \frac{p_\mathrm{r} \left( {1-q_{\mathrm{r}/\mathrm{r}} } \right) }{1-p_\mathrm{r} }} \right] } \right) \nonumber \\&\times \left( {1-\exp \left[ {-\alpha \frac{3}{4}\left( {1-\delta } \right) q_{\mathrm{r}/\mathrm{r}} } \right] } \right) \nonumber \\&+\,2\left( {1-\delta } \right) p_\mathrm{r} \left( {1-q_{\mathrm{r}/\mathrm{r}} } \right) \left( {1-\exp \left[ {-\alpha \left( {\frac{3}{4}\left( {1-\delta } \right) \frac{p_\mathrm{r} \left( {1-q_{\mathrm{r}/\mathrm{r}} } \right) }{1-p_\mathrm{r} }+\frac{1}{4}} \right) } \right] } \right) \nonumber \\&+\,\delta ^{2}p_\mathrm{r} q_{\mathrm{r}/\mathrm{r}} \left( {1-\exp \left[ {-\alpha \frac{3}{4}\left( {1-\delta } \right) q_{\mathrm{r}/\mathrm{r}} } \right] } \right) ^{2}\nonumber \\&+\,2\delta \left( {1-\delta } \right) p_\mathrm{r} q_{\mathrm{r}/\mathrm{r}} \left( {1-\exp \left[ {-\alpha \left( {\frac{3}{4}\left( {1-\delta } \right) q_{\mathrm{r}/\mathrm{r}} +\frac{1}{4}} \right) } \right] } \right) \nonumber \\&+\,\left( {1-\delta } \right) ^{2}p_\mathrm{r} q_{\mathrm{r}/\mathrm{r}} \end{aligned}$$

(39)

The top of Eqs. 36 and 39 constitute a closed dynamical system of two variables, $p_\mathrm{r}$ and $q_{\mathrm{r}/\mathrm{r}}$.

When we apply the same method to the case of sexual reproduction, we get the dynamics of local density as follows:

$$\begin{aligned} {p}'_{\mathrm{rr}}= & {} {p}'_\mathrm{r} {q}'_{\mathrm{r}/\mathrm{r}} =g_\mathrm{s} \left( {p_\mathrm{r} ,q_{\mathrm{r}/\mathrm{r}} } \right) =\left( {1-2p_\mathrm{r} +p_\mathrm{r} q_{\mathrm{r}/\mathrm{r}} } \right) \nonumber \\&\times \left( {1-\exp \left[ {-\beta \frac{3}{5}\left( {1-\delta } \right) \frac{p_\mathrm{r} \left( {1-q_{\mathrm{r}/\mathrm{r}} } \right) }{1-p_\mathrm{r} }} \right] } \right) ^{2} \nonumber \\&+\,2\delta p_\mathrm{r} \left( {1-q_{\mathrm{r}/\mathrm{r}} } \right) \left( {1-\exp \left[ {-\beta \frac{3}{5}\left( {1-\delta } \right) \frac{p_\mathrm{r} \left( {1-q_{\mathrm{r}/\mathrm{r}} } \right) }{1-p_\mathrm{r} }} \right] } \right) \nonumber \\&\times \left( {1-\exp \left[ {-\beta \frac{3}{5}\left( {1-\delta } \right) q_{\mathrm{r}/\mathrm{r}} } \right] } \right) \nonumber \\&+\,2\left( {1-\delta } \right) p_\mathrm{r} \left( {1-q_{\mathrm{r}/\mathrm{r}} } \right) \left( {1-\exp \left[ {-\beta \left( {\frac{3}{5}\left( {1-\delta } \right) \frac{p_\mathrm{r} \left( {1-q_{\mathrm{r}/\mathrm{r}} } \right) }{1-p_\mathrm{r} }+\frac{1}{5}} \right) } \right] } \right) \nonumber \\&\times \left( {1-\exp \left[ {-\beta \left( {\frac{3}{5}\left( {1-\delta } \right) q_{\mathrm{r}/\mathrm{r}} +\frac{1}{5}} \right) } \right] } \right) \nonumber \\&+\,\delta ^{2}p_\mathrm{r} q_{\mathrm{r}/\mathrm{r}} \left( {1-\exp \left[ {-\beta \frac{3}{5}\left( {1-\delta } \right) q_{\mathrm{r}/\mathrm{r}} } \right] } \right) ^{2} \nonumber \\&+\,2\delta \left( {1-\delta } \right) p_\mathrm{r} q_{\mathrm{r}/\mathrm{r}} \left( {1-\exp \left[ {-\beta \left( {\frac{3}{5}\left( {1-\delta } \right) q_{\mathrm{r}/\mathrm{r}} +\frac{1}{5}} \right) } \right] } \right) ^{2} \nonumber \\&+\,\left( {1-\delta } \right) ^{2}p_\mathrm{r} q_{\mathrm{r}/\mathrm{r}} \left( {1-\exp \left[ {-\beta \left( {\frac{3}{5}\left( {1-\delta } \right) q_{\mathrm{r}/\mathrm{r}} +\frac{2}{5}} \right) } \right] } \right) ^{2} \end{aligned}$$

(40)

The bottom of Eqs. 36 and 39 also constitute a closed dynamical system of two variables. Hence the population dynamics of bamboo can be expressed as follows:

$$\begin{aligned} {p}'_\mathrm{r}= & {} \left\{ {{\begin{array}{ll} {f_\mathrm{c} \left( {p_\mathrm{r} ,q_{r/r} } \right) }&{}\quad {\hbox {if }t\hbox { mod } \tau _\mathrm{r} \ne \hbox {0}} \\ {f_\mathrm{s} \left( {p_\mathrm{r} ,q_{r/r} } \right) }&{}\quad {\hbox {otherwise}} \\ \end{array} }} \right. \end{aligned}$$

(41)

$$\begin{aligned} {q}'_{\mathrm{r}/\mathrm{r}}= & {} \left\{ {{\begin{array}{ll} {{g_\mathrm{c} \left( {p_\mathrm{r} ,q_{r/r} } \right) }/{f_\mathrm{c} \left( {p_\mathrm{r} ,q_{r/r} } \right) }}&{}\quad {\hbox {if }t\hbox { mod } \tau _\mathrm{r} \ne \hbox {0}} \\ {{g_\mathrm{s} \left( {p_\mathrm{r} ,q_{r/r} } \right) }/{f_\mathrm{s} \left( {p_\mathrm{r} ,q_{r/r} } \right) }}&{}\quad {\hbox {otherwise}} \\ \end{array} }} \right. \end{aligned}$$

(42)

Hence we can apply standard analysis to a pair of non-linear difference equation.