Modeling Antibiotic Use Strategies in Intensive Care Units: Comparing De-escalation and Continuation

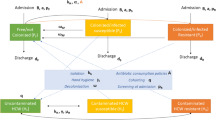
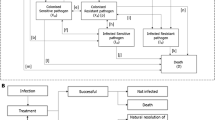
Abstract

Antimicrobial de-escalation refers to the treatment mechanism of switching from empiric antibiotics with good coverage to alternatives based on laboratory susceptibility test results, with the aim of avoiding unnecessary use of broad-spectrum antibiotics. In a previous study, we have developed multi-strain and multi-drug models in an intensive care unit setting, to evaluate the benefits and trade-offs of de-escalation in comparison with the conventional strategy called antimicrobial continuation. Our simulation results indicated that for a large portion of credible parameter combinations, de-escalation reduces the use of the empiric antibiotic but increases the probabilities of colonization and infections. In this paper, we first simplify the previous models to compare the long-term dynamical behaviors between de-escalation and continuation systems under a two-strain scenario. The analytical results coincide with our previous findings in the complex models, indicating the benefits and unintended consequences of de-escalation strategy result from the nature of this treatment mechanism, not from the complexity of the high-dimensional systems. By extending the models to three-strain scenarios, we find that de-escalation is superior than continuation in preventing outbreaks of invading strains that are resistant to empiric antibiotics. Thus decisions on antibiotic use strategies should be made specifically according to ICU conditions and intervention objectives.

Appendix

1.1 Proof of Theorem 1

Proof

Sketch of the proof: we can easily get the local stability results by analyzing the eigenvalues of the system linearized at the equilibria. The global stability results can be checked by the LaSalle’s invariant principle. When ${\mathcal {R}}_1^{\text {CT}}<1$, the Lyapunov function is defined as

$$\begin{aligned} V_1(S,X_0,X_1):=S-S^*-S^*\ln \tfrac{S}{S^*}+X_0-X_0^*-X_0^*\ln \tfrac{X_0}{X_0^*}+X_1, \end{aligned}$$

hence we can get the global stability of $(S^*,X_0^*,0)$.

For ${\mathcal {R}}_1^{\text {CT}}>1$, a routine calculation gives us the unique resistant strain-prevalent equilibrium

$$\begin{aligned} {\bar{S}}=\tfrac{\mu }{\beta _1},\,\bar{X_0}=\tfrac{1-p}{1-\tfrac{\beta _0}{\beta _1}}\cdot \tfrac{\lambda }{\mu },\, \bar{X_1}=\tfrac{p-\tfrac{\beta _0}{\beta _1}}{1-\tfrac{\beta _0}{\beta _1}}\cdot \tfrac{\lambda }{\mu }-\tfrac{\mu }{\beta _1}, \end{aligned}$$

and we can construct the Lyapunov function

$$\begin{aligned} V_2(S, X_0, X_1):= S-{\bar{S}}-{\bar{S}}\ln \tfrac{S}{{\bar{S}}}+X_0-\bar{X_0}-\bar{X_0}\ln \tfrac{X_0}{\bar{X_0}}+X_1-\bar{X_1}-\bar{X_1}\ln \tfrac{X_1}{\bar{X_1}}. \end{aligned}$$

to show the global stability of $({\bar{S}}, \bar{X_0}, \bar{X_1})$. $\square$

1.2 Proof of Theorem 2

Proof

First, we construct a Lyapunov function to show the global stability, we continue using the notation $X_0:=C_0+I_0$ and define $V_3: (0,+\infty )\times (0,+\infty )\times (0,+\infty )\times [0,+\infty )\rightarrow {\mathbb {R}}$ where

$$\begin{aligned} V_3(S, C_0, I_0, X_1):= S-S^*-S^*\ln \tfrac{S}{S^*}+X_0-X_0^*-X_0^*\ln \tfrac{X_0}{X_0^*}+X_1. \end{aligned}$$

Proposition 2 guarantees that the function is well-defined, taking the derivative of $V_3$ along the solution, and we have

$$\begin{aligned} \begin{aligned} \tfrac{\mathrm{d} V_3}{\mathrm{d}t}(S, C_0, I_0, X_1)=&-\tfrac{\mu +\beta _0 X_0^*}{S}(S-S^*)^2-\tfrac{\mu -\beta _0 S^*}{X_0}(X_0-X_0^*)^2\\&-X_1 (\mu -\beta _1 S^* - \beta _1 \tfrac{I_0}{X_0} X_0^*) \end{aligned} \end{aligned}$$

By the positivity of solution, we have $\tfrac{I_0}{X_0}=\tfrac{I_0}{I_0+C_0}\le 1$. Thus, the last item in the above equation can be estimated as $-X_1 (\mu -\beta _1 S^* - \beta _1 \tfrac{I_0}{X_0} X_0^*)\le -X_1 (\mu - \beta _1 S^* - \beta _1 X_0^*)=-X_1(\mu - \beta _1 \tfrac{\lambda }{\mu })\le 0$ for $\beta _1< \mu ^2/\lambda$. It is also easy to check $\mu -\beta _0 S^*\le 0$, so $\tfrac{\mathrm{d} V_3}{\mathrm{d}t}(S, C_0, I_0, X_1)\le 0$ for $\beta _1< \mu ^2/\lambda$.

Notice that $\tfrac{\mathrm{d} V_3}{\mathrm{d}t}(S, C_0, I_0, X_1)= 0$ if and only if either $\{S=S^*, X_0=X_0^*, X_1=0\}$ or $\{S=S^*,\, X_0=X_0^*, S+I_0=\tfrac{\mu }{\beta _1}\}$. Denote the largest invariant set that contains $\{S=S^*, X_0=X_0^*, X_1=0\}$ as ${\mathcal {M}}_1$. Then for any initial condition $(S(0),C_0(0), I_0(0), X_1(0)) \in {\mathcal {M}}_1$, we have the corresponding solution to system (4) satisfying ${\dot{S}}(0)=\dot{X_0}(0)={\dot{X}}_1(0)=0$ so there is no initial rate of change for the three compartments, and we should have $S(t)=S^*,\,X_0(t)=X_0^*, \,X_1(t)=0$. Therefore, ${\mathcal {M}}_1\subset \{S=S^*, X_0=X_0^*, X_1=0\}$, and hence ${\mathcal {M}}_1 = \{S=S^*, X_0=X_0^*, X_1=0\}$.

Denote the largest invariant set that contains $\{S=S^*,\, X_0=X_0^*, S+I_0=\tfrac{\mu }{\beta _1}\}$ to be ${\mathcal {M}}_2$. Then for any initial condition $(S(0),C_0(0), I_0(0), X_1(0)) \in \{S=S^*,\, X_0=X_0^*, S+I_0=\tfrac{\mu }{\beta _1}\}$, we have the corresponding solution to system (4) satisfying ${\dot{S}}(0)=\dot{X_0}(0)={\dot{X}}_1(0)=0$, then $S(t)=S^*,\,X_0(t)=X_0^*$, and $X_1(t)=X_1(0)$. As the population in all three compartments are constant, we have $S^*+X_0^*+X_1(0)=\tfrac{\lambda }{\mu }$, and hence $X_1(0)=0$; therefore, ${\mathcal {M}}_2\subset {\mathcal {M}}_1$.

For any initial condition $(S(0),C_0(0), I_0(0), X_1(0))$, the system (4) has a unique solution $(S(t), C_0(t), I_0(t), X_1(t))$ such that for any $\varepsilon >0$, there exists a $t_0>0$ and for all $t>t_0$, we have $|C_0(t)+I_0(t)-X_0^*|<\varepsilon$ and $|X_1(t)|<\varepsilon$. And we have the estimation

$$\begin{aligned}&\delta (X_0^*-\varepsilon )-(\varepsilon \beta _1+\delta +\tau +\mu ) I_0(t)\nonumber \\&\quad<{\dot{I}}_0(t)<\delta (X_0^*+\varepsilon )-(-\varepsilon \beta _1+\delta +\tau +\mu ) I_0(t), \end{aligned}$$

thus we have

$$\begin{aligned} \tfrac{\delta }{\varepsilon \beta _1+\delta +\tau +\mu }(X_0^*-\varepsilon )\le \lim _{t\rightarrow +\infty } I_0(t) \le \tfrac{\delta }{-\varepsilon \beta _1+\delta +\tau +\mu }(X_0^*+\varepsilon ), \end{aligned}$$

and since it is for any $\varepsilon >0$, we know that $\lim _{t \rightarrow +\infty } I_0(t) = I_0^*$, and hence $\displaystyle {\lim _{t \rightarrow +\infty } C_0(t)} = C_0^*$. $\square$

1.3 Proof of Theorem 3

Proof

System (4) can be framed as a general system of ODEs with the bifurcation parameter $\beta _1$:

$$\begin{aligned} \frac{\mathrm{d}x}{\mathrm{d}t}=f(x,\beta _1),\quad f:{\mathbb {R}}^4\times {\mathbb {R}},\,f\in C^2({\mathbb {R}}^4\times {\mathbb {R}}). \end{aligned}$$

Denote the resistant strain-free equilibrium $(S^*,C_0^*,I_0^*,0)$ as $x^*$ and we know that

$$\begin{aligned} f(x^*,\beta _1)=0\quad \text {for all}\quad \beta _1>0. \end{aligned}$$

Next, we verify the assumptions of Theorem 4.1 in Castillo-Chavez and Song (2004). Firstly, the matrix of the linearized system at $x^*$ is

$$\begin{aligned} A=D_xf(x^*,\beta _1^{\dag })= \begin{bmatrix} -\beta _0 X_0^* -\mu&-\beta _0 S^*&-\beta _0 S^*&-\beta _1^{\dag } S^*\\ \beta _0 X_0^*&\beta _0 S^* -\delta -\mu&\beta _0 S^*+\tau&0\\ 0&\delta&-(\tau +\mu )&-\beta _1^{\dag } I_0^*\\ 0&0&0&0 \end{bmatrix}, \end{aligned}$$

and 0 is a simple eigenvalue of A and all the other eigenvalues of A are negative real numbers. Next, we compute the right eigenvector $\mathbf{w}=(w_i)_{i=1}^{4}$ and have

$$\begin{aligned} w_1=\tfrac{(\mu +\delta -\beta _0 S^*)w_2-(\beta _0 S^*+\tau )w_3}{\beta _0 X_0^*},\quad \text {and}\quad w_4=\tfrac{\delta w_2 - (\mu +\tau )w_3}{\beta _1^{\dag }I_0^*}, \end{aligned}$$

where we pick

$$\begin{aligned} w_2=1-\tfrac{\beta _0 S^*+\tau }{\beta _0 X_0^*}-\tfrac{\mu +\tau }{\beta _1^{\dag }I_0^*} \quad \text {and}\quad w_3=-1-\tfrac{\mu +\delta -\beta _0 S^*}{\beta _0 X_0^*}-\tfrac{\delta }{\beta _1^{\dag }I_0^*}. \end{aligned}$$

Simplifying the expressions of $w_1$ and $w_4$, we have

$$\begin{aligned}&w_4=\tfrac{\mu +\tau +\delta }{\beta _1^{\dag } I_0^* X_0^*}\left( \tfrac{\mu }{\beta _0}+\tfrac{\lambda }{\mu }-2 S^*\right) >0,\,\,\text {by knowing that } S^*<\min \left\{ \tfrac{\mu }{\beta _0},\tfrac{\lambda }{\mu }\right\} ,\\&w_1=\left( \tfrac{\beta _0}{\beta _1^{\dag }}-1\right) \tfrac{S^*}{\beta _0 X_0^* I_0^*}(\mu +\tau +\delta ). \end{aligned}$$

Note from the Remark 1 in Castillo-Chavez and Song (2004) $w_1,w_2,w_3$ are not necessarily positive, but it is crucial to have $w_4>0$ as it corresponds to a positive perturbation of the equilibrium $x^*$ on its $X_1$ component.

Compute the left eigenvector $\mathbf{v}=(v_i)_{i=1}^4$ and we have $v_1=v_2=v_3=0,$ and $v_4=1$. We are thus able to calculate the following:

$$\begin{aligned} \begin{aligned}&a=\sum _{k,i,j=1}^{n}v_k w_i w_j \tfrac{\partial ^2 f_k}{\partial x_i \partial x_j}(x^*,\beta _1^{\dag })=2\beta _1^{\dag }w_4(w_1+w_3),\\&b=\sum _{k,i=1}^{n} v_k w_i \tfrac{\partial ^2 f_k}{\partial x_i \partial \beta _1}(x^*,\beta _1^{\dag })=\tfrac{\mu }{\beta _1^{\dag }}v_4 w_4>0. \end{aligned} \end{aligned}$$

Clearly, $w_3<0$ and if $\beta _0<\beta _1^{\dag }$, we have $w_1<0$, thus $a<0$. Otherwise, if $\beta _0\ge \beta _1^{\dag }$, we have

$$\begin{aligned} \begin{aligned} w_1+w_3&=\tfrac{(\mu +\delta -\beta _0 S^*)w_2+(\beta _0 X_0^* - \beta _0 S^* - \tau )w_3}{\beta _0 X_0^*}\\&=\tfrac{-\beta _0(\mu +\tau +\delta )(\tfrac{\mu }{\beta _0}-S^*)-\beta _0\beta _1^{\dag }X_0^*I_0^*-\beta _0 I_0^*(\beta _1^{\dag }I_0^*+\delta )-\tau I_0^*(\beta _0-\beta _1^{\dag })}{\beta _0 \beta _1^{\dag } X_0^* I_0^*}<0, \end{aligned} \end{aligned}$$

and thus $a<0$, which completes the proof. $\square$

1.4 Proof of Proposition 4

Proof

From (14), we have

$$\begin{aligned} g({\widetilde{S}})=0 \Longleftrightarrow f({\widetilde{S}})\left( {\widetilde{S}}-\tfrac{\mu }{\beta _1}\right) =\tfrac{\mu +\tau +\delta }{\beta _1}\left( {\widetilde{S}}-\tfrac{\mu }{\beta _0}\right) \left( {\widetilde{S}}-\tfrac{\mu }{\beta _1}\right) -(1-p)\tfrac{\lambda \delta }{\beta _0\beta _1}. \end{aligned}$$

Then, condition (13) is equivalent to

$$\begin{aligned} 0<{\widetilde{S}}<\min \left\{ \tfrac{\mu }{\beta _1},\tfrac{\delta +\mu }{\beta _0}\right\} \quad \text {and} \quad {\widetilde{S}}^2-\left( \tfrac{\mu }{\beta _0}+\tfrac{\mu }{\beta _1}\right) {\widetilde{S}}-(1-p)\tfrac{\lambda \delta }{\beta _0(\mu +\tau +\delta )}+\tfrac{\mu ^2}{\beta _0\beta _1}<0, \end{aligned}$$

which is equivalent to

$$\begin{aligned}&0<{\widetilde{S}}<\min \left\{ \tfrac{\mu }{\beta _1},\tfrac{\delta +\mu }{\beta _0}\right\} \quad \text {and}\\&\tfrac{1}{2}\bigl (\tfrac{\mu }{\beta _0}+\tfrac{\mu }{\beta _1}-\sqrt{(\tfrac{\mu }{\beta _0}-\tfrac{\mu }{\beta _1})^2+\tfrac{4(1-p)\lambda \delta }{\beta _0(\mu +\tau +\delta )}}\bigr )<{\widetilde{S}}\\&\qquad <\tfrac{1}{2}\bigl (\tfrac{\mu }{\beta _0}+\tfrac{\mu }{\beta _1}+\sqrt{(\tfrac{\mu }{\beta _0}-\tfrac{\mu }{\beta _1})^2+\tfrac{4(1-p)\lambda \delta }{\beta _0(\mu +\tau +\delta )}}\bigr ). \end{aligned}$$

Notice that

$$\begin{aligned}&\tfrac{1}{2}\bigl (\tfrac{\mu }{\beta _0}+\tfrac{\mu }{\beta _1}-\sqrt{(\tfrac{\mu }{\beta _0}-\tfrac{\mu }{\beta _1})^2+\tfrac{4(1-p)\lambda \delta }{\beta _0(\mu +\tau +\delta )}}\bigr )\\&\quad<\tfrac{1}{2}\bigl (\tfrac{\mu }{\beta _0}+\tfrac{\mu }{\beta _1}-|\tfrac{\mu }{\beta _0}-\tfrac{\mu }{\beta _1}|\bigr )<\min \left\{ \tfrac{\mu }{\beta _0},\tfrac{\mu }{\beta _1}\right\} , \end{aligned}$$

and

$$\begin{aligned}&\tfrac{1}{2}\bigl (\tfrac{\mu }{\beta _0}+\tfrac{\mu }{\beta _1}+\sqrt{(\tfrac{\mu }{\beta _0}-\tfrac{\mu }{\beta _1})^2+\tfrac{4(1-p)\lambda \delta }{\beta _0(\mu +\tau +\delta )}}\bigr )\\&\quad>\tfrac{1}{2}\bigl (\tfrac{\mu }{\beta _0}+\tfrac{\mu }{\beta _1}+|\tfrac{\mu }{\beta _0}-\tfrac{\mu }{\beta _1}|\bigr )>\max \left\{ \tfrac{\mu }{\beta _0},\tfrac{\mu }{\beta _1}\right\} . \end{aligned}$$

Thus, condition (13) is equivalent to condition (16). $\square$

1.5 Proof of Theorem 4

Next, we state some facts about the boundaries of region $\Gamma$ introduced in Proposition 5.

Lemma 1

The following properties of function h are defined in (17) and $S^*$ are easy to be verified.

(H.1):

$h(\beta _1)$ is a decreasing function for $\beta _1>0$, and $\displaystyle {\lim _{\beta _1\rightarrow 0^+} h(\beta _1)}=\tfrac{2\mu }{\beta _0}>S^*$;

(H.2):

$h(\beta _1)=S^*$ if and only if $\beta _1=\beta _1^{\dag }$;

(H.3):

$h(\beta _1)<0$ for $\beta _1>\tfrac{\mu ^2(\mu +\tau +\delta )}{(1-p)\lambda \delta }$;

(H.4):

$S^*<\tfrac{\mu +\delta }{\beta _0}$;

(H.5):

$\tfrac{\mu +\delta }{\beta _0}<\tfrac{\mu }{\beta _1}$ if and only if $\beta _1<\tfrac{\mu \beta _0}{\mu +\delta }$.

With the above information, the area $\Gamma$ is illustrated as the shaded areas in Fig. 2. We will need the following Lemma to show the existence of the resistant strain-prevalent equilibria.

Lemma 2

In the following statements, we begin to regard the function g(S) introduced in (9) with coefficients defined in (10) as a function of two variables, $g(S,\beta _1)$. The following facts about $g(S,\beta _1)$ are true.

(G.1):

$g(h(\beta _1),\beta _1)<0$ for $\beta _1>\beta _1^{\dag }$, and $g(h(\beta _1),\beta _1)=0$ when $\beta _1=\beta _1^{\dag }$ and $h(\beta _1^{\dag })=S^*$;

(G.2):

$g(S^*,\beta _1)=0$ if and only if $\beta _1=\beta _1^{\dag }$ or $\beta _1=\beta _0$, $g(S^*,\beta _1)<0$ only when $\beta _1$ lies in between the two roots, otherwise $g(S^*,\beta _1)>0$;

(G.3):

$g(\tfrac{\mu }{\beta _1},\beta _1)>0$ for all $\beta _1>0$;

(G.4):

$g(0,\beta _1)<0$ for all $\beta _1>0$.

(G.5):

$g(\tfrac{\mu +\delta }{\beta _0},\beta _1)=0$ if and only if $\beta _1=\beta _0$ or $\beta _1=\tfrac{\mu (\mu +\delta +\tau )\beta _0}{(\mu +\delta )(\mu +\delta +\tau )-(1-p)\beta _0\lambda }$.

(G.6):

$\tfrac{\mu }{\beta _0}>\tfrac{\lambda }{\mu }$ implies $\beta _1^{\dag }>\beta _0$, hence $\beta _1^{\dag }<\beta _0$ implies $\tfrac{\mu }{\beta _0}\le \tfrac{\lambda }{\mu }$.

(G.7):

$g(S,\beta _1^{\dag })=0$ has $S^*$ as one root, and has no root in $(S^*,\min \{\tfrac{\mu +\delta }{\beta _0},\tfrac{\mu }{\beta _1^{\dag }}\})$ when $\beta _1^{\dag }<\beta _0$.

Proof

$(G.3){-}(G.5)$ can be checked either algebraically by hand or symbolically by software Wolfram Mathematica, and we will show the proofs of the other facts.

• Proof of (G.1) We first locate the solution $\beta _1$ of $g(h(\beta _1),\beta _1)=0$. From the proof of Proposition 4, we know that $S=h(\beta _1)$ is a root of the following quadratic equation

  $$\begin{aligned} \tfrac{\mu +\tau +\delta }{\beta _1}(S-\tfrac{\mu }{\beta _0})(S-\tfrac{\mu }{\beta _1})-(1-p)\tfrac{\lambda \delta }{\beta _0\beta _1}=0, \end{aligned}$$

  hence by (14), $g(h(\beta _1),\beta _1)=f(h(\beta _1),\beta _1)(h(\beta _1)-\tfrac{\mu }{\beta _1})$. Then $g(h(\beta _1),\beta _1)=0$ if and only if $f(h(\beta _1),\beta _1)=0$ since $h(\beta _1)\ne \tfrac{\mu }{\beta _1}$ for any $\beta _1>0$. Denote the equilibrium we look for as $(h(\beta _1),I_0(\beta _1),C_0(\beta _1),X_1(\beta _1))$, from (11)–(12), we have $f(h(\beta _1),\beta _1)=0$ if and only if $C_0(\beta _1)=\tfrac{\lambda }{\mu }-\tfrac{\mu }{\beta _1}$ and $X_1(\beta _1)=0$. Thus, we are looking for an equilibrium with its $X_1$ component being 0. An easy calculation shows that we have either $h(\beta _1)=S_+^*$ (where $S_+^*>S^*$) or $h(\beta _1)=S^*$. As $h(\beta _1)$ is a strictly decreasing function, the solution to $h(\beta _1)=S_+^*>S^*$ is strictly less than $\beta _1^{\dag }$. By (H.2) in Lemma 1, $h(\beta _1)=S^*$ yields $\beta _1=\beta _1^{\dag }$. That is, there is no $\beta _1>\beta _1^{\dag }$ such that $g(h(\beta _1),\beta _1)=0$.

  Next we determine the sign of $g(h(\beta _1),\beta _1)$. Observe that $f(h(\beta _1),\beta _1)$ is a continuous function about $\beta _1>0$, then by the intermediate value theorem, $f(h(\beta _1),\beta _1)$ will not change its sign for $\beta _1>\beta _1^{\dag }$. Therefore, in order to know the sign of $f(h(\beta _1),\beta _1)$, we only need to test it at a specific $\beta _1$ value, which we choose to be $\tfrac{\mu ^2(\mu +\tau +\delta )}{(1-p)\lambda \delta }$ and $h(\tfrac{\mu ^2(\mu +\tau +\delta )}{(1-p)\lambda \delta })=0$. An easy calculation yields $f(0,\tfrac{\mu ^2(\mu +\tau +\delta )}{(1-p)\lambda \delta })=\tfrac{p\lambda }{\beta _0}(\tfrac{\delta }{\mu }+1)>0$. Also for all $\beta _1>\beta _1^{\dag }$ we have $h(\beta _1)<\tfrac{\mu }{\beta _1}$, hence $g(h(\beta _1),\beta _1)=f(h(\beta _1),\beta _1)(h(\beta _1)-\tfrac{\mu }{\beta _1})<0$.

• Proof of (G.2) By (10), $g(S^*,\beta _1)$ can be seen as a quadratic function about $\tfrac{\mu }{\beta _1}$ with positive coefficient of the second-order term, it is easy to check that $\tfrac{\mu }{\beta _0}$ and $\tfrac{\mu }{\beta _1^{\dag }}$ are the two roots for $g(S^*,\beta _1)=0$, we therefore complete the proof.

• Proof of (G.6) Assume $\tfrac{\mu }{\beta _0}>\tfrac{\lambda }{\mu }$, notice that $S^*<\min \{\tfrac{\mu }{\beta _0},\tfrac{\lambda }{\mu }\}$, then

  $$\begin{aligned} \tfrac{\mu }{\beta _1^{\dag }}=\tfrac{\delta }{\mu +\tau +\delta }\tfrac{\lambda }{\mu }+\tfrac{\mu +\tau }{\mu +\tau +\delta }S^*<\tfrac{\mu }{\beta _0} \end{aligned}$$

  implies $\beta _1^{\dag }>\beta _0$.

• Proof of (G.7) When $\beta _1=\beta _1^{\dag }$ we have $\tfrac{\mu }{\beta _1^{\dag }}=\tfrac{\delta }{\mu +\tau +\delta }\tfrac{\lambda }{\mu }+\tfrac{\mu +\tau }{\mu +\tau +\delta }S^*$ and rewrite (15) as

  $$\begin{aligned} g(S,\beta _1^{\dag })= & {} \left( S-\tfrac{\mu }{\beta _1^{\dag }}\right) \bigl [S^2-(\tfrac{\lambda }{\mu }-\tfrac{\tau }{\beta _0}+\tfrac{\lambda \delta }{\mu ^2}+\tfrac{\mu +\tau }{\mu }S^*)S+\tfrac{p\lambda }{\beta _0}+\tfrac{\lambda \delta }{\mu \beta _0}\bigr ]\\&+(1-p)\tfrac{\lambda \delta }{\beta _0\beta _1^{\dag }}. \end{aligned}$$

  Then, the roots of $g(S,\beta _1^{\dag })=0$ can be obtained by investigating the intersections between the third-order polynomial $y=P(S):=(S-\tfrac{\mu }{\beta _1^{\dag }})\bigl [S^2-(\tfrac{\lambda }{\mu }-\tfrac{\tau }{\beta _0}+\tfrac{\lambda \delta }{\mu ^2}+\tfrac{\mu +\tau }{\mu }S^*)S+\tfrac{p\lambda }{\beta _0}+\tfrac{\lambda \delta }{\mu \beta _0}\bigr ]$ and the horizontal line $y=-(1-p)\tfrac{\lambda \delta }{\beta _0\beta _1^{\dag }}$.

  Next we look at the roots of the quadratic equation $S^2-(\tfrac{\lambda }{\mu }-\tfrac{\tau }{\beta _0}+\tfrac{\lambda \delta }{\mu ^2}+\tfrac{\mu +\tau }{\mu }S^*)S+\tfrac{p\lambda }{\beta _0}+\tfrac{\lambda \delta }{\mu \beta _0}$. The condition of $\beta _1^{\dag }<\beta _0$ is equivalent to

  $$\begin{aligned} \tfrac{\mu }{\beta _1^{\dag }}=\tfrac{\delta }{\mu +\tau +\delta }\tfrac{\lambda }{\mu }+\tfrac{\mu +\tau }{\mu +\tau +\delta }S^*>\tfrac{\mu }{\beta _0} \end{aligned}$$

  and equivalent to

  $$\begin{aligned} S^*>\tfrac{\mu }{\beta _0}-\tfrac{\delta }{\mu +\tau }(\tfrac{\lambda }{\mu }-\tfrac{\mu }{\beta _0}), \end{aligned}$$

  then we can estimate

  $$\begin{aligned} \tfrac{\lambda }{\mu }-\tfrac{\tau }{\beta _0}+\tfrac{\lambda \delta }{\mu ^2}+\tfrac{\mu +\tau }{\mu }S^*>\tfrac{\delta +\mu }{\beta _0}+\tfrac{\lambda }{\mu }. \end{aligned}$$

  Now, we check the determinant of the quadratic equation

  $$\begin{aligned} \Delta =\left( \tfrac{\lambda }{\mu }-\tfrac{\tau }{\beta _0}+\tfrac{\lambda \delta }{\mu ^2}+\tfrac{\mu +\tau }{\mu }S^*\right) ^2 -4\tfrac{p\lambda }{\beta _0}-4\tfrac{\lambda \delta }{\mu \beta _0}>\left( \tfrac{\mu +\delta }{\beta _0}-\tfrac{\lambda }{\mu }\right) ^2. \end{aligned}$$

  Thus, the quadratic equation has two real roots with the bigger one

  $$\begin{aligned} x_1>\max \{\tfrac{\mu +\delta }{\beta _0},\tfrac{\lambda }{\mu }\}, \end{aligned}$$

  it is easy to see that $\tfrac{\mu }{\beta _1^{\dag }}=\tfrac{\delta }{\mu +\tau +\delta }\tfrac{\lambda }{\mu }+\tfrac{\mu +\tau }{\mu +\tau +\delta }S^*<\tfrac{\lambda }{\mu }$, so we have $x_1>\tfrac{\mu }{\beta _1^{\dag }}$. Therefore, $\tfrac{\mu }{\beta _1^{\dag }}$ is not the largest root of the third-order polynomial P(S), and the intersections between $y=P(S)$ and line $y=-(1-p)\tfrac{\lambda \delta }{\beta _0\beta _1^{\dag }}$ are illustrated in Fig. 8. In this way, we can see that $S^*$ must be the smallest root of $g(S,\beta _1^{\dag })=0$ and there is no other root lying in the interval $(S^*,\tfrac{\mu }{\beta _1^{\dag }})$, and there is no other roots lying in the even smaller interval $(S^*,\min \{\tfrac{\mu +\delta }{\beta _0},\tfrac{\mu }{\beta _1^{\dag }}\})$.

$\square$

Fig. 8

Auxiliary figure for the proof of (G.7) in Lemma 2 (Color figure online)

Proof of Theorem 4

We only need to show the existence of an ${\widetilde{S}}$ that satisfies condition (16). Proof of 1: In the case of $\beta _1^{\dag }>\beta _0$, for $\beta _1>\beta _1^{\dag }>\beta _0$, we have $\tfrac{\mu }{\beta _1}<\tfrac{\mu +\delta }{\beta _0}$; then, condition (16) is reduced to $\max \{0,h(\beta _1)\}<{\widetilde{S}}<\tfrac{\mu }{\beta _1}$. By (G.1) and (G.4) in Lemma 2, we have $g(\max \{0,h(\beta _1)\},\beta _1)<0$, and by (G.2) and (G.3) in Lemma2, we have $g(\min \{S^*,\tfrac{\mu }{\beta _1}\},\beta _1)>0$. The intermediate value theorem guarantees that $g({\widetilde{S}},\beta _1)$ has a root ${\widetilde{S}}$ in between $\max \{0,h(\beta _1)\}$ and $\min \{S^*,\tfrac{\mu }{\beta _1}\}$, and ${\widetilde{S}}<S^*$.

Proof of 2 We split the proof for the case of $\beta _1^{\dag }<\beta _0$ into the following two sub-cases.

(1) If $\tfrac{\mu }{\mu +\delta }\beta _0<\beta _1^{\dag }<\beta _0$, For $\beta _1>\beta _1^{\dag }>\tfrac{\mu }{\mu +\delta }\beta _0$, we have $\tfrac{\mu }{\beta _1}<\tfrac{\mu +\delta }{\beta _0}$; then, condition (16) is reduced to $\max \{0,h(\beta _1)\}<{\widetilde{S}}<\tfrac{\mu }{\beta _1}$.

By (G.1) and (G.4) in Lemma 2, we have $g(\max \{0,h(\beta _1)\},\beta _1)<0$, and by (G.2) and (G.3) Lemma 2, we have $g(\min \{S^*,\tfrac{\mu }{\beta _1}\})>0$ for $\beta _1\in (\beta _0,+\infty )$, then the intermediate value theorem guarantees that $g({\widetilde{S}},\beta _1)$ has a root ${\widetilde{S}}$ in between $\max \{0,h(\beta _1)\}$ and $\min \{S^*,\tfrac{\mu }{\beta _1}\}$ for $\beta _1\in (\beta _0,+\infty )$, and ${\widetilde{S}}<S^*$.

Again by (G.2) in Lemma 2, we have $g(S^*,\beta _1)<0$ for $\beta _1\in (\beta _1^{\dag },\beta _0)$, and by (G.3) in Lemma2, the intermediate value theorem guarantees that $g({\widetilde{S}},\beta _1)$ has a root ${\widetilde{S}}$ in between $S^*$ and $\tfrac{\mu }{\beta _1}$ for $\beta _1\in (\beta _1^{\dag },\beta _0)$ and clearly ${\widetilde{S}}>S^*$.

(2) If $\beta _1^{\dag }<\tfrac{\mu }{\mu +\delta }\beta _0$, we here discuss the existence of ${\widetilde{S}}$ in three intervals of $\beta _1$.

(2a) For $\beta _1\in (\beta _0,+\infty )$, we have $\tfrac{\mu }{\beta _1}<\tfrac{\mu +\delta }{\beta _0}$ and the condition (16) is reduced to $\max \{0,h(\beta _1)\}<{\widetilde{S}}<\tfrac{\mu }{\beta _1}$. Follow the same discussion as in case (1), we have the existence of ${\widetilde{S}}<S^*$.

(2b) For $\beta _1\in (\tfrac{\mu }{\mu +\delta }\beta _0,\beta _0)$, we have the condition (16) reduced to

$$\begin{aligned} \max \{0,h(\beta _1)\}<{\widetilde{S}}<\tfrac{\mu }{\beta _1}. \end{aligned}$$

By (G.2) and (G.3) in Lemma 2, we can conclude the existence of ${\widetilde{S}}>S^*$.

(2c) For $\beta _1\in (\beta _1^{\dag },\tfrac{\mu }{\mu +\delta }\beta _0)$, we have the condition (16) reduced to

$$\begin{aligned} \max \{0,h(\beta _1)\}<{\widetilde{S}}<\tfrac{\mu +\delta }{\beta _0}. \end{aligned}$$

Then in order to prove the conclusion, we only need to show that $g(\tfrac{\mu +\delta }{\beta _0},\beta _1)>0$ for $\beta _1^{\dag }\in (\beta _1^{\dag },\tfrac{\mu }{\mu +\delta }\beta _0)$. From (10), $g(\tfrac{\mu +\delta }{\beta _0},\beta _1)$ can be regarded as a quadratic function about $\tfrac{\mu }{\beta _1}$ with positive coefficient of the second-order term, thus the interval for $g(\tfrac{\mu +\delta }{\beta _0},\beta _1)>0$ is determined by the two zeros of the function which were obtained in (G.5) in Lemma 2. Firstly, if $\tfrac{\mu (\mu +\delta +\tau )\beta _0}{(\mu +\delta )(\mu +\delta +\tau )-(1-p)\beta _0\lambda }>0$, it is easy to check that $\tfrac{\mu }{\mu +\delta }\beta _0<\tfrac{\mu (\mu +\delta +\tau )\beta _0}{(\mu +\delta )(\mu +\delta +\tau )-(1-p)\beta _0\lambda }$, and $g(\tfrac{\mu +\delta }{\beta _0},\beta _1)>0$ for $\beta _1<\tfrac{\mu }{\mu +\delta }\beta _0$. Secondly, if $\tfrac{\mu (\mu +\delta +\tau )\beta _0}{(\mu +\delta )(\mu +\delta +\tau )-(1-p)\beta _0\lambda }<0$, we have $g(\tfrac{\mu +\delta }{\beta _0},\beta _1)>0$ if and only if $\tfrac{\mu }{\beta _1}>\tfrac{\mu }{\beta _0}$ or $\tfrac{\mu }{\beta _1}<\tfrac{\mu (\mu +\delta +\tau )\beta _0}{(\mu +\delta )(\mu +\delta +\tau )-(1-p)\beta _0\lambda }$ which is equivalent to $\beta _1<\beta _0$. Thus, we have $g(\tfrac{\mu +\delta }{\beta _0},\beta _1)>0$ for all $\beta _1\in (\beta _1^{\dag },\tfrac{\mu }{\mu +\delta }\beta _0)$. $\square$

1.6 Proof of Corollary 1

Proof

It is a well-known result that if the discriminant of a third-order polynomial is strictly greater than zero, then the polynomial has three distinct real roots of multiplicity 1, hence each of the real roots S of $g(S,\beta _1)=0$ is continuously dependent on $\beta _1$. As (G.3) and (G.4) in Lemma 2 guarantee the existence of a real root in $(0,\tfrac{\mu }{\beta _1})$, we denote $S^{-}(\beta _1)$ as the continuous branch that represents the smallest root in $(0,\tfrac{\mu }{\beta _1})$, and $S^{+}(\beta _1)$ as the one that represents the largest root in $(0,\tfrac{\mu }{\beta _1})$. Then, both $S^{-}(\beta _1)$ and $S^{+}(\beta _1)$ are well-defined and continuous for all $\beta _1>\beta _1^{\dag }$.

• 1. If $\beta _1^{\dag }>\beta _0$. For $\beta _1$ being sufficiently large, condition (16) is equivalent to $0<{\widetilde{S}}<\tfrac{\mu }{\beta _1}$, hence $S^+(\beta _1)$ stays in the region

  $$\begin{aligned} \Gamma _1:=\left\{ (\beta _1,S): \beta _1\ge \beta _1^{\dag },\,\max \{0,h(\beta _1)\} \le S \le \min \left\{ \tfrac{\mu }{\beta _1},S^*\right\} \right\} \end{aligned}$$

  for sufficiently large $\beta _1$. By $(G.1){-}(G.4)$ in Lemma 2 and that $S^+(\beta _1)$ is a continuous curve, $S^+(\beta _1)$ must stay in region $\Gamma _1$ and only touches and crosses the boundary of $\Gamma _1$ through the point $(\beta _1^{\dag },S^*)$. Hence, both $S^{+}(\beta _1)$ and $S^{-}(\beta _1)$ stay below $S^*$.

• 2. (2a): If $\tfrac{\mu }{\mu +\delta }\beta _0<\beta _1^{\dag }<\beta _0$. By (G.1), (G.3), (G.4), (G.7) in Lemma 2, we know that the curve $S^{+}(\beta _1)$ stays in region

  $$\begin{aligned} \Gamma _2:=\left\{ (\beta _1,S): \beta _1\ge \beta _1^{\dag },\,\max \{0,h(\beta _1)\}\le S \le \tfrac{\mu }{\beta _1}\right\} . \end{aligned}$$

  Then, the bifurcation branch only touches and crosses the boundary of $\Gamma _2$ through the point $(\beta _1^{\dag },S^*)$. Also from Theorem 4, there exists a ${\widetilde{S}} \in (S^*,\tfrac{\mu }{\beta _1})$ for $\beta _1\in (\beta _1^{\dag },\beta _0)$, so $S^{+}(\beta _1)$ must pass through the points $(\beta _1^{\dag },S^*)$ and $(\beta _0,S^*)$ and stays above $S^*$ for $\beta _1\in (\beta _1^{\dag },\beta _0)$ and for $\beta _1>\beta _0$, $S^{+}(\beta _1)<S^*$.

  (2b): If $\beta _1^{\dag }<\tfrac{\mu }{\mu +\delta }\beta _0$. From the proof of (2c) in Theorem 4, the curve $g(S,\beta _1)=0$ intersects the horizontal line $S=\tfrac{\mu +\delta }{\beta _0}$ at two points and both of them are outside of the region

  $$\begin{aligned} \Gamma _3:=\left\{ (\beta _1,S): \beta _1\ge \beta _1^{\dag },\,\max \{0,h(\beta _1)\}\le S \le \min \{\tfrac{\mu +\delta }{\beta _0},\tfrac{\mu }{\beta _1}\}\right\} . \end{aligned}$$

  By $(G.1){-}(G.4),(G.7)$ in Lemma 2, we know that the bifurcation branch $S^{+}(\beta _1)$ stays in region $\Gamma _3$, it only touches and crosses the boundary of $\Gamma _3$ through the point $(\beta _1^{\dag },S^*)$, but for $\beta _1\in (\beta _1^{\dag },\beta _0)$, we have $S^{+}(\beta _1)>S^*$ and for $\beta _1>\beta _0$, $S^{+}(\beta _1)<S^*$.$\square$

1.7 Proof of Corollary 2

Proof

If the discriminant of a third-order polynomial is strictly smaller than zero, then the polynomial has only one real root of multiplicity 1, hence ${\widetilde{S}}$ is unique and continuously dependent on $\beta _1$. From Theorem 4, we have that ${\widetilde{S}}<S^*$. $\square$

1.8 Proof of Theorem 5

We will apply Theorem 1.3.2 in Zhao (2003) to show the uniform persistence, and hence we need to formulate the problem as follows.

Consider the solution space ${\mathbb {X}}:=\{(S,I_0,C_0,X_1):S,I_0,C_0, X_1 \ge 0\},$ the interior subspace of ${\mathbb {X}}$: ${\mathbb {X}}_0:=\{(S,I_0,C_0,X_1):S,I_0,C_0, X_1 > 0\},$ and the boundary of ${\mathbb {X}}_0$ in ${\mathbb {X}}$: $\partial {\mathbb {X}}_0:={\mathbb {X}}\setminus {\mathbb {X}}_0=\{(S,I_0,C_0,X_1):S=0 \,\text {or} \,I_0=0\,\text {or}\,C_0=0\,\text {or}\, X_1 = 0\}.$ We denote $\Phi _t:{\mathbb {X}}\rightarrow {\mathbb {X}}$, $t\ge 0$ as the semiflow defined by the solution of system (4), and $M_{\partial }:=\{x\in \partial {\mathbb {X}}_0:\Phi _t(x)\in \partial {\mathbb {X}}_0,\,t\ge 0\}.$ Denote d(x, y) as the Euclidean distance between two points $x,y\in {\mathbb {R}}^4$, and $d(x,E):=\inf \{d(x,y):y\in E\}$ as the distance between a point x and a set $E\subseteq {\mathbb {R}}^4$. As ${\mathbb {X}}_0$ is positively invariant, $p(x):=d(x,\partial {\mathbb {X}}_0)$ can be seen as a generalized distance function for $\Phi$.

Further, we denote the baseline system with only strain 0 as

$$\begin{aligned}&{\dot{S}}=p\lambda -\beta _0 (C_0+I_0) S -\mu S,\nonumber \\&\dot{C_0}=(1-p)\lambda +\beta _0 (C_0+I_0) S +\tau I_0 - (\delta +\mu ) C_0,\\&\dot{I_0}=\delta C_0 - (\tau +\mu )I_0.\nonumber \end{aligned}$$

(20)

Lemma 3

$M_{\partial }=\{(S,I_0,C_0,X_1):X_1=0\}\cap \partial {\mathbb {X}}_0$.

Proof

If $x\in \{(S,I_0,C_0,X_1):X_1=0\}\cap \partial {\mathbb {X}}_0$, then $\Phi _t(x)$ is the solution to system (20) and $\Phi _t(x)\in \{(S,I_0,C_0,X_1):X_1=0\}\cap \partial {\mathbb {X}}_0\subseteq M_{\partial }$; hence, $\{(S,I_0,C_0,X_1):X_1=0\}\cap \partial {\mathbb {X}}_0\subseteq M_{\partial }.$ For any $x\in M_{\partial }$, suppose for contradiction that $x\in \{(S,I_0,C_0,X_1):X_1>0\}\cap \partial {\mathbb {X}}_0$; then, Proposition 2 implies $\Phi _t(x)\in \{(S,I_0,C_0,X_1):S,I_0,C_0,X_1>0\}\not \subseteq \partial {\mathbb {X}}_0$. Therefore, we have $x\in \{(S,I_0,C_0,X_1):X_1=0\}\cap \partial {\mathbb {X}}_0$. $\square$

Lemma 4

$\{(S^*,I_0^*,C_0^*,0)\}$ is isolated in ${\mathbb {X}}$ for $\beta _1>\beta _1^{\dag }$.

Proof

Choose $\varepsilon =\bigl (\beta _1(S^*+I_0^*)-\mu \bigr )/3>0$, denote ${\mathcal {B}}_0$ as the ball centered at $(S^*,I_0^*,C_0^*,0)$ with radius $\varepsilon$, and denote the maximal invariant set in ${\mathcal {B}}_0$ as M. For any point $x\in {\mathcal {B}}_0\setminus \{(S^*,I_0^*,C_0^*,0)\}$ and $\Phi _t(x)\in M\subseteq {\mathcal {B}}_0$ for all $t>0$, denote $(S(t),I_0(t),C_0(t),X_1(t)):=\Phi _t(x)$, then we have $|S(t)-S^*|<\varepsilon$ and $|I_0(t)-I_0^*|<\varepsilon$ for all $t>0$. However, from the last equation of system (4), we have $\dot{X_1}(t)=[\beta _1(S(t)+I_0(t))-\mu ]X_1(t)>[\beta _1(S^*+I_0^*)-2\varepsilon _0-\mu ]X_1(t)=\varepsilon X_1(t)$ for all $t>0$, then $\dot{X_1}(t)>\varepsilon _1 X_1(t)$ implies $\lim \limits _{t\rightarrow +\infty } X(t)=+\infty$ which leads to a contradiction. Therefore, the maximal invariant set in ${\mathcal {B}}_0$ is the set that contains only the equilibrium $\{(S^*,I_0^*,C_0^*,0)\}$. $\square$

Proof of Theorem 5

Apply Theorem 1.3.2 in Zhao (2003) to show the uniform persistence. By Proposition 2, ${\mathbb {X}}_0$ is positively invariant for the semiflow $\Phi _t$ generated by the solution to system (4), and $\Phi _t$ is compact and point dissipative, hence there is a global attractor for $\Phi _t$.

Let $\{(S^*,I_0^*,C_0^*,0)\}$ be the finite sequence that only consists of one set, which is obviously disjoint, compact, and from Lemma 4 it is an isolated invariant set in $\partial {\mathbb {X}}_0$. Next, we check with the following properties.

(a):

From Lemma 3, for any $x\in M_{\partial }$ we know that $\Phi _t(x)$ is the solution to system (20) and by our analysis of the baseline system, we have $\omega (x)=\{(S^*,I_0^*,C_0^*,0)\}$.

(b):

There is apparently no subset of $\{(S^*,I_0^*,C_0^*,0)\}$ that forms a cycle.

(c):

$\{(S^*,I_0^*,C_0^*,0)\}$ is isolated in ${\mathbb {X}}$ from Lemma 4.

(d):

As stated before, we define $p(x):=d(x,\partial {\mathbb {X}}_0)$, we need to show that for any $x\in {\mathbb {X}}\setminus \partial {\mathbb {X}}_0$, $\lim \limits _{t\rightarrow +\infty } d(\Phi _t(x),(S^*,I_0^*,C_0^*,0))\ne 0$, and similar argument as the proof in Lemma 4 is sufficient.

It follows from Theorem 1.3.2 in Zhao (2003) that there exists $\eta >0$ such that for any $x\in {\mathbb {X}}\setminus M_{\partial }$, we have $\min \limits _{y\in \omega (x)}p(y)>\eta .$ That is,

$$\begin{aligned} \liminf \limits _{t\rightarrow +\infty }S(t)>\eta ,\quad \liminf \limits _{t\rightarrow +\infty }I_0(t)>\eta ,\quad \liminf \limits _{t\rightarrow +\infty }C_0(t)>\eta , \quad \liminf \limits _{t\rightarrow +\infty }X_1(t)>\eta , \end{aligned}$$

for any nonnegative initial condition $(S(0),I_0(0),C_0(0),X_1(0))$ with $X_1(0)>0$. $\square$

1.9 Proof of Theorem 6

Proof

Firstly, we compute the difference between $\beta _1^{\dag }$ and $\beta _0$:

$$\begin{aligned} \beta _1^{\dag }-\beta _0=\tfrac{\mu }{S^*+I_0^*}-\beta _0=\tfrac{\mu }{\tfrac{\lambda }{\mu }\tfrac{\delta }{\mu +\delta +\tau }+\tfrac{\mu +\tau }{\mu +\delta +\tau }S^*}-\beta _0. \end{aligned}$$

Therefore, $\beta _1^{\dag }-\beta _0$ has the same sign with the following function $d(\beta _0)$:

$$\begin{aligned} d(\beta _0):= & {} \left( \mu -\tfrac{1}{2}\mu \tfrac{\mu +\tau }{\mu +\delta +\tau }\right) -\left( \tfrac{\lambda }{\mu }\tfrac{\delta }{\mu +\delta +\tau }+\tfrac{1}{2}\tfrac{\lambda }{\mu }\tfrac{\mu +\tau }{\mu +\delta +\tau }\right) \beta _0\\&+\tfrac{1}{2}\tfrac{\mu +\tau }{\mu +\delta +\tau }\sqrt{\left( \tfrac{\lambda \beta _0}{\mu }+\mu \right) ^2-4p\lambda \beta _0}. \end{aligned}$$

Clearly, $d(0)=\mu >0$, and

$$\begin{aligned} \begin{aligned} d(\beta _0)&<\left( \mu -\tfrac{1}{2}\mu \tfrac{\mu +\tau }{\mu +\delta +\tau }\right) -\left( \tfrac{\lambda }{\mu }\tfrac{\delta }{\mu +\delta +\tau }+\tfrac{1}{2}\tfrac{\lambda }{\mu }\tfrac{\mu +\tau }{\mu +\delta +\tau }\right) \beta _0+\tfrac{1}{2}\tfrac{\mu +\tau }{\mu +\delta +\tau }\left( \tfrac{\lambda \beta _0}{\mu }+\mu \right) \\&=\mu -\tfrac{\lambda }{\mu }\tfrac{\delta }{\mu +\delta +\tau }\beta _0 \rightarrow -\infty \quad \text {as}\quad \beta _0\rightarrow +\infty , \end{aligned} \end{aligned}$$

thus $d(\beta _0)<0$ for $\beta _0$ being sufficiently large. Since $d(\beta _0)$ is a continuous function, there exists at least one intersection between its curve and the positive branch of the $\beta _0$ axis. Observe that $d(\beta _0)=0$ has at most two real roots; hence, we can conclude that there exists a unique positive solution to $d(\beta _0)=0$, and we denote it as $\beta _0^*$. So $d(\beta _0)>0$ on $(0,\beta _0^*)$ and $d(\beta _0)<0$ on $(\beta _0^*,+\infty )$, which completes the proof. $\square$