1 Introduction

Estimating the ultimate capacity of a concrete structure is essential to determining appropriate safety margins. Changes in regulations combined with the objective of building sustainable structures have led engineers to develop efficient modeling tools that remain easy to use. The model presented in this paper has been created for such a purpose.

Concrete is considered as brittle in tension and more ductile under compressive loading. As opposed to uniaxial tension, under which just a single crack propagates, compression caused by the presence of heterogeneities (aggregates surrounded by a cement matrix) produces transverse tensile strains that generate mesoscopic cracks nucleating perpendicularly to the direction of extension. These mesoscopic cracks then coalesce until reaching the point of complete rupture. A pure mode I (extension) is thus considered for the purpose of describing behavior in both tension and compression. This situation can be extended to multiaxial loading at low and moderate confinement that allows for extension in at least one direction. When the material is highly confined, hydrostatic pressure serves to compact the porous cement matrix and shear favors mode II.

Within this framework, it has been shown (Mazars [1]) that two distinct damage modes essentially need to be considered:

  • the extension allowed (EA) domain: uni-, bi- or triaxial situations allowing for extension (\(\varepsilon_{i}\) > 0) in at least one direction and, accordingly, for a local cracking (mode I);

  • the no extension allowed (NEA) domain: a triaxial situation at high confinement generating both the collapse of the cement porous matrix, as a result of the spherical part of the stress tensor, and shear cracking (mode II) due to the deviatoric part.

In the framework of continuum media, to simulate concrete behavior, either plasticity (Ottosen [2], Dragon et al. [3]), fracture-based approaches (Bazant [4], Carpinteri [5]), damage models (Mazars [1], Mazars et al. [6], Simo et al. [7], Jirasek [8]) or a plastic-damage model (Lee and Fenves [9], Jason et al. [10]) is used. Depending on the specific case, one or the other approach may be suitable for certain situations (whether classical or not) found in common structures for conventional loads.

For severe loadings relative to natural or technological hazards (e.g., earthquakes, blasts, impacts), additional aspects must be taken into consideration, namely: the dynamic and cyclic nature of the loading and, for local impacts, the high confinement pressure. Some models provide a description of the cyclic behavior (la Borderie et al. [11], Halm et al. [12], Richard et al. [13]). Very few models however are capable of simulating loading with both confinement and strain rate effects (Pontiroli et al. [14], Gatuingt et al. [15]), though their use often remains complex.

This paper will present a strategy for modeling these types of behavior, in emphasizing efficiency and simplicity. To achieve this objective, a damage model provides good candidate strategies. One of the first models created within such a framework and specifically intended for concrete is Mazars’ damage model [1]. Efficient yet limited to “classical” monotonic loadings, this new proposal, called the “μ model” (μ for Mazars Unilateral), was developed as part of the thermodynamics of irreversible processes (Lemaitre et al. [16]) and has shown itself capable of describing a very broad range of nonlinear behavior (monotonic, cyclic, dynamic, etc.).

2 Theoretical aspects

2.1 Underlying assumptions

The main objective herein is to build as complete and simple a model as possible, which implies formulating the set of main assumptions listed below:

  • Concrete behavior is considered as the combination of elasticity and damage;

  • The damage description is assumed to be isotropic and directly affects the stiffness evolution of the material. Let \(\underline{\underline{{\underline{\underline{\Lambda }} }}}\) be the stiffness matrix of the original material, then the matrix for the damaged material is given by:

    $$\underline{\underline{{\underline{\underline{\Lambda }} }}}_{d} = \underline{\underline{{\underline{\underline{\Lambda }} }}} (1 - d)$$
    (1)

  • As opposed to classical damage models, d denotes the effective damage. Classically speaking, damage is a variable that describes the microcracking state of the material (Lemaitre and Chaboche [16]). Moreover, d describes the effect of damage on the stiffness activated by loading. In a cracked structure, d must then be able to describe the effects of crack opening and closure (i.e., unilateral effects).

  • Two principal damage modes are considered cracking (due to tension) and crushing (due to compression), to be subsequently associated with two thermodynamic variables Y t and Y c, which characterize the extreme loading state reached in the tensile part and compressive part, respectively, of the strain space.

2.2 Main concepts

In this context, the Helmotz free energy can be written as:

$$\rho \varPsi = \frac{1}{2}\underline{\underline{{\underline{\underline{\Lambda }} }}} (1 - d):\underline{\underline{\varepsilon }} :\underline{\underline{\varepsilon }}$$
(2)

with

$$d = f(\mathop Y\nolimits_{\text{t}} ,\mathop Y\nolimits_{\text{c}} )$$
(3)

The state laws then allow defining:

$$\underline{\underline{\sigma }} = \rho \frac{\partial \varPsi }{{\partial \underline{\underline{\varepsilon }} }} = \underline{\underline{{\underline{\underline{\Lambda }} }}} (1 - d):\varepsilon$$
(4)

According to thermodynamic rules, the energy ratio dissipated during the damage process must be non-negative and moreover respects the Clausius–Duhem inequality:

$$\underline{\underline{\sigma }} :\mathop \varepsilon \limits^{^\circ } - \rho \mathop \varPsi \limits^{^\circ } \ge 0\,\qquad(\mathop x\limits^{^\circ }=\frac{{\text{d}}{x}}{\text{d}t})$$
(5)

Combining (3), (4) and (5) yields:

$$- \rho \frac{\partial \varPsi }{{\partial \mathop Y\nolimits_{\text{t}} }}\mathop {\mathop Y\nolimits_{\text{t}} }\limits^{^\circ } - \rho \frac{\partial \varPsi }{{\partial \mathop Y\nolimits_{\text{c}} }}\mathop {{{Y_{\text{c}} }} }\limits^{^\circ } \ge 0$$
(6)

or:

$$- \rho \frac{\partial \varPsi }{\partial d}\frac{\partial d}{{\partial \mathop Y\nolimits_{\text{t}} }}\mathop {\mathop Y\nolimits_{\text{t}} }\limits^{^\circ } - \rho \frac{\partial \varPsi }{\partial d}\frac{\partial d}{{\partial \mathop Y\nolimits_{\text{c}} }}\mathop {{{Y_{\text{c}} }} }\limits^{^\circ } \ge 0$$
(7)

\(- \frac{\partial \varPsi }{\partial d} = \frac{1}{2}\underline{\underline{{\underline{\underline{\Lambda }} }}} :\varepsilon :\varepsilon\) is the damage energy release rate, which always remains positive; hence, the Clausius–Duhem inequality is verified if:

$$\frac{\partial d}{{\partial \mathop Y\nolimits_{\text{t}} }}\mathop {\mathop Y\nolimits_{\text{t}} }\limits^{^\circ } \ge 0\,\quad{\text{and}}\,\quad\frac{\partial d}{{\partial \mathop Y\nolimits_{\text{c}} }}\mathop {{{Y_{\text{c}} }} }\limits^{^\circ } \ge 0$$
(8)

2.2.1 Constitutive equations

Let’s now consider, like in the previous model (Mazars [1]), the equivalent strain concept; here we define \(\varepsilon_{\text{t}}\) and \(\varepsilon_{\text{c}}\) as the equivalent strain for cracking and crushing, respectively:

$$\mathop \varepsilon \nolimits_{\text{t}} = \frac{{\mathop I\nolimits_{\varepsilon } }}{2(1 - 2\nu )} + \frac{{\sqrt {\mathop J\nolimits_{\varepsilon } } }}{2(1 + \nu )}$$
(9)
$$\mathop \varepsilon \nolimits_{\text{c}} = \frac{{\mathop I\nolimits_{\varepsilon } }}{5(1 - 2\nu )} + \frac{{6\sqrt {\mathop J\nolimits_{\varepsilon } } }}{5(1 + \nu )}$$
(10)

\(\mathop I\nolimits_{\varepsilon } = \mathop \varepsilon \nolimits_{1} + \mathop \varepsilon \nolimits_{2} + \mathop \varepsilon \nolimits_{3}\) (first invariant of the strain tensor) and \(\mathop J\nolimits_{\varepsilon } = 0.5[(\mathop \varepsilon \nolimits_{1} - \mathop \varepsilon \nolimits_{2} )^{2} + (\mathop \varepsilon \nolimits_{2} - \mathop \varepsilon \nolimits_{3} )^{2} + (\mathop \varepsilon \nolimits_{3} - \mathop \varepsilon \nolimits_{1} )^{2} ]\) (directly linked to the second invariant of the deviatoric part of the strain tensor).

Two loading surfaces are to be associated:

$$\mathop f\nolimits_{\text{t}} = \mathop \varepsilon \nolimits_{\text{t}} - \mathop Y\nolimits_{\text{t}} \,\quad{\text{and}\quad}\,\mathop f\nolimits_{\text{c}} = \mathop \varepsilon \nolimits_{\text{c}} - \mathop Y\nolimits_{\text{c}}$$
(11)

with Y t and Y c defining the maximum values reached during the loading path:

$$\mathop Y\nolimits_{\text{t}} = Sup[\mathop \varepsilon \nolimits_{{0{\text{t}}}} ,\hbox{max} \mathop\varepsilon \nolimits_{\text{t}} ]\,\quad{\text{and}\quad}\,\mathop Y\nolimits_{\text{c}} = Sup[\mathop \varepsilon \nolimits_{{0{\text{c}}}} ,\hbox{max} \mathop\varepsilon \nolimits_{\text{c}} ]$$
(12)

\(\varepsilon_{{0{\text{t}}}}\) and \(\varepsilon_{{0{\text{c}}}}\) are the initial thresholds of \(\varepsilon_{\text{t}}\) and \(\varepsilon_{\text{c}}\) respectively.

2.2.2 Damage evolution

The effective damage d is directly correlated with the thermodynamic variables Y t and Y c through the driving variable Y:

$$Y = r\mathop Y\nolimits_{\text{t}} + (1 - r)\mathop Y\nolimits_{\text{c}}$$
(13)
$$r = \frac{{\sum {\left\langle {\mathop {\overline{\sigma } }\nolimits_{i} } \right\rangle_{ + } } }}{{\sum {\left| {\mathop {\overline{\sigma } }\nolimits_{i} } \right|} }}$$
(14)

where r is the triaxial factor (Lee and Fenves [9]), which evolves in the stress space from 0 in the stress compression domain to 1 in the stress tensile domain, \(\overline{{\underline{\underline{\sigma }} }} = \frac{{\underline{\underline{\sigma }} }}{(1 - d)} = \Lambda :\underline{\underline{\varepsilon }} :\underline{\underline{\varepsilon }}\) is the so-called “effective stress”, \(\left\langle x \right\rangle_{ + }\) is the positive part of x and |x| is the absolute value of x.

As was the case for the Mazars’ model, the damage evolution law is defined by:

$$d = 1 - \frac{{\left( {1 - A} \right)\mathop Y\nolimits_{0} }}{Y} - A\exp \left( { - B\left( {Y - \mathop Y\nolimits_{0} } \right)} \right)$$
(15)

where Y 0 is the initial threshold for Y:

$$\mathop Y\nolimits_{0} = r\mathop \varepsilon \nolimits_{0t} + \left( {1 - r} \right)\mathop \varepsilon \nolimits_{0c}$$
(16)

At this stage, it can be noticed that under the condition r = constant (radial paths), the Clausius–Duhem inequality, Eq. (8), will be verified if:

$$\frac{\partial d}{{\partial \mathop Y\nolimits_{t} }}\mathop {\mathop Y\nolimits_{t} }\limits^{^\circ } = \frac{\partial d}{\partial Y}\frac{\partial Y}{{\partial \mathop Y\nolimits_{t} }}\mathop {Y_{t} }\limits^{^\circ } = \frac{\partial d}{\partial Y}r\mathop {Y_{t} }\limits^{^\circ } \ge 0$$
(17)
$$\frac{\partial d}{{\partial \mathop Y\nolimits_{c} }}\mathop {\mathop Y\nolimits_{c} }\limits^{^\circ } = \frac{\partial d}{\partial Y}\frac{\partial Y}{{\partial \mathop Y\nolimits_{c} }}\mathop {Y_{c} }\limits^{^\circ } = \frac{\partial d}{\partial Y}(1 - r)\mathop {Y_{c} }\limits^{^\circ } \ge 0$$
(18)

\(\mathop {Y_{t} }\limits^{^\circ } ,\mathop {Y_{c} }\limits^{^\circ } ,\) r and (1−r) are always non-negative; then, (17) and (18) are verified if:

$$\frac{\partial d}{\partial Y} = (1 - A)\frac{{Y_{0} }}{{\mathop Y\nolimits^{2} }} + AB\exp ( - B(Y - \mathop Y\nolimits_{0} )) \ge 0$$
(19)

The variables A and B determine the shape of the effective damage evolution laws and subsequently the behavioral laws.

The choice of relationship for A and B addresses the following points:

  • Optimally reproducing the entire set of \(\sigma\)–\(\varepsilon\) curves for the various loading paths in the stress space;

  • For the specific case of shear, enabling reproduction of the sliding effects related to friction whenever the concrete is cracked, thanks to a residual stress.

  • Allowing for easy identification of material parameters from uniaxial experiments.

Then:

$$A = \mathop A\nolimits_{\text{t}} (2\mathop r\nolimits^{2} (1 - 2k) - r(1 - 4k)) + \mathop A\nolimits_{\text{c}} (2\mathop r\nolimits^{2} - 3r + 1)$$
(20)
$$B = \mathop r\nolimits^{{(\mathop r\nolimits^{2} - 2r + 2)}} \mathop B\nolimits_{\text{t}} + (1 - \mathop r\nolimits^{{(\mathop r\nolimits^{2} - 2r + 2)}} )\mathop B\nolimits_{\text{c}}$$
(21)

When r = 0 (compressive stress domain), A = A c and B = B c ; conversely, when r = 1 (tensile stress domain), A = A t and B = B t . A t , B t , A c , B c , are material parameters directly identified from compression tests and tension, or flexural bending tests. k is used to calibrate the asymptotic stress value at large displacement in shear: k = A (r = 0.5)/A t.

Under the previous conditions (r = constant), it is straightforward to show that \(\frac{\partial d}{\partial Y} \ge 0\) for typical values of A t, B t, A c and B c. Radial paths are the most common for classical structural loadings. For more complex loadings, r can evolve while on the given loading path. In this case, the Clausius–Duhem inequality (5) includes another term, \(\frac{\partial d}{\partial r}\mathop r\limits^{^\circ }\), and, along the same lines as above, this inequality will be verified if in addition:

$$\frac{\partial d}{\partial r}\mathop r\limits^{^\circ } \ge 0$$
(22)

During a complex loading path, the numerical verification of Eq. (22) allows ensuring the thermodynamic consistency of the solution to the problem. This step has been performed for series of loadings that include a strong variation of r (e.g., loading paths describing circles on the surface of a sphere centered at the origin of the strain space), in demonstrating that Eq. (22) is always respected for all cases treated.

2.3 Model validation

2.3.1 Calculation procedure: model responses for various loading paths

Figure 1 displays the evolution principle of the various variables along a tension–compression path; it shows, for the entire loading path, that the thermodynamic variables Y t and Y c are continuously increasing. Compared to other unilateral models, this trend is unique and highlights an irregular evolution in damage variable d given its dependence on r. In that framework, effective damage can be interpreted as the part of damage activated by local stress. In the case of prior damage created in tension (see Fig. 1 for t > t2), if during a subsequent loading the local stress acts in the crack-closing direction, then the effective damage is equal to 0 (see Fig. 1 for t3 < t < t4). If, on the contrary, the stress acts in the crack-opening direction, the effective damage remains d.

Fig. 1
figure 1

Evolution of internal variables Y t and Y c, their combination Y, and damage d, during a tension– compression loading

Full size image

The stress–strain response for such a loading is given in Fig. 2. The unilateral effect is clearly exhibited when, from tension (t = t3), the stress goes into compression (t = t5).

Fig. 2
figure 2

Tension–compression loading path exhibiting the unilateral effect (time references are in accordance with Fig. 1)

Full size image

Kupfer et al. [17] conducted a series of tests to investigate the response of plain concrete subjected to a two-dimensional loading. During these investigations, concrete plates (200 mm × 200 mm × 50 mm) were loaded until failure at prescribed ratios of \(\sigma_{1}\)/\(\sigma_{2}\), with \(\sigma_{3}\) set equal to zero. \(\sigma_{i}\) denotes the principal stresses.

The concrete specimen characteristics are listed in Table 1. Model parameters have been fitted so as to obtain the same strengths (f t, f c) under uniaxial tensile and uniaxial compressive loadings, respectively.

Table 1 Concrete characteristics, for the Kupfer tests
Full size table

Results from running the μ model have been compared with experimental results for both a tension–compression test and a bi-compression test, with \(\sigma_{1}\) < 0 and the ratio \(\sigma_{2}\)/\(\sigma_{1}\) = −0.052 and +0.52, respectively (Fig. 3). Let’s underscore that only the characteristics in Table 1 have been used to assign the model’s material parameters, thus transforming these results into a real prediction. At the top of the curve and due to loading controls, the final experimental point corresponds to collapse of the specimen.

Fig. 3
figure 3

Comparison between numerical curves and experimental points from Kupfer et al. [17]: a for a traction–compression loading with \(\sigma_{2} /\sigma_{1}\) = −0.052 (σ1 < 0), and b for a biaxial compression loading with \(\sigma_{2} /\sigma_{1}\) = 0.52 (\(\sigma_{1}\) < 0)

Full size image

In both cases, the μ model yields a very good prediction of maximum strength and quite good results for the strain evolution in various directions, except for extension, in the vicinity of the peak load. This outcome stems from the fact that the Poisson’s ratio remains constant in an isotropic formulation.

For the traction–compression test (\(\sigma_{2}\)/\(\sigma_{1}\) = −0.052; \(\sigma_{1}\) < 0), in order to show how works the unilateral effect, a second stage of the loading path has been applied: \(\sigma_{2}\)/\(\sigma_{1}\) = 0 and \(\sigma_{1}\) > 0. Figure 4 gives the response of the model for the two stages of the loading path. Figure 4b, shows that during stage I, due to the compression applied in direction 1, the tensile strength in direction 2 is less than 50 % of the uniaxial strength ft. Figure 4a shows that after stage I, the initial stiffness is recovered for direction 1 (unilateral effect) and the tensile strength is almost the same as that of the original material.

Fig. 4
figure 4

Biaxial responses of the μ model: stage I, \(\sigma_{2} /\sigma_{1}\) = −0.052 (\(\sigma_{1}\) < 0); stage II, \(\sigma_{2} /\sigma_{1}\) = 0 (\(\sigma_{1}\) > 0); a response showing that after the stage I, the stiffness and the tensile strength direction 1 are recovered (\(\sigma_{1}\), \(\varepsilon_{1}\)); b response showing that during stage I the tensile strength, in direction 2 (\(\sigma_{2}\), \(\varepsilon_{2}\)), is less than 50 % of the uniaxial tensile strength ft

Full size image

2.3.2 Failure surface

Figure 5 shows, in the plane \(\sigma_{3}\) = 0, the traces of both the surface initiation of damage (d = 0) and the failure surface (maximum stress envelope: points A and M on the uniaxial curve in Fig. 2). This same figure plots experimental data for the failure surface obtained from several biaxial tests along various loading paths, by Kupfer et al. [18] on an ordinary concrete. This model offers very good results with just a few differences near the bisector in the bi-compression area.

Fig. 5
figure 5

μ model in the plane \(\sigma_{3}\) = 0: traces of the damage initiation surface (dashed line) and of the failure surface compared to experimental results provided by Kupfer et al. [18]

Full size image

3 Applications on beams under cyclic loading

Applications covered by the μ model are mainly severe loadings on concrete structures. Among these applications, earthquakes would be an important issue: earthquakes generate nonlinear cyclic loadings on structural elements. The strain rate is small enough to be eliminated as an issue, unlike with blasts and shocks. The LMT Laboratory at ENS Cachan (France) has conducted an experimental campaign on reinforced concrete (RC) beams in order to study phenomena that play a major role in the response of RC structures during an earthquake (Ragueneau et al. [19], Crambuer et al. [20]). Phenomena such as damage evolution during increased loading, unilateral effects and energy dissipation due to cyclic loads have all been analyzed. These results will serve for the applications that follow.

3.1 Experimental program

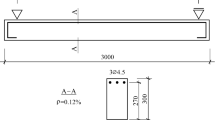
A series of rectangular RC beams were tested according to the protocol given in Fig. 6. The specimens measured 1.65 m long by 0.22 m high by 0.15 m wide. The entire campaign consisted of various longitudinal reinforcement steel ratios, though in this paper only the two specimens reinforced with four 12 mm rebar are considered (Fig. 6a). The concrete is a regular C30/37, whose characteristics are listed in Table 2.

Fig. 6
figure 6

Three-point bending test: a specimen geometry and boundary conditions, b loading programme: series of three cycles from ±1 mm to ±8 mm, c response throughout the entire loading program (beam No. 2)

Full size image
Table 2 Three point RC bend tests, experimental data and material specifications
Full size table

The RC beams are designed to be tested with a simple three-point bending set-up in the up and down vertical direction. A specific hinge device ensures a free-rotation condition at the end of the support beams. The loading path has been reproduced in Fig. 6b; it is displacement-controlled and includes sets of three cycles with gradually increasing intensity (from ±1 mm to ±8 mm). Figure 6c shows the force–displacement response of beam no. 2 for the full program, indicating: (i) the gradual decrease in stiffness due to concrete damage during the first series of cycles, and (ii) the appearance of rebar plasticity after the ±4 mm cycles and its continued prevalence beyond this stage.

3.2 Numerical modeling approach

The test specimen was modeled using Q4 (four-node) elements under a plane strain assumption and bar elements for rebar. The symmetry of the problem is used and the mesh for the half beam (711 nodes, 776 elements) is uniform over the central part of the beam. Boundary conditions are defined so as to correctly represent the experimental test (Fig. 7). The imposed displacement U y was applied on both the upper and lower parts within the central section of the beam.

Fig. 7
figure 7

Three-point bending tests, a mesh used, b elasto-plastic behaviour for steel [24]

Full size image

To avoid mesh sensitivity, the crack band approach based on the fracture energy concept has been introduced into this application (Bazant et al. [21]). The definition of G f was derived according to Planas et al. [22] and Bazant [23], meaning that in the central part of the beam (i.e., where damage and plasticity are concentrated), the size of elements is consistent with the crack band width:

$$h = \frac{{{2} \mathop G_{f} }}{{\mathop f^{2}_{t} }}\left( {\frac{1}{E} - \frac{1}{{\mathop E\nolimits_{t} }}} \right)^{ - 1}$$
(23)

with E t being the post-peak tangent stiffness for an equivalent triangular shape of the \(\sigma\)–\(\varepsilon\) curve.

The selected model parameter values have been adopted in accordance with the data provided in Table 2.

Regarding the rebar, bar elements are used in compliance with the elasto-plastic hardening model developed by Menegotto–Pinto [24]. Figure 7b displays the related \(\sigma\)–\(\varepsilon\) curve.

3.3 Results

3.3.1 Global results

Various situations have been modeled herein. Figure 8 compares the load–displacement curves resulting from the simulations with the experimental points:

  • For the total loading path, the calculation curve (Fig. 8a, solid line), performed without any cycle, shows good agreement with the envelope for the entire set of experimental curves.

  • For the same loading path with cycles up to ±2 mm, the comparison shows very good agreement (Fig. 8b).

  • For a cyclic loading of ±5 mm, including rebar plasticity (Fig. 8c), the results are also very satisfactory.

Fig. 8
figure 8

Bending test on RC beams as an experiment–calculation comparison: a comparison of the envelope of the total experimental response with a calculation driven without any cycle (beam No. 1), b comparison for the total path up to ±2 mm (beam No. 1), c cycle computed for ±5 mm compared to the experimental response up to ±5 mm (beam No. 2)

Full size image

It can be concluded from these results that the stiffness recovery, as modeled by the μ model, very accurately reproduces the experimental results and, moreover, the decision not to represent the permanent concrete strain does not penalize these results (some differences are only visible around the zero loading point when rebar plasticity has not been  activated– Fig. 8b).

3.3.2 Local results

Such a modeling approach serves to access local information indicating what happens inside the damaged areas both in concrete and in rebar. Figure 9 shows, at a given stage of the loading (±5mm), the strain field on the lateral beam surface. In Fig. 9b, the strain field is obtained by means of Digital Image Correlation (Ragueneau et al. [19]), which in turn identifies active cracks. Figure 9a highlights the strain concentrations, in correspondence with the crack bands where damage is localized and then where cracks are predicted by calculation. The dark grey area corresponds to a compressive strain, which is amplified in the compressed zones due to previous damage. A high level of agreement can be observed between these two images.

Fig. 9
figure 9

Strain field on the lateral surface of the beam at a given stage (±5 mm), providing a picture of the crack opening state: a calculation results, b test results obtained by digital image correlation (DIC)

Full size image

During a cyclic loading, at a given location, the effective damage d evolves until a maximum value of the load in one direction is reached. When the load is reversed, the local stress is also reversed. As presented Fig. 1, due to changes, first in the triaxial factor r (Eq. 14) and then in the damage driving variable Y (Eq. 13), this maximum value of d vanishes. This specific property may be used as a crack opening indicator.

Figure 10 provides the situation with d (the grey scale indicate where 0.98 < d < 1), for two different stages after a series of cycles extending to ±2 mm. The effective damage area is seen to represent a crack opening stage, as revealed by the Digital Image Correlation analysis, which is also depicted in Fig. 10.

Fig. 10
figure 10

Effective damage used as a crack opening indicator (d > 0.98) after cycles of up to ±2 mm and cracks observed by digital image correlation with deflection of: a −2 mm, b +2 mm

Full size image

However, if necessary, it is possible to visualize after a given loading path the total damage area thanks to the thermodynamic variables Y t and Y c. Two images can thus be derived: one is using Y t, while the other is using Y c, both of which are representative of cracking under tension and compression respectively.

These results reveal an efficient model, which has proven to be robust and effective in describing both cyclic behavior and crack opening behavior. The μ model is thus a good candidate for solving seismic problems.

4 Loading with confinement and strain rate effects

Among the range of severe loading situations involving concrete structures, blasts and impacts must be considered. To simulate these effects, the adopted modeling approach must include strain rate effects and confinement effects. This section will propose μ model improvements that allow simulating both phenomena.

4.1 Strain rate effects

The dependence of concrete strength on strain rate is well known, particularly under tension whereby inertia effects cannot explain the phenomenon. As presented in Pontiroli et al. [12], this effect is taken into account using a dynamic threshold \(\left( {\varepsilon_{{0{\text{t}}}}^{\text{d}} } \right)\) instead of a static one \(\left( {\varepsilon_{{0{\text{t}}}}^{\text{s}} } \right)\). The dynamic threshold is deduced from the static one through an increase factor dependent on the strain rate \(\dot{\varepsilon }\) (=d\(\varepsilon\) /dt):

$$\mathop R\nolimits_{t} = \mathop {\dot{\varepsilon }}\nolimits_{{0{\text{t}}}}^{\text{d}} /\mathop {\dot{\varepsilon }}\nolimits_{{0{\text{t}}}}^{\text{s}} = \hbox{min} \, [\hbox{max} \, (1.0 + a_{t} \dot{\varepsilon }^{bt} ,c_{t} \mathop {\dot{\varepsilon }}\nolimits^{dt} ), \, 5]$$
(23)

a t , b t , c t and d t are material coefficients defined by the user and derived from experimental results.

An experimental campaign has recently been conducted at the LEM3 Laboratory in Metz (France) (Forquin and Erzar [25], Erzar and Forquin [26]); it has focused on quasi-static tests and dynamic tests performed on both dry and wet concrete specimens. A high-speed hydraulic press was applied for the intermediate strain rate, and an experimental Hopkinson bar device, based on the spalling technique, was used for higher strain rates. From these tests, original identification techniques could be developed in order to deduce the tensile strength of the material.

For an ordinary concrete (f c = 30 MPa), the complete results are given in Fig. 11.

Fig. 11
figure 11

Concrete tensile strength versus strain rate: experiments [25] and the model with corresponding \(\sigma\)–\(\varepsilon\) curves, the peak of which increases with \(\dot{\varepsilon }\)

Full size image

In the μ model, the dynamic tensile strength is assumed to be the peak of the stress–strain curve: ft = E\(\varepsilon_{{0{\text{t}}}}^{\text{d}}\). From (23), f t = f(\(\dot{\varepsilon }\)) can be obtained. These results have also been plotted in Fig. 11, thus confirming that the calculations provide excellent results. It is a simple step to extend such a calculation to 3D situations by introducing \(\varepsilon_{{0{\text{t}}}}^{\text{d}}\) into Eqs. (12) and (16), in order to define the initial threshold of the 3D driving variable of damage, Y.

To highlight the ability of the μ model to describe high velocity problems, the spalling test conducted at LEM3 has been simulated. The test specimen was a cylinder (L = 140 mm, \(\phi\) = 45 mm) whose left edge was in contact with the Hopkinson bar, which generated the compressive wave on the right edge (Fig. 12c). The transmitted compressive pulse propagated along the specimen until reaching the free end, where it was reflected as a tensile pulse traveling in the opposite direction. When the amplitude of the reflected pulse has exceeded that of the incident pulse, a dynamic tensile loading spread across the specimen leading to a potential fracture; in Fig. 12d, the stress waves calculated for three specimen locations (120, 60 and 40 mm from the free edge) show that the stress at failure is reached at 8 ms for 14.9 MPa. Figure 12a also displays the experimental result obtained for a given pulse that led to multi-fracture of the specimen. Figure 12b shows a similar result for the calculation performed on a fiber beam model. Fracture is determined using an erosion technique: the element is eroded when strain reaches a very high value (\(\varepsilon\) > 10−2).

Fig. 12
figure 12

Spalling test: a post-test cracking on the concrete specimen [26], b damage resulting from a calculation exhibiting two main cracks, c pulse applied on the left edge of the specimen, d \(\sigma\)(t) response at three locations (120, 60, 40 mm from the right edge) exhibiting failure at 8 ms

Full size image

4.2 Confinement effects

Confinement corresponds to loadings in the tri-compression domain. The triaxial coefficient r, introduced in Eq. (14), lies within the confinement domain and equals 0. As mentioned in Sect. 1, damage modes depend on the presence or absence of extensions. At this point, two distinct domains can be considered: (i) the extension allowed (EA) domain, whereby during loading a positive strain exists in at least one direction; and (ii) a no extension allowed (NEA) domain, when loading prevents any kind of extension.

Positive strains within the EA domain can generate local damage and, as will be seen below, the μ model is a good candidate to describe this situation, which corresponds to a soft impact.

In contrast, within the NEA domain, phenomena are of two orders: (i) strong confinement leading to a gradual collapse of cement matrix porosity; and (ii) the shear caused by stress triaxiality generates local mode II cracking. It has been shown that such phenomena can be advantageously modeled through introducing compaction and plasticity effects. Coupling of the μ model with a plasticity model, as performed in the PRM model [14], will be considered in future developments.

4.2.1 Low and moderate confinement

The loading state in this zone is given by: ∑\(\left\langle {\varepsilon_{i} } \right\rangle\) + ≠ 0, which can be written \(I_{\varepsilon + }\) ≠ 0. From the definition provided in Sect. 2, a confinement coefficient C is introduced in order to model confinement effects within the EA domain. This step affects the thermodynamic variable Y c. With r = 0, the variable Y (Eq. (13)) that controls damage then becomes:

$$Y = C \, Y_{c}$$
(24)

C is an indicator of the existence of a local extension and has been defined as follows:

$$\left\{ {\begin{array}{*{20}c} {C = 1} & {{\text{if }}r > 0} \\ {C = \frac{{\sum {\left\langle {\varepsilon_{i} } \right\rangle_{ + } } }}{{\sum {\left\langle {\varepsilon_{i0} } \right\rangle_{ + } } }} \Leftrightarrow C = \frac{{I_{\varepsilon + } }}{{I_{\varepsilon 0 + } }}} & {{\text{if }}r = 0} \\ \end{array} } \right.$$
(25)

\(I_{\varepsilon 0 + }\) is the projection of \(I_{\varepsilon + }\) on the nearest plane \(\sigma_{i}\) = 0. \(I_{\varepsilon 0 + }\) is thus calculated by setting 0 as the “strongest” stress (i.e., the lowest in absolute value terms) of the three principal stresses. From these equations, d can be calculated according to a classical approach using (15).

To analyze the model response within the EA domain, a cylindrical specimen subjected to a vertical compression \(\sigma_{1}\) and confinement \(\sigma_{2} = \sigma_{3}\) will be considered (see Fig. 13a). This test can be conducted in a cell adapted for concrete specimens.

Fig. 13
figure 13

Triaxial test: a specimen and loading path, after a radial path, \(\sigma_{2} = \sigma_{3} = {\text{S}}\) and \(\sigma_{1}\) increases until failure, b response of the μ model, c experimental results (Ramtani [27] and Gabet [28] )

Full size image

The loading path comprises two steps, i.e.:

  1. 1.

    radial path: \(\sigma_{2} = \sigma_{3} = \beta \sigma_{1}\) (where β is a constant)

  2. 2.

    triaxial path: \(\sigma_{2} = \sigma_{3} = S\) (S is a fixed level), with \(\sigma_{1}\) increasing until failure.

Poisson’s ratio \(\nu\) is responsible for the transverse extension. For a given value of \(\nu\), typically equal to 0.2, it is straightforward to show that C = 0 for β values greater than or equal to 0.25. To avoid any damage during the first step, β = 0.25 has been chosen. Afterwards, during the second step β (= S/ \(\sigma_{1}\)) decreases, allowing d to evolve until failure (Fig. 13).

Figure 13b displays the numerical results derived for the same concrete specimen used earlier and for S values of 0, 20, 35, 50 and 100 MPa. Fig. 13c presents the experimental results obtained by two researchers on a similar concrete and on similar loading paths (Ramtani [27], Gabet [28]). It can be observed that both, the trends and values at failure have been correctly simulated. At a high S value (i.e., 100 MPa) however, it is observed that the phenomena described for the NEA domain have been activated, particularly compaction damage, which along with extension damage serve to accelerate specimen collapse and thus explain the conservative strength value resulting from calculation. This loading situation provides the limitation of the present development of the μ model.

5 Conclusion

The μ model has been based on the principles of isotropic damage mechanics. Two thermodynamic variables have been defined to describe, within a 3D formulation, the unilateral behavior of concrete (crack opening and closure), which is essential for cyclic loadings, in particular the seismic behavior of concrete structures.

Built around a simple formulation that combines elasticity and damage and in respecting the thermodynamic principles of irreversible processes, this model is simply implemented into a finite element code. Furthermore, the material parameters (i.e. eight in all, including elastic parameters) are easily identified solely from individual tensile and compressive tests. A series of applications yields, both at the material level and on reinforced concrete structures, a set of satisfactory experimental results attesting to the model’s effectiveness.

Through variation in the strain rate of the initial threshold of the driving damage variable, it has been proven that the model is able to describe high-velocity loading. The model’s ability to account for low and moderate confinement, i.e. when the load allows for extensions (∑\(\left\langle {\varepsilon_{i} } \right\rangle\) + ≠ 0), was also discussed. Dynamic loadings at either low or high speed, such as a blast or impact, could then be simulated, although an improved description of compaction phenomena and shear-driven local mode II is required to produce a complete model capable of simulating the punching effects that lead to penetration and perforation.

In conclusion, this model can provide a useful tool for engineering applications, as was initially expected, and moreover is able to cover a wide diversity of monotonic or cyclic problems from quasi-static to high-velocity loadings (i.e., earthquakes, blasts, soft impacts). New developments are underway to both: (i) complete the 3D version for high confinement, and (ii) create simplified tools, such as multifiber beams, based on the μ model and enhanced to treat 3D structural problems including torsion, severe loading and cracking indicators [29, 30].