Bifurcation analysis of a composite cantilever beam via 1:3 internal resonance

Abstract

In this paper, we study a multiple scales perturbation and numerical solution for vibrations analysis and control of a system which simulates the vibrations of a nonlinear composite beam model. System of second order differential equations with nonlinearity due to quadratic and cubic terms, excited by parametric and external excitations, are presented. The controller is implemented to control one frequency at primary and parametric resonance where damage in the mechanical system is probable. Active control is applied to the system. The multiple scales perturbation (MSP) method is implemented to obtain an approximate analytical solution. The stability analysis of the system is obtained by frequency response (FR). Bifurcation analysis is conducted using various control parameters such as natural frequency (ω₁), detuning parameter (σ₁), feedback signal gain (β), control signal gain (γ), and other parameters. The dynamic behavior of the system is predicted within various ranges of bifurcation parameters. All of the stable steady state (point attractor), stable periodic attractors, unstable steady state, and unstable periodic attractors are determined efficiently using bifurcation analysis. The controller’s influence on system behavior is examined numerically. To validate our results, the approximate analytical solution using the MSP method is compared with the numerical solution using the Runge-Kutta (RK) method of order four.

Introduction

An active control system is defined necessarily in terms of that a mass of external power or energy is required. Fanson and Caughey [1] were the first to introduce the Positive Position Feedback (PPF) technique. Vibrations can be abolished via a movement of feedback signals conducted by the mentioned technique. Active constrained layer damping has been effectively implemented as an efficient method to control the vibration of various flexible mechanical structures [2,3,4,5,6,7,8,9]. Eissa and Sayed [10,11,12] examined the active controller’s effect on both spring and simple pendulum at the primary resonance using negative velocity feedback. El-Bassiouny [13], Eissa et al. [14,15,16,17], and Jaensch [18] confirmed how active control is functional in vibration attenuation at resonance for different vibration modes. They approved that the active control method has several advantages with respect to the passive one. Sadek et al. [19] employed piezoelectric-patch-actuators as active control to control the vibration of simply supported flexible plates. An optimal control law was deduced utilizing the maximum principle theory to calculate the voltage of the actuators. Wang et al. [20] used an inverse feed-forward controller method for directing polymer actuator displacement control. Dong et al. [21] investigated the active vibration control method to control piezoelectric smart structures using a system identification technique. Kapuria and Yasin [22] studied the active vibration repression of metal laminated plates through piezoelectric fiber-reinforced composite materials. Warminski et al. [23] studied the experimental and theoretical investigations of vibrations of an autoparametric system composed of two beams with rectangular cross-sections. The experimental response of the system, tuned at 1:4 internal resonance case, is performed for random and harmonic excitations. Warminski et al. [24] investigated the numerical and experimental solutions for various active controllers which applied to a nonlinear mechanical system. El-Ganaini et al. [25] considered the PPF controller to put down the vibration amplitude of a nonlinear dynamic model at primary resonance with 1 : 1 internal resonance. Hamed and Amer [26] studied an active controller for damping out the nonlinear vibration composite beam with parametric excitation force in the case of 1 : 2 internal resonances. Sayed and Kamel [27] examined the effect of a linear controller to control the vibration of each of the saturation control of a linear absorber and the vibrating system. Sayed and Kamel [28] applied an active control method with on 1 : 2 and 1 : 3 internal resonance to control the vibrations of a nonlinear vibrating system. Large deformation analysis for a cantilever beam with a variable bending stiffness under both static and dynamic loads is investigated by the direct integration scheme [29]. A simple boundary feedback control moment is proposed to stabilize a nonhomogeneous flexible beam with a tip mass [30]. They obtained the exponential stability, spectrum-determined growth condition, and optimal decay rate. Chentouf [31] considered the stabilization problem of a variant of the SCOLE model. He shows that the system uniformly stabilized by the proposed feedback law as soon as the boundary control force and control moment were presented in the feedback. Chentouf [32] studied a model that consists of a non-homogeneous flexible beam clamped at its left end to a rigid disk and free at the right end, where another rigid body is attached. They treated different physical situations and provided accordingly appropriate feedback control laws. Bağdatlı et al. [33] investigated nonlinear transverse vibrations of a tensioned Euler-Bernoulli beam resting on multiple supports. A perturbation technique was applied to the equations of motion to obtain approximate analytical solutions. He considered 3 : 1 internal resonance. Hegazy [34] studied the dynamic behavior and chaotic motion of a string-beam coupled system subjected to parametric excitation. He considered and examined the case of 3 : 1 internal resonance between the modes of the beam and the string, in the presence of subharmonic resonance for the beam. Cemil Tunç [35, 36] investigated the asymptotic stability and boundedness of all solutions of certain differential equations of fourth order.

In this paper, the solutions of nonlinear differential equations that represent composite beam vibrations are obtained. We control the vibration of the system via 1 : 3 active control techniques. We applied the MSP technique to solve those nonlinear equations. We extract the corresponding FR equations and present graphically at different system parameters. We apply the RK algorithm to confirm the obtained curves numerically. We applied Lyapunov’s first method to investigate the stability of the controlled system. To validate our results, we compare approximate solutions using the MSP method and numerical solutions using the RK method of order four. We predict the dynamic behavior of the system at various ranges of bifurcation parameters. We use bifurcation analysis to determine the efficiently stable steady state (point attractor), stable periodic attractor, unstable steady state, and unstable periodic attractors.

Equations of motion

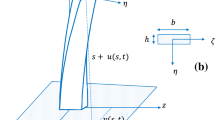
The modified nonlinear differential equations describe the oscillations of the nonlinear composite beam model [23, 24, 26] are given by:

$$ \ddot{u}+2{\upmu}_1{\upomega}_1\dot{u}+{\upomega}_1^2u+{\upalpha}_1{u}^3-\updelta \left(u{\dot{u}}^2+{u}^2\ddot{u}\right)={f}_1\cos {\Omega}_1t+u{f}_2\ \cos {\Omega}_2t+\upgamma {\nu}^3, $$

(1)

$$ \ddot{\nu}+2{\upmu}_2{\upomega}_2\dot{\nu}+{\upomega}_2^2\nu +{\upalpha}_2{\nu}^3=\upbeta u{\nu}^2, $$

(2)

with initial conditions $u(0)=0.02,\dot{u}(0)=0,\nu (0)=0.2,\dot{\nu}(0)=0,$ where u denotes the composite beam system displacement and ν denotes the controller displacement, and the derivatives with respect to the time t are denoted by dots. μ₁ and μ₂ are the parameters of the viscous damping coefficients, ω₁ is the natural frequency accompanied by the composite beam, and ω₂ is the natural frequencies associated with controller modes, Ω₁ and Ω₂ are the excitation frequencies, f₁ and f₂ are the excitation forces amplitudes, and γ and β are the control and feedback signal gains. δ, α₁ are the main system nonlinear stiffness coefficient which may be due to material of the beam non-homogeneity,α₂ nonlinear stiffness coefficient of the controller. The nonlinear parameters, linear viscous damping, and excitation forces are as follows:

$$ {\upmu}_n=\upvarepsilon {\hat{\upmu}}_n,{\upalpha}_n=\upvarepsilon {\hat{\upalpha}}_n,\updelta =\upvarepsilon \hat{\updelta},\upbeta =\upvarepsilon \hat{\upbeta},\upgamma =\upvarepsilon \hat{\upgamma},{f}_n=\upvarepsilon {\hat{f}}_n,\kern0.75em n=1,2, $$

(3)

where the parameter ε has a low value denoted as perturbation parameter and 0 < ε ≪ 1. Substituting Eq. (3) into Eqs. (1) and (2), we can obtain:

$$ \ddot{u}+2\upvarepsilon {\hat{\upmu}}_1{\upomega}_1\dot{u}+{\upomega}_1^2u+\upvarepsilon {\hat{\upalpha}}_1{u}^3-\upvarepsilon \hat{\updelta}\left(u{\dot{u}}^2+{u}^2\ddot{u}\right)=\upvarepsilon\ \left({\hat{f}}_1\cos {\Omega}_1t+u{\hat{f}}_2\ \cos {\Omega}_2t\right)+\upvarepsilon \hat{\upgamma}{\nu}^3, $$

(4)

$$ \ddot{\nu}+2\upvarepsilon {\hat{\upmu}}_2{\upomega}_2\dot{\nu}+{\upomega}_2^2\nu +\upvarepsilon {\hat{\upalpha}}_2{\nu}^3=\upvarepsilon \hat{\upbeta}u{\nu}^2. $$

(5)

The parameters ${\hat{\upalpha}}_1,{\hat{\upalpha}}_2,{\hat{\upmu}}_1,{\hat{\upmu}}_2,\hat{\updelta},\hat{\upbeta},\hat{\upgamma},{\hat{f}}_1$, and ${\hat{f}}_2$ are of the order 1. This means that all these parameters appear when comparing the coefficients of the parameter ε.

Existence and uniqueness theorem

The system of ODEs (1) and (2) with initial conditions $u(0)=0.02,\dot{u}(0)=0,\nu (0)=0.2,\dot{\nu}(0)=0$, can be transformed to a system of first order differential equations IVP in the following:

put u(t) = x₁(t) = x₁, then $\kern0.5em {\dot{x}}_1(t)={x}_2(t)={x}_2$

$$ {\dot{x}}_2(t)=\ddot{u}(t)=\left({f}_1\cos\ {\Omega}_1t+{x}_1{f}_2\ \cos\ {\Omega}_2t+\upgamma {x}_3^3-2{\upmu}_1{\upomega}_1{x}_2-{\upomega}_1^2{x}_1-{\upalpha}_1{x}_1^3+\updelta {x}_1{x}_2^2\right)/\left(1-\updelta {x}_1^2\right), $$

put v(t) = x₃(t) = x₃, then ${\dot{x}}_3(t)={x}_4(t)={x}_4$

$$ {\dot{x}}_4(t)=\ddot{v}(t)=\upbeta {x}_1{x}_3^2-2{\upmu}_2{\upomega}_2{x}_4-{\upomega}_2^2{x}_3-{\upalpha}_2{x}_3^3 $$

and the initial conditions become x₁(0) = 0.02, x₂(0) = 0, x₃(0) = 0.2, x₄(0) = 0.

Here, we concentrate on the solution of the first order IVP

$\dot{x_n}=f\left(t,{x}_n\right)$x_n(0) = x_0n    n = 1, 2, 3, 4 (*)

$$ {\dot{x}}_1(t)={x}_2(t) $$

$$ {\dot{x}}_2(t)=\left({f}_1\cos\ {\Omega}_1t+{x}_1{f}_2\ \cos\ {\Omega}_2t+\upgamma {x}_3^3-2{\upmu}_1{\upomega}_1{x}_2-{\upomega}_1^2{x}_1-{\upalpha}_1{x}_1^3+\updelta {x}_1{x}_2^2\right)/\left(1-\updelta {x}_1^2\right) $$

$$ {\dot{x}}_3(t)={x}_4(t) $$

$$ {\dot{x}}_4(t)=\upbeta {x}_1{x}_3^2-2{\upmu}_2{\upomega}_2{x}_4-{\upomega}_2^2{x}_3-{\upalpha}_2{x}_3^3 $$

Theorem 1 [37]. (Existence theorem) Suppose that f(t, x_n) is continuous function in some region R = {(t, x_n) : |t − 0| ≤ a, |x_n − x_0n| ≤ b}, (a, b > 0). Since f is continuous in a closed and bounded domain, it is necessarily bounded in R, i.e., there exists K > 0 such that |f(t, x_n)| ≤ K   ∀ (t, x_n) ∈ R . Then, the IVP (*) has at least one solution x_n = x_n(t) defined in the interval |t − 0| ≤ α where $\upalpha =\min \left(a,\frac{b}{K}\right)$ (note that the solution exists possibly in a smaller interval).

Theorem 2 [37]. (Uniqueness theorem) Suppose that f and $\frac{\partial f}{\partial {x}_n}$ are continuous function in R (defined in the existence theorem). Hence, both the f and $\frac{\partial f}{\partial {x}_n}$ are bounded in R, i.e., (a) |f(t, x_n)| ≤ K and (b) $\frac{\partial f}{\partial {x}_n}\le L\kern0.5em \forall \left(t,{x}_n\right)\in R$.

Then, the IVP (*) has at most one solution x_n = x_n(t) defined in the interval |t − 0| ≤ α where $\upalpha =\min \left(a,\frac{b}{K}\right)$. Combining with existence theorem, the IVP (*) has a unique solution x_n = x_n(t) defined in the interval |t − 0| ≤ α. By using Theorems (1) and (2), both the functions f(t, x_n) and its partial derivative are defined and continuous at all points$\left\{\left({x}_{\mathbf{1},}{x}_{\mathbf{2}},{x}_{\mathbf{3}},{x}_4\right):{x}_1\boldsymbol{\ne}\pm \sqrt{\frac{\mathbf{1}}{\boldsymbol{\updelta}}}\ \right\}$. The theorem guarantees that a solution to the IVP exists in some open interval and that this solution is unique.

Mathematical analysis

A first-order approximate solution of Eqs. (4) and (5) is conducted using the method of MSP [38, 39].

$$ u\left(t;\upvarepsilon \right)={u}_0\left({T}_0,{T}_1\right)+\upvarepsilon {u}_1\left({T}_0,{T}_1\right), $$

(6)

$$ \nu \left(t;\upvarepsilon \right)={\nu}_0\left({T}_0,{T}_1\right)+\upvarepsilon {\nu}_1\left({T}_0,{T}_1\right), $$

(7)

where T_n = εⁿt is the fast time scales for n = 0 and slow time scales for n = 1. In terms of T₀, T₁, the time derivatives are converted to the D operator according to:

$$ \frac{d}{dt}={D}_0+\upvarepsilon {D}_1,\kern0.5em \frac{d^2}{d{t}^2}={D}_0^2+2\upvarepsilon {D}_0{D}_1, $$

(8)

where ${D}_n=\frac{\partial }{\partial {T}_n}.$ After substituting Eqs. (6) and (7) and (8) into Eqs. (4) and (5) and comparing the coefficients of similar powers of the parameter ε in both sides, we obtain the following:

Order (ε⁰):

$$ \left({D}_0^2+{\upomega}_1^2\right){u}_0=0, $$

(9)

$$ \left({D}_0^2+{\upomega}_2^2\right){\nu}_0=0. $$

(10)

Order (ε):

$$ {\displaystyle \begin{array}{c}\left({D}_0^2+{\upomega}_1^2\right){u}_1=-2{D}_0{D}_1{u}_0-2{\hat{\upmu}}_1{\upomega}_1{D}_0{u}_0-{\hat{\upalpha}}_1{u}_0^3+\hat{\updelta}{u}_0{\left({D}_0{u}_0\right)}^2+\hat{\updelta}{u}_0^2{D}_0^2{u}_0+{\hat{f}}_1\mathit{\cos}{\Omega}_1{T}_0\\ {}+{u}_0{\hat{f}}_2\mathit{\cos}{\Omega}_2{T}_0+\hat{\upgamma}{\nu}_0^3,\end{array}} $$

(11)

$$ \left({D}_0^2+{\upomega}_2^2\right){\nu}_1=-2{D}_0{D}_1{\nu}_0-2{\hat{\upmu}}_2{\upomega}_2{D}_0{\nu}_0-{\hat{\upalpha}}_2{\nu}_0^3+\hat{\upbeta}{u}_0{\nu}_0^2. $$

(12)

The solutions of Eqs. (9) and (10) are represented in the complex form:

$$ {u}_0={A}_1{e}^{i{\upomega}_1{T}_0}+{\overline{A}}_1{e}^{-i{\upomega}_1{T}_0}, $$

(13)

$$ {\nu}_0={A}_2{e}^{i{\upomega}_2{T}_0}+{\overline{A}}_2{e}^{-i{\upomega}_2{T}_0}, $$

(14)

where A₁ and A₂ are complex function with T₁ as a complex argument, which assigned by removing of secular terms and small-divisor terms from the 1st order of approximation. Therefore, we investigate the case where Ω₁ ≅ ω₁, Ω₂ ≅ 2ω₁ and ω₁ ≅ 3ω₂. To examine quantitatively the closeness of the resonances, the detuning parameters σ₁, σ₂, and σ₃ are represented by Ω₁ = ω₁ + εσ₁, Ω₂ = 2ω₁ + εσ₂ and ω₁ = 3ω₂ + εσ₃. Substituting Eqs. (13) and (14) into Eqs. (11) and (12), we get:

$$ {\displaystyle \begin{array}{l}\left({D}_0^2+{\upomega}_1^2\right){u}_1=-2i{\upomega}_1{D}_1{A}_1{e}^{i{\upomega}_1{T}_0}+2i{\upomega}_1{D}_1{\overline{A}}_1{e}^{-i{\upomega}_1{T}_0}-2i{\hat{\upmu}}_1{\upomega}_1^2{A}_1{e}^{i{\upomega}_1{T}_0}+2i{\hat{\upmu}}_1{\omega}_1^2{\overline{A}}_1{e}^{-i{\upomega}_1{T}_0}\\ {}-{\hat{\upalpha}}_1{A}_1^3{e}^{3i{\upomega}_1{T}_0}-3{\hat{\upalpha}}_1{A}_1^2{\overline{A}}_1{e}^{i{\upomega}_1{T}_0}-3{\hat{\upalpha}}_1{A}_1{\overline{A}}_1^2{e}^{-i{\upomega}_1{T}_0}-{\hat{\upalpha}}_1{\overline{A}}_1^3{e}^{-3i{\upomega}_1{T}_0}-2{\upomega}_1^2\hat{\updelta}{A}_1^3{e}^{3i{\upomega}_1{T}_0}\\ {}-2{\upomega}_1^2\hat{\updelta}{A}_1^2{\overline{A}}_1{e}^{i{\upomega}_1{T}_0}-2{\upomega}_1^2\hat{\updelta}{\overline{A}}_1^2{A}_1{e}^{-i{\upomega}_1{T}_0}-2{\upomega}_1^2\hat{\updelta}{\overline{A}}_1^3{e}^{-3i{\upomega}_1{T}_0}+\left({\hat{f}}_1/2\right)\ {e}^{i\left({\upomega}_1+\upvarepsilon {\upsigma}_1\right){T}_0}\\ {}+\left({\hat{f}}_1/2\right){e}^{-i\left({\upomega}_1+\upvarepsilon {\upsigma}_1\right){T}_0}+\left({\hat{f}}_2/2\right){A}_1{e}^{i\left(3{\upomega}_1+\upvarepsilon {\upsigma}_2\right){T}_0}+\left({\hat{f}}_2/2\right){\overline{A}}_1{e}^{i\left({\upomega}_1+\upvarepsilon {\upsigma}_2\right){T}_0}\\ {}+\left({\hat{f}}_2/2\right){\overline{A}}_1{e}^{-i\left(3{\upomega}_1+\upvarepsilon {\upsigma}_2\right){T}_0}+\left({\hat{f}}_2/2\right){A}_1{e}^{-i\left({\upomega}_1+\upvarepsilon {\upsigma}_2\right){T}_0}+\hat{\upgamma}{A}_2^3{e}^{i\left({\upomega}_1-\upvarepsilon {\upsigma}_3\right){T}_0}\\ {}+3\hat{\upgamma}{A}_2^2{\overline{A}}_2{e}^{i{\upomega}_2{T}_0}+\hat{\upgamma}{\overline{A}}_2^3{e}^{-i\left({\upomega}_1-\upvarepsilon {\upsigma}_3\right){T}_0}+3\hat{\upgamma}{\overline{A}}_2^2{A}_2{e}^{-i{\upomega}_2{T}_0},\end{array}} $$

(15)

$$ {\displaystyle \begin{array}{c}\left({D}_0^2+{\upomega}_2^2\right){\nu}_1=-2i{\upomega}_2{D}_1{A}_2{e}^{i{\upomega}_2{T}_0}+2i{\upomega}_2{D}_1{\overline{A}}_2{e}^{-i{\upomega}_2{T}_0}-2i{\hat{\upmu}}_2{\upomega}_2^2{A}_2{e}^{i{\upomega}_2{T}_0}+2i{\hat{\upmu}}_2{\upomega}_2^2{\overline{A}}_2{e}^{-i{\upomega}_2{T}_0}\\ {}-{\hat{\upalpha}}_2{A}_2^3{e}^{3i{\upomega}_2{T}_0}-3{\hat{\upalpha}}_2{A}_2^2{\overline{A}}_2{e}^{i{\upomega}_2{T}_0}-3{\hat{\upalpha}}_2{A}_2{\overline{A}}_2^2{e}^{-i{\upomega}_2{T}_0}-{\hat{\upalpha}}_2{\overline{A}}_2^3{e}^{-3i{\upomega}_2{T}_0}\\ {}+\hat{\upbeta}{A}_1{A}_2^2{e}^{i\left({\upomega}_1+2{\upomega}_2\right){T}_0}+2\hat{\upbeta}{A}_1{A}_2{\overline{A}}_2{e}^{i{\upomega}_1{T}_0}+\hat{\upbeta}{A}_1{\overline{A}}_2^2{e}^{i\left({\upomega}_2+\upvarepsilon {\upsigma}_3\right){T}_0}\\ {}+\hat{\upbeta}{\overline{A}}_1{A}_2^2{e}^{-i\left({\upomega}_2+\upvarepsilon {\upsigma}_3\right){T}_0}+2\hat{\upbeta}{A}_2{\overline{A}}_1{\overline{A}}_2{e}^{-i{\upomega}_1{T}_0}+\hat{\upbeta}{\overline{A}}_1{\overline{A}}_2^2{e}^{-i\left({\upomega}_1+2{\upomega}_2\right){T}_0}.\end{array}} $$

(16)

We get the solvability conditions of the first-order expansion by eliminating the secular terms means the term that has some singularity (an unbounded term arising in time-dependent perturbation theory):

$$ 2i{\upomega}_1{D}_1{A}_1=-2i{\hat{\upmu}}_1{\upomega}_1^2{A}_1-3{\hat{\upalpha}}_1{A}_1^2{\overline{A}}_1-2{\upomega}_1^2\hat{\updelta}{A}_1^2{\overline{A}}_1+\frac{{\hat{f}}_1}{2}{e}^{i{\upsigma}_1{T}_1}+\frac{{\hat{f}}_2}{2}{\overline{A}}_1{e}^{i{\upsigma}_2{T}_1}+\hat{\upgamma}{A}_2^3{e}^{-i{\upsigma}_3{T}_1}, $$

(17)

$$ 2i{\upomega}_2{D}_1{A}_2=-2i{\hat{\upmu}}_2{\upomega}_2^2{A}_2-3{\hat{\upalpha}}_2{A}_2^2{\overline{A}}_2+\hat{\upbeta}{A}_1{\overline{A}}_2^2{e}^{i{\upsigma}_3{T}_1}. $$

(18)

By multiplying both sides of Eq. (8) be 2iω₁, 2iω₂, we obtain

$$ 2i{\upomega}_1\frac{d{A}_1}{dt}=\upvarepsilon 2\mathrm{i}{\upomega}_1{D}_1{A}_1, $$

(19)

$$ 2i{\upomega}_2\frac{d{A}_2}{dt}=\upvarepsilon 2\mathrm{i}{\upomega}_2{D}_1{A}_2. $$

(20)

Substituting Eqs. (17) and (18) into Eqs. (19) and (20), we obtain

$$ 2i{\upomega}_1\frac{d{A}_1}{dt}=\upvarepsilon \left(-2i{\hat{\upmu}}_1{\upomega}_1^2{A}_1-3{\hat{\upalpha}}_1{A}_1^2{\overline{A}}_1-2{\upomega}_1^2\hat{\updelta}{A}_1^2{\overline{A}}_1+\frac{{\hat{f}}_1}{2}{e}^{i{\upsigma}_1{T}_1}+\frac{{\hat{f}}_2}{2}{\overline{A}}_1{e}^{i{\upsigma}_2{T}_1}+\hat{\upgamma}{A}_2^3{e}^{-i{\upsigma}_3{T}_1}\right), $$

(21)

$$ 2i{\upomega}_2\frac{d{A}_2}{dt}=\upvarepsilon\ \left(-2i{\hat{\upmu}}_2{\upomega}_2^2{A}_2-3{\hat{\upalpha}}_2{A}_2^2{\overline{A}}_2+\hat{\upbeta}{A}_1{\overline{A}}_2^2{e}^{i{\upsigma}_3{T}_1}\ \right). $$

(22)

To analyze Eqs. (21) and (22), we can express A₁ and  A₂in polar form as

$$ {A}_1=\frac{1}{2}{a}_1{e}^{i{\upgamma}_1},{A}_2=\frac{1}{2}{a}_2{e}^{i{\upgamma}_2} $$

(23)

where a₁ and a₂ are the steady state amplitudes, and γ_s (s = 1, 2) are phases of the motion. Substituting Eq. (23) into Eqs. (21) and (22) and separating the real and imaginary parts, we get the following:

$$ {\dot{a}}_1=-{\upmu}_1{\upomega}_1{a}_1+\frac{f_1}{2{\upomega}_1}\mathit{\sin}{\uptheta}_1+\frac{f_2}{4{\upomega}_1}{a}_1\ \mathit{\sin}{\uptheta}_2+\frac{\upgamma}{8{\upomega}_1}{a}_2^3\ \mathit{\sin}{\uptheta}_3, $$

(24)

$$ {a}_1{\dot{\upgamma}}_1=\frac{3{\upalpha}_1}{8{\upomega}_1}{a}_1^3+\frac{\updelta}{4}{\upomega}_1{a}_1^3-\frac{f_1}{2{\upomega}_1}\mathit{\cos}{\uptheta}_1-\frac{f_2}{4{\upomega}_1}{a}_1\ \mathit{\cos}{\uptheta}_2-\frac{\upgamma}{8{\upomega}_1}{a}_2^3\ \mathit{\cos}{\uptheta}_3, $$

(25)

$$ {\dot{a}}_2=-{\upmu}_2{\upomega}_2{a}_2-\frac{\upbeta}{8{\upomega}_2}{a}_1{a}_2^2\mathit{\sin}{\uptheta}_3, $$

(26)

$$ {a}_2{\dot{\upgamma}}_2=\frac{3{\upalpha}_2}{8{\upomega}_2}{a}_2^3-\frac{\upbeta}{8{\upomega}_2}{a}_1{a}_2^2\mathit{\cos}{\uptheta}_3, $$

(27)

where

$$ {\uptheta}_1={\upsigma}_1{T}_1-{\upgamma}_1,{\uptheta}_2={\upsigma}_2{T}_1-2{\upgamma}_1,{\uptheta}_3=3{\upgamma}_2-{\upgamma}_1-{\upsigma}_3{T}_1. $$

(28)

Then, it follows from Eq. (28) that

$$ {\dot{\uptheta}}_1={\upsigma}_1-{\dot{\upgamma}}_1\Rightarrow {\dot{\upgamma}}_1={\upsigma}_1-{\dot{\uptheta}}_1,{\dot{\upgamma}}_2=\frac{1}{3}\left({\dot{\uptheta}}_3+{\upsigma}_3+{\upsigma}_1-{\dot{\uptheta}}_1\right). $$

(29)

Substituting Eq. (29) into Eqs. (25) and (27), we obtain

$$ {\dot{\uptheta}}_1={\upsigma}_1-\frac{3{\upalpha}_1}{8{\upomega}_1}{a}_1^2-\frac{\updelta}{4}{\upomega}_1{a}_1^2+\frac{f_1}{2{\upomega}_1{a}_1}\mathit{\cos}{\uptheta}_1+\frac{f_2}{4{\upomega}_1}\mathit{\cos}{\uptheta}_2+\frac{\upgamma}{8{\upomega}_1{a}_1}{a}_2^3\ \mathit{\cos}{\uptheta}_3, $$

(30)

$$ {\dot{\uptheta}}_3=-{\upsigma}_3-\frac{3{\upalpha}_1}{8{\upomega}_1}{a}_1^2-\frac{\updelta}{4}{\upomega}_1{a}_1^2+\frac{f_1}{2{\upomega}_1{a}_1}\mathit{\cos}{\uptheta}_1+\frac{f_2}{4{\upomega}_1}\mathit{\cos}{\uptheta}_2+\frac{\upgamma}{8{\upomega}_1{a}_1}{a}_2^3\ \mathit{\cos}{\uptheta}_3 $$

$$ +\frac{9{\upalpha}_2}{8{\upomega}_2}{a}_2^2-\frac{3\upbeta}{8{\upomega}_2}{a}_1{a}_2\ \mathit{\cos}{\uptheta}_3. $$

(31)

From Eqs. (24), (26), (30), and (31), the autonomous system of equations is:

$$ {\dot{a}}_1=-{\upmu}_1{\upomega}_1{a}_1+\frac{f_1}{2{\upomega}_1}\mathit{\sin}{\uptheta}_1+\frac{f_2}{4{\upomega}_1}{a}_1\ \mathit{\sin}{\uptheta}_2+\frac{\upgamma}{8{\upomega}_1}{a}_2^3\ \mathit{\sin}{\uptheta}_3, $$

(32)

$$ {\dot{\uptheta}}_1={\upsigma}_1-\frac{3{\upalpha}_1}{8{\upomega}_1}{a}_1^2-\frac{\updelta}{4}{\upomega}_1{a}_1^2+\frac{f_1}{2{\upomega}_1{a}_1}\mathit{\cos}{\uptheta}_1+\frac{f_2}{4{\upomega}_1}\mathit{\cos}{\uptheta}_2+\frac{\upgamma}{8{\upomega}_1{a}_1}{a}_2^3\ \mathit{\cos}{\uptheta}_3, $$

(33)

$$ {\dot{a}}_2=-{\upmu}_2{\upomega}_2{a}_2-\frac{\upbeta}{8{\upomega}_2}{a}_1{a}_2^2\ \mathit{\sin}{\uptheta}_3, $$

(34)

$$ {\displaystyle \begin{array}{c}{\dot{\uptheta}}_3=-{\upsigma}_3-\frac{3{\upalpha}_1}{8{\upomega}_1}{a}_1^2-\frac{\updelta}{4}{\upomega}_1{a}_1^2+\frac{f_1}{2{\upomega}_1{a}_1}\mathit{\cos}{\uptheta}_1+\frac{f_2}{4{\upomega}_1}\mathit{\cos}{\uptheta}_2+\frac{\upgamma}{8{\upomega}_1{a}_1}{a}_2^3\ \mathit{\cos}{\uptheta}_3\\ {}+\frac{9{\upalpha}_2}{8{\upomega}_2}{a}_2^2-\frac{3\upbeta}{8{\upomega}_2}{a}_1{a}_2\ \mathit{\cos}{\uptheta}_3\end{array}} $$

(35)

Steady state solution

In this work, the steady state motions are examined as follows:

$$ {\dot{a}}_1={\dot{a}}_2={\dot{\uptheta}}_1={\dot{\uptheta}}_2={\dot{\uptheta}}_3=0. $$

(36)

Then, it follows from Eq. (29) that

$$ {\dot{\upgamma}}_1={\upsigma}_1,{\dot{\upgamma}}_2=\frac{1}{3}\left({\upsigma}_1+{\upsigma}_3\right). $$

(37)

Then, the steady state solutions of Eqs. (32)–(35) are as follows:

$$ {\upmu}_1{\upomega}_1{a}_1-\frac{f_1}{2{\upomega}_1}\mathit{\sin}{\uptheta}_1-\frac{f_2}{4{\upomega}_1}{a}_1\ \mathit{\sin}{\uptheta}_2-\frac{\upgamma}{8{\upomega}_1}{a}_2^3\ \mathit{\sin}{\uptheta}_3=0, $$

(38)

$$ {\upsigma}_1-\frac{3{\upalpha}_1}{8{\upomega}_1}{a}_1^2-\frac{\updelta}{4}{\upomega}_1{a}_1^2+\frac{f_1}{2{\upomega}_1{a}_1}\mathit{\cos}{\uptheta}_1+\frac{f_2}{4{\upomega}_1}\mathit{\cos}{\uptheta}_2+\frac{\upgamma}{8{\upomega}_1{a}_1}{a}_2^3\ \mathit{\cos}{\uptheta}_3=0 $$

(39)

$$ {\upmu}_2{\upomega}_2{a}_2+\frac{\upbeta}{8{\upomega}_2}{a}_1{a}_2^2\ \mathit{\sin}{\uptheta}_3=0, $$

(40)

$$ {\displaystyle \begin{array}{c}{\upsigma}_3+\frac{3{\upalpha}_1}{8{\upomega}_1}{a}_1^2+\frac{\updelta}{4}{\upomega}_1{a}_1^2-\frac{f_1}{2{\upomega}_1{a}_1}\mathit{\cos}{\uptheta}_1-\frac{f_2}{4{\upomega}_1}\mathit{\cos}{\uptheta}_2-\frac{\upgamma}{8{\upomega}_1{a}_1}{a}_2^3\ \mathit{\cos}{\uptheta}_3-\frac{9{\upalpha}_2}{8{\upomega}_2}{a}_2^2\\ {}+\frac{3\upbeta}{8{\upomega}_2}{a}_1{a}_2\ \mathit{\cos}{\uptheta}_3=0.\end{array}} $$

(41)

In addition to a trivial one, two possible cases which will be described as follows exist.

• (1) a₁ ≠ 0, a₂ = 0 (system without control)

• (2) a₁ ≠ 0, a₂ ≠ 0 (system with control).

Case (1): We consider a₁ ≠ 0 and a₂ = 0 (system without control); the FR equation is described as follows:

$$ {\left({a}_1{\upsigma}_1-\frac{3{\upalpha}_1}{8{\upomega}_1}{a}_1^3-\frac{\updelta}{4}{\upomega}_1{a}_1^3\right)}^2+{\upmu}_1^2{\upomega}_1^2{a}_1^2-\frac{f_1^2}{4{\upomega}_1^2}-\frac{f_2^2}{16{\upomega}_1^2}{a}_1^2-\frac{f_1{f}_2}{8{\upomega}_1^2}{a}_1=0. $$

(42)

Case (2): It is considered a₁ ≠ 0 and a₂ ≠ 0 (system with control); the FR equations are described as follows:

$$ {\displaystyle \begin{array}{c}{\left({a}_1{\upsigma}_1-\frac{3{\upalpha}_1}{8{\upomega}_1}{a}_1^3-\frac{\updelta}{4}{\upomega}_1{a}_1^3\right)}^2+{\upmu}_1^2{\upomega}_1^2{a}_1^2-\frac{f_1^2}{4{\upomega}_1^2}-\frac{f_2^2}{16{\upomega}_1^2}{a}_1^2-\frac{f_1{f}_2}{8{\upomega}_1^2}{a}_1-\frac{\upgamma^2}{64{\upomega}_1^2}{a}_2^6\\ {}-\frac{f_1\upgamma}{8{\upomega}_1^2}{a}_2^3-\frac{f_2\upgamma}{16{\upomega}_1^2}{a}_1{a}_2^3=0\end{array}} $$

(43)

and

$$ {\displaystyle \begin{array}{c}{\left({\upsigma}_3+\frac{3{\upalpha}_1}{8{\upomega}_1}{a}_1^2+\frac{\updelta}{4}{\upomega}_1{a}_1^2-\frac{9{\upalpha}_2}{8{\upomega}_2}{a}_2^2\ \right)}^2+9{\upmu}_2^2{\upomega}_2^2-\frac{9{\upbeta}^2}{64{\upomega}_2^2}{a}_1^2{a}_2^2-\frac{f_1^2}{4{\upomega}_1^2{a}_1^2}-\frac{f_2^2}{16{\upomega}_1^2}\\ {}\kern0.5em -\frac{\upgamma^2}{64{\upomega}_1^2{a}_1^2}{a}_2^6-\frac{f_1{f}_2}{4{\upomega}_1^2{a}_1}-\frac{f_1\upgamma}{8{\upomega}_2^2{a}_1^2}{a}_2^3-\frac{f_2\upgamma}{16{\upomega}_2^2{a}_1}{a}_2^3=0.\end{array}} $$

(44)

Stability of the system

To derive the stability criteria, we assume that

$$ {a}_1={a}_{10}+{a}_{11},{a}_2={a}_{20}+{a}_{21}\ \mathrm{and}\ {\uptheta}_n={\uptheta}_{n0}+{\uptheta}_{n1}\kern0.75em \left(n=1,2,3\right), $$

(45)

where a₁₀, a₂₀, and θ_n0 satisfy Eqs. (38)–(41) and a₁₁, a₂₁, and θ_n1 are assumed to be small compared with a₁₀, a₂₀, and θ_n0. Substituting Eq. (45) into Eqs. (32)–(35), using Eqs. (38)–(41) and keeping only the linear terms in a₁₁, a₂₁, and θ_n1, we obtain:

$$ {\displaystyle \begin{array}{c}{\dot{a}}_{11}=\left(\frac{f_2}{4{\upomega}_1}\mathit{\sin}\left(2{\uptheta}_{10}\right)-{\upomega}_1{\upmu}_1\right){a}_{11}+\left(\frac{f_1}{2{\upomega}_1}\mathit{\cos}{\uptheta}_{10}+\frac{f_2}{2{\upomega}_1}{a}_{10}\ \mathit{\cos}\left(2{\uptheta}_{10}\right)\right){\uptheta}_{11}\\ {}+\left(\frac{3\upgamma}{8{\upomega}_1}{a}_{20}^2\ \mathit{\sin}{\uptheta}_{30}\right){a}_{21}+\left(\frac{\upgamma}{8{\upomega}_1}{a}_{20}^3\ \mathit{\cos}{\uptheta}_{30}\right){\uptheta}_{31},\end{array}} $$

(46)

$$ {\dot{\uptheta}}_{11}=\left(\frac{\upsigma_1}{a_{10}}-\frac{9{\upalpha}_1}{8{\upomega}_1}{a}_{10}-\frac{3\updelta}{4}{\upomega}_1{a}_{10}+\frac{f_2}{4{\upomega}_1{a}_{10}}\mathit{\cos}\left(2{\uptheta}_{10}\right)\right){a}_{11}-\left(\frac{f_1}{2{\upomega}_1{a}_{10}}\mathit{\sin}{\uptheta}_{10}\right.\left.+\frac{f_2}{2{\upomega}_1}\mathit{\sin}\left(2{\uptheta}_{10}\right)\right){\uptheta}_{11}+\left(\frac{3\upgamma}{8{\upomega}_1{a}_{10}}{a}_{20}^2\ \mathit{\cos}{\uptheta}_{30}\right){a}_{21}-\left(\frac{\upgamma}{8{\upomega}_1{a}_{10}}{a}_{20}^3\ \mathit{\sin}{\uptheta}_{30}\right){\uptheta}_{31}, $$

(47)

$$ {\dot{a}}_{21}=\left(\frac{\upbeta}{8{\upomega}_2}{a}_{20}^2\ \mathit{\sin}{\uptheta}_{30}\right){a}_{11}+\left(-{\upmu}_2{\upomega}_2+\frac{\upbeta}{4{\upomega}_2}{a}_{10}{a}_{20}\ \mathit{\sin}{\uptheta}_{30}\right){a}_{21}+\left(\frac{\upbeta}{8{\upomega}_2}{a}_{10}{a}_{20}^2\ \mathit{\cos}{\uptheta}_{30}\right){\uptheta}_{31}, $$

(48)

$$ {\displaystyle \begin{array}{c}{\dot{\uptheta}}_{31}=\left(-\frac{\upsigma_3}{a_{10}}-\frac{9{\upalpha}_1}{8{\upomega}_1}{a}_{10}-\frac{3\updelta}{4}{\upomega}_1{a}_{10}+\frac{9{\upalpha}_2}{8{\upomega}_2{a}_{10}}{a}_{20}^2-\frac{3\upbeta}{4{\upomega}_2}{a}_{20}\mathit{\cos}{\uptheta}_{30}+\frac{f_2}{4{\upomega}_1{a}_{10}}\mathit{\cos}\left(2{\uptheta}_{10}\right)\right){a}_{11}\\ {}-\left(\frac{f_1}{2{\upomega}_1{a}_{10}}\mathit{\sin}{\uptheta}_{10}+\frac{f_2}{2{\upomega}_1}\mathit{\sin}\left(2{\uptheta}_{10}\right)\right){\uptheta}_{11}+\left(\frac{3\upgamma}{8{\upomega}_1{a}_{10}}{a}_{20}^2\mathit{\cos}{\uptheta}_{30}+\frac{9{\upalpha}_2}{4{\upomega}_2}{a}_{20}\right.\\ {}\left.-\frac{3\upbeta}{8{\upomega}_2}{a}_{10}\mathit{\cos}{\uptheta}_{30}\right){a}_{21}+\left(\frac{3\upbeta}{8{\upomega}_2}{a}_{10}{a}_{20}\mathit{\sin}{\uptheta}_{30}-\frac{\upgamma}{8{\upomega}_1{a}_{10}}{a}_{20}^3\mathit{\sin}{\uptheta}_{30}\right){\uptheta}_{31}\end{array}}. $$

(49)

The system stability is analyzed by assessing the eigenvalues of the Jacobian matrix of the right-hand sides of the system of Eqs. (46)–(49). The equilibrium solution is considered stable when the real parts of the Jacobian matrix eigenvalues are negative. While the relevant solution is unstable if the corresponding real part of any of the eigenvalues is positive, the fixed points stability is investigated according to the following cases:

Case (1): Uncontrolled system, let a₂₁ = θ₃₁ = 0 in Eqs. (46)–(49); then, the above system is written in the matrix form as follows

$$ \left(\begin{array}{c}{a}_{11}.\\ {}{\uptheta}_{11}.\end{array}\right)=\left(\begin{array}{cc}{L}_1& {L}_2\\ {}{L}_3& {L}_4\end{array}\right)\left(\begin{array}{c}{a}_{11}\\ {}{\uptheta}_{11}\end{array}\right). $$

(50)

where

$$ {L}_1=-{\upmu}_1{\upomega}_1+\frac{f_2}{4{\upomega}_1}\mathit{\sin}\left(2{\uptheta}_1\right),{L}_2=\frac{f_1}{2{\upomega}_1}\mathit{\cos}{\uptheta}_1+\frac{f_2}{2{\upomega}_1}{a}_1\ \mathit{\cos}\left(2{\uptheta}_1\right), $$

$$ {L}_3=\frac{\upsigma_1}{a_1}-\frac{9}{8{\upomega}_1}{\upalpha}_1{a}_1-\frac{3\updelta}{4}{\upomega}_1{a}_1+\frac{f_2}{4{\upomega}_1{a}_1}\mathit{\cos}\left(2{\uptheta}_1\right),{L}_4=-\left(\frac{f_1}{2{\upomega}_1{a}_1}\mathit{\sin}{\uptheta}_1+\frac{f_2}{2{\upomega}_1}\mathit{\sin}\left(2{\uptheta}_1\right)\right). $$

Then, the characteristic equation is $\left|\begin{array}{cc}{L}_1-\lambda & {L}_2\\ {}{L}_3& {L}_4-\lambda \end{array}\right|=0,$

i.e., λ² + Bλ + C = 0, where B =  − (L₁ + L₄), C = (L₁L₄ − L₂L₃), and the obtained eigenvalues are as follows:

$$ \lambda =\frac{\left({L}_1+{L}_4\right)\pm \sqrt{{\left({L}_1+{L}_4\right)}^2-4\left({L}_1{L}_4-{L}_2{L}_3\right)}}{2}. $$

(51)

According to the Routh-Hurwitz criterion, the necessary and sufficient conditions of the roots of Eq. (51) have negative real parts, such that

$$ \left({L}_1+{L}_4\right)<0,\kern0.5em {L}_1{L}_4-{L}_2{L}_3>0 $$

Then, the fixed points are stable; otherwise, they are unstable.

Case (2): Controlled system when a₁₁ ≠ 0, θ₁₁ ≠ 0, a₂₁ ≠ 0, θ₃₁ ≠ 0 in Eqs. (46)–(49); then, we can write the above system in the matrix form as shown below:

$$ \left(\begin{array}{c}\begin{array}{c}{a}_{11}.\\ {}{\uptheta}_{11}.\end{array}\\ {}\begin{array}{c}{a}_{21}.\\ {}{\uptheta}_{31}.\end{array}\end{array}\right)=\left(\begin{array}{c}\begin{array}{c}{L}_1\kern0.5em {L}_2\kern0.5em \begin{array}{cc}{L}_9& {L}_{10}\end{array}\\ {}\begin{array}{cc}{L}_3& \begin{array}{cc}{L}_4& \begin{array}{cc}{L}_{11}& {L}_{12}\end{array}\end{array}\end{array}\end{array}\\ {}\begin{array}{c}\begin{array}{cc}{L}_5& \begin{array}{cc}{L}_6& \begin{array}{cc}{L}_{13}& {L}_{14}\end{array}\end{array}\end{array}\\ {}\begin{array}{cc}{L}_7& \begin{array}{cc}{L}_8& \begin{array}{cc}{L}_{15}& {L}_{16}\end{array}\end{array}\end{array}\end{array}\end{array}\right)\left(\begin{array}{c}\begin{array}{c}{a}_{11}\\ {}{\uptheta}_{11}\end{array}\\ {}\begin{array}{c}{a}_{21}\\ {}{\uptheta}_{31}\end{array}\end{array}\right). $$

(52)

The eigenvalue of the above system is as follows:

$$ \left|\begin{array}{c}\begin{array}{cc}{L}_1-\lambda & {L}_2\\ {}{L}_3\ & \kern1em {L}_4-\lambda \end{array}\\ {}\begin{array}{cc}{L}_5\kern2.25em & {L}_6\\ {}{L}_7\kern2.5em & {L}_8\end{array}\end{array}\kern2.00em \begin{array}{c}\begin{array}{cc}{L}_9\kern1.5em & \kern1.25em {L}_{10}\\ {}{L}_{11}\kern1.75em & \kern1em {L}_{12}\end{array}\\ {}\begin{array}{cc}{L}_{13}-\lambda & \kern0.75em {L}_{14}\\ {}{L}_{15}& \kern2em {L}_{16}-\lambda \end{array}\end{array}\right|=0, $$

(53)

i.e. λ⁴ + R₁λ³ + R₂λ² + R₃λ + R₄ = 0, (54)

where

$$ {L}_5=\frac{\upbeta}{8{\upomega}_2}{a}_2^2\ \mathit{\sin}{\uptheta}_3,{L}_6=0, $$

$$ {L}_7=\left(-\frac{\upsigma_3}{a_1}-\frac{9{\upalpha}_1}{8{\upomega}_1}{a}_1-\frac{3\updelta}{4}{\upomega}_1{a}_1+\frac{9{\upalpha}_2}{8{\upomega}_2{a}_1}{a}_2^2-\frac{3\upbeta}{4{\upomega}_2}{a}_2\mathit{\cos}{\uptheta}_3+\frac{f_2}{4{\upomega}_1{a}_1}\mathit{\cos}\left(2{\uptheta}_1\right)\right), $$

$$ {L}_8=-\left(\frac{f_1}{2{\upomega}_1{a}_1}\mathit{\sin}{\uptheta}_1+\frac{f_2}{2{\upomega}_1}\ \sin \left(2{\uptheta}_1\right)\right),{L}_9=\frac{3\upgamma}{8{\upomega}_1}{a}_2^2\ \mathit{\sin}{\uptheta}_3,{L}_{10}=\frac{\upgamma}{8{\upomega}_1}{a}_2^3\mathit{\cos}{\uptheta}_3, $$

$$ {L}_{11}=\frac{3\upgamma}{8{\upomega}_1{a}_1}{a}_2^2\ \mathit{\cos}{\uptheta}_3,\kern0.75em {L}_{12}=-\frac{\upgamma}{8{\upomega}_1{a}_1}{a}_2^3\ \mathit{\sin}{\uptheta}_3,\kern0.5em {L}_{13}=-{\upmu}_2{\upomega}_2+\frac{\upbeta}{4{\upomega}_2}{a}_1{a}_2\ \mathit{\sin}{\uptheta}_3, $$

$$ {L}_{14}=\frac{\upbeta}{8{\upomega}_2}{a}_1{a}_2^2\mathit{\cos}{\uptheta}_3,\kern0.75em {L}_{15}=\left(\frac{3\upgamma}{8{\upomega}_1{a}_1}{a}_2^2\mathit{\cos}{\uptheta}_3+\frac{9{\upalpha}_2}{4{\upomega}_2}{a}_2-\frac{3\upbeta}{8{\upomega}_2}{a}_1\mathit{\cos}{\uptheta}_3\right), $$

$$ {L}_{16}=\left(\frac{3\upbeta}{8{\upomega}_2}{a}_1{a}_2\mathit{\sin}{\uptheta}_3-\frac{\upgamma}{8{\upomega}_1{a}_1}{a}_2^3\mathit{\sin}{\uptheta}_3\right), $$

R₁, R₂, R₃ , and R₄ are functions of L_s (s = 1, 2, …, 16) which are given above. Based on the Routh-Hurwitz criterion, the necessary and sufficient conditions of the roots of Eq. (54) have negative real parts, such that

$$ {R}_1>0,{R}_1{R}_2-{R}_3>0,{R}_3\left({R}_1{R}_2-{R}_3\right)-{R}_1^2{R}_4>0,{R}_4>0. $$

(55)

In the following figures, the dashed lines refer to unstable solutions, while the solid lines refer to stable solutions.

Numerical results

Simulation results are illustrated in graphical forms such as the steady state amplitude of the composite beam system versus time history and detuning parameter σ₁ or the response of the composite beam system and controller at 1 : 3 internal resonance. The different parameters of the composite beam system shown in Fig. 1 are μ₁ = 0.001, f₁ = 0.01, f₂ = 0.05, α₁ = 0.002, ω₁ = 4, δ = 0.0001. Figure 1 declares that the steady state amplitude of the composite beam system is about 90 times that of the external excitation amplitude f₁.This is conducted when the controller is idle at the simultaneous primary and principal parametric resonance.

Fig. 1

System behavior without a controller at resonance Ω₁ ≅ ω₁, Ω₂ ≅ 2ω₁ for initial conditions $u(0)=.02,\dot{u}(0)=0$

Figure 2 shows that the time history for both composite beam system and controller amplitudes at Ω₁ ≅ ω₁, Ω₂ ≅ 2ω₁ at internal resonance ω₁ ≅ 3ω₂. From Fig. 2, it is observed that the energy is transmitted from the composite beam to the controller. To measure the effectiveness of the controller, we define E_a as flows (E_a= uncontrolled system amplitude/controlled system amplitude). Then, the effectiveness of the controller E_a is about 35. Figures 3, 4, 5, 6, and 7 indicate numerical results of the frequency response curves of the controlled system. Figure 3 illustrates that the response of the controlled system against σ₁. We note that the minimum response of the beam occurs when σ₁ = 0, which approves that the controller is able to eliminate the simultaneous primary and parametric resonance vibration effectively at the existence of the 1:3 internal resonance. Figure 4 shows that the influence of f₁ on the system amplitude response against the detuning parameter σ₁. From these figures, it is noticed that the increase in excitations force f₁ leads to an increase in the region of instability system. Figure 5 shows the effects of changing the control signal γ on the FR curves of both the controller and the beam system. Also, for decreasing γ, the effective frequency bandwidth of the saturation controller induces lowering the vibration impact of the composite beam. On the other hand, the controller’s excessive risk is decreased when the control signal is raised.

Fig. 2

System behavior with a controller at resonance Ω₁ ≅ ω₁, Ω₂ ≅ 2ω₁, ω₁ ≅ 3ω₂ for initial conditions $u(0)=0.02,\dot{u}(0)=0,\nu (0)=0.2,\dot{\nu}(0)=0.{\upmu}_1=0.001,{\upmu}_2=0.00098,{f}_1=0.01,{f}_2=0.05,{\upalpha}_1=0.002,{\upalpha}_2=0.002,{\upomega}_1=4,\updelta =0.0001,\upbeta =1,\upgamma =0.2$

Fig. 3

Effects of the detuning parameter σ₁ for μ₁ = 0.001, μ₂ = 0.00098, f₁ = 0.01, f₂ = 0.05, α₁ = 0.002, α₂ = 0.002, ω₁ = 4, δ = 0.0001, β = 1, γ = 0.2

Fig. 4

Effects of external excitation f₁. a f₁ = 0.3. b f₁ = 0.5

Fig. 5

Effects of control signal gain γ

Fig. 6

Effects of feedback signal gain β

Fig. 7

Effects of the natural frequency ω₁

Figure 6 demonstrates the effect of feedback signal β variation on the FR curves. Form this figure, we can see that decreasing the feedback signal obtained a better vibration lowering influence on the composite beam. Figure 7 indicates that the impacts of the natural frequency on the amplitude response curves against σ₁. Also, it is observed that for increasing the natural frequency, the effective frequency bandwidth of the controller and the better vibration damping influence of the composite beam.

Bifurcation analysis

Dynamic bifurcation analysis is performed using the XPPAUT 5 software package and AUTO-07p. Furthermore, MATLAB is used for investigating the dynamic behavior where the dynamic results are obtained at specific parameter values defined from AUTO 2007 [40,41,42,43]. The bifurcation analysis is performed for most of the controlling parameters such as parametric excitations parameters (f₂), nonlinear control parameter (α₂), detuning parameter (σ₁), feedback signal gain (β), control signal gain (γ), and the natural frequency (ω₁) as shown below.

Effect of the parametric excitation parameter (f₂)

Figure 8 a and b show the effect of the parametric excitation bifurcation parameter (f₂) on a₁ and a₂, respectively. The parameter values are indicated in Table 1. There is only Hopf bifurcation (HB) point at f₂ = 0.06839, where a₁ = 0.02473 and a₂ = 0.5691. In the region of (f₂ ≤ 0.06839), the system is dominated by a stable steady state, where a₁ is around 0.025 and a₂ is around 0.57. In the region of (0.06839 ≤ f₂ ≤ 0.09), the system is characterized by stable periodic attractor, where a₁ oscillated in the range of [0.02, 0.28] while a₂ oscillated in the range of [0.4, 1.32]; there is the unstable steady state in the same region (0.06839 ≤ f₂ ≤ 0.09) and unstable periodic attractor in (0.085 ≤ f₂ ≤ 0.09).

Fig. 8

Bifurcation diagram of f₂ as the bifurcation parameter. Stable steady state branch, thick black line; unstable steady state branch, thick broken black lines; stable periodic branch, black circles; unstable periodic branch, hollowed/white circles

Table 1 Parameter values

Effect of the nonlinear control parameter (α₂)

Figure 9 a and b indicate the effects of the nonlinear control parameter (α₂) as a bifurcation parameter on a₁ and a₂ at γ = 30 based on the two-parameter continuation technique [44], and the rest of the parameter’s values are shown in Table 1. There are two Hopf bifurcation points: the first Hopf HB₁ appears at the two points (α₂, a₁) = (0.478, 0.2006) and (α₂, a₂) = (0.478, 0.09285), while second Hopf HB₂ appears at the two points (α₂, a₁) = (0.1008, 0.1447) and (α₂, a₂) = (0.1008, 0.09622). The system behavior can be characterized as follow:

Fig. 9

Bifurcation diagram of nonlinear control parameter α₂ as the bifurcation parameter

Region (α₂ ≤ 0.1008): The bifurcation diagrams obtained in Fig. 9 a, and b show that there exists a point attractor only, if a₁ changes in the range of [0.148, 0.18] while a₂ changes in the range of [0.096, 0.1].

Region (0.1008 ≤ α₂ ≤ 0.478): The system is characterized by the unstable steady state through this region in the range (0.1008 ≤ α₂ ≤ 0.18); the system is dominated by the stable periodic attractor. Figure 10 a–c indicate the dynamics of the system at α₂ = 0.12 at the corresponding initial conditions. Figure 10 a shows the time course of a₁, where a₁ fluctuates in the range of [0.113, 0.185] while time traces of a₂ shows that a₂ fluctuates in the range [0.0885, 0.1035] as shown in Fig. 10b. The phase plane is shown in Fig. 10c confirms the oscillatory attractor which is the only attractor at α₂ = 0.12 as shown through the regular limit cycles of a₁ and a₂.

Fig. 10

α₂ point

Region (0.478 ≤ α₂): The system is dominated by a stable steady state. There is also an unstable periodic attractor. Figure 11 a and b show time traces of a₁ and a₂ at α₂ = 0.8 at the corresponding initial conditions where a₁ settles down at a₁ = 0.27 while a₂ = 0.0923. Phase plane (Fig. 11c) confirms the time traces in Fig. 11a, b where the system approached a point attractor.

Fig. 11

α₂ periodic

Effect of the detuning parameter (σ₁)

Figure 12 a and b show the bifurcation analysis using the detuning parameter (σ₁) as the bifurcation parameter at γ = 50 based on the two-parameter continuation technique [44], and the rest of the parameter’s values are indicated in Table 1. Two Hopf bifurcation points are available: HB₁ appears at σ₁ = 5.95 × 10⁻⁵, a₁ = 0.1722, and a₂ = 0.08094, while HB₂ is at σ₁ =  − 0.001926, a₁ = 0.1875,and a₂ = 0.08292 as shown in Fig. 12 a, b.

Fig. 12

Bifurcation diagram of detuning parameter σ₁ as the bifurcation parameter

Region (5.95 × 10⁻⁵ ≤ σ₁): The system is dominated by the point attractor where there is only a stable steady state.

Region (−0.001926 ≤ σ₁ ≤ 5.95 × 10⁻⁵): In this region, the system is dominated by the only periodic attractor. There is also an unstable steady state. The maximum frequency for a₁ and a₂ appears close to HB₁ at σ₁ = 0, where a₁ oscillates in the range of [0.02, 0.45] as shown in Fig. 12a, and a₂ oscillates in the range of [0.045, 0.135] as shown in Fig. 12b. However, this frequency decreases continuously as σ₁ decreases until reaching HB₂ as shown in Fig. 12a, b.

Region (σ₁ ≤  − 0.001926): In this region, the system is dominated by the point attractor where a stable steady state is available, where a₁ changes in the range [0.172, 0.19] while a₂ changes in the range [0.082, 0.09] as shown in Fig. 12a, b.

Effect of the feedback signal gain (β)

Figure 13 shows the effect of feedback signal β as the main bifurcation parameter where other parameter values are shown in Table 1. There is only one HB at β = 0.1776 and a₁ = 0.1544, and a₂ = 0.5116 as shown in Fig. 13a, b, respectively.

Fig. 13

Bifurcation diagram of feedback signal gain β as the bifurcation parameter

Region (0.1776 ≤ β): The system is controlled by only a stable steady state, where a₁ changes in the range of [0.1 0.1544] (Fig. 13a) while a₂ changes in the range of [0.1, 0.51].

Region (0.133 ≤ β ≤ 0.1776): In this region, the system is controlled by stable periodic attractor where a₁ changes in the range of [0.01, 1] as shown in Fig. 13a while a₂ oscillates in the range of [0.1, 1.4] as shown in Fig. 13b.

Region (β ≤ 0.133): The system has no stable behavior where there are unstable steady state and unstable periodic behavior as shown in Fig. 13a, b.

Effect of the control signal gain (γ)

Figure 14 shows the effect of control signal γ as the main bifurcation parameter where the rest of the parameter’s values are indicated in Table 1. There is only one HB at γ = 47.56 and a₁ = 0.1691, and a₂ = 0.08244 as shown in Fig. 14a, b, respectively. The behavior of the system can be described as follows:

Fig. 14

Bifurcation diagram of the control signal gains γ as the bifurcation parameter

Region (γ ≤ 47.56): The system is controlled by only a stable steady state where a₁ exists in the range of [0.01, 0.1691] (Fig. 14a) while a₂ changes in the range of [0.575, 0.08244] as shown in Fig. 14b.

Region (47.56 ≤ γ): In this region, the system is dominated by stable periodic attractor, where the frequency of a₁ increases as γ increases in the right side until it reaches the maximum at γ = 47.56, where a₁ oscillates in the range of [0.01, 0.95] as shown in Fig. 14a while a₂ oscillates in the range of [0.025, 0.18] as shown in Fig. 14b.

Effect of the natural frequency (ω₁)

The effect of ω₁ as the main bifurcation parameter is indicated in Fig. 15 where the other parameter values are taken from Table 1. There is only HB point at ω₁ = 3.283, a₁ = 0.01664, and a₂ = 0.5767 as shown in Fig. 15a, b. The system behavior due to changing ω₁ can be described as follows:

Fig. 15

Bifurcation diagram of natural frequency ω₁ as the bifurcation parameter

Region (3.283 ≤ ω₁): In this region, the system is controlled by point attractor, where a₁ changes in the range of [0.017, 0.02], and a₂ changes in the range of [0.57, 0.6] as shown in Fig. 15a, b, respectively.

Region (2.85 ≤ ω₁ ≤ 3.283): The system is dominated by periodic attractors where there are stable periodic attractors and unstable point attractors. Figure 15 a shows that the frequency of a₁ increases as ω₁ decreases in this region until it reaches the maximum at ω₁ = 2.85 where a₁ oscillates in the range [0.01, 0.24]. Figure 15b shows that the a₂ has the maximum frequency range of [0.5, 1.2] at ω₁ = 2.85.

Region (ω₁ ≤ 2.85): In this region, the system has unstable oscillations and unstable steady state. There is neither point nor periodic attractors as shown in Fig. 15a, b.

Numerical validation

Figure 16 shows time trace of the controlled system Eqs. (1) and (2) and the approximate modulated amplitudes of Eqs. (34)–(37) which obtained from perturbation analysis of the controlled system. From the comparison, we concluded that the predictions obtained from approximated analytical solutions using the MSP method agree well with the numerical solutions found by the RK.

Fig. 16

Comparison between RK and MSP methods at Ω₁ ≅ ω₁, Ω₂ ≅ 2ω₁, ω₁ ≅ 3ω₂

Figures 17 and 18 show a good agreement between the numerical solution of the original system (1) and (2) using the RK method and approximate solution using the MSP method. Also, the results obtained in Fig. 17 agreement with the results obtained in Fig. 5. The saturation phenomenon occurs for increasing feedback signal gain β as shown in Fig. 18.

Fig. 17

Comparison between RK and MSP methods at Ω₁ ≅ ω₁, Ω₂ ≅ 2ω₁, ω₁ ≅ 3ω₂

Fig. 18

Comparison between RK and MSP methods at Ω₁ ≅ ω₁, Ω₂ ≅ 2ω₁, ω₁ ≅ 3ω₂

Comparison with previous work

In [26], the active vibration controller 1:2 for suppressing the vibration of the nonlinear composite beam subjected to parametric excitation force only has been studied. In this paper, an active vibration controller 1:3 for suppressing the vibration of the nonlinear composite beam subjected to parametric and external excitation forces has been studied. Bifurcation analysis is conducted using various control parameters such as natural frequency (ω₁), detuning parameter (σ₁), feedback signal gain (β), control signal gain (γ), and other parameters. The dynamic behavior of the system is predicted within various ranges of bifurcation parameters. All of the stable steady state (point attractor), stable periodic attractor, unstable steady state, and unstable periodic attractors were determined efficiently using bifurcation analysis. The controller’s influence on system behavior is examined numerically.

Conclusions

The main objective of the work is to control the vibration of a nonlinear composite cantilever beam with external and parametric excitation forces. We applied the MSP technique to solve those nonlinear equations. We applied Lyapunov’s first method to investigate the stability of the controlled system. The corresponding FR equations have been extracted and presented graphically at different system parameters. The obtained curves were confirmed numerically applying the RK algorithm. Bifurcation analysis was conducted using many bifurcation parameters such as f₂, α₂, σ₁, β, γ, and ω₁. The nonlinear controller has been studied at Ω₁ ≅ ω₁, Ω₂ ≅ 2ω₁, ω₁ ≅ 3ω₂. To validate our results, the approximated analytical solution using the MSP perturbation method is compared with the numerical solution using the RK method of order four. From a previous comprehensive study, the following points are concluded:

• 1. The composite beam amplitude in the case of no controller at the simultaneous principal and primary parametric resonance Ω₁ ≅ ω₁, Ω₂ ≅ 2ω₁ is multiplied to about 30 times of the parametric excitation amplitude f₂.

• 2. The controller 1 : 3 is efficient for lowering the high steady state amplitude vibration of the composite beam.

• 3. Increasing the feedback signal β obtained the better of the vibration damping effect of the composite beam.

• 4. For increasing the linear damping μ₁ and natural frequency ω₁, the efficient frequency bandwidth of the controller and the better of vibration damping the composite beam influence.

• 5. For decreasing the control signal γ and excitation forces f₁ and f₂, the effective frequency bandwidth of the saturation controller can be improved and increase the vibration reduction action of the composite beam.

• 6. The overload controller risk decreases as the control signal γ increases.

• 7. The saturation phenomenon occurs for increasing feedback signal gain β.

• 8. The excitation force amplitude is increased as the steady state amplitude increased and lost its stability.

• 9. The composite beam amplitude is inversely proportional to the damping coefficient μ₁ and natural frequency ω₁.

• 10. The validation of our results has been done, where the approximate analytical solutions are compatible with the numerical solutions.

• 11. The dynamic system behavior was determined at different regions of the bifurcation parameters where all stable steady state, stable periodic, unstable steady state, and periodic attractors were evaluated.

In future work, we present some suggestions for further developments. Involving higher order nonlinearities to make the mathematical model closer to the real-life of a composite cantilever beam. Also, we intend to implement another control.