Introduction

Non-linear beam vibration modeling helps in the design and analysis of mechanical structures subjected to dynamic loads. This includes applications in aerospace, automotive, and civil engineering, where accurate prediction of structural responses under varying conditions is crucial for ensuring safety and performance [1, 2]. In both industry and construction, beams are one of the most important structural elements. In addition to applications in micro- and nano-scale structures, this structural member can also be used in macro-scale structures, such as airplane wings, flexible satellites, and bridge spans [3,4,5]. It is, therefore, possible to model and analyze many members of the structure as beams. To achieve a suitable design in beam-shaped members, it is particularly important to understand how the beam vibrates in transverse modes and to determine its natural frequencies. It is more evident that fatigue of the beam's constituent materials and its overall structural failure occurs in large-range vibrations, where effects raised around the natural frequency play an even greater role [6,7,8,9,10]. As a result, the non-linear effects in the equations governing beam vibrations are of greater importance [11].

Non-linear terms in vibration equations can be derived from geometrical, inertial, or material sources [12]. The stretching of the middle plane and the presence of large curvatures can result in geometric non-linearity. Material non-linearity is a result of a non-linear relationship between stress and strain in the beam material. Additionally, asymmetrically distributed and concentrated masses contribute to the non-linearity of inertia. In some studies, the vibration behavior of mechanical systems has been modeled using multi-degree-of-freedom models [13,14,15,16,17] or continuous media theory [18, 19]. Based on Euler-Bernoulli's theory, it is assumed that beam cross-sections remain perpendicular to the main axis during deformation [20]. According to this theory, transverse vertical strains and shear deformations are not taken into account. A study conducted by Abohamer et al. [21] delves into the dynamic analysis of a novel three-degree-of-freedom mechanism comprising two interconnected segments. The system is subject to external harmonic forces to induce motion. The dynamical system’s stability and vibration, as explored by Abohamer et al. [22], have been rigorously modeled. The homotopy analysis method was used by Javidi et al. [23] to investigate the non-linear behavior of a beam under axial load and to obtain a suitable expression to express the frequency of such non-linear behavior. This method was applied by Sediqi et al. [24] to analyze beam vibrations with non-linear damping, and acceptable results were obtained. Liu et al. have investigated the non-linear forced vibrations of functionally graded three-phase composite cylindrical shells [25]. Zheng et al. [26] studies focus on examining how rotating composite blades chaotically respond to vibrations, specifically looking at resonant responses and the occurrence of double-parameter multi-pulse vibrations. Liu et al. [27] investigated three specific phenomena in the context of a large deployable space antenna experiencing thermal load and internal resonance at a 1:3 ratio. The three phenomena being studied are non-linear vibrations, Andronov-Hopf bifurcations, and Pomeau-Manneville intermittent chaos. This research is the first of its kind to explore these aspects of the LDSA under these specific conditions. Liu et al. [28] studied the non-linear breathing vibrations of an eccentric rotating composite laminated circular cylindrical shell subjected to lateral and temperature excitations. The governing equations of motion are established based on Donnell thin shear deformation theory, von Karman-type non-linear relation, and Hamilton's principle. Mejia-Nava et al. [29] investigated the conditions of creating a non-linear bifurcation in cantilever beams through analytical analysis. Using the multiple time scale method, Ding et al. [30] considered the non-linear vibrations of a supported beam with asymmetric elastic supports, taking into account the effects of shear deformation and rotational inertia. Akkoca et al. [31] modeled the equations for a beam and took into account the effect of elongation in the middle plane. The frequency response of the device was then studied using the multiple time scale method in two modes, primary and secondary resonance. Lewandowski [32] demonstrates a method for analyzing steady-state vibrations of geometrically non-linear systems utilizing a harmonic balance approach with an exponential version. An analysis of the method and the numerical procedure corresponding to it is provided in detail. Geometric non-linearity is described through the von Karman theory. According to the first-order shear deformation theory, Sohani et al. [33] present an analytical procedure for forecasting the non-linear natural frequencies of beams. It is assumed by the non-linear kinematics assumptions that the transverse deflection and mid-plane stretching, which, utilizing von Kármán connections, are defined, will exhibit moderately large deformations. Hooke's law is utilized as the constitutive equation because the strains are small. Hamilton's principle is utilized to derive coupled non-linear longitudinal-transverse motion equations. In the results, the axial and transverse amplitudes of vibrations have a significant effect on the non-linear frequencies. Zamani et al. conducted an examination of large-amplitude free vibrations of simply supported beams [34] utilizing the method of finite elements. According to the Rayleigh-Ritz method, they presented an analytical expression.

Numerous investigations in the realm of beam vibration analysis from a non-linear perspective primarily focus on the inclusion of the third-order non-linear term while disregarding the influence of higher-order terms, subsequently resolving the issue through analytical methods [35,36,37]. A comprehensive review of existing literature underscores a notable gap in the exploration of non-linear beam vibrations under parametric excitation. This article seeks to address this gap by first establishing the governing equations for the non-linear vibrations of a three-dimensional Euler-Bernoulli beam subjected to parametric excitations and midplane elongation. Subsequently, the force response, as well as the beam's frequency response, are ascertained utilizing the multiple time scale method. A detailed examination of the beam’s frequency response is undertaken to elucidate the occurrences of supercritical pitchfork bifurcation and continuous or safe bifurcations. Various design parameters are scrutinized to assess their influence on this significant non-linear phenomenon.

Equations of motion

The geometric model of the clamped-clamped beam and coordinate system are shown in Fig. 1. Partial differential equations controlling the Euler-Bernoulli beam's transverse vibrations, taking into account the variable axial force along the length of the beam, are obtained as follows [38].

$$\begin{gathered} \frac{{\partial T\left( {x,t} \right)}}{\partial x} = p_{X} \hfill \\ m\frac{{\partial^{2} V\left( {x,t} \right)}}{{\partial t^{2} }} - \frac{\partial }{\partial x}\left[ {T\left( {x,t} \right)\frac{{\partial V\left( {x,t} \right)}}{\partial x}} \right] + \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {EI\frac{{\partial^{2} V\left( {x,t} \right)}}{{\partial x^{2} }}} \right]\,\,\, = p_{Y} \hfill \\ m\frac{{\partial^{2} W\left( {x,t} \right)}}{{\partial t^{2} }} - \frac{\partial }{\partial x}\left[ {T\left( {x,t} \right)\frac{{\partial W\left( {x,t} \right)}}{\partial x}} \right] + \frac{{\partial^{2} }}{{\partial x^{2} }}\left[ {EI\frac{{\partial^{2} W\left( {x,t} \right)}}{{\partial x^{2} }}} \right]\,\,\, = p_{Z} \hfill \\ \end{gathered}$$
(1)
Fig. 1
figure 1

Geometric of the clamped-clamped Euler-Bernoulli beam

Full size image

In Eq. (1), V(x,t) and W(x,t) are the transverse deformation of the beam in two directions perpendicular to the longitudinal axis of the beam. I is the moment of cross-sectional of inertia, m is the mass per unit length, E is the modulus of elasticity, T is the axial force along the length of the beam, t is time, x is displacement, and (px, py, pz) are forces components acting on the beam. In the derivation of these equations, it is assumed that transverse vibrations are carried out slowly; that is, the speed of beam oscillations is low. Also, dynamic stimulation is applied slowly in the upper support. Therefore, the longitudinal inertia term is omitted in these equations.

Galerkin technique is utilized to convert partial differential equations into ordinary differential equations. For this purpose, the hypothesis solution of Eq. (1) is considered as

$$V\left( {x,t} \right) = \Phi_{1} (x)v(t),\,\,\,\,\,\,W\left( {x,t} \right) = \Phi_{2} (x)w(t)$$
(2)

In line with using the Galerkin technique for the present problem, in Eq. (2), \(\Phi_{1} (x)\) and \(\Phi_{2} (x)\) are assumed as one of the linear modes of beam vibrations in its transverse directions. Therefore, v(t) and w(t) are the time-dependent amplitudes of beam vibrations. The boundary conditions for the beam in Fig. 1 are as follows:

$$V(0,t) = \frac{\partial V(0,t)}{{\partial x}} = 0,\,\,\,V(L,t) = \frac{\partial V(L,t)}{{\partial x}} = 0$$
(2a)
$$W(0,t) = \frac{\partial W(0,t)}{{\partial x}} = 0,\,\,\,W(L,t) = \frac{\partial W(L,t)}{{\partial x}} = 0$$
(2b)
$$U(0,t) = 0,\,\,\,U\left( {L,t} \right) = s_{0} + f(t)$$
(2c)

In the above equations, s0 and f(t) are, respectively, the initial static displacement and the dynamic displacement applied to the left support of the beam. According to the defined boundary conditions, at first, the upper support of the beam is under initial static displacement. Then, during vibrations, stimulation is applied to it in the form of dynamic displacement through the upper support. From Eq. (2a), an expression can be obtained to express the axial force. By performing mathematical operations, the axial force is obtained by ignoring its changes along the length of the beam and by ignoring volume forces and other external forces, as follows:

$$T\left( t \right) = \frac{{EAU_{0} }}{L} + \frac{EA}{L}\left\{ {f\left( t \right) + \frac{1}{2}\int\limits_{0}^{L} {\left( {\left( {\frac{\partial W}{{\partial x}}} \right)^{2} + \left( {\frac{\partial V}{{\partial x}}} \right)^{2} } \right)dx} } \right\}$$
(3)

As can be seen in Eq. (3), the obtained axial force is only a function of time. In the continuation of using the Galerkin method, it is assumed that [39, 40]:

$$\phi_{1} \left( x \right) = \phi_{2} \left( x \right) = \cosh \left( {\lambda x} \right) - \cos \left( {\lambda x} \right) + \frac{{\cosh \left( {\lambda L} \right) - \cos \left( {\lambda L} \right)}}{{\sinh \left( {\lambda L} \right) - \sin \left( {\lambda L} \right)}}\left[ {\sinh \left( {\lambda x} \right) - \sin \left( {\lambda x} \right)} \right]$$
(4)

By inserting Eq. (3) into Eq. (1), the following equation can be written:

$$EI\frac{{\partial^{4} V}}{{\partial X^{4} }} - \frac{EA}{L}\frac{\partial }{\partial X}\left[ {\left( {s_{0} + \left\{ {f\left( t \right) + \frac{1}{2}\int\limits_{0}^{L} {\left( {\left( {\frac{\partial W}{{\partial x}}} \right)^{2} + \left( {\frac{\partial V}{{\partial x}}} \right)^{2} } \right)dx} } \right\}} \right)\frac{\partial V}{{\partial X}}} \right] + \,\,m\frac{{\partial^{2} V}}{{\partial t^{2} }} = 0$$
(5a)
$$EI\frac{{\partial^{4} W}}{{\partial X^{4} }} - \frac{EA}{L}\frac{\partial }{\partial X}\left[ {\left( {s_{0} + \left\{ {p\left( t \right) + \frac{1}{2}\int\limits_{0}^{L} {\left( {\left( {\frac{\partial W}{{\partial x}}} \right)^{2} + \left( {\frac{\partial V}{{\partial x}}} \right)^{2} } \right)dx} } \right\}} \right)\frac{\partial W}{{\partial X}}} \right] + \,\,m\frac{{\partial^{2} W}}{{\partial t^{2} }} = 0$$
(5b)

By using Eq. (4), the boundary conditions are defined for the beam, and by applying the Galerkin technique to the latter equations, the following system of equations is achieved. The weight function used in the Galerkin technique is the same as the first linear mode of the clamped-clamped beam.

$$\,\left\{ \begin{gathered} \ddot{v}\left( t \right)\, + \,\left( {\omega_{0}^{2} \, + \,\lambda f(t)} \right)v(t)\, + \,\beta \left( {v(t)^{3} \, + \,v(t)w(t)^{2} } \right)\, = \,0 \hfill \\ \ddot{w}\left( t \right)\, + \,\left( {\omega_{0}^{2} \, + \,\lambda f(t)} \right)w(t)\, + \,\beta \left( {w(t)^{3} \, + \,w(t)v(t)^{2} } \right)\, = \,0 \hfill \\ \end{gathered} \right.$$
(6)

The Eq. (6) is the characteristic equation of beam vibrations. The coefficients introduced in Eq. (6) are given in the appendix. In the following, the solution of this system of equations will be discussed. The basic conditions for solving this system of equations are considered as zero initial conditions.

Methods

While numerical solution and finite element methods have seen significant development across various engineering disciplines [41,42,43,44,45], the provision of analytical methods remains crucial for addressing non-linear equations and comprehensively understanding system behavior. The multiple time scale method [46,47,48], also known as multiscale analysis or hierarchical modeling, is a technique commonly employed in dynamical systems and mathematical modeling to analyze systems with weakly non-linear behavior. In our study, we utilized the multiple time scale method to address the complex interactions and dynamics observed in the non-linear vibration of the beam. The system of Eq. (6) is solved utilizing the multiple time scale technique. According to this method, these equations are rewritten as follows [49]:

$$\begin{gathered} \ddot{v}\left( t \right)\, + \,\omega_{0}^{2} v(t)\, + \varepsilon \left[ {\,\lambda p(t)v(t)\, + \,\alpha v(t)^{3} \, + \,\,\beta v(t)w(t)^{2} } \right]\, = \,0 \hfill \\ \ddot{w}\left( t \right)\, + \,\omega_{0}^{2} \,w\left( t \right) + \varepsilon \,\left[ {\lambda p(t)w(t)\, + \,\alpha w(t)^{3} \, + \,\,\beta w(t)v(t)^{2} } \right]\, = \,0 \hfill \\ \end{gathered}$$
(7)

In Eq. (7), ε is a small parameter. According to the multiple time scale method, the answer is considered as Eq. (8):

$$\left\{ \begin{gathered} v(T_{0} ,T_{1} ) = v_{0} \left( {T_{0} ,T_{1} } \right) + \varepsilon v_{1} \left( {T_{0} ,T_{1} } \right) \hfill \\ w(T_{0} ,T_{1} ) = w_{0} \left( {T_{0} ,T_{1} } \right) + \varepsilon w_{1} \left( {T_{0} ,T_{1} } \right) \hfill \\ \end{gathered} \right.$$
(8)

In this equation, T0=t and T1=εt represent fast and slow time scales. Next, the linear damping term is added to Eq. (7), and then Eq. (8) is inserted into Eq. (7). After that, by adjusting the obtained equations according to the power of the small parameter ε on both sides of the equations, in such a way that equal coefficients ε are placed on both sides of the equation, the collection of linear differential equations that follows is gained:

$$O\left( {\varepsilon^{0} } \right):\,\,\,\,\,\left\{ \begin{gathered} \ddot{v}_{0} \left( {T_{0} ,T_{1} } \right) + \omega_{0}^{2} v_{0} \left( {T_{0} ,T_{1} } \right) = 0 \hfill \\ \ddot{w}_{0} \left( {T_{0} ,T_{1} } \right) + \omega_{0}^{2} w_{0} \left( {T_{0} ,T_{1} } \right) = 0 \hfill \\ \end{gathered} \right.$$
(9a)
$$O\left( {\varepsilon^{1} } \right):\,\,\,\left\{ \begin{gathered} \ddot{v}_{1} \left( {T_{0} ,T_{1} } \right) + \omega_{0}^{2} v_{1} \left( {T_{0} ,T_{1} } \right) = \delta p\left( t \right)v_{0} \left( {T_{0} ,T_{1} } \right) + \alpha v_{0} \left( {T_{0} ,T_{1} } \right)w_{0} \left( {T_{0} ,T_{1} } \right)^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 2\frac{{\partial^{2} v_{0} \left( {T_{0} ,T_{1} } \right)}}{{\partial T_{0} \partial T_{1} }} + \mu \frac{{\partial v_{0} \left( {T_{0} ,T_{1} } \right)}}{{\partial T_{0} }} + \alpha v_{0} \left( {T_{0} ,T_{1} } \right)^{3} \hfill \\ \,\,\,\,\, \hfill \\ \ddot{w}_{1} \left( {T_{0} ,T_{1} } \right) + \omega_{0}^{2} w_{1} \left( {T_{0} ,T_{1} } \right) = \delta p\left( t \right)w_{0} \left( {T_{0} ,T_{1} } \right)\,\, + \alpha w_{0} \left( {T_{0} ,T_{1} } \right)v_{0} \left( {T_{0} ,T_{1} } \right)^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + 2\frac{{\partial^{2} w_{0} \left( {T_{0} ,T_{1} } \right)}}{{\partial T_{0} \partial T_{1} }} + \mu \frac{{\partial w_{0} \left( {T_{0} ,T_{1} } \right)}}{{\partial T_{0} }} + \alpha w_{0} \left( {T_{0} ,T_{1} } \right)^{3} \hfill \\ \, \hfill \\ \end{gathered} \right.$$
(9b)

In Eq. (9), μ is the linear damping coefficient. As can be seen, the solutions of Eq. (9) are interdependent. The solution of the first device is obtained in the form of Eq. (10):

$$\left\{ \begin{gathered} v_{0} \left( {T_{0} ,T_{1} } \right) = A_{1} \left( {T_{1} } \right)e^{{i\omega_{0} T_{0} }} + \overline{A}_{1} \left( {T_{1} } \right)e^{{ - i\omega_{0} T_{0} }} \hfill \\ w_{0} \left( {T_{0} ,T_{1} } \right) = A_{2} \left( {T_{1} } \right)e^{{i\omega_{0} T_{0} }} + \overline{A}_{2} \left( {T_{1} } \right)e^{{ - i\omega_{0} T_{0} }} \hfill \\ \end{gathered} \right.$$
(10)

The parametric excitation, which is applied in the form of displacement at the end of the beam in Fig. 1, is expressed by Eq. (11):

$$f\left( t \right) = \frac{1}{2}K\left( {e^{{i\Omega T_{0} }} + e^{{ - i\Omega T_{0} }} } \right)$$
(11)

In Eq. (10), K is the beam support's dynamic displacement range, as well as Ω is the excitation frequency. By defining the resonance deviation parameter as below, it is possible to check the force response of the system in the sub-harmonic mode [50]. Assuming that the external excitation has primary resonances, the excitation frequency is assumed to be:

$$\Omega = 2\omega_{0} + \varepsilon \sigma$$

in which σ is the detuning parameter. By inserting Eq. (10) into Eq. (9), to prevent the occurrence of secular terms in the solution of the problem, the coefficient \(e^{{i\omega_{0} T_{0} }}\) should be set to zero, as a result:

$$\left\{ \begin{gathered} - 2\left( {i\frac{{\partial A_{1} \left( {T_{1} } \right)}}{{\partial T_{1} }}} \right)\omega_{0} + \frac{1}{2}\alpha \left( {3A_{1} \left( {T_{1} } \right)^{2} + \overline{A}_{2}^{2} \left( {T_{1} } \right)} \right)\,\,\overline{A}_{1} \left( {T_{1} } \right)\, + \,\frac{1}{2}A_{1} \left( {T_{1} } \right)\left( {2\overline{A}_{2} \left( {T_{1} } \right)A_{2} \left( {T_{1} } \right)\alpha + i\mu \omega_{0} } \right) = 0 \hfill \\ - 2\left( {i\frac{{\partial A_{2} \left( {T_{1} } \right)}}{{\partial T_{1} }}} \right)\omega_{0} + \frac{1}{2}\alpha \left( {3A_{2} \left( {T_{1} } \right)^{2} + \overline{A}_{1}^{2} \left( {T_{1} } \right)} \right)\,\,\overline{A}_{2} \left( {T_{1} } \right) + \frac{1}{2}A_{2} \left( {T_{1} } \right)\left( {2\overline{A}_{1} \left( {T_{1} } \right)A_{1} \left( {T_{1} } \right)\alpha + i\mu \omega_{0} } \right) = 0 \hfill \\ \end{gathered} \right.$$
(12)

It is assumed that

$$\left\{ \begin{gathered} A_{1} \left( {T_{1} } \right) = \frac{1}{2}a_{1} \left( {T_{1} } \right)e^{{i\beta_{1} \left( {T_{1} } \right)}} ,\,\,\,\overline{A}_{1} \left( {T_{1} } \right) = \frac{1}{2}a_{1} \left( {T_{1} } \right)e^{{ - i\beta_{1} \left( {T_{1} } \right)}} \hfill \\ A_{2} \left( {T_{1} } \right) = \frac{1}{2}a_{2} \left( {T_{1} } \right)e^{{i\beta_{2} \left( {T_{1} } \right)}} ,\,\,\,\overline{A}_{2} \left( {T_{1} } \right) = \frac{1}{2}a_{2} \left( {T_{1} } \right)e^{{ - i\beta_{2} \left( {T_{1} } \right)}} \hfill \\ \end{gathered} \right.$$
(13)

where ai and βi, i = 1 and 2 are unknown constants. By incorporating these equations into Eq. (12), there are

$$\begin{gathered} - \frac{1}{4}K\delta a_{1} \left( {T_{1} } \right)e^{{i\left( {\sigma T_{1} - \beta_{1} } \right)}} - i\omega_{0} a_{1}^{\prime } \left( {T_{1} } \right)e^{{i\beta_{1} \left( {T_{1} } \right)}} + \omega_{0} a_{1} \left( {T_{1} } \right)\beta^{\prime}_{1} \left( {T_{1} } \right)e^{{i\beta_{1} \left( {T_{1} } \right)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{3}{8}\alpha a_{1} \left( {T_{1} } \right)^{3} e^{{i\beta_{1} \left( {T_{1} } \right)}} - \frac{1}{8}\alpha a_{1} \left( {T_{1} } \right)a_{2} \left( {T_{1} } \right)^{2} e^{{i\left( {2\beta_{2} \left( {T_{1} } \right) - \beta_{1} \left( {T_{1} } \right)} \right)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{1}{4}\alpha a_{1} \left( {T_{1} } \right)a_{2} \left( {T_{1} } \right)^{2} e^{{i\beta_{1} \left( {T_{1} } \right)}} - \frac{1}{2}ia_{1} \left( {T_{1} } \right)\mu \omega_{0} e^{{i\beta_{1} \left( {T_{1} } \right)}} = 0 \hfill \\ \end{gathered}$$
(14a)
$$\begin{gathered} - \frac{1}{4}K\delta a_{2} \left( {T_{1} } \right)e^{{i\left( {\sigma T_{1} - \beta_{2} } \right)}} - i\omega_{0} a_{2}^{\prime } \left( {T_{1} } \right)e^{{i\beta_{2} \left( {T_{1} } \right)}} + \omega_{0} a_{2} \left( {T_{1} } \right)\,\beta^{\prime}_{2} \left( {T_{1} } \right)e^{{i\beta_{2} \left( {T_{1} } \right)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{3}{8}\alpha a_{2} \left( {T_{1} } \right)^{3} e^{{i\beta_{2} \left( {T_{1} } \right)}} - \frac{1}{8}\alpha a_{2} \left( {T_{1} } \right)a_{1} \left( {T_{1} } \right)^{2} e^{{i\left( {2\beta_{1} \left( {T_{1} } \right) - \beta_{2} \left( {T_{1} } \right)} \right)}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, - \frac{1}{4}\alpha a_{2} \left( {T_{1} } \right)a_{1} \left( {T_{1} } \right)^{2} e^{{i\beta_{2} \left( {T_{1} } \right)}} - \frac{1}{2}ia_{2} \left( {T_{1} } \right)\,\mu \omega_{0} e^{{i\beta_{2} \left( {T_{1} } \right)}} = 0 \hfill \\ \end{gathered}$$
(14b)

By performing a series of mathematical operations on Eq. (14), the following equation is obtained:

$$\begin{gathered} \frac{1}{4}K\delta a_{1} \left( {T_{1} } \right)sin\left( {\sigma T_{1} - 2\beta_{1} } \right) + \omega_{0} a_{1}^{\prime } \left( {T_{1} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \frac{1}{8}\alpha a_{1} \left( {T_{1} } \right)\,\,a_{2} \left( {T_{1} } \right)^{2} sin\left( {2\beta_{2} \left( {T_{1} } \right) - 2\beta_{1} \left( {T_{1} } \right)} \right) + \frac{1}{2}a_{1} \left( {T_{1} } \right)\mu \omega_{0} = 0 \hfill \\ \end{gathered}$$
(15a)
$$\begin{gathered} - \frac{1}{4}K\delta a_{1} \left( {T_{1} } \right)sin\left( {\sigma T_{1} - 2\beta_{1} } \right) + \omega_{0} a_{1} \left( {T_{1} } \right)\beta^{\prime}_{1} \left( {T_{1} } \right) - \,\,\frac{3}{8}\alpha a_{1} \left( {T_{1} } \right)^{3} \hfill \\ \,\,\,\,\,\,\,\,\,\, - \frac{1}{8}\alpha a_{1} \left( {T_{1} } \right)a_{2} \left( {T_{1} } \right)^{2} \cos \,\left( {2\beta_{2} \left( {T_{1} } \right) - 2\beta_{1} \left( {T_{1} } \right)} \right) - \frac{1}{4}\alpha a_{1} \left( {T_{1} } \right)a_{2} \left( {T_{1} } \right)^{2} = 0 \hfill \\ \end{gathered}$$
(15b)

The parameters are defined as follows:

$$\left\{ \begin{gathered} \sigma T_{1} - 2\beta_{1,2} = \psi_{1,2} \hfill \\ 2\beta_{1} - 2\beta_{2} = \eta \hfill \\ \end{gathered} \right.$$
(16)

According to the examination of vibrations around the stable point of motion, such as the center points in the phase plane diagrams, Eq. (17) is written:

$$a^{\prime}_{1,2} \left( {T_{1} } \right) = 0,\,\,\psi^{\prime}_{1,2} = 0$$
(17)

The above equations state that, near the stable points of the vibrating system, the oscillations’ amplitude and phase will not change. According to the mentioned points, the system’s frequency response equations can be gained as follows:

$$\begin{gathered} \left( {\frac{1}{4}K\delta a_{1} } \right)^{2} = \left( {\frac{1}{8}\alpha a_{1} a_{2}^{2} \sin \left( \eta \right) + \frac{1}{2}a_{1} \mu \omega_{0} } \right)^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,\,\,\left( {\frac{{\omega_{0} a_{1} \sigma }}{2} - \frac{3}{8}\alpha a_{1}^{3} - \frac{1}{4}\alpha a_{1} a_{2}^{2} - \frac{1}{8}\alpha a_{1} a_{2}^{2} \cos \left( \eta \right)} \right)^{2} \hfill \\ \end{gathered}$$
(18a)
$$\begin{gathered} \left( {\frac{1}{4}K\delta a_{2} } \right)^{2} = \left( {\frac{1}{8}\alpha a_{2} a_{1}^{2} \sin \left( \eta \right) + \frac{1}{2}a_{2} \mu \omega_{0} } \right)^{2} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,\,\,\left( {\frac{{\omega_{0} a_{2} \sigma }}{2} - \frac{3}{8}\alpha a_{2}^{3} - \frac{1}{4}\alpha a_{2} a_{1}^{2} - \frac{1}{8}\alpha a_{2} a_{1}^{2} \cos \left( \eta \right)} \right)^{2} \hfill \\ \end{gathered}$$
(18b)

Equation (18) has two obvious and non-obvious solutions. The obvious solution of this equation is a1=a2=0. From solving the system of Eq. (18), it can be concluded that a1=a2. Therefore, according to this result, the frequency response and the amplitude, depending on the time of movement, in the sub-harmonic mode for the non-trivial solution, will be obtained in the following implicit form:

$$\left( {\frac{1}{2}K\delta } \right)^{2} = \left( {\mu \omega_{0} } \right)^{2} + \left( {\omega_{0} \sigma - \frac{3}{2}\alpha a_{1}^{2} } \right)^{2}$$
(19)

on the other hand

$$\beta_{1} = \frac{1}{{\omega_{0} }}\left\{ {\left[ {\left( {\frac{1}{4}\delta K} \right)^{2} - \left( {\frac{1}{2}\mu \omega_{0} } \right)^{2} } \right]^{\frac{1}{2}} + \frac{3}{4}\alpha a_{1}^{2} } \right\}T_{1} + \beta_{0}$$
(20)

In Eq. (20), β0 is the constant of integration. As a result, according to Eq. (8), the first approximation for the time response is calculated as follows:

$$v\left( t \right) = a_{1} \cos \,\left( {\left( {\omega_{0} + \frac{\varepsilon }{{\omega_{0} }}\left\{ {\left[ {\left( {\frac{1}{4}\delta K} \right)^{2} - \left( {\frac{1}{2}\mu \omega_{0} } \right)^{2} } \right]^{\frac{1}{2}} + \frac{3}{4}\alpha a_{1}^{2} } \right\}} \right)t + \beta_{0} } \right)$$
(21)

For vibrations in the z direction, a similar expression will be obtained according to the result.

Results and discussion

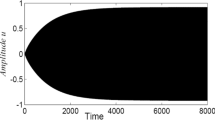
The present problem has been solved numerically to demonstrate the accuracy and correctness of the analytical solution made in this study. Figure 2 illustrates the time-dependent amplitudes of beam vibrations in one of the transverse directions. The analytical results obtained from the method of multiple time scales are in agreement with those obtained from the four-order Runge–Kutta method, as seen in the comparison figure.

Fig. 2
figure 2

Comparison of the analytical solution of multiple time scales and the fourth-order numerical solution Runge-Kutta

Full size image

Figure 3 compares the time trace of deflection obtained through our present method with the deflection response of the beam's center as determined by Barari et al. [51]. In this case, only transverse vibrations are considered and the other component of out-of-plane vibrations is neglected. A notable observation from these figures is the congruent deflection behavior exhibited by the center of the beam over an extended period, aligning with semi-analytical approaches documented in the literature. Furthermore, a parametric study has been conducted to scrutinize the time-marching response of the central deflection of the beam.

Fig. 3
figure 3

A comparison of the time history of the central deflection curve of the beam

Full size image

For different values of the resonance deviation parameter, Fig. 4 shows the force response of beam vibrations. According to this figure, the phenomenon of non-linear bifurcation may occur, both safely and catastrophic bifurcations, accompanied by the phenomenon of mutation. In the case of the parameter of deviation from negative resonance, the obvious answer will be transferred to the non-obvious answer without the occurrence of mutation, whereas when the parameter becomes positive, the transition will be accompanied by mutation. It can be seen that the bifurcation starting point for σ = 0, σ = 0.1, and σ = 0.5 occurs in the force range of K = 0.98, K = 1.95, and K = 0.2 respectively. Therefore, with the increase of the detuning parameter and the distance of the frequency of the excitation force from the natural frequency of the structure, the domain of the bifurcation phenomenon increases. Based on the analysis conducted by Nayfeh [52], stable and unstable parts of the answers have been separated. The force response of beam vibrations is illustrated in Fig. 5 as a function of the non-linear term coefficient. Using this figure, it can be seen that the starting point of bifurcation does not change when the coefficient of the non-linear term is changed. The system’s frequency response is shown in Fig. 6, which is obtained by solving Eq. (19). Based on the graph depicted in this figure, it can be seen that the graph is inclined to the right. This indicates that the hardening type has a non-linear effect on the beam equations. Conversely, the phenomenon of consecutive non-linear bifurcations is evident. The starting points of the non-linear bifurcation are specified in this figure.

Fig. 4
figure 4

The influence of resonance deviation parameter on force response curve

Full size image
Fig. 5
figure 5

The force response curve’s impact from the non-linear term coefficient

Full size image
Fig. 6
figure 6

Frequency response of beam vibrations

Full size image

In particular, when considering structures with doubly-clamped ends, the phenomenon of hardening resonance can be attributed to the tension induced during the oscillatory transverse motion of the beam. This tension, stemming from the dynamic interaction between the beam's motion and its clamped supports, contributes significantly to the observed hardening behavior in the system's resonance response. As displayed in Fig. 7, the force response diagram for several different values of the linear damping coefficient is shown at the point σ = 0.1. As can be displayed in this figure, with the rise of the damping coefficient, the phenomenon of critical bifurcation tends to be a safe bifurcation without mutation phenomenon. Also, by raising the value of the linear damping coefficient, the starting point of bifurcation moves away from the coordinate origin. Figure 8 examines the effect of the parametric excitation coefficient on the frequency response of the system. As it is known, this parameter affects the starting point of non-linear bifurcation.

Fig. 7
figure 7

Non-linear bifurcation diagram for σ = 0.1

Full size image
Fig. 8
figure 8

Excitation coefficient's impact on frequency response

Full size image

According to Fig. 9, increasing the non-linear coefficient results in the graph becoming more skewed to the right, which is to say, it becomes more hardening. The results suggest that non-linear effects exhibit a hardening behavior of the system’s equivalent spring. Additionally, as these effects become more pronounced, there is a discernible increase in the degree of amplitude distortion towards the right. Given that the natural frequency is one of the pivotal factors influencing the dynamics of forced vibrations in structures subjected to parametric excitation, its value was thoroughly examined in this study. Figure 10 illustrates the outcomes, indicating a substantial impact of this parameter on the frequency curve of the beam. Specifically, it induces a softening behavior in the stiff spring, as evidenced by the observed trends. Unlike the parametric excitation coefficient, this parameter reduces the hardening effect and also reduces the starting point of the non-linear bifurcation, as opposed to the non-linear stiffness coefficient.

Fig. 9
figure 9

Effect of non-linear term coefficients on frequency response

Full size image
Fig. 10
figure 10

The effect of the linear natural frequency of the system on the frequency response

Full size image

Conclusions

In conclusion, this study contributes to the field of structural dynamics by presenting a comprehensive analysis of the non-linear vibrations of beams. By considering the effect of mid-plane elongation in the analysis, the study offers valuable insights into the intricate dynamics of three-dimensional beams. The incorporation of this aspect enhances the accuracy and relevance of the analysis, thereby advancing our understanding of beam vibrations and their implications for structural design. Moving forward, the study’s conclusions can serve as a foundation for further research in this area and inform the development of more robust design methodologies for industrial and construction structures.

Incorporating the elongation of the beam’s middle plane led to the emergence of non-linear terms in the equations, contributing to a hardening state in the frequency response diagram. Notably, an increase in the coefficient of these non-linear terms was observed to reduce the fluctuation period, elucidating the intricate dynamics of the system. Analysis of the force response graphs revealed the presence of non-linear bifurcations, signifying critical transitions in the system's behavior. Notably, adjustments to the parameters of deviation from resonance and damping coefficient could transform critical bifurcations into safe ones, highlighting the potential for control and mitigation strategies. Furthermore, an examination of the frequency response demonstrated that increasing the linear frequency led to a decrease in non-linear stiffness and displacement at the starting points of non-linear bifurcations. This insight into the interplay between linear and non-linear dynamics sheds light on the system’s response to varying excitation conditions. Moreover, variations in excitation amplitude were found to induce changes in the starting points of non-linear bifurcations, underscoring the sensitivity of the system to external influences.

Overall, the findings underscore the complex interplay between parametric excitation, non-linear dynamics, and damping effects in beam vibrations. These insights have implications for the design and control of structures subjected to dynamic loading conditions, offering avenues for optimizing performance and mitigating undesirable responses.