Introduction

Marshall and Olkin (1997) developed a new family of distributions with an additional shape parameter called Marshall and Olkin-G (MO-G) family. The survival function of MO-G family is

$$ S(x)=\frac{\lambda \overline{G}\left(x,\psi \right)}{1-\overline{\lambda}\overline{G}\left(x,\psi \right)},\lambda >0,\overline{\lambda}=1-\lambda, x\in \Re, $$
(1)

where G(x, ψ) is the baseline cumulative distribution function(cdf) which may depend on the vector parameter ψ.

Many famous MO-G families and its special distributions are available in literature such as Marshall-Olkin-G (Marshall and Olkin; 1997), the MO extended Lomax (Ghitany et al.; 2007), MO semi-Burr and MO Burr (Jayakumar and Mathew; 2008), MO q-Weibull (Jose et al.; 2010), MO extended Lindley (Ghitany et al.; 2012), the generalized MO-G (Nadarajah et al. (2013), the MO Fréchet (Krishna et al; 2013), the MO family (Cordeiro and Lemonte; 2013), MO extended Weibull(Santos-Neto et al.; 2014), the beta MO-G (Alizadeh et al. 2015), the MO generalized exponential (Ristić, & Kundu; 2015), MO gamma-Weibull (Saboor and Pogány; 2016), MO generalized-G (Yousof et al.; 2018), MO additive Weibull (Afify et al.; 2018) and Weibull MO family (Korkmaz et al.; 2019).

This paper is sketched into the following sections. In Section 2, BIIIMO-G family is development via the T-X family technique. The basic structural properties and sub-models are also studied. In Section 3, two special models are studied. Section 4, deals with linear representations for the cdf and pdf of the BIIIMO-G family. In Section 5, moments, incomplete moments, inequality measures and some other properties are theoretically derived. In Section 6, stress-strength reliability and multicomponent stress-strength reliability of the model are studied. In Section 7, BIIIMO-G family is characterized via (i) conditional expectation; (ii) ratio of truncated moments and (iii) reverse hazard rate function. In Section 8, the maximum likelihood method is employed to estimate the parameters of the Burr III Marshall Olkin Weibull (BIIIMO-W) and Burr III Marshall Olkin Lindley (BIIIMO-L) distributions. In section 9, a simulation study is performed to illustrate the performance of the maximum likelihood estimates (MLEs). In Section 10, the potentiality of BIIIMO-G family is demonstrated by its application to real data sets: survival times of leukemia patients and bladder cancer patients’ data. Goodness of fit of the probability distribution through different methods is studied. Section 11 contains concluding remarks.

Development of BIIIMO-G family

Alzaatreh et al. (2013) proposed a T-X family technique for the development of the wider families based on any probability density function (pdf). The cdf of the T-X family of distributions is given by

$$ F(x)={\int}_{a_1}^{W\left[G\left(x;\psi \right)\right]}r(t)\ dt,\kern4.25em x\in \mathrm{\mathbb{R}}, $$
(2)

where r(t) is the pdf of a random variable (rv) T, where T ∈ [a1, a2] for − ∞  ≤ a1 < a2 < ∞ and W[G(x; ψ)] is a function of the baseline cumulative distribution function (cdf) of a rv X, depending on the vector parameter ψ and satisfies three conditions i) W[G(x; ψ)] ∈ [a1, a2], ii) W[G(x; ψ)] is differentiable and monotonically increasing and iii) \( \underset{x\to -\infty }{\lim }W\left[G\left(x;\psi \right)\right]\to {a}_1 \) and \( \underset{x\to \infty }{\lim}\kern0.24em \left[G\left(x;\psi \right)\right]\to {a}_2 \). The pdf corresponding to (2) is

$$ f(x)=\left\{\frac{\partial }{\partial x}W\left[G\left(x;\psi \right)\right]\right\}r\left\{W\left[G\left(x;\psi \right)\right]\right\},\kern4.25em x\in \mathbb{R}.\kern1.25em $$
(3)

In this article, the BIIIMO-G family is developed via the T-X family technique by setting.

r(t) = αβt−β − 1{1 + t−β}−α − 1, t > 0, α > 0, β > 0, and \( W\left[G\left(x;\psi \right)\right]=-\log \left[\frac{\lambda \overline{G}\left(x,\psi \right)}{1-\overline{\lambda}\overline{G}\left(x,\psi \right)}\right] \). Then, the cdf of BIIIMO-G family is

$$ F\left(x;\alpha, \beta, \lambda, \psi \right)={\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}\left(x;\psi \right)}{1-\overline{\lambda}\overline{G}\left(x;\psi \right)}\right)\right]}^{-\beta}\right\}}^{-\alpha },x\in \mathbb{R},\kern1em $$
(4)

where  α > 0, β > 0, λ > 0 and ψ > 0 are parameters.

The pdf corresponding to (4) is given by

$$ {\displaystyle \begin{array}{l}f\left(x;\alpha, \beta, \lambda, \psi \right)=\frac{\alpha \beta g\left(x;\psi \right)}{\overline{G}\left(x;\psi \right)\left(1-\overline{\lambda}\overline{G}\left(x;\psi \right)\right)}{\left[-\log \left(\frac{\lambda \overline{G}\left(x;\psi \right)}{1-\overline{\lambda}\overline{G}\left(x;\psi \right)}\right)\right]}^{-\beta -1}\times \\ {}\kern11.51999em {\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}\left(x;\psi \right)}{1-\overline{\lambda}\overline{G}\left(x;\psi \right)}\right)\right]}^{-\beta}\right\}}^{-\alpha -1},x\in \mathbb{R},\end{array}} $$
(5)

where g(x; ψ) is the baseline pdf. In future, a rv with pdf (5) is denoted by X~BIIIMO − G(α, β, λ, ψ). The dependence on the parameter vector ψ can be omitted and simply write as g(x) = g(x; ψ),

G(x) = G(x; ψ) and f(x) = f(x; α, β, λ, ψ).

Let T be a BIII random variable with shape parameters α, β. The BIIIMO-G rv with cdf (4) can be obtained from

$$ \Pr \left(\mathrm{X}<x\right)=\Pr \left(T\le -\log \left[\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right]\right). $$

Hence, the rv \( X={G}^{-1}\left[\frac{\lambda -\lambda \exp \left(-T\right)}{\lambda +\overline{\lambda}\exp \left(-T\right)}\right] \) has the BIIIMO-G distribution. The quantile function (qf) of X is the solution of the non-linear equation

$$ x=Q(u)={Q}_G\left(1-{\left\{\overline{\lambda}+\lambda \exp \left[{\left({u}^{-\frac{1}{\alpha }}-1\right)}^{-\frac{1}{\beta }}\right]\right\}}^{-1}\right), $$

where QG(.) = G−1(.) is the qf of the baseline distribution. Hence, if U is a uniform rv on (0, 1), then X = Q(U) follows the BIIIMO-G family.

Transformations and compounding

The BIIIMO-G family is derived through (i) ratio of the exponential and gamma random variables and (ii) compounding generalized inverse Weibull-MO (GIW-MO) and gamma distributions.

Lemma

  1. i.

    Let the random variable Z1 have the exponential distribution with parameter value 1 and the random variable Z2 have the fractional gamma i.e., Z2~Gamma(α,  1). Then, for

    $$ {Z}_1={\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\kern0.24em {Z}_2, $$

we have

$$ X={G}^{-1}\left\{\frac{\lambda +\lambda \exp \left[{\left(\frac{\;{Z}_2}{\;{Z}_1}\right)}^{\frac{1}{\beta }}\right]}{\overline{\lambda}+\lambda \exp \left[{\left(\frac{\;{Z}_2}{\;{Z}_1}\right)}^{\frac{1}{\beta }}\right]}\right\}\sim BIIIMO-G\left(\alpha, \beta, \lambda, \psi \right). $$
(6)
  1. ii.

    If Y|β, λ, θ~GIWMO(y; β, λ, θ)  and  θ|α~gamma(θ; α), then integrating the effect of θ with the help of

    $$ f\left(y,\alpha, \beta, \lambda \right)=\underset{0}{\overset{\infty }{\int }}g\left(\left.y\right|\beta, \lambda, \theta \right)g\left(\left.\theta \right|\alpha \right) d\theta, $$

we have Y~BIIIMO − G(α, β, λ, ψ)..

Structural properties of BIIIMO-G family

The survival, hazard, cumulative hazard, reverse hazard functions and the Mills ratio of a random variable X with BIIIMO-G family are, respectively given, by

$$ S(x)=1-{\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{-\alpha }, $$
(7)
$$ h(x)=\frac{\frac{\alpha \beta g(x)}{\overline{G}(x)\left(1-\overline{\lambda}\overline{G}(x)\right)}{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta -1}}{{\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{\alpha +1}-\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}, $$
(8)
$$ r(x)=\frac{d}{dx}\ln {\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{-\alpha }, $$
(9)
$$ H(x)=-\ln \left[1-{\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{-\alpha}\right], $$
(10)

and

$$ m(x)=\frac{{\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{\alpha +1}-\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}{\alpha \beta \frac{\lambda g(x)}{\overline{G}(x)\left(1-\overline{\lambda}\overline{G}(x)\right)}{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta -1}}. $$
(11)

The elasticity \( e(x)=\frac{d\mathrm{lnF}(x)}{d\ln x}= xr(x) \) for BIIIMO-G family is

$$ e(x)=\frac{d}{d\ln x}\ln {\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{-\alpha }. $$
(12)

The elasticity of BIIIMO-G family shows the behavior of the accumulation of probability in the domain of the random variable.

Sub-models

The BIIIMO-G family has the following sub models (Table 1).

Table 1 Sub-models of BIIIMO distribution
Full size table

Special BIIIMO-G models

The BIIIMO-G family density (5) produces greater flexibility than any baseline distribution for data modeling. It can be most tractable, when the functions g(x; ψ) and G(x; ψ) have simple analytic expressions. Then, two special sub-models of BIIIMO-G family are introduced.

The BIIIMO-Weibull (BIIIMO-W) distribution

The cdf and pdf of the Weibull random variable are \( g\left(x;b\right)=b\;{x}^{b-1}{e}^{-{x}^b},x>0,b>0 \) and \( G\left(x;b\right)=1-{e}^{-{x}^b},x\ge 0,b>0 \) where ψ = b. Then, the pdf of the BIIIMO-W model is given by

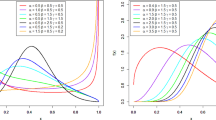
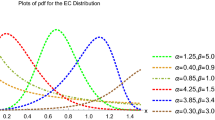
$$ {\displaystyle \begin{array}{l}f\left(x;\alpha, \beta, \lambda, b\right)=\frac{b\alpha \beta {x}^{b-1}}{\left(1-\overline{\lambda}{e}^{-{x}^b}\right)}{\left[-\log \left(\frac{\lambda {e}^{-{x}^b}}{1-\overline{\lambda}{e}^{-{x}^b}}\right)\right]}^{-\beta -1}\times \\ {}\kern11.51999em {\left\{1+\gamma {\left[-\log \left(\frac{\lambda {e}^{-{x}^b}}{1-\overline{\lambda}{e}^{-{x}^b}}\right)\right]}^{-\beta}\right\}}^{-\alpha -1},x>0,\end{array}} $$

The following graphs show that shapes of BIIIMO-W density are arc, bimodal, exponential, left- skewed, right-skewed and symmetrical (Fig. 1). The BIIIMO-W distribution has uni-model, bimodal, increasing, increasing and decreasing, inverted bathtub and modified bathtub hazard rate function (hrf) Fig. 2.

Fig. 1
figure 1

Plot of pdf of BIIIMO-W distribution for selected parameter values

Full size image
Fig. 2
figure 2

Plots of hrf of BIIIMO-W distribution for selected parameter values

Full size image

The Burr III Marshal Olkin-Lindley (BIIIMO-L) distribution

The cdf and pdf of the Lindley random variable are \( g\left(x;\psi \right)=\frac{b^2}{\left(1+b\right)}\;\left(1+x\right){e}^{- bx},x>0,b>0 \) and \( G\left(x;\psi \right)=1-\left(1+\frac{bx}{1+b}\right){e}^{- bx},x\ge 0 \) where ψ = b. Then, the pdf of the BIIIMO-L model are given by

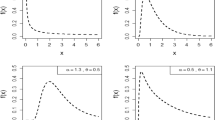
$$ {\displaystyle \begin{array}{l}f\left(x;\alpha, \beta, \lambda, b\right)=\frac{\alpha \beta \frac{b^2}{\left(1+b\right)}\;\left(1+x\right){e}^{- bx}}{\left(1+\frac{bx}{1+b}\right){e}^{- bx}}{\left\{-\log \left[\frac{\lambda \left(1+\frac{bx}{1+b}\right){e}^{- bx}}{1-\overline{\lambda}\left(1+\frac{bx}{1+b}\right){e}^{- bx}}\right]\right\}}^{-\beta -1}\times \\ {}\kern10.79999em {\left(1+{\left\{-\log \left[\frac{\lambda \left(1+\frac{bx}{1+b}\right){e}^{- bx}}{1-\overline{\lambda}\left(1+\frac{bx}{1+b}\right){e}^{- bx}}\right]\right\}}^{-\beta}\right)}^{-\alpha -1},x>0,\end{array}} $$

The following graphs show that shapes of BIIIMO-L density are J, revers J, arc, exponential, left- skewed, right-skewed and symmetrical (Fig. 3). The BIIIMO-L distribution has unimodal, increasing, increasing and decreasing, decreasing-increasing-decreasing inverted bathtub, bathtub and modified bathtub hazard rate function (Fig. 4).

Fig. 3
figure 3

Plots of pdf of BIIIMO-L distribution for selected parameter values

Full size image
Fig. 4
figure 4

Plots of hrf of BIIIMO-L distribution for selected parameter values

Full size image

Useful expansions

In this sub-section, the linear representations for the cdf and pdf of the BIIIMO-G family are obtained. The cdf in (4) can be expressed as

$$ F(x)=1-\sum \limits_{i\ge 1}^{\infty }{\left(-1\right)}^{i+1}\left({}_i^{\alpha +i-1}\right){\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{- i\beta}, $$

Following (Tahir et al. 2016), we have

$$ {\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{- i\beta}=\frac{\sum \limits_{k=0}^{\infty }{p}_k{\left[1-\left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^k}{\sum \limits_{k=0}^{\infty }{q}_k{\left(1-\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)}^k}, $$

where

$$ {p}_0=1, $$
$$ {p}_1=-\frac{1}{2} i\beta, $$
$$ {p}_2=\frac{1}{24}\left[3{\left( i\beta \right)}^2-5 i\beta \right], $$
$$ {p}_3=\frac{1}{48}\left[-{\left( i\beta \right)}^3+5{\left( i\beta \right)}^2-6 i\beta \right], $$
$$ {p}_4=\frac{1}{5760}\left[15{\left( i\beta \right)}^4-150{\left( i\beta \right)}^3+48{\left( i\beta \right)}^2-502 i\beta \right] $$

etc., and

$$ \kern0.24em {q}_k={q}_k\left( i\beta \right)=\sum \limits_{j=k}^{\infty }{\left(-1\right)}^{k+j}\left({}_j^{i\beta}\right)\left({}_k^j\right) $$

Then, we arrive at

$$ F(x)=1-\sum \limits_{i\ge 1}^{\infty }{\left(-1\right)}^{i+1}\left({}_i^{\alpha +i-1}\right)\frac{\sum \limits_{k=0}^{\infty }{p}_k{\left[1-\left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^k}{\sum \limits_{k=0}^{\infty }{q}_k{\left(1-\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)}^k}, $$

Using

$$ \frac{\sum \limits_{k=0}^{\infty }{b}_k{x}^k}{\sum \limits_{k=0}^{\infty }{a}_k{x}^k}=\frac{1}{a_0}\sum \limits_{k=0}^{\infty }{c}_k{x}^k, $$

where \( {c}_n-\frac{1}{a_0}\sum \limits_{k=1}^n{c}_{n-k}{a}_k-{b}_n=0 \) (see Gradshteyn and Ryzhik 2014),

we obtain \( F(x)=1-\frac{\sum \limits_{i\ge 1}^{\infty }{\left(-1\right)}^{1+i}\left({}_i^{\alpha +i-1}\right)}{q_0}\sum \limits_{k=0}^{\infty }{c}_k\underset{A}{\underbrace{{\left[1-\left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^k}}. \)

By applying the power series to the quantity A,

$$ {\left(1-z\right)}^{k-1}=\sum \limits_{h=0}^{\infty }{\left(-1\right)}^h\left({}_h^{k-1}\right){z}^h, $$

where |z| < 1 and b is a real non-integer, we obtain

$$ F(x)=1-\sum \limits_{i\ge 1}^{\infty }{\left(-1\right)}^{1+i}\left({}_{\kern0.84em i}^{\alpha +i-1}\right)\frac{1}{q_0}\left[{c}_0+\sum \limits_{k=1}^{\infty }{c}_k\sum \limits_{h=1}^k{\left(-1\right)}^h{\lambda}^h\left({}_h^k\right)\overline{G}{(x)}^h\underset{B}{\underbrace{{\left[1-\left(1-\lambda \right)\overline{G}(x)\right]}^{-h}}}\right]. $$
(13)

For 0 < λ ≤ 1, applying \( {\left(1-x\right)}^{-n}=\sum \limits_{\mathrm{\ell}=0}^{\infty}\left({}_{n-1}^{n+\mathrm{\ell}-1}\right){x}^{\mathrm{\ell}} \) to the quantity B, we arrive

$$ {\displaystyle \begin{array}{l}F(x)=1-\sum \limits_{i\ge 1}^{\infty }{\left(-1\right)}^{1+i}\left({}_{\kern0.72em i}^{\alpha +i-1}\right)\frac{1}{q_0}\left[{c}_0+\sum \limits_{k=1}^{\infty }{c}_k\sum \limits_{h=1}^k{\left(-1\right)}^h\left({}_h^k\right){\lambda}^h\sum \limits_{j=0}^{\infty}\left({}_{n-1}^{n+j-1}\right){\left(1-\lambda \right)}^j\overline{G}{(x)}^{j+h}\right]\\ {}=1+\left[\begin{array}{l}\sum \limits_{i\ge 1}^{\infty}\frac{c_0}{q_0}{\left(-1\right)}^{2+i}\left({}_{\kern0.72em i}^{\alpha +i-1}\right)\\ {}+\sum \limits_{j=0}^{\infty}\sum \limits_{h=1}^k\sum \limits_{k=1}^{\infty}\sum \limits_{i\ge 1}^{\infty}\frac{c_k}{q_0}{\left(-1\right)}^{2+h+i}{\left(1-\lambda \right)}^j{\lambda}^h\left({}_h^k\right)\left({}_{n-1}^{n+j-1}\right)\left({}_{\kern0.72em i}^{\alpha +i-1}\right)\overline{G}{(x)}^{j+h}\end{array}\right]\end{array}} $$
$$ F(x)=1+\sum \limits_{i\ge 1}^{\infty }{v}_i+\sum \limits_{j=0}^{\infty}\sum \limits_{h=1}^k\sum \limits_{k=1}^{\infty }{v}_{\mathrm{j},h}{\overline{H}}_{j+h}(x), $$
(14)

where

$$ {v}_{j,h}=\sum \limits_{i\ge 1}^{\infty}\frac{c_k}{q_0}{\left(-1\right)}^{2+h+i}{\left(1-\lambda \right)}^j{\lambda}^h\left({}_h^k\right)\left({}_{n-1}^{n+j-1}\right)\left({}_{\kern0.72em i}^{\alpha +i-1}\right) $$
$$ {v}_i=\frac{c_0}{q_0}{\left(-1\right)}^{2+i}\left({}_{\kern0.72em i}^{\alpha +i-1}\right) $$

and

$$ {\overline{H}}_{\theta }(x)=\overline{G}{(x)}^{\theta } $$

is the cdf of the Lehmann type II Exp (1-G) model with power θ > 0.

By differentiating (14) we get.

$$ f(x)=\sum \limits_{j=0}^{\infty}\sum \limits_{h=1}^k\sum \limits_{k=1}^{\infty }{v}_{\mathrm{j},h}{h}_{j+h}(x), $$
(15)

and

$$ {h}_{\theta }(x)=\theta g(x)\overline{G}{(x)}^{\theta -1} $$

is the pdf of the Lehmann type II Exp (1-G) model with power θ > 0. Equations (14) and (15) reveal that the BIIIMO-G density can be written as linear combinations of the Lehmann type II Exp(1-G) density functions. So, all properties of the new family can be derived based on the Lehmann type II Exp(1-G) density.

Moments

Moments, incomplete moments, inequality measures and some other properties are theoretically derived in this section.

Moments about origin

The rth moment of X, say \( {\mu}_r^{\prime } \), follows from (15) as

$$ {\mu}_r^{\hbox{'}}=E\left({X}^r\right)=\sum \limits_{j=0}^{\infty}\sum \limits_{h=1}^{\mathrm{k}}\sum \limits_{k=1}^{\infty}\;{v}_{j,h}E\left({Y}_m^r\right) $$
(16)

Henceforth, Ym denotes the Lehmann type II exp-(1-G) distribution with power parameter m.

The nth central moment of X, say Mn, is given by

$$ {M}_n=E{\left(X-{\mu}_1^{\prime}\right)}^n=\sum \limits_{r=0}^n\sum \limits_{j=0}^{\infty}\sum \limits_{h=1}^{\mathrm{k}}\sum \limits_{k=1}^{\infty }{\mathrm{v}}_{j,h}{\left(-1\right)}^{n-r}\left(\begin{array}{l}n\\ {}r\end{array}\right){\mu}_r^{\prime \left(n-r\right)}E\left({Y}_m^r\right) $$
(17)

The cumulants (κn) of X follow recursively from

$$ {\kappa}_n={\mu}_n^{\hbox{'}}-\sum \limits_{r=0}^{n-1}\left(\begin{array}{l}n-1\\ {}r-1\end{array}\right){\kappa}_r{\mu}_{n-r}^{\prime } $$
(18)

where \( {\kappa}_1={\mu}_1^{\prime },{\kappa}_2={\mu}_2^{\prime }-{\mu}_1^{\prime 2},{\kappa}_3={\mu}_3^{\prime }-3{\mu}_2^{\prime }{\mu}_1^{\prime }+{\mu}_1^{\prime 3} \), etc. The skewness and kurtosis measures can be calculated from the ordinary moments using well-known relationships.

Generating function

The moment generating function (mgf) MX(t) = E(et X) of X is given by

$$ {M}_X(t)={\sum \limits}_{j=0}^{\infty }{\sum \limits}_{h=1}^{\mathrm{k}}{\sum \limits}_{k=1}^{\infty }{\mathrm{v}}_{j,h}{M}_m(t), $$
(19)

where Mm(t) is the mgf of Ym. Hence, MX(t) can be determined from Lehmann type II exp-(1-G) generating function.

Incomplete moments

The sth incomplete moment, say Is(t), of X can be expressed from (15) as

$$ {I}_s(t)=\underset{-\infty }{\overset{t}{\int }}{x}^sf(x) dx={\sum \limits}_{j=0}^{\infty }{\sum \limits}_{h=1}^{\mathrm{k}}{\sum \limits}_{k=1}^{\infty }{\mathrm{v}}_{j,h}{\int}_{-\infty}^t{x}^s{h}_{j+h}(x) dx $$
(20)

A general formula for the first incomplete moment, I1(t), can be derived from the last equation (with s = 1).

The first incomplete moment can be applied to construct Bonferroni and Lorenz curves defined for a given probability π by \( B\left(\pi \right)={I}_1(q)/\left(\pi {\mu}_1^{\prime}\right) \) and \( L\left(\pi \right)={I}_1(q)/{\mu}_1^{\prime } \), respectively, where \( {\mu}_1^{\prime }=E(X) \) and q = Q(π) is the qf of X at π. The mean deviations about the mean \( \left[{\delta}_1=E\left(|X-{\mu}_1^{\prime }|\right)\right] \) and about the median [δ2 = E(|X − M|)] of X are given by \( {\delta}_1=2{\mu}_1^{\hbox{'}}F\left({\mu}_1^{\hbox{'}}\right)-2{I}_1\left({\mu}_1^{\hbox{'}}\right) \) and \( {\delta}_2={\mu}_1^{\prime }-2{I}_1(M) \), respectively, where \( {\mu}_1^{\prime }=E(X) \), \( M= Median(X)=Q\left(\frac{1}{2}\right) \) is the median and \( F\left({\mu}_1^{\prime}\right) \) is easily calculated from (4).

Table 2 shows the numerical measures of the median, mean, standard deviation, skewness and Kurtosis of the BIIIMO-W distribution for selected parameter values to describe their effect on these measures.

Table 2 Median, mean, standard deviation, skewness and Kurtosis of the BIIIMO-W distribution
Full size table

Table 3 shows the numerical measures of the median, mean, standard deviation, skewness and Kurtosis of the BIIIMO-L distribution for selected parameter values to describe their effect on these measures.

Table 3 Median, mean, standard deviation, skewness and Kurtosis of the BIIIMO-Lindley Distribution
Full size table

Reliability measures

In this section, different reliability measures for the BIIIMO-G family are studied.

Stress-strength reliability of BIIIMO-G family

Let  X1 ∼ BIIIMO − G(α1, β, λ, ψ), X2 ∼ BIIIMO − G(α2, β, λ, ψ) and X1 represents strength and X2 represents stress. Then, the reliability of the component is:

$$ {\displaystyle \begin{array}{c}\mathrm{R}=\Pr \left({\mathrm{X}}_2<{X}_1\right)=\underset{-\infty }{\overset{\infty }{\int }}\underset{-\infty }{\overset{x_1}{\int }}f\left({x}_1,{x}_2\right){dx}_2{dx}_1=\underset{0}{\overset{\infty }{\int }}{f}_{x_1}(x){F}_{x_2}(x) dx,\\ {}R=\underset{0}{\overset{\infty }{\int }}\frac{\alpha_1\beta g(x)}{\overline{G}(x)\left(1-\overline{\lambda}\overline{G}(x)\right)}{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta -1}{\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{-{\alpha}_1-1}{\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{-{\alpha}_2} dx=\frac{\alpha_1}{\left({\alpha}_1+{\alpha}_2\right)}\end{array}} $$
(21)

Therefore R is independent of β, λ and ψ.

Multicomponent stress-strength reliability estimator R s, κ based on BIIIMO-G family

Suppose a machine has at least “s” components working out of “ κ ” components. The strengths of all components of system are X1, X2, . …Xκ and stress Y is applied to the system. Both the strengths X1, X2, . …Xκ are i.i.d. and are independent of stress Y. F and G are the cdf of X and Y respectively. The reliability of a machine is the probability that the machine functions properly.

Let  X ∼ BIIIMO − G(α1, β, λ, ψ), Y ∼ BIIIMO − G(α2, β, λ, ψ) with common parameters β, λ, ψ and unknown shape parameters α1  and α2. The multicomponent stress- strength reliability for BIIIMO-G family is given by (Bhattacharyya and Johnson 1974).

$$ {R}_{s,\mathrm{m}}=P\left( strengths> stress\right)=P\left[ at\; least"s" of\;\left({\mathrm{X}}_1,{\mathrm{X}}_2,.\dots {\mathrm{X}}_{\kappa}\right)\; exceed\;Y\right], $$
(22)
$$ {R}_{s,\kappa }=\sum \limits_{l=s}^{\kappa}\left({}_{\mathrm{\ell}}^{\kappa}\right)\underset{0}{\overset{\infty }{\int }}{\left[1-F(y)\right]}^l\kern0.24em {\left[F(y)\right]}^{\kappa -l} dG(y) $$
(23)
$$ {R}_{s,\kappa }=\sum \limits_{\mathrm{\ell}=s}^{\kappa}\left(\begin{array}{l}\kappa \\ {}\mathrm{\ell}\end{array}\right)\left[\begin{array}{l}\underset{0}{\overset{\infty }{\int }}{\left(1-{\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{-{\alpha}_1}\kern0.24em \right)}^{\mathrm{\ell}}\;{\left({\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{-{\alpha}_1}\right)}^{\left(\kappa -\mathrm{\ell}\right)}\times \\ {}\kern1.08em \frac{\alpha_2\beta g(x)}{\overline{G}(x)\left(1-\overline{\lambda}\overline{G}(x)\right)}{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta -1}{\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{-{\alpha}_2-1}\end{array}\right] dx $$

Let \( t={\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{-{\alpha}_2} \), then we obtain

$$ {R}_{s,\kappa }=\sum \limits_{\mathrm{\ell}=s}^{\kappa}\left(\begin{array}{l}\kappa \\ {}\mathrm{\ell}\end{array}\right)\underset{0}{\overset{1}{\int }}{\left(1-{t}^v\right)}^{\mathrm{\ell}}\;{t}^{v\left(\kappa -\mathrm{\ell}\right)} dt. $$
$$ Let\kern0.36em z={t}^{\nu },t={z}^{\frac{1}{\nu }},\kern0.48em dt=\frac{1}{\nu }{z}^{\frac{1}{\nu }-1} dz $$

, then

$$ {R}_{s,\kappa }=\sum \limits_{\mathrm{\ell}=s}^{\kappa}\left(\begin{array}{l}\kappa \\ {}\mathrm{\ell}\end{array}\right)\underset{0}{\overset{1}{\int }}{\left(1-{t}^v\right)}^{\mathrm{\ell}}\;{t}^{v\left(\kappa -\mathrm{\ell}\right)} dt, $$
$$ {R}_{s,\kappa }=\sum \limits_{\mathrm{\ell}=s}^{\kappa}\left(\begin{array}{l}\kappa \\ {}\mathrm{\ell}\end{array}\right)\underset{0}{\overset{1}{\int }}{\left(1-z\right)}^{\mathrm{\ell}}\;{z}^{\left(\kappa -\mathrm{\ell}\right)}\frac{1}{\nu }{z}^{\frac{1}{\nu }-1} dz, $$
$$ {R}_{s,\kappa }=\frac{1}{\nu}\sum \limits_{\mathrm{\ell}=s}^{\kappa}\left(\begin{array}{l}\kappa \\ {}\mathrm{\ell}\end{array}\right)B\left(1+\mathrm{\ell},\kappa -\mathrm{\ell}+\frac{1}{\nu}\right)., $$
$$ {R}_{s,\kappa }=\frac{1}{\nu}\sum \limits_{\mathrm{\ell}=s}^{\kappa}\frac{\kappa !}{\left(\kappa -\mathrm{\ell}\right)!}{\left[\prod \limits_{j=0}^{\mathrm{\ell}}\left(\kappa -j+\frac{1}{\nu}\right)\right]}^{-1} where\kern0.24em v=\frac{\alpha_2}{\alpha_1} $$
(24)

The probability Rs, κ in (24) is called multicomponent stress-strength model reliability.

Characterizations

In this section, BIIIMO-G family is characterized via: (i) conditional expectation; (ii) ratio of truncated moments and (iii) reverse hazard rate function.

Characterization based on conditional expectation

Here BIIIMO-G family is characterized via conditional expectation.

Proposition

Let X : Ω → (0, ∞) be a continuous random variable with cdf F(x)

(  0 < F(x) < 1  for  x ≥ 0), then for α > 1, X has cdf (4) if and only if

$$ E\left\{\left.{\left[-\log \left(\frac{\lambda \overline{G}(X)}{1-\overline{\lambda}\overline{G}(X)}\right)\right]}^{-\beta}\right|X<t\right\}=\frac{1}{\left(\alpha -1\right)}\left\{1+\alpha {\left[-\log \left(\frac{\lambda \overline{G}(t)}{1-\overline{\lambda}\overline{G}(t)}\right)\right]}^{-\beta}\right\},\kern0.84em for\ t>0 $$
(25)

Proof. If pdf of X is (5), then

$$ E\left\{\left.{\left[-\log \left(\frac{\lambda \overline{G}(X)}{1-\overline{\lambda}\overline{G}(X)}\right)\right]}^{-\beta}\right|X<t\right\}={\left(F(t)\right)}^{-1}\underset{0}{\overset{t}{\int }}{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta }f(x) dx $$

\( ={\left(F(t)\right)}^{-1}\underset{0}{\overset{t}{\int }}\left(\begin{array}{l}{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\alpha\;\beta \frac{g(x)}{\overline{G}(x)\left(1-\overline{\lambda}\overline{G}(x)\right)}\times \\ {}\kern3.839998em {\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta -1}{\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{-\alpha -1}\end{array}\right)\kern0.24em dx \)Upon integration by parts and simplification, we obtain

$$ E\left\{\left.{\left[-\log \left(\frac{\lambda \overline{G}(X)}{1-\overline{\lambda}\overline{G}(X)}\right)\right]}^{-\beta}\right|X<t\right\}=\frac{1}{\left(\alpha -1\right)}\left\{1+\alpha {\left[-\log \left(\frac{\lambda \overline{G}(t)}{1-\overline{\lambda}\overline{G}(t)}\right)\right]}^{-\beta}\right\},\kern1.09em t>0. $$

Conversely, if (25) holds, then

$$ \underset{0}{\overset{t}{\int }}{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta }f(x) dx=\frac{F(t)}{\left(\alpha -1\right)}\left\{1+\alpha {\left[-\log \left(\frac{\lambda \overline{G}(t)}{1-\overline{\lambda}\overline{G}(t)}\right)\right]}^{-\beta}\right\} $$
(26)

Differentiating (26) with respect to t, we obtain.

\( {\left[-\log \left(\frac{\lambda \overline{G}(t)}{1-\overline{\lambda}G(t)}\right)\right]}^{-\beta }f(t)=\frac{f(t)}{\left(\alpha -1\right)}\left\{1+\alpha {\left[-\log \left(\frac{\lambda \overline{G}(t)}{1-\overline{\lambda}\overline{G}(t)}\right)\right]}^{-\beta}\right\}-\frac{F(t)}{\left(\alpha -1\right)}\left[\frac{\alpha \beta g(t)}{\overline{G}(x)\left(1-\overline{\lambda}\overline{G}(t)\right)}{\left[-\log \left(\frac{\lambda \overline{G}(t)}{1-\overline{\lambda}\overline{G}(t)}\right)\right]}^{-\beta -1}\right] \)After simplification and integration we arrive at

$$ F(t)={\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(t)}{1-\overline{\lambda}\overline{G}(t)}\right)\right]}^{-\beta}\right\}}^{-\alpha },t\ge 0 $$

Characterization of BIIIMO-G family through ratio of truncated moments

Here BIIIMO-G family is characterized using Theorem G (Glänzel; 1987) on the basis of a simple relationship between two truncated moments of X.

Proposition

Let X : Ω → ℝ be a continuous random variable.

$$ Let\kern0.24em {h}_1(x)=\frac{1}{\alpha }{\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{\alpha +1},x\in \mathrm{\mathbb{R}} $$

and

$$ {h}_2(x)=\frac{2{\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{\alpha +1}}{\alpha {\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{\beta }},x\in \mathrm{\mathbb{R}} $$

The random variable X has pdf (5) if and only if that the function p(x) (defined in theorem G) has the form \( p(x)={\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{\beta },\kern0.48em x\in \mathrm{\mathbb{R}}. \)

Proof. For random variable X with pdf (5),

$$ \left(1-F(x)\right)E\left(\left.{h}_1(X)\right|X\ge x\right)={\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta } $$

and

\( \kern0.36em \left(1-F(x)\right)E\left(\left.{h}_2(X)\right|X\ge x\right)={\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-2\beta },x\in \mathrm{\mathbb{R}}. \) \( \frac{E\left[\left.{h}_1(x)\right|X\ge x\right]}{E\left[\left.{h}_2(x)\right|X\ge x\right]}=p(x)={\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{\beta },\kern0.36em x\in \mathrm{\mathbb{R}}, \)

and

$$ {p}^{\prime }(x)=\frac{\beta g(x)}{\overline{G}(x)\left(1-\overline{\lambda}\overline{G}(x)\right)}{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{\beta -1},\kern0.36em x\in \mathbb{R}. $$

The differential equation

$$ {s}^{\prime }(x)=\frac{p^{\prime }(x){h}_2(x)}{p(x){h}_2(x)-{h}_1(x)}=\frac{2\beta g(t)}{\overline{G}(x)\left(1-\overline{\lambda}\overline{G}(t)\right)}{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-1} $$

has solution

$$ s(x)=\ln {\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{2\beta },\kern0.36em x\in \mathrm{\mathbb{R}}. $$

Therefore, in the light of theorem G, X has pdf (5).

Corollary

Let X : Ω → ℝ be a continuous random variable and let.

\( {h}_2(x)=\frac{2{\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{\alpha +1}}{\alpha {\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{\beta }},x\in \mathrm{\mathbb{R}} \). The pdf of X is (5) if and only if there exist functions

p(x)  and h1(x) defined in Theorem G, satisfying the differential equation

$$ \frac{p^{\prime }(x)}{p(x){h}_2(x)-{h}_1(x)}=\frac{\alpha \beta g(x)}{\overline{G}(x)\left(1-\overline{\lambda}\overline{G}(x)\right)}{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{\beta -1}{\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{-\alpha -1}. $$
(27)

Remark

The solution of (27) is

$$ p(x)={\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{2\beta}\int \left[\begin{array}{l}-{h}_1(x)\frac{\alpha \beta g(x)}{\overline{G}(x)\left(1-\overline{\lambda}\overline{G}(x)\right)}{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta -1}\times \\ {}\kern4.559998em {\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{-\alpha -1} dx\end{array}\right]+D, $$

where D is a constant.

Characterization of BIIIMO-G family via reverse Hazard rate function

Definition

Let X : Ω → (0, ∞) be a continuous random variable with cdf F(x) and pdf f(x).The reverse hazard function, rF, of a twice differentiable distribution function F, satisfies the differential equation

$$ \frac{d}{dx}\left[\ln f(x)\right]=\frac{r_F^{\prime }(x)}{r_F(x)}+{r}_F(x).\kern0.75em $$
(28)

Proposition

Let X : Ω → (0, ∞) be continuous random variable. The pdf of X is (5) if and only if its reverse hazard function, rF satisfies the first order differential equation

$$ {\mathrm{r}}_F^{\prime}\left(\mathrm{x}\right)\left(1+{\left\{-\log \left[\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right]\right\}}^{-\beta}\right)\hbox{-} \frac{\beta g(x){\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta -1}}{\overline{G}(x)\left(1-\overline{\lambda}\overline{G}(x)\right)}{r}_F(x)=\alpha \beta \frac{d}{dx}\left\{\frac{g(x){\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta -1}}{\overline{G}(x)\left(1-\overline{\lambda}\overline{G}(x)\right)}\right\}. $$
(29)

Proof If

X has pdf (5), then (29) holds. Now if (29) holds, then

$$ \frac{d}{dx}\left[{r}_F(x)\left(1+{\left\{-\log \left[\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right]\right\}}^{-\beta}\right)\right]=\alpha \beta \frac{d}{dx}\left\{\frac{g(x)}{\overline{G}(x)\left(1-\overline{\lambda}G(x)\right)}{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta -1}\right\}, $$

or

$$ {r}_F(x)=\frac{\alpha \beta g(x)}{\overline{G}(x)\left(1-\overline{\lambda}\overline{G}(x)\right)}{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta -1}{\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}(x)}{1-\overline{\lambda}\overline{G}(x)}\right)\right]}^{-\beta}\right\}}^{-1},x\in \mathrm{\mathbb{R}}, $$

which is the reverse hazard function of the BIIIMO-G Family.

Maximum likelihood estimation

In this section, parameter estimates are derived using maximum likelihood method. The log-likelihood function for the vector of parameters Φ = (α, β, λ, ψτ) of BIIIMO-G family is

$$ \mathrm{\ell}\left(\Phi \right)=\mathrm{lnL}\left(\Phi \right)=\left(\begin{array}{l}n\ln \left(\alpha \right)+n\ln \left(\beta \right)+\sum \limits_{i=1}^n\ln g\left({x}_i;\psi \right)-\sum \limits_{i=1}^n\ln \overline{G}\left({x}_i;\psi \right)-\\ {}\sum \limits_{i=1}^n\ln \left(1-\overline{\lambda}\overline{G}\left({x}_i;\psi \right)\right)-\left(\beta +1\right)\sum \limits_{i=1}^n\ln \left[-\log \left(\frac{\lambda \overline{G}\left({x}_i;\psi \right)}{1-\overline{\lambda}\overline{G}\left({x}_i;\psi \right)}\right)\right]-\\ {}\left(\alpha +1\right)\sum \limits_{i=1}^n\ln \left\{1+{\left[-\log \left(\frac{\lambda \overline{G}\left({x}_i;\psi \right)}{1-\overline{\lambda}\overline{G}\left({x}_i;\psi \right)}\right)\right]}^{-\beta}\right\}\end{array}\right)\kern0.24em $$
(30)

In order to compute the estimates of the parameters α, β, λ, ψτ, the following nonlinear equations must be solved simultaneously:

$$ \frac{\delta }{\delta \alpha}\mathrm{\ell}\left(\Phi \right)=\frac{n}{\alpha }-\sum \limits_{i=1}^n\ln \left\{1+{\left[-\log \left(\frac{\lambda \overline{G}\left({x}_i;\psi \right)}{1-\overline{\lambda}\overline{G}\left({x}_i;\psi \right)}\right)\right]}^{-\beta}\right\}=0, $$
(31)
$$ \frac{\delta }{\delta \beta}\mathrm{\ell}\left(\Phi \right)=\frac{n}{\beta }-\sum \limits_{i=1}^n\ln \left[-\log \left(\frac{\lambda \overline{G}\left({x}_i;\psi \right)}{1-\overline{\lambda}\overline{G}\left({x}_i;\psi \right)}\right)\right]+\left(\alpha +1\right)\sum \limits_{i=1}^n\ln \left[-\log \left(\frac{\lambda \overline{G}\left({x}_i;\psi \right)}{1-\overline{\lambda}\overline{G}\left({x}_i;\psi \right)}\right)\right]{\left\{{\left[-\log \left(\frac{\lambda \overline{G}\left({x}_i;\psi \right)}{1-\overline{\lambda}\overline{G}\left({x}_i;\psi \right)}\right)\right]}^{\beta }+1\right\}}^{-1}, $$
(32)
$$ \frac{\delta }{\delta \psi}\mathrm{\ell}\left(\Phi \right)=\left(\begin{array}{l}\sum \limits_{i=1}^n\frac{g^{\prime}\left({x}_i;\psi \right)}{g\left({x}_i;\psi \right)}+\sum \limits_{i=1}^n\frac{g^{\prime}\left({x}_i;\psi \right)}{\overline{G}\left({x}_i;\psi \right)}-\sum \limits_{i=1}^n\frac{\overline{\lambda}{g}^{\prime}\left({x}_i;\psi \right)}{\left[1-\overline{\lambda}\overline{G}\left({x}_i;\psi \right)\right]}\\ {}-\left(\beta +1\right)\sum \limits_{i=1}^n\frac{g^{\prime}\left({x}_i;\psi \right){\left[-\log \left(\frac{\lambda \overline{G}\left({x}_i;\psi \right)}{1-\overline{\lambda}\overline{G}\left({x}_i;\psi \right)}\right)\right]}^{-1}}{\left(\overline{G}\left({x}_i;\psi \right)-\overline{\lambda}{\overline{G}}^2\left({x}_i;\psi \right)\right)}\\ {}-\left(\alpha +1\right)\beta \sum \limits_{i=1}^n\left\{1+{\left[-\log \left(\frac{\lambda \overline{G}\left({x}_i;\psi \right)}{1-\overline{\lambda}\overline{G}\left({x}_i;\psi \right)}\right)\right]}^{\beta}\right\}\frac{g^{\prime}\left({x}_i;\psi \right){\left[-\log \left(\frac{\lambda \overline{G}\left({x}_i;\psi \right)}{1-\overline{\lambda}\overline{G}\left({x}_i;\psi \right)}\right)\right]}^{\beta -1}}{\left(\overline{G}\left({x}_i;\psi \right)-\overline{\lambda}{\overline{G}}^2\left({x}_i;\psi \right)\right)}\end{array}\right)=0. $$
(33)

where \( {g}^{\prime}\left({x}_i;\psi \right)=\frac{\delta }{\delta \psi}g\left({x}_i;\psi \right). \)

Simulation studies

In this Section, we perform the simulation study to see the performance of MLE’s of BIIIMO-L distribution. The random number generation is obtained with inverse of its cdf. The MLEs, say \( \left({\hat{\alpha}}_i,{\hat{\beta}}_i,{\hat{\lambda}}_i,{\hat{b}}_i\right) \) for i = 1,2,…,N, have been obtained by CG routine in R programme.

The simulation study is based on graphical results. We generate N = 1000 samples of sizes n = 20,30,…,1000 from BIIIMOL distribution and get true values of α = 1.5, β = 2.55, λ = 0.095 and b = 5 for this simulation study. We also calculate the mean, standard deviations (sd), bias and mean square error (MSE) of the MLEs. The bias and MSE are calculated by (for h = α, β, λ, b)

$$ {Bias}_h=\frac{1}{N}{\sum}_{i=1}^N\left({\hat{h}}_i-h\right) $$

and

$$ {MSE}_h=\frac{1}{N}{\sum}_{i=1}^N{\left({\hat{h}}_i-h\right)}^2. $$

The results are given by Fig. 5. Figure 5 reveals that the empirical means tend to the true parameter values and that the sds, biases and MSEs decrease when the sample size increases as expected. These results are in agreement with first-order asymptotic theory.

Fig. 5
figure 5

Simulation results of the special BIIIMO-L distribution

Full size image

Applications

The BIIIMO-W and BIIIMO-L distributions are compared with sub- and competing models. Different goodness fit measures such Cramer-von Mises (W*), Anderson Darling (A*), Kolmogorov- Smirnov statistics with p-values [K-S(p-values], Akaike information criterion (AIC), consistent Akaike information criterion (CAIC), Bayesian information criterion (BIC), Hannan-Quinn information criterion (HQIC) and likelihood ratio statistics are computed for survival times of leukemia patients and bladder cancer patients using R-Packages(AdequacyModel and zipfR). In first application, we compare BIIIMO-W distribution with Weibull Marshall Olkin-Weibull (WMO-W), odd Burr III Weibull (OBIII-W), Kumaraswamy Weibull (Kum.-W), beta Weibull (Beta-W), generalized gamma Weibull, Weibull and Burr III (BIII) distributions. In second application, we compare BIIIMO-Lindley (BIIIMO-L) distribution with odd Burr III Lindley (OBIII-L), Mc-Donald- Lindley (Mc-L), Kumaraswamy Lindley (Kum.-L), beta Lindley (Beta-L), Weibull power Lindley (W-PL), Kumaraswamy power Lindley (Kum.- PL), Lindley and Burr III (BIII) distributions.

The better fit corresponds to smaller W*, A*, K-S, \( -2\overset{\frown }{\mathrm{\ell}} \), AIC, CAIC, BIC and HQIC value. The maximum likelihood estimates (MLEs) of unknown parameters and values of goodness of fit measures are computed for BIIIMO-W, BIIIMO-L distributions and their sub-models and competing models. The MLEs, their standard errors (in parentheses) and goodness-of-fit statistics like W*, A*, K-S (p-value) are given in Tables 4 and 5. Tables 6 and 7 displays goodness-of-fit values.

Table 4 MLEs, their standard errors (in parentheses) and Goodness-of-fit statistics for data set I
Full size table
Table 5 MLEs, their standard errors (in parentheses) and Goodness-of-fit statistics for data set II
Full size table
Table 6 Goodness-of-fit statistics for data set I
Full size table
Table 7 Goodness-of-fit statistics for data set II
Full size table

Data set I

The survival times (days) of 40 patients suffering from leukemia (Abouammoh et al. 1994) are: 115,181, 255, 418, 441, 461, 516, 739, 743,789,807, 865, 924, 983, 1024,1062, 1063,1165, 1191, 1222,1251,1277, 1290,1357,1369, 1408,1455, 1478, 1222,1549, 1578, 1578, 1599, 1603, 1605, 1696, 1735, 1799, 1815,1852.

The BIIIMO-W distribution is best fitted than sub-models and competing models because the values of all criteria are smaller for BIIIMO-W distribution.

We can also perceive that the BIIIMO-W distribution is best fitted model than other sub-models and competing models because BIIIMO-W distribution offers the closer fit to empirical data (Fig. 6).

Fig. 6
figure 6

Fitted pdf, cdf, survival and pp. plots of the BIIIMO-W distribution for survival times data

Full size image

Data set II

The survival times of 128 bladder cancer patients (Lee and Wang 2003) are 0.08, 2.09, 3.48, 4.87, 6.94, 8.66, 13.11, 23.63, 0.20, 2.23, 3.52, 4.98, 6.97, 9.02, 13.29, 0.40, 2.26, 3.57, 5.06, 7.09, 9.22, 13.80, 25.74, 0.50, 2.46, 3.64, 5.09, 7.26, 9.47, 14.24, 25.82, 0.51, 2.54, 3.70, 5.17, 7.28, 9.74, 14.76, 26.31, 0.81, 2.62, 3.82, 5.32, 7.32, 10.06, 14.77, 32.15, 2.64, 3.88, 5.32, 7.39, 10.34, 14.83, 34.26, 0.90, 2.69, 4.18, 5.34, 7.59, 10.66, 15.96, 36.66, 1.05, 2.69, 4.23, 5.41, 7.62, 10.75, 16.62, 43.01, 1.19, 2.75, 4.26, 5.41, 7.63, 17.12, 46.12, 1.26, 2.83, 4.33, 5.49, 7.66, 11.25, 17.14, 79.05, 1.35, 2.87, 5.62, 7.87, 11.64, 17.36, 1.40, 3.02, 4.34, 5.71, 7.93, 11.79, 18.10, 1.46, 4.40, 5.85, 8.26, 11.98, 19.13, 1.76, 3.25, 4.50, 6.25, 8.37, 12.02, 2.02, 3.31, 4.51, 6.54, 8.53, 12.03, 20.28, 2.02, 3.36, 6.76, 12.07, 21.73, 2.07, 3.36, 6.93, 8.65, 12.63, 22.69

The BIIIMO-L distribution is best fitted than sub-models and competing models because the values of all criteria are smaller for BIIIMO-L distribution.

We can also perceive that the BIIIMO-L distribution is best fitted model than other sub-models and competing models because BIIIMO-L distribution offers the closer fit to empirical data (Fig. 7).

Fig. 7
figure 7

Fitted pdf, cdf, survival and pp. plots of the BIIIMO-Lindley distribution for survival times data

Full size image

Concluding remarks

We have developed the BIIIMO-G family via the T-X family technique. We have studied properties such as sub-models; descriptive measures based on the quantiles, moments, inequality measures, stress-strength reliability and multicomponent stress-strength reliability model. The BIIIMO-G family is characterized via different techniques. The MLEs for the BIIIMO-G family have been computed. A simulation studies is performed to illustrate the performance of the maximum likelihood estimates (MLEs). Applications of the BIIIMO-G model to real data sets (survival times of leukemia patients and bladder cancer patients data) are presented to show the significance and flexibility of the BIIIMO-G family. Goodness of fit shows that the BIIIMO-G family is a better fit. We have demonstrated that the BIIIMO-G family is empirically better for lifetime applications.