The Marshall-Olkin extended Weibull family of distributions

Abstract

We introduce a new class of models called the Marshall-Olkin extended Weibull family of distributions based on the work by Marshall and Olkin (Biometrika 84:641–652, 1997). The proposed family includes as special cases several models studied in the literature such as the Marshall-Olkin Weibull, Marshall-Olkin Lomax, Marshal-Olkin Fréchet and Marshall-Olkin Burr XII distributions, among others. It defines at least twenty-one special models and thirteen of them are new ones. We study some of its structural properties including moments, generating function, mean deviations and entropy. We obtain the density function of the order statistics and their moments. Special distributions are investigated in some details. We derive two classes of entropy and one class of divergence measures which can be interpreted as new goodness-of-fit quantities. The method of maximum likelihood for estimating the model parameters is discussed for uncensored and multi-censored data. We perform a simulation study using Markov Chain Monte Carlo method in order to establish the accuracy of these estimators. The usefulness of the new family is illustrated by means of two real data sets.

Mathematics Subject Classification (2010)

60E05; 62F03; 62F10; 62P10

1 Introduction

The Weibull distribution has assumed a prominent position as statistical model for data from reliability, engineering and biological studies (McCool 2012). This model has been exaustively used for describing hazard rates – an important quantity of survival analysis. In the context of monotone hazard rates, some results from the literature suggest that the Weibull law is a reasonable choice due to its negatively and positively skewed density shapes. However, this distribution is not a good model for describing phenomenon with non-monotone failure rates, which can be found on data from applications in reliability and biological studies. Thus, extended forms of the Weibull model have been sought in many applied areas. As a solution for this issue, the inclusion of additional parameters to a well-defined distribution has been indicated as a good methodology for providing more flexible new classes of distributions.

Marshall and Olkin (1997) derived an important method of including an extra shape parameter to a given baseline model thus defining an extended distribution. The Marshall and Olkin (“$\mathcal{ℳ}\mathcal{O}$” for short) transformation furnishes a wide range of behaviors with respect to the baseline distribution. The geometrical and inferential properties associated with the generated distribution depend on the values of the extra parameter. These characteristics provide more flexibility to the $\mathcal{ℳ}\mathcal{O}$ generated distributions. Considering the proportional odds model, Sankaran and Jayakumar (2008) presented a detailed discussion about the physical interpretation of the $\mathcal{ℳ}\mathcal{O}$ family.

This family has a relationship with the odds ratio associated with the baseline distribution. Let X be a distributed $\mathcal{ℳ}\mathcal{O}$ random variable which describes the lifetime relative to each individual in the population with a vector of p-covariates z=(z₁,…,z _p )^⊤, where (·)^⊤ denotes the transposition operator. Then, the cumulative distribution function (cdf) of X is given by

$$\overline{F}(x;\mathit{z})=\frac{k\left(\mathit{z}\right)\overline{G}\left(x\right)}{1-[1-k(\mathit{z}\left)\right]\overline{G}\left(x\right)},$$

(1)

where k(z)=λ _G (x)/λ _F (x ; z) is a non-negative function such that z is independent of the time x, λ _F (x ; z) is the proportional odds model [for a discussion about such modeling, see Sankaran and Jayakumar (2008)] and ${\lambda }_G\left(x\right)=G\left(x\right)/\overline{G}\left(x\right)$ represents an arbitrary odds for the baseline distribution.

In this paper, we consider k(z)=δ. Before, however, it is important to highlight two important properties of the $\mathcal{ℳ}\mathcal{O}$ transformation: (i) the stability and (ii) geometric extreme stability (Marshall and Olkin 1997). In other words, the $\mathcal{ℳ}\mathcal{O}$ distribution possesses a stability property in the sense that if the method is applied twice, it returns to the same distribution. In addition, the following stochastic behavior can also be verified: let {X₁,…,X _N } be a random sample from the population random variable equipped with the survival function (1) at k(z)=δ. Suppose that N has the geometric distribution with probability p and that this quantity is independent of X _i , for i=1,…,N. Then, U=m i n(X₁,…,X _N ) and V=m a x(X₁,…,X _N ) are random variables having survival functions (1) such that k(z) can be equal to p and p⁻¹, respectively, i.e., the $\mathcal{ℳ}\mathcal{O}$ transform satisfies the geometric extreme stability property.

Due to these advantages, many papers have employed the $\mathcal{ℳ}\mathcal{O}$ transformation. In Marshall and Olkin work, the exponential and Weibull distributions were generalized. Subsequently, the $\mathcal{ℳ}\mathcal{O}$ extension was applied to several well-known distributions: Weibull (Ghitany et al.2005, Zhang and Xie 2007), Pareto (Ghitany 2005), gamma (Ristić et al.2007), Lomax (Ghitany et al.2007) and linear failure-rate (Ghitany and Kotz 2007) distributions. More recently, general results have been addressed by Barreto-Souza et al. (2013) and Cordeiro and Lemonte (2013). In this paper, we aim to apply the $\mathcal{ℳ}\mathcal{O}$ generator to the extended Weibull ($\mathcal{E}\mathcal{W}$) class of distributions to obtain a new more flexible family to describe reliability data. The proposed family can also be applied to other fields including business, environment, informatics and medicine in the same way as it was originally done with the Birnbaum-Saunders and other lifetime distributions.

Let $\overline{G}\left(x\right)=1-G\left(x\right)$ and g(x)=d G(x)/d x be the survival and density functions of a continuous random variable Y with baseline cdf G(x). Then, the $\mathcal{ℳ}\mathcal{O}$ extended distribution has survival function given by

$$\overline{F}(x;\delta )=\frac{\delta \overline{G}\left(x\right)}{1-\overline{\delta }\overline{G}\left(x\right)}=\frac{\delta \overline{G}\left(x\right)}{G\left(x\right)+\delta \overline{G}\left(x\right)},x\in \mathcal{X}\subseteq \mathbb{R},\delta >0,$$

(2)

where $\overline{\delta }=1-\mathrm{\delta .}$

Clearly, δ=1 implies $\overline{F}\left(x\right)=\overline{G}\left(x\right)$. The family (2) has probability density function (pdf) given by

$$f(x;\delta )=\frac{\mathrm{\delta g}\left(x\right)}{{[1-\overline{\delta }\overline{G}(x\left)\right]}^2},x\in \mathcal{X}\subseteq \mathbb{R},\delta >0.$$

Its hazard rate function (hrf) becomes

$$\tau (x;\delta )=\frac{g\left(x\right)}{\overline{G}\left(x\right)[1-\overline{\delta }\overline{G}(x\left)\right]},x\in \mathcal{X}\subseteq \mathbb{R},\delta >0.$$

Further, the class of extended Weibull ($\mathcal{E}\mathcal{W}$) distributions pioneered by Gurvich et al. (1997) has achieved a prominent position in lifetime models. Its cdf is given by

$$G(x;\alpha ,\mathit{\xi })=1-exp[-\mathrm{\alpha H}(x;\mathit{\xi }\left)\right],x\in \mathcal{D}\subseteq {\mathbb{R}}_{+},\alpha >0,$$

(3)

where H(x;ξ) is a non-negative monotonically increasing function which depends on the parameter vector ξ. The corresponding pdf is given by

$$g(x;\alpha ,\mathit{\xi })=\alpha exp[-\mathrm{\alpha H}(x;\mathit{\xi }\left)\right]h(x;\mathit{\xi }),$$

(4)

where h(x;ξ) is the derivative of H(x;ξ).

Different expressions for H(x;ξ) in Equation (3) define important models such as:

• (i) H(x;ξ)=x gives the exponential distribution;

• (ii) H(x;ξ)=x ² leads to the Rayleigh (Burr type-X) distribution;

• (iii) H(x;ξ)= log(x/k) leads to the Pareto distribution;

• (iv) H(x;ξ)=β ⁻¹[ exp(β x)−1] gives the Gompertz distribution.

In this paper, we derive a new family of distributions by compounding the $\mathcal{ℳ}\mathcal{O}$ and $\mathcal{E}\mathcal{W}$ classes. We define a new generated family in order to provide a “better fit” in certain practical situations. The compounding procedure follows by taking the $\mathcal{E}\mathcal{W}$ class (3) as the baseline model in Equation (2). The Marshall-Olkin extended Weibull ($\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}$) family of distributions contains some special models as those listed in Table 1 with the corresponding H(·;·) and h(·;·) functions and the parameter vectors.

Table 1 Special models and the corresponding functions H ( x ; ξ ) and h ( x ; ξ )

The paper unfolds as follows. Section 2 presents the cdf and pdf of the proposed distribution and some expansions for the density function. The main statistical properties of the new family are derived in Section 3 including the moments, moment generating function (mgf) and incomplete moments, quantile function (qf), random number generator, skewness and kurtosis measures, order statistics, mean deviations and average lifetime functions. In Section 4, we derive four measures of information theory: Shannon and Rényi entropies, cross entropy and Kullback-Leibler divergence. The maximum likelihood method to estimate the model parameters is adopted in Section 5. Two special models are studied in some details in Section 6. We perform a simulation study using Monte Carlo’s experiments in order to assess the accuracy of the maximum likelihood estimators (MLEs) in Section 7.1 and two applications to real data in Section 7.2. Conclusions and some future lines of research are addressed in Section 8.

2 The $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}$ family

The cdf of the new family of distributions is given by

$$F(x;\delta ,\alpha ,\mathit{\xi })=\frac{1-exp[-\mathrm{\alpha H}(x;\mathit{\xi }\left)\right]}{1-\overline{\delta }exp[-\mathrm{\alpha H}(x;\mathit{\xi }\left)\right]},x\in \mathcal{D},$$

(5)

where α>0 and δ>0. Using (5), we can express its survival function as

$$\overline{F}(x;\delta ,\alpha ,\mathit{\xi })=\frac{\delta exp[-\mathrm{\alpha H}(x;\mathit{\xi }\left)\right]}{1-\overline{\delta }exp[-\mathrm{\alpha H}(x;\mathit{\xi }\left)\right]},x\in \mathcal{D}$$

(6)

and the associated hrf reduces to

$$\tau (x;\delta ,\alpha ,\mathit{\xi })=\frac{\alpha h(x;\mathit{\xi })}{1-\overline{\delta }exp[-\mathrm{\alpha H}(x;\mathit{\xi }\left)\right]},x\in \mathcal{D.}$$

(7)

The corresponding pdf is given by

$$f(x;\delta ,\alpha ,\mathit{\xi })=\frac{\delta \alpha h(x;\mathit{\xi })exp[-\mathrm{\alpha H}(x;\mathit{\xi }\left)\right]}{{\{1-\overline{\delta }exp[-\mathrm{\alpha H}(x;\mathit{\xi })\left]\right\}}^2},$$

(8)

where H(x;ξ) can be any special distribution listed in Table 1.

Hereafter, let X be a random variable having the $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}$ pdf (8) with parameters δ,α and ξ, say $X\sim \mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}(\delta ,\alpha ,\mathit{\xi })$. Equation (8) extends several distributions which have been studied in the literature.

The $\mathcal{ℳ}\mathcal{O}$ Pareto (Ghitany 2005) is obtained by taking H(x; ξ)= log(x/k)(x≥k). Further, for H(x; ξ)=x^γ we obtain the $\mathcal{ℳ}\mathcal{O}$ Weibull (Ghitany et al. 2005, Zhang and Xie 2007). The $\mathcal{ℳ}\mathcal{O}$ Lomax (Ghitany et al. 2007) and $\mathcal{ℳ}\mathcal{O}$ log-logistic are derived from (8) by taking H(x; ξ)= log(1+x^c) with c=1 and H(x; ξ)= log(1+x^c) with α=1, respectively. For H(x; ξ)=a x+b x²/2 and α=1, Equation (8) reduces to the $\mathcal{ℳ}\mathcal{O}$ linear failure rate (Ghitany and Kotz 2007). In the same way, for H(x; ξ)= log(1+x^c), we have the $\mathcal{ℳ}\mathcal{O}$ Burr XII (Jayakumar and Mathew 2008). Finally, we obtain the $\mathcal{ℳ}\mathcal{O}$ Fréchet (Krishna et al. 2013) from Equation (8) by setting H(x; ξ)=x^−γ. Table 1 displays some useful quantities and corresponding parameter vectors for special distributions.

A general approximate goodness-of-fit test for the null hypothesis H₀:X₁,…,X _n with X _i following F(x;θ), where the form of F is known but the p-vector θ=(δ,α,ξ)^⊤ is unknown, was proposed by Chen and Balakrishnan (1995). This method is based on the Cramér-von Mises (CM) and Anderson-Darling (AD) statistics and, in general, the smaller the values of these statistics, the better the fit. In this paper, such methodology is applied to provide goodness-of-fit tests for the distributions under study.

Some results in the following sections can be obtained numerically in any software such as MAPLE (Garvan 2002), MATLAB (Sigmon and Davis 2002), MATHEMATICA (Wolfram 2003), Ox (Doornik 2007) and R (R Development Core Team 2009). The Ox (for academic purposes) and R are freely available at http://www.doornik.com and http://www.r-project.org, respectively. The results can be computed by taking in the sums a large positive integer value in place of ∞.

2.1 Expansions for the density function

For any positive real number a, and for |z|<1, we have the generalized binomial expansion

$${(1-z)}^{-a}=\sum _{k=0}^{\infty }\frac{{\left(a\right)}_k}{k!}{z}^k,$$

(9)

where (a) _k =Γ(a+k)/Γ(a)=a(a+1)…(a+k−1) is the ascending factorial and Γ(·) is the gamma function. Applying (9) to (8), for 0<δ<1, gives

$$f(x;\delta ,\alpha ,\mathit{\xi })=\sum _{j=0}^{\infty }{\eta }_{j}g(x;(j+1)\alpha ,\mathit{\xi }),$$

(10)

where ${\eta }_j=\delta \overline{\delta }{j}^{}$ and g(x;(j+1)α,ξ) denotes the $\mathcal{E}\mathcal{W}$ density function with parameters (j+1)α and ξ. Otherwise, for δ>1, after some algebra, we can express (8) as

$$f(x;\delta ,\alpha ,\mathit{\xi })=\frac{g(x;\alpha ,\mathit{\xi })}{\delta {\left\{1-\left(1-1/\delta \right)[1-exp(-\mathrm{\alpha H}(x;\mathit{\xi })\left)\right]\right\}}^2}.$$

(11)

In this case, we can verify that |(1−1/δ)[1− exp(−α H(x;ξ))]|<1. Then, applying twice the expansion (9) in Equation (11), we obtain

$$f(x;\delta ,\alpha ,\mathit{\xi })=\sum _{j=0}^{\infty }{\nu }_{j}g(x;(j+1)\alpha ,\mathit{\xi }),$$

(12)

where

$${\nu }_j={\nu }_j\left(\delta \right)=\frac{{(-1)}^j}{\delta (j+1)!}\sum _{k=j}^{\infty }(k+1)!{(1-1/\delta )}^k.$$

We can verify that $\sum _{j=0}^{\infty }{\eta }_j=\sum _{j=0}^{\infty }{\nu }_j=1$. Then, the $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}$ density function can be expressed as an infinite linear combination of $\mathcal{E}\mathcal{W}$ densities. Equations (10) and (12) have the same form except for the coefficients η j′s in (10) and ν j′s in (12). They depend only on the generator parameter δ. For simplicity, we can write

$$f(x;\delta ,\alpha ,\mathit{\xi })=\sum _{j=0}^{\infty }{w}_{j}g(x;(j+1)\alpha ,\mathit{\xi }),$$

(13)

where

$$w_j=\left\{\begin{array}{ll}{\eta }_j,& \text{if}0<\delta <1,\\ {\nu }_j,& \text{if}\delta >1,\end{array}\right.$$

and η _j and ν _j are given by (10) and (12), respectively. Thus, some mathematical properties of (13) can be obtained directly from those $\mathcal{E}\mathcal{W}$ properties. For example, the ordinary, incomplete, inverse and factorial moments and the mgf of X follow immediately from those quantities of the $\mathcal{E}\mathcal{W}$ distribution.

3 General properties

3.1 Moments, generating function and incomplete moments

The n th ordinary moment of X can be obtained from (13) as

$$\begin{array}{lcr}\mathrm{E}\left(X^n\right)& =& \sum _{j=0}^{\infty }{w}_{j}E\left(Y_j^n\right),\end{array}$$

where from now on $Y_j\sim \mathcal{E}\mathcal{W}\left(\right(j+1)\alpha ,\mathit{\xi })$ denotes a random variable having the $\mathcal{E}\mathcal{W}$ density function g(y;(j+1)α,ξ).

The mgf and the k th incomplete moment of X follow from (13) as

$$M_X\left(t\right)=E\left({\mathrm{e}}^{\mathit{\text{tX}}}\right)=\sum _{j=0}^{\infty }{w}_j{M}_j\left(t\right)$$

and

$$\begin{array}{l}{T}_k\left(z\right)=\sum _{j=0}^{\infty }{w}_j{T}_k^{\left(j\right)}\left(z\right),\end{array}$$

(14)

where M _j (t) is the mgf of Y _j and $T_k^{\left(j\right)}\left(z\right)={\int }_{-\infty }^z{x}^{k}g(x;(j+1)\alpha ,\mathit{\xi })\mathrm{d}x$ comes directly from the $\mathcal{E}\mathcal{W}$ model.

3.2 Quantile function and random number generator

The qf of X follows by inverting (5) and it can be expressed in terms of H⁻¹(·) as

$$Q\left(u\right)=H^{-1}\left(\frac{1}{\alpha }log\left(\frac{1-\overline{\delta }u}{1-u}\right),\mathit{\xi }\right).$$

(15)

In Table 2, we provide the function H⁻¹(x;ξ) for some special models.

Table 2 The H ⁻¹ ( x ; ξ ) function

Hence, the generator for X can be given by the algorithm:

The $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}$ distributions can be very useful in modeling lifetime data and practitioners may be interested in fitting one of these models. We provide a script using the R language to generate the density, distribution function, hrf, qf, random numbers, Anderson-Darling test, Cramer-von Mises test and likelihood ratio (LR) tests. This script can be be obtained from the authors upon requested.

3.3 Mean deviations

The mean deviations of X about the mean and the median are given by

$${\delta }_1={\int }_{\mathcal{D}}|x-\mu |f(x;\delta ,\alpha ,\mathit{\xi })\mathrm{d}x\text{and}{\delta }_2={\int }_{\mathcal{D}}|x-M|f(x;\delta ,\alpha ,\mathit{\xi })\mathrm{d}x,$$

respectively, where μ=E(X) denotes the mean and M=M e d i a n(X) the median. The median follows from the nonlinear equation F(M;δ,α,ξ)=1/2. So, these quantities reduce to

$${\delta }_1=2\mu F(\mu ;\delta ,\alpha ,\mathit{\xi })-2T_1\left(\mu \right)\text{and}{\delta }_2=\mu -2T_1\left(M\right),$$

where T₁(z) is the first incomplete moment of X obtained from (14) as

$$T_1\left(z\right)=\sum _{j=0}^{\infty }{w}_j{T}_1^{\left(j\right)}\left(z\right),$$

and $T_1^{\left(j\right)}\left(z\right)={\int }_{-\infty }^{z}xg(x;(j+1)\alpha ,\mathit{\xi })\mathrm{d}x$ is the first incomplete moment of Y _j .

An important application of the mean deviations is related to the Bonferroni and Lorenz curves. These curves are useful in economics, reliability, demography, medicine and other fields. For a given probability p, they are defined by B(p)=T₁(q)/(p μ) and L(p)=T₁(q)/μ, respectively, where q=Q(p) is the qf of X given by (15) at u=p.

3.4 Average lifetime and mean residual lifetime functions

The average lifetime is given by

$$\begin{array}{l}{t}_m={\int }_0^{\infty }\left[1-F(x;\delta ,\alpha ,\mathit{\xi })\right]\mathrm{d}x=\sum _{j=0}^{\infty }{w}_j{\int }_0^{\infty }\overline{G}(x;(j+1)\alpha ,\mathit{\xi })\mathrm{d}\mathrm{x.}\end{array}$$

In fields such as actuarial sciences, survival studies and reliability theory, the mean residual lifetime has been of much interest; see, for a survey, Guess and Proschan (1988). Given that there was no failure prior to x₀, the residual life is the period from time x₀ until the time of failure. The mean residual lifetime is given by

$$\begin{array}{lcr}m(x_0;\delta ,\alpha ,\mathit{\xi })& =& \mathrm{E}\left(X-x_0|X\ge x_0;\delta ,\alpha ,\mathit{\xi }\right)=\underset{\{x:x>x_0\}}{\int }\frac{(x-x_0)f(x;\delta ,\alpha ,\mathit{\xi })}{\text{Pr}(X>x_0)}\mathrm{d}x\\ =& {\left[\text{Pr}(X>x_0)\right]}^{-1}{\int }_0^{\infty }yf(x_0+y;\delta ,\alpha ,\mathit{\xi })\mathrm{d}y\hfill \\ =& {\left[\overline{F}(x_0;\delta ,\alpha ,\mathit{\xi })\right]}^{-1}\sum _{j=0}^{\infty }{w}_j{\int }_0^{\infty }yg(x_0+y;(j+1)\alpha ,\mathit{\xi })\mathrm{d}\mathrm{y.}\hfill \end{array}$$

The last integral can be computed from the baseline $\mathcal{E}\mathcal{W}$ distribution. Further, m(x₀;δ,α,ξ)→E(X) as x₀→0.

4 Information theory measures

The seminal idea about information theory was pioneered by Hartley (1928), who defined a logarithmic measure of information for communication. Subsequently, Shannon (1948) formalized this idea by defining the entropy and mutual information concepts. The relative entropy notion (which would later be called divergence) was proposed by Kullback and Leibler (1951). The Kullback-Leibler’s measure can be understood like a comparison criterion between two distributions. In this section, we derive two classes of entropy measures and one class of divergence measures which can be understood as new goodness-of-fit quantities such those discussed by Seghouane and Amari (2007). All these measures are defined for one element or between two elements in the $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}$ family.

4.1 Rényi entropy

The Rényi entropy of X with pdf (8) is given by

$$H_{\text{R}}^s\left(X\right)=\frac{1}{1-s}log\left({\int }_{\mathcal{D}}f{(x;\delta ,\alpha ,\mathit{\xi })}^s\mathrm{d}x\right),$$

where s∈(0,1)∪(1,∞).

It is a difficult problem to obtain $H_{\text{R}}^s\left(X\right)$ in closed-form for the $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}$ family. So, we derive an expansion for this quantity.

By using (9), f(x;δ,α,ξ)^s can be expanded as

$$f{(x;\delta ,\alpha ,\mathit{\xi })}^s=\sum _{j=0}^{\infty }{w}_j^{\prime }exp[-(j+s\left)\mathrm{\alpha H}\right(x;\mathit{\xi }\left)\right]h{(x;\mathit{\xi })}^s,$$

(16)

where

$$w_j^{\prime }=\left\{\begin{array}{ll}{\eta }_j^{\prime }(\alpha ,\delta )=\frac{{\alpha }^s{\delta }^s{\left(2s\right)}_j{\overline{\delta }}^j}{j!},& \text{for}0<\delta <1,\\ {\nu }_j^{\prime }(\alpha ,\delta )=\frac{{\alpha }^s{\delta }^{-s}}{j!}\sum _{k=0}^{\infty }\frac{{\left(2s\right)}_k{\left(k\right)}_j}{k!}{(1-1/\delta )}^k,& \text{for}\delta >1.\end{array}\right.$$

The proof of this expansion is given in Appendix 8.

Finally, based on Equation (16), the Rényi entropy can be expressed as

$$H_{\text{R}}^s\left(X\right)=\frac{1}{1-s}log\left\{\sum _{j=0}^{\infty }\underset{j}{\overset{\prime }{w}}{\int }_{\mathcal{D}}exp[-(j+s\left)\mathrm{\alpha H}\right(x;\mathit{\xi }\left)\right]h{(x;\mathit{\xi })}^s\mathrm{d}x\right\}.$$

An advantage of this expansion is its dependence of an integral which has closed-form for some $\mathcal{E}\mathcal{W}$ distributions.

4.2 Shannon entropy

The Shannon entropy of X is given by

$$H_{\text{S}}\left(X\right)={\mathrm{E}}_X\left\{-log\left[f\right(X;\delta ,\alpha ,\mathit{\xi }\left)\right]\right\},$$

where the log-likelihood function corresponding to one observation follows from (8) as

$$\begin{array}{l}log\left[f\right(x;\delta ,\alpha ,\mathit{\xi }\left)\right]=log\left(\mathrm{\delta \alpha }\right)+log\left[h\right(x;\mathit{\xi }\left)\right]-\mathrm{\alpha H}(x;\mathit{\xi })-2log\left\{1-\overline{\delta }exp[-\mathrm{\alpha H}(x;\mathit{\xi }\left)\right]\right\}.\end{array}$$

Thus, it can be reduced to

$$H_{\text{S}}\left(X\right)=-log\left(\mathrm{\alpha \delta }\right)+2\mathrm{E}\left\{log\left[1-\bar{\delta }\bar{G}(X;\mathit{\xi })\right]\right\}-\mathrm{E}\left\{log\left[h(X;\mathit{\xi })\right]\right\}+\alpha \mathrm{E}\left[H(X;\mathit{\xi })\right].$$

4.3 Cross entropy and Kullback-Leibler divergence and distance

Let X and Y be two random variables with common support ${\mathbb{R}}_{+}$ whose densities are f _X (x;θ₁) and f _Y (y;θ₂), respectively. Cover and Thomas (1991) defined the cross entropy as

$$C_X\left(Y\right)={\mathrm{E}}_X\left\{-log\left[f_Y(X;{\mathit{\theta }}_2)\right]\right\}=-{\int }_0^{\infty }{f}_X(z;{\mathit{\theta }}_1)log\left[f_Y(z;{\mathit{\theta }}_2)\right]\mathrm{d}\mathrm{z.}$$

We consider that $X\sim \mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}({\delta }_x,{\alpha }_x,{\mathit{\xi }}_x)$ and $Y\sim \mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}({\delta }_y,{\alpha }_y,{\mathit{\xi }}_y)$. After some algebraic manipulations, we obtain

$$\begin{array}{ll}{C}_X\left(Y\right)& =-{\int }_{\mathcal{D}}{f}_X(z;{\delta }_x,{\alpha }_x,{\mathit{\xi }}_x)log\left[f_Y(z;{\delta }_y,{\alpha }_y,{\mathit{\xi }}_y)\right]\mathrm{d}z\\ =-log\left({\delta }_y{\alpha }_y\right)-{\mathrm{E}}_X\left\{log\left[h(X;{\mathit{\xi }}_y)\right]\right\}+{\alpha }_y{\mathrm{E}}_X\left[H(X;{\mathit{\xi }}_y)\right]\\ +2{\mathrm{E}}_X\left\{log\left[1-\bar{\delta }\bar{G}(X;{\mathit{\xi }}_y)\right]\right\}.\end{array}$$

(17)

An important measure in information theory is the Kullback-Leibler divergence given by

$$D\left(X\right|\left|Y\right)=C_X\left(Y\right)-H_{\text{S}}\left(X\right)={\mathrm{E}}_X\left\{log\left[\frac{f_X(X;{\delta }_x,{\alpha }_x,{\mathit{\xi }}_x)}{f_Y(X;{\delta }_y,{\alpha }_y,{\mathit{\xi }}_y)}\right]\right\}.$$

(18)

Applying (4.2) and (17) in Equation (18) gives

$$\begin{array}{ll}D\left(X\right|\left|Y\right)=& log\left(\frac{{\delta }_x{\alpha }_x}{{\delta }_y{\alpha }_y}\right)+{\mathrm{E}}_X\left\{log\left[\frac{h(X;{\mathit{\xi }}_x)}{h(X;{\mathit{\xi }}_y)}\right]\right\}+2{\mathrm{E}}_X\left\{log\left[\frac{1-\bar{\delta }\bar{G}(X;{\mathit{\xi }}_y)}{1-\bar{\delta }\bar{G}(X;{\mathit{\xi }}_x)}\right]\right\}\\ +{\alpha }_y{E}_X\left[H\right(X;{\mathit{\xi }}_y\left)\right]-{\alpha }_x{E}_X\left[H\right(X;{\mathit{\xi }}_x\left)\right].\end{array}$$

(19)

According to Cover and Thomas (1991), the Kullback-Leibler measure D(X||Y) is the quantification of the error considering that the Y model is true when the data follow the X distribution. For example, this measure has been proposed as essential parts of test statistics, which has seen strongly applied to contexts of radar synthetic aperture image processing in both univariate (Nascimento et al. 2010) and polarimetric (or multivariate) (Nascimento et al. 2014) perspectives.

In order to work with measures that satisfied the non-negativity, symmetry and definiteness properties, Nascimento et al. (2010) considered the symmetrization of (19)

$$\begin{array}{ll}{d}_{\text{KL}}(X,Y)& =\frac{1}{2}\left[D\left(X\right|\left|Y\right)+D\left(Y\right|\left|X\right)\right]\\ ={\int }_{\mathcal{D}}\underset{\equiv \mathit{\text{IntegrandKL}}(x,y)}{\underbrace{\left(f_X\left(x;{\delta }_x,{\alpha }_x,{\mathit{\xi }}_x\right)-f_Y\left(x;{\delta }_y,{\alpha }_y,{\mathit{\xi }}_y\right)\right)log\left(\frac{f_X(x;{\delta }_x,{\alpha }_x,{\mathit{\xi }}_x)}{f_Y(x;{\delta }_x,{\alpha }_x,{\mathit{\xi }}_x)}\right)}}\mathrm{d}x,\end{array}$$

which is given by

$$\begin{array}{ll}2d_{\text{KL}}(X,Y)& ={\alpha }_y\left\{{\mathrm{E}}_X\left[H(X;{\mathit{\xi }}_y)\right]-{\mathrm{E}}_Y\left[H(Y;{\mathit{\xi }}_y)\right]\right\}+{\alpha }_x\left\{{\mathrm{E}}_Y\left[H(Y;{\mathit{\xi }}_x)]-{\mathrm{E}}_X[H(X;{\mathit{\xi }}_x)\right]\right\}\\ +{\mathrm{E}}_X\left\{log\left[\frac{h\left(X;{\mathit{\xi }}_x\right)}{h\left(X;{\mathit{\xi }}_y\right)}\right]\right\}+{\mathrm{E}}_Y\left\{log\left[\frac{h\left(Y;{\mathit{\xi }}_y\right)}{h\left(Y;{\mathit{\xi }}_x\right)}\right]\right\}\\ +2{\mathrm{E}}_X\left\{log\left[\frac{1-\bar{\delta }\bar{G}\left(X;{\mathit{\xi }}_y\right)}{1-\bar{\delta }\bar{G}\left(X;{\mathit{\xi }}_x\right)}\right]\right\}+2{\mathrm{E}}_Y\left\{log\left[\frac{1-\bar{\delta }\bar{G}\left(Y;{\mathit{\xi }}_x\right)}{1-\bar{\delta }\bar{G}\left(Y;{\mathit{\xi }}_y\right)}\right]\right\}.\end{array}$$

(20)

Although this measure does not satisfy the triangle inequality, it is usually called the Kullback-Leibler distance (Jensen-Shannon divergence). The new measure can be used to answer questions like “how could one quantify the difference in selecting the Phani model with three parameters as the baseline distribution instead of the Weibull Kies distribution which has four parameters?”.

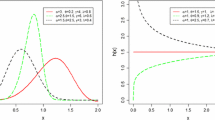
As an illustration for (20), we initially consider two distinct elements of the generated special model from the specifications: H(x;β)=β⁻¹[ exp(β x)−1] and h(x;β)= exp(β x) in (8). This model will be presented with more details in future sections and its parametric space is represented by the vector (δ,α,β). Suppose that we are interested in quantifying the influence of a nuisance degree ε in the parameter α over the distance between two distinct elements, (2,1,3) and (2,1+ε,3), at such parametric space. Figure 1(a) displays the integrand of (20) for ε=0.1, 1, 2 and 4 for which the distances (or areas) associated with d_KL(X,Y) are 6.50×10⁻³, 3.56×10⁻¹, 9.46×10⁻¹ and 2.25, respectively. It is notable that d_KL(X,Y) takes smaller values for more closer points (or, equivalently, for more closer fits) and, therefore, (20) consists of new goodness-of-fit measures. In Figures 1(b) and 1(c), we show the influence of η=α/β on d_KL([δ,α,β],[δ,α,β+ε]) (for β=δ=3 and α∈{1,3,9}) and of δ on d_KL([δ,α,β],[δ+ε,α,β]) (for β=α=3 and δ∈{3,4,5}). For all cases, the contamination ε takes values in the interval (−2.9,2.9).

Figure 1

MSE curves for δ ∈{0 . 3,0 . 8,1,2,4}, η =0 . 5,1,2 and n =200. (a) Behavior of the function IntegrandKL. (b) Influence of η=α/β under β=δ=3 and α∈{1,3,9}. (c) Influence of δ under (α,β)=(3,3).

5 Estimation

Here, we present a general procedure for estimating the $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}$ parameters from one observed sample and from multi-censored data. Additionally, we provide a discussion about how one can test the significance of additional parameter at the proposed class. Let x₁,…,x _n be a sample of size n from X. The log-likelihood function for the vector of parameters θ=(δ,α,ξ^⊤)^⊤ can be expressed as

$$\begin{array}{l}\ell \left(\mathit{\theta }\right)=nlog\left(\mathrm{\delta \alpha }\right)+\sum _{i=1}^{n}log\left[h(x_i;\mathit{\xi })\right]-\alpha \sum _{i=1}^{n}H(x_i;\mathit{\xi })-2\sum _{i=1}^{n}log\left\{1-\overline{\delta }exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]\right\}.\end{array}$$

From the above log-likelihood, the components of the score vector, $\mathbf{U}\left(\theta \right)={(U_{\delta },U_{\alpha },U_{\mathit{\xi }}^{\top })}^{\top }$, are given by

$$\begin{array}{ll}{U}_{\delta }\left(\mathit{\theta }\right)=\frac{\mathrm{\partial \ell }\left(\theta \right)}{\mathrm{\partial \delta }}=& \frac{n}{\delta }-2\sum _{i=1}^n\frac{exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]}{1-\overline{\delta }exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]},\\ U_{\alpha }\left(\mathit{\theta }\right)=\frac{\mathrm{\partial \ell }\left(\theta \right)}{\mathrm{\partial \alpha }}=& \frac{n}{\alpha }-\sum _{i=1}^{n}H(x_i;\mathit{\xi })-2\overline{\delta }\sum _{i=1}^n\frac{H(x_i;\mathit{\xi })exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]}{1-\overline{\delta }exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]}\text{and}\\ U_{{\mathit{\xi }}_k}\left(\mathit{\theta }\right)=\frac{\mathrm{\partial \ell }\left(\theta \right)}{\partial {\mathit{\xi }}_k}=& \sum _{i=1}^n\frac{1}{h(x_i;\mathit{\xi })}\frac{\mathrm{\partial h}(x_i;\mathit{\xi })}{\partial {\mathit{\xi }}_k}-\alpha \sum _{i=1}^n\frac{\mathrm{\partial H}(x_i;\mathit{\xi })}{\partial {\mathit{\xi }}_k}\\ -2\overline{\delta }\alpha \sum _{i=1}^n\frac{\mathrm{\partial H}(x_i;\mathit{\xi })}{\partial {\mathit{\xi }}_k}\frac{exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]}{1-\overline{\delta }exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]}.\end{array}$$

Finally, the partitioned observed information matrix for the $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}$ family is

whose elements are

$$\begin{array}{l}{U}_{\mathrm{\delta \delta }}\left(\mathit{\theta }\right)=-n{\delta }^{-2},U_{\mathrm{\delta \alpha }}\left(\mathit{\theta }\right)=2\sum _{i=1}^n\frac{H(x_i;\mathit{\xi })exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]}{{\left\{1-\overline{\delta }exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]\right\}}^2},\\ U_{\delta {\mathit{\xi }}_k}\left(\mathit{\theta }\right)=2\alpha \sum _{i=1}^n\frac{\mathrm{\partial H}(x_i;\mathit{\xi })}{\partial {\mathit{\xi }}_k}\frac{exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]}{{\left\{1-\overline{\delta }exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]\right\}}^2},\\ U_{\mathrm{\alpha \alpha }}\left(\mathit{\theta }\right)=-\frac{n}{{\alpha }^2}+2\overline{\delta }\sum _{i=1}^n\frac{H{(x_i;\mathit{\xi })}^{2}exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]}{{\left\{1-\overline{\delta }exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]\right\}}^2},\\ U_{\alpha {\mathit{\xi }}_k}\left(\mathit{\theta }\right)=-2\overline{\delta }\sum _{i=1}^n\frac{\mathrm{\partial H}(x_i;\mathit{\xi })}{\partial {\mathit{\xi }}_k}\frac{exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]}{1-\overline{\delta }exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]}\left[1-\frac{\mathrm{\alpha H}(x_i;\mathit{\xi })}{1-\overline{\delta }exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]}\right]\\ +\sum _{i=1}^n\frac{\mathrm{\partial H}(x_i;\mathit{\xi })}{\partial {\mathit{\xi }}_k}\text{and}\\ U_{{\mathit{\xi }}_k{\mathit{\xi }}_j}\left(\mathit{\theta }\right)=\sum _{i=1}^n\frac{1}{h(x_i;\mathit{\xi })}\left[\frac{{\partial }^{2}h(x_i;\mathit{\xi })}{\partial {\mathit{\xi }}_k{\mathit{\xi }}_j}-\frac{1}{h(x_i;\mathit{\xi })}\frac{\mathrm{\partial h}(x_i;\mathit{\xi })}{\partial {\mathit{\xi }}_k}\frac{\mathrm{\partial h}(x_i;\mathit{\xi })}{\partial {\mathit{\xi }}_j}\right]-\alpha \sum _{i=1}^n\frac{{\partial }^{2}H(x_i;\mathit{\xi })}{\partial {\mathit{\xi }}_k{\mathit{\xi }}_j}\\ -2\alpha \overline{\delta }\sum _{i=1}^n\frac{exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]}{1-\overline{\delta }exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]}\left[\frac{{\partial }^{2}H(x_i;\mathit{\xi })}{\partial {\mathit{\xi }}_k{\mathit{\xi }}_j}-\frac{\mathrm{\partial H}(x_i;\mathit{\xi })}{\partial {\mathit{\xi }}_k}\frac{\mathrm{\alpha H}(x_i;\mathit{\xi })}{1-\overline{\delta }exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]}\right].\end{array}$$

When some standard regularity conditions are satisfied (Cox and Hinkley 1974), one can verify that $\sqrt{n}\left({\left[\hat{\alpha },\hat{\delta },\hat{\mathit{\xi }}\right]}^{\top }-{\left[\alpha ,\delta ,\mathit{\xi }\right]}^{\top }\right)$ converges in distribution to the multivariate $N_{p+2}\left(0,\mathcal{K}{\left(\right[\alpha ,\delta ,\mathit{\xi }\left]\right)}^{-1}\right)$ distribution, where p denotes the dimension of ξ and $\mathcal{K}\left(\right[\alpha ,\delta ,\mathit{\xi }\left]\right)$ is the expected information matrix for which the limit identity ${lim}_{n\to \infty }{J}_n\left(\right[\alpha ,\delta ,\mathit{\xi }\left]\right)=\mathcal{K}\left(\right[\alpha ,\delta ,\mathit{\xi }\left]\right)$ is satisfied. Based on this result, one can compute confidence regions for the $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}$ parameters. Such regions can be used as decision criteria in several practical situations.

For checking if δ is statistically different from one, i.e. for testing the null hypothesis H₀:δ=1 against H₁:δ≠1, we use the LR statistic given by $\text{LR}=2\left\{\ell \left(\hat{\mathit{\theta }}\right)-\ell \left(\tilde{\mathit{\theta }}\right)\right\}$, where $\hat{\mathit{\theta }}$ is the vector of unrestricted MLEs under H₁ and $\tilde{\mathit{\theta }}$ is the vector of restricted MLEs under H₀. Under the null hypothesis, the limiting distribution of LR is a ${\chi }_1^2$ distribution. If the test statistic exceeds the upper 100(1−α)% quantile of the ${\chi }_1^2$ distribution, then we reject the null hypothesis.

Censored data occur very frequently in lifetime data analysis. Some mechanisms of censoring are identified in the literature as, for example, types I and II censoring (Lawless 2003). Here, we consider the general case of multi-censored data: there are n=n₀+n₁+n₂ subjects of which n₀ is known to have failed at the times $x_1,\dots ,x_{n_0}$, n₁ is known to have failed in the interval [ s_i−1,s _i ], i=1,…,n₁, and n₂ survived to a time r _i , i=1,…,n₂, but not observed any longer. Note that type I censoring and type II censoring are contained as particular cases of multi-censoring. The log-likelihood function of θ=(δ,α,ξ^⊤)^⊤ for this multi-censoring data reduces to

$$\begin{array}{lcr}\ell \left(\mathit{\theta }\right)& =& n_{0}log\left(\mathrm{\delta \alpha }\right)+\sum _{i=1}^{n_0}log\left[h(x_i;\mathit{\xi })\right]-\alpha \sum _{i=1}^{n_0}H(x_i;\mathit{\xi })-2\sum _{i=1}^{n_0}log\left\{1-\overline{\delta }exp[-\mathrm{\alpha H}(x_i;\mathit{\xi }\left)\right]\right\}\hfill \\ +\sum _{i=1}^{n_1}log\left\{\frac{1-exp[-\alpha H(s_i;\mathit{\xi }\left)\right]}{1-\overline{\delta }exp[-\alpha H(s_i;\mathit{\xi }\left)\right]}-\frac{1-exp[-\alpha H(s_{i-1};\mathit{\xi }\left)\right]}{1-\overline{\delta }exp[-\alpha H(s_{i-1};\mathit{\xi }\left)\right]}\right\}\hfill \\ +n_{2}log\left(\delta \right)-\alpha \sum _{i=1}^{n_2}H(r_i;\mathit{\xi })-2\sum _{i=1}^{n_2}log\left\{1-\overline{\delta }exp[-\mathrm{\alpha H}(r_i;\mathit{\xi }\left)\right]\right\}.\hfill \end{array}$$

(21)

The score functions and the observed information matrix corresponding to (21) is too complicated to be presented here.

6 Two special models

In this section, we study two special $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}$ models, namely the Marshall-Olkin modified Weibull ($\mathcal{ℳ}\mathcal{O}\mathcal{ℳ}\mathcal{W}$) and Marshall-Olkin Gompertz ($\mathcal{ℳ}\mathcal{O}\mathcal{G}$) distributions. We provide plots of the density and hazard rate functions for some parameters to illustrate the flexibility of these distributions.

6.1 The $\mathcal{ℳ}\mathcal{O}\mathcal{ℳ}\mathcal{W}$ model

For H(x;λ,γ)=x^γ exp(λ x) and h(x;λ,γ)=x^γ−1 exp(λ x)(γ+λ x), we obtain the $\mathcal{ℳ}\mathcal{O}\mathcal{ℳ}\mathcal{W}$ distribution. Its density function is given by

$$\begin{array}{l}f(x;\alpha ,\delta ,\lambda ,\gamma )=\mathrm{\delta \alpha }(\gamma +\mathrm{\lambda x})x^{\gamma -1}\frac{exp[\mathrm{\lambda x}-\alpha x^{\gamma }exp(\mathrm{\lambda x}\left)\right]}{{\left\{1-\overline{\delta }exp[-\alpha x^{\gamma }exp(\mathrm{\lambda x}\left)\right]\right\}}^2},x>0,\end{array}$$

where λ,γ≥0. If δ=1, it leads to the special case of the modified Weibull ($\mathcal{ℳ}\mathcal{W}$) distribution (Lai et al.2003). In addition, when λ=0, it gives the Weibull distribution. Its cdf and hrf are given by

$$F(x;\alpha ,\delta ,\lambda ,\gamma )=\frac{1-exp[-\alpha x^{\gamma }exp(\mathrm{\lambda x}\left)\right]}{1-\overline{\delta }exp[-\alpha x^{\gamma }exp(\mathrm{\lambda x}\left)\right]}$$

and

$$\tau (x;\alpha ,\delta ,\lambda ,\gamma )=\frac{\alpha x^{\gamma -1}exp\left(\mathrm{\lambda x}\right)(\gamma +\mathrm{\lambda x})}{1-\overline{\delta }exp[-\alpha x^{\gamma }exp(\mathrm{\lambda x}\left)\right]},$$

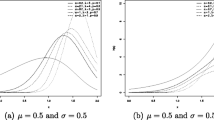
respectively. In Figures 2(a), 2(b), 2(c) and 2(d), we note some different shapes of the $\mathcal{ℳ}\mathcal{O}\mathcal{ℳ}\mathcal{W}$ pdf. Further, Figures 3(a), 3(b), 3(c) and 3(d) display plots of the $\mathcal{ℳ}\mathcal{O}\mathcal{ℳ}\mathcal{W}$ hrf, which can have increasing, decreasing, non-monotone and bathtub forms.

Figure 2

The$\mathcal{ℳ}\mathcal{O}\mathcal{ℳ}\mathcal{W}$ density functions. (a) For α=0.5,λ=2.0,γ=0.5. (b) For δ=2.0,λ=2.0,γ=0.5. (c) For δ=5.0,δ=2.0,γ=0.5. (d) For α=0.5,δ=2.0,λ=2.0.

Figure 3

The$\mathcal{ℳ}\mathcal{O}\mathcal{W}\mathcal{N}$ hrfs. (a) For α=0.5,λ=2.0,γ=0.5. (b) For δ=2.0,λ=2.0,γ=0.5. (c) For δ=5.0,δ=2.0,γ=0.5. (d) For α=0.5,δ=2.0,λ=2.0.

The r th raw moment of the $\mathcal{ℳ}\mathcal{O}\mathcal{ℳ}\mathcal{W}$ distribution comes from (13) as

$$\mathrm{E}\left(X^r\right)=\sum _{j=1}^{\infty }{w}_j{\mu }_r\left(j\right),$$

(22)

where ${\mu }_r\left(j\right)={\int }_0^{\infty }{x}^{r}g(x;(j+1)\alpha ,\gamma ,\lambda ))\mathrm{d}x$ denotes the r th raw moment of the $\mathcal{ℳ}\mathcal{W}$ distribution with parameters (j+1)α,γ and λ. Carrasco et al. (2008) determined an infinite representation for μ _r (j) given by

$${\mu }_r\left(j\right)=\sum _{i_1,\dots ,i_r=1}^{\infty }\frac{A_{i_1,\dots ,i_r}\Gamma (s_r/\gamma +1)}{{\left[\right(j+1\left)\alpha \right]}^{s_r/\gamma }},$$

(23)

where

$$A_{i_1,\dots ,i_r}=a_{i_1},\dots ,a_{i_r}\text{and}{s}_r=i_1,\dots ,i_r,$$

and

$$a_i=\frac{{(-1)}^{i+1}{i}^{i-2}}{(i-1)!}{\left(\frac{\lambda }{\gamma }\right)}^{i-1}.$$

Hence, the $\mathcal{ℳ}\mathcal{O}\mathcal{ℳ}\mathcal{W}$ moments can be obtained directly from (22) and (23).

Let x₁,…,x _n be a sample of size n from $X\sim \mathcal{ℳ}\mathcal{O}\mathcal{ℳ}\mathcal{W}(\alpha ,\delta ,\lambda ,\gamma )$. The log-likelihood function for the vector of parameters θ=(α,δ,λ,γ)^⊤ can be expressed as

$$\begin{array}{lcr}\ell \left(\mathit{\theta }\right)& =& nlog\left(\mathrm{\delta \alpha }\right)+\sum _{i=1}^{n}log(\gamma +\lambda x_i)+(\gamma -1)\sum _{i=1}^{n}log\left(x_i\right)+\lambda \sum _{i=1}^n{x}_i-\alpha \sum _{i=1}^n\underset{i}{\overset{\lambda }{x}}exp\left(\lambda x_i\right)\hfill \\ -2\sum _{i=1}^{n}log\left(1-\overline{\delta }exp\left[-\alpha \underset{i}{\overset{\gamma }{x}}exp\left(\lambda x_i\right)\right]\right).\hfill \end{array}$$

6.2 The $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ model

For H(x;β)=β⁻¹[ exp(β x)−1] and h(x;β)= exp(β x), we obtain the $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ distribution. Its pdf is given by

$$\begin{array}{l}f(x;\alpha ,\delta ,\beta )=\frac{\mathrm{\delta \alpha }exp\left\{\mathrm{\beta x}-\alpha /\beta [exp(\mathrm{\beta x})-1]\right\}}{{\left\{1-\overline{\delta }exp\left\{-\alpha /\beta [exp(\mathrm{\beta x})-1]\right\}\right\}}^2},x>0,\end{array}$$

where −∞<β<∞. For δ=1, it follows the Gompertz distribution as a special case. The $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ model is a special case of the Marshall-Olkin Makeham distribution (EL-Bassiouny and Abdo 2009). The cdf and hrf of the $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ distribution are given by

$$F(x;\alpha ,\delta ,\beta )=\frac{1-exp\left\{-\alpha /\beta [exp(\mathrm{\beta x})-1]\right\}}{1-\overline{\delta }exp\left\{-\alpha /\beta [exp(\mathrm{\beta x})-1]\right\}}$$

and

$$\tau (x;\alpha ,\delta ,\beta )=\frac{\alpha exp\left(\mathrm{\beta x}\right)}{1-\overline{\delta }exp\left\{-\alpha /\beta [exp(\mathrm{\beta x})-1]\right\}}.$$

Figures 4(a), 4(b) and 4(c) display some plots of the density functions for some values of α, δ and β. The hrf of the Gompertz distribution is increasing (β>0) and decreasing (β<0). Besides these two forms, Figures 5(a), 5(b) and 5(c) indicate that the $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ hrf can be bathtub shaped.

Figure 4

The$\mathcal{ℳ}\mathcal{O}\mathcal{G}$ density functions. (a) For α=0.5,β=0.7. (b) For δ=2.0,β=2.0. (c) For δ=5.0,α=1.5.

Figure 5

The$\mathcal{ℳ}\mathcal{O}\mathcal{G}$ hrfs. (a) For α=25,β=2.0. (b) For δ=0.2,β=0.5. (c) For α=0.01,δ=0.5.

From Equation (15), the $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ qf becomes

$$Q\left(u\right)={\beta }^{-1}log\left[\frac{\beta }{\alpha }log\left(\frac{1-\overline{\delta }u}{1-u}\right)+1\right].$$

Let x₁,…,x _n be a sample of size n from the $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ model. The log-likelihood function for the vector of parameters θ=(δ,α,β)^⊤ can be expressed as

$$\begin{array}{ll}\ell \left(\mathit{\theta }\right)& =nlog\left(\mathrm{\delta \alpha }\right)+\beta \sum _{i=1}^n{x}_i-\frac{\alpha }{\beta }\sum _{i=1}^n\left[exp\left(\beta x_i\right)-1\right]\\ -2\sum _{i=1}^{n}log\left(1-\overline{\delta }exp\left\{-\alpha [exp(\beta x_i)-1]/\beta \right\}\right).\end{array}$$

7 Simulation and applications

This section is divided in two parts. First, we perform a simulation study in order to assess the performance of the MLEs on some points at the parametric space of one of the special models. Second, an application to real data provides evidence in favor of one distribution in the $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}$ class.

7.1 Simulation study

We present a simulation study by means of Monte Carlo’s experiments in order to assess the performance of the MLEs described in Section 5. To that end, we work with the $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ distribution. One of advantages of this model is that its cdf has tractable analytical form. This fact implies in a simple random number generation (RNG) determined by the $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ qf given in Section 6.2. The $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ generator is illustrated in Figure 6.

Figure 6

Illustration of the $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ generator for two points at the parametric space.

The simulation study is conducted in order to quantify the influence of η=α/β over the estimation of the extra parameter δ. It is known that η>1 gives the Gompertz distribution which presents mode at zero or, for η<1, having their modes at x^∗=β⁻¹ [1 − log(η)]. An initial discussion using the Kullback-Leibler distance derived in Section 4.3 points out that increasing the contamination (or the bias of the estimates) can affect the quality of fit.

In this study, the following scenarios are taken into account. For the sample size n=50,100,150,200, we adopt as the true parameters the following cases:

• Scenario η<1: (α,β)=(1,2) and δ∈{0.3,1,4};

• Scenario η=1: (α,β)=(2,2) and δ∈{0.3,1,4};

• Scenario η>1: (α,β)=(4,2) and δ∈{0.3,1,4}.

Also, we use 10,000 Monte Carlo’s replications and, at each one of them, we quantify (i) the average of the MLEs and (ii) the mean square error (MSEs).

Table 3 gives the results of the simulation study. In general, the MLEs present smaller values of the biases and MSEs when the sample size increases. It is important to highlight the following atypical case: for the MLEs of α at the scenarios (α,δ,β)∈{(1,4,2),(2,1,2),(4,0.3,2),(4,1,2)} and of δ at (4,0.3,2), the associated biases do not have an inverse monotonic relationship with sample sizes, as expected.However, based on the fact that their MSEs tend to zero, we can expect that there exists a sample size n₀ such that biases of the MLEs decrease when the sample sizes increase from n₀.

Table 3 Performance of the MLEs for the $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ distribution

The results provide evidence that the scenarios under the condition η>1 yield a hard estimation (having larger variation ranges of the MSEs than those obtained for the cases when η<1) for α and β parameters, and that the MLEs present smaller values of the MSEs under such conditions. Figure 7 illustrates the above behavior for the cases δ∈{0.3,0.8,1,2,4} and n=200. In summary, the scenario with less numerical problems is (η,δ)=(2,0.1), whereas that one which requires more attention for estimating the $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ parameters is (η,δ)=(0.5,4).

Figure 7

MSE curves for δ ∈{0 . 3,1,4}, η =0 . 5,1,2 and n =200. (a)$\mathit{\text{MSE}}\left(\hat{\alpha }\right)$, (b)$\mathit{\text{MSE}}\left(\hat{\beta }\right)$, (c)$\mathit{\text{MSE}}\left(\hat{\delta }\right)$.

7.2 Applications

Here, the usefulness of the $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}$ distribution is illustrated by means of two real data sets.

7.2.1 Uncensored data

Here, we compare the fits of some special models of the $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{W}$ family using a real data set. The estimation of the model parameters is performed by the maximum likelihood method discussed in Section 5. We use the maxLik function of the maxLik package in R language. In this function, if the argument “method” is not specified, a suitable method is selected automatically. For this application, we use the Newton-Raphson method. The data represent the percentage of body fat determined by underwater weighing for 250 men. For more details about the data see http://lib.stat.cmu.edu/datasets/bodyfat.

Table 4 provides some descriptive measures. They suggest an empirical distribution which is slightly asymmetric and platykurtic.

Table 4 Descriptive statistics

We compare the classical models and generalized models within the $\mathcal{ℳ}\mathcal{O}$ family. The null hypothesis H₀:δ=1 is tested against H₁:δ≠1 using the LR statistic. The comparisons are presented in Table 5. For the $\mathcal{ℳ}\mathcal{O}\mathcal{W}$ and $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{P}$ models, one cannot say that the parameter δ is statistically different from one at the 10% significance level. Based on this result, we fit the , exponential power ($\mathcal{E}\mathcal{P}$), $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ and Marshall-Olkin flexible Weibull extension ($\mathcal{ℳ}\mathcal{O}\mathcal{F}\mathcal{W}\mathcal{E}$) models to the current data (see Table 1). These models are compared with two other three-parameter models, namely: the modified Weibull ($\mathcal{ℳ}\mathcal{W}$) and generalized Birnbaum-Saunders ($\mathcal{G}\mathcal{ℬ}\mathcal{S}$) (Owen 2006) distributions. The $\mathcal{G}\mathcal{ℬ}\mathcal{S}$ density is given by

$$f(x;\varphi ,\eta ,\kappa )=\frac{1}{\varphi \sqrt{2\mathrm{\pi \eta }}{x}^{\kappa }}\left(1-\kappa +\frac{\mathrm{\eta \kappa }}{x}\right)exp\left[-\frac{1}{2{\varphi }^2}\frac{{(x-\eta )}^2}{\eta x^{2\kappa }}\right],x>0.$$

Table 5 Comparison of fitted models using the LR test

In Table 6, we present the MLEs (standard errors in parentheses) of the parameters of the fitted $\mathcal{ℳ}\mathcal{O}\mathcal{F}\mathcal{W}\mathcal{E}$, $\mathcal{ℳ}\mathcal{O}\mathcal{G}$, $\mathcal{E}\mathcal{P}$, , $\mathcal{ℳ}\mathcal{W}$ and $\mathcal{G}\mathcal{ℬ}\mathcal{S}$ distributions. Also, we provide the goodness-of-fit measures (p-values in parentheses). Thus, these values indicate that the null models are strongly rejected for the $\mathcal{ℳ}\mathcal{O}\mathcal{F}\mathcal{W}\mathcal{E}$ and $\mathcal{ℳ}\mathcal{O}\mathcal{G}$ distributions, since the associated p-values are much lower than 0.001.

Table 6 MLEs and goodness-of-fit statistics

Table 7 gives the values of the Akaike information criterion (AIC), Bayesian information criterion (BIC), consistent Akaike information criterion (CAIC) and Hannan-Quinn information criterion (HQIC). Since the values of the AIC, CAIC and HQIC are smaller for the $\mathcal{ℳ}\mathcal{O}\mathcal{F}\mathcal{W}\mathcal{E}$ distribution compared to those values of the other fitted models. Thus, this new distribution seems to be a very competitive model to explain the current data.

Table 7 Statistics AIC, BIC, CAIC and HQIC

Figures 8(a) and 8(b) display the estimated density and survival functions of the $\mathcal{ℳ}\mathcal{O}\mathcal{F}\mathcal{W}\mathcal{E}$ distribution. The plots confirm the excellent fit of this distribution to the data. Figure 8(c) shows that the estimated $\mathcal{ℳ}\mathcal{O}\mathcal{F}\mathcal{W}\mathcal{E}$ hrf is an increasing curve.

Figure 8

Plots of the estimated. (a) density, (b) survivor function (c) and hrf of the $\mathcal{ℳ}\mathcal{O}\mathcal{F}\mathcal{W}\mathcal{E}$ model.

7.2.2 Censored data

Now, we consider a set of remission times from 137 cancer patients [Lee and Wang (2003), pag. 231]. Lee and Wang (2003) showed that the log-logistic ($\mathcal{ℒ}\mathcal{ℒ}$) model provides a good fit to the data. Ghitany et al. (2005) compared the fits of the $\mathcal{ℳ}\mathcal{O}\mathcal{W}$ and models to these data. Now, we present a more detailed study by comparing the fitted , $\mathcal{ℒ}\mathcal{ℒ}$, $\mathcal{E}\mathcal{P}$, $\mathcal{ℳ}\mathcal{O}\mathcal{W}$, Marshall-Olkin log-logistic ($\mathcal{ℳ}\mathcal{O}\mathcal{ℒ}\mathcal{ℒ}$), $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{P}$ and $\mathcal{G}\mathcal{ℬ}\mathcal{S}$ models to these data. The functions H(x;γ,c)= log(1+γ x^c) and h(x;γ,c)=γ c x^c−1/(1+γ x^c) are associated with the $\mathcal{ℒ}\mathcal{ℒ}$ model.

The hypothesis that the underlying distribution is (or $\mathcal{E}\mathcal{P}$) versus the alternative hypothesis that the distribution is the $\mathcal{ℳ}\mathcal{O}\mathcal{W}$ (or $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{P}$) is rejected with p-value = 0.0055 (or p-value = <0.0001). Further, the hypothesis test that the underlying distribution is $\mathcal{ℒ}\mathcal{ℒ}$ versus the $\mathcal{ℳ}\mathcal{O}\mathcal{ℒ}\mathcal{ℒ}$ distribution yields the p-value =1.0000. Thus, we compare the $\mathcal{ℳ}\mathcal{O}\mathcal{W}$, $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{P}$, $\mathcal{ℒ}\mathcal{ℒ}$ and $\mathcal{G}\mathcal{ℬ}\mathcal{S}$ models to determine which model gives the best fit to the current data.

Table 8 lists the MLEs (and corresponding standard errors in parentheses) of the parameters and the values of the AD and CM statistics (their p-values in parentheses). The figures in this table, specially the p-values, suggest that the $\mathcal{ℳ}\mathcal{O}\mathcal{W}$ distribution yields a better fit to these data than the other three distributions.

Table 8 MLEs and goodness-of-fit statistics

Table 9 lists the values of the AIC, BIC, CAIC and HQIC statistics. The figures in this table indicate that there is a competitiveness among the $\mathcal{ℳ}\mathcal{O}\mathcal{W}$, $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{P}$ and $\mathcal{ℒ}\mathcal{ℒ}$ models. However, if we observe the Figures 9(a), 9(b) and 9(c), we note that the $\mathcal{ℳ}\mathcal{O}\mathcal{W}$ and $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{P}$ models present better fits to the current data.

Table 9 Statistics AIC, BIC, CAIC and HQIC

Figure 9

Plots of the estimated. (a) Q-Q plot of $\mathcal{ℳ}\mathcal{O}\mathcal{W}$, (b)$\mathcal{ℒ}\mathcal{ℒ}$, (c)$\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{P}$ distributions and (d) Kaplan-Meier curve estimated survival and upper and lower 95% confidence limits for the cancer patients.

Figure 9(d) really shows that the $\mathcal{ℳ}\mathcal{O}\mathcal{W}$ and $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{P}$ distributions present good fits to the current data. We can conclude that the $\mathcal{ℳ}\mathcal{O}\mathcal{W}$ and $\mathcal{ℳ}\mathcal{O}\mathcal{E}\mathcal{P}$ distributions are excellent alternatives to explain this data set.

8 Conclusion

In this paper, the Marshall-Olkin extended Weibull family of distributions is proposed and some of its mathematical properties are studied. The maximum likelihood procedure is used for estimating the model parameters. Two special models in the family are described with some details. In order to assess the performance of the maximum likelihood estimates, a simulation study is performed by means of Monte Carlo experiments. Special models of the proposed family are compared (through goodness-of-fit measures) with other well-known lifetime models by means of two real data sets. The proposed model outperforms classical lifetime models to these data.

Appendix: An expansion for f(x;δ,α,ξ)F(x;δ,α,ξ)^c

Here, we obtain an expansion for the quantity f(x;δ,α,ξ)F(x;δ,α,ξ)^c. First, we consider an expansion for F(x;δ,α,ξ)^c. Based on (5), the power of the cdf can be expressed as

$$F{(x;\delta ,\alpha ,\xi )}^c=\underset{\equiv A}{\underbrace{{\{1-exp[-\mathrm{\alpha H}(x;\mathit{\xi })\left]\right\}}^c}}\underset{\equiv B}{\underbrace{{\{1-\overline{\delta }exp[-\mathrm{\alpha H}(x;\mathit{\xi })\left]\right\}}^{-c}}}.$$

Applying expansion (9), we have

$$A=\sum _{k=0}^{\infty }{(-1)}^k\left(\genfrac{}{}{0ex}{}{c}{k}\right)exp[-\mathrm{k\alpha H}(x;\mathit{\xi }\left)\right].$$

Now, we expand the quantity B. Equation (9) under the restriction δ<1 (implying that $\overline{\delta }exp[-\mathrm{\alpha H}(x;\mathit{\xi }\left)\right]<1$) yields

$$B=\sum _{j=0}^{\infty }\frac{{\left(c\right)}_j}{j!}{\overline{\delta }}^{j}exp[-\mathrm{j\alpha H}(x;\mathit{\xi }\left)\right].$$

Moreover, it is clear that δ=1 implies B=1. Finally, for δ>1 (i.e., $\{1-\overline{\delta }exp[-\mathrm{\alpha H}(x;\mathit{\xi })\left]\right\}>1$), the quantity B can be rewritten as

$$B={\left\{1-[1-{\{1-\overline{\delta }exp[-\mathrm{\alpha H}(x;\mathit{\xi })\left]\right\}}^{-1}]\right\}}^c.$$

Using the binomial expansion, we have

$$B=\sum _{j=0}^{\infty }{(-1)}^j\left(\genfrac{}{}{0ex}{}{c}{j}\right){\left[1-{\left\{1-\overline{\delta }exp\left[-\mathrm{\alpha H}(x;\mathit{\xi })\right]\right\}}^{-1}\right]}^j.$$

Thus,

$$\begin{array}{ll}F{(x;\delta ,\alpha ,\xi )}^c& ={\mathbb{I}}_{(\delta <1)}\sum _{j,k=0}^{\infty }{(-1)}^k\frac{{\left(c\right)}_j}{j!}\left(\genfrac{}{}{0ex}{}{c}{k}\right){\overline{\delta }}^{j}exp[-(j+k\left)\mathrm{\alpha H}\right(x;\mathit{\xi }\left)\right]\\ +{\mathbb{I}}_{(\delta =1)}\sum _{k=0}^{\infty }{(-1)}^k\left(\genfrac{}{}{0ex}{}{c}{k}\right)exp[-\mathrm{k\alpha H}(x;\mathit{\xi }\left)\right]\\ +{\mathbb{I}}_{(\delta >1)}\sum _{j,k=0}^{\infty }{(-1)}^{j+k}\left(\genfrac{}{}{0ex}{}{c}{k}\right)\left(\genfrac{}{}{0ex}{}{c}{j}\right)exp[-\mathrm{k\alpha H}(x;\mathit{\xi }\left)\right]\\ \times {[1-{\{1-\overline{\delta }exp[-\mathrm{\alpha H}(x;\mathit{\xi })\left]\right\}}^{-1}]}^j.\end{array}$$

Hence, based on Equation (13), the following expansion holds

$$\begin{array}{ll}f(x;\delta ,\alpha ,\xi )F{(x;\delta ,\alpha ,\xi )}^c& =\left(\sum _{v=0}^{\infty }{w}_{v}g\left(x;(v+1)\alpha ,\mathit{\xi }\right)\right)F{(x;\delta ,\alpha ,\xi )}^c={\mathbb{I}}_{(\delta <1)}\sum _{j,k,v=0}^{\infty }{(-1)}^k\\ \times w_v\frac{{\left(c\right)}_j}{j!}\left(\genfrac{}{}{0ex}{}{c}{k}\right){\overline{\delta }}^{j}exp[-(j+k\left)\mathrm{\alpha H}\right(x;\mathit{\xi }\left)\right]g(x;(v+1)\alpha ,\mathit{\xi })\\ +{\mathbb{I}}_{(\delta =1)}\sum _{k,v=0}^{\infty }{(-1)}^k{w}_v\left(\genfrac{}{}{0ex}{}{c}{k}\right)exp[-\mathrm{k\alpha H}(x;\mathit{\xi }\left)\right]g(x;(v+1)\alpha ,\mathit{\xi })\\ +{\mathbb{I}}_{(\delta >1)}\sum _{j,k,v=0}^{\infty }{(-1)}^{j+k}{w}_v\left(\genfrac{}{}{0ex}{}{c}{k}\right)\left(\genfrac{}{}{0ex}{}{c}{j}\right)exp[-\mathrm{k\alpha H}(x;\mathit{\xi }\left)\right]\\ \times {\left[1-{\{1-\overline{\delta }exp[-\mathrm{\alpha H}(x;\mathit{\xi })\left]\right\}}^{-1}\right]}^{j}g(x;(v+1)\alpha ,\mathit{\xi }).\end{array}$$

(24)