Constrained multi-fidelity surrogate framework using Bayesian optimization with non-intrusive reduced-order basis

Abstract

This article addresses the problem of constrained derivative-free optimization in a multi-fidelity (or variable-complexity) framework using Bayesian optimization techniques. It is assumed that the objective and constraints involved in the optimization problem can be evaluated using either an accurate but time-consuming computer program or a fast lower-fidelity one. In this setting, the aim is to solve the optimization problem using as few calls to the high-fidelity program as possible. To this end, it is proposed to use Gaussian process models with trend functions built from the projection of low-fidelity solutions on a reduced-order basis synthesized from scarce high-fidelity snapshots. A study on the ability of such models to accurately represent the objective and the constraints and a comparison of two improvement-based infill strategies are performed on a representative benchmark test case.

Introduction

Several computation techniques with varying fidelity¹ have been developed over the past decades for the simulation of fluid dynamics. Figure 1 illustrates the trade-off between duration and accuracy for some of these techniques. High-Fidelity (HF) simulation techniques such as 3D-RANS and LES have reached a maturity that allows them to be predictive enough to be used within aeronautical parts design optimization loops [39]. However, these imply extensive computer resources utilization ranging from hours to full days of computation on supercomputer architectures and the generation of several gigabytes of data. On the other hand, Low-Fidelity (LF) such as 2D-Euler, 1D models, categorization [20, 37], mesh reduction [5, 27] or relaxing convergence criteria [16], can be used to compute coarse fluid flow approximations using limited resources and time.

Fig. 1

Illustration of the trade-off between duration and accuracy for different computational fluid dynamics (CFD) techniques

This work addresses the problem of constrained derivative-free optimization with multiple fidelity sources. In the single-fidelity Surrogate-Based Optimization (SBO) framework, cheap to evaluate approximation models of the objective and constraints are used alongside an infill criterion to build a sequential Design of Experiments (DoE) optimization strategy. Multi-Fidelity (MF) approaches extend this framework by leveraging both low and high-fidelity simulators. Some approaches enhance LF simulations using additive [42], multiplicative [2] or hybrid [50] corrections or space mapping [29], learned from HF simulations. Other approaches, such as co-kriging [21, 28] or co-RBF [18], exploit the correlation between the different fidelity levels to produce a MF surrogate model. Another approach is to use hierarchical Kriging [49] to build surrogate models recursively at each fidelity level.

The efficiency of MF models depends on the compromise between the cost and accuracy of the responses. The general concept of MF infill strategies consists in establishing low-cost enrichment criteria of LF models to predict new HF sample’s most promising locations [30, 47]. Hierarchical methods identify promising points before evaluating them with the HF model [13, 17] within an optimization. Those methods can also be used with a Genetic Algorithm [45]. Other articles proposed to use trust-region methods to manage the infill criteria, both in the gradient-based [1] and the derivative-free frameworks [33, 34]. Albeit promising, those methods are likely to remain local. Recently, attention has been turned toward the Surrogate-Based-Optimization framework: approaches in the literature [30] are based either on the prediction error [27] or statistical criteria [25, 31].

In this article, we adopt the Bayesian optimization approach to select promising locations for HF evaluations. The main idea is to choose a prior model for expensive quantities of interest to optimize. The evaluation points are selected sequentially to obtain a small average error between the approximation and the optimal point under the selected prior, see e.g., Kushner, Zilinskas, and Mockus [51] for additional references in the field. Regarding single-objective bound-constrained optimization, the Expected Improvement (EI) was popularised by Jones et al. [25] in the Efficient Global Optimization (EGO) framework. Later, the EI criterion has been extended to handle constraints and to address multi-objective problems.² Picheny et al. [38] compared existing infill criteria such as EI, Augmented EI used by Huang et al. [22], and the Weighted Integrated Mean Square Error (Weighted IMSE) criterion for noisy optimization benchmark. The weighted EI extension is proposed by Sobester et al. [48] in order to control the balance between exploitation and exploration in a constrained optimization framework. In [44] the EGO was generalized for multidimensional variables in the noisy Gaussian process and gradient-knowledge framework. With similar noise assumptions, Kandasamy et al. [26] used the Thompson sampling criterion to consider the variability of the evaluation time when maximizing an unknown function from noisy evaluation in a parallel computing framework. A multi-fidelity extension of the EI criterion to the sequential Kriging was proposed by Huang et al. [23, 24]. This criterion allows for adding the cheapest best current LF sample. In our case, the sampling is focusing on the HF level. For the additional references, see [46], where Bayesian techniques are reviewed for applications such as constraint, single-fidelity, and multiple fidelity optimization.

Vectorial surrogate models can be used to account for features of interest that are difficult to represent with scalar models, such as discontinuities or shocks, which are typically encountered in aerodynamic simulations. The parametrization of full-field models is often used with a reduced-order model and relies on a separation between space variables and design variables. Methods such as Principal Component Analysis (PCA), Proper Orthogonal Decomposition (POD) [32], developed in the field of turbulence [8], Reduced Basis Methods (RBM) [3, 43] or Proper Generalized Decomposition (PGD) [12] can be employed to this end. The benefits of using such an approach in surrogate-based optimization are shown in [15]. The present work aims at predicting the system response based on a limited number of prior HF evaluations and the LF vector responses. To this end, the Non-Intrusive Reduced Basis (NIRB) [11] methodology is extended to a multi-fidelity optimization context called Multi-Fidelity Non-Intrusive Reduced Basis (MFNIRB) with a correction method within the Bayesian optimization framework.

The paper begins with an overview of the surrogate model used in the proposed enrichment strategy. The reduced basis methodology needed to represent the bi-level fidelity vector responses is also introduced. Then, the proposed infill strategy is detailed. Finally, a bi-fidelity level benchmark derived from aerodynamic simulation [7] illustrates the proposed approach.

Method

Multi-fidelity model

Given a design space ${\mathcal {D}}$ of dimension d and a physical domain $\Omega \subset {\mathbb {R}}^{\{2,\,3\}}$, the optimization problem considered in this work is to find values ${\varvec{\vartheta }}^\star \in {\mathcal {D}}$ of the design variables ${\varvec{\vartheta }}$ that minimize some scalar objective function ${\mathcal {J}}(\varvec{f}( \mathbf{x} ,\varvec{\vartheta }))$ while respecting $n_{c}$ real-valued constraint functions $(c_h)_{1 \le h \le n_c}$.

$$\begin{aligned} \begin{aligned} \underset{\varvec{\vartheta }\in {\mathcal {D}}\subset {\mathbb {R}}^{d}}{\text {minimize}}\quad {\mathcal {J}}({\varvec{f}}(\mathbf{x} ,\varvec{\vartheta })),\\ \text {s.t.} \quad&c_{h}({\varvec{f}}(\mathbf{x} ,\varvec{\vartheta }))\le 0,\quad h=\{1,...,n_{c}\}, \\ \end{aligned} \end{aligned}$$

(1)

where the objective function ${\mathcal {J}}$ and the constraint functions $(c_h)_{1 \le h \le n_c}$ are evaluated by running computer simulations yielding a vector ${\varvec{f}}( \mathbf{x} ,\varvec{\vartheta })$ of values at a fixed set $\mathbf{x} =(x_i)_{1 \le i \le n}$ of n discrete positions in the physical domain $\Omega$.

Given a design of M experiments $\{ {{\varvec{\vartheta }}}^{(1)}, \ldots ,{{\varvec{\vartheta }}}^{(M)} \} \in {\mathcal {D}}^M$, according to the Model Order Reduction paradigm [3, 9], a separated representation of ${\varvec{f}}(\mathbf{x} ,\varvec{\vartheta })$ can be formulated as

$$\begin{aligned} \varvec{f}(\mathbf{x} ,\varvec{\vartheta }) \approx \sum ^{m}_{k=1}\varvec{\varphi }_{k}(\mathbf{x} )\,\alpha _{k}(\varvec{\vartheta }),\quad \mathbf{x} \in \Omega ,\, \varvec{\vartheta }\in {\mathcal {D}} , \end{aligned}$$

(2)

where the basis vectors ${\varvec{\varphi }}_{k}$ are the left singular vectors, corresponding to $m\le M<<~n$ non-zero singular values of the so-called snapshot matrix

$$\begin{aligned} \mathbf{S} =[\varvec{f}(\mathbf{x} ,{{\varvec{\vartheta }}}^{(1)})\ ...\ \varvec{f}(\mathbf{x} ,{{\varvec{\vartheta }}}^{(M)})]. \end{aligned}$$

(3)

The basis vectors ${\varvec{\varphi }}_k$ depend on the discretization of the physical domain and only the coefficients $\alpha _k$ depend on the design variables ${\varvec{\vartheta }}$. Note that since only a low number of HF snapshots is assumed available, we are skipping the usual truncation phase. However, the number m of basis vectors is not strictly equal to M due to the possible presence of null singular values.

Rather than expressing $\alpha _k({\varvec{\vartheta }})$ explicitly using surrogate modeling techniques [15] or by solving a Galerkin-projected problem [14], the proposed multi-fidelity approach relies on the assumption that a LF solution $\varvec{f}^{LF}(\mathbf{x} ,{{\varvec{\vartheta }}})$ is available at a significantly lower computational effort than the HF solution $\varvec{f}(\mathbf{x} ,{{\varvec{\vartheta }}})$. The multi-fidelity approximations $\alpha ^{MF}_k$ of the coefficients $\alpha _k$ can then be obtained by projecting $\varvec{f}^{LF}(\mathbf{x} ,{{\varvec{\vartheta }}})$ on ${\varvec{\varphi }}_k$ [10]:

$$\begin{aligned} \alpha ^{MF}_k({{\varvec{\vartheta }}})={{\varvec{\varphi }}}^T_k(\mathbf{x} )\varvec{f}^{LF}(\mathbf{x} ,\varvec{\vartheta }),\quad \mathbf{x} \in \Omega . \end{aligned}$$

(4)

A multi-fidelity approximation model $\varvec{f}^{MF}(\mathbf{x} ,\varvec{\vartheta })$ of $\varvec{f}(\mathbf{x} ,\varvec{\vartheta })$ can thus be formulated as

$$\begin{aligned} \varvec{f}^{MF}(\mathbf{x} ,\varvec{\vartheta })=\sum _{k=1}^{m}\varvec{\varphi }_{k}(\mathbf{x} )\alpha _{k}^{MF}({{\varvec{\vartheta }}}), \varvec{\vartheta }\in {\mathcal {D}}. \end{aligned}$$

(5)

Note, that this formulation does not necessarily interpolate the data, namely

$$\begin{aligned} \varvec{f}^{MF}(\mathbf{x} ,{\varvec{\vartheta }}^{(i)})\ne \varvec{f}(\mathbf{x} ,{\varvec{\vartheta }}^{(i)}),\quad 1 \le i \le M,\, \mathbf{x} \in \Omega , \end{aligned}$$

(6)

and, as a consequence, the interpolation errors,

$$\begin{aligned} \left\{ \begin{array}{lcll} \Delta _{{\mathcal {J}}}\left( {\varvec{\vartheta }}^{(i)}\right) &{}=&{} {\mathcal {J}}\left( \varvec{f}(\mathbf{x} ,{\varvec{\vartheta }}^{(i)})\right) -{\mathcal {J}}\left( \varvec{f}^{MF}(\mathbf{x} ,{\varvec{\vartheta }}^{(i)})\right) , &{} \\ \Delta _{c_h}\left( {\varvec{\vartheta }}^{(i)}\right) &{}=&{} c_h\left( \varvec{f}(\mathbf{x} ,{\varvec{\vartheta }}^{(i)})\right) -c_h\left( \varvec{f}^{MF}(\mathbf{x} ,{\varvec{\vartheta }}^{(i)})\right) , &{} 1 \le h \le n_c \end{array} \right. \end{aligned}$$

(7)

are non-null.

In this work, it is assumed that the approximation $\varvec{f}^{MF}$ is unbiaised and the correction terms $\Delta _{{\mathcal {J}}}({\varvec{\vartheta }})$ and $\Delta _{c_h}({\varvec{\vartheta }})$ are modeled using Gaussian processes with zero mean and parametrized covariance kernels $k_{{\varvec{\theta }}}$

$$\begin{aligned} \Delta (\varvec{\vartheta }) \sim \mathcal {GP}(0,k_{{\varvec{\theta }}}({{\varvec{\vartheta }}},{{\varvec{\vartheta }}})),\, {{\varvec{\vartheta }}}\in {\mathcal {D}}. \end{aligned}$$

Conditional on the observations, the GP posterior distribution [41] at a new sampling point ${\varvec{\vartheta }}$ is a random variable with a normal distribution characterized by its mean

$$\begin{aligned} {\overline{\Delta }}_M{(\varvec{\vartheta })}={\varvec{k}^{T}_{{\varvec{\theta }}}}(\varvec{\vartheta }) \cdot \varvec{{K}_{{\varvec{\theta }}}}^{-1} \cdot \left[ \Delta ({\varvec{\vartheta }}^{(1)}),\, \ldots ,\, \Delta ({\varvec{\vartheta }}^{(M)})\right] ^T, \end{aligned}$$

and its variance

$$\begin{aligned} \sigma _M^2(\varvec{\vartheta })=k_{{\varvec{\theta }}}({\varvec{\vartheta }},{\varvec{\vartheta }})-\varvec{k_{{\varvec{\theta }}}}^T \cdot \varvec{K_{{\varvec{\theta }}}}^{-1} \cdot \varvec{k_{{\varvec{\theta }}}}, \end{aligned}$$

with $\varvec{K_{{\varvec{\theta }}}}$ the $M \times M$ covariance matrix between the M sample points

$$\begin{aligned} K_{{{\varvec{\theta }}}, ij}=k_{{\varvec{\theta }}}({{\varvec{\vartheta }}}^{(i)},{{\varvec{\vartheta }}}^{(j)}), \quad 1 \le i,\,j \le M, \end{aligned}$$

and ${{\varvec{k}}}_{{\varvec{\theta }}}$ the vector of covariates between the M sample points and $\varvec{\vartheta }$, defined by

$$\begin{aligned} {{\varvec{k}}}_{{\varvec{\theta }}}(\varvec{\vartheta })=\left[ k_{{\varvec{\theta }}}(\varvec{\vartheta },\varvec{\vartheta }^{(1)}),\, \ldots ,\, k_{{\varvec{\theta }}}(\varvec{\vartheta },\varvec{\vartheta }^{(M)})\right] ^{T}. \end{aligned}$$

The approximation of the cost functional for an arbitrary parameter set $\varvec{\vartheta }$ is thus defined as

$$\begin{aligned} \widetilde{{\mathcal {J}}}(\varvec{\vartheta })= {\mathcal {J}}(\varvec{f}_{MF}(\mathbf{x} ,\varvec{\vartheta })) +\Delta _{{\mathcal {J}}}(\varvec{\vartheta }). \end{aligned}$$

(8)

In analogous manner, the constraint functions are modeled as :

$$\begin{aligned} {\widetilde{c}}_{h}(\varvec{\vartheta })=c_{h}(\varvec{f}_{MF}(\mathbf{x} , \varvec{\vartheta })) + \Delta _{c_h}(\varvec{\vartheta }), \quad h=\{1,\,\ldots \,,\,n_{c}\} . \end{aligned}$$

(9)

In the following sections, the MF model refers to the MFNIRB model (the corrected MF prediction). The objective and constraints are expressed respectively by ${\mathcal {J}}^{MF}(\varvec{\vartheta })$ and $c_{h}^{MF}(\varvec{\vartheta })$ instead of ${\mathcal {J}}(\varvec{f}_{MF}(\mathbf{x} ,\varvec{\vartheta }))$ and $c_h(\varvec{f}_{MF}(\mathbf{x} ,\varvec{\vartheta }))$ to simplify the notations.

Improvement-based infill criteria

Assuming that a feasible solution exists in the DoE,³ the current best point can be defined as

$$\begin{aligned} {\mathcal {J}}_{best} = \min \left\{ {\mathcal {J}}(\mathbf{x} , \varvec{\vartheta });\,\varvec{\vartheta }\in {\mathcal {C}} \right\} , \end{aligned}$$

(10)

where ${\mathcal {C}}=\{\varvec{\vartheta }\in {\mathcal {D}};\,c_h(\varvec{\vartheta })\le 0,\,1\le h \le n_c\}$ denotes the feasible solution set. The improvement yielded by the observation of a new point ${\varvec{\vartheta }}$ can then be defined as

$$\begin{aligned} I(\varvec{\vartheta })=\max ({\mathcal {J}}_{best}-\widetilde{{\mathcal {J}}}(\varvec{\vartheta }),0) \cdot \varvec{1}_{\varvec{\vartheta }\in {\mathcal {C}}}. \end{aligned}$$

(11)

Assuming that the constraints involved in the optimization problem are independent, the probability that a given $\varvec{\vartheta }\in {\mathcal {D}}$ belongs to the feasible set ${\mathcal {C}}$ can be computed using the closed-form formula

$$\begin{aligned} \displaystyle PF\left( \varvec{\vartheta }\right) = \prod _{h=1}^{n_{c}} P\left( {\tilde{c}}_h(\varvec{\vartheta })\le 0\right) =\prod _{h=1}^{n_{c}}\Phi \left( \frac{-\widetilde{{\mathcal {J}}}_{c_h}}{\sigma _{c_h}}\right) , \end{aligned}$$

(12)

where $\sigma _{c_h}^2$ is the posterior variance associated to constraint $c_h$, $1 \le h \le n_c$.

If it is further assumed that the objective and constraints are independent, the probability of improvement can be expressed as

$$\begin{aligned} PI_c(\varvec{\vartheta })=\Phi \left( \frac{{\mathcal {J}}_{best} - \widetilde{{\mathcal {J}}}(\varvec{\vartheta })}{\sigma (\varvec{\vartheta })}\right) \cdot PF\left( \varvec{\vartheta }\right) . \end{aligned}$$

(13)

The EI in the presence of constraints is defined as the expected value of $I(\vartheta )$ conditional on the observations (see, e.g., [4]). Under the same assumptions

$$\begin{aligned} EI_{c}(\varvec{\vartheta })=EI(\varvec{\vartheta })\times PF(\varvec{\vartheta }), \end{aligned}$$

(14)

with

$$\begin{aligned} EI(\varvec{\vartheta }) = \left\{ \begin{array}{ll} \max \left( {\mathcal {J}}_{best}-\widetilde{{\mathcal {J}}}(\varvec{\vartheta }),\,0\right) &{} \text{ if } \quad \sigma (\varvec{\vartheta }) = 0, \\ ({\mathcal {J}}_{best}-\widetilde{{\mathcal {J}}}(\varvec{\vartheta }))\Phi \left( \frac{{\mathcal {J}}_{best}-\widetilde{{\mathcal {J}}}(\varvec{\vartheta })}{\sigma (\varvec{\vartheta })}\right) + \sigma (\varvec{\vartheta })\phi \left( \frac{{\mathcal {J}}_{best}-\widetilde{{\mathcal {J}}}(\varvec{\vartheta })}{\sigma (\varvec{\vartheta })}\right) &{} \text{ if } \quad \sigma (\varvec{\vartheta }) > 0 , \end{array} \right. \end{aligned}$$

(15)

where $\phi (.)$ and $\Phi (.)$ denote respectively the standard normal probability density function and the normal cumulative distribution functions, $\widetilde{{\mathcal {J}}}(\varvec{\vartheta })$ being the posterior mean of ${\mathcal {J}}$.

Either $EI_c$ and $PI_c$ can be used as an Infill Criterion (IC) within the optimization loop to select the most promising infill point. Whereas the PI favors the regions of likely improvement, the EI corresponds to the posterior expectation of the improvement function and hence achieves a natural trade-off between regions of high improvement and regions of high variance.

The maximum value of IC determines the new points to be added to the training set, such as

$$\begin{aligned} \varvec{\vartheta }_{new}^{*}=\mathop {\hbox {arg max}}\limits _{\varvec{\vartheta }} IC(\widetilde{{\mathcal {J}}}(\varvec{\vartheta })), \end{aligned}$$

(16)

where IC is an infill criterion using values of the approximate cost function $\widetilde{{\mathcal {J}}}$.

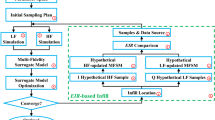
The algorithm 1 summarizes the proposed optimization procedure. After sampling M snapshots from the HF black-box solver, the orthogonal basis $\Upphi = (\varphi _k)_{1 \le k \le m}$ can be obtained with the Singular Value Decomposition (SVD). Thereby, the multi-fidelity projection coefficients (see Eq. (4)) are evaluated using $\Upphi$ and M snapshots sampling of the LF simulation. The multi-fidelity quantities of interest are formulated, then corrected as in equations (8) and (9) to evaluate the quantities $\widetilde{{\mathcal {J}}}$ and $\widetilde{c_h}$, $h=\{1,\,...\,,\,n_c\}$. The IC uses these quantities to find the next candidate. Since the IC is likely to be multi-modal, a global optimization algorithm should be used to solve the auxiliary optimization problem (16).

Numerical results

Problem definition

The optimization benchmark problem [7] is used for the following numerical experiments

$$\begin{aligned} \left. \begin{array}{rl} \text {minimize} &{} {\mathcal {J}}(\varvec{\vartheta }) \\ \text {s.t.} &{} \varvec{\vartheta }\in {\mathcal {D}},\, c_1(\varvec{\vartheta }) \le 0,\, c_2(\varvec{\vartheta }) \le 0, \end{array} \right. \end{aligned}$$

(17)

where ${\mathcal {D}} = \left[ 4,6\right] \times \left[ 10,14\right]$ is a bi-dimensional design space and the objective and constraints functions are defined by

$$\begin{aligned} \left\{ \begin{array}{lclcl} {\mathcal {J}} &{}:&{} \varvec{\vartheta }\in {\mathcal {D}} &{} \mapsto &{} \underset{x_i \in [0,\,1]}{\min }\,\varvec{f}(\mathbf{x} ,\,\varvec{\vartheta }) \\ c_1 &{}:&{} \varvec{\vartheta }\in {\mathcal {D}} &{} \mapsto &{} \underset{x_i \in [0,\,1]}{\mathop {\hbox {arg min}}\limits }\,\varvec{f}(\mathbf{x} ,\,\varvec{\vartheta }) - 0.75 \\ c_2 &{}:&{} \varvec{\vartheta }\in {\mathcal {D}} &{} \mapsto &{} 7.5 - \underset{x_i \in [0,\,1]}{\max }\,\varvec{f}(\mathbf{x} ,\,\varvec{\vartheta }), \end{array} \right. \end{aligned}$$

(18)

using either the HF model $f_{HF}$ or the LF model $f_{LF}$ defined as

$$\begin{aligned} \left\{ \begin{array}{lcccl} f_{HF} &{}:&{} {\mathbb {R}}^n \times {\mathcal {D}} &{} \rightarrow &{} {\mathbb {R}} \\ &{}&{} (x,\,\vartheta ) &{} \mapsto &{} \frac{1}{2}(6x-2)^{2}\sin (\vartheta _{2}x-4)+\sin (10\cos (\vartheta _{1}x)) \\ f_{LF} &{}:&{} {\mathbb {R}}^n \times {\mathcal {D}} &{} \rightarrow &{} {\mathbb {R}} \\ &{}&{} (x,\,\vartheta ) &{} \mapsto &{} \frac{1}{2}(6x-2)^{2}\sin (\vartheta _{2}x-4)+10(x-\frac{1}{2}). \end{array} \right. \end{aligned}$$

(19)

These benchmark functions feature two fidelity levels of the full-field model. It has been generalized to enable a variable Low- to High-fidelity distance

$$\begin{aligned} \varvec{f}_{LF}(\mathbf{x} ,{\varvec{\vartheta }},\alpha ) = \alpha \varvec{f}_{LF}(\mathbf{x} ,{\varvec{\vartheta }}) + (1-\alpha )\varvec{f}_{HF}(\mathbf{x} ,{\varvec{\vartheta }}), \end{aligned}$$

(20)

by introducing the parameter $\alpha \in [0,1]$. We first consider the numerical experiment with $\alpha = 1,$ then variable values of $\alpha$ are taken into account.

This test problem is illustrated in Fig. 2. The non-feasible regions are delimited by continuous and discontinuous lines corresponding to the $c_1$ and $c_2$ constraints. The red and blue lines represent the targeted HF and the LF values. As can be observed on subfigures 1c and d, the constraint $c_1$ features diagonal discontinuities and a sharp cliff in the region of high $\varvec{\vartheta }_2$ values (Fig. 1c) but none of them are present in the LF model (Fig. 1d). Similarly, the region of feasibility for the constraint $c_2$ is poorly represented by the LF model (see subfigures 1e and f). Besides, it features three disconnected feasible regions which make finding the global optimum a difficult optimization problem. Considering the objective function ${\mathcal {J}}$, it can be observed on subfigures 1a and b that the LF model fails to represent the influence of the $\varvec{\vartheta }_2$ variable, which makes it rather deceptive.

Fig. 2

Values of the objective function (first row) and of the constraints functions $c_1$ (second row) and $c_2$ (third row) of HF (left column) and LF (right column)

Convergence of the multi-fidelity model

In this section 3.2, the optimization problem (18) is used, with $\alpha = 1$, to illustrate the convergence of the MF model proposed in Section  towards the HF model with an increasing number of available HF simulations. The ordinary Kriging (OK) is compared to this model to illustrate the impact and the potential benefit of the MF trend compared to a constant trend based kriging (trend of the OK). The OK model is generated using the pykriging library [36] adapted to each experiment in sections 3.2, 3.3 and 3.4.

The constraints $c_{h}(\varvec{\vartheta })$, ${\widetilde{c}}^{MF}_{h}(\varvec{\vartheta })$ (see Eq. (9)) and ${\widetilde{c}}^{OK}_{h}(\varvec{\vartheta })$ obtained for Latin Hypercube designs respectively made of 4, 40 and 400 points are illustrated in Figs. 4 and 5 for $h=1$ and $h=2$ respectively, the red and black lines represent respectively the constraints limits of the HF and the approximates values (obtained with the MF and the OK models). The relative errors between the HF real values and MF models for the objective ${\mathcal {J}}$ and for the constraints $c_1$ and $c_2$ are given in Table 1 and the snapshots obtained using either the MF, LF and HF function values are represented on Fig. 3 for the 4 points DoE. For each curve, the up and down triangles represent respectively the maximum and the minimum values of the $f(\mathbf{x} )$. The vertical line represents the upper-bound of 0.75 on $c_1$ and the horizontal line represents the lower-bound of 7.5 on $c_2$ (see Eq. (18)).

Table 1 Mean over the design variables $\varvec{\vartheta }$ of the “HF-to-MF” models relative error for the objective and constraints when the number of available HF simulations successively equals to 4, 40 and 400 points

Fig. 3

Snapshots obtained for the 4 points DoE when the HF (continuous red curves), LF (dashed blue curves), and MF (dotted purple curves) models are used with $\alpha = 1$

The LF snapshots minimum values illustrated in Fig. 3 are located in the lower part of the vertical upper-bound line. The $c_1$ constraint is confirmed to be constant as observed on Fig. 1d and there are no non-feasible areas for this constraint (see Fig. 1b). The LF test function is not able to capture $c_1$ features. The multi-fidelity function values are approaching better the variation of minimum values locations (Fig. 3). Table 1 compares HF to multi-fidelity and corrected multi-fidelity quantities of interest.

Fig. 4

The convergence of the MF trend, MF and OK models of the $c_1$. In c–h, the left, the middle and the right columns show the values of $c_{1}^{MF}$, ${\widetilde{c}}_{1}^{MF}$ (see Eq. (9)) and ${\widetilde{c}}_{1}^{OK}$. The points in the DoE are represented as white dots

Fig. 5

The convergence of the MF trend, MF and OK models of $c_2$. In c–h, the left, the middle and the right columns show the values of $c_{2}^{MF}$, ${\widetilde{c}}_{2}^{MF}$ (see Eq. (9)) and ${\widetilde{c}}_{2}^{OK}$. The points in the DoE are represented as white dots

For both the objective and the constraints, the prediction errors of the MF models decrease as the size of the DoE increases. The features of the HF models are well captured, especially when the additive correction is applied (see Eq. (8)), with an average relative prediction error ranging from 0.04% to 0.35% which represents a reduction of 0.48% to 8.12% of the relative error (see Table 1 and Figs. 4 and 5). The corrected model is performing better than the LF and the uncorrected multi-fidelity models. The corrected MF model errors for a training set of 400 points are lower than the uncorrected one. Moreover, the increase of the training set sizes from 40 up to 400 generates a small reduction in the MF trend model error, which seems to reach an asymptote ($0.47\%$ drop of the objective and $0.02\%$ increase in $c_1$).

In Figs. 4 and 5, the MF model and the MF trend values are compared to an OK model and values of HF and LF constraints (evaluated by the functions defined by (19)). The OK model cannot capture discontinuities for a low-size training set (4 training points), whereas, the corrected model is better capturing the discontinuities even for scarce DoE size. The MF uncorrected model on Figs. 4 and 5 converges to the LF values, whereas, as for kriging, the corrected MF is converging to the HF targeted values.

Regarding the constraint $c_1$, for which the LF model is unable to capture the features of the HF model, Fig. 4 shows that the corrected MF model can capture both the high values of the constraint and the diagonal discontinuities. The LF model for constraint $c_2$ is more informative than the one for constraint $c_1$. Nevertheless, it fails to represent the three disconnected basins featured by the HF model, whereas Fig. 5 shows that these basins are recovered by the correction term using only 40 points.

Multi-fidelity convergence for variable Low- to High- fidelity distance

Section  illustrates the behavior of the MF model and trend in comparison to an OK model for a single run at each DoE level. As the Latin Hypercube Sampling used to generate the DoE exhibits non-deterministic behavior in successive runs, the present section is devoted to the statistical behavior over repeated runs.

This study focuses on the local results at the optimal targeted value. The criterion evaluated is defined at the theoretical optimal point $\varvec{\vartheta }^{*}$ by

$$\begin{aligned} \delta {\mathcal {J}} = \frac{||{\mathcal {J}}_{HF}(\varvec{\vartheta }^{*})-{\mathcal {J}}(\varvec{\vartheta }^{*})||}{||{\mathcal {J}}_{HF}(\varvec{\vartheta }^{*})||} \end{aligned}$$

(21)

where ${\mathcal {J}}$ can be equal to $\widetilde{{\mathcal {J}}}_{OK}$ or $\widetilde{{\mathcal {J}}}_{MF}$ .

The objective is to evaluate the capacity of MF models with different HF-LF distances (variable $\alpha$, see Eq. (20)) to respond accurately to the optimization problem.

It is advised to use a size of 10 times the number of variables as the initial set of experiments [25], leading to a minimum of 20 points initial set of experiments to obtain sufficient coverage. The MF model is then evaluated with a 20 initial training set. Results obtained for two different DoEs of 20 simulations (M=20) are presented in Fig. 6a, b for varying $\alpha$ values.

Fig. 6

Evolution of the relative error for a sample experiment. The black dots are the DoE points and the red star is the location of the theoretical optimum of the HF model

At the examples shown in Fig. 6, the MF trend intersects the OK model relative error between $\alpha = 0.2$ and $\alpha = 0.3$, its performances decreasing for higher $\alpha$ values, $\alpha \ge 0.3$ (Fig. 6a). MF model outperforms OK model for all $\alpha$ values in Fig. 6b while it remains less interesting for $\alpha \ge 0.4$ in the experiment in the Fig. 6a. Figure 6 presents some variability in the MF performance, therefore, Fig. 7 gives the mean and standard deviation for a series of 40 runs of the three models. In each run, a new LHS DoE is generated, and the results are computed for increasing values of $\alpha$.

Fig. 7

Evolution of the relative error at the theoretical optimal point for multiple runs. The mean error values are represented by purple continuous and dotted lines for the MF model and its trend, the OK by a red line, with their corresponding standard deviation (shaded areas) obtained from 40 independant LHS experiments for each $\alpha$ value. Same LHS DoE is used for model comparison

The average behaviour of the MF trend outperforms the OK model up to $\alpha \le 0.2$, while the average behaviour of the corrected MF model is systematically better for all values of $\alpha$, up to the maximum distance $\alpha = 1$. Given the standard deviation, Fig. 7 shows that the MF trend is very stable, unlike the OK and MF models. Given this variability, MF seems to outperform the OK model up to $\alpha = 0.7$, and we can consider that the proposed MF model is more accurate up to $\alpha \approx 0.7$.

This study illustrates the impact of the trend on a Kriging model. When the $\alpha$ decreases, the trend error MF is reduced, and consequently, the MF model (the corrected trend MF) is improved. The proposed MF model can be an alternative to classical Kriging (here OK model) when the available LF data are sufficiently close to the HF data, however, obtained at a cost comparable to the Kriging model evaluation.

Comparison of infill criteria

The last sections illustrate the behavior of MF in comparison to an OK for different DoE sizes and multiple MF configurations by using the parameter $\alpha$. In the present section, the value of $\alpha$ is fixed to 1, the highest HF-LF distance case, denoting the original benchmark problem [6]. Optimization strategies using either the $EI_c$ and $PI_c$ infill criteria defined in Section  are applied on the test problem of Section . The convergence was tested with high DoE coverage (up to 400 points). The objective of this section is to improve the model convergence with a smaller DoE.

Starting from a Latin Hypercube design of 20 experiments (which corresponds to $M=10d$ as recommended by [25]), either $EI_c$ and $PI_c$ are performed for the OK and corrected MF models. The results obtained after 5 iterations using $EI_c$ criterion that take into account the probability of feasibility of the constraints $c_1$ and $c_2$ are reported in Fig. 8. The cartographies showing the values of each criterion in the last iteration for MF and OK models are shown in Fig. 8e, f.

Fig. 8

Optimization results obtained using the $EI_c$ criterion. Starting from 20 points (first row), the algorithm is iterated for 5 iterations (the other subfigures)

The first experiment (Fig. 8), indicates that OK and MF optimums are in the targeted location for less than 5 infill iterations after a similar initial DoE of 20 training points. The model OK best point was obtained after only 3 iterations. The infill points are mainly covering the region of the theoretical exact best point, particulary for the model OK. The MF infill points are more distanced for iterations 1, 3, and 4 and can be considered more as an exploratory enrichment. The last maximal value of the MF $EI_c$ is located at the theoretical optimal point. The MF model is better representing the $c_1$ constraint at the initial iteration and remains very similar to an OK after few iterations. The global searching phase is brief and converge to the right area for this initial DoE size for both models. However, in this case, the optimal point was determined for less infill points for OK than for MF model. In this case, OK outperforms the MF model.

In the section , it was observed that the MF model was better representing the contraints than the OK model in a small DoE size of M = 4. The DoE size for both models is then decreased to 4 points in the following experiment to test the IC capabilities of MF in comparison to OK models for a lowest evaluation costs (Fig. 9).

Fig. 9

Optimization results obtained using the $EI_c$ $\cdot$ and $PI_c$ Starting from 4 points (first row), the algorithm is iterated for 21 iterations. The first column corresponds to results using the MF model, and the second column results using the OK model

In Fig. 9, initial models are expected to be less accurate, being insufficiently explored. The objective is to test the ICs capacity to reach the optimal point or the right region of interest. In Fig. 9c, the MF model best point was obtained after only 3 iterations in the case of $EI_c$ infill comparing to 15 iterations for the OK model (Fig. 9d). Concerning the $PI_c$ infill, the best point is obtained after 20 iterations for MF model and 18 for OK model (Fig. 9e, f). For both models, the points added are clustering in the right region of interest (close to the location of the best point). On the other hand, the $EI_c$ criterion on Fig. 9c, d appears more spread than $PI_c$ on Fig. 9f, e. The convergence of all cases is acheieved after a lower number of iterations for the $EI_c$ than $PI_c$. An explanation can be that the $PI_c$ infill criterion’s exploration capacity remains poor for both models. In conclusion, the $EI_c$ overperforms the $PI_c$ and compared to the OK model, this study shows that the enriched MF model results are better when the initial DoE remains relatively small thanks to a more efficient exploration of the design space.

Comparison of multi-fidelity and ordinary Kriging enriched surrogate models

In the last section, two enrichment criteria are explored in the multi-fidelity (MF) and single-fidelity (OK) frameworks. In the presented cases, the enrichment was able to find the regions of the optimal values. These observations imply that the MF can be used as a surrogate model in the constrained optimization problem to reduce its cost. The present section aims at quantifying the gain induced by the enrichment strategy. The reference solution for a random design space is compared to a sequentially enriched space. Experiments are performed for multiple runs with random LHS DoEs, for varying values of $\alpha$ using the $EI_c$ criterion.

Figure 10 describes the evolution of the local relative error (defined by (21)) of the objective function at the optimum location with and without the enrichment. The same LHS training sets are used for the MF and the OK model to compare both procedures. The dotted lines represent values obtained after insertion of 4 infill points to a 20 points LHS DoE.

Fig. 10

Evolution of the relative error for enriched and random DoE for multiple runs

The OK values obtained from the random and the enriched DoE have the same values, the local error is not improved by the enrichment. Even for the MF model, the enrichment does not significantly reduce the error. The gap remains very low until $\alpha =0.5$, where the impact of the enrichment in the error reduction appears higher, particularly for MF distances starting from $\alpha >0.5$. Moreover, the standard deviation is strongly correlated to $\alpha$ as it tends toward 0, allowing a very low uncertainty about the MF results for small $\alpha$. As a result of this study, when the LF function is close enough to the HF function, the approximation’s confidence is higher than for a single-fidelity surrogate model. In this boundary case, the MF is shown to be better for a well-chosen LF-HF combination.

Conclusions

The proposed methodology uses a multi-fidelity model approximation to accelerate the optimization process by applying additive corrections based on the Gaussian process. The method improves the surrogate model by using statistical infill criteria adapted to account for the violation of constraints such as the probability of improvement and the expected improvement criteria.

In the presented cases, the enrichment strategy allows finding the region of interest when the distance between the low- and the high-fidelity models is the highest. The optimization cost was lower for the multi-fidelity model with a small initial design of experiments than for the ordinary Kriging when using the expected improvement infill criterion. This can be further improved with a lower distance between the high and the low-fidelity response values used in the optimization framework. On the other hand, it has to be observed that the model’s quality is less improved than these models’ capacity to solve an optimization problem. A global quality criterion would have to be considered to qualify the multi-fidelity enrichment’s overall gain as a follow-up to this study.

Corrected multi-fidelity is a promising approach for capturing various delicate high-fidelity features. Based on this paper’s results, the reduced-order model of full-field multi-fidelity can provide additional information on complex systems’ behavior compared to usual scalar substitutes. Further work is needed to combine the infill criteria into an optimized strategy adapted to more sophisticated feature sets required to treat real engineering optimization test cases.