Geometrically exact planar Euler-Bernoulli beam and time integration procedure for multibody dynamics

Abstract

A new formulation of geometrically exact planar Euler-Bernoulli beam in multi-body dynamics is proposed. For many applications, the use of the Euler-Bernoulli model is sufficient and has the advantage of being a nodal displacement-only formulation avoiding the integration of rotational degrees of freedom. In this paper, an energy momentum method is proposed for the nonlinear in-plane dynamics of flexible multi-body systems, including the effects of revolute joints with or without torsional springs. Large rotational angles of the joints are accurately calculated. Several numerical examples demonstrate the accuracy and the capabilities of the new formulation.

Introduction

Flexible multi-body dynamics has been an intensive topic of research for the last decades due to its many applications in different areas of engineering. Examples of multi-body dynamical systems can be found in aerospace, mechanical, manufacturing and transportation engineering. Manipulators, robots and space structures [1, 2, 4,5,6,7,8, 19] are examples of multi-body dynamical systems. Also bio-dynamical systems e.g human bodies and animals are best understood as multi-body dynamical systems [9,10,11].

It’s clear that a rigid multi-body formulation is no longer suitable for today’s engineering applications and the flexibility of the members need to be considered [12, 13]. For systems experiencing large deformations, special formulations should be used. The classical geometrically exact beam theory, first introduced by Reissner [14] in an intrinsic form and implemented by Simo and Vu-Quoc [15], introduces a rotation vector as a degree of freedom of the system. Different implementations can be found in the literature depending on the type of updating schemes adopted for the rotational degrees of freedom including co-rotational frames for planar beams [16, 17] and inertial frames [18].

However, the integration of rotational parameters cannot be achieved using standard solvers for ordinary differential equations on vector space. In multi-body dynamics, the rotation tensor is also discontinuous at the joints. Problems associated with integration of rotational degrees of freedom are discussed in [17, 19] to which the reader is referred. Alternatively, the Absolute Nodal Coordinate Formulation (ANCF), first proposed by Shabana [2, 19,20,21,22,23,24] for the analysis of large deformation problem in multi-body dynamics, has gained some popularity in the multi-body dynamics community. The beam element in ANCF is described by using a global slope coordinates that define the element orientation.

In most multi-body dynamics applications, the members are slender beams. Hence, an Euler-Bernoulli model could be completely sufficient with the great advantage of delivering a nodal displacement-only formulation. Nevertheless, for some applications, the shear flexibility of the beam cannot be neglected. The standard Timoshenko-type beams finite element formulations do suffer from locking phenomena [21, 25,26,27,28,29,30]. However, it should be mentioned that more complex formulations addressing locking are available among which those based on the helicoidal approach [31,32,33,34,35].

Indeed, besides the kinematics description, the time integration scheme is also at the heart of multi-body dynamics. Especially when dealing with high non-linearity, classical time integrations cannot be employed because of numerical instabilities [36,37,38,39,40,41,42]. The use of long-term stable time integration schemes is then crucial.

In an attempt to avoid rotational degrees of freedom while still accounting for full geometric non-linearity, the present authors resorted to the classical Bernoulli beam and developed a suitable energy-momentum method which provides both high levels of accuracy and numerical stability. In this paper, we extend our approach to account for multi-body dynamics, where beams are connected via revolute joints with or without torsional springs. At the heart of our approach is to consider the strain fields obtained by integrating the strain rates. Not only the displacements and strains, but also the rotation angles of the joints are integrated. It will be shown that the finite rotation angles of the joints can be accurately obtained. Furthermore, the conservation of energy will be proved formally and numerically. We restrict ourselves to planar motion and show that the discontinuity at the joint rotation can be removed using a displacement-only formulation.

The paper is organized as follows. A review of the equations describing the deformation of a planar rod is given in “Rod kinematics and strain measures” section. In “Revolute joint with torsional spring” section, we develop a new method to circumvent the rotation discontinuity for two planar rods connected by a revolute joint with a torsional spring. “Hamilton’s principle and the dynamic equations” section is dedicated to Hamilton’s principle and the corresponding dynamic equations. The finite element method and the energy-momentum time integration are detailed in “Finite element formulation and time integration scheme” section. In particular, formal proof of energy and angular momentum conservation are given. In “Numerical examples” section, we provide a range of numerical examples demonstrating the strength and applicability of the new approach.

Rod kinematics and strain measures

In this section, we briefly introduce the beam’s strain measures. We consider a general Cartesian co-ordinate basis $\textit{\textbf{e}}_i, i=1,2,3$ and a curve $\textit{\textbf{X}}_0(s)$, with s being the arc-length. We understand $\textit{\textbf{X}}_0(s)$ as describing the centre line of the rod cross section. We restrict ourselves to in-plane deformations taking place in the $\textit{\textbf{e}}_1-\textit{\textbf{e}}_2$ plane and introduce the tangent vector $\displaystyle {\textit{\textbf{G}}_0=\frac{\text {d} \textit{\textbf{X}}_0(s)}{\text {d} s}}$. Perpendicular to this vector, we define $\textit{\textbf{N}}$ to be the normal vector with z as the corresponding coordinate in the direction of $\textit{\textbf{N}}$.

In addition to the Cartesian system, we define a suitable convected curvilinear coordinate system given by the triple $(s,z,x_3)$. We define the vector $\textit{\textbf{X}}(s,z)=\textit{\textbf{X}}_0(s)+z\,\textit{\textbf{N}}(s)$ as the position vector of points in the direction of $\textit{\textbf{N}}$ at the reference configuration. In a general cross section, the boundary is defined by z being a function of $x_3$. Note that the third direction is not explicitly included in this equation, though it is implicitly understood that it is in the direction of $\textit{\textbf{e}}_3$ and that the deformation is independent of that direction. Consequently, a local basis in the reference configuration is defined by the triple $(\textit{\textbf{G}}, \textit{\textbf{N}}, \textit{\textbf{e}}_3)$, with $\displaystyle {\textit{\textbf{G}}=\frac{\partial \textit{\textbf{X}}}{\partial s},\textit{\textbf{N}}=\frac{\partial \textit{\textbf{X}}}{\partial z}=\frac{\partial \textit{\textbf{X}}}{\partial z}\vert _{z=0}}$ and $\displaystyle {\textit{\textbf{G}}_0=\textit{\textbf{G}}\mid _{z=0}}$. We have also the following relations $\textit{\textbf{G}}\cdot \textit{\textbf{N}}=\textit{\textbf{G}}_0\cdot \textit{\textbf{N}}=0,\vert \textit{\textbf{N}}\vert =1, \textit{\textbf{N}}=\textit{\textbf{e}}_3\times \frac{\textit{\textbf{G}}}{|\textit{\textbf{G}}|}=\textit{\textbf{e}}_3\times \textit{\textbf{G}}_0,$ where $\vert \bullet \vert$ denotes the absolute value of a vector, $\times$ and $(\cdot )$ denotes the cross and scalar product of vectors, respectively. The corresponding contra-variant basis vectors are then given by $(\textit{\textbf{G}}^*,\textit{\textbf{N}},\textit{\textbf{e}}_3)$, with $\textit{\textbf{G}}^*=\frac{\textit{\textbf{G}}}{\vert \textit{\textbf{G}}\vert ^2}$.

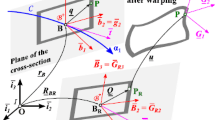
A deformation is given as $\textit{\textbf{x}} = \varvec{\varphi }(\textit{\textbf{X}})$ which defines the actual configuration. For our geometrically exact beam theory, we make use of the Bernoulli model where the cross sections are assumed to be rigid and remain perpendicular to the center line. Thus, the corresponding tangent vectors at the deformed configuration are defined as $(\textit{\textbf{g}}, \textit{\textbf{n}}, \textit{\textbf{e}}_3)$ with $\textit{\textbf{g}}_0=\textit{\textbf{g}}\vert _{z=0}$, and the following relations hold (Fig. 1)

$$\begin{aligned} \textit{\textbf{g}}&=\frac{\partial \textit{\textbf{x}}}{\partial s}, \end{aligned}$$

(1)

$$\begin{aligned} \textit{\textbf{n}}&=\textit{\textbf{e}}_3\times \frac{\textit{\textbf{g}}}{\vert \textit{\textbf{g}}\vert }=\textit{\textbf{e}}_3\times \frac{\textit{\textbf{g}}_0}{|\textit{\textbf{g}}_0|}. \end{aligned}$$

(2)

Fig. 1

Kinematic of beam element

The displacement of material points in the direction of $\textit{\textbf{n}}$ can be characterized by the following relation

$$\begin{aligned} \textit{\textbf{x}}=\textit{\textbf{X}}(s)-z\,\textit{\textbf{N}}(s)+\textit{\textbf{u}}(s)+z\,\textit{\textbf{n}}(s)= \textit{\textbf{X}}_0(s)+\textit{\textbf{u}}(s)+z\,\textit{\textbf{n}}(s). \end{aligned}$$

(3)

where $\textit{\textbf{u}}(s)$ is the displacement vector of the centre line. From this we obtain immediately $\textit{\textbf{g}}=\textit{\textbf{X}}_{0_{,s}}+\textit{\textbf{u}}_{,s}+z\,\textit{\textbf{n}}_{,s}.$ The deformation gradient is written down in the curvilinear basis system as $\mathbf {F}=\textit{\textbf{g}}\otimes \textit{\textbf{G}}^*+\textit{\textbf{n}}\otimes \textit{\textbf{N}}+\textit{\textbf{e}}_3\otimes \textit{\textbf{e}}_3.$ The Green strain tensor is defined as $\mathbf {E}=\frac{1}{2}(\mathbf {C}-\mathbf {I})$, where $\mathbf {C}=\mathbf {F}^\text {T}\mathbf {F}$. It has only one non-trivial component $E_{11}$ which is

$$\begin{aligned} E_{11}=\textit{\textbf{u}}_{,s}\cdot {\textit{\textbf{X}}_0}_{,s}+\frac{1}{2}\, \textit{\textbf{u}}_{,s}\cdot \textit{\textbf{u}}_{,s}&+z\left[ \textit{\textbf{n}}_{,s}\cdot ({\textit{\textbf{X}}_0}_{,s}+\textit{\textbf{u}}_{,s}) -\textit{\textbf{N}}_{,s}\cdot {\textit{\textbf{X}}_0}_{,s} \right] , \end{aligned}$$

(4)

where the term in $z^2$ has been neglected since the thickness of the beam is small compared to its length. $E_{11}$ is split into two components as $E_{11}=\varepsilon _{11}+z\,\kappa$, the definition of which are given by

$$\begin{aligned} \varepsilon&=\textit{\textbf{u}}_{,s}\cdot {\textit{\textbf{X}}_0}_{,s}+\frac{1}{2}\, \textit{\textbf{u}}_{,s}\cdot \textit{\textbf{u}}_{,s}\, , \end{aligned}$$

(5)

$$\begin{aligned} \kappa&=\textit{\textbf{n}}_{,s}\cdot ({\textit{\textbf{X}}_0}_{,s}+\textit{\textbf{u}}_{,s})-\textit{\textbf{N}}_{,s}\cdot {\textit{\textbf{X}}_0}_{,s}. \end{aligned}$$

(6)

The latter is the classical change of curvature.

Revolute joint with torsional spring

Let’s consider first the frictionless planar revolute joint (see Fig. 2). This type of joints is very common in mechanisms and allows only a relative rotation between two rods. We call the two cross-sections with a hinge, A and B.

Fig. 2

Revolute pair

The orientations of the cross sections are determined by their respective normal vectors. Denoting the relative rotation at the joint $\omega$, one has $\omega =\gamma -\Gamma$, where $\Gamma$ is defined to be the angle between the vectors $\textit{\textbf{N}}_B$ and $\textit{\textbf{N}}_A$. Similarly, the same holds for $\gamma$ at the deformed configuration. We recall that $\Gamma$ and $\gamma$ can be defined as the absolute value of the rotation vectors parallel to $\textit{\textbf{e}}_3$ with the corresponding rotations from $\textit{\textbf{N}}_B$ to $\textit{\textbf{N}}_A$ and from $\textit{\textbf{n}}_B$ to $\textit{\textbf{n}}_A$, respectively. These rotations are to be defined via the kinematic quantities $\textit{\textbf{N}}_A$, $\textit{\textbf{N}}_B$, $\textit{\textbf{n}}_A$ and $\textit{\textbf{n}}_B$. From Fig. 2, one can derive the following relations:

$$\begin{aligned} \left( \textit{\textbf{N}}_B\times \textit{\textbf{N}}_A\right) \cdot \textit{\textbf{e}}_3&=\vert \textit{\textbf{N}}_B\vert \vert \textit{\textbf{N}}_A\vert \sin \Gamma =\sin \Gamma , \end{aligned}$$

(7)

$$\begin{aligned} \textit{\textbf{N}}_B\cdot \textit{\textbf{N}}_A&=\vert \textit{\textbf{N}}_B\vert \vert \textit{\textbf{N}}_A\vert \cos \Gamma =\cos \Gamma , \end{aligned}$$

(8)

$$\begin{aligned} \left( \textit{\textbf{n}}_B\times \textit{\textbf{n}}_A\right) \cdot \textit{\textbf{e}}_3&=\vert \textit{\textbf{n}}_B\vert \vert \textit{\textbf{n}}_A\vert \sin \gamma =\sin \gamma , \end{aligned}$$

(9)

$$\begin{aligned} \textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A&=\vert \textit{\textbf{n}}_B\vert \vert \textit{\textbf{n}}_A\vert \cos \gamma =\cos \gamma , \end{aligned}$$

(10)

from which it follows

$$\begin{aligned}&\Gamma =\left( \arcsin \left( \left( \textit{\textbf{N}}_B\times \textit{\textbf{N}}_A\right) \cdot \textit{\textbf{e}}_3\right) -\frac{\pi }{2}\right) \frac{\textit{\textbf{N}}_B\cdot \textit{\textbf{N}}_A}{\vert \textit{\textbf{N}}_B\cdot \textit{\textbf{N}}_A\vert }+\frac{\pi }{2} , \end{aligned}$$

(11)

$$\begin{aligned}&\gamma =\left( \arcsin \left( \left( \textit{\textbf{n}}_B\times \textit{\textbf{n}}_A\right) \cdot \textit{\textbf{e}}_3\right) -\frac{\pi }{2}\right) \frac{\textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A}{\vert \textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A\vert }+\frac{\pi }{2}+2k\pi , \end{aligned}$$

(12)

with k being some integer. The expression for $\omega$ now reads

$$\begin{aligned} \omega =&\left( \arcsin \left( \left( \textit{\textbf{n}}_B\times \textit{\textbf{n}}_A\right) \cdot \textit{\textbf{e}}_3\right) -\frac{\pi }{2}\right) \frac{\textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A}{\vert \textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A\vert }\nonumber \\&-\left( \arcsin \left( \left( \textit{\textbf{N}}_B\times \textit{\textbf{N}}_A\right) \cdot \textit{\textbf{e}}_3\right) -\frac{\pi }{2}\right) \frac{\textit{\textbf{N}}_B\cdot \textit{\textbf{N}}_A}{\vert \textit{\textbf{N}}_B\cdot \textit{\textbf{N}}_A\vert }+2k\pi . \end{aligned}$$

(13)

Since the hinge can freely rotate, the only kinematic condition is that the displacement $\textit{\textbf{u}}$ defined in (3) is the same at sections A and B:

$$\begin{aligned} \textit{\textbf{u}}_A=\textit{\textbf{u}}_B . \end{aligned}$$

(14)

Note that there is no condition about the continuity of the first derivative of $\textit{\textbf{u}}$ between the bodies.

When an elastic torsional spring is added to the revolute joint, it generates an internal moment which is a function of the relative rotation between the two bodies of the system, see Fig. 3. The elastic energy stored in the torsional spring when it deforms is written as

$$\begin{aligned} U_{s}=\frac{1}{2}\, C \, \omega ^2 , \end{aligned}$$

(15)

with C as the spring constant.

Fig. 3

Revolute pair with torsional spring

Hamilton’s principle and the dynamic equations

We assume our multi-body system to be conservative. Hamilton’s principle states that the action functional is stationary. That is

$$\begin{aligned} \delta \int _{t_1}^{t_2}{\mathcal {L}}\, \text {d} t=0 \, , \end{aligned}$$

(16)

where t refers to time, $t_1$ and $t_2$ are boundaries of the time interval, ${\mathcal {L}}$ is defined as the Lagrangian given by

$$\begin{aligned} {\mathcal {L}}=T-\Psi _{int}-\Psi _{ext} . \end{aligned}$$

(17)

Here T is the kinetic energy of the system and $\Psi _{int}$, $\Psi _{ext}$ are the internal and the external potentials, respectively. The quantities in (17) are defined as

$$\begin{aligned} T&=\frac{1}{2}\int _{\mathcal {\textit{\textbf{B}}}}\rho \,\dot{\textit{\textbf{x}}}\cdot \dot{\textit{\textbf{x}}}\,\text {d}V \, , \end{aligned}$$

(18)

$$\begin{aligned} \Psi _{int}&=\frac{1}{2}\int _{\mathcal {\textit{\textbf{B}}}} (E \,E_{11}\,E_{11})\,\text {d} V+\frac{1}{2}\,\sum _{k=1}^K C_k\,\omega _k^2 \, , \end{aligned}$$

(19)

$$\begin{aligned} \Psi _{ext}&=-\int _L \textit{\textbf{q}}(s)\cdot \textit{\textbf{u}}(s)\,\text {d} s -\sum _{i=1}^N\textit{\textbf{P}}_i\,\textit{\textbf{u}}_i -\sum _{j=1}^M{M_{3j}\,\theta _j} \, , \end{aligned}$$

(20)

where E is Young’s modulus, L is the total length of all members, K is the number of torsional springs, $\textit{\textbf{q}}(s)$ is the distributed external force, $\textit{\textbf{P}}_i, i=1,...,N$ and $\textit{\textbf{u}}_i$ are the concentrated forces and the corresponding displacements, respectively, $M_{3j}, j=1,...,M$ and $\theta _j$ are concentrated external moments and the corresponding rotation angles, respectively. From  (16),  (17), together with an integration over the cross section, and due to the fact that the variations vanish at the boundaries, standard arguments of the calculus of variation deliver

$$\begin{aligned}&\int _{L}\rho A\ddot{\textit{\textbf{u}}}\cdot \delta \textit{\textbf{u}}\,\text {d}s+\int _{L}\rho I\ddot{\textit{\textbf{n}}}\cdot \delta {\textit{\textbf{n}}}\,\text {d}s +\int _{L} \left( EA\, \varepsilon _{11} \,\delta \varepsilon _{11}+EI \,\kappa \,\delta \kappa \right) \,\text {d} s+C\,\omega \,\delta \omega \nonumber \\&\quad -\int _L \textit{\textbf{q}}(s)\cdot \delta \textit{\textbf{u}}(s)\,\text {d} s - \sum _{i=1}^N\textit{\textbf{P}}_i\cdot \delta \textit{\textbf{u}}_i-\sum _{j=1}^M{M_{3j}\,\delta \theta _j} = 0 \, , \end{aligned}$$

(21)

with I and A being the moment of inertia and the cross-section area, respectively.

Since $\textit{\textbf{u}}$ is the only degree of freedom of the system, we have to relate the relative rotations to it and to its derivatives. Calculation of $\delta \theta$ starts from the fact that $\theta$ is the angle between $\textit{\textbf{N}}$ and $\textit{\textbf{n}}$, we have

$$\begin{aligned} \sin \theta&=\left( \textit{\textbf{N}}\times \textit{\textbf{n}}\right) \cdot \textit{\textbf{e}}_3 \, , \end{aligned}$$

(22)

$$\begin{aligned} \cos \theta \delta \theta&=\delta (\left( \textit{\textbf{N}}\times \textit{\textbf{n}}\right) \cdot \textit{\textbf{e}}_3) \, , \end{aligned}$$

(23)

$$\begin{aligned} \delta \theta&=\frac{\partial (\left( \textit{\textbf{N}}\times \textit{\textbf{n}}\right) \cdot \textit{\textbf{e}}_3)}{\partial {\textit{\textbf{u}}}_{,s}} \frac{1}{\textit{\textbf{N}}\cdot \textit{\textbf{n}}}\cdot \delta {\textit{\textbf{u}}}_{,s} \, . \end{aligned}$$

(24)

Accordingly, the functional in (21) can be written as follows

$$\begin{aligned}&\int _{L}\rho A\, \ddot{\textit{\textbf{u}}}\cdot \delta \textit{\textbf{u}}\,\text {d}s+\int _{L}\rho I\,\ddot{\textit{\textbf{n}}}\cdot \frac{\partial {\textit{\textbf{n}}}}{\partial {\textit{\textbf{u}}}_{,s}}\,\delta {\textit{\textbf{u}}}_{,s}\,\text {d}s +\int _{L} EA\, \varepsilon _{11}\, \frac{\partial \varepsilon _{11}}{\partial {\textit{\textbf{u}}}_{,s}}\,\delta {\textit{\textbf{u}}}_{,s}\,\text {d}s\nonumber \\&\quad +\int _{L} EI\, \kappa \left( \frac{\partial \kappa }{\partial {\textit{\textbf{u}}}_{,s}}\, \delta {\textit{\textbf{u}}}_{,s}+\frac{\partial \kappa }{\partial {\textit{\textbf{u}}}_{,ss}}\,\delta {\textit{\textbf{u}}}_{,ss}\right) \,\text {d}s+\sum _{k=1}^K C_k\,\omega _k\left( \frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^A}\,\delta {\textit{\textbf{u}}}_{,s}^A+\frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^B}\,\delta {\textit{\textbf{u}}}_{,s}^B\right) \nonumber \\&\quad -\int _L \textit{\textbf{q}}(s)\cdot \delta \textit{\textbf{u}}(s)\,\text {d}s- \sum _{i=1}^N\textit{\textbf{P}}_i\cdot \delta \textit{\textbf{u}}_i -\sum _{j=1}^M{M_{3j}\,\frac{\partial (\left( \textit{\textbf{N}}\times \textit{\textbf{n}}\right) \cdot \textit{\textbf{e}}_3)}{\partial {\textit{\textbf{u}}}_{,s}} \,\frac{1}{\textit{\textbf{N}}\cdot \textit{\textbf{n}}}\cdot \delta {\textit{\textbf{u}}}_{,s}}=0 \, , \end{aligned}$$

(25)

where ${\textit{\textbf{u}}}_{,s}^A$ and ${\textit{\textbf{u}}}_{,s}^B$ define the vectors ${\textit{\textbf{n}}}^A$ and ${\textit{\textbf{n}}}^B$, respectively. In general, the above equation takes the form

$$\begin{aligned} \rho \textit{\textbf{m}}\left( \ddot{\textit{\textbf{u}}},\dot{\textit{\textbf{u}}},\ddot{\textit{\textbf{u}}}_{,s},\textit{\textbf{u}},{\textit{\textbf{u}}}_{,s}\right) +\textit{\textbf{k}}\left( {\textit{\textbf{u}}}_{,s},{\textit{\textbf{u}}}_{,ss}\right) -\textit{\textbf{f}}\left( \textit{\textbf{u}},{\textit{\textbf{u}}}_{,s}\right) ={\textit{\textbf{0}}} \end{aligned}$$

(26)

where $\textit{\textbf{m}}$, $\textit{\textbf{k}}$, $\textit{\textbf{f}}$ are the generalized mass vector, the generalized internal force vector and the generalized external force vector, respectively. The total energy of the system, which in most cases coincides with the Hamiltonian, is defined by $\displaystyle {{\mathscr {H}}=T+\Psi _{int}+\Psi _{ext}=\text {constant}}$.

Equation (26) is the starting point for a numerical treatment which includes also the time integration scheme. For more details about the mass matrix, internal and external force vector, please refer to the Appendix A.

Finite element formulation and time integration scheme

Finite element discretisation

As a result of the Bernoulli hypothesis, functional (25) contains second derivatives. Hence, within a finite element method, the first derivative must exhibit continuity. We resort to the standard approach of utilizing Hermite polynomial within a finite element context. Each node comprises four degrees of freedom which are the displacement and their derivatives: $u_1, u_2, u'_1, u'_2$. For the displacement field the interpolations read

$$\begin{aligned} \textit{\textbf{u}}= & {} \mathcal {\textit{\textbf{N}}}\,\textit{\textbf{U}} \, , \end{aligned}$$

(27)

$$\begin{aligned} \textit{\textbf{u}}_{,s}= & {} \mathcal {\textit{\textbf{N}}}_{,s}\,\textit{\textbf{U}} \, , \end{aligned}$$

(28)

$$\begin{aligned} \textit{\textbf{u}}_{,ss}= & {} \mathcal {\textit{\textbf{N}}}_{,ss}\,\textit{\textbf{U}} \, , \end{aligned}$$

(29)

where

$$\begin{aligned} \mathcal {\textit{\textbf{N}}}= & {} \left( \begin{array}{cccccccc} N1 &{} 0 &{} N2 &{} 0 &{} N3 &{} 0 &{} N4 &{} 0 \\ 0 &{} N1 &{} 0 &{} N2 &{} 0 &{} N3 &{} 0 &{} N4 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{array} \right) \, ,\nonumber \\ \textit{\textbf{U}}^T= & {} \left( {u_1}^{I} \, {u_2}^{I} \, {u'_1}^{I} \, {u'_2}^{I} \, {u_1}^{II} \, {u_2}^{II} \, {u'}_1^{II} \, {u'}_2^{II}\right) \, , \end{aligned}$$

(30)

and

$$\begin{aligned} N1&=\frac{\zeta ^3}{4}-\frac{3\zeta }{4}+\frac{1}{2} \, , \end{aligned}$$

(31)

$$\begin{aligned} N2&=\frac{l\zeta ^3}{8}-\frac{l\zeta ^2}{8}-\frac{l\zeta }{8}+\frac{l}{8} \, , \end{aligned}$$

(32)

$$\begin{aligned} N3&=\frac{-\zeta ^3}{4}+\frac{3\zeta }{4}+\frac{1}{2} \, , \end{aligned}$$

(33)

$$\begin{aligned} N4&=\frac{l\zeta ^3}{8}+\frac{l\zeta ^2}{8}-\frac{l\zeta }{8}-\frac{l}{8} \, , \end{aligned}$$

(34)

with $\zeta =\left[ -1,1\right]$ and l is the length of the element.

An energy-momentum time integration scheme

Since the achievement of Simo and Tarnow [38], it has been realized that time integration schemes should reproduce conservation properties of the analytical model in the discrete case. Especially, energy conservation or energy control is considered key to long-term stable integration. In what follows, we will extend an energy-momentum method previously developed by [43,44,45] to cover the case of multibody dynamics.

Assuming that at time step n, all kinematical fields and velocities are known, we need to find these quantities for time step $n+1$. Consider $\xi$ to be a scalar which defines any position within the time interval $\Delta t$, with $0\le \xi \le 1$. We start with the following expressions:

$$\begin{aligned}&\textit{\textbf{x}}_{n+\xi }=\xi \textit{\textbf{x}}_{n+1}+(1-\xi )\textit{\textbf{x}}_{n} , \end{aligned}$$

(35)

$$\begin{aligned}&\dot{\textit{\textbf{x}}}_{n+\xi }=\frac{\textit{\textbf{x}}_{n+1}-\textit{\textbf{x}}_{n}}{\Delta t} , \end{aligned}$$

(36)

$$\begin{aligned}&\ddot{\textit{\textbf{x}}}_{n+\xi }=\frac{\dot{\textit{\textbf{x}}}_{n+1}-\dot{\textit{\textbf{x}}}_{n}}{\Delta t} . \end{aligned}$$

(37)

The first relation defines a convex set, the following two are true for some values of $\xi$. The midpoint rule corresponds to the choice $\xi =0.5$. Consequently, to integrate $\textit{\textbf{u}}$ one has,

$$\begin{aligned}&\dot{\textit{\textbf{u}}}_{n+\frac{1}{2}}=\frac{\Delta u}{\Delta t} \, , \end{aligned}$$

(38)

$$\begin{aligned}&\dot{\textit{\textbf{u}}}_{n+1}=\frac{2\Delta u}{\Delta t}-\dot{\textit{\textbf{u}}}_{n} \, , \end{aligned}$$

(39)

$$\begin{aligned}&\ddot{\textit{\textbf{u}}}_{n+\frac{1}{2}}=\frac{2\Delta u}{\Delta t^2}-\frac{2 \dot{\textit{\textbf{u}}}_{n}}{\Delta t} \, , \end{aligned}$$

(40)

where $\Delta u= \textit{\textbf{u}}_{n+1}-\textit{\textbf{u}}_{n}$. The key step in our energy-momentum method is to integrate strain velocity fields to define the strain fields instead of using Eq. (5), (6). The same is done for the highly non-linear kinematic relations as in Eqs. (2) and (13), where velocities are defined for these too. The equations are used to merely define the velocity fields themselves. One has

$$\begin{aligned} {\dot{\varepsilon }}&=\frac{\Delta \textit{\textbf{u}}_{,s}}{\Delta t}\cdot {\textit{\textbf{X}}_0}_{,s}+\textit{\textbf{u}}_{,s}\cdot \frac{\Delta \textit{\textbf{u}}_{,s}}{\Delta t} \, , \end{aligned}$$

(41)

$$\begin{aligned} {\dot{\kappa }}&= \frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,s}}\cdot \frac{\Delta \textit{\textbf{u}}_{,s}}{\Delta t}+\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,ss}}\cdot \frac{\Delta \textit{\textbf{u}}_{,ss}}{\Delta t} \, , \end{aligned}$$

(42)

$$\begin{aligned} \dot{\textit{\textbf{n}}}&=\frac{\partial \textit{\textbf{n}}}{\partial \textit{\textbf{u}}_{,s}}\cdot \frac{\Delta \textit{\textbf{u}}_{,s}}{\Delta t} \, , \end{aligned}$$

(43)

$$\begin{aligned} {\dot{\omega }}&= \frac{\partial \omega }{\partial \textit{\textbf{u}}_{,s}^A}\cdot \frac{\Delta \textit{\textbf{u}}_{,s}}{\Delta t}^A+\frac{\partial \omega }{\partial \textit{\textbf{u}}_{,s}^B}\cdot \frac{\Delta \textit{\textbf{u}}_{,s}}{\Delta t}^B \, , \end{aligned}$$

(44)

Given the strain fields and the kinematic quantities $\textit{\textbf{n}}$ and $\omega$ at time $t_n$, the strain fields and the same kinematic quantities at step $n+1$ are then defined as follows:

$$\begin{aligned} \varepsilon _{n+\frac{1}{2}}&=\varepsilon _{n}+ \frac{1}{2} \, \Delta t \, {\dot{\varepsilon }}_{n+\frac{1}{2}} \end{aligned}$$

(45)

$$\begin{aligned} \kappa _{n+\frac{1}{2}}&=\kappa _{n}+ \frac{1}{2} \, \Delta t \, {\dot{\kappa }}_{n+\frac{1}{2}} \end{aligned}$$

(46)

$$\begin{aligned} \ddot{\textit{\textbf{n}}}_{n+\frac{1}{2}}&= \frac{\dot{\textit{\textbf{n}}}_{n+1}-\dot{\textit{\textbf{n}}}_{n}}{\Delta t} \end{aligned}$$

(47)

$$\begin{aligned} \omega _{n+\frac{1}{2}}&=\omega _{n}+ \frac{1}{2}\, \Delta t \, {\dot{\omega }}_{n+\frac{1}{2}} \end{aligned}$$

(48)

With these so defined quantities, the midpoint rule provides energy conservation. Using (48), the value of $\omega$ could be calculated exactly without limitation (for example $2\pi$) because only the difference of $\omega$ is of importance.

The field equations

To obtain our field equations we start from functional (25)

$$\begin{aligned}&\int _{L}\rho A\,\ddot{\textit{\textbf{u}}}\cdot \delta \textit{\textbf{u}}\,\text {d}s+\int _{L}\rho I\,\ddot{\textit{\textbf{n}}}\cdot \frac{\partial {\textit{\textbf{n}}}}{\partial {\textit{\textbf{u}}}_{,s}}\,\delta {\textit{\textbf{u}}}_{,s}\,\text {d}s+\int _{L} EA\, \varepsilon _{11}\, \frac{\partial \varepsilon _{11}}{\partial {\textit{\textbf{u}}}_{,s}}\,\delta {\textit{\textbf{u}}}_{,s}\,\text {d}s\nonumber \\&\quad +\int _{L} EI\,\kappa \left( \frac{\partial \kappa }{\partial {\textit{\textbf{u}}}_{,s}}\,\delta {\textit{\textbf{u}}}_{,s}+\frac{\partial \kappa }{\partial {\textit{\textbf{u}}}_{,ss}}\,\delta {\textit{\textbf{u}}}_{,ss}\right) \,\text {d}s+\sum _{k=1}^K C_k \, \omega _k\left( \frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^A}\,\delta {\textit{\textbf{u}}}_{,s}^A+\frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^B}\,\delta {\textit{\textbf{u}}}_{,s}^B\right) \nonumber \\&\quad -\int _L \textit{\textbf{q}}(s)\cdot \delta \textit{\textbf{u}}(s)\,\text {d}s- \sum _{i=1}^N\textit{\textbf{P}}_i\cdot \delta \textit{\textbf{u}}_i -\sum _{j=1}^M{M_{3j}\,\frac{\partial (\left( \textit{\textbf{N}}\times \textit{\textbf{n}}\right) \cdot \textit{\textbf{e}}_3)}{\partial {\textit{\textbf{u}}}_{,s}} \frac{1}{\textit{\textbf{N}}\cdot \textit{\textbf{n}}}\cdot \delta {\textit{\textbf{u}}}_{,s}}=0. \end{aligned}$$

(49)

Using the following identities:

$$\begin{aligned}&\ddot{\textit{\textbf{n}}}\cdot \frac{\partial \textit{\textbf{n}}}{\partial \textit{\textbf{u}}_{,s}}\cdot \delta \textit{\textbf{u}}_{,s}=\left( \ddot{\textit{\textbf{n}}}\cdot \frac{\partial \textit{\textbf{n}}}{\partial \textit{\textbf{u}}_{,s}}\cdot \delta \textit{\textbf{u}} \right) _{,s} -\left( \ddot{\textit{\textbf{n}}}\cdot \frac{\partial \textit{\textbf{n}}}{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}\cdot \delta \textit{\textbf{u}} \, , \end{aligned}$$

(50)

$$\begin{aligned}&\varepsilon \,\frac{\partial \varepsilon }{\partial \textit{\textbf{u}}_{,s}}\cdot \delta \textit{\textbf{u}}_{,s}=\left( \varepsilon \,\frac{\partial \varepsilon }{\partial \textit{\textbf{u}}_{,s}}\cdot \delta \textit{\textbf{u}} \right) _{,s}-\left( \varepsilon \,\frac{\partial \varepsilon }{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}\cdot \delta \textit{\textbf{u}} \, , \end{aligned}$$

(51)

$$\begin{aligned}&\kappa \,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,s}}\cdot \delta \textit{\textbf{u}}_{,s}=\left( \kappa \,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,s}}\cdot \delta \textit{\textbf{u}} \right) _{,s}-\left( \kappa \,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}\cdot \delta \textit{\textbf{u}} \, , \end{aligned}$$

(52)

$$\begin{aligned}&\kappa \,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,ss}}\cdot \delta \textit{\textbf{u}}_{,ss}=\left( \kappa \,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,ss}}\cdot \delta \textit{\textbf{u}}_{,s}\right) _{,s}-\left( \left( \kappa \,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,ss}}\right) _{,s} \cdot \delta \textit{\textbf{u}}\right) _{,s}+\left( \kappa \,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,ss}}\right) _{,ss}\cdot \delta \textit{\textbf{u}} \, , \end{aligned}$$

(53)

together with Gauss’s theorem, the above functional can be rewritten to give

(54)

Because the variations are arbitrary, one Euler-Lagrange equation with two boundary conditions follow from the above functional:

$$\begin{aligned}&\rho A\,\ddot{\textit{\textbf{u}}}-\rho I\left( \ddot{\textit{\textbf{n}}}\cdot \frac{\partial \textit{\textbf{n}}}{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}-EA\left( \varepsilon \,\frac{\partial \varepsilon }{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}-EI\left( \kappa \,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}+EI\left( \kappa \,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,ss}}\right) _{,ss}=\textit{\textbf{q}}(s) \, , \end{aligned}$$

(55)

(56)

(57)

Proof of conservation of angular momentum

Let’s recall that ${\textit{\textbf{x}}_0}=\textit{\textbf{X}}_0+\textit{\textbf{u}}$. To prove the conservation of angular momentum we start by taking the cross product of Eqs. (55), (56) with ${\textit{\textbf{x}}_0}_{n+\frac{1}{2}}$ and the cross product of Eq. (57) with ${{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}$:

$$\begin{aligned}&{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \rho A\, \ddot{\textit{\textbf{u}}}_{n+\frac{1}{2}}-{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \rho I\left( \ddot{\textit{\textbf{n}}}_{n+\frac{1}{2}}\cdot \frac{\partial \textit{\textbf{n}}}{\partial \textit{\textbf{u}}_{,s}}\right) _{,s} -{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times EA\left( \varepsilon _{n+\frac{1}{2}}\,\frac{\partial \varepsilon }{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}\nonumber \\&\quad -{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times EI\left( \kappa _{n+\frac{1}{2}}\,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}+{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times EI\left( \kappa _{n+\frac{1}{2}}\,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,ss}}\right) _{,ss} ={\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \textit{\textbf{q}}(s) \, ,\quad \quad \end{aligned}$$

(58)

(59)

(60)

Integrating Eq. (58) gives

$$\begin{aligned}&\int _L{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \rho A\, \ddot{\textit{\textbf{u}}}_{n+\frac{1}{2}}\,\text {d} s- \int _L{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \rho I\left( \ddot{\textit{\textbf{n}}}_{n+\frac{1}{2}}\cdot \frac{\partial \textit{\textbf{n}}}{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}\,\text {d} s \nonumber \\&\quad -\int _L{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times EA\left( \varepsilon _{n+\frac{1}{2}}\,\frac{\partial \varepsilon }{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}\,\text {d} s-\int _L{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times EI\left( \kappa _{n+\frac{1}{2}}\,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}\,\text {d} s \nonumber \\&\quad +\int _L{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times EI\left( \kappa _{n+\frac{1}{2}}\,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,ss}}\right) _{,ss}\,\text {d} s =\int _L{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \textit{\textbf{q}}(s)\,\text {d} s. \end{aligned}$$

(61)

Using the following identities:

$$\begin{aligned}&{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \left( \ddot{\textit{\textbf{n}}}_{n+\frac{1}{2}}\cdot \frac{\partial \textit{\textbf{n}}}{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}= \left( {\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \ddot{\textit{\textbf{n}}}_{n+\frac{1}{2}}\cdot \frac{\partial \textit{\textbf{n}}}{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}- \left( {{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \ddot{\textit{\textbf{n}}}_{n+\frac{1}{2}}\cdot \frac{\partial \textit{\textbf{n}}}{\partial \textit{\textbf{u}}_{,s}}\right) \, , \end{aligned}$$

(62)

$$\begin{aligned}&{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \left( \varepsilon _{n+\frac{1}{2}}\frac{\partial \varepsilon }{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}=\left( {\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \varepsilon _{n+\frac{1}{2}}\frac{\partial \varepsilon }{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}- \left( {{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \varepsilon _{n+\frac{1}{2}}\frac{\partial \varepsilon }{\partial \textit{\textbf{u}}_{,s}}\right) \, , \end{aligned}$$

(63)

$$\begin{aligned}&{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \left( \kappa _{n+\frac{1}{2}}\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}=\left( {\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \kappa _{n+\frac{1}{2}}\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}- \left( {{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \kappa _{n+\frac{1}{2}}\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,s}}\right) \, , \end{aligned}$$

(64)

$$\begin{aligned}&{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \left( \kappa _{n+\frac{1}{2}}\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,ss}}\right) _{,ss}=\left( {\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \left( \kappa _{n+\frac{1}{2}}\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,ss}}\right) _{,s}\right) _{,s}\nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad -\left( {{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \left( \kappa _{n+\frac{1}{2}}\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,ss}}\right) \right) _{,s}\nonumber \\&\qquad \qquad \qquad \qquad \qquad \qquad +{{\textit{\textbf{x}}_0}_{,ss}}_{n+\frac{1}{2}}\times \left( \kappa _{n+\frac{1}{2}}\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,ss}}\right) . \end{aligned}$$

(65)

together with subsequent application of Gauss’s theorem, Eq. (61) presents us with the following statement

(66)

Using (59) and (60), the last statement results in

$$\begin{aligned}&\int _L{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \rho A\,\ddot{\textit{\textbf{u}}}_{n+\frac{1}{2}}\,\text {d} s +\int _L{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \rho {I}\left( \ddot{\textit{\textbf{n}}}_{n+\frac{1}{2}}\cdot \frac{\partial \textit{\textbf{n}}}{\partial {{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}}\right) \,\text {d} s \nonumber \\&\quad +\int _L{{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}}\times EA\left( \varepsilon _{n+\frac{1}{2}}\,\frac{\partial \varepsilon }{\partial {{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}}\right) \,\text {d} s\nonumber \\&\quad +\int _L{{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}}\times E{I}\left( \kappa _{n+\frac{1}{2}}\,\frac{\partial \kappa }{\partial {{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}}\right) \,\text {d} s \nonumber \\&\quad +\int _L{{\textit{\textbf{x}}_0}_{,ss}}_{n+\frac{1}{2}}\times E{I}\left( \kappa _{n+\frac{1}{2}}\,\frac{\partial \kappa }{\partial {\textit{\textbf{x}}_0}_{,ss}}\right) \,\text {d} s =\int _L{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \textit{\textbf{q}}(s)\,\text {d} s +\sum _{i=1}^N{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \textit{\textbf{P}}_i\nonumber \\&\quad -\sum _{k=1}^K C_k\omega _k\left( {{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^A}+{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^B}\right) \nonumber \\&\quad +\sum _{j=1}^M{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times M_{3j}\,\frac{\partial (\left( \textit{\textbf{N}}\times \textit{\textbf{n}}\right) \cdot \textit{\textbf{e}}_3)}{\partial {\textit{\textbf{u}}}_{,s}} \frac{1}{\textit{\textbf{N}}\cdot \textit{\textbf{n}}}. \end{aligned}$$

(67)

Now we are going to prove that

$$\begin{aligned} {\textit{\textbf{x}}_0}_{,s}\times \left( \frac{\partial (\left( \textit{\textbf{N}}\times \textit{\textbf{n}}\right) \cdot \textit{\textbf{e}}_3)}{\partial {\textit{\textbf{u}}}_{,s}} \frac{1}{\textit{\textbf{N}}\cdot \textit{\textbf{n}}}\right) =\textit{\textbf{e}}_3. \end{aligned}$$

(68)

In component form, the normal vector $\textit{\textbf{n}}$ defined in (2) reads

$$\begin{aligned} n_j={{{x_0}_k}_{,s}}\,\epsilon _{kj3}\,\frac{1}{\vert {\textit{\textbf{x}}_0}_{,s}\vert }. \end{aligned}$$

(69)

Here $\epsilon _{3jk}$ is the permutation symbol defined by $\epsilon _{3jk}= \left\{ \begin{array}{ccc} \text {1 for even permutation 3,j,k}\\ \text {--1 for even permutation 3,j,k}\\ \text {0 for two equal values of 3,j,k} \end{array} \right\}$.

Let us introduce $V_0=\left( \textit{\textbf{N}}\times \textit{\textbf{n}}\right) \cdot \textit{\textbf{e}}_3:$

$$\begin{aligned} V_0=N_i \,n_j \,\epsilon _{ij3}=N_i\,{{x_0}_k}_{,s}\,(\delta _{ik}\,\delta _{jj}-\delta _{ij}\,\delta _{kj})\frac{1}{\vert {\textit{\textbf{x}}_0}_{,s}\vert }=\frac{N_i\,{{x_0}_i}_{,s}}{\vert {\textit{\textbf{x}}_0}_{,s}\vert }. \end{aligned}$$

(70)

where $\delta _{ij}$ is the Kronecker delta defined as

$\delta _{ij}=\left\{ \begin{array}{cc} {1 if i=j}\\ {0 if i\ne j} \end{array}\right.$. Hence, one has now

$$\begin{aligned} \frac{\partial V_0}{\partial {{\textit{\textbf{x}}_0}_i}_{,s}}=\frac{{{x_0}_j}_{,s}\, N_m \,{{x_0}_l}_{,s}\,\epsilon _{ml3}\,\epsilon _{ij3}}{\vert {\textit{\textbf{x}}_0}_{,s}\vert ^3}. \end{aligned}$$

(71)

The term ${\textit{\textbf{N}}\cdot \textit{\textbf{n}}}$ can be rewritten as follows

$$\begin{aligned} {\textit{\textbf{N}}\cdot \textit{\textbf{n}}}=N_m{{x_0}_l}_{,s}\,\epsilon _{lm3}\,\frac{1}{\vert {\textit{\textbf{x}}_0}_{,s}\vert } \end{aligned}$$

(72)

which, together with (71), provides

$$\begin{aligned} \left( \frac{\partial (\left( \textit{\textbf{N}}\times \textit{\textbf{n}}\right) \cdot \textit{\textbf{e}}_3)}{\partial {\textit{\textbf{u}}}_{,s}} \frac{1}{\textit{\textbf{N}}\cdot \textit{\textbf{n}}}\right) \cdot \textit{\textbf{e}}_j= {{{x_0}_k}_{,s}}\,\epsilon _{kj3}\,\frac{1}{\vert {\textit{\textbf{x}}_0}_{,s}\vert ^2}. \end{aligned}$$

(73)

With this relation at hand, Eq. (69) gives

$$\begin{aligned} \frac{\partial (\left( \textit{\textbf{N}}\times \textit{\textbf{n}}\right) \cdot \textit{\textbf{e}}_3)}{\partial {\textit{\textbf{u}}}_{,s}} \frac{1}{\textit{\textbf{N}}\cdot \textit{\textbf{n}}}= \frac{\textit{\textbf{n}}}{\vert {\textit{\textbf{x}}_0}_{,s}\vert }=\textit{\textbf{e}}_3\times \frac{{\textit{\textbf{x}}_0}_{,s}}{\vert {\textit{\textbf{x}}_0}_{,s}\vert ^2}. \end{aligned}$$

(74)

Finally we get

$$\begin{aligned} {\textit{\textbf{x}}_0}_{,s}\times \left( \frac{\partial (\left( \textit{\textbf{N}}\times \textit{\textbf{n}}\right) \cdot \textit{\textbf{e}}_3)}{\partial {\textit{\textbf{u}}}_{,s}} \frac{1}{\textit{\textbf{N}}\cdot \textit{\textbf{n}}}\right) ={\textit{\textbf{x}}_0}_{,s}\times \left( \textit{\textbf{e}}_3\times \frac{{\textit{\textbf{x}}_0}_{,s}}{\vert {\textit{\textbf{x}}_0}_{,s}\vert ^2}\right) =\textit{\textbf{e}}_3. \end{aligned}$$

(75)

Hence, (68) is proven.

Then, we are going to prove that

$$\begin{aligned} \sum _{k=1}^K C_k\,\omega _k\,\left( {{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^A}+{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^B}\right) =0. \end{aligned}$$

(76)

Consider first $\displaystyle {{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^A}}$ with $\omega$ defined in (13), one has

$$\begin{aligned} \frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^A}=\frac{\partial }{\partial {\textit{\textbf{u}}}_{,s}^A}\left( \arcsin \left( \left( \textit{\textbf{n}}_B\times \textit{\textbf{n}}_A\right) \cdot \textit{\textbf{e}}_3\right) \frac{\textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A}{\vert \textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A\vert }\right) -\frac{\pi }{2}\frac{\partial }{\partial {\textit{\textbf{u}}}_{,s}^A}\left( \frac{\textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A}{\vert \textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A\vert }\right) \end{aligned}$$

(77)

and

$$\begin{aligned} \frac{\partial }{\partial {\textit{\textbf{u}}}_{,s}^A}\left( \frac{\textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A}{\vert \textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A\vert }\right) =\frac{\textit{\textbf{n}}_B}{\vert \textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A\vert }\frac{\partial \textit{\textbf{n}}_A}{\partial \textit{\textbf{u}}_{,s}^A} -\frac{\left( \textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A\right) ^2}{\sqrt{\left( \vert \textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A\vert \right) ^6}}\,\textit{\textbf{n}}_B\,\frac{\partial \textit{\textbf{n}}_A}{\partial \textit{\textbf{u}}_{,s}^A}=0. \end{aligned}$$

(78)

Consider next,

$$\begin{aligned}&{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \frac{\partial }{\partial {\textit{\textbf{u}}}_{,s}^A}\left( \arcsin \left( \left( \textit{\textbf{n}}_B\times \textit{\textbf{n}}_A\right) \cdot \textit{\textbf{e}}_3\right) \frac{\textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A}{\vert \textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A\vert }\right) \nonumber \\&\quad =\frac{{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \left( \left( \textit{\textbf{n}}_B\times \frac{\partial \textit{\textbf{n}}_A}{\partial \textit{\textbf{u}}_{,s}^A}\right) \textit{\textbf{e}}_3\right) }{\sqrt{1-\left( \left( \textit{\textbf{n}}_B\times \textit{\textbf{n}}_A\right) \cdot \textit{\textbf{e}}_3\right) ^2}}\frac{\textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A}{\vert \textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A\vert }\nonumber \\&\quad =\frac{\textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A}{\left( \textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A\right) ^2}\,{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \left( \left( \textit{\textbf{n}}_B\times \frac{\partial \textit{\textbf{n}}_A}{\partial \textit{\textbf{u}}_{,s}^A}\right) \textit{\textbf{e}}_3\right) . \end{aligned}$$

(79)

Using similar procedure to get the results from (70) to (75) by replacing $\textit{\textbf{N}}$ by $\textit{\textbf{n}}_B$, we proved that

$$\begin{aligned} \frac{\textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A}{\left( \textit{\textbf{n}}_B\cdot \textit{\textbf{n}}_A\right) ^2}\,{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \left( \left( \textit{\textbf{n}}_B\times \frac{\partial \textit{\textbf{n}}_A}{\partial \textit{\textbf{u}}_{,s}^A}\right) \textit{\textbf{e}}_3\right) =\textit{\textbf{e}}_3. \end{aligned}$$

(80)

Similarly for $\displaystyle {{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^B}}$ , we get $\displaystyle {{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^B}=-\textit{\textbf{e}}_3}$. Hence, (76) is proven.

Having Eqs. (75) and (76) at hand , Eq. (67) can be simplified to give

$$\begin{aligned}&\int _L{{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}}\times \rho A\, \ddot{\textit{\textbf{u}}}_{n+\frac{1}{2}}\,\text {d} s+\int _L{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \rho I \left( \ddot{\textit{\textbf{n}}}_{n+\frac{1}{2}}\cdot \frac{\partial \textit{\textbf{n}}}{\partial {{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}}\right) \,\text {d} s \nonumber \\&\quad +\int _L{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}} \times EA\left( \varepsilon _{n+\frac{1}{2}}\,\frac{\partial \varepsilon }{\partial {{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}}\right) \,\text {d} s+\int _L{{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}} \times E{I}\left( \kappa _{n+\frac{1}{2}}\,\frac{\partial \kappa }{\partial {{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}}\right) \,\text {d} s \nonumber \\&\quad +\int _L{{\textit{\textbf{x}}_0}_{,ss}}_{n+\frac{1}{2}} \times E{I}\left( \kappa _{n+\frac{1}{2}}\,\frac{\partial \kappa }{\partial {{\textit{\textbf{x}}_0}_{,ss}}_{n+\frac{1}{2}}}\right) \,\text {d} s \nonumber \\&= \int _L{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \textit{\textbf{q}}(s)\,\text {d} s+\sum _{i=1}^N{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \textit{\textbf{P}}_i+\sum _{j=1}^M M_{3j}. \end{aligned}$$

(81)

To further simplify this expression, we first are going to prove that

$$\begin{aligned} {\textit{\textbf{x}}_0}_{,s}\times \left( \ddot{\textit{\textbf{n}}} \cdot \frac{\partial \textit{\textbf{n}}}{\partial {\textit{\textbf{x}}_0}_{,s}}\right) =\ddot{\textit{\textbf{n}}}\times \left( {\textit{\textbf{x}}_0}_{,s} \cdot \frac{\partial \textit{\textbf{n}}}{\partial {\textit{\textbf{x}}_0}_{,s}}\right) . \end{aligned}$$

(82)

Let’s consider the second term in  (81). After some lengthy algebraic manipulations, Eq. (69) deliver

$$\begin{aligned} \frac{\partial n_k}{\partial {{x_0}_i}_{,s}}&=\frac{\epsilon _{3ik}}{\vert {\textit{\textbf{x}}_0}_{,s}\vert }-\epsilon _{3jk}\frac{{{x_0}_j}_{,s} \,{{x_0}_i}_{,s}}{\vert {\textit{\textbf{x}}_0}_{,s}\vert ^3} \, , \end{aligned}$$

(83)

$$\begin{aligned} \left( \ddot{\textit{\textbf{n}}} \cdot \frac{\partial \textit{\textbf{n}}}{\partial {\textit{\textbf{x}}_0}_{,s}}\right) \cdot \textit{\textbf{e}}_i&=\frac{\partial n_k}{\partial {{x_0}_i}_{,s}} \,\ddot{n}_k =\frac{\epsilon _{3ik}}{\vert {\textit{\textbf{x}}_0}_{,s}\vert }\ddot{n}_k-\epsilon _{3jk}\frac{{{x_0}_j}_{,s} \,{{x_0}_i}_{,s}\,\ddot{n}_k}{\vert {\textit{\textbf{x}}_0}_{,s}\vert ^3} \, , \end{aligned}$$

(84)

$$\begin{aligned} \left( {\textit{\textbf{x}}_0}_{,s}\times \left( \ddot{\textit{\textbf{n}}} \cdot \frac{\partial \textit{\textbf{n}}}{\partial {\textit{\textbf{x}}_0}_{,s}}\right) \right) \cdot \textit{\textbf{e}}_a&=\epsilon _{abi}\,{x_{0_b}}_{,s}\,\frac{\partial n_k}{\partial {{x_0}_i}_{,s}}\, \ddot{n}_k =-\delta _{a3}\,\frac{{x_{0_b}}_{,s}\,\ddot{n}_b}{\vert {\textit{\textbf{x}}_0}_{,s}\vert } \, , \end{aligned}$$

(85)

where use of ${x_{0_3}}_{,s}=0$ has been made. Consider further the expression $\displaystyle {\ddot{\textit{\textbf{n}}}\times \left( {\textit{\textbf{x}}_0}_{,s} \cdot \frac{\partial \textit{\textbf{n}}}{\partial {\textit{\textbf{x}}_0}_{,s}}\right) }$, which is equivalent to

$$\begin{aligned} \left( \ddot{\textit{\textbf{n}}}\times \left( {\textit{\textbf{x}}_0}_{,s} \cdot \frac{\partial \textit{\textbf{n}}}{\partial {\textit{\textbf{x}}_0}_{,s}}\right) \right) \cdot \textit{\textbf{e}}_a=-\delta _{a3}\frac{{x_{0_b}}_{,s}\,\ddot{n}_b}{\vert {\textit{\textbf{x}}_0}_{,s}\vert }. \end{aligned}$$

(86)

From (85) and (86), we conclude:

$$\begin{aligned} {\textit{\textbf{x}}_0}_{,s}\times \left( \ddot{\textit{\textbf{n}}} \cdot \frac{\partial \textit{\textbf{n}}}{\partial {\textit{\textbf{x}}_0}_{,s}}\right) =\ddot{\textit{\textbf{n}}}\times \left( {\textit{\textbf{x}}_0}_{,s} \cdot \frac{\partial \textit{\textbf{n}}}{\partial {\textit{\textbf{x}}_0}_{,s}}\right) . \end{aligned}$$

(87)

Hence (82) is proven.

Consider next

$$\begin{aligned} \left( {\textit{\textbf{x}}_0}_{,s} \cdot \frac{\partial \textit{\textbf{n}}}{\partial {\textit{\textbf{x}}_0}_{,s}}\right) \cdot \textit{\textbf{e}}_i=\frac{\partial n_k}{\partial {{x_0}_i}_{,s}} {{x_0}_k}_{,s}=\frac{\epsilon _{3ik}}{\vert {\textit{\textbf{x}}_0}_{,s}\vert }{{x_0}_k}_{,s} = -n_i. \end{aligned}$$

(88)

From  (87) and  (88) we can write:

$$\begin{aligned} {{\textit{\textbf{x}}_0}_{,s}}_{n+\frac{1}{2}}\times \left( \ddot{\textit{\textbf{n}}}_{n+\frac{1}{2}} \cdot \frac{\partial \textit{\textbf{n}}}{\partial {\textit{\textbf{x}}_0}_{,s}}\right) =-\ddot{\textit{\textbf{n}}}_{n+\frac{1}{2}}\times \textit{\textbf{n}}_{n+\frac{1}{2}}. \end{aligned}$$

(89)

Consider further the third term in  (81) and recall the expression for $\varepsilon$ defined in  (6), one has

$$\begin{aligned} \frac{\partial \varepsilon }{\partial \textit{\textbf{u}}_{,s}}={\textit{\textbf{x}}_0}_{,s}. \end{aligned}$$

(90)

Hence,

$$\begin{aligned} {\textit{\textbf{x}}_0}_{,s} \times EA\left( \varepsilon \,\frac{\partial \varepsilon }{\partial \textit{\textbf{u}}_{,s}}\right) =0. \end{aligned}$$

(91)

Finally, we are going to prove the following statement

$$\begin{aligned} {\textit{\textbf{x}}_0}_{,s} \times \left( \kappa \,\frac{\partial \kappa }{\partial {\textit{\textbf{x}}_0}_{,s}}\right) +{\textit{\textbf{x}}_0}_{,ss} \times \left( \kappa \,\frac{\partial \kappa }{\partial {\textit{\textbf{x}}_0}_{,ss}}\right) =0. \end{aligned}$$

(92)

Consider the last two integrals in  (81). The expression for $\kappa$, found in  (6), can be rewritten as follows:

$$\begin{aligned} \kappa&=\epsilon _{3ji}\,\frac{{{x_0}_i}_{,s}\,{{x_0}_j}_{,ss} }{\vert {\textit{\textbf{x}}_0}_{,s}\vert }-{N_i}_{,s}\,{{X_0}_i}_{,s}, \end{aligned}$$

(93)

which gives

$$\begin{aligned} \frac{\partial \kappa }{\partial {x_{0_l}}_{,s}}=\frac{\epsilon _{3jl}\,{{x_0}_j}_{,ss}}{\vert {\textit{\textbf{x}}_0}_{,s}\vert }-\frac{\epsilon _{3ji}\,{{x_0}_i}_{,s}\,{{x_0}_j}_{,ss}}{\vert {\textit{\textbf{x}}_0}_{,s}\vert ^3}\,{x_{0_l}}_{,s} \qquad \text {and} \qquad \frac{\partial \kappa }{\partial {{x_0}_{,ss}}_l}=\frac{\epsilon _{3li}\,{{x_0}_i}_{,s}}{\vert {\textit{\textbf{x}}_0}_{,s}\vert }. \end{aligned}$$

(94)

The term $\displaystyle {{\textit{\textbf{x}}_0}_{,s} \times \left( \kappa \,\frac{\partial \kappa }{\partial {\textit{\textbf{x}}_0}_{,s}}\right) }$ results in

$$\begin{aligned} \left( {\textit{\textbf{x}}_0}_{,s} \times \left( \kappa \,\frac{\partial \kappa }{\partial {\textit{\textbf{x}}_0}_{,s}}\right) \right) \cdot \textit{\textbf{e}}_a ={x_{0_m}}_{,s}\,\frac{\partial \kappa }{\partial {x_{0_l}}_{,s}}\,\epsilon _{mla}=\delta _{a3}\,\frac{{{x_0}_j}_{,s}\,{{x_0}_j}_{,ss}}{\vert {\textit{\textbf{x}}_0}_{,s}\vert }. \end{aligned}$$

Further, for $\displaystyle {{\textit{\textbf{x}}_0}_{,ss} \times \left( \kappa \,\frac{\partial \kappa }{\partial {\textit{\textbf{x}}_0}_{,ss}}\right) }$, it follows

$$\begin{aligned} \left( {\textit{\textbf{x}}_0}_{,ss} \times \left( \kappa \,\frac{\partial \kappa }{\partial {\textit{\textbf{x}}_0}_{,ss}}\right) \right) \cdot \textit{\textbf{e}}_a={{x_0}_{,ss}}_m\,\frac{\partial \kappa }{\partial {{x_0}_{,ss}}_l}\,\epsilon _{mla} =-\delta _{3a}\,\frac{{{x_0}_{,ss}}_i \, {{x_0}_i}_{,s}}{\vert {\textit{\textbf{x}}_0}_{,s}\vert }. \end{aligned}$$

(95)

Hence, Eqs. (95) and (95) mean nothing but

$$\begin{aligned} {\textit{\textbf{x}}_0}_{,s} \times \left( \kappa \,\frac{\partial \kappa }{\partial {\textit{\textbf{x}}_0}_{,s}}\right) +{\textit{\textbf{x}}_0}_{,ss} \times \left( \kappa \,\frac{\partial \kappa }{\partial {\textit{\textbf{x}}_0}_{,ss}}\right) =0. \end{aligned}$$

(96)

Using  (96), (91), (89) in  (81), we get

$$\begin{aligned}&\rho A\int _L {\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \ddot{\textit{\textbf{u}}}_{n+\frac{1}{2}}\,\text {d}s+\rho {I}\int _L\textit{\textbf{n}}_{n+\frac{1}{2}}\times \ddot{\textit{\textbf{n}}}_{n+\frac{1}{2}} \,\text {d}s\nonumber \\&\quad =\int _L{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \textit{\textbf{q}}(s)\,\text {d}s +\sum _{i=1}^N{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \textit{\textbf{P}}_i+\sum _{j=1}^M M_{3j}. \end{aligned}$$

(97)

which is equivalent to

$$\begin{aligned}&\rho A\int _L\left( {\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \ddot{\textit{\textbf{u}}}_{n+\frac{1}{2}}+\dot{{\textit{\textbf{x}}_0}}_{n+\frac{1}{2}}\times \dot{\textit{\textbf{u}}}_{n+\frac{1}{2}}\right) \,\text {d}s \nonumber \\&\quad +\rho {I}\int _L\left( \textit{\textbf{n}}_{n+\frac{1}{2}}\times \ddot{\textit{\textbf{n}}}_{n+\frac{1}{2}}+\dot{\textit{\textbf{n}}}_{n+\frac{1}{2}}\times \dot{\textit{\textbf{n}}}_{n+\frac{1}{2}}\right) \,\text {d}s \nonumber \\&\quad =\int _L{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \textit{\textbf{q}}(s)\,\text {d}s +\sum _{i=1}^N{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \textit{\textbf{P}}_i+\sum _{j=1}^M M_{3j}. \end{aligned}$$

(98)

since $\displaystyle {\dot{{\textit{\textbf{x}}_0}}_{n+\frac{1}{2}}\times \dot{\textit{\textbf{u}}}_{n+\frac{1}{2}}={\textit{\textbf{0}}}, \, \dot{\textit{\textbf{n}}}_{n+\frac{1}{2}}\times \dot{\textit{\textbf{n}}}_{n+\frac{1}{2}}=0}$, together with the use of the midpoint rule, the expression reads

$$\begin{aligned}&\rho A\int _L\left( \frac{{\textit{\textbf{x}}_0}_{n+1}+{\textit{\textbf{x}}_0}_{n}}{2}\times \frac{\dot{\textit{\textbf{u}}}_{n+1}-\dot{\textit{\textbf{u}}}_{n}}{\Delta t}+\frac{{\textit{\textbf{x}}_0}_{n+1}-{\textit{\textbf{x}}_0}_{n}}{\Delta t}\times \frac{\dot{\textit{\textbf{u}}}_{n+1}+\dot{\textit{\textbf{u}}}_{n}}{2}\right) \,\text {d}s \nonumber \\&\qquad +\rho {I}\int _L \left( \frac{\textit{\textbf{n}}_{n+1}+\textit{\textbf{n}}_{n}}{2}\times \frac{\dot{\textit{\textbf{n}}}_{n+1}-\dot{\textit{\textbf{n}}}_{n}}{\Delta t} \frac{\textit{\textbf{n}}_{n+1}-\textit{\textbf{n}}_{n}}{\Delta t}\times \frac{\dot{\textit{\textbf{n}}}_{n+1}+\dot{\textit{\textbf{n}}}_{n}}{2}\right) \,\text {d}s \nonumber \\&\quad =\int _L{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \textit{\textbf{q}}(s)\,\text {d}s +\sum _{i=1}^N{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \textit{\textbf{P}}_i+\sum _{j=1}^M M_{3j}. \end{aligned}$$

(99)

The expression is equivalent to the concise one

$$\begin{aligned}&\rho A\int _L\left( {\textit{\textbf{x}}_0}_{n+1}\times \dot{\textit{\textbf{u}}}_{n+1}-{\textit{\textbf{x}}_0}_{n}\times \dot{\textit{\textbf{u}}}_n\right) \,\text {d}s +\rho {I}\int _L\left( \textit{\textbf{n}}_{n+1}\times \dot{\textit{\textbf{n}}}_{n+1}-\textit{\textbf{n}}_n\times \dot{\textit{\textbf{n}}}_n\right) \,\text {d}s\nonumber \\&\quad =\int _L{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \textit{\textbf{q}}(s)\,\text {d}s+\sum _{i=1}^N{\textit{\textbf{x}}_0}_{n+\frac{1}{2}}\times \textit{\textbf{P}}_i+\sum _{j=1}^M M_{3j}. \end{aligned}$$

(100)

which indicates that in the case of vanishing moments, we immediately infer

$$\begin{aligned} {{\varvec{{\mathcal {J}}}}}_{n+1}-{{\varvec{{\mathcal {J}}}}}_{n}={\textit{\textbf{0}}}. \end{aligned}$$

(101)

This means nothing but the conservation of the total angular momentum.

Proof of conservation of the total energy

In the following, we will give a concise proof of energy conservation which is different than the proof presented earlier in [45].

Starting from Eq. (21), one can choose the variation to coincide with the velocity vector at time $n+\frac{1}{2}$. Functional (21) takes now the form

$$\begin{aligned}&\int _L\rho A\, \ddot{\textit{\textbf{u}}}_{n+\frac{1}{2}}\cdot \dot{\textit{\textbf{u}}}_{n+\frac{1}{2}}\,\text {d}s+\int _L\rho I\,\ddot{\textit{\textbf{n}}}_{n+\frac{1}{2}}\cdot \dot{\textit{\textbf{n}}}_{n+\frac{1}{2}}\,\text {d}s\nonumber \\&\qquad +\int _L EA\, \varepsilon _{n+\frac{1}{2}}\,{\dot{\varepsilon }}_{n+\frac{1}{2}}\,\text {d}s+\int _L EI \,\kappa _{n+\frac{1}{2}}\,{\dot{\kappa }}_{n+\frac{1}{2}}\,\text {d}s +\sum _{k=1}^K C_k\,{\omega _k}_{n+\frac{1}{2}}\,\dot{{\omega }_k}_{n+\frac{1}{2}}\nonumber \\&\quad =\int _L\textit{\textbf{q}}(s)\cdot \dot{\textit{\textbf{u}}}_{n+\frac{1}{2}}\,\text {d}s +\sum _{i=1}^N\textit{\textbf{P}}_i\cdot \dot{\textit{\textbf{u}}}_{n+\frac{1}{2}}+\sum _{j=1}^M M_{3j}\,{\dot{\theta }}_{n+\frac{1}{2}}, \end{aligned}$$

(102)

which, with the use of the midpoint rule, is equivalent to

$$\begin{aligned}&\int _L\rho A\, \frac{\left( \dot{\textit{\textbf{u}}}_{n+1}-\dot{\textit{\textbf{u}}}_{n}\right) \cdot \left( \dot{\textit{\textbf{u}}}_{n+1}+\dot{\textit{\textbf{u}}}_{n}\right) }{2\, \Delta t}\,\text {d}s +\int _L\rho {I}\, \frac{\left( \dot{\textit{\textbf{n}}}_{n+1}-\dot{\textit{\textbf{n}}}_{n}\right) \cdot \left( \dot{\textit{\textbf{n}}}_{n+1}+\dot{\textit{\textbf{n}}}_{n}\right) }{2\,\Delta t}\,\text {d}s\nonumber \\&\qquad +\int _L EA \,\frac{\left( {\varepsilon }_{n+1}-{\varepsilon }_{n}\right) \left( {\varepsilon }_{n+1}+{\varepsilon }_{n}\right) }{2\,\Delta t}\,\text {d}s+\int _L EI\,\frac{\left( {\kappa }_{n+1}-{\kappa }_{n}\right) \left( {\kappa }_{n+1}+{\kappa }_{n}\right) }{2\,\Delta t}\,\text {d}s \nonumber \\&\qquad +\sum _{k=1}^K C_k\,\frac{\left( {{\omega }_k}_{n+1}-{{\omega }_k}_{n}\right) \left( {{\omega }_k}_{n+1}+{{\omega }_k}_{n}\right) }{2\,\Delta t}\nonumber \\&\quad =\int _L \textit{\textbf{q}}(s)\cdot \frac{{\textit{\textbf{u}}}_{n+1}-{\textit{\textbf{u}}}_{n}}{\Delta t}\,\text {d}s+\sum _{i=1}^N\textit{\textbf{P}}_i\cdot \frac{{\textit{\textbf{u}}_i}_{n+1}-{\textit{\textbf{u}}_i}_{n}}{\Delta t}+\sum _{j=1}^M{M_{3j}\,\frac{{\theta _j}_{n+1}-{\theta _j}_{n}}{\Delta t}}. \end{aligned}$$

(103)

The last equation leads to

$$\begin{aligned}&\frac{1}{2}\int _L\rho A\left( \dot{\textit{\textbf{u}}}_{n+1}^2-\dot{\textit{\textbf{u}}}_{n}^2\right) \,\text {d}s +\frac{1}{2}\int _L\rho {I}\left( \dot{\textit{\textbf{n}}}_{n+1}^2-\dot{\textit{\textbf{n}}}_{n}^2\right) \,\text {d}s\nonumber \\&\qquad +\frac{1}{2}\int _L EA \left( \varepsilon _{n+1}^2-\varepsilon _{n}^2\right) \,\text {d}s +\frac{1}{2}\int _L EI\left( \kappa _{n+1}^2-\kappa _{n}^2\right) \,\text {d}s +\frac{1}{2} \sum _{k=1}^K C_k\,\left( {\omega _k}_{n+1}^2-{\omega _k}_{n}^2\right) \nonumber \\&\quad =\int _L \textit{\textbf{q}}(s)\cdot \left( {{\textit{\textbf{u}}}_{n+1}-{\textit{\textbf{u}}}_{n}}\right) \,\text {d} s +\sum _{i=1}^N\textit{\textbf{P}}_i\cdot \left( {{\textit{\textbf{u}}_i}_{n+1}-{\textit{\textbf{u}}_i}_{n}}\right) +\sum _{j=1}^M{M_{3j}\left( {{\theta _j}_{n+1}-{\theta _j}_{n}}\right) }. \quad \quad \end{aligned}$$

(104)

Assuming that the external loading is conservative, from Eq. (104) we finally obtain

$$\begin{aligned} \left[ T+\Psi _{int}+\Psi _{ext}\right] _{n+1}=\left[ T+\Psi _{int}+\Psi _{ext}\right] _{n}. \end{aligned}$$

(105)

which proves nothing but the conservation of the total energy. We refer the reader to Appendix for the proof of conservation of linear momentum. It is worthwhile to note that in some cases high frequency damping is a desirable quality of the integration scheme. This can be achieved by considering material-type viscosity in addition to the elastic response. However, this is out of the scope of this paper. Alternatively, slight modification of the present integration scheme can result in numerical damping, though this approach is not pursued here any further.

Numerical examples

To demonstrate the performance of the above method in geometrically exact multi-body dynamics, we investigate a range of examples, each of which will be run for one million time steps. The joint is modeled by revolute pair with or without a torsional spring.

Nonlinear dynamics of a flexible two-body system

The first example deals with a classical multi-body dynamics system consisting of two flexible rod-like bodies connected through a revolute joint without torsional spring. The two-body system is attached to a pinned support and subjected to a conservative horizontal force applied at one third of the beam length from the joint (see Fig. 4). The load increases linearly to a peak and decreases at the same rate to zero as shown in Fig. 5.

Fig. 4

Flexible two-body system

Fig. 5

Loading history

Parameters:

Beam length $L ~= ~5$ m, Height $H~=~4$ m

Cross section area $A~ = ~0.3 ~\text {m}^2$, Cross section inertia $I~ =~ 0.0022~\text {m}^4$

Young’s Modulus $E~ =~ 200~\text {GPa}$, Density $\rho ~ = ~7850 ~\text {kg/m}^3$

Number of element = 6, Number of steps = $10^{6}$

Time increment $\Delta t ~= ~10^{-3}$ s

Figure 6 shows the number of iteration necessary in order for the Newton-Raphson method to converge. For $\Delta t=10^{-2}$ s no more that 5 iterations are are needed to achieve convergence whereas for $\Delta t=10^{-3}$ s 3 iterations are sufficient to reach dynamic equilibrium.

Fig. 6

Number of iterations until convergence

Further, we investigate the influence of the time step size on the results. In Fig. 7, the vertical displacement of the free edge (end) of the two-body system versus time is plotted for different time steps: $\Delta t\le 10^{-3}$, $\Delta t=10^{-2}$, $\Delta t=0.1$ and $\Delta t=0.2$. For $\Delta t\le 10^{-3}$ and $\Delta t=1E-2$, the results are similar and only a slight deviation can be observed for $\Delta t=0.1$ and $\Delta t=0.2$. However, in term of energy conservation, Fig. 8 shows that numerically the energy conservation is achieved with high degree of accuracy for $\Delta t\le 10^{-3}$ and $\Delta t=10^{-2}$ whereas for larger time steps ($\Delta t\ge 0.1$), a numerical increase of energy can be observed. It should be noted however that for flexible beams with very high stiffness as considered in the present example, large time steps are physically not meaningful.

Fig. 7

Displacements for different $\Delta t$

Fig. 8

Energy history for different dt

The results of our energy-momentum method are now compared to solutions using classical midpoint rules. Figure 9 shows that the classical midpoint rule already suffers from blow up at $t=7$ s with $\Delta t=10^{-2}$ s. The energy blow-up can be seen in Fig. 10.

Fig. 9

Vertical displacement of second body‘s edge for $\Delta t=10^{-2}$ s

Fig. 10

Energy for $\Delta t=10^{-2}$ s

Nonlinear dynamics of a deformable multi-body system with flexible joint

To investigate the performance of the method for multi-body systems with torsional springs, we consider the previous example and equip the revolute joint with a flexible torsional spring (see Fig. 11). The system is subjected to a conservative horizontal force applied at free end of the multi-body system. The loading history is depicted in Fig. 12. The calculation was performed considering one million time steps with $\Delta t=10^{-3}$ s.

Fig. 11

Multi-body figure

Fig. 12

Loading history

Parameters:

Beam length $L ~= ~5$ m, Height $H~=~4$ m

Cross section area $A ~=~ 0.1 ~\text {m}^2$, Cross section inertia $I ~=~ 8.33\times 10^{-5} ~\text {m}^4$

Young’s Modulus $E ~= ~200 ~\text {GPa}$, Density $\rho ~ =~ 7850 ~\text {kg/m}^3$

Number of elements = 6, Time increment $\Delta t ~= ~10^{-3}$ s

Number of steps = $10^{6}$, Spring constant $C~=~10^{4}~\text {Nm/rad}$

Figures 13 and 14 show the horizontal and vertical displacements at the free end of the two-body system. The conservation of energy is depicted in Fig. 15. The time history of the rotation angle of the hinge is shown in Fig. 16. The rotation angle increases up to about 8 rad. It should be stressed that this smooth behaviour of the rotation angle is a direct outcome of the time integration method where the spring rotation angle is computed by integrating the rotational velocity via Eq. (44) and (48). Some snap shots of the two-body motion are shown in Fig. 17 together with the corresponding time and the value of the hinge rotation angle.

Fig. 13

Horizontal displacement versus time

Fig. 14

Vertical displacement versus time

Fig. 15

Energy time history

Fig. 16

Spring rotation angle time history

Fig. 17

Multi-body snap-shots

Finally, to demonstrate not only the stability and conservation properties of the proposed scheme but also its ability to compute finite spring rotation, we examine the response of this multi-body system using the standard mid-point time integration scheme. Figure 18 shows the displacement of the load application point versus time. An instability can be observed at about $t=95$ s. The time history of the spring rotation angle is plotted in Fig. 19. It can be seen that $\omega$ has a correct value for $\omega =[-\pi ,\pi ]$. When the spring rotation angle reaches $\pm \pi$, we observe a sharp jump in its value, which is clearly incorrect. Hence, the displacements are also not inappropriate. This behaviour is a consequence of the use of Eq. (13) which provides a straightforward means to calculate the spring rotation. This equation is well defined only for angle amplitudes less than $\left|\pi \right|$. Again, a smooth behaviour is possible if the spring rotation angle is computed using the proposed integration method (Eqs. (44) and (48)) where only the increment of $\omega$ is of importance. The energy also suffers from the blow-up phenomena as shown Fig. 20.

Fig. 18

Displacement time history—classical midpoint rule for $\Delta t=10^{-3}$ s

Fig. 19

Spring rotation angle time history—classical midpoint rule for $\Delta t=10^{-3}$ s

Fig. 20

Energy time history—classical midpoint rule for $\Delta t=10^{-3}$ s

Free moving multi-body system

To further asses the performance of the formulation, we consider a free moving multi-body system. More specifically, we investigate the motion of a two-elements mechanism connected to each other by a torsional spring (see Fig. 21). The mechanism is subjected to two external bending moments applied at each end. The time evolution of the loading is depicted in Fig. 22. The calculation has been performed considering one million time steps.

Fig. 21

Multi-body figure

Fig. 22

Loading history

P

Parameters:

Beam length $L~ =~ 5$ m, Height $H~=~4.8$ m

Cross section area $A ~=~ 0.05 ~\text {m}^2$, Cross section inertia $I~ =~ 1.042\times 10^{-5} ~\text {m}^4$

Young’s Modulus $E~ =~ 200~\text {GPa}$, Density $\rho ~=~ 7850 ~\text {kg/m}^3$

Number of elements = 6, Time increment $\Delta t~=~10^{-4}$ s

Number of steps = $10^{6}$, Spring constant $C~=~10^{4}~\text {Nm/rad}$

In this example, not only the conservation of energy (see Fig. 23), but also the conservation of linear momentum (see Fig. 24), and the angular momentum (Fig. 25) are captured. Similarly, the time history of the rotation angle of the hinge and some snap-shots of the motion are illustrated in Figs. 26 and 27, respectively.

Fig. 23

Energy history

Fig. 24

Momentum history

Fig. 25

Angular momentum history

Fig. 26

Spring rotation angle history

Fig. 27

Multi-body snap-shots

Slider-crank system

The last example deals with the classical slider-crank mechanism composed of two flexible beams connected by a revolute joint (see 28). On one side, the mechanism is attached to a pinned support. On the other side, the mechanical system is connected to a weightless slider using a revolute joint. The slider can move only in the horizontal direction and is subjected to an externally applied moment acting at the beam end cross-section connected to the pinned support. As a consequence of the loading, the beam rotates about the out-of-plane axis and the mechanism converts a rotary motion to a straight-line motion. The flexible beam element parameters are given below and the loading history is shown in Fig. 29.

Fig. 28

Multi-body system

Fig. 29

Loading history

Fig. 30

Energy history

Fig. 31

Horizontal displacement of the slider

Fig. 32

Multi-body snap-shots

Parameters:

Beam length $L_1~ =~ 3~\text {m}, L_2~ =~ 10$ m, Height $H~=~2~\text {m}$

Cross section area $A ~=~ 0.3 ~\text {m}^2$, Cross section inertia $I~ = ~0.0022 ~\text {m}^4$

Young’s Modulus $E ~=~ 200~\text {GPa}$, Density $\rho ~= ~7850 ~\text {kg/m}^3$

Number of elements = 6, Time increment $\Delta t ~= ~10^{-4}$ s

Number of steps = $10^{6}$

Fig. 33

Horizontal displacement

Fig. 34

Vertical displacement

Another excellent performance of the formulation is shown with this classical example of multibody mechanism. The energy is perfectly conserved for the whole time (see Fig. 30). The displacement time history of the slider is depicted in Fig. 31, here again no sign of instability is observed. Snap-shots of the motion are presented in Fig. 32.

Conclusions

A new approach for geometrically exact Euler-Bernoulli beam in planar multi-body dynamics has been proposed. A new energy-momentum method was designed for long-term dynamics. The advantage of a displacement-only formulation was clearly demonstrated. While the present paper considers only revolute joints, the methodology is general and could be applied to other types of joints as well. Also, the planar nature of the formulations in this paper is not a restriction. A fully three-dimensional formulation is being currently developed. Also a possible modification of the present formulation to incorporate high-frequency damping can be easily implemented, an aspect which was out of the scope in this paper (Figs. 33 and 34).

Appendices

Appendix A. Linearisation of functional

In order to solve (25), the discretisation in time and space as presented in “Finite element formulation and time integration scheme” section and the numerical linerisation have been used. To compute the integral, we use the classical Gaussian quadrature. Consider one beam element, Eq. (25) is evaluated at $t_{n+\frac{1}{2}}$

(A.1)

where l is the initial length of the element. The latter equation can be rewritten as follows

(A.2)

Let’s decompose $\textit{\textbf{G}}$ as follows $\textit{\textbf{G}}=\rho \, \textit{\textbf{m}}+\textit{\textbf{k}}-\textit{\textbf{f}}=0,$ where

$$\begin{aligned} \textit{\textbf{m}}&=\int _{l} A\, \mathcal {\textit{\textbf{N}}}^\text {T}\left( 2\frac{\Delta \textit{\textbf{u}}}{\Delta t^2}-2\frac{\dot{\textit{\textbf{u}}}_n}{\Delta t}\right) \,\text {d} s +\int _{l} I\,\mathcal {\textit{\textbf{N}}}_{,s}^\text {T}\left( 2\frac{\Delta \textit{\textbf{n}}}{\Delta t^2}-2\frac{\dot{\textit{\textbf{n}}}_n}{\Delta t}\right) \cdot \frac{\partial {\textit{\textbf{n}}}}{\partial {\textit{\textbf{u}}}_{,s}}\,\text {d} s. \end{aligned}$$

(A.3)

$$\begin{aligned} \textit{\textbf{k}}&=\int _{l} EA\, \mathcal {\textit{\textbf{N}}}_{,s}^\text {T} \,\varepsilon _{11} \,\frac{\partial \varepsilon _{11}}{\partial {\textit{\textbf{u}}}_{,s}}\,\text {d} s +\int _{l} EI \left( \mathcal {\textit{\textbf{N}}}_{,s}^\text {T}\,\kappa \,\frac{\partial \kappa }{\partial {\textit{\textbf{u}}}_{,s}}+\mathcal {\textit{\textbf{N}}}_{,ss}^\text {T}\,\kappa \,\frac{\partial \kappa }{\partial {\textit{\textbf{u}}}_{,ss}}\right) \,\text {d} s\nonumber \\&\quad +\sum _{k=1}^K \mathcal {\textit{\textbf{N}}}_{,s}^\text {T}\,C_k\,\omega _k\,\frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}}. \end{aligned}$$

(A.4)

$$\begin{aligned} \textit{\textbf{f}}&=\int _l \mathcal {\textit{\textbf{N}}}^\text {T}\textit{\textbf{q}}(s)\cdot \,\text {d} s + \sum _{i=1}^N\mathcal {\textit{\textbf{N}}}^\text {T}\textit{\textbf{P}}_i +\sum _{j=1}^M{M_{3j}\,\mathcal {\textit{\textbf{N}}}_{,s}^\text {T}\,\frac{\partial (\left( \textit{\textbf{N}}\times \textit{\textbf{n}}\right) \cdot \textit{\textbf{e}}_3)}{\partial {\textit{\textbf{u}}}_{,s}} \,\frac{1}{\textit{\textbf{N}}\cdot \textit{\textbf{n}}}}. \end{aligned}$$

(A.5)

In Eq. (A.2), $\Delta \textit{\textbf{U}}$ is the unknown as every thing is known at time step n. The linerization is made by taking the variation of $\textit{\textbf{G}}$ with respect to $\Delta \textit{\textbf{U}}$ as follows

$$\begin{aligned} \Delta \textit{\textbf{m}}&=\int _{l} A\, \mathcal {\textit{\textbf{N}}}^\text {T} 2\frac{\textit{\textbf{1}}}{dt^2}\,\mathcal {\textit{\textbf{N}}}\, \delta \Delta \textit{\textbf{U}} \, \text {d} s\nonumber \\&\quad +\int _{l} I\, \mathcal {\textit{\textbf{N}}}_{,s}^\text {T}\, \frac{\partial }{\partial \Delta \textit{\textbf{u}}_{,s}}\left( \left( 2\frac{\Delta \textit{\textbf{n}}}{\Delta t^2}-2\frac{{\dot{n}}_n}{\Delta t}\right) \cdot \frac{\partial {\textit{\textbf{n}}}}{\partial {\textit{\textbf{u}}}_{,s}}\right) \mathcal {\textit{\textbf{N}}}_{,s}\delta \Delta \textit{\textbf{U}}\,\text {d} s =\textit{\textbf{M}} \,\delta \Delta \textit{\textbf{U}}. \end{aligned}$$

(A.6)

$$\begin{aligned} \Delta \textit{\textbf{k}}&=\int _{l} EA\, \mathcal {\textit{\textbf{N}}}_{,s}^\text {T}\,\frac{\partial }{\partial \Delta \textit{\textbf{u}}_{,s}}\left( \varepsilon _{11}\, \frac{\partial \varepsilon _{11}}{\partial {\textit{\textbf{u}}}_{,s}}\right) \mathcal {\textit{\textbf{N}}}_{,s}\,\delta \Delta \textit{\textbf{U}}\,\text {d} s\nonumber \\&\qquad +\int _{l} EI \left( \mathcal {\textit{\textbf{N}}}_{,s}^\text {T}\,\frac{\partial }{\partial \Delta \textit{\textbf{u}}_{,s}}\left( \kappa \,\frac{\partial \kappa }{\partial {\textit{\textbf{u}}}_{,s}}\right) \mathcal {\textit{\textbf{N}}}_{,s}\right. +\mathcal {\textit{\textbf{N}}}_{,s}^\text {T}\, \frac{\partial }{\partial \Delta \textit{\textbf{u}}_{,s}}\left( \kappa \,\frac{\partial \kappa }{\partial {\textit{\textbf{u}}}_{,ss}}\right) \mathcal {\textit{\textbf{N}}}_{,ss}\nonumber \\&\qquad +\mathcal {\textit{\textbf{N}}}_{,ss}^\text {T}\, \frac{\partial }{\partial \Delta \textit{\textbf{u}}_{,s}}\left( \kappa \,\frac{\partial \kappa }{\partial {\textit{\textbf{u}}}_{,ss}}\right) \,\mathcal {\textit{\textbf{N}}}_{,s} \left. +\mathcal {\textit{\textbf{N}}}_{,ss}^\text {T}\,\frac{\partial }{\partial \Delta \textit{\textbf{u}}_{,ss}}\left( \kappa \,\frac{\partial \kappa }{\partial {\textit{\textbf{u}}}_{,ss}}\right) \,\mathcal {\textit{\textbf{N}}}_{,ss}\right) \,\delta \Delta \textit{\textbf{U}}\,\text {d} s \,\nonumber \\&\qquad +\sum _{k=1}^K \mathcal {\textit{\textbf{N}}}_{,s}^\text {T}\, \frac{\partial }{\partial \Delta \textit{\textbf{u}}_{,ss}}\left( C_k\,\omega _k\,\frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}}\right) \mathcal {\textit{\textbf{N}}}_{,s}\,\delta \Delta \textit{\textbf{U}}\nonumber \\&=\textit{\textbf{K}} \delta \Delta \textit{\textbf{U}}. \end{aligned}$$

(A.7)

$$\begin{aligned} \Delta \textit{\textbf{f}}&=\sum _{j=1}^M{M_{3j}\,\mathcal {\textit{\textbf{N}}}_{,s}^\text {T}\,\frac{\partial \left( \frac{\partial (\left( \textit{\textbf{N}}\times \textit{\textbf{n}}\right) \cdot \textit{\textbf{e}}_3)}{\partial {\textit{\textbf{u}}}_{,s}} \frac{1}{\textit{\textbf{N}}\cdot \textit{\textbf{n}}}\right) }{\partial \Delta \textit{\textbf{u}}_{,ss}} }\,\mathcal {\textit{\textbf{N}}}_{,s}\,\delta \Delta \textit{\textbf{U}}=\textit{\textbf{F}} \,\delta \Delta \textit{\textbf{U}}. \end{aligned}$$

(A.8)

Thus, the tangent matrix is $\textit{\textbf{W}}_{element}=\rho \, \textit{\textbf{M}}+\textit{\textbf{K}}-\textit{\textbf{F}}$. Finally, one can write $\textit{\textbf{W}}_{element}\delta \Delta \textit{\textbf{U}}= \left( \rho \textit{\textbf{m}}+\textit{\textbf{k}}-\textit{\textbf{f}}\right)$. Practically, the residual vector and tangent matrix containing the torsional springs could be calculated directly at global level not at element level as follows

$$\begin{aligned}&\sum _{k=1}^K C_k\,\omega _k\,\delta \omega _k=\sum _{k=1}^K C_k\,\omega _k\left( \frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^A}\,\delta {\textit{\textbf{u}}}_{,s}^A+\frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^B}\,\delta {\textit{\textbf{u}}}_{,s}^B\right) \nonumber \\&\quad =\sum _{k=1}^K C_k\,\omega _k\left( \frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^A}\,\mathcal {\textit{\textbf{N}}}_{,s}\,\textit{\textbf{T}}_1\,\delta \varvec{\Phi }+\frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^B}\,\mathcal {\textit{\textbf{N}}}_{,s}\,\textit{\textbf{T}}_2\,\delta \varvec{\Phi }\right) . \end{aligned}$$

(A.9)

where $\varvec{\Phi }$ is the global degrees of freedom. $\textit{\textbf{T}}_1$ and $\textit{\textbf{T}}_2$ are the localised matrix of the two elements connected by the torsional spring. The global residual vector related to torsional springs is written as follows

$$\begin{aligned} \textit{\textbf{s}}_p=\sum _{k=1}^K \left( \textit{\textbf{T}}_1^\text {T}\,\mathcal {\textit{\textbf{N}}}_{,s}^\text {T}\,C_k\,\omega _k\,\frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^A}+\textit{\textbf{T}}_2^\text {T}\,\mathcal {\textit{\textbf{N}}}_{,s}^\text {T}\,C_k\,\omega _k\,\frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^B}\right) . \end{aligned}$$

(A.10)

Thus, the corresponding global tangent matrix reads

$$\begin{aligned} \textit{\textbf{S}}_p&=\sum _{k=1}^K \left( \textit{\textbf{T}}_1^\text {T}\,\mathcal {\textit{\textbf{N}}}_{,s}^\text {T} \,C_k\,\frac{\partial }{\partial \Delta \textit{\textbf{u}}_{,s}^A}\left( \omega _k\frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^A}\right) \mathcal {\textit{\textbf{N}}}_{,s} \textit{\textbf{T}}_1 +\textit{\textbf{T}}_1^\text {T}\,\mathcal {\textit{\textbf{N}}}_{,s}^\text {T}\, C_k\,\frac{\partial }{\partial \Delta \textit{\textbf{u}}_{,s}^B}\left( \omega _k\frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^A}\right) \mathcal {\textit{\textbf{N}}}_{,s} \textit{\textbf{T}}_2\right. \nonumber \\&\quad +\left. \textit{\textbf{T}}_2^\text {T}\,\mathcal {\textit{\textbf{N}}}_{,s}^\text {T}\,C_k\,\frac{\partial }{\partial \Delta \textit{\textbf{u}}_{,s}^A}\left( \omega _k\frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^B}\right) \mathcal {\textit{\textbf{N}}}_{,s} \textit{\textbf{T}}_1 + \textit{\textbf{T}}_2^\text {T}\mathcal {\textit{\textbf{N}}}_{,s}^\text {T} \,C_k\,\frac{\partial }{\partial \Delta \textit{\textbf{u}}_{,s}^B}\left( \omega _k\frac{\partial \omega }{\partial {\textit{\textbf{u}}}_{,s}^B}\right) \mathcal {\textit{\textbf{N}}}_{,s} \,\textit{\textbf{T}}_2\right) . \end{aligned}$$

(A.11)

Appendix B. Proof of conservation of linear momentum

To prove the conservation of linear momentum, we start by integrating the field Eq. (55) which provides us with the statement

$$\begin{aligned}&\int _L \rho A\ddot{\textit{\textbf{u}}}_{n+\frac{1}{2}}\,\text {d} s -\int _L\left( \rho I\left( \ddot{\textit{\textbf{n}}}_{n+\frac{1}{2}}\cdot \frac{\partial \textit{\textbf{n}}}{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}-EA\left( \varepsilon _{n+\frac{1}{2}}\,\frac{\partial \varepsilon }{\partial \textit{\textbf{u}}_{,s}}\right) _{,s}\right) \,\text {d} s \nonumber \\&\quad -\int _L \left( EI\left( \kappa _{n+\frac{1}{2}}\,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,s}}\right) _{,s} +EI\left( \kappa _{n+\frac{1}{2}}\,\frac{\partial \kappa }{\partial \textit{\textbf{u}}_{,ss}}\right) _{,ss} \right) \,\text {d} s =\int _L\textit{\textbf{q}}(s)\,\text {d} s . \end{aligned}$$

(B.1)

The subsequent application of Gauss’s theorem results in

(B.2)

A view on the boundary condition (56), reveals the general momentum equation

$$\begin{aligned} \int _L \rho A\, \ddot{\textit{\textbf{u}}}_{n+\frac{1}{2}}\,\text {d} s =\int _L\textit{\textbf{q}}(s)\,\text {d} s +\sum _{i=1}^N\textit{\textbf{P}}_i=0, \end{aligned}$$

(B.3)

which indicates that in the case of vanishing external forces

$$\begin{aligned}&\int _L\textit{\textbf{q}}(s)\,\text {d} s +\sum \textit{\textbf{P}}_i=0, \end{aligned}$$

(B.4)

the midpoint rule provides us with the statement

$$\begin{aligned} \int _L \rho A \, \frac{\dot{\textit{\textbf{u}}}_{n+1}-\dot{\textit{\textbf{u}}}_{n}}{\Delta t}\,\text {d} s =0, \end{aligned}$$

(B.5)

leading to

$$\begin{aligned}&\int _L \rho A\left( {\dot{\textit{\textbf{u}}}_{n+1}-\dot{\textit{\textbf{u}}}_{n}}\right) \,\text {d} s =0, \end{aligned}$$

(B.6)

$$\begin{aligned}&\textit{\textbf{p}}_{n+1}-\textit{\textbf{p}}_{n}=0. \end{aligned}$$

(B.7)

Hence, the conservation of linear momentum is now proven.