Abstract
In this paper, the parameter identification of gene regulatory network with time-varying delay is studied. Firstly, we introduce the differential equation model of gene regulatory network with unknown parameters and time delay. Secondly, for the unknown parameters in the time-varying model, a corresponding system with adaptive parameters and adaptive controller is introduced, and the parameter identification problem of the original model is transformed into the synchronization problem of the two systems. Thirdly, we design an effective adaptive controller and an adaptive law for parameters and construct a Lyapunov functional. Then we give a strict theoretical proof that the adaptive parameters can converge to unknown parameters by Barbalat’s lemma. Finally, a numerical example is given to verify the validity of the theoretical results.
Similar content being viewed by others
1 Introduction
As a complex system, genetic regulatory networks (GRNs) could describe the complicated regulatory mechanism in living cells, which consist of DNA, RNA (especially mRNA), proteins, and some other micro-molecules [1, 2]. In the past decades, GRNs have attracted many researchers from some different fields, such as applied mathematics, systems biology, molecular biology, etc. Several kinds of models have been proposed and investigated, for example, Boolean networks model [3], Bayesian networks model [4], weighted matrices model [5], differential equation model [6], and so on.
Among those models, the differential equation models could describe the change in concentration of proteins and mRNA, which could reflect the nonlinear dynamical behaviors of biological process, thus, the differential equation models have been discussed widely in recent years. The differential equation models were modeled to describe gene expression process in [7] at first. Then, many results about dynamic analysis about GRNs have been published. For example, stability [8–10], stabilization [11–14], bifurcation [15–17], state estimation [18–20], and so on.
In the above results, the models are known. In many real world GRNs, one can determine the structure of the differential equation model according to some indetermination. However, the parameters of models may be unknown or different in various cells. Consequently, parameter identification of unknown GRNs is an interesting and important work. The common strategy of parameter identification is translating it into an optimization problem, in which the unknown parameters could be regarded as decision variables, while minimizing the error between pseudo state and real state could be regarded as optimization objective. Then, the problem could be solved by intelligent optimization algorithms. For example, Zhao and Yin have studied the parameter identification problem in geomechanics by particle swarm optimization and support vector machine methods [21]. Parameter identification of solar cell models according to artificial bee swarm optimization algorithm has been investigated in [22]. More recently, parameter identification of photovoltaic models using an improved JAYA optimization algorithm has been discussed in [23]. As for the GRNs, Tang and Wang have considered the problem of parameter identification of unknown delayed GRNs by a switching particle swarm optimization algorithm [24].
There were also some results about parameter identification problem for differential equations via adaptive synchronization method. In which, an auxiliary system would be constructed as a response system. Then, the adaptive laws would be designed to synchronize the auxiliary system to the unknown system. Meanwhile, the parameters in the auxiliary system were also updated with some adaptive laws. When the synchronization was achieved, the adaptive parameters were supposed to approach the unknown parameters. This significant method was proposed by Chen and Lv in [25]. Then, some related results have also been published, one can see [26–30]. For different models, the adaptive laws would be designed in different forms, which brings difficulties and challenges to this method.
Time delay often occurs due to transportation lag. And the existence of delays is a frequently result in instability, bifurcation, and chaos for dynamical systems. Therefore, there are many results about time delay systems [31–35]. Inspired by the above analysis, this paper studies the parameter identification problem of GRNs with time delay. We design some effective adaptive laws of linear feedback controllers and parameters in an auxiliary system. According to rigorous theoretical analysis, the synchronization could be achieved between the auxiliary system and the unknown system. Meanwhile, all the unknown parameters in the time-delayed GRNs could be estimated. The rest of the paper is organized as follows: In Sect. 2, we introduce the models of GRNs at first, and then the parameter identification problem is converted into a synchronization problem, some useful lemmas are also given in this section. The main results about synchronization and parameter identification are presented in Sect. 3. Then, some examples are given to demonstrate the effectiveness of our results in Sect. 4. Conclusions are finally drawn in Sect. 5.
2 Preliminaries
2.1 Basic model of GRN
In this paper, we consider the following GRN model with time-varying delay, which has been proposed in [6]:
where \(m(t)=[m_{1}(t),m_{2}(t),\ldots,m_{n}(t)]^{T}\in\mathbb{R}^{n}\), \(p( t ) = [p_{1}(t),p_{2}(t),\ldots,p_{n}(t)]^{T}\in\mathbb{R}^{n}\), and \(m_{i}(t)\), \(p_{i}(t)\) are concentrations of ith mRNA and ith protein at the time t, respectively. Based on the central dogma, a simplified dynamic system of gene regulation can be described as Fig. 1. \(A = \operatorname{diag}\{ {{a_{1}},{a_{2}}, \ldots,{a_{n}}} \}\) >0 and \(C = \operatorname{diag}\{{{c_{1}},{c_{2}}, \ldots,{c_{n}}} \}> 0\) are the degradation rates of the mRNAs and proteins, respectively. The nonlinear function \(f(\cdot)\) denotes feedback regulation from protein to transcription factor with \(f(\cdot )=[f_{1}(\cdot), f_{2}(\cdot),\ldots,f_{n}(\cdot)]\in\mathbb{R}^{n}\), and \(f_{i}(x)\) is a monotonic increasing function with a Hill form:
where \(H_{i}\) called the Hill coefficients, \(\beta_{i}\) are positive constants, \(i=1,2,\ldots,n\). \(D = \operatorname{diag}\{{d_{1}},{d_{2}}, \ldots,{d_{n}}\}\), and \(d_{i}\) is the translation rate of ith protein. \(\tau_{1}(t)\) and \(\tau_{2}(t)\) are time-varying delays, which denote the translation delay and the feedback regulation delay, respectively. \(L =[l_{1}, l_{2},\ldots,l_{n}]^{T}\in\mathbb{R}^{n}\), where \(l_{i} = \sum_{j \in{I_{i}}} {{\alpha_{ij}}} \), in which \({I_{i}}\) is the set of all the repressors of gene i. \(W = ( {{w_{ij}}} ) \in{\mathbb{R}^{n \times n}}\) with
Assumption 1
We assume that the time-varying delays \(\tau_{1}(t)\) and \(\tau_{2}(t)\) are satisfied: \(\dot{\tau}_{i}(t)\leq\mu_{i}<1\), \(i=1,2\).
Assumption 2
It is obvious that the function \(f_{i}(\cdot)\) satisfies the Lipschitz condition, we assume that there are constants \(h_{i}\geq0\), \(i=1,2,\ldots,n\), such that, for any \(x,y\in\mathbb{R}\), one has \(|f_{i}(y)-f_{i}(x)|\leq h_{i}|y-x|\), \(i=1,2,\ldots,n\).
Remark 1
The above two assumptions are very common. Clearly, Assumption 1 is certainly ensured if the transmission delay is constant, and many results have the same assumption, see for example [36–39] and the references therein. In addition, Assumption 2 can guarantee the existence and uniqueness of the solution for system (1); thus, the proof of the existence and uniqueness of the solution for system (1) is omitted here.
Remark 2
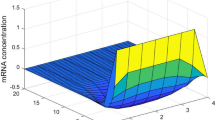
Time-varying delays have been considered in the above GRN model. Time delays are unavoidable in real world. Indeed, systems with time delays exhibit much more complicated dynamical behaviors than ordinary differential equations without time delays. Figure 2 shows some different dynamical behaviors under different time delays for GRN (1). In which, let \(\tau_{1}(t)=\tau_{2}(t)=\tau(t)\), the other parameters are the same as the ones in the simulation part.
Dynamical behaviors of GRN (1) with different time delays
2.2 Description of parameter identification and transformation
Noting that in many real situations the parameter matrices A, C, W, and D maybe unknown, we identify those unknown parameters by adaptive synchronization method in this paper. Model (1) could be regarded as a driven system. We construct the following response system:
where \(\hat{m}(t)=[\hat{m}_{1}(t),\hat{m}_{2}(t),\ldots,\hat{m}_{n}(t)]^{T} \in\mathbb{R}^{n}\), \(\hat{p}( t )= [\hat{p}_{1}(t),\hat {p}_{2}(t),\ldots, \hat{p}_{n}(t)]^{T}\in\mathbb{R}^{n}\), \(\hat{A}(t)=(\hat{a}_{ij}(t))_{n \times n}\), \(\hat{W}(t)=(\hat{w}_{ij}(t))_{n\times n}\), \(\hat{C}(t)=( \hat{c}_{ij}(t))_{n\times n}\), and \(\hat{D}(t)=(\hat{d}_{ij}(t))_{n \times n}\) are the estimations of unknown parameters A, W, C, and D, respectively. \(u_{1}(t)\) and \(u_{2}(t)\) are the feedback controllers to be designed later. Because there are unknown parameters A, W, C, and D in the driven system, we cannot construct an identical system. In addition, the complete synchronization between (1) and (2) cannot be achieved by the static linear feedback control method. Therefore, the adaptive control strategy is used in this manuscript; meanwhile, the parameters \(\hat{A}(t)\), \(\hat{W}(t)\), \(\hat{C}(t)\), and \(\hat{D}(t)\) are also assumed to be time-varying.
3 Main results
3.1 The design of adaptive laws
Let \(x(t)=\hat{m}(t)-m(t)=[x_{1}(t),x_{2}(t),\ldots,x_{n}(t)]^{T}\in \mathbb{R}^{n}\), \(y(t)=\hat{p}(t)-p(t)=[y_{1}(t),y_{2}(t),\ldots, y_{n}(t)]^{T} \in\mathbb{R}^{n}\). The adaptive controllers
where \(E_{1}(t)=\operatorname{diag}\{\varepsilon^{x}_{1}(t),\varepsilon^{x} _{2}(t),\ldots,\varepsilon^{x}_{n}(t)\}\) and \(E_{1}(t)=\operatorname{diag}\{ \varepsilon^{y}_{1}(t),\varepsilon^{y}_{2}(t),\ldots,\varepsilon^{y}_{n}(t) \}\) are dynamical feedback control gain matrices. Then, it is easy to get the error system as follows:
where \(\tilde{f}(y)(t-\tau_{1}(t))=f(y(t-\tau_{1}(t))+p(t-\tau _{1}(t)))-f(p(t- \tau_{1}(t)))\), \(\tilde{A}(t)=A-\hat{A}(t)\), \(\tilde{W}(t)=W-\hat{W}(t)\), \(\tilde{C}(t)=C-\hat{C}(t)\) and \(\tilde{D}(t)=D-\hat{D}(t)\).
In this paper, we design the adaptive laws as follows:
where \(\eta^{x}_{i}>0\), \(\eta^{y}_{i}>0\), \(\sigma^{x}_{i}>0\), \(\sigma^{y}_{i}>0\), \(\gamma^{x}_{ij}>0\), \(\gamma^{y}_{ij}>0\) are arbitrary constants for \(i,j=1,2,\ldots,n\).
3.2 The main theorem
Theorem 1
Under Assumptions1, 2and controllers\(u_{1}(t)=E_{1}(t)x(t)\)and\(u_{2}(t)=E_{2}(t)y(t)\)with adaptive laws (4), the synchronization can be achieved between (1) and (2). Furthermore, the unknown parameters can be estimated, that is, \(\lim_{t\rightarrow+\infty}(a_{i}-\hat{a}_{i}(t))=0\), \(\lim_{t\rightarrow+\infty}(w_{ij}-\hat{w}_{ij}(t))=0\), \(\lim_{t\rightarrow+\infty}(c_{i}-\hat{c}_{i}(t))=0\), \(\lim_{t\rightarrow+\infty}(d_{ij}-\hat{d}_{ij}(t))=0\), \(j=1,2,\ldots,n\).
Proof
Construct a Lyapunov function:
where \(l>\max(\lambda_{\max} (\frac{1}{2}W{W^{T}}-A+\frac{1}{2(1-\mu_{1})}LI),\lambda_{\max} (\frac{1}{2}D{D^{T}}-C+\frac{1}{2(1-\mu_{2})}I))+1>0\) is a constant. Although the parameters W, A, D, C are unknown, one can select l to be a sufficiently large constant to guarantee the above inequality.
Along any trajectory of the error system, the derivative is
By Assumption 1, we know that \(\dot{\tau}_{i}(t)\leq\mu_{i}<1\), \(i=1,2\), and hence \(-\frac{1-\dot{\tau}_{i}(t)}{1-\mu_{i}}\leq-1\), then
According to (4), one has
Then one can obtain
Based on Assumption 2, we know
where \(h = \max \{ {h_{i}^{2}|i = 1,2, \ldots,n} \} \).
According to the above inequations, we get
where I is a unit matrix, \({\lambda_{\max}} ( M )\) is an eigenvalue of the maximum of M. Based on the definition of l, we know that
It is obvious that \(\dot{V}(t)=0\) if and only if \(x(t)=0\) and \(y(t)=0\). Under the conditions \(x(t)=0\) and \(y(t)=0\), one can get the largest invariant \(\mathbb{E}=\{\hat{A}(t)=A,\hat{C}=C,\hat{W}=W, \hat{D}=D,E_{1}(t)=\hat{E}_{1},E_{2}(t)=\hat{E}_{2}\}\), where the feedback control gains \(\hat{E}_{1}\) and \(\hat{E}_{2}\) depend on the initial value of error system (3). Then, based on the well-known Lyapunov–LaSalle type theorem for functional differential equations (Theorem 3.1, p. 119 [40]), the trajectories of error dynamical system (3) will converge into the largest invariant \(\mathbb{E}\) as \(t\rightarrow+\infty\), which implies that the synchronization can be achieved between (1) and (2). Moreover, \(\lim_{t\rightarrow+\infty}(a_{i}-\hat{a}_{i})= \lim_{t\rightarrow+\infty}(w_{ij}-\hat{w}_{ij})=\lim_{t\rightarrow+\infty}(c_{i}-\hat{c}_{i})=\lim_{t\rightarrow+\infty}(d_{ij}-\hat{d}_{ij})=0\) (\(\forall i,j=1,2,\ldots,n\)). This completes the proof of this theorem. □
4 Numerical simulations
In this section, a numerical example is given to show the effectiveness of the proposed results.
Example 1
Consider the following the GRN with several unknown parameters:
where
and \(\tau_{1}(t)=\tau_{2}(t)=1\), there are limit cycles among mRNAs and proteins under those parameters, respectively. One can see in Fig. 3 and Fig. 4. The time-response of \(m_{i}(t)\) and \(p_{i}(t)\) can be seen in Fig. 5 and Fig. 6, respectively. Indeed, for different parameters, the GRN may be stable, unstable, period, or even chaotic. However, synchronization between two stable or unstable systems maybe meaningless. Consequently, we selected the above parameters to get a period orbit. Note that this dynamical behavior is sensitive to the parameters. For example, if we let \(w_{21}=-1.4\), other parameters are the same as above, without any control, one can see the time response between (6) and (7) in Fig. 7 and Fig. 8, respectively.
We construct the following response GRN four unknown parameters \(a_{33}\), \(c_{22}\), \(w_{21}\), \(d_{33}\):
with
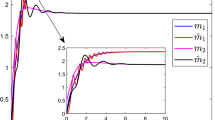
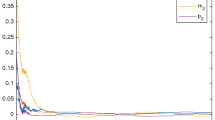
In the following simulations, we take \(m(s)=[0.1,0.5,1]^{T}\), \(p(s)=[0.7,0.4,0.1]^{T}\), \(\hat{m}(s)=[0.5,0.8,0.9]^{T}\), \(\hat{p}(s)=[1.2,1.3,2]^{T}\) when \(s\in[-1,0]\), and \(a_{33}(0)=c_{22}(0)=w _{21}(0)=d_{33}(0)=\varepsilon^{x}_{i}(0)=\varepsilon^{y}_{i}(0)=0\), \(i=1,2,3\), the updated gains are set as \(\eta^{x}_{i}=\eta^{y}_{i}=0.1\), \(\sigma^{x}_{i}=\sigma^{y}_{i}=5\), \(\gamma^{x}_{ij}=\gamma^{y}_{ij}=5\), \(i,j=1,2,3\). Then, one can get the following results. The synchronization between (6) and (7) can be obtained, one can see in Figs. 9 and 10. In addition, the unknown parameters can be estimated, which has been shown in Figs. 11 and 12, respectively. Finally, the adaptive control gain \(\varepsilon_{i}(t)\), \(i=1,2,\ldots,6\), can be see in Fig. 13.
5 Conclusion
In this paper, the adaptive synchronization method has been applied to identify the unknown parameters of a time-delayed GRN. A dynamical linear feedback controller and adaptive parameters updated laws have been designed to synchronize the auxiliary system to the unknown GRN. Then, based on the Lyapunov stability theorem and Barbalat’s lemma, the synchronization results could be guaranteed, the unknown parameters could also be identified. An example is given to show the effectiveness of the theoretical results.
References
Olson Eric, N.: Gene regulatory networks in the evolution and development of the heart. Science 313(5795), 1922–1927 (2006)
Karlebach, G., Shamir, R.: Modelling and analysis of gene regulatory networks. Nat. Rev. Mol. Cell Biol. 9(10), 770–780 (2008)
Shmulevich, I., Dougherty, E.R., Kim, S., Zhang, W.: Probabilistic Boolean networks: a rule-based uncertainty model for gene regulatory networks. Bioinformatics 18(2), 261–274 (2002)
Husmeier, D.: Sensitivity and specificity of inferring genetic regulatory interactions from microarray experiments with dynamic Bayesian networks. Bioinformatics 19(17), 2271–2282 (2003)
Weaver, D.C., Workman, C.T., Stormo, G.D.: Modeling regulatory networks with weight matrices. Pac. Symp. Biocomput. 4, 112–123 (1999)
Chen, L., Aihara, K.: Stability of genetic regulatory networks with time delay. IEEE Trans. Circuits Syst. I, Fundam. Theory Appl. 49(5), 602–608 (2002)
Chen, T., He, H.L., Church, G.M.: Modeling gene expression with differential equations. Pac. Symp. Biocomput. 29, 29–40 (1999)
Li, C., Chen, L., Aihara, K.: Stability of genetic networks with sum regulatory logic: lure system and lmi approach. IEEE Trans. Circuits Syst. I, Regul. Pap. 53(11), 2451–2458 (2006)
Ren, F., Cao, J.: Asymptotic and robust stability of genetic regulatory networks with time-varying delays. Neurocomputing 71(4), 834–842 (2008)
Chesi, G., Hung, Y.S.: Stability analysis of uncertain genetic sum regulatory networks. Automatica 44(9), 2298–2305 (2008)
Chen, B.S., Chang, Y.T., Wang, Y.C.: Robust h1-stabilization design in gene networks under stochastic molecular noises: fuzzy-interpolation approach. IEEE Trans. Syst. Man Cybern., Part B, Cybern. 38(1), 25–42 (2008)
Li, L., Yang, Y.: On sampled-data control for stabilization of genetic regulatory networks with leakage delays. Neurocomputing 149, 1225–1231 (2015)
Chen, W., Chen, D., Hu, J., Liang, J., Dobaie, A.M.: A sampled-data approach to robust h∞ state estimation for genetic regulatory networks with random delays. Int. J. Control. Autom. Syst. 16(2), 491–504 (2018)
Wan, X., Wang, Z., Wu, M., Liu, X.: State estimation for discrete time-delayed genetic regulatory networks with stochastic noises under the round-Robin protocols. IEEE Trans. Nanobiosci. 17(2), 145–154 (2018)
Huang, C., Cao, J., Xiao, M.: Hybrid control on bifurcation for a delayed fractional gene regulatory network. Chaos Solitons Fractals 87, 19–29 (2016)
Xiao, M., Zheng, W.X., Jiang, G., Cao, J.: Stability and bifurcation analysis of arbitrarily high-dimensional genetic regulatory networks with hub structure and bidirectional coupling. IEEE Trans. Circuits Syst. I, Regul. Pap. 63(8), 1243–1254 (2016)
Tao, B., Xiao, M., Sun, Q., Cao, J.: Hopf bifurcation analysis of a delayed fractional-order genetic regulatory network model. Neurocomputing 275, 677–686 (2018)
Liang, J., Lam, J., Wang, Z.: State estimation for Markov-type genetic regulatory networks with delays and uncertain mode transition rates. Phys. Lett. A 373(47), 4328–4337 (2009)
Liang, J., Lam, J.: Robust state estimation for stochastic genetic regulatory networks. Int. J. Syst. Sci. 41(1), 47–63 (2010)
Li, Q., Shen, B., Liu, Y., Alsaadi, F.E.: Event-triggered h∞ state estimation for discrete-time stochastic genetic regulatory networks with Markovian jumping parameters and time-varying delays. Neurocomputing 174, 912–920 (2016)
Zhao, H., Yin, S.: Geomechanical parameters identification by particle swarm optimization and support vector machine. Appl. Math. Model. 33(10), 3997–4012 (2009)
Askarzadeh, A., Rezazadeh, A.: Artificial bee swarm optimization algorithm for parameters identification of solar cell models. Appl. Energy 102, 943–949 (2013)
Yu, K., Liang, J.J., Qu, B.Y., Chen, X., Wang, H.: Parameters identification of photovoltaic models using an improved jaya optimization algorithm. Energy Convers. Manag. 150, 742–753 (2017)
Tang, Y., Wang, Z., Fang, J.: Parameters identification of unknown delayed genetic regulatory networks by a switching particle swarm optimization algorithm. Expert Syst. Appl. 38(3), 2523–2535 (2011)
Chen, S., Lü, J.: Parameters identification and synchronization of chaotic systems based upon adaptive control. Phys. Lett. A 299(4), 353–358 (2002)
Hu, M., Xu, Z., Zhang, R., Hu, A.: Parameters identification and adaptive full state hybrid projective synchronization of chaotic (hyper-chaotic) systems. Phys. Lett. A 361(3), 231–237 (2007)
Yu, W., Cao, J.: Adaptive synchronization and lag synchronization of uncertain dynamical system with time delay based on parameter identification. Phys. A, Stat. Mech. Appl. 375(2), 467–482 (2007)
Lu, J., Cao, J.: Synchronization-based approach for parameters identification in delayed chaotic neural networks. Phys. A, Stat. Mech. Appl. 382(2), 672–682 (2007)
Zhao, H., Li, L., Peng, H., Xiao, J., Yang, Y., Zheng, M.: Impulsive control for synchronization and parameters identification of uncertain multi-links complex network. Nonlinear Dyn. 83(3), 1437–1451 (2016)
Zhao, H., Li, L., Xiao, J., Yang, Y., Zheng, M.: Parameters tracking identification based on finite-time synchronization for multi-links complex network via periodically switch control. Chaos Solitons Fractals 104, 268–281 (2017)
Huang, C., Yang, Z., Yi, T., Zou, X.: On the basins of attraction for a class of delay differential equations with non-monotone bistable nonlinearities. J. Differ. Equ. 256, 2101–2114 (2014)
Wang, F., Yang, Y., Hu, M.: Asymptotic stability of delayed fractional-order neural networks with impulsive effects. Neurocomputing 154, 239–244 (2015)
Huang, C., Qiao, Y., Huang, L., Agarwal, R.: Dynamical behaviors of a food-chain model with stage structure and time delays. Adv. Differ. Equ. 2018, 186 (2018) https://doi.org/10.1186/s13662-018-1589-8
Long, X., Gong, S.: New results on stability of Nicholson’s blowflies equation with multiple pairs of time-varying delays. Appl. Math. Lett. 100, 106027 (2020) https://doi.org/10.1016/j.aml.2019.106027
Huang, C., Zhang, H., Cao, J., Hu, H.: Stability and Hopf bifurcation of a delayed prey-predator model with disease in the predator. Int. J. Bifurc. Chaos 29, 1–23 (2019)
Liu, F., Song, Q., Wen, G., Cao, J., Yang, X.: Bipartite synchronization in coupled delayed neural networks under pinning control. Neural Netw. 108, 146–154 (2018)
Fan, Y., Huang, X., Shen, H., Cao, J.: Switching event-triggered control for global stabilization of delayed memristive neural networks: an exponential attenuation scheme. Neural Netw. 117, 216–224 (2019)
Yang, X., Cao, J., Liang, J.: Exponential synchronization of memristive neural networks with delays: interval matrix method. IEEE Trans. Neural Netw. Learn. Syst. 28, 1878–1888 (2017)
Yang, W., Wang, Y., Shen, Y., Pan, L.: Cluster synchronization of coupled delayed competitive neural networks with two time scales. Nonlinear Dyn. 90, 2767–2782 (2017)
Hale, J.: Theory of Functional Differential Equation. Springer, New York (1977)
Acknowledgements
The authors are highly grateful to anonymous reviewers for their careful reading of this paper and their insightful comments and suggestions.
Availability of data and materials
Not applicable.
Funding
This work is not supported by any funds.
Author information
Authors and Affiliations
Contributions
All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Liu, C., Wang, F. Parameter identification of genetic regulatory network with time-varying delays via adaptive synchronization method. Adv Differ Equ 2020, 127 (2020). https://doi.org/10.1186/s13662-020-2537-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-020-2537-y