Introduction

With the deepening research on biological network, neural network, gene network and other excellent achievements have been produced in recent years [1,2,3,4,5,6]. Especially, as a powerful research tool for cell recognition, metabolism and signal transduction in the growth and reproduction processes of organisms, a mess of experts and scholars pay a widely sight of genetic regulatory networks (GRNs) in the field of biomedical and bioengineering [1, 2]. There exist two common phenomenons in the process of gene regulation. The first is hysteresis by slow conduction of gene regulation [7]. The second is reaction-diffusion phenomenon by the nonuniform concentration distribution of cell components in various regions, which means that the concentration changes of mRNA and protein in time and space from one layer to another must be considered. In recent years, some related research results have been presented for these dynamic characteristics of GRNs [8,9,10,11,12].

Since 1961, P. Dorato proposed the detailed finite-time stability (FTS) theory to describe the system performance indicators and state trajectories in a short time area in [13], the study of FTS has attracted wide attention in various fields. As we all know, Lyapunov theory is very important and universal to study the various dynamic characteristics of complex systems, and a large number of excellent results have been produced on the basis of this theory [14,15,16,17,18,19]. Therefore, it is convenient and effective to use Lyapunov theory to study the FTS of GRNs. Several excellent results for FTS analysis of the delayed GRNs with reaction-diffusion terms (DGRNs-RDTs) have proposed in [10,11,12, 20]. By applying the secondary delay-partition approach to divide the time-delay interval into two subintervals, the FTS conditions of DGRNs-RDTs are established in [10]. The problem of FTS for uncertain DGRNs-RDTs is analyzed by using the reconstructed uncertainties in [11, 20]. In [12], the FTS criteria of DGRNs-RDTs in relation to the character of delay and reaction-diffusion is established based on an LKF with quad-slope integrations. The common goal of the above literatures is to obtain the stability criterion with low conservatism, which is also the research purpose of this paper.

In the aspect of reducing the conservativeness of stability, delay information is often used to construct different LKF and different stability criteria have been obtained. For example, by introducing a fraction of the time delay, a novel stability result is obtained [21, 22]. In [10, 23], using such an idea that the whole delay interval is nonuniformly decomposed into multiple subintervals, several stability criteria are proposed. In [24], along with the routine of dynamic programming, a multiple dynamic contraction mapping idea and homeomorphism theory are combined and a nonuniformly weighting-delay-based analysis method is developed to analyze the stability of neural networks. In the above literatures, the stability of the system is analyzed by constructing a complex LKF. However, it is also an effective way to analyze stability, that is, to construct a simple LKF that contains system information as completely as possible. In addition, the utilization of the information on the slope of the regulatory function plays an important role in conservativeness as [25]. Currently, the slope information of nonlinear regulatory function is used by transforming it into the state-dependent inequality like \((G_1x-F(x))(G_2x-F(x))\le 0\) in FTS analysis. Namely, only the minimum slope matrix \(G_1\) and the maximum slope matrix \(G_2\) of the nonlinear regulatory function are used in [10,11,12, 20]. To this end, we will make a breakthrough in the use of nonlinear regulatory function, and construct an LKF with low complexity. The deterministic nonlinear regulator function information will be converted into polytope information based on a linear parameterization analysis method, which will increase the utilization of system information in the analysis process.

The main contributions of this paper can be summarized as follows: (i) the nonlinear DGRNs-RDTs is transformed into an equivalent linear one with time-varying bounded uncertainties based on the proposed linear parameterization method; (ii) a new generalized convex combination lemma is proposed to deal with the multiple bounded uncertainties; (iii) a FTS criterion of DGRNs-RDTs is established.

The remainder of this paper is distributed as follows. In Sect. 2, the problem description and some preliminaries, assumptions, definition are introduced. In Sect. 3, two main results are proposed, i.e., a linear parameterization method and sufficient FTS conditions of DGRNs-RDTs. In Sect. 4, two numerical examples are given to prove the validity of the theoretical results. Some summaries are drawn in Sect. 5.

Problem formulation and preliminaries

Consider the following DGRNs-RDTs:

$$\begin{aligned} \frac{\partial {\tilde{\mathfrak {O}}}_{i}(t, \varepsilon )}{\partial t}= & {} \sum _{\curlyvee =1}^m\frac{\partial }{\partial \varepsilon _{\curlyvee }}\left( K_{i_\curlyvee }\frac{\partial \tilde{\mathfrak {O}}_{i}(t, \varepsilon )}{\partial \varepsilon _\curlyvee }\right) -a_{i}\tilde{\mathfrak {O}}_{i}(t,\varepsilon )\nonumber \\&+\sum _{j=1}^nb_{ij}f_{j}(\tilde{\mathfrak {H}}_{j}(t-\mathfrak {A}(t),\varepsilon ))+q_{i}, \end{aligned}$$
(1a)
$$\begin{aligned} \frac{\partial \tilde{\mathfrak {H}}_{i}(t, \varepsilon )}{\partial t}= & {} \sum _{\curlyvee =1}^m\frac{\partial }{\partial \varepsilon _{\curlyvee }}\left( K^*_{i_\curlyvee }\frac{\partial \tilde{\mathfrak {H}}_{i}(t, \varepsilon )}{\partial \varepsilon _\curlyvee }\right) -c_{i}\tilde{\mathfrak {H}}_{i}(t,\varepsilon )\nonumber \\&+d_{i}\tilde{\mathfrak {O}}_{i}(t-\mathfrak {L}(t),\varepsilon ), \end{aligned}$$
(1b)

where \(i\in \mathfrak {I}_n=\{1,2, \dots , n\}\), \(\tilde{\mathfrak {O}}_{i}(t,\varepsilon )\) and \(\tilde{\mathfrak {H}}_{i}(t,\varepsilon )\) are the i-th node mRNA and protein concentrations at time t, respectively, \(\varepsilon =(\varepsilon _1, \varepsilon _2,\dots ,\varepsilon _m)^{T}\in \varOmega \subset {\mathbb {R}}^{m}\) represents the space variable, \(\varOmega =\{\varepsilon : |\varepsilon _\curlyvee |\le M_\curlyvee , \curlyvee \in \mathfrak {I}_m\}\) is a compact set in \(\mathbb {R}^{n}\) with smooth boundary \(\partial \varOmega \), \(M_\curlyvee >0\) is constant, \(K_{i_\curlyvee }>0\) and \(K^*_{i_\curlyvee }>0\) are the positive definite matrices; \(d_i\) represents the translation rate, \(a_i\) and \(c_i\) are the degradation rates, \(b_{ij}\) is represented as follows:

$$\begin{aligned} b_{ij}= \left\{ \begin{array}{ll} \alpha _{ij}, &{} \hbox {if transcription factor }j\hbox { activates gene }i, \\ 0, &{} \hbox {if there is no link from node }j\hbox { to node }i,\\ -\alpha _{ij}, &{} \hbox {if transcription factor }j\hbox { represses gene } i, \end{array} \right. \end{aligned}$$

\(q_{i}=\varSigma _{j\in \mathfrak {Z}_{i}} \alpha _{ij}\) stands for the basal metabolic rate, \(\mathfrak {Z}_{i}\) represents the set of repressers of gene i, \(f_{j}(s)=(\frac{s}{\beta _{j}})^{\lambda _{j}}/(1+(\frac{s}{\beta _{j}})^{\lambda _{j}})\) denotes the Hill feedback regulation function, where \(\beta _{j}>0\) and \(\lambda _{j}>0\) are the constants; \(\mathfrak {A}(t)\) and \(\mathfrak {L}(t)\) are the time-varying delays and satisfying:

$$\begin{aligned}&0\le \mathfrak {A}(\cdot )\le \tilde{\mathfrak {A}}, \dot{\mathfrak {A}}(\cdot )\le \mu _{\mathfrak {A}}, \ \mathfrak {A}\in \{0,\tilde{\mathfrak {A}}\},\nonumber \\&0\le \mathfrak {L}(\cdot )\le \tilde{\mathfrak {L}}, \dot{\mathfrak {L}}(\cdot )\le \mu _{\mathfrak {L}},\ \mathfrak {L}\in \{0,\tilde{\mathfrak {L}}\}, \end{aligned}$$
(2)

where \(\tilde{\mathfrak {A}}\), \(\tilde{\mathfrak {L}}\), \(\mu _{\mathfrak {A}}\) and \(\mu _{\mathfrak {L}}\) are non-negative real constants.

Let

$$\begin{aligned} \mathfrak {O}^*(\varepsilon )= & {} \mathrm {col}\left( \mathfrak {O}^*_1(\varepsilon ), \ \mathfrak {O}^*_2(\varepsilon ), \ \dots , \ \mathfrak {O}^*_n(\varepsilon )\right) , \\ \mathfrak {H}^*(\varepsilon )= & {} \mathrm {col}(\mathfrak {H}^*_1(\varepsilon ), \ \mathfrak {H}^*_2(\varepsilon ), \dots ,\mathfrak {H}^*_n(\varepsilon )) \end{aligned}$$

be the equilibrium point of DGRNs-RDTs (1). Obviously, we can easily transfer \((\mathfrak {O}^*(\varepsilon ),\mathfrak {H}^*(\varepsilon ))\) to the origin through the following transformations

$$\begin{aligned} \mathfrak {O}_i(t,\varepsilon )= & {} \tilde{\mathfrak {O}}_i(t,\varepsilon )-\mathfrak {O}^*_{i}(\varepsilon ),\\ \mathfrak {H}_i(t,\varepsilon )= & {} \tilde{\mathfrak {H}}_i(t,\varepsilon )-\mathfrak {H}^*_{i}(\varepsilon ), i\in \mathfrak {I}_n. \end{aligned}$$

Then, DGRNs-RDTs (1) is converted into a compact matrix form:

$$\begin{aligned} \frac{\partial \mathfrak {O}(t, \varepsilon )}{\partial t}= & {} \sum _{\curlyvee =1}^m\frac{\partial }{\partial \varepsilon _{\curlyvee }}\left( K_{\curlyvee }\frac{\partial \mathfrak {O}(t, \varepsilon )}{\partial \varepsilon _\curlyvee }\right) -A\mathfrak {O}(t, \varepsilon )\nonumber \\&+BF(\bar{\mathfrak {H}}(t-\mathfrak {A}(t),\varepsilon )), \end{aligned}$$
(3a)
$$\begin{aligned} \frac{\partial \mathfrak {H}(t, \varepsilon )}{\partial t}= & {} \sum _{\curlyvee =1}^m\frac{\partial }{\partial \varepsilon _{\curlyvee }}\left( K^*_{\curlyvee }\frac{\partial \mathfrak {H}(t, \varepsilon )}{\partial \varepsilon _\curlyvee }\right) -C\mathfrak {H}(t,\varepsilon )\nonumber \\&+D\mathfrak {O}(t-\mathfrak {L}(t), \varepsilon ), \end{aligned}$$
(3b)

where \(A=\mathrm {diag}(a_{1},a_{2},\dots ,a_{n}),C = \mathrm {diag}(c_{1},c_{2},\dots ,c_{n}), B=[b_{ij}]\in \mathbb {R}^{n}, D=\mathrm {diag}(d_{1}\), \(\ d_{2}, \ \ \dots , \ \ d_{n}), \ \ \ K_{\curlyvee }=\mathrm {diag}\,(K_{1_\curlyvee }, \ K_{2_\curlyvee }, \ \dots ,\ K_{n_\curlyvee }), \ \ K^*_{\curlyvee }=\mathrm {diag}\,(K^*_{1_\curlyvee }, \ \ K^*_{2_\curlyvee }, \ \dots , K^*_{n_\curlyvee })\), \(\mathfrak {O}(t, \ \varepsilon )=\mathrm {col}(\mathfrak {O}_{1}(t,\varepsilon ), \ \ \mathfrak {O}_{2}(t,\varepsilon ), \ \ \dots \, \ \ \mathfrak {O}_{n}(t,\varepsilon )), \mathfrak {H}(t,\varepsilon )=\mathrm {col}\,(\mathfrak {H}_{1}(t,\varepsilon ), \ \ \mathfrak {H}_{2}(t,\varepsilon )\), \( \dots ,\ \ \mathfrak {H}_{n}\,(t,\varepsilon )),\ \ F(\bar{\mathfrak {\mathfrak {H}}}\,(z,\varepsilon ))=\mathrm {col}\,(F_{1}(\bar{\mathfrak {H}}_1\,(z,\varepsilon )), \ \ F_{2}\,(\bar{\mathfrak {H}}_2\,(z,\varepsilon )), \ \ \dots \ , \ \ F_{n}\,(\bar{\mathfrak {H}}_n\,(z,\varepsilon ))\), \( F_{j}\,(\bar{\mathfrak {H}}_{j}\,(t-\mathfrak {A}(t),\varepsilon )) = f_{j}(\tilde{\mathfrak {H}}_{j}(t-{\mathfrak {A}}(t),\varepsilon ))-f_{j}(\mathfrak {H}^*_{j}(\varepsilon )) .\)

Assumption 1

[12] The DGRNs-RDTs (3) satisfy the following Dirichlet boundary conditions and initial conditions:

$$\begin{aligned}&\mathfrak {O}_i(t,\varepsilon )=0, \varepsilon \in \partial \varOmega ,t\in [-h,+\infty ), \\&\mathfrak {H}_i(t,\varepsilon )=0, \varepsilon \in \partial \varOmega ,t\in [-h,+\infty ), i\in \mathfrak {I}_n,\\&\mathfrak {O}_i(t,\varepsilon )=\phi _i(t,\varepsilon ), \varepsilon \in \partial \varOmega ,t\in [-h,0),\\&\mathfrak {H}_i(t,\varepsilon )=\varphi _i(t,\varepsilon ), \varepsilon \in \partial \varOmega ,t\in [-h,0), \end{aligned}$$

where \(h=\max \{\tilde{\mathfrak {A}},\tilde{\mathfrak {L}}\}\), \(\phi (t,\varepsilon )\), \(\varphi (t,\varepsilon )\in C^{1}([-h,0]\times \varOmega ,\mathbb {R}^n)\), \(C^1([-h,0]\times \varOmega ,\mathbb {R}^n)\) is a continuous function in Banach space , and the norm on this map is defined as

$$\begin{aligned} \Vert y(t,\varepsilon )\Vert _{h}= & {} \max \left\{ \sup \limits _{t\in [-h,0]}\Vert y(t,\varepsilon )\Vert ,\sup \limits _{t\in [-d,0]}\left\| \frac{\partial y(t,\varepsilon )}{\partial t}\right\| ,\right. \\&\quad \left. \sup \limits _{t\in [-h,0]}\left\| \frac{\partial y(t,\varepsilon )}{\partial \varepsilon _\curlyvee }\right\| \right\} . \end{aligned}$$

Assumption 2

The activation function \(f_{j}(\cdot )\) is a monotonically nondecreasing Hill feedback regulation function, and satisfies the peculiar formulas (see [26, 27]):

$$\begin{aligned} f_{j}(0)=0,\ g_{j1}\le {\frac{f_{j}(\chi _{1})-f_{j}(\chi _{2})}{\chi _{1}-\chi _{2}}}\le {g_{j2}} \end{aligned}$$
(4)

for any distinct \(\chi _{1}\), \(\chi _{2}\) \(\in \) \(\mathbb {R}\) , where \(g_{j1}\) and \(g_{j2}\) are nonnegative constants.

Definition 1

[28] For given positive constants \(c_1\), \(c_2\) and T, the trivial solution of DGRNs-RDTs (3) is finite-time-stable, if

$$\begin{aligned}&\Vert \phi (t,\varepsilon )\Vert ^{2}_{h}+\Vert \varphi (t,\varepsilon )\Vert ^{2}_{h}\le c_1,\\&\quad \Rightarrow \Vert \mathfrak {O}(t,\varepsilon )\Vert ^{2}+\Vert \mathfrak {H}(t,\varepsilon )\Vert ^{2}\le c_2, \end{aligned}$$

for

$$\begin{aligned} \Vert \tilde{y}(t,\varepsilon )\Vert= & {} \left( \int ^{}_{\varOmega }\tilde{y}^{T}(t,\varepsilon )\tilde{y}(t,\varepsilon )\text {d}\varepsilon \right) ^{1/2}, \tilde{y}(t,\varepsilon )\\&\quad \in \{\mathfrak {O}(t,\varepsilon ),\mathfrak {H}(t,\varepsilon )\}, t\in [0,T]. \end{aligned}$$

Remark 1

Under the assumptions of the Dirichlet boundary conditions and the Lipschitz conditions of \(f_j(\cdot )\), the existence of the equilibrium point \((\mathfrak {O}^*(\varepsilon ),\mathfrak {H}^*(\varepsilon ))\) can be easily derived by using the fixed point theory (see, [29, 30]).

Remark 2

Under normal circumstances, the concentrations inside and outside of the cell are inconsistent. To more meaningfully and truthfully study the problem of GRNs, it is necessary to consider the influence of concentration changes during the movement of genes. At present, many excellent results have been proposed on DGRNs-RDTs [10,11,12, 20, 31, 32]. This paper studies the DGRNs-RDTs (1), which consider the gradient of mRNA and protein concentration like the terms of \(\frac{\partial }{\partial \varepsilon _{\curlyvee }}(K_{i_\curlyvee }\frac{\partial \tilde{\mathfrak {O}}_{i}(t, \varepsilon )}{\partial \varepsilon _\curlyvee })\) and \(\frac{\partial }{\partial \varepsilon _{\curlyvee }}(K^*_{i_\curlyvee }\frac{\partial \tilde{\mathfrak {H}}_{i}(t, \varepsilon )}{\partial \varepsilon _\curlyvee })\). In addition, the lower boundary \(g_{j1}\) of nonlinear regulation function slope property is defined as 0 in [11, 12, 20, 31, 32]. In this paper, the regulation function slope property is defined to satisfy the condition (4) to comprehensively consider the stability problem.

Main results

In this section, the nonlinear DGRNs-RDTs (3) is translated into an equivalent linear one with bounded uncertainties, and a new generalized convex combination lemma is proposed. Then, FTS criterion of the new linear model is established under Dirichlet boundary conditions in terms of LMIs.

A linear parameterization approach

In order to dispose the nonlinearity in DGRNs-RDTs (3), we propose the following linear parameterization method based on the Lagrange’s mean-value theorem (LMVT)

By using the LMVT, there exist variable \(\xi _{j}(t,\varepsilon )\ge 0\), between \(\tilde{\mathfrak {H}}_{j}(t-\mathfrak {L}(t),\varepsilon )\) and \(\mathfrak {H}^{*}_{j}(\varepsilon )\), \(j\in \mathfrak {I}_n\), such that

$$\begin{aligned}&F_j(\bar{\mathfrak {H}}(t-\mathfrak {A}(t),\varepsilon ))\nonumber \\&\quad =f'_j(\xi _{j}(t,\varepsilon ))(\tilde{\mathfrak {H}}_{j}(t-\mathfrak {L}(t),\varepsilon )-\mathfrak {H}^{*}_{j}(\varepsilon ))\nonumber \\&\quad =f'_j(\xi _{j}(t,\varepsilon ))\mathfrak {H}_{j}(t-\mathfrak {L}(t),\varepsilon )\nonumber \\&\quad =\theta _{j}(t,\varepsilon )\mathfrak {H}_{j}(t-\mathfrak {L}(t),\varepsilon ), \end{aligned}$$
(5)

where \(f'_j(\xi _{j}(t,\varepsilon ))=\theta _{j}(t,\varepsilon )\).

According to Assumption 1 and the definition of function derivative, it follows that \(g_{j1}\le \theta _{j}(t,\varepsilon )\le g_{j2}\) for all \(t\ge 0\) and \(j\in \mathfrak {I}_n\). These variables \(\theta _{j}(t,\varepsilon )\) will be defined as uncertainties in the rest of this paper.

For simplicity of notations, we define \(\theta _{\varepsilon _{j}}(t)\), \(\mathfrak {O}_\varepsilon (t)\) and \(\mathfrak {H}_\varepsilon (t)\) to replace \(\theta _{j}(t,\varepsilon )\), \(\mathfrak {O}(t,\varepsilon )\) and \(\mathfrak {H}(t,\varepsilon )\). Then, we can transform DGRNs-RDTs (3) to

$$\begin{aligned} \frac{\partial \mathfrak {O}_\varepsilon (t)}{\partial t}= & {} \sum _{\curlyvee =1}^m\frac{\partial }{\partial \varepsilon _{\curlyvee }}\left( K_{\curlyvee }\frac{\partial \mathfrak {O}_\varepsilon (t)}{\partial \varepsilon _\curlyvee }\right) \nonumber \\&-A\mathfrak {O}_\varepsilon (t)+B\theta _\varepsilon (t)\mathfrak {H}_\varepsilon (t-\mathfrak {A}(t)), \end{aligned}$$
(6a)
$$\begin{aligned} \frac{\partial \mathfrak {H}_\varepsilon (t)}{\partial t}= & {} \sum _{\curlyvee =1}^m\frac{\partial }{\partial \varepsilon _{\curlyvee }}\left( K^*_{\curlyvee }\frac{\partial \mathfrak {H}_\varepsilon (t)}{\partial \varepsilon _\curlyvee }\right) -C\mathfrak {H}_\varepsilon (t)\nonumber \\&+D\mathfrak {O}_\varepsilon (t-\mathfrak {L}(t)), \end{aligned}$$
(6b)

where \(\theta _\varepsilon (t)= \mathrm {diag}(\theta _{\varepsilon _{1}}(t), \theta _{\varepsilon _{2}}(t), \dots , \theta _{\varepsilon _{n}}(t))\).

Based on the linear parameterization method above, the nonlinear GRNs is transformed into an equivalent linear one with uncertain forms.

Remark 3

Linearization refers to finding the linear approximation function of the nonlinear function at the fixed point or equilibrium point \(x_0\). The most widely used Linearization method is the Taylor series expansion, that is, the Taylor series expansion is performed at fixed point \(x_0\) and the higher-order terms are ignored to obtain a linear function with increment as the variable like \(f(x)-f(x_0)=(\frac{d(f(x))}{dx})_{x_0}(x-x_0)\) in [33]. This method requires the variation range of the variable near the fixed point \(x_0\) is small, and the resulting linear function changes with the choice of fixed point. The linear parameterization method above is to transform the nonlinear regulation function into an equivalent linear uncertainty function that satisfies the principle of superposition. In addition, the linear parameterization method is obtained by using the information of equilibrium point, but there is no requirement for the changes of state variable near the equilibrium point. Then, the linear parameterization method proposed is not a strict linearization method, but it is more accurate to convert the nonlinear function into a linear one, and the method can better reflect the slope information of the nonlinear function. The proposed linear parameterization method is the main highlight and key point of this paper, and promotes the subsequent FTS analysis.

Remark 4

Improving the utilization of system information can effectively reduce the conservativeness. As shown in [25], the activation function is divided into two parts to improve the utilization of its slope information, thereby reducing the conservativeness of the stability criterion. In this paper, in order to increase the utilization of system information, the nonlinear regulation function is transformed into equation (5) based on the linear parameterization method. That is, the slope information of the regulation function is converted into the uncertainties boundary information. Then, the \(2^n\) uncertainties boundary information matrices like \(G = \mathrm {diag}(g_{1s_j},g_{2s_j},\dots ,g_{ns_j}) (s_j\in \mathfrak {I}_2)\) will be considered to replace the upper and lower bound matrices in [10,11,12, 25]. Therefore, based on the linear parameterization method, a more accurate feasible region of the FTS conditions can be obtained by using the above \(2^n\) boundary information matrices.

Lemma 1

For a matrix \(\sigma = \left\{ \mathrm {diag}(\tilde{\sigma }_1,\tilde{\sigma }_2,\dots ,\tilde{\sigma }_n):u_{j1}\le \tilde{\sigma }_j\le u_{j2}, \ j\in \mathfrak {I}_n\right\} \) and any appropriate dimensional constant matrices \(\tilde{A}\), \(\tilde{B}\) and \(\tilde{C}\), the following inequality holds:

$$\begin{aligned} \tilde{A}+\tilde{B}^{T}\sigma \tilde{C}<0,\ if \ and \ only \ if,\ \tilde{A}+\tilde{B}^{T}U_{s_1,s_2, \dots , s_n}\tilde{C}<0, \end{aligned}$$

where \(U_{s_1,s_2, \dots , s_n}=\mathrm {diag}(u_{1s_j},u_{2s_j},\dots ,u_{ns_j})\), \(s_j\in \mathfrak {I}_2\). That is, \(U_{s_1,s_2, \dots , s_n}\) represents \(2^n\) matrices formed by the random combination of the upper and lower boundaries of \(\tilde{\sigma }_j\) in the matrix \(\sigma \).

Proof

The above lemma is equivalent to

$$\begin{aligned} \tilde{A}+\sum \limits _{j=1}^n \tilde{B}^{T}\sigma _j\tilde{C}<0,j\in \mathfrak {I}_n \end{aligned}$$
(7)

if and only if

$$\begin{aligned} \varOmega _{s_{1},s_{2},\dots ,s_{n}} :=\tilde{A}+\sum \limits _{j=1}^n\tilde{B}^{T}U_{js_j}\tilde{C}<0,s_j\in \{1,2\}, \ j\in \mathfrak {I}_n,\nonumber \\ \end{aligned}$$
(8)

where \(\sigma _{j}\) and \(U_{js_j}\) are diagonal matrix belong to \(R^{n\times n}\) with \(\tilde{\sigma }_j\) and \(u_{js_j}\) in the j-th site and 0 elsewhere, respectively.

The “only if” part follows immediately derived from \(u_{j1}\le \tilde{\sigma }_j\le u_{j2},j\in \mathfrak {I}_n\). Now we show the “if” part.

According to the convex combination lemma [34], and \(u_{j1}\le \tilde{\sigma }_j\le u_{j2}\), there exist positive \(\mathfrak {X}_{j1}\) and \(\mathfrak {X}_{j2}\) satisfying \(\mathfrak {X}_{j1}+\mathfrak {X}_{j2}=1\) such that \(\tilde{\sigma }_j=\mathfrak {X}_{j1}u_{j1}+\mathfrak {X}_{j2}u_{j2}\), \(j\in \mathfrak {I}_n\).

The left and right sides of inequality (8) are multiplied by \(\mathfrak {X}_{11}\) and \(\mathfrak {X}_{12}\) for \(s_1=1\) and \(s_1=2\), respectively. Then, we can derive \(\varTheta _{s_{2},\dots ,s_{n}} :=\mathfrak {X}_{11}\varOmega _{1,s_{2} ,\dots , s_{n}}+\mathfrak {X}_{12}\varOmega _{2, s_{2} , ..., s_{n}}<0\), that is,

$$\begin{aligned} \varTheta _{s_{2},\dots ,s_{n}}&=\mathfrak {X}_{11}(\tilde{A}+\sum \limits _{j=2}^n\tilde{B}^{T}U_{js_j}\tilde{C}+\tilde{B}^{T}U_{11}\tilde{C})\\&\quad +\mathfrak {X}_{12}\left( \tilde{A}+\sum \limits _{j=2}^n\tilde{B}^{T}U_{js_j}\tilde{C}+\tilde{B}^{T}U_{12}\tilde{C}\right) \\&=\tilde{A}+\tilde{B}^{T}\sigma _1\tilde{C} +\sum \limits _{j=2}^n\tilde{B}^{T}U_{js_j}\tilde{C} <0. \end{aligned}$$

Likewise, we can get \(\varTheta _{s_{3},\dots ,s_{n}} :=\mathfrak {X}_{21}\varOmega _{1,s_{3} ,\dots , s_{n}}+\mathfrak {X}_{22}\varOmega _{2,s_{3} ,..., s_{n}}<0\), that is,

$$\begin{aligned} \varTheta _{s_{3},\dots ,s_{n}}&=\mathfrak {X}_{21}\left( \tilde{A}+\tilde{B}^{T}\sigma _1\tilde{C} +\sum \limits _{j=3}^n\tilde{B}^{T}U_{js_j}\tilde{C} +\tilde{B}^{T}U_{21}\tilde{C}\right) \\&\quad +\mathfrak {X}_{22}\left( \tilde{A}+\tilde{B}^{T}\sigma _1\tilde{C} +\sum \limits _{j=3}^n\tilde{B}^{T}U_{js_j}\tilde{C}\right. \\&\quad \left. +\tilde{B}^{T}U_{22}\tilde{C}\right) \\&=\tilde{A}+\sum \limits _{j=1}^2\tilde{B}^{T}\sigma _j\tilde{C} +\sum \limits _{j=3}^n\tilde{B}^{T}U_{js_j}\tilde{C} <0. \end{aligned}$$

Continuous calculation based on the above algorithm, and ultimately we can obtain \(\tilde{A}+\sum \nolimits _{j=1}^n \tilde{B}^{T}\sigma _j\tilde{C}<0\), the proof is completed. \(\square \)

Remark 5

The lemma above is a new result of convex combination with multiple bounded uncertainty parameters. Specifically, the convex combination lemma in [34] is a special case of above lemma, for \(j=1\), and \(\mathfrak {X}_{j1}\), \(\tilde{B}^{T}U_{j1}\tilde{C}\), \(\tilde{B}^{T}U_{j2}\tilde{C}\) are defined as \(\alpha \), \(X_1\), \(X_2\), respectively. That is, \(\tilde{A}+\alpha X_1+(1-\alpha )X_2<0\) if and only if \(\tilde{A}+ X_1<0\) and \(\tilde{A}+X_2<0\). Therefore, the lemma above generalizes the corresponding results in [34] to a situation with n bounded uncertainties.

FTS analysis for DGRNs-RDTs

For notational ease, set

$$\begin{aligned} \eta _\varepsilon (t)&=\mathrm {col}\left( \mathfrak {O}_\varepsilon (t)\,\mathfrak {O}_\varepsilon (t-\tilde{\mathfrak {A}})\,\mathfrak {O}_\varepsilon (t-\mathfrak {A}(t))\,\frac{1}{\tilde{\mathfrak {A}}-\mathfrak {A}(t)}\right. \\&\qquad \int ^{t-\mathfrak {A}(t)}_{t-\tilde{\mathfrak {A}}}\mathfrak {O}_\varepsilon (s)\mathrm {d}s \ \mathfrak {H}_\varepsilon \ (t-\tilde{\mathfrak {L}}) \\&\qquad \mathfrak {H}_\varepsilon (t-\mathfrak {L}(t)) \ \ \ \,\frac{\partial \mathfrak {O}_\varepsilon (t)}{\partial t} \\&\qquad \frac{\partial \mathfrak {H}_\varepsilon (t)}{\partial t}\ \ \ \ \,\mathfrak {H}_\varepsilon (t)\ \ \ \ \frac{1}{\mathfrak {A}(t)} \,\int ^{t}_{t-\mathfrak {A}(t)} \,\mathfrak {O}_\varepsilon (s)\mathrm {d}s \\&\qquad \frac{1}{(\tilde{\mathfrak {A}}-\mathfrak {A}(t))^2}\int ^{t-\mathfrak {A}(t)}_{t-\tilde{\mathfrak {A}}}\int ^{t-\mathfrak {A}(t)}_{t-\alpha }\mathfrak {O}_\varepsilon (s)\mathrm {d}s\mathrm {d}\alpha \\&\qquad \frac{1}{\mathfrak {A}^2(t)}\int ^{t}_{t-\mathfrak {A}(t)}\int ^{t}_{\alpha }\mathfrak {O}_\varepsilon (s)\mathrm {d}s\mathrm {d}\alpha \\&\qquad \left. \frac{1}{\tilde{\mathfrak {L}}-\mathfrak {L}(t)}\int ^{t-\mathfrak {L}(t)}_{t-\tilde{\mathfrak {L}}}\mathfrak {H}_\varepsilon (s)\mathrm {d}s \right. \\&\qquad \frac{1}{(\tilde{\mathfrak {L}}-\mathfrak {L}(t))^2}\int ^{t-\mathfrak {L}(t)}_{t-\tilde{\mathfrak {L}}}\int ^{t-\mathfrak {L}(t)}_{\alpha }\mathfrak {H}_\varepsilon (s)\mathrm {d}s\mathrm {d}\alpha \\&\qquad \left. \frac{1}{\mathfrak {L}(t)}\int ^{t}_{t-\mathfrak {L}(t)}\mathfrak {H}_\varepsilon (s)\mathrm {d}s\quad \frac{1}{\mathfrak {L}^2(t)}\int ^{t}_{t-\mathfrak {L}(t)}\int ^{t}_{\alpha }\mathfrak {H}_\varepsilon (s)\mathrm {d}s\mathrm {d}\alpha \right) ,\\&l_i={\text {col}}(0_{(i-1)n\times n},\ I_n, \ 0_{(16-i)n\times n}),i\in \mathfrak {I}_{16},\\&\varUpsilon _\flat =[\varGamma _\flat \ \varGamma _{\flat +1}](\flat \in \mathfrak {I}_2)\\&\varGamma _1=[l_3-l_2 \ l_3+l_2-2l_{4} \ l_3-l_2+6l_{4}-12l_{11}],\\&\varGamma _2=[l_1-l_3 \ l_1+l_3-2l_{10} \ l_1-l_3+6l_{10}-12l_{12}],\\&\varGamma _3=[l_6-l_5 \ l_6+l_5-2l_{13} \ l_6-l_5+6l_{13}-12l_{14}],\\&\varGamma _4=[l_{9}-l_6 \ l_{9}+l_6-2l_{15} \ l_{9}-l_6+6l_{15}-12l_{16}],\\&\varGamma _5=[l_1-l_{10} \ l_1+2l_{10}-6l_{12}], \\&\varGamma _6=[l_3-l_{4} \ l_3+2l_{4}-6l_{11}],\\&\varGamma _7=[l_{9}-l_{15} \ l_{9}+2l_{15}-6l_{16}], \\&\varGamma _8=[l_6-l_{13} \ l_6+2l_{13}-6l_{14}]. \end{aligned}$$

Theorem 1

For given constants \(\tilde{\mathfrak {A}}\), \(\tilde{\mathfrak {L}}\), \(\mu _{\mathfrak {A}}\) and \(\mu _{\mathfrak {L}}\) satisfying (2), and positive scalars \(\rho \), \(c_1\), \(c_2\) and T, the DGRNs-RDTs (6) is finite-time-stable under Assumption 1 and 2, if there exist real symmetrical positive definite matrices \(Q_\iota \), diagonal positive definite matrices \(J_\varsigma \), \(Y_\varsigma \), and appropriate dimensional matrices \(\hat{H}_\varsigma \) \((\iota \in \mathfrak {I}_{10}, \varsigma \in \mathfrak {I}_2)\) such that the following LMIs hold:

$$\begin{aligned}&\varPi _{1_{s_1,s_2, \dots , s_n}}(\mathfrak {A},\mathfrak {L}) :=\varPhi _{1_{s_1,s_2, \dots , s_n}}\nonumber \\&\quad +\sum _{\hbar =2}^3\varPhi _{\hbar }+\varPhi _4(\mathfrak {A},\mathfrak {L})+\varPhi _5(\mathfrak {A},\mathfrak {L}){-}\rho l_1J_1l^{T}_1\nonumber \\&\quad -\rho l_{9}J_2l^{T}_{9}<0,s_j\in \mathfrak {I}_2 \end{aligned}$$
(9)
$$\begin{aligned}&\varPi _2:=c_1\mathrm {e}^{\rho T}(\lambda _1+\lambda _2)-c_2\lambda _{min}(J)\le 0, \ \varTheta _\varsigma \ge 0, \end{aligned}$$
(10)

where

$$\begin{aligned} \varPhi _{1_{s_1,s_2, \dots , s_n}}&=\varPhi _{11_{s_1,s_2,\dots , s_n}}+\varPhi _{11_{s_1,s_2, \dots , s_n}}'+\varPhi _{12}, \varPhi _{11_{s_1,s_2, \dots , s_n}}\\&=l_{1}J_1BG_{s_1,s_2, \dots , s_n}l^{T}_{6}+l_7Y_1B\\&\qquad \times G_{s_1,s_2, \dots ,s_n}l^{T}_{6}, \\&\varPhi _{12}=2l_1\left( -\frac{\pi ^{2}}{4}J_1K_M-J_1A\right) l^{T}_1\\&\qquad +2l_{9}\left( -\frac{\pi ^{2}}{4}J_2K^{*}_{M}-J_2C\right) l^{T}_{9}\\&\qquad -2(l_7Y_1l^{T}_7 +l_8Y_2l^{T}_8) -l_7Y_1Al^{T}_1-l_1AY_1l^{T}_7\\&\qquad +l_{9}J_2Dl^{T}_3+l_3DJ_2l^{T}_{9}-l_8Y_2Cl^{T}_{9}-l_{9}CY_2l^{T}_8 \\&\qquad +l_8Y_2Dl^{T}_3+l_3DY_2l^{T}_8,\\&\varPhi _2=l_1(Q_1+Q_2)l^{T}_1+l_{9}(Q_3+Q_4)l^{T}_{9}-l_{2}Q_2l^{T}_{2}\\&\qquad +(\mu _{\mathfrak {A}}-1)l_3Q_1l^{T}_3 -l_{5}Q_4l^{T}_{5}\\&\qquad +(\mu _{\mathfrak {L}}-1)l_6Q_3l^{T}_6,\,\varPhi _3=\tilde{\mathfrak {A}}l_7Q_5l^{T}_7+\tilde{\mathfrak {L}}l_8Q_6l^{T}_8\\&\qquad -\varUpsilon _1\varTheta _1\varUpsilon ^{T}_1-\varUpsilon _2\varTheta _2\varUpsilon ^{T}_2,\\&\varPhi _{4}(\mathfrak {A},\mathfrak {L})=\varPhi _{41}+\varPhi _{42}(\mathfrak {A},\mathfrak {L}), \\&\varPhi _{41}=\frac{\tilde{\mathfrak {A}}^{2}}{2}l_7\tilde{Q}_7l^{T}_7+\frac{\tilde{\mathfrak {L}}^{2}}{2}l_8\tilde{Q}_8l^{T}_8,\\&\varPhi _{42}(\mathfrak {A},\mathfrak {L})=-\varGamma _5\tilde{Q}_7\varGamma ^{T}_5-\varGamma _6\tilde{Q}_7\varGamma ^{T}_6\\&\qquad -\frac{\tilde{\mathfrak {A}}- \mathfrak {A}}{\tilde{\mathfrak {A}}}\varGamma _2\hat{Q}_7\varGamma ^{T}_2-\varGamma _7\tilde{Q}_8\varGamma ^{T}_7-\varGamma _8\tilde{Q}_8\varGamma ^{T}_8\\&\qquad -\frac{\tilde{\mathfrak {L}}-\mathfrak {L}}{\tilde{\mathfrak {L}}}\varGamma _4\hat{Q}_8\varGamma ^{T}_4,\\&\varPhi _{5}(\mathfrak {A},\mathfrak {L})=\frac{\tilde{\mathfrak {A}}^{3}}{6}l_7Q_9l^{T}_7+\frac{\tilde{\mathfrak {L}}^{3}}{6}l_8Q_{10}l^{T}_8 \\&\qquad -(\tilde{\mathfrak {A}}-\mathfrak {A})\varGamma _5\tilde{Q}_9\tilde{\varGamma }_5-(\tilde{\mathfrak {L}}-\mathfrak {L})\varGamma _8\tilde{Q}_{10}\tilde{\varGamma }_8\\&\qquad -\frac{3\mathfrak {A}}{2}(l_1-2l_{12})Q_9(l_1-2l_{12})^{T}\\&\qquad -\frac{3(\tilde{\mathfrak {A}}-\mathfrak {A})}{2}(l_3-2l_{11})Q_9(l_3-2l_{11})^{T}\\&\qquad -\frac{3\mathfrak {L}}{2}(l_{9}-2l_{16})Q_{10}(l_{9}-2l_{16})^{T}\\&\qquad -\frac{3(\tilde{\mathfrak {L}}-\mathfrak {L})}{2}(l_6-2l_{14})Q_{10}(l_6-2l_{14})^{T},\\&K_{M}=\mathrm {diag}\left( \sum _{\curlyvee =1}^m\frac{K_{1_\curlyvee }}{M^{2}_\curlyvee }, \sum _{\curlyvee =1}^m\frac{K_{2_\curlyvee }}{M^{2}_\curlyvee }, \dots \sum _{\curlyvee =1}^m\frac{K_{n_k}}{M^{2}_\curlyvee }\right) ,\, \, \\&K^{*}_{M}=\mathrm {diag}\left( \sum _{\curlyvee =1}^m\frac{K^{*}_{1_\curlyvee }}{M^{2}_\curlyvee }, \sum _{\curlyvee =1}^m\frac{K^{*}_{2_\curlyvee }}{M^{2}_\curlyvee }, \dots \right. \\&\qquad \left. \sum _{\curlyvee =1}^m\frac{K^{*}_{n_\curlyvee }}{M^{2}_\curlyvee }\right) , J=\mathrm {diag}(J_1,\ J_2),\, \, \\&\qquad \quad \tilde{Q}_{6+i}=\mathrm {diag}(2Q_{6+i}, 4Q_{6+i}),i\in \mathfrak {I}_4,\\&\qquad {\hat{Q}_{6+\mathfrak {j}}=\mathrm {diag}(Q_{6+\mathfrak {j}}, 3Q_{6+\mathfrak {j}},5Q_{6+\mathfrak {j}})},\\&\qquad \quad \varTheta _\varsigma = \begin{bmatrix} \hat{Q}_{4+\varsigma } &{}\hat{H}_{\varsigma }\\ \hat{H}_{\varsigma }^{T} &{}\hat{Q}_{4+\varsigma }\end{bmatrix}, {\mathfrak {j}\in \mathfrak {I}_2},\\&\lambda _{1}=\lambda _{max}(J_1)+\tilde{\mathfrak {A}}\lambda _{max}(Q_1)+\tilde{\mathfrak {A}}\lambda _{max}(Q_2)\\&\qquad +\frac{1}{6}\tilde{\mathfrak {A}}^{3}\lambda _{max}(Q_7)+\sum _{\curlyvee =1}^m\lambda _{max}(Y_1)\lambda _{max}(K_{\curlyvee })\\&\qquad +\frac{1}{2}\tilde{\mathfrak {A}}^{3}\lambda _{max}(Q_5) +\frac{1}{24}\tilde{\mathfrak {A}}^{4}\lambda _{max}(Q_9), \\&G_{s_1,s_2, \dots , s_n}=\mathrm {diag}(g_{1s_j},g_{2s_j},\dots ,g_{ns_j}), \lambda _{2}\\&\qquad =\lambda _{max}(J_2)+\tilde{\mathfrak {L}}\lambda _{max}(Q_3)+\tilde{\mathfrak {L}}\lambda _{max}(Q_4)\\&\qquad +\frac{1}{6}\tilde{\mathfrak {L}}^{3}\lambda _{max}(Q_8)+\sum _{\curlyvee =1}^m\lambda _{max}(Y_2)\lambda _{max}(K^{*}_{\curlyvee }) \\&\qquad +\frac{1}{2}\tilde{\mathfrak {L}}^{3}\lambda _{max}(Q_6)+\frac{1}{24}\tilde{\mathfrak {L}}^{4}\lambda _{max}(Q_{10}). \end{aligned}$$

Proof

Define an LKF candidate for DGRNs-RDTs (6) as:

$$\begin{aligned} V(t, \mathfrak {O}, \mathfrak {H})=\sum _{i=1}^5V_{i}(t, \mathfrak {O}, \mathfrak {H}), \end{aligned}$$

where

$$\begin{aligned} V_{1}(t, \mathfrak {O}, \mathfrak {H})&= \int ^{}_{\varOmega }\mathfrak {O}^{T}_\varepsilon (t)J_{1}\mathfrak {O}_\varepsilon (t)\mathrm {d}\varepsilon +\int ^{}_{\varOmega }\mathfrak {H}^{T}_\varepsilon (t)J_{2}\mathfrak {H}_\varepsilon (t)\mathrm {d}\varepsilon \\&\quad +\sum _{\curlyvee =1}^m\int ^{}_{\varOmega }\frac{\partial \mathfrak {O}^{T}_\varepsilon (t)}{\partial \varepsilon _\curlyvee }Y_1 K_\curlyvee \\&\quad \times \frac{\partial \mathfrak {O}_\varepsilon (t)}{\partial \varepsilon _\curlyvee }\mathrm {d}\varepsilon +\sum _{\curlyvee =1}^m\int ^{}_{\varOmega }\frac{\partial \mathfrak {H}^{T}_\varepsilon (t)}{\partial \varepsilon _\curlyvee }Y_2K^{*}_\curlyvee \frac{\partial \mathfrak {H}_\varepsilon (t)}{\partial \varepsilon _\curlyvee }\mathrm {d}\varepsilon ,\\ V_{2}(t, \mathfrak {O}, \mathfrak {H})&=\int ^{}_{\varOmega }\int ^{t}_{t-\mathfrak {A}(t)}\mathfrak {O}^{T}_\varepsilon (s)Q_{1}\mathfrak {O}_\varepsilon (s)\mathrm {d}s\mathrm {d}\varepsilon \\&\quad +\int ^{}_{\varOmega }\int ^{t}_{t-\tilde{\mathfrak {A}}}\mathfrak {O}^{T}_\varepsilon (s)Q_{2}\mathfrak {O}_\varepsilon (s)\mathrm {d}s\mathrm {d}\varepsilon \\&\quad +\int ^{}_{\varOmega }\int ^{t}_{t-\mathfrak {L}(t)}\mathfrak {H}^{T}_\varepsilon (s)Q_{3}\mathfrak {H}_\varepsilon (s)\mathrm {d}s\mathrm {d}\varepsilon \\&\quad +\int ^{}_{\varOmega }\int ^{t}_{t-\tilde{\mathfrak {L}}}\mathfrak {H}^{T}_\varepsilon (s)Q_{4}\mathfrak {H}_\varepsilon (s)\mathrm {d}s\mathrm {d}\varepsilon ,\\ V_{3}(t, \mathfrak {O}, \mathfrak {H})&=\tilde{\mathfrak {A}}\int ^{}_{\varOmega }\int ^{0}_{-\tilde{\mathfrak {A}}}\int ^{t}_{t+\nu }\frac{\partial \mathfrak {O}^{T}_\varepsilon (s)}{\partial s}Q_5\frac{\partial \mathfrak {O}_\varepsilon (s)}{\partial s}\mathrm {d}s\mathrm {d}\nu \mathrm {d}\varepsilon \\&\quad +\tilde{\mathfrak {L}}\int ^{}_{\varOmega }\int ^{0}_{-\tilde{\mathfrak {L}}}\int ^{t}_{t+{\nu }}\frac{\partial \mathfrak {H}^{T}_\varepsilon (s)}{\partial s}Q_6\frac{\partial \mathfrak {H}_\varepsilon (s)}{\partial s}\mathrm {d}s\mathrm {d}\nu \mathrm {d}\varepsilon ,\\ V_{4}(t, \mathfrak {O}, \mathfrak {H})&=\int ^{}_{\varOmega }\int ^{0}_{-\tilde{\mathfrak {A}}}\int ^{0}_{\lambda }\int ^{t}_{t+\nu }\frac{\partial \mathfrak {O}^{T}_\varepsilon (s)}{\partial s}Q_7\frac{\partial \mathfrak {O}_\varepsilon (s)}{\partial s}\mathrm {d}s\mathrm {d}\nu \mathrm {d}\lambda \mathrm {d}\varepsilon \\&\quad +\int ^{}_{\varOmega }\int ^{0}_{-\tilde{\mathfrak {L}}}\int ^{0}_{\lambda }\int ^{t}_{t+\nu }\frac{\partial \mathfrak {H}^{T}_\varepsilon (s)}{\partial s}Q_8\frac{\partial \mathfrak {H}_\varepsilon (s)}{\partial s}\mathrm {d}s\mathrm {d}\nu \mathrm {d}\lambda \mathrm {d}\varepsilon ,\\ V_{5}(t, \mathfrak {O}, \mathfrak {H})&=\int ^{}_{\varOmega }\int ^{0}_{-\tilde{\mathfrak {A}}}\int ^{0}_{\lambda }\int ^{0}_{\alpha }\int ^{t}_{t+\nu }\frac{\partial \mathfrak {O}^{T}_\varepsilon (s)}{\partial s}\\&\qquad Q_9\frac{\partial \mathfrak {O}_\varepsilon (s)}{\partial s}\mathrm {d}s\mathrm {d}\nu \mathrm {d}\alpha \mathrm {d}\lambda \mathrm {d}\varepsilon \\&\quad +\int ^{}_{\varOmega }\int ^{0}_{-\tilde{\mathfrak {L}}}\int ^{0}_{\lambda }\int ^{0}_{\alpha }\int ^{t}_{t+\nu }\nonumber \\&\qquad \frac{\partial \mathfrak {H}^{T}_\varepsilon (s)}{\partial s}Q_{10}\frac{\partial \mathfrak {H}_\varepsilon (s)}{\partial s}\mathrm {d}s\mathrm {d}\nu \mathrm {d}\alpha \mathrm {d}\lambda \mathrm {d}\varepsilon . \end{aligned}$$

Computing the derivative of\(V(t, {\mathfrak {O}, \mathfrak {H}})\) along the trajectories of DGRNs-RDTs (6), then

$$\begin{aligned} \frac{\partial V(t, {\mathfrak {O},\mathfrak {H}})}{\partial t}=\sum _{i=1}^5\frac{\partial V_{i}(t, \mathfrak {O}, \mathfrak {H})}{\partial t}, \end{aligned}$$
(11)

with the specific differentials as follow:

$$\begin{aligned} \frac{\partial V_{1}(t, \mathfrak {O}, \mathfrak {H})}{\partial t}&=2\int ^{}_{\varOmega }\mathfrak {O}^{T}_\varepsilon (t)J_{1}\left( \sum _{\curlyvee =1}^m\frac{\partial }{\partial \varepsilon _{\curlyvee }}(K_{\curlyvee }\frac{\partial \mathfrak {O}_\varepsilon (t)}{\partial \varepsilon _\curlyvee }\right) \nonumber \\&\quad -A\mathfrak {O}_\varepsilon (t)+B\theta _\varepsilon (t)\mathfrak {H}_\varepsilon (t-\mathfrak {L}(t)))\mathrm {d}\varepsilon \nonumber \\&\quad +2\int ^{}_{\varOmega }\mathfrak {H}^{T}_\varepsilon (t)J_{2}\left( \sum _{\curlyvee =1}^m\frac{\partial }{\partial \varepsilon _{\curlyvee }}(K^*_{\curlyvee }\frac{\partial \mathfrak {H}_\varepsilon (t)}{\partial \varepsilon _\curlyvee }\right) \nonumber \\&\quad -C\mathfrak {H}_\varepsilon (t)+D\mathfrak {O}_\varepsilon (t-\mathfrak {A}(t)))\mathrm {d}\varepsilon \nonumber \\&\quad +2\sum _{\curlyvee =1}^m\int ^{}_{\varOmega }\frac{\partial \mathfrak {O}^{T}_\varepsilon (t)}{\partial \varepsilon _\curlyvee }Y_1K_\curlyvee \frac{\partial }{\partial \varepsilon _\curlyvee }\left( \frac{\partial \mathfrak {O}_\varepsilon (t)}{\partial t}\right) \mathrm {d}\varepsilon \nonumber \\&\quad +2\sum _{\curlyvee =1}^m\int ^{}_{\varOmega }\frac{\partial \mathfrak {H}^{T}_\varepsilon (t)}{\partial \varepsilon _\curlyvee }Y_2K^{*}_\curlyvee \frac{\partial }{\partial \varepsilon _\curlyvee }\left( \frac{\partial \mathfrak {H}_\varepsilon (t)}{\partial t}\right) \mathrm {d}\varepsilon , \end{aligned}$$
(12)
$$\begin{aligned} \frac{\partial V_{2}(t, \mathfrak {O}, \mathfrak {H})}{\partial t}&\le \int ^{}_{\varOmega }\eta ^{T}_\varepsilon (t)\varPhi _2\eta _\varepsilon (t)\mathrm {d}\varepsilon ,\nonumber \\ \frac{\partial V_{3}(t, \mathfrak {O}, \mathfrak {H})}{\partial t}&=\tilde{\mathfrak {A}}^{2}\int ^{}_{\varOmega }\frac{\partial \mathfrak {O}^{T}_\varepsilon (t)}{\partial t}Q_5\frac{\partial \mathfrak {O}_\varepsilon (t)}{\partial t}\mathrm {d}\varepsilon \nonumber \\&\quad -\tilde{\mathfrak {A}}\int ^{}_{\varOmega }\int ^{t}_{t-\tilde{\mathfrak {A}}}\frac{\partial \mathfrak {O}^{T}_\varepsilon (s)}{\partial t}Q_5\frac{\partial \mathfrak {O}_\varepsilon (s)}{\partial \varepsilon _\curlyvee }\mathrm {d}s\mathrm {d}\varepsilon \nonumber \\&\quad +\tilde{\mathfrak {L}}^{2}\int ^{}_{\varOmega }\frac{\partial \mathfrak {H}^{T}_\varepsilon (t)}{\partial t}Q_6\frac{\partial \mathfrak {H}_\varepsilon (t)}{\partial t}\mathrm {d}\varepsilon \nonumber \\&\quad -\tilde{\mathfrak {L}}\int ^{}_{\varOmega }\int ^{t}_{t-\tilde{\mathfrak {L}}}\frac{\partial \mathfrak {H}^{T}_\varepsilon (s)}{\partial t}Q_6\frac{\partial \mathfrak {H}_\varepsilon (s)}{\partial \varepsilon _\curlyvee }\mathrm {d}s\mathrm {d}\varepsilon ,\nonumber \\ \frac{\partial V_{4}(t, \mathfrak {O}, \mathfrak {H})}{\partial t}&=\frac{\tilde{\mathfrak {A}}^{2}}{2}\int ^{}_{\varOmega }\frac{\partial \mathfrak {O}^{T}_\varepsilon (t)}{\partial t}Q_7\frac{\partial \mathfrak {O}_\varepsilon (t)}{\partial t}\mathrm {d}\varepsilon \nonumber \\&\quad -\int ^{}_{\varOmega }\int ^{0}_{-\tilde{\mathfrak {A}}}\int ^{t}_{t+\lambda }\frac{\partial \mathfrak {O}^{T}_\varepsilon (s)}{\partial s}Q_7\nonumber \\&\quad \times \frac{\partial \mathfrak {O}_\varepsilon (s)}{\partial s}\mathrm {d}s\mathrm {d}\lambda \mathrm {d}\varepsilon \nonumber \\&\quad +\frac{\tilde{\mathfrak {L}}^{2}}{2}\int ^{}_{\varOmega }\frac{\partial \mathfrak {H}^{T}_\varepsilon (t)}{\partial t}Q_8\frac{\partial \mathfrak {H}_\varepsilon (t)}{\partial t}\mathrm {d}\varepsilon \nonumber \\&\quad -\int ^{}_{\varOmega }\int ^{0}_{-\tilde{\mathfrak {L}}}\int ^{t}_{t+\lambda }\frac{\partial \mathfrak {H}^{T}_\varepsilon (s)}{\partial s}Q_8\frac{\partial \mathfrak {H}_\varepsilon (s)}{\partial s}\mathrm {d}s\mathrm {d}\lambda \mathrm {d}\varepsilon , \nonumber \\ \frac{\partial V_{5}(t, \mathfrak {O}, \mathfrak {H})}{\partial t}&=\frac{\tilde{\mathfrak {A}}^{3}}{6}\int ^{}_{\varOmega }\frac{\partial \mathfrak {O}^{T}_\varepsilon (t)}{\partial t}Q_9\frac{\partial \mathfrak {O}_\varepsilon (t)}{\partial t}\mathrm {d}\varepsilon \nonumber \\&\quad -\int ^{}_{\varOmega }\int ^{0}_{-\tilde{\mathfrak {A}}}\int ^{0}_{\alpha }\int ^{t}_{t+\lambda }\frac{\partial \mathfrak {O}^{T}_\varepsilon (s)}{\partial s}Q_9\nonumber \\&\quad \frac{\partial \mathfrak {O}_\varepsilon (s)}{\partial s}\mathrm {d}s\mathrm {d}\lambda \mathrm {d}\alpha \mathrm {d}\varepsilon \nonumber \\&\quad +\frac{\tilde{\mathfrak {L}}^{3}}{6}\int ^{}_{\varOmega }\frac{\partial \mathfrak {H}^{T}_\varepsilon (t)}{\partial t}Q_{10}\frac{\partial \mathfrak {H}_\varepsilon (t)}{\partial t}\mathrm {d}\varepsilon \nonumber \\&\quad -\int ^{}_{\varOmega }\int ^{0}_{-\tilde{\mathfrak {L}}}\int ^{0}_{\alpha }\int ^{t}_{t+\lambda }\frac{\partial \mathfrak {H}^{T}_\varepsilon (s)}{\partial s}\nonumber \\&\qquad {Q_{10}}\frac{\partial \mathfrak {H}_\varepsilon (s)}{\partial s}\mathrm {d}s\mathrm {d}\lambda \mathrm {d}\alpha \mathrm {d}\varepsilon . \end{aligned}$$
(13)

Firstly, by applying Lemma 3 in [32], Green formula and Assumption 1, we derive

$$\begin{aligned} \frac{\partial V_{1}(t, \mathfrak {O}, \mathfrak {H})}{\partial t}\le&\int ^{}_{\varOmega }\eta ^{T}_\varepsilon (t)(\varPhi _{12}+\tilde{\varPhi }_{11}{(t)}+\tilde{\varPhi }_{11}'{(t)})\eta _\varepsilon (t)\mathrm {d}\varepsilon , \end{aligned}$$
(14)

where \(\tilde{\varPhi }_{11}(t)=l_{1}J_1B\theta _\varepsilon (t)l^{T}_{6}+l_7Y_1B\theta _\varepsilon (t)l^{T}_6\).

Then, based on the second inequality in (10), according to reciprocally convex technique and Wirtinger-type integral inequality in [35] and [36], respectively, we obtain

$$\begin{aligned} \frac{\partial V_{3}(t, \mathfrak {O}, \mathfrak {H})}{\partial t}&\le \int ^{}_{\varOmega }\eta ^{T}_\varepsilon (t)\varPhi _3\eta _\varepsilon (t)\mathrm {d}\varepsilon , \end{aligned}$$
(15)
$$\begin{aligned} \frac{\partial V_{4}(t, \mathfrak {O}, \mathfrak {H})}{\partial t}&\le \int ^{}_{\varOmega }\eta ^{T}_\varepsilon (t)\varPhi _4(\mathfrak {A}(t),\mathfrak {L}(t))\eta _\varepsilon (t)\mathrm {d}\varepsilon . \end{aligned}$$
(16)

In addition, based on Jensen’s inequality and Wirtinger-type integral Lemma in [36] and [37], respectively, one can derive

$$\begin{aligned} \frac{\partial V_{5}(t, \mathfrak {O}, \mathfrak {H})}{\partial t}\le \int ^{}_{\varOmega }\eta ^{T}_\varepsilon (t)\varPhi _5(\mathfrak {A}(t),\mathfrak {L}(t))\eta _\varepsilon (t)\mathrm {d}\varepsilon . \end{aligned}$$
(17)

Therefore, substituting (12)-(17) into (11), we obtain

$$\begin{aligned} \frac{\partial V(t, \mathfrak {O}, \mathfrak {H})}{\partial t}\le \int ^{}_{\varOmega }\eta ^{T}_\varepsilon (t)\hat{\varPi }_1(\mathfrak {A}(t),\mathfrak {L}(t))\eta _\varepsilon (t)\mathrm {d}\varepsilon , \end{aligned}$$
(18)

where

$$\begin{aligned} \hat{\varPi }_1(\mathfrak {A}(t),\mathfrak {L}(t))= & {} \tilde{\varPhi }_{11}(t)+\tilde{\varPhi }_{11}'(t)+\varPhi _{12}+\varPhi _{2}+\varPhi _3\\&+\varPhi _4(\mathfrak {A}(t),\mathfrak {L}(t))+\varPhi _5(\mathfrak {A}(t),\mathfrak {L}(t)). \end{aligned}$$

According to the formula (18), we have

$$\begin{aligned} \frac{\partial V(t, \mathfrak {O}, \mathfrak {H})}{\partial t}&\le \int ^{}_{\varOmega }\eta ^{T}_\varepsilon (t){\tilde{\varPi }_1}(\mathfrak {A}(t),\mathfrak {L}(t))\eta _\varepsilon (t)\mathrm {d}\varepsilon \nonumber \\&\quad +\rho \int ^{}_{\varOmega }\mathfrak {O}^{T}_\varepsilon (t)J_{1}\mathfrak {O}_\varepsilon (t)+\mathfrak {H}^{T}_\varepsilon (t)J_{2}\mathfrak {H}_\varepsilon (t)\mathrm {d}\varepsilon \nonumber \\&\le \int ^{}_{\varOmega }\eta ^{T}_\varepsilon (t)\tilde{\varPi }_1(\mathfrak {A}(t),\mathfrak {L}(t))\eta _\varepsilon (t)\mathrm {d}\varepsilon \nonumber \\&\quad +\rho V(t, \mathfrak {O}, \mathfrak {H}), \end{aligned}$$
(19)

where \(\tilde{\varPi }_1(\mathfrak {A}(t),\mathfrak {L}(t))=\hat{\varPi }_1(\mathfrak {A}(t),\mathfrak {L}(t)) {-}\rho l_1J_1l^{T}_1{-}\rho l_{9}J_2l^{T}_{9}\).

Apparently, \(\tilde{\varPhi }_{11}(t)\), \(\varPhi _4(\mathfrak {A}(t),\mathfrak {L}(t))\) and \(\varPhi _5(\mathfrak {A}(t),\mathfrak {L}(t))\) are closely related to \(\mathfrak {A}(t)\), \(\mathfrak {L}(t)\) and the diagonal matrix compose of n time-varying bounded uncertain terms \(\theta _\varepsilon (t)\), respectively. Then, applying the lemma 1 to inequality (9), and using inequality (2), we can derive

$$\begin{aligned} \tilde{\varPi }_1(\mathfrak {A}(t),\mathfrak {L}(t))<0, \end{aligned}$$
(20)

and

$$\begin{aligned} \frac{\partial V(t, \mathfrak {O}, \mathfrak {H})}{\partial t}\le \rho V(t, \mathfrak {O}, \mathfrak {H}). \end{aligned}$$
(21)

Integrating from 0 to t on the both sides of the inequality (21), and \(t\in [0,T]\), we obtain

$$\begin{aligned} V(t, \mathfrak {O}, \mathfrak {H})\le V(0,\mathfrak {O}_\varepsilon (0),\mathfrak {H}_\varepsilon (0))+\int ^{t}_{0}\rho V(s, \mathfrak {O}, \mathfrak {H})\mathrm {d}s. \end{aligned}$$
(22)

From Gronwall inequality in [10], we derive \( V(T, \mathfrak {O}, \mathfrak {H})\le e^{\rho T}V(0,\mathfrak {O}_\varepsilon (0),\mathfrak {H}_\varepsilon (0)). \) Noting that \( V(0,\mathfrak {O}_\varepsilon (0),\mathfrak {H}_\varepsilon (0)) =\sum _{i=1}^5V_i(0,\mathfrak {O}_\varepsilon (0),\mathfrak {H}_\varepsilon (0)) \le \lambda _{1}\Vert \phi (t)\Vert ^{2}_{h}+\lambda _{2}\Vert \varphi (t)\Vert ^{2}_{h}\) \(\le (\lambda _{1}+\lambda _{2})(\Vert \phi (t)\Vert ^{2}_{h}+\Vert \varphi (t)\Vert ^{2}_{h})\).

Then, we get

$$\begin{aligned} V(T, \mathfrak {O}, \mathfrak {H})\le e^{\rho T}(\lambda _{1}+\lambda _{2})(\Vert \phi (t)\Vert ^{2}_{h}+\Vert \varphi (t)\Vert ^{2}_{h}), \end{aligned}$$
(23)

and

$$\begin{aligned} V(T, \mathfrak {O}, \mathfrak {H})&\ge \lambda _{min}(J_1)\Vert \mathfrak {O}_\varepsilon (t)\Vert ^{2} +\lambda _{min}(J_2)\Vert \mathfrak {H}_\varepsilon (t)\Vert ^{2}\nonumber \\&\ge \lambda _{min}(J)(\Vert \mathfrak {O}_\varepsilon (t)\Vert ^{2}+\Vert \mathfrak {H}_\varepsilon (t)\Vert ^{2}). \end{aligned}$$
(24)

Now, based on inequality (24), we can get that

$$\begin{aligned} \Vert \mathfrak {O}_\varepsilon (t)\Vert ^{2}+\Vert \mathfrak {H}_\varepsilon (t)\Vert ^{2} \le \frac{e^{\rho T}(\lambda _{1}+\lambda _{2})(\Vert \phi (t)\Vert ^{2}_{h}+\Vert \varphi (t)\Vert ^{2}_{h})}{\lambda _{min}(J)}. \end{aligned}$$

Therefore, we can derive that the DGRNs-RDTs (6) is finite-time-stable according to Definition 1 and inequality (9)-(10). The proof is completed. \(\square \)

Remark 6

In this paper, the slope information of regulatory function is more fully utilized rather than the fixed lower bound matrix like \(G_1=diag(g_{11}, g_{21},\dots , g_{n1})\) and the upper matrix like \(G_2=diag(g_{12}, g_{22},\dots , g_{n2})\) in [10,11,12, 25]. In detail, compared with the two slope information matrices mentioned above, the applicable slope information matrices can be increased to \(2^{n}\) by random combination of upper and lower boundaries of n uncertain items like \(G_{s_1,s_2,\dots ,s_n}=diag(g_{1s_j}, g_{2s_j},\dots , g_{ns_j}),\ s_j\in \{1,2\}\). That is, the condition (9) represents \(2^n\) inequalities. Although the method proposed in this paper increases the computational burden, it also obtains a more accurate feasible region of FTS criterion.

Remark 7

As shown in [12], the fourth-order integral term can more completely reflect the system state information. Then, the same fourth-order integral term like \(\int ^{}_{\varOmega }\int ^{0}_{-\tilde{\mathfrak {A}}}\int ^{0}_{\lambda }\int ^{0}_{\alpha }\int ^{t}_{t+\nu }\frac{\partial \mathfrak {O}^{T}_\varepsilon (s)}{\partial s}Q_9{\frac{\partial \mathfrak {O}_\varepsilon (s)}{\partial s}}\mathrm {d}s\mathrm {d}\nu \mathrm {d}\alpha \mathrm {d}\lambda \mathrm {d}\varepsilon \) is introduced into the LKF in this paper. However, different from the LKF in [12], the item like \(\int ^{}_{\varOmega }\int ^{t}_{t-\sigma (t)}f^{T}(p(s,x))Q_5\) \(\times f(p(s,x))\mathrm {d}s\mathrm {d}\varepsilon \) of LKF is removed because the information of \(f(\cdot )\) is transformed into the information of uncertainties and system states. Then, the LKF will be more simple and can fully reflect the system information. In addition, the slope information of the nonlinear regulation function is used more complete and flexible like \(G_{s_1,s_2, \dots , s_n}\) than the fixed form like \((G_1x-F(x))(G_2x-F(x))\le 0\). Therefore, the less conservative FTS criterion will be obtained by utilizing more information of GRNs in this paper.

Numerical example

To demonstrate the effectiveness of the theoretical, we will consider two numerical examples.

Example 1

Consider the following DGRNs-RDTs (3):

$$\begin{aligned} \frac{\partial \mathfrak {O}_\varepsilon (t)}{\partial t}= & {} \frac{\partial }{\partial \varepsilon _{\curlyvee }}\left( 0.1\frac{\partial \mathfrak {O}_\varepsilon (t)}{\partial \varepsilon _\curlyvee }\right) -0.8\mathfrak {O}_\varepsilon (t)\nonumber \\&-0.5F(\bar{\mathfrak {H}}_\varepsilon (t-\mathfrak {A}(t))), \end{aligned}$$
(25a)
$$\begin{aligned} \frac{\partial \mathfrak {H}_\varepsilon (t)}{\partial t}= & {} \frac{\partial }{\partial \varepsilon _{\curlyvee }}\left( 0.2\frac{\partial \mathfrak {H}_\varepsilon (t)}{\partial \varepsilon _\curlyvee }\right) -0.3\mathfrak {H}_\varepsilon (t)+\mathfrak {O}_\varepsilon (t-\mathfrak {L}(t)),\nonumber \\ \end{aligned}$$
(25b)

Assume \(\beta _{1}=1\), \(\lambda _{1}=2\), \(f_{1}(s)=\frac{s^2}{1+s^2}\), \(g_{11}=0.1\), \(g_{12}=0.65\), \(M_1=1\), \({\rho =0.001}\), \(\mu _{\mathfrak {A}}=\mu _{\mathfrak {L}}=2\), \(c_1=0.0878\), \(c_2=8\), \(T=20\), and the initial conditions are \(\phi _\varepsilon (t)=\varphi _\varepsilon (t)=1.3\).

Fig. 1
figure 1

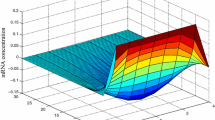
The trajectory of mRNA concentration \(\mathfrak {O}_\varepsilon (t)\) for DGRNs-RDTs (3)

Full size image

Then, we can testify the FTS conditions (9)-(10) are feasible by using the Toolbox YALMIP of MATLAB for \(\tilde{\mathfrak {A}}=\tilde{\mathfrak {L}}\in {(0,\ 1.5696]}\). Furthermore, a set of feasible solutions for conditions (9)-(10) are listed as follows:

$$\begin{aligned} J_1= & {} 0.3309,\ \ J_2=0.0386,\ Y_1=0.2379,\,Y_2=0.0766, \\ Q_1= & {} 5.7004\times 10^{-7},\\ Q_2= & {} 7.2424\times 10^{-5}, \,Q_3=1.2048\times 10^{-7},\\ Q_4= & {} 0.0212,\,Q_5=0.0964, Q_6=0.0311,\\ Q_7= & {} 1.3461\times 10^{-6},\,Q_8=1.8126\times 10^{-6},\\ Q_9= & {} 5.6286\times 10^{-4},\,Q_{10}=1.8126\times 10^{-6},\\ \hat{H}_1= & {} \begin{bmatrix} 0.0002&{}\quad 0.0001&{}\quad 0\\ 0.0001&{}\quad 0.0636&{}\quad 0.0001\\ 0&{}\quad 0.0001&{}\quad 0.1178\end{bmatrix},\\ \hat{H}_2= & {} \begin{bmatrix} 0&{}\quad 0&{}\quad 0\\ 0&{}\quad 0.0211&{}\quad 0\\ 0&{}\quad 0&{}\quad 0.0364\end{bmatrix}. \end{aligned}$$

Next, when \(\mathfrak {A}(t)=\mathfrak {L}(t)=0.5\), the state trajectories of DGRNs-RDTs (3) are shown in Figures 1 and 2. They reflect that the concentration trajectories of protein and mRNA gradually converge to the zero equilibrium point under \(T=20s\), which also show that the theoretical results of this paper are valid.

Example 2

We consider the DGRNs-RDTs (3) and its parameters as follow:

$$\begin{aligned}&K_{1}=K_{2}=\mathrm {diag}(0.1,0.1), \ \ K^*_{1}=K^*_{2}=\mathrm {diag}(0.2,0.2),\\&A=\mathrm {diag}(0.2,0.2),\ \ B=\mathrm {diag}(-0.55,-0.55),\\&C=\mathrm {diag}(0.3,0.3),\ D=diag(1,1), \end{aligned}$$

Assume \(\beta _{j}=1\), \(\lambda _{j}=2\), \(f_{j}(s)=\frac{s^2}{1+s^2}\), \(g_{j1}=0\), \(g_{j2}=0.65\), \(M_j=1\), \(\rho =0.002\), \(\mu _{\mathfrak {A}}=\mu _{\mathfrak {L}}=2\), \(c_1=0.0878\), \(c_2=8\), \(T=10\), \(\tilde{\mathfrak {A}}=\tilde{\mathfrak {L}}\in (0,\ 1.068]\), \(j\in \mathfrak {I}_2\).

Fig. 2
figure 2

The trajectory of protein concentration \(\mathfrak {H}_\varepsilon (t)\) for DGRNs-RDTs (3)

Full size image

We verify the FTS criterion (9)-(10) is viable by applying the Toolbox YALMIP of MATLAB under the numerical example mentioned above. In addition, we test the FTS conditions of this system are also feasible in [12].

Comparing the two slope information matrix in [12], we obtain four boundary matrices from two time-varying bounded uncertain term formed by the two regulation function \(F_{1}(s)\) and \(F_{2}(s)\) based on the proposed linear parameterization method.

However, substituting \(\tilde{\mathfrak {A}}=\tilde{\mathfrak {L}}\in (0,\ 1.152]\), and all other parameters of the mentioned model above remain the same, we testify the FTS conditions (9)-(10) proposed in this paper are solvable. Meanwhile, the corresponding conditions proposed in [12] are infeasible, which declare the stability criterion is ineffective for the considered system.

The simulation results of this example demonstrate the effectiveness of the theoretical verification in this paper, and attest the stability criterion proposed has a less conservative than the conditions in [12], and allows a larger time-delay upper bounds.

Conclusion

A linear parameterization method is proposed to study the finite-time stability (FTS) of delayed genetic regulatory networks with reaction-diffusion terms. The main contributions of this paper are as follows. (1) Based on the proposed linear parameterization method, the nonlinear system is transformed into an equivalent linear one with time-varying bounded uncertain terms. (2) The slope information of regulatory function is transformed into the boundary information of uncertain terms, which can make the information more fully and flexibly used. And a new generalized convex combination lemma with multiple bounded uncertainty parameters is proposed. (3) A stability criterion is established to guarantee FTS based on the proposed technique lemma. In the future, how to extend the method proposed in this paper to the study of state estimation and control problems, see [3, 5, 8] are the further research topics.