Markov switched stochastic Nicholson-type delay system with patch structure

Abstract

Considering stochastic perturbations of white and color noises, we introduce the Markov switched stochastic Nicholson-type delay system with patch structure. By constructing a traditional Lyapunov function we show that solutions of the addressed system are not only positive, but also do not explode to infinity in finite time and, in fact, are ultimately bounded. Then we estimate its ultimate boundedness, moment, and Lyapunov exponent. Finally, we present an example of numerical simulations to verify theoretical results.

1 Introduction

Considering that in the models of marine protected areas and B-cell chronic lymphocytic leukemia [1] the mortality rate is perturbed by the white noise of the environment, Yi and Liu [2] and Wang et al. [3] have presented a stochastic Nicholson-type delay system with patch structure:

$$ \begin{aligned}[b] d{x}_{i}(t)&= \Biggl[- \Biggl(a_{i}+ \sum_{j=1,j\neq i}^{n}b_{ij} \Biggr)x_{i}(t)+ \sum_{j=1,j\neq i}^{n}b_{ji} x_{j}(t) \\ &\quad+p_{i}x_{i}(t- \tau_{i})e^{-\gamma_{i}x_{i}(t-\tau_{i})} \Biggr]\,dt+\sigma _{i}{x}_{i}(t)\,dB_{i}(t), \end{aligned} $$

(1.1)

where $i\in I:=\{1,2,\ldots,n\}$, $x_{i}(t)$ is the size of the population at time t, $a_{i}$ is the per capita daily adult death rate, $p_{i}$ is the maximum per capita daily egg production, $\frac{1}{\gamma _{i}}$ is the size at which the population reproduces at its maximum rate, $\tau_{i}$ is the generation time, $b_{ij}$ ($i\neq j$) is the migration coefficient from compartment i to compartment j, $B_{i}(t)$ is an independent white noise with $B_{i}(0)=0$ and intensity $\sigma _{i}^{2}$. It is well known that the scalar Nicholson blowflies delay differential equation originated from [4, 5], and Berezansky et al. [6] summarized some results and introduced several open problems to attract many scholars [7–18]. Stochastic system (1.1) can be regarded as a generalization of the deterministic Nicholson blowflies model.

In the real world, it is complex for any practical system, since besides white noises, there are color noise interferences. One type of color noises is the so-called telegraph noise, which causes the system to switch from one environmental regime to another [19] and can mostly be modeled by a continuous-time Markov chain to describe the switching process between two or more regimes. To the best of our knowledge, almost no one or a few researchers consider the Markov switched stochastic Nicholson-type delay system with patch structure. This prompts us to propose the following stochastic system:

$$ \begin{aligned}[b] d{x}_{i}(t)&= \Biggl[- \Biggl(a_{i} \bigl(\xi(t) \bigr)+\sum_{j=1,j\neq i}^{n}b_{ij} \bigl(\xi(t) \bigr) \Biggr)x_{i}(t)+\sum _{j=1,j\neq i}^{n}b_{ji} \bigl(\xi(t) \bigr) x_{j}(t) \\ &\quad+p_{i} \bigl(\xi(t) \bigr)x_{i}(t- \tau_{i})e^{-\gamma_{i}(\xi(t))x_{i}(t-\tau_{i})} \Biggr]\,dt+\sigma _{i} \bigl( \xi(t) \bigr)x_{i}(t)\,dB_{i}(t) \end{aligned} $$

(1.2)

with initial conditions

$$ \xi(0)=\iota\in{S},\qquad x_{i}(s)=\varphi_{i}(s)\in C \bigl([-\tau _{i},0],[0,+\infty\bigr) ),\quad \varphi_{i}(0)>0, i\in I, $$

(1.3)

where $\xi(t)$ ($t\geq0$) is a continuous-time irreducible Markov chain with invariant distribution $\pi=(\pi_{k}, k\in{ S})$, which takes values in a finite state space ${S}=\{1,2,\ldots, N\}$, and its generator $Q=(\nu_{ij})_{N\times N}$ satisfies

$$P \bigl(\xi(t+\delta)=j|\xi(t)=i \bigr)=\left \{ \textstyle\begin{array}{l@{\quad}l} \nu_{ij}\delta+o(\delta) & \mbox{if } i\neq j,\\ 1+\nu_{ii}\delta+o(\delta) & \mbox{if } i=j, \end{array}\displaystyle \right . \quad\mbox{as } \delta\rightarrow0^{+}. $$

Here $\nu_{ij}\geq0$ for $i, j\in{S}$ with $i\neq j$, and $\sum_{j=1}^{j=N}\nu_{ij}=1$ for each $i\in{S}$, $B_{i}(t)$ are independent Brownian motions with $B_{i}(0)=0$ ($i\in I$), and they are independent of the Markov chain $\xi(t)$. For $i,j\in I$ and $k\in {S}$, the parameters $\tau_{i}$, $a_{i}(k)$, and $\gamma_{i}(k)$ are positive, and $b_{ij}(k)$, $p_{i}(k)$, and $\sigma_{i}^{2}(k)$ are nonnegative constants. Since system (1.2) describes the dynamics of a Markov switched stochastic Nicholson-type delay system with patch structure, it is important to study whether or not the solution:

• remains positive or never becomes negative,

• does not explode to infinity in finite time,

• is ultimately bounded in mean, and

• to estimate the moment and sample Lyapunov exponent.

In this paper, we discuss these problems one by one. In Sect. 2, we consider the existence and uniqueness of the global positive solution of (1.2)–(1.3). Next, we study its ultimate boundedness in mean, its moment, and its sample Lyapunov exponent in Sect. 3. We carry out an example and its numerical simulation to illustrate theoretical results in Sect. 4. Finally, we provide a brief conclusion to summarize our work.

2 Preliminary results

In this section, we introduce some basic definitions and lemmas, which are important for the proof of the main result. Unless otherwise specified, $(\varOmega,\{\mathcal{F}_{t}\}_{t\geq 0},\mathcal{P})$ is a complete probability space with filtration $\{ \mathcal{F}_{t}\}_{t\geq0}$ satisfying the usual conditions (i.e., it is right continuous, and $\mathcal{F}_{0}$ contains all $\mathcal{P}$-null sets). Let $B_{i}(t)$ ($i\in I$) be independent standard Brownian motions defined on this probability space. For simplicity, in the following sections, we use the following notation:

$$\begin{gathered} h^{-}=\min_{j\in{S}} \bigl\{ h(j) \bigr\} ,\qquad h^{+}=\max_{j\in{S}} \bigl\{ h(j) \bigr\} ,\qquad \tau =\min _{i\in I} \{\tau_{i}\}, \\ \mathbb{R}_{+}=(0,\infty),\qquad \mathbb{R}^{n}_{+}= \{ x_{i}\in\mathbb{R}_{+},i\in I\}.\end{gathered} $$

Let $p\geq1$ be such that for each $i\in I$, $A_{i}(p,\xi(t))>0$, and $C_{i}(p,\xi(t))$ is bounded, where

$$\begin{gathered} A_{i} \bigl(p,\xi(t) \bigr)=a_{i} \bigl(\xi(t) \bigr)- \frac{p-1}{p}\sum_{j=1,j\neq i}^{n} \bigl(b_{ji} \bigl(\xi (t) \bigr)-b_{ij} \bigl(\xi(t) \bigr) \bigr)-\frac{p-1}{2}\sigma_{i}^{2} \bigl( \xi(t) \bigr), \\ C_{i} \bigl(p,\xi(t) \bigr)=p\max_{x\in\mathbb{R}_{+}} \biggl\{ -A_{i} \bigl(\xi(t) \bigr)x^{p}+\frac{ p_{i}(\xi (t))}{e \gamma_{i}(\xi(t))}x^{p-1} \biggr\} .\end{gathered} $$

It is easy to see that for $i\in I$, $A_{i}(1,\xi(t))=a_{i}(\xi(t))>0$ and by continuity we can find ${p>1}$ such that $A_{i}(p,\xi(t))>0$. Considering the function $F(x):=-\alpha x^{p}+\beta x^{p-1}$, we can easily obtain that $F(x)$ increases on $[0, \frac{\beta(p-1)}{\alpha p}]$ and decreases on $[\frac{\beta(p-1)}{\alpha p}, +\infty)$, where $\alpha,\beta>0$ and $p>1$. Also, $F(0)=F(\frac{\beta}{\alpha})=0$, $\lim_{x\rightarrow+\infty} F(x)=-\infty$, and $\max_{x\in\mathbb {R}_{+}}F(x)=F(\frac{\beta(p-1)}{\alpha p})$ is bounded. Thus it is natural that $C_{i}(p,\xi(t))=pF(\frac{ p_{i}(\xi(t))(p-1)}{ep \gamma_{i}(\xi (t))A_{i}(\xi(t))})$ is also bounded.

Definition 2.1

(see [20])

System (1.2) is said to be ultimately bounded in mean if there is a positive constant L independent of initial conditions (1.3) such that

$$\limsup_{t\rightarrow\infty}E \bigl\vert x(t) \bigr\vert \leq L. $$

Lemma 2.1

For$A\in\mathbb{R}$, $B\in\mathbb{R}_{+}$, we have$\frac {Ax^{2}+Bx}{1+x^{2}}\leq G(A,B)$for$x\in\mathbb{R}$, where

$$G(A,B)=\left \{ \textstyle\begin{array}{l@{\quad}l} (A+\sqrt{A^{2}+B^{2}})/2, &A\geq0,\\ -B^{2}/4A, &A< 0. \end{array}\displaystyle \right . $$

Proof

By Lemma 1.2 of [21] the result easily follows, so we omit the proof. □

Lemma 2.2

For any given initial conditions (1.3), there exists a unique solution$x(t)=(x_{1}(t),\ldots,x_{n}(t))$of system (1.2) on$[0,\infty)$, which remains in$\mathbb{R}^{n}_{+}$with probability one, that is, $x(t)\in\mathbb{R}^{n}_{+}$for all$t\geq0$almost surely.

Proof

Because all coefficients of system (1.2) are locally Lipschitz continuous, for any given initial condition (1.3), there exists a unique maximal local solution $x(t)$ on $[-\tau, \nu_{e})$, where $\nu _{e}$ is the explosion time.

Firstly, we prove that $x(t)$ is positive on $[0, \nu_{e})$ almost surely. For $t\in[0,\tau]$, system (1.2) with initial conditions given in (1.3) becomes the system of stochastic linear differential equations:

$$ \left \{ \textstyle\begin{array}{l} d{x}_{i}(t)=[-(a_{i}(\xi(t))+\sum_{j=1,j\neq i}^{n}b_{ij}(\xi (t)))x_{i}(t)+\sum_{j=1,j\neq i}^{n}b_{ji}(\xi(t)) x_{j}(t)\\ \phantom{d{x}_{i}(t)=}{}+\alpha_{i}(\xi(t))]\,dt+\sigma_{i}(\xi(t))x_{i}(t)\,dB_{i}(t),\\ \xi(0)=\iota\in{S},\qquad x_{i}(0)=\varphi_{i}(0)>0,\quad i\in I, \end{array}\displaystyle \right . $$

(2.1)

where $\alpha_{i}(\xi(t))=p_{i}(\xi(t))\varphi_{i}(t-\tau_{i})e^{-\gamma_{i}(\xi (t))\varphi_{i}(t-\tau_{i})}\geq0$ a.s., $t\in[0,\tau]$. From the stochastic comparison theorem [22], $x_{i}(t)\geq I_{i}(t)$ a.s. for $t\in[0,\tau]$, where $I_{i}(t)$ ($i\in I$) are the solutions of the stochastic differential equations

$$ \left \{ \textstyle\begin{array}{l} d{I}_{i}(t)=[-(a_{i}(\xi(t))+\sum_{j=1,j\neq i}^{n}b_{ij}(\xi(t))) I_{i}(t)+\alpha_{i}(\xi(t))]\,dt+\sigma_{i}(\xi(t))I_{i}(t)\,dB_{i}(t),\\ \xi(0)=\iota\in{S},\qquad I_{i}(0)=\varphi_{i}(0)>0,\quad i\in I. \end{array}\displaystyle \right . $$

(2.2)

For $t\in[0,\tau]$, system (2.2) has the explicit solutions

$$I_{i}(t)=e^{\eta_{i}(\xi(t))} \biggl(\varphi_{i}(0)+ \int_{0}^{t}e^{-\eta_{i}(\xi(s))}\alpha _{i} \bigl(\xi(s) \bigr)\,ds \biggr)>0\quad \mbox{a.s.,} $$

where $\eta_{i}(\xi(t))=-(a_{i}(\xi(t))+\sum_{j=1,j\neq i}^{n}b_{ij}(\xi (t))-\frac{\sigma^{2}_{i}(\xi(t))}{2})t+\sigma_{i}(\xi(t)) B_{i}(t)$. Hence, for $t\in[0,\tau]$, $i\in I$, we have $x_{i}(t)\geq I_{i}(t)>0$ a.s.

Using the same method, we have $x_{i}(t)>0$ a.s. for $t\in[\tau, 2\tau]$, $i\in I$. Moreover, repeating this procedure, we also have $x_{i}(t)>0$ ($i\in I$) a.s. on $[m\tau, (m+1)\tau]$ for any integer $m\geq1$. Thus system (1.2) with initial conditions (1.3) has the unique positive solution $x(t)$ almost surely for $t\in[0, \tau_{e})$.

Next, we prove that $x(t)$ exists globally. Let $m_{0}\geq1$ be sufficiently large such that $\max_{-\tau\leq t\leq0}\varphi_{i}(t)< m_{0}$, $i\in I$. For every integer $m\geq m_{0}$, define the stopping time

$$\nu_{m}=\inf \bigl\{ t\in[0, \nu_{e}): x_{i}(t)\geq m \mbox{ for some } i\in I \bigr\} , $$

where throughout this paper, $\inf\emptyset:=\infty$. Obviously, $\nu _{m}$ is increasing as $m\rightarrow\infty$. Set $\nu_{\infty}=\lim_{m\rightarrow\infty}\nu_{m}$, where $\nu_{\infty}\leq\nu_{e}$ a.s. If we can prove that $\nu_{\infty}=\infty$ a.s., then $\nu_{e}=\infty$ and $x(t)\in R^{n}_{+}$ for all $t\geq0$ a.s. For this purpose, we need to show that $\nu _{\infty}=\infty$ a.s. Define $V(x)=\sum_{i=1}^{n}(x_{i}-1-\ln x_{i})$. For $t\in[0, \nu_{m}\wedge T)$, it is easy to show by Itô formula that

$$ dV(x)=LV \bigl(x,x(t-\tau),\xi(t) \bigr)+\sum_{i=1}^{n} \sigma_{i} \bigl(\xi (t) \bigr) \bigl(x_{i}(t)-1 \bigr) \,dB_{i}(t), $$

(2.3)

where $m\geq m_{0}$ and $T>0$ are arbitrary, and

$$ \begin{gathered}[b] LV \bigl(x,x(t-\tau),\xi(t) \bigr) \\ \quad= \sum_{i=1}^{n} [-a_{i} \bigl(\xi(t) \bigr)x_{i}(t)+a_{i} \bigl(\xi(t) \bigr)+\sum_{j=1,j\neq i}^{n}b_{ij} \bigl(\xi(t) \bigr)+\frac{1}{2}\sigma_{i}^{2} \bigl(\xi(t) \bigr)-\frac{\sum_{j=1,j\neq i}^{n}b_{ij}(\xi(t))) x_{j}(t)}{x_{i}(t)}\hspace{-36pt} \\ \qquad{}+p_{i} \bigl(\xi(t) \bigr)x_{i}(t- \tau_{i})e^{-\gamma_{i}(\xi(t))x_{i}(t-\tau_{i})}-\frac {p_{i}(\xi(t))x_{i}(t-\tau_{i})e^{-\gamma_{i}(\xi(t))x_{i}(t-\tau_{i})}}{x_{i}(t)} \\ \quad\leq \max_{j\in{S}}\sum_{i=1}^{n} \Biggl[a_{i}(j)+\sum_{j=1,j\neq i}^{n}b_{ij}(j)+ \frac{1}{2}\sigma_{i}^{2}(j)+ \frac{p_{i}(j)}{e\gamma_{i}(j)} \Biggr]:=K.\end{gathered} $$

(2.4)

In the last inequality, we used the fact that $\sup_{x\geq 0}xe^{-x}=\frac{1}{e}$. For any $m\geq m_{0}$, integrating both sides of (2.3) from 0 to $\nu_{m}\wedge T$ and taking expectations yield that

$$ EV \bigl(x(\nu_{m}\wedge T) \bigr)\leq V \bigl(x(0) \bigr)+ \int_{0}^{\nu_{m}\wedge T}K \,dt\leq V \bigl(x(0) \bigr)+KT:=K_{1}. $$

(2.5)

Since for every $\omega\in\{\nu_{m}\leq T\}$, there exists at least one of $x_{i}(\nu_{m},\omega)$ ($i\in I$) equal to m, we have that $V(x(\nu _{m}\wedge T))\geq(m-1-\ln m)$. Then from (2.5) it follows that

$$K_{1}\geq EV \bigl(x(\nu_{m}\wedge T) \bigr)\geq E \bigl[I_{\{\nu_{m}\leq T\}}(\omega)V \bigl(x(\nu _{m}\wedge T) \bigr) \bigr]\geq P{\{\nu_{m}\leq T\}}(m-1-\ln m), $$

where $I_{\{\nu_{m}\leq T\}}$ is the indicator function of $\{\nu_{m}\leq T\}$. Letting $m\rightarrow\infty$ gives $\lim_{m\rightarrow\infty}P\{ \nu_{m}\leq T\}=0$, and hence $P\{\nu_{\infty}\leq T\}=0$. Since $T>0$ is arbitrary, we must have $P\{\nu_{\infty}<\infty\}=0$. So $P\{\nu_{\infty}=\infty\}=1$ as required, which completes the proof of Lemma 2.2. □

Remark 2.1

Without color noises (i.e., $\xi(t)\equiv$ constant), system (1.2) is a stochastic Nicholson-type delay system with white noises in [2, 3]. Moreover, without migrations (i.e., $b_{ij}(\xi(t))\equiv 0$, $i,j\in I$), system (1.2) is a direct extension of n stochastic Nicholson’s blowflies delay differential equations that includes the stochastic model in [21, 23], and the restricted conditions $a_{i}>\frac{\sigma_{i}^{2}}{2}$ ($i\in I$) in [23, 24] for the existence and uniqueness of global positive solution are unnecessary. Thus Lemma 2.2 generalizes and improves Lemma 2.2 in [23, 24], Lemma 2.2 in [3], Theorem 2.1 in [21], and Theorem 2.1 in [2].

3 Main results

By Lemma 2.2, we show that the solution of the Markov switched stochastic Nicholson-type delay system (1.2) with initial conditions (1.3) remain in $\mathbb{R}^{n}_{+}$ almost surely and do not explode to infinity in finite time. This good property gives a great opportunity to study more complicated dynamic behaviors of system (1.2). In this section, we study the remaining problems: estimating the ultimate boundedness in mean, the average in time of the pth moment, and a sample Lyapunov exponent for system (1.2).

Theorem 3.1

For any given initial conditions (1.3), the solution$x(t)=(x_{1}(t),\ldots,x_{n}(t))$of system (1.2) has the property

$$ \limsup_{t\rightarrow\infty}E \bigl\vert x(t) \bigr\vert \leq \frac{nc}{a}, $$

(3.1)

where$a=\min_{i\in I}\{a_{i}^{-}\}$, $c=\max_{i\in I}\{(\frac{p_{i}}{e\gamma _{i}})^{+} \}$, that is, system (1.2) is ultimately bounded in mean.

Proof

By Lemma 2.2 the global solution $x(t)$ of (1.2) is positive on $t\geq0$ with probability one. It follows from (1.2) and the fact $\sup_{x\geq0}xe^{-x}=\frac{1}{e}$ that

$$ \begin{aligned}[b] d\sum_{i=1}^{n}x_{i}(t) & = \sum_{i=1}^{n} \bigl[-a_{i} \bigl(\xi(t) \bigr)x_{i}(t)+p_{i} \bigl(\xi (t) \bigr)x_{i}(t-\tau_{i})e^{-\gamma_{i}(\xi(t))x_{i}(t-\tau_{i})} \bigr]\,dt \\ &\quad+\sum_{i=1}^{n} \sigma_{i} \bigl(\xi(t) \bigr)x_{i}(t) \,dB_{i}(t) \\ &\leq\sum_{i=1}^{n} \biggl[-a_{i} \bigl(\xi(t) \bigr)x_{i}(t)+ \frac{p_{i}(\xi(t))}{e\gamma_{i}(\xi (t))} \biggr]\,dt+\sum_{i=1}^{n} \sigma_{i} \bigl(\xi(t) \bigr)x_{i}(t) \,dB_{i}(t) \\ &\leq\sum_{i=1}^{n} \bigl[-ax_{i}(t)+c \bigr]\,dt+\sum_{i=1}^{n} \sigma_{i} \bigl(\xi (t) \bigr)x_{i}(t) \,dB_{i}(t), \end{aligned} $$

(3.2)

which, together with Itô’s formula, implies that

$$ d \Biggl[\sum_{i=1}^{n} e^{at}x_{i}(t) \Biggr]\leq nce^{at}\,dt+\sum _{i=1}^{n}\sigma_{i} \bigl( \xi (t) \bigr)e^{at} x_{i}(t)\,dB_{i}(t). $$

(3.3)

Integrating both sides of (3.3) from 0 to t and then taking the expectations, we have

$$ e^{a t}E \Biggl(\sum_{i=1}^{n}x_{i}(t) \Biggr)\leq\sum_{i=1}^{n}x_{i}(0)+ \frac{nc}{a} \bigl(e^{a t}-1 \bigr). $$

(3.4)

This implies

$$ \limsup_{t\rightarrow\infty}E \Biggl(\sum_{i=1}^{n}x_{i}(t) \Biggr)\leq\frac{nc}{a}. $$

(3.5)

Since $E|x(t)|=E\sqrt{\sum_{i=1}^{n}x_{i}^{2}(t)}\leq E(\sum_{i=1}^{n}x_{i}(t))$, it is easy to get $\limsup_{t\rightarrow\infty}E|x(t)|\leq\frac {nc}{a}$, which is the required statement (3.1). The proof is now completed. □

Theorem 3.2

The solution$x(t)=(x_{1}(t),\ldots,x_{n}(t))$of (1.2) with initial conditions (1.3) satisfies

$$\begin{aligned}& \limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t}E \Biggl(\sum _{i=1}^{n}x_{i}^{p}(s) \Biggr)\,ds\leq \sum_{j\in{S}}\sum _{i=1}^{n}C_{i}(p,j)\pi _{j}\leq\sum_{i=1}^{n}C_{i}^{+}(p), \end{aligned}$$

(3.6)

$$\begin{aligned}& \begin{aligned}[b]{-}H_{i}^{+}&\leq-\sum _{j\in{S}} \pi_{j}H_{i}(j)\leq\liminf _{t\rightarrow \infty} \frac{1}{t}\ln x_{i}(t) \leq \limsup_{t\rightarrow\infty} \frac {1}{t}\ln x_{i}(t) \\ &\leq\sum_{j\in{S}}\pi_{j}G(j)\leq G^{+} \quad\textit{a.s.},\end{aligned} \end{aligned}$$

(3.7)

where$A(\xi(t))=-\min_{i\in I}A_{i}(2,\xi(t))$, $B(\xi(t))= \sqrt{ \sum_{i=1}^{n}\frac{p_{i}^{2}(\xi(t))}{e^{2}\gamma^{2}_{i}(\xi(t))}}$, $G(\xi (t))=G(A(\xi(t)),B(\xi(t)))$, and$H_{i}(\xi(t))=a_{i}(\xi(t))+\sum_{j=1,j\neq i}^{n}b_{ij}(\xi(t))+\frac{1}{2}\sigma_{i}^{2}(\xi(t))$, $i\in I$.

Proof

In view of Itô’s formula, Young’s inequality, and the fact $\sup_{x\geq0}xe^{-x}=\frac{1}{e}$, from (1.2) it follows that

$$\begin{aligned} &d \Biggl(\sum_{i=1}^{n}x_{i}^{p}(t) \Biggr) \\ &\quad= \sum_{i=1}^{n} p \Biggl[ \Biggl(-a_{i} \bigl(\xi(t) \bigr)-\sum_{j=1,j\neq i}^{n}b_{ij} \bigl(\xi(t) \bigr)+\frac{p-1}{2}\sigma_{i}^{2} \bigl(\xi (t) \bigr) \Biggr)x_{i}^{p}(t) \\ &\qquad{}+\sum_{j=1,j\neq i}^{n}b_{ji} \bigl(\xi(t) \bigr)x_{j}(t)x_{i}^{p-1}(t)+ p_{i} \bigl(\xi (t) \bigr)x_{i}^{p-1}(t) x_{i}(t-\tau_{i})e^{-\gamma_{i}(\xi(t))x_{i}(t-\tau _{i})} \Biggr]\,dt \\ &\qquad{}+\sum_{i=1}^{n} p \sigma_{i} \bigl(\xi(t) \bigr)x_{i}^{p}(t) \,dB_{i}(t) \\ &\quad\leq\sum_{i=1}^{n} p \Biggl[ \Biggl(-a_{i} \bigl(\xi(t) \bigr)+\frac{p-1}{p}\sum _{j=1,j\neq i}^{n} \bigl(b_{ji} \bigl(\xi(t) \bigr)-b_{ij} \bigl(\xi(t) \bigr) \bigr)+\frac{p-1}{2} \sigma_{i}^{2} \bigl(\xi (t) \bigr) \Biggr)x_{i}^{p}(t) \\ &\qquad{}+\frac{ p_{i}(\xi(t))}{e \gamma_{i}(\xi(t))}x_{i}^{p-1}(t) \Biggr] \,dt+\sum_{i=1}^{n} p \sigma_{i} \bigl( \xi(t) \bigr)x_{i}^{p}(t) \,dB_{i}(t) \\ &\quad=\sum_{i=1}^{n}p \biggl[-A_{i} \bigl(p,\xi(t) \bigr)x_{i}^{p}(t)+ \frac{ p_{i}(\xi(t))}{e \gamma _{i}(\xi(t))}x_{i}^{p-1}(t) \biggr]\,dt+\sum _{i=1}^{n} p \sigma_{i} \bigl(\xi (t) \bigr)x_{i}^{p}(t)\,dB_{i}(t) \\ &\quad\leq\sum_{i=1}^{n} C_{i} \bigl(p,\xi(t) \bigr)\,dt+\sum_{i=1}^{n} p \sigma_{i} \bigl(\xi (t) \bigr)x_{i}^{p}(t) \,dB_{i}(t). \end{aligned}$$

Since the Markov chain $\xi(t)$ has an invariant distribution $\pi=(\pi _{i}, i\in{ S})$, this implies

$$\begin{aligned} \limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t}E \Biggl(\sum _{i=1}^{n}x_{i}^{p}(s) \Biggr)\,ds \leq& \limsup_{t\rightarrow\infty}\frac {1}{t} \Biggl[E \Biggl(\sum_{i=1}^{n}x_{i}^{p}(0) \Biggr)+ \int_{0}^{t}\sum_{i=1}^{n} C_{i} \bigl(p,\xi(s) \bigr)\,ds \Biggr] \\ =&\sum_{j\in{S}}\sum_{i=1}^{n}C_{i}(p,j) \pi_{j} \\ \leq&\sum_{i=1}^{n}C_{i}^{+}(p). \end{aligned}$$

Using Itô’s formula, the Young and Cauchy inequalities, and the fact $\sup_{x\geq0}xe^{-x}=\frac{1}{e}$ again, from (1.2) and Lemma 2.1 we get that

$$\begin{aligned} \ln \bigl(1+ \bigl\vert x(t) \bigr\vert ^{2} \bigr) =&\ln \bigl(1+ \bigl\vert x(0) \bigr\vert ^{2} \bigr)+ \sum _{i=1}^{n} \int_{0}^{t}\frac {2}{1+ \vert x(s) \vert ^{2}} \\ &{}\times \Biggl[ \Biggl(-a_{i} \bigl(\xi(s) \bigr)-\sum _{j=1,j\neq i}^{n}b_{ij} \bigl(\xi(s) \bigr)+ \frac{1}{2}\sigma _{i}^{2} \bigl(\xi(s) \bigr) \Biggr)x_{i}^{2}(s) \\ &{}+\sum_{j=1,j\neq i}^{n}b_{ji} \bigl(\xi(s) \bigr)x_{i}(s)x_{j}(s)+p_{i} \bigl(\xi(s) \bigr)x_{i}(s) x_{i}(s- \tau)e^{-\gamma_{i}(\xi(s))x_{i}(s-\tau)} \Biggr]\,ds \\ &{}+\sum_{i=1}^{n} \biggl[M_{i}(t)- \int_{0}^{t}\frac{2\sigma_{i}^{2}(\xi (s))x_{i}^{4}(s)}{(1+ \vert x(s) \vert )^{2}}\,ds \biggr] \\ \leq&\ln \bigl(1+ \bigl\vert x(0) \bigr\vert ^{2} \bigr)+ \sum _{i=1}^{n} \int_{0}^{t}\frac{2}{1+ \vert x(s) \vert ^{2}} \\ &{}\times \Biggl[ \Biggl(-a_{i} \bigl(\xi(s) \bigr)+ \frac{1}{2}\sum_{j=1,j\neq i}^{n} \bigl(b_{ji} \bigl( \xi (s) \bigr)-b_{ij} \bigl(\xi(s) \bigr) \bigr)+\frac{1}{2} \sigma_{i}^{2} \bigl( \xi(s) \bigr) \Biggr)x_{i}^{2}(s) \\ &{}+\frac{p_{i}(\xi(s))}{e\gamma_{i}(\xi(s))}x_{i}(s) \Biggr]\,ds+\sum _{i=1}^{n} \biggl[M_{i}(t)- \int_{0}^{t}\frac{2\sigma_{i}^{2}(\xi (s))x_{i}^{4}(s)}{(1+ \vert x(s) \vert ^{2})^{2}}\,ds \biggr] \\ =&\ln \bigl(1+ \bigl\vert x(0) \bigr\vert ^{2} \bigr)+ 2\sum _{i=1}^{n} \int_{0}^{t}\frac{-A_{i}(2,\xi (s))x_{i}^{2}(s)+\frac{p_{i}(\xi(s))}{e\gamma_{i}(\xi (s))}x_{i}(s)}{1+ \vert x(s) \vert ^{2}}\,ds \\ &{}+\sum_{i=1}^{n} \biggl[M_{i}(t)- \int_{0}^{t}\frac{2\sigma_{i}^{2}(\xi (s))x_{i}^{4}(s)}{(1+ \vert x(s) \vert ^{2})^{2}}\,ds \biggr] \\ \leq&\ln \bigl(1+ \bigl\vert x(0) \bigr\vert ^{2} \bigr)+ 2 \int_{0}^{t}\frac{A(\xi(s)) \vert x(s) \vert ^{2}+B(\xi (s)) \vert x(s) \vert }{1+ \vert x(s) \vert ^{2}}\,ds \\ &{}+\sum_{i=1}^{n} \biggl[M_{i}(t)- \int_{0}^{t}\frac{2\sigma_{i}^{2}(\xi (s))x_{i}^{4}(s)}{(1+ \vert x(s) \vert ^{2})^{2}}\,ds \biggr] \\ \leq&\ln \bigl(1+ \bigl\vert x(0) \bigr\vert ^{2} \bigr)+ 2 \int_{0}^{t}G \bigl(\xi(s) \bigr)\,ds \\ &{}+\sum_{i=1}^{n} \biggl[M_{i}(t)- \int_{0}^{t}\frac{2\sigma_{i}^{2}(\xi (s))x_{i}^{4}(s)}{(1+ \vert x(s) \vert ^{2})^{2}}\,ds \biggr], \end{aligned}$$

(3.8)

where $M_{i}(t)=2\int_{0}^{t}\frac{\sigma_{i}(\xi(\xi(s)) x_{i}^{2}(s)}{1+|x(s)|^{2}}\,dB_{i}(s)$, $i\in I$.

Meanwhile, the exponential martingale inequality (Theorem 1.7.4 of [25]) implies that, for every $l>0$,

$$P \biggl\{ \sup_{0\leq t\leq l} \biggl[M_{i}(t)- \int_{0}^{t}\frac{2\sigma_{i}^{2}(\xi (s))x_{i}^{4}(s)}{(1+ \vert x(s) \vert ^{2})^{2}}\,ds \biggr]>2 \ln l \biggr\} \leq\frac{1}{l^{2}},\quad i\in I. $$

Using the convergence of $\sum_{l=1}^{\infty}\frac{1}{l^{2}}$ and the Borel–Cantelli lemma (Lemma 1.2.4 of [25]), we obtain that there exists a set $\varOmega_{0}\in\mathcal{F}$ with $P(\varOmega_{0})=1$ and a random integer $l_{0}=l_{0}(\omega)$ such that, for every $\omega\in \varOmega_{0}$,

$$ M_{i}(t)\leq \int_{0}^{t}\frac{2\sigma_{i}^{2}(\xi (s))x_{i}^{4}(s)}{(1+ \vert x(s) \vert ^{2})^{2}}\,ds+2\ln l $$

(3.9)

for all $0\leq t\leq l$, $l\geq l_{0}$, $i\in I$. Substituting (3.9) into (3.8), for any $\omega\in\varOmega_{0}$, $l\geq l_{0}$, $0< l-1\leq t\leq l$, we have

$$\begin{aligned} \frac{1}{t}\ln \bigl(1+ \bigl\vert x(t) \bigr\vert ^{2} \bigr) \leq&\frac{1}{l-1} \bigl[\ln \bigl(1+ \bigl\vert x(0) \bigr\vert ^{2} \bigr) \bigr]+ \frac{2}{t} \int_{0}^{t}G \bigl(\xi (s) \bigr)\,ds+ \frac{2n\ln l}{l-1}. \end{aligned}$$

Letting $l\rightarrow\infty$ and recalling that the Markov chain $\xi (t)$ has an invariant distribution $\pi=(\pi_{j}, j\in{ S})$, we get that

$$\begin{aligned} \limsup_{t\rightarrow\infty}\frac{1}{t}\ln x_{i}(t) \leq&\limsup_{t\rightarrow\infty}\frac{1}{2t}\ln \bigl(1+ \bigl\vert x(t) \bigr\vert ^{2} \bigr) \\ \leq&\limsup_{l\rightarrow\infty}\frac{1}{2(l-1)} \biggl[\ln \bigl(1+ \bigl\vert x(0) \bigr\vert ^{2} \bigr)+\frac {2n\ln l}{l-1} \biggr] \\ &+\limsup_{t\rightarrow\infty} \frac{1}{t} \int_{0}^{t}G \bigl(\xi(s) \bigr)\,ds \\ =&\sum_{j\in{S}}\pi_{j}G(j)\leq G^{+} \quad\text{a.s.}, i\in I. \end{aligned}$$

By Itô’s formula, from system (1.2) we obtain that

$$\begin{aligned} \ln x_{i}(t) =&\ln x_{i}(0)+ \int_{0}^{t} \Biggl[-a_{i} \bigl( \xi(s) \bigr)-\sum_{j=1,j\neq i}^{n}b_{ij} \bigl(\xi(s) \bigr)-\frac{1}{2}\sigma_{i}^{2} \bigl(\xi(s) \bigr) \\ &+\frac{\sum_{j=1,j\neq i}^{n}b_{ji}(\xi(t)) x_{j}(t)}{x_{i}(s)}+\frac {p_{i}(\xi(s))x_{i}(s-\tau_{i})e^{-\gamma_{i}(\xi(s))x_{i}(s-\tau _{i})}}{x_{i}(s)} \Biggr]\,ds \\ &+ \int_{0}^{t}\sigma_{i} \bigl(\xi(s) \bigr)\,dB_{i} \bigl(\xi(s) \bigr) \\ \geq&\ln x_{i}(0)- \int_{0}^{t}H_{i} \bigl(\xi(s) \bigr)\,ds+ \int_{0}^{t}\sigma_{i} \bigl(\xi(s) \bigr)\,dB_{i} \bigl(\xi (s) \bigr)\quad \mbox{a.s.}, \end{aligned}$$

which, with the help of the large number theorem for martingales (Theorem 1.3.4 [25]) and the invariant distribution of the Markov chain $\xi(t)$, implies

$$\liminf_{t\rightarrow\infty}\frac{1}{t}\ln x_{i}(t) \geq-\lim_{t\rightarrow \infty}\frac{1}{t} \int_{0}^{t}H_{i} \bigl(\xi(s) \bigr)\,ds=-\sum_{j\in{S}}\pi _{j}H_{i}(j) \geq-H_{i}^{+},\quad i\in I. $$

The proof is completed. □

Remark 3.1

Under the conditions $\alpha>\frac{\sigma^{2}}{2}$ in [23, 24] and $2(a_{1}+b_{2})-\sigma_{1}^{2}-(b_{1}+b_{2})\theta>0$, $2(a_{2}+b_{1})-\sigma _{2}^{2}-(b_{1}+b_{2})/\theta>0$ in [2], and $\lambda_{\max }^{+}(-DA-A^{T}D+D)<0$ in [3], the authors of [2, 3] and [23, 24] have estimated the ultimate boundedness, moment, and Lyapunov exponent of a relevant stochastic Nicholson-type model, respectively. However, these estimates in Theorems 3.1 and 3.2 of this paper are independent of any a priori conditions and only depend on the invariant distribution π of the Markov chain $\xi(t)$. In particular, these estimates can also be applied for no migration cases in [21]. Therefore Theorems 3.1 and 3.2 are a generalization and improvement of the corresponding results in [2, 3, 21, 23, 24]. Indeed, the stochastic models of [2, 3, 23, 24] are only concerned with white noises, but not with color noises. Moreover, we prove the existence of global positive solutions and estimate their ultimate boundedness, moment, and Lyapunov exponent without the restricted conditions $\alpha>\frac{\sigma^{2}}{2}$ in [23, 24], $2(a_{1}+b_{2})-\sigma_{1}^{2}-(b_{1}+b_{2})\theta>0$, $2(a_{2}+b_{1})-\sigma _{2}^{2}-(b_{1}+b_{2})/\theta>0$ in [2], and $\lambda_{\max}^{+}(-DA-A^{T}D+D)<0$ in [3]. Although Zhu et al. [21] have considered both white and color noises in stochastic Nicholson’s blowflies model, it is a scalar equation, and its initial condition $\varphi(s)\in C([-\tau ,0],(0,+\infty))$ is more strict than the initial conditions (1.3) in this paper. Then the model considered in this paper, the Markov switched stochastic Nicholson-type delay system with patch structure includes the models of [2, 3, 21, 23, 24] with $n=1,2$ and a constant Markov chain $\xi(t)$.

4 An example and its numerical simulations

In this section, we give an example with simulations to check our main results.

Example 4.1

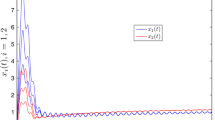
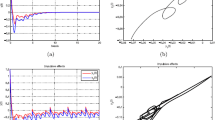
We choose ${S}=\{1,2,3\}$, $P=[-9,4,5;2,-5,3;2,2,-4]$, $a_{1}=[0.2,0.25,0.3]$, $a_{2}=[0.1,0.15,0.2]$, $a_{3}=[0.13,0.18,0.22]$, $b_{12}=[0.3,0.4,0.5]$, $b_{13}=[0.2,0.3,0.4]$, $b_{21}=[0.3,0.4,0.5]$, $b_{23}=[0.1,0.2,0.3]$, $b_{31}=[0.2,0.3,0.4]$, $b_{32}=[0.1,0.2,0.3]$, $p_{1}=[1.5,1.6,1.7]$, $p_{2}=[1.4,1.5,1.6]$, $p_{3}=[1.3,1.4,1.5]$, $\gamma _{1}=[1,1.5,2]$, $\gamma_{2}=[2,2.5,3]$, $\gamma_{3}=[1.5,2,2.5]$, $\sigma _{1}=[0.8,0.9,1]$, $\sigma_{2}=[0.7,0.8,0.9]$, $\sigma_{3}=[0.9,1,1.1]$, $\tau =1$ and initial conditions $\varphi_{1}(s)=1.1$, $\varphi_{2}(s)=1$, $\varphi _{3}(s)=0.9$, $s\in[-1,0]$. Then the irreducible Markov chain $\xi(t)$ has a unique stationary distribution $\pi=(0.1818,0.3377,0.4805)$. It follows from Lemma 2.2 that system (1.2) has a unique global solution $x(t)=(x_{1}(t), x_{2}(t), x_{3}(t))$, which remains in $\mathbb{R}^{3}_{+}$ with probability one, as shown in Fig. 1(a). According to the numerical methods of stochastic differential equations in [26, 27], we give the following discrete algorithm to simulate Example 4.1:

$$ \begin{aligned}[b] x_{i}^{n+1}&=x_{i}^{n}+ \Delta t \Biggl[- \Biggl(a_{i}(\xi_{n})+\sum _{j=1,j\neq i}^{n}b_{ij}(\xi _{n}) \Biggr)x_{i}^{n}+\sum_{j=1,j\neq i}^{n}b_{ji}( \xi_{n}) x_{j}^{n} \\ &\quad+p_{i}(\xi_{n})x_{i}^{n-k}e^{-\gamma_{i}(\xi_{n})x_{i}^{n-k}} \Biggr]+\sigma_{i}(\xi _{n})x_{i}^{n} \sqrt{\Delta t} U_{i}^{n} ,\quad n=0,1,2,\ldots,200, \end{aligned} $$

(4.1)

where $i=1,2,3$, $\Delta t=0.01$, $k=100$, $\xi_{n}\in{S}$ (Fig. 1(b)) is a 3-state Markov chain with generator P, $\{ U_{i}^{n}\}$ is a sequence of mutually independent random variables with $E U_{i}^{n}=0$ and $E (U_{i}^{n})^{2}=1$, independent of the Markov chain $\xi_{n}$.

Figure 1

Numerical solutions of Markov switched stochastic Nicholson-type delay system with patch structure (4.1) for initial values $\varphi_{1}(s)=1.1$, $\varphi_{2}(s)=1$, $\varphi_{3}(s)=0.9$, $s\in[-1,0]$

Furthermore, from Theorems 3.1 and 3.2 we have the following estimates:

$$\begin{gathered}\limsup_{t\rightarrow\infty}E \bigl|x(t) \bigr|\leq \frac {45}{e}\approx16.5546,\\ \limsup_{t\rightarrow\infty} \frac{1}{t} \int _{0}^{t}E\bigl(x_{1}^{2}(s)+x_{2}^{2}(s)+x_{3}^{2}(s) \bigr)\,ds\leq199.51, \\ -4.4\leq\liminf_{t\rightarrow\infty}\frac{1}{t}\ln x_{1}(t) \leq\limsup_{t\rightarrow \infty}\frac{1}{t} \ln x_{1}(t)\leq199.51\quad \text{a.s.}, \\ -3.205\leq\liminf_{t\rightarrow\infty}\frac{1}{t}\ln x_{2}(t) \leq\limsup_{t\rightarrow \infty}\frac{1}{t} \ln x_{2}(t)\leq199.51\quad \text{a.s.}, \\ -3.505\leq\liminf_{t\rightarrow\infty}\frac{1}{t}\ln x_{3}(t) \leq\limsup_{t\rightarrow \infty}\frac{1}{t} \ln x_{3}(t)\leq199.51\quad \text{a.s.}\end{gathered} $$

5 Conclusions

This paper is concerned with n connected Nicholson’s blowflies models under perturbations of white and color noises. Using a traditional Lyapunov function, we show that the solution of the Markov switched stochastic Nicholson-type delay system with patch structure remains positive and does not explode in finite time. Meanwhile, we estimate its ultimate boundedness, pth moment, and Lyapunov exponent. From Remarks 2.1 and 3.1 we find that the results obtained in this paper extend and improve some results in [2, 3, 21, 23, 24, 28, 29]. Inspired by the latest stochastic models in [30, 31], in the future work, we will deeply study dynamic behaviors of the addressed system, such as persistence, extinction, and so on.