1 Introduction

The advancement in the theory of the fractional calculus is more than three centuries old evolving along with the classical integer order calculus. Due to the superior merits of memory and hereditary properties, fractional calculus is getting more attention among researchers [1, 2]. Nowadays, fractional derivatives have been extensively used to model mechanical and electrical properties of assorted real materials. Furthermore, fractional derivatives have also been broadly used into different types of physical, chemical and biological phenomena [3–5]. Discrete fractional calculus has generated interest in recent years (see [6] and the references therein). For the trend of fractional calculus with different types of discrete exponential and Mittag-Leffler kernels we attract the attention of the reader to the recent manuscripts [7, 8] on kernels. This trend took place after the publication of continuous counterparts [9, 10]. Specially, fractional difference equations have become a popular topic recently. Using different approaches existence, uniqueness and then analysis of attractivity, stability and asymptotic stability of the solutions of fractional difference equations are most important topics in this direction [11–15].

Fixed point theorems are widely used for existence and uniqueness purposes. Furthermore, they are used to investigate the attractivity of solutions as well as stability and the asymptotic stability. In 2017, Abdeljawad et al. [16] used the Krasnoselskii fixed point theorem for a Caputo q-difference equation to investigate the existence of a solution. In 2018, Zhang and Zhou investigated existence and attractivity of solutions of Riemann–Liouville-like fractional difference equations using the Picard iteration method and then they used Schauder’s fixed point theorem for the required results [17]. Furthermore, they also proved results using weighted space. In 2018, Ardjouni et al. [18] used the Krasnoselskii fixed point theorem for a stability analysis of a nabla fractional difference equation. In 2018, Arjumand worked on existence and stability analysis of a non-linear Caputo fractional differential equation using the Krasnoselskii fixed point theorem by considering the solution of a fractional differential equation [19]. Besides, for help on stability refer to [20–25] and the references therein. Motivated by all the above-mentioned papers, here we consider the following fractional difference equation with initial condition:

$$ {}^{c}\nabla ^{\nu }_{0}x(t)=\lambda x(t)+\mathscr{F}\bigl(t,x(t)\bigr), \quad x(0)=x_{0}, t \in \mathbb{N}_{0}.$$
(1)

Here \({}^{c}\nabla ^{\nu }_{0}\) represents the Caputo nabla fractional difference operator with \(0<\nu \leq 1\) and a continuous function \(\mathscr{F}\) is defined as \(\mathscr{F}:\mathbb{N}_{0}\times \mathbb{R}\rightarrow \mathbb{R}\) with \(\mathscr{F}(t,0)=0\). Here we use the approach as mentioned in [19] by considering the solution of Eq. (1) in terms of the nabla discrete Mittag-Leffler function and then using its properties, we discuss the existence of solutions and then attractivity, stability and finally asymptotic stability of solutions of the above-mentioned problem. To the best of our knowledge, this approach to studying the stability using the fixed point theorem has never been followed by any researcher.

We arranged our current paper as follows: Sect. 2 contains some basic definitions, notations, lemmas and graphic analysis for the nabla discrete Mittag-Leffler functions. Section 3 intends to investigate the existence and stability results. Finally an example is provided with concluding remarks.

2 Preliminaries and essential tools

In this section, we present some basic nabla notations, definitions [6, 26, 27] and lemmas that are helpful in proving our main results. The graphs of the nabla discrete Mittag-Leffler functions will be shown and the behavior at infinity will be investigated as well.

Definition 1

For \(x:\mathbb{N}_{a+1}\rightarrow \mathbb{R}\) and \(\nu >0\), the nabla fractional sum is defined as

$$ \nabla ^{-\nu }_{a} x(t)=\frac{1}{\varGamma (\nu )}\sum _{\tau =a+1}^{t} \bigl(t-\rho (\tau )\bigr)^{\overline{\nu -1}}x( \tau ), \quad t\in \mathbb{N}_{a}, $$

where \(\rho (\tau )=\tau -1\). Meanwhile, \(\nabla _{a}^{-0}\) is taken as the identity operator.

Definition 2

For \(x:\mathbb{N}_{a}\rightarrow \mathbb{R}\), \(\nu \in \mathbb{R}^{+}\) and choose a natural number n such that \(n-1<\nu < n\), then the νth order nabla fractional difference is defined as

$$ \nabla ^{\nu }_{a} x(t)=\frac{1}{\varGamma (-\nu )}\sum _{\tau =a+1}^{t} \bigl(t-\rho (\tau )\bigr)^{\overline{-\nu -1}}x( \tau ), \quad t\in \mathbb{N}_{a+1}, $$

where \(\nabla _{a}^{0}\) is taken as the identity operator.

Definition 3

For \(x:\mathbb{N}_{a-n+1}\rightarrow \mathbb{R}\) and \(\nu >0\). The νth order Caputo nabla fractional difference of x is given by

$$ {}^{c}\nabla _{a}^{\nu }x(t)=\nabla _{a}^{-(n-\nu )} \bigl[ \nabla ^{n}x(t) \bigr] , \quad t \in \mathbb{N}_{a+1}, n=\lceil \nu \rceil . $$

Here \({}^{c}\nabla _{a}^{0}\) is taken as the identity operator.

Definition 4

([28])

Any subset of sequences in \(l_{0}^{\infty }\) is called uniformly Cauchy (or equi Cauchy) if for every \(\epsilon >0\), we have an integer N such that, for any sequence \(x= \lbrace x(n) \rbrace \) and \(i,j>N\), we must have \(|x(i)-x(j)|< \epsilon \).

Theorem 1

([28], Discrete Arzela–Ascoli’s theorem)

Any subset of\(l_{0}^{\infty }\)which is bounded and uniformly Cauchy is called relatively compact.

Theorem 2

([17], Schauder’s fixed point theorem)

Let\(\mathscr{N}\)be a non-empty, closed and convex subset of a Banach spaceS. Further assume a continuous mapping\(\mathscr{T} : \mathscr{N}\rightarrow \mathscr{N}\)such that\(\mathscr{T}\mathscr{N}\)is a relatively compact subset ofS. Then\(\mathscr{T}\)admits a unique fixed point in\(\mathscr{N}\). That is, \(\mathscr{T}x = x\)for\(x\in \mathscr{N}\).

Theorem 3

(Banach contraction principle)

Let\(\mathscr{N}\)be a non-empty complete metric space with a contraction mapping\(\mathscr{T}:\mathscr{N}\rightarrow \mathscr{N}\). Then\(\mathscr{T}\)has at least one fixed point in\(\mathscr{N}\). That is, there exists\(x \in \mathscr{N}\)such that\(\mathscr{T}x = x\).

Now we state Krasnoselskii’s fixed point theorem.

Theorem 4

([29], Krasnoselskii fixed point theorem)

Let\(\mathscr{N}\)be a non-empty, closed and convex subset of a Banach space\((S, \Vert \cdot \Vert )\). Suppose that\(\mathscr{T}_{1}\)and\(\mathscr{T}_{2}\)maps\(\mathscr{N}\)intoSsuch that

  1. (i)

    \(\mathscr{T}_{1}x+\mathscr{T}_{2}y\in \mathscr{N}\)for all\(x,y\in \mathscr{N}\),

  2. (ii)

    \(\mathscr{T}_{1}\)is continuous and\(\mathscr{T}_{1}\mathscr{N}\)is contained in a compact set ofS,

  3. (iii)

    \(\mathscr{T}_{2}\)is a contraction.

Then\(\mathscr{T}\)admits a fixed point in\(\mathscr{N}\)such that\(\mathscr{T}_{1}x+\mathscr{T}_{2}x=x\).

Lemma 1

([27])

Let\(0<\nu \leq 1\), \(a\in \mathbb{R}\)and consider the nabla Caputo nonhomogeneous fractional difference equation

$$ {}^{c}\nabla ^{\nu }_{a}z(t)=\lambda z(t)+ \mathscr{F}(t), \quad z(a)=a_{0}, t \in \mathbb{N}_{a},$$
(2)

then its solution is given by

$$ z(t)=a_{0}E_{\overline{\nu }}(\lambda ,t-a)+\sum _{\tau =a+1}^{t}E_{ \overline{\nu ,\nu }}\bigl(\lambda ,t-\rho (\tau )\bigr)\mathscr{F}(\tau ). $$
(3)

Remark 1

Following the above lemma, the solution of problem (1) is given by

$$ x(t)=x_{0}E_{\overline{\nu }}(\lambda ,t)+\sum _{\tau =1}^{t}E_{ \overline{\nu ,\nu }}\bigl(\lambda ,t-\rho (\tau )\bigr)\mathscr{F}\bigl(\tau ,x( \tau )\bigr).$$
(4)

Definition 5

([27])

For \(\lambda \in \mathbb{R}\), \(|\lambda |<1\) and \(\nu ,\beta ,t\in \mathbb{C}\) with \(\Re (\nu )>0\), the nabla discrete Mittag-Leffler functions are defined as follows:

$$ E_{\overline{\nu ,\beta }}(\lambda ,t)=\sum_{m=0}^{\infty } \lambda ^{m} \frac{t^{\overline{m\nu +\beta -1}}}{\varGamma (m\nu +\beta )}. $$

For \(\beta =1\), the one parameter nabla discrete Mittag-Leffler function can be written as

$$ E_{\overline{\nu }}(\lambda ,t)=\sum_{m=0}^{\infty } \lambda ^{m} \frac{t^{\overline{m\nu }}}{\varGamma (m\nu +1)}. $$

Remark 2

(The graphs and behavior of nabla discrete Mittag-Leffler functions at ∞)

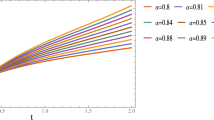
Motivated by Remark 1 in [30] and for the sake of benefiting in the proof of our main results, the numerical evidence, as illustrated in Fig. 1 and Fig. 2, shows that, for \(t\in \mathbb{R^{+}}\), \(0<\nu \leq 1\), the one and two parameter nabla discrete Mittag-Leffler functions are decreasing functions of t and are bounded above by 1. That is, \(E_{\overline{\nu }}(\lambda ,t)\leq 1\) and \(E_{\overline{\nu ,\nu }}(\lambda ,t)\leq 1\), where \(-1<\lambda <0\) and \(-\nu <\lambda <0\). Moreover, it is to be noted that \(\lim_{t\rightarrow \infty }E_{\overline{\nu }}(\lambda ,t)=0\) and \(\lim_{t\rightarrow \infty }E_{\overline{\nu ,\nu }}(\lambda ,t)=0\).

Figure 1
figure 1

\(E_{\overline{\nu }}(\lambda ,t)\) for \(\lambda =-0.5\), \(\nu =0.6,0.8,1\)

Full size image
Figure 2
figure 2

\(E_{\overline{\nu ,\nu }}(\lambda ,t)\) for \(\lambda =-0.5\), \(\nu =0.6,0.8,1\)

Full size image

Definition 6

([19])

\(x=\varphi (t)\) being a solution of Eq. (1) is called:

  1. (i)

    stable, if for every \(\epsilon >0\) and \(t_{0}\geq 0\), there exists a \(\delta >0\) depending on \(t_{0}\) and ϵ such that, for \(|x_{0}-\varphi (t_{0})|\leq \delta (t_{0},\epsilon )\), we have, for all \(t\geq t_{0}\), \(|x(t,x_{0},t_{0})-\varphi (t)|<\epsilon \);

  2. (ii)

    attractive, if there exists \(\zeta (t_{0})>0\) such that \(\Vert x_{0} \Vert \leq \zeta \) implies \(\lim_{t\rightarrow \infty }x(t,x_{0},t_{0}) =0\);

  3. (iii)

    asymptotically stable if it is attractive and stable.

3 Main results

In this section, we present existence and stability of the solutions of Eq. (1).

3.1 The existence and uniqueness theorems

Let \(l_{0}^{\infty }\) be the set of all real sequences \(x= \lbrace x(t) \rbrace _{t=0}^{\infty }\) from the starting point \(t=0\). The space is endowed with the supremum norm \(\Vert x \Vert =\sup_{t\in \mathbb{N}_{0}} \vert x(t) \vert \). \(l_{0}^{\infty }\) is a Banach space.

Theorem 5

Let us consider the solution of Eq. (1) as mentioned in Eq. (4). Assume a continuous and bounded function\(\mathscr{F}\), which obeys

\((A_{1})\):

\(\mathscr{F}:\mathbb{N}_{0}\times \mathbb{R}\rightarrow \mathbb{R}\)satisfies the Lipschitz condition with\(\mathscr{L}>0\)being a Lipschitz constant,

$$ \bigl\Vert \mathscr{F}(t,x)-\mathscr{F}(t,y) \bigr\Vert \leq \mathscr{L} \Vert x-y \Vert , \quad \forall t\in \mathbb{N}_{0}^{b}, b>0. $$

Then using Schauder’s fixed point theorem, there exists at least one solution of Eq. (1).

Proof

Let us consider a non-empty, closed and convex subset \(\mathscr{K}= \lbrace x:x\in l_{0}^{\infty }, \Vert x \Vert \leq \varLambda \rbrace \); also assume that \(\Vert \mathscr{F}(t,x) \Vert \leq \mathscr{R}\), \(\forall (t,x) \in \mathbb{N}_{0}^{b} \times \mathbb{R}\). Furthermore, consider a mapping \(\mathscr{T}\) on \(\mathscr{K}\) as given by

$$ \mathscr{T}x(t)=x_{0}E_{\overline{\nu }}(\lambda ,t)+\sum _{\tau =1}^{t}E_{ \overline{\nu ,\nu }}\bigl(\lambda ,t-\rho (\tau )\bigr)\mathscr{F}\bigl(\tau ,x( \tau )\bigr). $$

First of all we show that \(\mathscr{T}\) maps \(\mathscr{K}\) into \(\mathscr{K}\):

$$\begin{aligned} \bigl\vert \mathscr{T}x(t) \bigr\vert &= \Biggl\vert x_{0}E_{\overline{\nu }}( \lambda ,t)+\sum_{\tau =1}^{t}E_{\overline{\nu ,\nu }} \bigl(\lambda ,t- \rho (\tau )\bigr)\mathscr{F}\bigl(\tau ,x(\tau )\bigr) \Biggr\vert \\ &\leq \vert x_{0} \vert \bigl\vert E_{\overline{\nu }}(\lambda ,t) \bigr\vert + \int _{0}^{t} \bigl\vert E_{ \overline{\nu ,\nu }}\bigl( \lambda ,t-\rho (\tau )\bigr) \bigr\vert \bigl\vert \mathscr{F}\bigl(\tau ,x( \tau )\bigr) \bigr\vert \nabla \tau \\ &\leq \vert x_{0} \vert +\mathscr{R}b \leq \varLambda . \end{aligned}$$

Now we have to show that \(\mathscr{T}\) is relatively compact, for this purpose consider \(0\leq t_{1}\leq t_{2}\leq b\) so we get

$$\begin{aligned} & \bigl\vert \mathscr{T}x(t_{2})-\mathscr{T}x(t_{1}) \bigr\vert \\ &\quad \leq \bigl\vert x_{0}\bigl(E_{\overline{\nu }}(\lambda ,t_{2})-E_{ \overline{\nu }}(\lambda ,t_{1})\bigr) \bigr\vert \\ &\qquad {}+ \Biggl\vert \Biggl( \sum_{\tau =1}^{t_{2}}E_{\overline{\nu ,\nu }} \bigl( \lambda ,t_{2}-\rho (\tau )\bigr) -\sum _{\tau =1}^{t_{1}}E_{ \overline{\nu ,\nu }}\bigl(\lambda ,t_{1}-\rho (\tau )\bigr) \Biggr) \mathscr{F}\bigl(\tau ,x(\tau ) \bigr) \Biggr\vert \\ &\quad \leq \bigl\vert x_{0}\bigl(E_{\overline{\nu }}(\lambda ,t_{2})-E_{ \overline{\nu }}(\lambda ,t_{1})\bigr) \bigr\vert \\ &\qquad {}+ \Biggl\vert \Biggl( \sum_{\tau =1}^{t_{1}}E_{\overline{\nu ,\nu }} \bigl( \lambda ,t_{2}-\rho (\tau )\bigr) -\sum _{\tau =1}^{t_{1}}E_{ \overline{\nu ,\nu }}\bigl(\lambda ,t_{1}-\rho (\tau )\bigr) \Biggr) \mathscr{F}\bigl(\tau ,x(\tau ) \bigr) \Biggr\vert \\ &\qquad {}+ \Biggl\vert \sum_{\tau =t_{1}+1}^{t_{2}}E_{\overline{\nu ,\nu }} \bigl( \lambda ,t_{2}-\rho (\tau )\bigr) \mathscr{F}\bigl(\tau ,x(\tau )\bigr) \Biggr\vert \\ &\quad \leq \bigl\vert x_{0}\bigl(E_{\overline{\nu }}(\lambda ,t_{2})-E_{ \overline{\nu }}(\lambda ,t_{1})\bigr) \bigr\vert \\ &\qquad {}+ \int _{0}^{t_{1}} \bigl\vert \bigl( E_{\overline{\nu ,\nu }} \bigl(\lambda ,t_{2}- \rho (\tau )\bigr) -E_{\overline{\nu ,\nu }}\bigl(\lambda ,t_{1}-\rho (\tau )\bigr) \bigr) \bigr\vert \bigl\vert \mathscr{F} \bigl(\tau ,x(\tau )\bigr) \bigr\vert \nabla \tau \\ &\qquad {}+ \int _{t_{1}}^{t_{2}} \bigl\vert E_{\overline{\nu ,\nu }}\bigl( \lambda ,t_{2}- \rho (\tau )\bigr) \bigr\vert \bigl\vert \mathscr{F}\bigl(\tau ,x(\tau )\bigr) \bigr\vert \nabla \tau \\ &\quad \leq \bigl\vert x_{0}\bigl(E_{\overline{\nu }}(\lambda ,t_{2})-E_{ \overline{\nu }}(\lambda ,t_{1})\bigr) \bigr\vert \\ &\qquad {}+ \int _{0}^{t_{1}} \bigl\vert \bigl( E_{\overline{\nu ,\nu }} \bigl(\lambda ,t_{2}- \rho (\tau )\bigr) -E_{\overline{\nu ,\nu }}\bigl(\lambda ,t_{1}-\rho (\tau )\bigr) \bigr) \bigr\vert \mathscr{R}\nabla \tau \\ &\qquad {}+\mathscr{R} (t_{2}-t_{1}). \end{aligned}$$

Hence it follows that \(\vert \mathscr{T}x(t_{2})-\mathscr{T}x(t_{1}) \vert \rightarrow 0\) as \(t_{1}\rightarrow t_{2}\).

Now in order to show the continuity of \(\mathscr{T}\), let us consider a sequence \(x_{n}\) which converges to x, then we have

$$\begin{aligned} \bigl\vert \mathscr{T}x_{n}(t)-\mathscr{T}x(t) \bigr\vert &\leq \Biggl\vert \sum_{\tau =1}^{t}E_{ \overline{\nu ,\nu }} \bigl(\lambda ,t-\rho (\tau )\bigr) \bigl( \mathscr{F}\bigl(\tau ,x_{n}( \tau )\bigr)-\mathscr{F}\bigl(\tau ,x(\tau )\bigr) \bigr) \Biggr\vert \\ &\leq \int _{0}^{t} \bigl\vert E_{\overline{\nu ,\nu }}\bigl( \lambda ,t-\rho ( \tau )\bigr) \bigr\vert \bigl\vert \mathscr{F}\bigl(\tau ,x_{n}(\tau )\bigr)-\mathscr{F}\bigl( \tau ,x(\tau )\bigr) \bigr\vert \nabla \tau \\ &\leq \mathscr{L} \Vert x_{n}-x \Vert \int _{0}^{t} \nabla \tau \leq \mathscr{L}b \Vert x_{n}-x \Vert , \end{aligned}$$

we can see easily \(\mathscr{T}x_{n}\rightarrow \mathscr{T}x\) as \(x_{n}\rightarrow x\). Hence using Arzela–Ascoli’s theorem, \(\mathscr{T}\mathscr{K,}\) being a bounded and uniformly Cauchy subset of \(l_{0}^{\infty }\), is relatively compact.

Hence by Schauder’s fixed point theorem there exists at least one fixed point of \(\mathscr{T}\) in \(\mathscr{K}\). Furthermore, if all functions x in \(\mathscr{K}\) tend to 0 as \(t\rightarrow \infty \) then solutions of Eq. (1) tend to zero as \(t\rightarrow \infty \) and hence are called attractive solutions. □

3.2 The stability results

In the light of the fixed point results presented in the above subsection, we present some stability results in what follows.

Theorem 6

Assume that a bounded, continuous function\(\mathscr{F}\)satisfies the following conditions,

\((A_{2})\):

\(\Vert \mathscr{F}(t,x)-\mathscr{F}(t,y) \Vert \leq \mathscr{L}(t) \Vert x-y \Vert \),

\((A_{3})\):

\(\int _{0}^{t} \mathscr{L}(\tau )\nabla \tau \rightarrow 0 \)as\(t \rightarrow \infty \), where\(\mathscr{M}=\sup_{t\in \mathbb{N}_{0}} \int _{0}^{t} \mathscr{L}( \tau )\nabla \tau \),

then using the Banach contraction principle, there exists a unique solution of Eq. (1). Moreover, the solution is attractive.

Proof

Define a set \(\mathscr{E}= \lbrace x\in l_{0}^{\infty }, \Vert x \Vert \leq \epsilon \text{ and } x(t)\rightarrow 0 \text{ as }t\rightarrow \infty \rbrace \). Furthermore, assume that

$$ \bigl\vert \mathscr{F}(t,x) \bigr\vert \leq \bigl\vert \mathscr{F}(t,x)- \mathscr{F}(t,0) \bigr\vert + \bigl\vert \mathscr{F}(t,0) \bigr\vert \leq \mathscr{L}(t) \vert x-0 \vert +0=\mathscr{L}(t) \Vert x \Vert . $$

Now we define a mapping \(\mathscr{T}\) on \(\mathscr{E}\) as follows:

$$ \mathscr{T}x(t)=x_{0}E_{\overline{\nu }}(\lambda ,t)+\sum _{\tau =1}^{t}E_{ \overline{\nu ,\nu }}\bigl(\lambda ,t-\rho (\tau )\bigr)\mathscr{F}\bigl(\tau ,x( \tau )\bigr). $$

Continuity of \(\mathscr{T}x\) is followed by \(x\in \mathscr{E}\). First of all we prove that \(\mathscr{T}\) maps \(\mathscr{E}\) into itself:

$$\begin{aligned} \bigl\vert \mathscr{T}x(t) \bigr\vert &= \Biggl\vert x_{0}E_{\overline{\nu }}( \lambda ,t)+\sum_{\tau =1}^{t}E_{\overline{\nu ,\nu }} \bigl(\lambda ,t- \rho (\tau )\bigr)\mathscr{F}\bigl(\tau ,x(\tau )\bigr) \Biggr\vert \\ &\leq \vert x_{0} \vert \bigl\vert E_{\overline{\nu }}(\lambda ,t) \bigr\vert + \int _{0}^{t} \bigl\vert E_{ \overline{\nu ,\nu }}\bigl( \lambda ,t-\rho (\tau )\bigr) \bigr\vert \bigl\vert \mathscr{F}\bigl(\tau ,x( \tau )\bigr) \bigr\vert \nabla \tau \\ &\leq \vert x_{0} \vert + \int _{0}^{t} \mathscr{L}(\tau ) \bigl\Vert x(\tau ) \bigr\Vert \nabla \tau \\ &\leq \vert x_{0} \vert +\epsilon \int _{0}^{t} \mathscr{L}(\tau )\nabla \tau \leq \vert x_{0} \vert +\epsilon \mathscr{M}\leq \epsilon . \end{aligned}$$

Hence \(\mathscr{T}\) maps \(\mathscr{E}\) into itself. Now we show that \(\mathscr{T}x(t)\rightarrow 0\) as \(t\rightarrow \infty \). We can see easily in Figs. 1 and 2 that \(\lim_{t\rightarrow \infty } E_{\overline{\nu }}(\lambda ,t) \rightarrow 0\) and \(\lim_{t\rightarrow \infty } E_{\overline{\nu ,\nu }}(\lambda ,t- \rho (\tau ))\rightarrow 0\). So we have \(\lim_{t\rightarrow \infty } x_{0}E_{\overline{\nu }}(\lambda ,t) \rightarrow 0\). Also

$$\begin{aligned} \biggl\vert \int _{0}^{t} E_{\overline{\nu ,\nu }}\bigl(\lambda ,t-\rho (\tau )\bigr) \mathscr{F}\bigl(\tau ,x(\tau )\bigr)\nabla \tau \biggr\vert & \leq \int _{0}^{t} \bigl\vert E_{ \overline{\nu ,\nu }}\bigl( \lambda ,t-\rho (\tau )\bigr) \bigr\vert \bigl\vert \mathscr{F}\bigl(\tau ,x( \tau )\bigr) \bigr\vert \nabla \tau \\ &\leq \int _{0}^{t} \bigl\vert E_{\overline{\nu ,\nu }}\bigl( \lambda ,t-\rho (\tau )\bigr) \bigr\vert \mathscr{L}(\tau ) \bigl\Vert x(\tau ) \bigr\Vert \nabla \tau \\ &\leq \epsilon \int _{0}^{t}\mathscr{L}(\tau )\nabla \tau \leq \epsilon \mathscr{M}. \end{aligned}$$

Thus \(\vert \int _{0}^{t} E_{\overline{\nu ,\nu }}(\lambda ,t-\rho ( \tau ))\mathscr{F}(\tau ,x(\tau ))\nabla \tau \vert \rightarrow 0\) as \(t\rightarrow \infty \). Hence \(\mathscr{T}x(t)\rightarrow 0\) as \(t\rightarrow \infty \). Now we show that \(\mathscr{T}\) is a contraction mapping:

$$\begin{aligned} \bigl\vert \mathscr{T}x(t)-\mathscr{T}y(t) \bigr\vert &\leq \int _{0}^{t} \bigl\vert E_{ \overline{\nu ,\nu }}\bigl( \lambda ,t-\rho (\tau )\bigr) \bigr\vert \bigl\vert \mathscr{F}\bigl(\tau ,x( \tau )\bigr)-\mathscr{F}\bigl(\tau ,y(\tau )\bigr) \bigr\vert \nabla \tau \\ &\leq \Vert x-y \Vert \int _{0}^{t} \mathscr{L}(\tau )\nabla \tau \leq \mathscr{M} \Vert x-y \Vert . \end{aligned}$$

For \(\mathscr{M}<1\), \(\mathscr{T}\) is contraction. Hence by the contraction mapping principle Eq. (1) has a unique solution and furthermore, since all functions x in \(\mathscr{E}\) tend to 0 as \(t\rightarrow \infty \), a solution of Eq. (1) tends to zero as \(t\rightarrow \infty \), and hence is called an attractive solution. □

Theorem 7

Letxbe solution of Eq. (1) andx̂be a solution of Eq. (1) satisfying the initial condition\(\hat{x}(0)=\hat{x}_{0}\). Moreover, let there for very small\(\epsilon >0\)exist\(\delta =(1-\mathscr{M}) \epsilon \). Then solutions of Eq. (1) are stable.

Proof

Since x is a solution of Eq. (1) and x̂ is also a solution of Eq. (1) satisfying the initial condition \(\hat{x}(0)=\hat{x}_{0}\), we have

$$\begin{aligned} \bigl\vert x(t)-\hat{x}(t) \bigr\vert &\leq \bigl\vert x_{0}E_{\overline{\nu }}(\lambda ,t)- \hat{x}_{0}E_{\overline{\nu }}( \lambda ,t) \bigr\vert \\ &\quad {}+ \Biggl\vert \sum_{\tau =1}^{t}E_{\overline{\nu ,\nu }} \bigl(\lambda ,t-\rho ( \tau )\bigr)\mathscr{F}\bigl(\tau ,x(\tau )\bigr)-\sum _{\tau =1}^{t}E_{ \overline{\nu ,\nu }}\bigl(\lambda ,t- \rho (\tau )\bigr)\mathscr{F}\bigl(\tau , \hat{x}(\tau )\bigr) \Biggr\vert \\ &\leq \vert x_{0}-\hat{x}_{0} \vert \bigl\vert E_{\overline{\nu }}(\lambda ,t) \bigr\vert + \int _{0}^{t} \bigl\vert E_{\overline{\nu ,\nu }}\bigl( \lambda ,t-\rho (\tau )\bigr) \bigr\vert \bigl\vert \mathscr{F}\bigl(\tau ,x( \tau )\bigr)-\mathscr{F}\bigl(\tau ,\hat{x}(\tau )\bigr) \bigr\vert \nabla \tau \\ &\leq \vert x_{0}-\hat{x}_{0} \vert + \int _{0}^{t}\mathscr{L}(\tau ) \bigl\vert x(\tau )- \hat{x}(\tau ) \bigr\vert \nabla \tau \leq \vert x_{0}- \hat{x}_{0} \vert + \Vert x- \hat{x} \Vert \int _{0}^{t}\mathscr{L}(\tau )\nabla \tau \\ &\leq \vert x_{0}-\hat{x}_{0} \vert + \Vert x- \hat{x} \Vert \mathscr{M}. \end{aligned}$$

Hence we have

$$ \Vert x-\hat{x} \Vert \leq \frac{1}{1-\mathscr{M}} \Vert x_{0}- \hat{x}_{0} \Vert . $$

Then, for any \(\epsilon >0\), let \(\delta =(1-\mathscr{M})\epsilon \) so for \(\Vert x_{0}-\hat{x}_{0} \Vert <\delta \) we have \(\Vert x-\hat{x} \Vert <\epsilon \). Therefore, the solutions of Eq. (1) are stable. This completes the proof. □

Remark 3

From Theorem (6) and Theorem (7), it is clear that a solution of Eq. (1) is asymptotically stable.

Theorem 8

Assume that we have a bounded, continuous function\(\mathscr{F}\)satisfying assumptions\((A_{2})\)and\((A_{3})\). Then using Krasnoselskii’s fixed point theorem, Eq. (1) has at least one solution.

Proof

Let us consider a non-empty, closed, convex subset of a Banach space \(l_{0}^{\infty }\) defined as \(\mathscr{N}= \lbrace x:x\in l_{0}^{\infty }, |x(t)|\leq m, \forall t\in \mathbb{N}_{0} \rbrace \). Furthermore, define operators \(\mathscr{T}_{1}\) and \(\mathscr{T}_{2}\) on \(\mathscr{N}\) as follows:

$$\begin{aligned}& \mathscr{T}_{1}x(t)=x_{0}E_{\overline{\nu }}(\lambda ,t), \\& \mathscr{T}_{2}x(t)=\sum_{\tau =1}^{t}E_{\overline{\nu ,\nu }} \bigl( \lambda ,t-\rho (\tau )\bigr)\mathscr{F}\bigl(\tau ,x(\tau )\bigr)= \int _{0}^{t}E_{ \overline{\nu ,\nu }}\bigl(\lambda ,t-\rho ( \tau )\bigr)\mathscr{F}\bigl(\tau ,x( \tau )\bigr)\nabla \tau . \end{aligned}$$

As is well known, x being fixed point of the operator \(\mathscr{T}x=\mathscr{T}_{1}x+\mathscr{T}_{2}x\) is a solution of Eq. (1). Following the three steps as mentioned in Theorem 4, we present our proof as follows.

In the first step, we prove that \(\mathscr{T}\) maps \(\mathscr{N}\) into \(\mathscr{N}\) i.e. for any \(x,y\in \mathscr{N}\), we have to show that \(\mathscr{T}_{1}x(t)+\mathscr{T}_{2}y(t)\in \mathscr{N}\):

$$\begin{aligned} \bigl\vert \mathscr{T}_{1}x(t)+\mathscr{T}_{2}y(t) \bigr\vert &= \Biggl\vert x_{0}E_{ \overline{\nu }}(\lambda ,t)+\sum _{\tau =1}^{t}E_{ \overline{\nu ,\nu }}\bigl(\lambda ,t- \rho (\tau )\bigr)\mathscr{F}\bigl(\tau ,y( \tau )\bigr) \Biggr\vert \\ &\leq \bigl\vert x_{0}E_{\overline{\nu }}(\lambda ,t) \bigr\vert + \Biggl\vert \sum_{\tau =1}^{t}E_{ \overline{\nu ,\nu }} \bigl(\lambda ,t-\rho (\tau )\bigr)\mathscr{F}\bigl(\tau ,y( \tau )\bigr) \Biggr\vert \\ &\leq \vert x_{0} \vert + \int _{0}^{t} \bigl\vert E_{\overline{\nu ,\nu }}\bigl( \lambda ,t-\rho ( \tau )\bigr) \bigr\vert \bigl\vert \mathscr{F}\bigl(\tau ,y( \tau )\bigr) \bigr\vert \nabla \tau \\ &\leq \vert x_{0} \vert + \int _{0}^{t}\mathscr{L}(\tau ) \bigl\vert y(\tau ) \bigr\vert \nabla \tau \\ &\leq \vert x_{0} \vert + \mathscr{M}m \leq m. \end{aligned}$$

Hence \(\mathscr{T}\mathscr{N}\subset \mathscr{N}\). In the second step, in order to prove that \(\mathscr{T}_{1}\) is continuous, let us consider a sequence \({x_{n}}\) such that \(x_{n}\rightarrow x\).

$$ \bigl\vert \mathscr{T}_{1}x_{n}(t)-\mathscr{T}_{1}x(t) \bigr\vert = \bigl\vert x_{0}E_{ \overline{\nu }}(\lambda ,t)-x_{0}E_{\overline{\nu }}(\lambda ,t) \bigr\vert =0, $$

so for \(x_{n}\rightarrow x\), \(\mathscr{T}_{1}x_{n}\rightarrow \mathscr{T}_{1}x\). Hence \(\mathscr{T}_{1}\) is continuous. Now we show that \(\mathscr{T}_{1}(\mathscr{N})\) resides in a relatively compact set of \(l_{0}^{\infty }\). Taking \(t_{1}\leq t_{2}\leq H\), we have

$$\begin{aligned} \bigl\vert \mathscr{T}_{1}x(t_{2})-\mathscr{T}_{1}x(t_{1}) \bigr\vert &= \bigl\vert x_{0}E_{ \overline{\nu }}(\lambda ,t_{2})-x_{0}E_{\overline{\nu }}(\lambda ,t_{1}) \bigr\vert \\ &= \vert x_{0} \vert \bigl\vert E_{\overline{\nu }}(\lambda ,t_{2})-E_{\overline{\nu }}( \lambda ,t_{1}) \bigr\vert \end{aligned}$$

as \(t_{1}\rightarrow t_{2}\), we get \(|\mathscr{T}_{1}x(t_{2})-\mathscr{T}_{1}x(t_{1})|\rightarrow 0\). Hence \(\mathscr{T}_{1}(\mathscr{N})\) resides in a relatively compact set of \(l_{0}^{\infty }\).

In the last step, we show that \(\mathscr{T}_{2}\) is contraction. Letting \(x,y\in \mathscr{N}\), we have

$$\begin{aligned} & \bigl\vert \mathscr{T}_{2}x(t)-\mathscr{T}_{2}y(t) \bigr\vert \\ &\quad = \Biggl\vert \sum_{\tau =1}^{t}E_{\overline{\nu ,\nu }} \bigl(\lambda ,t-\rho ( \tau )\bigr)\mathscr{F}\bigl(\tau ,x(\tau )\bigr)-\sum _{\tau =1}^{t}E_{ \overline{\nu ,\nu }}\bigl(\lambda ,t- \rho (\tau )\bigr)\mathscr{F}\bigl(\tau ,y( \tau )\bigr) \Biggr\vert \\ &\quad = \biggl\vert \int _{0}^{t}E_{\overline{\nu ,\nu }}\bigl(\lambda ,t-\rho ( \tau )\bigr) \mathscr{F}\bigl(\tau ,x(\tau )\bigr)\nabla \tau - \int _{0}^{t}E_{ \overline{\nu ,\nu }}\bigl(\lambda ,t-\rho ( \tau )\bigr)\mathscr{F}\bigl(\tau ,y( \tau )\bigr)\nabla \tau \biggr\vert \\ &\quad \leq \int _{0}^{t} \bigl\vert E_{\overline{\nu ,\nu }}\bigl( \lambda ,t-\rho (\tau )\bigr) \bigr\vert \bigl\vert \bigl( \mathscr{F}\bigl( \tau ,x(\tau )\bigr)-\mathscr{F}\bigl(\tau ,y(\tau )\bigr)\bigr) \bigr\vert \nabla \tau \\ &\quad \leq \int _{0}^{t}\mathscr{L}(\tau ) \bigl\vert x(\tau )-y(\tau ) \bigr\vert \nabla \tau \\ &\quad \leq \Vert x-y \Vert \int _{0}^{t}\mathscr{L}(\tau )\nabla \tau \leq \mathscr{M} \Vert x-y \Vert . \end{aligned}$$

For \(\mathscr{M}<1\), \(\mathscr{T}_{2}\) is contraction.

Hence according to Theorem 4, \(\mathscr{T}\) has a fixed point in \(\mathscr{N}\) which is a solution of Eq. (1). □

Remark 4

According to Theorem (8), the solutions of Eq. (1) exist and are in \(\mathscr{N}\). Furthermore, if all functions x in \(\mathscr{N}\) tend to 0 as \(t\rightarrow \infty \), then the solutions of Eq. (1) are attractive.

Remark 5

From Theorem 7 and Theorem 8, it is clear that the solution of Eq. (1) is asymptotically stable.

4 Example

Consider the fractional difference equation as follows:

$$ {}^{c}\nabla ^{0.6}_{0}x(t)=-0.5x(t)+t^{\overline{-1.7}} \sin x(t), \quad x(0)=x_{0}, t\in \mathbb{N}_{1},$$
(5)

where \(\mathscr{F}(t,x(t))= t^{\overline{-1.7}}\sin x(t)\), \(t\in \mathbb{N}_{1}\).

According to Lemma 1, a solution of the problem under consideration can be written as

$$ x(t)=x_{0}E_{\overline{0.6}}(-0.5,t)+\sum_{\tau =1}^{t}E_{ \overline{0.6,0.6}} \bigl(-0.5,t-\rho (\tau )\bigr)\tau ^{\overline{-1.7}}\sin x( \tau ). $$
(6)

We can see easily that the function \(\mathscr{F}(t,x(t))\) satisfies condition \((A_{1})\), so by Theorem 5, there exists at least one solution of problem (5).

Moreover,

$$\begin{aligned} \bigl\Vert \mathscr{F}(t,x)-\mathscr{F}(t,y) \bigr\Vert &= \bigl\Vert t^{ \overline{-1.7}}\sin x-t^{\overline{-1.7}}\sin y \bigr\Vert \\ &\leq \mathscr{L}(t) \Vert x-y \Vert , \end{aligned}$$

where \(\mathscr{L}(t)=t^{\overline{-1.7}}\). Calculation shows that \(\mathscr{M}=\sup_{t\in \mathbb{N}_{1}}\int _{0}^{t}\mathscr{L}( \tau )\nabla \tau <1\) and \(\int _{0}^{t} \mathscr{L}(\tau )\nabla \tau \rightarrow 0\) as \(t \rightarrow \infty \). Hence conditions \((A_{2})\) and \((A_{3})\) are satisfied. So by Theorems 6 and 8, there exists at least one solution of problem (5). Moreover, by Theorem 7 the solution is stable. Furthermore, the solution x of problem (5) tends to 0 as \(t\rightarrow \infty \). Hence the solution is asymptotically stable.

5 Conclusion

Stability analysis is one of the most important topics due to its real-life applications in controlling systems. Fractional differential as well as fractional difference equations are widely used in real-life models, fixed point theorems are essential tools for stability analysis. In this paper, we have used Schauder’s fixed point theorem, the Banach contraction principle and Krasnoselskii’s fixed point theorem to study the existence and stability. The analysis of the results heavily depends on the nabla discrete Mittag-Leffler functions.