1 Introduction

The study of FDEs is a vital area for research both theoretically and in application point of view. For the recent applications of FDEs in the field of physics, biophysics, bioengineering, control theory, aerodynamics, biochemistry viscoelasticity, electrochemistry, mathematical biology, economic, signal and image processing etc. (see [1–6]). In last few decades the area related to the existence theory of solutions/positive solutions of the aforesaid equations has been got much attentions from researchers. Plenty of results can be traced out in literature concerning with existence theory for solutions to FDEs, for more discussion and results see [7–21]. Since most of the applied phenomenons and process can be modeled in the form of coupled systems of classical/non-integer order differential equations. Therefore, many authors have been concentrated to establish the existence theory of solutions for the mentioned systems. In this regard, plenty of research articles can be found in literature, few of them are [22–28]. Recently, Sudsutad and Tariboon [22], studied the following class with three point integral boundary conditions:

$$ \textstyle\begin{cases} {}^{C}\mathcal{D}^{\alpha} u(t)=\phi(t,u(t)),\quad t\in\mathcal {J}:=[0,1],\\ u(0)=0, \qquad u(1)=\frac{\delta}{\Gamma(\theta)}\int_{0}^{\eta}(\eta -s)^{\theta-1} u(s) \,ds. \end{cases} $$
(1)

Here \(\alpha\in(1, 2]\), \(\eta, \delta\in(0, 1)\) and we have the nonlinear functions \(\phi\in(\mathcal{J}\times \mathbf{R}, \mathbf{R}^{+})\); \(^{C}\mathcal{D}\) is the Caputo fractional derivative. Sufficient conditions for existence of solutions were formed to the class (1) of FDEs.

Recently another aspects devoted to the stability and numerical analysis of FDEs have been attracted by many researchers. Since in most of the situations, to find exact solutions to nonlinear problems is a challenging task and often it is quite difficult job to search out the exact solution. Therefore, strong motivations have been observed from the researchers to find best approximate solutions to nonlinear problems. For the mentioned task, they used different techniques like decomposition methods [29], homotopy methods [30], and integral transform methods [31], etc. One of the most powerful tools for numerical solutions to nonlinear and linear problems of (DEs) and FDEs is devoted to the generalized differential transform method (GDTM). The mentioned transform has been applied in various articles to treat nonlinear problems of FDEs for numerical solutions; see [32–35]. It is to be noted that there is no classical method to handle the nonlinear problems of FDEs for getting explicit solutions. This is due to the complexity of fractional calculus involved in the considered problems. Therefore, we need a reliable approach to find approximate solutions in the form of series to the proposed problems. On the other hand it is also important and interesting task if corresponding to the approximate solutions stability is achieved. Very recently stability analysis of FDEs has attracted great attention. Various type of stability analysis like Lyapunov type stability, Mittag Leffler type stability has been considered in many papers; see [36–38]. In last few years Hyers–Ulam type stability has given much attention. Because, it is quit useful in many applications like as numerical analysis, optimization, biology, economics, physics, dynamics, where finding the exact solution is quite difficult. For more information about Hyers–Ulam stability, we refer [39–45].

The class of FDEs devoted to integral boundary conditions has been studied by many authors; see [46–48]. This is due to the fact that integral boundary conditions have various applications in applied fields including blood flow problems, chemical engineering, thermo-elasticity, underground water flow, population dynamics, and so forth. Further the concerned differential equations under movable type integral boundary conditions are connected with mathematical physics, mechanics, engineering, economics and so on. They come up when values of the function on the boundary are connected to its value inside the domain. Sometimes, it is better to impose integral conditions because they lead to more precise measure than the local conditions. Therefore in last few years many authors have paid more and more attention to investigate the existence of solutions to FDEs under movable type boundary conditions; see [49–51]. For FDEs with integral boundary conditions and comments on their importance, we refer the reader to [52, 53] and the references therein.

Inspired from the aforesaid work, the aims and objectives of this paper is concerning to establish the existence theory to the following movable type boundary value problem of FDEs:

$$ \textstyle\begin{cases} {}^{C}D^{\alpha} u(t)=\phi(t,v(t)),\qquad {}^{C}D^{\beta} v(t)=\psi(t,u(t)), \quad t\in\mathcal{J},\\ u(0)=0,\qquad v(0)=0 , \qquad u(1)=\int_{0}^{\eta}u(s) \,ds,\qquad v(1)=\int_{0}^{\xi}v(s) \,ds, \end{cases} $$
(2)

where \(\alpha, \beta\in(1, 2]\) and \(\eta, \xi\in(0, 1)\) and \(\phi, \psi\in(\mathcal{J}\times[0, \infty), [0, \infty))\). It is to be noted that boundary conditions in system (2) are movable over the interval \(\mathcal{J}\). Then by using various tools of fixed point theory to obtain sufficient conditions for existence and uniqueness of positive solution. Furthermore, the approximate solutions are obtained by using (GDTM). Also, the Hyers–Ulam stability analysis is carried out for the corresponding numerical solutions about an exact (unique) solution. The established analysis and theory is demonstrated by providing examples. Further we remark that the considered coupled system include two, three, multi point, and nonlocal boundary value problems as special cases.

2 Background materials

In this section, we recall some basic results needed for our investigations.

Definition 2.1

([2–5])

The fractional integral of order \(q\in\mathbf{R_{+}}\) of a function \(x: (0, \infty)\rightarrow \mathbf{R}\) is defined as

$$ \mathcal{I}^{q} x(t)=\frac{1}{\Gamma(q)} \int_{a}^{t}(t-s)^{q-1} x(s) \,ds $$

provided the integral converges on \(\mathbf{R}^{+}\).

Definition 2.2

([2–5])

The derivative for a function \(x\in\mathbf{R}^{+}\rightarrow \mathbf{R}\) defined by

$$ {}^{C}\mathcal{D}^{q} x(t)=\frac{1}{\Gamma(m-q)} \int_{a}^{t} (t-s)^{m-q-1}x^{(m)}(s) \,ds, $$

where \(m=[q]+1\) and \([q]\) represents the integer part of q, is called Caputo fractional derivative.

Lemma 2.3

([1, 6])

The solution of the homogeneous FDE

$${}^{C}\mathcal{D}^{q} x(t)=0 $$

is given by

$$ x(t)=k_{0}+k_{1}t+k_{2}t^{2}+ \cdots+k_{m-1}t^{m-1}, $$

such that \(k_{i}\in\mathbf{R}\), \(j=0,1,2,\dots,m-1\). In view of this result, the solutions of the non-homogeneous FDE

$${}^{C}\mathcal{D}^{q} x(t)=y(t) $$

is given by

$$x(t)=\mathcal{I}^{q}y(t)+k_{0}+k_{1}t+k_{2}t^{2}+ \cdots+k_{m-1}t^{m-1}, $$

for some \(k_{i}\in\mathbf{R}\), \(j=0,1,2,\dots,m-1\).

Lemma 2.4

([1, 6])

For \(q>0\), the following result holds:

$$ \mathcal{I}^{q}\bigl[^{C}\mathcal{D}^{q} x(t) \bigr]=x(t)+k_{0}+k_{1}t+k_{2}t^{2}+ \cdots +k_{m-1}t^{m-1}, $$

where \(k_{i}\in\mathbf{R}\), \(j=0,1,2,\dots,m-1\).

Definition 2.5

([32–34])

For a function \(x(t)\), the generalized differential transform (GDT) is defined by

$$ x(k)=\frac{1}{\Gamma(kq+1)} \biggl[\frac{d^{kq}x(t)}{dt^{kq}} \biggr],\quad \text{at } t=t_{0}, k=1,2,\dots. $$

The inverse differential transform of \(x(k)\) is given by

$$ x(t)=\sum_{k=0}^{\infty}x(k) (t-t_{0})^{qk}. $$

In real world problems, the solution \(x(t)\) is formulated in the finite series form as

$$ x(t)=\sum_{k=0}^{i}x(k) (t-t_{0})^{qk}. $$

Let \(\mathbf{E}= \{u(t): u(t)\in C(\mathcal{J})\}\) be the Banach space endowed with norm \(\Vert u \Vert _{\mathbf{E}}= \max_{t\in\mathcal{J}} \vert u(t) \vert \). Then obviously the product \(\mathbf{E} \times\mathbf{E}\) is also a Banach space endowed with a norm \(\Vert (u,v) \Vert _{\mathbf{E} \times\mathbf{E} }=\max\{ \Vert u \Vert _{\mathbf{E}}, \Vert v \Vert _{\mathbf{E}}\}\).

Definition 2.6

([40, 41])

Let E be a Banach space and \(\mathcal{N}:\mathbf {E}\rightarrow\mathbf{E}\) be an operator. Then the operator equation given by

$$ x= \mathcal{N}x $$
(3)

is said to be Hyers–Ulam stable if for the inequality given as

$$ \vert x-\mathcal{N}x \vert \leq\epsilon, \quad t\in \mathcal{J}, $$

there exists a constant \(\mathcal{K}_{\mathcal{N}}>0\) such that for each solution \(x\in C(\mathcal{J}, \mathbf{R})\), of (3), we have a unique solution \(z\in C(\mathcal{J}, \mathbf{R})\) of the operator equation (3) satisfying the given relation

$$ \bigl\vert x(t)-z(t) \bigr\vert \leq\mathcal{K}_{\mathcal{N}} \epsilon,\quad t\in\mathcal{J}. $$

Consider \(\mathcal{N}_{i}:\mathbf{E}\rightarrow\mathbf{E}\), for \(i=1,2\) be two operators, then in view of Definition 2.6, the coupled system of operators equations given as

$$ \begin{aligned} &u(t) = \mathcal{N}_{1} v(t), \\ &v(t) = \mathcal{N}_{2} u(t), \end{aligned} $$
(4)

is said to be Hyers–Ulam stable if for the system of inequalities

$$ \begin{aligned} & \bigl\vert u(t)- \mathcal{N}_{1}v(t) \bigr\vert \leq\varepsilon_{1},\quad t \in\mathcal{J}, \\ & \bigl\vert v(t)- \mathcal{N}_{2}u(t) \bigr\vert \leq \varepsilon_{2},\quad t\in\mathcal{J}, \end{aligned} $$
(5)

there exist constants \(\varepsilon_{1},\varepsilon_{2}\), such that for any solution \((u, v)\) of (4) there is a unique solution \((x, y)\) of system (4) with \(K_{\mathcal{N}_{1}}>0\), \(K_{\mathcal {N}_{2}}>0\), which satisfy the following result:

$$\begin{aligned} \begin{aligned} & \bigl\vert u(t)-x(t) \bigr\vert \leq K_{\mathcal{N}_{1}}\varepsilon_{1}, \quad t\in\mathcal{J}, \\ & \bigl\vert v(t)-y(t) \bigr\vert \leq K_{\mathcal{N}_{2}}\varepsilon_{2}, \quad t\in\mathcal{J}. \end{aligned} \end{aligned}$$

3 Existence results

In this section we obtain the equivalent coupled system of integral equations of the considered problem (2). Further we also establish the required conditions for the existence of at least one solution for the proposed problem.

Theorem 3.1

For \(h\in C(\mathcal{J}, \textbf{R})\), the linear fractional order boundary value problem

$$ \begin{aligned} & {}^{C}\mathcal{D}^{\alpha} u(t)=h(t),\quad 1< \alpha\leq2, t\in\mathcal{J}, \\ & u(0)=0,\qquad u(1)= \int_{0}^{\eta}u(s) \,ds, \quad \eta\in(0, 1) \end{aligned} $$
(6)

has a solution given by

$$\begin{aligned} u(t) =&\frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-s)^{\alpha-1}h(s) \,ds \\ &{}-\frac{2t}{{(2-\eta^{2})}{\Gamma(\alpha)}} \biggl[ \int _{0}^{1}(1-s)^{\alpha-1} h(s) \,ds - \int_{0}^{\eta}\biggl( \int_{0}^{s}(s-\tau)^{\alpha-1}\biggr)h(\tau)\,d \tau ) \,ds \biggr]. \end{aligned}$$
(7)

Proof

Thanks to Lemma 2.4 and upon application of \(\mathcal{I}^{\alpha }\) on both sides of (6) yields

$$ u(t)=\mathcal{I}^{\alpha}h(t)-k_{0}-k_{1} t,\quad k_{0}, k_{1}\in\mathbf{R}. $$
(8)

From which we get

$$ \int_{0}^{\eta}u(s) \,ds=\frac{1}{\Gamma(\alpha)} \int_{0}^{\eta}\biggl( \int_{0}^{s}(s-\tau)^{\alpha-1} h(\tau) \,d\tau \biggr) \,ds-k_{0}\eta- k_{1}\frac{\eta^{2}}{2}. $$
(9)

In view of condition \(u(0)=0\) from (9), we get \(k_{0}=0\). Further using the boundary condition \(u(1)=\int_{0}^{\eta}u(s) \,ds\), then (9) produces

$$\begin{aligned} k_{1}=\frac{2}{(2-\eta^{2})\Gamma(\alpha)} \biggl[ \int_{0}^{1}(1-s)^{\alpha-1}h(s) \,ds - \int_{0}^{\eta}\biggl( \int_{0}^{s}(s-\tau)^{\alpha-1} h(\tau) \,d\tau \biggr) \,ds \biggr]. \end{aligned}$$

Plugging the values of \(k_{0}\) and \(k_{1}\) in (8), we receive the solution (7) of linear boundary value problems (6). □

In view of Theorem 3.1, we get the following lemma.

Lemma 3.2

The system of boundary value problems (2) under consideration is equivalent to the following coupled system of nonlinear integral equations:

$$ \left \{ \textstyle\begin{array}{rcl} u(t)&=&\frac{1}{\Gamma(\alpha)}\int_{0}^{t}(t-s)^{\alpha-1}\phi(s,v(s)) \,ds\\ &&{}-\frac{2t}{{(2-\eta^{2})}{\Gamma(\alpha)}} [\int _{0}^{1}(1-s)^{\alpha-1} \phi(s,v(s)) \,ds\\ &&{} -\int_{0}^{\eta}(\int_{0}^{s}(s-\tau)^{\alpha-1})\phi(\tau,v(\tau))\,d\tau ) \,ds ],\\ v(t)&=&\frac{1}{\Gamma(\beta)}\int_{0}^{t}(t-s)^{\beta-1}\psi(s,u(s)) \,ds\\ &&{}-\frac{2t}{{(2-\xi^{2})}{\Gamma(\beta)}} [\int _{0}^{1}(1-s)^{\beta-1} \psi(s,u(s)) \,ds\\ &&{} -\int_{0}^{\xi}(\int_{0}^{s}(s-\tau)^{\beta-1})\psi(\tau,u(\tau))\,d\tau ) \,ds ]. \end{array}\displaystyle \right . $$
(10)

Further, define \(\mathcal{N}_{1} :\mathbf{E}\rightarrow\mathbf{E}\) and \(\mathcal{N}_{2}:\mathbf{E}\rightarrow\mathbf{E} \) by

$$ \begin{aligned} \mathcal{N}_{1}v(t)={}& \frac{1}{\Gamma(\alpha)} \int _{0}^{t}(t-s)^{\alpha-1}\phi\bigl(s,v(s) \bigr) \,ds \\ &{} -\frac{2t}{{(2-\eta^{2})}{\Gamma(\alpha)}} \biggl[ \int_{0}^{1}(1-s)^{\alpha-1} \phi\bigl(s,v(s) \bigr) \,ds \\ &{} - \int_{0}^{\eta}\biggl( \int_{0}^{s}(s-\tau)^{\alpha-1}\biggr)\phi\bigl( \tau,v(\tau)\bigr)\,d\tau ) \,ds \biggr], \\ \mathcal{N}_{2}u(t)={}&\frac{1}{\Gamma(\beta)} \int_{0}^{t}(t-s)^{\beta-1}\psi \bigl(s,u(s) \bigr) \,ds \\ &{} -\frac{2t}{{(2-\xi^{2})}{\Gamma(\beta)}} \biggl[ \int_{0}^{1}(1-s)^{\beta-1} \psi\bigl(s,u(s) \bigr) \,ds \\ &{} - \int_{0}^{\xi}\biggl( \int_{0}^{s}(s-\tau)^{\beta-1}\biggr)\psi\bigl( \tau,u(\tau)\bigr)\,d\tau ) \,ds \biggr]. \end{aligned} $$
(11)

Thanks to Lemma 3.2, the corresponding coupled system of operators equations to coupled system (10) of integral equations is

$$ \textstyle\begin{cases} u(t)= \mathcal{N}_{1}v(t),\\ v(t)= \mathcal{N}_{2}u(t). \end{cases} $$
(12)

Therefore, we define \(\mathcal{N}: \mathbf{E}\times\mathbf {E}\rightarrow\mathbf{E}\times\mathbf{E} \) by \(\mathcal{N}(u,v)=(\mathcal{N}_{1}v,\mathcal{N}_{2}u)\). Therefore we investigate the fixed points of the operator \(\mathcal{N}\) which are the corresponding solutions of the proposed problem (10).

Lemma 3.3

(Krasnoselskii’s fixed point theorem)

If \(\mathbf{C}\subset\mathbf{E}\) be a closed convex and nonempty set and \(\mathbf{T}, \mathbf{S}\) be two operators such that

  1. (i)

    \(\mathbf{T}w_{1}+\mathbf{S}w_{2} \in\mathbf{C} \) for every \(w_{1}, w_{2} \in\mathbf{C}\);

  2. (ii)

    T is compact and continuous;

  3. (iii)

    S is contraction mapping,

then one can find at least one \(w \in\mathbf{C}\) with \(w=\mathbf {T}w+\mathbf{S}w\).

The given notations are adopted for easiness

$$\Delta_{1}=\frac{1}{\Gamma (\alpha+1)} \biggl(1+\frac{2[\alpha+1+\eta^{\alpha+1}]}{(\alpha+1)(2-\eta ^{2})} \biggr) \quad \text{and}\quad \Delta_{2}= \frac{1}{\Gamma (\beta+1)} \biggl(1+\frac{2[\beta+1+\xi^{\beta+1}]}{(\beta+1)(2-\xi ^{2})} \biggr). $$

We assume that the following hypotheses hold:

\((C_{1})\) :

\(\phi, \psi: \mathcal{J} \times[0, \infty)\rightarrow [0, \infty)\) are continuous, for \(t \in\mathcal{J}, u, v, \bar{u}, \bar{v} \in\mathbf{R}\);

\((C_{2})\) :

There exists a constant \(\Lambda_{\phi}>0\) such that

$$\bigl\lvert \phi(t,u)-\phi(t,\bar{u})\bigr\rvert \leq\Lambda_{\phi}\lvert u-\bar {u}\rvert, $$

for \(t \in\mathcal{J}, u,\bar{u} \in\mathbf{R}\);

\((C_{3})\) :

There exists a constant \(\Lambda_{\psi}>0\) such that

$$\bigl\lvert \psi(t,v)-\psi(t,\bar{v})\bigr\rvert \leq\Lambda_{\psi}\lvert v-\bar{v} \rvert, $$

for \(t \in\mathcal{J}, v,\bar{v} \in\mathbf{R}\).

Fist of all, we prove uniqueness of the solutions via the Banach contraction theorem.

Theorem 3.4

If assumptions \((C_{1})\)–\((C_{3})\) hold together with \(\Delta_{1}\Lambda _{\phi}<1\) and \(\Delta_{2}\Lambda_{\psi}<1\), then the BVP (2) under our consideration has a unique solution.

Proof

Let us take \(\mathbf{A}=\max_{t \in\mathcal{J}} \vert \phi(t,0) \vert \text{ and } \mathbf{B}=\max_{t \in \mathcal{J}} \vert \psi(t,0) \vert \) and choose

$$r\geq\max \biggl\{ \frac{\Delta_{1}\mathbf{A}}{1-\Delta_{1}\Lambda_{\phi}}, \frac{\Delta_{2}\mathbf{B}}{1-\Delta_{2}\Lambda_{\psi}} \biggr\} . $$

Let

$$\mathbf{C}=\bigl\{ (u,v) \in\mathbf{E}\times\mathbf{E} : \bigl\Vert (u,v) \bigr\Vert _{\mathbf {E}\times\mathbf{E}}\leq r\bigr\} \subset\mathbf{E}\times\mathbf{E} $$

be a closed bounded and convex set. Then, under the assumptions \((C_{1})\) and \((C_{2})\), taking \((u,v)\in\mathbf{C}\), we have

$$\begin{aligned} \bigl\vert \mathcal{N}_{1}v(t) \bigr\vert \leq&\frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-s)^{\alpha-1} \bigl\vert \phi \bigl(s,v(s)\bigr) \bigr\vert \,ds +\frac{ \vert 2t \vert }{{(2-\eta^{2})}{\Gamma(\alpha)}} \int_{0}^{1}(1-s)^{\alpha-1} \bigl\vert \phi \bigl(s,v(s)\bigr) \bigr\vert \,ds \\ &{} +\frac{ \vert 2t \vert }{{(2-\eta^{2})}{\Gamma(\alpha)}} \int_{0}^{\eta}\biggl( \int_{0}^{s}(s-\tau)^{\alpha-1} \bigl\vert \phi\bigl(\tau,v(\tau)\bigr) \bigr\vert \,d\tau \biggr) \,ds \\ \leq &\frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-s)^{\alpha-1}\bigl( \bigl\vert \phi\bigl(s,v(s)\bigr)-\phi (s,0) \bigr\vert + \bigl\vert \phi(s,0) \bigr\vert \bigr) \,ds \\ &{}+\frac{ \vert 2t \vert }{{(2-\eta^{2})}{\Gamma(\alpha)}} \int_{0}^{1}(1-s)^{\alpha-1}\bigl( \bigl\vert \phi\bigl(s,v(s)\bigr)-\phi(s,0) \bigr\vert + \bigl\vert \phi(s,0) \bigr\vert \bigr) \,ds \\ &{} +\frac{ \vert 2t \vert }{{(2-\eta^{2})}{\Gamma(\alpha)}} \int_{0}^{\eta}\biggl( \int_{0}^{s}(s-\tau)^{\alpha-1}\bigl( \bigl\vert \phi\bigl(\tau,v(\tau)\bigr)-\phi (\tau,0) \bigr\vert + \bigl\vert \phi(\tau,0) \bigr\vert \bigr)\,d\tau \biggr) \,ds \\ \leq&\frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-s)^{\alpha-1}( \Lambda_{\phi}r+\mathbf{A}) \,ds +\frac{ \vert 2t \vert }{{(2-\eta^{2})}{\Gamma(\alpha)}} \int_{0}^{1}(1-s)^{\alpha -1}( \Lambda_{\phi}r+\mathbf{A}) \,ds \\ &{}+\frac{ \vert 2t \vert }{{(2-\eta^{2})}{\Gamma(\alpha)}} \int_{0}^{\eta}\biggl( \int_{0}^{s}(s-\tau)^{\alpha-1}( \Lambda_{\phi}r+\mathbf{A})\,d\tau \biggr) \,ds, \end{aligned}$$

which yields

$$\begin{aligned} \bigl\vert \mathcal{N}_{1}v(t) \bigr\vert \leq\frac{(\Lambda_{\phi}r+\mathbf{A})}{\Gamma (\alpha+1)} \biggl(t^{\alpha}+\frac{ \vert 2t \vert }{{(2-\eta^{2})}} +\frac{ \vert 2t \vert }{{(2-\eta^{2})(\alpha+1)}}\eta^{\alpha+1} \biggr). \end{aligned}$$

Therefore, on using \(t\leq1\), we have

$$ \Vert \mathcal{N}_{1}v \Vert _{\mathbf{E}}\leq \frac{(\Lambda_{\phi}r+\mathbf {A})}{\Gamma(\alpha+1)} \biggl(1+\frac{2(\alpha+1+\eta^{\alpha +1})}{{(2-\eta^{2})(\alpha+1)}} \biggr) \leq(\Lambda_{\phi}r+\mathbf{A})\Delta_{1}\leq r. $$
(13)

Along the same lines, one has

$$ \Vert \mathcal{N}_{2}u \Vert _{\mathbf{E}}\leq( \Lambda_{\psi}r+\mathbf{B})\Delta _{2}\leq r. $$
(14)

Thus taking (13) and (14) together, we get

$$\bigl\Vert \mathcal{N}(u,v) \bigr\Vert _{\mathbf{E}\times\mathbf{E}}\leq r. $$

Also, taking \((u,v), (\bar{u}, \bar{v}) \in\mathbf{C}\), \(t\in\mathcal {J}\), we consider

$$\begin{aligned} \bigl\vert \mathcal{N}_{1}v(t)- \mathcal{N}_{1}\bar{v}(t) \bigr\vert \leq&\frac{1}{\Gamma (\alpha)} \int_{0}^{t}(t-s)^{\alpha-1} \bigl\vert \phi \bigl(s,v(s)\bigr)-\phi\bigl(s,\bar{v}(s)\bigr) \bigr\vert \,ds \\ &{}+\frac{ \vert 2t \vert }{(2-\eta^{2})\Gamma(\alpha)} \int_{0}^{1}(1-s)^{\alpha-1} \bigl\vert \phi \bigl(s,v(s)\bigr)-\phi\bigl(s,\bar{v}(s)\bigr) \bigr\vert \,ds \\ &{}+\frac{ \vert 2t \vert }{(2-\eta^{2})\Gamma(\alpha)} \int_{0}^{\eta}\biggl( \int _{0}^{1}(s-\tau)^{\alpha-1} \bigl\vert \phi\bigl(s,v(s)\bigr)-\phi\bigl(s,\bar{v}(s)\bigr) \bigr\vert \,d\tau \biggr) \,ds \\ \leq&\frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-s)^{\alpha-1} \Lambda_{\phi}\bigl\vert v(s)-\bar{v}(s) \bigr\vert \,ds\\ &{} + \frac{ \vert 2t \vert }{(2-\eta^{2})\Gamma (\alpha)} \int_{0}^{1}(1-s)^{\alpha-1} \Lambda_{\phi}\bigl\vert v(s)-\bar{v}(s) \bigr\vert \,ds \\ &{} +\frac{ \vert 2t \vert }{(2-\eta^{2})\Gamma (\alpha)} \int_{0}^{\eta}\biggl( \int_{0}^{1}(1-s)^{\alpha-1} \Lambda_{\phi}\bigl\vert v(s)-\bar {v}(s) \bigr\vert \,d\tau \biggr) \,ds, \end{aligned}$$

which implies that

$$\begin{aligned} \Vert \mathcal{N}_{1}v-\mathcal{N}_{1}\bar{v} \Vert _{\mathbf{E}}\leq\frac {\Lambda_{\phi}}{\Gamma (\alpha+1)} \biggl[ \Vert v-\bar{v} \Vert _{\mathbf{E}}+\frac{2 \Vert v-\bar{v} \Vert _{\mathbf{E}}}{(2-\eta^{2})} +\frac{2\eta^{\alpha+1} \Vert v-\bar{v} \Vert _{\mathbf{E}}}{(2-\eta^{2})(\alpha +1)} \biggr]\leq \Delta_{1}\Lambda_{\phi} \Vert v-\bar{v} \Vert _{\mathbf{E}}. \end{aligned}$$

In the same fashion, we can also get

$$\begin{aligned} \Vert \mathcal{N}_{2}u-\mathcal{N}_{2}\bar{u} \Vert _{\mathbf{E}}\leq\Delta _{2}\Lambda_{\psi} \Vert u-\bar{u} \Vert _{\mathbf{E}}. \end{aligned}$$
(15)

Thanks to the conditions \(\Delta_{1}\Lambda_{\phi}<1\) and \(\Delta_{2}\Lambda _{\psi}<1\)

$$ \bigl\Vert \mathcal{N}(u,v)-\mathcal{N}(\bar{u},\bar{v}) \bigr\Vert _{\mathbf{E}\times \mathbf{E}}\leq \bigl\Vert (u,v)-(\bar{u},\bar{v}) \bigr\Vert _{\mathbf{E}\times \mathbf{E}}. $$

Thus \(\mathcal{N}\) is a contraction operator. In view of the Banach contraction theorem, the considered BVP (2) has a unique solution. □

Further, we define the operators \(\mathbf{T}_{1}, \mathbf{S}_{1} :\mathbf {E}\rightarrow\mathbf{E}\) and \(\mathbf{T}_{2}, \mathbf{S}_{2} :\mathbf{E}\rightarrow\mathbf{E}\) by

$$ \begin{aligned} &\mathbf{T}_{1}v(t)= \frac{1}{\alpha} \int_{0}^{t}(t-s)^{\alpha-1}\phi \bigl(s,v(s) \bigr) \,ds, \\ &\begin{aligned} \mathbf{S}_{1}v(t)={}&{-}\frac{2t}{\Gamma(\alpha) (2-\eta^{2})} \biggl[ \int _{0}^{\eta}\biggl( \int_{0}^{s} (s-\tau)^{\alpha-1} \phi\bigl( \tau,v(\tau)\bigr)\,d\tau \biggr) \,ds\\ &{}- \int_{0}^{1}(1-s)^{\alpha-1}\phi \bigl(s,v(s) \bigr) \,ds \biggr], \end{aligned} \\ & \mathbf{T}_{2}u(t)=\frac{1}{\beta} \int_{0}^{t}(t-s)^{\beta-1}\psi\bigl(s,u(s) \bigr) \,ds, \\ & \begin{aligned} \mathbf{S}_{2}u(t)={}&{-}\frac{2t}{\Gamma(\beta) (2-\xi^{2})} \biggl[ \int_{0}^{\xi}\biggl( \int_{0}^{s} (s-\tau)^{\beta-1}\psi\bigl( \tau,u(\tau)\bigr)\,d\tau \biggr) \,ds\\ &{}- \int_{0}^{1}(1-s)^{\beta-1}\psi\bigl(s,u(s) \bigr) \,ds \biggr]. \end{aligned} \end{aligned} $$
(16)

In view of (16), we may write \(\mathcal{N}_{1}=\mathbf{T}_{1}+\mathbf {S}_{1}\), \(\mathcal{N}_{2}=\mathbf{T}_{2}+\mathbf{S}_{2}\) and, consequently, the operator N can be expressed as

$$\mathbf{N}=\mathbf{T}+\mathbf{S},\quad \text{such that } \mathbf{T}(u,v)=( \mathbf{T}_{1}v,\mathbf{T}_{2}u), \mathbf{S}(u,v)=(\mathbf {S}_{1}v,\mathbf{S}_{2}u). $$

Assume that for the positive constants \(\mathcal{M}_{\phi}\), \(\mathcal {M}_{\psi}\), \(\Omega_{\phi}\), \(\Omega_{\psi}\), the growth conditions provided by

\((C_{4})\) :

\(\vert \phi(t,v(t)) \vert \leq\mathcal{M}_{\phi} \Vert v \Vert _{\mathbf{E}}+\Omega_{\phi}\) over \(\mathcal{J}\times\mathbf{E}\) and \(\vert \psi(t,u(t)) \vert \leq\mathcal{M}_{\psi} \Vert u \Vert _{\mathbf{E}}+\Omega_{\psi}\) over \(\mathcal{J}\times\mathbf{E}\) are satisfied.

Theorem 3.5

Under the hypotheses \((C_{1}), (C_{4})\) and conditions

$$\frac{2\Lambda_{\phi}(\alpha+1+\eta^{\alpha+1})}{\Gamma(\alpha+2)(2-\eta ^{2})}< 1, \qquad \frac{2\Lambda_{\psi}(\beta+1+\xi^{\beta+1})}{\Gamma (\beta+2)(2-\xi^{2})}< 1, $$

hold. Then the BVP (2) proposed by us has at least one solution.

Proof

The continuity of ϕ and ψ implies that the operator \(\mathcal{N}\) is continuous. Let \(\mathbf{D}\subset\mathbf{C} \subseteq\mathbf{E}\times \mathbf{E}\) be bounded set. Then, for all \((u,v)\in\mathbf{D}\) and using \((C_{4})\), one has

$$\begin{aligned} \bigl\vert (\mathbf{T}_{1}v) (t) \bigr\vert = \biggl\vert \frac{1}{\Gamma(\alpha)} \int _{0}^{t}(t-s)^{\alpha-1}\phi\bigl(s,v(s) \bigr) \,ds \biggr\vert \leq\frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-s)^{\alpha-1}\bigl( \Omega_{\phi} \Vert v \Vert _{\mathbf{E}}+\mathcal{M}_{\phi} \bigr) \,ds, \end{aligned}$$

which implies that

$$\Vert \mathbf{T}_{1}v \Vert _{\mathbf{E}}\leq \frac{(\Omega_{\phi} \Vert v \Vert _{\mathbf {E}}+\mathcal{M}_{\mathcal{\phi}})}{\Gamma(\alpha+1)}. $$

In the same fashion, we get

$$\Vert \mathbf{T}_{2}u \Vert _{\mathbf{E}}\leq \frac{(\Omega_{\psi} \Vert u \Vert _{\mathbf {E}}+\mathcal{M}_{\psi})}{\Gamma(\beta+1)}. $$

Therefore the boundedness of \(\mathbf{T}(\mathbf{D})\) follows.

To show that S is equi-continuous, let \(t, \hat{t}\in[0,1]\) with \(t <\hat{t}\) and any \((u,v)\in\mathbf{E}\times\mathbf{E}\), we have

$$\begin{aligned} \bigl\vert \mathbf{T}_{1}v(t_{1})-\mathbf{T}_{1}v(t_{2}) \bigr\vert =&\frac{1}{\Gamma(\alpha )} \biggl\vert \int_{0}^{t}\bigl[(t_{2}-s)^{\alpha-1}-(t_{1}-s)^{\alpha-1} \bigr]\phi \bigl(s,v(s)\bigr) \,ds \\ &{}+ \int_{t}^{\hat{t}}(t_{2}-s)^{\alpha-1}\phi \bigl(s,v(s)\bigr) \,ds \biggr\vert , \end{aligned}$$

which implies that

$$\begin{aligned} \bigl\Vert \mathbf{T}_{1}v(t_{1})- \mathbf{T}_{1}v(t_{2}) \bigr\Vert _{{\mathbf{E}}} \leq \frac{(\Omega_{\phi} \Vert v \Vert _{\mathbf{E}}+ \mathcal{M}_{\phi})}{\Gamma(\alpha+1)} \bigl\vert 2(\hat{t}-t)^{\alpha }+{t}^{\alpha}-{ \hat{t}}^{\alpha} \bigr\vert . \end{aligned}$$
(17)

Repeating the same arguments, we have

$$\begin{aligned} \bigl\Vert \mathbf{T}_{2}u(t_{1})- \mathbf{T}_{2}u(t_{2}) \bigr\Vert _{{\mathbf{E}}} \leq \frac{(\Omega_{\psi} \Vert u \Vert _{{\mathbf{E}}}+ \mathcal{M}_{\psi})}{\Gamma (\beta+1)} \bigl\vert 2(\hat{t}-t)^{\beta}+{t}^{\beta}-{ \hat{t}}^{\beta} \bigr\vert . \end{aligned}$$
(18)

As in the right hand sides of (17) and (18), when \(t\rightarrow\hat{t}\), then the right hand sides of the mentioned relations approach to zero. Therefore using Arzela–Ascoli’s theorem, T is equi-continuous and compact.

Further, we need to prove that S is a contraction. Taking \(v, \bar{v} \in\mathbf{E}\), we get

$$\begin{aligned} \begin{aligned} \bigl\vert \mathbf{S}_{1}v(t)- \mathbf{S}_{1}\bar{v}(t) \bigr\vert \leq{}& \frac{ \vert 2t \vert }{(2-\eta ^{2})\Gamma (\alpha)} \int_{0}^{1}(1-s)^{\alpha-1} \bigl\vert \phi \bigl(s,v(s)\bigr)-\phi\bigl(s,\bar{v}(s)\bigr) \bigr\vert \,ds \\ &{}+\frac{ \vert 2t \vert }{(2-\eta^{2})\Gamma (\alpha)} \int_{0}^{\eta}\biggl( \int_{0}^{1}(s-\tau)^{\alpha-1} \bigl\vert \phi\bigl(s,v(s)\bigr)-\phi \bigl(s,\bar{v}(s)\bigr) \bigr\vert \,d\tau \biggr) \,ds \\ \leq{} & \frac{2 \vert t \vert \Lambda_{\phi} \vert v-\bar{v} \vert (\alpha+1+\eta^{\alpha+1})}{ \vert 2-\eta^{2} \vert \Gamma(\alpha+2)}, \end{aligned} \end{aligned}$$

which yields \(\Vert \mathbf{S}_{1}v-\mathbf{S}_{1}\bar{v} \Vert _{\mathbf{E}} \leq \frac{2\Lambda_{\phi}(\alpha+1+\eta^{\alpha+1})}{(2-\eta^{2})\Gamma(\alpha +2)} \Vert v-\bar{v} \Vert _{\mathbf{E}}\). Along the same lines, one can get

$$\begin{aligned} \Vert \mathbf{S}_{2}u-\mathbf{S}_{2}\bar{u} \Vert _{\mathbf{E}} \leq \frac{2\Lambda_{\psi}(\beta+1+\xi^{\beta+1})}{(2-\xi^{2})\Gamma(\beta +2)} \Vert u-\bar{u} \Vert _{\mathbf{E}}. \end{aligned}$$

Therefore S is a contraction, using Lemma 3.3, we see that \(\mathcal{N}\) has at least one fixed point which is the corresponding solution of (2). □

4 Numerical solutions for the problem (2)

Numerical methods play a key role in the area of nonlinear mathematics. To find an exact solution to every BVP of classical nonlinear differential equations is nearly impossible. Thus, it would be quite impossible to solve BVPs of nonlinear FDEs equations for their exact solutions. Therefore without implementing numerical methods it is not possible to obtain good numerical solution to a BVP of FDEs. Further numerical methods are powerful tools to be used to find approximate solutions of aforementioned problems. Some of these methods use transformation in order to reduce equations into simpler equations or systems of equations and some other methods give the solution in a series form which converges to the exact solution of an equation or system of equations. There are large number of numerical methods which have been used to find approximate solutions to nonlinear BVPs of DEs and FDEs in literature. One of them is the differential transform method. The said method was first introduced by Zhou [54] who solved linear and nonlinear initial value problems in electric circuit analysis. Further the aforesaid transform was extended to generalized form in [55]. The authors named this new version the generalized differential transform (GDTM). With the help of this method one constructs an analytical solution in the form of a polynomial. It is different from the traditional higher order Taylor series method, which requires symbolic computation of the necessary derivatives of the data functions. The Taylor series method computationally takes a long time for large orders and its computational cost is also high. The GDTM is an iterative procedure for obtaining analytic Taylor series solutions to FDEs with boundary or initial conditions. Keeping in mind the mentioned point, we will use generalized differential transform (GDTM) to obtain numerical solutions to the considered BVP (2). In view of (GDTM), the kth order approximate solution of the proposed problem is given as

$$ u(t)=\sum_{k=0}^{i} U(k)t^{k\sigma}, \qquad v(t)=\sum_{k=0}^{i} V(k)t^{k\sigma}. $$
(19)

Here σ is the order of the differential transform. σ must be selected such that it is compatible with both orders α, β, that is, there exist l, \(m,n\in\mathbf{N}\) such that \(l\sigma=1\), \(m\sigma=\alpha\), and \(n\sigma=\beta\). \(U(k)\) and \(V(k)\) are the generalized differential transforms of \(u(t)\) and \(v(t)\), and satisfies the relation

$$ \begin{aligned} &U(k+m)=\frac{\Gamma((m+k)\sigma-\alpha+1)}{\Gamma((m+k)\sigma+1)} F\bigl(k,V(k) \bigr), \\ &V(k+n)=\frac{\Gamma((n+k)\sigma-\beta+1)}{\Gamma((n+k)\sigma+1)} G\bigl(k,U(k)\bigr). \end{aligned} $$
(20)

Here \(F(k,V(k))\) and \(G(k,U(k))\) are the sigma order differential transform of \(\phi(t,v(t)\) and \(\psi(t,u(t)\), respectively, and can be calculated using theorems developed in [32].

Using the first initial condition, we have \(U(0)=0\) and \(V(0) =0\). Further, for initial conditions, we have

$$ \begin{aligned} &U(k)=0,\quad \text{for all }k \mbox{ such that }k\sigma < 1, \\ &V(k)=0,\quad \text{for all }k\mbox{ such that }k\sigma < 1, \\ &U(l)=c_{1},\qquad V(l)=c_{2}, \\ &U(k)=0,\quad \text{for } l< k< m, \\ &V(k)=0,\quad \text{for } l< k< n. \end{aligned} $$
(21)

Here \(c_{1}\) and \(c_{2}\) are unknown constants, which can be obtained using the moving boundary conditions. Using the recurrence relation (20), we can obtain a solution in the following form:

$$ \begin{aligned}& u(t)=\sum_{k=0}^{i} U_{(c_{1},c_{2})}(k) t^{k\sigma}, \\ & v(t)=\sum_{k=0}^{i} V_{(c_{1},c_{2})}(k) t^{k\sigma}. \end{aligned} $$
(22)

Here \(U_{(c_{1},c_{2})}(k),V_{(c_{1},c_{2})}(k)\) are coefficients still depending on \(c_{1}\) and \(c_{2}\). Using the moving boundary conditions, we may write

$$ \begin{aligned} &u(1)=\sum_{k=0}^{i} U_{(c_{1},c_{2})}(k),\qquad v(1)=\sum_{k=0}^{i} V_{(c_{1},c_{2})}(k), \\ & \int_{0}^{\eta}u(t)\,dt=\sum _{k=0}^{i} U_{(c_{1},c_{2})}(k)\frac{\Gamma(1+k\sigma )}{\Gamma(2+k\sigma)} \eta^{k\sigma+1}, \\ & \int_{0}^{\xi}v(t)\,dt=\sum _{k=0}^{i} V_{(c_{1},c_{2})}(k)\frac{\Gamma(1+k\sigma )}{\Gamma(2+k\sigma)} \xi^{k\sigma+1}. \end{aligned} $$
(23)

From (23), we can easily get two relations of the unknown \(c_{1}\) and \(c_{2}\) in the form

$$ \begin{aligned} &\sum_{k=0}^{i} U_{(c_{1},c_{2})}(k) \biggl(1-\frac{\Gamma(1+k\sigma)}{\Gamma (2+k\sigma)}\eta^{k\sigma+1} \biggr)=0, \\ &\sum_{k=0}^{i} V_{(c_{1},c_{2})}(k) \biggl(1-\frac{\Gamma(1+k\sigma)}{\Gamma (2+k\sigma)}\xi^{k\sigma+1} \biggr)=0. \end{aligned} $$
(24)

Equation (24) can be solved for \(c_{1}\) and \(c_{2}\) and using the values of \(c_{1}\) and \(c_{2}\) in Eq. (22), we get the approximate solution of the proposed problem (2).

5 Hyers–Ulam stability

In this section, we provide some sufficient conditions for Hyers–Ulam type stability results to the solutions of BVPs (2) with movable type integral boundary conditions. The method which was provided by Hyers, and which produces the additive mapping is called a direct method. This method is the most important and most powerful tool for studying the stability of various differential, functional and integral equations. The classical concept of Hyers–Ulam stability has applicable significance since it means that if we are dealing with Hyers–Ulam stable system then one does not seek the exact solution. All what is required is to find a function which satisfies a suitable approximation inequations. It is quite remarkable that Hyers–Ulam stability concept is very useful in many applications, such as numerical analysis, optimization, etc., where finding the exact solution is quite difficult or impossible for a problem of differential and integral equations. We find sufficient conditions to guarantee the movable integrable sample path is Hyers–Ulam stable. To derive the formal results about the Hyers–Ulam stability for BVPs (2), we give the following conditions first.

Let there exist functions \(w,z \in C(\mathcal{J}, \mathbf{R})\) which depend upon \(u, v\), respectively, such that

  1. (i)

    \(\vert w(t) \vert \leq\varepsilon_{1}\), \(\vert z(t) \vert \leq\varepsilon_{2}\), \(t\in\mathcal{J}\);

  2. (ii)

    \(\left \{ \begin{array}{ll} {}^{C}\mathcal{D}^{\alpha}u(t)=\phi(t, v(t))+w(t),\ t\in\mathcal{J,} \\ {}^{C}\mathcal{D}^{\beta}v(t)=\psi(t, u(t))+z(t),\ t\in\mathcal{J}. \end{array} \right .\)

Lemma 5.1

Let \((u, v)\in C(\mathcal{J}, \mathbf{R})\times C(\mathcal{J}, \mathbf{R})\) be any solution of the system of inequalities (5), then the following inequalities hold for \(K_{1}=\frac{\varepsilon_{1}[(2-\eta^{2})(\alpha+1)+2]}{(2-\eta^{2})\Gamma (\alpha+1)},\ K_{2}=\frac{\varepsilon_{2}[(2-\xi^{2})(\beta+1)+2]}{(2-\xi ^{2})\Gamma(\beta+1)}\):

$$ \textstyle\begin{cases} \vert u(t)-\mathcal{N}_{1}v(t) \vert \leq K_{1}\varepsilon_{1},& t\in\mathcal{J},\\ \vert v(t)-\mathcal{N}_{2}u(t) \vert \leq K_{2}\varepsilon_{2},& t\in\mathcal{J}, \end{cases} $$

where \(\mathcal{N}_{1}v(t)\), \(\mathcal{N}_{2}u(t)\) are given in (11).

Proof

From the Condition (ii), we have

$$ \textstyle\begin{cases} {}^{C}\mathcal{D}^{\alpha}u(t)=\phi(t,v(t))+w(t),\quad t\in\mathcal{J},\\ {}^{C}\mathcal{D}^{\beta}v(t)=\psi(t, u(t))+z(t),\quad t\in\mathcal{J},\\ u(0)=v(0)=0,\qquad u(1)=\int_{0}^{\eta}u(s) \,ds,\qquad v(1)=\int_{0}^{\xi}v(s) \,ds. \end{cases} $$
(25)

Then, in view of Lemma 3.2, the solution of (25) is given by

$$ \left \{ \textstyle\begin{array}{rcl} u(t)&=&\frac{1}{\Gamma(\alpha)}\int_{0}^{t}(t-s)^{\alpha-1}\phi(s,v(s)) \,ds\\ &&{}-\frac{2t}{{(2-\eta^{2})}{\Gamma(\alpha)}} [\int _{0}^{1}(1-s)^{\alpha-1} \phi(s,v(s)) \,ds\\ &&{} -\int_{0}^{\eta}(\int_{0}^{s}(s-\tau)^{\alpha-1})\phi(\tau,v(\tau))\,d\tau ) \,ds ]\\ &&{}+ \frac{1}{\Gamma(\alpha)}\int_{0}^{t}(t-s)^{\alpha-1}w(s) \, ds\\ &&{}-\frac{2t}{{(2-\eta^{2})}{\Gamma(\alpha)}} [\int _{0}^{1}(1-s)^{\alpha-1} w(s) \,ds\\ &&{} -\int_{0}^{\eta}(\int_{0}^{s}(s-\tau)^{\alpha-1})w(\tau))\,d\tau ) \,ds ],\\ v(t)&=&\frac{1}{\Gamma(\beta)}\int_{0}^{t}(t-s)^{\beta-1}\psi(s,u(s)) \,ds\\ &&{}-\frac{2t}{{(2-\xi^{2})}{\Gamma(\beta)}} [\int _{0}^{1}(1-s)^{\beta-1} \psi(s,u(s)) \,ds\\ &&{} -\int_{0}^{\xi}(\int_{0}^{s}(s-\tau)^{\beta-1})\psi(\tau,u(\tau))\,d\tau ) \,ds ]\\ &&{}+\frac{1}{\Gamma(\beta)}\int_{0}^{t}(t-s)^{\beta-1}z(s) \,ds\\ &&{}-\frac{2t}{{(2-\xi^{2})}{\Gamma(\beta)}} [\int _{0}^{1}(1-s)^{\beta-1} z(s) \,ds -\int_{0}^{\xi}(\int_{0}^{s}(s-\tau)^{\beta-1})z(\tau)\,d\tau ) \,ds ]. \end{array}\displaystyle \right . $$
(26)

From the first equation of system (26) and \(\eta^{\alpha+1}<1\), \(t\leq1\), we have

$$ \begin{aligned} & \biggl\vert u(t)- \biggl[ \frac{1}{\Gamma(\alpha)} \int _{0}^{t}(t-s)^{\alpha-1}\phi\bigl(s,v(s) \bigr) \,ds \\ & \qquad {}-\frac{2t}{{(2-\eta^{2})}{\Gamma(\alpha)}} \biggl( \int _{0}^{1}(1-s)^{\alpha-1} \phi\bigl(s,v(s) \bigr) \,ds \\ & \qquad {}- \int_{0}^{\eta}\biggl( \int_{0}^{s}(s-\tau)^{\alpha-1}\biggr)\phi\bigl( \tau,v(\tau)\bigr)\,d\tau \biggr) \,ds ) \biggr] \biggr\vert \\ & \quad \leq \biggl\vert \frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-s)^{\alpha -1}w(s) \,ds - \frac{2t}{{(2-\eta^{2})}{\Gamma(\alpha)}} \int_{0}^{1}(1-s)^{\alpha-1} w(s) \,ds \biggr\vert \\ & \qquad {}+ \biggl\vert \frac{2t}{{(2-\xi^{2})}{\Gamma(\beta)}} \int_{0}^{\eta}\biggl( \int_{0}^{s}(s-\tau)^{\alpha-1}\biggr)w(\tau)) \,d\tau ) \,ds \biggr\vert \\ & \quad \leq \biggl\vert \frac{1}{\Gamma(\alpha)} \int_{0}^{t}(t-s)^{\alpha -1}w(s) \,ds \biggr\vert + \biggl\vert \frac{2t}{{(2-\xi^{2})}{\Gamma(\beta)}} \int _{0}^{\eta}\biggl( \int_{0}^{s}(s-\tau)^{\alpha-1}\biggr)w(\tau)) \,d\tau ) \,ds \biggr\vert , \end{aligned} $$

from which we have

$$ \bigl\vert u(t)-\mathcal{N}_{1}v(t) \bigr\vert \leq K_{1}\varepsilon_{1},\quad \text{where } K_{1}= \frac{\varepsilon_{1}[(2-\eta^{2})(\alpha+1)+2]}{(2-\eta^{2})\Gamma(\alpha+1)}. $$
(27)

Along the same lines, we can also obtain

$$ \begin{aligned}& \biggl\vert v(t)- \biggl( \frac{1}{\Gamma(\beta)} \int _{0}^{t}(t-s)^{\beta-1}\psi\bigl(s,u(s) \bigr) \,ds \\ &\qquad {}-\frac{2t}{{(2-\xi^{2})}{\Gamma(\beta)}} \biggl[ \int _{0}^{1}(1-s)^{\beta-1} \psi\bigl(s,u(s) \bigr) \,ds \\ &\qquad {}- \int_{0}^{\xi}\biggl( \int_{0}^{s}(s-\tau)^{\beta-1}\biggr)\psi\bigl( \tau,u(\tau)\bigr)\,d\tau \biggr) \,ds \biggr] ) \biggr\vert \\ & \quad \leq \biggl\vert \frac{1}{\Gamma(\beta)} \int_{0}^{t}(t-s)^{\beta -1}z(s) \,ds \biggr\vert + \biggl\vert \frac{2t}{{(2-\xi^{2})}{\Gamma(\beta)}} \int_{0}^{\xi}\biggl( \int_{0}^{s}(s-\tau)^{\beta-1}\biggr)z(\tau)) \,d\tau ) \,ds \biggr\vert , \end{aligned} $$

which yields

$$ \bigl\vert v(t)-\mathcal{N}_{2}u(t) \bigr\vert \leq K_{2}\varepsilon_{2},\quad \text{where } K_{2}= \frac {\varepsilon_{2}[(2-\xi^{2})(\beta+1)+2]}{(2-\xi^{2})\Gamma(\beta+1)}. $$
(28)

 □

Theorem 5.2

Under the assumptions \((C_{2})\), \((C_{3})\), the solutions of the coupled system (10) is Hyers–Ulam stable if

$$\max \biggl\{ \frac{K_{1}\varepsilon_{1}+\Delta_{1}\Lambda_{\phi}K_{2}\varepsilon _{2}}{\Delta},\ \frac{K_{2}\varepsilon_{2}+\Delta_{2}\Lambda_{\psi}K_{1}\varepsilon _{1}}{\Delta} \biggr\} < 1, $$

where \(\Delta_{1}\Delta_{2}\lambda_{\phi}\Lambda_{\psi}\neq1\).

Proof

Let \((u, v)\in C(\mathcal{J}, \mathbf{R})\times C(\mathcal{J}, \mathbf {R})\) be any solution of the system of inequalities given by

$$ \begin{aligned}& \bigl\vert {}^{C} \mathcal{D}^{\alpha}u(t)-\phi\bigl(t, v(t)\bigr) \bigr\vert \leq \varepsilon_{1},\quad t\in \mathcal{J}, \\ & \bigl\vert {}^{C}\mathcal{D}^{\beta}v(t)-\psi\bigl(t, u(t) \bigr) \bigr\vert \leq\varepsilon_{2},\quad t\in \mathcal{J}, \end{aligned} $$
(29)

and \((x,y)\in C(\mathcal{J}, \mathbf{R})\times C(\mathcal{J}, \mathbf {R})\) be the unique solution of the following coupled system:

$$ \textstyle\begin{cases} {}^{C}\mathcal{D}^{\alpha}x(t)-\phi(t, y(t))=0,\quad t\in\mathcal{J},\\ {}^{C}\mathcal{D}^{\beta}y(t)-\psi(t, x(t))=0,\quad t\in\mathcal{J},\\ x(0)=y(0)=0,\qquad x(1)=\int_{0}^{\eta}x(s) \,ds,\qquad y(1)=\int_{0}^{\xi}y(s) \,ds. \end{cases} $$
(30)

Then, in view of Lemma 3.2 and (11), the solutions of (30) can be written as

$$ \left \{ \textstyle\begin{array}{rcl} x(t)&=&\frac{1}{\Gamma(\alpha)}\int_{0}^{t}(t-s)^{\alpha-1}\phi(s,y(s)) \,ds -\frac{2t}{{(2-\eta^{2})}{\Gamma(\alpha)}}\int_{0}^{1}(1-s)^{\alpha-1} \phi(s,y(s)) \,ds\\ &&{}+\frac{2t}{{(2-\eta^{2})}{\Gamma(\alpha)}}\int_{0}^{\eta}(\int_{0}^{s}(s-\tau)^{\alpha-1})\phi(\tau,y(\tau))\,d\tau ) \,ds=\mathcal {N}_{1}y(t),\\ y(t)&=&\frac{1}{\Gamma(\beta)}\int_{0}^{t}(t-s)^{\beta-1}\psi(s,x(s)) \,ds -\frac{2t}{{(2-\xi^{2})}{\Gamma(\beta)}}\int_{0}^{1}(1-s)^{\beta-1} \psi(s,x(s)) \,ds\\ &&{}+\frac{2t}{{(2-\xi^{2})}{\Gamma(\beta)}}\int_{0}^{\xi}(\int _{0}^{s}(s-\tau)^{\beta-1})\psi(\tau,x(\tau))\,d\tau ) \,ds=\mathcal{N}_{2}x(t). \end{array}\displaystyle \right . $$
(31)

Thanks to Lemma 5.1, we consider

$$ \begin{aligned}\bigl\vert u(t)-x(t) \bigr\vert &= \bigl\vert u(t)-\mathcal{N}_{1}y(t) \bigr\vert \\ & \leq \bigl\vert u(t)-\mathcal{N}_{1}y(t) \bigr\vert + \bigl\vert \mathcal{N}_{1}v(t)-\mathcal {N}_{1}y(t) \bigr\vert . \end{aligned} $$

This, upon computation, yields

$$ \Vert u-x \Vert _{\mathbf{E}}\leq K_{1} \varepsilon_{1}+\Delta_{1}\Lambda_{\phi} \Vert v-y \Vert _{\mathbf{E}}. $$
(32)

Repeating in the same fashion the second part of the system (31), we have

$$ \Vert v-y \Vert _{\mathbf{E}}\leq K_{2} \varepsilon_{2}+\Delta_{2}\Lambda_{\psi} \Vert u-x \Vert _{\mathbf{E}}. $$
(33)

Re-arranging and writing inequations (32) and (33) as

$$ \begin{aligned} & \Vert u-x \Vert _{\mathbf{E}}- \Delta_{1}\Lambda_{\phi} \Vert v-y \Vert _{\mathbf{E}}\leq K_{1}\varepsilon_{1}, \\ & \Vert v-y \Vert _{\mathbf{E}}-\Delta _{2}\Lambda_{\psi} \Vert u-x \Vert _{\mathbf{E}}\leq K_{2}\varepsilon_{2}, \\ & \left ( \textstyle\begin{array}{c@{\quad}c} 1 & -\Delta_{1}\Lambda_{\phi}\\ -\Delta_{2}\Lambda_{\psi}& 1 \end{array}\displaystyle \right )\left ( \textstyle\begin{array}{c} \Vert u-x \Vert _{\mathbf{E}} \\ \Vert v-y \Vert _{\mathbf{E}} \end{array}\displaystyle \right )\leq \left ( \textstyle\begin{array}{c} K_{1}\varepsilon_{1} \\ K_{2}\varepsilon_{2} \end{array}\displaystyle \right ). \end{aligned} $$
(34)

After computation, and using \(\Delta=1-\Delta_{1}\Delta_{2}\Lambda_{\phi}\Lambda_{\psi}\), (34) implies that

$$ \begin{aligned}& \Vert u-x \Vert _{\mathbf{E}}\leq \frac{K_{1}\varepsilon_{1}+\Delta_{1}\Lambda_{\phi}K_{2}\varepsilon_{2}}{\Delta}, \\ & \Vert v-y \Vert _{\mathbf{E}}\leq\frac{K_{2}\varepsilon_{2}+\Delta_{2}\Lambda_{\psi}K_{1}\varepsilon_{1}}{\Delta}, \end{aligned} $$
(35)

from which we have

$$ \bigl\Vert (u, v)-(x,y) \bigr\Vert _{\mathbf{E}\times\mathbf{E}}\leq\max \biggl\{ \frac {K_{1}\varepsilon_{1}+\Delta_{1}\Lambda_{\phi}K_{2}\varepsilon_{2}}{\Delta},\ \frac {K_{2}\varepsilon_{2}+\Delta_{2}\Lambda_{\psi}K_{1}\varepsilon_{1}}{\Delta} \biggr\} . $$
(36)

Hence the solution of the coupled system (10) is Hyers–Ulam stable. □

6 Examples

Example 6.1

Taking the given BVP with integral boundary conditions

$$ \begin{aligned}& {}^{C}\mathcal{D}^{\frac{7}{4}} u(t)=\frac{ \vert v(t) \vert }{(t+3)^{3}(1+ \vert v(t) \vert )},\qquad {}^{C}\mathcal{D}^{\frac{3}{2}} v(t)=\frac{9 \vert u(t) \vert }{32\pi(1+4 \vert u(t) \vert )},\quad t\in\mathcal{J}, \\ & u(0)=v(0)=0,\qquad u(1)= \int_{0}^{\eta}u(s) \,ds, \qquad v(1)= \int_{0}^{\xi}v(s) \,ds. \end{aligned} $$
(37)

We have \(\phi(t,v)=\frac{ \vert v(t) \vert }{(t+3)^{3}(1+ \vert v(t) \vert )}, \psi(t,u)=\frac {9 \vert u(t) \vert }{32\pi(1+4 \vert u(t) \vert )}, \alpha=\frac{7}{4}, \beta=\frac{3}{2}\). Now,

$$\bigl\vert \phi(t,v)-\phi(t,\bar{v}) \bigr\vert \leq\frac{1}{27} \vert v-\bar{v} \vert ,\qquad \bigl\vert \psi(t,u)-\psi(t,\bar{u}) \bigr\vert \leq\frac{9}{32\pi} \vert u-\bar{u} \vert . $$

Therefore, for all \(\eta, \xi\in(0, 1)\), we have

$$\begin{aligned} &\Delta_{1}\Lambda_{\phi}=\frac{\Lambda_{\phi}}{\Gamma(\alpha+1)} \biggl(1+ \frac {2[\alpha+1+\eta^{\alpha+1}]}{(\alpha+1)(2-\eta^{2})} \biggr)< 1,\\ & \Delta_{2}\Lambda_{\psi}= \frac{\Lambda_{\psi}}{\Gamma(\beta+1)} \biggl(1+\frac{2[\beta+1+\xi^{\beta+1}]}{(\beta+1)(2-\xi^{2})} \biggr)< 1, \end{aligned}$$

where \(\Lambda_{\phi}=\frac{1}{27}\), \(\Lambda_{\psi}=\frac{9}{32\pi}\). Therefore, by using Lemma 3.4, the BVP (37) has unique solution.

We find the approximate solutions of the problem using the method developed in Sect. 4. We select \(\sigma=1/4\), which implies that \(l=4\), \(m=7\), and \(n=6\). The recurrence relations corresponding to BVP (37) are given as

$$ \begin{aligned} &U(k+7)=\frac{\Gamma((7+k)\frac{1}{4}-\frac{7}{4}+1)}{\Gamma((7+k)\frac {1}{4}+1)} F\bigl(k,V(k) \bigr), \\ &V(k+6)=\frac{\Gamma((6+k)\frac{1}{4}-\frac{3}{2}+1)}{\Gamma((6+k)\frac {1}{4}+1)} G\bigl(k,U(k)\bigr). \end{aligned} $$
(38)

F and G are differential transform of \(\phi,\psi\). The initial conditions become

$$ \begin{aligned} &U(0)=0,\qquad U(1)=0,\qquad U(2)=0,\qquad U(3)=0,\\ & U(4)=c_{1},\qquad U(5)=0,\qquad U(6)=0, \\ &V(0)=0,\qquad V(1)=0,\qquad V(2)=0,\qquad V(3)=0,\\ & V(4)=c_{2},\qquad V(5)=0. \end{aligned} $$
(39)

After calculating recurrence relation and calculating the values of \(c_{1}\) and \(c_{2}\), we get \(u(t)\) and \(v(t)\) as given (note that here we truncate the relation at \(k=20\)). The approximate solution is given by

$$ \left \{ \textstyle\begin{array}{rcl} u(t) &=& \frac{35\text{,}538\text{,}947\text{,}983\text{,}423 t^{\frac{3}{4}}}{2\text{,}358\text{,}454\text{,}139\text{,}013\text{,}643} - \frac {3\text{,}318\text{,}660\text{,}919\text{,}569\text{,}631 t^{\frac{7}{4}}}{288\text{,}230\text{,}376\text{,}151\text{,}711\text{,}744} + \frac {4\text{,}827\text{,}143\text{,}155\text{,}737\text{,}645 t^{\frac{11}{4}}}{1\text{,}152\text{,}921\text{,}504\text{,}606\text{,}846\text{,}976}\\ &&{}- \frac{107\text{,}269\text{,}847\text{,}905\text{,}281 t^{\frac{15}{4}}}{36\text{,}028\text{,}797\text{,}018\text{,}963\text{,}968} + \frac{7\text{,}226\text{,}600\text{,}279\text{,}934\text{,}721 t^{\frac{19}{4}}}{2\text{,}305\text{,}843\text{,}009\text{,}213\text{,}693\text{,}952} - \frac {2\text{,}513\text{,}600\text{,}097\text{,}368\text{,}599 t^{\frac{23}{4}}}{576\text{,}460\text{,}752\text{,}303\text{,}423\text{,}488},\\ v(t)&=&\frac{30\text{,}329\text{,}568\text{,}610\text{,}629 t^{\frac{3}{2}}}{2\text{,}251\text{,}799\text{,}813\text{,}685\text{,}248} - \frac {543\text{,}250\text{,}089\text{,}644\text{,}091 t^{\frac{3}{4}}}{36\text{,}028\text{,}797\text{,}018\text{,}963\text{,}968}. \end{array}\displaystyle \right . $$
(40)

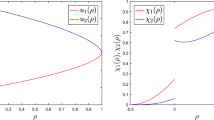
Since \((0, 0)\) is the unique solution of Example 6.1. It is easy to prove that the conditions of Theorem 5.2 are fulfilled for the approximate solution \((u, v)\) obtained in (40) for different \(t\in(0, 1)\). Therefore solution \((u, v)\) is Hyers–Ulam stable corresponding to the unique solution \((0, 0)\). The plots of the approximate solutions at different choices of parameters η and ξ are displayed in Fig. 1. In order to verify the accuracy of the boundary conditions, we simulate the scheme for different sets of η and ξ, and measure the absolute difference in boundary conditions using the relations as

$$ E_{u}= \biggl\vert u(1)- \int_{0}^{\eta}u(s) \,ds \biggr\vert , \qquad E_{v}= \biggl\vert v(1)- \int_{0}^{\xi}v(s) \,ds \biggr\vert . $$
(41)

For different choices of η and ξ and different scale level k, the absolute difference in boundary conditions of \(u(t)\) is displayed in Table 1. In Table 2 the absolute difference in boundary conditions of \(v(t)\) are displayed.

Figure 1
figure 1

Plots of approximate solution \((u, v)\) of Example 6.1 for different choices of parameters

Full size image
Table 1 Absolute error in boundary conditions of \(u(t)\) of Example 6.1 using different choice of parameters
Full size table
Table 2 Absolute error in boundary conditions of \(v(t)\) of Example 6.1 using different choice of parameters
Full size table

Example 6.2

Consider the given coupled system of BVP

$$ \textstyle\begin{cases} {}^{C}\mathcal{D}^{\frac{3}{2}} u(t)=\frac{ \vert v(t) \vert }{10(1+t)^{3}+ \vert v(t) \vert },\quad t\in[0,1],\\ {}^{C}\mathcal{D}^{\frac{3}{2}} v(t)=\frac{9 \vert u(t) \vert }{32\pi(1+4 \vert u(t) \vert )},\quad t\in[0,1],\\ u(0)=0,\qquad v(0)=0,\qquad \int_{0}^{\eta}u(s) \,ds=u(1),\qquad \int_{0}^{\eta}v(s) \,ds=v(1). \end{cases} $$
(42)

Since

$$ \bigl\vert \phi(t,v)-\phi(t,\bar{v}) \bigr\vert \leq\frac{1}{10} \vert v-\bar{v} \vert ,\qquad \bigl\vert \psi(t,u)-\psi(t,\bar{u}) \bigr\vert \leq\frac{5}{16\pi} \vert u-\bar{u} \vert , $$

as \(\Lambda_{\phi}=\frac{1}{10}\), \(\Lambda_{\psi}=\frac{5}{16\pi}\), \(\alpha =\beta=\frac{3}{2}\), then one can easily check that \(\Delta_{1}\Lambda _{\phi}<1\), \(\Delta_{2}\Lambda_{\psi}<1\), for all \(\eta, \xi\in(0, 1)\). Thanks to Lemma 3.4, the system of BVP (6.2) has a unique solution. Further, we approximate the solution of this problem with the proposed method. The error in the boundaries are given in Tables 3 and 4, respectively. The approximate solutions are displayed in Fig. 2. One can easily see from these tables that the absolute error at boundaries is much more less than 10−17. Obviously \((0, 0)\) is the unique solution and computing its approximate solution through (GDTM), one has

$$ \textstyle\begin{cases} u(t)= \frac{403\text{,}345\text{,}956\text{,}861 t^{\frac{3}{2}}}{4\text{,}451\text{,}799\text{,}813\text{,}685\text{,}248} + \frac {556\text{,}325\text{,}002 t^{\frac{3}{4}}}{890\text{,}287\text{,}901\text{,}234},\\ v(t)=\frac{1\text{,}234\text{,}567\text{,}890 t^{\frac{3}{2}}}{456\text{,}789\text{,}054\text{,}677} +\frac{3\text{,}456\text{,}789\text{,}345 t^{\frac{3}{4}}}{8\text{,}765\text{,}432\text{,}190}. \end{cases} $$
(43)

In view of Theorem 5.2, the approximate solution (43) is Hyers–Ulam stable corresponding to the unique solution \((0, 0)\).

Figure 2
figure 2

Plots of approximate solution \((u, v)\) of Example (6.2) at different choices of parameters

Full size image
Table 3 Absolute error in boundary conditions of \(u(t)\) of Example 6.2 using different choice of parameters
Full size table
Table 4 Absolute error in boundary conditions of \(v(t)\) of Example 6.2 using different choice of parameters
Full size table

7 Conclusion

We have derived some necessary conditions for the existence, uniqueness and Hyers–Ulam stability for the solutions of the considered BVP (2). The required results have been obtained by using classical fixed point theory due to Banach and Krasnoselskii. Moreover, an effort based on generalized differential transform has been made to find approximate solutions of the considered problem. As compared to the present literature devoted to the investigation of FDEs, our paper is different in few ways. We have investigated approximate solutions to highly nonlinear BVPs of FDEs by using GDTM together with the existence theory. The relevant aspect for such type of nonlinear problems has very rarely investigated. Furthermore we have also established some adequate conditions for the Hyers–Ulam type stability to the solutions of the proposed problem. For the justification, we have provided interesting examples. From the experimental results we observe that the approximate solution satisfies the moving point boundary conditions with a great accuracy and also the corresponding solutions are Hyers–Ulam stable.