1 Introduction

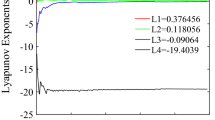
Chaos is a complex dynamic phenomenon in nonlinear dynamical system, which exists widely in nature. Chaos theory and its application have aroused great interest of scholars in various fields. Most of the research objects are three-dimensional chaotic systems, the biggest feature is that there is only a positive Lyapunov exponent, which reflects that the trajectory of the nonlinear system only generates instability (divergence or expansion) in a certain direction, and develops exponentially. However, there are high-dimensional nonlinear systems in a wide range of the fields of nature, social sciences, engineering, etc. These systems may have two or more positive Lyapunov exponents, which is why they are called hyperchaotic. Compared with chaotic motion, hyperchaotic motion is more complicated and has more advantages in engineering and scientific applications. Therefore, hyperchaotic systems have greater research value and prospects.

Over the years, scholars have done some research on hyperchaos in nonlinear circuits, secure communications, lasers, kolpoz oscillators, control and synchronization [1–5]. In 1979, Rössler presented the concept of hyperchaos in his speech on applied mathematics, and proposed the Rössler hyperchaos system [6]. The precise definition of hyperchaotic system includes: (i) autonomous differential equations with at least four phase spaces; (ii) dissipative structure; (iii) at least two unstable directions, of which at least one direction is nonlinear [7]. Due to the multiple positive Lyapunov exponents produced by hyperchaotic systems, its dynamic characteristics are difficult to predict and control. This characteristic is widely used in communication systems by scholars [8]. In 1999, Meyer et al. studied the hyperchaotic property of generalized Rössler system [9]. In 2005, based on the Chen system, Chen et al. proposed the hyperchaotic Chen system [10]. In 2016, based on the Lorenz system, Zarei et al. proposed a new four-dimensional quadratic autonomous hyperchaotic attractor. It can generate double-wing chaotic and hyperchaotic attractors with only one equilibrium point [11]. In 2017, Zhou et al. proposed a four-dimensional smooth quadratic autonomous hyperchaotic system with complex dynamics, and analyzed the stability of the hyperchaotic system, pitchfork bifurcation, Hopf bifurcation and other local dynamics problems by using the central manifold theorem and bifurcation theory [12]. In 2019, Rajagopal et al. proposed an improved hyperchaotic van der Pol–Duffing snap oscillator. Using a Lyapunov exponent, equilibrium point stability analysis and bifurcation diagram, various dynamic properties of the system were studied [13].

Under certain conditions, some complex invariant sets can be separated from the isolated zero-Hopf equilibrium point, so in some cases, the zero-Hopf equilibrium point may mean the generation of local chaos. There have been many studies on zero-Hopf bifurcation of three-dimensional systems. In 2014, by using the averaging theory, Garcia et al. provided an analytic proof of the existence of zero-Hopf bifurcation in systems with two slow speeds and one fast variable, and to describe the stability or instability of periodic orbits in such zero-Hopf bifurcation [14]. In 2017, Ginoux et al. used the second-order averaging theory to prove that there are two types of zero-Hopf bifurcation in the predator–prey Volterra–Gauss system under different parameters. Under the first parameter condition, the system has a periodic orbit, and under the second parameter condition, the system has five periodic orbits [15]. In 2018, Li et al. considered the existence of zero-Hopf bifurcation and periodic solutions for the improved Chua system by applying the averaging theory [16]. In 2018, Salih studied the zero-Hopf bifurcation of the three-dimensional Lotka–Volterra systems [17]. In 2018, Candido et al. studied the zero-Hopf bifurcation of 16 three-dimensional differential systems without equilibrium by using the averaging theory [18]. However, due to the higher dimension and complexity of hyperchaotic systems, few scholars are currently engaged in the analysis of hyperchaotic theory, there is still very little work done on zero-Hopf bifurcation for n-dimensional systems with \(n\geq{4}\). In 2014, Lorena et al. studied the zero-Hopf bifurcation of a class of Lorenz hyperchaotic systems and the generation of periodic solutions with the change of parameters, which was the first work on the zero-Hopf bifurcation problem in four-dimensional systems [7]. In 2015, Maza studied the zero-Hopf bifurcation of hyperchaotic Chen system, and proved that hyperchaotic Chen system has two periodic orbits at the zero-Hopf equilibrium point by using the averaging theory [19]. In 2017, Chen et al. studied zero-Hopf bifurcation of generalized Lorenz–Stenflo hyperchaotic system and obtained two periodic solutions generated from bifurcation points [20].

In order to fully understand the dynamics of a system, it is necessary to study its periodic solutions. In recent years, scholars have studied the periodic solutions of many classical systems. In 2017, Liu et al. studied the existence of periodic solutions for the Newtonian equation of motion with p-Laplacian operator by asymptotic behavior of potential function [21]. In 2018, Wang et al. considered the existence of periodic solutions for a non-autonomous second-order Hamiltonian systems [22]. In 2018, Wang et al. studied the multiplicity of periodic solutions of one kind of planar Hamiltonian systems with a nonlinear term satisfying semi-linear conditions [23]. In 2019, Chiraz proved the existence of periodic solutions for some non-densely non-autonomous delayed partial differential equations [24].

In this paper, from the perspective of local dynamics, a four-dimensional smooth quadratic autonomous hyperchaotic system [12] is studied:

$$\begin{aligned} \textstyle\begin{cases} \dot{x}=a(y-x),\\ \dot{y}=bx-y-xz+u,\\ \dot{z}=-cz+xy,\\ \dot{u}=-du-jx+exz, \end{cases}\displaystyle \end{aligned}$$
(1)

where a, b, c, d, j, e are real parameters.

The system (1) is constructed by adding one state variable to the well-known Lorenz system, which has rich and complex dynamic behaviors. With the change of parameters, the system can evolve into periodic, quasi-periodic, chaotic and hyperchaotic states, and attractors in these states are different from ordinary attractors. In this paper, we study the zero-Hopf bifurcation of the system (1) at equilibrium point, and the generation of periodic solutions as parameters change.

2 Zero-Hopf bifurcation analysis

We can verify that, for any choice of the parameters, \(E_{0}(0,0,0,0)\) is always an equilibrium point for the hyperchaotic system (1). Moreover, when \(c=0\), system (1) has a line equilibrium \((0,0,z,0)\); when \(\frac{-c(d+j-bd)}{d-e}>{0}\), system (1) has a pair of symmetrical equilibria:

$$\begin{gathered} E_{1} { \biggl(}\sqrt{\frac{-c(d+j-bd)}{d-e}},\sqrt{ \frac {-c(d+j-bd)}{d-e}},-\frac{d+j-bd}{d-e},-\sqrt{\frac {-c(d+j-bd)}{d-e}} \frac{e+j-be}{d-e} { \biggr)}, \\ E_{2} { \biggl(}-\sqrt{\frac{-c(d+j-bd)}{d-e}},-\sqrt{ \frac {-c(d+j-bd)}{d-e}},-\frac{d+j-bd}{d-e},\sqrt{\frac {-c(d+j-bd)}{d-e}} \frac{e+j-be}{d-e} { \biggr)}.\end{gathered} $$

In the next theorem, we will give the zero-Hopf equilibrium point of the system (1).

Theorem 1

The hyperchaotic system (1) has a zero-Hopf equilibrium localized at equilibrium\(E_{0}\)if the following conditions are satisfied: \(a=-1\), \(1-b<0\), \(c=j=d=0\). Moreover, the eigenvalues at\(E_{0}\)for the parameter conditions are 0, 0, \(\pm\sqrt{b-1}i\).

In the rest of this section, we will study the zero-Hopf bifurcation and periodic solutions of the hyperchaotic system (1) at the equilibrium point \(E_{0}\).

Theorem 2

For\(c\neq{0}\), \(j\neq{0}\), \(d\neq{0}\), \(e\neq{0}\), \(b>1\), we consider the hyperchaotic system (1) with\(a=-1+\varepsilon {a_{1}}\), \(c=\varepsilon{c_{1}}\), \(j=\varepsilon{j_{1}}\), \(d=\varepsilon {d_{1}}\), where\(\varepsilon>0\)is a sufficiently small parameter and\(a_{1}\), \(c_{1}\), \(j_{1}\), \(d_{1}\)are nonzero real parameters. The following statements hold.

  1. (i)

    If\(a_{1}\neq{d_{1}}\), \(\frac {c_{1}(a_{1}(b-1)^{2}-j_{1})}{e}>0\), the system(1) has a zero-Hopf bifurcation and produces a periodic solution\(\varepsilon\varPhi _{1}(t,\varepsilon)\)at the equilibrium point\(E_{0}\). Moreover, the periodic solution\(\varepsilon\varPhi_{1}(t,\varepsilon)\)is stable if\(a_{1}< d_{1}\), \(c_{1}>0\), \(4j_{1}+(-4a_{1}+c_{1})(b-1)^{2}>0\), \(j_{1}-a_{1}(b-1)^{2}<0\); or\(a_{1}< d_{1}\), \(c_{1}>0\), \(4j_{1}+(-4a_{1}+c_{1})(b-1)^{2}<0\).

  2. (ii)

    If\(a_{1}\neq{d_{1}}\), \(\frac {c_{1}(d_{1}(b-1)^{2}-j_{1})}{e}>0\), the system (1) has a zero-Hopf bifurcation and produces two periodic solutions\(\varepsilon\varPhi _{2}(t,\varepsilon)\), \(\varepsilon\varPhi_{3}(t,\varepsilon)\)at the equilibrium point\(E_{0}\). Moreover, the periodic solutions\(\varepsilon \varPhi_{2}(t,\varepsilon)\)and\(\varepsilon\varPhi_{3}(t,\varepsilon)\)are stable if\(a_{1}< d_{1}\), \(c_{1}>0\), \(-8j_{1}+(8d_{1}+c_{1})(b-1)^{2}>0\), \(-j_{1}+d_{1}(b-1)^{2}<0\); or\(a_{1}< d_{1}\), \(c_{1}>0\), \(-8j_{1}+(8d_{1}+c_{1})(b-1)^{2}<0\).

3 Averaging theory of periodic orbits

The averaging theory is a classical and mature tool for studying the dynamic behavior of nonlinear dynamical systems, especially for the study of periodic solutions. In recent years, it has been improved and applied well. The classical averaging theory [25] is as follows.

Consider differential system:

$$\begin{aligned} \dot{\textbf{x}}=\varepsilon{F(t,\textbf{x})}+ \varepsilon^{2}G(t, \textbf {x},\varepsilon), \end{aligned}$$
(2)

with \(\textbf{x}\in{D}\), where D is an open subset of \(R^{n}\), \(t\geq {0}\). We assume that \(F(t,\textbf{x})\) and \(G(t,\textbf{x},\varepsilon )\) are T-periodic in t. We define the averaged function

$$\begin{aligned} f(\textbf{x})=\frac{1}{T} \int_{0}^{T}F(t,\textbf{x})\,dt. \end{aligned}$$
(3)

Theorem 3

Make the following assumptions:

  1. (i)

    F, its Jacobian\(\partial{F}/\partial {\textbf{x}}\)and its Hessian\(\partial^{2}{F}/\partial{\textbf {x}^{2}}\); G, its Jacobian\(\partial{G}/\partial{\textbf{x}}\)are defined, continuous and bounded by a constant independent ofεin\([0,\infty)\times{D}\)and\(\varepsilon\in(0,\varepsilon_{0}]\).

  2. (ii)

    Tis a constant independent ofε.

Then the following conclusions can be obtained:

  1. (a)

    Ifpis the zero of the averaged function\(f(\textbf{x})\), and

    $$\begin{aligned} { \operatorname{det} { \biggl(}\frac{\partial{f}}{\partial{\textbf {x}}} { \biggr)}\bigg|_{\textbf{x}=p}} \neq{0}, \end{aligned}$$
    (4)

    then there exists aT-periodic solution\(\textbf {x}(t,\varepsilon)\)of system (2) such that\(\textbf{x}(0,\varepsilon )\rightarrow{p}\)as\(\varepsilon\rightarrow{0}\).

  2. (b)

    If the eigenvalue of the Jacobian matrix\((\frac{\partial {f}}{\partial{\textbf{x}}})\)has a negative real part, the periodic solution\(\textbf{x}(t,\varepsilon)\)is asymptotically stable.

4 Proofs

In this section we will provide the proofs of Theorem 1 and Theorem 2.

Proof of Theorem 1

The characteristic equation at the equilibrium point \(E_{0}\) is obtained:

$$\begin{aligned} \begin{aligned}[b] &\lambda^{4}+(1+a+c+d) \lambda^{3}+(a-ab+c+ac+d+ad+cd) \lambda^{2} \\ &\quad+(ac-abc+ad-abd+cd+acd+aj)\lambda+acd-abcd+acj=0. \end{aligned} \end{aligned}$$
(5)

When \(a=-1\), \(1-b<0\), \(c=j=d=0\), Eq. (5) has roots \(\lambda_{1}=\lambda_{2}=0\), \(\lambda_{3,4}=\pm\sqrt{b-1}i\). That is, the equilibrium point \(E_{0}\) is a zero-Hopf equilibrium of the hyperchaotic system (1).

Theorem 1 is proved. □

Proof of Theorem 2

Let \(b-1=\omega^{2}\), where \(\omega >0\). Then, by \(a=-1+\varepsilon{a_{1}}\), \(c=\varepsilon {c_{1}}\), \(j=\varepsilon{j_{1}}\), \(d=\varepsilon{d_{1}}\), \(b-1=\omega^{2}\), the hyperchaotic system (1) can be written as

$$\begin{aligned} \textstyle\begin{cases} \dot{x}=-(y-x)+\varepsilon{a_{1}}(y-x),\\ \dot{y}=(\omega^{2}+1)x-y+u-xz,\\ \dot{z}=-\varepsilon{c_{1}}z+xy,\\ \dot{u}=-\varepsilon{j_{1}}x-\varepsilon{d_{1}}u+exz. \end{cases}\displaystyle \end{aligned}$$
(6)

Furthermore, we rescale the variables. Let \(x=\varepsilon{\widetilde {x}}\), \(y=\varepsilon{\widetilde{y}}\), \(z=\varepsilon{\widetilde {z}}\), \(u=\varepsilon{\widetilde{u}}\), and denoting again the variables \((\widetilde{x},\widetilde{y},\widetilde{z},\widetilde{u})^{T}\) by \((x,y,z,u)^{T}\), then system (6) will be changed to

$$\begin{aligned} \textstyle\begin{cases} \dot{x}=-(y-x)+\varepsilon({a_{1}}(y-x)),\\ \dot{y}=(\omega^{2}+1)x-y+u-\varepsilon{xz},\\ \dot{z}=\varepsilon(-{c_{1}}z+xy),\\ \dot{u}=\varepsilon(-{j_{1}}x-{d_{1}}u+exz). \end{cases}\displaystyle \end{aligned}$$
(7)

Now we shall write the linear part at the origin of the system (7) when \(\varepsilon=0\) into its real Jordan normal form, i.e. as

$$\begin{aligned} \begin{pmatrix} 0&-\omega&0&0\\ \omega&0&0&0\\ 0&0&0&0\\ 0&0&0&0 \end{pmatrix} . \end{aligned}$$

For doing that we consider the linear change

$$\begin{aligned} \begin{aligned} x=-\frac{Z}{\omega^{2}}+\frac{X\omega+Y}{1+\omega^{2}}, \qquad y=Y- \frac {Z}{\omega^{2}},\qquad z=U, u=Z. \end{aligned} \end{aligned}$$
(8)

By using the new variables \((X,Y,Z,U)\), the system (7) can be written as follows:

$$ \left \{ \textstyle\begin{array}{ll} \dot{X}=&-Y\omega+\varepsilon { (} \frac{-\omega^{2}(1+\omega ^{2})(d_{1}Z+a_{1}\omega)(-X+Y\omega)+j_{1}(-\omega^{2}(Y+X\omega)+Z(1+\omega ^{2}))}{\omega^{3}+\omega^{5}} \\ &{}+\frac{(e-1)(\omega^{2}(Y+X\omega)+Z(1+\omega^{2}))U}{\omega^{3}+\omega ^{5}} { )}, \\ [3pt] \dot{Y}=&X\omega+\varepsilon { (}\frac{j_{1}(-\omega^{2}(Y+X\omega )+Z(1+\omega^{2}))+e(\omega^{2}(Y+X\omega)+Z(1+\omega^{2}))U}{\omega ^{4}+\omega^{6}} \\ [3pt] &{}-\frac{\omega^{2}(Y+X\omega)U+(d_{1}Z-UZ)(1+\omega^{2})}{\omega ^{2}+\omega^{4}} { )}, \\ [3pt] \dot{Z}=&\varepsilon { (}\frac{j_{1}(-\omega^{2}(Y+X\omega)+Z(1+\omega ^{2}))+e(\omega^{2}(Y+X\omega)+Z(1+\omega^{2}))U-d_{1}Z\omega^{2}(1+\omega ^{2})}{\omega^{2}+\omega^{4}} { )}, \\ [3pt] \dot{U}=&\varepsilon { (}\frac{-c_{1}U(\omega^{4}+\omega^{6})+(Z-Y\omega ^{2})(-\omega^{2}(Y+X\omega)+Z(1+\omega^{2}))}{\omega^{4}+\omega ^{6}} { )}. \end{array}\displaystyle \right . $$
(9)

Then we use the cylindrical coordinates \(X=r\cos{\theta}\), \(Y=r\sin{\theta }\), and obtain

$$ \left \{ \textstyle\begin{array}{ll} \dot{r}=&\frac{\varepsilon}{\omega^{4}+\omega^{6}} { (}r \omega ^{4} (a_{1}-j_{1}+U-eU+a_{1} \omega^{2} )\cos{\theta}^{2}-r\omega ^{2} (j_{1}+U (e+\omega^{2} ) )\sin{ \theta}^{2} \\ &{}+Z (1+\omega^{2} ) (j_{1}+eU+(-d_{1}+U) \omega^{2} )\sin{\theta}-\omega\cos {\theta} (U (-1+2e+ \omega^{2} )\sin{\theta} \\ &{}+r\omega^{2} (2j_{1}+a_{1} \omega^{2} (1+\omega^{2} ) )+Z (1+\omega ^{2} ) (-j_{1}+U-eU+d_{1} \omega^{2} ) ) { )}, \\ \dot{\theta}=&\omega+\frac{\varepsilon}{r(\omega^{4}+\omega^{6})} ( -r\omega^{3} (j_{1}+U (e+\omega^{2} ) )\cos{ \theta}^{2}+\omega\sin{\theta } (Z (1+\omega^{2} ) (-j_{1}+U-eU \\ &{}+d_{1}\omega^{2} )+r\omega^{2} (j_{1}+(-1+e)U+a_{1}\omega^{2} (1+ \omega ^{2} ) )\sin{\theta} )+\cos{\theta} (Z (1+ \omega^{2} ) (j_{1}+eU \\ &{}+(-d_{1}+U)\omega^{2} )-r\omega^{2} (j_{1}-j_{1}\omega^{2}+\omega ^{2} (a_{1}+2U+a_{1} \omega^{2} )+e (U-U\omega^{2} ) )\sin{ \theta} ) { )}, \\ \dot{Z}=&\varepsilon ( -d_{1}Z-(j_{1}+eU) { (}-\frac{Z}{\omega ^{2}}+\frac{r\omega\cos{\theta}+r\sin{\theta}}{1+\omega^{2}} { )} { )}, \\ \dot{U}=&\varepsilon ( -c_{1}U+ { (} \frac{Z}{\omega^{2}}-r\sin {{\theta}} { )} { (}-\frac{Z}{\omega^{2}}+ \frac{r\omega\cos{\theta }+r\sin{\theta}}{1+\omega^{2}} { )} { )}. \end{array}\displaystyle \right . $$
(10)

We take θ as a new independent variable and obtain the system

$$ \left \{ \textstyle\begin{array}{ll} \frac{dr}{d\theta}&=\varepsilon { (} \frac{1}{\omega^{5}+\omega ^{7}} (r\omega^{4} (a_{1}-j_{1}+U-eU+a_{1} \omega^{2} )\cos{\theta}^{2}-r\omega ^{2} (j_{1}+U (e+\omega^{2} ) )\sin{ \theta}^{2} \\ &\phantom{=}{}+Z (1+\omega^{2} ) (j_{1}+eU+(-d_{1}+U) \omega^{2} )\sin{\theta}-\omega\cos {\theta} (Z (1+ \omega^{2} ) (-j_{1}+U-eU \\ &\phantom{=}{}+d_{1}\omega^{2} )+r\omega^{2} (2j_{1}+a_{1}\omega^{2} (1+\omega ^{2} ) )+U (-1+2e+\omega^{2} )\sin{ \theta} ) ) { )}+o (\varepsilon^{2} ) \\ &=\varepsilon{F_{1}(\theta,r,Z,U)}+o (\varepsilon^{2} ), \\ \frac{dZ}{d\theta}&=\varepsilon { (}\frac{1}{\omega^{3}+\omega ^{5}} (Z (1+ \omega^{2} ) (j_{1}+eU-d_{1} \omega^{2} )-r\omega^{2}(j_{1}+eU) ( \omega \cos{\theta}+\sin{\theta}) ) { )}+o (\varepsilon^{2} ) \\ &=\varepsilon{F_{2}(\theta,r,Z,U)}+o (\varepsilon^{2} ), \\ \frac{dU}{d\theta}&=\varepsilon { (}\frac{-c_{1}U}{\omega}+ \frac {(Z-r\omega^{2}\sin{\theta})(Z+Z\omega^{2}-r\omega^{2}(\omega\cos{\theta }+\sin{\theta}))}{\omega^{5}+\omega^{7}} { )}+o (\varepsilon^{2} ) \\ &=\varepsilon{F_{3}(\theta,r,Z,U)}+o (\varepsilon^{2} ). \end{array}\displaystyle \right . $$
(11)

Using the notation of averaging theory introduced in Theorem 3, we get \(t=\theta\), \(T=2\pi\), \(\textbf{x}=(r,Z,U)\) and

$$\begin{aligned} \begin{aligned} F(\theta,r,Z,U)= \begin{pmatrix} F_{1}(\theta,r,Z,U)\\ F_{2}(\theta,r,Z,U)\\ F_{3}(\theta,r,Z,U) \end{pmatrix} ,\qquad f(r,Z,U)= \begin{pmatrix} f_{1}(r,Z,U)\\ f_{2}(r,Z,U)\\ f_{3}(r,Z,U) \end{pmatrix} . \end{aligned} \end{aligned}$$

Then we compute the integrals, i.e.

$$\begin{aligned} \begin{aligned} &f_{1}(r,Z,U)=\frac{1}{2\pi} \int_{0}^{2\pi}F_{1}(\theta,r,Z,U)\,d \theta=-\frac {r(j_{1}+eU-a_{1}\omega^{2})}{2\omega^{3}}, \\ &f_{2}(r,Z,U)=\frac{1}{2\pi} \int_{0}^{2\pi}F_{2}(\theta,r,Z,U)\,d \theta=\frac {Z(j_{1}+eU-d_{1}\omega^{2})}{\omega^{3}}, \\ &f_{3}(r,Z,U)=\frac{1}{2\pi} \int_{0}^{2\pi}F_{3}(\theta,r,Z,U)\,d \theta=\frac {-2c_{1}U+\frac{2Z^{2}}{\omega^{4}}+\frac{r^{2}}{1+\omega^{2}}}{2\omega}. \end{aligned} \end{aligned}$$

Solving the equations \(f_{1}(r,Z,U)=f_{2}(r,Z,U)=f_{3}(r,Z,U)=0\), we can get the following four solutions:

$$\begin{aligned} \begin{aligned} &s_{0}=(0,0,0), \\ &s_{1}= \biggl(\sqrt{\frac{2c_{1}(1+\omega^{2})(a_{1}\omega^{2}-j_{1})}{e}},0,\frac {a_{1}\omega^{2}-j_{1}}{e} \biggr), \\ &s_{2}= \biggl(0,\omega^{2}\sqrt{\frac{c_{1}(d_{1}\omega^{2}-j_{1})}{e}}, \frac {d_{1}\omega^{2}-j_{1}}{e} \biggr), \\ &s_{3}= \biggl(0,-\omega^{2}\sqrt{\frac{c_{1}(d_{1}\omega^{2}-j_{1})}{e}}, \frac {d_{1}\omega^{2}-j_{1}}{e} \biggr). \end{aligned} \end{aligned}$$

Finally, we analyze these four solutions, respectively.

  1. (I)

    For the first solution \(s_{0}\), it has the Jacobian

    $$\begin{aligned} { \operatorname{det} { \biggl(}\frac{\partial{f}}{\partial{\textbf {x}}}(s_{0}) { \biggr)}}=0. \end{aligned}$$

    Then, by Theorem 3, we know the periodic solution cannot be determined.

  2. (II)

    For the second solution \(s_{1}\), when \(\frac{c_{1}(a_{1}\omega^{2}-j_{1})}{e}>0\), \(s_{1}\) is a real solution. The solution \(s_{1}\) has the Jacobian

    $$\begin{aligned} { \operatorname{det} { \biggl(}\frac{\partial{f}}{\partial{\textbf {x}}}(s_{1}) { \biggr)}}=\frac{c_{1}(a_{1}\omega^{2}-j_{1})(a_{1}-d_{1})}{\omega^{5}}. \end{aligned}$$

    When \(a_{1}\neq{d_{1}}\), \({\operatorname{det}(\frac{\partial{f}}{\partial {S}}(s_{1}))}\neq{0}\). Then according to Theorem 3, we see that the system (11) has a periodic solution \(\textbf{x}_{1}(\theta,\varepsilon)\) such that \(\textbf{x}_{1}(0,\varepsilon)=s_{1}+o(\varepsilon)\). Bring the solution back to the system (9), and we have a periodic solution \(\varPhi_{1}(t,\varepsilon)=(X(t,\varepsilon),Y(t,\varepsilon ),Z(t,\varepsilon),U(t,\varepsilon))\). Then the system (6) has a periodic solution \((x(t,\varepsilon),y(t,\varepsilon),z(t,\varepsilon ),u(t,\varepsilon))=\varepsilon(X(t,\varepsilon),Y(t,\varepsilon ),Z(t,\varepsilon),U(t,\varepsilon))=\varepsilon\varPhi_{1}(t,\varepsilon)\).

To determine the stability of the periodic solution \(\varepsilon\varPhi _{1}(t,\varepsilon)\), we calculate the eigenvalues of the Jacobian matrix \(\frac{\partial{f}}{\partial{\textbf{x}}}(s_{1})\). The eigenvalues are given as follows:

$$\begin{aligned} &\lambda_{1}=\frac{a_{1}-d_{1}}{\omega},\qquad\lambda_{2,3}= \frac{-c_{1}\omega\pm \sqrt{c_{1}(4j_{1}+(-4a_{1}+c_{1})\omega^{2})}}{2\omega^{2}}. \end{aligned}$$

Now we discuss the stability of the periodic solution when the eigenvalues are real and imaginary, respectively, and obtain the following solutions.

  1. (i)

    When \(c_{1}(4j_{1}+(-4a_{1}+c_{1})(b-1)^{2})>0\), \(\lambda _{2}\) and \(\lambda_{3}\) are real. In this case, the periodic solution \(\varepsilon\varPhi_{1}(t,\varepsilon)\) is stable if \(a_{1}< d_{1}\), \(c_{1}>0\), \(j_{1}-a_{1}(b-1)^{2}<0\).

  2. (ii)

    When \(c_{1}(4j_{1}+(-4a_{1}+c_{1})\omega^{2})<0\), \(\lambda _{2}\) and \(\lambda_{3}\) are imaginary. In this case, the periodic solution \(\varepsilon\varPhi_{1}(t,\varepsilon)\) is stable if \(a_{1}< d_{1}\), \(c_{1}>0\).

  3. (iii)

    For the solutions \(s_{2}\) and \(s_{3}\), when \(\frac {c_{1}(d_{1}\omega^{2}-j_{1})}{e}>0\), \(s_{2}\), \(s_{3}\) are real solutions. The solution \(s_{2}\) and \(s_{3}\) have the same Jacobian

    $$\begin{aligned} { \operatorname{det} { \biggl(}\frac{\partial{f}}{\partial{\textbf {x}}}(s_{2}) { \biggr)}=\operatorname{det} { \biggl(}\frac{\partial{f}}{\partial{\textbf {x}}}(s_{3}) { \biggr)}}= \frac{c_{1}(d_{1}\omega^{2}-j_{1})(-a_{1}+d_{1})}{\omega^{5}}. \end{aligned}$$

    When \(a_{1}\neq{d_{1}}\), \({\operatorname{det}(\frac{\partial{f}}{\partial {\textbf{x}}}(s_{2},s_{3}))}\neq{0}\). According to the averaging theory, if there exists \(r=\varepsilon{r_{1}}+o(\varepsilon^{2})>0\), then system (11) has two additional periodic solutions \(\textbf{x}_{2}(\theta ,\varepsilon)\), \(\textbf{x}_{3}(\theta,\varepsilon)\) such that \(\textbf {x}_{2}(0,\varepsilon)=s_{2}+o(\varepsilon)\), \(\textbf{x}_{3}(0,\varepsilon )=s_{3}+o(\varepsilon)\). Bring the solutions back to the system (9), and we have two periodic solutions \(\varPhi_{2}(t,\varepsilon )=(X(t,\varepsilon),Y(t,\varepsilon),Z(t,\varepsilon),U(t,\varepsilon ))\), \(\varPhi_{3}(t,\varepsilon)=(X(t,\varepsilon),Y(t,\varepsilon ),Z(t,\varepsilon),U(t,\varepsilon))\). Then the system (6) has the periodic solutions \(\varepsilon\varPhi_{2}(t,\varepsilon)\), \(\varepsilon \varPhi_{3}(t,\varepsilon)\).

After calculation, we see that the Jacobian matrices \(\frac{\partial {f}}{\partial{\textbf{x}}}(s_{2})\), \(\frac{\partial{f}}{\partial{\textbf {x}}}(s_{3})\) have the same eigenvalues. The eigenvalues are given as follows:

$$\begin{aligned} &\lambda_{1}=\frac{a_{1}-d_{1}}{2\omega},\qquad\lambda_{2,3}= \frac{-c_{1}\omega\pm \sqrt{c_{1}(-8j_{1}+(8d_{1}+c_{1})\omega^{2})}}{2\omega^{2}}. \end{aligned}$$

Similarly, we discuss the case where the eigenvalues are real and imaginary, respectively. Then we arrive at the following conclusions.

  1. (i)

    When \(c_{1}(-8j_{1}+(8d_{1}+c_{1})(b-1)^{2})>0\), \(\lambda _{2}\) and \(\lambda_{3}\) are real. In this case, the periodic solutions \(\varepsilon\varPhi_{2}(t,\varepsilon)\), \(\varepsilon\varPhi_{3}(t,\varepsilon )\) are stable if \(a_{1}< d_{1}\), \(c_{1}>0\), \(-j_{1}+d_{1}(b-1)^{2}<0\).

  2. (ii)

    When \(c_{1}(-8j_{1}+(8d_{1}+c_{1})(b-1)^{2})<0\), \(\lambda _{2}\) and \(\lambda_{3}\) are imaginary. In this case, the periodic solutions \(\varepsilon\varPhi_{2}(t,\varepsilon)\), \(\varepsilon\varPhi _{3}(t,\varepsilon)\) are stable if \(a_{1}< d_{1}\), \(c_{1}>0\).

Theorem 2 is proved. □

5 Conclusion

Four-dimensional hyperchaotic systems have complex dynamic behavior and are widely used. In this paper, we study a four-dimensional smooth quadratic autonomous hyperchaotic system, and we prove that the system has a zero-Hopf bifurcation at the origin of coordinates. The existence of periodic solutions of the system is proved by the classical averaging method, and the stability conditions of periodic solutions are given. In fact, there are many other rich dynamic properties of this hyperchaotic system that are not fully exploited. We hope to have other discoveries about this system in the future work.