1 Introduction

Recently, epidemiological models have received much attention from scientists. Since the pioneering work of Kermack-Mckendrick, there have been many relevant papers [1–8], but only single-species is considered in these models. However, species does not exist alone; while species spreads the disease in the natural world, it also competes with other species for resource to exist, or is predated by their enemies. Therefore, it is more important to consider the effect of multi-species when we consider the dynamical behaviors of epidemiological models. There are not many papers [9–18] considering these two areas.

Due to its universal existence and importance, the dynamic relationship between the predator and the prey has been a dominant theme in ecology. The predator’s functional response is one significant component of the predator-prey relationship. Generally, the classical Holling types I-III are only related to the density of the prey, and Hassell-Varley type [19], Beddington-DeAngelis type [20–23] as well as Crowley-Martin type [24] are functions of both the prey and the predator densities. A lot of data show that the functional response related to prey and predator densities performs much better. The classical predator-prey model with Beddington-DeAngelis type functional response is

$$ \left \{ \textstyle\begin{array}{l} x'(t) = x(t)[b_{1}-a_{11}x(t)-\frac{a_{12}y(t)}{1+mx(t)+ny(t)}], \\ y'(t) = y(t)[-b_{2}+\frac{a_{21}x(t)}{1+mx(t)+ny(t)}-a_{22}y(t)], \end{array}\displaystyle \right . $$
(1)

where \(x=x(t)\) and \(y=y(t)\) represent prey and predator densities at time t, all the coefficients are positive. We can refer to [20, 21, 25] for the biological representation of each coefficient in model (1).

In this paper, we first introduce a deterministic predator-prey model with disease in the predator and Beddington-DeAngelis functional response. We assume that the disease only spreads among the predator population based on the basic epidemiological model, namely the SI:

$$ \left \{ \textstyle\begin{array}{l} x'(t) = x(t)[r-a_{11}x(t)-\frac{a_{12}y_{1}(t)}{1+mx(t)+ny_{1}(t)}], \\ y'_{1}(t) = y_{1}(t)[-d_{2}-a_{22}y_{1}(t)+\frac {a_{21}x(t)}{1+mx(t)+ny_{1}(t)}-\beta y_{2}(t)], \\ y'_{2}(t) =y_{2}(t)[\beta y_{1}(t)-d_{3}-a_{33}y_{2}(t)]. \end{array}\displaystyle \right . $$
(2)

Let \(x(t)\) denote the population density of prey, \(y_{1}(t)\) and \(y_{2}(t)\) represent the population density of the susceptible predator and the infected predator, respectively.

Model (2) is derived under the following assumptions: r is the intrinsic growth rate of the prey, \(a_{11}\) is the overcrowding rate of prey population, and \(a_{12}\) is the capturing rate of the predator. \(d_{2}\) is the death rate of the susceptible predator, \(a_{22}\) is the overcrowding rate of the susceptible predator. \(\frac{a_{21}}{a_{12}}\) is the rate of conversion of nutrient into the reproduction of the predator. β is the transmission rate of the disease. We assume that infected predators do not have capturing ability and do not recover or become immune, \(d_{3}\) and \(a_{33}\) are the death rate and the overcrowding rate of the infected predator, all the coefficients are positive here. System (2) has four non-negative equilibria \(O(0,0,0)\), \(E_{1}(\frac {r}{a_{11}},0,0)\), the disease-free equilibrium \(E_{2}(\hat{x},\hat {y}_{1},0)\) and the positive equilibrium \(E^{*}=(x^{*},y_{1}^{*},y_{2}^{*})\). \(E_{2}\) exists if

$$ a_{21}r>d_{2}(a_{11}+mr).$$
(3)

\(E^{*}\) exists if

$$ a_{21}r>\biggl(d_{2}+\frac{d_{3}a_{22}}{\beta}\biggr) \biggl(a_{11}+mr+\frac{nd_{3}a_{11}}{\beta }\biggr). $$
(4)

Define the basic reproduction number \(R_{0}=\frac{a_{21}r}{(d_{2}+\frac {d_{3}a_{22}}{\beta})(a_{11}+mr+\frac{nd_{3}a_{11}}{\beta})}\), obviously, \(E^{*}\) exists when \(R_{0}>1\). In addition, we can compute a useful result: \(\hat{y}_{1}<\frac{d_{3}}{\beta}\) if \(R_{0}<1\).

In fact, all the populations in the natural world are inevitably affected by environmental white noise which is an important component in reality. Therefore, many stochastic models for single-species or multi-species have been developed [26–30]. In this paper, considering the effect of environmental noise, we introduce stochastic perturbation into some parameters. As we known, r is the intrinsic growth rate of preys, \(d_{2}\) and \(d_{3}\) are both death rates of susceptible predators and infected predators. In practice, these parameters can be estimated by an average value plus an error term. By the well-known central limit theorem, we know the error term follows a normal distribution and sometimes depends on how much the current population sizes differ from the equilibrium state. Hence, we consider the perturbation as the following form [31–36]:

$$r\rightarrow r+\sigma_{1}\dot{B}_{1}(t),\qquad -d_{2}\rightarrow-d_{2}+\sigma_{2}\dot {B}_{2}(t),\qquad -d_{3}\rightarrow-d_{3}+ \sigma_{3}\dot{B}_{3}(t), $$

where \(\sigma_{i}^{2}\) (\(i=1,2,3\)) is the intensity of noise and \(\dot {B}_{i}(t)\) (\(i=1,2,3\)) is a standard Brownian motion. Corresponding to the deterministic model (2), a stochastic system has the following form:

$$ \left \{ \textstyle\begin{array}{l} dx(t) = x(t)[r-a_{11}x(t)-\frac {a_{12}y_{1}(t)}{1+mx(t)+ny_{1}(t)}]\,dt+\sigma_{1} x(t)\, dB_{1}(t), \\ dy_{1}(t) = y_{1}(t)[-d_{2}-a_{22}y_{1}(t)+\frac {a_{21}x(t)}{1+mx(t)+ny_{1}(t)}-\beta y_{2}(t)]\, dt+\sigma_{2} y_{1}(t)\, dB_{2}(t), \\ dy_{2}(t) =y_{2}(t)[\beta y_{1}(t)-d_{3}-a_{33}y_{2}(t)]\, dt+\sigma_{3} y_{2}(t)\, dB_{3}(t). \end{array}\displaystyle \right . $$
(5)

Throughout this paper, unless otherwise specified, let \((\Omega ,\mathcal{F},\mathcal{P})\) be a complete probability space with a filtration \({\{\mathcal{F}_{t}\}}_{t\in R}\) satisfying the usual conditions (i.e., it is right continuous and increasing and \(\mathcal{F}_{0}\) contains all \(\mathcal{P}\)-null sets).

The qualitative analysis of system (2) is in Additional file 1, here we mainly discuss the stochastic system. In the following section, we derive the existence of a positive solution of system (5), an estimate of the solution, and give the conditions of persistence in the mean or extinction for both populations. We also show that there exists a stationary distribution of the solution. As a result, conditions of global stability for model (2) are obtained.

2 Existence of the positive solution

In order for a stochastic differential equation to have a unique global solution for any given initial value, the coefficients of the equation are generally required to satisfy the linear growth condition and the local Lipschitz condition [37].

Theorem 1

For any initial value \(x_{0}>0\), \(y_{10}>0\) and \(y_{20}>0\), there is a unique solution \((x(t), y_{1}(t), y_{2}(t))\) of system (5) on \(t\geq0\), and the solution will remain in \(R_{+}^{3}\) with probability 1.

Proof

Define a \(C^{2}\)-function \(V: R_{+}^{3}\rightarrow R_{+}\) by \(V(x,y_{1},y_{2})=(x-1-\log x)+(y_{1}-1-\log y_{1})+(y_{2}-1-\log y_{2})\), by a similar way of the proof in Theorem 2.1 of [34], Theorem 2.1 of [35] and Lemma 2 of [36], we can have the required assertion. □

Though we cannot get an explicit solution for model (5), an estimate of positive solution of (5) can be derived, we firstly show a very useful lemma derived from [38].

Consider the equation

$$ dN(t)=N(t)\bigl[\bigl(a(t)-b(t)N(t)\bigr)\, dt+\alpha(t)\, dB(t) \bigr]. $$
(6)

Lemma 1

Assume that \(a(t)\), \(b(t)\) and \(\alpha(t)\) are bounded continuous functions defined on \([0, \infty)\), \(a(t)>0\) and \(b(t)>0\). Then there exists a unique continuous positive solution \(N(t)\) for any initial value \(N(0)=N_{0}>0\), which is global and represented by

$$ N(t)= \frac{\exp\{\int_{0}^{t}[a(s)-\frac{\alpha^{2}(s)}{2}]\, ds+\alpha(s)\, dB(s)\} }{1/N_{0}+\int_{0}^{t}b(s)\exp\{\int_{0}^{s}[a(\tau)-\frac{\alpha^{2}(\tau )}{2}]\, d\tau+\alpha(\tau)\, dB(\tau)\}\, ds},\quad t\geq0. $$
(7)

Since the solution is positive, we have \(dx(t) \leq x(t)[r-a_{11}x(t)]\, dt+\sigma_{1} x(t)\, dB_{1}(t)\) from system (5), let

$$\Phi(t)=\frac{\exp^{(r-\frac{\sigma_{1}^{2}}{2})t+\sigma _{1}B_{1}(t)}}{1/x_{0}+a_{11}\int_{0}^{t}\exp^{(r-\frac{\sigma _{1}^{2}}{2})s+\sigma_{1}B_{1}(s)}\, ds}, $$

by Lemma 1, it is easy to see that \(\Phi(t)\) is the unique solution of the following equation:

$$ \left \{ \textstyle\begin{array}{l} d\Phi(t)=\Phi(t)(r-a_{11}\Phi(t))\, dt+\sigma_{1}\Phi(t)\, dB_{1}(t), \\ \Phi(0)=x_{0}. \end{array}\displaystyle \right . $$

The comparison theorem for stochastic equations yields \(x(t)\leq\Phi (t)\), \(t\geq0\), a.s. Besides,

$$dy_{1}(t) \leq y_{1}(t)\biggl[-d_{2}-a_{22}y_{1}(t)+ \frac{a_{21}}{m}\biggr]\, dt+\sigma_{2} y_{1}(t)\, dB_{2}(t). $$

Obviously, by Lemma 1,

$$\Psi_{1}(t)=\frac{\exp^{(\frac{a_{21}}{m}-d_{2}-\frac{\sigma _{2}^{2}}{2})t+\sigma_{2}B_{2}(t)}}{\frac{1}{y_{10}}+a_{22}\int_{0}^{t}\exp ^{(\frac{a_{21}}{m}-d_{2}-\frac{\sigma_{2}^{2}}{2})s+\sigma_{2}B_{2}(s)}\, ds} $$

is the solution to the equation

$$ \left \{ \textstyle\begin{array}{l} d\Psi_{1}(t)=\Psi_{1}(t)(\frac{a_{21}}{m}-d_{2}-a_{22}\Psi_{1}(t))\, dt+\sigma _{2}\Psi_{1}(t)\, dB_{2}(t), \\ \Psi_{1}(0)=y_{10}, \end{array}\displaystyle \right . $$

and \(y_{1}(t)\leq\Psi_{1}(t)\), \(t\geq0\), a.s. On the other hand,

$$dx(t)\geq x(t)\biggl[r-a_{11}x(t)-\frac{a_{12}}{n}\biggr]\, dt+ \sigma_{1} x(t)\, dB_{1}(t), $$

similarly, we can get \(x(t)\geq\phi(t)\), \(t\geq0\), a.s., where

$$\phi(t)=\frac{\exp^{(r-\frac{a_{12}}{n}-\frac{\sigma_{1}^{2}}{2})t+\sigma _{1}B_{1}(t)}}{1/x_{0}+a_{11}\int_{0}^{t}\exp^{(r-\frac{a_{12}}{n}-\frac{\sigma _{1}^{2}}{2})s+\sigma_{1}B_{1}(s)}\, ds} $$

is the solution of

$$ \left \{ \textstyle\begin{array}{l} d\phi(t)=\phi(t)(r-\frac{a_{12}}{n}-a_{11}\phi(t))\, dt+\sigma_{1}\phi (t)\, dB_{1}(t), \\ \phi(0)=x_{0}. \end{array}\displaystyle \right . $$

It is easy to see that \(dy_{2}(t)\leq y_{2}(t)[\beta\Psi _{1}(t)-d_{3}-a_{33}y_{2}(t)]\, dt+\sigma_{3} y_{2}(t)\, dB_{3}(t)\), we also have \(y_{2}(t)\leq\Psi_{2}(t)\), \(t\geq0\), a.s., and

$$\Psi_{2}(t)=\frac{\exp\{\int_{0}^{t}(\beta\Psi_{1}(s)-d_{3}-\frac{\sigma _{3}^{2}}{2})\,ds+\sigma_{3}\,dB_{3}(s)\}}{\frac{1}{y_{20}}+a_{33}\int_{0}^{t}\exp\{ \int_{0}^{s}(\beta\Psi_{1}(\tau)-d_{3}-\frac{\sigma_{3}^{2}}{2})\,d\tau+\sigma _{3}\,dB_{3}(\tau)\}\,ds} $$

is the solution of

$$ \left \{ \textstyle\begin{array}{l} d\Psi_{2}(t)=\Psi_{2}(t)(\beta\Psi_{1}(t)-d_{3}-a_{33}\Psi_{2}(t))\,dt+\sigma _{3}\Psi_{2}(t)\,dB_{3}(t), \\ \Psi_{2}(0)=y_{20}. \end{array}\displaystyle \right . $$

By system (5), we have \(dy_{1}(t)\geq y_{1}(t)[-d_{2}-a_{22}y_{1}(t)+\frac{a_{21}\phi(t)}{1+m\Phi (t)+n\Psi_{1}(t)}-\beta\Psi_{2}(t)]\,dt+\sigma_{2} y_{1}(t)\,dB_{2}(t)\). Therefore, we derive \(y_{1}(t)\geq\psi_{1}(t)\), \(t\geq0\), a.s., where

$$\psi_{1}(t)=\frac{\exp\{\int_{0}^{t}(\frac{a_{21}\phi(s)}{1+m\Phi(s)+n\Psi _{1}(s)}-d_{2}-\beta\Psi_{2}(s)-\frac{\sigma_{2}^{2}}{2})\,ds+\sigma_{2}\,dB_{2}(s)\} }{\frac{1}{y_{10}}+a_{22}\int_{0}^{t}\exp\{\int_{0}^{s}(\frac{a_{21}\phi (\tau)}{1+m\Phi(\tau)+n\Psi_{1}(\tau)}-d_{2}-\beta\Psi_{2}(\tau)-\frac{\sigma _{2}^{2}}{2})\,d\tau+\sigma_{2}\,dB_{2}(\tau)\}\,ds} $$

is a solution of

$$ \left \{ \textstyle\begin{array}{l} d\psi_{1}(t)=\psi_{1}(t)(\frac{a_{21}\phi(t)}{1+m\Phi(t)+n\Psi _{1}(t)}-d_{2}-\beta\Psi_{2}(t)-a_{22}\psi_{1}(t))\,dt+\sigma_{2}\psi_{1}(t)\,dB_{2}(t), \\ \psi_{1}(0)=y_{10}. \end{array}\displaystyle \right . $$

We can also get \(y_{2}(t)\geq\psi_{2}(t)\), \(t\geq0\), a.s., where

$$\psi_{2}(t)=\frac{\exp\{\int_{0}^{t}(\beta\psi_{1}(s)-d_{3}-\frac{\sigma _{3}^{2}}{2})\,ds+\sigma_{3}\,dB_{3}(s)\}}{\frac{1}{y_{20}}+a_{33}\int_{0}^{t}\exp\{ \int_{0}^{s}(\beta\psi_{1}(\tau)-d_{3}-\frac{\sigma_{3}^{2}}{2})\,d\tau+\sigma _{3}\,dB_{3}(\tau)\}\,ds} $$

is a solution of

$$ \left \{ \textstyle\begin{array}{l} d\psi_{2}(t)=\psi_{2}(t)(\beta\psi_{1}(t)-d_{3}-a_{33}\psi_{2}(t))\,dt+\sigma _{3}\psi_{2}(t)\,dB_{3}(t), \\ \psi_{2}(0)=y_{20}, \end{array}\displaystyle \right . $$

then we derive the following theorem.

Theorem 2

Assume \((x(t), y_{1}(t), y_{2}(t))\) on \(t\geq0\) is the positive solution of system (5) for initial value \(x_{0}>0\), \(y_{10}>0\) and \(y_{20}>0\), then there exist functions \(\Phi(t)\), \(\phi(t)\), \(\Psi_{i}(t)\), \(\psi_{i}(t)\) (\(i=1, 2\)), defined as above, such that

$$\phi(t)\leq x(t)\leq\Phi(t),\qquad \psi_{i}(t)\leq y_{i}(t)\leq\Psi_{i}(t)\quad (i=1, 2), t\geq0,\textit{a.s.} $$

3 Persistence in the mean and extinction

In order to consider the conditions of persistence in the mean and extinction for the prey and predator population, at first, we give two useful lemmas. Applying Itô’s formula to system (5) yields

$$ \left \{ \textstyle\begin{array}{l} d\ln x(t) =[r-\frac{1}{2}\sigma_{1}^{2}-a_{11}x(t)-\frac {a_{12}y_{1}(t)}{1+mx(t)+ny_{1}(t)}]\,dt+\sigma_{1}\,dB_{1}(t), \\ d\ln y_{1}(t) = [-d_{2}-\frac{1}{2}\sigma_{2}^{2}-a_{22}y_{1}(t)+\frac {a_{21}x(t)}{1+mx(t)+ny_{1}(t)}-\beta y_{2}(t)]\,dt+\sigma_{2}\,dB_{2}(t), \\ d\ln y_{2}(t) =[\beta y_{1}(t)-d_{3}-\frac{1}{2}\sigma _{3}^{2}-a_{33}y_{2}(t)]\,dt+\sigma_{3}\,dB_{3}(t). \end{array}\displaystyle \right . $$
(8)

Lemma 2

The solution \((x(t),y_{1}(t),y_{2}(t))\) of system (5) for any initial value \((x_{0}, y_{10}, y_{20})\in R_{3}^{+}\) satisfies the following inequalities:

$$\limsup_{t\rightarrow\infty}\frac{\ln x(t)}{t} \leq0, \qquad \limsup _{t\rightarrow\infty}\frac{\ln y_{1}(t)}{t} \leq0,\qquad \limsup _{t\rightarrow\infty}\biggl(\frac{\ln y_{1}(t)}{t}+\frac{\ln y_{2}(t)}{t}\biggr) \leq0. $$

Proof

It follows from Eq. (8) that

$$ \left \{ \textstyle\begin{array}{l} d\ln x(t) \leq[r-\frac{1}{2}\sigma_{1}^{2}-a_{11}x(t)]\,dt+\sigma _{1}\,dB_{1}(t), \\ d\ln y_{1}(t) \leq [\frac{a_{21}}{m}-d_{2}-\frac{1}{2}\sigma _{2}^{2}-a_{22}y_{1}(t)]\,dt+\sigma_{2}\,dB_{2}(t), \\ d\ln y_{2}(t) =[\beta y_{1}(t)-d_{3}-\frac{1}{2}\sigma _{3}^{2}-a_{33}y_{2}(t)]\,dt+\sigma_{3}\,dB_{3}(t). \end{array}\displaystyle \right . $$

Consider the following system:

$$ \left \{ \textstyle\begin{array}{l} d\ln u(t) = [r-\frac{1}{2}\sigma_{1}^{2}-a_{11}u(t)]\,dt+\sigma_{1}\,dB_{1}(t), \\ d\ln v_{1}(t) = [\frac{a_{21}}{m}-d_{2}-\frac{1}{2}\sigma _{2}^{2}-a_{22}v_{1}(t)]\,dt+\sigma_{2}\,dB_{2}(t), \\ d\ln v_{2}(t) =[\beta v_{1}(t)-d_{3}-\frac{1}{2}\sigma _{3}^{2}-a_{33}v_{2}(t)]\,dt+\sigma_{3}\,dB_{3}(t), \end{array}\displaystyle \right . $$
(9)

with initial value \((x_{0}, y_{10}, y_{20})\in R_{3}^{+}\). By the comparison theorem for stochastic differential equations, we have

$$x(t)\leq u(t),\qquad y_{i}(t)\leq v_{i}(t)\quad (i=1,2), t \in[0,+\infty), \mbox{a.s.} $$

In fact, by virtue of Theorem 3.3 and Corollary 3.4 in [39], we can get

$$\limsup_{t\rightarrow\infty}\frac{\ln u(t)}{t} \leq0,\qquad \limsup _{t\rightarrow\infty}\frac{\ln v_{1}(t)}{t} \leq0. $$

Hence, \(\limsup_{t\rightarrow\infty}\frac{\ln x(t)}{t} \leq0\), \(\limsup_{t\rightarrow\infty}\frac{\ln y_{1}(t)}{t} \leq0\). In the following, we show that \(\limsup_{t\rightarrow\infty}(\frac{\ln y_{1}(t)}{t}+\frac{\ln y_{2}(t)}{t}) \leq0\).

Applying Itô’s formula to \(\exp(t)\ln v_{i}(t)\) (\(i=1,2\)) results in

$$ \left \{ \textstyle\begin{array}{l} \exp(t)\ln v_{1}(t) =\ln y_{10}+\int_{0}^{t}\exp(s)[\ln v_{1}(s)+\frac {a_{21}}{m}-d_{2}-\frac{1}{2}\sigma_{2}^{2}-a_{22}v_{1}(s)]\,ds \\ \hphantom{\exp(t)\ln v_{1}(t) =}{}+M_{1}(t), \\ \exp(t)\ln v_{2}(t) =\ln y_{20}+\int_{0}^{t}\exp(s)[\ln v_{2}(s)+\beta v_{1}(s)-d_{3}-\frac{1}{2}\sigma_{3}^{2}-a_{33}v_{2}(s)]\,ds \\ \hphantom{\exp(t)\ln v_{2}(t) =}{}+M_{2}(t), \end{array}\displaystyle \right . $$
(10)

where \(M_{i}(t)=\int_{0}^{t}\sigma_{i} \exp(s)\,dB_{i}(s)\) (\(i=1,2\)) is a real-valued continuous local martingale with quadratic form \(\langle M_{i}(t),M_{i}(t)\rangle=\int_{0}^{t}\sigma_{i}^{2} \exp(2s)\,ds\).

By virtue of the exponential martingale inequality of [40], for any positive constants T, δ and η, we have

$$P\biggl\{ \sup_{0\leq t\leq T}\biggl[M_{i}(t)- \frac{\delta}{2}\bigl\langle M_{i}(t),M_{i}(t)\bigr\rangle \biggr]>\eta\biggr\} \leq\exp(-\delta\eta). $$

Choosing \(T=\gamma k\), \(\delta=\exp(-\gamma k)\), \(\eta=\theta\exp(\gamma k)\ln k\) gives that

$$P\biggl\{ \sup_{0\leq t\leq\gamma k}\biggl[M_{i}(t)- \frac{\exp(-\gamma k)}{2}\bigl\langle M_{i}(t),M_{i}(t)\bigr\rangle \biggr]>\theta\exp(\gamma k)\ln k\biggr\} \leq k^{-\theta}, $$

where \(k\in N\), \(\theta>1\) and \(\gamma>1\). It follows from the Borel-Cantelli lemma that there exists \(\Omega_{i}\subset\Omega\) (\(i=1,2\)) with \(P(\Omega_{i})=1\) such that for any \(\omega\in\Omega_{i}\), an integer \(k_{i}=k_{i}(\omega)\) satisfying

$$M_{i}(t)\leq\frac{\exp(-\gamma k)}{2}\bigl\langle M_{i}(t),M_{i}(t) \bigr\rangle +\theta \exp(\gamma k)\ln k $$

for all \(0\leq t\leq\gamma k\) and \(k\geq k_{i}(\omega)\) can be found. Now let \(\Omega_{0}=\bigcap_{i=1}^{2}\Omega_{i}\), clearly, \(P(\Omega_{0})=1\). Moreover, let \(k_{0}(\omega)=\max\{k_{i}(\omega),i=1,2\}\), then for any \(\omega\in\Omega _{0}\), it follows from Eq. (10) that

$$ \left \{ \textstyle\begin{array}{l} \exp(t)\ln v_{1}(t)\leq\ln y_{10}+\int_{0}^{t}\exp(s)[\ln v_{1}(s)+\frac {a_{21}}{m}-d_{2}-\frac{1}{2}\sigma_{2}^{2}-a_{22}v_{1}(s)]\,ds \\ \hphantom{\exp(t)\ln v_{1}(t)\leq}{}+\int_{0}^{t}\exp(s)\frac{\sigma_{2}^{2}}{2}\exp(s-\gamma k)\,ds+\theta\exp (\gamma k)\ln k, \\ \exp(t)\ln v_{2}(t)\leq\ln y_{20}+\int_{0}^{t}\exp(s)[\ln v_{2}(s)+\beta v_{1}(s)-d_{3}-\frac{1}{2}\sigma_{3}^{2}-a_{33}v_{2}(s)]\,ds \\ \hphantom{\exp(t)\ln v_{2}(t)\leq}{}+\int_{0}^{t}\exp(s)\frac{\sigma_{3}^{2}}{2}\exp(s-\gamma k)\,ds+\theta\exp (\gamma k)\ln k \end{array}\displaystyle \right . $$
(11)

for all \(0\leq t\leq\gamma k\) and \(k\geq k_{i}(\omega)\). Then

$$\begin{aligned}& \exp(t)\bigl[\ln v_{1}(t)+\ln v_{2}(t)\bigr] \\& \quad \leq \ln y_{10}+\ln y_{20}+\int_{0}^{t} \exp(s)\biggl[\ln v_{1}(s)-(a_{22}-\beta)v_{1}(s)+ \frac{a_{21}}{m} \\& \qquad {}-d_{2}-\frac{1}{2}\sigma_{2}^{2}+\ln v_{2}(s)-a_{33}v_{2}(s)-d_{3}- \frac {1}{2}\sigma_{3}^{2}\biggr]\,ds \\& \qquad {}+\int _{0}^{t}\exp(s)\sum_{i=2}^{3} \frac{\sigma _{i}^{2}}{2}\exp(s-\gamma k)\,ds \\& \qquad {}+2\theta\exp(\gamma k)\ln k. \end{aligned}$$

It is easy to see that for any \(0\leq s\leq\gamma k\) and \((u(s),v_{1}(s),v_{2}(s))\in R_{+}^{3}\), there exists a constant A independent of k such that

$$\begin{aligned}& \ln v_{1}(s)-(a_{22}-\beta)v_{1}(s)+ \frac{a_{21}}{m}-d_{2}-\frac{1}{2}\sigma_{2}^{2} +\ln v_{2}(s)-a_{33}v_{2}(s)-d_{3}- \frac{1}{2}\sigma_{3}^{2} \\& \quad {} +\sum_{i=2}^{3}\frac{\sigma_{i}^{2}}{2} \exp(s-\gamma k)\leq A. \end{aligned}$$

Hence, it follows that for all \(0\leq t\leq\gamma k\), with \(k\geq k_{0}(\omega)\), we have

$$\exp(t)\bigl[\ln v_{1}(t)+\ln v_{2}(t)\bigr]\leq \ln y_{10}+\ln y_{20}+\int_{0}^{t}A \exp(s)\,ds+2\theta\exp(\gamma k)\ln k. $$

Thus,

$$\ln v_{1}(t)+\ln v_{2}(t)\leq\exp(-t)[ \ln y_{10}+\ln y_{20}]+A\bigl[1-\exp (-t)\bigr]+2\theta\exp(-t) \exp(\gamma k)\ln k. $$

Consequently, for \(\gamma(k-1)\leq t\leq\gamma k\) and \(k\geq k_{0}(\omega )\), it follows that

$$\begin{aligned} \frac{\ln v_{1}(t)}{t}+\frac{\ln v_{2}(t)}{t} \leq&\frac{1}{t}\exp(-t)[ \ln y_{10}+\ln y_{20}]+\frac{A[1-\exp(-t)]}{t} \\ &{}+\frac{2\theta\exp(-\gamma(k-1))\exp(\gamma k)\ln k}{t}. \end{aligned}$$

Now let \(k\rightarrow+\infty\), then \(t\rightarrow+\infty\), we have

$$\limsup_{t\rightarrow\infty}\biggl(\frac{\ln v_{1}(t)}{t}+\frac{\ln v_{2}(t)}{t} \biggr) \leq0. $$

Therefore,

$$\limsup_{t\rightarrow\infty}\biggl(\frac{\ln y_{1}(t)}{t}+\frac{\ln y_{2}(t)}{t} \biggr) \leq0. $$

 □

Definition 1

  1. (1)

    The population \(x(t)\) is said to be non-persistent in the mean if \(\langle x(t)\rangle^{*}=0\), where \(\langle f(t)\rangle =\frac{1}{t}\int_{0}^{t}f(s)\,ds\), \(f^{*}=\limsup_{t\rightarrow+\infty }f(t)\), \(f_{*}=\liminf_{t\rightarrow+\infty}f(t)\).

  2. (2)

    The population \(x(t)\) is said to be weakly persistent in the mean if \(\langle x(t)\rangle^{*}>0\).

  3. (3)

    The population \(x(t)\) is said to be strongly persistent in the mean if \(\langle x(t)\rangle_{*}>0\).

Lemma 3

[41]

Suppose that \(x(t)\in C[\Omega\times R_{+},R_{+}^{0}]\), where \(R_{+}^{0}:=\{a|a>0,a\in R\}\).

  1. (I)

    If there are positive constants \(\lambda_{0}\), T and \(\lambda\geq0\) such that

    $$\ln x(t)\leq\lambda t-\lambda_{0}\int_{0}^{t}x(s) \,ds+\sum_{i=1}^{n}\beta_{i}B_{i}(t) $$

    for \(t\geq T\), where \(\beta_{i}\) is a constant, \(1\leq i\leq n\), then \(\langle x\rangle^{*}\leq\lambda/\lambda_{0}\), a.s. (i.e., almost surely).

  2. (II)

    If there are positive constants \(\lambda_{0}\), T and \(\lambda\geq 0\) such that

    $$\ln x(t)\geq\lambda t-\lambda_{0}\int_{0}^{t}x(s) \,ds+\sum_{i=1}^{n}\beta_{i}B_{i}(t) $$

    for \(t\geq T\), where \(\beta_{i}\) is a constant, \(1\leq i\leq n\), then \(\langle x\rangle_{*}\geq\lambda/\lambda_{0}\), a.s.

Theorem 3

For the prey population, we have:

  1. (i)

    If \(r<\frac{1}{2}\sigma_{1}^{2}\), then the prey population \(x(t)\) will go to extinction a.s.

  2. (ii)

    If \(r=\frac{1}{2}\sigma_{1}^{2}\), then the prey population \(x(t)\) is non-persistent in the mean a.s.

  3. (iii)

    If \(r>\frac{1}{2}\sigma_{1}^{2}\), then the prey population \(x(t)\) is weakly persistent in the mean a.s.

  4. (iv)

    If \(r>\frac{1}{2}\sigma_{1}^{2}+\frac{a_{12}}{n}\), then the prey population \(x(t)\) is strongly persistent in the mean a.s.

Proof

It follows from the first equation of system (5) that

$$dx(t) \leq x(t)\bigl[r-a_{11}x(t)\bigr]\,dt+\sigma_{1}x(t) \,dB_{1}(t), $$

the right-hand side is a logistic system, because of the comparison theorem, Theorem 2, Theorem 7 and Theorem 8 in [42], we can get consequences (i) and (ii).

(iii) We need to show that there exists a constant \(\rho>0\) such that for any solution of system (5) with initial value \((x_{0}, y_{10},y_{20})\in R_{+}^{3}\) satisfying \(\langle x(t)\rangle^{*}\geq\rho >0\). Now we assume that the contrast is true, let \(\varepsilon_{1}>0\) sufficiently small such that \((-d_{2}-\frac{\sigma _{2}^{2}}{2})+a_{21}\varepsilon_{1}<0\), \((r-\frac{1}{2}\sigma _{1}^{2})-a_{11}\varepsilon_{1}>0\), then for \(\varepsilon_{1}>0\), there exists a solution \((\bar{x},\bar{y}_{1} ,\bar{y}_{2})\) with initial value \((x_{0}, y_{10},y_{20})\in R_{+}^{3}\) such that \(P\{\langle\bar{x}(t)\rangle^{*}<\varepsilon_{1}\}>0\).

By virtue of system (8), we have

$$\frac{\ln\bar{y}_{1}(t)-\ln y_{10}}{t}\leq\biggl(-d_{2}-\frac{\sigma _{2}^{2}}{2} \biggr)+a_{21}\bigl\langle \bar{x}(t)\bigr\rangle +\sigma_{2} \frac{B_{2}(t)}{t}. $$

We also have \(\lim_{t\rightarrow+\infty}\frac{B_{2}(t)}{t}=0\), thus \(\limsup_{t\rightarrow+\infty}\frac{\ln\bar{y}_{1}(t)}{t}\leq (-d_{2}-\frac{\sigma_{2}^{2}}{2})+a_{21}\varepsilon_{1}<0\), then \(\lim_{t\rightarrow+\infty}\bar{y}_{1}(t)=0\).

It follows from system (8) that

$$d\ln\bar{x}(t) \geq\biggl[r-\frac{1}{2}\sigma_{1}^{2}-a_{11} \bar {x}(t)-a_{12}\bar{y}_{1}(t)\biggr]\,dt+ \sigma_{1}\,dB_{1}(t). $$

Integrating both sides from \([0, t]\) and multiplying by \(\frac{1}{t}\), we obtain

$$\frac{\ln\bar{x}(t)-\ln x_{0}}{t}\geq\biggl(r-\frac{1}{2}\sigma _{1}^{2} \biggr)-a_{11}\bigl\langle \bar{x}(t)\bigr\rangle -a_{12}\bigl\langle \bar {y}_{1}(t)\bigr\rangle +\sigma_{1} \frac{B_{1}(t)}{t}, $$

then \(\limsup_{t\rightarrow+\infty}\frac{\ln\bar{x}(t)}{t}\geq(r-\frac {1}{2}\sigma_{1}^{2})-a_{11}\varepsilon_{1}>0\), which contradicts Lemma 2. Therefore, our assumption is false, \(\langle x(t) \rangle^{*}>0\), the prey population \(x(t)\) will be weakly persistent in the mean a.s.

(iv) It is easy to get

$$dx(t)\geq x(t)\biggl[\biggl(r-\frac{a_{12}}{n}\biggr)-a_{11}x(t) \biggr]\,dt+\sigma_{1}x(t)\,dB_{1}(t). $$

Similarly, by the comparison theorem, Theorem 2 and Theorem 10 in [42], result (iv) is obtained. □

Remark 1

By Theorem 3, we find that \(r-\frac {1}{2}\sigma_{1}^{2}\) is the threshold between weak persistence in the mean and extinction for the prey population. If \(\frac{1}{2}\sigma _{1}^{2}>r\), then the prey population will be extinct in the future, no matter whether the predator exists. It implies that environmental random perturbation plays a very important role in the biological system.

Theorem 4

For the predator population, we have:

  1. (i)

    If \(a_{21}(r-\frac{1}{2}\sigma_{1}^{2})< a_{11}(d_{2}+\frac{\sigma _{2}^{2}}{2})\), then the susceptible predator population \(y_{1}(t)\) will go to extinction a.s.

  2. (ii)

    If \(a_{21}(r-\frac{1}{2}\sigma_{1}^{2})=a_{11}(d_{2}+\frac{\sigma _{2}^{2}}{2})\), then the susceptible predator population \(y_{1}(t)\) is non-persistent in the mean a.s.

  3. (iii)

    If \(\beta a_{21}(r-\frac{1}{2}\sigma_{1}^{2})<\beta a_{11}(d_{2}+\frac{\sigma_{2}^{2}}{2})+a_{11}a_{22}(d_{3}+\frac{\sigma _{3}^{2}}{2})\), then the infected predator population \(y_{2}(t)\) will go to extinction a.s.

  4. (iv)

    If \(\beta a_{21}(r-\frac{1}{2}\sigma_{1}^{2})=\beta a_{11}(d_{2}+\frac{\sigma_{2}^{2}}{2})+a_{11}a_{22}(d_{3}+\frac{\sigma _{3}^{2}}{2})\), then the infected predator population \(y_{2}(t)\) is non-persistent in the mean a.s.

Proof

(i) If \(r\leq\frac{1}{2}\sigma_{1}^{2}\), then it follows from Theorem 3 that \(\langle x(t)\rangle^{*}=0\). By the second equation of system (8), we have

$$ \frac{\ln y_{1}(t)-\ln y_{10}}{t}\leq\biggl(-d_{2}-\frac{\sigma _{2}^{2}}{2} \biggr)+a_{21}\bigl\langle x(t)\bigr\rangle +\sigma_{2} \frac{B_{2}(t)}{t}. $$
(12)

Hence, \([t^{-1}\ln y_{1}(t)]^{*}\leq(-d_{2}-\frac{\sigma _{2}^{2}}{2})<0\), then \(\lim_{t\rightarrow+\infty}y_{1}(t)=0\).

Now we consider that if \(r> \frac{1}{2}\sigma_{1}^{2}\), it follows from the first equation of system (8) that

$$\frac{\ln x(t)-\ln x_{0}}{t}\leq\biggl(r-\frac{1}{2}\sigma _{1}^{2} \biggr)-a_{11}\bigl\langle x(t) \bigr\rangle +\sigma_{1} \frac{B_{1}(t)}{t}. $$

Applying Lemma 3 leads to

$$ \bigl\langle x(t) \bigr\rangle ^{*}\leq \frac{r-\frac{1}{2}\sigma_{1}^{2}}{a_{11}}. $$
(13)

Substituting the above inequality into (12) gives

$$ \bigl[t^{-1}\ln y_{1}(t)\bigr]^{*} \leq\biggl(-d_{2}-\frac{\sigma _{2}^{2}}{2}\biggr)+a_{21}\bigl\langle x(t)\bigr\rangle ^{*}\leq\frac{a_{21}(r-\frac {1}{2}\sigma_{1}^{2})-a_{11}(d_{2}+\frac{\sigma_{2}^{2}}{2})}{a_{11}}< 0, $$
(14)

which implies that \(\lim_{t\rightarrow+\infty}y_{1}(t)=0\) a.s.

(ii) Assume \(\langle y_{1}(t)\rangle^{*}>0\), then it follows from Lemma 2 that \([t^{-1}\ln y_{1}]^{*}=0\). Making use of (14), we can see

$$ 0=\bigl[t^{-1}\ln y_{1}(t) \bigr]^{*}\leq\biggl(-d_{2}-\frac{\sigma _{2}^{2}}{2} \biggr)+a_{21}\bigl\langle x(t)\bigr\rangle ^{*}. $$
(15)

On the other hand, for sufficiently small \(\varepsilon_{3}>0\), there exists \(T_{3}>0\) such that for all \(t>T_{3}\), \(a_{21}\langle x(t) \rangle< a_{21}\langle x(t) \rangle^{*}+\varepsilon_{3}\).

Substituting these inequalities into the second equation of system (8) yields that

$$\begin{aligned} \frac{\ln y_{1}(t)-\ln y_{10}}{t}&\leq\biggl(-d_{2}-\frac{\sigma _{2}^{2}}{2} \biggr)+a_{21}\bigl\langle x(t)\bigr\rangle -a_{22}\bigl\langle y_{1}(t)\bigr\rangle +\sigma_{2}\frac{B_{2}(t)}{t} \\ &\leq \biggl(-d_{2}-\frac{\sigma_{2}^{2}}{2}\biggr)+a_{21}\bigl\langle x(t)\bigr\rangle ^{*}+\varepsilon_{3}-a_{22} \bigl\langle y_{1}(t)\bigr\rangle +\sigma_{2} \frac{B_{2}(t)}{t}, \end{aligned}$$

then application of Lemma 3 and (15) results in

$$\bigl\langle y_{1}(t)\bigr\rangle ^{*}\leq \frac{(-d_{2}-\frac{\sigma _{2}^{2}}{2})+a_{21}\langle x(t)\rangle^{*}+\varepsilon_{3}}{a_{22}}. $$

Condition \(a_{21}(r-\frac{1}{2}\sigma_{1}^{2})=a_{11}(d_{2}+\frac{\sigma _{2}^{2}}{2})\) means that \(r> \frac{1}{2}\sigma_{1}^{2}\), because of (13) and the arbitrariness of \(\varepsilon_{3}\),

$$ \bigl\langle y_{1}(t)\bigr\rangle ^{*}\leq \frac{a_{21}(r-\frac{1}{2}\sigma _{1}^{2})-a_{11}(d_{2}+\frac{\sigma_{2}^{2}}{2})}{a_{11}a_{22}}=0, $$
(16)

which is a contradiction to our assumption, therefore, \(\langle y_{1}(t)\rangle^{*}=0\) a.s.

(iii) If \(a_{21}(r-\frac{1}{2}\sigma_{1}^{2})\leq a_{11}(d_{2}+\frac {\sigma_{2}^{2}}{2})\), then from (i) and (ii), we get \(\langle y_{1}(t)\rangle^{*}=0\). Hence, it follows from the third equation of system (8) that

$$ \frac{\ln y_{2}(t)-\ln y_{20}}{t}=\beta\bigl\langle y_{1}(t)\bigr\rangle -d_{3}-\frac {1}{2}\sigma_{3}^{2}-a_{33} \bigl\langle y_{2}(t)\bigr\rangle +\sigma_{3} \frac{B_{3}(t)}{t}. $$
(17)

Taking superior limit leads to \([t^{-1}\ln y_{2}(t)]^{*}\leq-d_{3}-\frac{1}{2}\sigma_{3}^{2}<0\), then \(\lim_{t\rightarrow+\infty}y_{2}(t)=0\) a.s.

If \(a_{21}(r-\frac{1}{2}\sigma_{1}^{2})>a_{11}(d_{2}+\frac{\sigma _{2}^{2}}{2})\), \(r>\frac{1}{2}\sigma_{1}^{2}\) must be verified, thus by the proof of (ii), we have (16), that is,

$$\bigl\langle y_{1}(t)\bigr\rangle ^{*}\leq \frac{a_{21}(r-\frac{1}{2}\sigma _{1}^{2})-a_{11}(d_{2}+\frac{\sigma_{2}^{2}}{2})}{a_{11}a_{22}}. $$

At this time, making use of (16), we obtain

$$\begin{aligned} \bigl(t^{-1}\ln y_{2}(t)\bigr)^{*} &\leq \beta \bigl\langle y_{1}(t)\bigr\rangle ^{*}-d_{3}- \frac {1}{2}\sigma_{3}^{2} \\ &\leq \frac{\beta a_{21}(r-\frac{1}{2}\sigma_{1}^{2})-\beta a_{11}(d_{2}+\frac{\sigma_{2}^{2}}{2})-a_{11}a_{22}(d_{3}+\frac{\sigma _{3}^{2}}{2})}{a_{11}a_{22}} \\ &< 0, \end{aligned}$$

then \(\lim_{t\rightarrow+\infty}y_{2}(t)=0\) as desired.

(iv) If \(\beta a_{21}(r-\frac{1}{2}\sigma_{1}^{2})=\beta a_{11}(d_{2}+\frac{\sigma_{2}^{2}}{2})+a_{11}a_{22}(d_{3}+\frac{\sigma _{3}^{2}}{2})\), then \(a_{21}(r-\frac{1}{2}\sigma_{1}^{2})>a_{11}(d_{2}+\frac{\sigma _{2}^{2}}{2})\) and \(r>\frac{1}{2}\sigma_{1}^{2}\). By the properties of superior limit, for sufficiently small \(\varepsilon_{4}>0\), there exists a constant \(T_{4}>0\) such that for all \(t>T_{4}\), \(\langle y_{1}(t)\rangle<\langle y_{1}(t)\rangle^{*}+\frac{\varepsilon _{4}}{\beta}\).

Substituting (16) and the above results into (17) yields

$$\begin{aligned} \frac{\ln y_{2}(t)-\ln y_{20}}{t} \leq&\frac{\beta a_{21}(r-\frac {1}{2}\sigma_{1}^{2})-\beta a_{11}(d_{2}+\frac{\sigma _{2}^{2}}{2})}{a_{11}a_{22}}+\varepsilon_{4}-d_{3}- \frac{\sigma _{3}^{2}}{2}-a_{33}\bigl\langle y_{2}(t)\bigr\rangle \\ &{}+\sigma_{3}\frac{B_{3}(t)}{t} \\ \leq& \frac{\beta a_{21}(r-\frac{1}{2}\sigma_{1}^{2})-\beta a_{11}(d_{2}+\frac{\sigma_{2}^{2}}{2})-a_{11}a_{22}(d_{3}+\frac{\sigma _{3}^{2}}{2})}{a_{11}a_{22}}+\varepsilon_{4} \\ &{}-a_{33}\bigl\langle y_{2}(t)\bigr\rangle + \sigma_{3}\frac{B_{3}(t)}{t}. \end{aligned}$$

By Lemma 3, \(\langle y_{2}(t)\rangle^{*}\leq\frac{1}{a_{33}}[\frac{\beta a_{21}(r-\frac{1}{2}\sigma_{1}^{2})-\beta a_{11}(d_{2}+\frac{\sigma _{2}^{2}}{2})-a_{11}a_{22}(d_{3}+\frac{\sigma _{3}^{2}}{2})}{a_{11}a_{22}}+\varepsilon_{4}]=\frac{\varepsilon _{4}}{a_{33}}\). Considering the arbitrariness of \(\varepsilon_{4}\), we have \(\langle y_{2}(t)\rangle^{*}\leq0\). Notice the positivity of the solution \((x(t),y_{1}(t), y_{2}(t))\), it is easy to get \(\langle y_{2}(t)\rangle^{*}=0\) a.s. □

Remark 2

Observing conditions (i) and (iii) of Theorem 4, we can see that if condition (i) is true, (iii) must be verified. That is to say, if the susceptible predator population goes to extinction, the infected predator population will also die out, which is consistent with the reality. Though we have some difficulties to research persistence for the predator population now, we can consider it in another way in Section 5.

Remark 3

It follows from Theorems 3, 4 and Theorem A.4 in Additional file 1 that the solution of stochastic system (5) satisfies \(\langle x(t)\rangle^{*}\leq\frac{r-\frac{1}{2}\sigma_{1}^{2}}{a_{11}}\) when \(r>\frac{1}{2}\sigma_{1}^{2}\). If \(r>\frac{1}{2}\sigma_{1}^{2}+\frac {a_{12}}{n}\), then \(\langle x(t)\rangle_{*}\geq\frac{r-\frac{1}{2}\sigma_{1}^{2}-\frac {a_{12}}{n}}{a_{11}}\). When \(\sigma_{1}^{2}=0\), the upper bound and lower bound are the same with \(\overline{K}\) and \(\underline{K}\) in Theorem A.4, this is consistent with our expectations. Besides, if \(a_{21}(r-\frac{1}{2}\sigma_{1}^{2})>a_{11}(d_{2}+\frac{\sigma _{2}^{2}}{2})\), \(\langle y_{1}(t)\rangle^{*}\leq\frac{a_{21}(r-\frac {1}{2}\sigma_{1}^{2})-a_{11}(d_{2}+\frac{\sigma_{2}^{2}}{2})}{a_{11}a_{22}}\). \(\langle y_{2}(t)\rangle^{*}\leq\frac{\beta a_{21}(r-\frac{1}{2}\sigma _{1}^{2})-\beta a_{11}(d_{2}+\frac{\sigma _{2}^{2}}{2})-a_{11}a_{22}(d_{3}+\frac{\sigma _{3}^{2}}{2})}{a_{11}a_{22}a_{33}}\) if \(\beta a_{21}(r-\frac{1}{2}\sigma _{1}^{2})>\beta a_{11}(d_{2}+\frac{\sigma _{2}^{2}}{2})+a_{11}a_{22}(d_{3}+\frac{\sigma_{3}^{2}}{2})\). These results are all the same conclusions with \(\overline{K}_{1}\) and \(\overline{K}_{2}\) in Theorem A.4 when \(\sigma_{i}^{2}=0\) (\(i=1,2,3\)). Furthermore, we find that the upper bound and lower bound of the solution for the stochastic system are smaller than those for the deterministic system. It means environmental random perturbation can reduce the size of the population to a certain extent.

4 The long time behavior of solution

For system (2), by analyzing the characteristic equation of four equilibria, we can easily get sufficient conditions of local stability for these equilibria. At this time, we know \(O(0,0,0)\) is saddle, not stable. If \(a_{21}r< d_{2}(a_{11}+mr)\), then \(E_{1}\) is locally asymptotically stable, and the disease-free equilibrium \(E_{2}\) does not exist. When \(r>\frac{a_{12}}{n}\), \(a_{21}r>d_{2}(a_{11}+mr)\) and \(R_{0}<1\) are verified, the disease-free equilibrium \(E_{2}(\hat{x},\hat{y}_{1},0)\) is locally asymptotically stable, \(E^{*}\) does not exist; when \(R_{0}>1\) and \(r>\frac{a_{12}}{n}\), the positive equilibrium \(E^{*}\) is locally asymptotically stable.

For stochastic system (5), \(E_{1}\) and \(E_{2}\) are no longer equilibria, but in this section we can study the asymptotic behavior of solution around them. Meanwhile, the conditions of global asymptotic behavior for \(E_{1}\) and \(E_{2}\) are derived.

Theorem 5

If \(a_{21}r< a_{11}d_{2}\), then for any given initial value \((x_{0},y_{10},y_{20})\in R_{+}^{3}\), the solution \(X(t)=(x(t),y_{1}(t),y_{2}(t))\) of system (5) has the property

$$\limsup_{t\rightarrow+\infty}\frac{1}{t}\int_{0}^{t}E \bigl[\bigl\Vert X(s)-E_{1}\bigr\Vert ^{2}\bigr]\,ds\leq \frac{a_{21}\sigma_{1}^{2}r}{2\mu a_{11}}, $$

here \(\mu=\min\{a_{21}a_{11}, a_{12}a_{11}, a_{12}a_{33}\}\).

Proof

Define a function \(V(t)=c_{1}(x-\frac{r}{a_{11}}-\frac {r}{a_{11}}\log\frac{a_{11}x}{r})+c_{2}y_{1}+c_{3}y_{2}\), where \(c_{i}\) (\(i=1,2,3\)) are positive constants to be determined later. Then the function \(V(t)\) is positive definite, and

$$\begin{aligned} dV(t) =& c_{1}\biggl(x-\frac{r}{a_{11}}\biggr)\biggl[r-a_{11}x- \frac {a_{12}y_{1}}{1+mx+ny_{1}}\biggr]\,dt \\ &{}+\frac{c_{1}\sigma_{1}^{2}r}{2a_{11}}\,dt+c_{1}\biggl(x- \frac {r}{a_{11}}\biggr) \sigma_{1}\,dB_{1}(t) \\ &{}+c_{2}y_{1}\biggl[-d_{2}-a_{22}y_{1}+ \frac{a_{21}x}{1+mx+ny_{1}}-\beta y_{2}\biggr]\,dt+c_{2}\sigma _{2}y_{1}\,dB_{2}(t) \\ &{}+c_{3}y_{2}[\beta y_{1}-d_{3}-a_{33}y_{2}] \,dt+c_{3}\sigma_{3}y_{2}\,dB_{3}(t). \end{aligned}$$

Here,

$$\begin{aligned} LV =&c_{1}\biggl(x-\frac{r}{a_{11}}\biggr)\biggl[-a_{11} \biggl(x-\frac{r}{a_{11}}\biggr)-\frac {a_{12}y_{1}}{1+mx+ny_{1}}\biggr]+\frac{c_{1}\sigma_{1}^{2}r}{2a_{11}} \\ &{}+c_{2}y_{1}\biggl[-d_{2}-a_{22}y_{1}+ \frac{a_{21}x}{1+mx+ny_{1}}-\beta y_{2}\biggr]+c_{3}y_{2}[ \beta y_{1}-d_{3}-a_{33}y_{2}] \\ =& -c_{1}a_{11}\biggl(x-\frac{r}{a_{11}} \biggr)^{2}-\frac {c_{1}a_{12}xy_{1}}{1+mx+ny_{1}}+\frac{c_{1}a_{12}\frac{r}{a_{11}}y_{1}}{1+mx+ny_{1}} +\frac{c_{1}\sigma_{1}^{2}r}{2a_{11}} \\ &{}-c_{2}d_{2}y_{1}-c_{2}a_{22}y_{1}^{2}+ \frac{c_{2}a_{21}xy_{1}}{1+mx+ny_{1}}-c_{2}\beta y_{1}y_{2}+c_{3} \beta y_{1}y_{2}-c_{3}d_{3}y_{2}-c_{3}a_{33}y_{2}^{2}. \end{aligned}$$

Let \(c_{1}=a_{21}\), \(c_{2}=c_{3}=a_{12}\), then

$$\begin{aligned} LV =&-c_{1}a_{11}\biggl(x-\frac{r}{a_{11}} \biggr)^{2}+\frac{c_{1}a_{12}\frac {r}{a_{11}}y_{1}}{1+mx+ny_{1}}+\frac{c_{1}\sigma_{1}^{2}r}{2a_{11}} \\ &{} -c_{2}d_{2}y_{1}-c_{2}a_{22}y_{1}^{2}-c_{3}d_{3}y_{2}-c_{3}a_{33}y_{2}^{2} \\ \leq& -c_{1}a_{11}\biggl(x-\frac{r}{a_{11}} \biggr)^{2}-\biggl(c_{2}d_{2}-c_{1}a_{12} \frac {r}{a_{11}}\biggr)y_{1} \\ &{}-c_{2}a_{22}y_{1}^{2}-c_{3}d_{3}y_{2}-c_{3}a_{33}y_{2}^{2}+ \frac{c_{1}\sigma_{1}^{2}r}{2a_{11}}. \end{aligned}$$

If \(a_{11}d_{2}>a_{21}r\), thus

$$LV\leq-c_{1}a_{11}\biggl(x-\frac {r}{a_{11}} \biggr)^{2}-c_{2}a_{22}y_{1}^{2}-c_{3}a_{33}y_{2}^{2}+ \frac{c_{1}\sigma _{1}^{2}r}{2a_{11}}, $$

therefore,

$$\begin{aligned} dV \leq& -\biggl[c_{1}a_{11}\biggl(x-\frac {r}{a_{11}} \biggr)^{2}+c_{2}a_{22}y_{1}^{2}+c_{3}a_{33}y_{2}^{2} \biggr]\,dt+\frac{c_{1}\sigma _{1}^{2}r}{2a_{11}}\,dt \\ &{}+c_{1}\biggl(x-\frac{r}{a_{11}}\biggr)\sigma_{1} \,dB_{1}(t)+c_{2}\sigma_{2}y_{1} \,dB_{2}(t)+c_{3}\sigma _{3}y_{2} \,dB_{3}(t). \end{aligned}$$

Integrating both sides of the above inequality from 0 to t, then taking expectations, yields

$$0\leq E\bigl[V(t)\bigr]\leq V(0)-\mu\int_{0}^{t}E \biggl[\biggl(x(s)-\frac {r}{a_{11}}\biggr)^{2}+y_{1}(s)^{2}+y_{2}(s)^{2} \biggr]\,ds+\frac{c_{1}\sigma_{1}^{2}r}{2a_{11}}t, $$

which leads to

$$\limsup_{t\rightarrow+\infty}\frac{1}{t}\int_{0}^{t}E \biggl[\biggl(x(s)-\frac {r}{a_{11}}\biggr)^{2}+y_{1}(s)^{2}+y_{2}(s)^{2} \biggr]\,ds\leq \frac{c_{1}\sigma_{1}^{2}r}{2\mu a_{11}}, $$

here \(\mu=\min\{a_{21}a_{11}, a_{12}a_{11}, a_{12}a_{33}\}\). The result is straightforward. □

When \(\sigma_{i}=0\) (\(i=1,2,3\)), system (5) becomes system (2). By Theorem 5, we know the stability of equilibrium \(E_{1}\).

Corollary 1

If \(a_{21}r< a_{11}d_{2}\), the equilibrium \(E_{1} (\frac{r}{a_{11}},0,0)\) of system (2) is globally asymptotically stable.

Remark 4

It is not difficult to find that the solution of stochastic system (5) fluctuates around equilibrium \(E_{1} (\frac{r}{a_{11}},0,0)\) of system (2) when \(E_{1}\) is globally asymptotically stable. The intensity of fluctuation is relevant to \(\sigma_{1}^{2}\). The smaller \(\sigma_{1}^{2}\) is, the weaker the fluctuation is.

Theorem 6

Assume \(a_{21}r>d_{2}(a_{11}+mr)\), \(a_{11}>m(r-a_{11}\hat {x})\) and \(R_{0}<1\), for any given initial value \((x_{0},y_{10},y_{20})\in R_{+}^{3}\), the solution \(X(t)=(x(t),y_{1}(t),y_{2}(t))\) of system (5) has the property

$$\limsup_{t\rightarrow+\infty}\frac{1}{t}\int_{0}^{t}E \bigl[\bigl\Vert X(s)-E_{2}\bigr\Vert ^{2}\bigr]\,ds\leq \frac{c_{1}\hat{x}\sigma_{1}^{2}}{2\tilde{\mu }}+\frac{c_{2}\hat{y}_{1}\sigma_{2}^{2}}{2\tilde{\mu}}, $$

where \(c_{1}=a_{21}(1+n\hat{y}_{1})\), \(c_{2}=c_{3}=a_{12}(1+m\hat{x})\) and \(\tilde {\mu}=\min\{[a_{11}-m(r-a_{11}\hat{x})]c_{1}, c_{2}a_{22}, c_{3}a_{33}\}\).

Proof

Define a \(C^{2}\) function \(V: R_{+}^{3}\rightarrow R_{+}\) by

$$V(t)=c_{1}\biggl(x-\hat{x}-\hat{x}\log\frac{x}{\hat{x}} \biggr)+c_{2}\biggl(y_{1}-\hat{y}_{1}-\hat {y}_{1}\log\frac{y_{1}}{\hat{y}_{1}}\biggr)+c_{3}y_{2}, $$

where \(c_{i}>0\) (\(i=1,2,3\)) are constants to be chosen later. Make system (5) into the following form:

$$\left \{ \textstyle\begin{array}{l} dx = x[-a_{11}(x-\hat{x})+a_{12}\frac{m\hat{y}_{1}(x-\hat{x})-(y_{1}-\hat {y}_{1})(1+m\hat{x})}{(1+mx+ny_{1})(1+m\hat{x}+n\hat{y}_{1})}]\,dt+\sigma_{1} x\, dB_{1}(t), \\ dy_{1} = y_{1}[-a_{22}(y_{1}-\hat{y}_{1})+a_{21}\frac{(x-\hat{x})(1+n\hat {y}_{1})-n\hat{x}(y_{1}-\hat{y}_{1})}{(1+mx+ny_{1})(1+m\hat{x}+n\hat {y}_{1})}-\beta y_{2}]\,dt+\sigma_{2} y_{1}\,dB_{2}(t), \\ dy_{2} =y_{2}[\beta y_{1}-d_{3}-a_{33}y_{2}]\,dt+\sigma_{3} y_{2}\,dB_{3}(t). \end{array}\displaystyle \right . $$

From Itô’s formula, we compute

$$\begin{aligned} dV =&\biggl[-c_{1}a_{11}(x-\hat{x})^{2}+ \frac{c_{1}a_{12}m\hat{y}_{1}(x-\hat {x})^{2}}{(1+mx+ny_{1})(1+m\hat{x}+n\hat{y}_{1})} \\ &{}-\frac{c_{1}a_{12}(1+m\hat{x})(x-\hat{x})(y_{1}-\hat {y}_{1})}{(1+mx+ny_{1})(1+m\hat{x}+n\hat{y}_{1})}\biggr]\,dt+c_{1}\sigma_{1}(x-\hat{x})\,dB_{1}(t) \\ &{}+ \frac{c_{1}\hat{x}\sigma _{1}^{2}}{2}\,dt+\biggl[-c_{2}a_{22}(y_{1}- \hat{y}_{1})^{2}+ \frac{c_{2}a_{21}(1+n\hat{y}_{1})(x-\hat{x})(y_{1}-\hat {y}_{1})}{(1+mx+ny_{1})(1+m\hat{x}+n\hat{y}_{1})} \\ &{}-\frac{c_{2}a_{21}n\hat{x}(y_{1}-\hat{y}_{1})^{2}}{(1+mx+ny_{1})(1+m\hat {x}+n\hat{y}_{1})}-c_{2}\beta y_{2}(y_{1}- \hat{y}_{1})+\frac{c_{2}\hat{y}_{1}\sigma _{2}^{2}}{2}\biggr]\,dt \\ &{}+c_{2}(y_{1}- \hat{y}_{1})\sigma_{2}\,dB_{2}(t)+\bigl[c_{3}y_{2}(\beta y_{1}-d_{3}-a_{33}y_{2}) \bigr]\,dt+c_{3}\sigma_{3} y_{2} \,dB_{3}(t). \end{aligned}$$

Make \(c_{1}=a_{21}(1+n\hat{y}_{1})\), \(c_{2}=a_{12}(1+m\hat{x})\), therefore

$$\begin{aligned} LV \leq& -c_{1}a_{11}(x-\hat{x})^{2}+ \frac{c_{1}m(r-a_{11}\hat{x})(x-\hat {x})^{2}}{1+mx+ny_{1}}-c_{2}a_{22}(y_{1}- \hat{y}_{1})^{2} \\ &{} -c_{2}\beta y_{1}y_{2}+c_{2} \beta\hat{y}_{1}y_{2}+c_{3}\beta y_{1}y_{2}-c_{3}d_{3}y_{2}-c_{3}a_{33}y_{2}^{2}+ \frac{c_{1}\hat{x}\sigma_{1}^{2}}{2}+ \frac{c_{2}\hat{y}_{1}\sigma_{2}^{2}}{2}. \end{aligned}$$

Let \(c_{2}=c_{3}\), then

$$\begin{aligned} LV \leq& -c_{1}a_{11}(x-\hat{x})^{2}+c_{1}m(r-a_{11} \hat{x}) (x-\hat {x})^{2}-c_{2}a_{22}(y_{1}- \hat{y}_{1})^{2} \\ &{}-(c_{3}d_{3}-c_{2} \beta\hat{y}_{1})y_{2}-c_{3}a_{33}y_{2}^{2}+ \frac{c_{1}\hat{x}\sigma_{1}^{2}}{2}+ \frac{c_{2}\hat{y}_{1}\sigma_{2}^{2}}{2}. \end{aligned}$$

When \(R_{0}<1\), we have \(d_{3}-\beta\hat{y}_{1}>0\), thus

$$LV\leq -c_{1}\bigl[a_{11}-m(r-a_{11}\hat{x}) \bigr](x-\hat{x})^{2}-c_{2}a_{22}(y_{1}- \hat{y}_{1})^{2} -c_{3}a_{33}y_{2}^{2}+ \frac{c_{1}\hat{x}\sigma_{1}^{2}}{2}+ \frac{c_{2}\hat{y}_{1}\sigma_{2}^{2}}{2}. $$

If \(a_{11}>m(r-a_{11}\hat{x})\), set \(\tilde{\mu}=\min\{ [a_{11}-m(r-a_{11}\hat{x})]c_{1}, c_{2}a_{22}, c_{3}a_{33}\}\), integrating both sides from 0 to t, taking expectations leads to

$$0\leq EV(t)\leq V(0)-\tilde{\mu}\int_{0}^{t}E \bigl[\bigl(x(s)-\hat {x}\bigr)^{2}+\bigl(y_{1}(s)- \hat{y}_{1}\bigr)^{2}+y_{2}^{2}(s)\bigr] \,ds+\biggl(\frac{c_{1}\hat{x}\sigma_{1}^{2}}{2}+ \frac{c_{2}\hat{y}_{1}\sigma_{2}^{2}}{2}\biggr)t. $$

Dividing both sides by t and letting \(t\rightarrow+\infty\), we get

$$\limsup_{t\rightarrow+\infty}\frac{1}{t}\int_{0}^{t}E \bigl[\bigl(x(s)-\hat {x}\bigr)^{2}+\bigl(y_{1}(s)- \hat{y}_{1}\bigr)^{2}+y_{2}^{2}(s)\bigr] \,ds\leq \frac{c_{1}\hat{x}\sigma_{1}^{2}}{2\tilde{\mu}}+\frac{c_{2}\hat{y}_{1}\sigma _{2}^{2}}{2\tilde{\mu}}. $$

This completes the theorem. □

When \(\sigma_{i}=0\) (\(i=1,2,3\)), it is easy to get the following.

Corollary 2

Assume \(a_{21}r>d_{2}(a_{11}+mr)\), the disease-free equilibrium \(E_{2} (\hat {x},\hat{y}_{1},0)\) of system (2) is globally asymptotically stable when \(a_{11}>m(r-a_{11}\hat{x})\) and \(R_{0}<1\).

Remark 5

The solution of stochastic system (5) fluctuates around the disease-free equilibrium \(E_{2} (\hat{x},\hat {y}_{1},0)\) of deterministic system (2) when \(E_{2}\) is globally asymptotically stable. The values of \(\sigma_{1}^{2}\) and \(\sigma_{2}^{2}\) determine the extent of fluctuations.

Remark 6

According to \(\hat{y}_{1}=\frac{(1+m\hat{x})(r-a_{11}\hat {x})}{a_{21}-nr+na_{11}\hat{x}}\), we have \(\hat{x}>\frac {r}{a_{11}}-\frac{a_{12}}{na_{11}}\) when \(r>\frac{a_{12}}{n}\). The condition \(a_{11}>m(r-a_{11}\hat{x})\) in Theorem 6 is equivalent to \(\hat{x}>\frac{r}{a_{11}}-\frac{1}{m}\), thus, if \(ma_{12}< na_{11}\), the condition \(a_{11}>m(r-a_{11}\hat{x})\) must be verified. Therefore, the condition \(a_{11}>m(r-a_{11}\hat{x})\) in Theorem 6 can be replaced by the condition \(a_{12}<\min\{\frac{na_{11}}{m}, nr\}\) which is easier to verify.

5 Stationary distribution

Before giving the main theorems, we first give a lemma [43].

Let \(X(t)\) be a homogeneous Markov process in \(E_{l}\) (\(E_{l}\) denotes Euclidean l-space) described by the stochastic equation

$$ dX(t)=b(X)\,dt+\sum_{r=1}^{k} \sigma_{r}(X)\,dB_{r}(t). $$
(18)

The diffusion matrix is

$$A(x)=\bigl(a_{ij}(x)\bigr),\quad a_{ij}(x)=\sum _{r=1}^{k}\sigma_{r}^{i}(x) \sigma_{r}^{j}(x). $$

Assumption B

There exists a bounded domain \(U\subset E_{l}\) with regular boundary Γ, having the following properties:

  1. (B.1)

    In the domain U and some neighborhood thereof, the smallest eigenvalue of the diffusion matrix \(A(x)\) is bounded away from zero.

  2. (B.2)

    If \(x\in E_{l}\backslash U\), the mean time τ at which a path issuing from x reaches the set U is finite, and \(\sup_{x\in K}E_{x}\tau <\infty\) for every compact subset \(K \subset E_{l}\).

Lemma 4

[43]

If Assumption  B holds, then the Markov process \(X(t)\) has a stationary distribution \(\mu(\cdot)\). Let \(f(\cdot)\) be a function integrable with respect to the measure μ. Then

$$P_{x}\biggl\{ \lim_{T\rightarrow\infty} \frac{1}{T}\int _{0}^{T}f\bigl(X(t)\bigr)\,dt=\int _{E_{l}}f(x)\mu(dx)\biggr\} =1 $$

for all \(x\in E_{l}\).

Remark 7

To validate (B.1), it suffices to prove that F is uniformly elliptical in U, where \(F_{u}=b(x)\cdot u_{x}+[tr(A(x)u_{xx})]/2\), that is, there is a positive number M such that \(\sum_{i,j=1}^{k}a_{ij}(x)\xi_{i}\xi_{j}\geq M|\xi|^{2} \), \(x\in U\), \(\xi\in R^{k}\) (see p.103 of [44]). To verify (B.2), it is sufficient to show that there exists some neighborhood U and a non-negative \(C^{2}\)-function V such that for any \(x\in E_{l}\backslash U\), LV is negative. (For details, we refer to p.1163 of [45].)

Theorem 7

Assume \(R_{0}>1\) is satisfied, \(a_{11}>m(r-a_{11}x^{*})\), and \(w<\min\{a_{21}(a_{11}-m(r-a_{11}x^{*}))(1+ny_{1}^{*})(x^{*})^{2}, a_{12}a_{22}(1+mx^{*})(y_{1}^{*})^{2}, a_{12}a_{33}(1+mx^{*})(y_{2}^{*})^{2}\}\), where

$$w=\frac{a_{21}x^{*}\sigma_{1}^{2}(1+ny_{1}^{*})}{2}+\frac {a_{12}y_{1}^{*}\sigma_{2}^{2}(1+mx^{*})}{2}+\frac{a_{12}y_{2}^{*}\sigma _{3}^{2}(1+mx^{*})}{2}, $$

then there is a stationary distribution \(\mu(\cdot)\) for system (5) and it has ergodic property.

Proof

System (5) can be written as the form of system (18),

$$\begin{aligned} d \left ( \textstyle\begin{array}{@{}c@{}} x(t) \\ y_{1}(t) \\ y_{2}(t) \end{array}\displaystyle \right ) =&\left ( \textstyle\begin{array}{@{}c@{}} x(t)(r-a_{11}x(t)-\frac{a_{12}y_{1}(t)}{1+mx(t)+ny_{1}(t)}) \\ y_{1}(t)(-d_{2}-a_{22}y_{1}(t)+\frac{a_{21}x(t)}{1+mx(t)+ny_{1}(t)}-\beta y_{2}(t)) \\ y_{2}(t)(\beta y_{1}(t)-d_{3}-a_{33}y_{2}(t)) \end{array}\displaystyle \right ) \,dt \\ &{}+ \left ( \textstyle\begin{array}{@{}c@{}} \sigma_{1}x(t) \\ 0 \\ 0 \end{array}\displaystyle \right )\,dB_{1}(t)+ \left ( \textstyle\begin{array}{@{}c@{}} 0 \\ \sigma_{2}y_{1}(t) \\ 0 \end{array}\displaystyle \right )\,dB_{2}(t)+ \left ( \textstyle\begin{array}{@{}c@{}} 0 \\ 0 \\ \sigma_{3}y_{2}(t) \end{array}\displaystyle \right )\,dB_{3}(t) , \end{aligned}$$

and the diffusion matrix is

$$ A=\left ( \textstyle\begin{array}{@{}c@{\quad}c@{\quad}c@{}} \sigma_{1}^{2}x^{2} & 0 & 0 \\ 0 & \sigma_{2}^{2}y_{1}^{2} & 0 \\ 0 & 0 &\sigma_{3}^{2}y_{2}^{2} \end{array}\displaystyle \right ). $$

Define

$$\begin{aligned} V(x,y_{1},y_{2}) =&c_{1}\biggl(x-x^{*}-x^{*} \log\frac {x}{x^{*}}\biggr)+c_{2}\biggl(y_{1}-y_{1}^{*}-y_{1}^{*} \log\frac {y_{1}}{y_{1}^{*}}\biggr) \\ &{}+c_{3}\biggl(y_{2}-y_{2}^{*}-y_{2}^{*} \log\frac{y_{2}}{y_{2}^{*}}\biggr), \end{aligned}$$

where \(c_{i}\) (\(i=1,2,3\)) are positive constants to be determined. System (5) can be rewritten as

$$ \left \{ \textstyle\begin{array}{l} dx = [-xa_{11}(x-x^{*})+a_{12}x\frac {my_{1}^{*}(x-x^{*})-(y_{1}-y_{1}^{*})(mx^{*}+1)}{(1+mx+ny_{1})(1+mx^{*}+ny_{1}^{*})}]\,dt+\sigma _{1} x\, dB_{1}(t), \\ dy_{1} = [-a_{22}y_{1}(y_{1}-y_{1}^{*})-\beta y_{1}(y_{2}-y_{2}^{*})+a_{21}y_{1}\frac {(x-x^{*})(1+ny_{1}^{*})-nx^{*}(y_{1}-y_{1}^{*})}{(1+mx+ny_{1})(1+mx^{*}+ny_{1}^{*})}]\,dt \\ \hphantom{dy_{1} =}{}+\sigma_{2} y_{1}\,dB_{2}(t), \\ dy_{2} =[\beta y_{2}(y_{1}-y_{1}^{*})-a_{33}y_{2}(y_{2}-y_{2}^{*})]\,dt+\sigma_{3} y_{2}\,dB_{3}(t). \end{array}\displaystyle \right . $$
(19)

If \((x,y_{1},y_{2})\in R_{3}^{+}\), applying Itô’s formula to system (19) gives

$$\begin{aligned} LV =&c_{1}\biggl[\frac{x-x^{*}}{x}dx+\frac{x^{*}}{2x^{2}}(dx)^{2} \biggr]+c_{2}\biggl[\frac {y_{1}-y_{1}^{*}}{y_{1}}dy_{1}+ \frac{y_{1}^{*}}{2y_{1}^{2}}(dy_{1})^{2}\biggr] \\ &{}+c_{3} \biggl[\frac {y_{2}-y_{2}^{*}}{y_{2}}dy_{2}+\frac{y_{2}^{*}}{2y_{2}^{2}}(dy_{2})^{2} \biggr] \\ =&c_{1}\biggl[-a_{11}\bigl(x-x^{*} \bigr)^{2}+\frac {a_{12}my_{1}^{*}(x-x^{*})^{2}-a_{12}(y_{1}-y_{1}^{*})(x-x^{*})(mx^{*}+1)}{(1+mx+ny_{1})(1+mx^{*}+ny_{1}^{*})}+\frac {x^{*}\sigma_{1}^{2}}{2}\biggr] \\ &{}+c_{2}\biggl[-a_{22}\bigl(y_{1}-y_{1}^{*} \bigr)^{2}-\beta\bigl(y_{1}-y_{1}^{*} \bigr) \bigl(y_{2}-y_{2}^{*}\bigr) \\ &{}+ \frac {a_{21}(x-x^{*})(1+ny_{1}^{*})(y_{1}-y_{1}^{*})-a_{21}nx^{*}(y_{1}-y_{1}^{*})^{2}}{(1+mx+ny_{1})(1+mx^{*}+ny_{1}^{*})}+\frac{y_{1}^{*}\sigma_{2}^{2}}{2}\biggr] \\ &{} +c_{3}\biggl[\beta \bigl(y_{1}-y_{1}^{*}\bigr) \bigl(y_{2}-y_{2}^{*} \bigr)-a_{33}\bigl(y_{2}-y_{2}^{*} \bigr)^{2}+\frac {y_{2}^{*}\sigma_{3}^{2}}{2}\biggr] \\ =&-c_{1}a_{11}\bigl(x-x^{*}\bigr)^{2}+ \frac {c_{1}a_{12}my_{1}^{*}(x-x^{*})^{2}}{(1+mx+ny_{1})(1+mx^{*}+ny_{1}^{*})} \\ &{}-\frac {c_{1}a_{12}(y_{1}-y_{1}^{*})(x-x^{*})(mx^{*}+1)}{(1+mx+ny_{1})(1+mx^{*}+ny_{1}^{*})}+\frac{c_{1}x^{*}\sigma_{1}^{2}}{2}-c_{2}a_{22}\bigl(y_{1}-y_{1}^{*} \bigr)^{2} \\ &{}-c_{2}\beta \bigl(y_{1}-y_{1}^{*} \bigr) \bigl(y_{2}-y_{2}^{*}\bigr)+ \frac {c_{2}a_{21}(x-x^{*})(1+ny_{1}^{*})(y_{1}-y_{1}^{*})}{(1+mx+ny_{1})(1+mx^{*}+ny_{1}^{*})} \\ &{}-\frac {c_{2}a_{21}nx^{*}(y_{1}-y_{1}^{*})^{2}}{(1+mx+ny_{1})(1+mx^{*}+ny_{1}^{*})}+\frac {c_{2}y_{1}^{*}\sigma_{2}^{2}}{2} \\ &{}+c_{3}\beta \bigl(y_{1}-y_{1}^{*}\bigr) \bigl(y_{2}-y_{2}^{*} \bigr)-c_{3}a_{33}\bigl(y_{2}-y_{2}^{*} \bigr)^{2} +\frac{c_{3}y_{2}^{*}\sigma_{3}^{2}}{2}. \end{aligned}$$

Here, let \(c_{1}=a_{21}(1+ny_{1}^{*})\), \(c_{2}=c_{3}=a_{12}(1+mx^{*})\), therefore,

$$\begin{aligned} LV \leq&-c_{1}a_{11}\bigl(x-x^{*} \bigr)^{2}+\frac {c_{1}a_{12}my_{1}^{*}(x-x^{*})^{2}}{(1+mx+ny_{1})(1+mx^{*}+ny_{1}^{*})}-c_{2}a_{22} \bigl(y_{1}-y_{1}^{*}\bigr)^{2} \\ &{}-c_{3}a_{33}\bigl(y_{2}-y_{2}^{*} \bigr)^{2}+\frac{c_{1}x^{*}\sigma_{1}^{2}}{2}+\frac {c_{2}y_{1}^{*}\sigma_{2}^{2}}{2}+\frac{c_{3}y_{2}^{*}\sigma_{3}^{2}}{2} \\ \leq&-\biggl[a_{11}a_{21}\bigl(1+ny_{1}^{*} \bigr)-\frac {a_{21}a_{12}my_{1}^{*}(1+ny_{1}^{*})}{(1+mx^{*}+ny_{1}^{*})}\biggr]\bigl(x-x^{*}\bigr)^{2} \\ &{}-a_{12}a_{22} \bigl(1+mx^{*}\bigr) \bigl(y_{1}-y_{1}^{*} \bigr)^{2}-a_{12}a_{33}\bigl(1+mx^{*}\bigr) \bigl(y_{2}-y_{2}^{*}\bigr)^{2} \\ &{} + \frac{a_{21}x^{*}\sigma _{1}^{2}(1+ny_{1}^{*})}{2}+\frac{a_{12}y_{1}^{*}\sigma_{2}^{2}(1+mx^{*})}{2} +\frac{a_{12}y_{2}^{*}\sigma_{3}^{2}(1+mx^{*})}{2} \\ =& -\bigl[a_{11}a_{21}\bigl(1+ny_{1}^{*} \bigr)-a_{21}m\bigl(r-a_{11}x^{*}\bigr) \bigl(1+ny_{1}^{*}\bigr)\bigr]\bigl(x-x^{*} \bigr)^{2} \\ &{}-a_{12}a_{22}\bigl(1+mx^{*} \bigr) \bigl(y_{1}-y_{1}^{*}\bigr)^{2}-a_{12}a_{33}\bigl(1+mx^{*}\bigr) \bigl(y_{2}-y_{2}^{*}\bigr)^{2} \\ &{} + \frac{a_{21}x^{*}\sigma _{1}^{2}(1+ny_{1}^{*})}{2}+\frac{a_{12}y_{1}^{*}\sigma_{2}^{2}(1+mx^{*})}{2} +\frac{a_{12}y_{2}^{*}\sigma_{3}^{2}(1+mx^{*})}{2}. \end{aligned}$$

When \(w<\min\{a_{21}(a_{11}-m(r-a_{11}x^{*}))(1+ny_{1}^{*})(x^{*})^{2}, a_{12}a_{22}(1+mx^{*})(y_{1}^{*})^{2}, a_{12}a_{33}(1+ mx^{*})(y_{2}^{*})^{2}\}\), the ellipsoid

$$\begin{aligned}& -a_{21}\bigl(a_{11}-m\bigl(r-a_{11}x^{*} \bigr)\bigr) \bigl(1+ny_{1}^{*}\bigr) \bigl(x-x^{*} \bigr)^{2}-a_{12}a_{22}\bigl(1+mx^{*} \bigr) \bigl(y_{1}-y_{1}^{*}\bigr)^{2} \\& \quad {} -a_{12}a_{33}\bigl(1+mx^{*}\bigr) \bigl(y_{2}-y_{2}^{*}\bigr)^{2}+w=0 \end{aligned}$$

lies entirely in \(R_{+}^{3}\). We can take U to be a neighborhood of the ellipsoid with \(\overline{U}\subseteq E_{3}=R_{+}^{3}\), so for \((x,y_{1},y_{2})\in E_{3}\backslash U\), \(LV\leq-\overline{K}\) (\(\overline{K}\) is a positive constant), which implies that condition (B.2) in Lemma 4 is satisfied.

Besides, there is \(M=\min\{\sigma_{1}^{2}x^{2}, \sigma_{2}^{2}y_{1}^{2}, \sigma_{3}^{2}y_{2}^{2}, (x,y_{1},y_{2})\in\overline{U}\}>0\) such that

$$\sum_{i,j=1}^{3}a_{ij} \xi_{i}\xi_{j}=\sigma_{1}^{2}x^{2} \xi_{1}^{2}+\sigma _{2}^{2}y_{1}^{2} \xi_{2}^{2}+\sigma_{3}^{2}y_{2}^{2} \xi_{3}^{2}\geq M\|\xi\|^{2} $$

for all \((x,y_{1},y_{2})\in\overline{U}\), \(\xi\in R^{3}\), which implies that condition (B.1) in Lemma 4 is satisfied. Therefore, the stochastic system (5) has a stationary distribution \(\mu(\cdot)\) and it is ergodic. □

Without considering the random fluctuations of environment, that is say, \(\sigma_{i}\ (i=1,2,3)=0\), according to the proof of Theorem 7, it is easy to get the following conclusion.

Corollary 3

Assume \(R_{0}>1\), when \(a_{11}>m(r-a_{11}x^{*})\), the positive equilibrium \(E^{*}(x^{*},y_{1}^{*},y_{2}^{*})\) of system (2) is globally asymptotically stable.

6 Numerical simulation

In order to confirm the results of Sections 3 and 5, we numerically simulate the solution of stochastic system (5). For system (5), we use the Milstein method mentioned in Higham [46] to substantiate the analytical findings. We consider the following discrete equations:

$$\left \{ \textstyle\begin{array}{l} x_{k+1}=x_{k}+x_{k}[(r-a_{11}x_{k}-\frac {a_{12}y_{1,k}}{1+mx_{k}+ny_{1,k}})\Delta t+\sigma_{1}\varepsilon_{1k}\sqrt {\Delta t}+\frac{1}{2}\sigma_{1}^{2}(\varepsilon_{1k}^{2}-1)\Delta t], \\ y_{1,k+1} =y_{1,k}+y_{1,k}[(-d_{2}-a_{22}y_{1,k}+\frac {a_{21}x_{k}}{1+mx_{k}+ny_{1,k}}-\beta y_{2,k})\Delta t+\sigma_{2}\varepsilon _{2k}\sqrt{\Delta t} \\ \hphantom{y_{1,k+1} =}{}+\frac{1}{2}\sigma_{2}^{2}(\varepsilon_{2k}^{2}-1)\Delta t], \\ y_{2,k+1} =y_{2,k}+y_{2,k}[(\beta y_{1,k}-d_{3}-a_{33}y_{2,k})\Delta t+\sigma_{3}\varepsilon_{3k}\sqrt{\Delta t}+\frac{1}{2}\sigma _{3}^{2}(\varepsilon_{3k}^{2}-1)\Delta t], \end{array}\displaystyle \right . $$

where time increment \(\Delta t=0.1>0\), and \(\varepsilon_{ik}\) (\(i=1,2,3\)) are \(N(0,1)\) distributed independent random variables which can be generated numerically by pseudo-random number generators.

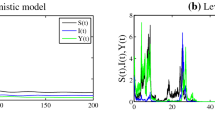
Here, let \(r=0.8\), \(a_{11}=0.2\), \(a_{12}=0.8\), \(m=n=0.5\), \(d_{2}=0.2\), \(a_{22}=0.2\), \(a_{21}=0.6\), \(\beta=0.4\), \(d_{3}=0.2\), \(a_{33}=0.1\), \(x_{0}=0.6\), \(y_{10}=0.4\), \(y_{20}=0.2\), then \(E^{*}(x^{*},y_{1}^{*},y_{2}^{*})=(3.0401, 0.6872, 0.7488)\). At first, in the absence of noise, in view of Corollary 3, the equilibrium \(E^{*}(x^{*},y_{1}^{*},y_{2}^{*})\) of deterministic system (2) is globally asymptotically stable, Figure 1 confirms it. We choose \(\sigma_{1}=0.08\), \(\sigma_{2}=0.02\), \(\sigma_{3}=0.05\), then (4) is satisfied, \(a_{11}>m(r-a_{11}x^{*})\), \(\omega\approx0.01\), and \(\min\{a_{21}(a_{11}-m(r-a_{11}x^{*}))(1+ny_{1}^{*})(x^{*})^{2}, a_{12}a_{22}(1+mx^{*})(y_{1}^{*})^{2}, a_{12}a_{33}(1+mx^{*})(y_{2}^{*})^{2}\}\approx0.113\). Hence, the conditions of Theorem 7 are verified, there is a stationary distribution for system (5). Figure 1 shows that the solution of (5) is fluctuating around the positive equilibrium \(E^{*}\) of deterministic system (2) in a small neighborhood. In the last figure from Figure 1, we can see that all the solutions of system (5) are around \(E^{*}\), which illustrates that there is a stationary distribution for system (5).

Figure 1
figure 1

Solutions of systems ( 2 ) and ( 5 ). The black lines represent solutions of deterministic system (2), red lines are solutions of stochastic system (5), the last figure of Figure 1 is the population distribution of system (5) around \(E^{*}\).

Full size image

Suffering large density of white noise, we can refer to Figure 2 which also simulates system (5). Here, we choose \(r=0.4\), \(\sigma_{1}=1\), \(\sigma _{2}=0.8\), \(\sigma_{3}=0.5\), the other parameters are the same, the conditions of Theorem 7 are not verified, then by Theorems 3 and 4, all the populations of stochastic system (5) will become extinct, which does not happen in the corresponding deterministic system (2). Figure 2 shows it.

Figure 2
figure 2

Solutions of systems ( 2 ) and ( 5 ). The red line represents the prey population, the purple line and black line are susceptible predator and infected predator population, respectively. The left figure is the solution of deterministic system (2), the right one is the solution of stochastic system (5).

Full size image

7 Conclusions

A stochastic model corresponding to a predator-prey model with Beddington-DeAngelis functional response and disease in the predator population is investigated. We show that system (5) has a unique global positive solution as this is essential in any population dynamics model. We also give an estimate of the solution by the comparison theorem. The threshold between persistence in the mean and extinction for prey population is given. Sufficient conditions of extinction for both the susceptible predator and the infected predator are obtained. Furthermore, sufficient conditions of permanence for deterministic system (2) are derived in Additional file 1, which can give us a contrast between stochastic system (5) and its corresponding deterministic system (2). This shows that environmental perturbation will make the reduced population size. There is a stationary distribution for system (5) when the environmental noise is very small, we can consider it as stability in stochastic sense. By the way, conditions of global stability of system (2) can be established. Numerical simulations illustrate that if the positive equilibrium of the deterministic system is globally stable, then the stochastic model will preserve this nice property provided the noise is sufficiently small, but it is not true when the noise is large. All these consequences imply that the environmental white noise has an important effect on biological systems; therefore, it is more realistic and suitable to include random effects in the models.

Some interesting questions deserve further investigation. Here, we cannot get the condition of persistence for the predator population at present. In fact, there are some difficulties that cannot be overcome at present, we leave them for future research. Moreover, it is interesting to study other parameters perturbed by the environmental noise.