Conditions for prosperity and depression of a stochastic R&D model under regime switching

Abstract

The stochastic research and development (R&D) model plays an important role in economic growth theories. To explain the growth performance of the economy under regime switching, we first establish sufficient criteria that ensure economic prosperity, nonprosperity and depression in the R&D model disturbed by white and color noise. Then, we determine the threshold between prosperity and depression. Furthermore, we estimate an upper bound of the growth rates of technological progress and capital accumulation in the prosperity case. The results indicate that color noise sensitively impacts the growth performance of the economy in the R&D model. Finally, numerical simulations are conducted to verify our theoretical work.

1 Introduction

The stochastic research and development (R&D) model has been the center of attention in economic growth theories for a long time, because it can be used to describe the growth rates of technological progress and capital accumulation [1–3]. Impacted by the existing economic reality, the uncertainty of the R&D model is affected by many factors, such as the accumulation of knowledge, government intervention, introduction of talent resources, and population fluctuation. The effect of uncertainty on the growth performance of the economy has been studied by several authors [4–8]. For example, Canton [6] analyzed a two-sector model of endogenous growth to reveal the impact of uncertainty on long-run economic growth. He showed that economic growth was higher in the presence of business cycles because people devoted more time to learning activities in an uncertain economic environment. To study endogenous economic growth, the authors of [2, 7, 8] regarded technological progress as a production process similar to the production of output, and the long-run economic growth rate was determined completely by the population growth rate. Based on various references [2, 7, 8], Romer [9] fully described the R&D model, interpreted the effectiveness of labor as knowledge, and modeled the determinants of its evolution over time. Wu et al. [4] introduced the uncertainty from population growth and transformed the R&D model of [9] into a simple form via Itô’s formula. They computed the sample average of the growth rates of both technology and capital accumulation and proved that the long-run growth rate of the economic system was ultimately bounded in mean. Zhang et al. [10] explored a numerical approximate method that could preserve the positivity of the numerical solution of the R&D model shown in [4] and revealed that the new numerical approximate method was effective and practical.

However, all these works [2, 4, 7–10] assumed that the parameters of the R&D model are all determined constants. In fact, a stochastic R&D system may experience abrupt changes in the structure and parameters. For example, the fixed capital of the listed company is affected by the stock price of the market. Capital accumulation may have optimistic asymptotic behavior when stock prices rise, and capital accumulation may have another asymptotic behavior if stock prices decrease; additionally, the company may enter another development level under the state of talent introduction. Meanwhile, a continuous time Markov chain, namely, color noise, can delineate the system switch from one environmental regime to another in a population system [11–17]. For instance, Liu et al. [13] showed that an ergodic Markov chain could accurately describe the stochastic phenomena of a population system in practice. Liu et al. [14] added Markovian switching to a stochastic multigroup mutualistic system and investigated the ergodicity property and positive recurrence, which provided a good explanation of some biological phenomena. Yu et al. [15] introduced Markovian switching to the phytoplankton–zooplankton model, they also analyzed the extinction, weak persistence, and nonpersistence in the mean. Zhao et al. [17] developed a stochastic phytoplankton allelopathy model with Markovian switching and showed that the Markovian switching had a great impact on the evolution of the phytoplankton populations.

Inspired by these studies, we introduce Markovian switching into the stochastic R&D model to describe the development trend of the economy under different situations. The switching is memoryless, and the waiting time for the next switch has an exponential distribution. Therefore, the research on the threshold between economic prosperity and depression in the R&D model under regime switching supports our trending analysis and forecasting of the economic environment. Motivated by these features, our natural aims in this paper are as follows:

• To get sufficient criteria that maintain economic strong prosperity, weak prosperity, nonprosperity, and depression in the mean.

• To obtain the threshold between stochastic depression and prosperity in the mean.

• To estimate the upper bound of the rates of both technological progress and capital accumulation in the prosperity case.

The rest of this paper is structured as follows. In Sect. 2, we recall the fundamental theory necessary for later discussion and provide sufficient conditions to ensure the existence of a global positive solution of the R&D model under white and color noise. Section 3 shows that the R&D model with regime switching shows either stochastic economic prosperity or depression under some assumptions and obtains the threshold between depression and prosperity. Finally, some numerical examples are presented to confirm our theory in Sect. 4.

2 Model formulation and preliminaries

2.1 Model formulation

Romer [9] fully described the deterministic R&D model based on [2, 7, 8]:

$$ \textstyle\begin{cases} Y(t)=[(1-a_{K})K(t)]^{1-\alpha}[A(t)(1-a_{L})L(t)]^{\alpha }=C_{Y}K^{1-\alpha}(t)(A(t)L(t))^{\alpha},\\ \dot{A}(t)=B[a_{K} K(t)]^{\xi}[a_{L} L(t)]^{\eta}A^{1+\theta }(t)=C_{K}K^{\xi}(t)A^{1+\theta}(t)L^{\eta}(t). \end{cases} $$

(1)

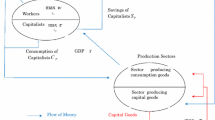
The deterministic R&D model involves four variables: labor (L), capital (K), technology (A), and output (Y). There are two sectors, a goods-producing sector, where output is produced, and an R&D sector, where additions to the stock of knowledge (technological progress) are produced. Fraction $a_{L}$ of the labor force is used in the R&D sector, and fraction $1-a_{L}$ is used in the goods-producing sector. Similarly, fraction $a_{K}$ of the capital stock is used in the R&D sector, and the remaining $1-a_{K}$ is used in the goods-producing sector. Technological progress is regarded as a production process, such as production of output in the model. Both sectors use the full stock of knowledge, where $C_{Y}=(1-a_{K})^{1-\alpha}(1-a_{L})^{\alpha}$, $C_{K}=Ba_{K}^{\xi}a_{L}^{\eta}$, B is a parameter which measures efficiency in the R&D sector. The population growth of model (1) is regarded as exogenous, and $\dot{L}(t)=nL(t)$.

Wu [4] introduced uncertainty resulting from population growth, and by means of Itô’s formula, the deterministic R&D model (1) can be simplified as a system of stochastic differential equations (SDEs):

$$ \textstyle\begin{cases} dx(t) =x(t)(\theta x(t)+\xi y(t)+\eta n-\frac{\eta\eta'}{2}\sigma ^{2})\,dt+\eta\sigma x(t)\,dw(t), \\ dy(t) = y(t)(\alpha x(t)-\alpha y(t)+\alpha n-\frac{\alpha\alpha '}{2}\sigma^{2})\,dt+\alpha\sigma y(t)\,dw(t), \end{cases} $$

(2)

where $\eta'=1-\eta$, $\alpha'=1-\alpha$, $x(t)=\frac{\dot {A}(t)}{A(t)}$, $y(t)=\frac{\dot{K}(t)}{K(t)}={\frac{sY(t)}{K(t)}}$, i.e., they represent the growth rates of technological progress in the R&D sector and the growth rates of capital accumulation in the goods-producing sector, $s\in(0, 1)$ means the saving rate, the depreciation rate here of capital $K(t)$ is not considered. Also $dL(t)=L(t)(ndt+\sigma\,dw(t))$, where $w(t)$ is a standard Brownian motion. The features of parameters in model (2) are shown in Table 1.

Table 1 Parameter values for R&D model (2)

To describe the stochastic R&D model under different states, we introduce Markovian switching in (2) and assume that there are m regimes, then model (2) obeys:

$$ \textstyle\begin{cases} dx(t) =x(t) [\theta(i) x(t)+\xi(i) y(t)+\eta(i) n(i)-\frac{\eta (i) \eta'(i)}{2}\sigma^{2}(i) ]\,dt+\eta(i)\sigma(i) x(t)\,dw(t), \\ dy(t) = y(t) [\alpha(i)x(t)-\alpha(i)y(t)+\alpha(i)n(i)-\frac {\alpha(i)\alpha'(i)}{2}\sigma^{2}(i) ]\,dt+\alpha(i)\sigma(i) y(t)\,dw(t), \end{cases} $$

(3)

in regime i ($1\leq i \leq m$). The switching between these m regimes is controlled by a Markov chain and the R&D model (2) with both white and color noise becomes

$$ \textstyle\begin{cases} dx(t)=x(t) [\theta(\varsigma(t)) x(t)+\xi(\varsigma(t)) y(t)+b_{x}(\varsigma(t)) ]\,dt+\eta(\varsigma(t)) \sigma (\varsigma(t)) x(t)\,dw(t), \\ dy(t)=y(t) [\alpha(\varsigma(t)) x(t)-\alpha(\varsigma(t)) y(t)+b_{y}(\varsigma(t)) ]\,dt+\alpha(\varsigma(t)) \sigma (\varsigma(t)) y(t)\,dw(t), \end{cases} $$

(4)

where

$$\begin{gathered}b_{x} \bigl(\varsigma(t) \bigr)=\eta \bigl( \varsigma(t) \bigr) n \bigl(\varsigma(t) \bigr)-\frac {\eta(\varsigma(t)) \eta'(\varsigma(t))}{2} \sigma^{2} \bigl(\varsigma (t) \bigr), \\ b_{y} \bigl(\varsigma(t) \bigr)=\alpha \bigl(\varsigma(t) \bigr)n \bigl( \varsigma(t) \bigr)- \frac{\alpha(\varsigma(t))\alpha'(\varsigma(t))}{2}\sigma ^{2} \bigl( \varsigma(t) \bigr).\end{gathered} $$

The analysis of the next sections is focused on model (4).

2.2 Preliminary results

For mathematical simplicity, we introduce several notations. Throughout this paper, let $(\varOmega, \mathfrak{F}, \{\mathfrak{F}_{t}\}_{t\geq 0}, \mathbb{P})$ be a complete probability space with a filtration $\{ \mathfrak{F}_{t}\}_{t\geq0}$ satisfying the usual conditions (that is, it is right continuous and increasing, while $\mathfrak{F}_{0}$ contains all $\mathbb{P}$-null sets), $\mathbb{E}$ denotes the expectation corresponding to $\mathbb{P}$. Let $\{w(t)\}_{t\geq0}$ be a standard Brownian motion defined on the above complete probability space. For a set A, we denote its indicator function by $\mathbf{1}_{A}$, namely $\mathbf{1}_{A}(x)=1$ if $x \in A$ and 0 otherwise. Denote by $\mathbb{R}^{n}_{+}$ the positive cone in $\mathbb{R}^{n}$, that is, $\mathbb{R}^{n}_{+}=\{x\in\mathbb{R}^{n}: x_{i}>0\text{ for all }1\leq i \leq n\}$. If $x\in\mathbb{R}^{n}$, its Euclidean norm is $|x|=(\sum^{n}_{i=1}x^{2}_{i})^{\frac{1}{2}}$ [18]. For two real numbers a and b, we use $a\vee b = \max\{a, b\}$ and $a\wedge b = \min\{a, b\}$. If A is a vector or matrix, its transpose is denoted by $A^{\top}$ and the trace norm of A is defined as $|A|=\sqrt{\operatorname{trace}(A^{\top}A)}$. If A is an $n\times n$ symmetric matrix, we introduce the following definition:

$$ \lambda^{+}_{\max}(A)=\sup_{x\in\mathbb{R}^{n}_{+}, |x|=1}x^{\top}Ax,\qquad\lambda_{\max}(A)=\sup_{x\in\mathbb{R}^{n}, |x|=1}x^{\top}Ax. $$

It is clear that $\lambda^{+}_{\max}(A)\leq\lambda_{\max}(A)$ and $x^{\top}Ax\leq\lambda^{+}_{\max}(A)|x|^{2}$ for any $x \in\mathbb {R}^{n}_{+}$ [19]. In model (4), $\{{\varsigma(t), t\geq0}\}$ is a right-continuous Markov chain on the probability space $(\varOmega, \mathfrak{F}, \{\mathfrak{F}_{t}\} _{t\geq0}, \mathbb{P})$ taking values in a finite-state $\mathbb {S}=\{1, 2, \dots, m\}$ with the generator $\varTheta=(\kappa _{ij})_{m\times m}$ given by

$$ \mathbb{P} \bigl\{ \varsigma(t+\delta)=j|\varsigma(t)=i \bigr\} = \textstyle\begin{cases} \kappa_{ij}\delta+o(\delta), &\text{if } i\neq j,\\ 1+\kappa_{ij}\delta+o(\delta), &\text{if } i=j, \end{cases} $$

where $\delta>0$. Here $\kappa_{ij}$ is the transition rate from i to j if $i\neq j$ while

$$ \kappa_{ii}=-\sum_{i\neq j} \kappa_{ij}. $$

In this paper we note that $\kappa_{ij}>0$ if $i\neq j$. As a standing hypothesis, we assume that the Markov chain $\{ \varsigma(t), t\geq0\}$ is independent of the Brownian motion $w (\cdot)$ and it is irreducible, which means that the system can switch from any regime to any other [20]. This is equivalent to the condition that for any $i, j \in\mathbb{S}$, there are finite numbers $i_{1}, i_{2}, \dots, i_{i}\in\mathbb{S}$ such that $\kappa_{i, i_{1}}\kappa_{i_{1}, i_{2}}\cdots\kappa_{i_{i}, j}>0$ and this implies the ergodicity property in view of Markov theory for finite states. If Θ has a trivial eigenvalue, then the algebraic interpretation of irreducbility is $\operatorname{rank}(\varTheta)=n-1$. Under this assumption, the Markov chain has a unique stationary distribution $\pi=(\pi_{1}, \pi_{2}, \dots, \pi_{m})\in\mathbb {R}^{1\times m}$ which can be determined by solving the linear equation $\pi\varTheta=0$, $\sum^{m}_{k=1}\pi_{k}=1$ and $\pi_{k}>0$, $\forall k\in \mathbb{S}$. The details of the theory have been studied by many authors [11–13, 21]. For any vector $\phi =(\phi(1), \phi(2), \dots, \phi(m))^{\top}$, we note that $\lim_{t\rightarrow\infty}\frac{1}{t}\int^{t}_{0}\phi(\varsigma(s))\, ds=\sum_{k \in\mathbb{S}}\pi_{k}\phi(k)$, $\hat{\phi}(k)=\{\min {\phi}(k)|k\in\mathbb{S}\}=\min_{\varsigma(t)=1}^{m}\phi(\varsigma (t))$ and $\check{\phi}(k)=\{\max{\phi}(k)|k\in\mathbb{S}\}=\max_{\varsigma(t)=1}^{m}\phi(\varsigma(t))$. Inspired by Liu and Wang in [16], we also list the following notations: $\langle f(t)\rangle=\frac{1}{t}\int_{0}^{t}f(s)\,ds$, $f_{*}=\liminf_{t\rightarrow\infty}f(t)$ and $f^{*}=\limsup_{t\rightarrow\infty}f(t)$.

Let $({z(t)}, \varsigma(t))$ be the diffusion process described by the following equation:

$$ \textstyle\begin{cases} d{z(t)}=f(z(t), \varsigma(t))\,dt+g(z(t), \varsigma(t)){\,dw(t)},\\ z(0)=z,\qquad \varsigma(0)=\varsigma, \end{cases} $$

(5)

where $w(\cdot)$ and $\varsigma(\cdot)$ are the d-dimensional Brownian motion and the right-continuous Markov chain in the above discussion, respectively. Functions $f(\cdot, \cdot): {\mathbb {R}}^{n}\times\mathbb{S}\rightarrow{\mathbb{R}}^{n}$, $g(\cdot, \cdot): {\mathbb{R}}^{n}\times\mathbb{S}\rightarrow{\mathbb{R}}^{n\times d}$ satisfy $g(z, k)g^{T}(z, k)=D(z, k)$. For each $k\in\mathbb{S}$, and for any twice continuously differentiable function $V(\cdot, k)$, $(z(t), \varsigma(t))$ has a generator L given as follows [12, 21]:

$$ LV(z, k)=\sum_{i=1}^{n}f_{i}(z, k)\frac{\partial V(z, k)}{\partial z_{i}}+\frac{1}{2} \sum_{i, j=1}^{n}D_{ij}(z, k)\frac{\partial^{2}V(z, k)}{\partial z_{i}\partial z_{j}}+\varTheta V(z, \cdot) (k), $$

where

For convenience, model (4) can be rewritten in matrix form as

$$ dX(t)=\operatorname{diag} \bigl(x(t), y(t) \bigr) \bigl\{ \bigl[A \bigl( \varsigma (t) \bigr)X(t)+B \bigl(\varsigma(t) \bigr) \bigr]\,dt+\beta \bigl( \varsigma(t) \bigr) \,dw(t) \bigr\} , $$

(6)

where

$$\begin{gathered}X(t)= \bigl(x(t),y(t) \bigr)^{\top},\quad\quad \beta \bigl(\varsigma(t) \bigr)= \bigl(\eta \bigl(\varsigma (t) \bigr)\sigma \bigl( \varsigma(t) \bigr),\alpha \bigl(\varsigma(t) \bigr) \sigma \bigl(\varsigma(t) \bigr) \bigr)^{\top}, \\ B \bigl(\varsigma(t) \bigr)= \bigl(b_{x}\varsigma(t), b_{y}\varsigma(t) \bigr)^{\top},\qquad A \bigl(\varsigma(t) \bigr)= \begin{pmatrix} \theta(\varsigma(t)) & \xi(\varsigma(t))\\ \alpha(\varsigma(t)) & -\alpha(\varsigma(t)) \end{pmatrix} . \end{gathered} $$

Theorem 2.1

For any$i\in\mathbb{S}$, if$\theta(i)+\xi(i)<0$holds, then for any given initial value$(x(0), y(0), \varsigma(0))\in\mathbb {R}_{+}\times\mathbb{R}_{+}\times\mathbb{S}$, there exists a unique solution to model (4) for$t\geq0$, and the solution will remain in$\mathbb{R}_{+}\times\mathbb {R}_{+}\times\mathbb{S}$almost surely.

Proof

The proof can be found in Appendix A. □

Theorem 2.1 implies that if the returns of technology scale to the capital and technology sectors are decreasing, then the technology and capital show positive long-run growth. This useful property offers us a great opportunity to construct different types of Lyapunov functions to research the asymptotic properties of model (4) in $\mathbb{R}^{2}_{+}$ in more detail. Next, we attempt to obtain sufficient criteria to ensure economic strong prosperity, weak prosperity, nonprosperity, and depression in the mean. Moreover, we obtain an estimate of the upper bound of economic growth rates.

3 The threshold between depression and prosperity in the mean

In the R&D model, we are concerned about whether the rates of technological progress and capital accumulation will continue to grow or be stable in the long term. In this section, our aim is to discuss the economic growth rate and give the threshold between depression and prosperity of the system. These are also the main conclusions of this paper.

Definition 3.1

• The R&D system (4) is said to be in depression, if $\lim_{t\rightarrow\infty}x(t)=0$ and $\lim_{t\rightarrow\infty }y(t)=0$ a.s.

• The R&D system (4) is said to be in nonprosperity if $\langle x(t)\rangle^{*}=0$ and $\langle y(t)\rangle^{*}=0$ a.s.

• The R&D system (4) is said to be in weak prosperity in the mean if $\langle x(t)\rangle^{*}>0$ and $\langle y(t)\rangle^{*}>0$ a.s.

• The R&D system (4) is said to be in strong prosperity in the mean if $\langle x(t)+y(t)\rangle_{*}>0$ a.s.

Remark 3.1

Definition 3.1 is inspired by [16]. Liu and Wang introduced weak and strong persistence in a stochastic single-specie model if $\lim\sup_{t\rightarrow\infty}\frac {1}{t}\int_{0}^{t} y(s)\,ds>0$ and $\lim\inf_{t\rightarrow\infty }\frac{1}{t}\int_{0}^{t} y(s)\,ds>0$ a.s., respectively. Clearly, the condition of strong prosperity in the mean is stronger than that of weak prosperity. However, we define strong prosperity differently from [16] to satisfy the following certifications and actual background.

Definition 3.2

The economic growth rate of model (4) is said to be stochastically ultimately bounded if for any $\varepsilon\in(0, 1)$, there exists a positive $B=B(\varepsilon)$ such that for any initial value $(x(0), y(0), \varsigma(0))\in\mathbb{R}_{+}\times\mathbb {R}_{+}\times\mathbb{S}$, the solution of model (4) has the property that

$$ \limsup_{t\rightarrow\infty} \mathbb{P} \bigl\{ \bigl\vert x(t) \bigr\vert \leq B(\varepsilon ) \bigr\} \geq1-\varepsilon, \qquad\limsup _{t\rightarrow\infty}\mathbb {P} \bigl\{ \bigl\vert y(t) \bigr\vert \leq B(\varepsilon) \bigr\} \geq1-\varepsilon. $$

Theorem 3.1

For any$i\in\mathbb{S}$, if$\theta(i)+\xi(i)<0$holds, then the expected growth rates of both technology and capital accumulation are ultimately bounded in the long-run.

Proof

According to Theorem 2.1, the solution $(x(t), y(t), \varsigma(t))\in \mathbb{R}_{+}\times\mathbb{R}_{+}\times \mathbb{S}$ a.s. For any $\gamma>0$, we define $V: \mathbb{R}_{+} \times\mathbb{R}_{+}\times\mathbb{R}_{+}\times\mathbb{S}\rightarrow \mathbb{R}_{+}$ as

$$ V(t, x, y, i)=e^{\gamma t} \biggl(x(t)-\frac{2\theta(i)+\xi(i)}{\alpha(i)}y(t) \biggr). $$

For any positive integer $k\geq(x^{2}(0)+y^{2}(0))^{\frac{1}{2}}$, define the stopping time as $\rho_{k}=\inf\{t\in(0, \tau_{e}): (x^{2}(t)+y^{2}(t))^{\frac{1}{2}}\geq k\}$. By the generalized Itô’s formula [21] applied to $V(t, x(t), y(t), i)$, we have

$$ \begin{aligned} LV \bigl(t, x(t), y(t), i \bigr) ={}&e^{\gamma t} \biggl\{ \theta(i)x^{2}(t)-2\theta(i)x(t)y(t)+ \bigl[2\theta(i) + \xi(i) \bigr]y^{2}(t) \\ &- \bigl[2\theta(i)+\xi(i) \bigr] \biggl[n(i)-\frac{(1-\alpha(i))}{2} \sigma^{2}(i) +\frac{\gamma(i)}{\alpha(i)} \biggr]y(t) \\ &+ \biggl[\eta(i)n(i)-\frac{\eta(i)(1-\eta(i))}{2}\sigma^{2}(i) +\gamma(i) \biggr]x(t) \biggr\} \\ &+\sum_{j=1}^{m}\kappa_{ij}e^{\gamma t} \biggl(x(t)-\frac{2\theta(j)+\xi (j)}{\alpha(j)}y(t) \biggr). \end{aligned} $$

Letting $\bar{D}(i)=\operatorname{diag}(1, -\frac{2\theta(i)+\xi(i)}{\alpha (i)})$, $F(i)=[\eta(i)n(i)-\frac{\eta(i)(1-\eta(i))}{2}\sigma^{2}(i) +\gamma(i), -(2\theta(i)+\xi(i))(n(i)-\frac{(1-\alpha (i))}{2}\sigma^{2}(i) +\frac{\gamma(i)}{\alpha(i)})]$, from the condition of $\theta (i)+\xi(i)<0$, we get that $\bar{D}(i)A$ is a negative definite matrix and, denoting $-\lambda:=\max_{i\in\mathbb{S}}\lambda ^{+}_{\max}\bar{D}(i)A$, then we have

$$ LV \bigl(t, x(t), y(t), i \bigr) \leq e^{\gamma t} \bigl\{ \bigl( \bigl\vert F(i) \bigr\vert +\kappa_{i} \bigr) \bigl\vert X(t) \bigr\vert -\lambda \bigl\vert X(t) \bigr\vert ^{2} \bigr\} \leq Ce^{\gamma t}. $$

(7)

where $\kappa_{i}=\sum_{j\neq i}\kappa_{ij}(1+(\frac{2\theta(j)+\xi (j)}{\alpha(j)})^{2})^{\frac{1}{2}}$, $C=\max_{i=1}^{m}\frac{(|F(i)|+\kappa_{i})^{2}}{4\lambda}$. Integrating both sides of (7) from 0 to $t\wedge\rho_{k}$ and taking expectations, we obtain

$$ \mathbb{E}V \bigl(t\wedge\rho_{k}, x(t\wedge\rho_{k}), y(t\wedge\rho_{k}), \varsigma(t\wedge\rho_{k}) \bigr) \leq V \bigl(0, x(0), y(0), \varsigma(0) \bigr)+\frac{C}{\gamma} \bigl(e^{\gamma (t\wedge\rho_{k})}-1 \bigr). $$

Letting $k\rightarrow\infty$, we get

$$ \mathbb{E}V \bigl(t, x(t), y(t), \varsigma(t) \bigr)\leq V \bigl(0, x(0), y(0), \varsigma(0) \bigr)+\frac{C}{\gamma} \bigl(e^{\gamma t}-1 \bigr), $$

while letting $t\rightarrow\infty$ yields

$$ \lim_{t\rightarrow\infty}\sup\mathbb{E} \biggl(x(t)-\frac{2\theta (\varsigma(t))+\xi(\varsigma(t))}{\alpha(\varsigma(t))}y(t) \biggr)\leq \frac{C}{\gamma}, $$

by the positivity property of V. Also letting $C_{1}=\frac{\check {\alpha}(\varsigma(t))}{2\check{\theta}(\varsigma(t)) +\check{\xi}(\varsigma(t))}$, we get

$$ \lim_{t\rightarrow+\infty}\sup\mathbb{E}x(t)\leq \frac{C}{\gamma },\qquad \lim_{t\rightarrow+\infty}\sup\mathbb{E}y(t)\leq -C_{1}\frac{C}{\gamma} , $$

(8)

as required. Now for any $\varepsilon>0$, let $B_{1}(\varepsilon)=\frac {C}{\varepsilon\gamma}$, then, according to the Chebyshev’s inequality, we have

$$ \mathbb{P} \bigl\{ \bigl\vert x(t) \bigr\vert >B_{1}( \varepsilon) \bigr\} \leq\frac{\mathbb {E}( \vert x(t) \vert )}{B_{1}(\varepsilon)}, $$

so

$$ \limsup_{t\rightarrow\infty} \mathbb{P} \bigl\{ \bigl\vert x(t) \bigr\vert >B_{1}(\varepsilon) \bigr\} \leq\varepsilon, $$

which implies that

$$ \limsup_{t\rightarrow\infty} \mathbb{P} \bigl\{ \bigl\vert x(t) \bigr\vert \leq B_{1}(\varepsilon ) \bigr\} \geq1-\varepsilon. $$

In the same way, letting $B_{2}(\varepsilon)=-\frac{\check{\alpha }(\varsigma(t))}{2\check{\theta}(\varsigma(t)) +\check{\xi}(\varsigma(t))}\frac{C}{\varepsilon\gamma}$, we have

$$ \limsup_{t\rightarrow\infty} \mathbb{P} \bigl\{ \bigl\vert y(t) \bigr\vert \leq B_{2}(\varepsilon ) \bigr\} \geq1-\varepsilon, $$

thus the proof is completed. □

Remark 3.2

We denote $L(x, y)=\theta x^{2}-2\theta x y+(2\theta+\xi)y^{2}+(\gamma +b_{x})x-\frac{y}{\alpha}(2\theta+\xi)(\gamma+b_{y})$. From [4], we know that the value of $L_{\max}$ can influence the rates of technological progress and capital accumulation in the R&D model with white noise. However, Theorem 3.1 shows that the value of $L_{\max}$ is not sufficient to determine the long-run economic trend under regime switching. Therefore, not only $L_{\max}$ but also the transition rate $\kappa_{ij}$ can control the bound of economic growth in the R&D model disturbed by both white and color noise.

Theorem 3.2

For any$\varsigma(t)\in\mathbb{S}$, if$\theta(\varsigma(t))+\xi (\varsigma(t))<0$, then there is a positive constantKsuch that for any initial value$(x(0), y(0), \varsigma(0))\in\mathbb{R}_{+}\times\mathbb{R}_{+}\times \mathbb{S}$, the solution of model (4) has the property that

$$ \begin{gathered} \limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t}\mathbb{E}x^{2}(s)\, ds \leq\frac{2K}{\lambda}, \\ \limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t}\mathbb{E}y^{2}(s)\, ds \leq\frac{2K}{\lambda}.\end{gathered} $$

Proof

By Theorem 2.1, the solution of model (4) will remain in $\mathbb{R}_{+}\times\mathbb{R}_{+}\times \mathbb{S}$ for all $t>0$ a.s., then we define a $C^{2}$-function $V: \mathbb{R}_{+}\times\mathbb{R}_{+}\times\mathbb{S}\rightarrow\mathbb {R}_{+}$ by

$$ V \bigl(x(t), y(t), i \bigr)=x(t)-\frac{2\theta(i)+\xi(i)}{\alpha(i)}y(t). $$

For any positive integer $k\geq(x^{2}(0)+y^{2}(0))^{\frac{1}{2}}$, we define the stopping time $\rho_{k}=\inf\{t\in(0, {\tau_{e}}): (x^{2}(t)+y^{2}(t))^{\frac{1}{2}}>k\}$, where $\tau_{e}$ is the explosion time defined in the proof of Theorem 2.1. By the generalized Itô’s formula, we can get

$$ \begin{aligned} LV \bigl(x(t), y(t), i \bigr)&=x(t) \bigl[\theta(i) x(t)+ \xi(i) y(t)+b_{x}(i) \bigr]+\sum_{j=1}^{m} \kappa_{ij}V \bigl(x(t), y(t), j \bigr) \\ &\quad-\frac{2\theta(i)+\xi(i)}{\alpha(i)}y(t) \bigl[\alpha(i) x(t)-\alpha (i) y(t)+b_{y}(i) \bigr], \end{aligned} $$

then integrating both sides from 0 to $t\wedge\rho_{k}$ and taking expectations, we have

$$ \begin{aligned}[b] &\mathbb{E} \biggl(x(t)- \frac{2\theta(i)+\xi(i)}{\alpha(i)}y(t) \biggr) \\ &\quad\leq \mathbb{E} \int_{0}^{t\wedge\rho_{k}} \biggl\{ \biggl\{ \biggl\vert \biggl[b_{x}(s), \frac{2\theta(i)+\xi(i)}{\alpha (s)} \biggr] \biggr\vert + \kappa_{i} \biggr\} \bigl\vert X(s) \bigr\vert -\lambda \bigl\vert X(s) \bigr\vert ^{2} \biggr\} \,ds \\ &\qquad+x(0)-\frac{2\theta(\varsigma(0))+\xi(\varsigma(0))}{\alpha (\varsigma(0))}y(0) \\ &\quad\leq x(0)-\frac{2\theta(\varsigma(0))+\xi(\varsigma(0))}{\alpha (\varsigma(0))}y(0)+Kt-\frac{\lambda}{2}\mathbb{E} \int_{0}^{t\wedge \rho_{k}} \bigl\vert X(s) \bigr\vert ^{2}\,ds, \end{aligned} $$

(9)

where $K=\max_{i\in\mathbb{S}}\frac{b_{x}^{2}(i)+(\frac{2\theta (i)+\xi(i)}{\alpha(i)}b_{y}(i))^{2}+\kappa^{2}_{i}}{\lambda}$, $\kappa_{i}$ and λ are the same as in Theorem 3.1. Using the Fubini theorem and letting $k\rightarrow\infty$, $t\rightarrow\infty$, respectively, we get

$$ \limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t}\mathbb {E} \bigl(x^{2}(s)+y^{2}(s) \bigr)\,ds\leq\frac{2K}{\lambda} , $$

(10)

as desired. □

Theorem 3.2 shows that the growth rates of both technological progress and capital accumulation are second moment bounded in the time average sense, and the conclusion is stronger than that of Theorem 3.1.

Lemma 3.3

For any$\varsigma(t)\in\mathbb{S}$, if$\theta(\varsigma(t))+\xi (\varsigma(t))<0$and$\bar{\theta}(\varsigma(t))+\frac{\xi (\varsigma(t))+\alpha(\varsigma(t))}{2}<0$holds, then the solution of model (4) has the explicit form

$$ \begin{gathered} x(t)+y(t) \\ \quad \leq \exp\biggl\{ \int_{0}^{t}\biggl[\bar{b}\bigl(\varsigma(s) \bigr)-\frac{1}{2}\sigma ^{2}\bigl(\varsigma(s)\bigr)\bar{ \eta}^{2}\bigl(\varsigma(s)\bigr)\biggr]\,ds+ \int_{0}^{t}\sigma \bigl(\varsigma(s)\bigr)\bar{ \eta}\bigl(\varsigma(s)\bigr) \,dw(s)\biggr\} \\ \qquad{}\Big/\biggl(\frac {1}{x(0)+y(0)}+ \int_{0}^{t}-\biggl(\frac{\bar{\theta}(\varsigma (s))}{2}+ \frac{\xi(\varsigma(s))+\alpha(\varsigma(s))}{4}\biggr) \\ \quad\quad{}\cdot \exp\biggl\{ \int_{0}^{t}\biggl(\bar{b}\bigl(\varsigma(\tau) \bigr)-\frac{1}{2}\sigma ^{2}\bigl(\varsigma(\tau)\bigr) \bar{\eta}^{2}\bigl(\varsigma(\tau)\bigr)\biggr)d\tau+ \int _{0}^{s}\sigma\bigl(\varsigma(\tau)\bigr) \bar{\eta}\bigl(\varsigma(\tau)\bigr) \,dw(\tau )\biggr\} \,ds\biggr), \end{gathered} $$

where$\bar{\theta}(\varsigma(t))=-\alpha(\varsigma(t))\vee\theta (\varsigma(t))$, $\bar{b}(\varsigma(t))=b_{x}(\varsigma(t))\vee b_{y}(\varsigma(t))$, $\bar {\eta}(\varsigma(t))=\eta(\varsigma(t))\vee\alpha(\varsigma (t))$, for any$\varsigma(t)\in\mathbb{S}$.

Proof

The proof of this result is deferred until Appendix B. □

Lemma 3.3 is a preparation for researching the threshold of model (4) in the following result.

Theorem 3.3

For any$\varsigma(t)\in\mathbb{S}$, if$\theta(\varsigma(t))+\xi (\varsigma(t))<0$and$\bar{\theta}(\varsigma(t))+\frac{\xi (\varsigma(t))+\alpha(\varsigma(t))}{2}<0$hold, when$\tilde{b}-\langle\frac{\sigma^{2}(\varsigma(t))\bar{\eta }^{2}(\varsigma(t))}{2}\rangle_{*}<0$, then the R&D system (4) will go into depression, where$\tilde{b}=\frac {1}{t}\int_{0}^{t}\bar{b}(\varsigma(s))\,ds$and$\bar{b}(\varsigma (s))$, $\bar{\theta}(\varsigma(t))$, $\bar{\eta}(\varsigma(t))$are the same as defined in Lemma3.3.

Proof

From Lemma 3.3, we can easily get that

$$ \begin{aligned}[b] \varphi(t)&\leq\varphi(0)\exp \biggl\{ \int_{0}^{t} \biggl[\bar {b} \bigl(\varsigma(s) \bigr)-\frac{1}{2}\sigma^{2} \bigl(\varsigma(s) \bigr) \bar{ \eta}^{2} \bigl(\varsigma(s) \bigr) \biggr]\,ds+ \int_{0}^{t}\sigma \bigl(\varsigma (s) \bigr) \bar{ \eta} \bigl(\varsigma(s) \bigr)\,dw(s) \biggr\} \hspace{-12pt} \\ &\leq\varphi(0)\exp \biggl\{ -t \biggl[ \biggl\langle \frac{1}{2}\sigma ^{2} \bigl(\varsigma(s) \bigr) \bar{\eta}^{2} \bigl( \varsigma(s) \bigr) \biggr\rangle -\frac{1}{t} \int_{0}^{t}\bar {b} \bigl(\varsigma(s) \bigr) \,ds\\&\quad- \frac{\int_{0}^{t}\sigma(\varsigma(s))\bar{\eta}(\varsigma(s))\, dw(t)}{t} \biggr] \biggr\} . \end{aligned} $$

(11)

Letting $\int_{0}^{t}\sigma(\varsigma(s))\bar{\eta}(\varsigma(s))\, dw(s)=M(t)$, $\frac{1}{t}\int_{0}^{t}\bar{b}(\varsigma(s))\,ds=\tilde {b}$ a.s., we known that $M(t)$ is a martingale which satisfies

$$ \bigl\langle M(t), M(t) \bigr\rangle _{t}\leq\check{ \sigma}^{2} \bigl(\varsigma (t) \bigr)\check{\bar{ \eta}}^{2} \bigl(\varsigma(t) \bigr)t, $$

then, due to the ergodicity of $\varsigma(t)$ and the strong law of large numbers for martingales, we can get

$$ \lim_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t}\bar{b} \bigl(\varsigma (t) \bigr) \,ds=\sum_{i=1}^{m}\pi_{i} \bar{b}(i) =\tilde{b} \quad \text{a.s.}, $$

(12)

so that taking limit superior of both sides of (11) leads to

$$ \limsup_{t\rightarrow\infty}\varphi(t)\leq\varphi(0)\exp \biggl\{ -t \biggl[ \biggl\langle \frac{1}{2}\sigma^{2} \bigl( \varsigma(t) \bigr)\bar{\eta}^{2} \bigl(\varsigma(t) \bigr) \biggr\rangle -\tilde{b} \biggr] \biggr\} . $$

(13)

Therefore the desired assertion follows from (13) immediately. □

Remark 3.3

In the corresponding deterministic R&D model, the growth rates of both technological progress and capital accumulation are determined entirely by the population growth rate. In the stochastic environment, due to the effect of white noise, if the expected population growth rate n satisfies $n<\frac{1-(\sqrt{\alpha}-\sqrt{\eta})^{2}}{2}\sigma^{2}$, then the population growth rate may have little influence on long-run economic growth because the economic growth rate will go to zero. However, the situation changes considerably for the stochastic R&D model under white and color noise. Theorem 3.3 shows that both the ergodicity of the Markov chain $\varsigma(t)$ and the transition rate $\kappa_{ij}$ from i to j affect the long-run growth rates of technological progress and capital accumulation in the stochastic R&D model under white and color noise.

Remark 3.4

Unless otherwise specified, the values of b̃, $\bar {b}(\varsigma(s))$, $\bar{\theta}(\varsigma(t))$, $\bar{\eta }(\varsigma(t))$ and $M(t)$ are consistent with Theorem 3.3 in the following.

Theorem 3.4

For any$\varsigma(t)\in\mathbb{S}$, if$\theta(\varsigma(t))+\xi (\varsigma(t))<0$and$\bar{\theta}(\varsigma(t))+\frac{\xi (\varsigma(t))+\alpha(\varsigma(t))}{2}<0$hold, when$\tilde{b}-\langle\frac{1}{2}\sigma^{2}(\varsigma(t))\bar{\eta }^{2}(\varsigma(t))\rangle_{*}=0$, then model (4) will be stochastically nonprosperous in the mean.

Proof

Using the generalized Itô’s formula to $\log\varphi(t)$, with $\varphi(t)$ defined in Lemma 3.3, we have

$$ \begin{aligned} d\log\varphi(t)={}& \biggl\{ \biggl[\frac{\bar{\theta}(\varsigma(t))}{2}+ \frac{\xi(\varsigma(t))+\alpha(\varsigma(t))}{4} \biggr]\varphi(t) +\bar{b}-\frac{1}{2} \sigma^{2} \bigl(\varsigma(t) \bigr)\bar{\eta} \bigl(\varsigma (t) \bigr) \biggr\} \,dt \\ &+\sigma \bigl(\varsigma(t) \bigr)\bar{\eta} \bigl(\varsigma(t) \bigr) \,dw(t), \end{aligned} $$

and then

$$ \begin{aligned}[b] \frac{1}{t}\log \frac{\varphi(t)}{\varphi(0)}={}&\frac{1}{t} \int _{0}^{t}\bar{b} \bigl(\varsigma(s) \bigr) \,ds +\frac{1}{t} \int_{0}^{t} \biggl[\frac{\bar{\theta}(\varsigma(t))}{2} + \frac{\xi(\varsigma(s))+\alpha(\varsigma(s))}{4} \biggr]\varphi (s)\,ds \\ &-\frac{1}{2t} \int_{0}^{t}\sigma^{2} \bigl( \varsigma(s) \bigr)\bar{\eta }^{2} \bigl(\varsigma(s) \bigr)\,ds + \frac{1}{t} \int_{0}^{t}\sigma \bigl(\varsigma(s) \bigr) \bar{ \eta} \bigl(\varsigma (s) \bigr)\,dw(s), \end{aligned} $$

(14)

so, according to Eq. (12), we have

$$ \begin{aligned}[b] \frac{1}{t}\log\frac{\varphi(t)}{\varphi(0)}&= \frac{1}{t} \int _{0}^{t}\bar{b} \bigl(\varsigma(s) \bigr) \,ds + \biggl\langle \biggl[\frac{\bar{\theta}(\varsigma(t))}{2}+\frac{{\xi (\varsigma(t))}+ \alpha(\varsigma(t))}{4} \biggr] \varphi(t) \biggr\rangle \\ &\quad- \frac{1}{2} \bigl\langle \sigma^{2} \bigl(\varsigma(t) \bigr)\bar{\eta}^{2} \bigl(\varsigma (t) \bigr) \bigr\rangle +\frac{M(t)}{t}.\end{aligned} $$

(15)

Making use of the strong law of large numbers for martingales yields $\lim_{t\rightarrow+\infty}\frac{M(t)}{t}=0$ a.s., so for any $\varepsilon>0$, there exists a constant T such that for any $t>T$, we have

$$\begin{aligned}& \frac{M(t)}{t}\leq\frac{\varepsilon}{3}, \end{aligned}$$

(16)

$$\begin{aligned}& \frac{1}{t} \int_{0}^{t}\bar{b} \bigl(\varsigma(s) \bigr) \,ds \leq\tilde{b}+\frac {\varepsilon}{3}, \end{aligned}$$

(17)

and

$$ \frac{1}{2} \bigl\langle \sigma ^{2} \bigl( \varsigma(t) \bigr)\bar{\eta}^{2} \bigl(\varsigma(t) \bigr) \bigr\rangle > \frac{1}{2} \bigl\langle \sigma^{2} \bigl( \varsigma(t) \bigr) \bar{\eta}^{2} \bigl(\varsigma (t) \bigr) \bigr\rangle _{*} - \frac{\varepsilon}{3}. $$

(18)

Substituting (16), (17), and (18) into Eq. (15), we get

$$ \begin{aligned} \frac{1}{t}\log\frac{\varphi(t)}{\varphi(0)}&\leq \tilde{b} + \biggl\langle \biggl[\frac{\bar{\theta}(\varsigma(t))}{2} +\frac{\xi(\varsigma(t))+\alpha(\varsigma(t))}{4} \biggr]\varphi (t) \biggr\rangle -\frac{1}{2} \bigl\langle \sigma^{2} \bigl(\varsigma(t) \bigr)\bar{\eta}^{2} \bigl( \varsigma (t) \bigr) \bigr\rangle _{*} +\varepsilon \\ &\leq \biggl[\tilde{b}-\frac{1}{2} \bigl\langle \sigma^{2} \bigl(\varsigma(t) \bigr)\bar {\eta}^{2} \bigl(\varsigma(t) \bigr) \bigr\rangle _{*}+\varepsilon \biggr] + \biggl\langle \biggl[\frac{\bar{\theta}(\varsigma(t))}{2} + \frac{\xi(\varsigma(t))+\alpha(\varsigma(t))}{4} \biggr]\varphi (t) \biggr\rangle , \end{aligned} $$

from which we deduce

$$\begin{aligned} \log\varphi(t)-\log\varphi(0)&\leq \biggl[\tilde{b}- \frac {1}{2} \bigl\langle \sigma^{2} \bigl(\varsigma(t) \bigr) \bar{\eta}^{2} \bigl(\varsigma (t) \bigr) \bigr\rangle _{*} +\varepsilon \biggr]t\\ &\quad+ \biggl\langle \biggl[\frac{\bar{\theta}(\varsigma(t))}{2}+ \frac{\xi(\varsigma(t))+\alpha(\varsigma(t))}{4} \biggr] \varphi (t) \biggr\rangle t \\ &\leq \biggl[\tilde{b}-\frac{1}{2} \bigl\langle \sigma^{2} \bigl(\varsigma(t) \bigr)\bar {\eta}^{2} \bigl(\varsigma(t) \bigr) \bigr\rangle _{*} +\varepsilon \biggr]t\\&\quad+\max_{\varsigma(t)=1}^{m} \biggl\{ \frac{\bar {\theta}(\varsigma(t))}{2} +\frac{\xi(\varsigma(t))+\alpha(\varsigma(t))}{4} \biggr\} \int _{0}^{t}\varphi(s)\,ds. \end{aligned}$$

Letting $\int_{0}^{t}\varphi(s)\,ds=g(t)$ and $\tilde{b}=\frac {1}{2}\langle\sigma^{2}(\varsigma(t))\bar{\eta}^{2}(\varsigma (t))\rangle_{*}$, we have

$$ -\max_{\varsigma(t)=1}^{m} \biggl\{ \frac{\bar{\theta}(\varsigma(t))}{2} + \frac{\xi(\varsigma(t))+\alpha(\varsigma(t))}{4} \biggr\} g(t)\leq \varepsilon t-\log\frac{\varphi(t)}{\varphi(0)}, $$

and then

$$ \exp \biggl\{ -\max_{\varsigma(t)=1}^{m} \biggl\{ \frac{\bar{\theta }(\varsigma(t))}{2} +\frac{\xi(\varsigma(t))+\alpha(\varsigma(t))}{4} \biggr\} g(t) \biggr\} \leq \frac{\varphi(0)e^{\varepsilon t}}{\varphi(t)}, $$

thus we deduce that

$$ \exp \biggl\{ -\max_{\varsigma(t)=1}^{m} \biggl\{ \frac{\bar{\theta }(\varsigma(t))}{2} +\frac{\xi(\varsigma(t))+\alpha(\varsigma(t))}{4} \biggr\} g(t) \biggr\} \frac{dg(t)}{dt} < \varphi(0)e^{\varepsilon t},\quad t>T. $$

Now by integrating this inequality from T to t results in

$$ \int_{T}^{t} \exp \biggl\{ -\max _{\varsigma(t)=1}^{m} \biggl[\frac{\bar {\theta}(\varsigma(t))}{2} + \frac{\xi(\varsigma(t))+\alpha(\varsigma(t))}{4} \biggr]g(t) \biggr\} \,dg(t) < \frac{\varphi(0)}{\varepsilon} \bigl(e^{\varepsilon t}-e^{\varepsilon T} \bigr). $$

(19)

Letting $-\max_{\varsigma(t)=1}^{m}\{\frac{\bar{\theta}(\varsigma(t))}{2} +\frac{\xi(\varsigma(t))+\alpha(\varsigma(t))}{4}\}=C_{2}$, from (19), we deduce that

$$ e^{C_{2}g(t)}\leq e^{C_{2}g(T)}+\frac{C_{2}\varphi(0)}{\varepsilon } \bigl(e^{\varepsilon t}-e^{\varepsilon T} \bigr), $$

hence

$$ \int_{0}^{t}\varphi(s)\,ds\leq \frac{1}{C_{2}}\log \biggl[e^{C_{2}g(T)}+\frac {C_{2}\varphi(0)}{\varepsilon} \bigl(e^{\varepsilon t}-e^{\varepsilon T} \bigr) \biggr], $$

and then

$$ \biggl(\frac{\int_{0}^{t}\varphi(s)\,ds}{t} \biggr)^{*}\leq\frac{1}{C_{2}} \biggl\{ \frac {\log[e^{C_{2}g(T)} +\frac{C_{2}\varphi(0)}{\varepsilon}(e^{\varepsilon t}-e^{\varepsilon T})]}{t} \biggr\} ^{*}. $$

By the L’Hospital’ s rule, we derive

$$ \lim_{t\rightarrow\infty}\frac{\log [e^{C_{2}g(T)}+\frac {C_{2}\varphi(0)}{\varepsilon}(e^{\varepsilon t}-e^{\varepsilon T}) ]}{t}=\lim_{t\rightarrow\infty} \frac{C_{2}\varphi(0)e^{\varepsilon t}}{e^{C_{2}g(T)}+\frac{C_{2}\varphi(0)}{\varepsilon}(e^{\varepsilon t}-e^{\varepsilon T})}=\varepsilon, $$

so we have $\langle\varphi(t)\rangle^{*}\leq\frac{\varepsilon}{C_{2}}$ and, letting ε down to zero, we get that $\langle\varphi (t)\rangle^{*}\leq0$. Then by the comparison theorem, we can check that $\langle x(t)\rangle^{*}=0$ and $\langle y(t)\rangle^{*}=0$. □

Theorem 3.5

For any$\varsigma(t)\in\mathbb{S}$, if$\theta(\varsigma(t))+\xi (\varsigma(t))<0$and$\bar{\theta}(\varsigma(t))+\frac{\xi (\varsigma(t))+\alpha(\varsigma(t))}{2}<0$hold, when$\tilde {b}-\frac{1}{2}\langle\sigma^{2}(\varsigma(t))\bar{\eta }^{2}(\varsigma(t))\rangle_{*}>0$, then the R&D system (4) will be stochastically weakly prosperous in the mean.

Proof

From Theorem 3.3, we know that $x(t)+y(t)\leq \varphi(t)$, where $\varphi(t)$ is defined in (35). Under hypothetical conditions and through Corollary 3.4 in [22], we get that $\limsup_{t\rightarrow\infty}\frac{\log\varphi(t)}{t}\leq0$ a.s. Consequently, we have

$$ \biggl(\frac{\log x(t)}{t} \biggr)^{*}\leq0, \qquad \biggl( \frac{\log y(t)}{t} \biggr)^{*}\leq0. $$

(20)

Now we need to prove

$$ 0< \limsup_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t} x(s)\,ds< \limsup _{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t} \varphi(s)\,ds. $$

In fact, we just assume $\mathbb{P}\{\varphi(t)^{*}=0\}>0$ is not true. Actually, from (14), we obtain that

$$ \begin{aligned}[b] &\frac{\log\varphi(t)}{t}-\frac{\log\varphi(0)}{t} - \biggl\langle \biggl[\frac{\bar{\theta}(\varsigma(t))}{2} -\frac{\xi(\varsigma(t))+\alpha(\varsigma(t))}{4} \biggr]\varphi (t) \biggr\rangle \\&\quad=\frac{1}{t} \int_{0}^{t}\bar{b} \bigl(\varsigma(s) \bigr) \,ds -\frac{1}{2} \bigl\langle \sigma^{2} \bigl(\varsigma(t) \bigr) \bar{\eta}^{2} \bigl(\varsigma (t) \bigr) \bigr\rangle + \frac{M(t)}{t}.\end{aligned} $$

(21)

We consider the set $\mathbb{U}=\{\omega|\langle\omega\rangle^{*}=0\}$, and then for any $\varphi(t)\in\mathbb{U}$, we can easily get that

$$ \biggl\langle \biggl[\frac{\xi(\varsigma(t))+\alpha(\varsigma(t))}{4} -\frac{\bar{\theta}(\varsigma(t))}{2} \biggr] \varphi(t) \biggr\rangle ^{*} \leq\max_{\varsigma(t)\in\mathbb{S}} \biggl\{ \frac{\xi(\varsigma (t))+\alpha(\varsigma(t))}{4}-\frac{\bar{\theta}(\varsigma (t))}{2} \biggr\} \bigl\langle \varphi(t) \bigr\rangle ^{*}=0. $$

In view of (21), we have

$$ \biggl(\frac{\log\varphi(t)}{t} \biggr)^{*}\geq\tilde{b}- \frac{1}{2} \bigl\langle \sigma^{2} \bigl(\varsigma(t) \bigr)\bar{\eta}^{2} \bigl(\varsigma (t) \bigr) \bigr\rangle _{*}, $$

so we just let $\tilde{b}- \frac{1}{2}\langle\sigma^{2}(\varsigma(t))\bar{\eta}^{2}(\varsigma (t))\rangle_{*}>0$ and deduce

$$ \mathbb{P} \biggl\{ \biggl(\frac{\log\varphi(t)}{t} \biggr)^{*}>0 \biggr\} >0, $$

so that

$$ \mathbb{P} \biggl\{ \biggl(\frac{\log x(t)}{t} \biggr)^{*}>0 \biggr\} >0, $$

which contradicts Eq. (20). We can use the same method to $y(t)$ and then the proof is completed. □

Remark 3.5

Theorems 3.3, 3.4, and 3.5 show that under the conditions $\theta(\varsigma(t))+\xi(\varsigma (t))<0$ and $\bar{\theta}(\varsigma(t))+\frac{\xi(\varsigma (t))+\alpha(\varsigma(t))}{2}<0$, $\tilde{b}-\frac{1}{2}\langle\sigma^{2}(\varsigma(t)) \bar{\eta}^{2}(\varsigma(t))\rangle_{*}$ is the threshold between stochastic depression, nonprosperity, and weak prosperity in the mean. Additionally, color noise plays an important role in determining depression or prosperity in model (4). That is, when the Markov chain spends more time in a good state, which means $\sum_{i=1}^{m}\pi_{i}\bar{b}(i)$ takes a large value, then the growth rates of economic progress and capital accumulation trend toward prosperity in the long run. Conversely, if the Markov chain spends more time in a bad state, it may lead the R&D system (4) toward depression.

Theorem 3.6

For any$\varsigma(t)\in\mathbb{S}$, if$\theta(\varsigma(t))+\xi (\varsigma(t))<0$holds, when$\bar{h}>\frac{1}{2} \langle \sigma^{2}(\varsigma(t)) [\eta(\varsigma(t))\wedge\alpha(\varsigma(t))]^{2} \rangle^{*}$, then the R&D system (4) will be stochastically strongly prosperous in the mean.

Proof

We now consider the system on the boundary

$$ \begin{aligned}[b] d\varPhi(t)&=\varPhi(t) \bigl\{ \bigl[\theta \bigl(\varsigma(t) \bigr)\wedge(-\alpha ) \bigl(\varsigma(t) \bigr) \bigr]\varPhi(t) + \bigl[b_{x} \bigl(\varsigma(t) \bigr)\wedge b_{y} \bigl( \varsigma(t) \bigr) \bigr] \bigr\} \,dt\\&\quad+\sigma \bigl(\varsigma (t) \bigr) \bigl[ \eta \bigl(\varsigma(t) \bigr)\wedge\alpha \bigl(\varsigma(t) \bigr) \bigr] \varPhi(t) \,dw(t).\end{aligned} $$

(22)

We can easily to check that $x(t)+y(t)\geq\varPhi(t)$ a.s. for any $t\geq0$. Applying the generalized Itô’s formula, we get from equation (22) that

$$ \begin{aligned}[b] \frac{\log\varPhi(t)-\log\varPhi(0)}{t}&= \bigl[\theta \bigl(\varsigma (t) \bigr)\wedge \bigl(-\alpha \bigl(\varsigma(t) \bigr) \bigr) \bigr] \bigl\langle \varPhi(t) \bigr\rangle +\frac {\int_{0}^{t}(b_{x}(\varsigma(s))\wedge b_{y}(\varsigma(s)))\,ds}{t} \\ &\quad-\frac{1}{2} \bigl\langle \sigma^{2} \bigl(\varsigma(t) \bigr) \bigl[\eta \bigl(\varsigma (t) \bigr)\wedge\alpha \bigl(\varsigma(t) \bigr) \bigr]^{2} \bigr\rangle +\frac{M(t)}{t}. \end{aligned} $$

(23)

Letting $b_{x}(\varsigma(t))\wedge b_{y}(\varsigma(t))=h(\varsigma(t))$, by the ergodicity of Markov chain $\varsigma(t)$, we have

$$ \frac{\int_{0}^{t} h(\varsigma(s))\,ds}{t}=\sum_{i\in\mathbb{S}}\pi _{i} h(i)=\bar{h} \quad\text{a.s.}, $$

and then Eq. (23) can be rewritten as

$$ \begin{aligned}[b] \frac{\log\varPhi(t)-\log\varPhi(0)}{t}&= \bigl[\theta \bigl(\varsigma (t) \bigr) \wedge \bigl(-\alpha \bigl(\varsigma(t) \bigr) \bigr) \bigr] \bigl\langle \varPhi(t) \bigr\rangle +\frac {\int_{0}^{t} h(\varsigma(s))\,ds}{t} \\&\quad-\frac{1}{2} \bigl\langle \sigma^{2} \bigl(\varsigma(t) \bigr) \bigl[\eta \bigl(\varsigma (t) \bigr) \wedge\alpha \bigl(\varsigma(t) \bigr) \bigr]^{2} \bigr\rangle + \frac{M(t)}{t},\end{aligned} $$

(24)

where $M(t)=\int_{0}^{t}\sigma(\varsigma(s))[\eta(\varsigma(s))\wedge \alpha(\varsigma(s))]\,dw(s)$. For each sufficiently small constant $\varepsilon>0$, there is a constant T such that for all $t>T$, we have

$$\begin{aligned}& \frac{M(t)}{t}>-\frac{\varepsilon}{3}, \end{aligned}$$

(25)

$$\begin{aligned}& \frac{1}{t} \int_{0}^{t} h \bigl(\varsigma(s) \bigr)\,ds> \bar{h}-\frac{\varepsilon}{3}, \end{aligned}$$

(26)

and

$$ \frac{1}{2} \bigl\langle \sigma^{2} \bigl( \varsigma(t) \bigr) \bigl[\eta \bigl(\varsigma (t) \bigr)\wedge\alpha \bigl( \varsigma(t) \bigr) \bigr]^{2} \bigr\rangle < \frac{1}{2} \bigl\langle \sigma^{2} \bigl(\varsigma(t) \bigr) \bigl[\eta \bigl( \varsigma (t) \bigr)\wedge\alpha \bigl(\varsigma(t) \bigr) \bigr]^{2} \bigr\rangle ^{*} + \frac{\varepsilon}{3}. $$

(27)

Substituting (25), (26), and (27) into Eq. (24), we have

$$ \begin{aligned}[b] \log\varPhi(t)-\log\varPhi(0)&\geq \biggl\{ \bar{h} -\frac{1}{2} \bigl\langle \sigma^{2} \bigl( \varsigma(t) \bigr) \bigl[\eta \bigl(\varsigma (t) \bigr)\wedge\alpha \bigl( \varsigma(t) \bigr) \bigr]^{2} \bigr\rangle ^{*}-\varepsilon \biggr\} t \\ &\quad+\min_{\varsigma(t)\in\mathbb{S}} \bigl[\theta \bigl(\varsigma(t) \bigr)\wedge \bigl(-\alpha \bigl(\varsigma(t) \bigr) \bigr) \bigr] \int_{0}^{t}\varPhi(s)\,ds\quad (t>T). \end{aligned} $$

(28)

Letting $\min_{\varsigma(t)=1}^{m}[\theta(\varsigma(t))\wedge (-\alpha(\varsigma(t)))]=\nu$, $\bar{h} -\frac{1}{2} \langle\sigma^{2}(\varsigma(t))[\eta(\varsigma (t))\wedge\alpha(\varsigma(t))]^{2} \rangle^{*}-\varepsilon=\mu$, $\int_{0}^{t}\varPhi(s)\,ds=f(t)$, inequality (28) can be rewritten as

$$ \log\frac{df(t)}{dt}>\log\varPhi(0)+\mu t+\nu \int_{0}^{t}\varPhi(s)\,ds. $$

(29)

Taking the exponential of both sides of (29), we have

$$ \frac{df(t)}{dt}>\varPhi(0)e^{\mu t+\nu\int_{0}^{t}\varPhi(s)\,ds}, $$

and, since $\int_{0}^{t}\varPhi(s)\,ds=f(t)$, we have that

$$ e^{-\nu f(t)}\frac{df(t)}{dt}>\varPhi(0)e^{\mu t}. $$

(30)

Integrating both sides of (30) from T to t, we obtain that

$$ -\frac{1}{\nu} \bigl[e^{-\nu f(t)}-e^{-\nu f(T)} \bigr]> \frac{\varPhi (0)}{\mu} \bigl(e^{\mu t}-e^{\mu T} \bigr). $$

Hence

$$ f(t)>-\frac{1}{\nu}\log \biggl[-\varPhi(0)\frac{\nu}{\mu}e^{\mu t}+ \varPhi(0)\frac{\nu}{\mu}e^{\mu T}+e^{-\nu f(T)} \biggr], $$

thus we can get

$$ \biggl\{ \frac{\int_{0}^{t}\varPhi(s)\,ds}{t} \biggr\} _{*} \geq-\frac{1}{\nu} \biggl\{ \frac{\log [-\varPhi(0)\frac{\nu }{\mu}e^{\mu t}+\varPhi(0)\frac{\nu}{\mu}e^{\mu T}+e^{-\nu f(T)} ]}{t} \biggr\} _{*}. $$

(31)

By the L’Hospital’s rule, we have

$$ \begin{aligned} &\liminf_{t\rightarrow\infty}- \frac{1}{\nu} \biggl\{ \frac{\log [-\varPhi(0)\frac{\nu}{\mu}e^{\mu t}+\varPhi(0)\frac{\nu}{\mu }e^{\mu T}+e^{-\nu f(T)} ]}{t} \biggr\} \\ &\quad=\liminf_{t\rightarrow\infty}-\frac{1}{\nu}\cdot \frac{-\varPhi (0)\nu e^{\mu t}}{-\varPhi(0)\frac{\nu}{\mu}e^{\mu t}+\varPhi (0)\frac{\nu}{\mu}e^{\mu T}+e^{-\nu f(T)}} \\ &\quad=-\frac{\mu}{\nu}. \end{aligned} $$

Since $\min_{\varsigma(t)=1}^{m}[\theta(\varsigma(t))\wedge (-\alpha(\varsigma(t)))]=\nu$, $\bar{h} -\frac{1}{2} \langle\sigma^{2}(\varsigma(t))[\eta(\varsigma (t))\wedge\alpha(\varsigma(t))]^{2} \rangle^{*}-\varepsilon=\mu$, we have

$$ \biggl\{ \frac{\int_{0}^{t}\varPhi(s)\,ds}{t} \biggr\} _{*}\geq\frac{\bar{h} -\frac{1}{2} \langle\sigma^{2}(\varsigma(t))[\eta(\varsigma (t))\wedge\alpha(\varsigma(t))]^{2} \rangle^{*}-\varepsilon}{-\min_{\varsigma(t)\in\mathbb{S}}[\theta(\varsigma(t))\wedge(-\alpha (\varsigma(t)))]}, $$

(32)

where ε is sufficiently small such that

$$ \bigl\langle \varPhi(t) \bigr\rangle _{*}>\frac{\bar{h} -\frac{1}{2} \langle\sigma^{2}(\varsigma(t))[\eta(\varsigma (t))\wedge\alpha(\varsigma(t))]^{2} \rangle^{*}}{-\min_{\varsigma (t)\in\mathbb{S}}[\theta(\varsigma(t))\wedge(-\alpha(\varsigma(t)))]}. $$

According to the assumption, we have $\langle x(t)+y(t)\rangle_{*}>0$. □

Remark 3.6

Theorem 3.6 shows that under the condition of $\bar{h} -\frac{1}{2} \langle\sigma^{2}(\varsigma(t))[\eta(\varsigma (t))\wedge\alpha(\varsigma(t))]^{2} \rangle^{*}>0$, both technological progress and capital accumulation will be increased significantly in the mean. Clearly, the condition of Theorem 3.6 is stronger than that of Theorem 3.5, which means that if $\sum_{i=1}^{m}\pi_{i} h(i)$ is relatively large or the uncertainty from white noise is relatively low, then the economy will be characterized by strong prosperity.

4 Numerical experiments

In this section, we verify our theory from the previous sections via numerical examples.

Example 4.1

Let $\varsigma(t)$ be a Markov chain on the state space $\mathbb{S}=\{ 1,2\}$, and the generator Θ is given as $\Theta =\left(\begin{array}{cc}-1& 1\\ 3& -3\end{array}\right)$. Fig. 1(a) shows sample paths of the Markov chain, which has two reachable states. The dwell time of the system in these two reachable states depends on the stationary distribution in Fig. 1(b). We can also know that the Markov chain $\varsigma(t)$ spends more time in state 1 and less time in state 2.

Figure 1

(a) Computer simulation of a sample path of Markov chain $\varsigma(t)$. (b) Probability density function (PDF) of Markov chain $\varsigma(t)$

Example 4.2

We choose parameter values for states $\varsigma(t)=1$ and $\varsigma (t)=2$ as in Table 2. The Markov chain has the generator $\Theta =\left(\begin{array}{cc}-2& 2\\ 1& -1\end{array}\right)$. It is easy to verify that the parameters satisfy the conditions of Theorem 3.3, according to which we can conclude that the system will be in depression, and the numerical simulation shown in Fig. 2 clearly supports our conclusion.

Figure 2

The time-series plots of $x(t)$ and $y(t)$ for model (4) with initial value $(x_{0}, y_{0})=(0.9, 0.6)$, and other parameters are taken as in Table 2

Table 2 Parameter values under finite regime switching of model (4)

Example 4.3

To show the strong prosperity of the R&D model, we choose parameters for states 1 and 2 as in Table 3. The generator of the Markov chain is $\Theta =\left(\begin{array}{cc}-2& 2\\ 5& -5\end{array}\right)$. According to Theorem 3.6, we can conclude that the model will be in strong prosperity, and the numerical simulation in Fig. 3 displays this phenomenon, as expected.

Figure 3

The time-series plots of $x(t)$ and $y(t)$ for model (4) with initial $(x_{0}, y_{0}) = (0.2, 0.8)$, and other parameters are taken as in Table 3

Table 3 Parameter values under finite regime switching of model (4)

Example 4.4

Inspired by [23], we obtain the stationary distributions of $x(t)$ and $y(t)$ for three different environmental forcing intensities according to 10,000 numerical simulation runs in Fig. 4. The smooth curves denote the probability density functions of $x(t)$ and $y(t)$. The change in the stationary distributions with increasing σ is illustrated by the distributions displayed in the left ($\sigma=0.1$), middle ($\sigma=0.4$), and right ($\sigma=0.9$) panels in Fig. 4. The parameters of states 1, 2 and 3 are selected according to Table 4.

Figure 4

Histogram of the probability density function of $x(100)$ and $y(100)$ for model (4), the smooth curves are the probability density functions of $x(t)$ and $y(t)$, respectively

Table 4 Parameter values under finite regime switching of model (4)

The results show that increasing the environmental forcing intensity may lead to changes in the mean values and skewness of the distribution for the R&D model. More precisely, the stationary distribution is close to a normal distribution at lower intensity (e.g., $\sigma=0.1$, see the left panel of Fig. 4), but the distribution is positively skewed at higher intensity (e.g., $\sigma=0.9$, see the right panel of Fig. 4).

5 Concluding remarks

The stochastic R&D model plays an important role in economic growth theories. The asymptotic properties of the R&D model, which is disturbed by white and color noise, is an open problem. In this paper, we obtain sufficient conditions of economic strong prosperity, weak prosperity, nonprosperity, and depression under regime switching. The most important contribution of this paper is that we precisely express the threshold between prosperity and depression. This means that:

• If $\tilde{b}-\langle\frac{\sigma^{2}(\varsigma(t))\bar{\eta }^{2}(\varsigma(t))}{2}\rangle_{*}<0$, then the economy is going into a depression in the long term.

• If $\tilde{b}-\langle\frac{\sigma^{2}(\varsigma(t))\bar{\eta }^{2}(\varsigma(t))}{2}\rangle_{*}=0$, then the economy is going into nonprosperity in the long term.

• If $\tilde{b}-\langle\frac{\sigma^{2}(\varsigma(t))\bar{\eta }^{2}(\varsigma(t))}{2}\rangle_{*}>0$, then the economy is going into weak prosperity in the long term.

We also find that the growth rates of economic progress and capital accumulation can easily increase in the long term if the Markov chain spends more time in the good states or if the uncertainty coming from white noise is relatively low in the sense that $\bar{h}>\frac {1}{2} \langle\sigma^{2}(\varsigma(t)) [\eta(\varsigma(t))\wedge\alpha(\varsigma(t))]^{2} \rangle^{*}$ (see Theorem 3.6). In contrast, if the Markov chain spends more time in the bad states or the uncertainty coming from white noise is relatively large in the sense that $\tilde{b}<\langle \frac{\sigma^{2}(\varsigma(t))\bar{\eta}^{2}(\varsigma(t))}{2}\rangle _{*}$, it may lead to R&D system depression (see Theorem 3.3). The conclusions of this paper may provide a good explanation for some economic fluctuation phenomena under regime switching. Some questions that need further discussion remain. For instance, it will be useful to extend the R&D model to consider Poisson jumps or time delays. We will make further efforts in this direction in the future.

Appendices

Appendix 1: Proof of Theorem 2.1

Proof

Since the coefficients of model (4) are locally Lipschitz continuous, for any given positive initial value $(x(0), y(0), \varsigma(0))$, there exists a unique maximal local solution $(x(t), y(t), \varsigma(t))$ on $t\in[0, \tau_{e})$, where $\tau_{e}$ is the explosion time. In order to explain why the local solution is global, we only need to prove $\tau_{e}=\infty$ with probability 1. Let $k_{0}$ be a sufficiently large positive constant such that $x(0) \in [\frac{1}{k_{0}}, k_{0}]$, and $y(0) \in[\frac{1}{k_{0}}, k_{0}]$. For each integer $k \geq k_{0}$, we define the stopping time

$$ \tau_{k}=\inf \biggl\{ t\in[0, \tau_{e}): x \bigl( \varsigma(t) \bigr) \notin \biggl(\frac {1}{k}, k \biggr), y \bigl( \varsigma(t) \bigr) \notin \biggl(\frac{1}{k}, k \biggr) \text{ for } \varsigma(t) \in\mathbb{S} \biggr\} . $$

It is easily to see that $\tau_{k}$ is increasing as $k\rightarrow \infty$, and note that $\lim_{k\rightarrow\infty}\tau_{k}=\tau _{\infty}$. If we prove that $\tau_{\infty}=\infty$ a.s., by the definition of stopping time $\tau_{e}$, it is obvious that $\tau _{e}=\infty$ a.s. Now we assume this statement is not true, hence there exists a pair of positive constant numbers $(T, \varepsilon)$ such that $\mathbb{P}\{\tau_{\infty}\leq T(\varepsilon)\}>\varepsilon$, $\varepsilon\in(0, 1)$. We choose $k_{1}$ greater than or equal to $k_{0}$ such that for any $k\geq k_{1}$, we have $\mathbb{P}\{\tau_{k}\leq T\}\geq\varepsilon$. Next, we define a $C^{2}$-function $V: \mathbb {R}_{+}\times\mathbb{R}_{+}\times\mathbb{S}\rightarrow\mathbb{R}_{+}$ by

$$ V \bigl(x(t), y(t), i \bigr)=c_{x}(i) \bigl[x(t)-1-\log x(t) \bigr]+c_{y}(i) \bigl[y(t)-1-\log y(t) \bigr], $$

where for each $i \in\mathbb{S}$, $c_{x}(i)$, $c_{y}(i)$ are both positive numbers. Applying the generalized Itô’s formula to V, we obtain

$$ \begin{aligned}[b] LV \bigl(x(t), y(t), i \bigr)={}&X^{\top}(t)\operatorname{diag} \bigl(c_{x}(i), c_{y}(i) \bigr)B(i)- \bigl(c_{x}(i), c_{y}(i) \bigr) \begin{pmatrix} \theta(i) x(t)+\xi(i) y(t)+b_{x}(i)\\ \alpha(i) x(t)-\alpha(i) y(t)+b_{y}(i) \end{pmatrix}\hspace{-24pt} \\ &+\frac{1}{2}X^{\top}(t) \begin{pmatrix} 2c_{x}(i)\theta(i) & c_{x}(i)\xi(i)+c_{y}(i)\alpha(i)\\ c_{x}(i)\xi(i)+c_{y}(i)\alpha(i) & -2c_{y}(i)\alpha(i) \end{pmatrix} X(t) \\ &+\frac{1}{2} \bigl(c_{x}(i)\eta^{2}(i) \sigma^{2}(i)+c_{y}(i)\alpha^{2}(i) \sigma^{2}(i) \bigr) +\sum_{j=1}^{m} \kappa_{ij}V \bigl(x(t), y(t), j \bigr). \end{aligned} $$

(33)

Under assertion $\theta(i)+\xi(i)<0$, we know that −A is a nonsingular M-matrix, so the matrix $\operatorname{diag}(c_{x}(i), c_{y}(i))(-A)+(-A)^{\top}\operatorname{diag}(c_{x}(i), c_{y}(i))$ is positive definite [4, 24]. Then we get that

$$ \begin{aligned} LV \bigl(x(t), y(t), i \bigr)&\leq\frac{1}{2} \bigl(c_{x}(i)\eta^{2}(i)\sigma^{2}(i) +c_{y}(i)\alpha^{2}(i)\sigma^{2}(i) \bigr)-c_{x}(i)b_{x}(i)-c_{y}(i)b_{y}(i) \\ &\quad+{X^{\top}(t)} \operatorname{diag} \bigl(c_{x}(i), c_{y}(i) \bigr){B(i)}- \bigl(c_{x}(i), c_{y}(i) \bigr)AX(t)\\&\quad+\sum_{j=1}^{m} \kappa_{ij}V \bigl(x(t), y(t), j \bigr) \\ &\leq K_{1} \bigl(1+ \bigl\vert X(t) \bigr\vert \bigr)+\sum _{j=1}^{m}\kappa_{ij}V \bigl(x(t), y(t), j \bigr), \end{aligned} $$

where $K_{1}$ depends on the norm of $\operatorname{diag}(c_{x}(i), c_{y}(i))$, $B(i)$, and $\beta(i)$. Now letting $K_{2}=\frac{c_{x}(i)}{c_{x}(j)}\vee \frac{c_{y}(i)}{c_{y}(j)}$ and $K_{3}=c_{x}(i)\wedge c_{y}(i)$, for each $i, j \in\mathbb{S}$, we have

$$ \begin{aligned} V \bigl(x(t), y(t), j \bigr)&=c_{x}(j) \bigl[x(t)-1-\log x(t) \bigr]+c_{y}(j) \bigl[y(t)-1-\log y(t) \bigr] \\ &\leq K_{2} \bigl\{ c_{x}(i) \bigl[x(t)-1-\log x(t) \bigr]+c_{y}(i) \bigl[y(t)-1-\log y(t) \bigr] \bigr\} \\ &=K_{2}V \bigl(x(t), y(t), i \bigr). \end{aligned} $$

Due to the monotonicity and using the minimum value of $x(t)-2\log x(t)$, we easily get the inequality $x(t) \leq2 (x(t)-\log x(t) )$. Similarly, we can get that $y(t) \leq2 (y(t)-\log y(t) )$. So we have

$$ \begin{aligned} \bigl\vert X(t) \bigr\vert &\leq4+2 \bigl[x(t)-1- \log x(t)+y(t)-1- \log y(t) \bigr] \\ &\leq4+\frac{2}{K_{3}} \bigl[c_{x}(i) \bigl(x(t)-1-\log x(t) \bigr)+c_{y}(i) \bigl(y(t)-1-\log y(t) \bigr) \bigr] \\ &=4+\frac{2}{K_{3}}V \bigl(x(t), y(t), i \bigr). \end{aligned} $$

Hence there is a positive constant $K_{4}$ depending on $K_{1}$, $K_{2}$, $K_{3}$, and $\kappa_{ij}$ such that

$$ LV \bigl(x(t), y(t), i \bigr)\leq K_{4} \bigl(1+V \bigl(x(t), y(t), i \bigr) \bigr), $$

so, by Eq. (33), we have

$$ \begin{aligned} \mathbb{E}V \bigl(x({t\wedge\tau_{k}}), y({t\wedge\tau_{k}}), \varsigma ({t\wedge\tau_{k}}) \bigr)&\leq V \bigl(x(0), y(0), \varsigma(0) \bigr)\\&\quad+\mathbb{E} \int _{0}^{{t\wedge\tau_{k}}}K_{4} \bigl(1+V \bigl(x(s), y(s), \varsigma(s) \bigr) \bigr)\,ds \\ &\leq K_{4} \int_{0}^{t}\mathbb{E}V \bigl(x({s\wedge \tau_{k}}), y \bigl(x({s\wedge\tau _{k}}) \bigr), \varsigma \bigl(x({s\wedge\tau_{k}}) \bigr) \bigr)\,ds \\ &\quad+V \bigl(x(0), y(0), \varsigma(0) \bigr)+K_{4}T. \end{aligned} $$

Using the Gronwall inequality, we get that

$$ \mathbb{E}V \bigl(x({T\wedge\tau_{k}}), y({T\wedge \tau_{k}}), \varsigma ({T\wedge\tau_{k}}) \bigr)\leq K_{5}e^{K_{4} T}, $$

(34)

where $K_{5}=V(x(0), y(0), \varsigma(0))+K_{4}T$. For $k\geq k_{1}$, denote $\varOmega_{k}=\{\tau_{k}\leq T\}$, hence $\mathbb{P}(\varOmega_{k})\geq \varepsilon$. Then for any $\omega\in\varOmega_{k}$, there exists some $i\in\mathbb{S}$ such that $x(\tau_{k}, \omega)=\frac{1}{k}$ or $x(\tau_{k}, \omega)=k$, and $y(\tau_{k}, \omega)=\frac{1}{k}$ or $y(\tau_{k}, \omega)=k$. Due to the monotonicity of V, we have

$$ V \bigl(x(\tau_{k}), y(\tau_{k}), \varsigma( \tau_{k}) \bigr)\geq \bigl[c_{x} \bigl(\varsigma ( \tau_{k}) \bigr)+c_{y} \bigl(\varsigma( \tau_{k}) \bigr) \bigr] \biggl[(k-1-\log k)\wedge \biggl( \frac{1}{k}-1+\log k \biggr) \biggr]. $$

From (34), we deduce that

$$\begin{aligned} K_{5}e^{K_{4}T}&\geq\mathbb{E} \bigl[I_{\varOmega_{k}(\omega)}V \bigl(x(\tau _{k}), y(\tau_{k}), \varsigma( \tau_{k}) \bigr) \bigr]\\&\geq \bigl[c_{x} \bigl(\varsigma ( \tau_{k}) \bigr)+c_{y} \bigl(\varsigma( \tau_{k}) \bigr) \bigr] \biggl[(k-1-\log k)\wedge \biggl( \frac{1}{k}-1+\log k \biggr) \biggr],\end{aligned} $$

and, letting $k\rightarrow\infty$, we have $K_{5}e^{K_{4}T}\geq\infty$, which is contradiction to $K_{5}e^{K_{4}T}< \infty$. The proof is completed. □

Appendix 2: Proof of Lemma 3.3

Proof

According to model (4) and generalization of Theorem 1.1 in [25], let us consider the following SDE:

$$ \begin{aligned}[b] d\varphi(t)&=\varphi(t) \biggl[ \biggl(\frac{\bar{\theta}(\varsigma (t))}{2}+ \frac{\xi(\varsigma(t))+ \alpha(\varsigma(t))}{4} \biggr)\varphi (t)+\bar{b} \bigl(\varsigma(t) \bigr) \biggr] \,dt\\&\quad+\sigma \bigl(\varsigma(t) \bigr) \bar{\eta} \bigl(\varsigma(t) \bigr) \varphi(t) \,dw(t),\end{aligned} $$

(35)

where $\theta(\varsigma(t))\vee(-\alpha(\varsigma(t)))=\bar {\theta}(\varsigma(t))$, $b_{x}(\varsigma(t))\vee b_{y}(\varsigma (t))=\bar{b}(\varsigma(t))$, $\eta(\varsigma(t))\vee\alpha (\varsigma(t))=\bar{\eta}(\varsigma(t))$. Applying generalized Itô’s formula to $\frac{1}{\varphi(t)}$, we have

$$ \begin{aligned}[b] d\frac{1}{\varphi(t)}&= \biggl[\frac{1}{\varphi(t)} \bigl( \sigma^{2} \bigl(\varsigma(t) \bigr)\bar{\eta }^{2} \bigl( \varsigma(t) \bigr) -\bar{b} \bigl(\varsigma(t) \bigr) \bigr)- \biggl( \frac{\bar{\theta}(\varsigma(t))}{2} +\frac{\xi(\varsigma(t))+\alpha(\varsigma(t))}{4} \biggr) \biggr]\,dt \\&\quad- \frac{1}{\varphi(t)}\sigma \bigl(\varsigma(t) \bigr)\bar{\eta} \bigl(\varsigma (t) \bigr)\,dw(t).\end{aligned} $$

(36)

Letting $\frac{1}{\varphi(t)}=\psi(t)$, from Eq. (36), we can get

$$ \begin{aligned}[b] d\psi(t)&= \biggl[\psi(t) \bigl(\sigma^{2} \bigl( \varsigma(t) \bigr)\bar{\eta }^{2} \bigl(\varsigma(t) \bigr) -\bar{b} \bigl(\varsigma(t) \bigr) \bigr) - \biggl(\frac{\bar{\theta}(\varsigma(t))}{2}+ \frac{\xi(\varsigma(t)) +\alpha(\varsigma(t))}{4} \biggr) \biggr]\,dt\\&\quad -\psi(t)\sigma \bigl(\varsigma(t) \bigr) \bar{\eta} \bigl( \varsigma(t) \bigr)\,dw(t),\end{aligned} $$

(37)

and the corresponding homogeneous linear equation of (37) is

$$ d\tilde{\psi}(t)= \bigl[\tilde{\psi}(t) \bigl( \sigma^{2} \bigl(\varsigma(t) \bigr)\bar {\eta}^{2} \bigl( \varsigma(t) \bigr) -\bar{b} \bigl(\varsigma(t) \bigr) \bigr) \bigr]\,dt-\tilde{ \psi} \sigma \bigl(\varsigma(t) \bigr) \bar{\eta} \bigl(\varsigma(t) \bigr) \,dw(t). $$

(38)

Now using Itô’s formula to $\log\tilde{\psi}(t)$, we have

$$ d\log\tilde{\psi}(t)= \biggl[\frac{1}{2}\sigma^{2} \bigl( \varsigma(t) \bigr)\bar {\eta}^{2} \bigl(\varsigma(t) \bigr) -\bar{b} \bigl(\varsigma(t) \bigr) \biggr]\,dt-\sigma \bigl(\varsigma(t) \bigr)\bar{\eta } \bigl(\varsigma(t) \bigr)\,dw(t), $$

which results in

$$ \tilde{\psi}(t)=\tilde{\psi}(0)\exp \biggl\{ \int_{0}^{t} \biggl[\frac {1}{2} \sigma^{2} \bigl(\varsigma(s) \bigr)\bar{\eta}^{2} \bigl( \varsigma(s) \bigr)-\bar{b} \bigl(\varsigma (s) \bigr) \biggr]\,ds - \int_{0}^{t}\sigma \bigl(\varsigma(s) \bigr) \bar{ \eta} \bigl(\varsigma(s) \bigr)\,dw(s) \biggr\} , $$

so that we obtain the explicit solution of (37) as

$$\begin{aligned} \psi(t)&=\exp \biggl\{ \int_{0}^{t} \biggl[\frac{1}{2} \sigma^{2} \bigl(\varsigma (s) \bigr)\bar{\eta}^{2} \bigl( \varsigma(s) \bigr) -\bar{b} \bigl(\varsigma(s) \bigr) \biggr]\,ds- \int_{0}^{t}\sigma \bigl(\varsigma(s) \bigr)\bar { \eta} \bigl(\varsigma(s) \bigr)\,dw(s) \biggr\} \\ &\quad \cdot\biggl\{ \psi(0)+ \int_{0}^{t}- \biggl(\frac{\bar{\theta}(\varsigma (t))}{2}+ \frac{\xi(\varsigma(t)) +\alpha(\varsigma(t))}{4} \biggr)\\&\quad\cdot\exp \biggl[ \int_{0}^{s} \biggl[\bar{b} \bigl(\varsigma(s) \bigr) -\frac{1}{2}\sigma^{2} \bigl(\varsigma(s) \bigr)\bar{ \eta}^{2} \bigl(\varsigma (s) \bigr) \biggr]\,d\tau \\ &\quad+ \int_{0}^{s}\sigma \bigl(\varsigma(s) \bigr) \bar{ \eta} \bigl(\varsigma(s) \bigr)\, dw(\tau) \biggr]\,ds \biggr\} , \end{aligned}$$

as required. □