Regime-Switching Sunspot Equilibria in a One-Sector Growth Model with Aggregate Decreasing Returns and Small Externalities

Abstract

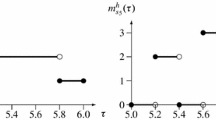
This paper shows that regime-switching sunspot equilibria easily arise in a one-sector growth model with aggregate decreasing returns and arbitrarily small externalities. We construct a regime-switching sunspot equilibrium under the assumption that the utility function of consumption is linear. We also construct a stochastic optimal growth model whose optimal process turns out to be a regime-switching sunspot equilibrium of the original economy under the assumption that there is no capital externality. We illustrate our results with numerical examples.

Appendices

Appendix A Proof of Lemma 6.3.1

Let $\{c^{*}_{t}, n^{*}_{t}, k^{*}_{t}\}_{t=0}^{\infty }$ be a feasible process satisfying (6.3.4)–(6.3.6) (with $c^{*}_{t}, n^{*}_{t}, k^{*}_{t}$ replacing $c_{t}, n_{t}, k_{t}$). To simplify notation, for $t \in \mathbb {Z}_{+}$ and $i = 1,2$ we define

$$\begin{aligned} f(t)&= f(k^{*}_{t}, n^{*}_{t}, k^{*}_{t}, n^{*}_{t}),\end{aligned}$$

(6.5.1)

$$\begin{aligned} f_{i}(t)&= f_{i}(k^{*}_{t}, n^{*}_{t}, k^{*}_{t}, n^{*}_{t}). \end{aligned}$$

(6.5.2)

We are to show that for any feasible process $\{c_{t}, n_{t}, k_{t}\}_{t=0}^{\infty }$, we have

$$\begin{aligned} E \sum _{t = 0}^{\infty } \beta ^{t} [u(c_{t}) - w(n_{t})] - E \sum _{t = 0}^{\infty } \beta ^{t} [u(c^{*}_{t}) - w(n^{*}_{t})] \leqslant 0. \end{aligned}$$

(6.5.3)

To this end, let $\{c_{t}, n_{t}, k_{t}\}_{t=0}^{\infty }$ be a feasible process. Fix $T \in \mathbb {N}_{+}$ for the moment. Let

$$\begin{aligned} \Delta _{T}&= E \sum _{t = 0}^{T} \beta ^{t} [u(c_{t}) - w(n_{t})] - E \sum _{t = 0}^{T} \beta ^{t}[ u(c^{*}_{t}) - w(n^{*}_{t})] \end{aligned}$$

(6.5.4)

$$\begin{aligned}&\leqslant E \sum _{t = 0}^{T} \beta ^{t} \{ u'(c^{*}_{t})(c_{t} - c^{*}_{t}) - w'(n^{*}_{t})(n_{t} - n^{*}_{t}) \}, \end{aligned}$$

(6.5.5)

where $u'(c^{*}_{t})$ is the right derivative of u at 0 if $c^{*}_{t} = 0$, and similarly for $w'(n^{*}_{t})$. We have

$$\begin{aligned} \nonumber \Delta _{T}&\leqslant E \sum _{t = 0}^{T} \beta ^{t} \{ u'(c^{*}_{t})[f(k_{t}, n_{t}, k^{*}_{t}, n^{*}_{t}) - f(t) \\&\qquad + \zeta (k_{t} - k^{*}_{t}) - (k_{t+1} - k^{*}_{t+1})] - w'(n^{*}_{t})(n_{t} - n^{*}_{t}) \}\end{aligned}$$

(6.5.6)

$$\begin{aligned} \nonumber&\leqslant E \sum _{t = 0}^{T} \beta ^{t} [u'(c^{*}_{t}) (f_{1}(t) + \zeta )(k_{t} - k^{*}_{t}) \\&\qquad + \{u'(c^{*}_{t}) f_{2}(t) - w'(n^{*}_{t})\} (n_{t} - n^{*}_{t}) - u'(c^{*}_{t}) (k_{t+1} - k^{*}_{t+1})]. \end{aligned}$$

(6.5.7)

Recalling the first-order condition (6.3.4) for $n_{t}$, we see that for all $t \in \mathbb {Z}_{+}$,

$$\begin{aligned} \{u'(c^{*}_{t}) f_{2}(t) - w'(n^{*}_{t})\} (n_{t} - n^{*}_{t}) \leqslant 0. \end{aligned}$$

(6.5.8)

Substituting into (6.5.7) we obtain

$$\begin{aligned} \Delta _{T}&\leqslant E \sum _{t = 0}^{T} \beta ^{t} [u'(c^{*}_{t}) (f_{1}(t) + \zeta )(k_{t} - k^{*}_{t}) - u'(c^{*}_{t}) (k_{t+1} - k^{*}_{t+1})]\end{aligned}$$

(6.5.9)

$$\begin{aligned}&= E \sum _{t = 0}^{T-1} \beta ^{t} [- u'(c^{*}_{t}) + \beta u'(c^{*}_{t+1}) (f_{1}(t+1) + \zeta )](k_{t+1} - k^{*}_{t+1}) \end{aligned}$$

(6.5.10)

$$\begin{aligned}&\qquad - \beta ^{T} E u'(c^{*}_{T})(k_{T+1} - k^{*}_{T+1}) \end{aligned}$$

(6.5.11)

$$\begin{aligned}&= E \sum _{t = 0}^{T-1} \beta ^{t} [- u'(c^{*}_{t}) + \beta E_{t} u'(c^{*}_{t+1}) (f_{1}(t+1) + \zeta )](k_{t+1} - k^{*}_{t+1}) \end{aligned}$$

(6.5.12)

$$\begin{aligned}&\qquad - \beta ^{T} E u'(c^{*}_{T})(k_{T+1} - k^{*}_{T+1}), \end{aligned}$$

(6.5.13)

where the last equality holds by the law of iterated expectations. Recalling the Euler condition (6.3.5) for $k_{t+1}$, we see that for all $t \in \mathbb {Z}_{+}$,

$$\begin{aligned}{}[- u'(c^{*}_{t}) + \beta E_{t} u'(c^{*}_{t+1}) (f_{1}(t+1) + \zeta )](k_{t+1} - k^{*}_{t+1}) \leqslant 0. \end{aligned}$$

(6.5.14)

Substituting into (6.5.13) we obtain

$$\begin{aligned} \Delta _{T}&\leqslant - \beta ^{T} E u'(c^{*}_{T})(k_{T+1} - k^{*}_{T+1}) \end{aligned}$$

(6.5.15)

$$\begin{aligned}&\leqslant \beta ^{T} E u'(c^{*}_{T}) k^{*}_{T+1} \rightarrow 0, \end{aligned}$$

(6.5.16)

where the second inequality holds since $k_{T+1} \geqslant 0$, and the convergence holds by the transversality condition (6.3.6). This completes the proof of Lemma 6.3.1.

Appendix B Proof of Proposition 6.4.1

Suppose that $\sigma = 0$. Then conditions (6.4.5) and (6.4.6) can be written as

$$\begin{aligned} s_{t} = 1 \quad&\Rightarrow \quad \rho \theta (k_{t})^{\alpha + \overline{\alpha }} (n_{t})^{\rho + \overline{\rho } -1} - \eta (n_{t})^{\gamma } {\left\{ \begin{array}{ll} = 0 &{} \text {if }n_{t} \in (0,1),\\ \geqslant 0 &{} \text {if }n_{t} = 1, \end{array}\right. } \end{aligned}$$

(6.5.17)

$$\begin{aligned} s_{t} = 0 \quad&\Rightarrow \quad n_{t} = 0. \end{aligned}$$

(6.5.18)

The Euler condition for $k_{t+1}$, (6.3.5), can be written as

$$\begin{aligned} \beta E_{t} [\alpha \theta (k_{t+1})^{\alpha + \overline{\alpha }-1}(n_{t+1})^{\rho + \overline{\rho }} + \zeta ] {\left\{ \begin{array}{ll} =1 &{} \text {if }k_{t+1} \in (0, g(k_{t}, n_{t})),\\ \geqslant 1 &{} \text {if }k_{t+1} = g(k_{t}, n_{t}),\\ \leqslant 1 &{} \text {if }k_{t+1} = 0.\end{array}\right. } \end{aligned}$$

(6.5.19)

The transversality condition (6.3.6) reduces to

$$\begin{aligned} \lim _{T \rightarrow \infty } \beta ^{T} E k_{T+1} = 0. \end{aligned}$$

(6.5.20)

Note that (6.5.17) and (6.5.18) can be combined into

$$\begin{aligned} n_{t} = m(k_{t}, s_{t}) \equiv s_{t} \min \left\{ \left[ \frac{\rho \theta }{\eta } (k_{t})^{\alpha + \overline{\alpha }} \right] ^{\frac{1}{\gamma + 1 - \rho - \overline{\rho }}} , 1 \right\} . \end{aligned}$$

(6.5.21)

Substituting into the left-hand side of (6.5.19) we obtain

$$\begin{aligned}&E_{t} [\alpha \theta (k_{t+1})^{\alpha + \overline{\alpha }-1}(n_{t+1})^{\rho + \overline{\rho }} + \zeta ]\end{aligned}$$

(6.5.22)

$$\begin{aligned}&= E_{t} [\alpha \theta (k_{t+1})^{\alpha + \overline{\alpha }-1} m(k_{t+1}, s_{t+1})^{\rho + \overline{\rho }} + \zeta ]\end{aligned}$$

(6.5.23)

$$\begin{aligned}&= {\left\{ \begin{array}{ll} p_{01} h(k_{t+1}) + \zeta &{} \text {if }s_{t} = 0,\\ p_{11} h(k_{t+1}) + \zeta &{} \text {if }s_{t} = 1, \end{array}\right. } \end{aligned}$$

(6.5.24)

where

$$\begin{aligned} h(k)&= \alpha \theta k^{\alpha + \overline{\alpha } - 1} m(k,1)^{\rho + \overline{\rho }} \end{aligned}$$

(6.5.25)

$$\begin{aligned}&= \min \left\{ \alpha \theta \left[ \frac{\rho \theta }{\eta } \right] ^{\frac{\rho + \overline{\rho }}{\gamma +1-\rho -\overline{\rho }}} k^{\frac{(\alpha + \overline{\alpha } - 1)(\gamma + 1) + \rho + \overline{\rho }}{\gamma +1-\rho - \overline{\rho }}}, \alpha \theta k^{\alpha + \overline{\alpha } - 1} \right\} . \end{aligned}$$

(6.5.26)

Both expressions in the curly brackets are strictly decreasing in k by (6.2.10) and (6.2.12) (note that $(\alpha +\overline{\alpha }-1)(\gamma +1) + \rho + \overline{\rho } < \alpha + \overline{\alpha } -1 + \rho + \overline{\rho } \leqslant 1$ by (6.2.12)). Thus $h(\cdot )$ is strictly decreasing, which implies that the inverse $h^{-1}(\cdot )$ exists. Indeed, for $z > 0$ we have

$$\begin{aligned} h^{-1}(z) = \min \left\{ \left[ \frac{z}{\alpha \theta } \left[ \frac{\eta }{\rho \theta } \right] ^{\frac{\rho + \overline{\rho }}{\gamma +1-\rho -\overline{\rho }}} \right] ^{\frac{\gamma +1-\rho - \overline{\rho }}{(\alpha + \overline{\alpha } - 1)(\gamma + 1) + \rho + \overline{\rho }}}, \left[ \frac{z}{\alpha \theta } \right] ^{\frac{1}{\alpha + \overline{\alpha } -1}} \right\} . \end{aligned}$$

(6.5.27)

Note that

$$\begin{aligned} \lim _{k \downarrow 0} h(k) = \infty . \end{aligned}$$

(6.5.28)

Substituting (6.5.22)–(6.5.24) into (6.5.19) we obtain

$$\begin{aligned} \beta [p_{s_{t}1} h(k_{t+1}) + \zeta ] {\left\{ \begin{array}{ll} =1 &{} \text {if }k_{t+1} \in (0, g(k_{t}, n_{t})), \\ \geqslant 1 &{} \text {if }k_{t+1} = g(k_{t}, n_{t}),\\ \leqslant 1 &{} \text {if }k_{t+1} = 0, \end{array}\right. } \end{aligned}$$

(6.5.29)

where $p_{s_{t}1} = p_{01}$ or $p_{11}$ depending on $s_{t} = 0$ or 1. For $p > 0$ define

$$\begin{aligned} q(p) = h^{-1} \left( \frac{1-\beta \zeta }{\beta p} \right) . \end{aligned}$$

(6.5.30)

Note from (6.5.28) that we can rule out the case $k_{t+1} = 0$ in (6.5.29). Hence we can write (6.5.29) as

$$\begin{aligned} k_{t+1} = \min \{q(p_{s_{t}1}), g(k_{t}, n_{t}) \}. \end{aligned}$$

(6.5.31)

We construct a process $\{c_{t}, n_{t}, k_{t}\}_{t=0}^{\infty }$ recursively as follows: given $k_{t} > 0$ and $s_{t} \in \{0,1\}$, let

$$\begin{aligned} n_{t} = m(k_{t}, s_{t}). \end{aligned}$$

(6.5.32)

Determine $k_{t+1}$ by (6.5.31). Let

$$\begin{aligned} c_{t} = g(k_{t}, n_{t}) - k_{t+1}. \end{aligned}$$

(6.5.33)

Draw $s_{t+1}$ according to (6.4.1). Determine $n_{t+1}$ by (6.5.32), and so on. By construction, this process is feasible and satisfies (6.5.17)–(6.5.19). It also satisfies (6.5.20) by (6.2.13). Thus it is a sunspot equilibrium. The conclusion of the proposition now follows.

C Proof of Proposition 6.4.2

Suppose that $\overline{\alpha } = 0$. Consider the stochastic optimal growth model (6.4.17)–(6.4.19). The Euler condition for $k_{t+1}$ is written as

$$\begin{aligned} \nonumber&-u'(c_{t}) + \beta E_{t} u'(c_{t+1}) [s_{t+1} \alpha \theta (k_{t+1})^{\alpha - 1}(n_{t+1})^{\rho + \overline{\rho }} + \zeta ] \\&\quad {\left\{ \begin{array}{ll} = 0 &{} \text {if }k_{t+1} \in (0, g(k_{t}, n_{t})),\\ \geqslant &{} \text {if }k_{t+1} = g(k_{t}, n_{t}),\\ \leqslant &{} \text {if }k_{t+1} = 0. \end{array}\right. } \end{aligned}$$

(6.5.34)

This is equivalent to the equilibrium Euler condition (6.3.5) for $k_{t+1}$ for the original economy (6.2.1)–(6.2.3) with $\overline{\alpha } = 0$ and (6.4.3). The first-order condition for $n_{t}$ for the above stochastic optimal growth model is given by

$$\begin{aligned} u'(c_{t}) s_{t} (\rho + \overline{\rho }) \theta (k_{t})^{\alpha } (n_{t})^{\rho + \overline{\rho } - 1} - \frac{\rho + \overline{\rho }}{\rho } w'(n_{t}) {\left\{ \begin{array}{ll} = 0 &{} \text {if }n_{t} \in (0,1),\\ \geqslant 0 &{} \text {if }n_{t} = 1, \\ \leqslant 0 &{} \text {if }n_{t} = 0, \end{array}\right. } \end{aligned}$$

(6.5.35)

which simplifies to

$$\begin{aligned} u'(c_{t}) s_{t} \rho \theta (k_{t})^{\alpha } (n_{t})^{\rho + \overline{\rho } - 1} - w'(n_{t}) {\left\{ \begin{array}{ll} = 0 &{} \text {if }n_{t} \in (0,1),\\ \geqslant 0 &{} \text {if }n_{t} = 1,\\ \leqslant 0 &{} \text {if }n_{t} = 0. \end{array}\right. } \end{aligned}$$

(6.5.36)

This is equivalent to (6.3.4) with $\overline{\alpha } = 0$ and (6.4.3). The transversality condition for the above problem is identical to (6.3.6).

Conditions (6.5.34) and (6.5.36) are necessary for optimality by standard arguments. The transversality condition (6.3.6) is also necessary by the argument of Kamihigashi (2005, Sect. 6).⁵ Given that the sunspot variable $s_{t}$ is discrete, we can easily establish the existence of an optimal process for the optimal stochastic growth model (6.4.17)–(6.4.19) by a standard argument (e.g., Ekeland and Scheinkman 1986). Let $\{c_{t}, n_{t}, k_{t}\}_{t=0}^{\infty }$ be an optimal process for (6.4.17)–(6.4.19). Then by the above argument, the process satisfies (6.3.4)–(6.3.6). Thus by Lemma 6.3.1, the process is an equilibrium of the original economy (6.2.1)–(6.2.3). Since it depends on $s_{t}$ in a nontrivial way, it is a sunspot equilibrium.