1 Introduction

Due to the important role that the time-varying Lyapunov equation plays in a broad spectrum of areas, there has been a rapid increase in its algorithm design, and many numerical methods and neural dynamics have been proposed to solve this problem and its time-invariant version; see, e.g., [1–6] on this subject. Let \(t_{\mathrm{0}}\in \mathbb{R}\) and \(t_{\mathrm{f}}\in \mathbb{R}\) denote the start and the final time instant of the solving process, respectively. The time-varying Lyapunov equation can be expressed as

$$ A(t)^{\top }X+XA(t)=B(t),\quad t\in [t_{\mathrm{0}},t_{\mathrm{f}}],$$
(1)

where \(A(t)\in \mathbb{R}^{n\times n}\) and \(B(t)\in \mathbb{R}^{n\times n}\) are smoothly time-variant matrix signals, and \(X\in \mathbb{R}^{n\times n}\) is the unknown matrix to be determined. In this paper, we are going to compute the online solution of problem (1) in real time, and the solution set of (1) is assumed to be nonempty throughout our discussions in this paper.

Since the seminal paper written by Hopfield [7], neural networks, especially recurrent neural networks, have been widely utilized to solve various time-invariant and time-varying problems. As an important subtopic of recurrent neural network, the Zhang neural network (ZNN) was firstly proposed by Zhang Yunong on March 2001 [1]. In recent years, ZNN has been generally deemed as a benchmark solver for various dynamics systems appeared in practice, such as the robots’ kinematic control, the pendulum system [8], the synchronization of chaotic sensor systems [9]. Based on a simple ordinary differential equation (ODE), i.e., the test problem to analyze the stability property of a numerical method for initial value problem, for the ZNN every component of an indefinite error function directly exponentially tends to zero, which endows ZNN with the ability to track the time-dependent solution of time-varying problems in an error-free manner. The ZNN has been intensively studied in the literature with its increasingly applications, and many more efficient variants of ZNN have been presented. For example, for potential digital hardware realization, several multi-step discrete-time ZNNs have been designed in [10–13]. To accelerate the convergence speed of the ZNN, a super-exponential ZNN with time-varying design parameter is proposed by Chen et al. [9]. Moreover, based on some deliberated designed activation functions, many continuous-time ZNNs with finite-time convergence property have been presented [14, 15].

Though the above ZNNs have received remarkable progress in various time-varying or future problem solving, they are sensitive to noise and prone to generating large error in a noiseless environment. However, noise is ubiquitous in real life, which cannot be ignored completely. For example, in the background extraction from surveillance video with missing and noisy data [16, 17], the observed data are often contaminated with additive Gaussian noise. The ZNN with anti-noise property has drawn increasing attention from researchers in recent years. To the best or our knowledge, Jin et al. [18] firstly designed an integration-enhanced ZNN formula to solve for real time-varying matrix inversion with additive constant noise. Then, Guo et al. [19] proposed a modified ZNN formula to solve a time-varying nonlinear equation with additive harmonic noise, whose convergence is analyzed based on an ingenious Lyapunov function. To analyze time-dependent matrix inversion with dynamic bounded gradually disappearing noise or dynamic bounded non-disappearing noise, a new noise-tolerant and predefined-time ZNN model is presented by Xiao et al. [20], in which the sign function plays an important role in proving its convergence and robustness.

However, the above three noise-tolerate ZNNs [18–20] all fail to deal with time-varying linear noise, which is unbounded and differs from the noise considered in the previous studies [18–20]. Thus there is much room for those papers to be improved. In this paper, based on a novel design formula, we are going to design a noise-tolerate continuous-time ZNN (termed NTCTZNN) to solve the time-varying Lyapunov equation which is contaminated with linear noise. The new ZNN is immune to linear noise and can counter its negative compact completely. Moreover, for potential digital hardware realization, the discrete-time version of NTCTZNN model is proposed on the basis of the Euler forward difference. A theoretical analysis of the proposed NTCTZNN and its discrete version is also discussed in detail.

In a nutshell, the contributions of this paper can be summarized as follows.

  • A novel noise-tolerant continuous-time Zhang neural network (termed NTCTZNN) with double integrals is proposed for solving the time-varying linear equations.

  • The proposed ZNN model is guaranteed to converge to the solution of the time-varying linear equations without noise or with constant noise or with time-varying linear noise.

  • A discrete-time version of the NTCTZNN model is proposed based on the Euler forward difference.

  • Numerical results including comparisons are presented to verify the obtained theoretical results.

The remainder of this paper is organized as follows. In Sect. 2, a novel noise-tolerant continuous-time ZNN (termed NTCTZNN) model is designed for the time-varying Lyapunov equation, and its convergence results are rigorously discussed. Section 3 describes the discrete version of the NTCTZNN (termed NTDTZNN), and proves its global convergence. Section 4 presents some numerical results to verify the efficiency of the NTCTZNN and the NTDTZNN. Finally, Sect. 5 concludes the paper with future research directions.

2 NTCTZNN model and its convergence

In this section, we shall design a novel noise-tolerant continuous-time Zhang neural network (NTCTZNN) for the time-varying Lyapunov equation and prove its convergence.

Firstly, let us review the noise-tolerant ZNN model with integral designed by Jin et al. [18]:

$$ \dot{e}(t)=-\gamma e(t)-\lambda \int _{0}^{t}e(\tau )\,d\tau ,$$
(2)

where \(\gamma >0\) and \(\lambda >0\) are two designed parameters. Setting \(e(t)=A(t)^{\top }X+XA(t)-B(t)\) in (2), we get a noise-tolerant continuous-time ZNN model for time-varying Lyapunov equation as follows:

$$\begin{aligned}& A(t)^{\top }\dot{X}(t)+\dot{X}(t)A(t) \\& \quad =-\gamma \bigl(A(t)^{\top }X(t)+X(t)A(t)-B(t) \bigr)-\lambda \int _{0}^{t} \bigl(A(\tau )^{\top }X( \tau )+X(\tau )A(\tau )-B(\tau ) \bigr)\,d\tau \\& \qquad {}- \bigl(\dot{A}(t)^{\top }X(t)+X(t)\dot{A}(t)-\dot{B}(t) \bigr)+ n(t), \end{aligned}$$
(3)

where \(n(t)\in \mathbb{R}^{n\times n}\) denotes an unknown additive noise. The noise-tolerant ZNN model (3) has the following convergence property.

Lemma 2.1

The noise-tolerant ZNN model (3) converges to a theoretical solution of problem (1) globally, no matter how large the unknown matrix-form constant noise is. In addition, it converges towards a theoretical solution of problem (1) with the upper bound of the limit of the steady-state residual error being\(\|a\|/\lambda \)in the presence of the unknown matrix-form time-varying linear noise, where\(n(t)=at\in \mathbb{R}^{n\times n}\)is a constant nose.

Proof

See Theorems 1–3 in [18]. □

To further improve the efficiency of noise-tolerant continuous-time ZNN model (3), we present a novel design formula with double integrals as follows:

$$ \dot{e}(t)=-\gamma e(t)-\lambda \int _{0}^{t}e(\tau )\,d\tau -\mu \int _{0}^{t}du \int _{0}^{u}e(v)\,dv.$$
(4)

Setting \(e(t)=A(t)^{\top }X+XA(t)-B(t)\) in the design formula (4), we get a new noise-tolerant continuous-time ZNN model for a time-varying Lyapunov equation:

$$\begin{aligned}& A(t)^{\top }\dot{X}(t)+\dot{X}(t)A(t) \\& \quad =-\gamma \bigl(A(t)^{\top }X(t)+X(t)A(t)-B(t) \bigr)-\lambda \int _{0}^{t} \bigl(A(\tau )^{\top }X( \tau )+X(\tau )A(\tau )-B(\tau ) \bigr)\,d\tau \\& \qquad {}-\mu \int _{0}^{t}du \int _{0}^{u} \bigl(A(v)^{\top }X(v)+X(v)A(v)-B(v) \bigr)\,dv \\& \qquad {} - \bigl(\dot{A}(t)^{\top }X(t)+X(t)\dot{A}(t)- \dot{B}(t) \bigr)+ n(t). \end{aligned}$$
(5)

Setting

$$ X_{2}(u)= \int _{0}^{u}\bigl(A(v)^{\top }X(v)+X(v)A(v)-B(v) \bigr)\,dv,\qquad X_{1}(t)= \int _{0}^{t}X_{2}(u)\,du, $$

the integral and differential equation (5) can be written as the following system of differential equations:

$$ \textstyle\begin{cases} \dot{X}_{1}(t)=X_{2}(t), \\ \dot{X}_{2}(t)=A(t)^{\top }X(t)+X(t)A(t)-B(t), \\ A(t)^{\top }\dot{X}(t)+\dot{X}(t)A(t)=-\gamma (A(t)^{\top }X(t)+X(t)A(t)-B(t) )-\lambda X_{2}(t) - \mu X_{1}(t) \\ \hphantom{A(t)^{\top }\dot{X}(t)+\dot{X}(t)A(t)=}{}- (\dot{A}(t)^{\top }X(t)+X(t) \dot{A}(t)-\dot{B}(t) )+ n(t). \end{cases} $$

In a practical computation, we need to transform the above system of differential equations in matrix form to that in vector form. Based on the Kronecker product ⊗ and the vec-operator vec, we get the NTCTZNN in vector form:

$$ \textstyle\begin{cases} \operatorname{vec}(\dot{X}_{1}(t))=\operatorname{vec}(X_{2}(t)), \\ \operatorname{vec}(\dot{X}_{2}(t))=\operatorname{vec}(A(t)^{\top }X(t)+X(t)A(t)-B(t)), \\ (I_{n}\otimes A(t)^{\top }+A(t)^{\top }\otimes I_{n} )\operatorname{vec}( \dot{X}(t))\\ \quad =\operatorname{vec} (-\gamma (A(t)^{\top }X(t)+X(t)A(t)-B(t) )-\lambda X_{2}(t) \\ \qquad {}- \mu X_{1}(t)- ( \dot{A}(t)^{\top }X(t)+X(t)\dot{A}(t)-\dot{B}(t) )+ n(t) ). \end{cases} $$

The design formula (4) can be utilized to solve the time-varying linear matrix equation and the time-varying Sylvester equation.

  1. (1)

    Consider the time-varying linear matrix equation

    $$ A(t)X=B(t), $$

    where \(A(t)\in \mathbb{R}^{m\times n}\), \(B(t)\in \mathbb{R}^{m\times p}\). Applying the design formula (4) to solve the above time-varying linear matrix equation, we have

    $$\begin{aligned}& \hat{A}(t)\operatorname{vec}\bigl(\dot{X}(t)\bigr) \\& \quad =-\gamma \bigl(\hat{A}(t)\operatorname{vec}(X)-\operatorname{vec} \bigl(B(t)\bigr) \bigr)- \lambda \int _{0}^{t} \bigl(\hat{A}(\tau ) \operatorname{vec}\bigl(X(\tau )\bigr)-\operatorname{vec}\bigl(B( \tau )\bigr) \bigr)\,d\tau \\& \qquad{} -\mu \int _{0}^{t}du \int _{0}^{u} \bigl(\hat{A}(v)\operatorname{vec} \bigl(X(v)\bigr)- \operatorname{vec}\bigl(B(v)\bigr) \bigr)\,dv- \bigl( \dot{\hat{A}}(t)\operatorname{vec}\bigl(X(v)\bigr) \\& \qquad {}-\operatorname{vec}\bigl( \dot{B}(t)\bigr) \bigr)+\operatorname{vec}\bigl( n(t)\bigr), \end{aligned}$$
    (6)

    where \(\hat{A}(t)=I_{p}\otimes A(t)\).

  2. (2)

    Consider the time-varying Sylvester equation

    $$ A_{1}(t)X+XA_{2}(t)=B(t), $$

    where \(A_{1}(t)\in \mathbb{R}^{m\times m}\), \(A_{2}(t)\in \mathbb{R}^{n\times n}\) and \(B(t)\in \mathbb{R}^{m\times n}\). Applying the design formula (4) to solve the time-varying Sylvester equation, we have

    $$\begin{aligned}& \hat{A}(t)\operatorname{vec}\bigl(\dot{X}(t)\bigr) \\& \quad =\operatorname{vec} \biggl(-\gamma \bigl(A(t)^{\top }X(t)+X(t)A(t)-B(t) \bigr) \\& \qquad {}- \lambda \int _{0}^{t} \bigl(A(\tau )^{\top }X( \tau )+X(\tau )A(\tau )-B(\tau ) \bigr)\,d\tau \\& \qquad {}-\mu \int _{0}^{t}du \int _{0}^{u} \bigl(A(v)^{\top }X(v)+X(v)A(v)-B(v) \bigr)\,dv \\& \qquad {}- \bigl(\dot{A}(t)^{\top }X(t)+X(t)\dot{A}(t)- \dot{B}(t) \bigr)+ n(t) \biggr), \end{aligned}$$
    (7)

    where \(\hat{A}(t)=I_{n}\otimes A_{1}(t)+A_{2}(t)^{\top }\otimes I_{m}\).

Assumption 2.1

To ensure the convergence property of the residual error\(\|e(t)\|\)generated by the NTCTZNN (5), the designed parametersγ, λandμare restricted to satisfy\(\gamma >0\), \(\lambda >0\), \(\mu >0\)and all the roots of the polynomial

$$ s^{3}+\gamma s^{2}+\lambda s+\mu =0,$$
(8)

are in the left half plane.

Remark 2.1

If we set \(\gamma =3\), \(\lambda =2\), \(\mu =1\), three roots of (8) are \(-0.7849 + 1.3071\mathrm{i}\), \(-0.7849 - 1.3071\mathrm{i}\), −0.4302. So Assumption 2.1 holds with \(\gamma =3\), \(\lambda =2\), \(\mu =1\).

According to a different type of the noise \(n(t)\), we divide the proof of the convergence of NTCTZNN (5) into the following four cases.

Case 1: If the unknown noise \(n(t)=0\in \mathbb{R}^{n\times n}\), we have the following convergence result.

Theorem 2.1

When\(n(t)=0\)andγ, λsatisfy the condition (8), the residual error\(\|e(t)\|\)generated by NTCTZNN (5) globally and exponentially converges to zero.

Proof

Set

$$ \varepsilon (t)= \int _{0}^{t}du \int _{0}^{u}e(v)\,dv $$

and let \(e_{ij}(t)\), \(\varepsilon _{ij}(t)\), \(\dot{\varepsilon }_{ij}(t)\), \(\ddot{\varepsilon }_{ij}(t)\) and \(\dddot{\varepsilon }_{ij}(t)\) be the ijth element of \(e(t)\), \(\varepsilon (t)\), \(\dot{\varepsilon }(t)\), \(\ddot{\varepsilon }(t)\) and \(\dddot{\varepsilon }(t)\), respectively. Then the ijth subsystem of the dynamical system (6) can be written as

$$ \dddot{\varepsilon }(t)+\gamma \ddot{\varepsilon }(t)+\lambda \dot{\varepsilon }(t)+\mu \varepsilon (t)=0,$$
(9)

whose characteristic equation is

$$ s^{3}+\gamma s^{2}+\lambda s+\mu =0.$$
(10)

The discriminant of the cubic equation (10) is defined as

$$ \Delta =3\bigl(4\lambda ^{3} - \lambda ^{2}\gamma ^{2} - 18\lambda \mu \gamma + 27\mu ^{2} + 4\mu \gamma ^{3}\bigr). $$

According to the Fan equations [21], if \(\gamma ^{2}=3\lambda \), \(\gamma \lambda =9\mu \), Eq. (10) has a real triple root, denoted by \(s_{1}\), which is a negative constant due to Assumption 2.1. So the general solution of the third-order ordinary differential equation (9) is

$$ \varepsilon _{ij}(t)=\bigl(c_{1ij}+c_{2ij}t+c_{3ij}t^{2} \bigr)\exp (s_{1}t),\quad \forall i,j=1,2,\ldots ,n, $$

where \(c_{1ij}\), \(c_{2ij}\), \(c_{3ij}\) are three constants determined by the initial conditions. Then, differentiating the above equation twice, we have

$$ e_{ij}(t)=\bigl[c_{1ij}s_{1}^{2}+(2+s_{1}t)c_{2ij}s_{1}+ \bigl(2+4ts_{1}+t^{2}s_{1}^{2} \bigr)c_{3ij}\bigr] \exp (s_{1}t). $$

The matrix form error \(e(t)\) is

$$ e(t)=\bigl[s_{1}^{2} c_{1}+(2+s_{1}t)s_{1} c_{2}+\bigl(2+4ts_{1}+t^{2}s_{1}^{2} \bigr)c_{3}\bigr] \exp (s_{1}t), $$

where \(c_{1}=(c_{1ij})\in \mathbb{R}^{n\times n}\), \(c_{2}=(c_{2ij})\in \mathbb{R}^{n\times n}\), \(c_{3}=(c_{3ij})\in \mathbb{R}^{n\times n}\). Then

$$ \bigl\Vert e(t) \bigr\Vert \leq \bigl[s_{1}^{2} \Vert c_{1} \Vert + \bigl\vert (2+s_{1}t)s_{1} \bigr\vert \Vert c_{2} \Vert + \bigl\vert 2+4ts_{1}+t^{2}s_{1}^{2} \bigr\vert \Vert c_{3} \Vert \bigr]\exp (s_{1}t). $$

The conclusion of this theorem holds from the above inequality and \(s_{1}<0\).

If \(\Delta >0\), Eq. (10) has a real root and two complex conjugate roots, denoted by

$$ s_{1},\qquad s_{2}=\alpha +\beta \mathrm{i},\qquad s_{3}=\alpha -\beta\mathrm{i}, $$

where \(\mathrm{i}=\sqrt{-1}\) denotes the imaginary unit. Since γ, λ and μ satisfy Assumption 2.1, we have \(s_{1}<0\), \(\alpha <0\). From the above analysis, the general solution of the third-order ordinary differential equation (9) is

$$ \varepsilon _{ij}(t)=c_{1ij}\exp (s_{1}t)+ \exp (\alpha t) \bigl(c_{2ij} \cos (\beta t)+c_{3ij}\sin ( \beta t)\bigr), $$

where \(c_{1ij}\), \(c_{2ij}\), \(c_{3ij}\) are three constants determined by the initial conditions. Then, differentiating the above equation twice, we have

$$ e_{ij}(t)=c_{1ij}z_{1}^{2}\exp (s_{1}t)+\bigl(\alpha ^{2}-\beta ^{2} \bigr)\exp ( \alpha t) \bigl(c_{2ij}\cos (\beta t)+c_{3ij} \sin (\beta t)\bigr). $$

The matrix form error \(e(t)\) is

$$ e(t)=c_{1}z_{1}^{2}\exp (s_{1}t)+\bigl(\alpha ^{2}-\beta ^{2} \bigr)\exp ( \alpha t) \bigl(c_{2}\cos (\beta t)+c_{3} \sin (\beta t)\bigr), $$

where \(c_{1}=(c_{1ij})\in \mathbb{R}^{n\times n}\), \(c_{2}=(c_{2ij})\in \mathbb{R}^{n\times n}\), \(c_{3}=(c_{3ij})\in \mathbb{R}^{n\times n}\). Then

$$ \bigl\Vert e(t) \bigr\Vert \leq \Vert c_{1} \Vert z_{1}^{2}\exp (s_{1}t)+ \bigl\vert \alpha ^{2}-\beta ^{2} \bigr\vert \bigl( \Vert c_{2} \Vert + \Vert c_{3} \Vert \bigr)\exp (\alpha t). $$

The conclusion of this theorem holds from the above inequality and \(s_{1}<0\) and \(\alpha <0\).

If \(\Delta =0\), Eq. (10) has a multiple root and all of its roots are real, denoted by \(s_{1}\), \(s_{2}=s_{3}\). The general solution of third-order ordinary differential equation (9) is

$$ \varepsilon _{ij}(t)=c_{1ij}\exp (s_{1}t)+(c_{2ij}+c_{3ij}t) \exp (s_{2}t),\quad \forall i,j=1,2,\ldots ,n, $$

where \(c_{1ij}\), \(c_{2ij}\), \(c_{3ij}\) are three constants determined by the initial conditions. Then, differentiating the above equation twice, we have

$$ e_{ij}(t)=c_{1ij}s_{1}^{2}\exp (s_{1}t)+\bigl[c_{3ij}+2c_{3ij}s_{2}+(c_{2ij}+c_{3ij}t)s_{2}^{2} \bigr] \exp (s_{2}t). $$

The matrix form error \(e(t)\) is

$$ e(t)=s_{1}^{2} c_{1}\exp (s_{1}t)+\bigl[c_{3}+2s_{2}c_{3}+(c_{2}+c_{3}t)s_{2}^{2} \bigr] \exp (s_{2}t), $$

where \(c_{1}=(c_{1ij})\in \mathbb{R}^{n\times n}\), \(c_{2}=(c_{2ij})\in \mathbb{R}^{n\times n}\), \(c_{3}=(c_{3ij})\in \mathbb{R}^{n\times n}\). Then

$$ \bigl\Vert e(t) \bigr\Vert \leq [s_{1}^{2} \Vert c_{1} \Vert \exp (s_{1}t)+\bigl[ \Vert c_{3} \Vert +2 \vert s_{2} \vert \Vert c_{3} \Vert +\bigl( \Vert c_{2} \Vert + \|c_{3}t\bigr)\|s_{2}^{2}\bigr]\exp (s_{2}t). $$

The conclusion of this theorem holds from the above inequality and \(s_{1}<0\) and \(s_{2}<0\).

If \(\Delta <0\), Eq. (10) has three distinct real roots, denoted by \(s_{1}\), \(s_{2}\), \(s_{3}\). The general solution of third-order ordinary differential equation (9) is

$$ \varepsilon _{ij}(t)=c_{1ij}\exp (s_{1}t)+c_{2ij} \exp (s_{2}t)+c_{3ij}t \exp (s_{3}t), \quad \forall i,j=1,2,\ldots ,n, $$

where \(c_{1ij}\), \(c_{2ij}\), \(c_{3ij}\) are three constants determined by the initial conditions. Then, differentiating the above equation twice, we have

$$ e_{ij}(t)=c_{1ij}s_{1}^{2}\exp (s_{1}t)+c_{2ij}\exp (s_{2}t)+c_{3ij} \exp (s_{3}t). $$

The matrix form error \(e(t)\) is

$$ e(t)=s_{1}^{2} c_{1}\exp (s_{1}t)+s_{2}^{2} c_{2}\exp (s_{2}t)+s_{3}^{2} c_{3}\exp (s_{3}t), $$

where \(c_{1}=(c_{1ij})\in \mathbb{R}^{n\times n}\), \(c_{2}=(c_{2ij})\in \mathbb{R}^{n\times n}\), \(c_{3}=(c_{3ij})\in \mathbb{R}^{n\times n}\). Then

$$ \bigl\Vert e(t) \bigr\Vert \leq s_{1}^{2} \Vert c_{1} \Vert \exp (s_{1}t)+s_{2}^{2} \Vert c_{2} \Vert \exp (s_{2}t)+s_{3}^{2} \Vert c_{3} \Vert \exp (s_{3}t). $$

The conclusion of this theorem holds from the above inequality and \(s_{1}<0\), \(s_{2}<0\) and \(s_{3}<0\). □

Case 2: If the unknown noise \(n(t)\) is a constant noise \(n(t)=a\in \mathbb{R}^{n\times n}\), we have the following convergence result.

Theorem 2.2

No matter how large the unknown constant noise\(n(t)=(a_{ij})\in \mathbb{R}^{n\times n}\)is, the residual error\(\|e(t)\|\)generated by NTCTZNN (5) for problem (1) converges to zero.

Proof

Obviously, the NTCTZNN (5) can be decoupled into \(n^{2}\) differential equations:

$$ \dot{e}_{ij}(t)=-\gamma e_{ij}(t)- \lambda \int _{0}^{t}e_{ij}(\tau )\,d \tau - \mu \int _{0}^{t}du \int _{0}^{u}e_{ij}(v) \,dv+a_{ij}.$$
(11)

Taking the Laplace transformation on both sides of (11), one has

$$ s\varepsilon _{ij}(s)-e_{ij}(0)=-\gamma \varepsilon _{ij}(s)- \frac{\lambda }{s}\varepsilon _{ij}(s)-\frac{\mu }{s^{2}}\varepsilon _{ij}(s)+ \frac{a_{ij}}{s},$$
(12)

where \(\varepsilon _{ij}(t)\) is the image function of \(e_{ij}(t)\). From (12), we have

$$ \varepsilon _{ij}(s)= \frac{e_{ij}(0)s^{2}+a_{ij}s}{s^{3}+\gamma s^{2}+\lambda s+\mu }. $$

Three poles of its transfer function are \(s_{1}\), \(s_{2}\) and \(s_{3}\), which are located on the left half-plane because γ, λ and μ satisfy Assumption 2.1. Thus the system (12) is stable and the final value theorem holds. That is,

$$ \lim_{t\rightarrow \infty }e_{ij}(t)=\lim_{s\rightarrow 0}s \varepsilon _{ij}(s)=\lim_{s\rightarrow 0} \frac{e_{ij}(0)s^{3}+ n_{ij}s^{2}}{s^{3}+\gamma s^{2}+\lambda s+\mu }=0. $$

This completes the proof. □

Case 3: If the unknown noise \(n(t)\) is a time-varying linear noise \(n(t)=at+b\in \mathbb{R}^{n\times n}\), we have the following convergence result.

Theorem 2.3

No matter how large the unknown linear noise\(\bar{ n}=at+b=(a_{ij}t+b_{ij})\in \mathbb{R}^{n\times n}\)is, the residual error\(\|e(t)\|\)generated by NTCTZNN (5) for problem (1) converges to zero.

Proof

Similar to the proof of Theorem 2.3, we have

$$ \lim_{t\rightarrow \infty }e_{ij}(t)=\lim_{s\rightarrow 0}s \varepsilon _{ij}(s)=\lim_{s\rightarrow 0} \frac{e_{ij}(0)s^{3}+b_{ij}s^{2}+a_{ij}s}{s^{3}+\gamma s^{2}+\lambda s+\mu }=0. $$

This completes the proof. □

Case 4: If the unknown noise \(n(t)\) is a time-varying quadratic noise \(n(t)=at^{2}+bt+c\in \mathbb{R}^{n\times n}\), we have the following convergence result.

Theorem 2.4

For the unknown quadratic noise\(\bar{ n}=at^{2}+bt+c=(a_{ij}t^{2}+b_{ij}t+c_{ij})\in \mathbb{R}^{n \times n}\), we have

$$ \lim_{t\rightarrow \infty } \bigl\Vert e(t) \bigr\Vert = \frac{2 \Vert a \Vert }{\mu }. $$

Proof

Similar to the proof of Theorem 2.3, we have

$$ \lim_{t\rightarrow \infty }e_{ij}(t)=\lim_{s\rightarrow 0}s \varepsilon _{ij}(s)=\lim_{s\rightarrow 0} \frac{e_{ij}(0)s^{3}+c_{ij}s^{2}+b_{ij}s+2a_{ij}}{s^{3}+\gamma s^{2}+\lambda s+\mu }= \frac{2a_{ij}}{\mu }. $$

This completes the proof. □

3 NTDTZNN and its convergence

For potential digital hardware realization, we shall present a noise-tolerant discrete-time ZNN (NTDTZNN) model for problem (1) and prove its global convergence.

We use the Euler forward difference to discretize the term \(\dot{X}(t)\) in NTCTZNN (5) and get the following NTDTZNN model:

$$\begin{aligned}& A_{k}^{\top }{X}_{k+1}+{X}_{k+1}A_{k} \\& \quad =A_{k}^{\top }{X}_{k}+{X}_{k}A_{k}- \gamma \tau e_{k}-\lambda \tau \sum_{j=1}^{k}e_{j}- \mu \tau \sum_{j=1}^{k}\sum _{i=1}^{j}e_{i} \\& \qquad{}-\tau \bigl( \dot{A}_{k}^{\top }X_{k}+X_{k} \dot{A}_{k}- \dot{B}_{k} \bigr)+\tau n_{k}, \end{aligned}$$
(13)

where \(\tau >0\) is the sampling gap.

Lemma 3.1

NTDTZNN (13) can be written as

$$ e_{k+1}+(\gamma \tau -1)e_{k}+\lambda \tau \sum_{j=1}^{k}e_{j}+ \mu \tau \sum_{j=1}^{k}\sum _{i=1}^{j}e_{i}-\tau n_{k}+ \mathcal{O}\bigl(\tau ^{2}\bigr)=0.$$
(14)

Proof

From (13), we have

$$\begin{aligned} &-\gamma \tau e_{k}-\lambda \tau \sum_{j=1}^{k}e_{j}- \mu \tau \sum_{j=1}^{k}\sum _{i=1}^{j}e_{i} \\ &\quad =A_{k}^{\top }({X}_{k+1}-X_{k})+({X}_{k+1}-X_{k})A_{k}+ \tau \bigl( \dot{A}_{k}^{\top }X_{k}+X_{k} \dot{A}_{k}-\dot{B}_{k} \bigr)-\tau n_{k} \\ &\quad =\tau \bigl(A_{k}^{\top }\dot{X}_{k}+ \dot{X}_{k}A_{k}\bigr)+\tau \bigl(\dot{A}_{k}^{\top }X_{k}+X_{k} \dot{A}_{k}-\dot{B}_{k} \bigr)-\tau n_{k}+ \mathcal{O}\bigl( \tau ^{2}\bigr) \\ &\quad =\tau \dot{e}_{k}-\tau n_{k}+\mathcal{O}\bigl( \tau ^{2}\bigr) \\ &\quad =e_{k+1}-e_{k}-\tau n_{k}+ \mathcal{O}\bigl(\tau ^{2}\bigr), \end{aligned}$$

in which the second and the fourth equalities follows from the Euler forward difference. Then the above equality can be easily further written as (14). This completes the proof. □

Theorem 3.1

Considering the linear noise\(n_{k}=ak+b\in \mathbb{R}^{n\times n}\), the limit of the residual error\(\|e_{k}\|\)generated by NTDTCNN (13) is\(O(h^{2})\)if and only if the parametersγ, λandτsatisfy

$$ \begin{aligned} &\mu \tau >0,\qquad \mu \tau + 4\gamma \tau + 2\lambda \tau < 8,\quad (\gamma \tau - 1)^{2}< 1, \\ &\bigl((\lambda + 2\gamma )\tau + (\gamma \tau - 1) \bigl((\lambda + \mu + \gamma )\tau - 3\bigr) - 3\bigr)^{2}< \bigl((\gamma \tau - 1)^{2} - 1\bigr)^{2}. \end{aligned} $$
(15)

Proof

Obviously, equality (14) also holds for k, that is,

$$ e_{k}+(\gamma \tau -1)e_{k-1}+\lambda \tau \sum_{j=1}^{k-1}e_{j}+ \mu \tau \sum_{j=1}^{k-1}\sum _{i=1}^{j}e_{i}-\tau n_{k-1}+ \mathcal{O}\bigl(\tau ^{2}\bigr)=0.$$
(16)

From (14)–(16), we can get

$$ e_{k+1}+\bigl((\gamma +\lambda )\tau -2 \bigr)e_{k}-(\gamma \tau -1)e_{k-1}+\mu \tau \sum _{i=1}^{k}e_{i}-ah+\mathcal{O}\bigl( \tau ^{2}\bigr)=0.$$
(17)

Similarly, equality (17) also holds for k, that is,

$$ e_{k}+\bigl((\gamma +\lambda ) \tau -2 \bigr)e_{k-1}-(\gamma \tau -1)e_{k-2}+ \mu \tau \sum _{i=1}^{k-1}e_{i}-a\tau + \mathcal{O}\bigl(\tau ^{2}\bigr)=0.$$
(18)

From (17)–(18), we thus have

$$ e_{k+1}+ \bigl((\gamma +\lambda +\mu )\tau -3 \bigr)e_{k}+\bigl(3-(2\gamma + \lambda ) \tau \bigr)e_{k-1}+( \gamma \tau -1)e_{k-2}+\mathcal{O}\bigl(\tau ^{2} \bigr)=0.$$
(19)

Setting \(\bar{e}_{k}=e_{k}-\mathcal{O}(\tau ^{2})\), equality (19) can rewritten as

$$ \bar{e}_{k+1}+ \bigl((\gamma +\lambda +\mu )\tau -3 \bigr)\bar{e}_{k}+\bigl(3-(2 \gamma +\lambda )\tau \bigr) \bar{e}_{k-1}+(\gamma \tau -1)\bar{e}_{k-2}=0.$$
(20)

The characteristic equation of (20) is

$$ v^{3}+ \bigl((\gamma +\lambda +\mu )\tau -3 \bigr)v^{2}+\bigl(3-(2\gamma + \lambda )\tau \bigr)v+\gamma \tau -1=0.$$
(21)

If all of the characteristic-equation roots’ moduli in (21) are less than 1, the NTDTZNN (13) is stable. According to the Jury stability criterion [22], it is easy to deduce that the roots of characteristic equation (21) is inside the unit circle if and only if the four inequalities in (15) hold. The proof is completed. □

Remark 3.1

If we set \(\gamma =5\), \(\lambda =2\), \(\mu =1\) and \(\tau =0.1\), it is easy to check that the four inequalities in (15) hold. If we set \(\gamma =5\), \(\lambda =2\), \(\mu =1\) and \(\tau =0.01\), it is easy to check that the fourth inequality in (15) does not hold.

Following a similar procedure, we can deduce the discrete form of the continuous-time ZNN in [18] for problem (1), which is denoted by NTDTZNN-p, as follows:

$$\begin{aligned}& A_{k}^{\top }{X}_{k+1}+{X}_{k+1}A_{k} \\& \quad =A_{k}^{\top }{X}_{k}+{X}_{k}A_{k}- \gamma \tau e_{k}-\lambda \tau \sum_{j=1}^{k}e_{j}- \tau \bigl(\dot{A}_{k}^{\top }X_{k}+X_{k} \dot{A}_{k}-\dot{B}_{k} \bigr)+\tau n_{k}. \end{aligned}$$
(22)

Corollary 3.1

NTDTZNN-p (22) with constant noise\(n(t)=a\)is convergent if and only if the parametersγ, λandτsatisfy

$$ \lambda \tau >0,\qquad 2\gamma \tau + \lambda \tau < 4,\quad ( \gamma \tau - 1)^{2}< 1.$$
(23)

Proof

Equality (22) can be written as

$$ e_{k+1}+(\gamma \tau -1)e_{k}+\lambda \tau \sum _{j=1}^{k}e_{j}- \tau n_{k}+\mathcal{O}\bigl(\tau ^{2}\bigr)=0, $$

which also holds for k, that is,

$$ e_{k}+(\gamma \tau -1)e_{k-1}+\lambda \tau \sum _{j=1}^{k-1}e_{j}- \tau n_{k-1}+\mathcal{O}\bigl(\tau ^{2}\bigr)=0. $$

Subtracting the above two equalities, we have

$$ e_{k+1}+\bigl((\gamma +\lambda )\tau -2\bigr)e_{k}-( \gamma \tau -1)e_{k-1}+ \mathcal{O}\bigl(\tau ^{2} \bigr)=0. $$

That is,

$$ \bar{e}_{k+1}+\bigl((\gamma +\lambda )\tau -2\bigr) \bar{e}_{k}-(\gamma \tau -1) \bar{e}_{k-1}=0, $$

whose characteristic equation is

$$ v^{2}+ \bigl((\gamma +\lambda )\tau -2 \bigr)v+1- \gamma \tau =0.$$
(24)

According to the Jury stability criterion [22] again, it is easy to deduce that the roots of characteristic equation (24) is inside the unit circle if and only if the three inequalities in (23) hold. The proof is completed. □

Remark 3.2

If we set \(\gamma =5\), \(\lambda =2\) and \(\tau =0.1\), it is easy to check that the three inequalities in (23) hold.

4 Numerical results

In this section, two simulation examples are included to substantiate the validity and fast convergence performance of NTCTZNN (5) and NTDTZNN (13). For comparative purposes, the CTZNN model in [8] (denoted by CTZNN), the NTCTZNN in [18] (denoted by NTCTZNN-p) and NTDTZNN-p (22) are included to solve time-varying Lyapunov equation.

By some simple manipulations, the CTZNN model in [8] for problem (1) is

$$\begin{aligned} A(t)^{\top }\dot{X}(t)+\dot{X}(t)A(t) =&-\gamma \bigl(A(t)^{\top }X(t)+X(t)A(t)-B(t) \bigr)\\ &{}- \bigl(\dot{A}(t)^{\top }X(t)+X(t)\dot{A}(t)-\dot{B}(t) \bigr)+ n(t), \end{aligned}$$

and the NTCTZNN model in [18] for problem (1) is

$$ \textstyle\begin{cases} \dot{X}_{1}(t)=X_{2}(t), \\ A(t)^{\top }\dot{X}(t)+\dot{X}(t)A(t)=-\gamma (A(t)^{\top }X(t)+X(t)A(t)-B(t) )-\lambda X_{1}(t) \\ \hphantom{A(t)^{\top }\dot{X}(t)+\dot{X}(t)A(t)=}{}- (\dot{A}(t)^{\top }X(t)+X(t) \dot{A}(t)-\dot{B}(t) )+ n(t). \end{cases} $$

In the following experiments, we set \(\gamma =5\), \(\lambda =2\), \(\mu =1\), \(h=0.1\), and

$$ \mathrm{Res}= \bigl\Vert A(t)^{\top }X(t)+X(t)A(t)-B(t) \bigr\Vert . $$

Example 4.1

Consider the following time-varying Lyapunov equation:

$$ A(t)^{\top }X+XA(t)=B(t),\quad t\in [0,50]~\mathrm{s}, $$

where

$$ A(t)= \begin{bmatrix} 3+\sin (t)& 1 \\ 1 &3+\cos (t)\end{bmatrix}, \qquad B(t)= \begin{bmatrix} \sin (t)& 1+\cos (t) \\ 1+\cos (t)& \sin (t)\end{bmatrix}. $$

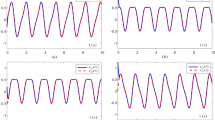
Firstly, we consider the zero noise \(n(t)=0\) and the constant noise \(n(t)=1\). The numerical results are plotted in Fig. 1.

Figure 1
figure 1

Numerical results of Example 4.1

Full size image

Secondly, we consider the linear noise \(n(t)=t+1\) and the quadratic noise \(n(t)=t^{2}+t+1\). The numerical results are plotted in Fig. 2.

Figure 2
figure 2

Numerical results of Example 4.1

Full size image

The numerical results are depicted in Figs. 1 and 2 indicate that: (1) For the zero noise, CTZNN becomes oscillating firstly, and NTCTZNN is the last one. The three tested models all can solve Example 4.1 with high accuracy. (2) For the constant noise, CTZNN fails to solve Example 4.1, and the other two models successfully solve Example 4.1. Moreover, we again find that NTCTZNN-p becomes oscillating firstly than NTCTZNN. (3) For the linear noise, both CTZNN and NTCTZNN-p fail to solve Example 4.1, while NTCTZNN successfully solve Example 4.1. (4) For the quadratic noise, all the three tested models do not work well, and the accuracy of NTCTZNN is about 1, which is in accordance with Theorem 2.4 (\(a_{ij}=1\), \(\mu =1\)). Overall, this example indicates that

$$ \mathrm{NTCTZNN}\succ \mathrm{NTCTZNN-p}\succ \mathrm{CTZNN}, $$

where \(A\succ B\) denotes the performance of model A is better than that of model B.

Example 4.2

Consider the following time-varying Lyapunov equation:

$$ A(t)^{\top }X+XA(t)=B(t),\quad t\in [0,50]~\mathrm{s}, $$

where

$$ A(t)= \begin{bmatrix} 3+t& 1+t \\ 1+t &3+t\end{bmatrix} , \qquad B(t)= \begin{bmatrix} t& 1+t \\ 1+t&t\end{bmatrix} . $$

We use the NTDTZNN (13) to solve this problem with constant noise \(n(t)=1\) or linear noise \(n(t)=t+1\). The numerical results are depicted in Fig. 3, from which we find that Res generated by NTDTZNN is oscillating decreasing. In fact, at the final time, 50 s, Res generated by NTDTZNN with the both types of noises is about 10−9, which indicates that NTDTZNN successfully solves this problem with high accuracy. For NTDTZNN with constant noise, the accuracy is about 10−7, a litter worse than that of NTDTZNN, but NTDTZNN with linear noise fails to solve this problem, which is in accordance with Corollary 3.1.

Figure 3
figure 3

Numerical results of Example 4.2

Full size image

5 Conclusions

In this paper, a novel noise-tolerant continuous-time ZNN (NTCTZNN) model and its discrete form (NTDTZNN) have been designed to solve a time-varying Laypunov equation. It has been proved that NTCTZNN and NTDTZNN inherently possess robustness to various type of noise. Numerical results as regards the two proposed models have been presented to substantiate their efficiency for solving time-varying Lyapunov equation.

In the future, we shall further improve NTCTZNN by introducing triple integrals to enhance its robustness to quadratic noise and study delayed ZNNs based on the theoretical results obtained in [23–28].