1 Introduction

As an important type of matrix equation, the Lyapunov equation is extensively applied in lots of engineering areas, including communication [1] and control [2,3,4,5]. Therefore, there is significant value in solving the Lyapunov equation. To solve this kind of equation, scholars have proposed some excellent algorithms, in which the most influential ones are traditional numerical algorithms [6,7,8,9]. Nonetheless, these numerical algorithms require extremely high time complexity, which impacts the application scope of the algorithms greatly.

Recently, the academic circles have achieved great development in the research on neural networks, and the application scope of these achievements covers multiple fields. Since gradient neural network (GNN) has the virtues of parallel distribution and hardware reliability, it is suitable for solving the stationary Lyapunov equation [10, 11]. GNN performs very well in solving the stationary Lyapunov equations, but it cannot solve the time-variant ones. If we use GNN to solve time-variant Lyapunov equation, a large delay error will occur, which results in that GNN cannot stabilize to the solution accurately.

In [12], a peculiar recurrent neural network was put forward. In this kind of neural network, the error always tends to zero, so this kind of neural network is referred to zeroing neural network. Many works have shown that ZNN can solve plenty of time-variant problems [13,14,15,16]. Nonetheless, the ordinary ZNN model has an obvious defect. For the ordinary ZNN model, it needs infinite time to stabilize to the theoretical solution, so the cost of time will be unacceptable.

To optimize the convergence times of ZNNs, finite-time stability and fixed-time stability were introduced into the research on ZNNs. As we know, the convergence speed of ZNN mainly depends on activation function (AF). By designing AFs based on finite-time stability theorems, ZNNs that can reach finite-time convergence were developed firstly [17, 18]. However, for finite-time stability-based ZNN, the convergence time is closely connected with the initial state of ZNN. If the initial state is undetermined, it will be impossible to calculate the convergence time, which limits the usability of finite-time stability-based ZNN. Furthermore, noise interference is inevitable in realistic applications, which may affect the convergence of ZNN. Hence, besides the convergence times of ZNNs, the robustness of ZNNs should also be investigated [19,20,21]. In [22], by designing AFs based on fixed-time stability theorems, Xiao et al. established two fresh fixed-time stability-based noise-resistant ZNN (NRZNN) models. These two models can not only converge in fixed-time but also tolerate various noises. For the above NRZNN models, the convergence times are bounded by an upper bound, which does’t rely on the initial values of NRZNNs and can be calculated based on the related parameters. However, it is tough to adjust the above-mentioned upper bound via the related parameters. Although subsequent researchers have greatly improved the fixed-time convergence speed [23,24,25], the upper bound of the convergence time still cannot be chosen arbitrarily in advance.

In recent years, predefined-time stability [26,27,28,29] was proposed. In fact, the related predefined-time stability theorems can be used to design predefined-time stability-based ZNN. For predefined-time stability-based ZNN, the convergence times are bounded by an upper bound, which does’t rely on the initial value of ZNN and can be an arbitrarily predefined time. Furthermore, the predefined time can be set as a model parameter in advance. However, until now, predefined-time stability has not been applied in the research on ZNNs, and it has not been applied in solving the Lyapunov equation either.

In this paper, we transform the problem of solving the time-variant Lyapunov equations into the convergence problem of ZNN. Two predefined-time stability theorems are used to devise new activation functions, and then we obtain two predefined-time stability-based ZNN (PTZNN) models. These two models still reserve the anti-noise virtue, and they can reach convergence within an arbitrarily predefined time. Lastly, we verify that the ZNNs developed in this paper are superior to the known ZNNs in solving the time-variant Lyapunov equation via numerical simulations. Compared with the ZNNs in [17, 18, 20, 22, 25], the ZNNs developed in this paper have the following obvious advantage: regardless of the initial values of ZNNs, the upper bound of the convergence times can be adjusted flexibly and set as a parameter of ZNNs in advance.

The remainder of this paper includes four sections. Essential preliminaries are presented in Sect. 2, and the theoretical results are given in Sect. 3. Numerical simulations are provided in Sect. 4, and Conclusions are given in Sect. 5.

2 Preliminaries and ZNN Model

Consider the time-variant Lyapunov equation as follows:

$$\begin{aligned} \begin{aligned} M ^ { T } ( t ) X ( t ) + X ( t ) M ( t ) = - Q ( t ) \end{aligned} \end{aligned}$$
(1)

where \( M(t)\in {\mathbb {R}}^{n\times n}\) denotes a known time-variant coefficient matrix; \( Q(t)\in {\mathbb {R}}^{n\times n}\) denotes a known time-variant matrix; \( X(t) \in {\mathbb {R}}^{n\times n}\) denotes the matrix which should be solved. Suppose that \(X^{*}(t)\) is the theoretical solution of Eq. (1).

First, we introduce a matrix-valued error E(t), where

$$\begin{aligned} \begin{aligned} E(t) = M^{T}(t)X(t)+X(t) M(t)+Q(t) \in {\mathbb {R}} ^ { n \times n }. \end{aligned} \end{aligned}$$
(2)

As we know, when the error E(t) converges to 0, the corresponding X(t) will be the solution of Eq. (1). Therefore, we should ensure E(t) can converge to 0 within some time.

To ensure the error E(t) can converge to 0, we adopt the following ZNN design:

$$\begin{aligned} \begin{aligned} \frac{ d E ( t ) }{ d t } = - \frac{ 1 }{ T _ { c } }\psi ( E ( t ) ), \end{aligned} \end{aligned}$$
(3)

where \(\psi ( \cdot ): {\mathbb {R}} ^ { n \times n }\rightarrow {\mathbb {R}} ^ { n \times n }\) stands for the array of activation functions; \({ T _ { c } }>0\) is the predefined time, and it denotes a known tunable parameter.

By substituting (2) into (3), we get the following ZNN model:

$$\begin{aligned} \begin{aligned} M ^{T}(t)\dot{X} (t)+\dot{X} (t)M(t)=&-\dot{M} ^ {T} (t) X (t) - X (t)\dot{M}(t)-\dot{Q}(t)\\&- \frac{1}{T_{c}}\psi (M^{T} (t) X (t)+ X (t) M (t) + Q (t)). \end{aligned} \end{aligned}$$
(4)

For this ZNN model, if we choose the suitable \(\psi ( \cdot )\), no matter X(t) begins with arbitrary initial state X(0), it can stabilize to the theoretical solution \(X^{*}(t)\) within the predefined time \(T _ { c }\).

In this part, consider nonlinear system \(\dot{x}(t)=f(x(t))\), where \(x(t) \in {\mathbb {R}}^{n}\); \(f: {\mathbb {R}}^{n} \rightarrow {\mathbb {R}}^{n}\) is a continuous function, and \(f(0)=0\).

Definition 1

No matter x(t) begins with arbitrary initial state x(0), if given any \(T_{c}>0\), x(t) can converge to 0 within \(T_{c}\), then the above nonlinear system is said to reach predefined-time stability, and \(T_{c}>0\) is the predefined time.

Lemma 1

[30]. Gamma function \(\Gamma (\cdot )\) is defined as \(\Gamma (z)=\int _{0}^{+\infty }e^{-t}t^{z-1}dt\). If continuous function \(V(\cdot ):{\mathbb {R}}^{n}\rightarrow {\mathbb {R}}_{+}\cup \{0\}\) satisfies

  1. (i)

    \(V(x(t))=0 \Leftrightarrow x(t)=0;\)

  2. (ii)

    \(\Vert x(t)\Vert \rightarrow +\infty \Rightarrow V(x(t))\rightarrow +\infty ;\)

  3. (iii)

    for \(\forall x(t)\in {\mathbb {R}}^{n}\) and \(\forall T_{c}>0\), there exist \(\alpha ,~\beta >0,~0<p<1\) and \(q>1\) such that

    $$\begin{aligned} {\dot{V}}(x(t))\le -\frac{T_{\max }}{T_{c}}\left( \alpha V^{p}(x(t))+\beta V^{q}(x(t))\right) , \end{aligned}$$

    where \(T_{\max }= \frac{\Gamma (\frac{1-p}{q-p})\Gamma (\frac{q-1}{q-p})}{\alpha (q-p)} \left( \frac{\alpha }{\beta }\right) ^{\frac{1-p}{q-p}}\), then the above nonlinear system reaches predefined-time stability, and \(T_{c}\) is the predefined time.

Lemma 2

[31]. If continuous function \(V(\cdot ):{\mathbb {R}}^{n}\rightarrow {\mathbb {R}}_{+}\cup \{0\}\) satisfies

  1. (i)

    \(V(x(t))=0 \Leftrightarrow x(t)=0;\)

  2. (ii)

    \(\Vert x(t)\Vert \rightarrow +\infty \Rightarrow V(x(t))\rightarrow +\infty ;\)

  3. (iii)

    for \(\forall x(t)\in {\mathbb {R}}^{n}\) and \(\forall T_{c}>0\), there exists \(0<p\le 1\) such that

    $$\begin{aligned} {\dot{V}}(x(t))\le -\frac{1}{p\cdot T_{c}}\exp (V^{p}(x(t)))V^{1-p}(x(t)), \end{aligned}$$

    then the above nonlinear system reaches predefined-time stability, and \(T_{c}\) is the predefined time.

3 The Predefined-Time Convergence of the PTZNN Models

Since the convergence speed of ZNN mainly depends on activation function (AF), we design two new AFs as follows:

$$\begin{aligned}{} & {} \begin{aligned} \psi _1(x)=w(a_{1}|x|^{p}+a_{2}|x|^{q}) {\text {sgn}}(x )+a_{3}x+a_{4}{\text {sgn}}(x), \end{aligned} \end{aligned}$$
(5)
$$\begin{aligned}{} & {} \begin{aligned} \psi _2(x)=\exp (|x|^{h})|x|^{1-h}{\text { sgn }} (x) / h + b _ {1} x + b _ {2} {\text { sgn }} ( x ), \end{aligned} \end{aligned}$$
(6)

where \(w= \frac{\Gamma (\frac{1-p}{q-p})\Gamma (\frac{q-1}{q-p})}{ a _ { 1 }(q-p)} \left( \frac{ a _ { 1 }}{ a _ { 2 }}\right) ^{\frac{1-p}{q-p}}\), \(a_{1},a_{2}>0\), \(a_{3},a_{4}\ge 0\), \(0<p<1\), \(q>1\), \(0<h<1\), \(b_{1},b_{2}\ge 0\).

Next, we shall propose two new PTZNN models based on these two AFs. Then we prove they can reach predefined-time stability, and the cases with noise disturbances are also considered.

A. Model-1

When AF array \(\psi _1(\cdot ): {\mathbb {R}} ^ { n \times n }\rightarrow {\mathbb {R}} ^ { n \times n }\) is applied to activate the ZNN model (4), we can gain the first PTZNN model:

$$\begin{aligned} \begin{aligned} M^{T}(t)\dot{X}(t) + \dot{X} (t) M (t) = -\dot{M} ^ {T} (t) X (t)-X (t)\dot{M}(t)- \dot{Q}(t)\\ -\frac{1}{T_{c} }\psi _1(M^{T} (t) X (t) + X (t) M(t) + Q (t)). \end{aligned} \end{aligned}$$
(7)

Theorem 1

Starting with a stochastic initial matrix \(X(0)\in {\mathbb {R}} ^ { n \times n }\), model (7) can output the theoretical solution of Eq. (1) within a predefined time \( T _ { c }\).

Proof

In fact, model (7) is equivalent to \({\dot{E}} (t) = - \frac{ 1 }{ T_{c} }\psi _1 (E(t))\), each subsystem of which can be written as

$$\begin{aligned} \begin{aligned} {\dot{e}} _ {ij} (t)=- \frac{1}{ T _ {c} }\psi _1 ( e_{ij} (t)),\ \ i,j \in \{ 1,2,\cdots ,n\}, \end{aligned} \end{aligned}$$
(8)

where \(E(t)=(e_{ij}(t))_{n\times n}\) and \({\dot{E}}(t)=({\dot{e}}_{ij}(t))_{n\times n}\).

If subsystem (8) can converge within \( T _ { c }\), then model (7) can converge within \( T _ { c }\). To prove subsystem (8) can reach predefined-time stability within \(T_{c}\), we choose Lyapunov function

$$\begin{aligned} V(t)=|e_{ij}(t)|. \end{aligned}$$

Its time derivative is

$$\begin{aligned} {\dot{V}}(t) = {\dot{e}}_{ij} (t) {\text {sgn}}(e_{ij}(t)) = -\frac{1}{T_{c}}\psi _1 (e_{ij}(t) ){\text {sgn}} (e_{ij} (t)). \end{aligned}$$

If the above equation is combined with AF(5), it follows that

$$\begin{aligned} \begin{aligned} {\dot{V}}(t)=&-\frac{w}{T_{c}}(a_{1}|e_{ij}(t)|^{p}+a_{2}|e_{ij}(t)|^{q}) -\frac{1}{T_{c}}(a_{3}|e_{ij}(t)|+a_{4})\\ \le&-\frac{w}{T_{c}}(a_{1}|e_{ij}(t)|^{p}+a_{2}|e_{ij}(t)|^{q})\\ =&-\frac{w}{T_{c}}(a_{1}V^{p}(t)+a_{2}V^{q}(t)). \end{aligned} \end{aligned}$$

Based on Lemma 1, subsystem (8) can reach predefined-time stability within \(T_{c}\). Therefore, model (7) can reach predefined-time stability within \(T_{c}\). \(\square \)

We can further consider PTZNN model with noise disturbance:

$$\begin{aligned} \begin{aligned} M^{T}(t)\dot{X}( t ) + \dot{X} (t) M (t) = -\dot{M} ^ {T} (t) X (t)-X (t)\dot{M} ( t )-\dot{Q}(t)\\ - \frac{1}{T_{c} }\psi _1(M^{T} (t) X ( t ) + X (t) M(t) + Q (t))+Y(t). \end{aligned} \end{aligned}$$
(9)

(1) Case 1: \(Y(t)=(y_{ij}(t))_{n\times n}\) is a dynamic bounded vanishing noise.

Theorem 2

If Y(t) is a dynamic bounded vanishing noise satisfying \(|y _ {ij}(t)|\le \delta |e_{ij}(t)|\), where \( \delta \in ( 0, + \infty )\). Starting with a stochastic initial matrix \(X(0)\in {\mathbb {R}} ^ { n \times n }\), model (9) can output the theoretical solution of Eq. (1) within a predefined time \( T _ { c }\), as long as \(a_{3}\ge \delta T_{c}\).

Proof

In fact, model (9) is equivalent to \({\dot{E}}(t)= -\frac{1}{T _ {c} }\psi _1 (E (t))+Y(t) \), each subsystem of which can be written as

$$\begin{aligned} \begin{aligned} {\dot{e}}_{ij}(t)=- \frac{ 1 }{T_{c}}\psi _1 (e_{ij}(t)) +{y} _ {ij}(t),\ \ i,j \in \{ 1,2,\cdots ,n\}, \end{aligned} \end{aligned}$$
(10)

where \(E(t)=(e_{ij}(t))_{n\times n}\), \({\dot{E}}(t)=({\dot{e}}_{ij}(t))_{n\times n}\) and \(Y(t)=(y_{ij}(t))_{n\times n}\).

To prove subsystem (10) can reach predefined-time stability within \(T_{c}\), we choose Lyapunov function

$$\begin{aligned} V(t) = |e_{ij}(t)|^{2}. \end{aligned}$$

Its time derivative is

$$\begin{aligned} {\dot{V}}(t)= 2e_{ij}(t){\dot{e}}_{ij}(t)= 2e_{ij}(t)\left( -\frac{1}{T_{c}}\psi _1(e_{ij}(t)) + y _{ij}(t)\right) . \end{aligned}$$

If the above equation is combined with AF(5) and \(a_{3}\ge \delta T_{c}\), it follows that

$$\begin{aligned}\begin{aligned} {\dot{V}}(t)=&-\frac{2w}{T_{c}}(a_{1}|e_{ij}(t)|^{p+1}+a_{2}|e_{ij}(t)|^{q+1})-\frac{2a_{4}}{T_{c}}|e_{ij}(t)|\\&+2\left( e_{ij}(t)y_{ij}(t)-\frac{a_{3}}{T_{c}}|e_{ij}(t)|^{2}\right) \\ \le&-\frac{2w}{T_{c}}(a_{1}|e_{ij}(t)|^{p+1}+a_{2}|e_{ij}(t)|^{q+1}) +2\left( \delta |e_{ij}(t)|^{2}-\frac{a_{3}}{T_{c}}|e_{ij}(t)|^{2}\right) \\ \le&-\frac{2w}{T_{c}}(a_{1}|e_{ij}(t)|^{p+1}+a_{2}|e_{ij}(t)|^{q+1})\\ =&-\frac{2w}{T_{c}}\left( a_{1}V^{\frac{p+1}{2}}+a_{2}V^{\frac{q+1}{2}}\right) =-\frac{w}{T_{c}}\left( 2a_{1}V^{\frac{p+1}{2}}+2a_{2}V^{\frac{q+1}{2}}\right) . \end{aligned} \end{aligned}$$

Moreover,

$$\begin{aligned}\begin{aligned} w=&\frac{\Gamma (\frac{1-p}{q-p})\Gamma (\frac{q-1}{q-p})}{ a _ { 1 }(q-p)} \left( \frac{ a _ { 1 }}{ a _ { 2 }}\right) ^{\frac{1-p}{q-p}}\\ =&\frac{\Gamma \left( \frac{1-\frac{p+1}{2}}{\frac{q+1}{2}-\frac{p+1}{2}}\right) \Gamma \left( \frac{\frac{q+1}{2}-1}{\frac{q+1}{2}-\frac{p+1}{2}}\right) }{2a_{1}\left( \frac{q+1}{2}-\frac{p+1}{2}\right) } \left( \frac{2a_{1}}{2a_{2}}\right) ^{\frac{1-\frac{p+1}{2}}{\frac{q+1}{2}-\frac{p+1}{2}}}. \end{aligned} \end{aligned}$$

Based on Lemma 1, subsystem (10) can reach predefined-time stability within \(T_{c}\). Therefore, model (9) can reach predefined-time stability within \(T_{c}\). \(\square \)

(2) Case 2: \(Y(t)=(y_{ij}(t))_{n\times n}\) is a dynamic bounded nonvanishing noise.

Theorem 3

If Y(t) is a dynamic bounded nonvanishing noise satisfying \(|y _ {ij}(t)|\le \delta \), where \( \delta \in ( 0, + \infty )\). Starting with a stochastic initial matrix \(X(0)\in {\mathbb {R}} ^ { n \times n }\), model (9) can output the theoretical solution of Eq. (1) within a predefined time \( T _ { c }\), as long as \(a_{4}\ge \delta T_{c}\).

Proof

Similarly to Theorem 2, we choose Lyapunov function

$$\begin{aligned} V(t) = |e_{ij}(t)|^{2}. \end{aligned}$$

Its time derivative is

$$\begin{aligned} {\dot{V}}(t)= 2e_{ij}(t){\dot{e}}_{ij}(t)= 2e_{ij}(t)\left( -\frac{1}{T_{c}}\psi _1(e_{ij}(t)) + y _{ij}(t)\right) . \end{aligned}$$

If the above equation is combined with AF (5) and \(a_{4}\ge \delta T_{c}\), it follows that

$$\begin{aligned} \begin{aligned} {\dot{V}}(t)=&-\frac{2w}{T_{c}}(a_{1}|e_{ij}(t)|^{p+1}+a_{2}|e_{ij}(t)|^{q+1})-\frac{2a_{3}}{T_{c}}|e_{ij}(t)|^{2}\\&+2\left( e_{ij}(t)y_{ij}(t)-\frac{a_{4}}{T_{c}}|e_{ij}(t)|\right) \\ \le&-\frac{2w}{T_{c}}(a_{1}|e_{ij}(t)|^{p+1}+a_{2}|e_{ij}(t)|^{q+1}) +2\left( \delta |e_{ij}(t)|-\frac{a_{4}}{T_{c}}|e_{ij}(t)|\right) \\ \le&-\frac{2w}{T_{c}}(a_{1}|e_{ij}(t)|^{p+1}+a_{2}|e_{ij}(t)|^{q+1})\\ =&-\frac{2w}{T_{c}}\left( a_{1}V^{\frac{p+1}{2}}+a_{2}V^{\frac{q+1}{2}}\right) =-\frac{w}{T_{c}}\left( 2a_{1}V^{\frac{p+1}{2}}+2a_{2}V^{\frac{q+1}{2}}\right) . \end{aligned} \end{aligned}$$

Similarly to Theorem 2, model (9) can reach predefined-time stability within \(T_{c}\). \(\square \)

B. Model-2

When AF array \(\psi _2(\cdot ): {\mathbb {R}} ^ { n \times n }\rightarrow {\mathbb {R}} ^ { n \times n }\) is applied to activate the ZNN model (4), we can gain the second PTZNN model:

$$\begin{aligned} \begin{aligned} M^{T}(t)\dot{X}( t ) + \dot{X} (t) M (t) = -\dot{M} ^ {T} (t) X (t)-X (t)\dot{M} ( t )- \dot{Q}(t) \\ - \frac{1}{T_{c} }\psi _2(M^{T} (t) X ( t ) + X (t) M(t) + Q (t)). \end{aligned} \end{aligned}$$
(11)

Theorem 4

Starting with a stochastic initial matrix \(X(0)\in {\mathbb {R}} ^ { n \times n }\), model (11) can output the theoretical solution of Eq. (1) within a predefined time \( T _ { c }\).

Proof

In fact, model (11) is equivalent to \({\dot{E}} (t) = - \frac{ 1 }{ T _ { c } }\psi _2 ( E ( t ) )\), each subsystem of which can be written as

$$\begin{aligned} \begin{aligned} {\dot{e}}_{ij} (t)=- \frac{ 1 }{T_{c}}\psi _2(e_{ij } (t)), \ \ i,j \in \{1,2,\cdots , n \}, \end{aligned} \end{aligned}$$
(12)

where \(E(t)=(e_{ij}(t))_{n\times n}\) and \({\dot{E}}(t)=({\dot{e}}_{ij}(t))_{n\times n}\).

To prove subsystem (12) can reach predefined-time stability within \(T_{c}\), we choose Lyapunov function

$$\begin{aligned} V(t)=|e_{ij}(t)|. \end{aligned}$$

Its time derivative is

$$\begin{aligned} {\dot{V}}(t) = {\dot{e}}_{ij} (t) {\text {sgn}}(e_{ij}(t)) = -\frac{1}{T_{c}}\psi _2 (e_{ij}(t) ){\text {sgn}} (e_{ij} (t)). \end{aligned}$$

If the above equation is combined with AF(6), it follows that

$$\begin{aligned} \begin{aligned} {\dot{V}}(t)&=-\frac{1}{T_{c}}\left( \exp (|e_{ij}(t)|^{h})|e_{ij}(t)|^{1-h}/h+b_{1}|e_{ij}(t)|+b_{2}\right) \\&\le -\frac{1}{T_{c}}\exp (|e_{ij}(t)|^{h})|e_{ij}(t)|^{1-h}/h\\&=-\frac{1}{hT_{c}}\exp (V^{h}(t))V^{1-h}(t). \end{aligned} \end{aligned}$$

Based on Lemma 2, subsystem (12) can reach predefined-time stability within \(T_{c}\). Therefore, model (11) can reach predefined-time stability within \(T_{c}\). \(\square \)

We can further consider PTZNN model with noise disturbance

$$\begin{aligned} \begin{aligned} M^{T}(t)\dot{X}( t ) + \dot{X} (t) M (t) = -\dot{M} ^ {T} (t) X (t)-X (t)\dot{M} ( t )-\dot{Q}(t) \\ - \frac{1}{T_{c} }\psi _2(M^{T} (t) X ( t ) + X (t) M(t) + Q (t))+Y(t). \end{aligned} \end{aligned}$$
(13)

(1) Case 1: \(Y(t)=(y_{ij}(t))_{n\times n}\) is a dynamic bounded vanishing noise.

Theorem 5

If Y(t) is a dynamic bounded vanishing noise is a dynamic bounded vanishing noise satisfying \(|y_ {ij}(t)|\le \delta |e_{ij}(t)|\), where \( \delta \in (0,+\infty )\). Starting with a stochastic initial matrix \(X(0)\in {\mathbb {R}} ^ { n \times n }\), model (13) can output the theoretical solution of Eq. (1) within a predefined time \( T _ { c }\), as long as \(b_{1}\ge \delta T_{c}\).

Proof

In fact, model (13) is equivalent to \({\dot{E}}(t)= -\frac{1}{T _ {c} }\psi _2(E (t))+Y(t) \), each subsystem of which can be written as

$$\begin{aligned} \begin{aligned} {\dot{e}}_{ij}(t)=- \frac{ 1 }{T_{c}}\psi _2 (e_{ij}(t)) +{y} _ {ij}(t), \ \ i,j \in \{1,2,\cdots , n \}, \end{aligned} \end{aligned}$$
(14)

where \(E(t)=(e_{ij}(t))_{n\times n}\), \({\dot{E}}(t)=({\dot{e}}_{ij}(t))_{n\times n}\) and \(Y(t)=(y_{ij}(t))_{n\times n}\).

To prove subsystem (14) can reach predefined-time stability within \(T_{c}\), we choose Lyapunov function

$$\begin{aligned} V(t) = |e_{ij}(t)|^{2}. \end{aligned}$$

Its time derivative is

$$\begin{aligned} {\dot{V}}(t)= 2e_{ij}(t){\dot{e}}_{ij}(t)= 2e_{ij}(t)\left( -\frac{1}{T_{c}}\psi _2(e_{ij}(t)) + y _{ij}(t)\right) . \end{aligned}$$

If the above equation is combined with AF(6) and \(b_{1}\ge \delta T_{c}\), it follows that

$$\begin{aligned} \begin{aligned} {\dot{V}}(t)=&-\frac{2}{T_{c}}\exp (|e_{ij}(t)|^{h}|e_{ij}(t)|^{2-h}/h-\frac{2b_{2}}{T_{c}}|e_{ij}(t)|\\&+2(e_{ij}(t)y_{ij}(t)-\frac{b_{1}}{T_{c}}|e_{ij}(t)|^{2})\\ \le&-\frac{2}{T_{c}}\exp (|e_{ij}(t)|^{h})|e_{ij}(t)|^{2-h}/h +2\left( \delta |e_{ij}(t)|^{2}-\frac{b_{1}}{T_{c}}|e_{ij}(t)|^{2}\right) \\ \le&-\frac{2}{T_{c}}\exp (|e_{ij}(t)|^{h})|e_{ij}(t)|^{2-h}/h\\ =&-\frac{1}{\frac{h}{2}T_{c}}\exp \left( V^{\frac{h}{2}}(t)\right) V^{\frac{2-h}{2}}(t). \end{aligned} \end{aligned}$$

Based on Lemma 2, subsystem (14) can reach predefined-time stability within \(T_{c}\). Therefore, model (13) can reach predefined-time stability within \(T_{c}\). \(\square \)

(2)Case 2: \(Y(t)=(y_{ij}(t))_{n\times n}\) is a dynamic bounded nonvanishing noise.

Theorem 6

If Y(t) is a dynamic bounded nonvanishing noise satisfying \(|y_ {ij}(t)|\le \delta \), where \( \delta \in (0,+\infty )\). Starting with a stochastic initial matrix \(X(0)\in {\mathbb {R}} ^ { n \times n }\), model (13) can output the theoretical solution of Eq. (1) within a predefined time \( T _ { c }\), as long as \(b_{2}\ge \delta T_{c}\).

Proof

Similarly to Theorem 5, we choose Lyapunov function

$$\begin{aligned} V(t) = |e_{ij}(t)|^{2}. \end{aligned}$$

Its time derivative is

$$\begin{aligned} {\dot{V}}(t)= 2e_{ij}(t){\dot{e}}_{ij}(t)= 2e_{ij}(t)(-\frac{1}{T_{c}}\psi _2(e_{ij}(t)) + y _{ij}(t)). \end{aligned}$$

If the above equation is combined with AF(6) and \(b_{2}\ge \delta T_{c}\), it follows that

$$\begin{aligned} \begin{aligned} {\dot{V}}(t)=&-\frac{2}{T_{c}}\exp (|e_{ij}(t)|^{h}|e_{ij}(t)|^{2-h}/h-\frac{2b_{1}}{T_{c}}|e_{ij}(t)|^{2}\\&+2(e_{ij}(t)y_{ij}(t)-\frac{b_{2}}{T_{c}}|e_{ij}(t)|)\\ \le&-\frac{2}{T_{c}}\exp (|e_{ij}(t)|^{h})|e_{ij}(t)|^{2-h}/h +2(\delta |e_{ij}(t)|-\frac{b_{2}}{T_{c}}|e_{ij}(t)|)\\ \le&-\frac{2}{T_{c}}\exp (|e_{ij}(t)|^{h})|e_{ij}(t)|^{2-h}/h\\ =&-\frac{1}{\frac{h}{2}T_{c}}\exp (V^{\frac{h}{2}}(t))V^{\frac{2-h}{2}}(t). \end{aligned} \end{aligned}$$

Similarly to Theorem 5, model (13) can reach predefined-time stability within \(T_{c}\). \(\square \)

Remark 1

At the beginning of this section, AF(5) and AF(6) are defined, and the conditions that the parameters in AF(5) and AF(6) should satisfy have also been given: \(w=\frac{\Gamma (\frac{1-p}{q-p})\Gamma (\frac{q-1}{q-p})}{ a _ { 1 }(q-p)} \left( \frac{ a _ { 1 }}{ a _ { 2 }}\right) ^{\frac{1-p}{q-p}}\), \(a_{1},a_{2}>0\), \(a_{3},a_{4}\ge 0\), \(0<p<1\), \(q>1\), \(0<h<1\), \(b_{1},b_{2}\ge 0\). Theorems 1-3 are related to AF(5), so the parameters in AF(5) must satisfy the following conditions: \(w=\frac{\Gamma (\frac{1-p}{q-p})\Gamma (\frac{q-1}{q-p})}{ a _ { 1 }(q-p)} \left( \frac{ a _ { 1 }}{ a _ { 2 }}\right) ^{\frac{1-p}{q-p}}\), \(a_{1},a_{2}>0\), \(a_{3},a_{4}\ge 0\), \(0<p<1\), \(q>1\). Moreover, in Theorem 2 the parameter \(a_{3}\) in AF(5) should satisfy \(a_{3}\ge \delta T_{c}\), and in Theorem 3 the parameter \(a_{4}\) in AF(5) should satisfy \(a_{4}\ge \delta T_{c}\), where \(T_{c}\) is the predefined time and \(\delta \) is a constant about noise. Theorems 4-6 are related to AF(6), so the parameters in AF(6) must satisfy the following conditions: \(0<h<1\), \(b_{1},b_{2}\ge 0\). Moreover, in Theorem 5 the parameter \(b_{1}\) in AF(6) should satisfy \(b_{1}\ge \delta T_{c}\), and in Theorem 6 the parameter \(b_{2}\) in AF(6) should satisfy \(b_{2}\ge \delta T_{c}\), where \(T_{c}\) is the predefined time and \(\delta \) is a constant about noise. If some parameters in AF(5) and AF(6) don’t satisfy the related conditions, the corresponding PTZNNs cannot reach predefined-time stability within \(T_{c}\), at least in theory.

4 Numerical Simulation

In this section, we verify the derived results via numerical simulations. Simulation results show that, the models developed in this paper are superior to the known models in solving the time-variant Lyapunov equation.

Example 1

Let \(a_ {1}=a_{2}=a_{3}=a_{4}=b_{1}=b_{2}= 1\), \(p=h=0.25\), \(q=4\). Through calculating, \(w=\frac{4\pi }{{15\sin (0.2\pi )}}\). The coefficient matrices of Eq. (1) are \(M(t) = \left[ \begin{array} { l l } {-1-\frac{1}{2} \cos (4t) } &{} { \frac{1}{2} \sin (4t)} \\ { \frac{1}{2} \sin (4t) } &{} {-1+ \frac{1}{2} \cos (4t) } \end{array} \right] \), \(Q (t) = \left[ \begin{array} { l l } {\sin (4t) } &{} { \cos (4t)} \\ { -\cos (4t) } &{} { \sin (4t)} \end{array} \right] \). We set the predefined time \(T_{c}=1\). The theoretical solution of Eq. (1) is

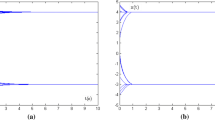
$$\begin{aligned} X^{*}(t) = \left[ \begin{array} { l l } \frac{-\sin (4t )(\cos (4t)-2)}{3} &{} \frac{-(2\cos (4t)-1)(\cos (4t) + 2 )}{6} \\ \frac{-(2\cos (4t)+1)(\cos (4t)-2)}{6} &{} \frac{ \sin (4t ) (\cos (4t)+2)}{3} \end{array} \right] . \end{aligned}$$

The noiseless Eq. (1) can be solved by using models (7) and (11). Figures 1, 2 and 3 show the main simulation results. The state solution of Eq. (1) based on model (7) and AF(5) is shown in Fig. 1, where \(X(t)=(x_{ij}(t))_{2\times 2}\), \(X^{*}(t)=(x_{ij}^{*}(t))_{2\times 2}\). Figure 1 illustrates that blue lines and red lines overlap within a short time, where blue line indicates the state solution of each subsystem starting from X(0), and red line indicates the exact solution of each subsystem. The state solution of Eq. (1) based on model (11) and AF(6) is shown in Fig. 2.

Fig. 1
figure 1

a-d illustrate the state solution of noiseless Eq. (1) based on model (7) and AF(5), where the parameters of Eq. (1) have been given in Example 1

Full size image
Fig. 2
figure 2

a-d illustrate the state solution of noiseless Eq. (1) based on model (11) and AF(6), where the parameters of Eq. (1) have been given in Example 1

Full size image
Fig. 3
figure 3

a and b illustrate the residual errors \(|| M^{T}(t)X(t)+X(t) M(t)+Q(t)||{_F}\) of noiseless Eq. (1) based on models (7) and (11), where the parameters of Eq. (1) have been given in Example 1

Full size image

Figure 3 illustrates the residual errors of noiseless Eq. (1) based on models (7) and (11). In Fig. 3, the residual error based on model (7) converges to zero within about 0.2, and the residual error based on model (11) converges to zero within about 0.3, which verifies the actual convergence times are not more than the predefined time \(T_{c}=1\).

Fig. 4
figure 4

The residual errors of Eq. (1) with different noises based on NRZNN, model (9) and model (13), where the parameters of Eq. (1) have been given in Example 1. (a) with noise \(y_{ij}(t) = 0\); (b) with noise \(y_{ij}(t)=0.3\sin (3t)\); (c) with noise \(y_{ij}(t)=1\); (d) with noise \(y_{ij}(t)=0.8|e_{ij}(t)|\), \(i,j\in \left\{ 1,2\right\} \)

Full size image

For comparison, noise-resistant ZNN (NRZNN), model (9) and model (13) are all used to solve Eq. (1) with different noises, and the corresponding residual errors are given in Fig. 4. Figure 4 illustrates that, regardless of the presence or type of noise, the convergence speeds based on model (9) and model (13) are almost not affected. However, if there exists noise, the convergence speed based on NRZNN slows down obviously. Therefore, we conclude that model (9) and model (13) have the better anti-noise performance, compared with the previous ZNN models.

Example 2

Let \(a_ {1}=a_{2}=a_{3}=a_{4}=b_{1}=b_{2}= 0.5\), \(p=h=0.5\), \(q=2\). Through calculating, \(w=1.5\pi \). The coefficient matrices of Eq. (1) are

$$\begin{aligned} M (t)= & {} \left[ \begin{array} { l l } { - 1 + 1.5 c ^ { 2 } } &{} { 1 - 1.5 s \times c } \\ {-1-1.5 s \times c } &{} {-1+1.5s^{2}}\end{array} \right] ,\\ Q ( t )= & {} \left[ \begin{array} { l l } { 2 s - 3 s \times c ^ { 2 } } &{} { - 0.5 c ( 1 - 6 s ^ { 2 } ) } \\ { 0.5 c ( 4 - 3 c ^ { 2 } + 3 s ^ { 2 } ) } &{} { 0.5 s ( 1 - 3 s ^ { 2 } + 3 c ^ { 2 } ) } \end{array} \right] , \end{aligned}$$

where s and c represent \(\sin (t)\) and \(\cos (t)\), respectively. We set the predefined time \(T_{c}=0.5\). The theoretical solution of Eq. (1) is

$$\begin{aligned} X^{*}(t) = \left[ \begin{array} { l l } { \sin (t) } &{} { \cos (t) } \\ { -\cos (t) } &{} { \sin (t) } \end{array} \right] . \end{aligned}$$
Fig. 5
figure 5

a-d illustrate the state solution of Eq. (1) based on model (9) and AF(5), where the constant noise is \(y_{ij}(t)=1\), and the parameters of Eq. (1) have been given in Example 2, \(i,j\in \left\{ 1,2\right\} \)

Full size image
Fig. 6
figure 6

a-d illustrate the state solution of Eq. (1) based on model (13) and AF(6), where the constant noise is \(y_{ij}(t)=1\), and the parameters of Eq. (1) have been given in Example 2, \(i,j\in \left\{ 1,2\right\} \)

Full size image

Equation (1) with constant noise \(y_{ij}(t)=1\) can be solved by using models (9) and (13), \(i,j\in \left\{ 1,2\right\} \). Figures 5, 6 show the main simulation results. The state solution of Eq. (1) based on model (9) and AF(5) is shown in Fig. 5, where \(X(t)=(x_{ij}(t))_{2\times 2}\), \(X^{*}(t)=(x_{ij}^{*}(t))_{2\times 2}\). Figure 5 illustrates that blue lines and red lines overlap within a short time (about 0.2), where blue line indicates the state solution of each subsystem starting from X(0), and red line indicates the exact solution of each subsystem. The state solution of Eq. (1) based on model (13) and AF (6) is shown in Fig. 6. The convergence times of both models are not greater than the predefined time \(T_{c}=0.5\).

Similarly to Example 1, NRZNN, model (9) and model (13) are all used to solve Eq. (1) with different noises, and the corresponding residual errors are given in Fig. 7. Figure 7 illustrates that, regardless of the presence or type of noise, the convergence speeds based on model (9) and model (13) are almost not affected. However, if there exists noise, the convergence speed based on NRZNN slows down obviously. Therefore, we conclude that model (9) and model (13) have the better anti-noise performance, compared with the previous ZNN models.

Fig. 7
figure 7

The residual errors of Eq. (1) with different noises based on NRZNN, model (9) and model (13), where the parameters of Eq. (1) have been given in Example 2. (a) with noise \(y_{ij}(t) = 0\); (b) with noise \(y_{ij}(t)=0.5\cos (1.8t)\); (c) with noise \(y_{ij}(t)=2\); (d) with noise \(y_{ij}(t)=0.6|e_{ij}(t)|\), \(i,j\in \left\{ 1,2\right\} \)

Full size image

5 Conclusions

In this paper, two PTZNN models are proposed by introducing predefined-time stability theorems into activation functions, and then they are applied to solve the time-variant Lyapunov equation. We prove the PTZNN models can reach predefined-time stability, and the noise-tolerant performance of the PTZNN models are also analyzed strictly. Finally, we verify that the models developed in this paper are superior to the known models in solving the time-variant Lyapunov equation via numerical simulations. Due to the existence of \(T_{\max }\), the predefined-time stability theorem in Lemma 1 is a bit complicated, so activation function (5) is also a bit complicated. In fact, there is another predefined-time stability theorem, which is the special case of Lemma 1 and more concise than Lemma 1. However, the above predefined-time stability theorem is not discussed in this paper. In the future, we shall use the above predefined-time stability theorem to solve some time-variant equations.