1 Introduction

In the last decades, big efforts have been made to develop and analyze mathematical models for the transmission of the mosquito-borne diseases such as malaria [1,2,3], dengue [4,5,6], Zika [7, 8], yellow fever [9], and chikungunya [10,11,12,13,14] to human population. Humans are infected by chikungunya virus (CHIKV) by infected Aedes albopictus and Aedes agypti mosquito. The syndrome of chikungunya includes: fever, headache, severe joint and muscle pain, rash, fatigue, and nausea. The basic mathematical model of within-host virus dynamics was proposed by [15] and has been extended in several works (see, e.g., [16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34]). Wang and Liu [35] have proposed and studied the following within-host CHIKV dynamics model which contains four compartments, uninfected-monocytes (s), infected monocytes (y), free CHIKV particles (p), and antibodies (x):

$$\begin{aligned}& \dot{s}(t) =\varrho -\xi s(t)-\omega _{1}s(t)p(t), \end{aligned}$$
(1)
$$\begin{aligned}& \dot{y}(t) =\omega _{1}s(t)p(t)-\epsilon y(t), \end{aligned}$$
(2)
$$\begin{aligned}& \dot{p}(t) =\varkappa y(t-\delta )-cp(t)-rx(t)p(t), \end{aligned}$$
(3)
$$\begin{aligned}& \dot{x}(t) =\lambda +\rho x\bigl(t-\delta ^{\ast }\bigr)p\bigl(t-\delta ^{\ast }\bigr)-mx(t). \end{aligned}$$
(4)

The susceptible monocytes are generated by rate ϱ, die with rate \(\xi s(t)\), and are attacked by CHIKV with rate \(\omega _{1}s(t)p(t)\). Constants ϵ, c, and m denote, respectively, the normal death rate constants of the infected monocytes, CHIKV, and antibodies. The parameter ϰ represents the production rate constant of the CHIKV. The term rate \(rx(t)p(t)\) represents the neutralization rate of CHIKV. Parameters λ and ρ represent the generation and proliferation rate constants of the antibodies. Parameter δ represents the maturation time of the newly produced CHIKV particles and \(\delta ^{\ast }\) represents the time that CHIKV stimulation needs for generating antibodies. Model (1)–(4) presented in [35] has recently been extended in [36, 37]. In [35] and [36, 37] it has been assumed that the uninfected monocyte becomes infected due to its contact with CHIKV (viral infection). It has been mentioned in [38] that the uninfected monocyte can also be infected when it contacts with infected monocyte (cellular infection). Cellular and viral infections have been considered in mathematical models of different viruses in many works (see, e.g., [39,40,41,42,43,44,45,46,47,48]).

The main contributions of the paper are summarized as follows:

(1) We incorporate both CHIKV-to-monocyte and infected-to-monocyte transmissions into the CHIKV dynamics model.

(2) The rate of infection in model (1)–(4) is bilinear in the CHIKV and the uninfected monocytes. The actual incidence rate is probably not strictly linear. A less than linear response in CHIKV and infected monocytes could occur due to saturation at high CHIKV or infected monocyte concentrations. Therefore, it is reasonable for us to assume that the infection rate of modeling CHIKV infection is given by saturated mass action.

(3) Latent viral reservoirs serve as a major barrier in curing viral infection. Although antiretroviral treatment reduces the level of viruses significantly, there is still a low viral load due to ongoing latently infected cells reservoir reactivation. Therefore, we propose a model which incorporates two classes of infected monocytes: latently infected monocytes (w), which contain the CHIKV but do not produce it, and actively infected monocytes (y), which produce the CHIKV particles.

(4) In [49], the authors described the CHIKV replication cycle (see Fig. 1): “The virus enters susceptible cells through endocytosis, mediated by an unknown receptor. As the endosome is acidic, conformational changes occur resulting in the fusion of the viral and host cell membranes, causing the release of the nucleocapsid into the cytoplasm. The RNA genome is first translated into the 4nsPs, which together will form the replication complex and assist in several downstream processes (depicted by dashed arrowed line in Fig. 1). Subsequently, the genome is replicated to its negative-sense strand, which in turn will be used as a template for the synthesis of the 49S viral RNA and 26S subgenomic mRNA. The 26S subgenomic mRNA will be translated to give the structural proteins (C–pE2–6K–E1). After a round of processing by serine proteases, the capsid is released into the cytoplasm. The remaining structural proteins are further modified post-translationally in the endoplasmic reticulum and subsequently in the Golgi apparatus. E1 and E2 associate as a dimer and are transported to the host plasma membrane, where they will ultimately be incorporated onto the virion surface as trimeric spikes. Capsid protein will form the icosahedral nucleocapsid that will contain the replicated 49S genomic RNA before being assembled into a mature virion ready for budding. During budding the virions will acquire a membrane bilayer from part of the host cell membrane.”

Figure 1
figure 1

CHIKV replication cycle [49]

Full size image

Therefore, this process may take time period which can be incorporated into the CHIKV model by considering three types of discrete or distributed time delays and latently infected cells.

(5) We study the basic and global properties of the proposed models.

We mention that the qualitative analysis presented in this paper is not simply a straightforward generalization of analogous calculations developed in [36] and [37] where only CHIKV-to-monocyte has been considered. This is due to the incorporation of both CHIKV-to-monocyte and infected-to-monocyte transmissions in the present models.

2 CHIKV model with discrete-delays

In this section we propose the following CHIKV dynamics model with three discrete-time delays and with both CHIKV-to-monocyte and infected-to-monocyte transmissions:

$$\begin{aligned}& \dot{s}(t) =\varrho -\xi s(t)- \frac{\omega _{1}s(t)p(t)}{1+\mu _{1}p(t)}-\frac{\omega _{2}s(t)y(t)}{1+ \mu _{2}y(t)}, \end{aligned}$$
(5)
$$\begin{aligned}& \dot{w}(t) =(1-n)e^{-a_{1}\delta _{1}} \biggl[ \frac{\omega _{1}s(t- \delta _{1})p(t-\delta _{1})}{1+\mu _{1}p(t-\delta _{1})}+ \frac{\omega _{2}s(t- \delta _{2})y(t-\delta _{1})}{1+\mu _{2}y(t-\delta _{1})} \biggr] -(b+d)w(t), \end{aligned}$$
(6)
$$\begin{aligned}& \dot{y}(t) =ne^{-a_{2}\delta _{2}} \biggl[ \frac{\omega _{1}s(t-\delta _{2})p(t- \delta _{2})}{1+\mu _{1}p(t-\delta _{2})}+ \frac{\omega _{2}s(t-\delta _{2})y(t- \delta _{2})}{1+\mu _{2}y(t-\delta _{2})} \biggr] +dw(t)-\epsilon y(t), \end{aligned}$$
(7)
$$\begin{aligned}& \dot{p}(t) =\varkappa e^{-a_{3}\delta _{3}}y(t-\delta _{3})-cp(t)-rx(t)p(t), \end{aligned}$$
(8)
$$\begin{aligned}& \dot{x}(t) =\lambda +\rho x(t)p(t)-mx(t), \end{aligned}$$
(9)

where w is the concentration of latently infected monocytes. The CHIKV-uninfected and infected-uninfected incidence rates are given by \(\frac{\omega _{1}ps}{1+\mu _{1}p}\) and \(\frac{\omega _{2}ys}{1+\mu _{2}y}\), where a fraction n (where \(0< n<1\)) will become actively infected monocyte and \((1-n)\) will become latently infected monocytes. Constant b denotes the normal death rate constant of the latently infected monocytes. The latently infected monocytes are activated at rate \(dw(t)\). Here, \(\delta _{1}\) and \(\delta _{2}\) are the times between CHIKV entry a susceptible monocyte to be latently and actively infected monocytes, respectively. The immature CHIKV needs time \(\delta _{3}\) to be mature. The factors \(e^{-a_{1}\delta _{1}}\), \(e^{-a_{2}\delta _{2}}\), and \(e^{-a_{3}\delta _{3}}\) represent the probability of surviving to the age of \(\delta _{1}\), \(\delta _{2}\), and \(\delta _{3}\), respectively. Here, \(a_{1}\), \(a_{2}\), and \(a_{3}\) are positive constants.

We consider the initial conditions

$$\begin{aligned}& \begin{gathered} s(\varphi ) =\vartheta _{1}(\varphi ), \quad\quad w(\varphi )=\vartheta _{2}( \varphi ),\quad\quad y(\varphi )=\vartheta _{3}(\varphi ),\\ p(\varphi )=\vartheta _{4}(\varphi ),\quad\quad x(\varphi )=\vartheta _{5}( \varphi ), \\ \vartheta _{i}(\varphi ) \geq 0,\quad \varphi \in {}[ -k,0] \quad \text{and}\quad \vartheta _{i}\in C\bigl([-k,0], \mathbb{R}_{\geq 0}\bigr), \quad i=1,2,\ldots,5, \end{gathered} \end{aligned}$$
(10)

where \(k= \max \{ \delta _{1},\delta _{2},\delta _{3}\}\) and C is the Banach space of continuous functions mapping the interval \([-k,0]\) into \(\mathbb{R}_{\geq 0}\).

2.1 Basic properties

In the next lemma we establish that the solutions of the system are nonnegative and ultimately bounded.

Lemma 1

The solutions of system (5)–(9) with the initial (10) are nonnegative and ultimately bounded.

Proof

Equations (5) and (9) give \(\dot{s}| _{s=0}= \varrho >0\), \(\dot{x}| _{x=0}=\lambda >0\). Thus, for all \(t\geq 0\), \(s(t)>0\), and \(x(t)>0\). Moreover, from Eqs. (6)–(8), we get

$$\begin{aligned}& \begin{aligned} w(t) ={}&\vartheta _{2}(0)e^{-(b+d)t}+(1-n)e^{-a_{1}\delta _{1}} \int _{0} ^{t}e^{-(b+d)(t-\theta )}s(\theta -\delta _{1}) \\ &{}\times \biggl[\frac{\omega _{1}p( \theta -\delta _{1})}{1+\mu _{1}p(\theta -\delta _{1})}+\frac{\omega _{2}y( \theta -\delta _{1})}{1+\mu _{2}y(\theta -\delta _{1})} \biggr]\,d \theta \geq 0, \end{aligned} \\& \begin{aligned} y(t) ={}&\vartheta _{3}(0)e^{-\epsilon t}+ne^{-a_{2}\delta _{2}} \int _{0}^{t}e^{-\epsilon (t-\theta )} \\ &{}\times \biggl[s(\theta -\delta _{2}) \biggl(\frac{ \omega _{1}p(\theta -\delta _{2})}{1+\mu _{1}p(\theta -\delta _{2})}+\frac{ \omega _{2}y(\theta -\delta _{2})}{1+\mu _{2}y(\theta -\delta _{2})} \biggr)+dw(\theta ) \biggr]\,d\theta \geq 0, \end{aligned} \\& p(t) =\vartheta _{4}(0)e^{-\int _{0}^{t}(c+rx(\varphi ))\,d\varphi }+ \int _{0}^{t}e^{-\int _{\theta }^{t}{(c+rx(\varphi ))\,d\varphi }}{\bigl\{ \varkappa e^{-a_{3}\delta _{3}}y(\theta -\delta _{3})\bigr\} \,d\theta } \geq 0 \quad \text{for } t\in {}[ 0,k]. \end{aligned}$$

By recursive argument, we show that \(w(t)\geq 0\), \(y(t)\geq 0\), and \(p(t)\geq 0\) for all \(t\geq 0\). From Eq. (5) we have \(\lim _{t \rightarrow \infty }\sup s(t)\leq \frac{\varrho }{\xi }\). Let us consider

$$ h_{1}(t)=(1-n)e^{-a_{1}\delta _{1}}s(t-\delta _{1})+ne^{-a_{2}\delta _{2}}s(t- \delta _{2})+w(t)+y(t), $$

then

$$\begin{aligned} \dot{h}_{1}(t) &=(1-n)e^{-a_{1}\delta _{1}} \biggl[\varrho -\xi s(t- \delta _{1})-\frac{\omega _{1}s(t-\delta _{1})p(t-\delta _{1})}{1+\mu _{1}p(t- \delta _{1})}-\frac{\omega _{2}s(t-\delta _{1})y(t-\delta _{1})}{1+\mu _{2}y(t-\delta _{1})} \biggr] \\ & \quad{}+ne^{-a_{2}\delta _{2}} \biggl[\varrho -\xi s(t-\delta _{2})- \frac{ \omega _{1}s(t-\delta _{2})p(t-\delta _{2})}{1+\mu _{1}p(t-\delta _{2})}-\frac{ \omega _{2}s(t-\delta _{2})y(t-\delta _{2})}{1+\mu _{2}y(t-\delta _{2})} \biggr] \\ & \quad{}+(1-n)e^{-a_{1}\delta _{1}} \biggl[\frac{\omega _{1}s(t-\delta _{1})p(t- \delta _{1})}{1+\mu _{1}p(t-\delta _{1})}+ \frac{\omega _{2}s(t-\delta _{1})y(t- \delta _{1})}{1+\mu _{2}y(t-\delta _{1})} \biggr]-(b+d)w(t) \\ & \quad{}+ne^{-a_{2}\delta _{2}} \biggl[\frac{\omega _{1}s(t-\delta _{2})p(t- \delta _{2})}{1+\mu _{1}p(t-\delta _{2})}+\frac{\omega _{2}s(t-\delta _{2})y(t- \delta _{2})}{1+\mu _{2}y(t-\delta _{2})} \biggr]+dw(t)-\epsilon y(t) \\ &=\varrho (1-n)e^{-a_{1}\delta _{1}}+\varrho ne^{-a_{2}\delta _{2}}-(1-n)e ^{-a_{1}\delta _{1}}\xi s(t-\delta _{1})-ne^{-a_{2}\delta _{2}}\xi s(t- \delta _{2}) \\ &\quad{} -bw(t)-\epsilon y(t) \\ &\leq \varrho -\sigma _{1}\bigl[(1-n)e^{-a_{1}\delta _{1}}s(t-\delta _{1})+ne ^{-a_{2}\delta _{2}}s(t-\delta _{2})+w(t)+y(t) \bigr] \\ &=\varrho -\sigma _{1}h_{1}(t), \end{aligned}$$

where \(\sigma _{1}= \min \{ \xi ,b,\epsilon \}\). It follows that \(\lim _{t\rightarrow \infty }\sup h_{1}(t)\leq \Delta _{1}\), where \(\Delta _{1}=\frac{\varrho }{\sigma _{1}} \). This yields \(\lim _{t\rightarrow \infty }\sup w(t)\leq \Delta _{1}\) and \(\lim _{t\rightarrow \infty }\sup y(t)\leq \Delta _{1}\). Define

$$ h_{2}(t)=p(t)+\frac{r}{\rho }x(t), $$

then

$$\begin{aligned} \dot{h}_{2}(t) &=\varkappa e^{-a_{3}\delta _{3}}y(t-\delta _{3})-cp(t)+\frac{r}{ \rho }\lambda -\frac{r}{\rho }mx(t) \\ &\leq \varkappa \Delta _{1}+\frac{r}{\rho }\lambda -\sigma _{2}\biggl[p(t)+\frac{r}{ \rho }x(t)\biggr] \\ &=\frac{\varkappa \rho \Delta _{1}+r\lambda }{\rho }-\sigma _{2}h_{2}(t), \end{aligned}$$

where \(\sigma _{2}= \min \{c,m\}\). Then \(\lim _{t\rightarrow \infty }\sup h_{2}(t)\leq \Delta _{2}\), where \(\Delta _{2}=\frac{ \varkappa \rho \Delta _{1}+r\lambda }{\rho \sigma _{2}}\). The nonnegativity of the solution implies that \(\lim _{t\rightarrow \infty }\sup p(t)\leq \Delta _{2}\) and \(\lim _{t\rightarrow \infty }\sup x(t)\leq \Delta _{3}\), where \(\Delta _{3}=\frac{ \rho }{r}\Delta _{2}\). This shows the ultimate boundedness of \(s(t)\), \(w(t)\), \(y(t)\), \(p(t)\), and \(x(t)\). □

Proving the nonnegativity and boundedness of solutions of the model assures the biological viability of the model; and so, we now move on to determining the equilibria of the system. So, in the next section, the threshold parameter for the existence of equilibria is calculated.

2.2 Equilibria

We define the basic reproduction number of model (5)–(9) as follows:

$$ \mathcal{R}_{0}=\frac{\alpha _{1}\varrho [ m\varkappa \omega _{1}e ^{-a_{3}\delta _{3}}+\omega _{2}(cm+r\lambda ) ] }{\xi \epsilon (cm+r \lambda )}, $$
(11)

where \(\alpha _{1}=\frac{d(1-n)e^{-a_{1}\delta _{1}}+n(b+d)e^{-a_{2} \delta _{2}}}{b+d}\). The parameter \(R_{0}\) represents the average number of secondary infections and it can be written as \(R_{0}=R_{01}+R_{02}\), where

$$\begin{aligned}& \mathcal{R}_{01} =\frac{\alpha _{1}\varrho m\varkappa \omega _{1}e ^{-a_{3}\delta _{3}}}{\xi \epsilon (cm+r\lambda )}, \\& \mathcal{R}_{02} =\frac{\alpha _{1}\varrho \omega _{2}}{\xi \epsilon }. \end{aligned}$$

In fact, \(R_{01}\) is the average number of secondary viruses caused by a virus, that is, the basic reproduction number corresponding to CHIKV-to-monocyte infection mode, while \(R_{02}\) is the average number of secondary infected monocytes caused by an infected monocyte, that is, the basic reproduction number corresponding to infected-to-monocyte infection mode.

Remark 1

We note that the basic reproduction number of model (1)–(4) presented in [35] is given by

$$ \mathcal{R}_{(1)-(4)}=\frac{\varrho m\varkappa \omega _{1}}{\xi \epsilon (cm+r\lambda )}, $$

which does not depend on the maturation time delay δ. Therefore, the time delay δ does not affect the stability properties of the equilibria. In contrast, since the basic reproduction number R of our proposed model depends on time delay parameters \(\delta _{1}\), \(\delta _{2}\), and \(\delta _{3}\), the time delay has significant effect on the stability properties of the equilibria.

Lemma 2

If \(\mathcal{R}_{0}\leq 1\), then system (5)–(9) has only one equilibrium \(\varOmega _{0}\), and if \(\mathcal{R}_{0}>1\), then the system has two equilibria \(\varOmega _{0}\)and \(\varOmega _{1}\).

The proof of Lemma 2 is given in the Appendix.

Remark 2

In the proof of Lemma 1, we follow the same lines as the proof of Theorem 2.1 in [35]. However, in [35], the existence of equilibria depended on the roots of quadratic equation

$$ q_{1}p^{2}+q_{2}p+q_{3}=0, $$
(12)

which is simpler than equation (12). This difference comes from the incorporation of infected-to-monocyte transmission in our model.

2.3 Global properties

The global stability of the equilibria will be established by constructing Lyapunov functions following the method presented [50] and followed by [51,52,53,54,55,56]. To construct the required Lyapunov functional, a positive definite function

$$ G(z)=z-1-\ln z $$

has been used. It can be easily proved that \(G(z)\geq 0\) for any \(z>0\). We use the notation \((s,w,y,p,x)=(s(t),w(t),y(t),p(t),x(t))\). Now the following two theorems are stated, respectively, for the global stability of \(\varOmega _{0}\) and \(\varOmega _{1}\).

Theorem 1

For system (5)–(9), if \(\mathcal{R} _{0}\leq 1\), then \(\varOmega _{0}\)is globally asymptotically stable (G.A.S.).

Proof

Construct a Lyapunov function \(U_{0}(s,w,y,p,x)\) as follows:

$$\begin{aligned} U_{0} &=\alpha _{1}s_{0}G \biggl( \frac{s}{s_{0}} \biggr)+\frac{d}{b+d}w+y+\frac{ \alpha _{1}\omega _{1}s_{0}}{c+rx_{0}}p+ \frac{r\alpha _{1}\omega _{1}s _{0}}{\rho (c+rx_{0})}x_{0}G \biggl(\frac{x}{x_{0}} \biggr) \\ & \quad{}+\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d} \int _{0}^{\delta _{1}} \biggl(\frac{ \omega _{1}s(t-\theta )p(t-\theta )}{1+\mu _{1}p(t-\theta )}+ \frac{ \omega _{2}s(t-\theta )y(t-\theta )}{1+\mu _{2}y(t-\theta )} \biggr)\,d \theta \\ & \quad{}+ne^{-a_{2}\delta _{2}} \int _{0}^{\delta _{2}} \biggl(\frac{\omega _{1}s(t- \theta )p(t-\theta )}{1+\mu _{1}p(t-\theta )}+ \frac{\omega _{2}s(t- \theta )y(t-\theta )}{1+\mu _{2}y(t-\theta )} \biggr)\,d\theta \\ & \quad{}+\frac{\alpha _{1}\omega _{1}s_{0}\varkappa e^{-a_{3}\delta _{3}}}{c+rx _{0}} \int _{0}^{\delta _{3}}y(t-\theta )\,d\theta . \end{aligned}$$

Clearly, \(U_{0}(s_{0},0,0,0,x_{0})=0\) and \(U_{0}(s,w,y,p,x)>0\) for all \(s,y,p,x>0\). Calculating \(\frac{dU_{0}}{dt}\) along system (5)–(9), we obtain

$$\begin{aligned} \frac{dU_{0}}{dt} &=\alpha _{1} \biggl(1-\frac{s_{0}}{s} \biggr) \biggl( \varrho -\xi s-\frac{\omega _{1}sp}{1+\mu _{1}p}-\frac{\omega _{2}sy}{1+ \mu _{2}y} \biggr) \\ & \quad{} +\frac{d}{b+d} \biggl[(1-n)e^{-a_{1}\delta _{1}}s(t-\delta _{1}) \biggl(\frac{ \omega _{1}p(t-\delta _{1})}{1+\mu _{1}p(t-\delta _{1})}+\frac{\omega _{2}y(t- \delta _{1})}{1+\mu _{2}y(t-\delta _{1})} \biggr)-(b+d)w \biggr] \\ & \quad{}+ne^{-a_{2}\delta _{2}}s(t-\delta _{2}) \biggl( \frac{\omega _{1}p(t- \delta _{2})}{1+\mu _{1}p(t-\delta _{2})}+\frac{\omega _{2}y(t-\delta _{2})}{1+ \mu _{2}y(t-\delta _{2})} \biggr)+dw-\epsilon y \\ &\quad{} +\frac{\alpha _{1}\omega _{1}s_{0}}{c+rx_{0}} \bigl(\varkappa e^{-a _{3}\delta _{3}}y(t-\delta _{3})-cp-rxp \bigr)+\frac{r\alpha _{1}\omega _{1}s_{0}}{\rho (c+rx_{0})} \biggl(1- \frac{x_{0}}{x} \biggr) (\lambda +\rho xp-mx ) \\ &\quad{} +\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d} \biggl[\frac{\omega _{1}sp}{1+ \mu _{1}p}+ \frac{\omega _{2}sy}{1+\mu _{2}y} \\ &\quad{}- \biggl(\frac{\omega _{1}s(t- \delta _{1})p(t-\delta _{1})}{1+\mu _{1}p(t-\delta _{1})}+\frac{\omega _{2}s(t-\delta _{1})y(t-\delta _{1})}{1+\mu _{2}y(t-\delta _{1})} \biggr) \biggr] \\ &\quad{} +ne^{-a_{2}\delta _{2}} \biggl[\frac{\omega _{1}sp}{1+\mu _{1}p}+\frac{ \omega _{2}sy}{1+\mu _{2}y}- \biggl(\frac{\omega _{1}s(t-\delta _{2})p(t- \delta _{2})}{1+\mu _{1}p(t-\delta _{2})}+\frac{\omega _{2}s(t-\delta _{2})y(t- \delta _{2})}{1+\mu _{2}y(t-\delta _{2})} \biggr) \biggr] \\ &\quad{} +\frac{\alpha _{1}\omega _{1}s_{0}}{c+rx_{0}}\varkappa e^{-a_{3} \delta _{3}} \bigl(y-y(t-\delta _{3}) \bigr). \end{aligned}$$
(13)

Simplify Eq. (13) as follows:

$$\begin{aligned} \frac{dU_{0}}{dt} &=-\alpha _{1}\xi \frac{(s-s_{0})^{2}}{s}- \frac{ \alpha _{1}\omega _{1}s_{0}\mu _{1}p^{2}}{1+\mu _{1}p}-\frac{\alpha _{1} \omega _{2}s_{0}\mu _{2}y^{2}}{1+\mu _{2}y} \\ & \quad{} +\epsilon \biggl(\frac{\alpha _{1}\omega _{2}s_{0}}{\epsilon }+ \frac{\alpha _{1}\omega _{1}s_{0}\varkappa e^{-a\delta _{3}}}{\epsilon (c+rx_{0})}-1 \biggr)y +\frac{r\alpha _{1}\omega _{1}s_{0}}{\rho (c+rx_{0})} \biggl(1-\frac{x _{0}}{x} \biggr) (mx_{0}-mx ) \\ &=-\alpha _{1}\xi \frac{(s-s_{0})^{2}}{s}-\frac{\alpha _{1}\omega _{1}s _{0}\mu _{1}p^{2}}{1+\mu _{1}p}- \frac{\alpha _{1}\omega _{2}s_{0}\mu _{2}y ^{2}}{1+\mu _{2}y}-\frac{r\alpha _{1}\omega _{1}s_{0}m}{\rho (c+rx_{0})}\frac{(x-x _{0})^{2}}{x} \\ &\quad{}+\epsilon ( \mathcal{R}_{0}-1)y. \end{aligned}$$
(14)

If \(\mathcal{R}_{0}\leq 1\), then \(\frac{dU_{0}}{dt}\leq 0\) for all \(s,w,y,p,x>0\). Moreover, \(\frac{dU_{0}}{dt}=0\) when \(s=s_{0}\), \(x=x_{0}\) and \(y=p=0\). Let \(D= \{ (s,w,y,p,x): \frac{dU_{0}}{dt}=0 \} \) and N be the largest invariant subset of D. The trajectory of model (5)–(9) tends to N [57]. All the elements of N satisfy \(y=p=0\). Then, from Eq. (7), we get

$$ \dot{y}(t)=0=dw(t)\quad \Longrightarrow \quad w(t)=0. $$

Hence, \(N= \{ \varOmega _{0} \} \). Therefore by LaSalle’s invariance principle for delay systems (Theorem 5.3 of Kuang [58]), we get \(\varOmega _{0}\) is G.A.S. when \(R_{0}\leq 1\). □

Theorem 2

For system (5)–(9), if \(\mathcal{R} _{0}>1\), then \(\varOmega _{1}\)is G.A.S.

Proof

Let a function \(U_{1}(s,w,y,p,x)\) be defined as follows:

$$\begin{aligned} U_{1} &=\alpha _{1}s_{1}G \biggl( \frac{s}{s_{1}} \biggr)+\frac{d}{b+d}w _{1}G \biggl( \frac{w}{w_{1}} \biggr)+y_{1}G \biggl(\frac{y}{y_{1}} \biggr) \\ & \quad{}+\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{\varkappa e^{-a_{3}\delta _{3}}(1+\mu _{1}p_{1})y_{1}}p_{1}G \biggl(\frac{p}{p_{1}} \biggr)+\frac{r \alpha _{1}\omega _{1}s_{1}p_{1}}{\rho \varkappa e^{-a_{3}\delta _{3}}(1+ \mu _{1}p_{1})y_{1}}x_{1}G \biggl(\frac{x}{x_{1}} \biggr) \\ & \quad{}+\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{1}s_{1}p_{1}}{1+ \mu _{1}p_{1}} \int _{0}^{\delta _{1}}G \biggl(\frac{s(t-\theta )p(t-\theta )(1+\mu _{1}p_{1})}{s_{1}p_{1}(1+\mu _{1}p(t-\theta ))} \biggr)\,d\theta \\ & \quad{}+\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{2}s_{1}y_{1}}{1+ \mu _{2}y_{1}} \int _{0}^{\delta _{1}}G \biggl(\frac{s(t-\theta )y(t-\theta )(1+\mu _{2}y_{1})}{s_{1}y_{1}(1+\mu _{2}y(\delta -\theta ))} \biggr)\,d \theta \\ & \quad{}+ne^{-a_{2}\delta _{2}}\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \int _{0}^{\delta _{2}}G \biggl(\frac{s(t-\theta )p(t-\theta )(1+\mu _{1}p _{1})}{s_{1}p_{1}(1+\mu _{1}p(\delta -\theta ))} \biggr)\,d\theta \\ & \quad{}+ne^{-a_{2}\delta _{2}}\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \int _{0}^{\delta _{2}}G \biggl(\frac{s(t-\theta )y(t-\theta )(1+\mu _{2}y _{2})}{s_{1}y_{1}(1+\mu _{2}y(\delta -\theta ))} \biggr)\,d\theta \\ & \quad{}+\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \int _{0}^{ \delta _{3}}G \biggl(\frac{y(t-\theta )}{y_{1}} \biggr)\,d\theta . \end{aligned}$$

Clearly, \(U_{1}(s,w,y,p,x)>0\) for all \(s,w,y,p,x>0\) and \(U_{1}(s_{1},w _{1},y_{1},p_{1},x_{1})=0\). Calculating \(\frac{dU_{1}}{dt}\) along the trajectories of (5)–(9), we obtain

$$\begin{aligned} \frac{dU_{1}}{dt} &=\alpha _{1} \biggl(1-\frac{s_{1}}{s} \biggr) \biggl( \varrho -\xi s-\frac{\omega _{1}sp}{1+\mu _{1}p}-\frac{\omega _{2}sy}{1+ \mu _{2}y} \biggr) \\ & \quad{}+\frac{d}{b+d} \biggl(1-\frac{w_{1}}{w} \biggr) \\ & \quad{}\times \biggl[(1-n)e^{-a_{1} \delta _{1}} \biggl(\frac{\omega _{1}s(t-\delta _{1})p(t-\delta _{1})}{1+\mu _{1}p(t-\delta _{1})}+\frac{\omega _{2}s(t-\delta _{1})y(t-\delta _{1})}{1+ \mu _{2}y(t-\delta _{1})} \biggr)-(b+d)w \biggr] \\ & \quad{}+ \biggl(1-\frac{y_{1}}{y} \biggr) \biggl[ne^{-a_{2}\delta _{2}} \biggl(\frac{ \omega _{1}s(t-\delta _{2})p(t-\delta _{2})}{1+\mu _{1}p(t-\delta _{2})}+\frac{ \omega _{2}s(t-\delta _{2})y(t-\delta _{2})}{1+\mu _{2}y(t-\delta _{2})} \biggr)+dw-\epsilon y \biggr] \\ &\quad{} +\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{\varkappa e^{-a_{3}\delta _{3}}(1+\mu _{1}p_{1})y_{1}} \biggl(1-\frac{p_{1}}{p} \biggr) \bigl( \varkappa e^{-a_{3}\delta _{3}}y(t-\delta _{3})-cp-rxp \bigr) \\ & \quad{}+\frac{r\alpha _{1}\omega _{1}s_{1}p_{1}}{\rho \varkappa e^{-a_{3} \delta _{3}}(1+\mu _{1}p_{1})y_{1}} \biggl(1-\frac{x_{1}}{x} \biggr) ( \lambda +\rho xp-mx ) \\ & \quad{}+\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{1}s_{1}p_{1}}{1+ \mu _{1}p_{1}} \biggl[ \frac{sp(1+\mu _{1}p_{1})}{s_{1}p_{1}(1+\mu _{1}p)}-\frac{s(t- \delta _{1})p(t-\delta _{1})(1+\mu _{1}p_{1})}{s_{1}p_{1}(1+\mu _{1}p(t- \delta _{1}))} \\ & \quad{}+\ln \biggl(\frac{s(t-\delta _{1})p(t-\delta _{1})(1+\mu _{1}p)}{sp(1+ \mu _{1}p(t-\delta _{1}))} \biggr) \biggr] \\ &\quad{} +\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{2}s_{1}y_{1}}{1+ \mu _{2}y_{1}} \biggl[ \frac{sy(1+\mu _{2}y_{1})}{s_{1}y_{1}(1+\mu _{2}y)}-\frac{s(t- \delta _{1})y(t-\delta _{1})(1+\mu _{2}y_{1})}{s_{1}y_{1}(1+\mu _{2}y(t- \delta _{1}))} \\ & \quad{}+\ln \biggl(\frac{s(t-\delta _{1})y(t-\delta _{1})(1+\mu _{2}y)}{sy(1+ \mu _{2}y(t-\delta _{1}))} \biggr) \biggr] \\ &\quad{} +ne^{-a_{2}\delta _{2}}\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl[\frac{sp(1+\mu _{1}p_{1})}{s_{1}p_{1}(1+\mu _{1}p)}- \frac{s(t- \delta _{2})p(t-\delta _{2})(1+\mu _{1}p_{1})}{s_{1}p_{1}(1+\mu _{1}p(t- \delta _{2}))} \\ & \quad{}+\ln \biggl(\frac{s(t-\delta _{2})p(t-\delta _{2})(1+\mu _{1}p)}{sp(1+ \mu _{1}p(t-\delta _{2}))} \biggr) \biggr] \\ & \quad{}+ne^{-a_{2}\delta _{2}}\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggl[\frac{sy(1+\mu _{2}y_{1})}{s_{1}y_{1}(1+\mu _{2}y)}- \frac{s(t- \delta _{2})y(t-\delta _{2})(1+\mu _{2}y_{1})}{s_{1}y_{1}(1+\mu _{2}y(t- \delta _{2}))} \\ & \quad{}+\ln \biggl(\frac{s(t-\delta _{2})y(t-\delta _{2})(1+\mu _{2}y)}{sy(1+ \mu _{2}y(t-\delta _{2}))} \biggr) \biggr] \\ &\quad{} +\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl[\frac{y}{y _{1}}- \frac{y(t-\delta _{3})}{y_{1}}+\ln \biggl( \frac{y(t-\delta _{3})}{y} \biggr) \biggr]. \end{aligned}$$
(15)

Simplifying Eq. (15), we get

$$\begin{aligned} \frac{dU_{1}}{dt} &=\alpha _{1} \biggl(1-\frac{s_{1}}{s} \biggr) (\varrho -\xi s)+\alpha _{1} \biggl(\frac{\omega _{1}s_{1}p}{1+\mu _{1}p}+ \frac{ \omega _{2}s_{1}y}{1+\mu _{2}y} \biggr) \\ & \quad{}-\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d} \biggl[\frac{\omega _{1}s(t- \delta _{1})p(t-\delta _{1})}{1+\mu _{1}p(t-\delta _{1})}+ \frac{\omega _{2}s(t-\delta _{1})y(t-\delta _{1})}{1+\mu _{2}y(t-\delta _{1})} \biggr]\frac{w _{1}}{w}+dw_{1} \\ & \quad{}-ne^{-a_{2}\delta _{2}} \biggl[\frac{\omega _{1}s(t-\delta _{2})p(t- \delta _{2})}{1+\mu _{1}p(t-\delta _{2})}+\frac{\omega _{2}s(t-\delta _{2})y(t- \delta _{2})}{1+\mu _{2}y(t-\delta _{2})} \biggr]\frac{y_{1}}{y}-dw\frac{y _{1}}{y}-\epsilon y+\epsilon y_{1} \\ & \quad{}-\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}\frac{y(t- \delta _{3})p_{1}}{y_{1}p}-\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{ \varkappa e^{-a_{3}\delta _{3}}(1+\mu _{1}p_{1})y_{1}}cp+ \frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{\varkappa e^{-a_{3}\delta _{3}}(1+\mu _{1}p _{1})y_{1}}cp_{1} \\ & \quad{}+\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{\varkappa e^{-a_{3}\delta _{3}}(1+\mu _{1}p_{1})y_{1}}rxp_{1}-\frac{\alpha _{1}\omega _{1}s_{1}p _{1}}{\varkappa e^{-a_{3}\delta _{3}}(1+\mu _{1}p_{1})y_{1}}rx_{1}p \\ & \quad{}+\frac{r\alpha _{1}\omega _{1}s_{1}p_{1}}{\rho \varkappa e^{-a_{3} \delta _{3}}(1+\mu _{1}p_{1})y_{1}} \biggl(1-\frac{x_{1}}{x} \biggr) (\lambda -mx) \\ & \quad{}+\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d} \biggl[\frac{\omega _{1}s_{1}p _{1}}{1+\mu _{1}p_{1}}\ln \biggl( \frac{s(t-\delta _{1})p(t-\delta _{1})(1+ \mu _{1}p)}{sp(1+\mu _{1}p(t-\delta _{1}))} \biggr) \\ & \quad{}+\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}}\ln \biggl(\frac{s(t- \delta _{1})y(t-\delta _{1})(1+\mu _{2}y)}{sy(1+\mu _{2}y(t-\delta _{1}))} \biggr) \biggr] \\ & \quad{}+ne^{-a_{2}\delta _{2}} \biggl[\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p _{1}}\ln \biggl( \frac{s(t-\delta _{2})p(t-\delta _{2})(1+\mu _{1}p)}{sp(1+ \mu _{1}p(t-\delta _{2}))} \biggr) \\ & \quad{}+\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y _{1}}\ln \biggl( \frac{s(t-\delta _{2})y(t-\delta _{2})(1+\mu _{2}y)}{sy(1+ \mu _{2}y(t-\delta _{2}))} \biggr) \biggr] \\ & \quad{}+\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl[\frac{y}{y _{1}}+\ln \biggl( \frac{y(t-\delta _{3})}{y} \biggr) \biggr]. \end{aligned}$$

Applying the equilibria conditions for \(\varOmega _{1}\),

$$\begin{aligned}& \varrho =\xi s_{1}+\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+\frac{ \omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}}, \quad\quad w_{1}=\frac{(1-n)e^{-a_{1}\delta _{1}}}{(b+d)} \biggl(\frac{ \omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+ \frac{\omega _{2}s_{1}y_{1}}{1+ \mu _{2}y_{1}} \biggr), \\& \begin{aligned} \epsilon y_{1} &=\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d} \biggl( \frac{ \omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+\frac{\omega _{2}s_{1}y_{1}}{1+ \mu _{2}y_{1}} \biggr)+ne^{-a_{2}\delta _{2}} \biggl( \frac{\omega _{1}s_{1}p _{1}}{1+\mu _{1}p_{1}}+\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr) \\ &=\alpha _{1} \biggl(\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+\frac{ \omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr), \end{aligned} \\& cp_{1} =\varkappa e^{-a_{3}\delta _{3}}y_{1}-rx_{1}p_{1}, \quad\quad \lambda =mx_{1}-\rho x_{1}p_{1}, \end{aligned}$$

we get

$$\begin{aligned} \frac{dU_{1}}{dt} &=\alpha _{1} \biggl(1-\frac{s_{1}}{s} \biggr) ( \xi s_{1}-\xi s )+\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d} \frac{ \omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl(1-\frac{s_{1}}{s} \biggr) \\ & \quad{}+ne ^{-a_{2}\delta _{2}} \frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl(1-\frac{s _{1}}{s} \biggr) \\ & \quad{}+\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{2}s_{1}y _{1}}{1+\mu _{2}y_{1}} \biggl(1- \frac{s_{1}}{s} \biggr)+ne^{-a_{2}\delta _{2}}\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggl(1- \frac{s_{1}}{s} \biggr) \\ & \quad{}+\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}\frac{(1+\mu _{1}p_{1})p}{(1+\mu _{1}p)p_{1}}+\frac{\alpha _{1}\omega _{2}s_{1}y_{1}}{1+ \mu _{2}y_{1}} \frac{(1+\mu _{2}y_{1})y}{(1+\mu _{2}y)y_{1}} \\ &\quad{} -\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{1}s_{1}p_{1}}{1+ \mu _{1}p_{1}} \biggl[ \frac{s(t-\delta _{1})p(t-\delta _{1})(1+\mu _{1}p _{1})w_{1}}{s_{1}p_{1}(1+\mu _{1}p(t-\delta _{1}))w} \biggr] \\ & \quad{}-\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{2}s_{1}y _{1}}{1+\mu _{2}y_{1}} \biggl[ \frac{s(t-\delta _{1})y(t-\delta _{1})(1+\mu _{2}y_{1})w_{1}}{s_{1}y_{1}(1+\mu _{2}y(t-\delta _{1}))w} \biggr] \\ & \quad{}+\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d} \biggl[\frac{\omega _{1}s _{1}p_{1}}{1+\mu _{1}p_{1}}+ \frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr] \\ & \quad{}-ne^{-a_{2}\delta _{2}}\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl[ \frac{s(t-\delta _{2})p(t-\delta _{2})(1+\mu _{1}p_{1})y_{1}}{s_{1}p_{1}(1+\mu _{1}p(t- \delta _{2}))y} \biggr] \\ & \quad{}-ne^{-a_{2}\delta _{2}} \frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggl[\frac{s(t-\delta _{2})y(t- \delta _{2}(1+\mu _{2}y_{1}))y_{1}}{s_{1}y_{1}(1+\mu _{2}y(t-\delta _{2}))y} \biggr] \\ & \quad{}-\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d} \biggl[\frac{\omega _{1}s _{1}p_{1}}{1+\mu _{1}p_{1}}+ \frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr] \frac{wy_{1}}{w_{1}y} \\ & \quad{}-\frac{\alpha _{1}\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}}\frac{y}{y _{1}}+\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d} \biggl[\frac{\omega _{1}s _{1}p_{1}}{1+\mu _{1}p_{1}}+ \frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr] \\ & \quad{}+ne^{-a_{2}\delta _{2}} \biggl[\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+\frac{\omega _{2}s _{1}y_{1}}{1+\mu _{2}y_{1}} \biggr] \\ & \quad{}-\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl[\frac{y(t- \delta _{3})p_{1}}{y_{1}p} \biggr]- \frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{1+ \mu _{1}p_{1}}\frac{p}{p_{1}}+\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d} \frac{ \omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \\ & \quad{}+ne^{-a_{2}\delta _{2}}\frac{ \omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \\ & \quad{}-\frac{2r\alpha _{1}s_{1}p_{1}\omega _{1}}{\varkappa e^{-a_{3}\delta _{3}}(1+\mu _{1}p_{1})y_{1}}x_{1}p_{1}+ \frac{r\alpha _{1}s_{1}p_{1} \omega _{1}}{\varkappa e^{-a_{3}\delta _{3}}(1+\mu _{1}p_{1})y_{1}}x_{1}p _{1} \biggl( \frac{x}{x_{1}} \biggr) \\ & \quad{}+\frac{r\alpha _{1}s_{1}p_{1}\omega _{1}}{ \varkappa e^{-a_{3}\delta _{3}}(1+\mu _{1}p_{1})y_{1}}x_{1}p_{1} \biggl(\frac{x _{1}}{x} \biggr) \\ & \quad{}-\frac{r\alpha _{1}s_{1}p_{1}m\omega _{1}}{\rho \varkappa e^{-a_{3} \delta _{3}}(1+\mu _{1}p_{1})y_{1}}\frac{(x-x_{1})^{2}}{x} \\ & \quad{}+\frac{d(1-n)e ^{-a_{1}\delta _{1}}}{b+d} \frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \ln \biggl[\frac{s(t-\delta _{1})p(t-\delta _{1})(1+\mu _{1}p)}{sp(1+\mu _{1}p(t-\delta _{1}))} \biggr] \\ &\quad{} +\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{2}s_{1}y_{1}}{1+ \mu _{2}y_{1}}\ln \biggl[ \frac{s(t-\delta _{1})y(t-\delta _{1})(1+\mu _{2}y)}{sy(1+ \mu _{2}y(t-\delta _{1}))} \biggr] \\ & \quad{}+ne^{-a_{2}\delta _{2}}\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \ln \biggl[ \frac{s(t-\delta _{2})p(t-\delta _{2})(1+\mu _{1}p)}{sp(1+\mu _{1}p(t- \delta _{2}))} \biggr] \\ &\quad{} +ne^{-a_{2}\delta _{2}}\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \ln \biggl[ \frac{s(t-\delta _{2})y(t-\delta _{2})(1+\mu _{2}y)}{sy(1+\mu _{2}y(t- \delta _{2}))} \biggr] \\ & \quad{}+\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p _{1}}\ln \biggl[ \frac{y(t-\delta _{3})}{y} \biggr]. \end{aligned}$$
(16)

Using the following equations:

$$\begin{aligned}& \begin{aligned} \ln \biggl(\frac{s(t-\delta _{1})p(t-\delta _{1})(1+\mu _{1}p)}{sp(1+\mu _{1}p(t- \delta _{1}))} \biggr) &=\ln \biggl( \frac{s_{1}}{s} \biggr)+\ln \biggl(\frac{s(t- \delta _{1})p(t-\delta _{1})(1+\mu _{1}p_{1})w_{1}}{s_{1}p_{1}(1+\mu _{1}p(t- \delta _{1}))w} \biggr) \\ & \quad{}+\ln \biggl(\frac{wy_{1}}{w_{1}y} \biggr)+\ln \biggl( \frac{yp_{1}}{y _{1}p} \biggr)+\ln \biggl(\frac{1+\mu _{1}p}{1+\mu _{1}p_{1}} \biggr), \end{aligned} \\& \begin{aligned} \ln \biggl(\frac{s(t-\delta _{1})y(t-\delta _{1})(1+\mu _{2}y)}{sy(1+\mu _{2}y(t- \delta _{1}))} \biggr) &=\ln \biggl( \frac{s_{1}}{s} \biggr)+\ln \biggl(\frac{s(t- \delta _{1})y(t-\delta _{1})(1+\mu _{2}y_{1})w_{1}}{s_{1}y_{1}(1+\mu _{2}y(t- \delta _{1}))w} \biggr) \\ & \quad{} +\ln \biggl( \frac{wy_{1}}{w_{1}y} \biggr) +\ln \biggl(\frac{1+\mu _{2}y}{1+\mu _{2}y_{1}} \biggr), \end{aligned} \\& \begin{aligned} \ln \biggl(\frac{s(t-\delta _{2})p(t-\delta _{2})(1+\mu _{1}p)}{sp(1+\mu _{1}p(t- \delta _{2}))} \biggr) &=\ln \biggl( \frac{s_{1}}{s} \biggr)+\ln \biggl(\frac{s(t- \delta _{2})p(t-\delta _{2})(1+\mu _{1}p_{1})y_{1}}{s_{1}p_{1}(1+\mu _{1}p(t- \delta _{2}))y} \biggr) \\ & \quad{} +\ln \biggl( \frac{yp_{1}}{y_{1}p} \biggr) +\ln \biggl(\frac{1+\mu _{1}p}{1+\mu _{1}p_{1}} \biggr), \end{aligned} \\& \begin{aligned}[b] \ln \biggl(\frac{s(t-\delta _{2})y(t-\delta _{2})(1+\mu _{2}y)}{sy(1+\mu _{2}y(t- \delta _{2}))} \biggr) &=\ln \biggl(\frac{s_{1}}{s} \biggr)+\ln \biggl(\frac{s(t- \delta _{2})y(t-\delta _{2})(1+\mu _{2}y_{1})}{s_{1}y(1+\mu _{2}y(t-\delta _{2}))} \biggr) \\ &\quad{} +\ln \biggl(\frac{1+\mu _{2}y}{1+\mu _{2}y_{1}} \biggr), \end{aligned} \\& \ln \biggl(\frac{y(t-\delta _{3})}{y} \biggr) =\ln \biggl(\frac{y(t- \delta _{3})p_{1}}{y_{1}p} \biggr)+\ln \biggl(\frac{y_{1}p}{yp_{1}} \biggr), \end{aligned}$$

we get

$$\begin{aligned} \frac{dU_{1}}{dt} &=-\alpha _{1}\xi \frac{(s-s_{1})^{2}}{s}- \frac{r \alpha _{1}s_{1}p_{1}m\omega _{1}}{\rho \varkappa e^{-a_{3}\delta _{3}}(1+ \mu _{1}p_{1})y_{1}}\frac{(x-x_{1})^{2}}{x} \\ & \quad{}-\frac{r\alpha _{1}s_{1}p _{1}\omega _{1}}{\varkappa e^{-a_{3}\delta _{3}}(1+\mu _{1}p_{1})y_{1}}x _{1}p_{1} \biggl[2-\frac{x}{x_{1}}- \frac{x_{1}}{x} \biggr] \\ & \quad{}+\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d} \biggl(\frac{\omega _{1}s_{1}p _{1}}{1+\mu _{1}p_{1}}+ \frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr) \biggl[1-\frac{s_{1}}{s}+\ln \biggl( \frac{s_{1}}{s} \biggr) \biggr] \\ & \quad{}+ne^{-a_{2}\delta _{2}} \biggl(\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p _{1}}+\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr) \biggl[1-\frac{s _{1}}{s}+\ln \biggl(\frac{s_{1}}{s} \biggr) \biggr] \\ & \quad{}+\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl[\frac{(1+ \mu _{1}p_{1})p}{(1+\mu _{1}p)p_{1}}- \frac{p}{p_{1}}-1+\frac{1+\mu _{1}p}{1+ \mu _{1}p_{1}} \biggr] \\ & \quad{}+\frac{\alpha _{1}\omega _{2}s_{1}y_{1}}{1+\mu _{2}y _{1}} \biggl[\frac{(1+\mu _{2}y_{1})y}{(1+\mu _{2}y)y_{1}}- \frac{y}{y_{1}}-1+\frac{1+\mu _{2}y}{1+\mu _{2}y_{1}} \biggr] \\ & \quad{}+\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{1}s_{1}p_{1}}{1+ \mu _{1}p_{1}} \biggl[1- \frac{s(t-\delta _{1})p(t-\delta _{1})(1+\mu _{1}p _{1})w_{1}}{s_{1}p_{1}(1+\mu _{1}p(t-\delta _{1}))w} \\ & \quad{}+\ln \biggl(\frac{s(t- \delta _{1})p(t-\delta _{1})(1+\mu _{1}p_{1})w_{1}}{s_{1}p_{1}(1+\mu _{1}p(t- \delta _{1}))w} \biggr) \biggr] \\ & \quad{}+\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{2}s_{1}y_{1}}{1+ \mu _{2}y_{1}} \biggl[1- \frac{s(t-\delta _{1})y(t-\delta _{1})(1+\mu _{2}y _{1})w_{1}}{s_{1}y_{1}(1+\mu _{2}y(t-\delta _{1}))w} \\ & \quad{}+\ln \biggl(\frac{s(t- \delta _{1})y(t-\delta _{1})(1+\mu _{2}y_{1})w_{1}}{s_{1}y_{1}(1+\mu _{2}y(t- \delta _{1}))w} \biggr) \biggr] \\ &\quad{} +ne^{-a_{2}\delta _{2}}\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl[1-\frac{s(t-\delta _{2})p(t-\delta _{2})(1+\mu _{1}p_{1})y_{1}}{s _{1}p_{1}(1+\mu _{1}p(t-\delta _{2}))y} \\ & \quad{}+ \ln \biggl(\frac{s(t-\delta _{2})p(t- \delta _{2})(1+\mu _{1}p_{1})y_{1}}{s_{1}p_{1}(1+\mu _{1}p(t-\delta _{2}))y} \biggr) \biggr] \\ & \quad{}+ne^{-a_{2}\delta _{2}}\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggl[1-\frac{s(t-\delta _{2})y(t-\delta _{2}(1+\mu _{2}y_{1}))}{s_{1}(1+ \mu _{2}y(t-\delta _{2}))y} \\ & \quad{}+ \ln \biggl(\frac{s(t-\delta _{2})y(t-\delta _{2}(1+\mu _{2}y_{1}))}{s_{1}(1+\mu _{2}y(t-\delta _{2}))y} \biggr) \biggr] \\ & \quad{}+\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{1}s_{1}p_{1}}{1+ \mu _{1}p_{1}} \biggl[1- \frac{wy_{1}}{w_{1}y} +\ln \biggl(\frac{wy_{1}}{w _{1}y} \biggr) \biggr] \\ & \quad{}+ \frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggl[1-\frac{wy_{1}}{w_{1}y}+\ln \biggl(\frac{wy_{1}}{w_{1}y} \biggr) \biggr] \\ &\quad{} +\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl[1-\frac{y(t- \delta _{3})p_{1}}{y_{1}p}+\ln \biggl( \frac{y(t-\delta _{3})p_{1}}{y_{1}p} \biggr) \biggr] \\ & \quad{}+\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl[1- \frac{1+\mu _{1}p}{1+\mu _{1}p _{1}}+\ln \biggl(\frac{1+\mu _{1}p}{1+\mu _{1}p_{1}} \biggr) \biggr] \\ & \quad{}+\frac{\alpha _{1}\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggl[1-\frac{1+ \mu _{2}y}{1+\mu _{2}y_{1}}+\ln \biggl( \frac{1+\mu _{2}y}{1+\mu _{2}y_{1}} \biggr) \biggr]. \end{aligned}$$

Finally we get

$$\begin{aligned} \frac{dU_{1}}{dt} &=-\alpha _{1}\xi \frac{(s-s_{1})^{2}}{s}- \frac{ \alpha _{1}rs_{1}p_{1}\omega _{1}}{\rho \varkappa e^{-a_{3}\delta _{3}}(1+ \mu _{1}p_{1})y_{1}}\frac{\lambda }{x_{1}}\frac{(x-x_{1})^{2}}{x} \\ & \quad{}- \alpha _{1} \biggl(\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+\frac{ \omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr)G \biggl(\frac{s_{1}}{s} \biggr) \\ & \quad{}-\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl(\frac{ \mu _{1}(p-p_{1})^{2}}{(1+\mu _{1}p)(1+\mu _{1}p_{1})p_{1}} \biggr)- \frac{ \alpha _{1}\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggl(\frac{\mu _{2}(y-y _{1})^{2}}{(1+\mu _{2}y)(1+\mu _{2}y_{1})y_{1}} \biggr) \\ & \quad{}-\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{1}s_{1}p_{1}}{1+ \mu _{1}p_{1}}G \biggl( \frac{s(t-\delta _{1})p(t-\delta _{1})(1+\mu _{1}p _{1})w_{1}}{s_{1}p_{1}(1+\mu _{1}p(t-\delta _{1}))w} \biggr) \\ &\quad{} -\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{2}s_{1}y_{1}}{1+ \mu _{2}y_{1}}G \biggl( \frac{s(t-\delta _{1})y(t-\delta _{1})(1+\mu _{2}y _{1})w_{1}}{s_{1}y_{1}(1+\mu _{2}y(t-\delta _{1}))w} \biggr) \\ &\quad {} -ne^{-a_{2}\delta _{2}}\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}G \biggl(\frac{s(t-\delta _{2})p(t-\delta _{2})(1+\mu _{1}p_{1})y_{1}}{s _{1}p_{1}(1+\mu _{1}p(t-\delta _{2}))y} \biggr) \\ &\quad {} -ne^{-a_{2}\delta _{2}}\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}}G \biggl(\frac{s(t-\delta _{2})y(t-\delta _{2})(1+\mu _{2}y_{1})}{s_{1}(1+ \mu _{2}y(t-\delta _{2}))y} \biggr) \\ &\quad {} -\frac{d(1-n)e^{-a_{1}\delta _{1}}}{b+d}\frac{\omega _{1}s_{1}p_{1}}{1+ \mu _{1}p_{1}}G \biggl( \frac{wy_{1}}{w_{1}y} \biggr)-\frac{d(1-n)e^{-a_{1} \delta _{1}}}{b+d}\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}}G \biggl( \frac{wy _{1}}{w_{1}y} \biggr) \\ &\quad {} -\frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}G \biggl(\frac{y(t- \delta _{3})p_{1}}{y_{1}p} \biggr)- \frac{\alpha _{1}\omega _{1}s_{1}p_{1}}{1+ \mu _{1}p_{1}}G \biggl(\frac{1+\mu _{1}p}{1+\mu _{1}p_{1}} \biggr) \\ & \quad{}-\frac{ \alpha _{1}\omega _{2}s_{1}y_{1}}{1+\mu _{1}y_{1}}G \biggl(\frac{1+\mu _{1}y}{1+ \mu _{1}y_{1}} \biggr). \end{aligned}$$

Therefore, \(\frac{dU_{1}}{dt}\leq 0\) for all \(s,w,y,p,x>0\). Let \(\widetilde{D}= \{ (s,w,y,p,x):\frac{dU_{1}}{dt}=0 \} \) and Ñ be the largest invariant subset of D̃. The trajectory of model (5)–(9) tends to Ñ [57]. It can be verified that \(\frac{dU_{1}}{dt}=0\) implies \(s=s_{1}\), \(y=y_{1}\), \(p=p_{1}\), \(x=x_{1}\), and

$$\begin{aligned} \frac{s(t-\delta _{1})p(t-\delta _{1})(1+\mu _{1}p_{1})w_{1}}{s_{1}p_{1}(1+ \mu _{1}p(t-\delta _{1}))w} &=\frac{s(t-\delta _{1})y(t-\delta _{1})(1+ \mu _{2}y_{1})w_{1}}{s_{1}y_{1}(1+\mu _{2}y(t-\delta _{1}))w} \\ &=\frac{s(t-\delta _{2})p(t-\delta _{2})(1+\mu _{1}p_{1})y_{1}}{s_{1}p _{1}(1+\mu _{1}p(t-\delta _{2}))y} \\ &=\frac{s(t-\delta _{2})y(t-\delta _{2})(1+\mu _{2}y_{1})}{s_{1}(1+\mu _{2}y(t-\delta _{2}))y}=1. \end{aligned}$$

Applying the above relations to Eq. (6), we get \(w(t)=w_{1}\) and hence \(\widetilde{N}= \{ \varOmega _{1} \} \). This shows that all the sufficient conditions given in Corollary 5.2 of Kuang [58] are satisfied under the condition \(R_{0}>1\). This implies that \(\varOmega _{1}\) is G.A.S. when \(R_{0}>1\). □

3 CHIKV model with distributed delays

In this section, we consider CHIKV dynamics model with distributed delays:

$$\begin{aligned}& \dot{s}(t) =\varrho -\xi s(t)- \frac{\omega _{1}s(t)p(t)}{1+\mu _{1}p(t)}-\frac{\omega _{2}s(t)y(t)}{1+ \mu _{2}y(t)}, \end{aligned}$$
(17)
$$\begin{aligned}& \begin{aligned}[b] \dot{w}(t) &=(1-n) \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a_{1}\delta } \biggl[\frac{\omega _{1}s(t-\delta )p(t-\delta )}{1+\mu _{1}p(t-\delta )}+\frac{\omega _{2}s(t-\delta )y(t-\delta )}{1+\mu _{2}y(t-\delta )} \biggr]\,d \delta \\ &\quad{} -(b+d)w(t), \end{aligned} \end{aligned}$$
(18)
$$\begin{aligned}& \begin{aligned}[b] \dot{y}(t) &=n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2}\delta } \biggl[ \frac{\omega _{1}s(t-\delta )p(t-\delta )}{1+\mu _{1}p(t-\delta )}+\frac{ \omega _{2}s(t-\delta )y(t-\delta )}{1+\mu _{2}y(t-\delta )} \biggr] \,d \delta +dw(t) \\&\quad{} -\epsilon y(t), \end{aligned} \end{aligned}$$
(19)
$$\begin{aligned}& \dot{p}(t) =\varkappa \int _{0}^{\zeta _{3}}f_{3}(\delta )e^{-a_{3} \delta }y(t-\delta )\,d\delta -cp(t)-rx(t)p(t), \end{aligned}$$
(20)
$$\begin{aligned}& \dot{x}(t) =\lambda +\rho x(t)p(t)-mx(t), \end{aligned}$$
(21)

where \(f_{i}(\delta )>0\), \(i=1,2,3\), are probability distribution functions satisfying \(f_{i}(\delta )>0\), \(i=1,2,3\), and

$$ \int _{0}^{\zeta _{i}}f_{i}(\delta )\,d \delta =1, \qquad \int _{0}^{\zeta _{i}}f_{i}(u)e^{lu} \,du< \infty , \quad i=1,2,3, $$

where \(l>0\). Denote \(F_{i}=\int _{0}^{\zeta _{i}}f_{i}(\delta )e^{-a _{i}\delta }\,d\delta \), \(i=1,2,3\), thus \(0< F_{i}\leq 1\). The initial conditions for system (17)–(21) are given by Eq. (10) with \(k= \max \{ \zeta _{1},\zeta _{2},\zeta _{3}\}\).

3.1 Basic properties

Lemma 3

The solutions of system (17)–(21) with the initial (10) are nonnegative and ultimately bounded.

Proof

Equations (17) and (21) give \(\dot{s}| _{s=0}= \varrho >0\), \(\dot{x}| _{x=0}=\lambda >0\). Thus, for all \(t\geq 0\) \(s(t)>0\) and \(x(t)>0\). Moreover, from Eqs. (18)–(20), we get

$$\begin{aligned}& \begin{aligned} w(t) &=\vartheta _{2}(0)e^{-(b+d)t} \\ &\quad {} +(1-n) \int _{0}^{t}e^{-(b+d)(t-\theta )} \biggl( \int _{0}^{\zeta _{1}}f _{1}(\delta )e^{-a_{1}\delta }s(\theta -\delta ) \\ &\quad{}\times \biggl[\frac{\omega _{1}p(\theta -\delta )}{1+\mu _{1}p(\theta -\delta )}+ \frac{\omega _{2}y( \theta -\delta )}{1+\mu _{2}y(\theta -\delta )} \biggr]\,d\delta \biggr)\,d \theta \geq 0, \end{aligned} \\& \begin{aligned} y(t) &=\vartheta _{3}(0)e^{-\epsilon t} \\ &\quad {} +n \int _{0}^{t}e^{-\epsilon (t-\theta )} \biggl( \int _{0}^{\zeta _{2}}f _{2}(\delta )e^{-a_{2}\delta }s(\theta -\delta ) \\ &\quad{}\times \biggl[\frac{\omega _{1}p(\theta -\delta )}{1+\mu _{1}p(\theta -\delta )}+ \frac{\omega _{2}y( \theta -\delta )}{1+\mu _{2}y(\theta -\delta )} \biggr]\,d\delta +dw( \theta ) \biggr)\,d\theta \geq 0, \end{aligned} \\& \begin{aligned} p(t) ={}&\vartheta _{4}(0)e^{-\int _{0}^{t}(c+rx(\varphi ))\,d\varphi }+ \int _{0}^{t}e^{-\int _{\theta }^{t}(c+rx(\varphi ))\,d\varphi } \int _{0} ^{\zeta _{3}}f_{3}(\delta )e^{-a_{3}\delta }\varkappa y(\theta -\delta )\,d\delta \,d\theta \\ \geq {}&0 \quad \text{for } t\in {}[ 0,k]. \end{aligned} \end{aligned}$$

By recursive argument, we show that \(w(t)\geq 0\), \(y(t)\geq 0\), and \(p(t)\geq 0\) for all \(t\geq 0\). For the boundedness of the solution, we have from Eq. (17) \(\lim _{t\rightarrow \infty } \sup s(t)\leq \frac{\varrho }{\xi }\). Let us consider

$$ g_{1}(t)=(1-n) \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a_{1}\delta }s(t- \delta )\,d\delta +n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2}\delta }s(t- \delta )\,d\delta +w(t)+y(t), $$

then

$$\begin{aligned} \dot{g}_{1}(t) &=(1-n) \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a_{1} \delta } \biggl[\varrho -\xi s(t-\delta )-s(t-\delta ) \\ &\quad{}\times\biggl( \frac{\omega _{1}p(t-\delta )}{1+\mu _{1}p(t-\delta )}+\frac{\omega _{2}y(t-\delta )}{1+ \mu _{2}y(t-\delta )} \biggr) \biggr]\,d\delta \\ &\quad {} +n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2}\delta } \biggl[\varrho -\xi s(t-\delta )-s(t-\delta ) \\ &\quad{}\times\biggl( \frac{\omega _{1}p(t-\delta )}{1+ \mu _{1}p(t-\delta )}+\frac{\omega _{2}y(t-\delta )}{1+\mu _{2}y(t- \delta )} \biggr) \biggr]\,d\delta \\ &\quad {} +(1-n) \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a_{1}\delta }s(t- \delta ) \biggl(\frac{\omega _{1}p(t-\delta )}{1+\mu _{1}p(t-\delta )}+ \frac{ \omega _{2}y(t-\delta )}{1+\mu _{2}y(t-\delta )} \biggr)\,d\delta \\ &\quad{} -(b+d)w(t) \\ &\quad {} +n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2}\delta }s(t-\delta ) \biggl(\frac{\omega _{1}p(t-\delta )}{1+\mu _{1}p(t-\delta )}+ \frac{ \omega _{2}y(t-\delta )}{1+\mu _{2}y(t-\delta )} \biggr)\,d\delta +dw(t)- \epsilon y(t) \\ &=\varrho (1-n) \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a_{1}\delta }\,d \delta +\varrho n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2}\delta }\,d \delta \\ &\quad {} -\xi (1-n) \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a_{1}\delta }s(t- \delta )\,d\delta -\xi n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2} \delta }s(t-\delta )\,d\delta \\ &\quad {} -bw(t)-\epsilon y(t) \\ &\leq \varrho -\sigma _{1} \biggl((1-n) \int _{0}^{\zeta _{1}}f_{1}( \delta )e^{-a_{1}\delta }s(t-\delta )\,d\delta + \int _{0}^{\zeta _{2}}f _{2}(\delta )e^{-a_{2}\delta }s(t-\delta )\,d\delta +w(t)+y(t) \biggr) \\ &=\varrho -\sigma _{1}g_{1}(t). \end{aligned}$$

It follows that \(\lim _{t\rightarrow \infty }\sup g_{1}(t) \leq \Delta _{1}\). Since \(s(t)>0\), \(w(t)\geq 0 \), and \(y(t)\geq 0\), then \(\lim _{t\rightarrow \infty }\sup w(t)\leq \Delta _{1}\) and \(\lim _{t\rightarrow \infty }\sup y(t)\leq \Delta _{1}\). Moreover, we define

$$ g_{2}(t)=p(t)+\frac{r}{\rho }x(t), $$

then

$$\begin{aligned} \dot{g}_{2}(t) &=\varkappa \int _{0}^{\zeta _{3}}f_{3}(\delta )e^{-a _{3}\delta }y(t-\delta )\,d\delta -cp+\frac{r}{\rho }\lambda - \frac{r}{ \rho }mx \\ &\leq \varkappa \Delta _{1}+\frac{r}{\rho }\lambda -\sigma _{2} \biggl(p(t)+\frac{r}{ \rho }x(t) \biggr) \\ &=\frac{\varkappa \rho \Delta _{1}+r\lambda }{\rho }-\sigma _{2}g_{2}(t). \end{aligned}$$

Then \(\lim _{t\rightarrow \infty }\sup g_{2}(t)\leq \Delta _{2}\). The nonnegativity of the solution implies that \(\lim _{t \rightarrow \infty }\sup p(t)\leq \Delta _{2}\) and \(\lim _{t \rightarrow \infty }\sup x(t)\leq \Delta _{3}\). This shows the ultimate boundedness of \(s(t)\), \(w(t)\), \(y(t)\), \(p(t)\), and \(x(t)\). □

3.2 Equilibria

Define the basic reproduction number

$$ \mathcal{R}_{0}^{D}=\frac{\alpha _{1}^{D}(m\varkappa \omega _{1}F_{3}+cm \omega _{2}+r\lambda \omega _{2})\varrho }{\xi \epsilon (cm+r\lambda )}, $$

where \(\alpha _{1}^{D}=\frac{d}{b+d}(1-n)F_{1}+nF_{2}\).

Lemma 4

If \(\mathcal{R}_{0}^{D}\leq 1\), then system (17)–(21) has only one equilibrium \(\varOmega _{0}\), and if \(\mathcal{R}_{0}^{D}>1\), then the system has two equilibria \(\varOmega _{0}\)and \(\varOmega _{1}\).

The proof of Lemma 4 is given in the Appendix.

3.3 Global properties

Theorem 3

For system (17)–(21), if \(\mathcal{R}_{0}^{D}\leq 1\), then \(\varOmega _{0}\)is G.A.S.

Proof

Let a function \(V_{0}(s,w,y,p,x)\) be defined as follows:

$$\begin{aligned} V_{0} &=\alpha _{1}^{D}s_{0}G \biggl(\frac{s}{s_{0}} \biggr)+ \frac{d}{b+d}w+y+ \frac{\alpha _{1}^{D}\omega _{1}s_{0}}{c+rx_{0}}p+\frac{r \alpha _{1}^{D}\omega _{1}s_{0}}{\rho (c+rx_{0})}x_{0}G \biggl( \frac{x}{x _{0}} \biggr) \\ &\quad {} +\frac{d(1-n)}{b+d} \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a_{1} \delta } \int _{0}^{\delta } \biggl[\frac{\omega _{1}s(t-\theta )p(t- \theta )}{1+\mu _{1}p(t-\theta )}+ \frac{\omega _{2}s(t-\theta )y(t- \theta )}{1+\mu _{2}y(t-\theta )} \biggr]\,d\theta \,d\delta \\ &\quad {} +n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2}\delta } \int _{0}^{ \delta } \biggl[\frac{\omega _{1}s(t-\theta )p(t-\theta )}{1+\mu _{1}p(t- \theta )}+ \frac{\omega _{2}s(t-\theta )y(t-\theta )}{1+\mu _{2}y(t- \theta )} \biggr]\,d\theta \,d\delta \\ &\quad {} +\frac{\alpha _{1}^{D}\omega _{1}s_{0}\varkappa }{c+rx_{0}} \int _{0} ^{\zeta _{3}}f_{3}(\delta )e^{-a_{3}\delta } \int _{0}^{\delta }y(t- \theta )\,d\theta \,d\delta . \end{aligned}$$

Calculating \(\frac{dV_{0}}{dt}\) along system (17)–(21), we obtain

$$\begin{aligned} \frac{dV_{0}}{dt} &=\alpha _{1}^{D} \biggl(1- \frac{s_{0}}{s} \biggr) \biggl(\varrho -\xi s-\frac{\omega _{1}sp}{1+\mu _{1}p}- \frac{\omega _{2}sy}{1+ \mu _{2}y} \biggr) \\ & \quad{}+\frac{d}{b+d} \biggl[(1-n) \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a _{1}\delta } \biggl[\frac{\omega _{1}s(t-\delta )p(t-\delta )}{1+\mu _{1}p(t- \delta )}+\frac{\omega _{2}s(t-\delta )y(t-\delta )}{1+\mu _{2}y(t- \delta )} \biggr]\,d \delta \\ & \quad{}-(b+d)w \biggr] \\ & \quad{}+n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2}\delta } \biggl[\frac{ \omega _{1}s(t-\delta )p(t-\delta )}{1+\mu _{1}p(t-\delta )}+\frac{ \omega _{2}s(t-\delta )y(t-\delta )}{1+\mu _{2}y(t-\delta )} \biggr]\,d \delta +dw-\epsilon y \\ &\quad{} +\frac{\alpha _{1}^{D}\omega _{1}s_{0}}{c+rx_{0}} \biggl(\varkappa \int _{0} ^{\zeta _{3}}f_{3}(\delta )e^{-a_{3}\delta }y(t-\delta )\,d\delta -cp-rxp \biggr) \\ & \quad{}+\frac{r\alpha _{1}^{D}\omega _{1}s_{0}}{\rho (c+rx_{0})} \biggl(1-\frac{x _{0}}{x} \biggr) (\lambda +\rho xp-mx ) \\ &\quad{} +\frac{d(1-n)}{b+d} \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a_{1} \delta } \biggl[\frac{\omega _{1}sp}{1+\mu _{1}p}+\frac{\omega _{2}sy}{1+ \mu _{2}y}- \frac{\omega _{1}s(t-\delta )p(t-\delta )}{1+\mu _{1}p(t- \delta )} \\ & \quad{}-\frac{\omega _{2}s(t-\delta )y(t-\delta )}{1+\mu _{2}y(t- \delta )} \biggr]\,d\delta \\ & \quad{}+n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2}\delta } \biggl[\frac{ \omega _{1}sp}{1+\mu _{1}p}+\frac{\omega _{2}sy}{1+\mu _{2}y}- \frac{\omega _{1}s(t-\delta )p(t-\delta )}{1+\mu _{1}p(t-\delta )} \\ & \quad{}-\frac{\omega _{2}s(t- \delta )y(t-\delta )}{1+\mu _{2}y(t-\delta )} \biggr]\,d\delta \\ & \quad{}+\frac{\alpha _{1}^{D}\omega _{1}s_{0}}{c+rx_{0}}\varkappa \int _{0} ^{\zeta _{3}}f_{3}(\delta )e^{-a_{3}\delta }\bigl(y-y(t-\delta )\bigr)\,d\delta . \end{aligned}$$
(22)

Collecting terms of Eq. (22), we get

$$\begin{aligned} \frac{dV_{0}}{dt} &=-\alpha _{1}^{D}\xi \frac{(s-s_{0})^{2}}{s}-\frac{ \alpha _{1}^{D}\omega _{1}s_{0}\mu _{1}p^{2}}{1+\mu _{1}p}-\frac{\alpha _{1}^{D}\omega _{2}s_{0}\mu _{2}y^{2}}{1+\mu _{2}y}+\epsilon \biggl( \frac{ \alpha _{1}^{D}\omega _{2}s_{0}}{\epsilon }+\frac{\alpha _{1}^{D}\omega _{1}s_{0}\varkappa F_{3}}{\epsilon (c+rx_{0})}-1 \biggr)y \\ & \quad{}+\frac{r\alpha _{1}^{D}\omega _{1}s_{0}}{\rho (c+rx_{0})} \biggl(1-\frac{x _{0}}{x} \biggr) (mx_{0}-mx ) \\ &=-\alpha _{1}^{D}\xi \frac{(s-s_{0})^{2}}{s}- \frac{\alpha _{1}^{D} \omega _{1}s_{0}\mu _{1}p^{2}}{1+\mu _{1}p}-\frac{\alpha _{1}^{D}\omega _{2}s_{0}\mu _{2}y^{2}}{1+\mu _{2}y}-\frac{r\alpha _{1}^{D}\omega _{1}s _{0}m}{\rho (c+rx_{0})} \frac{(x-x_{0})^{2}}{x} \\ & \quad{}+\epsilon \bigl(\mathcal{R} _{0}^{D}-1 \bigr)y. \end{aligned}$$
(23)

If \(\mathcal{R}_{0}^{D}\leq 1\), then \(\frac{dV_{0}}{dt}\leq 0\) for all \(s,w,y,p,x>0\). Moreover, \(\frac{dV_{0}}{dt}=0\) when \(s=s_{0}\), \(x=x_{0}\), and \(y=p=0\). Similar to the proof of Theorem 1, one can show that \(\frac{dV_{0}}{dt}=0\) at \(\varOmega _{0}\). Applying LaSalle’s invariance principle [58], we get that if \(R_{0}^{D}\leq 1\), then \(\varOmega _{0}\) is G.A.S. □

Theorem 4

For system (17)–(21), if \(\mathcal{R}_{0}^{D}>1\), then \(\varOmega _{1}\)is G.A.S.

Proof

Let \(V_{1}(s,w,y,p,x)\) be defined as follows:

$$\begin{aligned} V_{1} &=\alpha _{1}^{D}s_{1}G \biggl(\frac{s}{s_{1}} \biggr)+ \frac{d}{b+d}w_{1}G \biggl(\frac{w}{w_{1}} \biggr)+y_{1}G \biggl( \frac{y}{y _{1}} \biggr) \\ &\quad {} +\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{\varkappa F_{3}(1+\mu _{1}p_{1})y_{1}}p_{1}G \biggl(\frac{p}{p_{1}} \biggr)+\frac{r\alpha _{1} ^{D}\omega _{1}s_{1}p_{1}}{\rho \varkappa F_{3}(1+\mu _{1}p_{1})y_{1}}x _{1}G \biggl(\frac{x}{x_{1}} \biggr) \\ &\quad {} +\frac{d(1-n)}{b+d}\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \int _{0} ^{\zeta _{1}}f_{1}(\delta )e^{-a_{1}\delta } \int _{0}^{\delta }G \biggl(\frac{s(t- \theta )p(t-\theta )(1+\mu _{1}p_{1})}{s_{1}p_{1}(1+\mu _{1}p(t-\theta ))} \biggr)\,d\theta \,d\delta \\ &\quad {} +\frac{d(1-n)}{b+d}\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{1}y_{1}} \int _{0} ^{\zeta _{1}}f_{1}(\delta )e^{-a_{1}\delta } \int _{0}^{\delta }G \biggl(\frac{s(t- \theta )y(t-\theta )(1+\mu _{2}y_{1})}{s_{1}y_{1}(1+\mu _{2}y(t-\theta )} \biggr)\,d\theta \,d\delta \\ &\quad {} +\frac{n\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \int _{0}^{\zeta _{2}}f _{2}(\delta )e^{-a_{2}\delta } \int _{0}^{\delta }G \biggl(\frac{s(t- \theta )p(t-\theta )(1+\mu _{1}p_{1})}{s_{1}p_{1}(1+\mu _{1}p(t-\theta ))} \biggr)\,d\theta \,d\delta \\ &\quad {} +\frac{n\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \int _{0}^{\zeta _{2}}f _{2}(\delta )e^{-a_{2}\delta } \int _{0}^{\delta }G \biggl(\frac{s(t- \theta )y(t-\theta )(1+\mu _{2}y_{1})}{s_{1}y_{1}(1+\mu _{2}y(t-\theta )} \biggr)\,d\theta \,d\delta \\ &\quad {} +\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{F_{3}(1+\mu _{1}p_{1})} \int _{0}^{\zeta _{3}}f_{3}(\delta )e^{-a_{3}\delta } \int _{0}^{\delta }G \biggl(\frac{y(t-\theta )}{y_{1}} \biggr)\,d\theta \,d\delta . \end{aligned}$$

Then

$$\begin{aligned} \frac{dV_{1}}{dt} &=\alpha _{1}^{D} \biggl(1- \frac{s_{1}}{s} \biggr) \biggl(\varrho -\xi s-\frac{\omega _{1}sp}{1+\mu _{1}p_{1}}- \frac{\omega _{2}sy}{1+ \mu _{2}y_{1}} \biggr) \\ & \quad{}+\frac{d}{b+d} \biggl(1-\frac{w_{1}}{w} \biggr) \biggl[(1-n) \int _{0}^{ \zeta _{1}}f_{1}(\delta )e^{-a_{1}\delta } \biggl(\frac{\omega _{1}s(t- \delta )p(t-\delta )}{1+\mu _{1}p(t-\delta )} \\ & \quad{}+\frac{\omega _{2}s(t- \delta )y(t-\delta )}{1+\mu _{2}y(t-\delta )} \biggr)\,d \delta -(b+d)w \biggr] \\ &\quad{} + \biggl(1-\frac{y_{1}}{y} \biggr) \biggl[n \int _{0}^{\zeta _{2}}f_{2}( \delta )e^{-a_{2}\delta } \biggl(\frac{\omega _{1}s(t-\delta )p(t-\delta )}{1+\mu _{1}p(t-\delta )} \\ & \quad{}+\frac{\omega _{2}s(t-\delta )y(t-\delta )}{1+ \mu _{2}y(t-\delta )} \biggr)\,d \delta +dw-\epsilon y \biggr] \\ &\quad{} +\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{\varkappa F_{3}(1+\mu _{1}p_{1})y_{1}} \biggl(1-\frac{p_{1}}{p} \biggr) \biggl[ \varkappa \int _{0} ^{\zeta _{3}}f_{3}(\delta )e^{-a_{3}\delta }y(t-\delta )\,d\delta -cp-rxp \biggr] \\ & \quad{}+\frac{r\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{\rho \varkappa F_{3}(1+ \mu _{1}p_{1})y_{1}} \biggl(1-\frac{x_{1}}{x} \biggr) (\lambda +\rho xp-mx ) \\ & \quad{}+\frac{d(1-n)}{b+d} \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a_{1} \delta } \biggl[\frac{\omega _{1}sp}{1+\mu _{1}p}-\frac{\omega _{1}s(t- \delta )p(t-\delta )}{(1+\mu _{1}p(t-\delta ))} \\ & \quad{}+\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}\ln \biggl(\frac{s(t- \delta )p(t-\delta )(1+\mu _{1}p)}{sp(1+\mu _{1}p(t-\delta ))} \biggr) \biggr] \,d\delta \\ & \quad{}+\frac{d(1-n)}{b+d} \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a_{1} \delta } \biggl[\frac{\omega _{2}sy}{1+\mu _{2}y}-\frac{\omega _{2}s(t- \delta )y(t-\delta )}{(1+\mu _{2}y(t-\delta ))} \\ & \quad{}+\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}}\ln \biggl(\frac{s(t- \delta )y(t-\delta )(1+\mu _{2}y)}{sy(1+\mu _{2}y(t-\delta ))} \biggr) \biggr] \,d\delta \\ &\quad{} +n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2}\delta } \biggl[\frac{ \omega _{1}sp}{1+\mu _{1}p}-\frac{\omega _{1}s(t-\delta )p(t-\delta )}{(1+ \mu _{1}p(t-\delta ))} \\ &\quad{} +\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}\ln \biggl(\frac{s(t- \delta )p(t-\delta )(1+\mu _{1}p)}{sp(1+\mu _{1}p(t-\delta ))} \biggr) \biggr] \,d\delta \\ &\quad{} +n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2}\delta } \biggl[\frac{ \omega _{2}sy}{1+\mu _{2}y}-\frac{\omega _{2}s(t-\delta )y(t-\delta )}{(1+ \mu _{2}y(t-\delta ))} \\ & \quad{}+\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}}\ln \biggl(\frac{s(t- \delta )y(t-\delta )(1+\mu _{2}y)}{sy(1+\mu _{2}y(t-\delta ))} \biggr) \biggr] \,d\delta \\ & \quad{}+\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{F_{3}(1+\mu _{1}p_{1})} \int _{0}^{\zeta _{3}}f_{3}(\delta )e^{-a_{3}\delta } \biggl[\frac{y}{y _{1}}-\frac{y(t-\delta )}{y_{1}}+\ln \biggl(\frac{y(t-\delta )}{y_{1}} \biggr) \biggr]\,d\delta . \end{aligned}$$
(24)

Simplify Eq. (24) as follows:

$$\begin{aligned} \frac{dU_{1}}{dt} &=\alpha _{1}^{D} \biggl(1- \frac{s_{1}}{s} \biggr) ( \varrho -\xi s)+\alpha _{1}^{D} \biggl( \frac{\omega _{1}s_{1}p}{1+\mu _{1}p}+ \frac{\omega _{2}s_{1}y}{1+\mu _{2}y} \biggr) \\ & \quad{}-\frac{d(1-n)}{b+d} \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a_{1} \delta _{1}} \\ & \quad{}\times\biggl[\frac{\omega _{1}s(t-\delta )p(t-\delta )w_{1}}{1+\mu _{1}p(t-\delta )w}+\frac{\omega _{2}s(t-\delta )y(t-\delta )w_{1}}{1+ \mu _{2}y(t-\delta )w} \biggr]\,d \delta +dw_{1} \\ & \quad{}-n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2}\delta } \biggl[\frac{ \omega _{1}s(t-\delta )p(t-\delta )y_{1}}{(1+\mu _{1}p(t-\delta ))y}+\frac{ \omega _{2}s(t-\delta )y(t-\delta )y_{1}}{(1+\mu _{2}y(t-\delta ))y} \biggr]\,d \delta -dw\frac{y_{1}}{y} \\ & \quad{}-\epsilon y+\epsilon y_{1} \\ & \quad{}-\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{F_{3}(1+\mu _{1}p_{1})} \int _{0}^{\zeta _{3}}f_{3}(\delta )e^{-a_{3}\delta } \biggl(\frac{y(t- \delta )p_{1}}{y_{1}p} \biggr)\,d\delta - \frac{\alpha _{1}^{D}\omega _{1}s _{1}p_{1}}{\varkappa F_{3}(1+\mu _{1}p_{1})y_{1}}cp \\ & \quad{}+\frac{\alpha _{1} ^{D}\omega _{1}s_{1}p_{1}}{\varkappa F_{3}(1+\mu _{1}p_{1})y_{1}}cp_{1} \\ & \quad{}+\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{\varkappa F_{3}(1+\mu _{1}p_{1})y_{1}}rxp_{1}-\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{ \varkappa F_{3}(1+\mu _{1}p_{1})y_{1}}rx_{1}p \\ & \quad{}+ \frac{r\alpha _{1}^{D} \omega _{1}s_{1}p_{1}}{\rho \varkappa F_{3}(1+\mu _{1}p_{1})y_{1}} \biggl(1-\frac{x_{1}}{x} \biggr) (\lambda -mx) \\ &\quad{} +\frac{d(1-n)}{b+d} \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a_{1} \delta } \biggl[\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}\ln \biggl(\frac{s(t- \delta )p(t-\delta )(1+\mu _{1}p)}{sp(1+\mu _{1}p(t-\delta ))} \biggr) \\ & \quad{}+\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}}\ln \biggl(\frac{s(t- \delta )y(t-\delta )(1+\mu _{2}y)}{sy(1+\mu _{2}y(t-\delta ))} \biggr) \biggr] \,d\delta \\ &\quad{} +n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2}\delta } \biggl[\frac{ \omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}\ln \biggl(\frac{s(t-\delta )p(t- \delta )(1+\mu _{1}p)}{sp(1+\mu _{1}p(t-\delta ))} \biggr) \\ & \quad{}+\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}}\ln \biggl(\frac{s(t- \delta )y(t-\delta )(1+\mu _{2}y)}{sy(1+\mu _{2}y(t-\delta ))} \biggr) \biggr] \,d\delta \\ & \quad{}+\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{F_{3}(1+\mu _{1}p_{1})} \int _{0}^{\zeta _{3}}f_{3}(\delta )e^{-a_{3}\delta } \biggl[\frac{y}{y _{1}}+\ln \biggl(\frac{y(t-\delta )}{y} \biggr) \biggr]\,d\delta . \end{aligned}$$

Applying the equilibrium conditions for \(\varOmega _{1}\):

$$\begin{aligned}& \varrho =\xi s_{1}+\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+\frac{ \omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}}, \quad \quad w_{1}=\frac{(1-n)F_{1}}{(b+d)} \biggl(\frac{\omega _{1}s _{1}p_{1}}{1+\mu _{1}p_{1}}+ \frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr), \\& \begin{aligned} \epsilon y_{1} &=\frac{d(1-n)F_{1}}{b+d} \biggl( \frac{\omega _{1}s_{1}p _{1}}{1+\mu _{1}p_{1}}+\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr)+nF_{2} \biggl( \frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+\frac{ \omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr) \\ &=\alpha _{1}^{D} \biggl(\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+ \frac{ \omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr), \end{aligned} \\& cp_{1} =\varkappa F_{3}y_{1}-rx_{1}p_{1}, \quad\quad \lambda =mx_{1}-\rho x_{1}p_{1}, \end{aligned}$$

we get

$$\begin{aligned} \frac{dU_{1}}{dt} &=\alpha _{1}^{D} \biggl(1- \frac{s_{1}}{s} \biggr) (\xi s_{1}-\xi s )+ \frac{d(1-n)F_{1}}{b+d}\frac{\omega _{1}s _{1}p_{1}}{1+\mu _{1}p_{1}} \biggl(1-\frac{s_{1}}{s} \biggr)+nF_{2}\frac{ \omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl(1-\frac{s_{1}}{s} \biggr) \\ &\quad{} +\frac{d(1-n)F_{1}}{b+d}\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y _{1}} \biggl(1- \frac{s_{1}}{s} \biggr)+nF_{2}\frac{\omega _{2}s_{1}y_{1}}{1+ \mu _{2}y_{1}} \biggl(1- \frac{s_{1}}{s} \biggr) \\ & \quad{}+\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}\frac{(1+ \mu _{1}p_{1})p}{(1+\mu _{1}p)p_{1}}+\frac{\alpha _{1}^{D}\omega _{2}s _{1}y_{1}}{1+\mu _{2}y_{1}} \frac{(1+\mu _{2}y_{1})y}{(1+\mu _{2}y)y_{1}} \\ & \quad{}-\frac{d(1-n)}{b+d} \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a_{1} \delta }\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl[\frac{s(t- \delta )p(t-\delta )(1+\mu _{1}p_{1})w_{1}}{s_{1}p_{1}(1+\mu _{1}p(t- \delta ))w} \biggr]\,d \delta \\ & \quad{}-\frac{d(1-n)}{b+d} \int _{0}^{\zeta _{1}}f_{1}(\delta )e^{-a_{1} \delta }\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggl[\frac{s(t- \delta )y(t-\delta )(1+\mu _{2}y_{1})w_{1}}{s_{1}y_{1}(1+\mu _{2}y(t- \delta ))w} \biggr]\,d \delta \\ & \quad{}+\frac{d(1-n)}{b+d}F_{1} \biggl[\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+ \frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr] \\ & \quad{}-n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2}\delta }\frac{\omega _{1}s_{1}p _{1}}{1+\mu _{1}p_{1}} \biggl[\frac{s(t-\delta )p(t-\delta )(1+\mu _{1}p _{1})y_{1}}{s_{1}p_{1}(1+\mu _{1}p(t-\delta ))y} \biggr]\,d \delta \\ & \quad{}-n \int _{0}^{\zeta _{2}}f_{2}(\delta )e^{-a_{2}\delta }\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggl[\frac{s(t-\delta )y(t-\delta )(1+ \mu _{2}y_{1})y_{1}}{s_{1}y_{1}(1+\mu _{2}y(t-\delta ))y} \biggr]\,d \delta \\ & \quad{}-\frac{d(1-n)}{b+d}F_{1} \biggl[\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+ \frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr]\frac{wy _{1}}{w_{1}y}-\frac{\alpha _{1}^{D}\omega _{2}s_{1}y_{1}}{1+\mu _{2}y _{1}} \frac{y}{y_{1}} \\ & \quad{}+\frac{d(1-n)}{b+d}F_{1} \biggl[ \frac{\omega _{1}s _{1}p_{1}}{1+\mu _{1}p_{1}}+ \frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr] \\ & \quad{}+nF_{2} \biggl[\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+\frac{ \omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr]-\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{F_{3}(1+\mu _{1}p_{1})} \int _{0}^{\zeta _{3}}f_{3}( \delta )e^{-a_{3}\delta } \biggl[\frac{y(t-\delta )p_{1}}{y_{1}p} \biggr]\,d \delta \\ & \quad{} - \frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}\frac{p}{p _{1}} \\ & \quad{}+\frac{d(1-n)}{b+d}F_{1} \frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+nF_{2} \frac{\omega _{1}s _{1}p_{1}}{1+\mu _{1}p_{1}}-\frac{2r\alpha _{1}^{D}s_{1}p_{1}\omega _{1}}{ \varkappa F_{3}(1+\mu _{1}p_{1})y_{1}}x_{1}p_{1} \\ & \quad{}+\frac{r\alpha _{1}^{D}s_{1}p_{1}\omega _{1}}{\varkappa F_{3}(1+\mu _{1}p_{1})y_{1}}x_{1}p_{1} \biggl( \frac{x}{x_{1}} \biggr)+\frac{r\alpha _{1}^{D}s_{1}p_{1}\omega _{1}}{\varkappa F_{3}(1+\mu _{1}p_{1})y_{1}}x _{1}p_{1} \biggl(\frac{x_{1}}{x} \biggr) \\ & \quad{}-\frac{r\alpha _{1}^{D}s_{1}p_{1}m \omega _{1}}{\rho \varkappa F_{3}(1+\mu _{1}p_{1})y_{1}} \frac{(x-x_{1})^{2}}{x} \\ & \quad{}+\frac{d(1-n)}{b+d}\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \int _{0} ^{\zeta _{1}}f_{1}(\delta )e^{-a_{1}\delta }\ln \biggl[\frac{s(t-\delta )p(t-\delta )(1+\mu _{1}p)}{sp(1+\mu _{1}p(t-\delta ))} \biggr]\,d\delta \\ & \quad{}+\frac{d(1-n)}{b+d}\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \int _{0} ^{\zeta _{1}}f_{1}(\delta )e^{-a_{1}\delta }\ln \biggl[\frac{s(t-\delta )y(t-\delta )(1+\mu _{2}y)}{sy(1+\mu _{2}y(t-\delta ))} \biggr]\,d\delta \\ & \quad{}+\frac{n\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \int _{0}^{\zeta _{2}}f _{2}(\delta )e^{-a_{2}\delta }\ln \biggl[\frac{s(t-\delta )p(t-\delta )(1+\mu _{1}p)}{sp(1+\mu _{1}p(t-\delta ))} \biggr]\,d\delta \\ &\quad{} +\frac{n\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \int _{0}^{\zeta _{2}}f _{2}(\delta )e^{-a_{2}\delta }\ln \biggl[\frac{s(t-\delta )y(t-\delta )(1+\mu _{2}y)}{sy(1+\mu _{2}y(t-\delta ))} \biggr]\,d\delta \\ & \quad{}+\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{F_{3}(1+\mu _{1}p_{1})} \int _{0}^{\zeta _{3}}f_{3}(\delta )e^{-a_{3}\delta }\ln \biggl[\frac{y(t- \delta )}{y} \biggr]\,d\delta . \end{aligned}$$

Using the following equations:

$$\begin{aligned}& \begin{aligned} \ln \biggl(\frac{s(t-\delta )p(t-\delta )(1+\mu _{1}p)}{sp(1+\mu _{1}p(t- \delta ))} \biggr) &=\ln \biggl( \frac{s_{1}}{s} \biggr)+\ln \biggl(\frac{s(t- \delta )p(t-\delta )(1+\mu _{1}p_{1})w_{1}}{s_{1}p_{1}(1+\mu _{1}p(t- \delta ))w} \biggr) \\ &\quad {} +\ln \biggl( \frac{wy_{1}}{w_{1}y} \biggr)+\ln \biggl(\frac{yp _{1}}{y_{1}p} \biggr) +\ln \biggl(\frac{1+\mu _{1}p}{1+\mu _{1}p_{1}} \biggr), \end{aligned} \\& \begin{aligned} \ln \biggl(\frac{s(t-\delta )y(t-\delta )(1+\mu _{2}y)}{sy(1+\mu _{2}y(t- \delta ))} \biggr) &=\ln \biggl( \frac{s_{1}}{s} \biggr)+\ln \biggl(\frac{s(t- \delta )y(t-\delta )(1+\mu _{2}y_{1})w_{1}}{s_{1}y_{1}(1+\mu _{2}y(t- \delta ))w} \biggr) \\ &\quad {} +\ln \biggl( \frac{wy_{1}}{w_{1}y} \biggr) +\ln \biggl(\frac{1+\mu _{2}y}{1+\mu _{2}y_{1}} \biggr), \end{aligned} \\& \begin{aligned} \ln \biggl(\frac{s(t-\delta )p(t-\delta )(1+\mu _{1}p)}{sp(1+\mu _{1}p(t- \delta ))} \biggr) &=\ln \biggl( \frac{s_{1}}{s} \biggr)+\ln \biggl(\frac{s(t- \delta )p(t-\delta )(1+\mu _{1}p_{1})y_{1}}{s_{1}p_{1}(1+\mu _{1}p(t- \delta ))y} \biggr) \\ &\quad {} +\ln \biggl( \frac{yp_{1}}{y_{1}p} \biggr) +\ln \biggl(\frac{1+\mu _{1}p}{1+\mu _{1}p_{1}} \biggr), \end{aligned} \\& \begin{aligned} \ln \biggl(\frac{s(t-\delta )y(t-\delta )(1+\mu _{2}y)}{sy(1+\mu _{2}y(t- \delta ))} \biggr)& =\ln \biggl(\frac{s_{1}}{s} \biggr)+\ln \biggl(\frac{s(t- \delta )y(t-\delta )(1+\mu _{2}y_{1})}{s_{1}y(1+\mu _{2}y(t-\delta ))} \biggr) \\ &\quad{} +\ln \biggl(\frac{1+\mu _{2}y}{1+\mu _{2}y_{1}} \biggr),\end{aligned} \\& \ln \biggl(\frac{y(t-\delta )}{y} \biggr) =\ln \biggl(\frac{y(t-\delta )p_{1}}{y_{1}p} \biggr)+\ln \biggl(\frac{y_{1}p}{yp_{1}} \biggr), \end{aligned}$$

we get

$$\begin{aligned} \frac{dU_{1}}{dt} &=-\alpha _{1}^{D}\xi \frac{(s-s_{1})^{2}}{s} -\frac{r \alpha _{1}^{D}s_{1}p_{1}m\omega _{1}}{\rho \varkappa F_{3}(1+\mu _{1}p _{1})y_{1}}\frac{(x-x_{1})^{2}}{x} \\ &\quad {}- \frac{r\alpha _{1}^{D}s_{1}p_{1} \omega _{1}}{\varkappa F_{3}(1+\mu _{1}p_{1})y_{1}}x_{1}p_{1} \biggl[2- \frac{x}{x _{1}}-\frac{x_{1}}{x} \biggr] \\ &\quad {} +\frac{d(1-n)}{b+d}F_{1} \biggl(\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+ \frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr) \biggl[1-\frac{s _{1}}{s}+\ln \biggl( \frac{s_{1}}{s} \biggr) \biggr] \\ &\quad {} +nF_{2} \biggl(\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+ \frac{ \omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr) \biggl[1-\frac{s_{1}}{s}+ \ln \biggl( \frac{s_{1}}{s} \biggr) \biggr] \\ &\quad {} +\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl[\frac{(1+ \mu _{1}p_{1})p}{(1+\mu _{1}p)p_{1}}- \frac{p}{p_{1}}-1+\frac{1+\mu _{1}p}{1+ \mu _{1}p_{1}} \biggr] \\ &\quad {}+\frac{\alpha _{1}^{D}\omega _{2}s_{1}y_{1}}{1+\mu _{2}y _{1}} \biggl[\frac{(1+\mu _{2}y_{1})y}{(1+\mu _{2}y)y_{1}}- \frac{y}{y_{1}}-1+\frac{1+\mu _{2}y}{1+\mu _{2}y_{1}} \biggr] \\ &\quad {} +\frac{d(1-n)}{b+d}\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \int _{0} ^{\zeta _{1}}f_{1}(\delta )e^{-a_{1}\delta } \biggl[1-\frac{s(t-\delta )p(t- \delta )(1+\mu _{1}p_{1})w_{1}}{s_{1}p_{1}(1+\mu _{1}p(t-\delta _{1}))w} \\ &\quad {} +\ln \biggl(\frac{s(t-\delta )p(t-\delta )(1+\mu _{1}p_{1})w_{1}}{s _{1}p_{1}(1+\mu _{1}p(t-\delta ))w} \biggr) \biggr]\,d\delta \\ &\quad {} +\frac{d(1-n)}{b+d}\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \int _{0} ^{\zeta _{1}}f_{1}(\delta )e^{-a_{1}\delta } \biggl[1-\frac{s(t-\delta )y(t- \delta )(1+\mu _{2}y_{1})w_{1}}{s_{1}y_{1}(1+\mu _{2}y(t-\delta ))w} \\ &\quad {} +\ln \biggl(\frac{s(t-\delta )y(t-\delta )(1+\mu _{2}y_{1})w_{1}}{s _{1}y_{1}(1+\mu _{2}y(t-\delta ))w} \biggr) \biggr]\,d\delta \\ &\quad {} +n\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \int _{0}^{\zeta _{2}}f _{2}(\delta )e^{-a_{2}\delta } \biggl[1-\frac{s(t-\delta )p(t-\delta )(1+ \mu _{1}p_{1})y_{1}}{s_{1}p_{1}(1+\mu _{1}p(t-\delta ))y} \\ &\quad {} +\ln \biggl(\frac{s(t-\delta )p(t-\delta )(1+\mu _{1}p_{1})y_{1}}{s _{1}p_{1}(1+\mu _{1}p(t-\delta ))y} \biggr) \biggr]\,d\delta \\ &\quad {} +n\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \int _{0}^{\zeta _{2}}f _{2}(\delta )e^{-a_{2}\delta } \biggl[1-\frac{s(t-\delta )y(t-\delta )(1+ \mu _{2}y_{1})y_{1}}{s_{1}y_{1}(1+\mu _{2}y(t-\delta ))y} \\ &\quad {} +\ln \biggl(\frac{s(t-\delta )y(t-\delta )(1+\mu _{2}y_{1})y_{1}}{s _{1}y_{1}(1+\mu _{2}y(t-\delta ))y} \biggr) \biggr]\,d\delta \\ &\quad {} +\frac{d(1-n)}{b+d}F_{1} \frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl[1-\frac{wy_{1}}{w _{1}y}+\ln \biggl(\frac{wy_{1}}{w_{1}y} \biggr) \biggr] \\ &\quad {}+ \frac{d(1-n)}{b+d}F _{1}\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggl[1- \frac{wy_{1}}{w _{1}y}+\ln \biggl(\frac{wy_{1}}{w_{1}y} \biggr) \biggr] \\ &\quad {} +\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{F_{3}(1+\mu _{1}p_{1})} \int _{0}^{\zeta _{3}}f_{3}(\delta )e^{-a_{3}\delta } \biggl[1-\frac{y(t- \delta )p_{1}}{y_{1}p}+\ln \biggl( \frac{y(t-\delta )p_{1}}{y_{1}p} \biggr) \biggr]\,d\delta \\ &\quad {} +\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl[1-\frac{1+ \mu _{1}p}{1+\mu _{1}p_{1}}+\ln \biggl( \frac{1+\mu _{1}p}{1+\mu _{1}p_{1}} \biggr) \biggr] \\ &\quad {}+ \frac{\alpha _{1}^{D} \omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggl[1- \frac{1+ \mu _{2}y}{1+\mu _{2}y_{1}}+\ln \biggl(\frac{1+\mu _{2}y}{1+\mu _{2}y_{1}} \biggr) \biggr]. \end{aligned}$$

Finally we get

$$\begin{aligned} \frac{dU_{1}}{dt} &=-\alpha _{1}^{D}\xi \frac{(s-s_{1})^{2}}{s}-\frac{ \alpha _{1}^{D}rs_{1}p_{1}\omega _{1}}{\rho \varkappa F_{3}(1+\mu _{1}p _{1})y_{1}}\frac{\lambda }{x_{1}} \frac{(x-x_{1})^{2}}{x}\\ &\quad {}-\alpha _{1} ^{D} \biggl( \frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr)G \biggl(\frac{s_{1}}{s} \biggr) \\ &\quad {} -\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \biggl(\frac{ \mu _{1}(p-p_{1})^{2}}{(1+\mu _{1}p)(1+\mu _{1}p_{1})p_{1}} \biggr)- \frac{ \alpha _{1}^{D}\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggl(\frac{\mu _{2}(y-y _{1})^{2}}{(1+\mu _{2}y)(1+\mu _{2}y_{1})y_{1}} \biggr) \\ &\quad {} -\frac{d(1-n)}{b+d}\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \int _{0} ^{\zeta _{1}}f_{1}(\delta )e^{-a_{1}\delta }G \biggl(\frac{s(t-\delta )p(t- \delta )(1+\mu _{1}p_{1})w_{1}}{s_{1}p_{1}(1+\mu _{1}p(t-\delta ))w} \biggr)\,d\delta \\ &\quad {} -\frac{d(1-n)}{b+d}\frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \int _{0} ^{\zeta _{1}}f_{1}(\delta )e^{-a_{1}\delta }G \biggl(\frac{s(t-\delta )y(t- \delta )(1+\mu _{2}y_{1})w_{1}}{s_{1}y_{1}(1+\mu _{2}y(t-\delta ))w} \biggr)\,d\delta \\ &\quad {} -\frac{n\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}} \int _{0}^{\zeta _{2}}f _{2}(\delta )e^{-a_{2}\delta }G \biggl(\frac{s(t-\delta )p(t-\delta )(1+ \mu _{1}p_{1})y_{1}}{s_{1}p_{1}(1+\mu _{1}p(t-\delta ))y} \biggr)\,d\delta \\ &\quad {} -\frac{n\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \int _{0}^{\zeta _{2}}f _{2}(\delta )e^{-a_{2}\delta }G \biggl(\frac{s(t-\delta )y(t-\delta (1+ \mu _{2}y_{1}))}{s_{1}(1+\mu _{2}y(t-\delta ))y} \biggr)\,d\delta \\ &\quad {} -\frac{d(1-n)}{b+d}F_{1} \biggl[\frac{\omega _{1}s_{1}p_{1}}{1+\mu _{1}p_{1}}+ \frac{\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}} \biggr]G \biggl(\frac{wy _{1}}{w_{1}y} \biggr) \\ &\quad {} -\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{F_{3}(1+\mu _{1}p_{1})} \int _{0}^{\zeta _{3}}f_{3}(\delta )e^{-a_{3}\delta }G \biggl(\frac{y(t- \delta )p_{1}}{y_{1}p} \biggr)-\frac{\alpha _{1}^{D}\omega _{1}s_{1}p_{1}}{1+ \mu _{1}p_{1}}G \biggl(\frac{1+\mu _{1}p}{1+\mu _{1}p_{1}} \biggr) \\ &\quad {}-\frac{ \alpha _{1}^{D}\omega _{2}s_{1}y_{1}}{1+\mu _{2}y_{1}}G \biggl( \frac{1+\mu _{2}y}{1+\mu _{2}y_{1}} \biggr). \end{aligned}$$

Therefore, \(\frac{dV_{1}}{dt}\leq 0\) for all \(s,w,y,p,x>0\). Let \(L= \{ (s,w,y,p,x):\frac{dV_{1}}{dt}=0 \} \) and Q be the largest invariant subset of L. The trajectory of model (17)–(21) tends to Q [57]. It can be verified that \(\frac{dV_{1}}{dt}=0\) implies \(s=s_{1}\), \(y=y_{1}\), \(p=p_{1}\), \(x=x_{1}\), and

$$\begin{aligned} \frac{s(t-\delta )p(t-\delta )(1+\mu _{1}p_{1})w_{1}}{s_{1}p_{1}(1+\mu _{1}p(t- \delta ))w} &=\frac{s(t-\delta )y(t-\delta )(1+\mu _{2}y_{1})w_{1}}{s _{1}y_{1}(1+\mu _{2}y(t-\delta ))w} \\ &=\frac{s(t-\delta )p(t-\delta )(1+\mu _{1}p_{1})y_{1}}{s_{1}p_{1}(1+\mu _{1}p(t- \delta ))y} \\ &=\frac{s(t-\delta )y(t-\delta (1+\mu _{2}y_{1}))}{s_{1}(1+ \mu _{2}y(t-\delta ))y}=1, \quad \delta \in {}[ 0,k]. \end{aligned}$$

Applying the above relations to Eq. (19), we get \(w(t)=w_{1}\), and hence \(Q= \{ \varOmega _{1} \} \). Applying LaSalle’s invariance principle [58], we get \(\varOmega _{1}\) is G.A.S. when \(R_{0}^{D}>1\). □

4 Numerical simulations

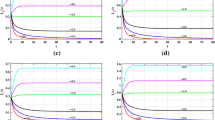
The previous sections described the analytical results and provided a qualitative interpretation of the solutions of the underlying delay differential equation models. In this section, exhaustive numerical exploration has been done to explore the long-term dynamics of the CHIKV model and the various properties of the solutions. We conduct numerical simulations for system (5)–(9) with values of the parameters listed in Table 1. We consider two cases of the effect of \(\delta _{1}\), \(\delta _{2}\), \(\delta _{3}\) and \(\mu _{1}\), \(\mu _{2}\) as follows.

Table 1 The value of the parameters of model (5)–(9)
Full size table

Case 1

We let \(\delta =\delta _{1}=\delta _{2}=\delta _{3}\) and \(\omega _{1}=\omega _{2}=0.05\) by using the following initial conditions:

$$\begin{aligned}& \vartheta _{1}(\varphi )=14,\quad\quad \vartheta _{2}(\varphi )=0.3,\quad\quad \vartheta _{3}( \varphi )=1.0,\\ & \vartheta _{4}( \varphi )=1.5,\quad\quad \vartheta _{5}(\varphi )=2.5, \quad \varphi \in {}[ -k,0]. \end{aligned}$$

We can see in Fig. 2, for smaller values of δ, e.g., \(\delta =0.0,0.5,1.0\), then \(\mathcal{R}_{0}>1\), and the trajectory of the system converges to the equilibrium \(\varOmega _{1}\); whereas when δ becomes larger, e.g., \(\delta =1.5,1.9\), then \(\mathcal{R} _{0}\leq 1\), and the system has one equilibrium \(\varOmega _{0}\). Also, for this case, the concentrations of the uninfected monocytes and antibodies return to their values, while the CHIKV particles are cleared from the body. Let \(\delta ^{ct}\) be the critical value of the parameter δ such that

$$ \mathcal{R}_{0}=\frac{\alpha _{1}(m\varkappa \omega _{1}e^{-a_{3}\delta ^{ct}}+cm\omega _{2}+r\lambda \omega _{2})\varrho }{\xi \epsilon (cm+r \lambda )}=1. $$

Using the data given in Table 1, we obtain \(\delta ^{ct}=1.278\). The variations of \(\mathcal{R}_{0}\) w.r.t. δ are listed in Table 2. We can observe that as δ is increased, \(\mathcal{R}_{0}\) is decreased. Moreover, we have the following cases:

  1. (i)

    if \(0\leq \delta <1.278\), then \(\varOmega _{1}\) exists and it is G.A.S.;

  2. (ii)

    if \(\delta \geq 1.278\), then \(\varOmega _{0}\) is G.A.S.

It is clearly seen that an increase in time delay will stabilize the system around \(\varOmega _{0}\). Biologically, the time delay has similar effect as the antiviral treatment, which can be used to eliminate the CHIKV. We observe that when the delay period is sufficiently long, the CHIKV replication will be cleared.

Figure 2
figure 2

The simulation of trajectories of system (5)–(9) for Case 1

Full size image
Table 2 The value of \(\mathcal{R}_{0}\) for different values of τ
Full size table

Case 2

We fix the value \(\omega _{1}=\omega _{2}=0.05\). Let us consider \(\mu =\mu _{1}=\mu _{2}\) and the initial

$$\begin{aligned}& \begin{gathered} \vartheta _{1}(\varphi )=16,\quad\quad \vartheta _{2}(\varphi )=0.05,\quad\quad \vartheta _{3}( \varphi )=0.2,\\ \vartheta _{4}( \varphi )=0.3,\quad\quad \vartheta _{5}(\varphi )=1.5, \quad \varphi \in {}[ -k,0].\end{gathered} \end{aligned}$$

The effect of the saturation on the CHIKV is shown in Fig. 3. It is shown that, as μ is increased, \(s(t) \) is increased (but does not reach \(s_{0}\)) while all of \(w(t)\), \(y(t)\), \(p(t)\), and \(x(t)\) are decreased (but do not reach zero).

Figure 3
figure 3

The simulation of trajectories of system (5)–(9) for Case 2

Full size image

5 Conclusion

In the literature, most of the published papers which proposed within-host CHIKV dynamics models assumed that the susceptible monocyte becomes infected by contacting with CHIKV (CHIKV-to-monocyte transmission). However, it was reported that the CHIKV can also spread by infected-to-monocyte transmission. In this paper, we formulated and analyzed within-host CHIKV dynamics models with latently infected cells and antibody immune response. We incorporated both CHIKV-to-monocyte and infected-to-monocyte transmissions. We assumed that the infection rate of modeling CHIKV infection is given by saturated mass action. We incorporated three types of discrete or distributed time delays into the model. To ensure the well-posedness of the model, we proved the nonnegativity and boundedness properties of the solutions. We derived the basic reproduction number \(\mathcal{R}_{0}\), which fully determines the existence and stability of the two equilibria of the model. The global stability of the equilibria of the model has been investigated by utilizing Lyapunov functionals and applying LaSalle’s invariance principle. We have proven that (i) if \(\mathcal{R}_{0}\leq 1\), then the CHIKV-free equilibrium \(\varOmega _{0}\) is globally asymptotically stable and the CHIKV is prophesied to be completely cleared from the body, and (ii) if \(\mathcal{R}_{0}>1\), then the infected equilibrium \(\varOmega _{1}\) is globally asymptotically stable and the CHIKV infection becomes chronic. We supported our theoretical results with numerical simulations.

Recently, many authors argued that the virus moves freely in body and follows the Fickian diffusion (see, e.g., [59] and [60]). Therefore, it is more reasonable to study reaction–diffusion versions of our models. Further, since the exact solutions of systems (5)–(9) and (17)–(21) are not known, therefore approximate solutions can only be found. Therefore, the corresponding discrete-time models of these systems need to be investigated (see, e.g., [61,62,63]). We leave these points as possible future works.