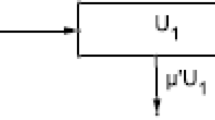1 Introduction

Humans have known about heroin and euphoria inducing properties for a long time. Heroin is also known as smacks, gag, horse, gear, and brown. Opium poppy is the major cause of drugs. In Neolithic times, the cultivation of these opium poppies was found as evidence. More than six thousand years ago, opium poppies were collected and consumed. In this way opium has remained popular drug for millennia. Opium dens were especially common during the 1800s, and first-time drug morphine was extracted from the opium poppy. Ultimately heroin introduced itself as an opiate drug extracted from morphine [1, 2]. In 1897, the Bayer pharmaceutical company of Germany refined heroin and started selling it as a cure for tuberculosis and addiction of drug morphine. Heroin is an opioid derivative, and an estimated 13.5 million people in the world take opioids. But approximately 9.2 million are heroin users. The average cost of a single dose of 0.1 g of heroin is $15 to $20 in the US costing between $150 and $200 per day for an addict to support their habit. According to the national survey on drug use and health (NSBUH), in 2014 about 430,000 Americans reported using heroin in that year with the greatest increase being by young adults aged 18 to 25. The number of people using heroin in 2016 was 948,000, which is nearly double the number of people from two years before [3]. These figures may even be low as it is likely that many heroin users simply do not take part in health service.

The biggest side effect of heroin is its addiction. Body changes and the traumatic mental side effects compel the user to increase the dose. The individuals who have been taking the drugs for quite some time will have high tolerance level hence making it all the more difficult to quit. If one decides to stop using heroin, the after effects include: extreme craving for the drug, restlessness, muscle, bone pain, diarrhea, and vomiting. These can persist between 48 to 72 hours. It also may take several attempts to get rid of it. Approximately, seventeen million peoples are directly affected by these types of drugs in the form of health problems all over the world.

2 Literature survey

In the last decade of the twentieth century various mathematical models were proposed to discuss the epidemic dynamics of heroin model. In 2009, Mulone and Straughan suggested in [4] that the model proposed by White and Comiskey in [5] has stable steady states. Wang, Yang, and Li in 2011 preferred bilinear incidence law over standard incidence in the heroin epidemic model. They proposed that the population is not constant with time in [6]. Samanta extended the model in [5] to non-autonomous epidemic form, which was an improved version of the periodic epidemic model. Here, the population has been treated periodically in [7]. Liu and Zhang worked on time delayed heroin epidemic model, which led to the formulation of a delay differential equation system in [8]. In 2013, Haung and Liu in [9] found that, under specific condition, the delay differential equation model can be converted into an ordinary differential equation model which resembles the renowned SIR epidemic model. Abdurahman, Zhang, and Teng in [10] changed a non-autonomous time delayed heroin epidemic model to an autonomous model. Here the non-standard finite difference pattern was applied to get the discretized heroin epidemic model. In 2015 the authors Fang et al. in [2, 11] formulated age-dependent susceptible and treat-age heroine epidemic models respectively. In 2016 Yang, Li, and Zhang in [12] inquired an age structured heroin model. Non-linear incidence rate was discussed instead of ordinary incidence rate. The time delayed heroin epidemic model was also proposed by the authors in [13]. Ma, Liu, and Li in [14] discussed various types of bifurcation of heroin epidemic model with non-linear contact rate. Besides, the age structured heroin epidemic model was also proposed in [15]. Wangari and Stone discussed the backward bifurcations and stability in the heroin model, and they considered that heroin users can be rehabilitated quickly in [16]. In 2018, a stochastic heroin epidemic model with bilinear incidence and varying population size was obtained from a deterministic version by Liu, Zhang, and Li in [17]. Liu, Zhang, and Xing inspected the vanishing and existence of ergodic stationary distribution in a stochastic heroine epidemic model. Stochastic Lyapunov function was developed to discuss the extinction of drug users among the population in [18]. Inspired by the previous work contributions, Zhang and Wang acquired a delayed heroin model in 2019. The authors studied the impact of the time delay on heroin model and concluded that the addicts are not cured quickly, rather they need a time period [19]. Random perturbations were introduced in the deterministic heroin epidemic model by Wei, Yang, and Li in [20].

Although huge improvements have been made towards the utilization of mathematical methods to model infectious disease, very little efforts have been made to impose this work on heroin epidemic models. In this paper, dynamic disease modeling is extended to the drug-using career. Here the drug users are interpreted as people who directly or indirectly hurt themselves or their families with their drug using habit [21]. The author has made his contributions towards the evolution of mathematical epidemiology. Social issues like drug and alcohol use are termed as epidemics, little work has been carried out towards the utilization of mathematical modeling techniques to these difficulties [22,23,24,25,26]. Different models of the transmission of heroin have been studied. The usual quantitative schemes like Euler and Runge–Kutta never maintain dynamical possessions as we have seen in the deterministic modeling. We have also seen that in Euler–Maruyama, stochastic Euler and stochastic Runge–Kutta do not maintain the dynamical possessions in stochastic case. So, from this a question arises and needs to be researched more: Could we develop the random emphatical scheme which maintains all the dynamical possessions [27,28,29]?

A rule introduced in the deterministic case has been used to start the notion stochastic non-standard finite difference scheme (SNSFD). These regulations were given by Mickens. This is the major point of this paper.

The flow of the paper is based on the following sections:

In Sect. 2, the deterministic heroin epidemic model is described. Section 3 explains the construction way of a stochastic heroin epidemic model and its equilibria. Section 4 explains the stochastic numerical schemes for the stochastic heroin epidemic model and its convergence analysis. In Sect. 5, the conclusion and directions are given.

3 Deterministic heroin epidemic model

We consider the heroin epidemic model presented in [5] in this section.

Let at any time t, the variables be described as S (denotes the susceptible group of people), \(\mathrm{U}_{1}\) (denotes the drug users who are not in treatment), and \(\mathrm{U}_{2} \) (denotes the drug users who are in treatment). In Fig. 1, the diagram of heroin epidemic model is presented.

Figure 1
figure 1

Flow diagram of heroin epidemic model

Full size image

The model parameters are described as Λ (denotes the individuals entering the susceptible population from general population), μ (denotes the general population natural decease rate), \(\delta_{1} \) (denotes the removal rate due to drug related deaths of users not in treatment and the recovery rate of those who stop using drugs without treatment), \(\delta_{2} \) (denotes the removal rate due to drug related deaths of users in treatment and the lucky cure rate that leads to drug-free life accompanied by immunity to drug addiction in the time period of modeling), \(\beta_{1} \) (denotes the probability of becoming a drug user), p (denotes the drug users who get treatment), and \(\beta_{3} \) (denotes the probability of a drug user in treatment relapsing to untreated use).

The deterministic equations of the heroin epidemic model are as follows:

$$\begin{aligned}& \frac{\mathrm{dS}}{\mathrm{dt}} =\varLambda\mathrm{N}- \frac{\beta_{1} \mathrm{U}_{1} \mathrm{S}}{\mathrm{N}} - \mu_{1} \mathrm{S}, \end{aligned}$$
(1)
$$\begin{aligned}& \frac{\mathrm{d} \mathrm{U}_{1}}{\mathrm{dt}} = \frac{\beta_{1} \mathrm{U}_{1} \mathrm{S}}{\mathrm{N}} -\mathrm{p} \mathrm{U}_{1} + \frac{\beta_{3} \mathrm{U}_{1} \mathrm{U}_{2}}{\mathrm{N}} - ( \mu+ \delta_{1} ) \mathrm{U}_{1}, \end{aligned}$$
(2)
$$\begin{aligned}& \frac{\mathrm{d} \mathrm{U}_{2}}{\mathrm{dt}} =\mathrm{p} \mathrm{U}_{1} - \frac{\beta_{3} \mathrm{U}_{1} \mathrm{U}_{2}}{\mathrm{N}} - ( \mu+ \delta_{2} ) \mathrm{U}_{2}, \end{aligned}$$
(3)

where

$$\mathrm{S}+ \mathrm{U}_{1} + \mathrm{U}_{2} =\mathrm{N} $$

put

$$\mathrm{S}= \frac{\mathrm{S}}{\mathrm{N}},\qquad \mathrm{U}_{1} = \frac{\mathrm{U}_{1}}{\mathrm{N}},\qquad \mathrm{U}_{2} = \frac{\mathrm{U}_{2}}{\mathrm{N}}. $$

The normalized form of model (1)–(3) is as follows:

$$\begin{aligned}& \frac{\mathrm{dS}}{\mathrm{dt}} =\varLambda- \beta_{1} \mathrm{U}_{1} \mathrm{S}- \mu_{1} \mathrm{S}, \end{aligned}$$
(4)
$$\begin{aligned}& \frac{\mathrm{d} \mathrm{U}_{1}}{\mathrm{dt}} = \beta_{1} \mathrm{U}_{1} \mathrm{S}- \mathrm{p} \mathrm{U}_{1} + \beta_{3} \mathrm{U}_{1} \mathrm{U}_{2} - \mu_{1} \mathrm{U}_{1}, \end{aligned}$$
(5)
$$\begin{aligned}& \frac{\mathrm{d} \mathrm{U}_{2}}{\mathrm{dt}} =\mathrm{p} \mathrm{U}_{1} - \beta_{3} \mathrm{U}_{1} \mathrm{U}_{2} - \mu_{1} \mathrm{U}_{2}, \end{aligned}$$
(6)

where the region for system (4)–(6) is \(\varGamma= \{ ( S, \mathrm{U}_{1}, \mathrm{U}_{2} ):\mathrm{S}+ \mathrm{U}_{1} + \mathrm{U}_{2} \leq \frac{\varLambda}{\mu_{1}}, \mathrm{S}\geq0, \mathrm{U}_{1} \geq0, \mathrm{U}_{2} \geq0 \}\). The given region is called feasible region for model (4)–(6). So, the solutions of model (4)–(6) lie in this region and are bounded.

3.1 Equilibria of heroin epidemic model

The equilibria of heroin model (4)–(6) are as follows:

  • Drug-free equilibrium is \(\mathrm{DFE}= ( \mathrm{S}, \mathrm{U}_{1}, \mathrm{U}_{2} ) = ( \frac{\varLambda}{\mu_{1}},0,0 )\),

  • Drug-present equilibrium is \(\mathrm{DPE}= ( \mathrm{S}^{*}, \mathrm{U}_{1}^{*}, \mathrm{U}_{2}^{*} )\),

where

$$\begin{gathered} \mathrm{U}_{1}^{*} = \frac{\varLambda- \mu_{1} \mathrm{S}^{*}}{\beta_{1} \mathrm{S}^{*}}, \qquad \mathrm{U}_{2}^{*} = \frac{\mathrm{p}+ \mu_{1} - \beta_{1} \mathrm{S}^{*}}{\beta_{3}}, \\ \mathrm{S}^{*} = \bigl[ \bigl( \beta_{1} ( \mathrm{p}+ \mu_{1} ) \mu_{2} +\mathrm{p} \beta_{3} \mu_{1} - \varLambda \beta_{1} \beta_{3} - \mu_{1} ( \mathrm{p}+ \mu_{1} ) \beta_{3} \bigr) \\ \phantom{\mathrm{S}^{*} =}{}\pm \bigl[ \bigl( \varLambda \beta_{1} \beta_{3} + \mu_{1} ( \mathrm{p}+ \mu_{1} ) \beta_{3} - \beta_{1} ( \mathrm{p}+ \mu_{1} ) \mu_{2} -\mathrm{p} \beta_{3} \mu_{1} \bigr)^{2} \\ \phantom{\mathrm{S}^{*} =}{} -4 \bigl( -\beta_{1}^{2} \mu_{2} - \mu_{1} \beta_{1} \beta_{3} \bigr) \bigl( \mathrm{p}+ \beta_{3} \varLambda- \beta_{3} \varLambda ( \mathrm{p}+ \mu_{1} ) \bigr)\bigr]^{1/2}\bigr] \\ \phantom{\mathrm{S}^{*} =}{} \big/ \bigl[2 \bigl( -\beta_{1}^{2} \mu_{2} - \mu_{1} \beta_{1} \beta_{3} \bigr)\bigr], \\ \mathrm{R}_{0}^{\mathrm{d}} = \frac{\beta_{1}}{ ( \mathrm{p}+ \mu_{1} )}.\end{gathered} $$

Note that \(\mathrm{R}_{0}^{\mathrm{d}}\) is heroin generation number.

4 Stochastic heroin epidemic model

Let us consider the vector \(\mathrm{W}= [\mathrm{S}, \mathrm{U}_{1}, \mathrm{U}_{2} ]^{\mathrm{T}}\), the transition probabilities of system (4)–(6) are as follows (see Table 1).

Table 1 Transition probabilities
Full size table

The expectation and variance of stochastic heroin epidemic model is defined as

$$\begin{gathered} \mathrm{E}^{*} [ \Delta \mathrm{W} ] = \sum _{\mathrm{i}=1}^{7} \mathrm{P}_{\mathrm{i}} \mathrm{T}_{\mathrm{i}}, \\ \text{Expectation} =\mathrm{E}^{*} [ \Delta \mathrm{W} ] = \left [ \textstyle\begin{array}{c} \mathrm{P}_{1} - \mathrm{P}_{2} - \mathrm{P}_{3}\\ \mathrm{P}_{2} - \mathrm{P}_{4} + \mathrm{P}_{5} - \mathrm{P}_{6}\\ \mathrm{P}_{4} - \mathrm{P}_{5} - \mathrm{P}_{7} \end{array}\displaystyle \right ] \Delta \mathrm{t}, \\ \mathrm{Var}= \mathrm{E}^{*} \bigl[ \Delta \mathrm{W} \Delta \mathrm{W}^{\mathrm{T}} \bigr] = \sum_{\mathrm{i}=1}^{7} \mathrm{P}_{\mathrm{i}} [\mathrm{T}_{\mathrm{i}} ] [\mathrm{T}_{\mathrm{i}} ]^{\mathrm{T}}, \\ \mathrm{E}^{*} \bigl[ \Delta \mathrm{W} \Delta \mathrm{W}^{\mathrm{T}} \bigr] = \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \mathrm{P}_{1} + \mathrm{P}_{2} + \mathrm{P}_{3} & - \mathrm{P}_{2} & 0\\ - \mathrm{P}_{2} & \mathrm{P}_{2} + \mathrm{P}_{4+} \mathrm{P}_{5} + \mathrm{P}_{6} & - \mathrm{P}_{4} - \mathrm{P}_{5}\\ 0 & - \mathrm{P}_{4} - \mathrm{P}_{5} & \mathrm{P}_{4} + \mathrm{P}_{5} + \mathrm{P}_{7} \end{array}\displaystyle \right ] \Delta \mathrm{t}.\end{gathered} $$

The general form of SDEs is as follows:

$$\begin{gathered} \frac{\mathrm{dW}(\mathrm{t})}{\mathrm{dt}} =\mathrm{f} \bigl( \mathrm{W}(\mathrm{t}), \mathrm{t} \bigr) +\mathrm{L}\bigl(\mathrm{W}(\mathrm{t}),\mathrm{t}\bigr) \frac{\mathrm{dB}(\mathrm{t})}{\mathrm{dt}}, \\ \text{Stochastic drift} =\mathrm{f} \bigl( \mathrm{W} ( \mathrm{t} ),\mathrm{t} \bigr) = \frac{\mathrm{E}^{*} [ \Delta \mathrm{W} ]}{\Delta \mathrm{t}}, \\ \text{Stochastic diffusion} =\mathrm{L} \bigl( \mathrm{W}(\mathrm{t}),\mathrm{t} \bigr) = \sqrt{\frac{\mathrm{E}^{*} [\Delta \mathrm{W} \Delta \mathrm{W}^{\mathrm{T}} ]}{\Delta \mathrm{t}}} . \end{gathered} $$

The SDE of system (4)–(6) is as follows:

$$ \mathrm{dW} ( \mathrm{t} ) =\mathrm{f} \bigl( \mathrm{W}(\mathrm{t}),\mathrm{t} \bigr) \,\mathrm{dt}+\mathrm{L} \bigl( \mathrm{W}(\mathrm{t}),\mathrm{t} \bigr) \,\mathrm{dB}(\mathrm{t}) $$
(7)

with initial conditions \(\mathrm{W} ( 0 ) = \mathrm{W}_{0} = [0.5,0.3, 0.2]^{\mathrm{T}}\), \(0\leq \mathrm{t}\leq \mathrm{T}\), and \(\mathrm{B}(\mathrm{t})\) is called Brownian motion.

4.1 Euler–Maruyama method

System (7) could be written and presented in [30] as follows:

$$ \mathrm{W}_{\mathrm{n}+1} = \mathrm{W}_{\mathrm{n}} + \mathrm{f} ( \mathrm{W}_{\mathrm{n}},\mathrm{t} ) \Delta \mathrm{t}+ \mathrm{L} ( \mathrm{W}_{\mathrm{n}},\mathrm{t} ) \Delta \mathrm{B}_{\mathrm{n}}, $$
(8)

where ‘Δt’ could be represented as a time step size and \(\Delta \mathrm{B}_{\mathrm{n}}\) is the standard normal distribution, i.e., \(\Delta \mathrm{B}_{\mathrm{n}} \sim \mathrm{N}(0, 1)\). For the solution of system (8), we shall use the parameter values presented in [5] (see Table 2).

Table 2 Parameter values [5]
Full size table

The solution of system (8), i.e., \(\mathrm{DFE} = ( \frac{\varLambda}{ \mu_{1}},0,0)\) and \(\mathrm{DPE} = ( 0.2713, 0.5372, 0.1915 )\). For the graphical illustration of system (8), see Fig. 2.

Figure 2
figure 2

(a) In drug users’ fraction Euler–Maruyama converges to drug-present equilibrium, while deterministic solution is the mean of Euler–Maruyama solution for \(\mathrm{h}=0.01\). (b) In drug users’ fraction Euler–Maruyama shows negativity and divergence for drug-present equilibrium for \(\mathrm{h}=4\)

Full size image

5 Parametric perturbation in heroin epidemic model

In this technique, we shall choose parameters from system (4)–(6) and change into the random parameters with small noise as \(\beta_{1}\, \mathrm{dt}= \beta_{1}\, \mathrm{dt}+\sigma\, \mathrm{dB}\). So, the stochastic heroin epidemic of system (4)–(6) is as follows [31]:

$$\begin{aligned}& \mathrm{dS}= ( \varLambda- \beta_{1} \mathrm{U}_{1} \mathrm{S}- \mu_{1} \mathrm{S} ) \,\mathrm{dt}-\sigma \mathrm{U}_{1} \mathrm{S}\,\mathrm{dB}, \end{aligned}$$
(9)
$$\begin{aligned}& \mathrm{d} \mathrm{U}_{1} = ( \beta_{1} \mathrm{U}_{1} \mathrm{S}-\mathrm{p} \mathrm{U}_{1} + \beta_{3} \mathrm{U}_{1} \mathrm{U}_{2} - \mu_{1} \mathrm{U}_{1} )\, \mathrm{dt}+\sigma \mathrm{U}_{1} \mathrm{S}\,\mathrm{dB}, \end{aligned}$$
(10)
$$\begin{aligned}& \mathrm{d} \mathrm{U}_{2} = ( \mathrm{p} \mathrm{U}_{1} - \beta_{3} \mathrm{U}_{1} \mathrm{U}_{2} - \mu_{2} \mathrm{U}_{2} )\, \mathrm{dt}. \end{aligned}$$
(11)

The Brownian motion is denoted by \(\mathrm{B}_{\mathrm{k}} ( \mathrm{t} )\) (\(\mathrm{k}=1,2,3\)). The stochasticity of system (9)–(11) is denoted by σ and \(\sigma_{1}\). System (9)–(11) has no analytic solution due to non-integral term of Brownian motion. So, in the coming section we shall assume some stochastic methods for the solution of system (9)–(11).

5.1 Equilibria of stochastic heroin epidemic model

The equilibria of system (9)–(11) are as follows:

  • Drug-free equilibrium is \(\mathrm{DFE}= ( S, \mathrm{U}_{1}, \mathrm{U}_{2} ) = ( \frac{\varLambda}{\mu_{1}},0,0 )\),

  • Drug-present equilibrium is \(\mathrm{DPE}= ( \mathrm{S}^{*}, \mathrm{U}_{1}^{*}, \mathrm{U}_{2}^{*} )\),

where

$$\begin{gathered} \mathrm{U}_{1}^{*} = \frac{\varLambda- \mu_{1} \mathrm{S}}{\beta_{1} \mathrm{S}}, \qquad \mathrm{U}_{2}^{*} = \frac{\mathrm{p}+ \mu_{1} - \beta_{1} \mathrm{S}}{\beta_{3}}, \\ \mathrm{S}^{*} = \bigl[ \bigl( \beta_{1} ( \mathrm{p}+ \mu_{1} ) \mu_{2} +\mathrm{p} \beta_{3} \mu_{1} - \varLambda \beta_{1} \beta_{3} - \mu_{1} ( \mathrm{p}+ \mu_{1} ) \beta_{3} \bigr) \\ \phantom{\mathrm{S}^{*} =}{}\pm \bigl[ \bigl( \varLambda \beta_{1} \beta_{3} + \mu_{1} ( \mathrm{p}+ \mu_{1} ) \beta_{3} - \beta_{1} ( \mathrm{p}+ \mu_{1} ) \mu_{2} -\mathrm{p} \beta_{3} \mu_{1} \bigr)^{2} -4 \bigl( -\beta_{1}^{2} \mu_{2} - \mu_{1} \beta_{1} \beta_{3} \bigr)\bigr]^{1/2} \\ \phantom{\mathrm{S}^{*} =}{}\times \bigl( \mathrm{p}+ \beta_{3} \varLambda- \beta_{3} \varLambda ( \mathrm{p}+ \mu_{1} ) \bigr)\bigr] \\ \phantom{\mathrm{S}^{*} =}{} \big/ \bigl[2 \bigl( -\beta_{1}^{2} \mu_{2} - \mu_{1} \beta_{1} \beta_{3} \bigr)\bigr].\end{gathered} $$

Lemma 5.1

The solution \(( \mathrm{S} ( \mathrm{t} ), \mathrm{U}_{1} ( \mathrm{t} ), \mathrm{U}_{2} ( \mathrm{t} ) )\) of system (9)–(11), for any assumed initial value \(( \mathrm{S} ( 0 ), \mathrm{U}_{1} ( 0 ), \mathrm{U}_{2} ( 0 ) ) \in \mathrm{R}_{+}^{3}\), has the following possessions, almost surely.

5.1.1 Stochastic threshold dynamics

Extinction

Let us introduce \(\mathrm{R}_{0}^{\mathrm{S}} = \mathrm{R}_{0}^{\mathrm{d}} - \frac{\sigma^{2} \mathrm{R}}{2 \mu_{1}^{2} ( \mathrm{P}+ \mu_{1} )^{3}}\).

Then we have the following.

Definition 5.1

For system (9)–(11) the drug users \(\mathrm{U}_{1}\)(t) are supposed to be extinct if \(\lim_{\mathrm{t}\rightarrow\infty} \mathrm{U}_{1} ( \mathrm{t} ) =0\) almost surely.

Theorem 5.1

If \(\sigma^{2} < \frac{\beta_{1} \mu_{1}}{ \varLambda}\) and \(\mathrm{R}_{0}^{\mathrm{S}}\) < 1, then the drug users of system (9)–(11) approach to zero exponentially almost surely.

Proof

Let us assume that \(( \mathrm{S} ( \mathrm{t} ), \mathrm{U}_{1} ( \mathrm{t} ), \mathrm{U}_{2} (\mathrm{t}) )\) is a solution of system (9)–(11) with holding the initial conditions \(( \mathrm{S} ( 0 ), \mathrm{U}_{1} ( 0 ), \mathrm{U}_{2} (0) ) \in \mathrm{R}_{+}^{3}\) by Ito’s formula.

Let \(\mathrm{f} (\mathrm{U}_{1} )= \ln (\mathrm{U}_{1} )\) and

$$\begin{gathered} \mathrm{d}\ln ( \mathrm{U}_{1} ) = \mathrm{f}' ( \mathrm{U}_{1} ) \,\mathrm{d} \mathrm{U}_{1} + \frac{1}{2} \mathrm{f}^{''} ( \mathrm{U}_{1} ) \mathrm{U}_{1}^{2} \bigl( \sigma^{2} \mathrm{S}^{2} \bigr) \,\mathrm{dt}, \\ \mathrm{d} \ln (\mathrm{U}_{1} )= \frac{1}{\mathrm{U}_{1}} \,\mathrm{d} \mathrm{U}_{1} + \frac{1}{2} \biggl(- \frac{1}{\mathrm{U}_{1}^{2}} \biggr) \mathrm{U}_{1}^{2} \bigl( \sigma^{2} \mathrm{S}^{2} \bigr) \,\mathrm{dt}, \\ \mathrm{d} \ln (\mathrm{U}_{1} )=\biggl( \beta_{1} \mathrm{S}-\mathrm{p}+ \beta_{3} \mathrm{U}_{2} - \mu_{1} - \frac{1}{2} \sigma^{2} \mathrm{S}^{2} \biggr)\,\mathrm{dt}+\sigma \mathrm{S}\,\mathrm{dt}.\end{gathered} $$

By integrating “0” to “t” on both sides, we have

$$\ln ( \mathrm{U}_{1} )= \ln \mathrm{U}_{1} ( 0 ) + \int_{0}^{\mathrm{t}} \biggl( \beta_{1} \mathrm{S}-\mathrm{p}+ \beta_{3} \mathrm{U}_{2} - \mu_{1} - \frac{1}{2} \sigma^{2} \mathrm{S}^{2} \biggr)\,\mathrm{dt}+ \int_{0}^{\mathrm{t}} \sigma \mathrm{S}\,\mathrm{dB}, $$

where \(\mathrm{M} ( \mathrm{t} ) = \int_{0}^{\mathrm{t}} \sigma \mathrm{S}\,\mathrm{dB}\) is the continuous martingale with \(\mathrm{M} ( 0 ) =0\).

If \(\sigma^{2} > \frac{\beta_{1} \mu_{1}}{\varLambda}\),

$$\begin{gathered} \ln (\mathrm{U}_{1} )\leq\biggl( \frac{\beta_{1}^{2}}{2 \sigma^{2}} -(\mathrm{p}+ \mu_{1} )\biggr)\mathrm{t}+ \mathrm{M}_{1} ( \mathrm{t} ) + \ln \mathrm{U}_{1} ( 0 ), \\ \frac{\ln (\mathrm{U}_{1} )}{\mathrm{t}} \leq- \biggl( ( \mathrm{p}+ \mu_{1} ) - \frac{\beta_{1}^{2}}{2 \sigma^{2}} \biggr) + \frac{\mathrm{M}_{1} ( \mathrm{t} )}{\mathrm{t}} + \frac{\ln \mathrm{U}_{1} (0)}{\mathrm{t}}. \end{gathered} $$

By above Lemma 5.1, if

$$\lim_{\mathrm{t}\rightarrow\infty} \frac{\mathrm{M}_{1} ( \mathrm{t} )}{\mathrm{t}} =0 $$

and

$$\lim_{\mathrm{t}\rightarrow\infty} \frac{\ln \mathrm{U}_{1} (\mathrm{t})}{ \mathrm{t}} \leq \biggl( ( \mathrm{P}+ \mu_{1} ) - \frac{\beta_{1}^{2}}{2 \sigma^{2}} \biggr) < 0, $$

then \(\sigma^{2} > \frac{\beta_{1}^{2}}{2(\mathrm{p}+ \mu_{1} )}\) and \(\lim_{\mathrm{t}\rightarrow\infty} \mathrm{U}_{1} (\mathrm{t}) =0\) almost surely.

If \(\sigma^{2} < \frac{\beta_{1} \mu_{1}}{\varLambda}\), then

$$\begin{aligned}& \ln \bigl( \mathrm{U}_{1} ( \mathrm{t} ) \bigr) \leq \biggl( \frac{\beta_{1} \varLambda}{\mu_{1}} - \frac{1}{2} \sigma^{2} \frac{\varLambda^{2}}{\mu_{1}^{2}} - ( \mathrm{p}+ \mu_{1} ) \biggr) \mathrm{t}+ \mathrm{M}_{1} ( \mathrm{t} ) + \ln \mathrm{U}_{1} ( 0 ), \\& \frac{\ln \mathrm{U}_{1} (\mathrm{t})}{\mathrm{t}} \leq ( \mathrm{p}+ \mu_{1} ) \biggl( \frac{\beta_{1} \varLambda}{\mu_{1} ( \mathrm{p}+ \mu_{1} )} - \frac{1}{2} \sigma^{2} \frac{\varLambda^{2}}{\mu_{1}^{2} ( \mathrm{p}+ \mu_{1} )} -1 \biggr) + \frac{\mathrm{M}_{1} ( \mathrm{t} )}{\mathrm{t}} + \frac{\ln \mathrm{U}_{1} (0)}{\mathrm{t}}. \end{aligned}$$
(12)

By taking the superior limit on both sides of (12), we have

$$\lim_{\mathrm{t}\rightarrow\infty} \sup \frac{\ln \mathrm{U}_{1} ( \mathrm{t} )}{\mathrm{t}} \leq ( \mathrm{P}+ \mu_{1} ) \bigl( \mathrm{R}_{0}^{\mathrm{S}} -1 \bigr), $$

when \(\mathrm{R}_{0}^{\mathrm{S}} <1\) we get

$$\lim_{\mathrm{t}\rightarrow\infty} \sup \frac{\ln \mathrm{U}_{1} ( \mathrm{t} )}{\mathrm{t}} \leq 0 \quad\Rightarrow \quad\lim _{\mathrm{t}\rightarrow\infty} \mathrm{U}_{1} ( \mathrm{t} ) =0 $$

almost surely

$$\mathrm{R}_{0}^{\mathrm{S}} = \mathrm{R}_{0}^{\mathrm{d}} - \frac{1}{2} \sigma^{2} \frac{\varLambda^{2}}{\mu_{1}^{2} ( \mathrm{p}+ \mu_{1} )} < 1. $$

The stochastic reproduction number \(\mathrm{R}_{0}^{\mathrm{S}} =0.3320<1\) means these measures are helpful in controlling the heroin in population and the stochastic reproduction number \(\mathrm{R}_{0}^{\mathrm{S}} =3.3320 >1\) means the heroin is endemic in population. □

5.2 Stochastic Euler method

System (9)–(11) could be written as follows [31,32,33]:

$$ \left . \textstyle\begin{array}{l} \mathrm{S}^{\mathrm{n}+1} = \mathrm{S}^{\mathrm{n}} +\mathrm{h} ( \varLambda- \beta_{1} \mathrm{U}_{1}^{\mathrm{n}} \Delta^{\mathrm{n}} - \mu_{1} \Delta^{\mathrm{n}} -\sigma \mathrm{U}_{1}^{\mathrm{n}} \mathrm{S}^{\mathrm{n}} \Delta \mathrm{B}_{\mathrm{n}} ) \\ \mathrm{U}_{1}^{\mathrm{n}+1} = \mathrm{U}_{1}^{\mathrm{n}} +\mathrm{h} ( \beta_{1} \mathrm{U}_{1}^{\mathrm{n}} \Delta^{\mathrm{n}} -\mathrm{p} \mathrm{U}_{1}^{\mathrm{n}} + \beta_{3} \mathrm{U}_{1}^{\mathrm{n}} \mathrm{U}_{2}^{\mathrm{n}} - \mu_{1} \mathrm{U}_{1}^{\mathrm{n}} -\sigma \mathrm{U}_{1}^{\mathrm{n}} \mathrm{S}^{\mathrm{n}} \Delta \mathrm{B}_{\mathrm{n}} ) \\ \mathrm{U}_{2}^{\mathrm{n}+1} = \mathrm{U}_{2}^{\mathrm{n}} +\mathrm{h} ( \mathrm{p} \mathrm{U}_{1}^{\mathrm{n}} - \beta_{3} \mathrm{U}_{1}^{\mathrm{n}} \mathrm{U}_{2}^{\mathrm{n}} - \mu_{2} \mathrm{U}_{2}^{\mathrm{n}} ) \end{array}\displaystyle \right \}, $$
(13)

where “h” is represented as a time step size and \(\Delta \mathrm{B}_{\mathrm{n}} \sim \mathrm{N}(0,1)\). The solution of system (13) is illustrated in Fig. 3.

Figure 3
figure 3

(a) In susceptible users’ fraction stochastic Euler method converges to drug-free equilibrium, while deterministic solution is the mean of stochastic Euler method solution for \(h=0.01\). (b) In susceptible users’ fraction stochastic Euler method fails to maintain the positivity and diverges for drug-free equilibrium for \(h=5\). (c) In drug users’ fraction stochastic Euler method converges to drug-present equilibrium, while deterministic solution is the mean of stochastic Euler method solution for \(h=0.01\). (d) In drug users’ fraction stochastic Euler method shows negativity and unstable behavior for drug-present equilibrium for \(h=5\)

Full size image

5.3 Stochastic Runge–Kutta method

System (9)–(11) could be written as follows [31,32,33]:

Stage 1

$$\begin{gathered} \mathrm{A}_{1} = \mathrm{h} \bigl( \varLambda- \beta_{1} \mathrm{U}_{1}^{\mathrm{n}} \mathrm{S}^{\mathrm{n}} - \mu_{1} \mathrm{S}^{\mathrm{n}} -\sigma \mathrm{U}_{1}^{\mathrm{n}} \mathrm{S}^{\mathrm{n}} \Delta \mathrm{B}_{\mathrm{n}} \bigr), \\ \mathrm{B}_{1} =\mathrm{h} \bigl( \beta_{1} \mathrm{U}_{1}^{\mathrm{n}} \mathrm{S}^{\mathrm{n}} -\mathrm{p} \mathrm{U}_{1}^{\mathrm{n}} + \beta_{3} \mathrm{U}_{1}^{\mathrm{n}} \mathrm{U}_{2}^{\mathrm{n}} - \mu_{1} \mathrm{U}_{1}^{\mathrm{n}} -\sigma \mathrm{U}_{1}^{\mathrm{n}} \mathrm{S}^{\mathrm{n}} \Delta \mathrm{B}_{\mathrm{n}} \bigr), \\ \mathrm{C}_{1} =\mathrm{h} \bigl( \mathrm{p} \mathrm{U}_{1}^{\mathrm{n}} - \beta_{3} \mathrm{U}_{1}^{\mathrm{n}} \mathrm{U}_{2}^{\mathrm{n}} - \mu_{2} \mathrm{U}_{2}^{\mathrm{n}} \bigr).\end{gathered} $$

Stage 2

$$\begin{gathered} \mathrm{A}_{2} = \mathrm{h} \biggl( \varLambda- \beta_{1} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{1}}{2} \biggr) \biggl( \mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{1}}{2} \biggr)\\ \phantom{\mathrm{A}_{2} =}{}- \mu_{1} \biggl( \mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{1}}{2} \biggr) -\sigma\biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{1}}{2} \biggr) \biggl( \mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{1}}{2} \biggr)\Delta \mathrm{B}_{\mathrm{n}} \biggr), \\ \mathrm{B}_{2} =\mathrm{h} \biggl( \beta_{1} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{1}}{2} \biggr) \biggl( \mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{1}}{2} \biggr) -\mathrm{p} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{1}}{2} \biggr) + \beta_{3} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{1}}{2} \biggr) \biggl( \mathrm{U}_{2}^{\mathrm{n}} + \frac{\mathrm{C}_{1}}{2} \biggr)\\ \phantom{\mathrm{B}_{2} =} {}- \mu_{1} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{1}}{2} \biggr) -\sigma \biggl(\mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{1}}{2} \biggr) \biggl(\mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{1}}{2} \biggr)\Delta \mathrm{B}_{\mathrm{n}} \biggr), \\ \mathrm{C}_{2} =\mathrm{h}\biggl[\mathrm{p} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{1}}{2} \biggr) - \beta_{3} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{1}}{2} \biggr) \biggl(\mathrm{U}_{2}^{\mathrm{n}} + \frac{\mathrm{C}_{1}}{2} \biggr) - \mu_{2} \biggl( \mathrm{U}_{2}^{\mathrm{n}} + \frac{\mathrm{C}_{1}}{2} \biggr) \biggr]. \end{gathered} $$

Stage 3

$$\begin{gathered} \mathrm{A}_{3} = \mathrm{h} \biggl( \varLambda- \beta_{1} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{2}}{2} \biggr) \biggl( \mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{2}}{2} \biggr)\\ \phantom{\mathrm{A}_{3} =}{}- \mu_{1} \biggl( \mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{2}}{2} \biggr)-\sigma\biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{2}}{2} \biggr) \biggl( \mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{2}}{2} \biggr)\Delta \mathrm{B}_{\mathrm{n}} \biggr), \\ \mathrm{B}_{3} =\mathrm{h} \biggl( \beta_{1} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{2}}{2} \biggr) \biggl( \mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{2}}{2} \biggr) -\mathrm{p} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{2}}{2} \biggr) + \beta_{3} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{2}}{2} \biggr) \biggl( \mathrm{U}_{2}^{\mathrm{n}} + \frac{\mathrm{C}_{2}}{2} \biggr) \\ \phantom{\mathrm{B}_{3} =}{}- \mu_{1} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{2}}{2} \biggr) -\sigma \biggl(\mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{2}}{2} \biggr) \biggl(\mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{2}}{2} \biggr)\Delta \mathrm{B}_{\mathrm{n}} \biggr), \\ \mathrm{C}_{3} =\mathrm{h}\biggl[\mathrm{p} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{2}}{2} \biggr) - \beta_{3} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{2}}{2} \biggr) \biggl(\mathrm{U}_{2}^{\mathrm{n}} + \frac{\mathrm{C}_{2}}{2} \biggr) - \mu_{2} \biggl( \mathrm{U}_{2}^{\mathrm{n}} + \frac{\mathrm{C}_{2}}{2} \biggr) \biggr]. \end{gathered} $$

Stage 4

$$\begin{gathered} \mathrm{A}_{4} = \mathrm{h} \biggl( \varLambda- \beta_{1} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{3}}{2} \biggr) \biggl( \mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{3}}{2} \biggr)\\ \phantom{\mathrm{A}_{4} =}{}- \mu_{1} \biggl( \mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{3}}{2} \biggr)-\sigma\biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{3}}{2} \biggr) \biggl( \mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{3}}{2} \biggr)\Delta \mathrm{B}_{\mathrm{n}} \biggr), \\ \mathrm{B}_{4} =\mathrm{h} \biggl( \beta_{1} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{3}}{2} \biggr) \biggl( \mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{3}}{2} \biggr) -\mathrm{p} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{3}}{2} \biggr) + \beta_{3} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{3}}{2} \biggr) \biggl( \mathrm{U}_{2}^{\mathrm{n}} + \frac{\mathrm{C}_{3}}{2} \biggr)\\ \phantom{\mathrm{B}_{4} =}{} - \mu_{1} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{3}}{2} \biggr) -\sigma \biggl(\mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{3}}{2} \biggr) \biggl(\mathrm{S}^{\mathrm{n}} + \frac{\mathrm{A}_{3}}{2} \biggr)\Delta \mathrm{B}_{\mathrm{n}} \biggr), \\ \mathrm{C}_{4} =\mathrm{h}\biggl[\mathrm{p} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{3}}{2} \biggr) - \beta_{3} \biggl( \mathrm{U}_{1}^{\mathrm{n}} + \frac{\mathrm{B}_{3}}{2} \biggr) \biggl(\mathrm{U}_{2}^{\mathrm{n}} + \frac{\mathrm{C}_{3}}{2} \biggr) - \mu_{2} \biggl( \mathrm{U}_{2}^{\mathrm{n}} + \frac{\mathrm{C}_{3}}{2} \biggr) \biggr]. \end{gathered} $$

Final stage

$$ \left . \textstyle\begin{array}{l} \mathrm{S}^{\mathrm{n}+1} = \mathrm{S}^{\mathrm{n}} + \frac{1}{6} [ \mathrm{A}_{1} +2 \mathrm{A}_{2} +2 \mathrm{A}_{3} + \mathrm{A}_{4} ] \\ \mathrm{U}_{1}^{\mathrm{n}+1} = \mathrm{U}_{1}^{\mathrm{n}} + \frac{1}{6} [ \mathrm{B}_{1} +2 \mathrm{B}_{2} +2 \mathrm{B}_{3} + \mathrm{B}_{4} ] \\ \mathrm{U}_{2}^{\mathrm{n}+1} = \mathrm{U}_{2}^{\mathrm{n}} + \frac{1}{6} [ \mathrm{C}_{1} +2 \mathrm{C}_{2} +2 \mathrm{C}_{3} + \mathrm{C}_{4} ] \end{array}\displaystyle \right \}, $$
(14)

where “h” is represented as a time step size and \(\Delta \mathrm{B}_{\mathrm{n}} \sim \mathrm{N}(0,1)\). The solution of system (14) is shown in Fig. 4.

Figure 4
figure 4

(a) In susceptible users’ fraction stochastic Runge–Kutta method converges to drug-free equilibrium, while deterministic solution is the mean of stochastic Runge–Kutta method solution for \(\mathrm{h}=0.01\). (b) In susceptible users’ fraction stochastic Runge–Kutta method solution is unbound for drug-free equilibrium for \(\mathrm{h}=0.01\). (c) In drug users’ fraction stochastic Runge–Kutta method converges to drug-present equilibrium, while deterministic solution is the mean of stochastic Runge–Kutta method solution for \(\mathrm{h}=0.01\). (d) In drug users fraction stochastic Runge–Kutta method shows failure of dynamical properties for drug-present equilibrium for \(\mathrm{h}=6\)

Full size image

5.4 Stochastic NSFD method

System (9)–(11) could be written as follows [31,32,33]:

$$ \left . \textstyle\begin{array}{l} \mathrm{S}^{\mathrm{n}+1} = \frac{\mathrm{S}^{\mathrm{n}} +\lambda\varLambda}{1+\mathrm{h} \beta_{1} \mathrm{U}_{1}^{\mathrm{n}} +\mathrm{h} \mu_{1} +\mathrm{h}\sigma \mathrm{U}_{1}^{\mathrm{n}} \Delta \mathrm{B}_{\mathrm{n}}} \\ \mathrm{U}_{1}^{\mathrm{n}+1} = \frac{\mathrm{U}_{1}^{\mathrm{n}} +\mathrm{h} \beta_{1} \mathrm{U}_{1}^{\mathrm{n}} \mathrm{S}^{\mathrm{n}} + \beta_{3} \mathrm{U}_{1}^{\mathrm{n}} \mathrm{U}_{2}^{\mathrm{n}} +\sigma \mathrm{U}_{1}^{\mathrm{n}} \mathrm{S}^{\mathrm{n}} \Delta \mathrm{B}_{\mathrm{n}}}{1+\mathrm{hp}+\mathrm{h} \mu_{1}} \\ \mathrm{U}_{2}^{\mathrm{n}+1} = \frac{\mathrm{U}_{2}^{\mathrm{n}} +\mathrm{hp} \mathrm{U}_{1}^{\mathrm{n}}}{1+\mathrm{h} \beta_{3} \mathrm{U}_{1}^{\mathrm{n}} +\mathrm{h} \mu_{2}} \end{array}\displaystyle \right \}, $$
(15)

where “h” is represented as a time step size and \(\Delta \mathrm{B}_{\mathrm{n}} \sim \mathrm{N}(0,1)\).

5.4.1 Analysis of the stochastic NSFD method

Let us assume some theorems as follows.

Theorem 5.2

System (15) has a unique positive solution \(( \mathrm{S}^{\mathrm{n}}, \mathrm{U}_{1}^{\mathrm{n}}, \mathrm{U}_{2}^{\mathrm{n}} )\in \mathrm{R}_{+}^{3}\) on \(\mathrm{n}\geq 0\), for any initial system \(( \mathrm{S}^{\mathrm{n}} (0), \mathrm{U}_{1}^{\mathrm{n}} (0), \mathrm{U}_{2}^{\mathrm{n}} (0)) \in \mathrm{R}_{+}^{3}\), almost surely.

Theorem 5.3

The set \(\varOmega= \{ ( \mathrm{S}^{\mathrm{n}}, \mathrm{U}_{1}^{\mathrm{n}}, \mathrm{U}_{2}^{\mathrm{n}} ) \in \mathrm{R}_{+}^{3}: \mathrm{S}^{\mathrm{n}} \geq0, \mathrm{U}_{1}^{\mathrm{n}} \geq0, \mathrm{U}_{2}^{\mathrm{n}} \geq0, \mathrm{S}^{\mathrm{n}} + \mathrm{U}_{1}^{\mathrm{n}} + \mathrm{U}_{2}^{\mathrm{n}} \leq \frac{\varLambda}{\mu_{1}} \}\) for all \(\mathrm{n}\geq0\) is a non-negative invariant for system (15).

Proof

System (15) could be written as follows:

$$\begin{gathered} \frac{\mathrm{S}^{\mathrm{n}+1} - \mathrm{S}^{\mathrm{n}}}{\mathrm{h}} =\varLambda- \beta_{1} \mathrm{U}_{1}^{\mathrm{n}} \mathrm{S}^{\mathrm{n}} - \mu_{1} \mathrm{S}^{\mathrm{n}} -\sigma \mathrm{U}_{1}^{\mathrm{n}} \mathrm{S}^{\mathrm{n}} \Delta \mathrm{B}_{\mathrm{n}}, \\ \frac{\mathrm{U}_{1}^{\mathrm{n}+1} - \mathrm{U}_{1}^{\mathrm{n}}}{ \mathrm{h}} = \beta_{1} \mathrm{U}_{1}^{\mathrm{n}} \mathrm{S}^{\mathrm{n}} -\mathrm{p} \mathrm{U}_{1}^{\mathrm{n}} + \beta_{3} \mathrm{U}_{1}^{\mathrm{n}} \mathrm{U}_{2}^{\mathrm{n}} - \mu_{1} \mathrm{U}_{1}^{\mathrm{n}} +\sigma \mathrm{U}_{1}^{\mathrm{n}} \mathrm{S}^{\mathrm{n}} \Delta \mathrm{B}_{\mathrm{n}}, \\ \frac{\mathrm{U}_{2}^{\mathrm{n}+1} - \mathrm{U}_{2}^{\mathrm{n}}}{ \mathrm{h}} =\mathrm{p} \mathrm{U}_{1}^{\mathrm{n}} - \beta_{3} \mathrm{U}_{1}^{\mathrm{n}} \mathrm{U}_{2}^{\mathrm{n}} - \mu_{2} \mathrm{U}_{2}^{\mathrm{n}}.\end{gathered} $$

So,

$$\begin{gathered} \frac{(\mathrm{S}^{\mathrm{n}+1} + \mathrm{U}_{1}^{\mathrm{n}+1} + \mathrm{U}_{2}^{\mathrm{n}+1} )-( \mathrm{S}^{\mathrm{n}} + \mathrm{U}_{1}^{\mathrm{n}} + \mathrm{U}_{2}^{\mathrm{n}} )}{\mathrm{h}} =\varLambda- \mu_{1} \bigl( \mathrm{S}^{\mathrm{n}} + \mathrm{U}_{1}^{\mathrm{n}} + \mathrm{U}_{2}^{\mathrm{n}} \bigr), \\ \mathrm{S}^{\mathrm{n}+1} + \mathrm{U}_{1}^{\mathrm{n}+1} + \mathrm{U}_{2}^{\mathrm{n}+1} = \bigl( \mathrm{S}^{\mathrm{n}} + \mathrm{U}_{1}^{\mathrm{n}} + \mathrm{U}_{2}^{\mathrm{n}} \bigr) +\mathrm{h}\varLambda- \mu_{1} \bigl( \mathrm{S}^{\mathrm{n}} + \mathrm{U}_{1}^{\mathrm{n}} + \mathrm{U}_{2}^{\mathrm{n}} \bigr), \\ \mathrm{S}^{\mathrm{n}+1} + \mathrm{U}_{1}^{\mathrm{n}+1} + \mathrm{U}_{2}^{\mathrm{n}+1} \leq \frac{\varLambda}{\mu_{1}} +\mathrm{h}\varLambda- \mathrm{h} \mu_{1} \biggl( \frac{\varLambda}{\mu_{1}} \biggr), \\ \mathrm{S}^{\mathrm{n}+1} + \mathrm{U}_{1}^{\mathrm{n}+1} + \mathrm{U}_{2}^{\mathrm{n}+1} \leq \frac{\varLambda}{\mu_{1}},\end{gathered} $$

almost surely. □

Theorem 5.4

Discrete dynamical system (15) has the same equilibria as those of Continuous dynamical system (9)–(11) for all \(\mathrm{n}\geq0\).

Proof

The equilibria of system (9)–(11) are as follows:

  • DFE, i.e., \(\mathrm{D}_{3} = ( \mathrm{S}^{\mathrm{n}}, \mathrm{U}_{1}^{\mathrm{n}}, \mathrm{U}_{2}^{\mathrm{n}} ) = ( \frac{\varLambda}{\mu_{1}},0,0 )\),

  • DPE, i.e., \(\mathrm{E}_{3} =( \mathrm{S}^{\mathrm{n}}, \mathrm{U}_{1}^{\mathrm{n}}, \mathrm{U}_{2}^{\mathrm{n}} )\),

where

$$\begin{gathered} \mathrm{U}_{1}^{\mathrm{n}} = \frac{\varLambda- \mu_{1} \mathrm{S}^{\mathrm{n}}}{\beta_{1} \mathrm{S}^{\mathrm{n}}}, \qquad \mathrm{U}_{2}^{\mathrm{n}} = \frac{\mathrm{p}+ \mu_{1} - \beta_{1} \mathrm{S}^{\mathrm{n}}}{\beta_{3}}, \\ \mathrm{S}^{\mathrm{n}} = \bigl[ \bigl( \beta_{1} ( \mathrm{p}+ \mu_{1} ) \mu_{2} +\mathrm{p} \beta_{3} \mu_{1} - \varLambda \beta_{1} \beta_{3} - \mu_{1} ( \mathrm{p}+ \mu_{1} ) \beta_{3} \bigr) \\ \phantom{\mathrm{S}^{\mathrm{n}} =}{}\pm \bigl[ \bigl( \varLambda \beta_{1} \beta_{3} + \mu_{1} ( \mathrm{p}+ \mu_{1} ) \beta_{3} - \beta_{1} ( \mathrm{p}+ \mu_{1} ) \mu_{2} -\mathrm{p} \beta_{3} \mu_{1} \bigr)^{2} \\ \phantom{\mathrm{S}^{\mathrm{n}} =}{}-4 \bigl( -\beta_{1}^{2} \mu_{2} - \mu_{1} \beta_{1} \beta_{3} \bigr) \bigl( \mathrm{p}+ \beta_{3} \varLambda- \beta_{3} \varLambda ( \mathrm{p}+ \mu_{1} ) \bigr)\bigr]^{1/2}\bigr] \\ \phantom{\mathrm{S}^{\mathrm{n}} =}{} \big/ \bigl[2 \bigl( -\beta_{1}^{2} \mu_{2} - \mu_{1} \beta_{1} \beta_{3} \bigr)\bigr],\end{gathered} $$

almost surely. □

Theorem 5.5

The eigenvalues of discrete dynamical system (15) lie in the unit circle for all \(\mathrm{n}\geq0\).

Proof

Let us consider F, G, and H from system (15) as follows:

$$\begin{gathered} \mathrm{F}= \frac{\mathrm{S}+\mathrm{h}\varLambda}{1+\mathrm{h} \beta_{1} \mathrm{U}_{1} +\mathrm{h} \mu_{1} +\mathrm{h}\sigma \mathrm{U}_{1} \Delta \mathrm{B}_{\mathrm{n}}}, \\ \mathrm{G}= \frac{\mathrm{U}_{1} +\mathrm{h} \beta_{1} \mathrm{U}_{1} \mathrm{S}+ \beta_{3} \mathrm{U}_{1} \mathrm{U}_{2} +\sigma \mathrm{U}_{1} \mathrm{S}\Delta \mathrm{B}_{\mathrm{n}}}{1+\mathrm{hp}+\mathrm{h} \mu_{1}}, \\ \mathrm{H}= \frac{\mathrm{U}_{2} +\mathrm{hp} \mathrm{U}_{1}}{1+\mathrm{h} \beta_{3} \mathrm{U}_{1} +\mathrm{h} \mu_{2}}.\end{gathered} $$

The Jacobean matrix is defined as

$$\mathrm{J}= \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \frac{\partial \mathrm{F}}{\partial \mathrm{S}} & \frac{\partial \mathrm{F}}{\partial \mathrm{U}_{1}} & \frac{\partial \mathrm{F}}{\partial \mathrm{U}_{2}} \\ \frac{\partial \mathrm{G}}{\partial \mathrm{S}} & \frac{\partial \mathrm{G}}{\partial \mathrm{U}_{1}} & \frac{\partial \mathrm{G}}{\partial \mathrm{U}_{2}} \\ \frac{\partial \mathrm{H}}{\partial \mathrm{S}} & \frac{\partial \mathrm{H}}{\partial \mathrm{U}_{1}} & \frac{\partial \mathrm{H}}{\partial \mathrm{U}_{2}} \end{array}\displaystyle \right ], $$

where

$$\begin{gathered} \frac{\partial \mathrm{F}}{\partial \mathrm{S}} = \frac{1}{ 1+\mathrm{h} \beta_{1} \mathrm{U}_{1} +\mathrm{h} \mu_{1} +\mathrm{h}\sigma \mathrm{U}_{1} \Delta \mathrm{B}_{\mathrm{n}}}, \\ \frac{\partial \mathrm{F}}{\partial \mathrm{U}_{1}} = \frac{- ( \mathrm{S}+\mathrm{h}\varLambda ) \mathrm{h} \beta_{1}}{ ( 1+\mathrm{h} \beta_{1} \mathrm{U}_{1} +\mathrm{h} \mu_{1} +\mathrm{h}\sigma \mathrm{U}_{1} \Delta \mathrm{B}_{\mathrm{n}} )^{2}},\qquad \frac{\partial \mathrm{F}}{\partial \mathrm{U}_{2}} =0, \\ \frac{\partial \mathrm{G}}{\partial \mathrm{S}} = \frac{\mathrm{h} \beta_{1} \mathrm{U}_{1}}{1+\mathrm{hp}+\mathrm{h} \mu_{1}},\qquad \frac{\partial \mathrm{G}}{\partial \mathrm{U}_{1}} = \frac{1+\mathrm{h} \beta_{1} \mathrm{S}+ \beta_{3} \mathrm{U}_{2}}{1+\mathrm{hp}+\mathrm{h} \mu_{1}},\qquad \frac{\partial \mathrm{G}}{\partial \mathrm{U}_{2}} = \frac{\beta_{3} \mathrm{U}_{1}}{1+\mathrm{hp}+\mathrm{h} \mu_{1}}, \\ \frac{\partial \mathrm{H}}{\partial \mathrm{S}} =0,\qquad \frac{\partial \mathrm{H}}{\partial \mathrm{U}_{1}} = \frac{\mathrm{hp}}{\mathrm{h} \beta_{3}},\qquad \frac{\partial \mathrm{H}}{\partial \mathrm{U}_{2}} = \frac{1}{1+\mathrm{h} \beta_{3} \mathrm{U}_{1} +\mathrm{h} \mu_{2}}. \end{gathered} $$

Now we want to linearize the model about the equilibria of model for drug-free equilibrium \(\mathrm{D}_{1} = ( \mathrm{S}, \mathrm{U}_{1}, \mathrm{U}_{2} ) = ( \frac{\varLambda}{\mu_{1}},0,0 )\) and \(\mathrm{R}_{0}^{\mathrm{S}} <1\).

The given Jacobean is

$$\mathrm{J}= \left [ \textstyle\begin{array}{c@{\quad}c@{\quad}c} \frac{1}{1+\mathrm{h} \mu_{1}} & \frac{- \mathrm{h} \beta_{1} ( \varLambda+ \mu_{1} \mathrm{h}\varLambda )}{\mu_{1} ( {1}+ \mathrm{h} \mu_{1} )^{{2}}} & 0 \\ 0 & \frac{\mu_{1} +\mathrm{h} \beta_{1} \varLambda}{\mu_{1} ( 1+\mathrm{hp}+\mathrm{h} \mu_{1} )} & 0 \\ 0 & \frac{\mathrm{hp}}{\mathrm{h} \beta_{3}} & \frac{1}{1+\mathrm{h} \mu_{2}} \end{array}\displaystyle \right ]. $$

The eigenvalues of J are as follows:

$$\begin{gathered} \lambda_{1} = \frac{1}{1+\mathrm{h} \mu_{1}} < 1,\qquad \lambda_{2} = \frac{\mu_{1} +\mathrm{h} \beta_{1} \varLambda}{\mu_{1} ( 1+\mathrm{hp}+\mathrm{h} \mu_{1} )} < 1,\qquad \mathrm{R}_{0}^{\mathrm{S}} < 1, \\ \lambda_{3} = \frac{1}{1+\mathrm{h} \mu_{2}} < 1.\end{gathered} $$

This is to guarantee the fact that all the eigenvalues of Jacobean lie in the unit circle. So, system (15) is LAS around \(\mathrm{D}_{1}\). So, the graphical illustration of system (15) is presented in Fig. 5.

Figure 5
figure 5

(a) In susceptible users’ fraction stochastic-NSFD converges to drug-free equilibrium, while the deterministic solution is the mean of stochastic NSFD solution for \(\mathrm{h}=0.01\). (b) In susceptible users’ fraction stochastic-NSFD preserves all dynamical properties for drug-free equilibrium for \(\mathrm{h}=100\). (c) In drug users’ fraction stochastic-NSFD converges to drug-present equilibrium, while deterministic solution is the mean of stochastic NSFD solution for \(\mathrm{h}=0.01\). (d) In drug users’ fraction stochastic-NSFD preserves all dynamical properties for drug-present equilibrium, while deterministic solution is the mean of stochastic NSFD solution for \(\mathrm{h}=100\)

Full size image

 □

5.5 Contrast section

Let us assume the comparison among the stochastic methods and the stochastic NSFD method in this section as follows.

5.6 Covariance of heroin epidemic model

Let us describe the covariance among the compartments of heroin epidemic model. For this, we have designed the correlation factors and its consequences as stated in Table 3.

Table 3 Covariance of model
Full size table

The inverse relationship approved that the number of susceptible users has increased with decrease in the remaining compartments of heroin epidemic model. So, the heroin epidemic model will be a drug-free model.

6 Results and discussion

In Fig. 2(a), the given Euler–Maruyama method converges to equilibria of model at \(\mathrm{h}=0.01\), and unstability could observed in Fig. 2(b). In Fig. 3(a) and 3(c) the stochastic Euler converges to both equilibria at \(\mathrm{h}=0.01\). But failure to maintain stability and non-negativity for both equilbria could be observed in Fig. 3(b) and 3(d). In Fig. 4(a) and 4(c), the stochastic Runge–Kutta converges to both equilibria of model at \(\mathrm{h}=0.01\), and in Fig. 4(b) and 4(d), the given method shows divergence. So, the stochastic explicit schemes are time dependent and conditionally convergent schemes. On the other hand, in Fig. 5, the stochastic NSFD converges to equilibria of the model for any time. In Fig. 6, we have showed the efficiency of the stochastic NSFD method with existing stochastic explicit methods for different time step sizes. Also, we can observe in the above graphical illustration that the deterministic solutions are called the average of stochastic solutions of a heroin epidemic system. So, the stochastic explicit methods are time dependent and conditionally convergent methods. This is the beauty of stochastic NSFD as compared to other stochastic explicit methods.

Figure 6
figure 6

(a) Drug users’ fraction with Euler–Maruyama and its average at \(\mathrm{h}=0.01\). (b) Drug users’ fraction with Euler–Maruyama and its average at \(\mathrm{h}=4\). (c) Drug users’ fraction with stochastic Euler and its average at \(\mathrm{h}=0.01\). (d) Drug users’ fraction with stochastic Euler and its average at \(\mathrm{h}=5\). (e) Drug users’ fraction with stochastic Runge–Kutta and its average at \(\mathrm{h}=0.01\). (f) Drug users’ fraction with stochastic Runge–Kutta and its average at \(\mathrm{h}=6\)

Full size image

7 Conclusion and directions

In comparison to the deterministic heroin epidemic model, the stochastic heroin epidemic model is a more reliable strategy. The stochastic numerical techniques are detail-oriented, and they work well for even minute time step size. They may lose the necessary properties of a continuous dynamical system due to divergence on specific values of time step size. The SNSFD for a heroin epidemic model is capable of preserving important properties like positivity, dynamical consistency, and boundedness. It is also appropriate for any time step size [27,28,29]. For our future work, we are aiming to execute SNSFD to sophisticated stochastic delay and spatio-temporal systems. Additionally, we could utilize the current numerical work in the extension of networking flows and fractional networking flows systems [34]. In the future, we are going to work for the reaction diffusion and fractional-order stochastic models.