Abstract
The stochastic P-bifurcation behavior of a bistable Van der Pol system with fractional time-delay feedback under Gaussian white noise excitation is studied. Firstly, based on the minimal mean square error principle, the fractional derivative term is found to be equivalent to the linear combination of damping force and restoring force, and the original system is further simplified to an equivalent integer order system. Secondly, the stationary Probability Density Function (PDF) of system amplitude is obtained by stochastic averaging, and the critical parametric conditions for stochastic P-bifurcation of system amplitude are determined according to the singularity theory. Finally, the types of stationary PDF curves of system amplitude are qualitatively analyzed by choosing the corresponding parameters in each area divided by the transition set curves. The consistency between the analytical solutions and Monte Carlo simulation results verifies the theoretical analysis in this paper.
Similar content being viewed by others
1 Introduction
Fractional calculus is a generalization of integer-order calculus, which has a history of more than 300 years. Integer-order derivatives cannot express the memory characteristics of viscoelastic substances, whereas fractional derivatives contain convolution, thus, they can express the memory effect and manifest a cumulative effect over time. Hence, fractional derivatives are suitable for describing memory characteristics [1,2,3,4] and have become a powerful mathematical tool to study anomalous diffusion, non-Newtonian fluid mechanics, viscoelastic mechanics, and soft-matter physics. In comparison to integer-order calculus, fractional derivatives can describe various reaction processes more accurately [5,6,7,8,9,10,11], thus, they are indispensable to studying the mechanical characteristics and fractional-order parametric influences on different systems.
In recent years, researchers have analyzed the dynamic behavior of nonlinear multi-stable systems under different noise excitations and achieved fruitful results. For the dynamic systems without time-delay, Wang et al. investigated the stochastic resonance in a FitzHugh–Nagumo model with an additive Lévy noise numerically; the numerical simulation results show the occurrence of the stochastic resonance phenomena in the given FHN system [12]. Xu et al. proposed a method to find an approximate theoretical solution to the mean first exit time of a one-dimensional bistable kinetic system subjected to additive Poisson white noise and derived the analytical solution to the mean first exit time by combining perturbation techniques with Laplace integral method [13]. Xu et al. discussed the constructive role of combined harmonic and random excitation on stochastic resonance (SR) in a Brusselator model; the simulation results showed that the intensity of the Gaussian colored noise and the amplitude of the periodic force can enhance SR [14]. Liu et al. investigated the active vibration suppression of a fractional two-degree-of-freedom viscoelastic airfoil model with a harmonic external force by means of the sliding mode control scheme, derived the amplitude-frequency relations by an extended averaging technique, and its correctness was verified by Monte Carlo simulations [15]. Li et al. developed a fractional-order predator-prey model by incorporating a constant prey refuge and feedback control and discussed the stability of equilibrium point by analyzing the characteristic equation of the system [16]. Zhu et al. designed a magnetic shape-memory alloy microgripper and studied its nonlinear dynamic characteristics under stochastic perturbation [17]. In addition, the authors investigated the dynamic behaviors of Van der Pol–Duffing oscillators under Lévy noise, color noise, and combined harmonic and random noise; moreover, the stochastic P-bifurcation behaviors of noise oscillators were discussed by analyzing the changes in the stationary probability density function of the systems [18,19,20,21,22]. Hao and Wu investigated the stochastic P-bifurcation of tri-stability in a generalized Duffing–Van der Pol oscillator system excited by additive Gaussian white noise, multiplicative colored noise, and combined additive and multiplicative Gaussian white noise; obtained the analytical expression for stationary PDF of amplitude; and analyzed the influences of noise intensity and system parameters on stochastic P-bifurcation of the system [23,24,25]. Chen et al. studied the response of a Duffing system with fractional damping under combined white noise and harmonic excitations and found that a small variation in the order of fractional derivative could induce stochastic P-bifurcation in the system [26]. Huang et al. discussed the response and the stationary PDF of a single-degree-of-freedom strongly nonlinear system under Gaussian white noise excitation [27]. Li et al. investigated the stochastic P-bifurcation behavior of a bistable Van der Pol–Duffing system with fractional derivatives under additive and multiplicative colored noise excitations and found that small changes in linear damping coefficient, in the order of fractional derivative, and in noise intensity can each lead to stochastic P-bifurcation in the system [28]. Liu et al. investigated a Duffing oscillator system with fractional damping under combined harmonic and Poisson white noise parametric excitations and analyzed the asymptotic Lyapunov stability of the system based on the largest Lyapunov exponent [29]. Morales-Delgado et al. studied the fractional-order dynamics of the oxygen diffusion through capillary to tissues under the influence of external forces considering the fractional operators of Liouville–Caputo and Caputo–Fabrizio and applied the Laplace homotopy method for analytical and numerical results [30]. Hammouch et al. constructed new explicit solutions for a time-fractional nonlinear Calogero–Bogoyavlenskii–Schiff equation in \((2+1)\) dimensions with conformable derivative and expressed the obtained solutions by different kinds of functions [31]. Saad et al. established an effective algorithm for the homotopy analysis method (HAM) to solve a cubic isothermal auto-catalytic chemical system and compared the HAM solutions with the solutions obtained by Mathematica in-built numerical solver [32]. Tariboon et al. defined new concepts of fractional quantum calculus by defining a new q-shifting operator and then discussed their basic properties [33]. Agarwal et al. introduced the solution of differential algebraic equations using two hybrid classes and their twin one-leg with the improved stability properties [34]. Saoudi et al. investigated the existence of solutions to the boundary value problem for the nonlinear fractional differential equations with Riemann–Liouville fractional derivative by employing the method of Nehari manifold combined with the fibering maps [35]. Agarwal et al. discussed solvability questions of a non-local problem with integral form transmitting conditions for diffusion-wave equation with the Caputo fractional derivative and proved the uniqueness of the solution of the formulated problem by using the energy integral method with some modifications [36].
For the dynamics of time-delay systems, Leung et al. investigated the dynamic behavior of two Duffing–Van der Pol oscillators with fractional derivative damping and time delay, found periodic solutions based on the residue harmonic balance method, and then accurately calculated the limited cycle frequency and amplitude [37]. Zhou et al. studied the dynamic stability and the Hopf bifurcation of a paddy ecosystem, obtained the necessary stability conditions for the system by analyzing its characteristic equation [38]. Chen et al. studied the primary resonance response of a Van der Pol system under fractional-order delayed negative feedback and forced excitation, obtained the approximate analytical solution for the system based on the averaging method [39]. Leung et al. analyzed a Van der Pol–Duffing oscillator with fractional derivatives and time delays based on the residue harmonic method and examined its periodic bifurcations using the fractional order, time delay, and feedback gain as continuation parameters [40]. Chen et al. proposed a stochastic averaging technique to analyze the dynamic behavior of a randomly excited strongly nonlinear system with a delayed feedback fractional-order proportional-derivative controller and obtained the stationary probability density function of the system [41]. Mathiyalagan and Balachandran investigated the finite-time stochastic stability of fractional-order singular systems with white noise and time delay and developed the necessary conditions for finite-time stability based on Gronwall’s approach and stochastic analysis [42]. Wen et al. studied the deterministic and autonomous Duffing systems with fractional time-delay coupled feedback and noticed that fractional time-delay coupled feedback played the roles both of velocity time-delay feedback and displacement time-delay feedback [43]. Liu et al. studied the Hopf bifurcation in a nonlinear electromechanical coupled system with time-delay feedback, obtained its characteristic root and stable domain, and finally, analyzed the relationship between feedback gain and stable domain [44]. Jiang et al. considered a classical Van der Pol oscillator with general time-delay feedback and found the Bogdanov–Takens bifurcation, triple-zero and Hopf-zero singularities in the system by analyzing the distribution of associated characteristic roots [45]. Liu et al. studied the Hopf bifurcation of a coupled relative-rotation system with time-delay feedback and obtained the periodic solutions of the system for both primary resonance and 1:1 internal resonance [46].
Due to the complexity of fractional derivatives, analyzing them is difficult, and the parametric vibration characteristics can only be analyzed qualitatively, while the critical conditions of parametric influences cannot be found. These problems affect the design and analysis of such systems, in part because the stochastic P-bifurcation of bi-stability for fractional-order time-delay coupled system has not been reported. In the present research, the nonlinear vibration of a generalized Van der Pol oscillator excited by Gaussian white noise excitation was considered as the example. The transition set curves of the fractional-order system and the critical parameters for stochastic P-bifurcation were determined by the singularity method. Furthermore, the nature of stationary PDF curves in each area of the parametric plane was analyzed. Finally, Monte Carlo simulation results were compared with analytical solutions obtained by stochastic averaging.
2 The derivation of equivalent system
The initial condition of the Riemann–Liouville derivative conveys no physical meaning, whereas the initial condition of the Caputo derivative describes a clear physical meaning and forms the initial conditions for integer-order differential equations. Therefore, the Caputo fractional derivative was used in the present paper:
where \(m - 1 < p \le m\), \(m \in N\), \(t \in [a,b]\), \(x^{(m)}(t)\) is the m-order derivative of \(x(t)\) and \(\varGamma (m)\) is the gamma function.
For a given physical system, because the initial moment of oscillators is \(t = 0\), the Caputo derivative is often used as the following form:
where \(m - 1 < p \le m\), \(m \in N\).
In this paper, we consider the generalized Van der Pol oscillator system with fractional-order time-delay coupled feedback excited by Gaussian white noise excitation:
where ε represents the linear damping coefficient, \(\alpha _{1}\), \(\alpha _{2}\), and \(\alpha _{3}\) represent the nonlinear damping coefficients of the system, w is the natural frequency, and τ is the time-delay introduced in the system. \({}_{0}^{C}D^{p}[x(t - \tau )]\) is the p (\(0 \le p \le 1\)) order Caputo derivative of \(x(t - \tau )\) with respect to t, which is definedby Eq. (2). \(\xi _{k}(t)\) (\(k = 1,2\)) are two independent Gaussian white noises, which satisfy
where \(D_{k}\) denotes the intensities of Gaussian white noises \(\xi _{k}(t)\) respectively, \(\delta (s)\) is the Dirac function, and s is the correlation time of Gaussian white noises \(\xi _{k}(t)\).
The fractional derivative has the contributions of damping force and restoring force [44,45,46,47,48,49,50], hence, we introduce the equivalent system as follows:
where \(C(p,\tau )\) and \(K(p,\tau )\) are the coefficients of equivalent damping force and equivalent restoring force of the fractional derivative \({}_{0}^{C}D^{p}[x(t - \tau )]\), respectively.
Applying the equivalent methods described in the literature [29, 49,50,51], the ultimate forms of \(C(p,\tau )\) and \(K(p,\tau )\) can be obtained as follows:
Therefore, the equivalent Van der Pol oscillator associated with system (5) can be represented as follows:
where
3 The stationary PDF of system amplitude
In the first example, the system described in Eq. (7) with \(\varepsilon = 0.2\), \(\alpha _{1} = 1.51\), \(\alpha _{2} = 2.85\), \(\alpha _{3} = - 1.693\), \(w = 1\), and \(\tau = 0.5\) was considered. For convenience in discussing parametric influence, the bifurcation diagram of the system amplitude with variation of the fractional order p is shown in Fig. 1 when \(D _{1} = D_{2}\ = 0\).
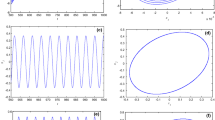
In Fig. 1, the Hopf bifurcation and the Fold bifurcation values are marked by \(p_{H} = 0.189\) and \(p_{F} = 0.245\), respectively, there are two attractors (equilibrium and limit cycle), where \(0.189 \le p \le 0.245\), and the corresponding result is shown in Fig. 2.
In the second example, the system with \(\varepsilon = - 0.5\), \(\alpha _{1} = 1.51\), \(\alpha _{2} = 2.85\), \(\alpha _{3} = - 1.693\), \(w = 1\), and \(p = 0.5\) was considered. The bifurcation diagram of the system amplitude with the variation in time-delay τ is displayed in Fig. 3 when \(D _{1} = D_{2}\ = 0\).
In Fig. 3, the Fold bifurcation and the Hopf bifurcation values are marked by \(\tau _{F} = 0.159\) and \(\tau _{H} = 0.262\), respectively. There are also two attractors (equilibrium and limit cycle), where \(0.159 \le \tau \le 0.262\), and the corresponding result is illustrated in Fig. 4.
Assuming that the solution of system (7) has the periodic form, we introduce the following transformation [52]:
where \(w_{0}\) is the natural frequency of equivalent system (7), \(a(t)\) and \(\theta (t)\) represent the amplitude and phase processes of system response respectively, they are both random processes.
Substituting Eq. (9) into Eq. (7), we can obtain
in which
Equation (10) can be treated as the Stratonovich stochastic differential equation, and by adding the relevant Wong–Zakai correction term, it can be transformed into the Itô stochastic differential equation as follows:
where \(B_{k}(t)\) are independent normalized Wiener processes and
By stochastic averaging [53] of averaging Eq. (12) over Φ, we can obtain the following averaged Itô equation:
where \(B_{1}(t)\) and \(B_{2}(t)\) are two unit Wiener processes that are independent of each other, and
Equations (14) and (15) imply that da does not depend on θ, the averaged Itô equation of \(a(t)\) is independent of \(\theta (t)\), and the random process \(a(t)\) is a one-dimensional diffusion process. Then the corresponding Fokker–Planck–Kolmogorov (FPK) equation of \(a(t)\) can be expressed as follows:
The boundary conditions are as follows:
Based on the boundary conditions (17), the stationary PDF of system amplitude can be described as
where C is the normalized constant that satisfies
Substituting Eq. (15) into Eq. (18), the explicit expression of stationary PDF of the system amplitude a can be obtained:
where
4 Stochastic P-bifurcation of system amplitude
Stochastic P-bifurcation means the changes in the number of peaks in the PDF curve. To obtain the critical parametric conditions for stochastic P-bifurcation, we analyze the influence of parameters on the system by using singularity theory.
For the sake of convenience, \(\bar{p}(a)\) can be expressed as follows:
where
According to the singularity theory [54], the stationary PDF of system amplitude needs to satisfy the conditions as follows:
Substituting Eq. (22) into Eq. (24), we can obtain the following condition [43, 50]:
where H is the condition for the changes in the number of peaks in the PDF curve.
As the existence of multiplicative noise generally makes the superposition principle invalid, the multiplicative noise excitation is more complex than additive noise excitation in the analysis of system response. Therefore, the stochastic P-bifurcation under additive and multiplicative Gaussian white noises is discussed separately below.
4.1 Additive noise excitation case
Additive noise refers to that the system is only affected by the external excitation, in this case, \(D_{1} \ne 0\), \(D_{2} = 0\), and Eq. (23) can be expressed as follows:
Substituting Eq. (26) into Eq. (25), the critical parametric conditions for stochastic P-bifurcation of system amplitude can be obtained as follows:
where amplitude a satisfies the following condition:
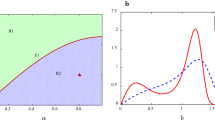
With parameters \(\varepsilon = 0.2\), \(\alpha _{1} = 1.51\), \(\alpha _{2} = 2.85\), \(\alpha _{3} = - 1.693\), \(w = 1\), and \(\tau = 0.5\), according to Eqs. (27) and (28), the transition set curves for stochastic P-bifurcation with the unfolding parameters p and \(D_{1}\) are displayed in Fig. 5.
Figure 5 reveals the effects with the variations of parameters p and \(D_{1}\) on the stochastic P-bifurcation of the system, and as can be seen from Fig. 5, the intercepts of transition set curves at \(D_{1} = 0\) represent the Hopf bifurcation value \(p_{H} = 0.189\) and the Fold bifurcation value \(p_{F} = 0.245\), respectively, which are well consistent with the deterministic bifurcation diagram in Fig. 1. Based on the singularity theory, the topological structures of the stationary PDF curves at different points \((p,D_{1})\) in the same area are qualitatively identical. By taking a point \((p,D_{1})\) in each area, we can obtain all varieties of the stationary PDF curves that are qualitatively different. The unfolding parametric plane \(p - D_{1}\) is divided into two sub-areas by the transition set curve; for the sake of convenience, each area in Fig. 5 is marked with a number.
The stationary PDF \(\bar{p}(a)\) and the joint PDF \(\bar{p}(x, \dot{x})\) are analyzed for a point \((p,D_{1})\) in each sub-area in Fig. 5, and the analytical solutions are compared with Monte Carlo simulation results for original system (3) based on the numerical method for fractional derivative [43, 55], and the corresponding results are displayed in Figs. 6 and 7.
As can be seen from Fig. 5, the parametric area where the PDF occurs bimodally is surrounded by an approximately triangular area. And when we take the parameter \((p, D_{1})\) in area 1, the PDFs for \(\bar{p}(a)\) and \(\bar{p}(x, \dot{x})\) have a stable limit cycle as shown in Fig. 6(a) and Fig. 7(a), the steady-state response of the system is mainly characterized by the large amplitude vibration; in area 2, the PDFs for \(\bar{p}(a)\) and \(\bar{p}(x, \dot{x})\)still have a stable limit cycle, while the probability near the origin is not zero, there are both the limit cycle and equilibrium in the system simultaneously, which implies that there are two more probable motions in the response of the system, and the shape of the stationary PDF is qualitatively different from the case when the parameter \((p, D_{1})\) is taken in area 1, as shown in Fig. 6(b) and Fig. 7(b).
With the parameters \(\varepsilon = - 0.5\), \(\alpha _{1} = 1.51\), \(\alpha _{2} = 2.85\), \(\alpha _{3} = - 1.693\), \(w = 1\), and \(p = 0.5\), according to Eqs. (27) and (28), the transition set curves for stochastic P-bifurcation with the unfolding parameters τ and \(D_{1}\) are displayed in Fig. 8.
In order to discuss the effects with the variations of parameters τ and \(D_{1}\) on the stochastic P-bifurcation of the system, the stationary PDF \(\bar{p}(a)\) and the joint PDF \(\bar{p}(x, \dot{x})\) are analyzed for a point \((\tau ,D_{1})\) in each sub-area in Fig. 8, then the analytical solutions are compared with the Monte Carlo simulation results for original system (3) using the numerical method for fractional derivative [43, 55], and the corresponding results are displayed in Fig. 9 and Fig. 10.
As can be seen from Fig. 8, the intercepts of transition set curves at \(D_{1} = 0\) represent the Fold bifurcation value \(\tau _{F} = 0.159\) and the Hopf bifurcation value \(\tau _{H} = 0.262\), respectively, which are well consistent with the deterministic bifurcation diagram in Fig. 3. The parametric area where the PDF occurs bimodally is similar to the case in Fig. 5 and is also surrounded by an approximately triangular area. And when we take the parameter \((\tau , D_{1})\) in area 1, the PDFs for \(\bar{p}(a)\) and \(\bar{p}(x, \dot{x})\) have a distinct peak near the origin, the system has only a stable equilibrium at the moment, the steady-state response of the system is mainly characterized by the small amplitude vibration, as shown in Fig. 9(a) and Fig. 10(a); in area 2, the PDFs for \(\bar{p}(a)\) and \(\bar{p}(x, \dot{x})\) have a stable limit cycle clearly, while the probability near the origin is not zero, showing that equilibrium coexists with the limit cycle in the system at this moment, which implies that there are two more probable motions in the response of the system and that stochastic jump may occur between the two more probable motions, and the shape of the stationary PDF has a qualitative change compared with the case in area 1, as shown in Fig. 9(b) and Fig. 10(b).
4.2 Multiplicative noise excitation case
In the case of \(D_{1} = 0\) and \(D_{2} \ne 0\), Eq. (23) can be transformed into
Substituting Eq. (29) into Eq. (25), the critical parametric condition for stochastic P-bifurcation of the system can be obtained as follows:
where amplitude a satisfies the following expression:
For more generalizations, we take values of ε, τ, and p, which are different from the values taken in the additive noise excitation case in this section, with the parameters \(\varepsilon = 0.5\), \(\alpha _{1} = 1.51\), \(\alpha _{2} = 2.85\), \(\alpha _{3} = - 1.693\), \(w = 1\), and \(\tau = 1\), according to Eqs. (30) and (31), the transition set curves for stochastic P-bifurcation with the unfolding parameters p and \(D_{2}\) are displayed in Fig. 11.
As can be seen from Fig. 11, the unfolding parametric plane \(p - D_{2}\) is divided into three sub-areas by the transition set curves, which is different from the case under the additive noise excitation as shown in Fig. 5; for the sake of convenience, each area in Fig. 11 is marked with a number. In order to reveal the influences with the variations of parameters p and \(D_{2}\) on the stochastic P-bifurcation of the system, the characteristics of the PDFs for \(\bar{p}(a)\) and \(\bar{p}(x, \dot{x})\) are analyzed for a point \((p,D _{2})\) in each sub-area in Fig. 11, then the analytical solutions are compared with the Monte Carlo simulation results for original system (3) based on the numerical method for fractional derivative [43, 55], and the corresponding results are displayed in Fig. 12 and Fig. 13.
It can be seen from Fig. 11 that the parametric area where the PDF curve occurs bimodally is surrounded by two lines. And when we take the parameter \((p,D_{2})\) as \(p = 0.3\), \(D_{2} = 0.6\) in area 1, the PDFs for \(\bar{p}(a)\) and \(\bar{p}(x, \dot{x})\) have a stable limit cycle at the moment, the steady-state response of the system is mainly characterized by the large amplitude vibration, as shown in the solid line in Fig. 12 and Fig. 13(a); when taking the parameter \((p,D_{2})\) as \(p = 0.4\), \(D _{2} = 1\) in area 2, the PDFs for \(\bar{p}(a)\) and \(\bar{p}(x, \dot{x})\)still have a stable limit cycle, while the probability near the origin is not zero, and the system has also a response whose amplitude is approximately zero, there are both the limit cycle and equilibrium in the system simultaneously, which implies that there are two more probable motions in the response of the system and that stochastic jump may occur between the two more probable motions, as shown in the dot line in Fig. 12 and Fig. 13(b); when taking the parameter \((p,D_{2})\) as \(p = 0.45\), \(D_{2} = 0.4\) in area 3, the PDFs for \(\bar{p}(a)\) and \(\bar{p}(x, \dot{x})\) appear in the form of the Dirac function, the steady-state response of the system is constant at 0, similar to the stable equilibrium in the deterministic system at this time, and the randomness of the system is suppressed, as shown in the dashed line in Fig. 12 and Fig. 13(c).
With parameters \(\varepsilon = 0.2\), \(\alpha _{1} = 1.51\), \(\alpha _{2} = 2.85\), \(\alpha _{3} = - 1.693\), \(w = 1\), and \(p = 0.1\), according to Eqs. (30) and (31), the transition set curves for stochastic P-bifurcation with the unfolding parameters τ and \(D_{2}\) are displayed in Fig. 14.
In order to reveal the influences with the variations of parameters τ and \(D_{2}\) on the stochastic P-bifurcation of the system, we analyze the characteristics of PDFs for \(\bar{p}(a)\) and \(\bar{p}(x, \dot{x})\) for a point \((\tau ,D_{2})\) in each sub-area in Fig. 14, then the analytical solutions are compared with the Monte Carlo simulation results for original system (3) based on the numerical method for fractional derivative [43, 55], and the corresponding results are illustrated in Fig. 15 and Fig. 16.
It can be seen from Fig. 14 that the parametric area where the PDF occurs bimodally is similar to the case in Fig. 11, and is also surrounded by two lines, while in other two sub-areas, the topological structures of the PDF curves are different from those in Fig. 11. When we take the parameter \((\tau ,D_{2})\) as \(\tau = 0.1\), \(D_{2} = 0.5\) in area 1, the PDFs for \(\bar{p}(a)\) and \(\bar{p}(x, \dot{x})\) appear in the form of Dirac function; the steady-state response amplitude of the system is constant at 0, similar to the stable equilibrium in the deterministic system at this time, and the randomness of the system is suppressed, as shown in the dashed line in Fig. 15 and Fig. 16(a). When taking the parameter \((\tau ,D_{2})\) as \(\tau = 0.25\), \(D_{2} = 0.8\) in area 2, the PDFs for \(\bar{p}(a)\) and \(\bar{p}(x, \dot{x})\) have a stable limit cycle, and the probability near the origin is not zero, showing that equilibrium coexists with the limit cycle in the system at the moment, which implies that there are two more probable motions in the response of the system and that stochastic jump may occur between the two more probable motions, as shown in the dot line in Fig. 15 and Fig. 16(b). When taking the parameter \((\tau ,D_{2})\) as \(\tau = 0.4\), \(D _{2} = 0.5\) in area 3, the PDFs for \(\bar{p}(a)\) and \(\bar{p}(x, \dot{x})\) have a stable limit cycle clearly at this time, the steady-state response of the system is mainly characterized by the large amplitude vibration, as shown in the solid line in Fig. 15 and Fig. 16(c).
It is evident that the stationary PDF \(\bar{p}(a)\) and the joint PDF \(\bar{p}(x, \dot{x})\) in any two adjacent areas in Figs. 5, 8, 11, and 14 are very qualitatively different. Regardless of the exact values of the unfolding parameters, if they cross any line in these figures, the system will demonstrate stochastic P-bifurcation behavior. Therefore, the transition set curves are just the critical parametric conditions for stochastic P-bifurcation of the system. The analytic solutions shown in Figs. 6, 9, 12, and 15 are well consistent with the Monte Carlo simulation results for original system (3), further verifying the theoretical analysis and showing that it is feasible to use the methods in this paper to analyze the stochastic P-bifurcation behavior of fractional-order systems with time-delay feedback.
In comparison to the integer-order controllers, the fractional-order controllers have better dynamic performances and robustness [41]. In recent years, multifarious fractional-order controllers have been developed [56,57,58,59], and we obtained the areas where system (3) will undergo stochastic P-bifurcation through the above analysis, it can make the system switch between monostable and bistable states by selecting the corresponding unfolding parameters, which should provide the theoretical guidance for fractional-order controller design.
5 Conclusions
In this paper, we studied the bistable stochastic P-bifurcation of a generalized Van der Pol system with the fractional time-delay feedback under additive and multiplicative Gaussian white noise excitations respectively. According to the principle of minimal mean square error, the original system was transformed into an equivalent integer-order system, and the stationary PDF for system amplitude was obtained by stochastic averaging. In addition, the critical parametric conditions for stochastic P-bifurcation of the system were obtained based on the singularity theory; according to this, we can maintain the system response for small amplitude near equilibrium or monostability by selecting the corresponding unfolding parameters, which can provide the theoretical guidance for system design and avoid the damage of the system caused by nonlinear jump or large amplitude vibration. Furthermore, the consistency between Monte Carlo simulation results and analytical solutions can also verify the theoretical analysis. It can be concluded that the fractional order p, time-delay τ, and noise intensities \(D_{1}\) and \(D_{2}\) can each cause stochastic P-bifurcation, and the number of peaks in stationary PDF curves can be controlled from one to two by selecting the corresponding unfolding parameters.
References
Xu, M., Tan, W.: Representation of the constitutive equation of viscoelastic materials by the generalized fractional element networks and its generalized solutions. Sci. China Ser. A 46, 145–157 (2003)
Sabatier, J., Agrawal, O., Machado, J.: Advances in Fractional Calculus. Springer, Dordrecht (2007)
Podlubny, I.: Fractional order systems and PID controller. IEEE Trans. Autom. Control 44, 208–214 (1999)
Monje, C., Chen, Y., Vinagre, B., Xue, D., Feliu, V.: Fractional-Order Systems and Controls: Fundamentals and Applications. Springer, London (2010)
Bagley, R., Torvik, J.: Fractional calculus—a different approach to the analysis of viscoelastically damped structures. AIAA J. 21, 741–748 (1983)
Bagley, R., Torvik, P.: Fractional calculus in the transient analysis of viscoelastically damped structures. AIAA J. 23, 918–925 (2012)
Tenreiro Machado, J.: And I say to myself: what a fractional world! Fract. Calc. Appl. Anal. 14, 635–654 (2011)
Machado, J.: Fractional order modelling of fractional-order holds. Nonlinear Dyn. 70, 789–796 (2012)
Machado, J.: Fractional Calculus: Application in Modeling and Control. Springer, New York (2013)
Machado, J., Costa, A., Quelhas, M.: Fractional dynamics in DNA. Commun. Nonlinear Sci. Numer. Simul. 16, 2963–2969 (2011)
Francesco, M.: Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos Solitons Fractals 7, 1461–1477 (1996)
Wang, Z., Xu, Y., Yang, H.: Lévy noise induced stochastic resonance in an FHN model. Sci. China, Technol. Sci. 59, 371–375 (2016)
Xu, Y., Li, H., Wang, H., Jia, W., Yue, X., Kurths, J.: The estimates of the mean first exit time of a bistable system excited by Poisson white noise. J. Appl. Mech. 84, 091004 (2017)
Xu, Y., Ma, J., Wang, H., Li, Y., Kurths, J.: Effects of combined harmonic and random excitations on a Brusselator model. Eur. Phys. J. B 90, 194 (2017)
Liu, Q., Xu, Y., Kurths, J.: Active vibration suppression of a novel airfoil model with fractional order viscoelastic constitutive relationship. J. Sound Vib. 432, 50–64 (2018)
Li, H., Muhammadhaji, A., Zhang, L., Teng, Z.: Stability analysis of a fractional-order predator–prey model incorporating a constant prey refuge and feedback control. Adv. Differ. Equ. 2018, 325 (2018)
Zhu, Z., Xu, J.: Nonlinear dynamic characteristics and optimal control of giant magnetostrictive laminated plate subjected to in-plane stochastic excitation. AIP Adv. 4, 031322 (2014)
Rong, H., Wang, X., Xu, W., Meng, G., Fang, T.: On double-peak probability density functions of a Duffing oscillator under narrow-band random excitations. Acta Phys. Sin. 54, 2557–2561 (2005) (in Chinese)
Rong, H., Wang, X., Meng, G., Xu, W., Fang, T.: On double peak probability density functions of Duffing oscillator to combined deterministic and random excitations. Appl. Math. Mech. 27, 1569–1576 (2006)
Gu, R., Xu, Y., Hao, M., Yang, Z.: Stochastic bifurcations in Duffing–van der Pol oscillator with Lévy stable noise. Acta Phys. Sin. 60, 157–161 (2011) (in Chinese)
Xu, Y., Gu, R., Zhang, H., Xu, W., Duan, J.: Stochastic bifurcations in a bistable Duffing–Van der Pol oscillator with colored noise. Phys. Rev. E 83, 056215 (2011)
Zakharova, A., Vadivasova, T., Anishchenko, V., Koseska, A., Kurths, J.: Stochastic bifurcations and coherence-like resonance in a self-sustained bistable noisy oscillator. Phys. Rev. E 81, 011106 (2010)
Wu, Z., Hao, Y.: Three-peak P-bifurcations in stochastically excited van der Pol–Duffing oscillator. Sci. China, Ser. G, Phys. Mech. Astron. 43, 524–529 (2013) (in Chinese)
Wu, Z., Hao, Y.: Stochastic P-bifurcations in tri-stable van der Pol–Duffing oscillator with multiplicative colored noise. Acta Phys. Sin. 64, 060501 (2015) (in Chinese)
Hao, Y., Wu, Z.: Stochastic P-bifurcation of tri-stable Van der Pol–Duffing oscillator. Chin. J. Theor. Appl. Mech. 45, 257–264 (2013) (in Chinese)
Chen, L., Zhu, W.: Stochastic jump and bifurcation of Duffing oscillator with fractional derivative damping under combined harmonic and white noise excitations. Int. J. Non-Linear Mech. 46, 1324–1329 (2011)
Huang, Z., Jin, X.: Response and stability of a SDOF strongly nonlinear stochastic system with light damping modeled by a fractional derivative. J. Sound Vib. 319, 1121–1135 (2009)
Li, W., Zhang, M., Zhao, J.: Stochastic bifurcations of generalized Duffing–van der Pol system with fractional derivative under colored noise. Chin. Phys. B 26, 62–69 (2017)
Liu, W., Zhu, W., Chen, L.: Stochastic stability of Duffing oscillator with fractional derivative damping under combined harmonic and Poisson white noise parametric excitations. Probab. Eng. Mech. 53, 109–115 (2018)
Morales-Delgado, V.F., Gómez-Aguilar, J.F., Saad, K.M., Muhammad, A.K., Agarwal, P.: Analytic solution for oxygen diffusion from capillary to tissues involving external force effects: a fractional calculus approach. Physica A 523, 48–65 (2019)
Hammouch, Z., Mekkaoui, T., Agarwal, P.: Optical solitons for the Calogero–Bogoyavlenskii–Schiff equation in \((2+1)\) dimensions with time-fractional conformable derivative. Eur. Phys. J. Plus 133, 248 (2018)
Saad, K.M., Iyiola, O.S., Agarwal, P.: An effective homotopy analysis method to solve the cubic isothermal auto-catalytic chemical system. AIMS Math. 3, 183–194 (2018)
Tariboon, J., Ntouyas, S.K., Agarwal, P.: New concepts of fractional quantum calculus and applications to impulsive fractional q-difference equations. Adv. Differ. Equ. 2015 18, 1–19 (2015)
Agarwal, P., Ibrahim, I.H., Yousry, F.M.: G-stability one-leg hybrid methods for solving DAEs. Adv. Differ. Equ. 2019, 103 (2019)
Saoudi, K., Agarwal, P., Kumam, P., Ghanmi, A., Thounthong, P.: The Nehari manifold for a boundary value problem involving Riemann–Liouville fractional derivative. Adv. Differ. Equ. 2018, 263 (2018)
Agarwal, P., Berdyshev, A., Karimov, E.: Solvability of a non-local problem with integral transmitting condition for mixed type equation with Caputo fractional derivative. Results Math. 71, 1235–1257 (2017)
Leung, A., Guo, Z., Yang, H.: Fractional derivative and time delay damper characteristics in Duffing–van der Pol oscillators. Commun. Nonlinear Sci. Numer. Simul. 18, 2900–2915 (2013)
Zhou, X., Wu, Z., Wang, Z., Zhou, T.: Stability and Hopf bifurcation analysis in a fractional-order delayed paddy ecosystem. Adv. Differ. Equ. 2018, 315 (2018)
Chen, J., Li, X., Tang, J., Liu, Y.: Primary resonance of van der Pol oscillator under fractional-order delayed feedback and forced excitation. Shock Vib. 11, 1–9 (2017)
Leung, A., Yang, H., Zhu, P.: Periodic bifurcation of Duffing–van der Pol oscillators having fractional derivatives and time delay. Commun. Nonlinear Sci. Numer. Simul. 19, 1142–1155 (2014)
Chen, L., Liang, X., Zhu, W., Zhao, Y.: Stochastic averaging technique for SDOF strongly nonlinear systems with delayed feedback fractional-order PD controller. Sci. China, Technol. Sci. 62, 287–297 (2019)
Mathiyalagan, K., Balachandran, K.: Finite-time stability of fractional-order stochastic singular systems with time delay and white noise. Complexity 21, 370–379 (2016)
Wen, S., Shen, Y., Yang, S.: Dynamical analysis of Duffing oscillator with fractional-order feedback with time delay. Acta Phys. Sin. 65, 158–167 (2016) (in Chinese)
Liu, S., Zhao, S., Wang, Z., Li, H.: Stability and Hopf bifurcation of a nonlinear electromechanical coupling system with time delay feedback. Chin. Phys. B 24, 345–353 (2015)
Jiang, W., Wei, J.: Bifurcation analysis in van der Pol’s oscillator with delayed feedback. J. Comput. Appl. Math. 213, 604–615 (2008)
Liu, S., Li, X., Tan, S., Li, H.: Hopf bifurcation control for a coupled nonlinear relative rotation system with time-delay feedbacks. Chin. Phys. B 23, 299–305 (2014)
Chen, L., Wang, W., Li, Z., Zhu, W.: Stationary response of Duffing oscillator with hardening stiffness and fractional derivative. Int. J. Non-Linear Mech. 48, 44–50 (2013)
Chen, L., Li, Z., Zhuang, Q.: First-passage failure of single-degree-of-freedom nonlinear oscillators with fractional derivative. J. Vib. Control 19, 2154–2163 (2013)
Shen, Y., Yang, S., Xing, H., Ma, H.: Primary resonance of Duffing oscillator with two kinds of fractional-order derivatives. Commun. Nonlinear Sci. Numer. Simul. 17, 3092–3100 (2012)
Yang, Y., Xu, W., Sun, Y., Gu, X.: Stochastic response of van der Pol oscillator with two kinds of fractional derivatives under Gaussian white noise excitation. Chin. Phys. B 25, 13–21 (2016)
Chen, L., Zhu, W.: Stochastic response of fractional-order van der Pol oscillator. Theor. Appl. Mech. Lett. 4, 68–72 (2014)
Spanos, P., Zeldin, B.: Random vibration of systems with frequency-dependent parameters or fractional derivatives. J. Eng. Mech. 123, 290–292 (1997)
Zhu, W.: Random Vibration. Science Press, Beijing (1992) (in Chinese)
Ling, F.: Catastrophe Theory and Its Applications. Shang Hai Jiao Tong University Press, Shanghai (1987) (in Chinese)
Petráš, I.: Fractional-Order Nonlinear Systems: Modeling, Analysis and Simulation. Higher Education Press, Beijing (2011)
Petráš, I.: Tuning and implementation methods for fractional-order controllers. Fract. Calc. Appl. Anal. 15, 282–303 (2012)
Agrawal, O.: A general formulation and solution scheme for fractional optimal control problems. Nonlinear Dyn. 38, 323–337 (2004)
Charef, A., Assabaa, M., Ladaci, S., Loiseau, J.: Fractional order adaptive controller for stabilised systems via high-gain feedback. IET Control Theory Appl. 7, 822–828 (2013)
Shah, P., Agashe, S.: Review of fractional PID controller. Mechatronics 38, 29–41 (2016)
Acknowledgements
The authors would like to thank the reviewers and editors for their conscientious reading and comments which were extremely helpful and useful for improving the article.
Availability of data and materials
Data supporting the results of this study are included in the article. All other data can be available from the corresponding author as required.
Funding
This work in this paper was supported by the National Basic Research Program of China (Grant No. 2014CB046805) and the National Natural Science Foundation of China (Grant No. 11372211).
Author information
Authors and Affiliations
Contributions
YL participated in the draft writing and the revision of the manuscript. ZW and GZ participated in the revision of the manuscript. FW and YW put forward some valuable suggestions. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no conflicts of interest in publishing of this paper.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Li, Y., Wu, Z., Zhang, G. et al. Stochastic P-bifurcation in a bistable Van der Pol oscillator with fractional time-delay feedback under Gaussian white noise excitation. Adv Differ Equ 2019, 448 (2019). https://doi.org/10.1186/s13662-019-2356-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13662-019-2356-1