Finite time synchronization of stochastic Markovian jumping genetic oscillator networks with time-varying delay and Lévy noise

Abstract

This paper is to investigate the finite-time synchronization of stochastic Markovian jumping genetic oscillator networks with time-varying delay and Lévy noise. At first, we generalize the finite-time stability theorem from the systems driven by Brownian motion to the Markovian jumping systems with Lévy noise. And then, we utilize the stochastic Lyapunov functional method and appropriate control to obtain sufficient conditions for finite-time synchronization. Finally, two numerical examples are presented to verify the effectiveness of the proposed criteria.

1 Introduction

Over the past few years, genetic oscillator networks (GONs) have received considerable attention in biological and biomedical sciences since they provide a powerful tool to elucidate the interactions between genes and proteins in gene expression and other gene regulation processes. As is known, GONs are inherently coupled complex biochemical systems, where proteins are synthesized from genes as transcriptional factors binding to the regulatory sites of their corresponding genes or other genes. Some important progress has been made in the development of GONs by means of various mathematical modeling, such as Boolean network model [1] and differential equation model [2]. Particularly, the differential equation model has obtained an increasing interest in qualitative and quantitative analysis [3,4,5].

Synchronization analysis of GONs is a hot topic in theory and numerical calculation. Usually, it is known that synchronization is essential for understanding biological rhythmic phenomena and molecular communication of living organisms [6, 7]. Very recently, some experimental results have implied that synchronization also plays a vital role in biomedical engineering. For instance, in Ref. [8] it has been found that synchronization can significantly increase the rate of homologous recombination during transformation in gene targeting, and in Ref. [9] it is showed that synchronization can enhance the anticancer activity of 2-deoxyglucose in breast cancer cells due to an increase in cellular glucose metabolism. Therefore, it is not surprising that many theoretical analyses on synchronization with or without control have been established for GONs in these years [6, 7, 10,11,12,13,14,15,16]. As we know, in Ref. [10] the global exponential synchronization of delay-coupled GONs was considered in absence of control, while in Ref. [11] the cluster synchronization problem of GONs was investigated based on aperiodically adaptive intermittent control, and in Ref. [12] the conditions for multisynchronization of GONs were given via partial impulsive control strategy. Among the various synchronization protocols including exponential synchronization and asymptotic synchronization, finite-time synchronization is faster in synchronization realization. Moreover, the finite-time control techniques have demonstrated better robustness and disturbance rejection properties [17, 18]. As a result, the finite-time synchronization has obtained much attention in complex networks except for GONs [19,20,21,22,23]. Note that the real cellular life is finite, so it should be more meaningful for considering finite-time synchronization in GONs.

Although deterministic differential equations can capture some mean-field characteristics of practical dynamic systems, stochastic differential equations are more important in modeling uncertainties inherent in real world [24,25,26,27,28]. Gene expression is an intrinsically stochastic process [29, 30]. It should be pointed out that all of the existing literature about stochastic GONs mainly focuses on a system driven by Brownian motion [7, 13, 16]. However, researchers observed that the products of mRNAs and proteins occur in a bursty, unpredictable, and intermittent manner from a large number of biology experiments [31]. These burst-like events lead to a pulsatile fashion of high transcriptional activity followed by long periods of inactivity [32] and obey heavy tailed distributions [33]. The characteristics of burst-like events appear to be properly modeled by the non-Gaussian Lévy process [34]. In fact, jump-diffusion Lévy process, which involves Brownian motion as a specific case, allows not only the number of individuals to change continuously most of the time but also random jump discontinuities to occur occasionally [35, 36]. Meanwhile, we also note that a large number of studies have considered the effects of two kinds of necessary factors, i.e., time delay [37, 38] and Markovian jumping [39,40,41], in GONs. On the one hand, time delay is a ubiquitous phenomenon in slow biochemical reactions of genetic oscillator regulatory process. On the other hand, the dynamical systems with Markovian jumping are appropriate to describe the situation where gene switches between an inactive state, in which no protein will be produced, and an active state [42]. This evidence demonstrates that it is more meaningful and challenging to explore synchronization for delayed GONs with Lévy noise and Markovian jumping despite increased mathematical complexity. Nevertheless, to the best of our knowledge, the problem of synchronization for GONs in the case of Lévy noise has not been studied.

Motivated by the above discussions, the purpose of this paper is to deal with the finite-time synchronization problem of stochastic Markovian jumping GONs with time-varying delay and Lévy noise. We will introduce vector form Lévy noise into GONs to make a system more realistic in the true biological environment of networks because each node is always influenced by different multidimensional noises. By contrast of the existing literature, the main contributions of this paper can be highlighted into three points. Firstly, a more general model is proposed in this paper via introducing vector form Lévy noise into GONs. Secondly, we extend the finite-time stability theorem previously developed for the systems driven by Brownian motion to the Markovian jumping systems with Lévy noise. Thirdly, the sufficient finite-time synchronization conditions for stochastic Markovian jumping GONs with time-varying delay and Lévy noise are derived with the help of appropriate control and stochastic Lyapunov functional method.

The paper is organized as follows. In Sect. 2, some preliminary model notations and a lemma of finite-time stability for the Markovian jumping systems driven by Lévy noise are given. In Sect. 3, by applying Itô’s formula and the finite-time stability theorem, we obtain sufficient conditions of finite-time synchronization for GONs. Additionally, some corollaries are reduced to extend our main results. In Sect. 4, two numerical examples are presented to verify the effectiveness of the proposed criteria. Finally, conclusions are drawn in Sect. 5.

Notations

Throughout this paper, unless otherwise specified, we let $(\varOmega ,\mathcal{F},\{\mathcal{F}_{t}\}_{t\geq 0},P)$ be a complete probability space with a filtration $\{\mathcal{F}_{t}\}_{t \geq 0}$ satisfying usual conditions (i.e., it is right-continuous and increasing while $\mathcal{F}_{0}$ contains all P-null sets). $R^{n}$ is the n-dimensional Euclidean space. $R_{+}$ denotes the set of positive real numbers. If x is a vector or matrix, its transpose is denoted by $x^{T}$. For vector $x\in R^{n}$, its norm is defined as $\Vert x \Vert =\sqrt{(x^{T}x)}$. $I_{n}$ denotes the n-dimensional identity matrix. $A>0$ implies that A is a symmetric and positive definite matrix. $\operatorname{diag}(\cdot )$ stands for a diagonal matrix. $E(\cdot )$ denotes the expectation operator with respect to some probability measure.

2 Preliminaries

Let $r(t)$, $t\geq 0$ be a right-continuous Markovian chain on the probability space taking values in a finite state set $S=\{1,2,\ldots ,M\}$ with generator $\varPi =(\pi _{ij})_{M\times M}$ given by

$$ P\bigl\{ r(t+\delta )=j\mid r(t)=i\bigr\} =\textstyle\begin{cases} \pi _{ij} \delta +o(\delta ); \quad \textrm{if } i\neq j, \\ 1+\pi _{ii} \delta +o(\delta ); \quad \textrm{if } i= j, \end{cases} $$

where $\delta >0$ and $\pi _{ij}\geq 0$ is the transition rate from i to j if $i\neq j$, while

$$ \pi _{ii}=-\sum_{i\neq j}\pi _{ij}. $$

It is well known that almost every sample path of $r(t)$ is a right-continuous step function.

Consider the Markovian jumping GONs with time-varying delay of the form

$$\begin{aligned} dx_{k}(t) =&\Biggl[A\bigl(r(t)\bigr)x_{k}(t)+B_{1} \bigl(r(t)\bigr)\tilde{f}\bigl(r(t),x_{k}(t)\bigr)-B _{2}\bigl(r(t)\bigr)\tilde{g}\bigl(r(t),x_{k}\bigl(t- \tau (t)\bigr)\bigr) \\ &{}+B_{2}\bigl(r(t)\bigr)\bar{e}_{n}+\sum _{l=1}^{N}G_{kl}\bigl(r(t)\bigr) \varGamma \bigl(r(t)\bigr)x _{l}(t)\Biggr]\,dt, \end{aligned}$$

(2.1)

where $x_{k}(t)\in R^{n}$, $k=1,\ldots ,N$, is the state vector of the kth genetic oscillator which represents the concentrations of proteins, RNAs, and chemical complexes at time t. $r(t)$ is a Markov chain in a finite state space S. In the networks, $A(r(t))$, $B_{1}(r(t))$, and $B_{2}(r(t))$ are matrices in $R^{n \times n}$. $\bar{e}_{n}=(1,\ldots ,1)^{T}_{n\times 1}$. $\varGamma (r(t)) \in R^{n \times n}$ is a constant inner coupling matrix of the genetic oscillators to be determined, it should be noted that $\varGamma (r(t))$ is not necessary to be diagonal in this paper. $G(r(t))=(G(r(t))_{kl})_{N \times N}$ is the irreducible coupling matrix, which is defined as follows: if there is a link from node l to node k, then $G(r(t))_{kl}$ is equal to a positive constant denoting the coupling strength of this link; otherwise, $G(r(t))_{kl} = 0$; $G(r(t))_{kk} = -\sum_{l=1,l\neq k}^{N}G_{kl}(r(t))$. $\tilde{f}(r(t), x_{k}(t))=[ \tilde{f}_{1}(r(t), x_{k1}(t)), \ldots , \tilde{f}_{n}(r(t), x_{kn}(t))]^{T} \in R^{n}$ and $\tilde{g}(r(t), x_{k}(t-\tau (t)))=[ \tilde{g}_{1}(r(t), x_{k1}(t-\tau (t))), \ldots , \tilde{g}_{n}(r(t), x_{kn}(t-\tau (t)))]^{T} \in R^{n}$ are the regulatory functions, which are monotonic increasing regulatory functions and usually are of the Michaelis–Menten or Hill form.

In this paper, we use the drive-response approach to derive the finite-time synchronization criteria, where system (2.1) can be regarded as the drive system with the state variate denoted by $x_{k}(t)$, and the response system with the state variate denoted by $y_{k}(t)$ can be described in the following stochastic Markovian jumping GONs with time-varying delay and Lévy noise according to Lévy–Itô decomposition theorem and the interlacing technique [35]:

$$\begin{aligned} dy_{k}(t) =&\Biggl[A\bigl(r(t)\bigr)y_{k}(t)+B_{1} \bigl(r(t)\bigr)\tilde{f}\bigl(r(t),y_{k}(t)\bigr)-B _{2}\bigl(r(t)\bigr)\tilde{g}\bigl(r(t),y_{k}\bigl(t- \tau (t)\bigr)\bigr) \\ &{}+B_{2}\bigl(r(t)\bigr)\bar{e}_{n}+\sum _{l=1}^{N}G_{kl}\bigl(r(t)\bigr) \varGamma \bigl(r(t)\bigr)y _{l}(t)+U_{k}\bigl(r(t) \bigr)\Biggr]\,dt \\ &{}+\sigma _{k}\bigl(r(t),y_{k}(t)-x_{k}(t),y_{k} \bigl(t-\tau (t)\bigr)-x_{k}\bigl(t-\tau (t)\bigr)\bigr)\,dW _{k}(t) \\ &{}+ \int _{\mathbb{Z}}h_{k}\bigl(r(t),y_{k}(t)-x_{k}(t),y_{k} \bigl(t-\tau (t)\bigr)-x _{k}\bigl(t-\tau (t)\bigr),z_{k} \bigr)\tilde{N}_{k}(dt,dz_{k}). \end{aligned}$$

(2.2)

It should be noticed that the initial values in the response system are different from those in the drive system, where $U_{k}(r(t))=(u_{k1}(r(t)),u _{k2}(r(t)),\ldots ,u_{kn}(r(t)))^{T} \in R^{n}$ is a control input vector. ${\sigma _{k}}: S\times R^{n}\times R^{n} \rightarrow R^{n \times n}$ and ${h_{k}}: S\times R ^{n}\times R^{n}\times \mathbb{Z} \rightarrow R^{n}$ are Lévy noise intensity functions. $W(t)=(W_{1}(t),\ldots ,W_{N}(t))^{T}$ is a vector Brownian motion defined on the probability space $(\varOmega , \mathcal{F},\{\mathcal{F}_{t}\}_{t\geq 0},P)$ with $\{\mathcal{F}_{t} \}_{t\geq 0}$ satisfying the usual conditions. $N(t, z)$ is an N-dimensional Poisson process and $N_{k}(dt,dz_{k})$ is Poisson counting measure with characteristic measure $\{\lambda _{k}, k=1, \ldots ,N\}$ on a measurable subset $\mathbb{Z}$ of $[0,\infty )$. $\tilde{N}_{k}(dt,dz_{k})=N_{k}(dt,dz_{k})-\lambda _{k}(dz_{k})\,dt$. Throughout the paper, it is assumed that $W_{k}$ and $W_{l}$, $N_{k}$, and $N_{l}$ are independent for all $k\neq l$, and $r(t)$, W and N are also independent.

Define the synchronization error vector $e_{k}(t)=y_{k}(t)-x_{k}(t)$, based on systems (2.1) and (2.2), we have the following error dynamic system:

$$\begin{aligned} de_{k}(t) =&\Biggl[A\bigl(r(t)\bigr)e_{k}(t)+B_{1} \bigl(r(t)\bigr)f\bigl(r(t),e_{k}(t)\bigr)-B_{2} \bigl(r(t)\bigr)g\bigl(r(t),e _{k}\bigl(t-\tau (t)\bigr)\bigr) \\ &{}+\sum_{l=1}^{N}G_{kl} \bigl(r(t)\bigr)\varGamma \bigl(r(t)\bigr)e_{l}(t)+U_{k} \bigl(r(t)\bigr)\Biggr]\,dt \\ &{}+\sigma _{k}\bigl(r(t),e_{k}(t),e_{k} \bigl(t-\tau (t)\bigr)\bigr)\,dW_{k}(t) \\ &{}+ \int _{\mathbb{Z}}h_{k}\bigl(r(t),e_{k}(t),e_{k} \bigl(t-\tau (t)\bigr),z_{k}\bigr) \tilde{N}_{k}(dt,dz_{k}), \end{aligned}$$

(2.3)

where $f(r(t), e_{k}(t))=\tilde{f}(r(t), y_{k}(t))-\tilde{f}(r(t), x _{k}(t))$, $g(r(t), e_{k}(t-\tau (t)))=\tilde{g}(r(t), y_{k}(t-\tau (t)))- \tilde{g}(r(t), x_{k}(t-\tau (t)))$. The initial value is given by $\{e(\bar{\theta }): -\tilde{\tau } \leq \bar{\theta } \leq 0\}=\xi _{0} \in R^{n}$. Throughout the paper, we assume that $f(r(t),0)=g(r(t),0)= \sigma (r(t),0,0)=h(r(t),0,0,0)=0$. Usually, with an appropriate control in the response system, the error state will approach zero. And in this case, it is said that the response system is synchronized with the drive system. In order to achieve finite-time synchronization, we take the control of the form

$$\begin{aligned} U_{k}\bigl(r(t)\bigr) =&-\eta _{1} \bigl(r(t)\bigr) e_{k}(t)-\vartheta \bigl(r(t)\bigr) \operatorname{sign}\bigl(e_{k}(t)\bigr) \bigl\vert e_{k}(t) \bigr\vert ^{\theta } \\ &{}-\vartheta \bigl(r(t)\bigr) \biggl( \int _{t-\tau (t)}^{t}\eta _{2}\bigl(r(s) \bigr) g^{T}\bigl(r(s), e _{k}(s)\bigr)g\bigl(r(s), e_{k}(s)\bigr)\,ds\biggr)^{\frac{1+\theta }{2}}\frac{e_{k}(t)}{ \Vert e _{k}(t) \Vert ^{2}} \\ &{}-\vartheta \bigl(r(t)\bigr) \biggl( \int _{t-\tau (t)}^{t}\eta _{3}\bigl(r(s) \bigr) e_{k}^{T}(s)e _{k}(s)\,ds \biggr)^{\frac{1+\theta }{2}}\frac{e_{k}(t)}{ \Vert e_{k}(t) \Vert ^{2}}, \end{aligned}$$

(2.4)

where $\operatorname{sign}(e_{k}(t))=\operatorname{diag}( \operatorname{sign}(e_{k1}(t)),\ldots ,\operatorname{sign}(e_{kn}(t)))$, $|e_{k}(t)|^{\theta }=(|e_{k1}(t)|^{\theta },\ldots , |e_{kn}(t)|^{ \theta })^{T}$. $\eta _{1}(r(t))$, $\eta _{2}(r(t))$, $\eta _{3}(r(t))$ are control strengths satisfying $\eta _{2}(r(t))>0$, $\eta _{3}(r(t))>0$. $\vartheta (r(t))>0$ is a tunable constant and the real number θ satisfies $0 < \theta <1$. For convenience, $r(t)$ and $r(t_{0})$ are written as i and $i_{0}$, respectively.

In order to derive the main results of this paper, we require the functions $\tilde{f}(\cdot ,\cdot )$, $\tilde{g}(\cdot ,\cdot )$, $\sigma (\cdot ,\cdot ,\cdot )$, and $h(\cdot ,\cdot ,\cdot ,\cdot )$ to satisfy the following assumptions.

$\mathbf{A}_{1}$ :

For $\forall x,y \in R^{n}$, the nonlinear functions f̃ and g̃ satisfy the following sector-like conditions:

$$ 0\leq \frac{\tilde{f}_{s}(i,x)-\tilde{f}_{s}(i,y)}{x-y}\leq \mu _{s} ^{i}, \qquad 0\leq \frac{\tilde{g}_{s}(i,x)-\tilde{g}_{s}(i,y)}{x-y} \leq \nu _{s}^{i}, \quad s=1, \ldots , n, $$

or equivalently,

$$\begin{aligned}& {\bigl(\tilde{f}(i,x)-\tilde{f}(i,y)\bigr)^{T}\bigl( \tilde{f}(i,x)-\tilde{f}(i,y)\bigr)\leq (x-y)^{T}\mu ^{i} \mu ^{i}(x-y),} \\& {\bigl(\tilde{g}(i,x)-\tilde{g}(i,y)\bigr)^{T}\bigl(\tilde{g}(i,x)- \tilde{g}(i,y)\bigr)\leq (x-y)^{T}\nu ^{i}\nu ^{i}(x-y),} \end{aligned}$$

where $\mu ^{i}=\operatorname{diag}\{\mu ^{i}_{1}, \ldots , \mu ^{i}_{n} \}$ and $\nu ^{i}=\operatorname{diag}\{\nu ^{i}_{1}, \ldots , \nu ^{i} _{n}\}$.

$\mathbf{A}_{2}$ :

Assume that the noise intensity functions $\sigma _{k}(\cdot ,\cdot ,\cdot )$ and $h_{k}(\cdot ,\cdot ,\cdot ,\cdot )$ satisfy the following conditions:

$$\begin{aligned}& \operatorname{trace}\bigl(\sigma _{k}^{T} \bigl(i,e_{k}(t),e_{k}\bigl(t-\tau (t)\bigr)\bigr)\sigma _{k}\bigl(i,e _{k}(t),e_{k}\bigl(t-\tau (t)\bigr)\bigr)\bigr) \\& \quad \leq e^{T}_{k}(t)\lambda _{1}^{i}e_{k}(t)+ e ^{T}_{k}\bigl(t-\tau (t)\bigr)\lambda _{2}^{i}e_{k}\bigl(t-\tau (t)\bigr) \end{aligned}$$

and

$$\begin{aligned}& \int _{\mathbb{Z}}h_{k}^{T} \bigl(i,e_{k}(t),e_{k}\bigl(t-\tau (t) \bigr),z_{k}\bigr)h_{k}\bigl(i,e _{k}(t),e_{k} \bigl(t-\tau (t)\bigr),z_{k}\bigr)\lambda _{k}(dz_{k}) \\& \quad \leq e^{T}_{k}(t)H_{1}^{i}e_{k}(t)+e^{T}_{k} \bigl(t-\tau (t)\bigr)H_{2}^{i}e _{k} \bigl(t-\tau (t)\bigr), \end{aligned}$$

where $\lambda _{1}^{i}$, $\lambda _{2}^{i}$, $H_{1}^{i}$, and $H_{2}^{i}$ are positive constant matrices of appropriate dimensions.

$\mathbf{A}_{3}$ :

There exist positive constants τ̃ and τ̄ such that

$$ 0 < \tau (t) \leq \tilde{\tau },\qquad \dot{\tau }(t) \leq \bar{\tau }. $$

For the system

$$\begin{aligned} dx(t) =&\bar{f}\bigl(r(t),t,x(t),x\bigl(t-\tau (t)\bigr)\bigr)\,dt+ \bar{g}\bigl(r(t),t,x(t),x\bigl(t- \tau (t)\bigr)\bigr)\,dW(t) \\ &{}+ \int _{\mathbb{Z}}\bar{h}\bigl(r(t),t,x(t),x\bigl(t-\tau (t)\bigr),z \bigr)\tilde{N}(dt,dz), \end{aligned}$$

(2.5)

where $x(t)\in R^{n}$, $\bar{f}: S\times R_{+} \times R^{n}\times R ^{n}\rightarrow R^{n}$, $\bar{g}: S\times R_{+} \times R^{n}\times R ^{n}\rightarrow R^{n \times n}$, and $\bar{h}: S\times R_{+} \times R ^{n}\times R^{n}\times \mathbb{Z} \rightarrow R^{n}$ are Borel-measurable functions. Given $V\in C^{2,1}(S\times R_{+}\times R ^{n}; R_{+})$, we define the operator LV by

$$\begin{aligned} LV(i,t,x) =&V_{t}(i,t,x)+V_{x}(i,t,x)\bar{f} \bigl(i,t,x(t),x\bigl(t-\tau (t)\bigr)\bigr) \\ &{}+\frac{1}{2}\operatorname{trace}\bigl[\bar{g}\bigl(i,t,x(t),x \bigl(t-\tau (t)\bigr)\bigr)V _{xx}(i,t,x)\bar{g}\bigl(i,t,x(t),x \bigl(t-\tau (t)\bigr)\bigr)\bigr] \\ &{}+ \int _{\mathbb{Z}}\sum_{k=1}^{N} \bigl\{ V\bigl(i,t,x+\bar{h}_{k}\bigl(i,t,x(t),x\bigl(t- \tau (t) \bigr),z_{k}\bigr)\bigr)-V(i,t,x) \\ &{}-V_{x}(i,t,x)\bar{h}_{k}\bigl(i,t,x(t),x\bigl(t- \tau (t)\bigr),z_{k}\bigr)\bigr\} \lambda _{k}(dz _{k}) +\sum_{j=1}^{M}q_{ij}V(j,t,x), \end{aligned}$$

where

$$ V_{x}(i,t,x)=\biggl(\frac{\partial V(i,t,x)}{\partial x_{1}},\ldots , \frac{ \partial V(i,t,x)}{\partial x_{n}}\biggr), \qquad V_{xx}(i,t,x)=\biggl( \frac{\partial ^{2} V(i,t,x)}{\partial x_{k}\partial x _{l}}\biggr)_{n\times n}. $$

For later use, we list Itô’s formula (see [38] and [39]) as follows:

$$\begin{aligned}& V\bigl(r(t),t,x(t)\bigr) \\& \quad =V\bigl(r(0),0,x(0)\bigr)+ \int _{0}^{t}LV(r(s),s,x(s),x\bigl(s-\tau (s) \bigr)\,ds \\& \qquad {}+ \int _{0}^{t}V_{x}\bigl(r(s),s,x(s) \bigr)\bar{g}\bigl(r(s),s,x(s),x\bigl(s-\tau (s)\bigr)\bigr)\,dW(s)+ \sum _{k=1}^{N} \int _{0}^{t} \int _{\mathbb{Z}}\bigl\{ V\bigl(r(s),s,x(s) \\& \qquad {}+\bar{h}_{k}\bigl(r(s),s,x(s),x\bigl(s-\tau (s) \bigr),z_{k}\bigr)\bigr)-V\bigl(r(s),s,x(s)\bigr)\bigr\} \tilde{N}(ds,dz_{k}) \\& \qquad {}+ \int _{0}^{t}\int _{R}\bigl\{ V\bigl(i_{0}+\bar{c} \bigl(r(s),m\bigr),s,x(s)\bigr)-V\bigl(r(s),s,x(s)\bigr)\bigr\} \bar{ \mu }(ds,dm), \end{aligned}$$

for the details on the function c̄ and the measure $\bar{ \mu }(ds,dm)$, see [43, 44].

Specially, given $V(i,t,e_{k})\in C^{2,1}(S\times R_{+}\times R^{n}; R _{+})$, and then the operator LV associated with stochastic model (2.3) is

$$\begin{aligned} LV(i,t,e_{k}) =&V_{t}(i,t,e_{k})+V_{e}(i,t,e_{k}) \Biggl[A^{i}e_{k}(t)+B_{1} ^{i}f\bigl(i,e_{k}(t)\bigr) \\ &{}-B_{2}^{i}g\bigl(i,e_{k}\bigl(t-\tau (t)\bigr)\bigr)+\sum_{l=1}^{N}G_{kl}^{i} \varGamma ^{i}e_{l}(t)+U_{k}^{i} \Biggr] \\ &{}+\frac{1}{2}\operatorname{trace}\bigl[\sigma _{k} \bigl(i,e_{k}(t),e_{k}\bigl(t- \tau (t)\bigr) \bigr)V_{ee}(i,t,e_{k})\sigma _{k} \bigl(i,e_{k}(t),e_{k}\bigl(t-\tau (t)\bigr)\bigr)\bigr] \\ &{}+ \int _{\mathbb{Z}}\bigl\{ V\bigl(i,t,e_{k}+h_{k} \bigl(i,e_{k}(t),e_{k}\bigl(t-\tau (t)\bigr),z _{k}\bigr)\bigr)-V(i,t,e_{k}) \\ &{}-V_{e}(i,t,e_{k})h_{k} \bigl(i,e_{k}(t),e_{k}\bigl(t-\tau (t) \bigr),z_{k}\bigr)\bigr\} \lambda _{k}(dz_{k}) +\sum_{j=1}^{M}\pi _{ij}V(j,t,e_{k}). \end{aligned}$$

Definition 2.1

([45])

A function $C: R_{+}\rightarrow R_{+}$ is said to be a class $\mathcal{K}$ function if it is continuous, strictly increasing, and $C(0)=0$. A class $\mathcal{K}$ function C is said to belong to class $\mathcal{K}_{\infty }$ if $C(x)\rightarrow \infty$ as $x\rightarrow \infty$.

Definition 2.2

([45])

The trivial solution of system (2.5) is finite-time stable in probability if the equation admits a unique solution for any initial value $x_{0}\in R^{n}$ and each $i\in S$; moreover, the following properties hold:

• (a) Finite-time attractiveness in probability: For any initial value $x_{0}\in R^{n}\backslash \{0\}$, the first hitting time $\tau _{h}(x _{0})=\inf \{t; x(i,t,x_{0})=0\}$, called the stochastic settling time, is finite almost surely, that is, $P\{\tau _{h}(x_{0})<\infty \}=1$;

• (b) Stability in probability: For each pair of $\varepsilon \in (0,1)$ and $b > 0$, there exists $\delta =\delta (\varepsilon , b)>0$ such that

  $$ P\bigl( \bigl\Vert x(i,t;x_{0}) \bigr\Vert < b \text{ for all } t\geq 0\bigr)\geq 1-\varepsilon , $$

  whenever $\|x_{0}\|< \delta$.

To end of this section, we introduce the following lemma which is useful in deriving sufficient conditions of finite-time synchronization.

Lemma 2.1

Suppose system (2.5) has a unique solution denoted by $x(i_{0}, t, x_{0})$, for any initial value $\{x(\bar{\theta }): - \tilde{\tau } \leq \bar{\theta } \leq 0\}=x_{0} \in R^{n}\backslash \{0\}$ and $r(t_{0})=i_{0}\in S$. Additionally, if there exists a function $V(i,t,x)\in C^{2,1}(S\times R_{+}\times R^{n}; R_{+})$, $\mathcal{K}_{\infty }$ class functions $C_{1}(\cdot )$ and $C_{2}(\cdot )$, and real numbers $c_{i}> 0$, $1> a >0$, such that

$$\begin{aligned}& C_{1}\bigl( \Vert x \Vert \bigr) \leq V(i, t, x)\leq C_{2} \bigl( \Vert x \Vert \bigr), \end{aligned}$$

(2.6)

$$\begin{aligned}& LV(i, t, x)\leq -c_{i}\bigl(V(i, t, x)\bigr)^{a}, \end{aligned}$$

(2.7)

then the trivial solution of system (2.5) is finite-time stable in probability.

Proof

Applying Itô’s formula and integrating the both sides from $t_{0}$ to t, then taking mathematical expectation for the both sides, it can be easily reduced that

$$\begin{aligned} EV(i,t,x) =&EV\bigl(i_{0},t_{0},x(t_{0}) \bigr)+E \int _{t_{0}}^{t}LV\bigl(i,s,x(s)\bigr)\,ds \\ \leq& EV\bigl(i_{0},t_{0},x(t_{0}) \bigr)-E \int _{t_{0}}^{t}c\bigl(V(i, s, x) \bigr)^{a}\,ds \\ \leq& EV\bigl(i_{0},t_{0},x(t_{0}) \bigr), \end{aligned}$$

where $c=\min_{i\in S}c_{i}$. Define $\tau _{b}=\inf \{t; \|x(t, x_{0})\|> b\}$. With the help of (2.6) and (2.7), it has

$$\begin{aligned} P(\tau _{b} \leq t)C_{1}\bigl( \Vert b \Vert \bigr) \leq& E\bigl[I_{\{\tau _{b} \leq t\}}V\bigl(r(\tau _{b}), \tau _{b},x(\tau _{b})\bigr)\bigr] \\ \leq &E\bigl[V\bigl(r(t\wedge \tau _{b}),t\wedge \tau _{b},x(t\wedge \tau _{b})\bigr)\bigr] \\ \leq& V\bigl(i_{0},t_{0},x(t_{0})\bigr) \\ \leq& C_{2}\bigl( \Vert x_{0} \Vert \bigr). \end{aligned}$$

Thus, by taking $\delta =(C_{2}(\varepsilon C_{1}(\|b\|)))^{-1}$, we can obtain that

$$ P(\tau _{b} \leq t)\leq \varepsilon , $$

whenever $\|x_{0}\|\leq \delta$. Letting $t\rightarrow \infty$, we derive $P(\tau _{b} \leq \infty )\leq \varepsilon$, which further leads to

$$ P\Bigl(\sup_{0\leq t} \bigl\Vert x(i_{0},t; x_{0}) \bigr\Vert \leq b\Bigr)\geq 1-\varepsilon \quad \forall t \in (t_{0}, \infty ). $$

(2.8)

Similar to Theorem 3.1 in [45], we can conclude that the trivial solution of system (2.5) is finite-time stable in probability. Moreover, according to Lemma 3.1 in [45], we have

$$ E\bigl[T_{0}\bigl(i_{0},t_{0},x(t_{0}) \bigr)\bigr]= \frac{V(r(t_{0}),t_{0},x(t_{0}))^{(1-a)}}{c(1-a)}+t_{0}, $$

which implies that $T_{0}(i_{0},t_{0},x(t_{0}))< \infty$ a.s. □

Remark 2.1

Since the presence of the Lévy noise item can make the problem complicated, Theorem 3.1 in [45] and Theorem 4.1 in [46] obtained the finite-time stability conditions for stochastic differential equations driven by Brownian motion cannot be straightaway used to discuss our main problems. In Lemma 2.1, we make a first attempt to give the finite-time stability theorem for the Markovian jump systems driven by Lévy noise, which improves and generalizes the related results in the previous literature.

3 Main results

In this section, the finite-time synchronization criteria for Markovian jumping GONs with time-varying delay and Lévy noise will be got under the above assumptions $\mathbf{A}_{1}$–$\mathbf{A}_{3}$ by means of the stochastic Lyapunov functional method and Lemma 2.1.

Definition 3.1

The genetic oscillator networks (2.1) and (2.2) are said to achieve finite-time synchronization in probability if the trivial solution of error system (2.3) is finite-time stable in probability.

Theorem 3.1

Suppose that error system (2.3) has a unique solution, and let assumptions $\mathbf{A}_{1}$–$\mathbf{A}_{3}$ hold. If there exists a symmetric positive definite matrix $P_{i}\in R^{n\times n}$ and positive definite diagonal matrices $\varSigma _{1i}, \varSigma _{2i} \in R ^{n\times n}$, $i\in S$, such that

$$\begin{aligned}& \begin{aligned} &I_{N}\otimes \bigl(-2\eta _{1}^{i} P_{i}+2P_{i}A^{i}+P_{i}B_{1}^{i} \varSigma _{1i}^{-1}B_{1}^{iT}P_{i}+ \mu ^{i}\varSigma _{1i}\mu ^{i} +P_{i}B_{2}^{i} \varSigma _{2i}^{-1}B_{2}^{iT}P_{i} \\ &\quad {}+\eta _{2}^{i}\nu ^{i}P_{i} \nu ^{i}+\rho (P_{i})\lambda _{1}^{i}+ \rho (P _{i})H_{1}^{i}+\eta _{3}^{i}P_{i}\bigr) +G^{i} \otimes P_{i}\varGamma ^{i}< 0, \\ &I_{N}\otimes \bigl(\nu ^{i}\varSigma _{2i} \nu ^{i}+\bar{\tau }\eta _{2}^{i}\nu ^{i}P_{i}\nu ^{i}+\rho (P_{i})\lambda _{2}^{i}+\rho (P_{i})H_{2}^{i} -(1-\bar{ \tau })\eta _{3}^{i}P_{i}\bigr) < 0, \\ &I_{N}\otimes (P_{j}-\varpi _{i})\leq 0, \quad i \neq j,\qquad I_{N}\otimes (P _{j}-\varpi _{i})> 0,\quad i= j, \end{aligned} \end{aligned}$$

(3.1)

then systems (2.1) and (2.2) are finite-time synchronization in probability in a finite time

$$ T^{*}=\frac{V(r(0),0,\xi _{0})^{(1-\theta )}}{\vartheta (1-\theta )}, $$

where $\vartheta =\min_{i\in S}\vartheta _{i}$ and ‘⊗’ represents the Kronecker product.

Proof

According to Lemma 2.1, it can be assumed that system (2.3) has a unique solution denoted by $e_{k}(i_{0}, t, \xi _{0})$ on $t \geq 0$ for any initial value $\xi _{0}\in R^{n}\backslash \{0\}$. For simplicity, $e_{k}(i_{0}, t, \xi _{0})$ is written as $e_{k}(t)$. For system (2.3), define $V(i,t,e_{k}(t))=V_{1}(i,t,e_{k}(t))+V_{2}(i,t,e _{k}(t))+V_{3}(i,t,e_{k}(t))$, where

$$\begin{aligned}& V_{1}\bigl(i,t,e_{k}(t)\bigr)=\sum _{k=1}^{N}e_{k}^{T}(t)P_{i}e_{k}(t)=e ^{T}(t) (I_{N}\otimes P _{i})e(t), \\& V_{2}\bigl(i,t,e_{k}(t)\bigr)=\sum _{k=1}^{N} \int _{t-\tau (t)}^{t}\eta _{2}^{i}g^{T} \bigl(i, e_{k}(s)\bigr)P _{i}g\bigl(i, e_{k}(s)\bigr)\,ds \\& \hphantom{V_{2}(i,t,e_{k}(t))}=\eta _{2}^{i} \int _{t-\tau (t)}^{t}g^{T}\bigl(i, e(s) \bigr) (I_{N}\otimes P_{i})g\bigl(i, e(s)\bigr)\,ds, \\& V_{3}\bigl(i,t,e_{k}(t)\bigr)=\sum _{k=1}^{N} \int _{t-\tau (t)}^{t}\eta _{3}^{i}e_{k}^{T}(s)P _{i}e_{k}(s)\,ds \\& \hphantom{V_{3}(i,t,e_{k}(t))}=\eta _{3}^{i} \int _{t-\tau (t)}^{t}e^{T}(s) (I_{N}\otimes P _{i})e(s)\,ds. \end{aligned}$$

Then applying Itô’s formula, we can derive

$$ LV=LV_{1}+LV_{2}+LV_{3}, $$

(3.2)

where

$$\begin{aligned}& LV_{1}=\sum_{j=1}^{M} \pi _{ij}V_{1}\bigl(j,t,e_{k}(t)\bigr)+2\sum _{k=1}^{N}e_{k}^{T}(t)P_{i} \Biggl[A^{i}e_{k}(t)+B_{1}^{i}f \bigl(i,e_{k}(t)\bigr) \\& \hphantom{LV_{1}=}{}-B_{2}^{i}g\bigl(i,e_{k} \bigl(t-\tau (t)\bigr)\bigr)+\sum_{l=1}^{N}G_{kl}^{i} \varGamma ^{i}e_{l}(t)+U_{k}^{i} \Biggr] \\& \hphantom{LV_{1}=}{}+\sum_{k=1}^{N} \operatorname{trace}\bigl(\sigma _{k}^{T} \bigl(i,e_{k}(t),e_{k}\bigl(t- \tau (t)\bigr) \bigr)P_{i}\sigma _{k}\bigl(i,e_{k}(t),e_{k} \bigl(t-\tau (t)\bigr)\bigr)\bigr) \\& \hphantom{LV_{1}=}{}+ \int _{\mathbb{Z}}\Biggl[\sum_{k=1}^{N} \bigl(e_{k}(t)+h_{k}\bigl(i,e_{k}(t),e _{k}\bigl(t-\tau (t)\bigr),z_{k}\bigr) \bigr)^{T}P_{i} \\& \hphantom{LV_{1}=}{}\times \bigl(e_{k}(t)+h_{k} \bigl(i,e_{k}(t),e_{k}\bigl(t-\tau (t) \bigr),z_{k}\bigr)\bigr) \\& \hphantom{LV_{1}=}{}-\sum_{k=1}^{N}e_{k}^{T}(t)P_{i}e_{k}(t)-2 \sum_{k=1} ^{N}e_{k}^{T}(t)P_{i}h_{k} \bigl(i,e_{k}(t),e_{k}\bigl(t-\tau (t) \bigr),z_{k}\bigr)\Biggr]\lambda _{k}(dz_{k}), \\& LV_{2}=\sum_{k=1}^{N} \eta _{2}^{i}g^{T}\bigl(i,e_{k}(t) \bigr) P_{i}g\bigl(i,e _{k}(t)\bigr) \\& \hphantom{LV_{2}=}{}-\bigl(1-\dot{\tau }(t)\bigr)\sum_{k=1}^{N}\eta _{2}^{i}g^{T}\bigl(i,e _{k} \bigl(t-\tau (t)\bigr)\bigr) P_{i}g\bigl(i,e_{k}\bigl(t- \tau (t)\bigr)\bigr) +\sum_{j=1}^{M}\pi _{ij}V_{2}\bigl(j,t,e_{k}(t)\bigr), \end{aligned}$$

and

$$\begin{aligned} LV_{3} =&\sum_{k=1}^{N} \eta _{3}^{i}e_{k}^{T}(t) P_{i}e_{k}(t)-\bigl(1- \dot{\tau }(t)\bigr)\sum _{k=1}^{N}\eta _{3}^{i}e_{k}^{T} \bigl(t-\tau (t)\bigr) P_{i}e_{k}\bigl(t-\tau (t)\bigr) \\ &{}+\sum_{j=1}^{M}\pi _{ij}V_{3}\bigl(j,t,e_{k}(t)\bigr). \end{aligned}$$

For $LV_{2}$ and $LV_{3}$, according to assumption $\mathbf{A}_{3}$, we have

$$\begin{aligned} LV_{2} \leq& \sum_{k=1}^{N} \eta _{2}^{i}g^{T}\bigl(i,e_{k}(t) \bigr) P_{i}g\bigl(i,e _{k}(t)\bigr) \\ &{}-(1-\bar{\tau })\eta _{2}^{i}\sum_{k=1}^{N}g^{T} \bigl(i,e _{k}\bigl(t-\tau (t)\bigr)\bigr) P_{i}g \bigl(i,e_{k}\bigl(t-\tau (t)\bigr)\bigr) \\ &{}+\sum_{j=1}^{M}\pi _{ij}V_{2}\bigl(j,t,e_{k}(t)\bigr) \end{aligned}$$

(3.3)

and

$$\begin{aligned} LV_{3} \leq& \sum_{k=1}^{N} \eta _{3}^{i}e_{k}^{T}(t)P_{i}e_{k}(t)-(1- \bar{ \tau })\eta _{3}^{i}\sum _{k=1}^{N}e_{k}^{T} \bigl(t-\tau (t)\bigr) P_{i}e _{k}\bigl(t-\tau (t)\bigr) \\ &{}+\sum_{j=1}^{M}\pi _{ij}V_{3}\bigl(j,t,e_{k}(t)\bigr). \end{aligned}$$

(3.4)

By using assumption $\mathbf{A}_{1}$, it yields

$$\begin{aligned}& 2\sum_{k=1}^{N}e_{k}^{T}(t)P_{i}B_{1}^{i}f \bigl(i,e_{k}(t)\bigr)-2 \sum_{k=1}^{N}e_{k}^{T}(t)P_{i}B_{2}^{i}g \bigl(i,e_{k}\bigl(t-\tau (t)\bigr)\bigr) \\& \quad \leq \sum_{k=1}^{N}[e_{k}^{T}(t)P_{i}B_{1}^{i} \varSigma _{1i}^{-1}B _{1}^{iT}P_{i}e_{k}(t)+f^{T} \bigl(i,e_{k}(t)\bigr)\varSigma _{1i}f \bigl(i,e_{k}(t)\bigr) \\& \qquad {}+e_{k}^{T}(t)P_{i}B_{2}^{i} \varSigma _{2i}^{-1}B_{2}^{iT}P_{i}e_{k}(t)+g ^{T}(i,e_{k}\bigl(t-\tau (t)\bigr)\varSigma _{2i}g\bigl(i,e_{k}\bigl(t-\tau (t)\bigr)\bigr) \\& \quad \leq \sum_{k=1}^{N}e_{k}^{T}(t) \bigl[P_{i}B_{1}^{i}\varSigma _{1i}^{-1}B _{1}^{iT}P_{i}+ \mu ^{i}\varSigma _{1i}\mu ^{i} +P_{i}B_{2}^{i}\varSigma _{2i} ^{-1}B_{2}^{iT}P_{i} \bigr]e_{k}(t) \\& \qquad {}+\sum_{k=1}^{N}e_{k}^{T} \bigl(t-\tau (t)\bigr)\bigl[\nu ^{i}\varSigma _{2i}\nu ^{i}\bigr]e_{k}\bigl(t-\tau (t)\bigr) \end{aligned}$$

(3.5)

and

$$\begin{aligned}& \sum_{k=1}^{N}\eta _{2}^{i}g^{T}\bigl(i,e_{k}(t) \bigr) P_{i}g\bigl(i,e_{k}(t)\bigr)+(\bar{ \tau }-1)\eta _{2}^{i}\sum_{k=1}^{N}g^{T} \bigl(i,e_{k}\bigl(t-\tau (t)\bigr)\bigr) P _{i}g \bigl(i,e_{k}\bigl(t-\tau (t)\bigr)\bigr) \\& \quad \leq \sum_{k=1}^{N}e_{k}^{T}(t) \bigl[\eta _{2}^{i}\nu ^{i}P_{i} \nu ^{i}\bigr]e_{k}(t)+\sum _{k=1}^{N}e_{k}^{T} \bigl(t-\tau (t)\bigr)\bigl[\bar{\tau } \eta _{2}^{i}\nu ^{i} P_{i}\nu ^{i}\bigr]e_{k} \bigl(t-\tau (t)\bigr). \end{aligned}$$

(3.6)

Moreover, it can be easily reduced that

$$ 2\sum_{k=1}^{N}e_{k}^{T}(t)P_{i} \sum_{l=1}^{N}G_{kl} ^{i}\varGamma ^{i}e_{l}(t) =2e^{T}(t) \bigl(G^{i}\otimes P_{i} \varGamma ^{i}\bigr)e(t) $$

(3.7)

and

$$ -2\vartheta _{i}\sum_{k=1}^{N}e_{k}^{T}(t)P_{i} \operatorname{sign}\bigl(e_{k}(t)\bigr)\big| e_{k}(t) \big| ^{\theta }\leq -2 \vartheta _{i}\Biggl(\sum _{k=1}^{N}e_{k}^{T}(t)P_{i}e_{k}(t) \Biggr)^{\frac{1+ \theta }{2}}. $$

(3.8)

With assumption $\mathbf{A}_{2}$ in mind, it is held that

$$\begin{aligned}& \sum_{k=1}^{N} \operatorname{trace}\bigl(\sigma _{k}^{T} \bigl(i,e_{k}(t),e_{k}\bigl(t- \tau (t)\bigr) \bigr)P_{i}\sigma _{k}\bigl(i,e_{k}(t),e_{k} \bigl(t-\tau (t)\bigr)\bigr)\bigr) \\& \quad \leq\rho (P_{i})\sum_{k=1}^{N} \bigl[e_{k}^{T}(t)\lambda _{1}^{i}e _{k}(t)+e_{k}^{T}\bigl(t-\tau (t)\bigr) \lambda _{2}^{i}e_{k}\bigl(t-\tau (t)\bigr) \bigr] \end{aligned}$$

(3.9)

and

$$\begin{aligned}& \int _{\mathbb{Z}}\Biggl[\sum_{k=1}^{N} \bigl(e_{k}(t)+h_{k}\bigl(i,e_{k}(t),e _{k}\bigl(t-\tau (t)\bigr),z_{k}\bigr) \bigr)^{T}P_{i}\bigl(e_{k}(t) +h_{k}\bigl(i,e_{k}(t),e_{k}\bigl(t- \tau (t)\bigr),z_{k}\bigr)\bigr) \\& \qquad {}-\sum_{k=1}^{N}e_{k}^{T}(t)P_{i}e_{k}(t)-2 \sum_{k=1} ^{N}e_{k}^{T}(t)P_{i}h_{k} \bigl(i,e_{k}(t),e_{k}\bigl(t-\tau (t) \bigr),z_{k}\bigr)\Biggr]\lambda _{k}(dz_{k}) \\& \quad = \int _{\mathbb{Z}}\sum_{k=1}^{N}h_{k}^{T} \bigl(i,e_{k}(t),e_{k}\bigl(t- \tau (t) \bigr),z_{k}\bigr)P_{i}h_{k} \bigl(i,e_{k}(t),e_{k}\bigl(t-\tau (t) \bigr),z_{k}\bigr)\lambda _{k}(dz_{k}) \\& \quad \leq \rho (P_{i})\sum_{k=1}^{N} \bigl[e_{k}^{T}(t)H_{1}^{i}e_{k}(t)+e _{k}^{T}\bigl(t-\tau (t)\bigr)H_{2}^{i}e_{k} \bigl(t-\tau (t)\bigr)\bigr], \end{aligned}$$

(3.10)

where $\rho (\cdot )$ denotes the spectral radius. Due to $\sum_{i,j\in S}\pi _{ij}=0$, for an arbitrary symmetric positive definite matrix $\varpi _{i}$, we obtain

$$ \biggl(\sum_{i,j\in S}\pi _{ij}\biggr) \varpi _{i}=0, \quad i\in S. $$

(3.11)

Then submitting (3.3)–(3.11) into (3.2), it follows

$$\begin{aligned} LV \leq& e^{T}(t)\bigl[I_{N}\otimes \bigl(-2 \eta _{1}^{i} P_{i}+2P_{i}A^{i}+P_{i}B _{1}^{i}\varSigma _{1i}^{-1}B_{1}^{iT}P_{i}+ \mu ^{i}\varSigma _{1i}\mu ^{i} +P _{i}B_{2}^{i}\varSigma _{2i}^{-1}B_{2}^{iT}P_{i} \\ &{}+\eta _{2}^{i}\nu ^{i}P_{i} \nu ^{i}+\rho (P_{i})\lambda _{1}^{i}+ \rho (P _{i})H_{1}^{i}+\eta _{3}^{i}P_{i}\bigr) +G^{i} \otimes P_{i}\varGamma ^{i}\bigr]e(t) \\ &{}+e^{T}\bigl(t-\tau (t)\bigr)\bigl[I_{N}\otimes \bigl(\nu ^{i}\varSigma _{2i}\nu ^{i}+\bar{ \tau }\eta _{2}^{i}\nu ^{i}P_{i} \nu ^{i}+\rho (P_{i})\lambda _{2}^{i}+ \rho (P_{i})H_{2}^{i} \\ &{}-(1-\bar{\tau })\eta _{3}^{i}P_{i} \bigr)\bigr]e\bigl(t-\tau (t)\bigr)+\sum_{j=1} ^{M}\pi _{ij}\biggl[e^{T}(t) \bigl(I_{N}\otimes (P_{j}-\varpi _{i}) \bigr)e(t) \\ &{}+ \int _{t-\tau (t)}^{t}\eta _{2}^{j} g^{T}\bigl(j, e(s)\bigr) \bigl(I_{N}\otimes (P _{j}-\varpi _{i})\bigr)g\bigl(j,e(s)\bigr)\,ds \\ &{}+ \int _{t-\tau (t)}^{t}\eta _{3}^{j}e^{T}(s) \bigl(I_{N}\otimes (P_{j}-\varpi _{i}) \bigr)e(s)\,ds\biggr]-2\vartheta _{i}\bigl(e^{T}(t) (I_{N}\otimes P_{i})e(t)\bigr)^{\frac{1+ \theta }{2}} \\ &{}-2\vartheta _{i}\biggl( \int _{t-\tau (t)}^{t}\eta _{2}^{i} g^{T}\bigl(i, e(s)\bigr) (I _{N}\otimes P_{i})g\bigl(i, e(s)\bigr)\,ds\biggr)^{\frac{1+\theta }{2}} \\ &{}-2\vartheta _{i}\biggl( \int _{t-\tau (t)}^{t}\eta _{3}^{i} e^{T}(s) (I_{N} \otimes P_{i})e(s)\,ds \biggr)^{\frac{1+\theta }{2}}. \end{aligned}$$

According to condition (3.1) and the inequality in [47] as follows:

$$\begin{aligned}& \Vert x_{1} \Vert ^{m}+ \Vert x_{2} \Vert ^{m}+\cdots + \Vert x_{n} \Vert ^{m} \\& \quad \geq \bigl( \Vert x_{1} \Vert ^{2}+ \Vert x_{2} \Vert ^{2}+\cdots + \Vert x_{n} \Vert ^{2}\bigr)^{\frac{m}{2}},\quad x_{1}, \ldots , x_{n}\in R^{n}, 0< m < 2, \end{aligned}$$

we can get

$$\begin{aligned} LV \leq& -2\vartheta _{i}\bigl(e^{T}(t) (I_{N}\otimes P_{i})e(t)\bigr)^{\frac{1+ \theta }{2}} \\ &{}-2\vartheta _{i}\biggl( \int _{t-\tau (t)}^{t}\eta _{2}^{i} g^{T}\bigl(i, e(s)\bigr) (I _{N}\otimes P_{i})g\bigl(i, e(s)\bigr)\,ds\biggr)^{\frac{1+\theta }{2}} \\ &{}-2\vartheta _{i}\biggl( \int _{t-\tau (t)}^{t}\eta _{3}^{i} e^{T}(s) (I_{N} \otimes P_{i})e(s)\,ds \biggr)^{\frac{1+\theta }{2}} \\ \leq& -2\vartheta _{i}\Biggl[\sum_{k=1}^{N}e_{k}^{T}(t)P_{i}e_{k}(t)+ \sum_{k=1}^{N} \int _{t-\tau (t)}^{t} \eta _{2}^{i}g^{T} \bigl(i, e_{k}(s)\bigr)P _{i}g\bigl(i, e_{k}(s)\bigr)\,ds \\ &{}+\sum_{k=1}^{N} \int _{t-\tau (t)}^{t} \eta _{3}^{i}e_{k}^{T}(s)P _{i}e_{k}(s)\,ds\Biggr]^{\frac{1+\theta }{2}} \\ =&-2\vartheta _{i} V\bigl(i,t,e_{k}(t) \bigr)^{\frac{1+\theta }{2}}. \end{aligned}$$

Based on Lemma 2.1, $V (i, t, e_{k}(t))$ converges to zero in a finite time, and the finite time is estimated by

$$ T^{*}=\frac{V(r(0),0,\xi _{0})^{(1-\theta )}}{\vartheta (1-\theta )}. $$

Consequently, systems (2.1) and (2.2) with control (2.4) are finite-time synchronized in probability in the finite time $T^{*}$. This completes the proof. □

Remark 3.1

As far as we know, all the existing stochastic models concerning GONs [7, 13, 16, 41] have considered the situation of Brownian motion. In this paper, the model discussed is universal, which replaces pure-diffusion Brownian motion with jump-diffusion Lévy process.

Remark 3.2

It should be noted that previous studies on synchronization problem of GONs [7, 10,11,12,13, 41] have just considered many types of synchronization including exponential synchronization and cluster synchronization but not finite-time synchronization. In this paper, we investigate finite-time synchronization problem of GONs for the first time. Moreover, compared with the studies on finite-time synchronization problem of complex networks [20,21,22,23], the problem of finite-time synchronization for the model driven by Lévy noise is also to be considered for the first time in this paper. Different from the classical Lyapunov stability, finite-time synchronization concerns the stability of the error system over a finite interval of time and plays an important role in the study of the transient behavior of systems.

When we do not consider time-varying delay, i.e., $\tau (t)=0$, error system (2.3) will be reduced to the following stochastic Markovian jumping GONs driven by Lévy noise:

$$\begin{aligned} de_{k}(t) =&\Biggl[A\bigl(r(t)\bigr)e_{k}(t)+B_{1} \bigl(r(t)\bigr)f\bigl(r(t),e_{k}(t)\bigr)-B_{2} \bigl(r(t)\bigr)g\bigl(r(t),e _{k}(t)\bigr) \\ &{}+\sum_{l=1}^{N}G_{kl} \bigl(r(t)\bigr)\varGamma \bigl(r(t)\bigr)e_{l}(t)+U_{k} \bigl(r(t)\bigr)\Biggr]\,dt \\ &{}+ \sigma _{k}\bigl(r(t),e_{k}(t) \bigr)\,dW_{k}(t) \\ &{}+ \int _{\mathbb{Z}}h_{k}\bigl(r(t),e_{k}(t),z_{k} \bigr)\tilde{N}_{k}(dt,dz_{k}), \quad k=1,\ldots ,N, \end{aligned}$$

(3.12)

with the control of the form

$$ U_{k}\bigl(r(t)\bigr)=-\eta _{1}\bigl(r(t)\bigr) e_{k}(t)-\vartheta \bigl(r(t)\bigr) \operatorname{sign} \bigl(e_{k}(t)\bigr) \bigl\vert e_{k}(t) \bigr\vert ^{\theta }. $$

(3.13)

Then we can easily get the following corollary.

Corollary 3.1

Suppose that error system (3.12) has a unique solution, and let assumptions $\mathbf{A}_{1}$–$\mathbf{A}_{2}$ hold. If there exists a symmetric positive definite matrix $P_{i}\in R^{n\times n}$ and positive definite diagonal matrices $\varSigma _{1i}, \varSigma _{2i}\in R ^{n\times n}$, $i\in S$, such that

$$\begin{aligned}& I_{N}\otimes \bigl(-2\eta _{1}^{i} P_{i}+2P_{i}A^{i}+P_{i}B_{1}^{i} \varSigma _{1i}^{-1}B_{1}^{iT}P_{i}+ \mu ^{i}\varSigma _{1i}\mu ^{i} +P_{i}B_{2}^{i} \varSigma _{2i}^{-1}B_{2}^{iT}P_{i} \\& \quad {}+\eta _{2}^{i}\nu ^{i}P_{i} \nu ^{i}+\rho (P_{i})\lambda _{1}^{i}+ \rho (P _{i})H_{1}^{i}+\eta _{3}^{i}P_{i}\bigr) +G^{i} \otimes P_{i}\varGamma ^{i}< 0, \\& I_{N}\otimes (P_{j}-\varpi _{i})\leq 0, \quad i\neq j,\qquad I_{N}\otimes (P _{j}-\varpi _{i})> 0,\quad i= j, \end{aligned}$$

then error system (3.12) is finite-time stable in probability in a finite time

$$ T^{*}=\frac{V(r(0),0,\xi _{0})^{(1-\theta )}}{\vartheta (1-\theta )}. $$

Proof

Define $V(i,t,e_{k}(t))=\sum_{k=1}^{N}e_{k} ^{T}(t)P_{i}e_{k}(t)$. The proof method is similar to that of Theorem 3.1, so we omit it. □

When we do not consider Markovian switching, i.e., Markovian chain $r(t)$ takes value in the state space $S=\{1\}$, error system (2.3) will be reduced to the following stochastic GONs with time-varying delay and Lévy noise:

$$\begin{aligned} de_{k}(t) =&\Biggl[Ae_{k}(t)+B_{1}f \bigl(e_{k}(t)\bigr)-B_{2}g\bigl(e_{k} \bigl(t-\tau (t)\bigr)\bigr)+ \sum_{l=1}^{N}G_{kl} \varGamma e_{l}(t)+U_{k}\Biggr]\,dt \\ &{}+\sigma _{k}\bigl(e_{k}(t),e_{k} \bigl(t-\tau (t)\bigr)\bigr)\,dW_{k}(t) \\ &{}+ \int _{\mathbb{Z}}h_{k}\bigl(e_{k}(t),e_{k} \bigl(t-\tau (t)\bigr),z_{k}\bigr)\tilde{N} _{k}(dt,dz_{k}), \quad k=1,\ldots ,N, \end{aligned}$$

(3.14)

with the control of the form

$$\begin{aligned} U_{k} =&-\eta _{1} e_{k}(t)- \vartheta \operatorname{sign}\bigl(e_{k}(t)\bigr) \bigl\vert e _{k}(t) \bigr\vert ^{\theta } \\ &{}-\vartheta \biggl( \int _{t-\tau (t)}^{t} \eta _{2}g^{T} \bigl(e_{k}(s)\bigr)g\bigl( e_{k}(s)\bigr)\,ds \biggr)^{\frac{1+ \theta }{2}}\frac{e_{k}(t)}{ \Vert e_{k}(t) \Vert ^{2}} \\ &{}-\vartheta \biggl( \int _{t-\tau (t)}^{t} \eta _{3}e_{k}^{T}(s)e_{k}(s) \,ds\biggr)^{\frac{1+ \theta }{2}}\frac{e_{k}(t)}{ \Vert e_{k}(t) \Vert ^{2}}. \end{aligned}$$

(3.15)

Then we can easily get the following corollary.

Corollary 3.2

Suppose that error system (3.14) has a unique solution, and let assumptions $\mathbf{A}_{1}$–$\mathbf{A}_{3}$ hold. If there exists a symmetric positive definite matrix $P\in R^{n\times n}$ and positive definite diagonal matrices $\varSigma _{1}, \varSigma _{2} \in R^{n\times n}$ such that

$$\begin{aligned}& I_{N}\otimes \bigl(-2\eta _{1} P+2PA+PB_{1}\varSigma _{1}^{-1}B_{1}^{T}P+ \mu \varSigma _{1}\mu +PB_{2}\varSigma _{2}^{-1}B_{2}^{T}P \\& \quad {}+\eta _{2}\nu P\nu +\rho (P)\lambda _{1}+\rho (P)H_{1}+\eta _{3}P\bigr)+G \otimes P\varGamma < 0, \\& I_{N}\otimes \bigl(\nu \varSigma _{2}\nu +\bar{\tau } \eta _{2}\nu P\nu +\rho (P) \lambda _{2}+\rho (P)H_{2} -(1-\bar{\tau })\eta _{3}P\bigr)< 0, \end{aligned}$$

then error system (3.14) is finite-time stable in probability in a finite time

$$ T^{*}= \frac{V(0,\xi _{0})^{\frac{1-\theta }{2}}}{\vartheta (1-\theta )}. $$

Proof

Define $V(t,e_{k}(t))=V_{1}(t,e_{k}(t))+V_{2}(t,e_{k}(t))+V _{3}(t,e_{k}(t))$, where

$$\begin{aligned}& V_{1}\bigl(t,e_{k}(t)\bigr)=\sum _{k=1}^{N}e_{k}^{T}(t)Pe_{k}(t), \\& V_{2}\bigl(t,e_{k}(t)\bigr)=\sum _{k=1}^{N} \int _{t-\tau (t)}^{t} \eta _{2}g ^{T}\bigl(e_{k}(s)\bigr)Pg\bigl(e_{k}(s) \bigr)\,ds, \\& V_{3}\bigl(t,e_{k}(t)\bigr)=\sum _{k=1}^{N} \int _{t-\tau (t)}^{t}\eta _{3}e _{k}^{T}(s)Pe_{k}(s)\,ds. \end{aligned}$$

Similarly, following the same steps as in Theorem 3.1, one can easily obtain Corollary 3.2. □

When we do not consider Lévy jump, i.e., $h_{k}(i,e_{k}(t),e_{k}(t- \tau (t)),z_{k})=0$, error system (2.3) will be reduced to the following stochastic Markovian jumping GONs with time-varying delay:

$$\begin{aligned} de_{k}(t) =&\Biggl[A\bigl(r(t)\bigr)e_{k}(t)+B_{1} \bigl(r(t)\bigr)f\bigl(r(t),e_{k}(t)\bigr)-B_{2} \bigl(r(t)\bigr)g\bigl(r(t),e _{k}\bigl(t-\tau (t)\bigr)\bigr) \\ &{}+\sum_{l=1}^{N}G_{kl} \bigl(r(t)\bigr)\varGamma \bigl(r(t)\bigr)e_{l}(t)+U_{k} \bigl(r(t)\bigr)\Biggr]\,dt \\ &{}+\sigma _{k}\bigl(r(t),e_{k}(t),e_{k} \bigl(t-\tau (t)\bigr)\bigr)\,dW_{k}(t), \quad k=1, \ldots ,N, \end{aligned}$$

(3.16)

with the control of the form

$$\begin{aligned} U_{k}\bigl(r(t)\bigr) =&-\eta _{1} \bigl(r(t)\bigr) e_{k}(t)-\vartheta \bigl(r(t)\bigr) \operatorname{sign}\bigl(e_{k}(t)\bigr) \bigl\vert e_{k}(t) \bigr\vert ^{\theta } \\ &{}-\vartheta \bigl(r(t)\bigr) \biggl( \int _{t-\tau (t)}^{t}\eta _{2}\bigl(r(s) \bigr) g^{T}\bigl(r(s), e _{k}(s)\bigr)g\bigl(r(s), e_{k}(s)\bigr)\,ds\biggr)^{\frac{1+\theta }{2}}\frac{e_{k}(t)}{ \Vert e _{k}(t) \Vert ^{2}} \\ &{}-\vartheta \bigl(r(t)\bigr) \biggl( \int _{t-\tau (t)}^{t} \eta _{3}\bigl(r(s) \bigr)e_{k}^{T}(s)e _{k}(s)\,ds \biggr)^{\frac{1+\theta }{2}}\frac{e_{k}(t)}{ \Vert e_{k}(t) \Vert ^{2}}. \end{aligned}$$

(3.17)

Then we can easily get the following corollary.

Corollary 3.3

Suppose that error system (3.16) has a unique solution, and let assumptions $\mathbf{A}_{1}$–$\mathbf{A}_{3}$ hold. If there exists a symmetric positive definite matrix $P_{i}\in R^{n\times n}$ and positive definite diagonal matrices $\varSigma _{1i}, \varSigma _{2i} \in R ^{n\times n}$, $i\in S$, such that

$$\begin{aligned}& I_{N}\otimes \bigl(-2\eta _{1}^{i} P_{i}+2P_{i}A^{i}+P_{i}B_{1}^{i} \varSigma _{1i}^{-1}B_{1}^{iT}P_{i}+ \mu ^{i}\varSigma _{1}\mu ^{i} +P_{i}B_{2}^{i} \varSigma _{2i}^{-1}B_{2}^{iT}P_{i} \\& \quad {}+\eta _{2}^{i}\nu ^{i}P_{i} \nu ^{i}+\rho (P_{i})\lambda _{1}^{i}+ \eta _{3}^{i}P_{i}\bigr)+G^{i} \otimes P_{i}\varGamma ^{i}< 0, \\& I_{N}\otimes \bigl(\nu ^{i}\varSigma _{2} \nu ^{i}+\bar{\tau }\eta _{2}^{i}\nu ^{i}P_{i}\nu ^{i}+\rho (P_{i})\lambda _{2}^{i} -(1-\bar{\tau }) \eta _{3} ^{i}P_{i}\bigr)< 0, \\& I_{N}\otimes (P_{j}-\varpi _{i})\leq 0, \quad i\neq j, \qquad I_{N}\otimes (P _{j}-\varpi _{i})> 0, \quad i= j, \end{aligned}$$

then error system (3.16) is finite-time stable in probability in a finite time

$$ T^{*}=\frac{V(r(0),0,\xi _{0})^{(1-\theta )}}{\vartheta (1-\theta )}. $$

Proof

Define $V(i,t,e_{k}(t))=V_{1}(i,t,e_{k}(t))+V_{2}(i,t,e _{k}(t))+V_{3}(i,t,e_{k}(t))$, where

$$\begin{aligned}& V_{1}\bigl(i,t,e_{k}(t)\bigr)=\sum _{k=1}^{N}e_{k}^{T}(t)P_{i}e_{k}(t), \\& V_{2}\bigl(i,t,e_{k}(t)\bigr)=\sum _{k=1}^{N} \int _{t-\tau (t)}^{t}\eta _{2}^{i} g^{T}\bigl(i, e_{k}(s)\bigr)P_{i}g\bigl(i, e_{k}(s)\bigr)\,ds, \\& V_{3}\bigl(i,t,e_{k}(t)\bigr)=\sum _{k=1}^{N} \int _{t-\tau (t)}^{t}\eta _{3}^{i}e_{k}^{T}(s)P_{i}e_{k}(s) \,ds. \end{aligned}$$

By means of Theorem 3.1, the results of Corollary 3.3 are obvious, hence we omit their proofs here. □

Remark 3.3

As is known, GONs are inherently coupled networks. The finite-time synchronization criteria of genetic regulatory networks without coupled interaction proposed in [23] cannot be used to guarantee the case of the GONs. As a result, Corollary 3.3 is more general than previous results.

4 Numerical examples

Here, we present two illustrative numerical examples to demonstrate the effectiveness of the main results.

Example 4.1

Consider the following genetic oscillator networks [6]:

$$\begin{aligned}& \begin{aligned} &\frac{dx_{ak}}{dt}=-d_{1} \bigl(r(t)\bigr)x_{ak}+\frac{\alpha (r(t))}{u(r(t))+x _{Ck}^{m}}, \\ &\frac{dx_{bk}}{dt}=-d_{2}\bigl(r(t)\bigr)x_{bk}+ \frac{\alpha (r(t))}{u(r(t))+x _{Ak}^{m}}, \\ &\frac{dx_{ck}}{dt}=-d_{3}\bigl(r(t)\bigr)x_{ck}+ \frac{\alpha (r(t))}{u(r(t))+x _{Bk}^{m}}+\frac{k(r(t))x_{Sk}}{u_{s}(r(t))+x_{Sk}}, \\ &\frac{dx_{Ak}}{dt}=-d_{4}\bigl(r(t)\bigr)x_{Ak}+ \beta _{1}\bigl(r(t)\bigr)x_{ak}, \\ &\frac{dx_{Bk}}{dt}=-d_{5}\bigl(r(t)\bigr)x_{Bk}+ \beta _{2}\bigl(r(t)\bigr)x_{bk}, \\ &\frac{dx_{Ck}}{dt}=-d_{6}\bigl(r(t)\bigr)x_{Ck}+ \beta _{3}\bigl(r(t)\bigr)x_{ck}, \\ &\frac{dx_{Sk}}{dt}=-\bigl[k_{1}\bigl(r(t)\bigr)+(1-Q_{0})k_{2} \bigl(r(t)\bigr)\bigr]x_{Sk}+k_{3}\bigl(r(t)\bigr)x _{Ak} \\ &\hphantom{\frac{dx_{Sk}}{dt}=}{}+\frac{k_{2}(r(t))Q_{0}}{N}\sum_{l=1}^{N}(x_{Sl}-x_{Sk}), \quad k=1,\ldots ,N, \end{aligned} \end{aligned}$$

(4.1)

where $x_{ak}$, $x_{bk}$, $x_{ck}$ and $x_{Ak}$, $x_{Bk}$, $x_{Ck}$ represent the dimensionless concentrations of genes tetR, cI, lacI and their product proteins TetR, CI, LacI, respectively. The concentration of AI inside the kth cell is denoted by $x_{Sk}$. More details are in Ref. [6]. In this example, $N=2$. Here, the Markov chain $r(t)$ is on the state space $S=\{1, 2\}$ with the generator $\Pi =\left[\begin{array}{cc}-4& 4\\ 6& -6\end{array}\right]$ and the following setting:

• when $r(t)=1$,

  $$\begin{aligned}& d_{1}=d_{3}=0.35,\qquad d_{2}=0.3, \qquad d_{4}=0.25,\qquad d_{5}=0.28, \qquad d_{6}=0.26, \\& \alpha =5.4,\qquad \beta _{1}=0.6,\qquad \beta _{2}=8.0, \\& \beta _{3}=0.015,\qquad m=4,\qquad Q_{0}=0.8,\qquad k=8.0, \qquad k_{1}=0.016, \\& k_{2}=0.4,\qquad k _{3}=0.018,\qquad u=1.3,\qquad u_{s}=5, \end{aligned}$$

• when $r(t)=2$,

  $$\begin{aligned}& d_{1}=d_{3}=0.33,\qquad d_{2}=0.3,\qquad d_{4}=0.23,\qquad d_{5}=0.27, \qquad d_{6}=0.27, \\& \alpha =4.9,\qquad \beta _{1}=0.5,\qquad \beta _{2}=9.0, \\& \beta _{3}=0.016,\qquad m=4,\qquad Q_{0}=0.8,\qquad k=8.0, \qquad k_{1}=0.016, \\& k_{2}=0.4, \qquad k _{3}=0.018,\qquad u=1.3,\qquad u_{s}=5. \end{aligned}$$

For system (4.1), its response system driven by Lévy noise can be described as system (2.2), in which $\tau (t)=0$, $\tilde{f}=[0, 0, 0, 0, 0, 0, \frac{x_{Sk}}{u_{s}(r(t))+x_{Sk}}]^{T}$, $B_{1}(r(t))$ is a $7\times 7$ matrix with all zero entries except for $B_{1}(3,7)=k(r(t))$, $\tilde{g}=[0, 0, 0, \frac{1}{u(r(t))+x_{Ak} ^{m}}, \frac{1}{u(r(t))+x_{Bk}^{m}}, \frac{1}{u(r(t))+x_{Ck}^{m}}, 0]^{T}$, $B_{2}(r(t))$ is a $7\times 7$ matrix with all zero entries except for $B_{2}(2,4)=B_{2}(3,5)=\frac{\alpha (r(t))}{u(r(t))}$. And when $r(t)=1$,

$$\begin{aligned}& \sigma _{1}\bigl(e_{1}(t)\bigr)= \operatorname{diag} \bigl\{ 0.5e_{11}(t),\ldots ,0.5e _{17}(t)\bigr\} , \\& \sigma _{2}\bigl(e_{2}(t)\bigr)= \operatorname{diag} \bigl\{ 0.5e_{21}(t),\ldots ,0.5e _{27}(t)\bigr\} , \\& h_{1}\bigl(e_{1}(t), z_{1}\bigr)= \bigl[0.35e_{11}(t)z_{1},\ldots ,0.35e_{17}(t)z _{1}\bigr]^{T}, \\& h_{2}\bigl(e_{2}(t), z_{2}\bigr)= \bigl[0.35e_{21}(t)z_{2},\ldots ,0.35e_{27}(t)z _{2}\bigr]^{T}. \end{aligned}$$

When $r(t)=2$,

$$\begin{aligned}& \sigma _{1}\bigl(e_{1}(t)\bigr)= \operatorname{diag} \bigl\{ 0.4e_{11}(t),\ldots ,0.4e _{17}(t)\bigr\} , \\& \sigma _{2}\bigl(e_{2}(t)\bigr)= \operatorname{diag} \bigl\{ 0.4e_{21}(t),\ldots ,0.4e _{27}(t)\bigr\} , \\& h_{1}\bigl(e_{1}(t), z_{1}\bigr)= \bigl[0.25e_{11}(t)z_{1},\ldots ,0.25e_{17}(t)z _{1}\bigr]^{T}, \\& h_{2}\bigl(e_{2}(t), z_{2}\bigr)= \bigl[0.25e_{21}(t)z_{2},\ldots ,0.25e_{27}(t)z _{2}\bigr]^{T}. \end{aligned}$$

The initial values $x_{1}(t)=[0.5, 0.3, 0.09, 0.6, 1.3, 5.03, 1.1]^{T}$, $x_{2}(t)=[10.5, 0.31, 0.08,0.062, 1.31, 5.02, 1.2]^{T}$, $y_{1}(t)=[6.3, 0.33, 0.1, 0.061, 1.29, 5.04, 1.1]^{T}$, $y_{2}(t)=[3.2, 0.29, 0.02, 0.059, 1.32, 5.08, 0.99]^{T}$.

It is easy to verify that the given parameters satisfy the assumptions of Corollary 3.1, and thus system (4.1) and (2.2) should be finite-time synchronization. The simulated results in Figs. 1–3 clearly confirm our theoretical results. As seen from Fig. 1, due to the influence of Lévy noise, the trajectory of the response system without control has an evident deviation from the trajectory of the drive system. But in Fig. 2, under the same intensity of Lévy noise, the response system with control is synchronized with the drive system after a short-time transient evolution even though those states start at different initial values. To further verify the effectiveness of the proposed control design, we take different values of $\eta _{1}^{i}$ and $\vartheta _{i}$ ($i=1,2$) in Fig. 3.

Figure 1

(a) shows the path of switching signal. (b) and (c) exhibit the time evolutions of the concentrations of tetR $x_{ak}$ ($k=1, 2$) for the drive system and the response system without control under Lévy noise

Figure 2

(a) and (b) exhibit the time evolutions of the concentrations of tetR $x_{ak}$ ($k=1, 2$) for the drive system and the response systems with control under Lévy noise. In (c), the evolutions of the error systems tend to zero as time increases, which illustrates the finite-time synchronization of the drive system and the response system

Figure 3

(a)–(c) show the time responses of the error variables of the concentrations of tetR $x_{ak}$ ($k=1, 2$) under control with (a) $\eta _{1}^{1}=3$, $\vartheta _{1}=1$, $\eta _{1}^{2}=4$, $\vartheta _{2}=1$, $\theta =0.2$; (b) $\eta _{1}^{1}=8$, $\vartheta _{1}=1$, $\eta _{1}^{2}=9$, $\vartheta _{2}=1$, $\theta =0.2$; (c) $\eta _{1}^{1}=8$, $\vartheta _{1}=5$, $\eta _{1}^{2}=9$, $\vartheta _{2}=6$, $\theta =0.2$

Example 4.2

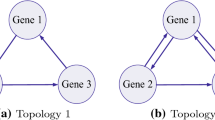
For systems (2.1) and (2.2), let $N=n=2$ and the Markov chain $r(t)$ be on the state space $S=\{1, 2\}$ with the generator $\Pi =\left[\begin{array}{cc}-7& 7\\ 3& -3\end{array}\right]$ and the following setting:

• when $r(t)=1$,

  $$\begin{array}{c}\tilde{f}(x_k(t))=\tilde{g}(x_k(t))=\frac{x_k{(t)}^2}{1+x_k{(t)}^2},\tau (t)=0.2-0.1cos(2t),\hfill \\ {\sigma }_1(e_1(t),e_1(t-\tau (t)))=diag\{0.5e_{11}(t),0.5e_{12}(t)\},\hfill \\ {\sigma }_2(e_2(t),e_2(t-\tau (t)))=diag\{0.5e_{21}(t-\tau (t)),0.5e_{22}(t-\tau (t))\},\hfill \\ h_1(e_1(t),e_1(t-\tau (t)),z_1)={[0.25e_{11}(t)z_1,0.25e_{12}(t)z_1]}^T,\hfill \\ h_2(e_2(t),e_2(t-\tau (t)),z_2)={[0.25e_{21}(t-\tau (t))z_2,0.25e_{22}(t-\tau (t))z_2]}^T,\hfill \\ A=\left[\begin{array}{cc}-1.0& 0.2\\ 0.5& -0.1\end{array}\right],B_1=\left[\begin{array}{cc}1.8& 0.3\\ 0.2& 3.5\end{array}\right],B_2=\left[\begin{array}{cc}-2.4& 0.01\\ 0.03& 3.5\end{array}\right],\hfill \\ G=\left[\begin{array}{cc}-1.0& 1.0\\ 1.0& -1.0\end{array}\right],\Gamma =\left[\begin{array}{cc}1.5& 0\\ 0& 1.5\end{array}\right],\lambda =1,\hfill \end{array}$$

• when $r(t)=2$,

  $$\begin{array}{c}\tilde{f}(x_k(t))=\tilde{g}(x_k(t))=\frac{x_k{(t)}^2}{1+x_k{(t)}^2},\tau (t)=0.2-0.1cos(2t),\hfill \\ {\sigma }_1(e_1(t),e_1(t-\tau (t)))=diag\{0.4e_{11}(t),0.4e_{12}(t)\},\hfill \\ {\sigma }_2(e_2(t),e_2(t-\tau (t)))=diag\{0.45e_{21}(t-\tau (t)),0.45e_{22}(t-\tau (t))\},\hfill \\ h_1(e_1(t),e_1(t-\tau (t)),z_1)={[0.3e_{11}(t)z_1,0.3e_{12}(t)z_1]}^T,\hfill \\ h_2(e_2(t),e_2(t-\tau (t)),z_2)={[0.2e_{21}(t-\tau (t))z_2,0.2e_{22}(t-\tau (t))z_2]}^T,\hfill \\ A=\left[\begin{array}{cc}-0.9& 0.1\\ 0.4& -0.5\end{array}\right],B_1=\left[\begin{array}{cc}-1.4& 0.2\\ 0.1& -2.1\end{array}\right],B_2=\left[\begin{array}{cc}2.5& 0.05\\ 0.01& 4.9\end{array}\right],\hfill \\ G=\left[\begin{array}{cc}-1.0& 1.0\\ 1.0& -1.0\end{array}\right],\Gamma =\left[\begin{array}{cc}1.0& 0\\ 0& 1.0\end{array}\right],\lambda =1,\hfill \end{array}$$

and the initial values $x_{1}(t)=[2.3, 0.3]^{T}$, $x_{2}(t)=[6.3, 1.3]^{T}$, $y_{1}(t)=[5.5, 4.0]^{T}$, $y_{2}(t)=[2.5, 7.5]^{T}$.

We find that the parameters given by Example 4.2 satisfy the assumptions of Theorem 3.1, which means that response system (2.2) should be finite-time synchronized with drive system (2.1) in theoretical analysis. The simulated results in Figs. 4–6 clearly confirm our conclusions. As seen from Fig. 4, due to the effect of Lévy noise, the trajectory of the response system without control is not synchronized with the trajectory of the drive system. But for the case with control in Fig. 5, the trajectory of the response system rapidly becomes the same as the trajectory of the drive system after a short-time transient evolution. Fig. 6 presents the synchronization time for different values of $\eta _{s}^{i}$, $\vartheta _{i}$ and θ ($s=1,2,3$, $i=1,2$).

Figure 4

(a) shows the path of switching signal. The time evolutions of genetic oscillators for the drive system ($x_{1}$, $x_{2}$) and the response system ($y_{1}$, $y_{2}$) without control under Lévy noise are illustrated in (b) and (c)

Figure 5

(a) and (b) exhibit the time evolutions of genetic oscillators for the drive system ($x_{1}$, $x_{2}$) and the response system ($y_{1}$, $y_{2}$) with control under Lévy noise. In (c), the evolutions of the error systems tend to zero as time increases, which illustrates the finite-time synchronization of the drive system and the response system

Figure 6

(a)–(c) show the time responses of the error variables under control with (a) $\eta _{1}^{1}=4$, $\eta _{2}^{1}=1$, $\eta _{3}^{1}=1$, $\vartheta _{1}=3$, $\eta _{1}^{2}=5$, $\eta _{2}^{2}=1$, $\eta _{3}^{2}=1$, $\vartheta _{2}=4$, $\theta =0.25$; (b) $\eta _{1}^{1}=9$, $\eta _{2}^{1}=1$, $\eta _{3}^{1}=1$, $\vartheta _{1}=3$, $\eta _{1}^{2}=10$, $\eta _{2}^{2}=1$, $\eta _{3}^{2}=1$, $\vartheta _{2}=4$, $\theta =0.25$; (c) $\eta _{1}^{1}=9$, $\eta _{2}^{1}=1$, $\eta _{3}^{1}=1$, $\vartheta _{1}=8$, $\eta _{1}^{2}=10$, $\eta _{2}^{2}=1$, $\eta _{3}^{2}=1$, $\vartheta _{2}=9$, $\theta =0.2$

Remark 4.1

It can be seen from Examples 4.1 and 4.2 that the effect of Lévy noise does play an important role in achieving the finite-time synchronization of GONs. Obviously, all of the criteria about finite-time synchronization in [20,21,22,23] cannot be applied in Examples 4.1 and 4.2 since they all ignored the perturbation of jump process.

5 Conclusions

In this paper, the problem of finite-time synchronization for stochastic Markovian jumping GONs with time-varying delay and Lévy noise has been investigated. It is worthy to point out that vector form Lévy noise is introduced in GONs and the finite-time synchronization problem for GONs is studied for the first time. Since the previous results concerning finite-time stability theorem cannot be straightway used to deal with our problem, we have generalized the finite-time stability theorem from the case of pure-diffusion Brownian motion to jump-diffusion Lévy process. By means of the stochastic Lyapunov functional method and the finite-time stability theorem, the sufficient criteria of finite-time synchronization for GONs with appropriate control have been given in Theorem 3.1. Moreover, we also have obtained sufficient conditions of finite-time synchronization for GONs under three situations, i.e., GONs without time-varying delay, Markovian switching or Lévy jump, in Corollary 3.1, 3.2 and 3.3. Finally, two numerical examples have been presented to confirm our theoretical results. These results not only have covered the gap that finite-time synchronization problem of GONs was not considered, but also are helpful for understanding the synchronization phenomena in living organisms and engineering applications.