1 Introduction

Miller and Ross [27], Oldham and Spanier [29], and Podlubny [31] have developed continuous fractional calculus. The discrete fractional calculus, due to its widespread applications in various branches of science and engineering, has become the object of many research works [1,2,3, 7, 14, 20]. Recently discrete delta fractional calculus has been developed by Atici and Eloe [12, 13, 15], Goodrich [21,22,23], and Holm [24]. For recent developments in the theory of discrete fractional calculus, applications of Mittag-Leffler function and fractional integral inequalities, we refer to [4,5,6, 8, 9, 16, 19, 25, 26, 32].

The integral transforms, like Mellin, Laplace, Fourier, were applied to obtain the solution of differential equations. These transforms made effectively possible to change a signal in the time domain into that in the frequency s-domain in the field of Digital Signal Processing (DSP) [34]. The more recent applications of fractional Fourier transform in X-ray models and simulations are developed in [28, 30]. In [33], the forward complex DFT, written in polar form, is given by

$$ X(t)=\frac{1}{N}\sum_{n=0}^{N-1}x(n)e^{-j2\pi tn/N} $$
(1)

and it takes different labels depending on the nature of \(x[n]\). The DFT \(X(t)=\frac{1}{N}\Delta ^{-1}x(n) e^{-j2\pi tn/N}| _{0}^{N}\) follows from the basic difference identity \(\Delta ^{-1}x(t)| _{0}^{N}= \sum_{n=0}^{N-1}x(n)\) in [10]. Let ℓ be the time between two successive signals. Replacing \(\Delta ^{-1}\) by \(\Delta _{\ell }^{-1}\), integer n by real t and the sequence \(x(n)\) by a function \(x(\xi )\), we get a Generalized Discrete Fourier Transform (GDFT)

$$ X(t)=\frac{h}{N}\Delta _{h}^{-1}x(\xi )e^{-j2\pi tt/N}\bigg| _{0}^{N}. $$
(2)

When \(h=1\) and \(h\rightarrow 0\), the GDFT becomes DFT given in (1) and FT defined as \(g(t)=\int _{-\infty }^{\infty }e ^{-j2\pi tx/N}f(t)\,dt\), respectively [11, 18].

The article is organized as follows. In Sect.  2 , the basic concepts about delta and its inverse difference operators are presented. In Sect.  3 , one dimensional fractional frequency Fourier transform is defined and its properties with numerical verification are given. In Sect.  4 , some results on convolution and fractional Fourier transform are discussed. Section  5 presents the conclusion.

2 Preliminaries

Here, we present some basic definitions, notations, and preliminaries. Let us denote by \(s_{r}^{m}\) and \(S_{r}^{m}\) the Stirling numbers of first and second kind, respectively. Denote by \(\mathbb{R}=(-\infty , \infty )\), \(L(\mathbb{R})=\) the set of all Lebesgue integrable functions on \(\mathbb{R}\). Let \(h>0,m\) be the positive integer, ν be a fraction, and ω be the frequency.

The polynomial factorial is defined by \(t_{h}^{(m)}=t(t-h)(t-2h) \cdots (t-(m-1)h)\), the relation between the polynomial and polynomial factorials is given by

$$ (\mathrm{i})\quad t_{h}^{(m)} = {\sum _{r=1}^{m}s_{r}^{m}h^{m-r}t^{r}}, \quad\quad (\mathrm{ii}) \quad t ^{m} = \sum _{r=1}^{m}S_{r}^{m}h^{m-r}t_{h}^{(r)}. $$
(3)

Definition 2.1

Let \(u(t)\), \(t\in [0,\infty )\), be a real- or complex-valued function and \(h>0\) be a fixed shift value. Then the h-difference operator \(\Delta _{h}\) on \(u(t)\) is defined as follows:

$$ \Delta _{h} u(t) =\frac{ u(t+h) - u(t)}{h}, $$
(4)

and its infinite h-difference sum is defined by

$$ \Delta _{h}^{-1}u(t)=h\sum _{r=0}^{\infty }u(t+rh). $$
(5)

Definition 2.2

Let \(u(t)\) and \(v(t)\) be two real-valued functions defined on \((-\infty ,\infty )\), and if \(\Delta _{h} v(t)=u(t)\), then the finite inverse principle law is given by

$$ v(t)-v(t-mh)=h\sum_{r=1}^{m} u(t-rh), \quad m \in Z^{+}. $$
(6)

Definition 2.3

([17], p. 5, Definition 2.6)

For \(h>0\) and \(\nu \in R\), the falling h-polynomial factorial function is defined by

$$ t_{h}^{(\nu )}=h^{\nu } \frac{\varGamma (\frac{k}{h}+1)}{\varGamma ( \frac{k}{h}+1-\nu )}, $$
(7)

where \(k_{h}^{({0})}=1\) and \(\frac{k}{h}+1,\frac{k}{h}+1-\nu \notin \{0,-1,-2,-3,\ldots\}\), since the division at a pole yields zero.

Applying Definition 2.1, we get the modified identities as follows:

$$ \begin{gathered} (\mathrm{i})\quad \Delta _{h} t_{h}^{(m)} = mt_{h}^{(m-1)}, \qquad (\mathrm{ii}) \quad \Delta _{h}^{-1} t_{h}^{(m)} = \frac{t_{h}^{(m+1)}}{m+1}, \\ (\mathrm{iii})\quad \Delta _{h}^{-1}t^{m}= \sum_{r=1}^{m} \frac{S_{r}^{m}h^{m-r}k_{h}^{(r)}}{r+1}. \end{gathered} $$
(8)

Lemma 2.4

Let \(h>0\) and \(u(t)\), \(w(t)\) be real-valued bounded functions. Then

$$ \Delta _{h}^{-1} \bigl(u(t)w(t) \bigr)=u(t) \Delta _{h}^{-1}w(t)-\Delta _{h} ^{-1} \bigl(\Delta _{h}^{-1}w(t+h) \Delta _{h} u(t) \bigr). $$
(9)

Proof

Applying (4) on the product of two functions \(u(t)v(t)\), we get

$$ \Delta _{h} u(t)v(t) =\frac{ u(t+h)v(t+h) - u(t)v(t)}{h}. $$
(10)

Now the proof follows by adding and subtracting \(\frac{ u(t)v(t+h)}{h}\), then applying \(\Delta _{h}^{-1}\) on both sides. □

Lemma 2.5

Let \(t\in (-\infty , \infty )\), \(h>0\), and \(\nu >0\), then we have

$$ \Delta _{h}^{-1}e^{-i\omega ^{1/\nu }t}= \frac{he^{-i\omega ^{1/\nu }t}}{(e ^{-i\omega ^{1/\nu }h}-1)}. $$
(11)

Proof

The proof follows by taking \(u(t)=e^{-i\omega ^{1/ \nu }t}\) in Definition 2.1 and applying \(\Delta _{h}^{-1}\). □

Corollary 2.6

Let \(t\in (-\infty , \infty )\), \(h>0\), and \(\nu >0\), then we have

$$ \frac{he^{-i\omega ^{1/\nu }t}}{(e^{-i\omega ^{1/\nu }h}-1)}- \frac{he ^{-i\omega ^{1/\nu }(t-mh)}}{(e^{-i\omega ^{1/\nu }h}-1)}=h\sum _{r=1}^{m} e^{-i\omega ^{1/\nu }(t-rh)}. $$
(12)

Proof

The proof follows by equation (11) and the finite inverse principle law given in (6). □

Example 2.7

For the particular values \(\nu =0.6\), \(s=0.2\), \(t=4\), \(m=2\), and \(h=3\), (12) is verified by MATLAB. The coding is given by \(3\times \operatorname{symsum}(\exp (-i \times (0.2)^{(1/0.6)}\times (4-3\times r)),r,1,2)=(3\times \exp (-i \times (0.2)^{(1/0.6)}\times 4))/(\exp (-i\times (0.2)^{(1/0.6)}\times 3)-1)-(3\times \exp (-i\times (0.2)^{(1/0.6)}\times -2))/(\exp (-i\times (0.2)^{(1/0.6)}\times 3)-1)\).

Theorem 2.8

Let \(t\in (-\infty , \infty )\) and \(h>0\). Then we have

$$ \Delta _{h}^{-1} \bigl(t_{h}^{(m)}e^{\pm i\omega ^{1/\nu }t} \bigr)=\sum^{m} _{r=0}\frac{(-1)^{r}(m)_{1}^{(r)}h^{r+1}t_{h}^{(m-r)}e^{\pm i \omega ^{1/\nu }(t+rh)}}{(e^{\pm i\omega ^{1/\nu }h}-1)^{r+1}}. $$
(13)

Proof

Taking \(u(t)=t_{h}^{(1)}\), \(w(t)=e^{i\omega ^{1/ \nu }t}\) in (9) and using (3), we get

$$ \Delta ^{-1}_{h} \bigl(t^{(1)}_{h}e^{i\omega ^{1/ \nu }t} \bigr)=\frac{ht_{h}^{(1)}e^{i\omega ^{1/\nu }t}}{(e^{i\omega ^{1/ \nu }h}-1)}-\frac{h^{2} e^{i\omega ^{1/\nu }(t+h)}}{(e^{i\omega ^{1/ \nu }h}-1)^{2}}. $$

Taking \(u(t)=t_{h}^{(2)}\), \(w(t)=e^{i\omega ^{1/\nu }t}\) in (9) and using (3), we get

$$ \Delta ^{-1}_{h} \bigl(t^{(2)}_{h}e^{i\omega ^{1/ \nu }t} \bigr)=\frac{ht_{h}^{(2)}e^{i\omega ^{1/\nu }t}}{(e^{i\omega ^{1/ \nu }h}-1)}-\frac{2h^{2} t_{h}^{(1)} e^{i\omega ^{1/\nu }(t+h)}}{(e ^{i\omega ^{1/\nu }h}-1)^{2}}+\frac{2h^{3} e^{i\omega ^{1/\nu }(t+2h)}}{(e ^{i\omega ^{1/\nu }h}-1)^{3}}, $$

which can be expressed as

$$ \Delta _{h}^{-1} \bigl(t_{h}^{(2)}e^{i\omega ^{1/ \nu }t} \bigr)=\sum^{2}_{r=0}\frac{(-1)^{r}(2)_{1}^{(r)}h^{r+1}t _{h}^{(2-r)}e^{i\omega ^{1/\nu }(t+rh)}}{(e^{i\omega ^{1/\nu }h}-1)^{r+1}}. $$

Now (13) follows by continuing the above process and then replacing i by −i. □

Theorem 2.9

Let \(t\in (-\infty , \infty )\) and \(h>0\). If \(e^{\pm i\omega ^{1/\nu }h} \neq 1\), then we have

$$ \Delta _{h}^{-1} \bigl(t^{n}e^{\pm i\omega ^{1/\nu }t} \bigr)=\sum^{n}_{m=0}S _{m}^{n}h^{n-m} \sum^{m}_{r=0}\frac{(-1)^{r}(m)_{1}^{(r)}h^{r+1}t _{h}^{(m-r)}e^{\pm i\omega ^{1/\nu }(t+rh)}}{(e^{\pm i\omega ^{1/\nu }h}-1)^{r+1}}. $$
(14)

Proof

The proof follows from the second term of (3) and (13). □

Theorem 2.10

Let \(t\in (-\infty , \infty )\) and \(h>0\). If \(a^{h}e^{\pm i\omega ^{1/ \nu }h}\neq 1\), then

$$ \Delta _{h}^{-1} \bigl(a^{t} e^{\pm i\omega ^{1/\nu }t} \bigr)=\frac{ha^{t}e^{ \pm i\omega ^{1/\nu }t}}{(a^{h}e^{\pm i\omega ^{1/\nu }h}-1)}. $$
(15)

Proof

Since

$$ \Delta _{h}a^{t}e^{\pm i\omega ^{1/\nu }t}=\frac{a^{t+h}e^{\pm i \omega ^{1/\nu }(t+h)}-a^{t}e^{\pm i\omega ^{1/\nu }t}}{h}= \frac{a^{t}e ^{\pm i\omega ^{1/\nu }t}}{h} \bigl[a^{h}e^{\pm i\omega ^{1/\nu }(h)}-1 \bigr], $$

the proof follows by taking \(\Delta _{h}^{-1}\) on both sides. □

3 1D fractional frequency Fourier transform and its properties

In this section, we define and obtain the properties of one dimensional fractional frequency Fourier transform and present the transforms of certain functions like trigonometric, hyperbolic, polynomials, etc. We also obtain some properties of Fourier transforms.

Definition 3.1

The fractional frequency Fourier transform (FFFT) of \(u(t)\) is defined as follows:

$$ F_{h,\nu } \bigl(u(t) \bigr)=U(\omega )=\Delta _{h}^{-1}u(t)e^{-i\omega ^{1/\nu }t}\big| _{t=-\infty }^{\infty }, $$
(16)

and the inverse generalized discrete Fourier transform of \(U(s)\) is given by

$$ u(t)=\frac{1}{2\pi }\Delta _{h}^{-1}U( \omega )e^{i\omega ^{1/\nu }t}\bigg| _{\omega =-\infty }^{\infty }. $$
(17)

Similarly, the fractional frequency Fourier sine and cosine transforms of \(u(t)\) are defined as follows:

$$\begin{aligned}& _{s}{}F_{h,\nu }{ \bigl(u(t) \bigr)}=U_{s}(\omega )=\Delta _{h}^{-1}u(t)\sin \omega ^{1/\nu }t\big| _{t=0}^{\infty }, \end{aligned}$$
(18)
$$\begin{aligned}& {}_{c}F_{h,\nu }{ \bigl(u(t) \bigr)}=U_{c}(\omega )=\Delta _{h}^{-1}u(t)\cos \omega ^{1/\nu }t\big| _{t=0}^{\infty }. \end{aligned}$$
(19)

The inverse of Fourier sine and cosine transforms of the above are respectively given by

$$\begin{aligned}& u(t)=\frac{2}{\pi }\Delta _{h}^{-1}U_{s}( \omega )\sin \omega ^{1/ \nu }t\bigg| _{s=0}^{\infty }, \end{aligned}$$
(20)
$$\begin{aligned}& u(t)=\frac{2}{\pi }\Delta _{h}^{-1}U_{c}( \omega )\cos \omega ^{1/ \nu }t\bigg| _{s=0}^{\infty }. \end{aligned}$$
(21)

Let \(c_{1}\) and \(c_{2}\) be constants. From Definition 3.1, we can obtain the following linearity, change of scale, and shifting properties of fractional frequency Fourier transform.

Property 3.2

If \(F_{h,\nu }(u(t))=U(\omega )\) and \(F_{h,\nu }(v(t))=V(\omega )\), then

$$\begin{aligned}& (\mathrm{i}) \quad F_{h,\nu } \bigl(c_{1}u(t)+c_{2}v(t) \bigr)=c_{1}U(\omega )+c_{2}V(\omega ), \end{aligned}$$
(22)
$$\begin{aligned}& (\mathrm{ii}) \quad \textit{If } F_{h,\nu } \bigl(u(t) \bigr)=U(\omega ), \textit{then } F_{h,\nu } \bigl(u(at) \bigr)= \frac{1}{a}U \biggl(\frac{\omega }{a} \biggr), \end{aligned}$$
(23)
$$\begin{aligned}& (\mathrm{iii}) \quad \textit{If } {} _{s}{}F_{h,\nu } \bigl(u(t) \bigr)=U_{s}(\omega ), \textit{then } {}_{s}{}F_{h,\nu } \bigl(u(at) \bigr)=\frac{1}{a}U_{s} \biggl(\frac{\omega }{a} \biggr), \end{aligned}$$
(24)
$$\begin{aligned}& (\mathrm{iv}) \quad \textit{If } {}_{c}F_{h,\nu } \bigl(u(t) \bigr)=U_{c}(\omega ), \textit{then } {}_{c}F_{h,\nu } \bigl(u(at) \bigr)=\frac{1}{a}U_{c} \biggl(\frac{\omega }{a} \biggr). \end{aligned}$$
(25)

Example 3.3

Take \(u(t)=t_{h}^{(3)}\) for \(-4< t<4\). Then from (13) we get

$$\begin{aligned} F_{h,\nu } \bigl(t_{h}^{(3)} \bigr) =&U(\omega )= \Delta _{h}^{-1}t_{h}^{(3)}e^{-i \omega ^{1/\nu }t}\big| _{t=-4}^{4}=\sum^{3}_{r=0} \frac{(-1)^{r}(3)_{1} ^{(r)}h^{r+1}t_{h}^{(3-r)}e^{- i\omega ^{1/\nu }(t+rh)}}{(e^{- i \omega ^{1/\nu }h}-1)^{r+1}}\bigg| _{t=-4}^{4} \\ =& \frac{h4_{h}^{(3)}e^{-4i\omega ^{1/\nu }}}{(e^{-i\omega ^{1/\nu }h}-1)}-\frac{3h ^{2}4_{h}^{(2)}e^{-i\omega ^{1/\nu }(4+h)}}{(e^{-i\omega ^{1/\nu }h}-1)^{2}}+\frac{6h ^{3}4_{h}^{(1)}e^{-i\omega ^{1/\nu }(4+2h)}}{(e^{-i\omega ^{1/\nu }h}-1)^{3}}-\frac{6e ^{-i\omega ^{1/\nu }(4+3h)}}{(e^{-i\omega ^{1/\nu }h}-1)^{4}} \\ &{}- \frac{h(-4)_{h}^{(3)}e^{4i\omega ^{1/\nu }}}{(e^{-i\omega ^{1/\nu }h}-1)}+\frac{3h ^{2}(-4)_{h}^{(2)}e^{-i\omega ^{1/\nu }(-4+h)}}{(e^{-i\omega ^{1/\nu }h}-1)^{2}}-\frac{6h ^{3}(-4)_{h}^{(1)}e^{-i\omega ^{1/\nu }(-4+2h)}}{(e^{-i\omega ^{1/ \nu }h}-1)^{3}} \\ &{}+ \frac{6e^{-i\omega ^{1/\nu }(-4+3h)}}{(e^{-i \omega ^{1/\nu }h}-1)^{4}}. \end{aligned}$$
(26)

For particular values of \(\nu =0.5\), \(\omega =3\), and \(h=1\), we provide MATLAB coding for verification as follows: \(U(\omega ) = \operatorname{symsum} ((4-r)\times (3-r)\times (2-r)\times \exp (-i\times 3^{(1/0.5)} \times (4-r) ), r,1,8 ) = (24\times (\exp (-i\times 3^{(1/0.5)}\times 4 ) ) )/ ( (\exp (-i \times 3^{(1/0.5)} )-1 ) ) - (36\times (\exp (-i\times 3^{(1/0.5)}\times 5 ) ) )/ ( (\exp (-i \times 3^{(1/0.5)} )-1 )^{2} ) + (24\times (\exp (-i\times 3^{(1/0.5)}\times 6 ) ) )/ ( (\exp (-i\times 3^{(1/0.5)} )-1 )^{3} ) - (6\times (\exp (-i\times 3^{(1/0.5)} \times 7 ) ) )/ ( (\exp (-i\times 3^{(1/0.5)} )-1 )^{4} ) + (120\times (\exp (i \times 3^{(1/0.5)}\times 4 ) ) )/ ( (\exp (-i\times 3^{(1/0.5)} )-1 ) ) + (60 \times (\exp (i\times 3^{(1/0.5)}\times 3 ) ) )/ ( (\exp (-i\times 3^{(1/0.5)} )-1 )^{2} ) + (24 \times (\exp (i\times 3^{(1/0.5)}\times 2 ) ) )/ ( (\exp (-i\times 3^{(1/0.5)} )-1 )^{3} ) + (6 \times (\exp (i\times 3^{(1/0.5)} ) ) )/ ( (\exp (-i\times 3^{(1/0.5)} )-1 )^{4} )\).

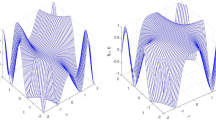
The outcomes are generated by MATLAB as diagrams. Figure  1 is the input function (signal) as polynomial factorial for the time factor t. Figure  2 is the fractional frequency Fourier transform in the frequency domain ω for the particular values of \(\omega =3\) and \(\nu =0.5\) which are generated. This shows that the signal runs smoothly in both real and imaginary parts of the frequency domain. One can generate functions easily by varying ω and ν to analyze the signal processing in the axis.

Figure 1
figure 1

Time domain \(\operatorname{Signal}(t)\)

Full size image
Figure 2
figure 2

Frequency (ω)

Full size image

4 Convolution product and fractional Fourier transform

In this section, we establish discrete convolution theorem and fractional Fourier transform based on generalized operator \(\Delta _{h}\). When \(h\rightarrow 0\), we get convolution theorem and Fourier transform.

Definition 4.1

Let u and v be two bounded functions on \((-\infty ,+\infty )\). Then the convolution of u and v is defined as

$$ w(x)=(u\circ v) (x)=\Delta _{h}^{-1}u(t)v(x-t)\big| _{t=- \infty }^{\infty }. $$
(27)

It is easy to see that \(u\circ v=v\circ u\).

Remark 4.2

When both u and v vanish on the negative real axis, \(v(x-t)=0\) if \(t>x\) and (27) becomes

$$ w(x)=(u\circ v) (x)=\Delta _{h}^{-1}u(t)v(x-t)\big| _{t=0}^{x}. $$
(28)

Theorem 4.3

Let \(\mathbb{R}=(-\infty ,\infty )\). Assume that \(u, v\in L( \mathbb{R})\) = set of all Lebesgue integrable functions on \(\mathbb{R}\) and that either u or v is bounded on \(\mathbb{R}\). Then the convolution

$$ w(x)=(u\circ v) (x)=\Delta _{h}^{-1}u(t)v(x-t)\big| _{-\infty }^{\infty } $$
(29)

exists for every x in \(\mathbb{R}\) and the function w so defined is bounded on \(\mathbb{R}\). If, in addition, the bounded function u or v is continuous on \(\mathbb{R}\), then w is also continuous on \(\mathbb{R}\) and \(w\in L(\mathbb{R})\).

Proof

Since \(u\circ v=v\circ u\), it suffices to consider the case in which v is bounded. Suppose \(\vert v \vert \leq M\). Then

$$ \bigl\vert u(t)v(x-t) \bigr\vert \leq M \bigl\vert u(t) \bigr\vert . $$
(30)

Since \(u(t)v(x-t)\) is a measurable function of t on \(\mathbb{R}\), from (27) and (30), we get \(\Delta _{\ell }^{-1} \vert u(t) v(x-t) \vert | _{-\infty }^{\infty }\leq M\Delta _{h}^{-1} \vert u(t) \vert | _{- \infty }^{\infty }\Rightarrow \vert w(x) \vert \leq M \Delta _{h}^{-1} \vert u(t) \vert | _{-\infty }^{\infty }\), which tells that w is bounded on \(\mathbb{R}\). Also, if v is continuous on \(\mathbb{R}\), then w is continuous on \(\mathbb{R}\). Now, for every compact interval \([a,b ]\), we have

$$\begin{aligned} \bigl(\Delta _{h}^{-1} \bigl\vert w(x) \bigr\vert \bigr)\big| _{a}^{b} \leq \Delta _{h}^{-1} \bigl\vert u(t) \bigr\vert _{-\infty }^{\infty }\Delta _{h}^{-1} \bigl\vert v(x-t) \bigr\vert _{a}^{b}\leq \Delta _{h}^{-1} \bigl\vert u(t) \bigr\vert _{-\infty }^{\infty }\Delta _{\ell }^{-1} \bigl\vert v(y) \bigr\vert _{-\infty }^{\infty }, \end{aligned}$$

where \(y=x-t\). □

Since w is bounded and continuous on \(\mathbb{R}\), \(w\in L(\mathbb{R})\).

5 Discrete convolution theorem for discrete Fourier transform

The following theorem illustrates the relation between convolution and Fourier transform.

Theorem 5.1

Assume that \(u,v\in L(\mathbb{R})\) and that at least one of u or v is continuous and bounded on \(\mathbb{R}\). Let h denote the convolution and \(w=u\circ v\). Then, for every real ν, we have

$$ \Delta ^{-1}_{h}w(x)e^{-ix\nu }\big| _{-\infty }^{\infty }= \bigl(\Delta ^{-1}_{h}u(t)e^{-it\nu } \bigr)\big| _{-\infty }^{\infty } \bigl(\Delta ^{-1}_{h}v(y)e^{-iy\nu } \bigr)\big| _{-\infty }^{\infty }. $$
(31)

Proof

Assume that v is continuous and bounded on \(\mathbb{R}\). Let \({a_{n}}\) and \({b_{n}}\) be two increasing sequences of positive real numbers such that \({a_{n}}\rightarrow +\infty \) and \({b_{n}}\rightarrow +\infty \). Define a sequence of functions \({u_{n}}\) on \(\mathbb{R}\) as \({u_{n}}(t)=\Delta ^{-1}_{h}e^{-ix \nu }v(x-t)| _{-a_{n}}^{b_{n}}\).

Since \(\vert \Delta ^{-1}_{h}e^{-ix\nu }v(x-t) \vert | _{-a_{n}}^{b_{n}}\leq \vert v \vert _{-\infty }^{\infty }\) for all compact intervals \([a,b]\). Now, for translation \(y=x-t\), we get

$$ \lim_{n\rightarrow \infty }u_{n}(t)=\Delta ^{-1}_{h}e ^{-ix\nu }v(x-t)\big| _{-\infty }^{\infty }= \Delta ^{-1}_{h}e ^{-i\nu (t+y)}v(y)\big| _{-\infty }^{\infty }. $$
(32)

By Lebesgue dominated convergence theorem,

$$ \lim_{n\rightarrow \infty }\Delta ^{-1}_{h}u(t)u_{n}(t)\Big| _{-\infty }^{\infty }= \bigl(\Delta ^{-1}_{h}u(t)e^{-it\nu } \bigr)\big| _{-\infty }^{\infty } \bigl(\Delta ^{-1}_{h}v(y)e^{-iy\nu } \bigr)\big| _{-\infty }^{\infty }. $$
(33)

But from (32) and (27), \(\lim_{n\rightarrow \infty }\Delta ^{-1}_{h}u(t)u_{n}(t)| _{- \infty }^{\infty }=\Delta ^{-1}_{h}e^{-ix\nu }w(x)| _{- \infty }^{\infty }\), which completes the proof. The discrete integral on the left also exists as an improper Riemann integral is continuous and bounded on \(\mathbb{R}\) and \(\Delta ^{-1}_{h} \vert w(x)e^{-ix \nu } \vert \leq \Delta ^{-1}_{h}w| _{-\infty }^{\infty }\) for every interval \([a,b]\). □

The following example provides the numerical verification of convolution and the solutions are analyzed by graphs.

Example 5.2

Consider the following functions:

$$ u(t)= \textstyle\begin{cases} a^{t} ,& \vert t \vert \leq 2, \\ 0,&\text{otherwise}, \end{cases}\displaystyle \qquad v(t)= \textstyle\begin{cases} e^{-i\omega ^{1/\nu }(x-t)} ,& \vert t \vert \leq 2, \\ 0, &\text{otherwise}. \end{cases} $$

Now from (27) we get \((u\circ v)(t) = \Delta _{h}^{-1}a^{t}e ^{-i\omega ^{1/\nu }t}| _{t=-2}^{2}\). Then, using (15) gives \((u\circ v)(t)=\frac{ha^{t}e^{\pm i\omega ^{1/\nu }t}}{(a^{h}e^{ \pm i\omega ^{1/\nu }h}-1)}| _{-2}^{2}\). By (6), we get

$$ (u\circ v) (t)=h\sum_{r=1}^{4}a^{2-rh}e^{-i\omega ^{1/\nu }(2-rh)}= \frac{ha ^{2}e^{\pm i\omega ^{1/\nu }2}}{(a^{h}e^{\pm i\omega ^{1/\nu }h}-1)}-\frac{ha ^{-2}e^{\pm i\omega ^{1/\nu }(-2)}}{(a^{h}e^{\pm i\omega ^{1/\nu }h}-1)}, $$
(34)

which is verified for the particular values \(h=3\), \(a=5\), \(\omega =0.3\), and \(\nu =0.2\) by MATLAB coding given below: \(\operatorname{symsum}(3\times 5^{(2-3 \times r)}\times \exp (-i\times (0.3)^{(1/0.2)}\times (2-r\times 3)),r,1,4)=75 \times \exp (-i\times (0.3)^{(1/0.2)}\times 2)/(125\times \exp (-i\times (0.3)^{(1/0.2)}\times 3)-1)-3 \times \exp (-i\times (0.3)^{(1/0.2)} \times -2)/(25\times (125\times \exp (-i\times (0.3)^{(1/0.2)}\times 3)-1))\).

6 Conclusion

In this work, we proved some properties and results with frequency fractional factor \(\omega ^{1/\nu }\) using the inverse difference operator. We defined one dimensional fractional frequency Fourier transform and its convolution. The biggest advantage of our findings is that, when \(h\rightarrow 0\) and \(\nu =1\), the one dimensional fractional frequency Fourier transform becomes the Fourier transform which exists in the literature. We believe that the new extension and definitions will be valuable for researchers to develop the models in Fourier transform. When the Fourier transform does not exist for any function (signal), we can apply one dimensional fractional Fourier transform using (5) and (16) and get several applications in the field of digital signal processing.