Abstract
Discrete Mittag-Leffler function of order 0 < α ≤ 1, , λ ≠ 1, satisfies the nabla Caputo fractional linear difference equation
Computations can show that the semigroup identity
does not hold unless λ = 0 or α = 1. In this article we develop a semigroup property for the discrete Mittag-Leffler function in the case α ↑ 1 is just the above identity. The obtained semigroup identity will be useful to develop an operator theory for the discrete fractional Cauchy problem with order α ∈ (0, 1).
Similar content being viewed by others
1 Introduction and Preliminaries
The fractional calculus started to be investigated deeply in both theorical and applied view points. One of the main reasons of the fast development of this type of calculus is that it incorporates, as a particular case, the classical calculus. Starting from this interesting point it is natural to ask if there is an extension of the fractional calculus and even more precisely if this generalization could find us new dimensions of some problems within the complex systems which up to now were not solved properly as in Biology, nanotechnology and medicine [1–6]. Mittag-Leffler functions play a very important role in the theory of fractional differential equations [1–4].
Recently there is a huge effort on the line of discretizing the fractional calculus operators and its applications in the control theory and the corresponding variational principles [9–17]. In our opinion the discrete fractional operators can play a crucial role both from the theoretical and applied point of view. However the combinations of the techniques from both fields are not always straithforward namely because the fractional operators are non-local. However, we expect that this new unification will provide new tools in understanding the hyper-complex dynamical systems.
In this article, the main aim is to establish a semi-group property for discrete Mittag-Leffler functions.
This article is organized as follows: The rest of this section contains definitions and preliminary concepts regarding the rising factorial function, the discrete Mittaf-Leffler functions, Caputo fractional difference and the discrete convolution. In Section 2, we find the nabla discrete transforms of certain discrete Mittag-Leffler functions by making use of the discrete convolution theorem, which will be helpful to proceed in obtaining our main results. Finally, Section 3 deals with a semigroup property for discrete Mittag-Leffler functions and some examples are given to illustrate our results.
For the sake of the nabla fractional calculus we have the following definition
Definition 1. (i) For a natural number m, the m rising (ascending) factorial of t is defined by
(ii) For any real number the α rising function is defined by
Regarding the rising factorial function we observe the following:
(i)
(ii)
where ρ(t) = t - 1.
Definition 2. The nabla discrete Laplace transform for a function f defined on is defined by
If f(t, s) is a function of two variables, we state explicitly to specify to which parameter we apply the transform.
Lemma 1. [11] For any ,
-
(i), |1 - z| < 1,
-
(ii), |1 - z| < b.
Definition 3. (Nabla Discrete Mittag-Leffler) For and α, β, with Re(α) > 0, the nabla discrete Mittag-Leffler functions are defined by
For β = 1, it is written that
Definition 4. For 0 < α ≤ 1 the α-order Caputo fractional derivative of a function f, which is defined on , is defined by
where ρ(s) = s - 1 and is the nabla left fractional sum of order α.
Note that if f is defined on , then is defined on .
Example 1. Let 0 < α ≤ 1, and consider the nabla left Caputo nonhomogeneous fractional difference equation
The solution of (8) has the form
Remark 1. If we solve the nabla discrete fractional system (8) with α = 1 and a0 = 1 we obtain the following solution
The first part of the solution is the nabla discrete exponential function . For the sake of more comparisons see reference ([18], p. 118).
Definition 5. Let , 0 < α < 1 and be a function. The nabla discrete convolution of with f is defined by
2 Discrete Laplace of Mittag-Leffler Type and Convolution Type Functions
Proposition 1. For any , and f defined on we have
Proof.
□
Lemma 2. Let f be defined on . Then
Proof.
□
Lemma 3. Let f be defined on and 0 < α ≤ 1. Then
Proof. By the help of Lemma 1, Proposition 1 and Lemma 2 we have
□
Lemma 4. Let 0 < α ≤ 1 and f be defined on . Then,
(i) .
(ii)
Proof. (i) From Example 1 we know that
Apply the nabla discrete Laplace transform to both sides, then Lemma 3 yields that
Hence, it follows.
-
(ii)
First it is easy to see that . If we apply
 and make use of (i) and Lemma 2, then we have that
and make use of (i) and Lemma 2, then we have that
□
3 A discrete Mittag-Leffler Semigroup Property
By direct calculations it can be showed that the following semigroup property for discrete Mittag-Leffler functions
does not hold unless λ = 0 or α = 1. For more consistency, we next show how certain discrete Mittag-Leffler functions do not satisfy the above mentioned semigroup property.
Example 2. For 0 < α ≤ 1 and λ ≠ 1 we have
and
Then, clearly
Theorem 1. For every real λ and 0 < α < 1 the following holds
for all t, .
Proof. For the sake of simplicity we set . By Definition 4 we have that for all t, ,
In the last equality the fact that solves Eq.(8) is used. Applying the nabla discrete transform 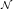 with respect to t to both sides of (18), we get by Lemma 3 that
with respect to t to both sides of (18), we get by Lemma 3 that
where and are the nabla discrete transforms of f(t + s) and with respect to t, respectively. By applying the nabla summation by parts and making use of (4) we have that
By Lemma 1 (i), we arrive at
which combining with the equality (19) leads to that
Then applying the inverse nabla discrete Laplace transform to both sides of (22), we get that
Arranging the limit of the sum in the left hand sum of (23) and making use of Proposition 1 it follows that
Splitting the sum in the left hand side of (24) yields directly equality (17).
□
Remark 2. We note that for α = 1, the summations in (17) are divergent. However, it can be shown that the semigroup property for is just the limit case state of equality (17) as α↑ 1. Indeed, if we multiply both sides of (17) with (1 - α) and use summation by parts, then, letting α ↑ 1 we get that the limit state of the left is and of the right is .
References
Miller KS, Ross B: Fractional difference calculus. In Proceedings of the International Symposium on Univalent Functions, Fractional Calculus and Their Applications. Nihon University, Koriyama, Japan; 1989:139–152.
Podlubny I: Fractional Differential Equations. Academic Press: San Diego CA; 1999.
Samko G, Kilbas AA: Marichev, Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach, Yverdon; 1993.
Kilbas A, Srivastava MH, Trujillo JJ: Theory and Application of Fractional Differential Equations. North Holland Mathematics Studies; 2006:204.
Magin RL: Fractional Calculus in Bioengineering. Begell House Publisher, Inc. Connecticut; 2006.
Baleanu D, Diethelm K, Scalas E, Trujillo JJ: Fractional Calculus Models and Numerical Methods (Series on Complexity, Nonlinearity and Chaos). World Scientific; 2012.
Abdeljawad T: On Riemann and Caputo fractional differences Original Research Article Computers and Mathematics with Applications. 2011, 62(3):1602–1611.
Abdeljawad T: Principles of delta and nabla fractional differences. 2011. arXiv:1112.5795v1
Atıcı FM, Eloe PW: A Transform method in discrete fractional calculus. International Journal of Difference Equations 2007, 2(2):165–176.
Atıcı FM, Eloe PW: Initial value problems in discrete fractional calculus. Proceedings of the American Mathematical Society 2009, 137: 981–989.
Atıcı FM, Eloe PaulW: Discrete fractional calculus with the nabla operator. Electronic Journal of Qualitative Theory of Differential equations, Spec Ed I 2009, (3):1–12.
Atıcı FM, şengül S: Modelling with fractional difference equations. Journal of Mathematical Analysis and Applications 2010, 369: 1–9. 10.1016/j.jmaa.2010.02.009
Bastos NunoRO, Ferreira RuiAC, Torres DelfimFM: Discrete-time fractional variational problems. Signal Processing 2011, 91(3):513–524. 10.1016/j.sigpro.2010.05.001
Gray HL, Zhang NF: On a new definition of the fractional difference. Math-ematicsof Computaion 1988, 50(182):513–529.
Anastassiou GA: Principles of delta fractional calculus on time scales and inequalities. Mathematical and Computer Modelling 2010, 52: 556–566. 10.1016/j.mcm.2010.03.055
Anastassiou GA: Foundations of nabla fractional calculus on time scales and inequalities. Computer and Mathematics with Applications 2010, 59: 3750–3762. 10.1016/j.camwa.2010.03.072
Abdeljawad T, Baleanu D: Fractional Differences and integration by parts. Journal of Computational Analysis and Applications 2011, 13(3):574–582.
Bohner M, Peterson A: Advances in Dynamic Equations on Time Scales. Birkhäuser, Boston; 2003.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
TA wrote the first draft of the paper, FJ has corrected this draft, DB has prepared the final version of the work and enhanced the revised version of the manuscript. The authors read carefully and approved the final version of the manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Abdeljawad, T., Jarad, F. & Baleanu, D. A semigroup-like Property for Discrete Mittag-Leffler Functions. Adv Differ Equ 2012, 72 (2012). https://doi.org/10.1186/1687-1847-2012-72
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1847-2012-72



