Control optimization and homoclinic bifurcation of a prey–predator model with ratio-dependent

Abstract

In this paper, a predator–prey model with ratio-dependent and impulsive state feedback control is constructed, where the pest growth rate is related to an Allee effect. Firstly, the existence condition of the homoclinic cycle is obtained by analyzing the control parameter q. The existence, uniqueness and asymptotic stability of the periodic orbit are discussed by using the geometric theory of the differential equations, the method of successor functions and analog of the Poincaré criterion. Secondly, we formulate a control optimization with a minimal total cost in pest management, and we obtain an optimal economic threshold. Finally, we verify the main results by numerical simulation.

1 Introduction

Differential equations can be applied extensively in many fields, including economic development, environmental protection, population ecology, infectious diseases and pharmacokinetics, and the cultivation of micro-organisms [1,2,3,4,5,6]. In [3], Cui et al. proposed the fractional differential equations and analyzed the uniqueness of solution for boundary value problems. Many researchers have obtained very good achievements in the field of stochastic differential equations [7,8,9,10,11,12].

In recent decades, many researchers have found that the occurrence of some biological phenomena and the optimal control of some life phenomena were not continuous processes, but the transient behavior of an impulse, so we should use impulsive differential equations to describe these phenomena. The theory of impulsive differential equations is proposed on the basis of continuous differential equation theory, which is difficult but valuable. It is widely applied in the harvest description [13,14,15,16], ecological resources [17,18,19,20,21,22,23,24,25,26], pest control [27,28,29,30,31] and epidemiologic control [32,33,34,35,36]. Many scholars investigated state-dependent pulse differential equations in predator–prey model to simulate the pest management including the periodic release of natural enemies [37,38,39] and the periodic release of natural enemies combined with periodic spraying of pesticides [40,41,42,43,44,45,46]. On the other hand, the bifurcation theory has been widely applied in the continuous dynamic system [47,48,49]. However, its application in impulsive dynamical system was little.

In [50], Zhang et al. proposed a predator–prey model with multi-state pulse feedback control as follows:

$$ \textstyle\begin{cases} \left . \textstyle\begin{array}{l} {\frac{dx(t)}{dt}=x(t) [r\ln \frac{K}{x(t)}-\rho y(t) ],} \\ {\frac{dy(t)}{dt}= [\mu \rho x(t)-d ]y(t),} \end{array}\displaystyle \right \} \quad x\neq h_{1},h_{2},\text{or }x=h_{1},y>y_{ML}, \\ \left . \textstyle\begin{array}{l} {\triangle x=0,} \\ {\triangle y=\zeta ,} \end{array}\displaystyle \right \} \quad x=h_{1},y\leq y_{ML}, \\ \left . \textstyle\begin{array}{l} {\triangle x=-px(t),} \\ {\triangle y=-qy(t)+\tau ,} \end{array}\displaystyle \right \} \quad x=h_{2}, \end{cases} $$

(1)

where $h_{1}$ and $h_{2}$ are the biological control level (i.e. the threshold with slight damage to the crops) and the chemical control level (i.e. pest economic injury threshold), respectively. $y_{\mathrm{ML}}$ represents the predator maintainable level at $x=h_{1}$. It is interesting and practically significant to involve chemical and biological controls at different economic thresholds, but there is a key problem to be identified in the model. Biological control can be adopted at $x=h_{1}$ and $y< y_{\mathrm{ML}}$, but for a higher pest density $x=h$, where $h_{1}< h< h_{2}$, there no control strategy is adopted, therefore the model is not flawless.

Based on above the factors, we propose a ratio-dependent predator–prey system with an integrated control strategy as follows:

$$ \textstyle\begin{cases} \left . \textstyle\begin{array}{l} {\frac{dx_{1}(t_{1})}{dt_{1}}=rx_{1}(t_{1}) [x_{1}(t_{1})-\alpha _{1} ] [1-\frac{x_{1}(t_{1})}{K} ] -\frac{mx_{1}(t _{1})y_{1}(t_{1})}{x_{1}(t_{1})+mby_{1}(t_{1})},} \\ {\frac{dy_{1}(t_{1})}{dt_{1}}= [-\beta _{1}+\frac{cmx_{1}(t_{1})}{x _{1}(t_{1})+mby_{1}(t_{1})} ]y_{1}(t_{1}),} \end{array}\displaystyle \right \} \quad x_{1}< h', \\ \left . \textstyle\begin{array}{l} {\triangle x_{1}(t_{1})=-p_{1}(x_{1})x_{1}(t_{1}),} \\ {\triangle y_{1}(t_{1})=-q_{1}(x_{1})y_{1}(t_{1})+\tau _{1}(x_{1}),} \end{array}\displaystyle \right \} \quad x_{1}=h',y_{1}\leq h_{h}', \end{cases} $$

(2)

where $\Delta x_{1}(t_{1})=x_{1}(t_{1}^{+})-x_{1}(t_{1})$, $\Delta y _{1}(t_{1})=y_{1}(t_{1}^{+})-y_{1}(t_{1})$, $x_{1}$ and $y_{1}$ represent the density of the prey and predator at time $t_{1}$, respectively. r denotes the intrinsic rate growth of pests. $h'\in [h_{1}',h_{2}']$ represents the threshold of pests, where $h_{1}'$ and $h_{2}'$ are biological control level and chemical control level, respectively. $K>0$ represents the environment carrying capacity of pests. m denotes the attack rate of predator. b denotes the handling time of a single pest by natural enemies. c is the conversion ratio of consumed pests into viable natural enemy offspring. $\beta _{1}$ is the death rate of predator. The parameter $\alpha _{1}$ represents the survival threshold of the pest population for the Allee effect. $0<\alpha _{1}<K$ is the survival threshold of the pest population for the strong Allee effect, $-K<\alpha _{1}<0$ is the survival threshold of the pest population for the weak Allee effect. In this paper, only $0<\alpha _{1}<K$ is taken into consideration. For reducing the parameters, we nondimensionalize system (2) with the following scaling:

$$ \frac{x_{1}}{K}=x, \quad\quad \frac{mby_{1}}{K}=y, \quad\quad rKt_{1}=t, $$

then the following form can be obtained:

$$ \textstyle\begin{cases} \left . \textstyle\begin{array}{l} {\frac{dx(t)}{dt}=x(t) [x(t)-\alpha ] [1-x(t) ]-\frac{ \lambda x(t)y(t)}{x(t)+y(t)}}, \\ {\frac{dy(t)}{dt}=\frac{\lambda _{1}x(t)y(t)}{x(t)+y(t)}-\beta y(t),} \end{array}\displaystyle \right \}\quad x< h, \\ \left . \textstyle\begin{array}{l} {\triangle x(t)=-p(x)x(t),} \\ {\triangle y(t)=-q(x)y(t)+\tau (x),} \end{array}\displaystyle \right \} \quad x=h,y\leq y_{h}, \end{cases} $$

(3)

where $\alpha =\frac{\alpha _{1}}{K}$, $\lambda =\frac{1}{rbK}$, $\lambda _{1}=\frac{cm}{rK}$, $\beta =\frac{\beta _{1}}{rK}$, $\tau =\frac{mb\tau _{1}}{K}$, $h=\frac{1}{K}h'$, $h_{1}=\frac{1}{K}h _{1}'$, $h_{2}=\frac{1}{K}h_{2}'$, and they are all positive constants. We can refer to [51, 52] for the analysis of the term $\frac{xy}{x+y}$ at $O(0,0)$. The parameters $p(x)$, $q(x)$, $\tau (x)$ are continuous functions defined on $[h_{1},h_{2}]$, where $\tau (h_{1})=\tau _{\max }$, $\tau (h_{2})=\tau _{\min }$, $p(h_{1})=0$, $p(h_{2})=p_{\max }$, $q(h_{1})=0$, $q(h_{2})=q_{\max }$. In this paper, the functions p, q, τ are defined in a linear form [53], i.e.

$$ \textstyle\begin{cases} p(x)=p_{\max }\frac{x-h_{1}}{h_{2}-h_{1}},\quad p_{\max }\in [0,1), \\ q(x)=q_{\max }\frac{x-h_{1}}{h_{2}-h_{1}},\quad q_{\max }\in [0,1), \\ \tau (x)=\tau _{\max }-(\tau _{\max }-\tau _{\min })\frac{x-h_{1}}{h_{2}-h _{1}}. \end{cases} $$

(4)

The organizational structure of this article is as follows. In Sect. 2, the existence of homocilinic cycle and existence, uniqueness and asymptotic stability of the periodic orbit of system (3) are proved. Furthermore, the optimization problem is formulated to reduce the total cost of pest control (i.e. the predator and the spraying agent). In Sect. 3, the numerical simulation of the concrete model is gradually carried out to verify the theoretical results. The final conclusion is drawn in Sect. 4.

2 Dynamical analysis of system (3)

2.1 Equilibria

Without impulse effect, system (3) becomes the following:

$$ \textstyle\begin{cases} {\frac{dx}{dt}=x(x-\alpha )(1-x)-\frac{\lambda xy}{x+y},} \\ {\frac{dy}{dt}=\frac{\lambda _{1}xy}{x+y}-\beta y.} \end{cases} $$

(5)

Theorem 2.1

([51])

System (5) has five equilibria: origin $O(0,0)$, two boundary equilibria: $N_{1}(\alpha ,0)$ and $N_{2}(1,0)$ and two positive equilibria: $E_{1}(x_{1},y_{1})$ and $E_{2}(x_{2},y _{2})$, where $x_{1}=\frac{1+\alpha -\sqrt{(1-\alpha )^{2}-4\lambda (1-\frac{\beta }{\lambda _{1}})}}{2}$, $y_{1}=\frac{(\lambda _{1}- \beta )x_{1}}{\beta }$, $x_{2}=\frac{1+\alpha +\sqrt{(1-\alpha )^{2}-4 \lambda (1-\frac{\beta }{\lambda _{1}})}}{2}$, $y_{2}=\frac{(\lambda _{1}-\beta )x_{2}}{\beta }$.

If $(H_{1})$ $x(t_{0})=x_{0}<\alpha$, $y(t_{0})=y_{0}>0$ holds, then the equilibrium $O(0,0)$ of system (5) is stable.

If $(H_{2})$ $\lambda _{1}>\beta$ holds, then the equilibrium $N_{1}$ is an unstable node and $N_{2}$ is a saddle point.

If $(H_{3})$ $\lambda _{1}<\beta$ holds, then the equilibrium $N_{1}$ is a saddle point and $N_{2}$ is a stable node.

If $(H_{4})$ $\lambda _{1}>\beta >\frac{\alpha _{1}}{4\lambda }[4\lambda -(1-\alpha )^{2}]>0$ holds, then equilibria $E_{1}$ and $E_{2}$ are positive equilibria.

If $(H_{5})$ $\operatorname{Tr}(J(E_{2}))=x_{2}(1+\alpha -2x_{2})+\frac{\beta ( \lambda -\lambda _{1})(\lambda _{1}-\beta )}{\lambda _{1}^{2}}<0$ holds, then point $E_{1}$ is a saddle point and point $E_{2}$ is a locally asymptotically stable node or focus (see Fig. 1).

Figure 1

Phase diagram of system (5) with $a=0.1$, $\lambda =0.5$, $\beta =0.55$, $\lambda _{1}=0.8$

2.2 Existence of the order one periodic orbit and homoclinic cycle of system (3)

By using the geometric theory of differential equations and the method of successor function, the existence of the order one periodic orbit and homoclinic cycle of system (3) is investigated in this section. For the actual biological significance, we always suppose that $\max \{\frac{1+\alpha -\sqrt{(1-\alpha )^{2}-4\lambda (1-\frac{ \beta }{\lambda _{1}})}}{2},h_{1}\}<(1-p)h<h<\min \{\frac{1+\alpha +\sqrt{(1- \alpha )^{2}-4\lambda (1-\frac{\beta }{\lambda _{1}})}}{2},h_{2}\}$ and conditions $(H_{4})$, $(H_{5})$ hold in the paper.

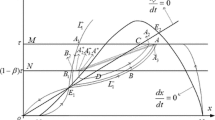
Set $M=\{(x,y)|x=h,0\leq y\leq y_{h}\}$ is called an impulsive set and set $N=\{(x,y)|x=(1-p)h,\tau \leq y\leq (1-q)y_{h}+\tau \}$ is called a phase set. For convenience, for any point L, let $x_{L}$ and $y_{L}$ denote its abscissa and ordinate, respectively. I is a continuous mapping which satisfies $I(M)=N$ and which is called an impulsive function. If $L(h,y_{L})\in M$, then the impulse function transfers the point L into $L^{+}$. We denote function $F(J)=J^{-}$ as the trajectory starting from the point $J\in N$ hits the impulse set M at the point $J^{-}$. In this paper, the tendency of trajectory is assumed to start from phase set. The unstable manifold and stable manifold of $E_{1}$ are denoted as $T_{1}^{-}(t,E_{1})$ and $T_{1}^{+}(t,E_{1})$, respectively. At time t, $T_{1}^{-}(t,E_{1})$ intersects phase set N at point $A_{1}$ and impulsive set M at point $B_{1}$. At time t, $T_{1}^{+}(t,E_{1})$ intersects phase set N at point $A_{2}$ and impulsive set M at point $B_{2}$. Isocline $\varGamma _{1}$: $\frac{dy}{dt}=0$ intersects phase set N at point A and impulsive set M at point B, where $y_{A}=\frac{h(1-p)( \lambda _{1}-\beta )}{\beta }$ and $y_{B}=\frac{(\lambda _{1}-\beta )h}{ \beta }$. The function $\varphi (y,q)=(1-q)y+\tau$ is monotonically decreasing about q, and monotonically increasing about y, thus there must exist a value $q_{*}\in (0,1)$ such that point B jumps to A after the impulse effect, i.e. $\varphi (y_{B},q_{*})=(1-q_{*})y _{B}+\tau =y_{A}$, we have $q_{*}=p+\frac{\beta \tau }{(\lambda _{1}- \beta )h}$, for convenience, we set $\delta =p+\frac{\beta \tau }{( \lambda _{1}-\beta )h}$. For any $q\in (0,1)$, the existence of order one periodic orbit of system (3) is to be proved in the cases of $0< q\leq \delta$ and $\delta < q<1$, respectively (see Fig. 2).

Figure 2

Illustration of system (5)

Case I $0< q\leq \delta$.

Theorem 2.2

• (a) If conditions $(H_{4})(H_{5})$ and $q=\delta$ hold, then system (3) admits a unique order one periodic orbit.

• (b) If conditions $(H_{4})(H_{5})$ and $0< q^{*}< q< q^{0}<\delta <1$ hold, then system (3) admits a unique order one periodic orbit.

Proof

The trajectory starting from the point $A\in N$ hits the point $B\in M$, then point $B\in M$ jumps to point $B^{+}$ after impulsive effect.

(a) Firstly, we prove the existence of the order one periodic orbit of system (3) in the case of $q=\delta$. In this case, $B^{+}$ coincides with point A, that is, $\widehat{AB}$ and $\overline{BA}$ constitute the order one periodic orbit.

(b) In this case, $B^{+}$ is above A. According to the impulsive equations of system (3), there surely has a value $q^{*} \in (0,\delta )$ satisfying $\varphi (y_{B_{1}},q^{*})=(1-q^{*})y_{B _{1}}+\tau =y_{A_{2}}$, that is, point $B_{1}$ jumps to point $A_{2}$ after impulse effect, also, there surely has a value $q^{0}\in (q^{*},\delta )$ satisfying $\varphi (y_{B_{1}},q^{0})=(1-q ^{0})y_{B_{1}}+\tau =y_{A}$. For any $q\in (q^{*},q^{0})$, point $B_{1}$ jumps to point $B_{1}^{+}$ after impulsive effect, we have $(1-q^{0})y_{B_{1}}+\tau =y_{A}<(1-q)y_{B_{1}}+\tau =y_{B_{1}^{+}}<(1-q ^{*})y_{B_{1}}+\tau =y_{A_{2}}$, that is, $y_{A}< y_{B_{1}^{+}}< y_{A _{2}}$. There must exist a trajectory going through point $B_{1}^{+}$ and intersecting the line $x=h$ at point $C_{1}$, and $I(C_{1})=C_{1} ^{+}$. In view of the disjointness of any two trajectories and the vector field of system (3), we have $y_{B_{1}}< y_{C_{1}}< y _{B}$, $(1-q)y_{B_{1}}+\tau =y_{B_{1}^{+}}<(1-q)y_{C_{1}}+\tau =y_{C _{1}^{+}}$, that is, $y_{C_{1}^{+}}>y_{B_{1}^{+}}$. Thus the successor function [54, Definition 3.3] of $B_{1}^{+}$: $g(B_{1} ^{+})=y_{C_{1}^{+}}-y_{B_{1}^{+}}>0$.

A point $C((1-p)h, y_{A_{2}}-\varepsilon )$ is selected in set N, where $\varepsilon >0$ is small enough, then point C is fully close to point $A_{2}$. Set $F(C)=C_{2}\in M$, we have $y_{C_{2}}>y_{B_{1}}$ due to continuous dependence of the solution on initial value and time, and $C_{2}$ is close enough to point $B_{1}$. Thus we have $y_{C_{2} ^{+}}>y_{B_{1}^{+}}$, and point $C_{2}^{+}$ is close enough to point $B_{1}^{+}$, then we have $y_{C_{2}^{+}}< y_{C}$, that is, $g(C)=y_{C _{2}^{+}}-y_{C}<0$. According to [54, Lemma 3.2, 3.3], there has a point $P\in (B_{1}^{+},C)$ such that $g(P)=0$, i.e. system (3) admits the order one periodic orbit, whose initial point is between point $B_{1}^{+}$ and point C in the set N (see Fig. 3(a)).

Figure 3

The existence and uniqueness of the order one periodic orbit of system (3) in case I. (a) The existence of the order one periodic solution of system (3). (b) The uniqueness of the order one periodic orbit of system (3)

Next, we prove the uniqueness of the order one periodic orbit of system (3). We arbitrarily select two points K and Q in the $\overline{AA_{2}}$, where $y_{A}< y_{K}< y_{Q}< y_{A_{2}}$. Set $F(K)=K_{1}\in M$, $F(Q)=Q_{1}\in M$, then we have $y_{Q_{1}}< y_{K_{1}}$, and $K_{1}$ and $Q_{1}$ are, respectively, mapped to $K_{1}^{+}\in N$ and $Q_{1}^{+}\in N$ after the impulse effect, then the successor functions of K, Q satisfy

$$\begin{aligned} g(K)-g(Q) =&(y_{K_{1}^{+}}-y_{K})-(y_{Q_{1}^{+}}-y_{Q}) \\ =&(y_{Q}-y_{K})+(y_{K_{1}^{+}}-y_{Q_{1}^{+}}) \\ =&(y_{Q}-y_{K})+(1-q)y_{K_{1}}+\tau -(1-q)y_{Q_{1}}-\tau \\ =&(y_{Q}-y_{K})+(1-q) (y_{K_{1}}-y_{Q_{1}})>0. \end{aligned}$$

Thus the successor function is monotonically increasing in the $\overline{AA_{2}}$, then there is only one point $P\in (A,A_{2})$ such that $g(P)=0$, i.e. system (3) has only an order one periodic orbit when q satisfies $0< q<\delta$ (see Fig. 3(b)). This completes the proof. □

Theorem 2.3

If conditions $(H_{4})$ and $(H_{5})$ and $q=q^{*}$ hold, then system (3) admits an order one homoclinic cycle; if $q\in (0,q^{*})$, system (3) does not admit an order one periodic orbit and the pests and natural enemy population will become extinct.

Proof

When $q=q^{*}$, we have $\varphi (y_{B_{1}}, q_{*})=(1-q^{*})y_{B_{1}}+ \tau =y_{A_{2}}$, then the closed curve $\overline{B_{1}A_{2}}\cup \widehat{A_{2}E_{1}}\cup \widehat{E_{1}B_{1}}$ forms a cycle which passes through the saddle $E_{1}$. Thus system (3) admits an order one homoclinic cycle (see Fig. 4).

Figure 4

The order one homoclinic cycle of system (3) in case I

When $q\in (0,q^{*})$, we have $(1-q)y_{B_{1}}+\tau =y_{B_{1}^{+}}>(1-q ^{*})y_{B_{1}}+\tau =y_{A_{2}}$ and the trajectory of system (3) starting from $B_{1}^{+}$ will tend to origin when $t\rightarrow +\infty$, and it has no impulse effect. Thus system (3) has no order one periodic orbit and the pest and natural enemy population will become extinct. This completes the proof. □

Case II $\delta < q<1$.

Theorem 2.4

If the conditions $(H_{4})(H_{5})$ and $\delta < q<1$ hold, then the system (3) admits the order one periodic orbit.

Proof

In this case, we know that $B^{+}$ is below A. Set $F(B^{+})=S_{1} \in M$, according to the property of orbit of system (3), we know $y_{B}>y_{S_{1}}$, thus we have $y_{B^{+}}>y_{S_{1}^{+}}$, then the successor function of point $B^{+}$ is $g(B^{+})=y_{S_{1}^{+}}-y_{B ^{+}}<0$. A point $H((1-p)h,\varepsilon )\in N$ is selected, where $\varepsilon <\tau$, and set $F(H)=H_{1}\in M$, after impulsive effect, point $H_{1}$ jumps to $H_{1}^{+}$, then $y_{H_{1}^{+}}=(1-q)y_{H_{1}}+ \tau >\varepsilon$, that is, $y_{H_{1}^{+}}>y_{H}$, thus we have $g(H)=y_{H_{1}^{+}}-y_{H}>0$. By [54, Lemma 3.2, 3.3], there exists a point $P\in (H,B^{+})$ satisfying $g(P)=0$, that is, system (3) admits the order one periodic orbit, whose initial point is between H and $B^{+}$ in the set N. This completes the proof (see Fig. 5).

Figure 5

The existence of the order one periodic orbit of system (3) in case II

 □

2.3 Stability of the order one periodic orbit of system (3)

Next, we study the stability of the order one periodic orbit of system (3).

Theorem 2.5

If conditions $(H_{4})$, $(H_{5})$, and $(1-\alpha )+\frac{\lambda h}{ \alpha }-\frac{\lambda _{1}\alpha y_{1}}{(1+h)^{2}}<0$ and $\vert \chi \vert <1$ hold, then the order one periodic orbit of system (3) is orbitally asymptotically stable, where

$$ \chi =\frac{ [(1-p)h-\alpha ] [1-(1-p)h ](h+ \eta _{1})}{(h-\alpha )(1-h)(h+\eta _{1})-\lambda \eta _{1}}. $$

Proof

Let $x=\xi (t)$, $y=\eta (t)$ be a T-periodic orbit of system (3) and $\xi _{1}=\xi (T)=h$, $\eta _{1}=\xi (T)$, $\xi _{0}= \xi (0)$, $\eta _{0}=\eta (0)$, $\xi _{1}^{+}=\xi (T^{+})$, $\eta _{1}^{+}= \eta (T^{+})$, then we have

$$ \xi _{1}^{+}=\xi _{0}=(1-p)h, \quad\quad \eta _{1}^{+}=\eta _{0}=(1-q)\eta _{1}+\tau . $$

Let $P(x,y)=x(x-\alpha )(1-x)-\frac{\lambda xy}{x+y}$, $Q(x,y)=\frac{ \lambda _{1}xy}{x+y}-\beta y$, $\varPhi (x,y)=-px$, $\varPsi (x,y)=-qy+ \tau$, $\varUpsilon (x,y)=x-h$.

Then

$$\begin{aligned}& \frac{\partial \varPhi }{\partial x}=-p, \quad\quad \frac{\partial \varPsi }{\partial x}=0, \quad\quad \frac{\partial \varPhi }{\partial y}=0,\quad\quad \frac{\partial \varPsi }{ \partial y}=-q, \quad\quad \frac{\partial \varUpsilon }{\partial x}=1, \frac{\partial \varUpsilon }{\partial y}=0, \\& \begin{aligned} \Delta _{1} &=\frac{P_{+}(\frac{\partial \varPsi }{\partial y}\frac{ \partial \varUpsilon }{\partial x}-\frac{\partial \varPsi }{\partial x}\frac{ \partial \varUpsilon }{\partial y}+\frac{\partial \varUpsilon }{\partial x})+Q _{+}(\frac{\partial \varPhi }{\partial x}\frac{\partial \varUpsilon }{ \partial y}-\frac{\partial \varPhi }{\partial y}\frac{\partial \varUpsilon }{\partial x}+\frac{\partial \varUpsilon }{\partial y})}{P\frac{\partial \varUpsilon }{\partial x}+Q\frac{\partial \varUpsilon }{\partial y}} \\ &=\frac{P(\xi _{1}^{+},\eta _{1}^{+})(-q\times 1-0\times 0+1)+Q(\xi _{1}^{+},\eta _{1}^{+})(-p\times 0-0\times 1+0)}{P(\xi _{1},\eta _{1}) \times 1+Q(\xi _{1},\eta _{1})\times 0} \\ &=\frac{(1-q)\xi _{0} [(\xi _{0}-\alpha )(1-\xi _{0})-\frac{\lambda \eta _{0}}{\xi _{0}+\eta _{0}} ]}{\xi _{1} [(\xi _{1}-\alpha )(1- \xi _{1})-\frac{\lambda \eta _{1}}{\xi _{1}+\eta _{1}} ]}, \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \int _{0}^{T}\biggl(\frac{\partial P}{\partial x}+ \frac{\partial Q}{\partial y}\biggr) =& \int _{0}^{T} \biggl[(x-\alpha ) (1-x)- \frac{\lambda y}{x+y}+\frac{ \lambda _{1}x}{x+y}-\beta \biggr]\,dt \\ & {} + \int _{0}^{T} \biggl[x(1+\alpha -2x)+ \frac{\lambda xy}{(x+y)^{2}}-\frac{ \lambda _{1}xy}{(x+y)^{2}} \biggr]\,dt \\ =& \int _{0}^{T} \biggl[\frac{\dot{x}(t)}{x(t)}+ \frac{\dot{y}(t)}{y(t)} \biggr]\,dt+ \int _{0}^{T} \biggl[x(1+\alpha -2x)+ \frac{\lambda xy}{(x+y)^{2}}-\frac{ \lambda _{1}xy}{(x+y)^{2}} \biggr]\,dt \\ =&\ln \frac{x(T)y(T)}{x(0)y(0)}+ \int _{0}^{T} \biggl[x(1+\alpha -2x)+ \frac{ \lambda xy}{(x+y)^{2}}-\frac{\lambda _{1}xy}{(x+y)^{2}} \biggr]\,dt \\ =&\ln \frac{\xi _{1}\eta _{1}}{\xi _{0}\eta _{0}}+ \int _{0}^{T} \biggl[x(1+ \alpha -2x)+ \frac{\lambda xy}{(x+y)^{2}}- \frac{\lambda _{1} xy}{(x+y)^{2}} \biggr]\,dt. \end{aligned}$$

Furthermore,

$$\begin{aligned} \mu _{2} =&\Delta _{1}\exp \int _{0}^{T} \biggl[\frac{\partial P}{\partial x}\bigl(\xi (t), \eta (t)\bigr)+\frac{\partial Q}{\partial y}\bigl(\xi (t),\eta (t)\bigr) \biggr]\,dt \\ =&\frac{(1-q)\xi _{0} [(\xi _{0}-\alpha )(1-\xi _{0})-\frac{\lambda \eta _{0}}{\xi _{0}+\eta _{0}} ]}{\xi _{1} [(\xi _{1}-\alpha )(1- \xi _{1})-\frac{\lambda \eta _{1}}{\xi _{1}+\eta _{1}} ]} \\ & {} \cdot \exp \biggl[\ln \frac{\xi _{1}\eta _{1}}{\xi _{0}\eta _{0}}+ \int _{0}^{T} \biggl(x(1+\alpha -2x)+ \frac{\lambda xy}{(x+y)^{2}}-\frac{ \lambda _{1} xy}{(x+y)^{2}} \biggr)\,dt \biggr] \\ =&\frac{(1-q)\eta _{1} [(\xi _{0}-\alpha )(1-\xi _{0})-\frac{ \lambda \eta _{0}}{\xi _{0}+\eta _{0}} ]}{\eta _{0} [(\xi _{1}- \alpha )(1-\xi _{1})-\frac{\lambda \eta _{1}}{\xi _{1}+\eta _{1}} ]} \\ & {} \cdot \exp \biggl[ \int _{0}^{T} \biggl(x(1+\alpha -2x)+ \frac{\lambda xy}{(x+y)^{2}}-\frac{\lambda _{1} xy}{(x+y)^{2}} \biggr)\,dt \biggr]. \end{aligned}$$

For any point $(x,y)\in \varTheta$, $\alpha < x<1$ and $y_{1}< y< h$, we have $(1-\alpha )+\frac{\lambda h}{\alpha }- \frac{\lambda _{1}\alpha y_{1}}{(1+h)^{2}}<0$, so we can get

$$ x(1+\alpha -2x)+\frac{\lambda xy}{(x+y)^{2}}- \frac{\lambda _{1}xy}{(x+y)^{2}}< (1-\alpha )+ \frac{\lambda h}{\alpha }-\frac{ \lambda _{1}\alpha y_{1}}{(1+h)^{2}}< 0, $$

and due to $\vert \chi \vert <1$, we have

$$ \biggl\vert \frac{(1-q)\eta _{1} [(\xi _{0}-\alpha )(1-\xi _{0})-\frac{ \lambda \eta _{0}}{\xi _{0}+\eta _{0}} ]}{\eta _{0} [(\xi _{1}- \alpha )(1-\xi _{1})-\frac{\lambda \eta _{1}}{\xi _{1}+\eta _{1}} ]} \biggr\vert < 1. $$

Therefore $\vert \mu _{2} \vert <1$. According to the analog of the Poincaré criterion [55, Theorem 2.3], we know that the order one periodic orbit of system (3) is orbitally asymptotically stable. This completes the proof. □

2.4 Determination of optimal pest economic threshold

In order to determine the optimum release amount of natural enemies and the optimal frequency of spraying chemical pesticide, we formulate the following optimization problem and find the optimal economic threshold.

Let $l_{1}$ represent the unit cost of the biological control, $l_{2}$ the unit cost of the chemical control. Our final purpose is to minimize the expenses of per unit period. We denote by F the total expenses in a period of system (3), which is a function of the chemical control strength $p(h)$ and release amount of natural enemies $\tau (h)$. Then we have $F(h)=l_{1}\tau (h)+l_{2}p(h)$. Thus we formulate the following optimization model:

$$\begin{aligned}& \min \frac{F(h)}{T(h)}\\& \text{s.t. }h_{1}< h< h_{2}. \end{aligned}$$

Solving the objective function yields the optimum economic threshold $h^{*}$, which results in the optimum release amount of the predator $\tau ^{*}=\tau (h^{*})$, the optimal chemical control strength $p^{*}=p(h^{*})$ and the optimal control period of chemical control $T^{*}=T(\tau ^{*},p^{*})$. However, it is important to be noted that the optimal economic threshold $h^{*}$ is dependent on the ratio of $\omega =\frac{l_{2}}{l_{1}}$.

3 Simulations and optimization

In order to verify the theoretical results obtained in this paper, a specific example is presented in this section. Let $\alpha =0.1$, $\lambda =0.5$, $\lambda _{1}=0.8$, $\beta =0.55$, $h_{1}=0.35$, $h_{2}=0.76$, $p _{\max }=0.3$, $\tau _{\max }=0.1$, $\tau _{\min }=0.01$, $q_{\max }=0.8$. By a simple calculation, the saddle point and locally asymptotically stable point are $E_{1}(0.3349,0.1522)$ and $E_{0}(0.7651,0.3478)$, respectively. We carry out simulations by changing the main parameter h and fixing all other parameters. The control parameters p, q, τ are calculated by (4).

3.1 Numerical simulations

Taking parameters α, λ, β, $\lambda _{1}$ into system (5), we can obtain

$$ \textstyle\begin{cases} {\frac{dx}{dt}=x(t) [x(t)-0.1 ] [1-x(t) ]-\frac{0.5 x(t)y(t)}{x(t)+y(t)},} \\ {\frac{dy}{dt}=\frac{0.8x(t)y(t)}{x(t)+y(t)}-0.55 y(t).} \end{cases} $$

(6)

Furthermore, Fig. 6(a) shows the phase portrait of $x(t)$ and $y(t)$, Fig. 6(b) shows time series of $x(t)$, Fig. 6(c) shows time series of $y(t)$. Let $p=0.27$, $h=0.61$, $\tau =0.18$, we shall get $\delta =p+\frac{\beta \tau }{(\lambda _{1}-\beta )h}=0.27+\frac{0.55 \times 0.18}{(0.8-0.55)\times 0.61}=0.92$. Let $q=0.01$ we shall get Fig. 7. Figures 7(a), 7(b) and 7(c) show that system (3) does not have order one periodic orbit and the pest and natural enemy population become extinct when $0< q< q^{*}$. Let $q=0.6$, $q=0.7$ and $q=0.8$ and we shall get a unique order one periodic solution and it is asymptotically stable (see Fig. 8). Furthermore, according to Fig. 8, we see that, as the parameter q increases, the period T becomes smaller. Figure 9 shows that system (3) admits the order one periodic orbit when $q>\delta$. According to Fig. 9, we see that, as the parameter q increases, the period T becomes smaller.

Figure 6

Numerical simulations without impulsive. (a) Phase portrait of $x(t)$ and $y(t)$. (b) Time series of $x(t)$. (c) Time series of $y(t)$

Figure 7

Numerical simulations in the case $0< q< q^{*}$. (a) Phase portrait of $x(t)$ and $y(t)$. (b) Time series of $x(t)$. (c) Time series of $y(t)$

Figure 8

Numerical simulations in the case $q^{*}< q<\delta$. (a) Phase portrait of $x(t)$ and $y(t)$. (b) Time series of $x(t)$. (c) Time series of $y(t)$

Figure 9

Numerical simulations in the case $\delta < q<1$. (a) Phase portrait of $x(t)$ and $y(t)$. (b) Time series of $x(t)$. (c) Time series of $y(t)$

3.2 Optimum pest control level

The impulse period T of the order one periodic orbit varies with the economic threshold h, as is shown in Fig. 10. And Fig. 11 shows the variation of cost per unit time $F/T$ and the period T with the pest control level h. Assume $l_{1}=10{,}000$, $l_{2}=100$, we shall get $\omega =\frac{l_{2}}{l_{1}}=1/100$.

Figure 10

Impulse period T of the order one periodic solution varies with the economic threshold h

Figure 11

Cost per unit time $F/T$ on the economic threshold h

The optimal pest threshold is $h^{*}=0.46$, the optimal chemical control strength is $p^{*}=0.0878$, the optimal release amount of the natural enemies is $\tau ^{*}=0.0737$. It is important to note that the optimum economic threshold h is dependent on ω, that is, the larger ω is, the lower h is, as is illustrated in Fig. 12.

Figure 12

The change in the cost per unit time $F/T$ on the economic threshold h for $\omega =1/200,1/100,1,100$

4 Conclusion

In this paper, a predator–prey model with ratio-dependent and impulsive state feedback control is proposed. We take control measures that combine biological control and chemical control. The aim of this study is to get optimum pest control level and minimize the cost of pest control.

Based on the above analysis, both the predator and the prey are extinct when $0< q< q^{*}$, that is, the order one periodic orbit does not exist when $0< q< q^{*}$, system (3) admits an order one homoclinic cycle for $q=q^{*}$; we obtain a unique and stable order one periodic orbit according to the geometric theory of the differential equations and the method of subsequence functions in the case of $q^{*}< q<\delta$; and system (3) admits the order one periodic orbit in the case of $\delta < q<1$.

In order to reduce the total cost of pest management, an optimization problem is formulated, and the optimal economic threshold and the minimum control cost are obtained. Finally, numerical simulation is carried out to verify the theoretical results.