1 Introduction

As we all know, the classical Lotka–Volterra model can well describe the competition among different populations, thus it has been one of the most important models in the field of mathematical ecology. In recent decades, it was found that the Lotka–Volterra model can do nothing about forecasting except portraying the densities of the interactive population, thus also cannot describe the competitive mechanism. The Lotka–Volterra model can only do feedback estimation by the result of competition and cannot properly estimate the important α and β parameters before the competition. During the mid-1970s, a competitive theory based on competition for resources was developed stimulated by dissatisfaction with the classical theory, the so-called resource competition model. Based on the Monod model, this model mainly focuses on the dynamical behavior while multiple populations compete for multiple resources. Tilman et al. established different consumer–resource models in [1, 2]; from then on, a large number of articles emerged, especially during the recent two or three decades (see [3,4,5,6]). Based on Tillman’s theory, scholars also proposed a new method that predicted the final competition results by using resource requirement among competing populations. However, owing to the complexity of competition among populations, that theory is still not perfect. Nowadays, the minimum requirements competition theory of Tillman’s is still popular. The theory considers that the final winner will be that population which has the minimum resource requirements. While the relative growth rate of a population is the minimum function of resources, it enhances the difficulty of research. Many researchers focused on the competition between two populations and one resource. Hsu [7] considered the disturbances from the opponents competing for resources and pointed out that the final winner among the predators depends on its initial population size. In 1999, Huisman (see [8]) went on studying the model established by Tillman in 1977. He pointed out that it was competition for resources that led to the bio-diversity, thereby studying the resources’ competition model was obvious and essential. Smith et al. (see [9]) proved, by using matrix theory, that there is no equilibrium point provided the population size exceeds the number of resources, while also considering that the relative mortality was equal to the transform rate among resources. There are many other works about this problem (see [10,11,12,13,14,15]).

At present, many researches of resources’ competition models are published in various ecology journals, that is to say, many researches are still based on experiment, while their theoretical results are scarce. Actually, the resources’ competition theory proposed by Tillman came from a laboratory chemostat cultivation and focused on the chemostat system which is still being studied. The model is as follows:

$$ \frac{dR}{dt} = D(S-R)-\frac{\mu_{m}RN}{(K+R)Y}, \qquad \frac{dN}{dt} = N\biggl(\frac{\mu_{m}RN}{K+R}-D\biggr), $$
(1)

where R is the density of nutrients in the system, D is the dilution rate or the input rate of nutrients, S denotes the supply of nutrients or resources, \(\mu_{m}\) denotes the maximum birth rate, N denotes the population density or size, K denotes the half-saturation constant, i.e., the amount of nutrients while the birth rate is half of \(\mu_{m}\), Y is the size of the produced population for individual units. There have been many results on this kind for chemostat models (see [16,17,18,19]). In order to better match up the reality, Tillman generalized the original model to have n populations and k nutrients (resources). The specific model is as follows [20]:

$$\begin{aligned} &\frac{dN_{i}(t)}{dt} = N_{i}(t) \bigl( \mu_{i}(R_{1},R_{2},\dots,R_{k})-m_{i} \bigr),\quad i=1,2,\dots,n, \end{aligned}$$
(2)
$$\begin{aligned} &\frac{dR_{j}(t)}{dt} = D \bigl(S_{j}-R_{j}(t) \bigr)-\sum _{i=1}^{n}C_{ji}\mu _{i}(R_{1},R_{2},\dots,R_{k})N_{i}(t),\quad j=1,2,\dots,k, \end{aligned}$$
(3)

where

$$ \mu_{i}(R_{1},R_{2}, \dots,R_{k})=\min \biggl(\frac{r_{i}R_{1}}{K_{1i}+R_{1}},\frac {r_{i}R_{2}}{K_{2i}+R_{2}}, \dots, \frac{r_{i}R_{k}}{K_{ki}+R_{k}} \biggr), $$
(4)

\(N_{i}\) denotes the density of population i, \(r_{i}\) denotes the maximal growth rate, \(m_{i}\) denotes the relative death rate of population i, \(N_{i}m_{i}\) denotes the death rate of population i, \(R_{j}\) denotes the amount of the jth available resource, D denotes the transformation rate of the system, \(S_{j}\) denotes the support of the jth resource, \(C_{ji}\) denotes the jth resource that gets consumed by the ith population, \(\sum_{i=1}^{n}C_{ji}\mu_{i}(R_{1},R_{2},\dots,R_{k})N_{i}\) denotes the total consumption by all the populations, \(DR_{j}\) denotes the self-consumption rate of the jth resource. The well-known Monod function in ecology describes the relative birth rate of the population which is the function of resources; \(K_{ji}\) in the Monod function denotes the corresponding resources when the population birth rate becomes half of \(r_{i}\). Equation (2) illustrates that the birth rate of a certain population depends on the resource which has the minimum support. Equation (3) shows that the amount of the jth resource depends on the support and consumption of resources.

In [21], Huisman et al. found that there would be several results and chaos when the number of populations became larger than the number of resources. Therefore, it is very difficult to study the problem where many populations compete for several resources. In view of its importance, the authors tried to focus on the asymptotic behavior when there are n populations competing for k resources. In fact, a biological system is inevitably affected by environmental noises (see [22]). May has pointed out that parameters in systems exhibited random fluctuations to a greater or lesser extent due to environmental noises [23]. Thus, it is meaningful to take environmental noises into consideration. The most important parameters for a population ecosystem are the intrinsic growth rate (= birth rate \(\mu_{i}-\mbox{ death rate }m_{i}\)), so we used the technique of parameter perturbation to examine the effect of environmental noise on intrinsic growth rate: \(\gamma_{i}=\mu_{i}-m_{i} \Longrightarrow(\mu_{i}+\alpha _{i1}\,dB_{1}(t))-(m_{i}+\alpha_{i2}\,dB_{2}(t))\). That is, the birth and death rates are subjected to a normal distribution with means \(\mu_{i}\) and \(m_{i}\). Owing to the complication of the system, we are only concerned with white noise. For many new conclusions on this kind of competition model with regime switching or impulsive effect, the readers are referred to [24,25,26]. In this paper, we will focus on the following model:

$$\begin{aligned} dN_{i}(t)={}& N_{i}(t) \bigl( \mu_{i}(R_{1},R_{2},\dots,R_{k})-m_{i} \bigr)\,dt \\ &{}+\alpha_{i1}N_{i}(t)\,dB_{1}(t)- \alpha_{i2}N_{i}(t)\,dB_{2}(t),\quad i=1,2,\dots,n, \end{aligned}$$
(5)
$$\begin{aligned} dR_{j}(t)={}& D\bigl(S_{j}-R_{j}(t)\bigr)\,dt- \sum_{i=1}^{n}C_{ji} \mu_{i}(R_{1},R_{2},\dots ,R_{k})N_{i}\,dt \\ &{}-\sum_{i=1}^{n}C_{ji} \alpha_{i1}N_{i}(t)\,dB_{1}(t),\quad j=1,2,\dots,k, \end{aligned}$$
(6)

where \(\alpha_{i1}\) and \(\alpha_{i2}\) (\(i=1,2,\dots,n\)) are all positive constants, and the rest are the same as in the former system. The system is understood in Itô rather than Stratonovich sense. As we all know, equations in Stratonovich sense are usually used in physics, while Itô equations are always used in mathematics, especially when the most widely used Euler scheme to find a numerical solution is employed. Itô approach can give an explicit function of the current coordinate, whereas Stratonovich approach yields SDEs with implicit solution functions. All in all, we still use Itô equations in this paper.

Seeing the complication of the stochastic model, only the white noise is considered. This paper consists of several parts: the existence of solution is studied in Sect. 2, the stochastic final boundedness is discussed in Sect. 3, path estimation is studied in Sect. 4, the persistence and extinction are finally discussed in Sect. 5.

2 Existence of positive solutions

Theorem 1

For any given initial condition \((N_{i}(0),R_{j}(0)) \in R_{+}^{n}\times R_{+}^{k}\) \((i=1,2,\dots,n; j=1,2,\dots,k)\), there exists a unique solution \((N(t),R(t))\) (where \((N(t)=(N_{1}(t), N_{2}(t),\dots, N_{n}(t)), R(t)=(R_{1}(t), R_{2}(t),\dots,R_{k}(t)))\) for system (5)–(6), and this solution remains in \(R_{+}^{n}\times R_{+}^{k}\) with probability 1.

Proof

Considering that the coefficients satisfy a local Lipchitz condition, there exists a unique local saturated solution \((N(t),R(t))\), \(t\in[0,\tau_{e})\) based on the given condition, where \(\tau_{e}\) is the exploration time. In order to prove that the solution is a global solution, \(\tau_{e}=\infty\) a.s. is needed. Let \(m_{0}\) be large enough, such that \((N_{i}(0),R_{j}(0))\in[m_{0}^{-1}, m_{0}]\ (i=1,2,\dots ,n; j=1,2,\dots,k)\). Then for any \(m\geq m_{0}\), we define a stopping time

$$\tau_{m}=\inf \Bigl\{ t\in[0,\tau_{e}):\min _{1\leq i\leq n; 1\leq j \leq k}\bigl\{ N_{i}(t),R_{j}(t)\bigr\} \leq m^{-1} \text{ or } \max_{1\leq i\leq n; 1\leq j \leq k}\bigl\{ N_{i}(t),R_{j}(t) \bigr\} \geq m \Bigr\} , $$

where \(\inf\emptyset=\infty\). Based on comparison theory, the following will be deduced under the condition \(t\leq\tau_{e}\):

$$ N_{i}(t)\vee R_{j}(t)\leq C_{1},\quad C_{1}>0. $$
(7)

Obviously, \(\tau_{m}\) is a monotonically increasing function of m. Let \(\tau_{\infty}=\lim_{m\rightarrow\infty}\tau_{m}\), and we define a twice differentiable function \(V:R_{+}^{n}\rightarrow R_{+}\) as follows:

$$V(N_{i},R_{j})=\sum_{i=1}^{n} \biggl(N_{i}(t)-b_{i}-b_{i}\ln\frac{N_{i}(t)}{b_{i}} \biggr) -\sum_{j=1}^{k} \biggl(R_{j}(t)-a_{j}-a_{j}\ln\frac{R_{j}(t)}{a_{j}} \biggr), $$

where \(a_{j}\ (1\leq j\leq k), b_{i}\ (1\leq i\leq n)\) are all positive constants to be defined. Then,

$$\begin{aligned} dV={}&\sum_{i=1}^{n} \biggl(1- \frac{b_{i}}{N_{i}(t)} \biggr)\,dN_{i}+\sum_{j=1}^{k} \biggl(1-\frac{a_{j}}{R_{j}(t)}\biggr)\,dR_{j}+ \frac{1}{2}\sum _{i=1}^{n}\frac{b_{i}}{N_{i}^{2}}(dN_{i})^{2} +\frac{1}{2}\sum_{j=1}^{k} \frac{a_{j}}{R_{j}^{2}}(dR_{j})^{2} \\ \leq{}& \sum_{i=1}^{n} \biggl(1- \frac{b_{i}}{N_{i}(t)} \biggr) \bigl(\mu _{i}(R_{1},R_{2}, \dots,R_{k})-m_{i} \bigr)\,dt \\ &{}+\sum_{j=1}^{k} \biggl(1- \frac{a_{j}}{R_{j}(t)} \biggr) \Biggl[D\bigl(S_{j}-R_{j}(t) \bigr)-\sum_{j=1}^{k}\sum _{i=1}^{n}C_{ji} \mu_{i}(R_{1},R_{2}, \dots,R_{k})N_{i} \Biggr]\,dt \\ &{}+\frac{1}{2}\sum_{i=1}^{n}b_{i} \bigl(\alpha_{i1}^{2}+\alpha_{i2}^{2} \bigr)\,dt+ \sum_{j=1}^{k}\sum _{i=1}^{n}a_{j}C_{ji}^{2} \alpha_{i1}^{2}\,dt \\ &{}+\sum_{i=1}^{n} \biggl(1- \frac{b_{i}}{N_{i}(t)} \biggr) \bigl(\alpha_{i1}N_{i}\,dB_{1}(t) -\alpha_{i2}N_{i}\,dB_{2}(t) \bigr) \\ \leq{}& \sum_{i=1}^{n}N_{i}(t) \mu_{i}(R_{1},R_{2},\dots,R_{k})\,dt+ \sum_{i=1}^{n}b_{i}m_{i}\,dt- \sum_{i=1}^{n}N_{i}(t)m_{i}\,dt \\ &{}-\sum_{i=1}^{n}b_{i} \mu_{i}(R_{1},R_{2},\dots,R_{k})\,dt + \sum_{j=1}^{k}DS_{j}dt+\sum _{j=1}^{k}Da_{j}dt \\ &{}-\sum_{j=1}^{k}\sum _{i=1}^{n}C_{ji}\mu(R_{1},R_{2}, \dots,R_{k})N_{i}\,dt +\sum_{j=1}^{k} \sum_{i=1}^{n}\frac{a_{j}}{R_{j}(t)}C_{ji} \mu_{i}(R_{1},R_{2},\dots ,R_{k})N_{i}\,dt \\ &{}+\frac{1}{2}\sum_{i=1}^{n}b_{i} \bigl(\alpha_{i1}^{2}+\alpha_{i2}^{2} \bigr)\,dt+\sum_{j=1}^{k} \sum _{i=1}^{n}a_{j}C_{ji}^{2} \alpha_{i1}^{2}\,dt -\sum_{i=1}^{n} \sum_{j=1}^{k} \biggl(1-\frac{a_{j}}{R_{j}} \biggr)C_{ji}\alpha _{i1}N_{i}\,dB_{1}(t) \\ &{}+\sum_{i=1}^{n} \biggl(1- \frac{b_{i}}{N_{i}(t)} \biggr) \bigl(\alpha _{i1}N_{i}\,dB_{1}(t)- \alpha_{i2}N_{i}\,dB_{2}(t) \bigr). \end{aligned}$$

Let

$$\begin{aligned} LV:={}&\sum_{i=1}^{n}N_{i}(t) \mu_{i}(R_{1},R_{2},\dots,R_{k})+\sum _{i=1}^{n}b_{i}m_{i} - \sum_{i=1}^{n}N_{i}(t)m_{i}- \sum_{i=1}^{n}b_{i} \mu_{i}(R_{1},R_{2},\dots,R_{k}) \\ &{}+\sum_{j=1}^{k}DS_{j}+\sum _{j=1}^{k}Da_{j}-\sum _{j=1}^{k}\sum_{i=1}^{n}C_{ji} \mu (R_{1},R_{2},\dots,R_{k})N_{i} \\ &{}+\sum_{j=1}^{k}\sum _{i=1}^{n} \frac {a_{j}}{R_{j}(t)}C_{ji} \mu_{i}(R_{1},R_{2},\dots,R_{k})N_{i} \\ &{}+\frac{1}{2}\sum_{i=1}^{n}b_{i} \bigl(\alpha_{i1}^{2}+\alpha_{i2}^{2} \bigr) +\sum_{j=1}^{k}\sum _{i=1}^{n}a_{j}C_{ji}^{2} \alpha_{i1}^{2}. \end{aligned}$$

For any \(1\leq i\leq n\), \(1\leq j\leq k\), we choose proper \(a_{j}\) and \(b_{i}\) such that

$$ \sum_{i=1}^{n}N_{i}(t) \mu_{i}(R_{1},R_{2},\dots,R_{k})-\sum _{i=1}^{n}b_{i}\mu _{i}(R_{1},R_{2},\dots,R_{k})\leq0, $$
(8)

and

$$-\sum_{j=1}^{k}\sum _{i=1}^{n}C_{ji}\mu(R_{1},R_{2}, \dots,R_{k})N_{i} +\sum_{j=1}^{k} \sum_{i=1}^{n}\frac{a_{j}}{R_{j}(t)} C_{ji}\mu_{i}(R_{1},R_{2},\dots ,R_{k})N_{i}\leq0, $$

then from (7), we know that when \(t\leq\tau_{e}\), there exists a \(\bar {K}>0\), such that

$$LV\leq\bar{K}, $$

thus

$$\begin{aligned} dV(N_{i},R_{j})\leq{}& \bar{K}\,dt+\sum _{i=1}^{n} \biggl(1-\frac{b_{i}}{N_{i}(t)} \biggr) \bigl( \alpha_{i1}N_{i}\,dB_{1}(t)-\alpha_{i2}N_{i}\,dB_{2}(t) \bigr) \\ &{}-\sum_{i=1}^{n}\sum _{j=1}^{k} \biggl(1-\frac{a_{j}}{R_{j}} \biggr)C_{ji}\alpha _{i1}N_{i}\,dB_{1}(t). \end{aligned}$$

Integrating from 0 to \(\tau_{m}\wedge T\), one obtains

$$E \bigl[V\bigl(N_{i}(\tau_{m} \wedge T), R_{j}( \tau_{m} \wedge T)\bigr) \bigr]\leq V\bigl(N_{i}(0),R_{j}(0) \bigr)+\bar{K}T. $$

Owing to

$$\begin{aligned} V \bigl(N_{i}(\tau_{m},\omega),R_{j}( \tau_{m},\omega) \bigr)\geq{}&\min_{1\leq j \leq k} \biggl\{ m-a_{j}-a_{j}\ln{\frac{m}{a_{j}}},\frac{1}{m}-a_{j}-a_{j} \ln{\frac {1}{ma_{j}}} \biggr\} \\ &{}\wedge\min_{1\leq j \leq n} \biggl\{ m-b_{i}-b_{i} \ln{\frac{m}{b_{i}}},\frac {1}{m}-b_{i}-b_{i}\ln{ \frac{1}{mb_{i}}} \biggr\} , \end{aligned}$$

we obtain

$$\begin{aligned} V\bigl(N_{i}(0),R_{j}(0)\bigr)+\bar{K}T\geq{}& E \bigl[1_{{\tau_{k} \leq T}}(\omega )V\bigl(N_{i}(\tau_{m}, \omega),R_{j}(\tau_{m},\omega)\bigr) \bigr] \\ \geq{}& P\{\tau_{m} \leq T\} \biggl(\min_{1\leq j \leq k} \biggl\{ m-a_{j}-a_{j}\ln {\frac{m}{a_{j}}}, \frac{1}{m}-a_{j}-a_{j}\ln{\frac{1}{ma_{j}}} \biggr\} \\ &{}\wedge\min_{1\leq i \leq n} \biggl\{ m-b_{i}-b_{i} \ln{\frac{m}{b_{i}}},\frac {1}{m}-b_{i}-b_{i}\ln{ \frac{1}{mb_{i}}} \biggr\} \biggr), \end{aligned}$$

where \(1_{{\tau_{m} \leq T}}\) is the characteristic function of the set \(\{\tau_{m} \leq T\}\). Letting \(m\rightarrow\infty\), it is easy to see that

$$\lim_{m\rightarrow\infty}P\{\tau_{m} \leq T\}=0, $$

that is,

$$P\{\tau_{\infty}\leq T\}=0, $$

and then for any \(T>0\), \(P\{\tau_{\infty}< \infty\}=0\). Therefore, \(P\{ \tau_{m}=\infty\}=1\) is obtained. □

3 Stochastic final boundedness of the system solutions

Definition 1

If for any \(\varepsilon\in(0,1)\), there exists a positive constant \(\hat{H}=\hat{H}(\varepsilon)\) such that for any given initial condition \((N(0),R(0))\), the solution \((N(t),R(t))\) of system (5)–(6) satisfies

$$\begin{aligned} &\limsup_{t\rightarrow\infty}P\bigl\{ \bigl\vert N(t) \bigr\vert \leq \hat{H}\bigr\} \geq1-\varepsilon, \\ &\limsup_{t\rightarrow\infty}P\bigl\{ \bigl\vert R(t) \bigr\vert \leq \hat{H}\bigr\} \geq1-\varepsilon, \end{aligned}$$

then the solution of system (5)–(6) is said to be stochastically finally bounded, where \(N(t)= (N_{1}(t),N_{2}(t),\dots,N_{n}(t) ), R(t)= (R_{1}(t), R_{2}(t),\dots,R_{k}(t) )\).

Remark 1

For any resource, \(R_{j}(t)\leq S_{j}\ (1\leq j\leq k)\), so it is reasonable to consider the boundedness of resource \(R(t)\).

Lemma 1

Let \(\theta\in(0,1)\), \(\bar{D}=\min_{1\leq i\leq n}\{ D, m_{i}\}\), \(\gamma=\bar{D}+\frac{1}{2}(1-\theta)\max_{1\leq i\leq n}\{ \alpha_{i2}^{2}\}>0\). Then for any \(\xi\in(0, \gamma\theta)\), there exists \(\hat{H}>0\), such that the solution of system (5)–(6) satisfies

$$\begin{aligned} &\limsup_{t\rightarrow\infty}E \bigl\vert R(t) \bigr\vert ^{\theta}\leq k^{\frac{\theta}{2}}\frac {\theta\hat{H}}{\xi}, \end{aligned}$$
(9)
$$\begin{aligned} &\limsup_{t\rightarrow\infty}E \Biggl(\sum_{i=1}^{n} \vert N_{i} \vert ^{\theta}\Biggr)\leq \frac{(\frac{\theta\hat{H}}{\xi})^{\theta}}{\sum_{j=1}^{k} (\sum_{i=1}^{n} \vert C_{ji} \vert ^{\frac{\theta}{\theta-1}} )^{\theta-1}}. \end{aligned}$$
(10)

Proof

From system (5)–(6), we can see that

$$ dR_{j}+\sum_{i=1}^{n}C_{ji} \,dN_{i}=D(S_{j}-R_{j})\,dt-\sum _{i=1}^{n}C_{ji}N_{i}m_{i}\,dt -\sum_{i=1}^{n}C_{ji} \alpha_{i2}N_{i}\,dB_{2}. $$
(11)

Let

$$ y_{j}=R_{j}+\sum _{i=1}^{n}C_{ji}N_{i}, $$
(12)

and for any \(\theta\in(0,1)\) define

$$\begin{aligned} V\bigl(N(t),R(t)\bigr)=\sum_{j=1}^{k}y_{j}^{\theta}. \end{aligned}$$
(13)

Then

$$\begin{aligned} dV\bigl(N(t),R(t)\bigr) =LV+\theta\sum_{j=1}^{k}y_{j}^{\theta-1} \sum_{i=1}^{n}C_{ji} \alpha_{i2}N_{i}\,dB_{2}, \end{aligned}$$
(14)

where

$$\begin{aligned} LV&=\theta\sum_{j=1}^{k}y_{j}^{\theta-1} \Biggl[D(S_{j}-R_{j})\,dt-\sum _{i=1}^{n}C_{ji}N_{i}m_{i} \Biggr]\frac{1}{2}\theta(\theta-1) \sum_{j=1}^{k}y_{j}^{\theta-2} \sum_{i=1}^{n}C_{ji}^{2}N_{i}^{2} \alpha_{i2}^{2} \\ &\leq \theta\sum_{j=1}^{k}y_{j}^{\theta-2} \biggl[-\bar {D}y_{j}^{2}+DS_{j}y_{j}+ \frac{1}{2}(\theta-1)\max_{1\leq i\leq n}\bigl\{ \alpha _{i2}^{2}\bigr\} y_{j}^{2} \biggr] \\ &=\theta\sum_{j=1}^{k}y_{j}^{\theta-2} \biggl[-\biggl(\bar{D}+\frac{1}{2}(1-\theta )\max_{1\leq i\leq n} \bigl\{ \alpha_{i2}^{2}\bigr\} \biggr)y_{j}^{2}+DS_{j}y_{j} \biggr] \\ &:= \theta\sum_{j=1}^{k}y_{j}^{\theta-2} \bigl[-\gamma y_{j}^{2}+DS_{j}y_{j} \bigr], \end{aligned}$$

with \(\bar{D}=\min_{1\leq i\leq n}\{D, m_{i}\}\), and from lemma assumptions we know that \(\gamma=\bar{D}+\frac{1}{2}(1-\theta)\max_{1\leq i\leq n}\{\alpha_{i2}^{2}\}>0\). Hence for any \(\xi\in(0, \gamma\theta)\), from Itô formula, we obtain

$$ d \bigl(e^{\xi t}V\bigl(N(t), R(t)\bigr) \bigr)=e^{\xi t}(\xi V+LV)\,dt+\theta e^{\xi t}\sum_{j=1}^{k}y_{j}^{\theta-1} \sum_{i=1}^{n}C_{ji}N_{i} \alpha_{i2}\,dB_{2}, $$
(15)

where

$$\begin{aligned} e^{\xi t}(\xi V+LV)&\leq \xi e^{\xi t}\sum _{j=1}^{k}y_{j}^{\theta}+e^{\xi t} \theta\sum_{j=1}^{k}y_{j}^{\theta-2} \bigl[-\gamma y_{j}^{2}+DS_{j}y_{j} \bigr] \\ &=\theta e^{\xi t}\sum_{j=1}^{k}y_{j}^{\theta-2} \biggl[\frac{\xi}{\theta }y_{j}^{2}-\gamma y_{j}^{2}+DS_{j}y_{j} \biggr] \\ &=\theta e^{\xi t}\sum_{j=1}^{k}y_{j}^{\theta-2} \biggl[\biggl(\frac{\xi}{\theta }-\gamma\biggr)y_{j}^{2}+DS_{j}y_{j} \biggr]. \end{aligned}$$

Thus, there exists a positive constant Ĥ such that

$$e^{\xi t}(\xi V+LV)\leq\theta e^{\xi t}\hat{H}. $$

So

$$ d(e^{\xi t}V\bigl(N(t), R(t)\bigr)\leq\theta e^{\xi t}\hat{H}\,dt+ \theta e^{\xi t}\sum_{j=1}^{k}y_{j}^{\theta-1} \sum_{i=1}^{n}C_{ji}N_{i} \alpha_{i2}\,dB_{2}. $$
(16)

Integrating (16) from 0 to t and taking expectation, we obtain

$$\begin{aligned} e^{t}E \bigl(V \bigl(N(t), R(t) \bigr) \bigr)\leq V \bigl(N(0),R(0) \bigr)+\frac {\theta\hat{H}}{\xi}e^{\xi t}-\frac{\theta\hat{H}}{\xi}, \end{aligned}$$

that is,

$$\begin{aligned} E\bigl(V\bigl(N(t), R(t)\bigr)\bigr)\leq \biggl(V\bigl(N(0),R(0)\bigr)- \frac{\theta\hat{H}}{\xi} \biggr)e^{-\xi t}+\frac{\theta\hat{H}}{\xi}. \end{aligned}$$

So

$$\limsup_{t\rightarrow\infty}E \Biggl(\sum_{j=1}^{k}y_{j}^{\theta}\Biggr)\leq \frac{\theta\hat{H}}{\xi}. $$

Also because

$$\vert y \vert ^{2}\leq k\max_{1\leq j\leq k}y_{j}^{2}, $$

the following inequality holds:

$$\vert y \vert ^{\theta}\leq k^{\frac{\theta}{2}}\max_{1\leq j\leq k}y_{j}^{\theta}\leq k^{\frac{\theta}{2}}V \bigl(N(t), R(t) \bigr). $$

Therefore,

$$\begin{aligned} \limsup_{t\rightarrow\infty}E \bigl\vert R(t) \bigr\vert ^{\theta}\leq\limsup_{t\rightarrow \infty}E \bigl\vert y(t) \bigr\vert ^{\theta}\leq k^{\frac{\theta}{2}}\frac{\theta\hat{H}}{\xi}. \end{aligned}$$
(17)

Also when \(0<\theta<1\), one has

$$\sum_{i=1}^{n}C_{ji}N_{i} \geq \Biggl(\sum_{i=1}^{n} \vert N_{i} \vert ^{\theta}\Biggr)^{\frac {1}{\theta}} \Biggl(\sum _{i=1}^{n} \vert C_{ji} \vert ^{\frac{\theta}{\theta-1}} \Biggr)^{\frac{\theta-1}{\theta}}. $$

Then from (17), we obtain

$$ \Biggl(\sum_{i=1}^{n} \vert N_{i} \vert ^{\theta}\Biggr)^{\frac{1}{\theta}} \sum _{j=1}^{k} \Biggl(\sum_{i=1}^{n} \vert C_{ji} \vert ^{\frac{\theta}{\theta-1}} \Biggr)^{\frac{\theta-1}{\theta}} \leq\sum _{j=1}^{k} \vert y_{j} \vert ^{\theta}\leq\frac {\theta\hat{H}}{\xi}. $$
(18)

The conclusion then follows by taking expectations of both sides of (17). □

Theorem 2

System (5)–(6) is stochastically finally bounded.

Proof

From (9), we know that there exists one positive constant \(K_{1}\) such that

$$\begin{aligned} \limsup_{t\rightarrow\infty}E \bigl(\sqrt{R(t)} \bigr)\leq K_{1}. \end{aligned}$$
(19)

For any \(\varepsilon>0\), let \(\bar{H}=\frac{K_{1}^{2}}{\varepsilon^{2}}\). Then the following can be obtained by using Chebyshev inequality:

$$P\bigl\{ \bigl\vert R(t) \bigr\vert >\bar{H}\bigr\} \leq\frac{E (\sqrt{R(t)} )}{\sqrt{\bar{H}}}. $$

Therefore,

$$\begin{aligned} \limsup_{t\rightarrow\infty}P\bigl\{ \bigl\vert R(t) \bigr\vert >\bar{H} \bigr\} \leq\frac{K_{1}}{\sqrt{\bar {H}}}=\varepsilon, \end{aligned}$$

that is,

$$\limsup_{t\rightarrow\infty}P\bigl\{ \bigl\vert R(t) \bigr\vert \leq \bar{H}\bigr\} \geq1-\varepsilon. $$

From (10), there exists a positive constant \(K_{2}\) such that

$$\begin{aligned} \limsup_{t\rightarrow\infty}E \bigl(\sqrt{N(t)} \bigr)\leq K_{2}. \end{aligned}$$
(20)

We can use the same method to prove that \(N(t)\) is also stochastically finally bounded. □

4 Path estimation of the system solutions

Theorem 3

For any given initial value \((N_{i}(0),R_{j}(0))\in R_{+}^{n}\times R_{+}^{k}\ (1\leq i\leq n; 1\leq j\leq k)\), the solution of system (5)–(6) satisfies

$$ \lim_{t\rightarrow\infty}\frac{R_{j}(t)}{t}=\frac{N_{i}(t)}{t}=0\quad \textit{a.s.} $$
(21)

Proof

Let \(y(t)=\sum_{j=1}^{k} (R_{j}(t)+\sum_{i=1}^{n}C_{ji}N_{i}(t) )\). We also define

$$ W(y)=(1+y)^{\eta}, $$
(22)

where η is a positive real number to be determined. By using Itô formula, we obtain

$$ dW(y)=LW(y)-\eta(1+y)^{\eta-1}\sum_{j=1}^{k} \sum_{i=1}^{n}C_{ji} \alpha_{i2}N_{i}\,dB_{2}, $$
(23)

where

$$\begin{aligned} LW(y)={}& \eta(1+y)^{\eta-1}\sum_{j=1}^{k}D \bigl(S_{j}-R_{j}(t)\bigr) -\eta(1+y)^{\eta -1}\sum _{j=1}^{k}\sum_{i=1}^{n}C_{ji}N_{i}m_{i} \\ &{}+\frac{1}{2}\eta(\eta-1) (1+y)^{\eta-2}\sum _{j=1}^{k}\sum_{i=1}^{n}C_{ji}^{2} \alpha_{i2}^{2}N_{i}^{2} \\ ={}&\eta(1+y)^{\eta-2}\sum_{j=1}^{k} \Biggl[D(1+y) \bigl(S_{j}-R_{j}(t)\bigr)-\sum _{i=1}^{n}C_{ji}N_{i}m_{i} \\ &{}+\frac{1}{2}(\eta-1)\sum_{i=1}^{n}C_{ji}^{2} \alpha_{i2}^{2}N_{i}^{2} \Biggr]. \end{aligned}$$

Let \(\hat{D}=\max_{i}\{m_{i},D\}\). Then

$$\begin{aligned} LW(y)\leq{}&\eta(1+y)^{\eta-2}\sum_{j=1}^{k} \Biggl[\hat {D}(1+y) \bigl(S_{j}-R_{j}(t)\bigr)-\sum _{i=1}^{n}\hat{D}C_{ji}N_{i} \\ &{}+\frac{1}{2}(\eta-1)\sum_{i=1}^{n}C_{ji}^{2} \alpha_{i2}^{2}N_{i}^{2} \Biggr] \\ ={} & \eta(1+y)^{\eta-2} \Biggl[\hat{D}(1+y)\sum _{j=1}^{k}S_{j}-\hat {D}y(1+y) \\ &{}+\frac{1}{2}(\eta-1)\sum_{i=1}^{n}C_{ji}^{2} \alpha_{i2}^{2}N_{i}^{2} \Biggr] \\ = {}& \eta(1+y)^{\eta-2} \Biggl[-\hat{D}y^{2}+\hat{D}\Biggl(\sum _{j=1}^{k}S_{j}-1\Biggr)y+\hat{D} \sum_{j=1}^{k}S_{j} \\ &{}+\frac{1}{2}(\eta-1)\max_{i}\bigl\{ \alpha_{i2}^{2}\bigr\} y^{2} \Biggr] \\ ={}&\eta(1+y)^{\eta-2} \Biggl\{ - \biggl[\hat{D}-\biggl(\frac{\eta-1}{2} \vee0\biggr)\max_{i}\bigl\{ \alpha_{i2}^{2} \bigr\} \biggr]y^{2} \\ &{}+\hat{D} \Biggl(\sum_{j=1}^{k}S_{j}-1 \Biggr)y+\hat{D}\sum_{j=1}^{k}S_{j} \Biggr\} . \end{aligned}$$

Choosing a proper \(\eta>0\) such that \(\hat{D}-(\frac{\eta-1}{2}\vee 0)\max_{i}\{\alpha_{i2}^{2}\}:= \gamma>0\), we claim that

$$LW(y)\leq\eta(1+y)^{\eta-2} \Biggl[-\gamma y^{2}+\hat{D}\Biggl( \sum_{j=1}^{k}S_{j}-1\Biggr)y+ \hat{D}\sum_{j=1}^{k}S_{j} \Biggr]. $$

For arbitrary \(\xi\in(0,\gamma\eta)\), applying Itô formula, one has

$$\begin{aligned} d\bigl[e^{\xi t}W(y)\bigr]={}&\xi e^{\xi t}W(y) \,dt+e^{\xi t}\,d\bigl(W(y)\bigr) \\ ={}& \bigl(\xi e^{\xi t}W(y)+e^{\xi t}LW(y) \bigr)\,dt \\ &{} -e^{\xi t}\eta(1+y)^{\eta-1} \sum_{j=1}^{k} \sum_{i=1}^{n}C_{ji}\alpha _{i2}N_{i}\,dB_{2}, \end{aligned}$$

where

$$\begin{aligned} &\xi e^{\xi t}W(y)+e^{\xi t}LW(y) \\ &\quad\leq \xi e^{\xi t}(1+y)^{\eta}+e^{\xi t} \eta(1+y)^{\eta-2} \Biggl[-\gamma y^{2}+\hat{D}\Biggl(\sum _{j=1}^{k}S_{j}-1\Biggr)y+\hat{D} \sum_{j=1}^{k}S_{j} \Biggr] \\ &\quad=\eta e^{\xi t}(1+y)^{\eta-2} \Biggl[\frac{\xi}{\eta}(1+y)^{2}- \gamma y^{2}+\hat{D}\Biggl(\sum_{j=1}^{k}S_{j}-1 \Biggr)y+\hat{D}\sum_{j=1}^{k}S_{j} \Biggr] \\ &\quad=\eta e^{\xi t}(1+y)^{\eta-2} \Biggl[-\biggl(\gamma- \frac{\xi}{\eta}\biggr) y^{2}+ \Biggl(\hat{D} \Biggl(\sum _{j=1}^{k}S_{j}-1 \Biggr)+ \frac{2\xi}{\eta} \Biggr)y+\hat{D}\sum_{j=1}^{k}S_{j} +\frac{\xi}{\eta} \Biggr]. \end{aligned}$$

Since \(\xi\in(0,\gamma\eta)\), there exists a positive number J such that

$$\xi e^{\xi t}W(y)+e^{\xi t}LW(y)\leq\eta J e^{\xi t}. $$

Then

$$d\bigl[\xi e^{\xi t}W(y)\bigr]\leq\eta J e^{\xi t}+e^{\xi t} \eta(1+y)^{\eta -1}\sum_{j=1}^{k}\sum _{i=1}^{n}C_{ji} \alpha_{i2}N_{i}\,dB_{2}. $$

Integrating from 0 to t the above inequality, and then taking expectation, we obtain

$$E\bigl[\xi e^{\xi t}W(y)\bigr]\leq W\bigl(y(0)\bigr)+ \frac{\eta J}{\xi}e^{\xi t}-\frac{\eta J}{\xi}, $$

that is,

$$E\bigl[W(y)\bigr]\leq \biggl[W\bigl(y(0)\bigr)-\frac{\eta J}{\xi} \biggr]e^{-\xi t}+\frac{\eta J}{\xi}, $$

and thus

$$\limsup_{t\rightarrow\infty}E \bigl[\bigl(1+y(t)\bigr)^{\eta}\bigr] \leq\frac{\eta J}{\xi}. $$

Because the following proof has nothing to do with the stochastic term, and its method is same as in [19], we omit it. Then

$$\lim_{t\rightarrow\infty}\frac{y(t)}{t} =\lim_{t\rightarrow\infty} \frac {1}{t} \Biggl[\sum_{j=1}^{k} \Biggl(R_{j}(t)+\sum_{i=1}^{n}C_{ji}N_{i}(t) \Biggr) \Biggr]=0 \quad\text{a.s.} $$

For any \(1\leq i\leq n, 1\leq j \leq k\), due to \(N_{i}(t)>0, R_{j}(t)>0\), we get

$$\lim_{t\rightarrow\infty}\frac{N_{i}(t)}{t}=\lim_{t\rightarrow\infty} \frac {R_{j}(t)}{t} \quad\text{a.s.} $$

This completes the proof of Theorem 3. □

5 Permanence and extinction

In this part, we will discuss the situation when the solution of system (5)–(6) will be permanent or extinct under some certain conditions. For the definitions see [27].

Theorem 4

Suppose that the noise intensity satisfies \(\max_{1\leq i\leq k}\{\alpha_{i1}^{2}+\alpha_{i2}^{2}\}<2D\). For an arbitrary initial condition \((N_{i}(0),R_{j}(0))\in R_{+}^{n}\times R_{+}^{k}\), if \(c\max_{1\leq j \leq k}\{S_{j}\}-m_{i}-\frac{1}{2}(\alpha_{i1}^{2}+\alpha _{i2}^{2})<0\) \((1\leq i \leq n)\), then the solution of system (5)–(6) satisfies

$$\limsup_{t\rightarrow\infty}\frac{\ln N_{i}(t)}{t}\leq c\max_{1\leq j \leq k} \{S_{j}\}-m_{i}-\frac{1}{2}\bigl( \alpha_{i1}^{2}+\alpha_{i2}^{2}\bigr)< 0\quad\textit{a.s.}\ (1\leq i\leq n), $$

that is, the solution of system (5)–(6) will exponentially fast become extinct almost surely. Here c is a positive constant, satisfying \(\max_{{1\leq i \leq n}, {1\leq j \leq k}}\frac{r_{i}}{K_{ji}+R_{j}}= c\).

Proof

Integrating from 0 to t both sides of (11) and then dividing by t, we get

$$\begin{aligned} &\frac{1}{t} \Biggl(R_{j}+\sum_{i=1}^{n}C_{ji}N_{i}(t) \Biggr)-\frac{1}{t} \Biggl(R_{j}(0)+\sum _{i=1}^{n}C_{ji}N_{i}(0) \Biggr) \\ &\quad=D \biggl(S_{j}-\frac{1}{t} \int_{0}^{t}R_{j}(s)\,ds \biggr)-\sum _{i=1}^{n}C_{ji}m_{i} \frac{1}{t} \int_{0}^{t}N_{i}(s)\,ds \\ &\qquad{}- \sum_{i=1}^{n}C_{ji} \alpha_{i2}\frac{1}{t} \int_{0}^{t}N_{i}(s)\,dB_{2}, \end{aligned}$$

that is,

$$ \frac{1}{t}R_{j}(s)\,ds+\frac{1}{D}\sum _{i=1}^{n}C_{ji}m_{i} \frac{1}{t} \int _{0}^{t}N_{i}(s) \,ds=S_{j} +\frac{\alpha_{j}(t)}{D}, $$
(24)

where

$$\begin{aligned} \alpha_{j}(t)={}&{-}\sum_{i=1}^{n}C_{ji} \alpha_{i2}\frac{1}{t} \int _{0}^{t}N_{i}(s)\,dB_{2} \\ &{}+\frac{1}{t} \Biggl(R_{j}(0) +\sum _{i=1}^{n}C_{ji}N_{i}(0) \Biggr) -\frac{1}{t} \Biggl(R_{j}+\sum_{i=1}^{n}C_{ji}N_{i} \Biggr). \end{aligned}$$

Applying Itô formula to (5), we can obtain

$$d\ln N_{i}= \biggl[\mu_{i}-m_{i}- \frac{1}{2}\bigl(\alpha_{i1}^{2}+\alpha_{i2}^{2} \bigr) \biggr]\,dt+\alpha_{i1}\,dB_{1}-\alpha_{i2} \,dB_{2}. $$

Integrating from 0 to t both sides of the above formula and then dividing by t, we get

$$\begin{aligned} \frac{\ln N_{i}}{t}={}&\frac{1}{t} \int_{0}^{t}\mu_{i}(s) \,ds-m_{i}-\frac{1}{2}\bigl(\alpha _{i1}^{2}+ \alpha_{i2}^{2}\bigr) \\ &{} +\frac{\alpha_{i1}B_{1}}{t}-\frac{\alpha_{i2}B_{2}}{t}+\frac{\ln N_{i}(0)}{t}. \end{aligned}$$
(25)

From assumption and (25), we obtain

$$\begin{aligned} \frac{\ln N_{i}}{t}\leq{}& \frac{1}{t}c \int_{0}^{t}R_{j}(s)\,ds-m_{i}- \frac {1}{2}\bigl(\alpha_{i1}^{2}+\alpha_{i2}^{2} \bigr) \\ &{}+\frac{\alpha_{i1}B_{1}}{t}-\frac{\alpha_{i2}B_{2}}{t}+\frac{\ln N_{i}(0)}{t} \\ \leq{}& -\frac{c}{D}m_{i}\max_{1\leq j\leq k}\sum _{l=1}^{n}C_{jl}\frac {1}{t} \int_{0}^{t}N_{l}(s)\,ds+c\max _{1\leq j\leq k}S_{j} \\ &{}-m_{i}-\frac{1}{2}\bigl(\alpha_{i1}^{2}+ \alpha_{i2}^{2}\bigr)+\beta_{i}(t) \\ ={}&c\max_{1\leq j\leq k}S_{j}- \biggl(m_{i}+ \frac{1}{2}\bigl(\alpha_{i1}^{2}+\alpha _{i2}^{2}\bigr) \biggr) \\ &{}-\frac{c}{D}m_{i}\max_{1\leq j\leq k}\sum _{l=1}^{n}C_{jl}\frac{1}{t} \int _{0}^{t}N_{l}(s)\,ds+ \beta_{i}(t), \end{aligned}$$

where \(\beta_{i}(t)=\frac{c\max_{j}\{\alpha_{j}(t)\}}{D}+\frac{\alpha _{i1}B_{1}}{t}-\frac{\alpha_{i2}B_{2}}{t}+\frac{\ln N_{i}(0)}{t}\). From Theorem 3 and the law of large numbers, we know that, when \(\max_{1\leq i\leq n}\{\alpha_{i1}^{2}+\alpha_{i2}^{2}\}<2D\) holds, \(\lim_{t\rightarrow \infty}\beta_{i}(t)=0\) a.s.

From the assumptions of the theorem, we get that for any \(1\leq i\leq n\), if \(m_{i}+\frac{1}{2}(\alpha_{i1}^{2}+\alpha_{i2}^{2})>c\max_{1\leq j\leq k}S_{j}\), and

$$ \limsup_{t\rightarrow\infty}\frac{\ln N_{i}(t)}{t}\leq c\max_{1\leq j\leq k}S_{j}- \biggl(m_{i}+\frac{1}{2}\bigl(\alpha_{i1}^{2}+ \alpha_{i2}^{2}\bigr) \biggr)< 0\quad \text{a.s.}\ (1\leq i\leq n), $$
(26)

then

$$\lim_{t\rightarrow\infty}N_{i}(t)=0 \quad \text{a.s.}, $$

which implies that the solution of system (5)–(6) becomes extinct in probability. □

Remark 2

From (26) we know that population will become extinct when the input of resources tends to zero.

Theorem 5

Assume that the noise intensity satisfies \(\max_{1\leq j\leq k}\{\alpha_{i1}^{2}+\alpha_{i2}^{2}\}<2D\). Then for any given initial condition \((N_{i}(0),R_{j}(0))\in R_{+}^{n}\times R_{+}^{k}\), if \(c_{i}\min_{1\leq j \leq k}\{S_{j}\}-m_{i}-\frac{1}{2}(\alpha_{i1}^{2}+\alpha _{i2}^{2})>0\) \((1\leq i \leq n)\), system (5)–(6) satisfies

$$\liminf_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t}N_{i}(s)\,ds\geq \frac {c_{i}\min_{1\leq j \leq k}\{S_{j}\}- m_{i}-\frac{1}{2}(\alpha_{i1}^{2}+\alpha _{i2}^{2})}{D}>0 \quad\textit{a.s.}\ (1\leq i\leq n), $$

that is, the solution of system (5)–(6) will be persistent in the mean.

Proof

Similarly as in the proof of Theorem 4, we can get

$$\begin{aligned} \frac{\ln N_{i}}{t}={}&\frac{1}{t} \int_{0}^{t}\mu_{i} \bigl(R_{1}(s),R_{2}(s), \dots ,R_{k}(s) \bigr)\,ds-m_{i}-\frac{1}{2}\bigl( \alpha_{i1}^{2}+\alpha_{i2}^{2}\bigr) \\ &{} +\frac{\alpha_{i1}B_{1}}{t}-\frac{\alpha_{i2}B_{2}}{t}+\frac{\ln N_{i}(0)}{t}. \end{aligned}$$
(27)

Notice that \(\mu_{i}(R_{1},R_{2},\dots,R_{k})=\min_{1\leq j\leq k}\{\frac {r_{i}R_{j}}{K_{ji}+R_{j}}\}\), where \(K_{ji}\leq S_{j}\), \(R_{j}\leq S_{j}\), so for any \(1\leq i\leq n, 1\leq j\leq k\),

$$\frac{r_{i}R_{j}}{K_{ji}+R_{j}}\geq\frac{r_{i}R_{j}}{2S_{j}}\geq\frac {r_{i}R_{j}}{2\max_{1\leq j\leq k}S_{j}}, $$

and then

$$\begin{aligned} \frac{\ln N_{i}}{t} \geq{}& \frac{r_{i}}{2\max_{1\leq j\leq k}S_{j}}\frac {1}{t} \int_{0}^{t}R_{j}(s)\,ds-m_{i}- \frac{1}{2}\bigl(\alpha_{i1}^{2}+\alpha_{i2}^{2} \bigr) \\ &{} +\frac{\alpha_{i1}B_{1}}{t}-\frac{\alpha_{i2}B_{2}}{t}+\frac{\ln N_{i}(0)}{t} \\ :={}& -c_{i}\sum_{i=1}^{n}C_{ji}m_{i} \frac{1}{t} \int_{0}^{t}N_{i}(s)\,ds+c_{i}S_{j} -m_{i}-\frac{1}{2}\bigl(\alpha_{i1}^{2}+ \alpha_{i2}^{2}\bigr)+\beta_{i}(t) \\ \geq{}&-D\frac{1}{t} \int_{0}^{t}N_{i}(s)\,ds+c_{i}S_{j} -m_{i}-\frac{1}{2}\bigl(\alpha_{i1}^{2}+ \alpha_{i2}^{2}\bigr)+\beta_{i}(t), \end{aligned}$$

where \(\beta_{i}(t)=\frac{c_{i}\min_{j}\{\alpha_{j}(t)\}}{D}+\frac{\alpha _{i1}B_{1}}{t}-\frac{\alpha_{i2}B_{2}}{t}+\frac{\ln N_{i}(0)}{t}\), \(c_{i}=\frac {r_{i}R_{j}}{2\max_{1\leq j\leq k}S_{j}}\).

Using Theorem 3 and the law of large numbers, \(\lim_{t\rightarrow\infty }\beta_{i}(t)=0\) a.s., whenever \(\max_{1\leq j\leq k}\{\alpha _{i1}^{2}, \alpha_{i2}^{2}\}<2D\) holds. From Lemma 5.1 of [28], we know that

$$\liminf_{t\rightarrow\infty}\frac{1}{t} \int_{0}^{t}N_{i}(s)\,ds\geq \frac {c_{i}S_{j}- m_{i}-\frac{1}{2}(\alpha_{i1}^{2}+\alpha_{i2}^{2})}{D}>0 \quad\text{a.s.}\ (1\leq i\leq n). $$

The proof is completed. □

6 Numerical examples

In this section we demonstrate the efficiency of the proposed condition of permanence and extinction with some illustrative examples.

Example 1

Consider the following two populations competing for two resources:

$$\begin{aligned} &dN_{1}=N_{1}(\mu_{1}-m_{1})\,dt+ \alpha_{11}N_{1}\,dB_{1}-\alpha_{12}N_{2} \,dB_{2}, \\ &dN_{2}=N_{2}(\mu_{2}-m_{2})\,dt+ \alpha_{21}N_{1}\,dB_{1}-\alpha_{22}N_{2} \,dB_{2}, \\ &dR_{1}= \bigl[D(S_{1}-R_{1})-C_{11} \mu_{1}N_{1}-C_{12}\mu_{2}N_{2} \bigr]\,dt -C_{11}\alpha_{11}N_{1} \,dB_{1}-C_{12}\alpha_{21}N_{2} \,dB_{1}, \\ &dR_{2}= \bigl[D(S_{2}-R_{2})-C_{21} \mu_{1}N_{1}-C_{22}\mu_{2}N_{2} \bigr]\,dt -C_{11}\alpha_{11}N_{1} \,dB_{1}-C_{12}\alpha_{21}N_{2} \,dB_{1}, \end{aligned}$$

where \(\mu_{1}(R_{1},R_{2})=\min (\frac{r_{1}R_{1}}{K_{11}+R_{1}},\frac {r_{1}R_{2}}{K_{21}+R_{2}} )\), \(\mu_{2}(R_{1},R_{2})=\min (\frac {r_{2}R_{1}}{K_{12}+R_{1}},\frac{r_{2}R_{2}}{K_{22}+R_{2}} )\).

Let \(\alpha_{11}=0.12\), \(\alpha_{12}=0.145\), \(\alpha_{21}=0.15\), \(\alpha _{22}=0.1\), \(r_{1}=0.35\), \(r_{2}=0.35\), \(K_{11}=0.4\), \(K_{12}=0.5\), \(K_{21}=0.3\), \(K_{22}=0.5\), \(m_{1}=0.5\), \(m_{2}=0.5\), \(S_{1}=411.5\), \(S_{2}=411.35\), \(D=0.2\), \(C_{11}=0.15\), \(C_{12}=0.15\), \(C_{21}=0.13\), \(C_{22}=0.15\).

Since

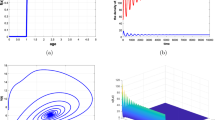
$$\max_{1\leq i\leq2}\bigl\{ \alpha_{i1}^{2}+ \alpha_{i2}^{2}\bigr\} =0.035< 2D=0.4. $$

Figure 1 illustrates that under given initial conditions, i.e., when \(N_{1}(t)=1\), \(N_{2}(t)=1\), \(R_{1}(t)=400\), \(R_{2}(t)=400\), \(N_{i}(t)\ (i=1, 2)\) will get extinct simultaneously since they satisfy the extinction condition, while only \(N_{2}\) will become extinct and \(N_{1}\) will stay alive permanently in Fig. 2.

Figure 1
figure 1

Time evolution of the system in Example 1 with initial condition \((1,400)\) when \(m_{1}=0.5\), \(m_{2}=0.5\)

Full size image
Figure 2
figure 2

Time evolution of the system in Example 1 with initial condition \((1,400)\) when \(m_{1}=0.325\), \(m_{2}=0.315\)

Full size image

Let \(\alpha_{11}=0.12\), \(\alpha_{12}=0.145\), \(\alpha_{21}=0.15\), \(\alpha _{22}=0.1\), \(r_{1}=0.35\), \(r_{2}=0.35\), \(K_{11}=0.4\), \(K_{12}=0.5\), \(K_{21}=0.3\), \(K_{22}=0.5\), \(m_{1}=0.325\), \(m_{2}=0.315\), \(S_{1}=411.5\), \(S_{2}=411.35\), \(C_{11}=0.15\), \(C_{12}=0.15\), \(C_{21}=0.13\), \(C_{22}=0.15\).

Since

$$\max_{1\leq i\leq2}\bigl\{ \alpha_{i1}^{2}+ \alpha_{i2}^{2}\bigr\} =0.035< 2D=0.4. $$

Figure 3 illustrates that population \(N_{1}\) will become extinct and \(N_{2}\) will be permanent, given the initial conditions \(N_{1}(t)=1\), \(N_{2}(t)=1\), \(R_{1}(t)=400\), \(R_{2}(t)=400\).

Figure 3
figure 3

Time evolution of the system in Example 1 with initial condition \((1,400)\) when \(m_{2}=0.325\), \(m_{1}=0.315\)

Full size image

Let \(\alpha_{11}=0.12\), \(\alpha_{12}=0.145\), \(\alpha_{21}=0.15\), \(\alpha _{22}=0.1\), \(r_{1}=0.35\), \(r_{2}=0.35\), \(K_{11}=0.4\), \(K_{12}=0.5\), \(K_{21}=0.3\), \(K_{22}=0.5\), \(m_{1}=0.5\), \(m_{2}=0.315\), \(S_{1}=411.5\), \(S_{2}=411.35\), \(C_{11}=0.15\), \(C_{12}=0.15\), \(C_{21}=0.13\), \(C_{22}=0.15\).

Since

$$\max_{1\leq i\leq2}\bigl\{ \alpha_{i1}^{2}+ \alpha_{i2}^{2}\bigr\} =0.035< 2D=0.4. $$

Figure 4 illustrates that population \(N_{1}\) and \(N_{2}\) will be both permanent, given the initial conditions \(N_{1}(t)=1\), \(N_{2}(t)=1\), \(R_{1}(t)=400\), \(R_{2}(t)=400\).

Figure 4
figure 4

Time evolution of the system in Example 1 with initial condition \((1,400)\) when \(m_{1}=0.5\), \(m_{2}=0.315\)

Full size image

More precisely, it can be observed that the populations get extinct or will both be permanent depending on the relationship between the intensity of environmental noises \(\alpha_{i}\), death rate \(m_{i}\), transformation rate of system D and supply of resources \(S_{i}\). That is, having enough resources and a lower death rate is beneficial to the survival of the population (see Fig. 4), and on the contrary, if there is a high-intensity environmental fluctuation, the population may suffer extinction (see Figs. 1–3). Thus, the environmental noise may affect the evolution trend of a population.

7 Conclusion

From a biological point of view, it is an interesting topic to consider the survival of the resource competition system with stochastic surrounding noises. In this paper, we suppose that the birth and death rates of the population system are both influenced by white noises of different intensity, and then study the stochastic resources’ competition system with n populations competing for k necessary resources. By using stochastic analysis, stochastic final boundedness of the ith population, moment boundedness and extinction or permanence under certain conditions in the system (5)–(6) are obtained. It is found that the requirement of white noise is identical with those in existing results, that is, populations will get extinct when the noise is very strong. Furthermore, a path estimate of the ith population is also obtained. For resources’ competition system, the birth rate of the population described by the minimum function is indeed affected by the number of resources, which is compatible with the known theory, in which those who have the least resource consumption will maintain persistence. However, as we know, there are many different random perturbations that should be considered, such as the telephone noise, Levy noise, etc. Due to the complexity of the system with n populations competing for k resources, in this paper, we only consider the white noise, however, we can consider the Markovian switching into model (5)–(6) in future, which takes the following form:

$$\begin{aligned} &dN_{i}(t)= N_{i}(t) \bigl(\mu_{i}\bigl(\xi(t) \bigr)-m_{i}\bigl(\xi(t)\bigr)\bigr)\,dt +\alpha_{i1}\bigl( \xi(t)\bigr)N_{i}(t)\,dB_{1}(t)-\alpha_{i2}\bigl( \xi(t)\bigr)N_{i}(t)\,dB_{2}(t), \\ &dR_{j}(t)= D\bigl(S_{j}-R_{j}(t)\bigr)\,dt-\sum _{i=1}^{n}C_{ji}\mu_{i} \bigl(\xi(t)\bigr)N_{i}\,dt -\sum_{i=1}^{n}C_{ji} \alpha_{i1}\bigl(\xi(t)\bigr)N_{i}(t)\,dB_{1}(t), \end{aligned}$$

where \(i=1,2,\dots,n\), \(j=1,2,\dots,k\), \(\xi(t)\) is a right-continuous Markov chain on a finite state space \(S={1,2,\dots,N}\) (for the definition of a Markov chain, the readers can see [29, 30]).