1 Introduction

Mathematical modeling plays an important role in understanding the dynamics of many infectious diseases. Thus, the use of modeling is crucial in order to analyze the spread, control strategies and the mechanisms of transmission of diseases. Over the years, numerous epidemiological models have been formulated mathematically (see, e.g., [1–6]). Although most of these models have been restricted to integer-order differential equations (IDEs), in the last three decades, it has turned out that many problems in different fields such as sciences, engineering, finance, economics and in particular epidemiology can be described successfully by the fractional-order differential equations (FDEs) (see, e.g., [7–12]). A property of these fractional-order models is their nonlocal property which does not exist in IDEs. Nonlocal property means that the next state of a model depends not only upon its current state but also upon all of its historical states [13]. The transformation of an integer-order model into a fractional-order model needs to be precise as to the order of differentiation α: a small change in α may cause a big change in the final results [14]. FDEs can be used to model certain phenomena which cannot be adequately modeled by IDEs [15]. FDEs are commonly used on biological systems since they are related in a natural way to systems with memory. Similar to a nonlinear differential system, a nonlinear fractional differential system may also have complex dynamics, such as chaos and bifurcation. Studying chaos in fractional-order dynamical systems is an attractive and interesting topic [16].

Discrete models constructed by the discretization of continuous models have been used to describe some epidemic models. Many significant and meaningful types of such research can be found in [17–27] and the references therein. The reason for the use of discrete models is that statistical data on epidemics are collected in discrete times and hence comparing data with output of a discrete model may be easier [28]. In general, the dynamical behavior of discrete fractional-order epidemic models may exhibit phenomena such as the period-doubling and chaotic behavior. Iwami et al. [29] have proposed a mathematical model in a continuous-time version to interpret a model of the spread of avian–human influenza epidemic. In [29], the dynamics of the spread into bird population and between bird and human populations have been thoroughly studied. The main objective of the current study is to extend the research done in [29] by employing fractional models with discrete-time systems. In this paper, a discrete-time SI is established by SI fractional-order epidemic model. This model contains two parameters in addition to those already existing in the original SI model proposed in [29]; time step parameter and fractional-order parameter. The occurrence of bifurcations as these parameters are varied is shown in Section 7. The stability of fixed points, the emergence of flip bifurcation and Neimark–Sacker bifurcation are also studied. Using the discretized-time SI model with fractional order is a new topic, thus this paper provides a new contribution to the literature.

This paper is organized as follows. In Section 2, the fractional-time SI epidemic model from its continuous-time counterpart is constructed. In Section 3, the discretized-time SI model with fractional-order parameter is established. Section 4 discusses the existence and stability of fixed points of the discretized-time SI model with fractional order. In Sections 5 and 6, flip and Neimark–Sacker bifurcations are demonstrated, respectively. In Section 7, some numerical examples are shown. A brief discussion of our results is given in Section 8.

2 The FDE epidemic model

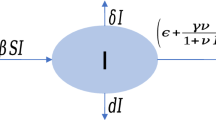
Let us consider the following IDE epidemic model:

$$ \begin{gathered} \frac{dS(t)}{dt} =\Lambda-\mu S-\beta SI, \\ \frac{dI(t)}{dt} =\beta SI- ( \mu+r ) I.\end{gathered} $$
(2.1)

This model is constructed by Iwami et al. [29] to explain the spreads of avian influenza through the bird world and describes the interactions between them. The population in this model is divided into susceptible birds with size S and infected birds with size I. The new birds birth rate is expressed by the parameter Λ. Susceptible birds die at the rate μ and infected birds die at the rate \(\mu+r\), where r is the additional death rate mediated by avian influenza. The parameter β is the bilinear incidence rate.

There are several definitions of fractional derivatives [30, 31]. One of the most common definitions is the Caputo definition [32]. This definition is often used in real applications and shown in Definition 1.

Definition 1

The fractional integral of order \(\beta\in \mathbb{R} ^{+}\) of the function \(f(t)\), \(t>0\), is defined by

$$I^{\beta}f(t)=\int_{0}^{t}\frac{ ( t-s ) ^{\beta-1}}{\Gamma ( \beta ) }f ( s ) \,ds,$$

and the fractional derivative of order \(\alpha\in ( n-1,n ) \) of \(f ( t ) \), \(t>0\), is defined by

$$D^{\alpha}f ( t ) =I^{n-\alpha}D^{n}f ( t ) ,\quad \alpha>0,$$

where \(f^{(n)}\) represents the nth order derivative of \(f(t)\), \(n=[\alpha]\) is the value of α rounded up to the nearest integer, \(I^{\beta}\)is the βth order Riemann-Liouville integer operator and \(\Gamma(\cdot)\) is Euler’s Gamma function. The operator \(D^{\alpha}\) is called the ‘αth order Caputo differential operator’.

Now, the fractional-order form of the SI epidemic model (2.1) can be formulated as follows:

$$ \begin{gathered} D_{t}^{\alpha}S(t) =\Lambda-\mu S-\beta SI, \\ D_{t}^{\alpha}I(t) =\beta SI- ( \mu+r ) I,\end{gathered} $$
(2.2)

where \(D_{t}^{\alpha}\) represents the Caputo fractional derivative, \(t>0\), and α is the fractional order satisfying \(\alpha\in ( 0,1 ] \).

3 Discretization process

There are many discretization methods that have been used to construct the discrete-time model using continuous-time methods such as explicit and implicit Euler’s method, Runge–Kutta method, predictor-corrector method and nonstandard finite difference methods [33–37]. Some of them are approximation for the derivative and some for the integral. In [38, 39] a discretization process was introduced to discretize FDEs. This discretization method is an approximation for the right hand side of the differential equation has the formula \(D^{\alpha}x ( t ) =f ( x ( t ) ) \), \(t>0\), \(\alpha\in ( 0,1 ) \). This method is now applied to the fractional-order SI model (2.2). Assume that \(S ( 0 ) =S_{0}\) and \(I ( 0 ) =I_{0}\) are the initial conditions of system (2.2). So, the discretization of the system (2.2) is given by the following formulas:

$$ \begin{gathered} D^{\alpha}S(t) =\Lambda-\mu S \biggl( \biggl[ \frac{t}{x} \biggr] x \biggr) -\beta S \biggl( \biggl[ \frac{t}{x} \biggr] x \biggr) I \biggl( \biggl[ \frac{t}{x} \biggr] x \biggr) , \\ D^{\alpha}I(t) =\beta S \biggl( \biggl[ \frac{t}{x} \biggr] x \biggr) I \biggl( \biggl[ \frac{t}{x} \biggr] x \biggr) - ( \mu+r ) I \biggl( \biggl[ \frac{t}{x} \biggr] x \biggr) .\end{gathered} $$
(3.1)

First, let \(t\in[ 0,h ) \), \(t/h\in [ 0,1 ) \). Then

$$ \begin{gathered} D_{t}^{\alpha}S(t) =\Lambda-\mu S_{0}-\beta S_{0}I_{0}, \\ D_{t}^{\alpha}I(t) =\beta S_{0}I_{0}- ( \mu+r ) I_{0},\end{gathered} $$
(3.2)

and the solution of (3.2) reduces to

$$ \begin{gathered} S_{1}(t) =S_{0}+J^{\alpha} [ \Lambda-\mu S_{0}-\beta S_{0}I_{0} ] =S_{0}+\frac{t^{\alpha}}{\Gamma ( 1+\alpha ) } [ \Lambda -\mu S_{0}-\beta S_{0}I_{0} ] , \\ I_{1}(t) =I_{0}+J^{\alpha} \bigl[ \beta S_{0}I_{0}- ( \mu+r ) I_{0} \bigr] =I_{0}+\frac{t^{\alpha}}{\Gamma ( 1+\alpha ) } \bigl[ \beta S_{0}I_{0}- ( \mu+r ) I_{0} \bigr] .\end{gathered} $$
(3.3)

Second, let \(t\in [ h,2h ) \), which makes \(1\leqslant t/h<2\). Thus, we obtain

$$ \begin{gathered} D_{t}^{\alpha}S(t) =\Lambda-\mu S_{1}-\beta S_{1}I_{1}, \\ D_{t}^{\alpha}I(t) =\beta S_{1}I_{1}- ( \mu+r ) I_{1},\end{gathered} $$
(3.4)

which have the following solutions:

$$ \begin{gathered} S_{2} ( t ) =S_{1} ( x ) +\frac{ ( t-h ) ^{\alpha}}{\Gamma ( 1+\alpha ) } \bigl[ \Lambda-\mu S_{1} ( x ) -\beta S_{1} ( x ) I_{1} ( x ) \bigr] , \\ I_{2}(t) =I_{1} ( x ) +\frac{ ( t-h ) ^{\alpha}}{\Gamma ( 1+\alpha ) } \bigl[ \beta S_{1} ( x ) I_{1} ( x ) - ( \mu+r ) I_{1} ( x ) \bigr] .\end{gathered} $$
(3.5)

Repeating the discretization process n times yields

$$ \begin{gathered} S_{n+1}(t) =S_{n} ( nx ) +\frac{ ( t-nh ) ^{\alpha}}{\Gamma ( 1+\alpha ) } \bigl[ \Lambda- \mu S_{n}(nx)-\beta S_{n}(nx)I_{n}(nx) \bigr] , \\ I_{n+1}(t) =I_{n} ( nx ) +\frac{ ( t-nh ) ^{\alpha}}{\Gamma ( 1+\alpha ) } \bigl[ \beta S_{n}(nx)I_{n}(nx)- ( \mu+r ) I_{n}(nx) \bigr] ,\end{gathered} $$
(3.6)

where \(t\in [ nh, ( n+1 ) h ) \). For \(t\rightarrow ( n+1 ) h\), system (3.6) is reduced to

$$ \begin{gathered} S_{n+1} =S_{n}+\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) } [ \Lambda-\mu S_{n}-\beta S_{n}I_{n} ] , \\ I_{n+1} =I_{n}+\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) } \bigl[ \beta S_{n}I_{n}- ( \mu+r ) I_{n} \bigr] .\end{gathered} $$
(3.7)

Remark 3.1

It should be noticed that if \(\alpha\rightarrow1\) in (3.7), the Euler discretization of SI model is obtained.

4 Stability of fixed points

In this section, an approach as in [40] is employed. The stability of the system (3.7) is studied around its fixed points. It is clear that the model (3.7) has always a disease free equilibrium point \(E_{0}=(\frac{\Lambda}{\mu},0)\) and an endemic equilibrium point \(E_{1}= ( \frac{\mu+r}{\beta},\frac{\Lambda}{\mu+r}-\frac{\mu}{\beta} ) \). Furthermore, the system (3.7) has basic reproduction number \(\Re_{0}=\frac{\beta\Lambda}{\mu ( \mu+r ) }>1\), then \(E_{1}\) can be reformulated as \(E_{1}= ( \frac{\mu+r}{\beta},\frac{\mu ( \Re _{0}-1 ) }{\beta} ) \). It can be seen that the free equilibrium point \(E_{0}\) always exists while the positive endemic \(E_{1}\) exists only when \(\Re_{0}>1\). So as to analyze the dynamical properties of (3.7), we compute the Jacobian matrix J of (3.7), and we evaluate at the fixed point \(E= ( S^{\ast},I^{\ast} ) \)

$$ J \bigl( S^{\ast},I^{\ast} \bigr) =\left ( \textstyle\begin{array} {c@{\quad}c}1-\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) } ( \mu+\beta I^{\ast } ) & -\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) }\beta S^{\ast }\\ \frac{h^{\alpha}}{\Gamma ( 1+\alpha ) }\beta I^{\ast} & 1+\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) } ( \beta S^{\ast}-\mu-r ) \end{array}\displaystyle \right ) . $$
(4.1)

In order to study the stability of the fixed points of the system (3.7), the two following lemmas are employed.

Lemma 4.1

([41, 42])

Let \(\lambda_{1}\) and \(\lambda_{2}\) be the two roots of matrix \(J ( M ) \), we have the following definitions:

  1. (i)

    If \(\vert \lambda_{1} \vert <1\) and \(\vert \lambda _{2} \vert <1\), then the equilibrium point of \(M ( x^{\ast },y^{\ast } ) \) is locally asymptotically stable (sink).

  2. (ii)

    If \(\vert \lambda_{1} \vert >1\) and \(\vert \lambda _{2} \vert >1\), then the equilibrium point of \(M ( x^{\ast },y^{\ast } ) \) is unstable (source).

  3. (iii)

    If \(\vert \lambda_{1} \vert <1\) and \(\vert \lambda _{2} \vert >1\) (or \(\vert \lambda_{1} \vert >1\) and \(\vert \lambda_{2} \vert <1\)), then the equilibrium point of \(M ( x^{\ast},y^{\ast} ) \) is unstable (saddle).

  4. (iv)

    If \(\vert \lambda_{1} \vert =1\) or \(\vert \lambda _{2} \vert =1\), then the equilibrium point of \(M ( x^{\ast },y^{\ast } ) \) is called non-hyperbolic.

Lemma 4.2

([43, 44])

Let \(F ( \lambda ) =\lambda^{2}-\operatorname{Tr}\lambda+\mathrm{Det}\). Suppose that \(F ( 1 ) >0\), \(\lambda_{1}\), \(\lambda_{2}\) are the two roots of \(F ( \lambda ) =0\). Then

  1. (i)

    \(\vert \lambda_{1} \vert <1\) and \(\vert \lambda _{2} \vert <1\) if and only if \(F ( -1 ) >0\) and \(\mathrm{Det}<1\);

  2. (ii)

    \(\vert \lambda_{1} \vert <1\) and \(\vert \lambda _{2} \vert >1\) or (\(\vert \lambda_{1} \vert >1\) and \(\vert \lambda_{2} \vert <1 \)) if and only if \(F ( -1 ) <0\);

  3. (iii)

    \(\vert \lambda_{1} \vert >1\) and \(\vert \lambda _{2} \vert >1\) if and only if \(F ( -1 ) >0\) and \(\mathrm{Det}>1\);

  4. (iv)

    \(\lambda_{1}=-1\) and \(\lambda_{2}\neq1\) if and only if \(F ( -1 ) =0\) and \(\mathrm{Tr}\neq0,2\);

  5. (v)

    \(\lambda_{1}\) and \(\lambda_{2}\) are complex and \(\vert \lambda _{1} \vert = \vert \lambda_{2} \vert \) if and only if \(\mathrm{Tr}^{2}-4\mathrm{Det}<0\) and \(\mathrm{Det}=1\).

Based on Lemmas 4.1 and 4.2, the following results can be achieved.

Theorem 4.3

If \(\Re_{0}<1\), then the free-equilibrium point \(E_{0}\) has at least four different topological types for all its values of parameters

  1. (i)

    \(E_{0}\) is a sink if \(0< h<\min \{ \sqrt[\alpha]{\frac{2\Gamma (1+\alpha)}{\mu}},\sqrt[\alpha]{\frac{2\Gamma(1+\alpha)}{ ( \mu +r ) ( 1-\Re_{0} ) }} \} \).

  2. (ii)

    \(E_{0}\) is a source if \(h>\max \{ \sqrt[\alpha]{\frac{2\Gamma (1+\alpha)}{\mu}},\sqrt[\alpha]{\frac{2\Gamma(1+\alpha)}{ ( \mu +r ) ( 1-\Re_{0} ) }} \} \).

  3. (iii)

    \(E_{0}\) is a saddle if \(\sqrt[\alpha]{\frac{2\Gamma(1+\alpha )}{ ( \mu+r ) ( 1-\Re_{0} ) }}< h<\sqrt[\alpha]{\frac {2\Gamma(1+\alpha)}{\mu}}\) or \(\sqrt[\alpha]{\frac{2\Gamma(1+\alpha )}{\mu}}< h<\sqrt[\alpha]{\frac{2\Gamma(1+\alpha)}{ ( \mu+r ) ( 1-\Re_{0} ) }}\).

  4. (iv)

    \(E_{0}\) is non-hyperbolic if \(h=\sqrt[\alpha]{\frac{2\Gamma (1+\alpha )}{\mu}}\) or \(h=\sqrt[\alpha]{\frac{2\Gamma(1+\alpha)}{ ( \mu +r ) ( 1-\Re_{0} ) }}\).

Proof

The Jacobian matrix of \(E_{0}\) is

$$J ( E_{0} ) =\left ( \textstyle\begin{array} {c@{\quad}c}1-\frac{h^{\alpha}\mu}{\Gamma ( 1+\alpha ) } & \frac{-h^{\alpha }\beta\Lambda}{\mu\Gamma ( 1+\alpha ) }\\ 0 & 1-\frac{h^{\alpha}(\mu+r) ( 1-\Re_{0} ) }{\Gamma ( 1+\alpha ) }\end{array}\displaystyle \right ).$$

The eigenvalues of \(J ( E_{0} ) \) are \(\lambda _{1}=1-\frac{h^{\alpha}\mu}{\Gamma ( 1+\alpha ) }\) and \(\lambda _{2}=1-\frac{h^{\alpha}(\mu+r) ( 1-\Re_{0} ) }{\Gamma ( 1+\alpha ) }\) where \(0<\alpha\leqslant1\) and h, \(\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) }>0\). Hence applying the stability conditions using Lemma 4.1 the results (i)–(iv) can be achieved. □

Theorem 4.4

If \(\Re_{0}>1\), we have

  1. (i)

    \(E_{1}\) is asymptotically stable (sink) if one of the following conditions holds:

    1. (i.1)

      \(\Delta\geqslant0\) and \(0< h< h_{1}\).

    2. (i.2)

      \(\Delta<0\) and \(0< h< h_{2}\).

  2. (ii)

    \(E_{1}\) is unstable (source) if one of the following conditions holds:

    1. (ii.1)

      \(\Delta\geqslant0\) and \(h>h_{3}\).

    2. (ii.2)

      \(\Delta<0\) and \(h>h_{2}\).

  3. (iii)

    \(E_{1}\) is unstable (saddle) if \(\Delta\geqslant0\) and \(h_{1}< h< h_{3}\).

  4. (iv)

    \(E_{1}\) is non-hyperbolic if one of the following conditions holds:

    1. (iv.1)

      \(\Delta\geqslant0\) and \(h=h_{1}\) or \(h_{3}\),

    2. (iv.2)

      \(\Delta<0\) and \(h=h_{2}\),

    where

    $$\begin{gathered} h_{1}=\sqrt[\alpha]{\frac{ ( \mu\Re_{0}-\sqrt{\Delta} ) \Gamma(1+\alpha)}{\mu ( \mu+r ) ( \Re_{0}-1 ) }}, \\ h_{2}=\sqrt[\alpha]{\frac{\Re_{0}\Gamma(1+\alpha)}{ ( \mu+r ) ( \Re_{0}-1 ) }}, \\ h_{3}=\sqrt[\alpha]{\frac{ ( \mu\Re_{0}+\sqrt{\Delta} ) \Gamma(1+\alpha)}{\mu ( \mu+r ) ( \Re_{0}-1 ) }},\end{gathered} $$

    and

    $$\Delta= \bigl[ \mu ( \Re_{0}-2 ) \bigr] ^{2}-4\mu r ( \Re_{0}-1 ) .$$

Proof

The Jacobian matrix of \(E_{1}\) can be written as

$$J ( E_{1} ) =\left ( \textstyle\begin{array} {c@{\quad}c}1-\frac{h^{\alpha}\mu\Re_{0}}{\Gamma ( 1+\alpha ) } & \frac{-h^{\alpha} ( \mu+r ) }{\Gamma ( 1+\alpha ) }\\ \frac{h^{\alpha}\mu ( \Re_{0}-1 ) }{\Gamma ( 1+\alpha ) } & 1 \end{array}\displaystyle \right ) .$$

The characteristic equation of \(J ( E_{1} ) \) has the form

$$\lambda^{2}-\mathrm{Tr} \bigl( J ( E_{1} ) \bigr) \lambda+\mathrm{Det} \bigl( J ( E_{1} ) \bigr) =0,$$

where

$$\mathrm{Tr} \bigl( J ( E_{1} ) \bigr) =2-\frac{h^{\alpha}\mu\Re_{0}}{\Gamma ( 1+\alpha ) }$$

and

$$\mathrm{Det} \bigl( J ( E_{1} ) \bigr) =\frac{h^{2\alpha}\mu ( \mu+r ) ( \Re_{0}-1 ) }{\Gamma^{2} ( 1+\alpha ) }-\frac{h^{\alpha}\mu\Re_{0}}{\Gamma ( 1+\alpha ) }+1.$$

Then the characteristic equation \(J ( E_{1} ) \) has two eigenvalues, which are

$$\lambda_{1,2}=1-\frac{h^{\alpha}\mu\Re_{0}}{2\Gamma ( 1+\alpha ) }\pm\frac{h^{\alpha}\sqrt{\Delta}}{2\Gamma ( 1+\alpha ) }.$$

By applying Lemmas 4.1, 4.2 and the Jury conditions [45], the stability conditions (i)–(iv) can be achieved. □

From the above analysis if the statement (iv.1) of Theorem 4.4 holds, then one of the eigenvalues of \(J ( E_{1} ) \) is −1 and the other is neither 1 nor −1. The statement (iv.1) can be reformulated as follows:

$$( \alpha,h,\beta,\Lambda,\mu,r ) \in\Omega_{1}\cup\Omega _{2},$$

where

$$\Omega_{1}= \bigl\{ ( \alpha,h,\beta,\Lambda,\mu,r ) :h=h_{1},\Delta\geq0,\Re_{0}>1 \bigr\} ,$$

and

$$\Omega_{2}= \bigl\{ ( \alpha,h,\beta,\Lambda,\mu,r ) :h=h_{3},\Delta\geq0,\Re_{0}>1 \bigr\} .$$

If the parameter h varies in the neighborhood of \(h_{1}\) and \(( \alpha,h,\beta,\Lambda,\mu,r ) \in\Omega_{1}\) or \(h_{3}\) and \(( \alpha,h,\beta,\Lambda,\mu,r ) \in\Omega_{2}\), the system (3.7) may undergo a flip bifurcation of equilibrium \(E_{1}\).

When the statement (iv.2) of Theorem 4.4 holds, then the two eigenvalues of \(J ( E_{1} ) \) are a pair of conjugate complex numbers and the modules of each of them equals 1. The statement (iv.2) can be reformulated as follows:

$$( \alpha,h,\beta,\Lambda,\mu,r ) \in\Omega_{3},$$

where

$$\Omega_{3}= \bigl\{ ( \alpha,h,\beta,\Lambda,\mu,r ) :h=h_{2},\Delta< 0,\Re_{0}>1 \bigr\} .$$

If the parameter h varies in the neighborhood of \(h_{2}\) and \(( \alpha,h,\beta,\Lambda,\mu,r ) \in\Omega_{3}\), the system (3.7) may undergo a Neimark–Sacker bifurcation of equilibrium \(E_{1}\).

5 Flip bifurcation analysis

Flip bifurcation of the equilibrium point \(E_{1}\) when parameters \(( \alpha,h,\beta,\Lambda,\mu,\gamma ) \) vary in the small neighborhood of \(\Omega_{1}\) or \(\Omega_{2}\) is discussed in this section. Let \(A_{1}=\frac{h^{\alpha}}{\Gamma ( 1+\alpha ) }\) and \(A_{\ast}\) be a perturbation of bifurcation parameter, then a perturbed form of model (3.7) can be formulated as follows:

$$ \begin{gathered} S_{n+1} =S_{n}+ ( A_{1}+A_{\ast} ) [ \Lambda-\mu S_{n}-\beta S_{n}I_{n} ] , \\ I_{n+1} =I_{n}+ ( A_{1}+A_{\ast} ) \bigl[ \beta S_{n}I_{n}- ( \mu+r ) I_{n} \bigr] .\end{gathered} $$
(5.1)

We translate \(E_{1} ( S^{\ast},I^{\ast} ) \) to the origin by using transformations \(X_{n}=S_{n}-S^{\ast}\) and \(Y_{n}=I_{n}-I^{\ast}\). Then (5.1) can reformulated as follows:

$$ \left ( \textstyle\begin{array}{c}X_{n+1}\\ Y_{n+1}\end{array}\displaystyle \right ) =\left ( \textstyle\begin{array}{c}a_{11}X_{n}+a_{12}Y_{n}+a_{13}X_{n}Y_{n}+ ( b_{11}X_{n}+b_{12}Y_{n}+b_{13}X_{n}Y_{n} ) A_{\ast}\\ a_{21}X_{n}+a_{22}Y_{n}+a_{23}X_{n}Y_{n}+ ( b_{21}X_{n}+b_{22}Y_{n}+b_{23}X_{n}Y_{n} ) A_{\ast}\end{array}\displaystyle \right ) , $$
(5.2)

where

$$\begin{gathered} a_{11}=1-\mu\Re_{0}A_{1},\qquad a_{12}=- ( \mu+r ) A_{1}, \qquad a_{13}=-\beta A_{1}, \\ b_{11}=-\mu\Re_{0}, \qquad b_{12}=- ( \mu+r ) ,\qquad b_{13}=-\beta, \\ a_{21}=\mu ( \Re_{0}-1 ) A_{1},\qquad a_{22}=1, \qquad a_{23}=\beta A_{1}, \\ b_{21}=\mu ( \Re_{0}-1 ) , \qquad b_{22}=0,\qquad b_{23}= \beta,\end{gathered}$$

and \(A=A_{1}\).

Let \(T_{1}=\bigl( {\scriptsize\begin{matrix}{}a_{11} & a_{12}\cr a_{21} & a_{22}\end{matrix}} \bigr) \), then the generalized eigenvectors of \(T_{1}\) corresponding to the eigenvalues \(\lambda_{1}\) and \(\lambda_{2}\) where \(\lambda_{1}=-1\) and \(\vert \lambda_{2} \vert \neq1\) are \(\bigl( {\scriptsize\begin{matrix}{} K_{1}\cr K_{2}\end{matrix}} \bigr) =K_{2}\bigl( {\scriptsize\begin{matrix}{} \frac{-a_{12}}{1+a_{11}}\cr 1 \end{matrix}} \bigr) \) and \(\bigl( {\scriptsize\begin{matrix}{} K_{3}\cr K_{4}\end{matrix}} \bigr) =K_{4}\bigl( {\scriptsize\begin{matrix}{} \frac{-a_{12}}{a_{11}-\lambda_{2}}\cr 1 \end{matrix}} \bigr) \), respectively. Here, we choose \(K_{2}=- ( 1+a_{11} ) \) and \(K_{4}=- ( a_{11}-\lambda_{2} ) \). Then we have an invertible matrix \(T_{2}=\bigl( {\scriptsize\begin{matrix}{} K_{1} & K_{3}\cr K_{2} & K_{4}\end{matrix}} \bigr) =\bigl( {\scriptsize\begin{matrix}{} a_{12} & a_{12}\cr -1-a_{11} & \lambda_{2}-a_{11}\end{matrix}} \bigr) \). Consider the following transformation:

$$\left ( \textstyle\begin{array} {c}X_{n}\\ Y_{n}\end{array}\displaystyle \right ) =T_{2}\left ( \textstyle\begin{array} {c}u_{n}\\ \upsilon_{n}\end{array}\displaystyle \right ) .$$

Taking \(T_{2}^{-1}\) on both sides of (5.2), we obtain

$$ \left ( \textstyle\begin{array} {c}u_{n+1}\\ \upsilon_{n+1}\end{array}\displaystyle \right ) =\left ( \textstyle\begin{array} {c@{\quad}c}-1 & 0\\ 0 & \lambda_{2}\end{array}\displaystyle \right ) \left ( \textstyle\begin{array} {c}u_{n}\\ \upsilon_{n}\end{array}\displaystyle \right ) +\left ( \textstyle\begin{array} {c}f_{1} ( X_{n},Y_{n},A_{\ast} ) \\ f_{2} ( X_{n},Y_{n},A_{\ast} ) \end{array}\displaystyle \right ) , $$
(5.3)

where

$$\begin{gathered} \begin{aligned}f_{1} ( X_{n},Y_{n},A_{\ast} ) ={}&\frac{ ( \lambda_{2}-a_{11} ) }{a_{12} ( \lambda_{2}+1 ) } \bigl( a_{13}X_{n}Y_{n}+ ( b_{11}X_{n}+b_{12}Y_{n}+b_{13}X_{n}Y_{n} ) A_{\ast } \bigr) \\ &-\frac{1}{ ( \lambda _{2}+1 ) } \bigl( a_{23}X_{n}Y_{n}+ ( b_{21}X_{n}+b_{22}Y_{n}+b_{23}X_{n}Y_{n} ) A_{\ast} \bigr) ,\end{aligned} \\ \begin{aligned}f_{2} ( X_{n},Y_{n},A_{\ast} ) ={}&\frac{ ( a_{11}+1 ) }{a_{12} ( \lambda_{2}+1 ) } \bigl( a_{13}X_{n}Y_{n}+ ( b_{11}X_{n}+b_{12}Y_{n}+b_{13}X_{n}Y_{n} ) A_{\ast} \bigr) \\ &+\frac{1}{ ( \lambda _{2}+1 ) } \bigl( a_{23}X_{n}Y_{n}+ ( b_{21}X_{n}+b_{22}Y_{n}+b_{23}X_{n}Y_{n} ) A_{\ast} \bigr) ,\end{aligned} \\ X_{n}=a_{12} ( u_{n}+\upsilon_{n} ) ,\qquad Y_{n}=- ( 1+a_{11} ) u_{n}+ ( \lambda_{2}-a_{11} ) \upsilon_{n},\end{gathered}$$

and

$$X_{n}Y_{n}=-a_{12} ( 1+a_{11} ) u_{n}^{2}+a_{12} ( \lambda_{2}-2a_{11}-1 ) u_{n}\upsilon_{n}+a_{12} ( \lambda _{2}-a_{11} ) \upsilon_{n}^{2}.$$

Now, the center manifold \(W^{c} ( 0,0,0 ) \) of (5.3) at the fixed point \(( 0,0 ) \) in a small neighborhood of \(A_{\ast}=0\) can be formulated. Hence, based on the center manifold theorem, we know there exists a center manifold

$$W^{c} ( 0,0,0 ) = \bigl\{ ( u_{n},\upsilon _{n},A_{\ast} ) \in \mathbb{R} ^{3}:\upsilon_{n}=\varphi ( u_{n},A_{\ast} ) ,\varphi ( 0,0 ) =0,D\varphi ( 0,0 ) =0 \bigr\} , $$

for \(u_{n}\), \(A_{\ast}\) sufficiently small. We assume a center manifold of the form

$$\varphi ( u_{n},A_{\ast} ) =a_{1}u_{n}^{2}+a_{2}A_{\ast}u_{n}+0 \bigl( \bigl( \vert u_{n} \vert + \vert A_{\ast } \vert \bigr) ^{3} \bigr) , $$

which must satisfy

$$ \begin{aligned}[b] N \bigl( \varphi ( u_{n},A_{\ast} ) \bigr)& =\varphi \bigl( -u_{n}+f_{1} \bigl( u_{n},\varphi ( u_{n},A_{\ast} ) \bigr) ,A_{\ast} \bigr) - \lambda_{2}\varphi ( u_{n},A_{\ast} ) -f_{2} \bigl( u_{n},\varphi ( u_{n},A_{\ast} ) ,A_{\ast} \bigr) \\& =0.\end{aligned} $$
(5.4)

By equating coefficients of like powers in (5.4) to zero, we obtain

$$\begin{gathered} a_{1}=\frac{ ( 1+a_{11} ) [ a_{13} ( 1+a_{11} ) +a_{12}a_{23} ] }{\lambda_{2}^{2}-1},\\ a_{2}=\frac{ ( 1+a_{11} ) [ b_{12} ( 1+a_{11} ) -a_{12}b_{11} ] }{a_{12} ( \lambda_{2}+1 ) ^{2}}+\frac{b_{22} ( 1+a_{11} ) -a_{12}b_{21}}{ ( \lambda_{2}+1 ) ^{2}}.\end{gathered}$$

Therefore, the map f, which is model (3.7) restricted to the center manifold \(W^{c} ( 0,0,0 ) \) takes the form

$$ f ( u_{n} ) =-u_{n}+\varphi_{1}u_{n}A_{\ast}+ \varphi_{2}u_{n}A_{\ast}^{2}+ \varphi_{3}u_{n}^{2}+\varphi_{4}u_{n}^{2}A_{\ast}+ \varphi_{5}u_{n}^{3}+0 \bigl( \bigl( \vert u_{n} \vert + \vert A_{\ast} \vert \bigr) ^{4} \bigr) , $$
(5.5)

where

$$ \begin{gathered} \varphi_{1} =\frac{1}{a_{12} ( \lambda_{2}+1 ) } \bigl\{ a_{12} \bigl[ b_{11} ( \lambda_{2}-a_{11} ) -a_{12}b_{21} \bigr] - ( 1+a_{11} ) \bigl[ b_{12} ( \lambda_{2}-a_{11} ) -a_{12}b_{22} \bigr] \bigr\} , \\ \varphi_{2} =\frac{a_{2}}{a_{12} ( \lambda_{2}+1 ) } \bigl\{ a_{12} \bigl[ b_{11} ( \lambda_{2}-a_{11} ) -a_{12}b_{21} \bigr] + ( \lambda_{2}-a_{11} ) \bigl[ b_{12} ( \lambda_{2}-a_{11} ) -a_{12}b_{22} \bigr] \bigr\} , \\ \varphi_{3} =\frac{-1}{\lambda_{2}+1} \bigl\{ ( 1+a_{11} ) \bigl[ a_{13} ( \lambda_{2}-a_{11} ) -a_{12}a_{23} \bigr] \bigr\} , \\ \begin{aligned}\varphi_{4} ={}& \frac{1}{a_{12} ( \lambda_{2}+1 ) } \bigl\{ a_{2}a_{12} ( \lambda_{2}+1 ) \bigl[ a_{13} ( \lambda _{2}-a_{11} ) -a_{12}a_{23} \bigr]\\ &+a_{1}a_{12} \bigl[ b_{11} ( \lambda_{2}-a_{11} ) -a_{12}b_{21} \bigr] \\ & + a_{1} ( \lambda_{2}-a_{11} ) \bigl[ b_{12} ( \lambda_{2}-a_{11} )-a_{12}b_{22} \bigr] \\ &-a_{12} ( 1+a_{11} ) \bigl[ b_{13} ( \lambda_{2}-a_{11} )-a_{12}b_{23} \bigr] \bigr\} ,\end{aligned} \\ \varphi_{5} =\frac{a_{1} ( \lambda_{2}-2a_{11}-1 ) }{\lambda _{2}+1} \bigl[ a_{13} ( \lambda_{2}-a_{11} ) -a_{12}a_{23} \bigr] .\end{gathered} $$
(5.6)

According to the flip bifurcation, the discriminatory quantities \(\chi _{1}\) and \(\chi_{1}\) are given by

$$ \begin{gathered} \chi_{1} = \biggl( \frac{\partial^{2}f}{\partial u_{n}\,\partial A_{\ast}}+\frac{1}{2} \frac{\partial f}{\partial A_{\ast}}\frac{\partial ^{2}f}{\partial u_{n}^{2}} \biggr) \bigg\vert _{ ( 0,0 ) }, \\ \chi_{2} = \biggl( \frac{1}{6}\frac{\partial^{3}f}{\partial u_{n}^{3}}+ \biggl( \frac{1}{2}\frac{\partial^{2}f}{\partial u_{n}^{2}} \biggr) ^{2} \biggr) \bigg\vert _{ ( 0,0 ) }.\end{gathered} $$
(5.7)

Thus, \(\chi_{1}=\varphi_{1}\) and \(\chi_{2}=\varphi_{5}+\varphi_{3}^{2}\). Therefore according to flip bifurcation conditions in [46], the following theorem can be stated.

Theorem 5.1

If \(\chi_{2}\neq0\), and the parameter \(A_{\ast}\) alters in the limiting region of the point \(( 0,0 ) \), then the system (5.1) passes through a flip bifurcation at the point \(E_{1} ( S^{\ast},I^{\ast} ) \). Further, the period-2 points that bifurcate from the fixed point \(E_{1} ( S^{\ast},I^{\ast} ) \) are stable if \(\chi_{2}>0\) and unstable if \(\chi_{2}<0\).

6 Neimark–Sacker bifurcation

A Neimark–Sacker bifurcation of the equilibrium point \(E_{1}\) occurs when parameters \(( \alpha,h,\beta,\Lambda,\mu,\gamma ) \) vary in the small neighborhood of \(\Omega_{3}\). A perturbation form of model (3.7) can be written as follows:

$$ \begin{gathered} S_{n+1} =S_{n}+ \bigl( A_{2}+A^{\ast} \bigr) [ \Lambda-\mu S_{n}-\beta S_{n}I_{n} ] , \\ I_{n+1} =I_{n}+ \bigl( A_{2}+A^{\ast} \bigr) \bigl[ \beta S_{n}I_{n}- ( \mu+r ) I_{n} \bigr] ,\end{gathered} $$
(6.1)

where \(\vert A^{\ast} \vert \ll 1\) is a limited perturbation parameter. Let \(X_{n}=S_{n}-S^{\ast}\), \(Y_{n}=I_{n}-I^{\ast}\), then the fixed point \(E_{1} ( S^{\ast},I^{\ast} ) \) to \(( 0,0 ) \) can be retranslated and (6.1) can be reformulated as follows:

$$ \left ( \textstyle\begin{array} {c}X_{n+1}\\ Y_{n+1}\end{array}\displaystyle \right ) =\left ( \textstyle\begin{array} {c}c_{11}X_{n}+c_{12}Y_{n}+c_{13}X_{n}Y_{n}\\ c_{21}X_{n}+c_{22}Y_{n}+c_{23}X_{n}Y_{n}\end{array}\displaystyle \right ) , $$
(6.2)

where

$$\begin{gathered} c_{11}=1-\mu\Re_{0} \bigl( A_{2}+A^{\ast} \bigr) ,\quad\quad c_{12}=- ( \mu+r ) \bigl( A_{2}+A^{\ast} \bigr) ,\quad\quad c_{13}=-\beta \bigl( A_{2}+A^{\ast} \bigr) , \\ c_{21}=\mu ( \Re_{0}-1 ) \bigl( A_{2}+A^{\ast} \bigr) ,\quad\quad c_{22}=1,\quad\quad c_{23}=\beta \bigl( A_{2}+A^{\ast} \bigr) ,\end{gathered} $$

and \(A=A_{2}\).

The characteristic equation associated with the linearization system of model (6.2) at \(( 0,0 ) \) is

$$ \omega^{2}+p \bigl( A^{\ast} \bigr) \omega+q \bigl( A^{\ast} \bigr) =0, $$
(6.3)

where

$$\begin{gathered} p \bigl( A^{\ast} \bigr) =-2-G \bigl( A_{2}+A^{\ast} \bigr) , \\ q \bigl( A^{\ast} \bigr) =1+G \bigl( A_{2}+A^{\ast} \bigr) +H \bigl( A_{2}+A^{\ast} \bigr) ^{2}, \\ G=c_{22}-c_{11},\quad \text{and}\quad H=c_{21}c_{12}-c_{11}c_{22}.\end{gathered}$$

Since the parameters \(( \alpha,h,\beta,\Lambda,\mu,r ) \in \Omega_{3}\) and \(A^{\ast}\) varies in a small neighborhood of \(A^{\ast}=0\), and the roots of (6.3) are pair of complex conjugate numbers \(\omega_{1}\) and \(\omega _{2}\) denoted by

$$\omega_{1,2}=1+\frac{G ( A_{2}+A^{\ast} ) }{2}\pm\frac{i ( A_{2}+A^{\ast} ) }{2}\sqrt{4H-G^{2}}, $$

we have

$$\vert \omega_{1,2} \vert =\sqrt{q \bigl( A^{\ast} \bigr) },\qquad \frac{d \vert \omega_{1,2} \vert }{dA^{\ast}} \bigg\vert _{A^{\ast }=0}=-\frac{G}{2}>0.$$

In addition, it is required that, when \(A^{\ast }=0\), \(\overline{\omega}^{n},\omega^{n}\neq1\) (\(n=1,2,3,4 \)), which is equivalent to \(p ( 0 ) \neq-2,0,1,2\). Since \(p^{2}(0)-4q(0)<0\) and \(q(0)=1\), we have \(p^{2}(0)<4\); then \(p(0)\neq\pm2\). It is only required that \(p(0)\neq0,1\), which leads to

$$ G^{2}\neq2H,3H. $$
(6.4)

Therefore, the eigenvalues \(\omega_{1,2}\) of fixed point \(( 0,0 ) \) of (6.2) does not lie on the intersection of the unit circle with the coordinate axes when \(A^{\ast}=0\).

Next, the normal form of model (6.2) when \(A^{\ast}=0\) is studied. Let \(\theta=\operatorname{Re} ( \omega_{1,2} ) \), \(\eta=\operatorname {Im} ( \omega_{1,2} ) \) and

$$ T=\left ( \textstyle\begin{array} {c@{\quad}c}c_{12} & 0\\ \theta-c_{11} & -\eta \end{array}\displaystyle \right ) =\left ( \textstyle\begin{array} {c@{\quad}c}c_{11} & 0\\ \frac{-1}{2}K & \frac{-1}{2}K\sqrt{4K-K^{2}}\end{array}\displaystyle \right ) . $$
(6.5)

Consider the translation below

$$ \left ( \textstyle\begin{array} {c}X_{n}\\ Y_{n}\end{array}\displaystyle \right ) =T\left ( \textstyle\begin{array} {c}u_{n}\\ \upsilon_{n}\end{array}\displaystyle \right ) . $$
(6.6)

Taking \(T^{-1}\) on both sides of (6.2), we obtain

$$ \left ( \textstyle\begin{array} {c}u_{n+1}\\ \upsilon_{n+1}\end{array}\displaystyle \right ) =\left ( \textstyle\begin{array} {c@{\quad}c}\theta& -\eta\\ \eta& \theta \end{array}\displaystyle \right ) \left ( \textstyle\begin{array} {c}u_{n}\\ \upsilon_{n}\end{array}\displaystyle \right ) +\left ( \textstyle\begin{array} {c}f ( u_{n}+\upsilon_{n} ) \\ g ( u_{n}+\upsilon_{n} ) \end{array}\displaystyle \right ) , $$
(6.7)

where

$$\begin{gathered}f ( u_{n}+\upsilon_{n} ) =c_{13} \bigl[ ( \theta -c_{11} ) u_{n}^{2}-\eta u_{n}\upsilon_{n} \bigr] , \\ g ( u_{n}+\upsilon_{n} ) = \bigl[ c_{13} ( c_{11}-\theta ) +c_{12}c_{23} \bigr] \biggl[ \frac{ ( c_{11}-\theta ) }{\eta}u_{n}^{2}+u_{n}\upsilon_{n} \biggr] , \\ X_{n}=c_{12}u_{n},\qquad Y_{n}= ( \theta-c_{11} ) u_{n}-\eta\upsilon _{n}.\end{gathered}$$

Now, we obtain

$$ \begin{gathered} \frac{\partial^{2}f}{\partial u_{n}^{2}} =2c_{13} ( \theta -c_{11} ) , \\ \frac{\partial^{2}f}{\partial u_{n}\,\partial\upsilon_{n}} =-\eta c_{13}, \\ \frac{\partial^{2}f}{\partial\upsilon_{n}^{2}} =0, \\ \frac{\partial^{3}f}{\partial u_{n}^{3}} =\frac{\partial ^{3}f}{\partial u_{n}^{2}\,\partial\upsilon_{n}}=\frac{\partial^{3}f}{\partial u_{n}\,\partial\upsilon_{n}^{2}}= \frac{\partial^{3}f}{\partial\upsilon_{n}^{3}}=0, \\ \frac{\partial^{2}g}{\partial u_{n}^{2}} =\frac{2 ( c_{11}-\theta ) }{\eta} \bigl[ c_{13} ( c_{11}-\theta ) +c_{12}c_{23} \bigr] , \\ \frac{\partial^{2}g}{\partial u_{n}\,\partial\upsilon_{n}} =c_{13} ( c_{11}-\theta ) +c_{12}c_{23}, \\ \frac{\partial^{2}g}{\partial\upsilon_{n}^{2}} =0, \\ \frac{\partial^{3}g}{\partial u_{n}^{3}} =\frac{\partial^{3}g}{\partial u_{n}^{2}\,\partial\upsilon_{n}}=\frac{\partial^{3}g}{\partial u_{n}\,\partial\upsilon_{n}^{2}}= \frac{\partial^{3}g}{\partial\upsilon _{n}^{3}}=0.\end{gathered} $$
(6.8)

According to the Neimark–Sacker bifurcation, the discriminatory quantity ℏ is given by

$$ \hslash=-\operatorname{Re} \biggl[ \frac{ ( 1-2\omega ) \overline{\omega}^{2}}{1-\omega}\xi_{11} \xi_{20} \biggr] -\frac{1}{2} \vert \xi_{11} \vert ^{2}- \vert \xi_{02} \vert ^{2}+ \operatorname{Re} ( \overline{\omega}\xi_{21} ) \neq0, $$
(6.9)

where

$$\begin{aligned}& \omega =\theta+i\eta, \\& \xi_{11} =\frac{1}{4} \biggl[ \frac{\partial^{2}f}{\partial u_{n}^{2}}+ \frac{\partial^{2}f}{\partial\upsilon_{n}^{2}}+i \biggl( \frac{\partial^{2}g}{\partial u_{n}^{2}}-\frac{\partial^{2}g}{\partial \upsilon_{n}^{2}} \biggr) \biggr] \bigg\vert _{ ( u_{n},\upsilon _{n} ) = ( 0,0 ) }, \\& \xi_{20} =\frac{1}{8} \biggl[ \frac{\partial^{2}f}{\partial u_{n}^{2}}- \frac{\partial^{2}f}{\partial\upsilon_{n}^{2}}+2\frac {\partial ^{2}g}{\partial u_{n}\,\partial\upsilon_{n}}+i \biggl( \frac{\partial^{2}g}{\partial u_{n}^{2}}- \frac{\partial^{2}g}{\partial\upsilon_{n}^{2}}-2\frac{\partial^{2}f}{\partial u_{n}\,\partial\upsilon_{n}} \biggr) \biggr] \bigg\vert _{ ( u_{n},\upsilon_{n} ) = ( 0,0 ) }, \\ & \\ & \xi_{02} =\frac{1}{8} \biggl[ \frac{\partial^{2}f}{\partial u_{n}^{2}}- \frac{\partial^{2}f}{\partial\upsilon_{n}^{2}}-2\frac {\partial ^{2}g}{\partial u_{n}\,\partial\upsilon_{n}}+i \biggl( \frac{\partial^{2}g}{\partial u_{n}^{2}}- \frac{\partial^{2}g}{\partial\upsilon_{n}^{2}}+2\frac{\partial^{2}f}{\partial u_{n}\,\partial\upsilon_{n}} \biggr) \biggr] \bigg\vert _{ ( u_{n},\upsilon_{n} ) = ( 0,0 ) }, \\& \begin{aligned}\xi_{21} ={}&\frac{1}{16} \biggl[ \frac{\partial^{3}f}{\partial u_{n}^{3}}+ \frac{\partial^{3}f}{\partial u_{n}\,\partial\upsilon_{n}^{2}}+\frac{\partial^{3}g}{\partial u_{n}^{2}\,\partial\upsilon_{n}}+\frac {\partial^{3}g}{\partial\upsilon_{n}^{3}}\\ &+i \biggl( \frac{\partial^{3}g}{\partial u_{n}^{3}}+\frac{\partial^{3}g}{\partial u_{n}\,\partial \upsilon _{n}^{2}}-\frac{\partial^{3}f}{\partial u_{n}^{2}\,\partial\upsilon_{n}}- \frac{\partial^{3}f}{\partial\upsilon_{n}^{3}} \biggr) \biggr] \bigg\vert _{ ( u_{n},\upsilon_{n} ) = ( 0,0 ) }.\end{aligned} \end{aligned}$$
(6.10)

From the above analysis and the theorem in [47], Theorem 6.1 can be stated.

Theorem 6.1

If conditions (6.4) and (6.10) hold, then the system (3.7) undergoes Neimark–Sacker bifurcation at the positive fixed point \(E_{1} ( S^{\ast },I^{\ast} ) \) when the parameter \(A^{\ast}\) varies in the small neighborhood of \(A_{2}\). Furthermore if (\(\hslash<0\), \(\hslash >0 \)) then (an attracting, a repelling) invariant closed curve bifurcates from the fixed point \(E_{1} ( S^{\ast},I^{\ast} ) \) for (\(A_{2}>A^{\ast}\), \(A_{2}< A^{\ast}\)), respectively.

7 Numerical examples

This section shows the bifurcation diagrams, phase portraits and maximum Lyapunov exponents for the model (3.7) to confirm the above theoretical analysis and to illustrate the complex dynamics of our model using numerical continuation. Bifurcation occurs when the stability of an equilibrium point changes [48]. In general, the dynamics of a discrete SI model with integer-order has been examined by Hu et al. [42]. As discussed earlier in Section 1, this paper focuses on varying the time step size parameter h and the fractional-order parameter α in the model (3.7), which can be seen as extension of the corresponding results given in [29, 42]. Based on the previous analysis, the parameters of the model (3.7) can be examined in the following two cases.

Case 1. Varying h in range \(2\leqslant h\leqslant2.85\) and fixing \(\Lambda=3.5\), \(\mu=0.145\), \(r=0.12\), \(\beta=0.09\), \(\alpha=0.99\) with initial conditions \(( S_{0},I_{0} ) = ( 3.1,7.8 ) \).

Case 2. Varying α in range \(0.8\leqslant\alpha\leqslant0.99\) and fixing \(\Lambda=1.5\), \(\mu=0.2\), \(r=0.3\), \(\beta=0.1\), \(h=8.1\), \(( S_{0},I_{0} ) = ( 5.1,0.9 ) \).

In Case 1, the basic reproduction number \(\Re_{0}=8.198>1\), thus the model (3.7) has one positive endemic equilibrium point \(E_{1} ( 2.944,11.596 ) \). Since \(\Delta=0.307>0\) and \(h_{1}=2.305\), according to Theorem 4.4, \(E_{1}\) is asymptotically stable (sink) when \(h<2.305\). When \(h=h_{1}\), flip bifurcation emerges from the equilibrium point \(E_{1}\) with \(\chi_{1}=-0.871\), \(\chi_{2}=0.015>0\) and \(( \alpha,h,\beta,\Lambda,\mu,r ) = ( 0.99,2.305,0.09,3.5,0.145,0.12 ) \in\Omega_{1}\). The occurrence of these bifurcations is illustrated in Figure 1(a)–(c). These figures show that \(E_{1}\) is stable when \(h<2.305\) and loses its stability through the flip bifurcation when \(h=2.305\). Period-2, 4, 8, 16 orbits appear as h increases in the range when \(h\in ( 2.305,2.83 ) \). The phase portraits for \(h\in ( 2.305,2.83 ) \) are plotted in Figure 2(a)–(d) to illustrate these observations further. The emergence of period-2, 4, 8 and 16 orbits are observed when \(h=2.5,2.75,2.8\) and 2.82 in Figure 2(a)–(d). Some interesting phenomena are also seen when h increases further: for instance, when \(h=2.9\) (Figure 2(e)), period-12 orbit appears. The occurrence of chaotic regions is also observed in Figure 1(a)–(c): these phenomena can be illustrated by the phase portrait in Figure 2(f) (e.g. when \(h=2.95\)). Maximal Lyapunov exponents (LEs) are computed in Figure 3 corresponding to observations in Figure 1(a)–(c). It is observed that some LE values are positive and some are negative, so there exist stable fixed points or stable period windows in the chaotic regions. Generally, a positive LE is considered to be one of the characteristics which imply the existence of chaos (e.g. when \(h>2.83\)).

Figure 1
figure 1

Flip bifurcation diagram of model (3.7) for \(h\in[2,3]\) with local amplification to (a)

Full size image
Figure 2
figure 2

Phase portraits diagram of model (3.7) for various h corresponding to Figure 1

Full size image
Figure 3
figure 3

Maximal Lyapunov exponents corresponding to Figure 1

Full size image

In Case 2, the basic reproduction number \(\Re_{0}=1.5>1\), thus, model (3.7) has one positive endemic equilibrium point \(E_{1} ( 5,1 ) \). Since \(\Delta=-0.11<0\), according to Theorem 4.4 \(E_{1}\) is asymptotically stable (sink) when \(\alpha<0.826\) and unstable when \(\alpha>0.826\). The Neimark–Sacker (N-S) bifurcation emerges from \(E_{1}\) at \(\alpha =0.826\) with \(\hslash=-0.778<0\) and \(( \alpha,h,\beta,\Lambda,\mu,r ) = ( 0.826,8.1,0.1,1.5,0.2,0.3 ) \in\Omega_{3}\). The occurrence of an N-S bifurcation is illustrated in Figure 4(a)–(c). Figure 4 shows that \(E_{1}\) is stable for \(\alpha<0.826\) and loses its stability through an N-S bifurcation at \(\alpha=0.826\). Attracting invariant circle appears as fractional-order parameter increases in the range of \(\alpha\in ( 0.826,0.87 ) \). The phase portraits for various α-values corresponding to Figure 4 are plotted in Figure 5(a)–(i) to illustrate these observations. Furthermore, the quasi-periodic orbits (\(\alpha=0.913\)) and periodic-13 orbits (\(\alpha=0.921\)) are observed within the chaotic regions in Figure 5(f) and (g), respectively. Attracting chaotic sets are also seen when α increases further and these observations are plotted in Figure 5(h)–(i). Maximal Lyapunov exponents corresponding to observations in Figure 4(a)–(c) are computed in Figure 6. It is observed that some LE values are positive and some are negative. So there exist stable fixed points or stable period windows in the chaotic regions (e.g. when \(\alpha>0.921\)).

Figure 4
figure 4

N-S bifurcation diagram of model (3.7) for \(\alpha\in [0.8,0.99]\) with local amplification to (a)

Full size image
Figure 5
figure 5figure 5

Phase portraits diagram of model (3.7) for various α corresponding to Figure 4

Full size image
Figure 6
figure 6

Maximal Lyapunov exponents corresponding to Figure 4

Full size image

8 Discussion and conclusion

A new discrete-time SI epidemic model has been discussed in this paper. Such a discrete-time model is obtained from the discretization of the fractional-time SI model. The discretization process provides crucial terms such as h (time step parameter) and α (fractional-order parameter), which are then varied in order to describe the dynamical behaviors of the model. As h and α are varied, the model exhibits several complicated dynamical behaviors including the emergence of flip and N-S bifurcations, period-2, 4, 8, 12, 13, 16 orbits, quasi-periodic orbits, attracting invariant circle and chaotic sets. Analytically, necessary and sufficient conditions on the parameters for the occurrence of flip and N-S bifurcations are derived. Moreover, numerical continuation is carried out to illustrate the validity of the analytical results and it is observed that both numerical and analytical findings are in good agreement. In conclusion, the proposed fractional-time SI model can engender more complex dynamical behaviors than its continuous model counterpart. Studying the dynamical behaviors of the full avian–human influenza SIR epidemic model described by a discrete-time with fractional-order version will be our future work.