1 Introduction

It is well known that cellular neural networks have attracted broad attention in numerous scientific fields due to their potential application prospect in psychophysics, speech, perception, robotics, pattern recognition, signal and image processing, optimization and population dynamics, and so on [2,3,4,5,6]. Noting that the design of cellular neural depends largely on the global exponential convergence natures, a lot of authors investigated the global exponential convergence of the equilibria and periodic solutions for cellular neural networks, and many outstanding achievements have been stated. For example, Zhang [7] focused on the exponential convergence for cellular neural networks with continuously distributed leakage delays. Applying the Lyapunov function method and differential inequality strategies, sufficient conditions that ensure that all solutions of the networks convergence exponentially to the zero equilibrium point are obtained. Liu [8] investigated the convergence for HCNNs with delays and oscillating coefficients in leakage terms. Using some suitable integral inequality technique, the authors established some sufficient conditions to ensure that all solutions of the networks convergence exponentially to the zero equilibrium point, Zhao and Wang [9] presented some sufficient conditions for exponential convergence via the Lyapunov functional method and differential inequality strategies for a SICNN with leakage delays and continuously distributed delays of neutral type. Chen and Yang [10] established an exponential convergence criteria for HRNNs with continuously distributed delays in the leakage terms by using the Lyapunov functional method and differential inequality strategies. For more results on this topic, we refer the readers to [11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42].

In 2008, Tang [1] considered the following delayed cellular neural networks with time-varying coefficients:

$$\begin{aligned} x_{i}^{\prime}(t) =&-c_{i}(t)x_{i}(t)+ \sum_{j=1}^{n}a_{ij}(t)f_{j} \bigl(x_{j}\bigl(t-\tau_{ij}(t)\bigr)\bigr) \\ &{} +\sum_{j=1}^{n}b_{ij}(t) \int_{0}^{\infty}K_{ij}(u)g_{j} \bigl(x_{j}(t-u)\bigr)\,du+I_{i}(t), \end{aligned}$$
(1.1)

where \(i = 1, 2, \ldots, n\), \(t\in R\), n corresponds to the number of units in a neural network, \(x_{i} (t)\) denotes the state vector of the ith unit at the time t, \(c_{i} (t)>0\) denotes the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs at the time t, \(a_{ij}(t)\) and \(b_{ij}(t)\) represent the connection weights at the time t, \(\tau_{ij}(t)\geq0\) denotes the transmission delay of the ith unit along the axon of the jth unit at the time t, \(I_{i}(t)\) denotes the external bias on the ith unit at the time t, \(f_{j}\) and \(g_{j}\) are activation functions of signal transmission, and \(K_{ij}(u)\) corresponds to the transmission delay kernel. Mathematical analysis technique was applied under the following conditions:

  1. (A1)

    For each \(j\in\{1,2,\ldots,n\}\), there exist nonnegative constants \(\bar{L}_{j}\) and \({L}_{j}\) such that

    $$\bigl\vert f_{j}(u) \bigr\vert \leq\bar{L}_{j} \vert u \vert ,\qquad \bigl\vert g_{j}(u) \bigr\vert \leq{L}_{j} \vert u \vert \quad \mbox{for all } u\in R. $$
  2. (A2)

    For \(i\in\{1,2,\ldots,n\}\), there exist constants \(T_{0}>0\), \(\eta>0\), \(\lambda>0\), and \({\xi}_{0}>0\) such that

    $$\begin{aligned}& -\bigl[c_{i}(t)-\lambda\bigr]\xi_{i}+\sum _{j=1}^{N} \bigl\vert a_{ij}(t) \bigr\vert e^{\lambda\tau}\bar {L}_{j}\xi_{j}+\sum _{j=1}^{N} \bigl\vert b_{ij}(t) \bigr\vert \int_{0}^{\infty}K_{ij}(u)e^{\lambda u}\,du {L}_{j}\xi_{j} \\& \quad < -\eta< 0\quad \mbox{for all } t>T_{0}, \end{aligned}$$

    where \(\tau=\max_{1\leq i,j\leq n}\{\sup_{t\in R}\tau_{ij}(t)\}\).

  3. (A3)

    For \(i\in\{1,2,\ldots,n\}\), \(I_{i}(t)=O(e^{-\lambda t})\).

Some sufficient conditions ensuring that all solutions of system (1.1) converge exponentially to zero equilibrium point were obtained. Here we would like to point out that Tang [1] investigated the exponential convergence by assuming that the leakage term coefficient functions \(c_{i}(t)\) are not oscillating, that is, \(c_{i}(t)>0\), \(i=1,2,\ldots,n\). However, in many cases, oscillating coefficients usually occur in linearizations of population dynamics models due to seasonal fluctuations, for example, in winter the death rate maybe greater than the birth rate [5, 43]. Thus the study on the exponential convergence for cellular neural networks with oscillating coefficients in the leakage terms has important principle value and important realistic significance.

In this paper, we further consider the exponential convergence for cellular neural networks (1.1). The initial conditions associated with (1.1) are given by

$$ x_{i}(s)=\varphi_{i}(s),\quad s\in(-\infty,0], \varphi_{i}\in BC, i=1,2,\ldots,n, $$
(1.2)

where BC denotes the set of all real-valued bounded and continuous functions defined on \((-\infty,0]\). Differently from the assumptions in [1], we establish other sufficient conditions that guarantee that all solutions of the considered neural networks converge exponentially to the zero equilibrium point. We believe that this research on the exponential convergence for cellular neural networks plays an important role in designing the cellular neural networks with time-varying delays. Our results are new and a good complement to the work of [1].

For simplicity, we denote by \(R^{p}\) (\(R=R^{1}\)) the set of all p-dimensional real vectors (real numbers). Set \(x(t)=(x_{1}(t),x_{2}(t),\ldots,x_{n}(t))^{T}\in R^{n}\). For any \(x(t)\in R^{n}\), we let \(|x|\) denote the absolute value vector given by \(|x|=(|x_{1}|,|x_{2}|,\ldots,|x_{n}|)^{T}\) and define \(\|x\|=\max_{1\leq i\leq n}|x_{i}(t)|\). For \(f\in BC\), we denote \(f^{+}=\sup_{t\in R}|f(t)|\) and \(f^{-}=\inf_{t\in R}|f(t)|\). Let \(\tau^{+}=\max_{1\leq i,j\leq n}\{\sup_{t\in R}\tau_{ij}(t)\}\).

Throughout this paper, we assume that the following conditions are satisfied:

  1. (H1)

    For \(i = 1, 2, \ldots, n\), there exist constants \(\bar{c}_{i}>0\) and \(M>0\) such that

    $$e^{-\int_{s}^{t} c_{i}(u)\,du} \leq M e^{-(t-s)\bar{c}_{i}}\quad \mbox{for all } t,s \in R \mbox{ such that } t-s\geq0. $$
  2. (H2)

    For \(j= 1, 2, \ldots, n\), there exist positive constants \(L_{j}^{f} \) and \(L_{j}^{g}\) such that

    $$\begin{aligned}& \bigl\vert f_{j}(u)-f_{j}(v) \bigr\vert \leq L_{j}^{f} \vert u-v \vert , \qquad \bigl\vert g_{j}(u)-g_{j}(v) \bigr\vert \leq L_{j}^{g} \vert u-v \vert , \\& f_{j}(0)=0,\qquad g_{j}(0)=0 \end{aligned}$$

    for \(u,v\in R\).

  3. (H3)

    For \(i,j = 1, 2, \ldots, n\), the delay kernel \(K_{ij}: [0,\infty)\rightarrow R\) is continuous and absolutely integrable.

  4. (H4)

    For \(i= 1, 2, \ldots, n\), there exists a positive constant \(\mu_{0}\) such that

    $$I_{i}(t)=O\bigl(e^{-\mu_{0} t}\bigr) \quad (t\rightarrow+\infty),\qquad \frac{MG_{i}}{\bar{c}_{i}}< 1, $$

    where

    $$G_{i}=\sum_{j=1}^{n}a_{ij}^{+}L_{j}^{f} +\sum_{j=1}^{n}b_{ij}^{+}L_{j}^{g} \int_{0}^{\infty}K_{ij}(u)\,du. $$

The remainder of the paper is organized as follows. In Sect. 2, we establish a sufficient condition which ensures the exponential convergence of all solutions of the considered neural networks. In Sect. 3, we give an example that illustrates the theoretical findings. The paper ends with a brief conclusion in Sect. 4.

2 Global exponential convergence

Theorem 2.1

If (H1)–(H4) hold, then for every solution \(x(t)=(x_{1}(t),x_{2}(t), \ldots,x_{n}(t))^{T}\) of system (1.1) with any initial value conditions (1.2), there exists a positive constant λ such that \(x_{i}(t)=O(e^{-\lambda t})\) as \(t\rightarrow+\infty\), \(i=1,2,\ldots,n\).

Proof

We first define the continuous function

$$ \varTheta_{i}(\epsilon)=-\bar{c}_{i}+ \epsilon+M \Biggl[\sum_{j=1}^{n}a_{ij}^{+}L_{j}^{f}e^{\epsilon \tau^{+}} +\sum_{j=1}^{n}b_{ij}^{+}L_{j}^{g} \int_{0}^{\infty}K_{ij}(u)e^{\epsilon u}\,du+\epsilon \Biggr], $$
(2.1)

where \(\epsilon\in[0, \min\{\mu_{0},\min_{1\leq i\leq n} \bar{c}_{i}\})\). By (H4) we get

$$\begin{aligned} \varTheta_{i}(0) =&-\bar{c}_{i}+M \Biggl[\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f}+ \sum_{j=1}^{n}b_{ij}^{+}L_{j}^{g} \int_{0}^{\infty}K_{ij}(u)\,du \Biggr] \\ =&\bar{c}_{i} \biggl(\frac{MG_{i}}{\bar{c}_{i}}-1 \biggr)< 0, \quad i=1,2,\ldots,n. \end{aligned}$$
(2.2)

In view of the continuity of \(\varTheta_{i}(\epsilon)\), we can choose a constant \(\lambda\in[0, \min\{\mu_{0},\min_{1\leq i\leq n} \bar{c}_{i}\})\) such that

$$\begin{aligned}& -\bar{c}_{i}+\lambda+M \Biggl[\sum_{j=1}^{n}a_{ij}^{+}L_{j}^{f}e^{\lambda \tau^{+}} +\sum_{j=1}^{n}b_{ij}^{+}L_{j}^{g} \int_{0}^{\infty}K_{ij}(u)e^{\lambda u}\,du+\lambda \Biggr] \\& \quad =(\bar{c}_{i}-\lambda) \biggl(\frac{M\gamma_{i}}{\bar{c}_{i}-\lambda}-1 \biggr)< 0, \quad i=1,2,\ldots,n, \end{aligned}$$
(2.3)

where

$$\gamma_{i}=\sum_{j=1}^{n}a_{ij}^{+}L_{j}^{f}e^{\lambda\tau^{+}} +\sum_{j=1}^{n}b_{ij}^{+}L_{j}^{g} \int_{0}^{\infty}K_{ij}(u)e^{\lambda u}\,du+\lambda. $$

Let \(x(t)=(x_{1}(t),x_{2}(t),\ldots,x_{n}(t))^{T}\) be the solution of system (1.1) with any initial value \(\varphi(t)=(\varphi_{1}(t),\varphi_{2}(t),\ldots,\varphi_{n}(t))^{T}\) satisfying (1.2) and \(\|\varphi\|_{0}=\sup_{t\leq0}\max_{1\leq i\leq n}|\varphi_{i}(t)|\). For any \(\varepsilon>0\), we have

$$ \bigl\Vert x(t) \bigr\Vert < \bigl( \Vert \varphi \Vert _{0}+ \varepsilon\bigr)e^{-\lambda t}< \varOmega \bigl( \Vert \varphi \Vert _{0}+\varepsilon\bigr)e^{-\lambda t} \quad \mbox{for all } t\in (- \infty,0], $$
(2.4)

where Ω is a sufficiently large constant such that

$$ \bigl\Vert I_{i}(t) \bigr\Vert < \lambda\varOmega\bigl( \Vert \varphi \Vert _{0}+\varepsilon\bigr)e^{-\lambda t} \quad \mbox{for all } t\in R $$
(2.5)

and

$$ \varOmega>\frac{\bar{c}_{i}-\lambda}{\gamma_{i}}+1, \quad i=1,2,\ldots,n. $$
(2.6)

It follows from (2.3) and (2.6) that

$$ \frac{1}{\varOmega}-\frac{\bar{c}_{i}-\lambda}{\gamma_{i}}< 0,\qquad \frac{M\gamma_{i}}{\bar{c}_{i}-\lambda}< 1,\quad i=1,2, \ldots,n. $$
(2.7)

Now we will prove that

$$ \bigl\Vert x(t) \bigr\Vert < \varOmega\bigl( \Vert \varphi \Vert _{0}+\varepsilon\bigr)e^{-\lambda t}\quad \mbox{for all } t>0. $$
(2.8)

If (2.8) does not hold, then there must exist i and \(t_{0}\) such that

$$ \textstyle\begin{cases} \Vert x(t_{0}) \Vert = \vert x_{i}(t_{0}) \vert =\varOmega( \Vert \varphi \Vert _{0}+\varepsilon)e^{-\lambda t_{0}},\\ \Vert x(t) \Vert < \varOmega ( \Vert \varphi \Vert _{0}+\varepsilon)e^{-\lambda t} \quad \mbox{for all } t\in(-\infty,t_{0}). \end{cases} $$
(2.9)

Notice that

$$\begin{aligned} x_{i}^{\prime}(s)+c_{i}(s)x_{i}(s) =&\sum _{j=1}^{n}a_{ij}(s)f_{j} \bigl(x_{j}\bigl(s-\tau_{ij}(s)\bigr)\bigr) \\ &{}+\sum_{j=1}^{n}b_{ij}(s) \int_{0}^{\infty}K_{ij}(u)g_{j} \bigl(x_{j}(s-u)\bigr)\,du \\ &{}+I_{i}(s),\quad s\in[0,t], t\in[0,t_{0}]. \end{aligned}$$
(2.10)

Multiplying both sides of (2.10) by \(e^{-\int_{0}^{s} c_{i}(u)\,du}\) and then integrating on \([0,t]\), we have

$$\begin{aligned} x_{i}(t) =&x_{i}(0)e^{-\int_{0}^{t} c_{i}(u)\,du}+ \int_{0}^{t}e^{-\int_{s}^{t} c_{i}(u)\,du} \Biggl[\sum _{j=1}^{n}a_{ij}(s)f_{j} \bigl(x_{j}\bigl(s-\tau_{ij}(s)\bigr)\bigr) \\ &{}+\sum_{j=1}^{n}b_{ij}(s) \int_{0}^{\infty}K_{ij}(u)g_{j} \bigl(x_{j}(s-u)\bigr)\,du +I_{i}(s) \Biggr],\quad t \in[0,t_{0}], \end{aligned}$$
(2.11)

and

$$\begin{aligned} \bigl\vert x_{i}(t_{0}) \bigr\vert =&\Bigg|x_{i}(0)e^{-\int_{0}^{t_{0}} c_{i}(u)\,du}+ \int_{0}^{t_{0}}e^{-\int_{s}^{t_{0}} c_{i}(u)\,du} \Bigg[\sum _{j=1}^{n}a_{ij}(s)f_{j} \bigl(x_{j}\bigl(s-\tau_{ij}(s)\bigr)\bigr) \\ &{}+\sum_{j=1}^{n}b_{ij}(s) \int_{0}^{\infty}K_{ij}(u)g_{j} \bigl(x_{j}(s-u)\bigr)\,du +I_{i}(s)\Bigg|. \end{aligned}$$
(2.12)

By (H1)–(H4) and (2.12) we get

$$\begin{aligned} \bigl\vert x_{i}(t_{0}) \bigr\vert \leq& M \bigl( \Vert \varphi \Vert _{0}+\varepsilon\bigr)e^{-\bar{c}_{i} t_{0}}+ \int_{0}^{t_{0}}Me^{-(t_{0}-s)\bar{c}_{i}} \Biggl[\sum _{j=1}^{n}a_{ij}^{+}L_{j}^{f}e^{\lambda \tau^{+}} \varOmega\bigl( \Vert \varphi \Vert _{0}+\varepsilon \bigr)e^{-\lambda s} \\ &{}+\sum_{j=1}^{n}b_{ij}^{+}L_{j}^{g} \int_{0}^{\infty}K_{ij}(u)e^{\lambda u}\,du\, \varOmega\bigl( \Vert \varphi \Vert _{0}+\varepsilon \bigr)e^{-\lambda s} +\lambda\varOmega\bigl( \Vert \varphi \Vert _{0}+\varepsilon\bigr)e^{-\lambda s} \Biggr]\,ds \\ \leq&\varOmega\bigl( \Vert \varphi \Vert _{0}+\varepsilon\bigr) \Biggl\{ \frac{M e^{-\bar{c}_{i} t_{0}}}{\varOmega}+ \int_{0}^{t_{0}}Me^{-(t_{0}-s)\bar{c}_{i}}e^{-\lambda s} \Biggl[\sum_{j=1}^{n}a_{ij}^{+}L_{j}^{f}e^{\lambda\tau^{+}} \\ &{}+\sum_{j=1}^{n}b_{ij}^{+}L_{j}^{g} \int_{0}^{\infty}K_{ij}(u)e^{\lambda u}\,du+\lambda \Biggr]\,ds \Biggr\} . \end{aligned}$$
(2.13)

By (2.3), (2.6), (2.7), and (2.13) we have

$$\begin{aligned} \bigl\vert x_{i}(t_{0}) \bigr\vert \leq&\varOmega \bigl( \Vert \varphi \Vert _{0}+\varepsilon\bigr) \biggl[ \frac{M e^{-\bar{c}_{i} t_{0}}}{\varOmega}+e^{-\bar{c}_{i} t_{0}} \int_{0}^{t_{0}}e^{(\bar{c}_{i}-\lambda)s}\,ds \gamma_{i} \biggr] M \\ =&\varOmega\bigl( \Vert \varphi \Vert _{0}+\varepsilon \bigr)e^{-\lambda t_{0}} \biggl[\frac{M e^{(\lambda-\bar{c}_{i}) t_{0}}}{\varOmega}+\frac{\gamma_{i}}{\bar{c}_{i}-\lambda} \bigl(1-e^{(\lambda-\bar{c}_{i}) t_{0}} \bigr) \biggr] M \\ =&\varOmega\bigl( \Vert \varphi \Vert _{0}+\varepsilon \bigr)e^{-\lambda t_{0}} \biggl[ \biggl(\frac{1}{\varOmega}-\frac{\gamma_{i}}{\bar{c}_{i}-\lambda } \biggr) e^{(\lambda-\bar{c}_{i}) t_{0}} +\frac{\gamma_{i}}{\bar{c}_{i}-\lambda} \biggr]M \\ < &\varOmega\bigl( \Vert \varphi \Vert _{0}+\varepsilon \bigr)e^{-\lambda t_{0}}\frac{\gamma_{i}}{\bar{c}_{i}-\lambda}M \\ < &\varOmega\bigl( \Vert \varphi \Vert _{0}+\varepsilon \bigr)e^{-\lambda t_{0}}, \end{aligned}$$
(2.14)

which contradicts (2.9). So (2.8) holds. Letting \(\varepsilon\rightarrow0^{+}\), it follows from (2.8) that

$$ \bigl\Vert x(t) \bigr\Vert < \varOmega \Vert \varphi \Vert _{0} e^{-\lambda t}\quad \mbox{for all } t>0. $$
(2.15)

The proof of Theorem 2.1 is complete. □

Remark 2.1

Tang [1] analyzed the exponential convergence for cellular neural network model (1.1) under conditions (A1)–(A3). In this paper, we discuss the exponential convergence for cellular neural network model (1.1) under conditions (H1)–(H4). Moreover, the analysis method is different from that in [1].

3 Example

In this section, we present an example to verify the analytical predictions obtained in the previous section. Consider the following cellular neural networks with time-varying delays:

$$ \textstyle\begin{cases} x_{1}^{\prime}(t)=-c_{1}(t)x_{1}(t)+\sum_{j=1}^{2}a_{1j}(t)f_{j}(x_{j}(t-\tau_{1j}(t))) \\ \hphantom{x_{1}^{\prime}(t)=}{}+\sum_{j=1}^{2}b_{1j}(t)\int_{0}^{\infty}K_{1j}(u)g_{j}(x_{j}(t-u))\,du+I_{1}(t),\\ x_{2}^{\prime}(t)=-c_{2}(t)x_{2}(t)+\sum_{j=1}^{2}a_{2j}(t)f_{j}(x_{j}(t-\tau_{2j}(t))) \\ \hphantom{x_{2}^{\prime}(t)=}{}+\sum_{j=1}^{2}b_{2j}(t)\int_{0}^{\infty}K_{2j}(u)g_{j}(x_{j}(t-u))\,du+I_{2}(t),\\ x_{3}^{\prime}(t)=-c_{3}(t)x_{3}(t)+\sum_{j=1}^{2}a_{3j}(t)f_{j}(x_{j}(t-\tau_{3j}(t))) \\ \hphantom{x_{3}^{\prime}(t)=}{}+\sum_{j=1}^{2}b_{3j}(t)\int_{0}^{\infty}K_{3j}(u)g_{j}(x_{j}(t-u))\,du+I_{3}(t), \end{cases} $$
(3.1)

where \(g_{j}(x)=f_{j}(x)=0.03\sin x^{2}\) (\(j=1,2,3\)) and

[ a 11 ( t ) a 12 ( t ) b 11 ( t ) b 12 ( t ) ] = [ 0.2 + 0.4 sin 4500 t 0.2 + 0.3 sin 4500 t 0.1 + 0.4 cos 4500 t 0.1 + 0.4 cos 4500 t ] , [ a 21 ( t ) a 22 ( t ) b 21 ( t ) b 22 ( t ) ] = [ 0.1 + 0.4 cos 5000 t 0.2 + 0.3 cos 5000 t 0.2 + 0.2 cos 5000 t 0.1 + 0.4 sin 5000 t ] , [ a 31 ( t ) a 32 ( t ) b 31 ( t ) b 32 ( t ) ] = [ 0.2 + 0.3 sin 6000 t 0.1 + 0.2 cos 6000 t 0.1 + 0.2 sin 6000 t 0.2 + 0.3 sin 6000 t ] , [ K 11 ( u ) K 12 ( u ) K 21 ( u ) K 22 ( u ) K 31 ( u ) K 32 ( u ) ] = [ | sin u | e − u | sin u | e − u | sin u | e − u | sin u | e − u | sin u | e − u | sin u | e − u ] , [ c 1 ( u ) I 1 ( u ) c 2 ( u ) I 2 ( u ) c 3 ( u ) I 3 ( u ) ] = [ 0.2 + 3 sin 6000 t e − 2 t sin t 0.1 + 2 sin 4000 t e − 3 t sin t 0.1 + 2 cos 5000 t e − 5 t sin t ] , [ τ 11 ( u ) τ 12 ( u ) τ 21 ( u ) τ 22 ( u ) τ 31 ( u ) τ 32 ( u ) ] = [ 0.2 sin 3 t 0.4 sin 3 t 0.1 sin 3 t 0.3 sin 3 t 0.2 sin 3 t 0.4 sin 3 t ] .

Then \(\bar{c}_{1}=0.2\), \(\bar{c}_{2}=0.1\), \(\bar{c}_{3}=0.1\), \(L_{j}^{f}=L_{j}^{g}=0.03\), and

[ a 11 + a 12 + b 11 + b 12 + ] = [ 0.6 0.5 0.5 0.5 ] , [ a 21 + a 22 + b 21 + b 22 + ] = [ 0.5 0.5 0.4 0.5 ] , [ a 31 + a 32 + b 31 + b 32 + ] = [ 0.5 0.3 0.3 0.5 ] .

Let \(M=e^{0.01}\). Then

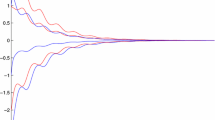
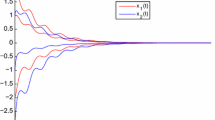
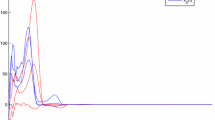
$$\begin{aligned}& G_{1}=\sum_{j=1}^{2}a_{1j}^{+}L_{j}^{f} +\sum_{j=1}^{2}b_{1j}^{+}L_{j}^{g} \int_{0}^{\infty}K_{1j}(u)\,du \\& \hphantom{G_{1}}=(0.6+0.5)\times0.03+(0.5+0.5)\times0.03\times0.5 \\& \hphantom{G_{1}}=0.0480, \\& G_{2}=\sum_{j=1}^{2}a_{2j}^{+}L_{j}^{f} +\sum_{j=1}^{2}b_{2j}^{+}L_{j}^{g} \int_{0}^{\infty}K_{2j}(u)\,du \\& \hphantom{G_{2}}=(0.5+0.5)\times0.03+(0.4+0.5)\times0.03\times0.5 \\& \hphantom{G_{2}}= 0.0313, \\& G_{3}=\sum_{j=1}^{2}a_{3j}^{+}L_{j}^{f} +\sum_{j=1}^{2}b_{3j}^{+}L_{j}^{g} \int_{0}^{\infty}K_{3j}(u)\,du \\& \hphantom{G_{3}}=(0.5+0.3)\times0.03+(0.3+0.5)\times0.03\times0.5\\& \hphantom{G_{3}}= 0.0360, \\& \frac{MG_{1}}{\bar{c}_{1}}=\frac{e^{0.01}\times0.0480}{0.2}= 0.2425 < 1, \\& \frac{MG_{2}}{\bar{c}_{2}}=\frac{e^{0.01}\times0.0313}{0.2}=0.3160 < 1, \\& \frac{MG_{3}}{\bar{c}_{3}}=\frac{e^{0.01}\times0.0360}{0.2}= 0.3640< 1. \end{aligned}$$

Thus all the conditions of Theorem 2.1 are satisfied. So we can conclude that all solutions of (3.1) converge exponentially to the zero equilibrium point \((0,0,0)^{T}\). This result is shown by computer simulation in Figs. 1–3.

Figure 1
figure 1

Time history of model (3.1)

Full size image
Figure 2
figure 2

Time history of system (3.1)

Full size image
Figure 3
figure 3

Time history of model (3.1)

Full size image

4 Conclusions

In this paper, we are concerned with a class of cellular neural networks with time-varying delays. Using the differential inequality under the unboundedness conditions of the activation functions, we establish a sufficient condition guaranteeing that all solutions of the considered neural networks converge exponentially to the zero equilibrium point. The obtained sufficient condition is easy to check in practice. The results derived in this paper are completely new and complement the previously known ones [1]. We present an example to illustrate the effectiveness of our theoretical results. The obtained results play a key role in designing neural networks and can be applied in many areas such as artificial intelligence, image recognition, disease diagnosis, and so on. Recently, pseudo-almost periodic solutions of cellular neural networks have also become a hot issue. However, there are rare results on pseudo-almost periodic solutions of cellular neural networks, which are worth studying in near future.