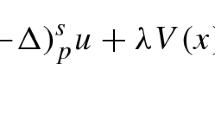Existence of multiple solutions for fractional p-Kirchhoff equations with concave-convex nonlinearities

Abstract

In this paper, we investigate the existence of multiple solutions for Kirchhoff-type equations involving nonlocal integro-differential operators with homogeneous Dirichlet boundary conditions as follows:

$$ \textstyle\begin{cases} M(\int_{\mathbb{R}^{2n}}\frac{|u(x)-u(y)|^{p}}{|x-y|^{n+sp}}\,dx\, dy)(-\triangle )_{p}^{s}u=\lambda|u|^{q-2}u+\frac{\alpha}{\alpha+\beta}|u|^{\alpha -2}u|v|^{\beta}, & \mbox{in }\Omega, \\ M(\int_{\mathbb{R}^{2n}}\frac{|v(x)-v(y)|^{p}}{|x-y|^{n+sp}}\,dx\, dy)(-\triangle )_{p}^{s}v=\mu|v|^{q-2}v+\frac{\beta}{\alpha+\beta}|v|^{\beta -2}v|u|^{\alpha}, & \mbox{in }\Omega, \\ u=v=0, & \mbox{in }\mathbb{R}^{n}\setminus\Omega, \end{cases} $$

where Ω is a smooth bounded set in $\mathbb{R}^{n}$, $n>ps$ with $s\in(0,1)$ fixed, ${\lambda,\mu}>0$ are two parameters, $1< q< p< p(\tau+1)<\alpha+\beta<p^{*}$, $p^{*}=\frac{np}{n-sp}$, M is a continuous function, given by $M(h)=k+lh^{\tau}$, $k>0$, $l,\tau\geq0$, and $(-\triangle)_{p}^{s}$ is the fractional p-Laplacian operator. We will prove that the problem has at least two solutions by using the Nehari manifold method and fibering maps.

1 Introduction

In this paper, we consider the following Kirchhoff-type problem involving fractional p-Laplacian and concave-convex nonlinearities:

$$ \textstyle\begin{cases} M(\int_{\mathbb{R}^{2n}}\frac{|u(x)-u(y)|^{p}}{|x-y|^{n+sp}}\,dx\, dy)(-\triangle )_{p}^{s}u=\lambda|u|^{q-2}u+\frac{\alpha}{\alpha+\beta}|u|^{\alpha -2}u|v|^{\beta}, & \mbox{in }\Omega, \\ M(\int_{\mathbb{R}^{2n}}\frac{|v(x)-v(y)|^{p}}{|x-y|^{n+sp}}\,dx\, dy)(-\triangle )_{p}^{s}v=\mu|v|^{q-2}v+\frac{\beta}{\alpha+\beta}|v|^{\beta -2}v|u|^{\alpha}, & \mbox{in }\Omega, \\ u=v=0,& \mbox{in }\mathbb{R}^{n}\setminus\Omega, \end{cases} $$

(1.1)

where Ω is a smooth bounded set in $\mathbb{R}^{n}$, $n>ps$ with $s\in (0,1)$ fixed, ${\lambda,\mu}>0$ are two parameters, $1< q< p< p(\tau+1)<\alpha+\beta<p^{*}$, $p^{*}=\frac{np}{n-sp}$ is the fractional Sobolev exponent, M is a special continuous function defined by $M(h)=k+lh^{\tau}$, $k>0$, $l,\tau\geq0$. $(-\triangle)_{p}^{s}$ is the fractional p-Laplacian operator given by

$$ (-\triangle)_{p}^{s}u(x)=2\lim _{\varepsilon\rightarrow0} \int_{\mathbb{R} ^{n}\setminus {B_{\varepsilon}(x)}} \frac{|u(x)-u(y)|^{p-2}(u(x)-u(y))}{|x-y|^{n+sp}}\,dx\,dy. $$

(1.2)

The Kirchhoff-type equation and system have a broad background in phase transitions, population dynamics, mathematical finance, etc. There have been a lot of excellent results related to the existence and multiplicity of solutions for this system. We refer the readers to [1–4] for Kirchhoff problems involving the classical Laplace operator and to [5, 6] for the p-Laplacian case. For the fractional system, please consult [7–21] and the references therein.

In [10] and [11], the authors discussed the system (or a single equation, that is, $u=v$) in the special case of $M\equiv 1$. They obtained some interesting results by using the Nehari manifold method. For the special case $p=2$ of this system, there are many results available in the existing literature, we refer the interested reader to [22, 23] for the case of the classical Laplacian and to [24–26] for the case of the fractional Laplacian. Moreover, the authors [18] studied bifurcation results for a fractional elliptic equation with critical exponent. There is also some work for the case that M is not a constant (see, for example, [9]). However, as far as we know, there are few results on the fractional p-Kirchhoff system with concave-convex nonlinearities. Motivated by the above work, in this paper we consider problem (1.1) for a more general case $M(h)=k+lh^{\tau}$. We obtained a new multiplicity result by using the Nehari manifold method and fibering maps.

In order to state our result, we introduce some notations. Suppose $s\in (0,1)$ and $p\in[1,\infty)$. Let $W^{s,p}$ be a fractional Sobolev space with the norm

$$ \|u\|_{W^{s,p} (\Omega)}= \|u\|_{L^{p}(\Omega)}+ \biggl( \int_{\Omega \times \Omega} \frac{|u(x)-u(y)|^{p}}{|x-y|^{n+sp}}\,dx\,dy \biggr)^{\frac{1}{p}}. $$

(1.3)

Set $Q=\mathbb{R}^{2n}\setminus(C\Omega\times{C\Omega})$ with $C\Omega=\mathbb{R}^{n}\setminus\Omega$. We define

$$ X = \biggl\{ u\Big|u:\mathbb{R}^{n}\rightarrow\mathbb{R}\mbox{ is measurable}, u|_{\Omega}\in L^{p}(\Omega),\mbox{and } \int_{Q}\frac{|u(x)-u(y)|^{p}}{|x-y|^{n+sp}}\,dx\,dy< \infty\biggr\} . $$

The space X is endowed with the norm

$$ \|u\|_{X}= \|u\|_{L^{p}(\Omega)}+ \biggl( \int_{Q} \frac{|u(x)-u(y)|^{p}}{|x-y|^{n+sp}}\,dx\,dy \biggr)^{\frac{1}{p}}. $$

(1.4)

Let $X_{0}$ be the completion of the space $C_{0}^{\infty}(\Omega)$ in X. The space $X_{0}$ is a Banach space which can be endowed with the norm

$$ \|u\|_{X_{0}}= \biggl( \int_{Q} \frac{|u(x)-u(y)|^{p}}{|x-y|^{n+sp}}\,dx\,dy \biggr)^{\frac{1}{p}}. $$

(1.5)

It is easy to see that this norm is equivalent to the usual one defined in (1.3).

As proved in [17, 24], we have the following results:

• (i) $X_{0}\hookrightarrow L^{r}(\Omega)$ is continuous for any $r\in [1,p^{*}]$ and compact for any $r\in[1,p^{*})$.

• (ii) For $\alpha+\beta\in(p,p^{*})$, let S denote the best Sobolev constant for the embedding $X_{0}\hookrightarrow L^{\alpha+\beta}(\Omega)$. Then, for $u\in X_{0}$, we have

  $$\begin{aligned} \begin{aligned}[b] \|u\|_{L^{\alpha+\beta}(\Omega)}&= \biggl( \int_{\Omega}|u|^{\alpha +\beta }\,dx \biggr)^{\frac{1}{ \alpha+\beta}} \leq S^{-\frac{1}{p}}\|u\|_{X_{0}} \\ &=S^{-\frac{1}{p}} \biggl( \int_{Q} \frac{|u(x)-u(y)|^{p}}{|x-y|^{n+sp}}\,dx\,dy \biggr)^{\frac{1}{p}}. \end{aligned} \end{aligned}$$

  (1.6)

Let $E=X_{0}\times X_{0}$ be the Cartesian product of two spaces, which is a reflexive Banach space with the norm

$$\begin{aligned} \bigl\Vert (u,v)\bigr\Vert =&\bigl(\Vert u\Vert _{X_{0}}^{p}+\Vert v\Vert _{X_{0}}^{p} \bigr)^{\frac{1}{p}} \\ =& \biggl( \int_{Q} \frac{|u(x)-u(y)|^{p}}{|x-y|^{n+sp}}\,dx\,dy+ \int_{Q} \frac{|v(x)-v(y)|^{p}}{|x-y|^{n+sp}}\,dx\,dy \biggr)^{\frac{1}{p}}. \end{aligned}$$

(1.7)

Definition 1.1

We say that $(u,v)\in E$ is a weak solution of problem (1.1) if for any $(\phi,\psi)\in E$ one has

$$\begin{aligned}& M\bigl(\Vert u\Vert _{X_{0}}\bigr) \int_{Q}\frac {|u(x)-u(y)|^{p-2}(u(x)-u(y))(\phi(x)-\phi (y))}{|x-y|^{n+sp}}\,dx\,dy \\& \qquad{}+M\bigl(\Vert v\Vert _{X_{0}}\bigr) \int_{Q}\frac {|v(x)-v(y)|^{p-2}(v(x)-v(y))(\psi (x)-\psi (y))}{|x-y|^{n+sp}}\,dx\,dy \\& \quad= \int_{\Omega}\bigl(\lambda|u|^{q-2}u\phi+ \mu|v|^{q-2}v\psi\bigr)\, dx+\frac {\alpha }{\alpha+\beta} \int_{\Omega}|u|^{\alpha-2}u|v|^{\beta}\phi\, dx \\& \qquad{}+\frac{\beta}{\alpha+\beta} \int_{\Omega}|u|^{\alpha}|v|^{\beta -2}v\psi \,dx. \end{aligned}$$

(1.8)

The main result of this paper is as follows.

Theorem 1.2

Let $s\in(0,1)$, $n>sp$. If $1< q< p< p(\tau+1)<\alpha+\beta<p^{*}$, then there exists $\Lambda_{0}>0$ such that for $0<\lambda+\mu <\Lambda_{0}$ problem (1.1) has at least two solutions.

Remark 1

To our best knowledge, there is no similar result of this system for the case $p=2$.

This paper is organized as follows. In Section 2, we give some preliminaries of a Nehari manifold and a variational setting of problem (1.1). Section 3 gives the proof of Theorem 1.2.

2 The variational setting

Define a functional $I(u,v):E\rightarrow\mathbb{R}$ as follows:

$$ I(u,v)=\frac{k}{p}\bigl\Vert (u,v)\bigr\Vert ^{p}+\frac{l}{\sigma}\bigl\Vert (u,v)\bigr\Vert ^{\sigma}- \frac {1}{m} \int_{\Omega}|u|^{\alpha}|v|^{\beta}\,dx - \frac{1}{q}G(u,v), $$

(2.1)

where $\sigma=p(\tau+1)$, and $m=\alpha+\beta$, and

$$ G(u,v)= \int_{\Omega}\bigl(\lambda|u|^{q}+\mu|v|^{q} \bigr)\,dx. $$

By a direct computation, we know that $I(u,v)\in C^{1}(E,\mathbb{R})$ and, for $\forall(\phi,\psi)\in E$, there holds

$$\begin{aligned} \bigl\langle I'(u,v),(\phi,\psi)\bigr\rangle = &M \bigl(\Vert u\Vert _{X_{0}}\bigr) \int_{Q}\frac {|u(x)-u(y)|^{p-2}(u(x)-u(y))(\phi(x)-\phi(y))}{|x-y|^{n+sp}}\,dx\, dy \\ &{}+M\bigl(\Vert v\Vert _{X_{0}}\bigr) \int_{Q}\frac {|v(x)-v(y)|^{p-2}(v(x)-v(y))(\psi (x)-\psi (y))}{|x-y|^{n+sp}}\,dx\,dy \\ &{}- \int_{\Omega}\bigl(\lambda|u|^{q-2}u\phi+ \mu|v|^{q-2}v\psi\bigr)\, dx-\frac {\alpha }{m} \int_{\Omega}|u|^{\alpha-2}u|v|^{\beta}\phi\,dx \\ &{}-\frac{\beta}{m} \int_{\Omega}|u|^{\alpha}|v|^{\beta-2}v\psi\,dx. \end{aligned}$$

(2.2)

Then the weak solutions of problem (1.1) correspond to the critical points of the functional I. Since I is not bounded below on E, we consider it on the Nehari manifold

$$ N=\bigl\{ (u,v)\in E\setminus{(0,0)}|\bigl\langle I'(u,v),(u,v)\bigr\rangle =0\bigr\} . $$

From (2.2), we have

$$ \bigl\langle I'(u,v),(u,v)\bigr\rangle = k\bigl\Vert (u,v)\bigr\Vert ^{p}+l\bigl\Vert (u,v)\bigr\Vert ^{\sigma}- \int _{\Omega}|u|^{\alpha}|v|^{\beta}\,dx -G(u,v). $$

(2.3)

Thus, $(u,v)\in N$ if and only if

$$ k\bigl\Vert (u,v)\bigr\Vert ^{p}+l\bigl\Vert (u,v) \bigr\Vert ^{\sigma}- \int_{\Omega}|u|^{\alpha}|v|^{\beta}\,dx -G(u,v)=0. $$

(2.4)

Particularly, the following equality holds on N:

$$\begin{aligned} I(u,v) =&k\biggl(\frac{1}{p}-\frac{1}{q}\biggr)\bigl\Vert (u,v)\bigr\Vert ^{p}+l\biggl(\frac {1}{\sigma }- \frac {1}{q}\biggr)\bigl\Vert (u,v)\bigr\Vert ^{\sigma}-\biggl( \frac{1}{m}-\frac{1}{q}\biggr) \int _{\Omega}|u|^{\alpha }|v|^{\beta}\,dx \\ =&k\biggl(\frac{1}{p}-\frac{1}{m}\biggr)\bigl\Vert (u,v)\bigr\Vert ^{p}+l\biggl(\frac {1}{\sigma}-\frac {1}{m}\biggr)\bigl\Vert (u,v)\bigr\Vert ^{\sigma}-\biggl(\frac{1}{q}- \frac{1}{m}\biggr)G(u,v). \end{aligned}$$

(2.5)

Define

$$ \Phi(u,v)=\bigl\langle I'(u,v),(u,v)\bigr\rangle ,\quad \forall(u,v) \in E. $$

Then, for any $(u,v)\in N$,

$$\begin{aligned}& \bigl\langle \Phi'(u,v),(u,v)\bigr\rangle \\& \quad=kp\bigl\Vert (u,v)\bigr\Vert ^{p}+l\sigma\bigl\Vert (u,v) \bigr\Vert ^{\sigma}-m \int_{\Omega}|u|^{\alpha}|v|^{\beta}\,dx -qG(u,v) \\& \quad=k(p-m)\bigl\Vert (u,v)\bigr\Vert ^{p}+l(\sigma-m)\bigl\Vert (u,v)\bigr\Vert ^{\sigma}-(q-m)G(u,v) \\& \quad=k(p-q)\bigl\Vert (u,v)\bigr\Vert ^{p}+l(\sigma-q)\bigl\Vert (u,v)\bigr\Vert ^{\sigma}-(m-q) \int_{\Omega}|u|^{\alpha}|v|^{\beta}\,dx. \end{aligned}$$

(2.6)

Thus, it is natural to split N into three parts:

$$\begin{aligned}& N^{+}=\bigl\{ (u,v)\in N:\bigl\langle \Phi'(u,v),(u,v) \bigr\rangle >0\bigr\} , \\& N^{-}=\bigl\{ (u,v)\in N:\bigl\langle \Phi'(u,v),(u,v)\bigr\rangle < 0 \bigr\} , \\& N^{0}=\bigl\{ (u,v)\in N:\bigl\langle \Phi'(u,v),(u,v)\bigr\rangle =0\bigr\} . \end{aligned}$$

(2.7)

We now derive some properties of $N^{+}$, $N^{-}$ and $N^{0}$.

Lemma 2.1

I is coercive and bounded below on N.

Proof

By Hölder’s inequality and (1.6), we have

$$\begin{aligned} \int_{\Omega}\lambda|u|^{q}\,dx \leq&\lambda \biggl( \int_{\Omega}1\, dx \biggr)^{\frac{m-q}{m}} \biggl( \int_{\Omega}|u|^{m}\,dx \biggr)^{\frac{q}{m}} = \lambda|\Omega|^{\frac{m-q}{m}}\|u\|_{m}^{q} \\ \leq&\lambda|\Omega |^{\frac {m-q}{m}}S^{-\frac{q}{p}}\|u\|_{X_{0}}^{q} \leq\lambda|\Omega|^{\frac{m-q}{m}}S^{-\frac{q}{p}}\bigl\Vert (u,v)\bigr\Vert ^{q}. \end{aligned}$$

Similarly,

$$ \int_{\Omega}\mu|v|^{q}\,dx \leq\mu| \Omega|^{\frac{m-q}{m}}S^{-\frac{q}{p}}\Vert v\Vert _{X_{0}}^{q} \leq\mu|\Omega|^{\frac{m-q}{m}}S^{-\frac{q}{p}}\bigl\Vert (u,v)\bigr\Vert ^{q}. $$

Then

$$ G(u,v)\leq(\lambda+\mu)|\Omega|^{\frac{m-q}{m}}S^{-\frac {q}{p}} \bigl\Vert (u,v)\bigr\Vert ^{q}. $$

(2.8)

It follows from (2.5) and (2.8) that

$$\begin{aligned} I(u,v) \geq& k\biggl(\frac{1}{p}-\frac{1}{m}\biggr) \bigl\Vert (u,v)\bigr\Vert ^{p}+l\biggl(\frac{1}{\sigma }- \frac{1}{m}\biggr)\bigl\Vert (u,v)\bigr\Vert ^{\sigma} \\ &{}-\biggl(\frac{1}{q}-\frac{1}{m}\biggr) (\lambda+\mu)| \Omega|^{\frac {m-q}{m}}S^{-\frac{q}{p}}\bigl\Vert (u,v)\bigr\Vert ^{q}. \end{aligned}$$

(2.9)

Since $q< p\leq\sigma< m$, from inequality (2.9), the functional I is coercive and bounded below on N. The proof is completed. □

Lemma 2.2

There exists $\Lambda_{0}>0$, given by

$$ \Lambda_{0}=\frac{k(m-p)}{(m-q)|\Omega|^{\frac{m-q}{m}}S^{-\frac{q}{p}}} \biggl(\frac{k(p-q)}{(m-q)S^{-\frac{m}{q}}} \biggr)^{\frac{p-q}{m-p}}, $$

such that for any $0<\lambda+\mu<\Lambda_{0}$ we have $N^{0}=\emptyset$.

Proof

We argue by contradiction. Assume that there exist $\lambda ,\mu>0$ with $0<\lambda+\mu<\Lambda_{0}$ such that $N^{0}\neq\emptyset$. Then, for $(u,v)\in N^{0}$, we have

$$ \bigl\langle I'(u,v),(u,v)\bigr\rangle =0 \quad\mbox{and}\quad \bigl\langle \Phi '(u,v),(u,v)\bigr\rangle =0. $$

Then it follows from (2.5)-(2.8) that

$$ \bigl\Vert (u,v)\bigr\Vert \leq \biggl(\frac{(m-q)(\lambda+\mu)|\Omega |^{\frac {m-q}{m}}S^{-\frac{q}{p}}}{k(m-p)} \biggr)^{\frac{1}{p-q}}. $$

(2.10)

On the other hand, by Young’s inequality, we have

$$\begin{aligned} \begin{aligned}[b] \int_{\Omega}|u|^{\alpha}|v|^{\beta}\,dx&\leq \frac{\alpha}{m} \int _{\Omega}|u|^{m} \,dx+\frac{\beta}{m} \int_{\Omega}|v|^{m} \,dx \\ & \leq\frac{\alpha}{m}S^{-\frac{m}{q}}\|u\|_{X_{0}}^{m}+ \frac{\beta }{m}S^{-\frac{m}{q}}\|v\|_{X_{0}}^{m} \leq S^{-\frac{m}{q}}\bigl\Vert (u,v)\bigr\Vert ^{m}. \end{aligned} \end{aligned}$$

(2.11)

From (2.5)-(2.7) and (2.11) it follows that

$$ k(p-q)\bigl\Vert (u,v)\bigr\Vert ^{p}\leq(m-q)S^{-\frac{m}{q}} \bigl\Vert (u,v)\bigr\Vert ^{m}. $$

We have

$$ \bigl\Vert (u,v)\bigr\Vert \geq \biggl(\frac{k(p-q)}{(m-q)S^{-\frac{m}{q}}} \biggr)^{\frac{1}{m-p}}. $$

(2.12)

By (2.10) and (2.12),

$$ \lambda+\mu\geq\frac{k(m-p)}{(m-q)|\Omega|^{\frac {m-q}{m}}S^{-\frac{q}{p}}} \biggl(\frac{k(p-q)}{(m-q)S^{-\frac{m}{q}}} \biggr)^{\frac {p-q}{m-p}}=\Lambda_{0}, $$

which contradicts $0<\lambda+\mu<\Lambda_{0}$. □

By Lemmas 2.1 and 2.2, we write $N=N^{+}+N^{-}$ for $0<\lambda +\mu<\Lambda_{0}$, and I is coercive and bounded from below on $N^{+}$ and $N^{-}$. We define

$$ C^{+}=\inf_{(u,v)\in N^{+}} I(u,v) ,\qquad C^{-}=\inf_{(u,v)\in N^{-}} I(u,v). $$

As proved in [27], we have the following lemma.

Lemma 2.3

For $0<\lambda+\mu<\Lambda_{0}$, suppose that $(u_{0},v_{0})$ is a local minimizer for I on N. Then, if $(u_{0},v_{0})\notin N^{0}$, $(u_{0},v_{0})$ is a critical point of I.

Lemma 2.4

• (a) If $0<\lambda+\mu<\Lambda_{0}$, then $C^{+}<0$.

• (b) If $0<\lambda+\mu<\frac{q}{p}\Lambda_{0}$, then $\exists d_{0}>0$ such that $C^{-}>d_{0}$.

Proof

(a) Let $(u,v)\in N^{+}$, it follows from (2.6) and (2.7) that

$$ \int_{\Omega}|u|^{\alpha}|v|^{\beta}\,dx< \frac{k(p-q)}{m-q}\bigl\Vert (u,v)\bigr\Vert ^{p}+\frac{l(\sigma -q)}{m-q} \bigl\Vert (u,v)\bigr\Vert ^{\sigma}. $$

(2.13)

Put (2.13) into (2.5),

$$ I(u,v)< -\frac{k(p-q)}{mpq}\bigl\Vert (u,v)\bigr\Vert ^{p}- \frac {l(p-q)(m-p)}{mpq}\bigl\Vert (u,v)\bigr\Vert ^{\sigma}< 0, $$

which implies $C^{+}=\inf_{(u,v)\in N^{+}} I(u,v)<0$.

(b) Let $(u,v)\in N^{-}$. By (2.5) and (2.8),

$$\begin{aligned} I(u,v) \geq&\frac{k(m-p)}{pm}\bigl\Vert (u,v)\bigr\Vert ^{p}-\frac {m-q}{mq}G(u,v) \\ \geq&\frac{k(m-p)}{pm}\bigl\Vert (u,v)\bigr\Vert ^{p}- \frac {m-q}{mq}(\lambda+\mu )|\Omega |^{\frac{m-q}{m}}S^{-\frac{q}{p}}\bigl\Vert (u,v)\bigr\Vert ^{q} \\ =&\bigl\Vert (u,v)\bigr\Vert ^{q} \biggl(\frac{k(m-p)}{pm}\bigl\Vert (u,v)\bigr\Vert ^{p-q}-\frac {m-q}{mq}(\lambda+\mu)| \Omega|^{\frac{m-q}{m}}S^{-\frac {q}{p}} \biggr). \end{aligned}$$

(2.14)

Combining (2.12) with (2.14), we have

$$ I(u,v)\geq \biggl(\frac{k(p-q)}{(m-q)S^{-\frac{m}{q}}} \biggr)^{\frac{q}{m-p}} \biggl( \frac{k(m-p)}{pm} \biggl(\frac{k(p-q)}{(m-q)S^{-\frac {m}{q}}} \biggr) ^{\frac{p-q}{m-p}}- \frac{m-q}{mq}(\lambda+\mu)|\Omega|^{\frac {m-q}{m}}S^{-\frac{q}{p}} \biggr). $$

Clearly, if $0<\lambda+\mu<\Lambda_{0}$, then there exists $d_{0}(p,q,\alpha,\beta,S)>0$ such that $C^{-}=\inf_{(u,v)\in N^{-}} I(u, v)>d_{0}$. □

For each $(u,v)\in E$, let

$$ \eta(t)=kt^{p-q}\bigl\Vert (u,v)\bigr\Vert ^{p}+lt^{\sigma-q}\Vert u,v\Vert ^{\sigma}-t^{m-q} \int _{\Omega}|u|^{\alpha}|v|^{\beta}\,dx. $$

(2.15)

Then

$$ \eta'(t)=t^{p-q-1}E(t), $$

where

$$ E(t)=k(p-q)\bigl\Vert (u,v)\bigr\Vert ^{p}+l(\sigma-q)t^{\sigma-p} \bigl\Vert (u,v)\bigr\Vert ^{\sigma}-(m-q)t^{m-p} \int_{\Omega}|u|^{\alpha}|v|^{\beta}\,dx. $$

Define

$$ t^{*}= \biggl(\frac{l(\sigma-q)(\sigma-p)\|(u,v)\|^{\sigma}}{(m-q)(m-p)\int _{\Omega}|u|^{\alpha}|v|^{\beta}\,dx} \biggr)^{\frac{1}{m-\sigma}}. $$

It is easy to check that $E(t)$ increases for $t\in[0,t^{*})$ and decreases for $t\in(t^{*},\infty)$, $E(t)$ achieves its maximum at $t^{*}$. Since $E(t)\rightarrow0$ as $t\rightarrow0^{+}$ and $E(t)\rightarrow-\infty$ as $t\rightarrow\infty$ and there exists unique $t_{l}$, $0< t^{*}< t_{l}$, such that $E(t_{l})=0$, so $\eta(t)$ achieves its maximum at $t_{l}$, increasing for $t\in[0,t_{l})$ and decreasing for $t\in(t_{l},\infty)$. When $l=0$, we have

$$ t_{0}= \biggl(\frac{k(p-q)\Vert (u,v)\Vert ^{p}}{(m-q)\int_{\Omega}|u|^{\alpha}|v|^{\beta}\,dx} \biggr)^{\frac{q}{m-p}}. $$

(2.16)

Obviously, $E(t_{0})=E(t_{l})=0$ and $t_{0}\leq t_{l}$ for $l\geq0$. Thus

$$ \eta(t_{l})\geq\frac{k(m-p)}{m-q}t_{l}^{p-q} \bigl\Vert (u,v)\bigr\Vert ^{p}\geq \frac {k(m-p)}{m-q}t_{0}^{p-q} \bigl\Vert (u,v)\bigr\Vert ^{p}=\eta(t_{0}). $$

(2.17)

Set

$$\begin{aligned}& \Psi_{0}(t)=\Phi(tu,tv)=\bigl\langle I'(tu,tv) (tu,tv) \bigr\rangle \\& \hphantom{\Psi_{0}(t)}=kt^{p}\bigl\Vert (u,v)\bigr\Vert ^{p}+lt^{\sigma}\bigl\Vert (u,v)\bigr\Vert ^{\sigma}-t^{m} \int_{\Omega}|u|^{\alpha}|v|^{\beta}\,dx-t^{q}G(u,v), \\& \Psi_{1}(t)=\bigl\langle \Phi'(tu,tv),(tu,tv)\bigr\rangle \\& \hphantom{\Psi_{1}(t)}=kpt^{p}\bigl\Vert (u,v)\bigr\Vert ^{p}+l \sigma t^{\sigma}\bigl\Vert (u,v)\bigr\Vert ^{\sigma}-mt^{m} \int_{\Omega}|u|^{\alpha}|v|^{\beta}\,dx-qt^{q}G(u,v). \end{aligned}$$

Then

$$ \Psi_{0}(t)=t^{q}\bigl(\eta(t)-G(u,v)\bigr). $$

(2.18)

Lemma 2.5

$(tu,tv)\in N^{+}$ (or $N^{-}$) if and only if $\Psi_{1}(t)>0$ (or $\Psi_{1}(t)<0$).

Proof

By (2.7), it is clear that $(tu,tv)\in N^{+}$ (or $N^{-}$) if and only if $(tu,tv)\in N$ and $\langle\Phi'(tu,tv),(tu,tv)\rangle>0$ (<0) for $t>0$. Note that

$$\Psi_{0}(t)=\Phi(tu,tv)=\bigl\langle I'(tu,tv), (tu,tv) \bigr\rangle ,\qquad \Psi _{1}(t)=\bigl\langle \Phi'(tu,tv),(tu,tv) \bigr\rangle . $$

Hence, $(tu,tv)\in N^{+}$ if and only if $\Psi_{0}(t)=0$ and $\Psi_{1}(t)>0$. □

Lemma 2.6

For each $(u,v)\in E\setminus{(0,0)}$ and $0<\lambda+\mu<\Lambda_{0}$, there exist $0< t_{1}< t_{l}< t_{2}$ such that $(t_{1}u,t_{1}v)\in N^{+}$, $(t_{2}u,t_{2}v)\in N^{-}$, and

$$ I(t_{1}u,t_{1}v)=\inf_{0\leq t\leq t_{l}}I(tu,tv),\qquad I(t_{2}u,t_{2}v)=\sup_{t\geq 0}I(tu,tv). $$

Proof

Set

$$\begin{aligned} \Psi_{2}(t) =&I(tu,tv) \\ =&\frac{kt^{p}}{p}\bigl\Vert (u,v)\bigr\Vert ^{p}+ \frac{lt^{\sigma}}{\sigma}\bigl\Vert (u,v)\bigr\Vert ^{\sigma}- \frac{t^{m}}{m} \int_{\Omega}|u|^{\alpha}|v|^{\beta}\,dx- \frac{t^{q}}{q}G(u,v). \end{aligned}$$

Since $0<\lambda+\mu<\Lambda_{0}$, by (2.8), (2.15) and (2.17), we have

$$ G(u,v)\leq(\lambda+\mu)|\Omega|^{\frac{m-q}{m}}S^{-\frac {q}{p}}\bigl\Vert (u,v) \bigr\Vert ^{q} \leq\eta(t_{0})\leq\eta(t_{l}). $$

Thus, there exist $t_{1}$ and $t_{2}$ such that $0< t_{1}< t_{l}< t_{2}$ and $\eta(t_{1})=\eta(t_{2})=G(u,v)$. It follows from (2.18) that $\Psi_{0}(t_{1})=0$ and $\Psi_{0}(t_{2})=0$, then $(t_{1}u,t_{1}v)\in N$ and $(t_{2}u,t_{2}v)\in N$. $\Psi_{1}(t_{1})=(t_{1})^{q+1}\eta'(t_{1})>0$. By Lemma 2.5, one has $(t_{1}u,t_{1}v)\in N^{+}$. Meanwhile, $\Psi_{1}(t_{2})=(t_{2})^{q+1}\eta'(t_{2})<0$, we obtain $(t_{2}u,t_{2}v)\in N^{-}$. By a direct calculation, we have $\Psi_{2}'(t)=t^{q-1}(\eta(t)-G(u,v))$. Since $\Psi_{2}'(t)<0$ for $t\in[0,t_{1})$ and $\Psi_{2}'(t)>0$ for $t\in[t_{1},t_{l})$, $I(t_{1}u,t_{1}v)=\inf_{0\leq t\leq t_{l}}I(tu,tv)$. Furthermore, we find that $\Psi_{2}'(t)>0$ for $t\in[t_{1},t_{2})$, $\Psi _{2}'(t)<0$ for $t\in[t_{2},+\infty)$ and $\Psi_{2}(t)\leq0$ for $t\in[0,t_{1}]$. Since $(t_{2}u,t_{2}v)\in N^{-}$, by Lemma 2.4, we obtain $\Psi_{2}(t_{2})>0$. Then $I(t_{2}u,t_{2}v)=\sup_{t\geq0}I(tu,tv)$. □

3 Proof of the main result

Lemma 3.1

If $0<\lambda+\mu<\Lambda_{0}$, then the functional I has a minimizer $(u_{1},v_{1})$ in $N^{+}$ satisfying

• (i) $I(u_{1},v_{1})=C^{+}<0$;

• (ii) $(u_{1},v_{1})$ is a solution of problem (1.1).

Proof

Since I is bounded from below on $N^{+}$, there exists a minimizing sequence $\{(u_{n}, v_{n})\}\in N^{+}$ such that

$$ \lim_{n\rightarrow\infty}I(u_{n},v_{n})=\inf _{(u,v)\in N^{+}}I(u,v)=C^{+}. $$

Since $I(u,v)$ is coercive and bounded from below on N, then $\{ (u_{n},v_{n})\}$ is bounded on E. Then there exists $(u_{1},v_{1})\in E$, up to a subsequence, that we still denote by $\{(u_{n},v_{n})\}$, such that, as $n\rightarrow \infty$,

$$\begin{aligned}& u_{n}\rightharpoonup u_{1},\qquad v_{n} \rightharpoonup v_{1},\quad \mbox{in }L^{r}(\Omega), \\& u_{n}(x)\rightarrow u_{1}(x),\qquad v_{n}(x) \rightarrow v_{1}(x),\quad \mbox{a.e. in }\Omega \end{aligned}$$

for any $1\leq r< p^{*}$, and by [28], Theorem IV-9, there exists $l(x)\in L^{r}(\mathbb{R}^{n})$ such that

$$ \bigl\vert u_{n}(x)\bigr\vert \leq l(x),\qquad \bigl\vert v_{n}(x)\bigr\vert \leq l(x),\quad \mbox{a.e. in } \mathbb{R}^{n} $$

for any $1\leq r< p^{*}$. By the dominated convergence theorem,

$$\begin{aligned} \lim_{n\rightarrow\infty} \int_{\Omega}\bigl(\lambda|u_{n}|^{q}+ \mu|v_{n}|^{q}\bigr)\,dx =& \int_{\Omega}\lim_{n\rightarrow\infty}\bigl( \lambda|u_{n}|^{q}+\mu |v_{n}|^{q}\bigr) \,dx \\ =& \int_{\Omega}\bigl(\lambda|u_{1}|^{q}+ \mu|v_{1}|^{q}\bigr)\,dx, \end{aligned}$$

and

$$ \lim_{n\rightarrow\infty} \int_{\Omega}|u_{n}|^{\alpha}|v_{n}|^{\beta}\, dx= \int _{\Omega}|u_{1}|^{\alpha}|v_{1}|^{\beta}\,dx. $$

By Lemma 2.6, there exists $t_{1}< t_{l}$ such that $(t_{1}u_{1},t_{1}v_{1})\in N^{+}$ and $\Psi_{0}(t_{1})=\langle I'(t_{1}u_{1},t_{1}v_{1}), (t_{1}u_{1},t_{1}v_{1})\rangle=0$.

Next we show that $(u_{n},v_{n})\rightarrow(u_{1},v_{1})$ strongly in E. Suppose otherwise, then

$$ \bigl\Vert (u_{1},v_{1})\bigr\Vert < \liminf _{n\rightarrow\infty}\bigl\Vert (u_{n},v_{n})\bigr\Vert . $$

As

$$\begin{aligned} \bigl\langle I'(t_{1}u_{n},t_{1}v_{n}),(t_{1}u_{n},t_{1}v_{n}) \bigr\rangle =&kt_{1}^{p}\bigl\Vert (u_{n},v_{n}) \bigr\Vert ^{p} +lt_{1}^{\sigma}\bigl\Vert (u_{n},v_{n})\bigr\Vert ^{\sigma}\\ &{}-t_{1}^{m} \int_{\Omega}|u_{n}|^{\alpha}|v_{n}|^{\beta}\,dx -t_{1}^{q}G(u_{n},v_{n}), \end{aligned}$$

and

$$\begin{aligned} \bigl\langle I'(t_{1}u_{1},t_{1}v_{1}),(t_{1}u_{1},t_{1}v_{1}) \bigr\rangle =&kt_{1}^{p}\bigl\Vert (u_{1},v_{1}) \bigr\Vert ^{p} +lt_{1}^{\sigma}\bigl\Vert (u_{1},v_{1})\bigr\Vert ^{\sigma}\\ &{}-t_{1}^{m} \int_{\Omega}|u_{1}|^{\alpha}|v_{1}|^{\beta}\,dx -t_{1}^{q}G(u_{1},v_{1}), \end{aligned}$$

we have

$$ \lim_{n\rightarrow\infty}\bigl\langle I'(t_{1}u_{n},t_{1}v_{n}),(t_{1}u_{n},t_{1}v_{n}) \bigr\rangle > \bigl\langle I'(t_{1}u_{1},t_{1}v_{1}),(t_{1}u_{1},t_{1}v_{1}) \bigr\rangle =\Psi_{0}(t_{1})=0. $$

That is, $\langle I'(t_{1}u_{n},t_{1}v_{n}),(t_{1}u_{n},t_{1}v_{n})\rangle>0$ for n large enough. Since $\{(u_{n},v_{n})\}\in N^{+}$, it is easy to see that $\langle I'(u_{n},v_{n}),(u_{n},v_{n})\rangle=0$, and $\langle I'(tu_{n},tv_{n}),(tu_{n},tv_{n})\rangle<0$ for $0< t<1$. So we have $t_{1}>1$. On the other hand, $I(tu_{1},tv_{1})$ is decreasing on $(0,t_{1})$, So

$$ I(t_{1}u_{1},t_{1}v_{1})\leq I(u_{1},v_{1})< \liminf_{n\rightarrow\infty }I(u_{n},v_{n})=C^{+}= \inf_{(u,v)\in N^{+}}I(u,v), $$

which is a contradiction. Hence $(u_{n},v_{n})\rightarrow(u_{1},v_{1})$ strongly in E. This implies

$$ I(u_{n},v_{n})\rightarrow I(u_{1},v_{1})= \inf_{(u,v)\in N^{+}}I(u,v)=C^{+}\quad \mbox{as } n\rightarrow\infty. $$

Namely, $(u_{1},v_{1})$ is a minimizer of I on $N^{+}$, by Lemma 2.2, $(u_{1},v_{1})$ is a solution of problem (1.1). □

Lemma 3.2

If $0<\lambda+\mu<\Lambda_{0}$, then the functional I has a minimizer $(u_{2},v_{2})$ in $N^{-}$ such that

• (i) $I(u_{2},v_{2})=C^{-}$;

• (ii) $(u_{2},v_{2})$ is a solution of problem (1.1).

Proof

Since I is bounded from below on $N^{-}$, there exists a minimizing sequence $\{(\bar{u}_{n}, \bar{v}_{n})\}\in N^{-}$ such that

$$ \lim_{n\rightarrow\infty}I(\bar{u}_{n},\bar{v}_{n})=C^{-}. $$

Since $I(u,v)$ is coercive, $\{(\bar{u}_{n},\bar{v}_{n})\}$ is bounded on E, up to a subsequence, we still denote it by $\{(\bar{u}_{n},\bar{v}_{n})\}$, then there exists $(u_{2},v_{2})\in E$ such that

$$ \bar{u}_{n}\rightharpoonup u_{2}, \qquad \bar{v}_{n}\rightharpoonup v_{2},\quad \mbox{in } L^{r}(\Omega) $$

for any $1\leq r< p^{*}$, and by [28], Theorem IV-9, and the dominated convergence theorem,

$$ \lim_{n\rightarrow\infty} G(\bar{u}_{n},\bar{v}_{n})= G(u_{2},v_{2}), $$

and

$$ \lim_{n\rightarrow\infty} \int_{\Omega} \vert \bar{u}_{n}\vert ^{\alpha} \vert \bar {v}_{n}\vert ^{\beta}\,dx= \int_{\Omega} \vert u_{2}\vert ^{\alpha} \vert v_{2}\vert ^{\beta}\,dx. $$

By Lemma 2.6, there exists unique $t_{2}$ such that $(t_{2}u_{2},t_{2}v_{2})\in N^{-}$. Next we show that $(\bar{u}_{n},\bar{v}_{n})\rightarrow(u_{2},v_{2})$ strongly in E. The proof of this claim is by contradiction. If the claim were not true, then

$$ \bigl\Vert (u_{2},v_{2})\bigr\Vert < \liminf _{n\rightarrow\infty}\bigl\Vert (\bar {u}_{n},\bar{v}_{n}) \bigr\Vert . $$

Since $(\bar{u}_{n},\bar{v}_{n})\in N^{-}$ and $I(\bar{u}_{n},\bar {v}_{n})\geq I(t\bar{u}_{n}, t\bar{v}_{n})$ for all $t>0$, then we have

$$ I(t_{2}u_{2},t_{2}v_{2})< \liminf _{n\rightarrow\infty}I(t_{2}\bar{u}_{n},t_{2} \bar{v}_{n}) \leq\liminf_{n\rightarrow\infty}I(\bar{u}_{n}, \bar{v}_{n})=C^{-}, $$

which is a contradiction. This implies

$$ I(\bar{u}_{n},\bar{v}_{n})\rightarrow I(u_{2},v_{2})= \inf_{(u,v)\in N^{-}}I(u,v)=C^{-} \quad\mbox{as }n\rightarrow\infty. $$

Namely, $(u_{2},v_{2})$ is a minimizer of I on $N^{-}$, by Lemma 2.2, $(u_{2},v_{2})$ is a solution of problem (1.1). □

Proof of Theorem 1.2

By Lemmas 3.1 and 3.2, we have that for $0<\lambda+\mu<\Lambda_{0}$, problem (1.1) has two solutions $(u_{1},v_{1})\in N^{+}$ and $(u_{2},v_{2})\in N^{-}$ in E. Since $N^{+}\cap N^{-}=\emptyset$, then these two solutions are distinct. □