1 Introduction

Throughout this paper, we always assume that \(H_{1}\), \(H_{2}\) and \(H_{3}\) are real Hilbert spaces with inner product \(\langle \cdot , \cdot \rangle \) and induced norm \(\|\cdot \|\). Let C and Q be nonempty closed and convex subsets of \(H_{1}\) and \(H_{2}\), respectively. Let \(A: H_{1}\rightarrow H_{2}\) be a bounded linear operator and I denote the identity operator. The split feasibility problem (SFP) is to find

$$ x\in C \quad \text{such that} \quad Ax\in Q, $$
(1.1)

which is first introduced by Censor and Elfving [8] in finite-dimensional Hilbert spaces for modeling inverse problems. The applications of the split feasibility problem are very comprehensive such as CT in medicine, intelligence antennas and the electronic warning systems in militarily, the development of fast image processing technology, etc. [5, 7, 9, 34].

To solve the problem (1.1), Byrne [4] proposed the CQ algorithm which generates a sequence \(\{x_{n}\}\) by

$$ x_{n+1}=P_{C}\bigl(x_{n}-\xi A^{\ast }(Ax_{n}-P_{Q}Ax_{n})\bigr), $$
(1.2)

and proved the sequence generated by (1.2) converges to the solution of (1.1), where \(A^{*}\) is the adjoint operator of A, \(\xi \in ( 0, 2 / L )\) and L denotes the largest eigenvalue of the matrix \(A^{T}A\). Furthermore, many authors studied the problem (1.1) and proposed some algorithms for solving it, please see [3, 6, 22, 25, 26, 32, 33, 35] and the references therein. Particular cases of the CQ algorithm are the Landweber and projected Landweber methods for obtaining exact or approximate solutions of the linear equations \(Ax=b\).

In [18, 19, 24, 30, 31, 34], a lot of algorithms were proposed for solving a multiple-sets split feasibility problem (MSFP), which is to find

$$ x\in \bigcap_{i=1}^{p}C_{i} \quad \text{such that}\quad Ax\in \bigcap_{j=1}^{r}Q_{j}, $$
(1.3)

where \(p, r\geq 1\) are integers, \(\{C_{i}\}_{i=1}^{p}\) and \(\{Q_{j}\} _{j=1}^{r}\) are nonempty closed convex subsets of \(H_{1}\) and \(H_{2}\), respectively. When \(p=r=1\), then MSFP (1.3) is known as SFP (1.1).

Since every closed convex subset of a Hilbert space is the fixed point set of its associating projection, the problem (1.1) and (1.3) are all special cases of the so-called multiple-set split common fixed point problem (MSCFP) which is to find

$$ x\in \bigcap_{i=1}^{p} \operatorname{Fix}(S_{i}) \quad \text{such that}\quad Ax \in \bigcap _{j=1}^{r}\operatorname{Fix}(T_{j}), $$
(1.4)

where \(p, r\geq 1\) are integers, \(\{S_{i}\}_{i=1}^{p}: H_{1}\rightarrow H_{1}\) and \(\{T_{j}\}_{j=1}^{r}: H_{2}\rightarrow H_{2}\) are nonlinear operators and \(\operatorname{Fix} (S_{i})\) and \(\operatorname{Fix} (T_{j})\) are the sets of fixed points of \(S_{i}\) and \(T_{j}\), respectively. In particular, if \(p=r=1\), then MSCFP (1.4) reduces to the split common fixed point problem (SCFP) [11, 20, 27, 29] to find

$$ x\in \operatorname{Fix}(S)\quad \text{such that}\quad Ax\in \operatorname{Fix}(T), $$
(1.5)

where \(S: H_{1}\rightarrow H_{1}\) and \(T: H_{2}\rightarrow H_{2}\) are nonlinear operators.

It is easy to see from [10, 15] that the above problems are the special cases of the following problem:

$$ \mbox{find a point $x^{*}\in X$ that solves IP1} $$

and such that

$$ \mbox{the point $y^{*}=Ax^{*}\in Y $ solves IP2}, $$

where IP1 and IP2 are inverse problems, which is called the split inverse problem (SIP).

Furthermore, we find that the equilibrium problem (EP) and the split variational inequality problem (SVI) are also special cases of SIP from [10, 11, 15, 21].

As the further extension of the split feasibility problem, Moudafi [22, 23] introduced the split equality feasibility problem (SEFP) to find

$$ x\in C,\quad y\in Q \quad \text{such that}\quad Ax=By, $$
(1.6)

where \(A: H_{1}\rightarrow H_{3}\) and \(B: H_{2}\rightarrow H_{3}\) are two bounded linear operators. Obviously, if \(B=I\) and \(H_{3}=H_{2}\), then (1.6) reduces to (1.1), which can be extended to be the split common fixed point problem (SCFPP); see [11] and the references therein. This kind of split equality feasibility problem (1.6) allows for asymmetric and partial relations between the variables x and y.

To solve the split equality feasibility problem (1.6), Moudafi [23] proposed the following alternating CQ algorithm:

$$ \textstyle\begin{cases} x_{n+1}=P_{C}(x_{n}-\gamma _{n}A^{\ast }(Ax_{n}-By_{n})), \\ y_{n+1}=P_{Q}(y_{n}+\gamma _{n}B^{\ast }(Ax_{n+1}-By_{n})). \end{cases} $$
(1.7)

Under suitable conditions, he proved the weak convergence of the sequence \(\{(x_{n},y_{n})\}\) to a solution of (1.6) in Hilbert spaces. About the study of algorithms and theories for solving (1.6), the reader can also see [14, 17] and the references therein.

In [23], Moudafi studied the split equality common fixed point problem (SECFP), which is to find

$$ x\in \operatorname{Fix}(S),\quad y\in \operatorname{Fix}(T)\quad \text{such that} \quad Ax=By, $$
(1.8)

and proposed the following iterative algorithm:

$$ \textstyle\begin{cases} x_{n+1}=S(x_{n}-\lambda _{n}A^{\ast }(Ax_{n}-By_{n})), \\ y_{n+1}=T(y_{n}+\beta _{n}B^{\ast }(Ax_{n+1}-By_{n})). \end{cases} $$
(1.9)

He proved the weak convergence of the sequences generated by scheme (1.9) under the condition that S and T are firmly quasi-nonexpansive mappings. The study of the problem (1.9) not only has theory interesting, but also has practical background. In [1, 2], Attouch et al. propose the inertial Nash equilibration processes, which is the link with decision sciences and game theory. The problem can be modeled as the following convex optimization problem:

$$ \min \bigl\{ f(x) + g(y) + \mu Q(x,y), x \in X, y \in Y \bigr\} , $$
(1.10)

where X, Y are real Hilbert spaces, \(f: X\rightarrow \mathbf{R} \cup \{+\infty \}\), \(g: Y\rightarrow R\cup \{+\infty \}\) are closed convex proper functions acting, respectively, on the spaces X and Y, \(Q: X\times Y \rightarrow R^{+}\) is a nonnegative quadratic form which couples the two variables x and y, and μ is a positive parameter. Let \(f(x)=\|x-z\|^{2} \), \(g(y)=\|y-v\|^{2}\), and \(Q(x,y)=\|Ax-By\|^{2}\), where \(z\in \operatorname{fix}(S)\), \(v\in \operatorname{fix}(T)\) and S, T are operators. Then the optimization solution of the problem (1.10) is the solution of (1.8).

Furthermore, Chang, Wang and Qin [13] modified the iterative scheme (1.9) and provided a unified framework for solving this problem without using the projection. The framework is as follows:

$$ \textstyle\begin{cases} u_{n}= x_{n}- \gamma _{n}A^{\ast }(Ax_{n}- By_{n} ), \\ x_{n+ 1} = \alpha _{n}x_{n} + (1-\alpha _{n}) [(1-\xi )I+ \xi S((1- \eta )I+\eta S)]u_{n}, \\ v_{n}= y_{n} + \gamma _{n}B^{\ast } (Ax_{n}-By_{n}), \\ y_{n+ 1}= \alpha _{n}y_{n}+ (1- \alpha _{n}) [(1-\xi )I+ \xi T((1- \eta )I+\eta T)]v_{n}, \end{cases} $$
(1.11)

where S: \(H_{1}\rightarrow H_{1}\) and T: \(H_{2}\rightarrow H_{2}\) are two L-Lipschitz and quasi-pseudo-contractive mappings with \(L \geq 1\), \(\operatorname{Fix}(T) \neq \emptyset \). They proved that the sequence \(\{(x_{n}, y_{n})\}\) generated by the above modification (1.11) converges weakly to a solution of problem (1.8).

In this paper, we propose an alternating iterative algorithm which modifies the iterative scheme (1.11). In the process of calculating \(v_{n}\), we use \(x_{n+1}\) instead of \(x_{n}\). And we modify the directions \(A^{*}(Ax_{n}-By_{n})\) and \(B^{*}(By_{n}-Ax_{n})\), which can make full use of the current information of the iterative points. Details please see Theorem 3.1 in Sect. 3. Furthermore, we prove that the sequence generated by the algorithm weakly converges to a solution of the split equality common fixed point problem (1.8). Numerical results show that the feasibility and efficiency of this algorithm by comparing the algorithm proposed in this paper with the algorithm in [13].

2 Preliminaries

In this section, we recall some concepts, definitions and conclusions, which are prepared for proving our main results. We write \(x_{n} \rightharpoonup x \) and \(x_{n} \rightarrow x\) to indicate that the sequence \(\{x_{n}\}\) converges weakly and strongly to x, respectively.

Definition 2.1

([28])

A mapping \(T: C\rightarrow C\) is called

  1. (i)

    quasi-nonexpansive, if \(\operatorname{Fix} (T) \neq \emptyset \) and

    $$ \bigl\Vert Tx- x^{\ast } \bigr\Vert \leq \bigl\Vert x- x^{\ast } \bigr\Vert , \quad \text{for all } x\in C \text{ and } x^{\ast } \in \operatorname{Fix}(T); $$
    (2.1)
  2. (ii)

    quasi-pseudo-contractive, if \(\operatorname{Fix} (T) \neq \emptyset \) and

    $$ \bigl\Vert Tx- x^{\ast } \bigr\Vert ^{2}\leq \bigl\Vert x- x^{\ast } \bigr\Vert ^{2} + \Vert Tx- x \Vert ^{2} , \quad \text{for all } x\in C \text{ and } x^{\ast } \in \operatorname{Fix}(T). $$
    (2.2)

A mapping \(P_{C}\) is said to be metric projection of \(H_{1}\) onto C if for every point \(x\in H_{1}\), there exists a unique nearest point in C denoted by \(P_{C}x\) such that

$$ \Vert x-P_{C}x \Vert \leq \Vert x-y \Vert , \quad \text{for all } y\in C. $$
(2.3)

The corresponding property of the mapping \(P_{C}\) can be seen from [16]. Furthermore, the demiclosedness principle plays an important role in our arguments.

A mapping \(T: H \rightarrow H\) is called demiclosed at the origin if for any sequence \(\{x_{n}\}\) which weakly converges to x, and the sequence \(\{T x_{n}\}\) strongly converges to 0, then \(Tx=0\).

To establish the main results, we need the following technical lemmas.

Lemma 2.1

([12])

Let H be a real Hilbert space, then the following conclusions hold:

$$\begin{aligned}& \Vert x- y \Vert ^{2} = \Vert x \Vert ^{2}+ \Vert y \Vert ^{2}-2\langle x, y\rangle ,\quad \forall x, y \in H, \end{aligned}$$
(2.4)
$$\begin{aligned}& \bigl\Vert \alpha x+(1-\alpha )y \bigr\Vert ^{2}= \alpha \Vert x \Vert ^{2}+ (1-\alpha ) \Vert y \Vert ^{2} \\& \hphantom{\bigl\Vert \alpha x+(1-\alpha )y \bigr\Vert ^{2}={}}- \alpha (1-\alpha ) \Vert x- y \Vert ,\quad \forall x, y\in H, \alpha \in [0, 1]. \end{aligned}$$
(2.5)

Lemma 2.2

Let H be a real Hilbert space and \(T: H\rightarrow H\) be a L-Lipschitz mapping with \(L\geq 1\).

Denote

$$ K: = (1-\xi )I+ \xi T\bigl((1-\eta )I+\eta T\bigr). $$
(2.6)

If \(0< \xi < \eta < \frac{1}{1+\sqrt{1+L^{2}}}\), then the following conclusions hold:

  1. (i)

    \(\operatorname{Fix}(T)= \operatorname{Fix} (T((1-\eta )I+ \eta T))= \operatorname{Fix}(K)\).

  2. (ii)

    If T is demiclosed at 0, then K is also demiclosed at 0.

  3. (iii)

    In addition, if \(T: H\rightarrow H\) is quasi-pseudo-contractive, then the mapping K is quasi-nonexpansive, that is,

    $$ \bigl\Vert Kx -u^{\ast } \bigr\Vert \leq \bigl\Vert x- u^{\ast } \bigr\Vert , \quad \forall x \in H \textit{ and } u^{\ast } \in \operatorname{Fix}(T)=\operatorname{Fix}(K). $$
    (2.7)

3 Main results

In this section, we assume that

  1. (i)

    \(H_{1}\), \(H_{2}\) and \(H_{3}\) are real Hilbert spaces. \(A: H_{1} \rightarrow H_{3}\) and \(B: H_{2}\rightarrow H_{3}\) are two bounded linear operators, \(A^{\ast }\) and \(B^{\ast }\) are their adjoint operators, respectively.

  2. (ii)

    \(S: H_{1}\rightarrow H_{1}\) and \(T: H_{2}\rightarrow H_{2}\) are all L-Lipschitz and quasi-pseudo-contractive mapping with \(L\geq 1\), \(0<\xi _{n} < \eta _{n} <\frac{1}{1+\sqrt{1+L^{2}}}\), \(\forall n\geq 1\), \(\operatorname{Fix}(S) \neq \emptyset \), and \(\operatorname{Fix}(T) \neq \emptyset\).

Our objective is to solve the split equality common fixed point problem to find

$$ x^{\ast } \in \operatorname{Fix}(S),\quad y^{\ast } \in \operatorname{Fix}(T) \quad \mbox{such that}\quad Ax^{\ast }=By^{\ast }. $$
(3.1)

Theorem 3.1

Let \(H_{1}\), \(H_{2}\), \(H_{3}\) and A, B, S, T are assumed as above. Assume that \(\{\alpha _{n}\} \) is a non-increasing sequence which satisfies \(0< \beta \leq \alpha _{n} \leq \theta < 1 \), where β and θ are real numbers. For arbitrary \(x_{0}\in H _{1}\), \(y_{0}\in H_{2} \), let \(\{x_{n}\}\), \(\{y_{n}\}\), \(\{u_{n}\}\) and \(\{v_{n}\}\) be generated by

$$ \textstyle\begin{cases} u_{n}= x_{n}- \gamma _{n}[(x_{n}-Kx_{n})+A^{\ast } (Ax_{n} - By_{n})], \\ x_{n+ 1}= \alpha _{n} x_{n}+ (1-\alpha _{n})Ku_{n}, \\ v_{n}= y_{n}- \gamma _{n}[(y_{n}-Gy_{n})- B^{\ast } (Ax_{n+1}-By_{n})], \\ y_{n+ 1}= \alpha _{n}y_{n}+ (1-\alpha _{n})Gv_{n}, \end{cases} $$
(3.2)

where

$$\begin{aligned}& K:=(1-\xi _{n} )I + \xi _{n} S\bigl((1-\eta _{n} )I + \eta _{n} S\bigr), \\& G:=(1-\xi _{n} )I + \xi _{n} T\bigl((1-\eta _{n} )I + \eta _{n} T\bigr). \end{aligned}$$

Assume S and T are demiclosed at 0, and \(\{\gamma _{n}\}\) is a non-decreasing sequence which satisfies

$$ \gamma _{n} \in \biggl(\varepsilon ,\frac{1}{1+c}-\varepsilon \biggr),\qquad c=\max \bigl\{ \Vert A \Vert ^{2}, \Vert B \Vert ^{2}\bigr\} , $$

where ε is small enough. Then the sequence \(\{(x_{n},y _{n} )\}\) generated by the algorithm weakly converges to the solution of (3.1).

Proof

Choose \(p\in \operatorname{Fix}(S)\), \(q\in \operatorname{Fix}(T)\) and \(Ap=Bq \). By the algorithm of Theorem 3.1, we have

$$\begin{aligned}& \Vert u_{n}-p \Vert ^{2} \\& \quad = \bigl\Vert x_{n}-\gamma _{n}\bigl[(x_{n}-Kx_{n})+A^{*}(Ax_{n}-By_{n}) \bigr]-p \bigr\Vert ^{2} \\& \quad = \Vert x_{n}-p \Vert ^{2}+\gamma _{n}^{2} \bigl\Vert (x_{n}-Kx_{n})+A^{*}(Ax_{n}-By_{n}) \bigr\Vert ^{2} \\& \qquad {} -2\gamma _{n}\bigl\langle x_{n}-p,(x_{n}-Kx_{n})+A^{*}(Ax_{n}-By_{n}) \bigr\rangle \\& \quad \leq \Vert x_{n}-p \Vert ^{2}+\gamma _{n}^{2}\bigl(1+ \Vert A \Vert ^{2}\bigr) \Vert x_{n}-Kx_{n} \Vert ^{2}+ \gamma _{n}^{2}\biggl(1+\frac{1}{ \Vert A \Vert ^{2}}\biggr) \bigl\Vert A^{*}(Ax_{n}-By_{n}) \bigr\Vert ^{2} \\& \qquad {} -2\gamma _{n}\langle x_{n}-p,x_{n}-Kx_{n} \rangle -2\gamma _{n}\bigl\langle x_{n}-p,A^{*}(Ax_{n}-By_{n}) \bigr\rangle . \end{aligned}$$
(3.3)

We have

$$\begin{aligned}& -2\langle x_{n}-p,x_{n}-Kx_{n} \rangle \\& \quad = -2 \Vert x_{n}-p \Vert ^{2}-2\langle x_{n}-p,p-Kx_{n}\rangle \\& \quad = -2 \Vert x_{n}-p \Vert ^{2}+ \Vert x_{n}-p \Vert ^{2}+ \Vert Kx_{n}-p \Vert ^{2}- \Vert Kx_{n}-x_{n} \Vert ^{2} \\& \quad \leq - \Vert Kx_{n}-x_{n} \Vert ^{2}, \end{aligned}$$
(3.4)
$$\begin{aligned}& -2\langle Ax_{n}-Ap,Ax_{n}-By_{n} \rangle = \Vert By_{n}-Ap \Vert ^{2}- \Vert Ax_{n}-Ap \Vert ^{2}- \Vert Ax_{n}-By_{n} \Vert ^{2}. \end{aligned}$$
(3.5)

Combining (3.4) and (3.5), then (3.3) can be written as

$$\begin{aligned}& \Vert u_{n}-p \Vert ^{2} \\& \quad \leq \Vert x_{n}-p \Vert ^{2}+\gamma _{n}^{2}\bigl(1+ \Vert A \Vert ^{2}\bigr) \Vert x_{n}-Kx_{n} \Vert ^{2}+ \gamma _{n}^{2}\bigl(1+ \Vert A \Vert ^{2}\bigr) \Vert Ax_{n}-By_{n} \Vert ^{2} \\& \qquad {} -\gamma _{n} \Vert Kx_{n}-x_{n} \Vert ^{2}+\gamma _{n} \Vert By_{n}-Ap \Vert ^{2}-\gamma _{n} \Vert Ax_{n}-Ap \Vert ^{2} \\& \qquad {} -\gamma _{n} \Vert Ax_{n}-By_{n} \Vert ^{2}. \end{aligned}$$
(3.6)

Similarly, we can obtain

$$\begin{aligned}& \Vert v_{n}-q \Vert ^{2} \\& \quad \leq \Vert y_{n}-q \Vert ^{2}+\gamma _{n}^{2}\bigl(1+ \Vert B \Vert ^{2}\bigr) \Vert y_{n}-Gy_{n} \Vert ^{2}+ \gamma _{n}^{2}\bigl(1+ \Vert B \Vert ^{2}\bigr) \Vert Ax_{n+1}-By_{n} \Vert ^{2} \\& \qquad {} -\gamma _{n} \Vert Gy_{n}-y_{n} \Vert ^{2}+\gamma _{n} \Vert Ax_{n+1}-Bq \Vert ^{2}-\gamma _{n} \Vert By_{n}-Bq \Vert ^{2} \\& \qquad {} -\gamma _{n} \Vert Ax_{n+1}-By_{n} \Vert ^{2}. \end{aligned}$$
(3.7)

Adding (3.6) and (3.7), by \(Ap=Bq\), we have

$$\begin{aligned}& \Vert u_{n}-p \Vert ^{2}+ \Vert v_{n}-q \Vert ^{2} \\& \quad \leq \Vert x_{n}-p \Vert ^{2}+ \Vert y_{n}-q \Vert ^{2}-\gamma _{n} \Vert Ax_{n}-Ap \Vert ^{2}+ \gamma _{n} \Vert Ax_{n+1}-Ap \Vert ^{2} \\& \qquad {} -\gamma _{n}\bigl(1-\gamma _{n}\bigl(1+ \Vert A \Vert ^{2}\bigr)\bigr) \Vert Kx_{n}-x_{n} \Vert ^{2} \\& \qquad {} -\gamma _{n}\bigl(1-\gamma _{n}\bigl(1+ \Vert A \Vert ^{2}\bigr)\bigr) \Vert Ax_{n}-By_{n} \Vert ^{2} \\& \qquad {} -\gamma _{n}\bigl(1-\gamma _{n}\bigl(1+ \Vert B \Vert ^{2}\bigr)\bigr) \Vert Gy_{n}-y_{n} \Vert ^{2} \\& \qquad {} -\gamma _{n}\bigl(1-\gamma _{n}\bigl(1+ \Vert B \Vert ^{2}\bigr)\bigr) \Vert Ax_{n+1}-By_{n} \Vert ^{2}. \end{aligned}$$
(3.8)

By K and G being quasi-nonexpansive and Eq. (2.5), we can write

$$\begin{aligned}& \Vert x_{n+1}-p \Vert ^{2} \\& \quad = \bigl\Vert \alpha _{n}x_{n}+(1-\alpha _{n})Ku_{n}-p \bigr\Vert ^{2} \\& \quad = \bigl\Vert \alpha _{n}(x_{n}-p)+(1-\alpha _{n}) (Ku_{n}-p) \bigr\Vert ^{2} \\& \quad = \alpha _{n} \Vert x_{n}-p \Vert ^{2}+(1- \alpha _{n}) \Vert Ku_{n}-p \Vert ^{2}-\alpha _{n}(1- \alpha _{n}) \Vert Ku_{n}-x_{n} \Vert ^{2} \\& \quad \leq \alpha _{n} \Vert x_{n}-p \Vert ^{2}+(1-\alpha _{n}) \Vert u_{n}-p \Vert ^{2}-\alpha _{n}(1-\alpha _{n}) \Vert Ku_{n}-x_{n} \Vert ^{2}. \end{aligned}$$
(3.9)

Similarly, we can obtain

$$\begin{aligned}& \Vert y_{n+1}-q \Vert ^{2} \\& \quad = \bigl\Vert \alpha _{n}y_{n}+(1-\alpha _{n})Gv_{n}-q \bigr\Vert ^{2} \\& \quad \leq \alpha _{n} \Vert y_{n}-q \Vert ^{2}+(1-\alpha _{n}) \Vert v_{n}-q \Vert ^{2}-\alpha _{n}(1-\alpha _{n}) \Vert Gv_{n}-y_{n} \Vert ^{2}. \end{aligned}$$
(3.10)

Adding (3.9) and (3.10), combining (3.8), we have

$$\begin{aligned}& \Vert x_{n+1}-p \Vert ^{2}+ \Vert y_{n+1}-q \Vert ^{2} \\& \quad \leq \alpha _{n}\bigl[ \Vert x_{n}-p \Vert ^{2}+ \Vert y_{n}-q \Vert ^{2}\bigr]+(1-\alpha _{n})\bigl[ \Vert u _{n}-p \Vert ^{2}+ \Vert v_{n}-q \Vert ^{2}\bigr] \\& \qquad {} -\alpha _{n}(1-\alpha _{n})\bigl[ \Vert Ku_{n}-x_{n} \Vert ^{2}+ \Vert Gv_{n}-y_{n} \Vert ^{2}\bigr] \\& \quad \leq \Vert x_{n}-p \Vert ^{2}+ \Vert y_{n}-q \Vert ^{2}-(1-\alpha _{n})\gamma _{n} \Vert Ax _{n}-Ap \Vert ^{2} \\& \qquad {} +(1-\alpha _{n})\gamma _{n} \Vert Ax_{n+1}-Ap \Vert ^{2} \\& \qquad {} -(1-\alpha _{n})\gamma _{n}\bigl(1-\gamma _{n} \bigl(1+ \Vert A \Vert ^{2}\bigr)\bigr) \Vert Kx_{n}-x_{n} \Vert ^{2} \\& \qquad {} -(1-\alpha _{n})\gamma _{n}\bigl(1-\gamma _{n} \bigl(1+ \Vert A \Vert ^{2}\bigr)\bigr) \Vert Ax_{n}-By_{n} \Vert ^{2} \\& \qquad {} -(1-\alpha _{n})\gamma _{n}\bigl(1-\gamma _{n} \bigl(1+ \Vert B \Vert ^{2}\bigr)\bigr) \Vert Gy_{n}-y_{n} \Vert ^{2} \\& \qquad {} -(1-\alpha _{n})\gamma _{n}\bigl(1-\gamma _{n} \bigl(1+ \Vert B \Vert ^{2}\bigr)\bigr) \Vert Ax_{n+1}-By _{n} \Vert ^{2} \\& \qquad {} -\alpha _{n}(1-\alpha _{n})\bigl[ \Vert Ku_{n}-x_{n} \Vert ^{2}+ \Vert Gv_{n}-y_{n} \Vert ^{2}\bigr]. \end{aligned}$$
(3.11)

Letting

$$ \varGamma _{n}(p,q)= \Vert x_{n}-p \Vert ^{2}+ \Vert y_{n}-q \Vert ^{2}-(1-\alpha _{n})\gamma _{n} \Vert Ax_{n}-Ap \Vert ^{2}. $$

From (3.11), \(\{\alpha _{n}\}\) and \(\{\gamma _{n}\}\) being non-increasing, we can get the following inequality:

$$\begin{aligned} \varGamma _{n+1}(p,q) \leq &\varGamma _{n}(p,q)-\alpha _{n}(1-\alpha _{n})\bigl[ \Vert Ku _{n}-x_{n} \Vert ^{2}+ \Vert Gv_{n}-y_{n} \Vert ^{2}\bigr] \\ &{}-(1-\alpha _{n})\gamma _{n}\bigl(1-\gamma _{n} \bigl(1+ \Vert A \Vert ^{2}\bigr)\bigr) \Vert Kx_{n}-x_{n} \Vert ^{2} \\ &{}-(1-\alpha _{n})\gamma _{n}\bigl(1-\gamma _{n} \bigl(1+ \Vert A \Vert ^{2}\bigr)\bigr) \Vert Ax_{n}-By_{n} \Vert ^{2} \\ &{}-(1-\alpha _{n})\gamma _{n}\bigl(1-\gamma _{n} \bigl(1+ \Vert B \Vert ^{2}\bigr)\bigr) \Vert Gy_{n}-y_{n} \Vert ^{2} \\ &{}-(1-\alpha _{n})\gamma _{n}\bigl(1-\gamma _{n} \bigl(1+ \Vert B \Vert ^{2}\bigr)\bigr) \Vert Ax_{n+1}-By _{n} \Vert ^{2}. \end{aligned}$$
(3.12)

From (3.12) and \(\gamma _{n} \in (\varepsilon ,\frac{1}{1+c}- \varepsilon )\), \(c=\max \{\|A\|^{2},\|B\|^{2}\}\), we have

$$ \varGamma _{n+1}(p,q)\leq \varGamma _{n}(p,q) $$

and

$$ \varGamma _{n}(p,q)\geq \bigl[1-(1-\alpha _{n})\gamma _{n} \Vert A \Vert ^{2}\bigr] \Vert x_{n}-p \Vert ^{2}+ \Vert y_{n}-q \Vert ^{2}\geq 0. $$

Therefore, the sequence \(\{\varGamma _{n}(p,q)\}\) is a non-increasing sequence and lower bounded by 0. As a result, \(\{\varGamma _{n}(p,q)\}\) converges to some finite limit. Suppose that is \(\varGamma (x^{*},y^{*})\). Hence, we know that the sequences \(\{x_{n}\}\) and \(\{y_{n}\}\) are bounded. Letting \(n\rightarrow \infty \) and taking the limit in the two sides of (3.12), we obtain

$$ \begin{aligned} & \Vert Ku_{n}-x_{n} \Vert \rightarrow 0;\qquad \Vert Kx_{n}-x_{n} \Vert \rightarrow 0;\qquad \Vert Ax_{n}-By_{n} \Vert \rightarrow 0; \\ & \Vert Gv_{n}-y_{n} \Vert \rightarrow 0;\qquad \Vert Gy_{n}-y_{n} \Vert \rightarrow 0;\qquad \Vert Ax_{n+1}-By_{n} \Vert \rightarrow 0. \end{aligned} $$
(3.13)

Now, let us prove that \(\{x_{n}\}\) and \(\{y_{n}\}\) are asymptotically regular, from (3.13), we can obtain

$$\begin{aligned} \lim _{n\rightarrow \infty } \Vert x_{n+1}-x_{n} \Vert = &\lim _{n\rightarrow \infty } \bigl\Vert \alpha _{n}x_{n}+(1- \alpha _{n})Ku_{n}-x _{n} \bigr\Vert \\ = &\lim _{n\rightarrow \infty } \bigl\Vert -(1-\alpha _{n})x_{n}+(1- \alpha _{n})Ku_{n} \bigr\Vert \\ = &\lim _{n\rightarrow \infty }(1-\alpha _{n}) \Vert Ku_{n}-x_{n} \Vert =0. \end{aligned}$$

Similarly, we have

$$ \lim _{n\rightarrow \infty } \Vert y_{n+1}-y_{n} \Vert =0. $$

From (3.13), we have

$$ \begin{aligned}[b] \lim _{n\rightarrow \infty } \Vert u_{n}-x_{n} \Vert &=\lim _{n\rightarrow \infty }\gamma _{n} \bigl\Vert (x_{n}-Kx_{n})+A^{*}(Ax_{n}-By _{n}) \bigr\Vert \\ &\leq \lim _{n\rightarrow \infty }\bigl[\gamma _{n} \Vert x_{n}-Kx_{n} \Vert + \gamma _{n} \bigl\Vert A^{*}(Ax_{n}-By_{n}) \bigr\Vert \bigr] \\ &\leq \lim _{n\rightarrow \infty }\bigl[ \Vert x_{n}-Kx_{n} \Vert +\gamma _{n} \Vert A \Vert \Vert Ax_{n}-By_{n} \Vert \bigr]=0. \end{aligned} $$
(3.14)

Similarly, we can obtain

$$ \lim _{n\rightarrow \infty } \Vert v_{n}-y_{n} \Vert =0. $$
(3.15)

Combining (3.13), (3.14) and (3.15), we can get

$$ \begin{aligned} &\lim _{n\rightarrow \infty } \Vert Ku_{n}-u_{n} \Vert =\lim _{n\rightarrow \infty }\bigl[ \Vert Ku_{n}-x_{n} \Vert + \Vert x_{n}-u_{n} \Vert \bigr]=0, \\ &\lim _{n\rightarrow \infty } \Vert Gv_{n}-v_{n} \Vert =\lim _{n\rightarrow \infty } \bigl[ \Vert Gv_{n}-y_{n} \Vert + \Vert y_{n}-v_{n} \Vert \bigr]=0. \end{aligned} $$
(3.16)

Since \(\{x_{n}\}\) and \(\{y_{n}\}\) are bounded sequences, there exist weakly convergent subsequences, say \(\{x_{n_{j}}\}\subset \{x_{n}\}\) and \(\{y_{n_{j}}\}\subset \{y_{n}\}\) such that \(x_{n_{j}} \rightharpoonup x^{\ast }\) and \(y_{n_{j}} \rightharpoonup y^{\ast }\). The Opial property guarantees that the weakly subsequential limit of \(\{(x_{n},y_{n})\}\) is unique. So we have \(x_{n} \rightharpoonup x^{\ast }\) and \(y_{n} \rightharpoonup y^{\ast }\).

On the other hand, from (3.14) and (3.15), we can obtain \(u_{n} \rightharpoonup x^{\ast }\) and \(v_{n} \rightharpoonup y^{ \ast }\). Since K and G are demiclosed at 0 and by (3.16), we have \(Kx^{\ast }= x^{\ast }\) and \(Gy^{\ast }= y^{\ast }\), which imply that \(x^{\ast } \in \operatorname{Fix}(K)\) and \(y^{\ast } \in \operatorname{Fix}(G)\), that is, \(x^{\ast } \in \operatorname{Fix}(S)\) and \(y^{\ast } \in \operatorname{Fix}(T)\) from Lemma 2.2(i).

Furthermore, since \(Ax_{n} - By_{n} \rightharpoonup Ax^{\ast } - By ^{\ast }\), by using the weakly lower-continuity of the squared norm, we have

$$ \bigl\Vert Ax^{\ast } - By^{\ast } \bigr\Vert ^{2}= \liminf _{n\rightarrow \infty } \Vert Ax_{n} - By_{n} \Vert ^{2}\leq \lim _{n\rightarrow \infty } \Vert Ax _{n} - By_{n} \Vert ^{2}= 0. $$
(3.17)

consequently, \(Ax^{\ast }= By^{\ast }\). The proof is completed. □

4 Numerical examples

In this section, we give an example to show some insight into the behavior of the algorithm presented in this paper. The whole codes are written in Matlab 7.0. All the numerical results are carried out on a personal Lenovo Thinkpad computer with Intel(R) Core(TM) i7-6500U CPU 2.50 GHz and RAM 8.00 GB.

Example 4.1

Let \(H_{1}=H_{2}=H_{3}=R^{5}\). \(S(x)=\frac{1}{5}\sin x\), \(T(x)=\frac{1}{10}\sin x\). \(A\in R^{5\times 5}\), \(B\in R^{5 \times 5}\) are as follows:

$$\begin{aligned}& A= \begin{pmatrix} 0.6674& 0.4429& 0.1642& 0.0410& 0.1124 \\ 0.9138& 0.8919& 0.1286& 0.1953& 0.9165 \\ 0.5186& 0.0535& 0.4354& 0.6849& 0.2078 \\ 0.6941& 0.7589& 0.9198& 0.0316& 0.0625 \\ 0.3730& 0.9534& 0.1759& 0.3807& 0.2593 \end{pmatrix}, \\& B= \begin{pmatrix} 0.4654& 0.2709& 0.1099& 0.3647& 0.0556 \\ 0.8159& 0.4763& 0.0070& 0.4048& 0.3070 \\ 0.3713& 0.6759& 0.6937& 0.9897& 0.7612 \\ 0.1701& 0.5584& 0.5488& 0.5779& 0.1563 \\ 0.2222& 0.1778& 0.9335& 0.6102& 0.8083 \end{pmatrix}. \end{aligned}$$

The problem is to find \(x^{\ast } \in \operatorname{Fix}(S)\), \(y^{\ast } \in \operatorname{Fix}(T)\) such that \(Ax^{\ast }=By^{\ast }\).

In the experiments, we take \(\alpha _{n}=\frac{1}{3}+\frac{1}{2^{n}}\), \(\xi _{n}=(1-(\frac{1}{2})^{n})\ast \frac{1}{1+\sqrt{1+L^{2}}}\), \(\eta _{n}=(1-(\frac{2}{3})^{n})\ast \frac{1}{1+\sqrt{1+L^{2}}}\), where L is not higher than the minimum value of the Lipschitzian constants of S and T. In this example, we set \(L=\sqrt{5}\). Set \(\gamma _{n}= \min \{\frac{1}{1+\lambda _{A}},\frac{1}{1+\lambda _{B}}\}/1.01\). The stopping criterion is \(\|Ax_{n}-By_{n}\| \leq 10^{-6}\).

In the following tables and figures, we denote the non-alternating iteration algorithm in [13] and the alternating iteration algorithm in this paper for solving split equality common fixed point problem by “NAIA” and “AIA”, respectively. And we set “k”, “s”, “\(x ^{*}\)” and “\(y^{*}\)” to express the number of iteration, CPU time in seconds and the final solution, respectively. Init. denotes the initial points. The numerical results can be seen from Tables 1 and 2.

Table 1 The numerical results of Example 4.1
Full size table
Table 2 The numerical results of Example 4.1
Full size table

Furthermore, for testing the stationary property of iterative number, we carry out 500 experiments for different initial points which are presented randomly, such as

  1. Case 1.

    \(x^{0}=\operatorname{rand}(5,1)\), \(y^{0}=\operatorname{rand}(5,1)\);

  2. Case 2.

    \(x^{0}=\operatorname{rand}(5,1)*10\), \(y^{0}=\operatorname{rand}(5,1)*10\);

  3. Case 3.

    \(x^{0}=\operatorname{rand}(5,1)*100\), \(y^{0}=\operatorname{rand}(5,1)*100\);

  4. Case 4.

    \(x^{0}=\operatorname{rand}(5,1)*1000\), \(y^{0}=\operatorname{rand}(5,1)*1000\),

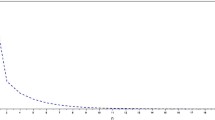
separately in Example 4.1, the results can be found in Figs. 1–4.

Figure 1
figure 1

The iterative number of NAIA and AIA for the initial point of Case 1

Full size image
Figure 2
figure 2

The iterative number of NAIA and AIA for the initial point of Case 2

Full size image
Figure 3
figure 3

The iterative number of NAIA and AIA for the initial point of Case 3

Full size image
Figure 4
figure 4

The iterative number of NAIA and AIA for the initial point of Case 4

Full size image

From Tables 1 and 2 and Figs. 1–4, we can see that the iterative number and CPU time of the alternating iteration algorithm in this paper are smaller than that of the non-alternating iteration algorithm in [13].

5 Conclusions

In this paper, we study the split equality common fixed point problem and propose an alternating iteration algorithm for solving this problem. We prove the weak convergence of the iteration sequence generated by the alternating iteration algorithm. At the same time, we solve a numerical example using the non-alternating iteration algorithm presented in [13] and the alternating iteration algorithm proposed in this paper. From the numerical results, we can see that the alternating iteration algorithm is superior to the non-alternating iteration algorithm with respect to the iterative number and CPU time for the example. Certainly, more examples are needed for validation.