Abstract
In this paper, we propose a new algorithm for solving the split common fixed point problem for infinite families of demicontractive mappings. Strong convergence of the proposed method is established under suitable control conditions. We apply our main results to study the split common null point problem, the split variational inequality problem, and the split equilibrium problem in the framework of a real Hilbert space. A numerical example supporting our main result is also given.
Similar content being viewed by others
1 Introduction
Let H be a real Hilbert space with inner product \(\langle\cdot ,\cdot\rangle\) and norm \(\|\cdot\|\). Let I denote the identity mapping. Let C and Q be nonempty closed convex subsets of real Hilbert spaces \(H_{1} \) and \(H_{2}\), respectively. Let \(A:H_{1}\to H_{2} \) be a bounded linear operator with adjoint operator \(A^{*}\).
The split feasibility problem (SFP), which was first introduced by Censor and Elfving [1], is to find
Let \(P_{C} \) and \(P_{Q} \) be the orthogonal projections onto the sets C and Q, respectively. Assume that (1) has a solution. It known that \(v^{*}\in H_{1} \) solves (1) if and only if it solves the fixed point equation
where \(\gamma>0 \) is any positive constant.
SFP has been used to model significant real-world inverse problems in sensor networks, radiation therapy treatment planning, antenna design, immaterial science, computerized tomography, etc. (see [2–4]).
The split common fixed point problem (SCFP) for mappings T and S, which was first introduced by Censor and Segal [5], is to find
where \(T:H_{1}\to H_{1} \) and \(S:H_{2}\to H_{2} \) are two mappings satisfying \(F(T)=\{x\in H_{1} : Tx=x\}\neq\emptyset\) and \(F(S)=\{ x\in H_{2} : Sx=x\}\neq\emptyset\), respectively. Since each closed and convex subset may be considered as a fixed point set of a projection onto the subset, the SCFP is a generalization of the SFP. Recently, the SFP and SCFP have been studied by many authors; see, for example, [6–11].
In 2010, Moudafi [11] introduced the following algorithm for solving (2) for two demicontractive mappings:
He proved that \(\{x_{n}\} \) converges weakly to some solution of SCFP.
The multiple set split feasibility problem (MSSFP), which was first introduced by Censor et al. [4], is to find
where \(\{C_{i}\}_{i=1}^{m} \) and \(\{Q_{i}\}_{i=1}^{r} \) are families of nonempty closed convex subsets of real Hilbert spaces \(H_{1} \) and \(H_{2}\), respectively. We see that if \(m=r=1\), then problem (4) reduces to problem (1).
Recently, Eslamian [12] considered the problem of finding a point
where \(A_{1}, A_{2}:H_{1}\to H_{2} \) are bounded linear operators, and \(U_{i}:H_{1}\to H_{1}\), \(T_{i}:H_{2}\to H_{2} \) and \(S_{i}:H_{2}\to H_{2}\), \(i=1,2,\ldots,m\). He also presented a new algorithm to solve (5) for finite families of quasi-nonexpansive mappings:
He proved that \(\{x_{n}\} \) converges strongly to some solution of (5) under some control conditions.
Question. Can we modify algorithm (6) to a simple one for solving the problem of finding
where \(A_{1}, A_{2}:H_{1}\to H_{2} \) are bounded linear operators, and \(\{U_{i}:H_{1}\to H_{1}: i\in\mathbb{N}\}\), \(\{T_{i}:H_{2}\to H_{2}: i\in\mathbb{N}\} \) and \(\{S_{i}:H_{2}\to H_{2}: i\in\mathbb {N}\} \) are infinite families of \(k_{3}\)-, \(k_{2}\)-, and \(k_{1}\)-demicontractive mappings, respectively.
In this work, we introduce a new algorithm for solving problem (7) for infinite families of demicontractive mappings and prove its strong convergence to a solution of problem (7).
2 Preliminaries
Throughout this paper, we adopt the following notations.
-
(i)
“→” and “⇀” denote the strong and weak convergence, respectively.
-
(ii)
\(\omega_{\omega}(x_{n}) \) denotes the set of the cluster points of \(\{x_{n}\} \) in the weak topology, that is, \(\exists\{x_{n_{i}}\} \) of \(\{x_{n}\} \) such that \(x_{n_{i}}\rightharpoonup x\).
-
(iii)
Γ is the solution set of problem (7), that is,
$$\Gamma= \Biggl\{ v^{*}\in\bigcap_{i=1}^{\infty} F(U_{i}) : A_{1}v^{*}\in \bigcap _{i=1}^{\infty}F(S_{i}) \text{ and } A_{2}v^{*}\in\bigcap_{i=1}^{\infty}F(T_{i}) \Biggr\} . $$
A mapping \(P_{C} \) is said to be a metric projection of H onto C if for every \(x\in H\), there exists a unique nearest point in C, denoted by \(P_{C}x \), such that
It is known that \(P_{C} \) is a firmly nonexpansive mapping. Moreover, \(P_{C} \) is characterized by the following property: \(\langle x-P_{C}x,y-P_{C}x\rangle\leq0\) for all \(x\in H\), \(y\in C\). A bounded linear operator \(B:H\to H \) is said to be strongly positive if there is a constant \(\xi>0\) such that
Definition 2.1
The mapping \(T:H\to H \) is said to be
-
(i)
L-Lipschitzian if there exists \(L>0 \) such that
$$\Vert Tu-Tv \Vert \leq L \Vert u-v \Vert \quad \text{for all } u,v\in H; $$ -
(ii)
α-contraction if T is α-Lipschitzian with \(\alpha\in[0,1)\), that is,
$$\Vert Tu-Tv \Vert \leq\alpha \Vert u-v \Vert \quad \text{for all } u,v \in H; $$ -
(iii)
nonexpansive if T is 1-Lipschitzian;
-
(iv)
quasi-nonexpansive if \(F(T)\neq\emptyset\) and
$$\Vert Tu-v \Vert \leq \Vert u-v \Vert \quad \text{for all } u\in H, v\in F(T); $$ -
(v)
firmly nonexpansive if
$$\Vert Tu-Tv \Vert ^{2}\leq \Vert u-v \Vert ^{2} - \bigl\Vert (u-v)-(Tu-Tv) \bigr\Vert ^{2}\quad \text{for all } u,v\in H; $$or equivalently, for all \(u,v\in H\),
$$\Vert Tu-Tv \Vert ^{2}\leq\langle Tu-Tv,u-v\rangle; $$ -
(vi)
λ-inverse strongly monotone if there exists \(\lambda>0 \) such that
$$\langle u-v,Tu-Tv\rangle\geq\lambda \Vert Tu-Tv \Vert ^{2} \quad \text{for all } u,v\in H; $$ -
(vii)
k-demicontractive if \(F(T)\neq\emptyset\) and there exists \(k\in[0,1) \) such that
$$\Vert Tu-v \Vert ^{2}\leq \Vert u-v \Vert ^{2} +k \Vert u-Tu \Vert ^{2}\quad \text{for all } u\in H, v\in F(T). $$
The following example is an infinite family of k-demicontractive mappings in \(\mathbb{R}^{2} \).
Example 2.2
For \(i\in\mathbb{N}\), let \(U_{i}:\mathbb{R}^{2}\to\mathbb{R}^{2} \) be defined for all \(x_{1},x_{2}\in\mathbb{R} \) by
and \(\|\cdot\| \) is the Euclidean norm on \(\mathbb{R}^{2}\). Observe that \(F(U_{i})=0\times\mathbb{R} \) for all \(i\in\mathbb{N} \), that is, if \(x=(x_{1},x_{2})\in\mathbb{R}\times\mathbb{R} \) and \(p=(0,p_{2}) \in F(U_{i})\), then
So, \(U_{i} \) are \(\frac{3}{4} \)-demicontractive mappings for all \(i\in\mathbb{N}\).
Definition 2.3
The mapping \(T:H\to H \) is said to be demiclosed at zero if for any sequence \(\{u_{n}\}\subset H \) with \(u_{n}\rightharpoonup u \) and \(Tu_{n}\to0\), we have \(Tu=0\).
Lemma 2.4
([13])
Assume that B is a self-adjoint strongly positive bounded linear operator on a Hilbert space H with coefficient \(\xi>0 \) and \(0<\mu \leq\|B\|^{-1}\). Then \(\|I-\mu B\|\leq1-\xi\mu\).
Lemma 2.5
([14])
Let H be a real Hilbert space. Then the following results hold:
-
(i)
\(\|u+v\|^{2}=\|u\|^{2}+2\langle u,v\rangle+\|v\|^{2} \) \(\forall u,v\in H\);
-
(ii)
\(\|u+v\|^{2}\leq\|u\|^{2}+2\langle v,u+v\rangle\) \(\forall u,v\in H\).
Lemma 2.6
([15])
Let \(\{a_{n}\} \) be a sequence of nonnegative real numbers satisfying the following relation:
where
-
(i)
\(\{\gamma_{n}\}\subset(0,1)\), \(\sum_{n=1}^{\infty}\gamma_{n} =\infty\);
-
(ii)
\(\limsup_{n\to\infty}\frac{\delta_{n}}{\gamma_{n}} \leq0\) or \(\sum_{n=1}^{\infty}|\delta_{n}|< \infty\).
Then \(\lim_{n\to\infty}a_{n}=0\).
Lemma 2.7
([16])
Let \(\{\kappa_{n}\} \) be a sequence of real numbers that does not decrease at infinity, that is, there exists at a subsequence \(\{\kappa _{n_{i}}\} \) of \(\{\kappa_{n}\} \) that satisfies \(\kappa _{n_{i}}<\kappa_{n_{i}+1} \) for all \(i\in\mathbb{N}\). For every \(n\geq n_{o}\), define the integer sequence \(\{\tau(n)\} \) as follows:
where \(n_{o}\in\mathbb{N} \) is such that \(\{l\leq n_{o} : \kappa_{l}< \kappa_{l+1}\}\neq\emptyset\). Then:
-
(i)
\(\tau(n_{o})\leq \tau(n_{o}+1)\leq\cdots\), and \(\tau(n)\to \infty\);
-
(ii)
for all \(n\geq n_{o}\), \(\max\{\kappa_{n},\kappa_{\tau(n)}\} \leq\kappa_{\tau(n)+1}\).
3 Results and discussion
In this section, we propose a new algorithm, which is a modification of (6) and prove its strong convergence under some suitable conditions. We start with the following important lemma.
Lemma 3.1
For two real Hilbert spaces \(H_{1} \) and \(H_{2}\), let \(A:H_{1}\to H_{2} \) be a bounded linear operator with adjoint operator \(A^{*}\). If \(T:H_{2}\to H_{2} \) is a k-demicontractive mapping, then
for all \(x^{*}\in H_{1} \) such that \(Ax^{*}\in F(T)\).
Proof
Suppose that \(T:H_{2}\to H_{2} \) is a k-demicontractive mapping and let \(x^{*}\in H_{1} \) be such that \(Ax^{*}\in F(T)\). Then we have
Since A is a bounded linear operator with adjoint operator \(A^{*}\) and T is a k-demicontractive mapping, by Lemma 2.5(ii) we deduce that
This completes the proof. □
Lemma 3.2
For two real Hilbert spaces \(H_{1} \) and \(H_{2}\), let \(A:H_{1}\to H_{2} \) be a bounded linear operator with adjoint operator \(A^{*}\), and let \(\{T_{i}:H_{2}\to H_{2}:i\in\mathbb{N}\} \) be an infinite family of k-demicontractive mappings. Let \(\{x_{n}\} \) be sequence in \(H_{1} \), and let
where \(\{\alpha_{n,i}\} \) is a real sequence in \([0,1] \) satisfying \(\sum_{i=1}^{n}\alpha_{n,i}=1\). Then we have
for all \(x^{*}\in H_{1} \) such that \(Ax^{*}\in\bigcap_{i=1}^{\infty }F(T_{i})\).
Proof
Let \(x^{*}\in H_{1} \) be such that \(Ax^{*}\in\bigcap_{i=1}^{\infty }F(T_{i})\). From (10) and Lemma 3.1 we obtain
This completes the proof. □
Lemma 3.3
Let \(\{T_{i}:H_{1}\to H_{1}:i\in\mathbb{N}\} \) be an infinite family of k-demicontractive mappings from a Hilbert space \(H_{1} \) to itself. Let \(\{x_{n}\} \) be sequence in \(H_{1} \), and let
where \(\{\alpha_{n,i}\} \) is a real sequence in \([0,1] \) satisfying \(\sum_{i=1}^{n}\alpha_{n,i}=1\). Then we have
for all \(x^{*}\in\bigcap_{i=1}^{\infty}F(T_{i})\).
Proof
The statement directly follows from Lemma 3.2 by putting \(H_{1}=H_{2} \) and \(A=I \). □
Now, we introduce a new algorithm for solving problem (7) for an infinite family of demicontractive mappings and then prove its strong convergence.
Theorem 3.4
Let \(H_{1}\) and \(H_{2}\) be two real Hilbert spaces, and let \(A_{1}, A_{2}: H_{1}\to H_{2} \) be two bounded linear operators with adjoint operators \(A_{1}^{*} \) and \(A_{2}^{*}\), respectively. Let \(f : H_{1} \to H_{1} \) be a ρ-contraction mapping, and let B be a self-adjoint strongly positive bounded linear operator on \(H_{1} \) with coefficient \(\xi>2\rho\) and \(\|B\|=1\). Let \(\{ S_{i}:H_{2}\to H_{2}:i\in\mathbb{N}\}\), \(\{ T_{i}:H_{2}\to H_{2}:i\in\mathbb{N}\} \), and \(\{U_{i}:H_{1}\to H_{1}:i\in\mathbb{N}\} \) be infinite families of \(k_{1}\)-, \(k_{2}\)-, and \(k_{3} \)-demicontractive mappings such that \(S_{i}-I\), \(T_{i}-I \), and \(U_{i}-I\) are demiclosed at zero, respectively. Suppose that \(\Gamma = \{v^{*}\in\bigcap_{i=1}^{\infty} F(U_{i}) : A_{1}v^{*}\in\bigcap_{i=1}^{\infty}F(S_{i}) \textit{ and } A_{2}v^{*}\in\bigcap_{i=1}^{\infty }F(T_{i}) \}\neq\emptyset\). For arbitrary \(x_{1}\in H_{1} \), let \(\{u_{n}\}\), \(\{v_{n}\}\), \(\{y_{n}\} \), and \(\{x_{n}\} \) be generated by
where \(\{\delta_{n}\}\), \(\{\theta_{n}\}\), \(\{\tau_{n}\}\), \(\{\sigma_{n}\}\), \(\{ \alpha_{n,i}\}\), \(\{\beta_{n,i}\} \), and \(\{\gamma_{n,i}\} \) are sequences in \([0,1] \) satisfying the following conditions:
-
(C1)
\(\sum_{i=1}^{n}\alpha_{n,i}= \sum_{i=1}^{n}\beta _{n,i} = \sum_{i=1}^{n}\gamma_{n,i}= 1\) for all \(n\in\mathbb{N}\);
-
(C2)
\(\liminf_{n\to\infty}\alpha_{n,i}>0\), \(\liminf_{n\to \infty}\beta_{n,i}>0 \), and \(\liminf_{n\to\infty}\gamma_{n,i}>0 \) for all \(i\in\mathbb{N}\);
-
(C3)
\(\lim_{n\to\infty}\sigma_{n}=0 \) and \(\sum_{n=1}^{\infty} \sigma_{n} = \infty\);
-
(C4)
\(0< a_{1}\leq\delta_{n}\leq a_{2}<\frac{1-k_{1}}{\| A_{1}\|^{2}}\);
-
(C5)
\(0< b_{1}\leq\theta_{n}\leq b_{2}<\frac{1-k_{2}}{\| A_{2}\|^{2}}\);
-
(C6)
\(0< c_{1}\leq\tau_{n}\leq c_{2}<1-k_{3}\).
Then the sequence \(\{x_{n}\} \) converges strongly to \(x^{*}=P_{\Gamma }(f+I-B)x^{*}\).
Proof
For any \(u,v\in H_{1}\), by Lemma 2.4 we have
that is, the mapping \(P_{\Gamma}(f+I-B) \) is a contraction. So, by the Banach contraction principle there is a unique element \(x^{*}\in H_{1} \) such that \(x^{*}=P_{\Gamma}(f+I-B)x^{*}\).
Let \(x^{*}=P_{\Gamma}(f+I-B)x^{*}\), that is, \(x^{*}\in\bigcap_{i=1}^{\infty} F(U_{i})\) is such that \(A_{1}x^{*}\in\bigcap_{i=1}^{\infty}F(S_{i})\) and \(A_{2}x^{*}\in\bigcap_{i=1}^{\infty }F(T_{i})\). From Lemmas 3.2 and 3.3 and from (12) we obtain
and
Therefore
By conditions (C4), (C5), and (C6) we have
By condition (C3) we may assume that \(\sigma_{n}\in(0,\|B\| ^{-1}) \) for all \(n\in\mathbb{N}\). By Lemma 2.4 we get \(\| I-\sigma_{n}B\|\leq1- \sigma_{n}\xi\). From (12) and (17) we get
Therefore \(\{x_{n}\} \) is bounded, and we also have that \(\{y_{n}\} \) and \(\{f(y_{n})\} \) are bounded. To this end, we consider the following two cases.
Case 1. Suppose that \(\{\|x_{n}-x^{*}\|\} _{n=n_{o}}^{\infty} \) is nonincreasing for some \(n_{o}\in\mathbb{N}\). Then we get that \(\lim_{n\to\infty} \|x_{n}-x^{*}\|\) exists. By (16), (17), and Lemma 2.5(i) we get
where
This implies, for \(j=1,2,\ldots,n\),
and
From (19), (20), (21), and conditions (C2)–(C6) we obtain
and
Next, we show that
To see this, choose a subsequence \(\{x_{n_{p}}\} \) of \(\{x_{n}\} \) such that
Since the sequence \(\{x_{n_{p}}\} \) is bounded, there exists a subsequence \(\{x_{n_{p_{j}}}\} \) of \(\{x_{n_{p}}\} \) such that \(x_{n_{p_{j}}}\rightharpoonup z\in H_{1}\). Without loss of generality, we may assume that \(x_{n_{p}}\rightharpoonup z\in H_{1}\). Since \(A_{1} \) is a bounded linear operator, this yields that \(A_{1}x_{n_{p}}\rightharpoonup A_{1}z\). By the demiclosedness principle of \(S_{i}-I \) at zero and (22) we get \(A_{1}z\in\bigcap_{i=1}^{\infty} F(S_{i})\). By (12) and (22) we have
Similarly, we also have \(\|v_{n}-u_{n}\|\to0 \) as \(n\to\infty\). Using the fact that \(x_{n_{p}}\rightharpoonup z \) and \(\|u_{n}-x_{n}\| \to0\), we conclude that \(u_{n_{p}}\rightharpoonup z\). Since \(A_{2} \) is a bounded linear operator, we get that \(A_{2}u_{n_{p}}\rightharpoonup A_{2}z\). By the demiclosedness principle of \(T_{i}-I \) at zero and (23) we get \(A_{2}z\in\bigcap_{i=1}^{\infty} F(T_{i})\). Again, since \(u_{n_{p}}\rightharpoonup z \) and \(\|v_{n}-u_{n}\|\to0\), we conclude that \(v_{n_{p}}\rightharpoonup z\). By the demiclosedness principle of \(U_{i}-I \) at zero and (24) we also have \(z\in\bigcap_{i=1}^{\infty} F(U_{i})\). Therefore \(z\in\Gamma\).
Since \(x^{*}=P_{\Gamma}(f+I-B)x^{*} \) and \(z\in\Gamma\), we get
Using Lemma 2.5 and (17), we have
This implies that
By (25), (26), and Lemma 2.6 we conclude that \(x_{n}\to x^{*} \) as \(n\to\infty\).
Case 2. Suppose that there exists an integer \(m_{o} \) such that
Put \(\kappa_{n}= \|x_{n}-x^{*}\|\) for all \(n\geq m_{o}\). Then we have \(\kappa_{m_{o}}\leq\kappa_{m_{o}+1}\). Let \(\{\mu(n)\} \) be the sequence defined by
for all \(n\geq m_{o}\). By Lemma 2.7 we obtain that \(\{\mu (n)\} \) is a nondecreasing sequence such that
By the same argument as in case 1 we obtain
and
By the demiclosedness principle of \(S_{i}-I\), \(T_{i}-I \), and \(U_{i}-I \) at zero, we have \(\omega_{\omega}(x_{\mu(n)})\subset\Gamma\). This implies that
By a similar argument from (26) we also have
So, we get \(\lim_{n\to\infty}\kappa_{\mu(n)} =0 \) and also have \(\lim_{n\to\infty}\kappa_{\mu(n)+1} =0\). By Lemma 2.7 we have
Therefore \(x_{n}\to x^{*} \) as \(n\to\infty\). This completes the proof. □
By setting \(T_{i}=I \) for all \(i\in\mathbb{N} \) in Theorem 3.4 we obtain the following result.
Corollary 3.5
Let \(H_{1}\) and \(H_{2}\) be two real Hilbert spaces, let \(A_{1}: H_{1}\to H_{2} \) be a bounded linear operator with adjoint operator \(A_{1}^{*}\). Let \(f : H_{1} \to H_{1} \) be a ρ-contraction mapping, and let B be a self-adjoint strongly positive bounded linear operator on \(H_{1} \) with coefficient \(\xi>2\rho\) and \(\|B\|=1\). Let \(\{S_{i}:H_{2}\to H_{2}:i\in\mathbb{N}\}\) and \(\{ U_{i}:H_{1}\to H_{1}:i\in\mathbb{N} \}\) be infinite families of \(k_{1}\)- and \(k_{3} \)-demicontractive mappings such that \(S_{i}-I\) and \(U_{i}-I\) are demiclosed at zero, respectively. Suppose that \(\Omega = \{v^{*}\in\bigcap_{i=1}^{\infty} F(U_{i}) : A_{1}v^{*}\in\bigcap_{i=1}^{\infty}F(S_{i}) \}\neq\emptyset\). For arbitrary \(x_{1}\in H_{1} \), let \(\{u_{n}\}\), \(\{y_{n}\} \), and \(\{x_{n}\} \) be generated by
where \(\{\delta_{n}\}\), \(\{\tau_{n}\}\), \(\{\sigma_{n}\}\), \(\{\alpha_{n,i}\} \), and \(\{\gamma_{n,i}\} \) are sequences in \([0,1] \) satisfying the following conditions:
-
(C1)
\(\sum_{i=1}^{n}\alpha_{n,i}=\sum_{i=1}^{n}\gamma_{n,i}= 1\) for all \(n\in\mathbb{N}\);
-
(C2)
\(\liminf_{n\to\infty}\alpha_{n,i}>0 \) and \(\liminf_{n\to\infty }\gamma_{n,i}>0 \) for all \(i\in\mathbb{N}\);
-
(C3)
\(\lim_{n\to\infty}\sigma_{n}=0 \) and \(\sum_{n=1}^{\infty} \sigma _{n} = \infty\);
-
(C4)
\(0< a_{1}\leq\delta_{n}\leq a_{2}<\frac{1-k_{1}}{\|A_{1}\|^{2}}\);
-
(C5)
\(0< c_{1}\leq\tau_{n}\leq c_{2}<1-k_{3}\).
Then the sequence \(\{x_{n}\} \) converges strongly to \(x^{*}=P_{\Omega }(f+I-B)x^{*}\).
Remark 3.6
By the same setting as in Corollary 3.5, Eslamian [17] used another algorithm for solving the same problem as in Corollary 3.5; see [17], Theorem 3.3. Note that each step of our algorithm is much easier for computation than that of Eslamian [17] because our algorithm concerns only the finite sum.
By setting \(f(y)=v \) for all \(y\in H_{1}\) and \(B=I \) in Theorem 3.4 we obtain the following result.
Corollary 3.7
Let \(H_{1}\) and \(H_{2}\) be two real Hilbert spaces, and let \(A_{1}, A_{2}: H_{1}\to H_{2} \) be two bounded linear operators with adjoint operators \(A_{1}^{*} \) and \(A_{2}^{*}\), respectively. Let \(\{ S_{i}:H_{2}\to H_{2}:i\in\mathbb{N}\}\), \(\{ T_{i}:H_{2}\to H_{2}:i\in \mathbb{N}\} \), and \(\{U_{i}:H_{1}\to H_{1}:i\in\mathbb{N}\} \) be infinite families of \(k_{1}\)-, \(k_{2}\)-, and \(k_{3} \)-demicontractive mappings such that \(S_{i}-I\), \(T_{i}-I \), and \(U_{i}-I\) are demiclosed at zero, respectively. Suppose that \(\Gamma= \{v^{*}\in \bigcap_{i=1}^{\infty} F(U_{i}) : A_{1}v^{*}\in\bigcap_{i=1}^{\infty }F(S_{i}) \textit{ and } A_{2}v^{*}\in\bigcap_{i=1}^{\infty}F(T_{i}) \}\neq\emptyset\). For arbitrary \(x_{1}\in H_{1} \), let \(\{u_{n}\}\), \(\{ v_{n}\}\), \(\{y_{n}\} \), and \(\{x_{n}\} \) be generated by
where \(\{\delta_{n}\}\), \(\{\theta_{n}\}\), \(\{\tau_{n}\}\), \(\{\sigma_{n}\}\), \(\{ \alpha_{n,i}\}\), \(\{\beta_{n,i}\} \), and \(\{\gamma_{n,i}\} \) are sequences in \([0,1] \) satisfying the following conditions:
-
(C1)
\(\sum_{i=1}^{n}\alpha_{n,i}= \sum_{i=1}^{n}\beta_{n,i} = \sum_{i=1}^{n}\gamma_{n,i}= 1\) for all \(n\in\mathbb{N}\);
-
(C2)
\(\liminf_{n\to\infty}\alpha_{n,i}>0\), \(\liminf_{n\to\infty}\beta _{n,i}>0 \), and \(\liminf_{n\to\infty}\gamma_{n,i}>0 \) for all \(i\in \mathbb{N}\);
-
(C3)
\(\lim_{n\to\infty}\sigma_{n}=0 \) and \(\sum_{n=1}^{\infty} \sigma _{n} = \infty\);
-
(C4)
\(0< a_{1}\leq\delta_{n}\leq a_{2}<\frac{1-k_{1}}{\|A_{1}\|^{2}}\);
-
(C5)
\(0< b_{1}\leq\theta_{n}\leq b_{2}<\frac{1-k_{2}}{\|A_{2}\|^{2}}\);
-
(C6)
\(0< c_{1}\leq\tau_{n}\leq c_{2}<1-k_{3}\).
Then the sequence \(\{x_{n}\} \) converges strongly to \(x^{*}=P_{\Gamma }(v)\).
It is known that every quasi-nonexpansive mapping is 0-demicontractive mapping, so the following result is directly obtained by Theorem 3.2.
Corollary 3.8
Let \(H_{1}\) and \(H_{2}\) be two real Hilbert spaces, and let \(A_{1}, A_{2}: H_{1}\to H_{2} \) be two bounded linear operators with adjoint operators \(A_{1}^{*} \) and \(A_{2}^{*}\), respectively. Let \(\{ S_{i}:H_{2}\to H_{2}:i\in\mathbb{N}\}\), \(\{ T_{i}:H_{2}\to H_{2}:i\in \mathbb{N}\} \), and \(\{U_{i}:H_{1}\to H_{1}:i\in\mathbb{N}\} \) be infinite families of quasi-nonexpansive mappings such that \(S_{i}-I\), \(T_{i}-I \), and \(U_{i}-I\) are demiclosed at zero, respectively. Suppose that \(\Gamma= \{v^{*}\in\bigcap_{i=1}^{\infty} F(U_{i}) : A_{1}v^{*}\in\bigcap_{i=1}^{\infty}F(S_{i}) \textit{ and } A_{2}v^{*}\in \bigcap_{i=1}^{\infty}F(T_{i}) \}\neq\emptyset\). For arbitrary \(x_{1}\in H_{1} \), let \(\{u_{n}\}\), \(\{v_{n}\}\), \(\{y_{n}\} \), and \(\{ x_{n}\} \) be generated by
where \(\{\delta_{n}\}\), \(\{\theta_{n}\}\), \(\{\tau_{n}\}\), \(\{\sigma_{n}\}\), \(\{ \alpha_{n,i}\}\), \(\{\beta_{n,i}\} \), and \(\{\gamma_{n,i}\} \) are sequences in \([0,1] \) satisfying the following conditions:
-
(C1)
\(\sum_{i=1}^{n}\alpha_{n,i}= \sum_{i=1}^{n}\beta_{n,i} = \sum_{i=1}^{n}\gamma_{n,i}= 1\) for all \(n\in\mathbb{N}\);
-
(C2)
\(\liminf_{n\to\infty}\alpha_{n,i}>0\), \(\liminf_{n\to\infty}\beta _{n,i}>0 \), and \(\liminf_{n\to\infty}\gamma_{n,i}>0 \) for all \(i\in \mathbb{N}\);
-
(C3)
\(\lim_{n\to\infty}\sigma_{n}=0 \) and \(\sum_{n=1}^{\infty} \sigma _{n} = \infty\);
-
(C4)
\(0< a_{1}\leq\delta_{n}\leq a_{2}<\frac{1}{\|A_{1}\|^{2}}\);
-
(C5)
\(0< b_{1}\leq\theta_{n}\leq b_{2}<\frac{1}{\|A_{2}\|^{2}}\);
-
(C6)
\(0< c_{1}\leq\tau_{n}\leq c_{2}<1\).
Then the sequence \(\{x_{n}\} \) converges strongly to \(x^{*}=P_{\Gamma }(v)\).
4 Applications
4.1 The split common null point problem
Let M be the set-valued mapping of H into \(2^{H}\). The effective domain of M is denoted by \(D(M)\), that is, \(D(M)=\{x\in H : Mx\neq\emptyset\}\). The mapping M is said to be monotone if
A monotone mapping M is said to be maximal if the graph \(G(M) \) is not properly contained in the graph of any other monotone map, where \(G(M)=\{(x,y)\in H\times H : y\in Mx\}\). It is known that M is maximal if and only if for \((x,u)\in H\times H\), \(\langle x-y,u-v\rangle\geq0 \) for every \((y,v)\in G(M) \) implies \(u\in Mx\). For the maximal monotone operator M, we can associate its resolvent \(J_{\delta}^{M} \) defined by
It is known that if M is a maximal monotone operator, then the resolvent \(J_{\delta}^{M} \) is firmly nonexpansive, and \(F(J_{\delta }^{M})=M^{-1}0\equiv\{x\in H : 0\in Mx\} \) for every \(\delta>0\).
Let \(H_{1} \) and \(H_{2} \) be two real Hilbert spaces. Let \(M_{i}:H_{1}\to2^{H_{1}}\), \(O_{i}:H_{2}\to2^{H_{2}}\), and \(P_{i}:H_{2}\to2^{H_{2}} \) be multivalued mappings. The split common null point problem (SCNPP) [18] is to find a point \(u^{*}\in H_{1} \) such that
and the points \(v_{j}^{*}=A_{j}u^{*}\in H_{2} \) satisfy
where \(A_{j}:H_{1}\to H_{2} \) (\(1\leq j\leq q\)) are bounded linear operators.
Now, we apply Theorem 3.4 to solve the problem of finding a point \(u^{*}\in H_{1} \) such that
and the points \(v^{*}=A_{1}u^{*}\in H_{2}\) and \(s^{*}=A_{2}u^{*}\in H_{2} \) satisfy
where \(A_{1}, A_{2}:H_{1}\to H_{2} \) are bounded linear operators.
Since every firmly nonexpansive mapping is a 0-demicontractive mapping, we obtain the following theorem for problem (32)–(33).
Theorem 4.1
Let \(H_{1}\) and \(H_{2}\) be two real Hilbert spaces, and let \(A_{1}, A_{2}: H_{1}\to H_{2} \) be two bounded linear operators with adjoint operators \(A_{1}^{*} \) and \(A_{2}^{*}\), respectively. Let \(f : H_{1} \to H_{1} \) be a ρ-contraction mapping, and let B be a self-adjoint strongly positive bounded linear operator on \(H_{1} \) with coefficient \(\xi>2\rho\) and \(\|B\|=1\). Let \(\{M_{i}:H_{1}\to 2^{H_{1}}: i\in\mathbb{N}\}\), \(\{O_{i}: H_{2}\to2^{H_{2}}: i\in\mathbb {N} \}\), and \(\{P_{i}:H_{2}\to2^{H_{2}}: i\in\mathbb{N}\} \) be maximal monotone mappings. Suppose that \(\Omega= \{v^{*}\in\bigcap_{i=1}^{\infty} M_{i}^{-1}0 : A_{1}v^{*}\in\bigcap_{i=1}^{\infty }O_{i}^{-1}0 \textit{ and } A_{2}v^{*}\in\bigcap_{i=1}^{\infty }P_{i}^{-1}0 \}\neq\emptyset\). For arbitrary \(x_{1}\in H_{1} \), let \(\{u_{n}\}\), \(\{v_{n}\}\), \(\{y_{n}\} \), and \(\{x_{n}\} \) be generated by
where \(r_{1}, r_{2}, r_{3}>0 \) and \(\{\delta_{n}\}\), \(\{\theta_{n}\}\), \(\{\tau _{n}\}\), \(\{\sigma_{n}\}\), \(\{\alpha_{n,i}\}\), \(\{\beta_{n,i}\}\), \(\{\gamma _{n,i}\} \) are sequences in \([0,1] \) satisfying the following conditions:
-
(C1)
\(\sum_{i=1}^{n}\alpha_{n,i}= \sum_{i=1}^{n}\beta_{n,i} = \sum_{i=1}^{n}\gamma_{n,i}= 1\) for all \(n\in\mathbb{N}\);
-
(C2)
\(\liminf_{n\to\infty}\alpha_{n,i}>0\), \(\liminf_{n\to\infty}\beta _{n,i}>0 \), and \(\liminf_{n\to\infty}\gamma_{n,i}>0 \) for all \(i\in \mathbb{N}\);
-
(C3)
\(\lim_{n\to\infty}\sigma_{n}=0 \) and \(\sum_{n=1}^{\infty} \sigma _{n} = \infty\);
-
(C4)
\(0< a_{1}\leq\delta_{n}\leq a_{2}<\frac{1}{\|A_{1}\|^{2}}\);
-
(C5)
\(0< b_{1}\leq\theta_{n}\leq b_{2}<\frac{1}{\|A_{2}\|^{2}}\);
-
(C6)
\(0< c_{1}\leq\tau_{n}\leq c_{2}<1\).
Then the sequence \(\{x_{n}\} \) converges strongly to \(x^{*}=P_{\Omega }(f+I-B)x^{*}\).
4.2 The split variational inequality problem
Let C and Q be nonempty closed convex subsets of two real Hilbert spaces \(H_{1} \) and \(H_{2}\), respectively. Let \(A:H_{1}\to H_{2} \) be a bounded linear operator, \(g:H_{1}\to H_{1} \), and \(h:H_{2}\to H_{2}\). The split variational inequality problem (SVIP) is to find a point \(u^{*}\in C \) such that
and the point \(v^{*}=Au^{*}\in Q \) satisfy
We denote the solution set of the SVIP by \(\varOmega=\operatorname{SVIP}(C,Q,g,h,A)\). The set of all solutions of variational inequality problem (35) is denoted by \(\operatorname{VIP}(C,g) \), and it is known that \(\operatorname{VIP}(C,g)=F(P_{C}(I-\lambda g)) \) for all \(\lambda>0\).
Let \(A_{1}, A_{2}:H_{1}\to H_{2} \) be two bounded linear operators, \(g_{i}:H_{1}\to H_{1} \), and \(h_{i}, l_{i}:H_{2}\to H_{2}\). In this section, we apply Theorem 3.4 to solve the problem of finding a point \(u^{*}\in\bigcap_{i=1}^{\infty}C_{i} \) such that
and the point \(v^{*}=A_{1}u^{*}\in\bigcap_{i=1}^{\infty}Q_{i}\), \(s^{*}=A_{2}u^{*}\in\bigcap_{i=1}^{\infty}K_{i} \) satisfy
where \(\{C_{i}\}_{i\in\mathbb{N}} \) is a family of nonempty closed convex subsets of a real Hilbert space \(H_{1} \), and \(\{Q_{i}\}_{i\in \mathbb{N}}\) and \(\{K_{i}\}_{i\in\mathbb{N}} \) are two families of nonempty closed convex subsets of a real Hilbert space \(H_{2}\). We now prove a strong convergence theorem for problem (37)–(38).
Theorem 4.2
Let \(\{C_{i}\}_{i\in\mathbb{N}} \) be the family of nonempty closed convex subsets of a real Hilbert space \(H_{1} \), let \(\{Q_{i}\}_{i\in \mathbb{N}}\) and \(\{K_{i}\}_{i\in\mathbb{N}} \) be two families of nonempty closed convex subsets of a real Hilbert space \(H_{2}\), and let \(A_{1}, A_{2}: H_{1}\to H_{2} \) be two bounded linear operators with adjoint operators \(A_{1}^{*} \) and \(A_{2}^{*}\), respectively. Let \(f : H_{1} \to H_{1} \) be a ρ-contraction mapping, and let B be a self-adjoint strongly positive bounded linear operator on \(H_{1} \) with coefficient \(\xi>2\rho\) and \(\|B\|=1\). Let \(\{ g_{i}:H_{1}\to H_{1}:i\in\mathbb{N}\}\), \(\{h_{i}:H_{2}\to H_{2};i\in \mathbb{N}\} \), and \(\{ l_{i}:H_{2}\to H_{2};i\in\mathbb{N}\} \) be \(r_{1}\)-, \(r_{2}\)-, and \(r_{3} \)-inverse strongly monotone mappings, respectively. Let \(r = \min\{r_{1},r_{2}, r_{3}\}\) and \(\mu\in (0,2r)\). Suppose that \(\Omega= \{v^{*}\in\bigcap_{i=1}^{\infty} \operatorname{VIP}(C_{i},g_{i}) : A_{1}v^{*}\in\bigcap_{i=1}^{\infty}\operatorname{VIP}(Q_{i},h_{i}) \textit{ and } A_{2}v^{*}\in\bigcap_{i=1}^{\infty}\operatorname{VIP}(K_{i},l_{i}) \} \neq\emptyset\). For arbitrary \(x_{1}\in H_{1} \), let \(\{u_{n}\}\), \(\{ v_{n}\}\), \(\{y_{n}\} \), and \(\{x_{n}\} \) be generated by
where \(\{\delta_{n}\}\), \(\{\theta_{n}\}\), \(\{\tau_{n}\}\), \(\{\sigma_{n}\}\), \(\{ \alpha_{n,i}\}\), \(\{\beta_{n,i}\}\), \(\{\gamma_{n,i}\} \) are sequences in \([0,1] \) satisfying the following conditions:
-
(C1)
\(\sum_{i=1}^{n}\alpha_{n,i}= \sum_{i=1}^{n}\beta_{n,i} = \sum_{i=1}^{n}\gamma_{n,i}= 1\) for all \(n\in\mathbb{N}\);
-
(C2)
\(\liminf_{n\to\infty}\alpha_{n,i}>0\), \(\liminf_{n\to\infty}\beta _{n,i}>0 \), and \(\liminf_{n\to\infty}\gamma_{n,i}>0 \) for all \(i\in \mathbb{N}\);
-
(C3)
\(\lim_{n\to\infty}\sigma_{n}=0 \) and \(\sum_{n=1}^{\infty} \sigma _{n} = \infty\);
-
(C4)
\(0< a_{1}\leq\delta_{n}\leq a_{2}<\frac{1}{\|A_{1}\|^{2}}\);
-
(C5)
\(0< b_{1}\leq\theta_{n}\leq b_{2}<\frac{1}{\|A_{2}\|^{2}}\);
-
(C6)
\(0< c_{1}\leq\tau_{n}\leq c_{2}<1\).
Then the sequence \(\{x_{n}\} \) converges strongly to \(x^{*}=P_{\Omega }(f+I-B)x^{*}\).
Proof
It is known that \(S_{i}:=P_{Q_{i}}(I-\mu h_{i})\), \(T_{i}=: P_{K_{i}}(I-\mu l_{i}) \), and \(U_{i}:=P_{C_{i}}(I-\mu g_{i}) \) are nonexpensive mappings for all \(\mu\in(0,2r) \), and hence they are 0-demicontractive mappings. We obtain the desired result from Theorem 3.4. □
4.3 The split equilibrium problem
Let \(H_{1} \) and \(H_{2} \) be two real Hilbert spaces, and let C and Q be nonempty closed convex subsets of \(H_{1} \) and \(H_{2}\), respectively. Let \(A:H_{1}\to H_{2} \) be a bounded linear operator, and let \(g:C\times C\to\mathbb{R} \) and \(h:Q\times Q\to\mathbb{R} \) be two bifunctions. The split equilibrium problem (SEP) is to find a point \(u^{*}\in C \) such that
and \(Au^{*}\in Q \) satisfy
The set of all solutions of equilibrium problem (40) is denoted by \(\operatorname{EP}(g)\).
Lemma 4.3
([19])
Let C be a nonempty closed convex subset of H, and let g be a bifunction of \(C\times C \) into \(\mathbb{R} \) satisfying the following conditions:
-
(A1)
\(g(x,x)=0 \) for all \(x\in C\);
-
(A2)
g is monotone, that is, \(g(x,y)+g(y,x)\leq0 \) for all \(x,y \in C\);
-
(A3)
for all \(x,y,z\in C\),
$$\limsup_{t\downarrow0}g\bigl(tz+(1-t)x,y\bigr)\leq g(x,y); $$ -
(A4)
\(g(x,\cdot) \) is convex and lower semicontinuous for all \(x\in C\).
Let \(g:C\times C\to\mathbb{R} \) be a bifunction satisfying conditions (A1)–(A4), and let \(r>0 \) and \(x\in H\). Then there exists \(z\in C \) such that
Lemma 4.4
([20])
Let C be a nonempty closed convex subset of H, and let g be a bifunction of \(C\times C \) into \(\mathbb{R} \) satisfying conditions (A1)–(A4). For \(r>0 \) and \(x\in H\), define the mapping \(T_{r}^{g}:H\to C \) of g by
Then the following hold:
-
(i)
\(T_{r}^{g} \) is single-valued;
-
(ii)
\(T_{r}^{g} \) is firmly nonexpansive;
-
(iii)
\(F(T_{r}^{g})=\operatorname{EP}(g)\);
-
(iv)
\(\operatorname{EP}(g) \) is closed and convex.
Let \(A_{1}, A_{2}:H_{1}\to H_{2} \) be two bounded linear operators, and let \(g_{i}:C_{i}\times C_{i}\to\mathbb{R} \) and \(h_{i}, l_{i}:Q_{i}\times Q_{i}\to\mathbb{R} \) be bifunctions for all \(i\in \mathbb{N}\). In this section, we apply Theorem 3.4 to solve the problem of finding a point
By Lemma 4.4(iii) we have that \(T_{r_{1}}^{h_{i}}\), \(T_{r_{2}}^{l_{i}} \), and \(T_{r_{3}}^{g_{i}} \) are firmly nonexpansive mappings, and hence they are 0-demicontractive mappings. We obtain the following result from Theorem 3.4.
Theorem 4.5
Let \(\{C_{i}\}_{i\in\mathbb{N}} \) be a family of nonempty closed convex subsets of a real Hilbert space \(H_{1} \), let \(\{Q_{i}\}_{i\in \mathbb{N}} \) and \(\{K_{i}\}_{i\in\mathbb{N}} \) be two families of nonempty closed convex subsets of a real Hilbert space \(H_{2}\), and let \(A_{1}, A_{2}: H_{1}\to H_{2} \) be two bounded linear operators with adjoint operators \(A_{1}^{*} \) and \(A_{2}^{*}\), respectively. Let \(f : H_{1} \to H_{1} \) be a ρ-contraction mapping, and let B be a self-adjoint strongly positive bounded linear operator on \(H_{1} \) with coefficient \(\xi>2\rho\) and \(\|B\|=1\). Let \(g_{i}:C_{i}\times C_{i}\to\mathbb{R} \) and \(h_{i}, l_{i}:Q_{i}\times Q_{i}\to\mathbb{R} \) be bifunctions satisfying conditions (A1)–(A4) for all \(i\in\mathbb{N}\). Suppose that \(\Omega=\{v^{*}\in\bigcap_{i=1}^{\infty}\operatorname{EP}(g_{i}) : A_{1}v^{*}\in\bigcap_{i=1}^{\infty }\operatorname{EP}(h_{i}) \textit{ and } A_{2}v^{*}\in\bigcap_{i=1}^{\infty }\operatorname{EP}(l_{i})\}\neq\emptyset\). For arbitrary \(x_{1}\in H_{1} \), let \(\{ u_{n}\}\), \(\{v_{n}\}\), \(\{y_{n}\} \), and \(\{x_{n}\} \) be generated by
where \(r_{1}, r_{2}, r_{3}>0 \) and \(\{\delta_{n}\}\), \(\{\theta_{n}\}\), \(\{\tau _{n}\}\), \(\{\sigma_{n}\}\), \(\{\alpha_{n,i}\}\), \(\{\beta_{n,i}\}\), \(\{\gamma _{n,i}\} \) are sequences in \([0,1] \) satisfying the following conditions:
-
(C1)
\(\sum_{i=1}^{n}\alpha_{n,i}= \sum_{i=1}^{n}\beta_{n,i} = \sum_{i=1}^{n}\gamma_{n,i}= 1\) for all \(n\in\mathbb{N}\);
-
(C2)
\(\liminf_{n\to\infty}\alpha_{n,i}>0\), \(\liminf_{n\to\infty}\beta _{n,i}>0 \), and \(\liminf_{n\to\infty}\gamma_{n,i}>0 \) for all \(i\in \mathbb{N}\);
-
(C3)
\(\lim_{n\to\infty}\sigma_{n}=0 \) and \(\sum_{n=1}^{\infty} \sigma _{n} = \infty\);
-
(C4)
\(0< a_{1}\leq\delta_{n}\leq a_{2}<\frac{1}{\|A_{1}\|^{2}}\);
-
(C5)
\(0< b_{1}\leq\theta_{n}\leq b_{2}<\frac{1}{\|A_{2}\|^{2}}\);
-
(C6)
\(0< c_{1}\leq\tau_{n}\leq c_{2}<1\).
Then the sequence \(\{x_{n}\} \) converges strongly to \(x^{*}=P_{\Omega }(f+I-B)x^{*}\).
5 Numerical example for the main result
We now give a numerical example of the studied method. Let \(H_{1}=H_{2}=(\mathbb{R}^{2},\|\cdot\|_{2})\). Define the mappings \(S_{i}:\mathbb{R}^{2}\to\mathbb{R}^{2}\), \(U_{i}:\mathbb{R}^{2}\to\mathbb{R}^{2} \), and \(T_{i}:\mathbb{R}^{2}\to\mathbb{R}^{2} \) by
and
for all \(x_{1}, x_{2}\in\mathbb{R}\). Then \(S_{i} \) are \(\frac {12}{25} \)-demicontractive mappings for all \(i\in\mathbb{N} \) and \(\bigcap_{i=1}^{\infty}F(S_{i})=\{(0,0)\}\), \(U_{i} \) are \(\frac{3}{4} \)-demicontractive mappings for all \(i\in\mathbb{N} \) and \(\bigcap_{i=1}^{\infty}F(U_{i})=0\times\mathbb{R} \), and \(T_{i} \) are 0-demicontractive mappings for all \(i\in\mathbb{N} \) and \(\bigcap_{i=1}^{\infty}F(T_{i})=\mathbb{R}\times0\). Next, we define the mappings \(f:\mathbb{R}^{2}\to\mathbb{R}^{2}\), \(B:\mathbb{R}^{2}\to\mathbb {R}^{2}\), \(A_{1}:\mathbb{R}^{2}\to\mathbb{R}^{2} \), and \(A_{2}:\mathbb {R}^{2}\to\mathbb{R}^{2} \) by
and
for all \(x_{1}, x_{2}\in\mathbb{R}\). Then f is a \(\frac{1}{8} \)-contraction, B is a self-adjoint strongly positive bounded linear operator with coefficient \(\xi=\frac{1}{2} \), and \(A_{1}\), \(A_{2} \) are bounded linear operators. Define the real sequence \(\{\alpha_{n,i}\}\), \(\{\beta_{n,i}\} \), and \(\{\gamma_{n,i}\} \) as follows:
and
that is,
and
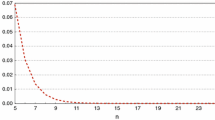
We see that \(\lim_{n\to\infty}\alpha_{n,i}= \frac{1}{2^{i}}\), \(\lim_{n\to\infty}\beta_{n,i}= \frac{1}{3^{i}} \), and \(\lim_{n\to\infty }\gamma_{n,i}= \frac{1}{2^{2i+3}} \) for \(i\in\mathbb{N}\). Now, we start with the initial point \(x_{1}=(1,1) \) and let \(\{ x_{n}\}\) be the sequence generated by (12). Suppose that \(x_{n} \) is of the form \(x_{n}=(a_{n}, b_{n})\). where \(a_{n}, b_{n} \in\mathbb{R}\). The criterion for stopping our testing method is taken as \(\| x_{n-1}-x_{n}\|_{2}<10^{-6}\). Choose \(\delta_{n}= \frac{n}{11n-1}\), \(\theta_{n}=\frac{n}{30n-1}\), \(\tau _{n}=\frac{n}{2n-1}\), and \(\sigma_{n}=\frac{1}{n^{0.01}} \) for all \(n\in\mathbb{N}\). Figure 1 shows the errors \(\| x_{n-1} -x_{n}\|_{2} \) of our proposed method. The values of \(x_{n} \) and \(\| x_{n-1}-x_{n}\|_{2} \) are shown in Table 1.
We observe from Table 1 that \(x_{n}\to(0,0)\in\Gamma\). We also note that the error is bounded by \(\| x_{30} -x_{31}\|_{2} <10^{-6}\), and we can use \(x_{31}=( 0.00000003, 0.00000117) \) to approximate the solution of (7) with accuracy at least 6 D.P.
6 Conclusion
We introduce a new algorithm for solving the split common fixed point problem (7) of the infinite families of demicontractive mappings in Hilbert spaces. Strong convergence of the proposed algorithm is obtained under some suitable control conditions. The main results of this paper can be considered as an extension of work by Eslamian [12] by providing an algorithm for finding a solution of problem (7), which is a generalization of problem (5).
Abbreviations
- SFP:
-
The split feasibility problem
- SCFP:
-
The split common fixed point problem
- MSSFP:
-
The multiple set split feasibility problem
- SCNPP:
-
The split common null point problem
- SVIP:
-
The split variational inequality problem
- SEP:
-
The split equilibrium problem
References
Censor, Y., Elfving, T.: A multiprojection algorithm using Bregman projections in a product space. Numer. Algorithms 8, 221–239 (1994)
Byrne, C.: Iterative oblique projection onto convex subsets ant the split feasibility problem. Inverse Probl. 18, 441–453 (2002)
Censor, Y., Bortfeld, T., Martin, B., Trofimov, A.: A unified approach for inversion problems in intensity-modulated radiation therapy. Phys. Med. Biol. 51, 2353–2365 (2006)
Censor, Y., Elfving, T., Kopf, N., Bortfeld, T.: The multiple set split feasibility problem and its applications. Inverse Probl. 21, 2071–2084 (2005)
Censor, Y., Segal, A.: The split common fixed point problem for directed operators. J. Convex Anal. 16, 587–600 (2009)
Moudafi, A.: A note on the split common fixed point problem for quasi-nonexpansive operators. Nonlinear Anal. 74, 4083–4087 (2011)
Qin, L.J., Wang, L., Chang, S.S.: Multiple-set split feasibility problem for a finite family of asymptotically quasi-nonexpansive mappings. Panam. Math. J. 22(1), 37–45 (2012)
Wang, F., Xu, H.K.: Approximation curve and strong convergence of the CQ algorithm for the split feasibility problem. J. Inequal. Appl. (2010). https://doi.org/10.1155/2010/102085
Xu, H.K.: A variable Krasnosekel’skii–Mann algorithm and the multiple-sets split feasibility problem. Inverse Probl. 22, 2021–2034 (2006)
Yang, Q.: The relaxed CQ algorithm for solving the split feasibility problem. Inverse Probl. 20, 1261–1266 (2004)
Moudafi, A.: The split common fixed point problem for demicontractive mappings. Inverse Probl. 26, 587–600 (2010)
Eslamian, M., Eslamian, P.: Strong convergence of a split common fixed point problem. Numer. Funct. Anal. Optim. 37, 1248–1266 (2016)
Marino, G., Xu, H.K.: A general iterative method for nonexpansive mappings in Hilbert spaces. J. Math. Anal. Appl. 318, 43–52 (2006)
Takahashi, W.: Introduction to Nonlinear and Convex Analysis. Yokohama Publishers, Yokohama (2009)
Xu, H.K.: Iterative algorithms for nonlinear operators. J. Lond. Math. Soc. 66, 240–256 (2002)
Mainge, P.E.: Approximation methods for common fixed points of nonexpansive mappings in Hilbert spaces. J. Math. Anal. Appl. 325, 469–479 (2007)
Eslamian, M.: General algorithms for split common fixed point problem of demicontractive mappings. Optimization 65(2), 443–465 (2016)
Byrne, C., Censor, Y., Gibali, A., Reich, S.: The split common null point problem. J. Nonlinear Convex Anal. 13, 759–775 (2012)
Blum, E., Oettli, W.: From optimization and variational inequalities to equilibrium problem. Math. Stud. 63, 123–145 (1994)
Combettes, P.L., Hirstoaga, A.: Equilibrium programming in Hilbert spaces. J. Nonlinear Convex Anal. 6, 117–136 (2005)
Acknowledgements
The authors would like to thank Chiang Mai University and Center of Excellence in Mathematics, CHE, Bangkok 10400, Thailand, for the financial support.
Availability of data and materials
Data sharing not applicable to this article as no datasets were generated or analyzed during the current study.
Author information
Authors and Affiliations
Contributions
Both authors contributed equally to the writing of this paper. Both authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Hanjing, A., Suantai, S. The split common fixed point problem for infinite families of demicontractive mappings. Fixed Point Theory Appl 2018, 14 (2018). https://doi.org/10.1186/s13663-018-0639-y
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13663-018-0639-y