1 Introduction

Recently, there has been overwhelming interest in the study of Mittag-Leffler functions. The Mittag-Leffler type functions have widespread applications in physics, biology, chemistry, engineering, and some other applied sciences. Some other aspects of the applications of these functions can be seen in fractional differential equations, stochastic systems, dynamical systems, statistical distributions, and chaotic systems. The geometric properties like starlikeness, convexity, and close-to-convexity of these functions have been investigated on a large scale by a number of researchers. We can easily see the direct usage of these functions to many techniques of fractional calculus. Gorenflo et al. [9], Kilbas et al. [14], and Srivastava et al. [34, 35] are a few leading precedents of these contributions. The Swedish mathematician G. M. Mittag-Leffler gave the idea of so-called Mittag-Leffler function \(E_{\alpha }(z)\), see [17]. Later, it was studied by Wiman [37, 38] who defined it in terms of power series depending on the complex parameter α. It may be regarded as a special function of \(z\in \mathbb{C} \). We define it as follows:

$$ \mathbb{E}_{\alpha }(z)=\sum_{n=0}^{\infty } \frac{z ^{n}}{\varGamma ( \alpha n+1 ) },\quad z\in \mathbb{C} ,\alpha\in \mathbb{C}. $$
(1.1)

We observe that the power series (1.1) converges in the whole complex plane for all \(\operatorname{Re}\alpha >0\), whereas it diverges everywhere on \(\mathbb{C} \backslash \{0\}\) for all \(\operatorname{Re}\alpha <0\). We also note that for \(\operatorname{Re}\alpha =0\), its radius of convergence is \(R=e^{\pi /2| \operatorname{Im}(z)|}\). Wiman [37, 38] gave the first two-parametric generalizations of the function defined in (1.1). It was later studied by Agarwal [4], Humbert [10], and Agarwal and Humbert [11]. We define it as follows:

$$ \mathbb{E}_{\alpha ,\beta } ( z ) =\sum^{\infty }_{n=0} \frac{z^{n}}{\varGamma ( \alpha n+\beta ) }, \quad \alpha ,\beta \in \mathbb{C} , \operatorname{Re} ( \alpha ) >0, \operatorname{Re} ( \beta ) >0, z\in \mathbb{C}. $$
(1.2)

For different values of parameters, the conditions of convergence vary. When α and β are positive and real, the above given series converges in the entire complex plane. Another important and interesting fact about Mittag-Leffler functions is that the one and two-parametric Mittag-Leffler functions are fractional extensions of the basic functions. That is, \(E_{1}(\pm z)=E_{1,1}(\pm z)=e^{\pm z}\), \(E_{1,2}(z)=(e^{z}-1)/z\), \(E_{2}(z)=E_{2,1}(z)=\cosh (\sqrt{z})\), \(E_{2,2}(z)=\sinh (\sqrt{z})/\sqrt{z}\). For more about Mittag-Leffler functions, see [1, 3, 12].

Let \(\mathcal{A}\) denote the class of functions f of the form

$$ f ( z ) =z+\sum_{n=2}^{\infty } a_{n}z ^{n}, $$
(1.3)

which are analytic in the open unit disc \(\mathcal{U}= \{ z \in \mathbb{C} : \vert z \vert <1 \} \). Let \(\mathcal{S}\) denote the class of all functions in \(\mathcal{A}\) which are univalent in \(\mathcal{U}\). Let \(\mathcal{S}^{\ast }(\mu )\), \(\mathcal{C}(\mu )\), and \(\mathcal{K}(\mu )\) denote the classes of starlike, convex, and close-to-convex of order μ, respectively, defined as follows:

$$\begin{aligned} &\mathcal{S}^{\ast } ( \mu ) = \biggl\{ f:f\in \mathcal{A}\text{ and } \operatorname{Re} \biggl( \frac{zf^{\prime } ( z ) }{f ( z ) } \biggr) >\mu , z\in \mathcal{U}, \mu \in [ 0,1 ) \biggr\} , \\ &\mathcal{C} ( \mu ) = \biggl\{ f:f\in \mathcal{A}\text{ and }\operatorname{Re} \biggl( 1+\frac{zf^{\prime \prime } ( z ) }{f^{\prime } ( z ) } \biggr) >\mu ,z\in \mathcal{U}, \mu \in [ 0,1 ) \biggr\} , \end{aligned}$$

and

$$ \mathcal{K} ( \mu ) = \biggl\{ f:f\in \mathcal{A}\text{ and }\operatorname{Re} \biggl( \frac{zf^{\prime } ( z ) }{g ( z ) } \biggr) >\mu , z\in \mathcal{U}, \mu \in [ 0,1 ) ,g\in \mathcal{S}^{\ast } \biggr\} . $$

It is clear that

$$ \mathcal{S}^{\ast } ( 0 ) =\mathcal{S}^{\ast }, \qquad \mathcal{C} (0 ) =\mathcal{C}, \quad \text{and}\quad \mathcal{K} ( 0 ) =\mathcal{K}. $$

The functions z, \(\frac{z}{ ( 1-z ) }\), \(\frac{z}{1-z^{2}}\), \(\frac{z}{1+z}\), \(\frac{z}{1+z^{2}}\) are starlike and univalent functions. It is convenient for f to be close-to-convex, when the corresponding function g has one of the aforementioned forms.

Consider a function \(f\in \mathcal{A}\) which is real on the segment \((-1,1)\). If f satisfies the relation

$$ \operatorname{Im} ( z ) \operatorname{Im}f ( z ) >0, \quad z\in \mathcal{U} \text{,} $$

then f is called a typically real function. The class of typically real functions \(\mathcal{T}\) was introduced by Robertson [26]. A function \(f\in \mathcal{S}\) is said to be convex in the direction of imaginary axis if and only if the domain \(f ( \mathcal{U} ) \) is convex in the direction of imaginary axis. That is, for every \(w_{1},w_{2}\in f ( \mathcal{U} ) \), \([w_{1},w_{2}] \subset f ( \mathcal{U} ) \) such that \(\operatorname{Re}w_{1}=\operatorname{Re}w_{2}\). Robertson [26] showed that a function \(f\in \mathcal{A}\) with real coefficients is convex in the direction of imaginary axis if \(zf^{\prime } ( z ) \) is typically real. It is equivalent to

$$ \operatorname{Re} \bigl[ \bigl( 1-z^{2} \bigr) f^{\prime} ( z ) \bigr] >0, \quad z\in \mathcal{U}. $$

Ruscheweyh [27] proved that if a function f \(\in \mathcal{T}\) and satisfies \(\operatorname{Re}f^{\prime }(z)>0\) for \(z\in \mathcal{U}\), then f is a starlike univalent function in \(\mathcal{U}\). The extension of this definition up to order μ was given by Mondal and Swaminathan in [18].

Let \(f\in \mathcal{A}\) of the form (1.3) and \(g\in \mathcal{A}\) be given by

$$ g(z)=z+\sum_{n=2}^{\infty }b_{n}\text{ }z^{n}. $$

Then convolution or Hadamard product of f and g is defined as

$$ ( f\ast g ) (z)=z+\sum_{n=2}^{\infty }a_{n}b_{n}z^{n} \quad ( z\in \mathcal{U} ) . $$

We also focus on the class of pre-starlike functions, initiated in [28]. The class \(\mathcal{R}_{\mu }\) denotes the class of pre-starlike functions of order μ and is defined as follows:

$$ \mathcal{R}_{\mu }=\left\{ f:f\in \mathcal{A}\text{ and } \left\{ \textstyle\begin{array}{l} \operatorname{Re}\frac{f ( z ) }{z}>0, \quad z\in \mathcal{U}\text{ for }\mu =1, \\ \frac{z}{ ( 1-z ) ^{2 ( 1-\mu ) }}\ast f ( z ) \in \mathcal{S}^{\ast } ( \mu ) , \quad z\in \mathcal{U} \text{ for }0\leq \mu < 1. \end{array}\displaystyle \right. \right\} $$

In particular, \(\mathcal{R}_{1/2}=\mathcal{S}^{\ast } ( 1/2 ) \) and \(\mathcal{R}_{0}=\mathcal{C}\). Sheil-Small et al. [32] generalized the class \(\mathcal{R}_{\mu }\) and defined the class \(\mathcal{R}[\rho ,\mu ]\). A function \(f\in \mathcal{A}\) is in the class \(\mathcal{R}[\rho ,\mu ]\) if \(f\ast \mathcal{S}_{\rho }\in \) \(\mathcal{S}^{\ast }(\mu )\), where \(\mathcal{S}_{\rho }=\frac{z}{(1-z)^{2-2 \rho }}\), \(0\leq \rho <1\). It is easy to see that \(\mathcal{R}[\mu , \mu ] = \mathcal{R}_{\mu }\). For more details, see [8, 29].

Observe that Mittag-Leffler function \(\mathbb{E}_{\alpha ,\beta }\) does not belong to the family \(\mathcal{A}\). Thus, it is natural to consider the following normalization of Mittag-Leffler functions:

$$\begin{aligned} &E_{\alpha ,\beta } ( z ) =z\varGamma ( \beta ) \mathbb{E}_{\alpha ,\beta } ( z ) =z+ \sum^{\infty }_{n=2}\frac{\varGamma ( \beta ) }{\varGamma ( \beta +\alpha ( n-1 ) ) }z ^{n}, \\ &\quad z,\alpha ,\beta \in \mathbb{C} , \operatorname{Re} ( \alpha ) >0, \operatorname{Re} ( \beta ) >0. \end{aligned}$$
(1.4)

Formula (1.4) holds for complex parameters α, β, and \(z\in \mathbb{C} \). In this paper, we shall restrict our attention to the case of real-valued α, β, and \(z\in \mathcal{U}\). For particular values of α and β, we obtain several functions, for example

$$\begin{aligned} &E_{1,3} ( z ) =\frac{2 ( e^{z}-z-1 ) }{z}, \qquad E_{1,4} ( z ) = \frac{6 ( e^{z}-z-1 ) -3z^{2}}{z ^{2}}, \\ &E_{2,2} ( z ) =\sqrt{z}\sinh \sqrt{z}, \qquad E_{3,1} ( z ) =\frac{z}{2} \biggl[ e^{z^{1/3}}+2e^{- \frac{1}{2}z^{1/3}}\cos \biggl( \frac{\sqrt{3}}{2}z^{1/3} \biggr) \biggr] . \end{aligned}$$

In some recent years, several researchers studied geometric properties such as starlikeness, convexity, and close-to-convexity of certain special functions; for details, see [5,6,7, 19, 21,22,23,24,25, 36] and the references therein. Also see [2, 13, 16, 30, 33] for some properties of special functions and mathematical inequalities. More recently, Sangal and Swaminathan [31] studied geometric properties of hypergeometric functions by using the positivity technique.

In this paper, we study pre-starlikeness and deduce the convexity and starlikeness of order \(1/2\). We also investigate the starlikeness of order \(2\mu +\eta -1\). Furthermore, we find the convexity of Mittag-Leffler functions in the direction of imaginary axis. The main tool in this investigation is the positivity technique.

2 Preliminaries

To obtain our main results, we need the following lemmas.

Lemma 2.1

([18])

Let \(\{ a_{k} \} _{k=1}^{\infty }\) be a sequence of positive numbers such that \(a_{1}=1\). If, for \(0\leq \mu <1\),

  1. (1)

    \(( 1-\mu ) a_{1}\geq ( 2-\mu ) a_{2} \geq 2^{ ( \mu +1 ) } ( 3-\mu ) a_{3}\),

  2. (2)

    \(( k-1-\mu ) ( k-\mu ) a_{k}\geq k ( k+1-\mu ) a_{k+1}\), \(\forall k\geq 3\).

Then \(f ( z ) =z+\sum^{\infty }_{k=2} a _{k}z^{k}\in \mathcal{S}^{\ast } ( \mu ) \).

Lemma 2.2

([20])

Let \(\eta \geq 0\), \(\mu \in \mathbb{R} \) such that \(0<\mu +\eta <1\) and \(n\in \mathbb{N} \). If \(d_{0}=d_{1}=1\) and \(d_{2k}=d_{2k+1}=\frac{(1+\eta )_{n-k}n!}{(n-k)!(1+\eta )_{n}}.\frac{( \mu +\eta )_{k}}{k!}\) for \(1\leq k\leq n\), then

  1. (i)

    \(\sum_{k=0}^{n}d_{k}\cos (k\theta )>0\Leftrightarrow \mu +\eta \leq \mu ^{\ast } ( \frac{1}{2} ) =0.691556\ldots\) ,

  2. (ii)

    \(\sum_{k=1}^{2n+1}\sin (k\theta )>0\Leftrightarrow \mu +\eta \leq \mu ^{\ast } ( \frac{1}{2} ) \),

  3. (iii)

    \(\sum_{k=1}^{2n}\sin (k\theta )>0\) for \(\mu +\eta \leq \frac{1+\eta }{2}\),

where \(\mu ^{\ast }(\gamma )\), \(\gamma \in ( 0,1 ] \) is the unique solution in \(] 0,1 [ \) of \(\int _{0}^{ ( \gamma +1 ) \pi }\frac{\sin ( t-\gamma \pi ) }{t ^{1-\mu }}\,dt=0\).

Koumandos and Ruscheweyh [15] obtained the value of \(\mu ^{ \ast }(\gamma )\). In this work, we use the particular value \(\mu ^{\ast } ( \frac{1}{2} ) =\mu _{0}^{\ast }\).

Lemma 2.3

([31])

Let \(0\leq \eta \leq 2\mu _{0}^{\ast }-1\), \(\mu \in \mathbb{R} \) such that \(0<\mu +\eta <1\) and \(n\in \mathbb{N} \). If \(\{ a_{k} \} _{k=1}^{\infty }\) is a decreasing sequence of non-negative numbers satisfying \(a_{0}>0\) and

$$ k ( n-k+1+\eta ) a_{2k}\leq (n-k+1) (k+\mu +\eta -1)a_{2k-1} \quad \textit{for }1\leq k \leq n, $$

then, for all \(0<\theta <\pi \),

$$ \sum_{k=0}^{n}a_{k}\sin k\theta >0\quad \Leftrightarrow\quad \mu +\eta \leq \frac{1+\eta }{2}. $$

Lemma 2.4

([31])

Let \(0\leq \eta \leq 2\mu _{0}^{\ast }-1\) and \(-\eta < \mu \leq \frac{1-\eta }{2}\), \(a_{1}=1\), \(a_{k}\geq 0\) satisfy

$$\begin{aligned} & \bigl[ k(1+\eta ) (1-\mu -\eta )-1+2\mu +\eta \bigr] a_{k} \\ &\quad \geq \bigl[ (k+1) (1+\eta ) (1-\mu -\eta )-1+2\mu +\eta \bigr] a _{k+1}, \end{aligned}$$
(2.1)
$$\begin{aligned} &(n-k+1) (k+\mu +\eta -1) \bigl[ 2k(1+\eta ) (1-\mu -\eta )-1+2\mu + \eta \bigr] a_{2k} \\ &\quad \geq k(n-k+1+\eta ) \bigl[ (2k+1) (1+\eta ) (1-\mu -\eta )-1+2\mu + \eta \bigr] a_{2k+1} \end{aligned}$$
(2.2)

for \(1\leq k\leq n\). Then \(f_{n}(z)=\sum_{k=1}^{n}a_{k}z^{k}\) is starlike of order \(\frac{1-2\mu -\eta }{(1+\eta )(1-\mu -\eta )}\). Moreover, in the limiting case, \(f(z)=\lim_{n\rightarrow \infty }f _{n}(z)=\sum_{k=1}^{\infty }a_{k}z^{k}\) is starlike of the same order if \(\{ a_{k} \} \) satisfy (2.1) and in addition

$$\begin{aligned} \begin{aligned}[b] &(k+\mu +\eta -1) \bigl[ 2k(1+\eta ) (1-\mu -\eta )-1+2\mu +\eta \bigr] a_{2k} \\ &\quad \geq k \bigl[ (2k+1) (1+\eta ) (1-\mu -\eta )-1+2\mu +\eta \bigr] a _{2k+1}\quad \textit{for }k\geq 1. \end{aligned} \end{aligned}$$
(2.3)

Lemma 2.5

([31])

Let \(\mu \in \mathbb{R} \) and \(\eta \geq 0\) such that \(0<\mu +\eta <1\), and let \(a_{1}=1\) and \(a_{k}\geq 0\) satisfy

$$\begin{aligned} 0 \leq& na_{n}\leq \cdots\leq (k+1)a_{k+1}\leq ka_{k}\leq \cdots\leq 3a_{3} \\ \leq &2a _{2}\leq \frac{\mu +\eta }{\mu _{0}^{\ast }},\quad \mu +\eta \in \bigl( 0,\mu _{0}^{\ast } \bigr] , \end{aligned}$$
(2.4)

and

$$ 2(n-k+1) (k+\mu +\eta -1)a_{2k}\geq (2k+1) (n-k+1+\eta )a_{2k+1},\quad 1\leq k\leq \biggl[ \frac{n}{2} \biggr] . $$
(2.5)

Then \(f_{n}(z)=z+\sum_{k=2}^{n}a_{k}z^{k}\) satisfies \(\operatorname{Re}(f_{n}^{\prime }(z))>1-\frac{\mu +\eta }{\mu _{0}^{\ast }}\).

3 Main results

Theorem 3.1

Let \(\alpha \geq 1\), \(\beta \geq 1\). Then \(E_{\alpha ,\beta } ( z ) \in \mathcal{R} [ \rho ,\mu ] \) for \(0\leq \mu <1\) and

$$ \frac{\varGamma ( \alpha +\beta ) }{\varGamma ( \beta ) }\geq \textstyle\begin{cases} T_{1} ( \rho ,\mu ) , \quad 0\leq \rho \leq \rho _{1} ( \mu ) , \\ \max \{ T_{1} ( \rho ,\mu ) , T_{2} ( \rho , \mu ) \frac{2\varGamma ^{2} ( \alpha +\beta ) }{\varGamma ( \beta ) \varGamma ( 2\alpha +\beta ) }, T _{3} ( \rho ,\mu ) \frac{\varGamma ( \alpha ( k-1 ) +\beta ) }{\varGamma ( \alpha k+\beta ) }\frac{ \varGamma ( \alpha +\beta ) }{\varGamma ( \beta ) } \} ,\\ \quad \rho _{1} ( \mu ) \leq \rho < 1, \end{cases} $$

where

$$\begin{aligned} T_{1} ( \rho ,\mu ) =&\frac{2 ( 2-\mu ) ( 1-\rho ) }{ ( 1-\mu ) },\qquad T_{2} ( \rho ,\mu ) =\frac{2^{\mu -1} ( 3-\mu ) ( 3-2\rho ) }{ ( 2-\mu ) }, \\ T_{3} ( \rho ,\mu ) =&\frac{2 ( 4-\mu ) ( 2-\rho ) }{ ( 2-\mu ) ( 3-\mu ) },\quad \rho _{1} ( \mu ) =1-\frac{2^{\mu } ( 3-\mu ) ( 1-\mu ) }{4 ( 2-\mu ) ^{2}-2.2^{\mu } ( 3-\mu ) ( 1-\mu ) }. \end{aligned}$$

Proof

Consider the function \(g ( z ) =z+\sum^{\infty }_{k=2} b_{k}z^{k}\), where \(b_{k}\) is given by

$$ b_{1}=1, \qquad b_{k+1}=\frac{\varGamma ( \alpha ( k-1 ) +\beta ) }{\varGamma ( \alpha k+\beta ) } \frac{ ( k+1-2\rho ) }{k}b_{k}, \quad \forall k\geq 1. $$

Now

$$\begin{aligned} & ( 1-\mu ) b_{1}- ( 2-\mu ) b_{2} \\ &\quad = ( 1-\mu ) -2 ( 2-\mu ) \frac{\varGamma ( \beta ) }{\varGamma ( \alpha +\beta ) } ( 1- \rho ) \\ &\quad =\frac{1}{\varGamma ( \alpha +\beta ) } \bigl[ ( 1- \mu ) \varGamma ( \alpha +\beta ) -2 ( 2-\mu ) ( 1-\rho ) \varGamma ( \beta ) \bigr] \geq 0 \end{aligned}$$

implies \(\varGamma ( \alpha +\beta ) \geq T_{1} ( \rho ,\mu ) \varGamma ( \beta ) \), where \(T_{1} ( \rho ,\mu ) =\frac{2 ( 2-\mu ) ( 1- \rho ) }{ ( 1-\mu ) }\). Again

$$\begin{aligned} & ( 2-\mu ) b_{2}-2^{\mu +1} ( 3-\mu ) b_{3} \\ &\quad = ( 2-\mu ) b_{2}-2^{\mu +1} ( 3-\mu ) \frac{ \varGamma ( \alpha +\beta ) }{\varGamma ( 2\alpha + \beta ) } \frac{ ( 3-2\rho ) }{2}b_{2} \\ &\quad =\frac{2 ( 2-\mu ) b_{2}}{\varGamma ( 2\alpha + \beta ) } \biggl[ \frac{\varGamma ( 2\alpha +\beta ) }{2}-T_{2} ( \rho , \mu ) \varGamma ( \alpha +\beta ) \biggr] \geq 0 \end{aligned}$$

with \(\frac{\varGamma ( \alpha +\beta ) }{\varGamma ( \beta ) }\geq 2T_{2} ( \rho ,\mu ) \frac{\varGamma ^{2} ( \alpha +\beta ) }{\varGamma ( \beta ) \varGamma ( 2\alpha +\beta ) }\), where \(T_{2} ( \rho ,\mu ) =\frac{2^{\mu -1} ( 3-\mu ) ( 3-2 \alpha ) }{ ( 2-\mu ) }\). Also consider

$$\begin{aligned} & ( k-1-\mu ) ( k-\mu ) b_{k}-k ( k+1- \mu ) b_{k+1} \\ &\quad = ( k-1-\mu ) ( k-\mu ) b_{k}-k ( k+1- \mu ) \frac{ ( k+1-2\rho ) }{k} \frac{\varGamma ( \alpha ( k-1 ) +\beta ) }{\varGamma ( \alpha k+ \beta ) }b_{k} \\ &\quad =\frac{b_{k}}{\varGamma ( \alpha k+\beta ) } \\ &\qquad {}\times\bigl[ ( k-1-\mu ) ( k-\mu ) \varGamma ( \alpha k+ \beta ) - ( k+1-\mu ) ( k+1-2\rho ) \varGamma \bigl( \alpha ( k-1 ) +\beta \bigr) \bigr] \\ &\quad = A ( k ) M ( k ) , \end{aligned}$$

where \(A ( k ) =\frac{b_{k}}{\varGamma ( \alpha k+ \beta ) }\) and

$$\begin{aligned} M ( k ) =& ( k-1-\mu ) ( k-\mu ) \varGamma ( \alpha k+\beta ) - ( k+1-\mu ) ( k+1-2\rho ) \varGamma \bigl( \alpha ( k-1 ) + \beta \bigr) \\ =&A ( \rho ,\mu ) ( k-3 ) ^{2}+B ( \rho ,\mu ) ( k-3 ) +D ( \rho ,\mu ) . \end{aligned}$$

Here

$$\begin{aligned} &A ( \rho ,\mu ) =\varGamma ( \alpha k+\beta ) -\varGamma \bigl( \alpha ( k-1 ) + \beta \bigr) \geq 0, \\ &B ( \rho ,\mu ) = ( 5-2\mu ) \varGamma ( \alpha k+\beta ) - ( 8-2\rho -\mu ) \varGamma \bigl( \alpha ( k-1 ) +\beta \bigr) \geq 0, \\ &D ( \rho ,\mu ) = ( 2-\mu ) ( 3- \mu ) \varGamma ( \alpha k+\beta ) -2 ( 4- \mu ) ( 2-\rho ) \varGamma \bigl( \alpha ( k-1 ) +\beta \bigr) \geq 0. \end{aligned}$$

This implies that

$$ \frac{\varGamma ( \alpha +\beta ) }{\varGamma ( \beta ) }\geq T_{3} ( \rho ,\mu ) \frac{\varGamma ( \alpha ( k-1 ) +\beta ) }{\varGamma ( \alpha k+\beta ) } \frac{\varGamma ( \alpha +\beta ) }{ \varGamma ( \beta ) }, $$

where \(T_{3} ( \rho ,\mu ) =\frac{2 ( 4-\mu ) ( 2-\alpha ) }{ ( 2-\mu ) ( 3-\mu ) }\). It is clear that \(A ( \rho ,\mu )\), \(B ( \rho ,\mu )\), \(D ( \rho ,\mu )\) are non-negative. Since each coefficient of \(( k-3 ) \) and the constant term in \(M ( k ) \) are non-negative, therefore \(M ( k ) \) is an increasing function for \(k\geq 3\). Also, for \(M ( 3 ) >0\), we have \(( k-1-\mu ) ( k- \mu ) b_{k}\geq k ( k+1-\mu ) b_{k+1}\). Thus \(b_{k}\) satisfies the conditions of Lemma 2.1 and hence \(g\in \mathcal{S}^{\ast } ( \mu ) \). After simple computations, we observe that \(g ( z ) =E_{\alpha ,\beta } ( z ) \ast \frac{z}{ ( 1-z ) ^{2-2\rho }}\). Therefore, by the definition of \(\mathcal{R} [ \rho ,\mu ]\), we have \(E_{\alpha ,\beta } ( z ) \in \mathcal{R} [ \rho , \mu ] \). Now consider

$$\begin{aligned} T_{3} ( \rho ,\mu ) -T_{1} ( \rho ,\mu ) =& \frac{2 ( 4-\mu ) ( 2-\rho ) }{ ( 2-\mu ) ( 3-\mu ) }-\frac{2 ( 2-\mu ) ( 1- \rho ) }{ ( 1-\mu ) } \\ =&\frac{2 ( 1-\mu ) ( 4-\mu ) ( 2- \rho ) -2 ( 2-\mu ) ^{2} ( 3-\mu ) ( 1-\rho ) }{ ( 1-\mu ) ( 2-\mu ) ( 3-\mu ) }. \end{aligned}$$

The numerator is negative for all μ and hence \(T_{3} ( \rho ,\mu ) \leq T_{1} ( \rho ,\mu ) \) for \(0\leq \rho \leq \rho _{0} ( \mu ) \). Similarly, if \(0\leq \rho \leq \rho _{1} ( \mu ) \), \(T_{1} ( \rho , \mu ) \geq T_{2} ( \rho ,\mu ) \) for all μ. Here,

$$\begin{aligned} \rho _{0} ( \mu ) =&1-\frac{ ( 4-\mu ) ( 1-\mu ) }{ ( 2-\mu ) ^{2} ( 3-\mu ) - ( 4-\mu ) ( 1-\mu ) }, \\ \rho _{1} ( \mu ) =&1-\frac{2^{\mu } ( 3-\mu ) ( 1-\mu ) }{4 ( 2-\mu ) ^{2}-2.2^{\mu } ( 3-\mu ) ( 1-\mu ) }. \end{aligned}$$

Clearly, we can investigate that, for \(0\leq \rho \leq \min \{ \rho _{0} ( \mu ) ,\rho _{1} ( \mu ) \} \),

$$ \max_{i=1,2,3} \bigl\{ T_{i} ( \rho ,\mu ) \bigr\} =T_{1} ( \rho ,\mu ) . $$

Now, we only need to check the \(\min \{ \rho _{0} ( \mu ) ,\rho _{1} ( \mu ) \} \). Consider

$$\begin{aligned} \rho _{1}-\rho _{0} =&-\frac{2^{\mu } ( 3-\mu ) ( 1- \mu ) }{4 ( 2-\mu ) ^{2}-2.2^{\mu } ( 3- \mu ) ( 1-\mu ) }+ \frac{ ( 4-\mu ) ( 1-\mu ) }{ ( 2-\mu ) ^{2} ( 3-\mu ) - ( 4-\mu ) ( 1-\mu ) } \\ =&\frac{N ( \mu ) }{ ( 4 ( 2-\mu ) ^{2}-2.2^{ \mu } ( 3-\mu ) ( 1-\mu ) ) ( ( 2-\mu ) ^{2} ( 3-\mu ) - ( 4-\mu ) ( 1-\mu ) ) }, \end{aligned}$$

where

$$\begin{aligned} N ( \mu ) =&2^{\mu } ( 3-\mu ) ( 1- \mu ) \bigl\{ ( 2-\mu ) ^{2} ( 3-\mu ) - ( 4-\mu ) ( 1-\mu ) \bigr\} \\ &{}+ ( 4-\mu ) ( 1-\mu ) \bigl\{ 4 ( 2- \mu ) ^{2}-2.2^{\mu } ( 3-\mu ) ( 1-\mu ) \bigr\} \\ < &0. \end{aligned}$$

This implies \(\rho _{0} ( \mu ) =\min \{ \rho _{0} ( \mu ) ,\rho _{1} ( \mu ) \} \), and the proof is complete. □

Theorem 3.2

Let \(0\leq \mu <1\), \(\alpha \geq 1\), \(\beta \geq 1\). If \(\frac{\varGamma ( \alpha +\beta ) }{\varGamma ( \beta ) } \geq 2 ( 2-\mu ) \), then \(E_{\alpha ,\beta } ( z ) \) is pre-starlike of order μ in \(\mathcal{U}\).

Proof

Consider \(T_{i} ( \rho ,\mu ) ,i=1,2,3\), as in Theorem 3.1. Replacing ρ by μ, we get

$$\begin{aligned} T_{1} ( \mu ) =&2 ( 2-\mu ) , \\ T_{2} ( \mu ) =&\frac{2^{\mu -1} ( 3-\mu ) ( 3-2\mu ) }{ ( 2-\mu ) }, \\ T_{3} ( \mu ) =&\frac{2 ( 4-\mu ) }{ ( 3- \mu ) }. \end{aligned}$$

It is noticed that, for \(0\leq \mu <1\),

$$\begin{aligned} T_{1} ( \mu ) -T_{2} ( \mu ) =&2 ( 2- \mu ) - \frac{2^{\mu -1} ( 3-\mu ) ( 3-2 \mu ) }{ ( 2-\mu ) } \\ =&\frac{2 ( 2-\mu ) ^{2}-2^{\mu -1} ( 3-\mu ) ( 3-2\mu ) }{ ( 2-\mu ) }>0. \end{aligned}$$

Similarly,

$$\begin{aligned} T_{1} ( \mu ) -T_{3} ( \mu ) =&2 ( 2- \mu ) - \frac{2 ( 4-\mu ) }{ ( 3-\mu ) } \\ =&\frac{2 ( 2-\mu ) ( 3-\mu ) -2 ( 4- \mu ) }{ ( 3-\mu ) }>0. \end{aligned}$$

Therefore, \(T_{1} ( \mu ) \) is maximum. Hence

$$ \frac{\varGamma ( \alpha +\beta ) }{\varGamma ( \beta ) }\geq \max \left\{ \textstyle\begin{array}{c} T_{1} ( \mu ) , T_{2} ( \mu ) \frac{2\varGamma ^{2} ( \alpha +\beta ) }{\varGamma ( \beta ) \varGamma ( 2\alpha +\beta ) }, \\ T_{3} ( \mu ) \frac{\varGamma ( \alpha ( k-1 ) +\beta ) }{\varGamma ( \alpha k+\beta ) }\frac{ \varGamma ( \alpha +\beta ) }{\varGamma ( \beta ) } \end{array}\displaystyle \right \} =T_{1} ( \mu ) . $$

This is equivalent to

$$ \frac{\varGamma ( \alpha +\beta ) }{\varGamma ( \beta ) }\geq 2 ( 2-\mu ) . $$
(3.1)

 □

Corollary 3.3

Let \(\alpha \geq 1\), \(\beta \geq 1\). Then \(E_{\alpha ,\beta } ( z ) \in \mathcal{C}\) if \(\frac{\varGamma ( \alpha +\beta ) }{\varGamma ( \beta ) }\geq 4\).

Proof

It is noticed that, for \(\mu =0\), we have \(\frac{z}{ ( 1-z ) ^{2}}\ast f ( z ) \in \mathcal{S}^{\ast }\). By using the definition of convolution, it is easy to see that \(zf^{\prime } ( z ) \in \mathcal{S}^{\ast }\). Therefore, by Alexander relation it follows that \(f\in \mathcal{C}\). We also see from Theorem 3.2 that

$$ T_{1} ( 0 ) =4,\qquad T_{2} ( 0 ) =\frac{9}{4}, \qquad T_{3} ( 0 ) =\frac{8}{3}. $$

Now

$$ T_{1} ( 0 ) -T_{2} ( 0 ) =4-\frac{9}{4}= \frac{7}{4}>0, $$

similarly,

$$ T_{1} ( 0 ) -T_{3} ( 0 ) =4-\frac{8}{3}= \frac{4}{3}>0. $$

Therefore, \(T_{1} ( 0 ) \) is maximum. Hence

$$ \frac{\varGamma ( \alpha +\beta ) }{\varGamma ( \beta ) }\geq 4. $$

This shows that \(E_{\alpha ,\beta } ( z ) \in \mathcal{C}\). □

Example 3.4

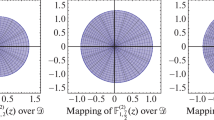
For \(\alpha =3\), \(\beta =1\), we have \(\frac{\varGamma ( \alpha + \beta ) }{\varGamma ( \beta ) }\geq 4\), therefore the function

$$ E_{3,1} ( z ) =\frac{z}{2} \biggl[ e^{z^{1/3}}+2e^{- \frac{1}{2}z^{1/3}} \cos \biggl( \frac{\sqrt{3}}{2}z^{1/3} \biggr) \biggr] $$

is in \(\mathcal{C}\).

Example 3.5

For \(\alpha =1\), \(\beta =4\), we have \(\frac{\varGamma ( \alpha + \beta ) }{\varGamma ( \beta ) }=4\), therefore the function

$$ E_{1,4} ( z ) =\frac{6 ( e^{z}-z-1 ) -3z^{2}}{z ^{2}} $$

is in \(\mathcal{C}\).

The mappings of these functions are given in Fig. 1.

Figure 1
figure 1

The mapping of \(\mathcal{U}\) by the indicated functions

Full size image

Corollary 3.6

Let \(\alpha \geq 1\), \(\beta \geq 1\). Then \(E_{\alpha ,\beta } ( z ) \in \mathcal{S}^{\ast } ( \frac{1}{2} ) \) if \(\frac{\varGamma ( \alpha +\beta ) }{\varGamma ( \beta ) }\geq 3\).

Proof

Consider \(T_{i} ( \rho ,\mu ) \), \(i=1,2,3\), as in Theorem 3.1. Replacing ρ by μ, we get

$$\begin{aligned} T_{1} ( \mu ) =&2 ( 2-\mu ) , \\ T_{2} ( \mu ) =&\frac{2^{\mu -1} ( 3-\mu ) ( 3-2\mu ) }{ ( 2-\mu ) }, \\ T_{3} ( \mu ) =&\frac{2 ( 4-\mu ) }{ ( 3- \mu ) }. \end{aligned}$$

For \(\mu =\frac{1}{2}\),

$$ T_{1} \biggl( \frac{1}{2} \biggr) =3,\qquad T_{2} \biggl( \frac{1}{2} \biggr) =\frac{5\sqrt{2}}{3},\qquad T_{3} \biggl( \frac{1}{2} \biggr) =\frac{14}{5}. $$

Now

$$ T_{1} \biggl( \frac{1}{2} \biggr) -T_{2} \biggl( \frac{1}{2} \biggr) =3-\frac{5 \sqrt{2}}{3}=\frac{9-5\sqrt{2}}{3}>0. $$

Similarly,

$$ T_{1} \biggl( \frac{1}{2} \biggr) -T_{3} \biggl( \frac{1}{2} \biggr) =3- \frac{14}{5}=\frac{1}{5}>0. $$

Therefore, \(T_{1} ( \frac{1}{2} ) \) is maximum. Hence

$$ \frac{\varGamma ( \alpha +\beta ) }{\varGamma ( \beta ) }\geq 3. $$

Therefore, for \(\alpha \geq 1\), \(\beta \geq 1\), and \(\frac{\varGamma ( \alpha +\beta ) }{\varGamma ( \beta ) } \geq 3\), \(E_{\alpha ,\beta } ( z ) \in \mathcal{S}^{\ast } ( \frac{1}{2} ) \). □

Example 3.7

For \(\alpha =1\), \(\beta =3\), we have \(\frac{\varGamma ( \alpha + \beta ) }{\varGamma ( \beta ) }=3\), therefore the function

$$ E_{1,3} ( z ) =\frac{2 ( e^{z}-z-1 ) }{z} $$

is in \(\mathcal{S}^{\ast } ( \frac{1}{2} ) \).

Example 3.8

For \(\alpha =2\), \(\beta =2\), we have \(\frac{\varGamma ( \alpha + \beta ) }{\varGamma ( \beta ) }=6\), therefore the function

$$ E_{2,2} ( z ) =\sqrt{z}\sinh \sqrt{z} $$

is in \(\mathcal{S}^{\ast } ( \frac{1}{2} ) \).

The mappings of these functions are given in Fig. 2.

Figure 2
figure 2

The mapping of \(\mathcal{U}\) by the indicated functions

Full size image

Theorem 3.9

Let \(\mu \geq 1\), \(\eta \geq \frac{-\mu +\sqrt{\mu ^{2}+4\mu -4}}{2}\) with \(\alpha \geq 1\), \(\beta \geq 2\) If \(M_{1}=(1+\eta )(1-\mu - \eta )>0\) and \(M_{2}=+2\mu +\eta -1>0\), then \(E_{\alpha ,\beta }(z)\) is starlike of order \(2\mu +\eta -1\).

Proof

It is observed that \(( E_{\alpha ,\beta } ) _{n}(z)= \sum_{k=1}^{\infty }a_{k}z^{k}\) gives \(a_{1}=1\) and \(a_{k}=\frac{ \varGamma ( \beta ) }{\varGamma ( \alpha ( k-1 ) +\beta ) }\) for \(k\geq 2\). The relation between \(a_{k}\) and \(a_{k+1}\) is

$$ a_{k+1}=\frac{\varGamma ( \alpha ( k-1 ) +\beta ) }{\varGamma ( \alpha k+\beta ) }a_{k}\quad \text{for }k \geq 1. $$

To prove this theorem, it is enough to show that \(\{ a_{k} \} \) satisfies conditions (2.1) and (2.3) of Lemma 2.4. Using the above relation and simple computations yields

$$\begin{aligned} & \bigl[ k(1+\eta ) (1-\mu -\eta )-1+2\mu +\eta \bigr] a_{k}- \bigl[ (k+1) (1+\eta ) (1-\mu -\eta )-1+2\mu +\eta \bigr] a_{k+1} \\ &\quad =\frac{\varGamma ( \alpha (k-1)+\beta ) a_{k}}{\varGamma ( \alpha k+\beta ) }h(k), \end{aligned}$$

where \(h(k)\) is defined as follows:

$$\begin{aligned} h(k) =&\frac{\varGamma ( \alpha k+\beta ) }{\varGamma ( \alpha (k-1)+\beta ) } \bigl[ k(1+\eta ) (1-\mu -\eta )-1+2 \mu +\eta \bigr] \\ &{}- \bigl[ (k+1) (1+\eta ) (1-\mu -\eta )-1+2\mu +\alpha \bigr] \\ =&\frac{\varGamma ( \alpha k+\beta ) }{\varGamma ( \alpha (k-1)+\beta ) } ( kM_{1}+M_{2} ) - \bigl[ (k+1)M _{1}+M_{2} \bigr] \\ =& \biggl[ \frac{k\varGamma ( \alpha k+\beta ) }{\varGamma ( \alpha (k-1)+\beta ) }-(k+1) \biggr] M_{1}+ \biggl[ \frac{ \varGamma ( \alpha k+\beta ) }{\varGamma ( \alpha (k-1)+ \beta ) }-1 \biggr] M_{2} >0. \end{aligned}$$
(3.2)

It is observed that under the conditions \(\mu \geq 1\), \(\eta \geq \frac{- \mu +\sqrt{\mu ^{2}+4\mu -4}}{2}\), \(\alpha \geq 1\), and \(\beta \geq 3\), expression (3.2) is positive for \(k\geq 1\). It remains to verify (2.3). That is,

$$\begin{aligned} &(k+\mu +\eta -1) \bigl[ 2k(1+\eta ) (1-\mu -\eta )-1+2\mu +\eta \bigr] a_{2k} \\ &\quad \geq k \bigl[ (2k+1) (1+\eta ) (1-\mu -\eta )-1+2\mu +\eta \bigr] a _{2k+1}. \end{aligned}$$

Clearly,

$$\begin{aligned} &(k+\mu +\eta -1) \bigl[ 2k(1+\eta ) (1-\mu -\eta )-1+2\mu +\eta \bigr] a_{2k} \\ &\quad {}-k \bigl[ (2k+1) (1+\eta ) (1-\mu -\eta )-1+2\mu +\eta \bigr] a_{2k+1}= \frac{ \varGamma ( \alpha (2k-1)+\beta ) a_{2k}}{2\varGamma ( \alpha (2k)+\beta ) }g(k), \end{aligned}$$

where \(g(k)\) is defined as follows:

$$\begin{aligned} g(k) =&\frac{\varGamma ( \alpha (2k)+\beta ) }{\varGamma ( \alpha (2k-1)+\beta ) }\bigl(k+\mu +\eta ^{\prime}-1\bigr) \bigl[ 2k(1+ \eta ) (1-\mu -\eta )-1+2\mu +\eta ) \bigr] \\ &{}- \bigl[ (2k+1) (1+\eta ) (1-\mu -\eta )-1+2\mu +\eta \bigr] \\ =&\frac{\varGamma ( \alpha (2k)+\beta ) }{\varGamma ( \alpha (2k-1)+\beta ) }(k+\mu +\eta -1) [ 2kM_{1}+M_{2} ] -k \bigl[ (2k+1)M_{1}+M_{2} \bigr] \\ =& \biggl[ \frac{\varGamma ( \alpha (2k)+\beta ) }{\varGamma ( \alpha (2k-1)+\beta ) }2k(k+\mu +\eta -1)-k(2k+1) \biggr] M_{1} \\ &{}+ \biggl[ \frac{\varGamma ( \alpha (2k)+\beta ) }{\varGamma ( \alpha (2k-1)+\beta ) }(k+\mu +\eta -1)-k \biggr] M _{2}>0. \end{aligned}$$
(3.3)

It is observed that under the conditions \(\mu \geq 1\), \(\eta \geq \frac{- \mu +\sqrt{\mu ^{2}+4\mu -4}}{2}\), \(2\mu +\eta >1\), \(\alpha \geq 1\), and \(\beta \geq 2\), expression (3.3) is positive for \(k\geq 1\), which completes the proof. □

Theorem 3.10

Let \(\mu \geq 1\), \(\eta \geq \frac{-\mu +\sqrt{\mu ^{2}+4\mu -4}}{2}\), \(2\mu +\eta >1\), \(\alpha \geq 1\), \(\beta \geq 2\), \(a_{1}=1\), \(a_{k}\geq 0\) satisfy

$$\begin{aligned} \begin{aligned} & ka_{k}-(k+1)a_{k+1} \geq 0,\quad k=1,2,3,\ldots,n-1, \\ & (n-k+1) (k+\mu +\eta -1) (2k-1)a_{2k-1} \geq 2k^{2}(n-k+1+ \eta )a_{2k},\\ &\quad k=4,5,\ldots, \biggl[ \frac{n+3}{2} \biggr] , \end{aligned} \end{aligned}$$
(3.4)

for \(k\geq 4\). Then \(( E_{\alpha ,\beta } ) _{n}(z)= \sum_{k=4}^{n}a_{k}z^{k}\) is convex in the direction of imaginary axis.

Proof

To show that Mittag-Leffler function is convex in the direction of imaginary axis, we will prove that \(z ( E_{\alpha ,\beta } ) _{n}^{\prime }(z) \) is a typically real function. Also \(( E_{ \alpha ,\beta } ) _{n}(z)\) has real coefficients. Set

$$\begin{aligned} z ( E_{\alpha ,\beta } ) _{n}^{\prime }(z) =&z+\sum _{k=2} ^{n}\frac{\varGamma ( \beta ) }{\varGamma ( \alpha ( k-1 ) +\beta ) }z^{k} \\ =&z+\sum_{k=2}^{n}b_{k}z^{k}, \end{aligned}$$

where \(b_{k}=\frac{\varGamma ( \beta ) }{\varGamma ( \alpha ( k-1 ) +\beta ) }\). To get the result, it is required that \(\{ b_{k} \} \) must satisfy the conditions mentioned in Lemma 2.3. Consider

$$\begin{aligned} kb_{k}-(k+1)b_{k+1} =&\varGamma ( \beta ) \biggl[ \frac{k}{ \varGamma ( \alpha ( k-1 ) +\beta ) }-\frac{k+1}{ \varGamma ( \alpha k+\beta ) } \biggr] \\ =&\varGamma ( \beta ) \biggl[ \frac{k\varGamma ( \alpha k+\beta ) -(k+1)\varGamma ( \alpha ( k-1 ) + \beta ) }{\varGamma ( \alpha k+\beta ) \varGamma ( \alpha ( k-1 ) +\beta ) } \biggr] >0 \end{aligned}$$

for \(k=1,2,3,\ldots,n-1\). Take

$$ (n-k+1) (k+\mu +\eta -1)b_{2k-1}-k(n-k+1+\eta )b_{2k}= \frac{b_{2k} \varGamma ( \alpha ( 2k-1 ) +\beta ) }{\varGamma ( \alpha ( 2k-2 ) +\beta ) }q(k), $$

here \(q(k)\) is defined as

$$ q(k)=(k+\mu +\eta -1) (n-k+1)-k(n-k+1+\eta )\frac{\varGamma ( \alpha ( 2k-2 ) +\beta ) }{\varGamma ( \alpha ( 2k-1 ) +\beta ) }. $$
(3.5)

Since Γ is an increasing function in \([ \frac{3}{2}, \infty )\), therefore (3.5) becomes positive when \(\mu \geq 1\), \(\eta \geq \frac{-\mu +\sqrt{\mu ^{2}+4 \mu -4}}{2}\), \(2\mu +\eta >1 \), \(\alpha \geq 1\), and \(\beta \geq 2\). Thus \(\{ b_{k} \} \) satisfies the conditions of Lemma 2.3. Therefore, by using the minimum principle for harmonic functions under the conditions \(\mu +\eta \in ( 0,\frac{1+\eta }{2} ] \),

$$ \operatorname{Im} \bigl( zf_{n}^{\prime } ( z ) \bigr) =\sum _{k=1}^{n}b_{k}r^{k} \sin k\theta >0,\quad \text{where }\theta \in \,] 0,\pi [ \text{ and }r\in \,] 0,1 [ $$

and

$$ \operatorname{Im} \bigl( zf_{n}^{\prime } ( z ) \bigr) =0\quad \text{for }z \in ( 0,1 ) . $$

The Schwarz reflection principle yields that \(\operatorname{Im} ( zf_{n}^{ \prime } ( z ) ) <0\) for \(\theta \in ( \pi ,2 \pi ) \). So \(zf_{n}^{\prime } ( z ) \) is a typically real function, which is equivalent to saying that \(f_{n}(z)\) is convex in the direction of imaginary axis. □

Theorem 3.11

Let \(\mu \in \mathbb{R} \) and \(\eta \geq 0\) such that \(2\mu +\eta >1\), and let \(a_{1}=1\) and \(a_{k}\geq 0\) satisfy

$$ 0\leq na_{n}\leq \cdots\leq (k+1)a_{k+1}\leq ka_{k}\leq \cdots\leq 3a_{3}\leq 2a _{2}\leq \frac{\mu +\eta }{\mu _{0}^{\ast }},\quad \mu +\eta \in \bigl( 0,\mu _{0}^{\ast } \bigr] , $$
(3.6)

and

$$ 2(n-k+1) (k+\mu +\eta -1)a_{2k}\geq (2k+1) (n-k+1+\eta )a_{2k+1},\quad 1\leq k\leq \biggl[ \frac{n}{2} \biggr] . $$
(3.7)

If \(\alpha \geq 1\) and \(\beta \geq 2\), then \(( E_{\alpha , \beta } ) _{n}(z)=z+\sum_{k=2}^{n}a_{k}z^{k}\) satisfies \(\operatorname{Re}(f_{n}^{\prime }(z))>1-\frac{\mu +\eta }{\mu _{0}^{\ast }}\).

Proof

Let \(\sigma -1=-\frac{\mu +\eta }{\mu _{0}^{\ast }}\) and \(( E _{\alpha ,\beta } ) _{n}(z)=z+\sum_{k=2}^{n}\frac{\varGamma ( \beta ) }{\varGamma ( \alpha ( k-1 ) + \beta ) }z^{k}\), where \(a_{k}=\frac{\varGamma ( \beta ) }{\varGamma ( \alpha ( k-1 ) +\beta ) }\). Then

$$ \frac{ ( E_{\alpha ,\beta } ) _{n}^{\prime }(z)-\sigma }{1- \sigma }=\sum_{k=0}^{n-1}c_{k}z^{k}, $$

where \(c_{k}=\frac{(k+1)b_{k+1}}{1-\sigma } \) and \(c_{0}=1\) for \(1 \leq k\leq n-1\). It is observed that under the conditions \(\alpha \geq 1\) and \(\beta \geq 2\) the coefficients \(a_{k}\) are positive. Therefore, \(c_{k}>0\) for \(k\geq 1\). To prove this theorem, we will show that the coefficients \(\{ c_{k} \} \) are decreasing and satisfy (2.5). Now, for this, consider

$$\begin{aligned} (k+1)a_{k+1}-(k+2)a_{k+2} =&\varGamma ( \beta ) \biggl[ \frac{k+1}{ \varGamma ( \alpha k+\beta ) }-\frac{k+2}{\varGamma ( \alpha ( k+1 ) +\beta ) } \biggr] \\ =&\varGamma ( \beta ) \biggl[ \frac{ ( k+1 ) \varGamma ( \alpha ( k+1 ) +\beta ) -(k+2) \varGamma ( \alpha k+\beta ) }{\varGamma ( \alpha k+ \beta ) \varGamma ( \alpha ( k+1 ) +\beta ) } \biggr] >0 \end{aligned}$$

for \(k=1,2,3,\ldots,n-2\). This shows that the coefficients of Mittag-Leffler function are decreasing and \(c_{1}< c_{0}\Rightarrow 2b _{2}<1-\sigma \). Now to have (2.5), consider

$$\begin{aligned} & ( n-k+1 ) ( \mu +\eta +k-1 ) a_{2k}-(n-k+1+ \eta ) (2k+1)a_{2k+1} \\ &\quad =\frac{ ( n-k+1 ) ( \mu +\eta +k-1 ) \varGamma ( \beta ) }{\varGamma ( \alpha ( 2k-1 ) + \beta ) }-\frac{(n-k+1+\eta )(2k+1)\varGamma ( \beta ) }{\varGamma ( \alpha ( 2k ) +\beta ) } \\ &\quad =\varGamma ( \beta ) \\ &\qquad {}\times \biggl[ \frac{ ( n-k+1 ) ( \mu +\eta +k-1 ) \varGamma ( \alpha ( 2k ) +\beta ) -(n-k+1+\eta )(2k+1)\varGamma ( \alpha ( 2k-1 ) +\beta ) }{\varGamma ( \alpha ( 2k ) +\beta ) \varGamma ( \alpha ( 2k-1 ) +\beta ) } \biggr] \\ &\quad >0,\quad \text{for }1\leq k\leq \biggl[ \frac{n}{2} \biggr] . \end{aligned}$$

It is clear that the above relation is positive for \(n\geq k\), \(\alpha \geq 1 \), and \(\beta \geq 2\). Also, Γ is an increasing function in \([ \frac{3}{2},\infty ) \). This yields (3.7). Using similar arguments and the minimum principle for harmonic function gives the required result. □

4 Conclusion

In this paper, we have studied the normalized Mittag-Leffler function of two parameters. We have investigated new properties including pre-starlikeness, convexity, and starlikeness of order \(1/2\). Sufficient conditions for the normalized Mittag-Leffler function to be starlike of order \(2\mu +\eta -1\) have also been studied. Moreover, we have found the convexity of Mittag-Leffler functions in the direction of imaginary axis.