1 Introduction

The method of separation of variables, also known as the Fourier method, is one of the most effective tools in analytically solving the problems from mathematical physics. This method will lead to the eigenvalue problem of self-adjoint operators (see, e.g., Sturm-Liouville problems). However, a great number of applied problems cannot be reduced to the above eigenvalue problem, e.g., the system characterized by the second order partial differential equation with a mixed partial derivative. As the orthogonality and the completeness of eigenvector systems can not be guaranteed for these problems, the traditional method of separation of variables fails to work.

In [1], using the simulation theory between structural mechanics and optimal control, the author introduced Hamiltonian systems into elasticity and related fields, and proposed the method of separation of variables based on Hamiltonian systems. In this method, the orthogonality and the completeness of eigenvector systems are, respectively, replaced by the symplectic orthogonality and the completeness in the Cauchy principal value (CPV) sense; the eigenvalue problem of self-adjoint operators becomes that of Hamiltonian operator matrices admitting the representation

$$ H= \begin{pmatrix} A & B \\ C & - A^{*} \end{pmatrix} :\mathcal{D}(H) \subseteq X\times X\to X \times X. $$
(1.1)

Here the asterisk denotes the adjoint operator, A is a closed linear operator with dense domain \(\mathcal {D}(A)\) in a Hilbert space X, and B, C are self-adjoint operators in X. In this direction, it has been shown that many non-self-adjoint problems in applied mechanics can be solved efficiently (see, e.g., [2–6]).

Over the past decade, the spectral problems of Hamiltonian operator matrices have been extensively considered in the literature [7–14]. But the completeness of the eigenvector or the root vector system [9, 10, 15] has not been completely understood.

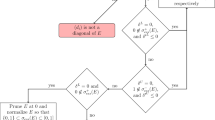
In this note, for the Hamiltonian operator matrix H, defined in (1.1), with at least one invertible off-diagonal entry, we consider its eigenvalue problem including the ascent, the algebraic multiplicity and the completeness. To be precise, we introduce the discriminant \(\Delta_{k} \) (\(k\in\Lambda\)) dependent on the first component of the eigenvectors of H. According to whether \(\Delta_{k}\) is equal to zero or not, we prove under certain assumptions that the algebraic multiplicity of every eigenvalue is 1 and the eigenvector system is complete in the CPV sense if \(\Delta _{k}\neq0\) for all \(k\in\Lambda\), and that the algebraic multiplicity of the eigenvalue is 2 and the root vector system is complete in the CPV sense if \(\Delta_{k_{0}}= 0\) for some \(k_{0}\in\Lambda\). We should mention the following: the assumption (3.4) in Section 3 does not necessarily hold for the whole domain of the involved operator, but only for the first component of the eigenvectors of H.

2 Preliminaries

Let \(\lambda\in\mathbb{C}\). For an operator T, we define \(N(T-\lambda)^{k}=\{x\in\mathcal{D}(T^{k})\mid (T-\lambda)^{k} x=0\}\). Recall that the smallest integer α such that \(N(T-\lambda)^{\alpha}=N(T-\lambda)^{\alpha+1}\) is called the ascent of λ and \(\operatorname{dim} N(T-\lambda)^{\alpha}\) is called the algebraic multiplicity of λ, which are denoted by \(\alpha(\lambda)\) and \(m_{a}(\lambda)\), respectively. The geometric multiplicity of λ is equal to \(\operatorname{dim} N(T-\lambda)\) and is at most the algebraic multiplicity. These two multiplicities are equal if T is self-adjoint. Note that the eigenvalue λ is called simple if the geometric multiplicity of λ is 1. We start with two basic concepts below.

Definition 2.1

[16]

Let T be a linear operator in a Banach space, and let u be an eigenvector of T associated with the eigenvalue λ. If

$$ Tu^{j}-\lambda u^{j} = u^{j-1},\quad j=1,2, \ldots,r,\qquad u^{0}=u, $$
(2.1)

then the vectors \(u^{1},\ldots, u^{r}\) are called the root vectors associated with the pair \((\lambda ,u)\), and \(\{u,u^{1},\ldots, u^{r} \}\) is called the Jordan chain associated with the pair \((\lambda ,u)\). Note that each \(u^{j}\) is called the jth order root vector associated with the pair \((\lambda ,u)\). The collection of all eigenvectors and root vectors of T is called its root vector system.

Definition 2.2

The symplectic orthogonal vector system \(\{u_{k},v_{k}\mid k\in\Lambda\}\) is said to be complete in the CPV sense in \(X\times X\), if for each \((f\ \ g)^{T}\in X\times X\), there exists a unique constant sequence \(\{c_{k},d_{k}\mid k\in\Lambda\}\) such that

$$ \left ( \begin{array}{@{}c@{}} f\\ g \end{array} \right )=\sum _{k\in\Lambda}c_{k}u_{k}+d_{k}v_{k}, $$

where Λ is an at most countable index set such as \(\{ 1, 2,\ldots\}\), \(\{ \pm 1, \pm2,\ldots\}\) and \(\{0, \pm1, \pm2,\ldots\}\). In general, the above formula is also called the symplectic Fourier expansion of \((f\ \ g)^{T}\) in terms of \(\{u_{k},v_{k}\mid k\in\Lambda\}\).

In the following, we review an important property of the Hamiltonian operator matrix H, and its proof may be found in [15].

Lemma 2.1

Let λ and μ be the eigenvalues of the Hamiltonian operator matrix H, and let the associated eigenvectors be \(u^{0}=(x^{0}\ \ y^{0})^{T}\) and \(v^{0}=(f^{0}\ \ g^{0})^{T}\), respectively. Assume that \(u^{1}=(x^{1}\ \ y^{1})^{T}\) and \(v^{1}=(f^{1}\ \ g^{1})^{T}\) are the first order root vectors associated with the pairs \((\lambda ,u^{0})\) and \((\mu,v^{0})\), respectively. If \(\lambda+\overline{\mu}\neq0\), then \(( u^{0},Jv^{0})=0\), \(( u^{0},Jv^{1})=0\), and \(( u^{1},Jv^{1})=0\), where

$$J=\left ( \begin{array}{@{}c@{\quad}c@{}} 0 & I\\ -I & 0 \end{array} \right ) $$

with I being the identity operator on X.

To prove the main results of this paper, we also need the following auxiliary lemma (see [17]).

Lemma 2.2

Let T be a linear operator in a Banach space. If \(\dim N(T)<\infty\), then \(\dim N(T^{k})\leq k \dim N(T)\) for \(k=1,2,\ldots\) .

3 Ascent and algebraic multiplicity

In this section, we present the results on the ascent and the algebraic multiplicity of the eigenvalues of the Hamiltonian operator matrix H and their proofs.

Theorem 3.1

Let ν be an eigenvalue of the Hamiltonian operator matrix H with invertible B, and let \((x\ \ y)^{T}\) be an associated eigenvector. If \((B^{-1}x, x)\neq0\), then \(y=\nu B^{-1}x-B^{-1}Ax\), and

$$ \nu=\frac{\operatorname{Im}(B^{-1}Ax, x)i+\sqrt{-(\operatorname{Im}(B^{-1}Ax, x))^{2} +(B^{-1}x,x)((Cx, x)+(B^{-1}Ax, Ax))}}{(B^{-1}x, x)} $$
(3.1)

or

$$ \nu=\frac{\operatorname{Im}(B^{-1}Ax,x)i-\sqrt{-(\operatorname{Im}(B^{-1}Ax, x))^{2} +(B^{-1}x,x)((Cx, x)+(B^{-1}Ax, Ax))}}{(B^{-1}x, x)}. $$
(3.2)

Proof

Since \((x\ \ y)^{T}\) is an eigenvector of H associated with the eigenvalue ν, we obtain

$$\begin{aligned} \left \{ \begin{array}{@{}l} A x+B y =\nu x, \\ C x-A^{*} y =\nu y. \end{array} \right . \end{aligned}$$
(3.3)

By the invertibility of B, the first relation of (3.3) implies \(y=\nu B^{-1}x-B^{-1}Ax\), and inserting it into the second relation yields

$$\begin{aligned} \nu^{2} B^{-1}x- \nu B^{-1}Ax+A^{*} \bigl(\nu B^{-1}x-B^{-1}Ax \bigr)-Cx=0. \end{aligned}$$

Taking the inner product of the above relation by x on the right, we have

$$\nu^{2} \bigl(B^{-1}x, x \bigr)- \nu \bigl( \bigl(B^{-1}Ax, x \bigr)- \bigl(B^{-1}x, Ax \bigr) \bigr)-(Cx, x)- \bigl(B^{-1}Ax,Ax \bigr)=0. $$

This together with the self-adjointness of B and \((B^{-1}x, x)\neq0\) demonstrates that (3.1) and (3.2) are valid. □

Write ν given by (3.1) and (3.2) as λ and μ, respectively. Then \(\lambda=a(x)i+b(x)\) and \(\mu=a(x)i-b(x)\), where \(a(x)=\frac{\operatorname{Im}(B^{-1}Ax, x)}{(B^{-1}x,x)}\), \(b(x)=\frac{\sqrt{\Delta(x)}}{(B^{-1}x, x)}\), and the discriminant

$$\Delta(x)=- \bigl(\operatorname{Im} \bigl(B^{-1}Ax,x \bigr) \bigr)^{2}+ \bigl(B^{-1}x,x \bigr) \bigl((Cx,x) + \bigl(B^{-1}Ax,Ax \bigr) \bigr). $$

Note that the self-adjointness of B and C implies \(\Delta(x)\in\mathbb{R}\), thus, the principal square root \(\sqrt{\Delta(x)}\in\mathbb{R}\) of \(\Delta(x)\) if \(\Delta(x)\geq0\) and \(\sqrt{\Delta(x)}=i\sqrt{-\Delta(x)}\in\{z \mid z=ir, r \in\mathbb{R}\}\) if \(\Delta(x)< 0 \).

Theorem 3.2

Let λ be an eigenvalue of the Hamiltonian operator matrix H with invertible B, and let \(u=(x\ \ y)^{T}\) be an associated eigenvector. If \((B^{-1}x, x)\neq0\), then the following statements hold.

  1. (i)

    If \(\Delta(x)\neq0\), then \(v=(x\ \ \mu B^{-1}x-B^{-1}Ax)^{T}\) is an eigenvector of H associated with the eigenvalue μ.

  2. (ii)

    If \(\Delta(x)= 0\) and

    $$ A^{*}B^{-1}x-B^{-1}Ax+2\lambda B^{-1}x=0, $$
    (3.4)

    then \(\mu=\lambda=a(x)i\), and there exists a vector \(v=(x\ \ \lambda B^{-1}x-B^{-1}Ax+B^{-1}x)^{T} \) such that \(Hv=\lambda v+u\), i.e., v is the first order root vector of H associated with the pair \((\lambda , u)\).

Proof

(i) Let \(\Delta(x)\neq0\). By Theorem 3.1, if λ is an eigenvalue of H, then μ is also an eigenvalue of H, and \(v=(x\ \ \mu B^{-1}x-B^{-1}Ax)^{T}\) is an eigenvector of H associated with the eigenvalue μ.

(ii) The assumption \(\Delta(x)= 0\) clearly implies \(\mu=\lambda=a(x)i\). By Theorem 3.1, we have \(y=\lambda B^{-1}x-B^{-1}Ax\), and hence

$$\begin{aligned} \lambda^{2} B^{-1}x- \lambda B^{-1}Ax+A^{*} \bigl(\lambda B^{-1}x-B^{-1}Ax \bigr)-Cx=0. \end{aligned}$$
(3.5)

To prove the assertion, it suffices to verify that

$$\begin{aligned} &H\left ( \begin{array}{@{}c@{}} x \\ \lambda B^{-1}x-B^{-1}Ax+B^{-1}x \end{array} \right ) -\lambda \left ( \begin{array}{@{}c@{}} x \\ \lambda B^{-1}x-B^{-1}Ax+B^{-1}x \end{array} \right )- \left ( \begin{array}{@{}c@{}} x \\ \lambda B^{-1}x-B^{-1}Ax \end{array} \right )=0, \end{aligned}$$

which immediately follows from (3.4) and (3.5). □

Remark 1

The assumption (3.4) is a natural hypothesis and aims to guarantee the existence of the first order root vector of H associated with the pair \((\lambda , u)\). In fact, if \(\lambda B^{-1}- B^{-1}A \) is self-adjoint, then (3.4) is obviously fulfilled. However, the self-adjointness of the operator is not necessary (see Example 5.2).

Theorem 3.2 reflects the location of eigenvalues of the Hamiltonian operator matrix H, i.e., they appear in the pair \((\lambda , \mu)\) of complex numbers. So, we have the results below.

Corollary 3.3

Let H be a Hamiltonian operator matrix with invertible B. If the first component x of every eigenvector of H satisfies \((B^{-1}x, x)\neq0\), then λ and μ appear pairwise. Moreover, if H only possesses at most countable eigenvalues, then we may set \(\{\lambda_{k},\mu_{k} \mid k\in\Lambda\}\), where

$$\begin{aligned}& \lambda_{k}=a_{k} i+b_{k}, \qquad \mu_{k}=a_{k} i-b_{k}, \\& a_{k}=a(x_{k})=\frac{\operatorname{Im}(B^{-1}Ax_{k}, x_{k})}{(B^{-1}x_{k}, x_{k})}, \qquad b_{k}=b(x_{k})=\frac{\sqrt{\Delta_{k}}}{(B^{-1}x_{k}, x_{k})},\quad \Delta_{k}= \Delta(x_{k}), \end{aligned}$$

Λ is an at most countable index set, and \(x_{k}\) is the first component of the eigenvector of H associated with the eigenvalue \(\lambda _{k}\) (or \(\mu_{k}\)).

The following theorem is the main result in this section, which gives the ascent and the algebraic multiplicity of the eigenvalues of the Hamiltonian operator matrix H.

Theorem 3.4

Let λ be a simple eigenvalue of the Hamiltonian operator matrix H with invertible B, and let \(u=(x\ \ y)^{T}\) be an associated eigenvector. If \((B^{-1}x, x)\neq0\), then we have:

  1. (i)

    if \(\Delta(x)\neq0\), then \(\alpha(\lambda)=\alpha(\mu)=1\), and hence \(m_{a}(\lambda)=m_{a}(\mu)=1\);

  2. (ii)

    if \(\Delta(x)= 0\) and (3.4) holds, then \(\alpha(\lambda)=2\), and hence \(m_{a}(\lambda)=2\).

Proof

(i) If λ is simple, then μ is also simple. By Theorem 3.2, their eigenvectors are \(u=(x\ \ \lambda B^{-1}x-B^{-1}Ax)^{T}\) and \(v=(x\ \ \mu B^{-1}x-B^{-1}Ax)^{T}\), respectively. Thus, we can obtain

$$ A^{*}B^{-1}x-B^{-1}Ax+2a(x)iB^{-1}x=0. $$
(3.6)

In the following, we only prove the results for λ, and the proof for μ is similar.

Assume \(\alpha(\lambda)\neq1\), then H has the first order root vector \(u^{1}=(x^{1}\ \ y^{1})^{T}\) associated with the pair \((\lambda ,u)\), i.e.,

$$\begin{aligned} \left \{ \begin{array}{@{}l} A x^{1}+B y^{1} =\lambda x^{1}+x, \\ C x^{1}-A^{*} y^{1} =\lambda y^{1}+\lambda B^{-1}x-B^{-1}Ax. \end{array} \right . \end{aligned}$$
(3.7)

From the first relation of (3.7), we have \(y^{1}=\lambda B^{-1}x^{1}-B^{-1}Ax^{1}+B^{-1}x\), and inserting it into the second equation yields

$$\lambda^{2} B^{-1}x^{1} - \lambda B^{-1}Ax^{1} + A^{*} \bigl(\lambda B^{-1}x^{1} - B^{-1}Ax^{1} + B^{-1}x \bigr)-Cx^{1} + 2\lambda B^{-1}x - B^{-1}Ax=0. $$

Taking the inner product of the above relation by x, we obtain

$$\begin{aligned} &\lambda^{2} \bigl(B^{-1}x^{1}, x \bigr)- \lambda \bigl( \bigl(B^{-1}Ax^{1}, x \bigr)- \bigl(B^{-1}x^{1}, Ax \bigr) \bigr)- \bigl(Cx^{1}, x \bigr)- \bigl(B^{-1}Ax^{1},Ax \bigr) \\ &\quad{}+2\lambda \bigl(B^{-1}x,x \bigr)- \bigl(B^{-1}Ax,x \bigr) + \bigl(B^{-1}x,Ax \bigr)=0. \end{aligned}$$

Since B is an invertible self-adjoint operator, \((B^{-1}A)^{*}=A^{*}B^{-1}\), which together with the self-adjointness of C deduces

$$\begin{aligned} &\lambda^{2} \bigl(x^{1}, B^{-1}x \bigr)- \lambda \bigl( \bigl(x^{1},A^{*}B^{-1}x \bigr)- \bigl(x^{1}, B^{-1}Ax \bigr) \bigr)- \bigl(x^{1}, Cx \bigr)- \bigl(B^{-1}Ax^{1},Ax \bigr) \\ &\quad{}+2\lambda \bigl(x,B^{-1}x \bigr)- \bigl(x,A^{*}B^{-1}x \bigr) + \bigl(x,B^{-1}Ax \bigr)=0, \end{aligned}$$

i.e.,

$$\begin{aligned} & \bigl(x^{1}, \overline{\lambda}^{2}B^{-1}x- \overline{\lambda} \bigl(A^{*}B^{-1}x- B^{-1}Ax \bigr)-Cx \bigr) - \bigl(B^{-1}Ax^{1},Ax \bigr) \\ &\quad{}+ \bigl(x,2\overline{\lambda}B^{-1}x-A^{*}B^{-1}x+B^{-1}Ax \bigr)=0. \end{aligned}$$
(3.8)

Thus, by (3.6) and (3.5), (3.8) is reduced to

$$\begin{aligned} \bigl(x^{1}, (\overline{\lambda}+\lambda) \bigl(( \overline{\lambda}-\lambda)B^{-1}x-A^{*}B^{-1}x+ B^{-1}Ax \bigr) \bigr)+2b(x) \bigl(x,B^{-1}x \bigr)=0. \end{aligned}$$
(3.9)

If \(\Delta(x)> 0\), then \(\overline{\lambda}-\lambda=-2a(x)i\), and hence \((\overline{\lambda}-\lambda)B^{-1}x-A^{*}B^{-1}x+ B^{-1}Ax=0\) by (3.6); if \(\Delta(x)< 0\), then \(\overline{\lambda}+\lambda=0\). To sum up,

$$(\overline{\lambda}+\lambda) \bigl((\overline{\lambda}-\lambda)B^{-1}x-A^{*}B^{-1}x+ B^{-1}Ax \bigr)=0 $$

when \(\Delta(x)\neq 0\). From (3.9), it follows that

$$2b(x) \bigl(x,B^{-1}x \bigr)=0, $$

which is a contradiction since \(\Delta(x)\neq0\) and \((x,B^{-1}x)\neq0\). Therefore, \(\alpha(\lambda)=1\). Since λ is simple, we immediately have \(m_{a}(\lambda)=1\).

(ii) By Theorem 3.2, we have \(N(H-\lambda)\subsetneqq N(H-\lambda)^{2}\), and then \(\alpha(\lambda)\geq2\). Assume \(N(H-\lambda)^{2}\subsetneqq N(H-\lambda)^{3}\), then there exists a vector \(u^{2}=(x^{2}\ \ y^{2})^{T}\in N(H-\lambda)^{3}\) such that \(u^{2}\notin N(H-\lambda)^{2}\). Obviously, \(0\neq(H-\lambda)u^{2}\in N(H-\lambda)^{2}\). From Lemma 2.2, it follows that \(\operatorname{dim}N(H-\lambda)^{2}=2\). So, \(N(H-\lambda)^{2}=\operatorname{span}\{u,u^{1}\}\), where \(u^{1}=(x \ \ \lambda B^{-1}x-B^{-1}Ax+B^{-1}x)^{T}\) is the first order root vector associated with the pair \((\lambda ,u)\). Let \((H-\lambda)u^{2}=l_{0}u+l_{1}u^{1}\), i.e.,

$$\left \{ \begin{array}{@{}l} A x^{2} + B y^{2} =\lambda x^{2}+(l_{0} + l_{1})x, \\ C x^{2} - A^{*} y^{2} =\lambda y^{2}+(l_{0} + l_{1})(\lambda B^{-1}x - B^{-1} Ax)+l_{1} B^{-1}x, \end{array} \right . $$

where \(l_{0},l_{1}\in\mathbb{C}\) and \(l_{1}\neq0\). Thus, \(y^{2}=\lambda B^{-1}x^{2}-B^{-1}Ax^{2}+(l_{0}+l_{1})B^{-1}x\) and

$$\begin{aligned} &\lambda^{2} B^{-1}x^{2}- \lambda B^{-1}Ax^{2}+A^{*} \bigl(\lambda B^{-1}x^{2}-B^{-1}Ax^{2}+(l_{0}+l_{1})B^{-1}x \bigr) -Cx^{2} \\ &\quad{}+(l_{0}+l_{1}) \bigl(2\lambda B^{-1}x-B^{-1}Ax \bigr)+l_{1}B^{-1}x=0. \end{aligned}$$

In view of \(\overline{\lambda}=-\lambda=-a(x)i\), taking the inner product of the above relation by x, we may have \((B^{-1}x,x)=0\), which contradicts the assumption \((B^{-1}x,x)\neq0\). Therefore, \(N(H-\lambda)\subsetneqq N(H-\lambda)^{2}=N(H-\lambda)^{3}\), i.e., \(\alpha(\lambda)=2\), which together with \(\operatorname{dim}N(H-\lambda)^{2}=2\) implies \(m_{a}(\lambda)=2\). □

Remark 2

If H is a compact operator, then \(\dim N(H-\lambda )<\infty\) for \(\lambda \neq0\). In the present article, we only consider the case that λ is a simple eigenvalue of H, i.e., \(\dim N(H-\lambda )=1\), and other cases need to be considered separately.

4 Completeness

In this section, the completeness of the eigenvector or root vector system of the Hamiltonian operator matrix H is given.

Theorem 4.1

Let H be a Hamiltonian operator matrix with invertible B, and let it only possess at most countable simple eigenvalues. Assume that the first component x of every eigenvector of H satisfies \((B^{-1}x, x)\neq0\) and \(\mathcal{D}(B)\subseteq\mathcal{D}(A^{*})\) (or \((A^{*}B^{-1}x, \widetilde{x})=0\) where x, \(\widetilde{x}\) are the, linear independent, first components of the eigenvectors associated with different eigenvalues of H). If \(\Delta(x)\neq 0\) for every x, then the eigenvector system of H is complete in the CPV sense in \(X\times X\) if and only if the collection of the first components of the eigenvector system of H is a Schauder basis in X.

Proof

By Corollary 3.3, the collection of all eigenvalues of H can be given by \(\{\lambda_{k},\mu_{k} \mid k\in\Lambda\}\). From the assumptions, \(\Delta_{k} \neq0\) immediately implies that \(b_{k}\neq0\) and \(\lambda_{k}\neq\mu_{k}\). According to Theorem 3.2, the eigenvectors associated with the eigenvalue \(\lambda_{k}\) and \(\mu_{k}\) are given by

$$ u_{k}=\left ( \begin{array}{@{}c@{}} x_{k} \\ \lambda_{k} B^{-1}x_{k}-B^{-1}Ax_{k} \end{array} \right ), \qquad v_{k}=\left ( \begin{array}{@{}c@{}} x_{k} \\ \mu_{k} B^{-1}x_{k}-B^{-1}Ax_{k} \end{array} \right ), $$

respectively. In addition, Theorem 3.4 shows that the algebraic multiplicity of every eigenvalue is 1. Thus, \(\{u_{k}, v_{k} \mid k\in\Lambda\}\) is an eigenvector system of H, and H has no root vectors.

Sufficiency. Since \(\Delta_{k} \in\mathbb{R}\), there are three cases to consider.

Case 1: \(\Delta_{k} > 0\) for each \(k\in\Lambda\). In this case, for each \(k,j\in\Lambda\),

$$ \lambda_{k}+\overline{\lambda}_{j}\neq0,\qquad \mu_{k}+\overline{\mu}_{j}\neq 0,\qquad \lambda_{k}+ \overline{\mu}_{j} \left \{ \begin{array}{@{}l@{\quad}l} = 0,& k=j,\\ \neq0, & k\neq j. \end{array} \right . $$
(4.1)

Then, by Lemma 2.1, we have

$$ \left \{ \begin{array}{@{}l} (u_{k},Ju_{j})=(\overline{\lambda}_{j}-\lambda _{k})(B^{-1}x_{k},x_{j})+(B^{-1}Ax_{k},x_{j})-(x_{k},B^{-1}Ax_{j})=0,\\ (v_{k},Jv_{j})=(\overline{\mu}_{j}-\mu _{k})(B^{-1}x_{k},x_{j})+(B^{-1}Ax_{k},x_{j})-(x_{k},B^{-1}Ax_{j})=0, \end{array} \right . $$

and hence

$$ (b_{j}-b_{k}) \bigl(B^{-1}x_{k},x_{j} \bigr)=0. $$
(4.2)

From (3.6) and (4.1), we obtain

$$\begin{aligned} \left \{ \begin{array}{@{}l} (u_{k},Jv_{j})= (\overline{\mu}_{j}-\lambda_{k})(B^{-1}x_{k},x_{j})+(B^{-1}Ax_{k},x_{j})-(x_{k},B^{-1}Ax_{j}) = \scriptsize{ \left \{ \begin{array}{@{}l@{\quad}l} -2\sqrt{\Delta_{k}}, & k=j, \\ 0, & k\neq j, \end{array} \right .} \\ (v_{k},Ju_{j})= (\overline{\lambda}_{j}- \mu_{k}) \bigl(B^{-1}x_{k},x_{j} \bigr)+ \bigl(B^{-1}Ax_{k},x_{j} \bigr)- \bigl(x_{k},B^{-1}Ax_{j} \bigr) = \scriptsize{ \left \{ \begin{array}{@{}l@{\quad}l} 2\sqrt{\Delta_{k}}, & k=j, \\ 0, & k\neq j. \end{array} \right .} \end{array} \right . \end{aligned}$$

Thus,

$$(b_{j}+b_{k}) \bigl(B^{-1}x_{k},x_{j} \bigr)=0,\quad k\neq j, $$

which together with (4.2) and \(b_{k}\neq0 \) (\(k\in\Lambda\)) yields

$$ \bigl(B^{-1}x_{k},x_{j} \bigr)=0,\quad k \neq j. $$
(4.3)

In what follows, we will prove the completeness of the eigenvector system \(\{u_{k},v_{ k} \mid k\in\Lambda\}\) of H in the CPV sense. For each \((f\ \ g)^{T}\in X\times X\), set

$$ c_{k}= \frac{\bigl( \bigl({\scriptsize\begin{matrix} f \cr g \end{matrix}}\bigr), Jv_{k} \bigr)}{ (u_{k},Jv_{k})},\qquad d_{k}= \frac{\bigl( \bigl( {\scriptsize\begin{matrix} f\cr g \end{matrix}}\bigr), J{u}_{k} \bigr)}{ (v_{k},J{u}_{k})}, \quad k\in\Lambda. $$
(4.4)

Then we see that

$$\begin{aligned} & \sum_{k\in\Lambda}c_{k}u_{k}+d_{k}v_{k} \\ &\quad= \sum_{k\in\Lambda} \left ( \begin{array}{@{}c@{}} \frac{(f,B^{-1}x_{k})}{(B^{-1}x_{k},x_{k})}x_{k}\\ \frac{(g,x_{k})}{(B^{-1}x_{k},x_{k})}B^{-1}x_{k}+ \frac{(f,B^{-1}Ax_{k})}{(B^{-1}x_{k},x_{k})}B^{-1}x_{k} -\frac{(f,B^{-1}x_{k})}{(B^{-1}x_{k},x_{k})}A^{*}B^{-1}x_{k} \end{array} \right ). \end{aligned}$$
(4.5)

Since the vector system \(\{x_{k}\mid k\in\Lambda\}\) consisting of the first components of the eigenvectors of H is a Schauder basis in X, there exists a unique sequence \(\{{e_{k}(f)}\mid k\in\Lambda \}\) of complex numbers such that

$$f=\sum_{k\in\Lambda}e_{k}(f) x_{k} $$

for each \(f\in X\). Taking the inner product of the above relation by \(B^{-1}x_{k}\) on the right, we clearly have \(e_{k}(f)=\frac{(f,B^{-1}x_{k})}{(B^{-1}x_{k},x_{k})}\), which shows that the first component of the right hand side of (4.5) is exactly the expression of f in terms of the basis \(\{x_{k}\mid k\in\Lambda\}\), i.e.,

$$ f=\sum_{k\in\Lambda} \frac{(f,B^{-1}x_{k})}{(B^{-1}x_{k},x_{k})}x_{k}. $$
(4.6)

Write

$$\Upsilon=\sum_{k\in\Lambda}\frac{(f,B^{-1}Ax_{k})}{(B^{-1}x_{k},x_{k})}B^{-1}x_{k} -\frac{(f,B^{-1}x_{k})}{(B^{-1}x_{k},x_{k})}A^{*}B^{-1}x_{k}. $$

If \(\mathcal{D}(B)\subseteq\mathcal{D}(A^{*})\), then \(A^{*}B^{-1}\) is bounded on the whole space X. So,

$$\begin{aligned} A^{*}B^{-1}f = A^{*}B^{-1}\sum _{k\in\Lambda} \frac{(f,B^{-1}x_{k})}{(B^{-1}x_{k},x_{k})}x_{k} = \sum _{k\in\Lambda} \frac{(f,B^{-1}x_{k})}{(B^{-1}x_{k},x_{k})}A^{*}B^{-1}x_{k}. \end{aligned}$$
(4.7)

From \((B^{-1}x_{k},x_{k})\neq0\) and (4.3), it follows that \(\{\frac{B^{-1}x_{k}}{(B^{-1}x_{k},x_{k})}\mid k\in\Lambda\}\) is also a Schauder basis in X, and hence

$$\begin{aligned} A^{*}B^{-1}f=\sum_{k\in\Lambda} \frac {(A^{*}B^{-1}f,x_{k})}{(B^{-1}x_{k},x_{k})}B^{-1}x_{k} =\sum _{k\in\Lambda} \frac{(f,B^{-1}Ax_{k})}{(B^{-1}x_{k},x_{k})}B^{-1}x_{k}. \end{aligned}$$
(4.8)

Hence, \(\Upsilon=0\) by (4.7) and (4.8). If \((A^{*}B^{-1}x, \widetilde{x})=0\), i.e., \((A^{*}B^{-1}x_{k}, x_{j})=0 \) (\(k\neq j\)), then for \(k\neq j\) we have

$$\biggl(\frac{(f,B^{-1}Ax_{k})}{(B^{-1}x_{k},x_{k})} B^{-1}x_{k} -\frac{(f,B^{-1}x_{k})}{(B^{-1}x_{k},x_{k})}A^{*}B^{-1}x_{k}, x_{j} \biggr) = 0,\quad k, j\in\Lambda, $$

and for \(k=j\), we have by (4.6) that

$$\begin{aligned} & \biggl(\frac{(f,B^{-1}Ax_{k})}{(B^{-1}x_{k},x_{k})}B^{-1} x_{k} - \frac{(f,B^{-1}x_{k})}{(B^{-1}x_{k},x_{k})}A^{*}B^{-1}x_{k}, x_{k} \biggr) \\ &\quad= \bigl(f,B^{-1}Ax_{k} \bigr)-\frac{(f,B^{-1}x_{k})}{(B^{-1}x_{k},x_{k})} \bigl(A^{*}B^{-1}x_{k}, x_{k} \bigr) \\ &\quad= \bigl(f,B^{-1}Ax_{k} \bigr)-\frac{(f,B^{-1}x_{k})}{(B^{-1}x_{k},x_{k})} \bigl(x_{k}, B^{-1}Ax_{k} \bigr)=0,\quad k, j\in \Lambda. \end{aligned}$$

Hence, \(\Upsilon=0\) since \(\{x_{k}\mid k\in\Lambda\}\) is a Schauder basis in X. Thus, we have shown so far that

$$ \sum_{k\in\Lambda}c_{k}u_{k} +d_{k}v_{k}=\sum_{k\in\Lambda} \left ( \begin{array}{@{}c@{}} \frac{(f,B^{-1}x_{k})}{(B^{-1}x_{k},x_{k})}x_{k}\\ \frac{(g,x_{k})}{(B^{-1}x_{k},x_{k})}B^{-1}x_{k} \end{array} \right )=\left ( \begin{array}{@{}c@{}} f \\ g \end{array} \right ). $$
(4.9)

Finally, we assume that there is another constant sequence \(\{\hat{c}_{k},\hat{d}_{k}\mid {k\in\Lambda}\}\) such that the expansion (4.9) is valid. Then we have

$$\begin{aligned} \sum_{k\in\Lambda}(c_{k}-\hat{c}_{k})u_{k}+(d_{k}- \hat{d}_{k})v_{k}=0, \end{aligned}$$

which clearly implies that \(c_{k}=\hat{c}_{k}\) and \(d_{k}=\hat{d}_{k}\) (\(k\in\Lambda\)). Thus, the expansion (4.9) is valid if and only if we choose \(c_{k}\), \(d_{k}\) (\(k\in\Lambda\)) defined by (4.4). Therefore, the eigenvector system \(\{u_{k},v_{k}\mid {k\in\Lambda} \}\) of H is complete in the CPV sense.

Case 2:

$$\Delta_{k} \left \{ \begin{array}{@{}l@{\quad}l} > 0, & k\in\Lambda_{1},\\ < 0, & k\in\Lambda_{2}, \end{array} \right . $$

where \(\Lambda=\Lambda_{1}\cup\Lambda_{2}\), \(\Lambda_{1}\neq\emptyset\), and \(\Lambda_{2}\neq\emptyset\). Then we find that

$$\begin{aligned}& \lambda_{k}+\overline{\lambda}_{j} \left \{ \begin{array}{@{}l@{\quad}l} = 0,& k=j\in\Lambda_{2},\\ \neq0, & \mbox{otherwise}, \end{array} \right .\qquad \mu_{k}+\overline{ \mu}_{j} \left \{ \begin{array}{@{}l@{\quad}l} = 0, & k=j\in\Lambda_{2},\\ \neq0, & \mbox{otherwise}, \end{array} \right .\\& \lambda_{k}+\overline{\mu}_{j} \left \{ \begin{array}{@{}l@{\quad}l} = 0, & k=j\in\Lambda_{1},\\ \neq0, & \mbox{otherwise}. \end{array} \right . \end{aligned}$$

Similar to the proof in Case 1, we can also obtain (4.3), and

$$ \left \{ \begin{array}{@{}l} \scriptsize{(u_{k},Ju_{j})= \left \{ \begin{array}{@{}l@{\quad}l} -2\sqrt{\Delta_{k}}, & k=j\in\Lambda_{2},\\ 0, & \mbox{otherwise}, \end{array} \right .} \qquad \scriptsize{(u_{k},Jv_{j})= \left \{ \begin{array}{@{}l@{\quad}l} -2\sqrt{\Delta_{k}}, & k=j \in\Lambda_{1},\\ 0, & \mbox{otherwise}, \end{array} \right .} \\ \scriptsize{(v_{k},Ju_{j})= \left \{ \begin{array}{@{}l@{\quad}l} 2\sqrt{\Delta_{k}}, & k=j \in\Lambda_{1},\\ 0, & \mbox{otherwise}, \end{array} \right .} \qquad \scriptsize{(v_{k},Jv_{j})= \left \{ \begin{array}{@{}l@{\quad}l} 2\sqrt{\Delta_{k}},& k=j \in\Lambda_{2},\\ 0, & \mbox{otherwise}. \end{array} \right .} \end{array} \right . $$

For \((f\ \ g)^{T}\in X\times X\), set

$$ c_{k}= \frac{\bigl( \bigl( {\scriptsize\begin{matrix} f \cr g \end{matrix}} \bigr), J{u}_{k} \bigr)}{ (u_{k},J{u}_{k})},\qquad d_{k}= \frac{\bigl( \bigl( {\scriptsize\begin{matrix} f\cr g \end{matrix}}\bigr), Jv_{k} \bigr)}{ (v_{k},Jv_{k})} $$

for \(k\in\Lambda_{2}\), and set

$$ c_{k}= \frac{\bigl( \bigl( {\scriptsize\begin{matrix} f \cr g \end{matrix}} \bigr), Jv_{k} \bigr)}{ (u_{k},Jv_{k})},\qquad d_{k}= \frac{\bigl( \bigl( {\scriptsize\begin{matrix} f\cr g \end{matrix}} \bigr), J{u}_{k} \bigr)}{ (v_{k},J{u}_{k})} $$

for \(k\in\Lambda_{1}\). Thus, we also have (4.5). The rest of the proof is analogous to that of Case 1.

Case 3: \(\Delta_{k} < 0\) for each \(k\in\Lambda\). Indeed, it suffices to note that

$$ \left \{ \begin{array}{@{}l} \scriptsize{(u_{k},Ju_{j})= \left \{ \begin{array}{@{}l@{\quad}l} -2\sqrt{\Delta_{k}}, & k=j,\\ 0,& k\neq j, \end{array} \right .} \\ \scriptsize{(v_{k},Jv_{j})= \left \{ \begin{array}{@{}l@{\quad}l} 2\sqrt{\Delta_{k}}, & k=j, \\ 0, & k\neq j, \end{array} \right .}\\ (u_{k},Jv_{j})=0, \end{array} \right . $$

and set

$$ c_{k}=\frac{\bigl( \bigl( {\scriptsize\begin{matrix} f \cr g \end{matrix}}\bigr), J{u}_{k} \bigr)}{ (u_{k},J{u}_{k})}, \qquad d_{k}=\frac{\bigl( \bigl( {\scriptsize\begin{matrix} f \cr g \end{matrix}} \bigr), Jv_{k} \bigr)}{ (v_{k},Jv_{k})} $$

for each \((f\ \ g)^{T}\in X\times X\).

Necessity. Assume that the eigenvector system \(\{u_{k},v_{ k} \mid k\in\Lambda\}\) of H is complete in the CPV sense, i.e., there exists a unique constant sequence \(\{c_{k},d_{k}\mid k\in\Lambda\}\) such that the equality (4.9) holds for each \((f\ \ g)^{T}\in X\times X\). In the following, we only consider Case 1 listed in the proof of sufficiency, and the proof of other cases is analogous. Taking the inner product of (4.9) by \(Ju_{k}\) and \(Jv_{k}\) on the right, respectively, we deduce that \(c_{k}\) and \(d_{k}\) (\(k\in\Lambda\)) are determined by (4.4). Thus,

$$f=\sum_{k\in\Lambda}c_{k}x_{k} +d_{k}x_{k}=\sum_{k\in\Lambda} \frac{(f,B^{-1}x_{k})}{(B^{-1}x_{k},x_{k})} x_{k}. $$

Therefore, by the arbitrariness of f, the vector system \(\{x_{k}\mid k\in\Lambda\}\) is a Schauder basis in X. The proof is finished. □

Theorem 4.2

Let H be a Hamiltonian operator matrix with invertible B, and let it only possess at most countable simple eigenvalues. Assume that the first component x of every eigenvector of H satisfies \((B^{-1}x, x)\neq0\) and \(\mathcal {D}(B)\subseteq\mathcal{D}(A^{*})\) (or \((A^{*}B^{-1}x, \widetilde{x})=0\) where x, \(\widetilde{x}\) are the, linear independent, first components of the eigenvectors associated with different eigenvalues of H). If there exists the first component \(\widehat{x}\) of an eigenvector of H associated with some eigenvalue \(\widehat{\lambda }\) such that \(\Delta(\widehat{x})=0\) and (3.4) holds, then the root vector system of H is complete in the CPV sense in \(X\times X\) if and only if the collection of the first components of the root vector system of H is a Schauder basis in X.

Proof

According to Corollary 3.3, we may assume that \(\{\lambda_{k},\mu_{k} \mid k\in\Lambda\}\) is the collection of all eigenvalues of H, where \(\Lambda=\Lambda_{3} \cup\Lambda_{4} \) with \(\Lambda_{3} =\{k\in\Lambda\mid \Delta_{k}=0\}\neq\emptyset\) and \(\Lambda_{4} =\{k\in\Lambda\mid \Delta_{k}\neq0\}\).

For \(k\in\Lambda_{3} \), we have \(\lambda_{k}=\mu_{k}=a_{k}i\). Then, by Theorem 3.2, the eigenvector \(u_{k}\) and the first order root vector \(v_{k}\) of H associated with the eigenvalue \(\lambda_{k}\) and the pair \((\lambda_{k}, u_{k})\) are given by

$$u_{k}=\left ( \begin{array}{@{}c@{}} x_{k} \\ \lambda_{k} B^{-1}x_{k}-B^{-1}Ax_{k} \end{array} \right ),\qquad v_{k}=\left ( \begin{array}{@{}c@{}} x_{k} \\ \lambda_{k} B^{-1}x_{k}-B^{-1}Ax_{k}+B^{-1}x_{k} \end{array} \right ), $$

respectively. By Theorem 3.4(ii), the algebraic multiplicity of the eigenvalue \(\lambda_{k}\) (\(k\in\Lambda_{3}\)) is 2. For \(k\in\Lambda_{4} \), we see that \(\lambda_{k}\neq\mu_{k}\). Then, by Theorem 3.2, the eigenvectors \(u_{k}\) and \(v_{k}\) of H associated with the eigenvalues \(\lambda_{k}\) and \(\mu_{k}\) are expressed as

$$u_{k}=\left ( \begin{array}{@{}c@{}} x_{k} \\ \lambda_{k} B^{-1}x_{k}-B^{-1}Ax_{k} \end{array} \right ),\qquad v_{k}=\left ( \begin{array}{@{}c@{}} x_{k} \\ \mu_{k} B^{-1}x_{k}-B^{-1}Ax_{k} \end{array} \right ), $$

respectively. By Theorem 3.4(i), the algebraic multiplicity of the eigenvalues \(\lambda_{k}\) and \(\mu_{k}\) (\(k\in\Lambda_{4}\)) are both 1. Thus, \(\{u_{k},v_{ k} \mid k\in\Lambda\}\) is a root vector system of the Hamiltonian operator matrix H.

When \(\Lambda_{4} \neq\emptyset\), we only prove the case that \(\Delta_{k}>0\) for \(k\in\Lambda_{4} \). The proof of the other cases can be similarly given. From Lemma 2.1, we have

$$ \left \{ \begin{array}{@{}l} (u_{k},J{u}_{j})=(v_{k},Jv_{j})=0, \quad k,j\in\Lambda,\\ \scriptsize{(u_{k},Jv_{j})= \left \{ \begin{array}{@{}l@{\quad}l} (B^{-1}x_{k},x_{k}), & k=j\in\Lambda_{3} , \\ -2\sqrt{\Delta_{k}}, & k=j\in\Lambda_{4} , \\ 0, & k\neq j, \end{array} \right .} \\ \scriptsize{(v_{k},Ju_{j})= \left \{ \begin{array}{@{}l@{\quad}l} -(B^{-1}x_{k},x_{k}), & k=j\in\Lambda_{3} , \\ 2\sqrt{\Delta_{k}}, & k=j\in\Lambda_{4} , \\ 0, & k\neq j. \end{array} \right .} \end{array} \right . $$

When \(\Lambda_{4} =\emptyset\), we obtain

$$ \left \{ \begin{array}{@{}l} (u_{k},J{u}_{j})=(v_{k},Jv_{j})=0,\\ \scriptsize{(u_{k},Jv_{j})= \left \{ \begin{array}{@{}l@{\quad}l} (B^{-1}x_{k},x_{k}), & k=j\in\Lambda, \\ 0, & k\neq j, \end{array} \right .} \\ \scriptsize{(v_{k},Ju_{j})= \left \{ \begin{array}{@{}l@{\quad}l} -(B^{-1}x_{k},x_{k}), & k=j\in\Lambda, \\ 0, & k\neq j. \end{array} \right . } \end{array} \right . $$

Then we set

$$ c_{k}= \frac{\bigl( \bigl( {\scriptsize\begin{matrix} f \cr g \end{matrix}} \bigr), Jv_{k} \bigr)}{ (u_{k},Jv_{k})},\qquad d_{k}= \frac{\bigl( \bigl( {\scriptsize\begin{matrix} f\cr g \end{matrix}} \bigr), J{u}_{k} \bigr)}{ (v_{k},J{u}_{k})}, \quad k\in\Lambda. $$

The rest of the proof is analogous to that of Case 1 in Theorem 4.1. □

5 Examples

In this section, some examples illustrating results of the previous sections are presented. To streamline the calculations, we work in the infinite-dimensional Hilbert space \(X=L^{2}(0,1)\), which consists of square integrable complex-valued functions on the unit interval (in the Lebesgue sense). Note that \(\mathcal{A}\) stands for the subspace of X consisting of all absolutely continuous functions.

Example 5.1

Let \(A=B=I\). Define the operator C in X by \(Cu=-u''-u\) for \(u\in \mathcal{D}(C)\), where

$$\mathcal{D}(C) = \bigl\{ u \in X\mid u, u' \in \mathcal{A}, u(0) =u(1), u'(0) =u'(1), -u''-u \in X \bigr\} . $$
(5.1)

Consider the Hamiltonian operator matrix given by \(H= \bigl( {\scriptsize\begin{matrix} I & I\cr -\frac{\partial^{2} }{\partial x^{2}}-I & -I \end{matrix}} \bigr)\) with the domain \(\mathcal{D}(C)\times X\).

Direct calculations show that the eigenvalues and associated eigenfunctions of H are given by

$$\begin{aligned}& \lambda_{k}=k\pi, \qquad \mu_{k}=-k\pi, \\& u_{k}=\bigl(\sin{k\pi x} \quad (k\pi-1)\sin{k\pi x}\bigr)^{T}, \qquad v_{k}=\bigl(\sin{k\pi x} \quad {-}(k\pi+1)\sin{k\pi x} \bigr)^{T},\quad k\in\Lambda, \end{aligned}$$

where \(\Lambda=\{ 1,2,\ldots\}\). Thus, the set \(\{x_{k}=\sin{k\pi x}\mid k\in\Lambda\}\) is a collection of the first components of the eigenfunction system \(\{u_{k},v_{ k} \mid k\in\Lambda\}\). Obviously,

$$\bigl(B^{-1}x_{k}, x_{k}\bigr)=(x_{k}, x_{k})\neq0 $$

and \(\mathcal{D}(B)\subseteq\mathcal{D}(A^{*})\). Since \(\Delta_{k}\neq0\) for every \(k\in\Lambda\), using Theorem 3.4, we have \(m_{a}(\lambda_{k})=m_{a}(\mu_{k})=1\). Besides, \(\{x_{k}=\sin{k\pi x}\mid k\in\Lambda\}\) is clearly a Schauder basis by observing that it is an orthogonal basis in X. According to Theorem 4.1, the eigenfunction system of H is complete in the CPV sense in \(X\times X\).

Example 5.2

Consider the boundary value problem

$$\begin{aligned} \left \{ \begin{array}{@{}l} 2u_{xx} + u_{xy}+2u_{yy}=0, \quad 0 < x < 1, 0 < y < h, \\ u(0,y) = u(1,y), \qquad u_{x}(0,y)=u_{x}(1,y), \quad 0\leq y \leq h. \end{array} \right . \end{aligned}$$
(5.2)

Set \(v=-\frac{1}{2}u_{x} - 2u_{y}\). Then we have the infinite-dimensional Hamiltonian system

$$\begin{aligned} \frac{\partial}{\partial y}\left ( \begin{array}{@{}c@{}} u \\ v \end{array} \right ) = \left ( \begin{array}{@{}c@{\quad}c@{}} -\frac{1}{4}\frac{\partial}{\partial x} & -\frac{1}{2}\\ \frac{15}{8}\frac{\partial^{2}}{\partial x^{2}} & -\frac{1}{4}\frac{\partial}{\partial x} \end{array} \right )\left ( \begin{array}{@{}c@{}} u \\ v \end{array} \right ). \end{aligned}$$

For the corresponding Hamiltonian operator matrix H, its entries are given by \(Au=-\frac{1}{4}u'\) for \(u\in\mathcal{D}(A)\), \(B=-\frac {1}{2}I\), and \(Cu=\frac{15}{8}u''\) for \(u\in\mathcal{D}(C)\), where

$$ \begin{aligned} &\mathcal{D}(A) = \bigl\{ u \in X\cap \mathcal{A} \mid u(0) =u(1), {u}' \in X \bigr\} , \\ &\mathcal{D}(C) = \bigl\{ u \in X\mid u, u' \in\mathcal{A}, u(0) =u(1), u'(0) =u'(1), u'' \in X \bigr\} . \end{aligned} $$
(5.3)

Set \(\Lambda=\{0, \pm1,\pm2,\ldots\}\). It is easy to see that \(\lambda _{0}=0\) is an eigenvalue of H and \(u_{0}=(1 \ \ 0)^{T}\) is its associated eigenfunction, and that the non-zero eigenvalues and associated eigenfunctions are given by

$$\begin{aligned}& \lambda_{k}=-\frac{k\pi}{2}i+\frac{\sqrt{15}k\pi}{2}, \qquad \mu_{k}=-\frac{k\pi}{2}i-\frac{\sqrt{15}k\pi}{2}, \\& u_{k}=\bigl( e^{2k\pi ix} \quad {-}\sqrt{15}k\pi e^{2k\pi ix} \bigr)^{T}, \qquad v_{k}= \bigl(e^{2k\pi ix} \quad \sqrt{15}k\pi e^{2k\pi ix}\bigr)^{T},\quad k\in\Lambda \backslash\{0 \}. \end{aligned}$$

Note that \(\Delta_{0}=0\) and \(\Delta_{k}\neq0\) (\(k\neq0\)), so we have \(\alpha(\lambda_{k})=\alpha(\mu_{k})=m_{a}(\lambda_{k})=m_{a}(\mu_{k})=1\) and \(\alpha(\lambda_{0})=m_{a}(\mu_{0})=2\) by Theorem 3.4. Then H has the first order root vector \(v_{0}=(1 \ \ {-}2)^{T}\) associated with the pair \((\lambda _{0},u_{0})\). Clearly, the collection \(\{x_{k}=e^{2k\pi ix}\mid k\in\Lambda\}\) of the first components of the root vector system \(\{u_{k},v_{ k} \mid k\in\Lambda\}\) is a Schauder basis in X. Also, we have

$$\begin{aligned}& \bigl(B^{-1}x_{k}, x_{k}\bigr)=-(x_{k}, x_{k})\neq0, \\& \bigl(A^{*}B^{-1}x_{k}, x_{j}\bigr)=0, \quad k\neq j, \\& A^{*}B^{-1}x_{0}-B^{-1}Ax_{0}+2 \lambda _{0}B^{-1}x_{0}=0. \end{aligned}$$

According to Theorem 4.2, \(\{u_{k},v_{k}\mid k\in\Lambda\}\) is complete in the CPV sense in \(X\times X\).