1 Introduction

A mobile intelligent robot is a useful tool which can lead to the target and at the same time avoid an obstacle when faced with it. Obstacle avoidance means that the robot avoids colliding with obstacles such as fixed objects or moving objects. So when a robot encounters with an obstacle, it must decide to avoid it and at the same time, consider the most efficient path to the target with a good decision; this decision is performed in this research using the state-dependent Riccati equation (SDRE) control method. The optimal control of nonlinear systems cannot be done similar to the methods of linear systems. One of the significant viewpoints for optimal control of nonlinear systems is using the SDRE. This method in addition to stability creates a proper functioning and robust for a wide range of nonlinear systems. Nonlinear optimal controller SDRE is a developed linear optimal control LQR, in which equations Riccati is state-dependent. Strategy SDRE has been introduced in the past decade. This strategy is a very effective algorithm for feedback nonlinear analysis that its states are nonlinear; however, a flexibility idea of through the weight matrix is dependent on the state. This involves factoring (ie, parameterization) of nonlinear dynamics to state vector and produces a value function for the matrix which is dependent on its state.

There are conventional methods of obstacle avoidance such as the path planning method [1], the navigation function method [2], and the optimal regulator [3]. Hence, an SDRE regulator [4, 5] is used for this paper. In recent years, many researchers have investigated the obstacle avoidance problem from different perspectives. SDRE technique developed as a design method, which provides a systematic and effective design of nonlinear controllers, filters, and observers. Because of its versatile features, SDRE is broadly used for different cases [6,7,8,9,10,11,12,13,14]. SDRE can also be used in the field of medicine, for example, in [15, 16] the presentation of the optimal chemotherapy protocol for cancer treatment, considering the metastasis, has used the full optimal SDRE feedback. In [17], the SDRE algorithm is studied on motion design of the cable-suspended robot with uncertainties and moving obstacles. A method for controlling the tracing of a robot has been developed by the SDRE. Vibration control of flexible-link manipulator in [18] is used in SDRE controller and Kalman filtering. The problem of estimating flexural states during the use of the SDRE for flexible control is the focus of this paper. Wanga et al. [19] present a novel H2 − H∞SDRE control approach with the purpose of providing a more effective control design framework for continuous-time nonlinear systems to achieve a mixed nonlinear quadratic regulator and H∞control performance criteria.

It should be noted that the algorithms discussed for avoiding an obstacle are different from each other, and each algorithm has proposed a separate and new method for avoiding obstacles. So far, novel methods to avoid obstacles in addition to the mentioned methods are also presented [20,21,22,23].

This paper is organized as follows: a description of the SDRE formulation is given in Section 2. Then, motion equations of the robot and its constraints are presented in Section 3. In Section 4, SDRE formulation of the robot is derived. And simulation results have been reported in Section 5. Finally, in Section 6, some conclusions are drawn from this research.

2 Methods

2.1 Problem formulation

Consider a nonlinear system that is autonomous, full-state observable and input affine that is presented as follows:

$$ \dot{x}(t)=f(x)+B(x)u(t),x(0)={x}_0 $$
(1)

Where x ∈ Rn is the state vector, u ∈ Rm is the input vector, and t ∈ [0, ∞), with functions f : Rn → Rnand B : Rn → Rn × m, and B(x) ≠ 0 ∀ x. Without any loss of generality, the origin is assumed to be an equilibrium point, such that f(0) = 0. In this context, the minimization of the infinite-time performance criterion is as follows:

$$ J\left({x}_0,u(.)\right)=\frac{1}{2}\int \left\{{x}^T(t)Q(x)x(t)+{u}^T(t)R(x)u(t)\right\} dt $$
(2)

Consider the above equation which is non-quadratic in x but quadratic in u. The state and input weighting matrices are assumed state-dependent such that Q : Rn → Rn × n and R : Rn → Rn × m. These design parameters satisfy Q(x) ≥ 0 and R(x) > 0 for all x [24].

2.2 SDRE nonlinear regulator problem

The SDRE methodology uses extended linearization as the key design concept in formulating the nonlinear optimal control problem. The linear control synthesis method for this case is the LQR synthesis method. SDRE feedback control is an “extended linearization control method” that provides a similar approach to the nonlinear regulation problem for the input-affine system (1) with cost functional (2). The nonlinear system of (1) can be rewritten in the linear structure using SDC form:

$$ \dot{x}(t)=A(x)x(t)+B(x)u(t) $$
(3)

SDC form is not unique and should be chosen in such a way that \( \left\{{Q}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}(x),A(x)\right\} \) and {A(x), B(x)} are pointwise observable and pointwise stabilizable, respectively.

Where W(x) is obtained from the solution of algebraic SDRE:

$$ W(x)A(x)+{A}^T(x)W(x)+Q(x)-W(x)B(x){R}^{-1}{B}^T(x)W(x)=0 $$
(4)

to get W(x) ≥ 0.

Where W(x) is the unique, symmetric, positive-definite solution of the algebraic state-dependent Riccati equation. As a result of this, the nonlinear control is obtained as:

$$ u(t)=-{R}^{-1}(x){B}^T(x)W(x)x(t) $$
(5)

The response obtained is locally asymptotically stable and is optimal [25].

2.3 SDRE nonlinear tracking problem

Consider an infinite-time nonlinear tracking problem. Minimize the following nonlinear cost function that is nonquadratic in x but is quadratic in u [26]:

$$ J=\frac{1}{2}{\int}_0^{\infty}\left\{{E}^T(t)Q(x)E(t)+{u}^T(t)R(x)u(t)\right\} dt $$
(6)

in which

$$ E(t)=X(t)-{X}_{desired}(t) $$
(7)

Q, R, x, and uare like the previous model and with the same conditions. By solving the Eq. (6), the input is obtained as the following equation:

$$ u(t)=-{R}^{-1}(x){B}^T(x)W(x)\left(X-{X}_d\right) $$
(8)

3 The four-wheeled car

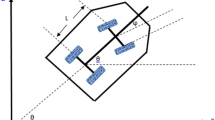
Here is considered a four-wheeled robot with front-wheel drive as Fig. 1. In this robot model, Rtu instantaneous turning radius, L length between the rear axle and the front of the robot, and (x, y) the robot’s position is measured at the center point of the rear wheels of the robot. The state vector consists of two-position variables (x, y), one orientation variable (θ), the speed of the robot (V), and front-wheel drive angle (α). Only the front wheels swivel in two directions, and the rear wheels swivel without slipping. The main reason for choosing this system for this project is the non-holonomic boundary movement of this system [27].

Fig. 1
figure 1

Four-wheeled car model with front-wheel steering

Full size image

Here, (V) and (θ) are considered as input vectors, but using these control inputs, this system is faced with solutions that are not smooth. It is very obvious that in practice mode, the speed of the vehicle’s robot and the wheel angle cannot change quickly and instantaneously. Therefore, to smooth the (V, θ) controls and make it possible to apply inputs to a real robot, a control level is added. In other words, (V, θ) is recorded as part of the state vector and (β, ψ) is added as a new control vector. These changes create smoother paths for (V, θ) that can be used in a real robot. Finally, with regard to all these points, the equation of motion for the robot kinematics derived as follows [27].

$$ \left[\begin{array}{c}\dot{x}\\ {}\dot{y}\\ {}\dot{\alpha}\\ {}\dot{V}\\ {}\dot{\theta}\end{array}\right]=\left[\begin{array}{c}V\cos \alpha \\ {}V\sin \alpha \\ {}\frac{V}{L}\tan \theta \\ {}\beta \\ {}\psi \end{array}\right] $$
(9)

3.1 Vehicle’s constraints

The constraints of the state and control inputs are as follows:

$$ {\displaystyle \begin{array}{l}x\in X=\left\{\begin{array}{c}x:0\le x(t)\le 10\\ {}y:0\le y(t)\le 10\\ {}\alpha :-3\pi \le \alpha \le 3\pi \\ {}V:-30\le V\le +30\\ {}\theta :-1\le \theta \le +1\end{array}\right\}\\ {}u\in U=\left\{\begin{array}{c}\beta :-10\le \alpha (t)\le 10\\ {}\psi :-0.33\le \psi (t)\le 0.33\end{array}\right\}\end{array}} $$
(10)

So far, dynamic equations of the robot and corresponding constraints on states and control input have been presented. In the following section, the proper formulation for utilizing SDRE approach for robot motion control will be presented.

4 Implementation of SDRE controller for the robot

4.1 SDC parameterization

The first step in designing the SDRE controller is to formulate the SDC. The most important point in SDC parameterization is that factorization should provide appropriate control over the entire area. SDC presentation of the system is written as follows [28].

$$ A(x)=\left[\begin{array}{ccccc}0& 0& {\beta}_{13}& {\beta}_{14}& 0\\ {}0& 0& {\beta}_{23}& {\beta}_{24}& 0\\ {}0& 0& 0& {\beta}_{34}& {\beta}_{35}\\ {}0& 0& 0& 0& 0\\ {}0& 0& 0& 0& 0\end{array}\right]B(x)=\left[\begin{array}{cc}0& 0\\ {}0& 0\\ {}0& 0\\ {}1& 0\\ {}0& 1\end{array}\right] $$
(11)
$$ {\displaystyle \begin{array}{l}{\beta}_{13}=\frac{\beta_1V\left(\cos \alpha -1\right)}{\alpha },{\beta}_{14}=\left(1-{\beta}_1\right)\left(\cos \alpha -1\right)+1\\ {}{\beta}_{23}={\beta}_2V\sin c\left(\alpha \right),{\beta}_{24}=\left(1-{\beta}_2\right)\sin \alpha \\ {}{\beta}_{34}=\left(1-{\beta}_3\right)\frac{\tan \theta }{L},{\beta}_{44}={\beta}_3\left(\frac{V}{L}\right)\left(\frac{\tan \theta }{\theta}\right)\end{array}} $$
(12)

4.2 Obstacle avoidance

In this paper, the concept of the APF method and the navigation function [29] is used to avoid collisions with obstacles during the robot’s movement. The navigation function that is similar to the APF, with the help of the sensor, will detect obstacles and avoid them and converge the robot toward the target. This function has the local minimum at the destination and a local maximum at the obstacles.

In the modified model, OBS can be decomposed into obsa and obsb. Where obsa is the component force under the direction along the line between the robot and the obstacle, and obsb is the component force under the direction along the line between the robot and the target. m is a weighting factor that one can set the distance of the robot from an obstacle during movement. By setting mand z, the desired result is achieved which is obstacle avoidance and reach the target. The proposed navigation function added to the cost function is as follows:

$$ \Big\{{\displaystyle \begin{array}{c}{R}_{\mathrm{at}}=\sqrt{{\left(x-{x}_d\right)}^2+{\left(y-{y}_d\right)}^2}\\ {}{R}_{\mathrm{rep}}=\sqrt{{\left(x-{x}_{\mathrm{ob}}\right)}^2+{\left(y-{y}_{\mathrm{ob}}\right)}^2}-{R}_{\mathrm{ob}}\\ {}{\mathrm{ob}\mathrm{s}}_a=m\left(\frac{{R_{\mathrm{at}}}^z}{{R_{\mathrm{rep}}}^2+0.1}\right)\\ {}{\mathrm{ob}\mathrm{s}}_b=\left(\frac{{R_{\mathrm{at}}}^{\left(z-1\right)}}{{R_{\mathrm{rep}}}^2+0.1}\right)\\ {}\mathrm{OBS}={\mathrm{ob}\mathrm{s}}_a+{\mathrm{ob}\mathrm{s}}_b\end{array}} $$
(13)

The form of obstacles is a sphere with center (xob, yob) and radius Rob, and it is supposed that they do not overlap each other. The purpose of this study is to design a control law by which the controlled object avoids obstacles and moves from an arbitrary initial point x0 to the destination point xd. In the next step, this obstacle avoidance equation is added to the cost function. The purpose here is to minimize the performance of the criterion function that is considered as follows:

$$ J=\frac{1}{2}{\int}_0^{\infty}\left\{{E}^T(t)Q(x)E(t)+{u}^T(t)R(x)u(t)+\mathrm{OBS}\right\} dt $$
(14)

Then, using the factoring, the matrix Q(x) is obtained as follows:

$$ {\displaystyle \begin{array}{c}Q(x)=\operatorname{diag}\left(\left[\frac{1}{{E_X}^2}\left(\mathrm{OBS}\right),\frac{1}{{E_Y}^2}\left(\mathrm{OBS}\right),1,1,1\right]\right)\\ {}\Big\{\begin{array}{c}{E}_X=x-{x}_d\\ {}{E}_Y=y-{y}_d\end{array}\end{array}} $$
(15)

EX and EY are errors of position. Q(x) is not a single matrix and many matrices are obtained for it. By using this formulation, the robot can now start from an initial point and reach a destination while avoiding obstacles. The useful property of the obstacle avoidance term in the cost function led to the increase in the cost function while the robot is nearing obstacle and decreasing when leaving it. Figure 2shows mesh plot of obstacle avoidance term in which the function has the global minimum at the destination and a local maximum at the obstacle. By rewriting (15), the second obstacle in the motion planning algorithm can be constructed as follows.

$$ Q(x)=\operatorname{diag}\left(\left[\frac{1}{{E_X}^2}\left({\mathrm{OBS}}_1+{\mathrm{OBS}}_2\right),\frac{1}{{E_Y}^2}\left({\mathrm{OBS}}_1+{\mathrm{OBS}}_2\right),1,1,1\right]\right) $$
(16)
Fig. 2
figure 2

The mesh plot of the obstacle avoidance term for obstacle point (x0, y0) = (−2, 4) and to target point (xd, yd) = (1, 5)

Full size image

5 Results and discussion

In this section, the effectiveness of the proposed method is verified by the simulation model of the robot. The general parameters include all states are as follows:

$$ {\displaystyle \begin{array}{l}{\beta}_1=0.715;{\beta}_2=0.8;{\beta}_3=0.5\\ {}R=\operatorname{diag}\left(\left[1,1\right]\right),L=0.5\end{array}} $$
(17)

Figure 2 shows the mesh plot of the obstacle avoidance term in which the function has the global minimum at the destination and a local maximum at the obstacle. It shows that the obstacles like the summit and the target act like the cavity and absorbs the robot into the inside itself.

In Fig. 3, obstacles have been considered as a circle of radius 0.4 and show that with SDRE method, the robot avoids obstacles and reaches the target with minimal cost. When the robot is faced by an obstacle; Q parameter is designed so that increases the cost function and in other words, finds the highest possible value to avoid colliding with the obstacle. Here, to avoid collision with the obstacle and reach the desired target, the value of m and z in the navigation obsis respectively put 5 and 2.

Fig. 3
figure 3

Path of the robot with the obstacle avoidance term in presence obstacle point (x0, y0) = (−2, 4) and target point (xd, yd) = (1, 5) with SDRE method

Full size image

Figure 4 shows two variables x and y in reaching the target point xd = (1, 5), and these figures show that the robot stops as soon as reaching to the target. Figure 5 shows that other states also regulated to zero after 3.1 s. Figure 6 shows control inputs that are applied to reach the desired target, after reaching the target became zero. The purpose of this control method is to find the control inputs that are applied to the system with Eq. (11); while stabilizing the system and satisfying the constraints defined for it, the defined cost function (16) is minimized, and the system state variables converge to zero with the least control effort. The figures obtained from the simulation show that SDRE method has achieved the desired goals. By comparing this method with the modified APF method, it is observed that this method selects a more optimal route according to the definition of the cost function for avoiding the obstacle and reaching the goal. The other difference is that in SDRE method, three parameters are added: vehicle velocity (V), the angle of the front wheels (α), and length of the car between the front and rear axles (L), to design appropriate control function in order to avoidance obstacles and reach the desired target.

Fig. 4
figure 4

x and y trajectories in presence obstacle point (x0, y0) = (−2, 4) and target point (xd, yd) = (1, 5) while avoiding an obstacle with SDRE method

Full size image
Fig. 5
figure 5

θ, V and φ trajectories in presence obstacle point (x0, y0) = (−2, 4) and target point (xd, yd) = (1, 5) while avoiding an obstacle with SDRE method

Full size image
Fig. 6
figure 6

Control inputs applied to the robot to reach the target point (xd, yd) = (1, 5) and in presence obstacle avoidance point (x0, y0) = (−2, 4) with SDRE method

Full size image

Without taking navigation function and supposing Q(x) = diag[100, 100, 1, 1, 1], Fig. 7 shows that the robot cannot reach the target with obstacle avoidance. Figure 8 of the LQR method in which a nonlinear system is linearized around the vector Xv = [1, 1, 1, 1, 1]Tand initial conditionsXp = [−3,3,0.0001,0.0001,0.0001]T. Figure 9 shows that although the control inputs became zero, as Fig. 8 depicts, the robot cannot avoid obstacles in reaching to the target. Like Fig. 8, in LQR method, with linearization of around none of the operating points and initial conditions, the robot cannot avoid obstacles in reaching to the target, so is concluded, by SDRE method where the matrix Adepends on its states, the answer is better.

Fig. 7
figure 7

Path of the robot without obstacle avoidance term and in presence obstacle point (x0, y0) = (−2, 4) and target point (xd, yd) = (1, 5)

Full size image
Fig. 8
figure 8

Path of the robot to the target point (xd, yd) = (1, 5) in presence obstacle point (x0, y0) = (−2, 4) with LQR method

Full size image
Fig. 9
figure 9

Control inputs applied to the robot to reach the target point (xd, yd) = (1, 5) and in presence obstacle point (x0, y0) = (−2, 4) with LQR method

Full size image

In the second section, the effectiveness of the proposed method is verified by the simulation model of the robot. The general parameters include all states are as follows:

$$ {\displaystyle \begin{array}{l}{\beta}_1=0.1;{\beta}_2=0.78;{\beta}_3=0.88\\ {}R=\operatorname{diag}\left(\left[1,1\right]\right),L=0.5\end{array}} $$
(18)

Figure 10 shows the mesh plot of the obstacle’s avoidance term in which the function has the global minimum at the destination and a local maximum at the obstacle. It shows that the obstacles like the summit and the target act like the cavity and absorbs the robot into the inside itself. Here, to avoid collision with the obstacle and reach the desired target, the value of m and z in the navigation obs is respectively put 0.5 and 2. In the face of obstacles more than an obstacle. The principles of work for other obstacles are like one obstacle, but in this case, a navigation function is put. For example, in Fig. 11, two obstacles have been considered as a circle of radius 0.25 and shows that with SDRE method; the robot avoids obstacles and reaches the target with minimal cost. Figure 12 shows the curve of two variable’s xand y in reaching the target point xd = (2, 5.5), and these figures show that the robot stops as soon as reaching to the target. Figure 13 shows that other states also regulated to zero after 4.2 s. Figure 14 shows control inputs that are applied to reach the desired target, after reaching the target the control attempt becomes zero.

Fig. 10
figure 10

The mesh plot of obstacle’s avoidance term in presence obstacle point’s (x01, y01) = (−1.5, 7.8), (x02, y02) = (0.1, 7) and target point (xd, yd) = (2, 5.5)

Full size image
Fig. 11
figure 11

Path of the robot in presence obstacle points (x01, y01) = (−1.5, 7.8), (x02, y02) = (0.1, 7) and target point (xd, yd) = (2, 5.5) while avoiding obstacles with SDRE method

Full size image
Fig. 12
figure 12

xand ytrajectories in presence obstacle points (x01, y01) = (−1.5, 7.8), (x02, y02) = (0.1, 7) and target point (xd, yd) = (2, 5.5) while avoiding obstacles with SDRE method

Full size image
Fig. 13
figure 13

θ, V and φ trajectories in presence obstacle points (x01, y01) = (−1.5, 7.8), (x02, y02) = (0.1, 7) and target point (xd, yd) = (2, 5.5) while avoiding obstacles with SDRE method

Full size image
Fig. 14
figure 14

Control inputs applied to the robot to reach the target point (xd, yd) = (2, 5.5) in presence obstacle points (x01, y01) = (−1.5, 7.8) and (x02, y02) = (0.1, 7) with SDRE method

Full size image

Without taking navigation function and supposing Q(x) = diag[100, 100, 1, 1, 1], Fig 15 shows that the robot cannot reach the target with obstacle avoidance. Figure 16 of the LQR method in which a nonlinear system is linearized around the vector Xv = [1, 1, 1, 1, 1]Tand initial conditions Xp = [−3,3,0.0001,0.0001,0.0001]T. Figure 17 shows that although the control inputs became zero, as Fig. 16 depicts, the robot cannot avoid obstacles in reaching to the target. Like Fig. 16, in LQR method, with linearization of around none of the operating points and initial conditions, the robot cannot avoid obstacles in reaching to the target, so is concluded, by SDRE method where the matrix Adepends on its states, the answer is better.

Fig. 15
figure 15

Path of the robot without obstacle avoidance term in presence obstacle points (x01, y01) = (−1.5, 7.8), (x02, y02) = (0.1, 7) and target point (xd, yd) = (2, 5.5)

Full size image
Fig. 16
figure 16

Path of the robot to the target point (xd, yd) = (2, 5.5) in presence obstacle points (x01, y01) = (−1.5, 7.8) and (x02, y02) = (0.1, 7) with LQR method

Full size image
Fig. 17
figure 17

Control inputs applied to the robot to reach the target point (xd, yd) = (2, 5.5) and in presence obstacle points (x01, y01) = (−1.5, 7.8) and (x02, y02) = (0.1, 7) with LQR method

Full size image

6 Conclusions

This paper focuses on the SDRE nonlinear regulator for solving the nonlinear optimal control problems. The existence of solutions as well as optimality and stability properties associated with SDRE controllers are the main of this paper. The paper is organized as follows. In Section 2, the formulation of the nonlinear optimal control problem, the concept of extended linearization and the SDRE controller for nonlinear optimal regulation are presented, then the additional degrees of freedom provided by the nonuniqueness of the SDC parameterization is reviewed. The necessary and sufficient conditions on the existence of solutions to the nonlinear optimal control problem, in particular, by SDRE feedback control, are reviewed. A theoretical study on the stability and optimality properties of SDRE feedback controls is pursued. SDRE method is compared with LQR method. It is concluded for that SDRE is a semilinear method, give the best answer than linear methods for nonlinear systems, because the basis of this method is that takes nonlinearity of the system and creates the nonlinear system that its state-dependent coefficient matrix structure has semilinear and minimum nonlinear performance index with semi-quadratic structure. The result is that contrary to controllers like LQR that first, they linearize nonlinear controllers, then the laws are designed for stability that can cause to remove some of the important elements of nonlinear systems that have a key role in system stability. In the method of SDRE, the important elements are not removed from the nonlinear system and as a result, according to the results of the various articles, it is concluded that the system is robust against disturbances and uncertainties and achieves better performance than LQR. Our target in this research is finding an equation control using the method SDRE for routing a robot and avoid collisions with obstacles and path optimization for the robot to reach the target. In the end, the proper suggestion for each robot’s path planning is to create an optimal combination algorithm according to the specific structure of each robot so that each algorithm can be covered the constraints of the other algorithm.