Abstract
Understanding nervous system function requires careful study of transient (non-equilibrium) neural response to rapidly changing, noisy input from the outside world. Such neural response results from dynamic interactions among multiple, heterogeneous brain regions. Realistic modeling of these large networks requires enormous computational resources, especially when high-dimensional parameter spaces are considered. By assuming quasi-steady-state activity, one can neglect the complex temporal dynamics; however, in many cases the quasi-steady-state assumption fails. Here, we develop a new reduction method for a general heterogeneous firing-rate model receiving background correlated noisy inputs that accurately handles highly non-equilibrium statistics and interactions of heterogeneous cells. Our method involves solving an efficient set of nonlinear ODEs, rather than time-consuming Monte Carlo simulations or high-dimensional PDEs, and it captures the entire set of first and second order statistics while allowing significant heterogeneity in all model parameters.
Similar content being viewed by others
1 Introduction
Advances in neural recording technologies have enabled experimentalists to simultaneously measure activity across different regions with cellular resolution [1,2,3,4]. However, it is still a technical challenge to measure the many biophysical parameters that govern this multi-region activity. This challenge is exacerbated by the fact that cortical neurons are heterogeneous (i.e., parameters vary across cells) [5] and have significant trial-to-trial noise [6]. Given these features, computational modeling of neural networks often requires exploration of a high-dimensional parameter space and lengthy, time-consuming Monte Carlo simulations. Thus, efficient methods to simulate [7] or approximate network statistics [8] are needed. Aside from computational benefits, streamlined equations for network activity offer potential benefits for mathematical analysis.
We previously developed a fast approximation method [9] for the complete first and second order statistics of a firing-rate network model based on the Wilson–Cowan model [10], and applied it to the olfactory sensory pathway [11]. However, those methods assumed that the statistics of neural activity are stationary (i.e., in steady state). Many neural systems rely on processing of time-varying, high frequency stimuli. The resulting neural responses are often transient, and a quasi-steady-state (QSS) approximation fails to capture the actual response statistics. For example, in the rodent vibrissa sensory [12], auditory [13,14,15], and electrosensory systems [16], stimuli and responses modulate on the order of a few milliseconds, i.e., much faster than the membrane time constants of neurons. Indeed, there is evidence that coding capabilities strongly depend on the timing of stimuli [17] (e.g., in the olfactory bulb [18,19,20]), further necessitating accurate modeling of time-varying neural activity. Modeling studies show the need to account for time-varying stimuli in calculating spiking statistics [21] and in capturing neural mechanisms such as divisive gain modulation [22]. Mathematical theory to efficiently characterize non-equilibrium heterogeneous spiking statistics is scarce despite the potential to shed light on crucial transient neural responses. Thus, it is clear that accurate modeling of time-varying neural activity would benefit mechanistic investigations of neural processing.
Here we present a method to approximate the non-equilibrium statistics of a general heterogeneous coupled firing-rate model of neural networks receiving background correlated noise, in which we: (i) assume weak coupling; equivalently, that neural activity is pairwise normal, and (ii) account for the entire probability distribution of inputs. The result is a computationally fast method because it requires the user to solve coupled nonlinear ODEs, rather than to simulate and average many realizations of coupled SDEs or numerically solve a high-dimensional PDE. The method performs much better than the related QSS method [9] in several representative examples; our code is freely available (see Availability of data and materials section).
2 Model equations and method
Each cell is modeled by a single activity variable \(x_{j}\), which may represent membrane voltage, calcium concentration, etc., and which evolves according to the following equation:
(see [10]), where \(F_{k}(\cdot )\geq 0\) is a nonlinear function mapping input activity to firing rate or response (often called the F-I curve). All cells receive background noise \(\eta _{j}\) uncorrelated in time but instantaneously correlated across different cells: \(\langle \eta _{j}(t) \rangle = 0\), \(\langle \eta _{j}(t) \eta _{j}(t') \rangle = \delta (t-t')\), and \(\langle \eta _{j}(t) \eta _{k}(t') \rangle = c_{jk} \delta (t-t')\) for \(j\neq k\) with \(c_{jk}\in (-1,1)\). The parameters \({\tilde{\mu }}_{j}\) and \({\tilde{\sigma }}_{j}\) model background noisy input. The parameter \(g_{jk}\) represents coupling strength from the presynaptic kth cell and is a signed quantity; \(g_{jk}<0\) represents inhibitory coupling (Fig. 1(A)).
(A) Schematic of network model. Top: Cells receive background correlated noise \(\xi_{j}(t)=\tilde{\sigma}_{j}\eta_{j}(t)\). Bottom: Network coupling via nonlinear function of activity that we choose to be a sigmoidal function. (B) A network of \(N_{c}=3\) coupled cells with randomly chosen parameters. With fast input \(\mu(t)\) (top-left) relative to the time scale, the actual non-equilibrium statistics (dash curves) are very different from the quasi-steady-state, or QSS (fixed \(\mu(t)\) at time t, solid curves). Upper right shows all three pairs of covariance of firing \(\operatorname {Cov}(\nu _{j},\nu_{k})\) for (\(j\neq k\)); bottom row shows the mean activity \(\mathbb{E}[X_{j}]\) and variance of firing \(\operatorname {Var}(\nu_{j})\). In all Monte Carlo simulations here and throughout the paper, we used 1 million realizations; see Sect. 2.3
We wish to compute all of the first and second order time-varying statistics:
where the angular brackets \(\langle \cdot \rangle \) denotes averaging over realizations.
2.1 Reduction of the Fokker–Planck equation
The corresponding probability density function \(p(\vec{x},t)\) of \(\vec{X}:=(x_{1},\dots ,x_{N_{c}})\), defined as \(p(\vec{x},t) \,d \vec{x}=P(\vec{X(t)}\in (\vec{x}, \vec{x}+dx))\), satisfies the Fokker–Planck equation [23]:
where \(D_{j,k}=c_{jk}\frac{\tilde{\sigma }_{j} \tilde{\sigma }_{k}}{ \tau _{j}\tau _{k}}\) (see Table 1), and the sum with \(D_{j,k}\) is taken over all \(N_{c}\times N_{c}\) pairs of \((j,k)\). For convenience we have defined the probability flux or current, as \(J_{l}(\vec{x},t) :=\frac{1}{\tau _{l}} [-x _{l}+ \tilde{\mu }_{l}+\sum_{k=1}^{N_{c}} g_{lk}F_{k}(x_{k}) ] p(\vec{x},t)\) in the right-most part of Eq. (2). This high-dimensional partial differential equation contains all of the statistics of the system.
2.2 Moment closure methods
One way to tackle high-dimensional systems is through “moment closure” methods, in which state variables are integrated or averaged out, and assumptions on moments used to reduce the number of equations. Such approaches have been used in the physical [24, 25] and life sciences [26,27,28]; see [29] for another type of reduction method for this kind of equation. Here, we propose a closure based on weak coupling, and therefore pairwise Gaussianity in the activity variables.
Without coupling, i.e. \(g_{jk}=0\), the steady-state solution of Eq. (2) is simply a multivariate Gaussian distribution with mean \(\vec{\mu }=[\tilde{\mu }_{1},\dots ,\tilde{\mu }_{N_{c}}]\) and covariance matrix \(\operatorname {Cov}_{j,k}=\frac{c_{jk}}{\tau _{j}+\tau _{k}} \tilde{\sigma }_{j} \tilde{\sigma }_{k}\) in the steady state. This motivates a closure of the system in which we assume X⃗ is Gaussian: i.e. \(X_{j}=\sigma _{j}+Y_{j} \mu _{j}\), where \(Y_{j} \) is a standard normal random variable, with parameters \(\mu _{j}\) and \(\sigma _{j}\) to be determined. We also assume the joint marginal distributions are bivariate Gaussian:
where \(\mathbb{N}\) denotes a bivariate Gaussian distribution, and \(d\widehat{x}_{j,k}\) denotes integrating over all \(N_{c}\) variables except \(x_{j}\) and \(x_{k}\).
Note that the integrated quantity \(\int \frac{\partial p(\vec{x},t)}{ \partial t}\,d\vec{x} = 0\), as any probability distribution must integrate to unity. We multiply Eq. (2) by \(x_{j}\) and integrate the equation over all \(N_{c}\) variables, \(d\vec{x}=dx_{j}\,d\widehat{x}_{j}\) (where again \(d\widehat{x}_{j}=dx_{1}\cdots dx_{j-1}\,dx _{j+1}\cdots dx_{N_{c}}\)):
where \(\frac{d\mu _{j}(t)}{dt} = \frac{\partial }{\partial t} \int x _{j} p(\vec{x},t)\,d\vec{x}\). Consider the first term on the RHS: when \(l\neq j\), we have \(\int \frac{\partial }{\partial x_{l}} J_{l}( \vec{x},t) x_{j}\,dx_{j}\,d\widehat{x}_{j}= \int \frac{\partial }{ \partial x_{l}} J_{l}(\vec{x},t)\,dx_{l} x_{j}\,dx_{j}\,d\widehat{x}_{l, j} =\int J_{l}\vert _{x_{l}=-\infty }^{x_{l}=\infty } x _{j}\,dx_{j}\,d\widehat{x}_{j} = \int 0 x_{j}\,dx_{j}\,d\widehat{x}_{j} = 0\). The last equality comes from no flux at ±∞: \(J_{l} \vert _{x_{l}=-\infty }^{x_{l}=\infty }=0\). A similar calculation applies to the second term, for all \(N_{c}\times N_{c}\) values of \((l_{1},l_{2})\): when \(l_{1}\neq j\) and \(l_{2}\neq j\), first integrate in \(x_{l_{1}}\) and \(x_{l_{2}}\), and then use the fact that there is no density at ±∞: \(p(\vec{x},t) \vert _{x_{l_{1/2}}=-\infty }^{x_{l_{1/2}}=\infty }=0\); when \(l_{1/2}=j\), first integrate in \(x_{j}\), then integrate by parts, using \(\partial _{j} p(\vec{x},t) x_{j}\vert _{x_{j}=-\infty }^{x_{j}=\infty }=0\) and \(\partial _{j} p(\vec{x},t) \vert _{x_{j}=-\infty }^{x_{j}= \infty }=0\). Therefore, Eq. (4) becomes
where we have used the approximation \(\int F_{k}(x_{k})p(\vec{x},t)\,d\vec{x}\approx \mathcal{E}_{1}(k)\) (see Table 1) by assuming the marginal \(x_{k}\) PDF is a normal distribution with mean \(\mu _{k}(t)\) and variance \(\sigma _{k}^{2}(t)\).
To derive a similar equation for the variance \(\sigma _{j}^{2}(t)\), we multiply Eq. (2) by \(x_{j}^{2}\) and again integrate over all variables:
where \(E_{j^{2}}(t)=\int x^{2}_{j} p(\vec{x},t)\,d\vec{x}\), and \(\sigma ^{2}_{j}(t)=E_{j^{2}}(t)- (\mu _{j}(t) )^{2}\).
Following the same type of manipulations and again using the no density condition at ±∞: \(p(\vec{x},t)\vert _{x_{l_{1/2}}=-\infty } ^{x_{l_{1/2}}=\infty }=0\), we get
We now employ our approximation, \(x_{j}=\mu _{j}(t)+y_{j}\sigma _{j}(t)\) where \(y_{j}\) is a standard normal random variable, to close the last term in Eq. (7). We further approximate \(\int y _{j} F_{k}(\mu _{k}(t)+y_{k}\sigma _{k}(t))p(\vec{x},t)\,d\vec{x}\) by assuming the joint marginal distribution of \((x_{j},x_{k})\) is bivariate normal, and use the definition of \(\mathcal{M_{F}}\) in Table 1: \(\int y_{j} F_{k}(\mu _{k}(t)+y_{k} \sigma _{k}(t))p(\vec{x},t)\,d\vec{x} \approx \mathcal{M_{F}}(j,k)\). Therefore, the equation for the second moment is
To derive the analogous equation for the \(\operatorname {Cov}_{j,k}(t)\), the procedure is almost exactly the same except that Eq. (2) is multiplied by \(x_{j} x_{k}\), and two terms from the sum (over probability fluxes \(J_{l}\)) contribute, when \(l=j\) and \(l=k\). The result is
When \(j=k\) in Eq. (9), we recover Eq. (8).
The full set of kinetic equations given by Eq. (5), (8), and (9) form a system of nonlinear coupled ODEs with \(N_{c} + N_{c}(N_{c}+1)/2\) variables. The statistics of the firing rate (i.e. \(\nu _{j} = F_{j}(x_{j})\)) are obtained from a standard change of variables.
If μ̃, σ̃ are constant in time, the system (Eq. (5), (8), (9)) settles to a steady state:
A common approximation to non-equilibrium statistics is to assume that the system immediately equilibrates to the steady-state solution of Eq. (1) at each time point for the time-dependent parameters \(\tilde{\mu }_{j}(t)\), \(\tilde{\sigma }_{j}(t)\), which we call the QSS method. We will find that the QSS method fails to capture meaningful features of network activity with relatively fast input.
2.3 Monte Carlo simulations
In the Results section, we compare our new method with Monte Carlo simulations. For all Monte Carlo simulations (i.e., both the actual non-equilibrium statistics and QSS), we used 1 million (\(1\times 10^{6}\)) realizations at each time point. The shaded error regions in all figures represent 1 standard deviation above and below the mean, which is approximated via the sample standard deviation on 1000 samples of 1000 realizations each: \(S=\sqrt{\frac{1}{999} \sum_{j=1}^{1000} ( X(j)- \overline{X} ) ^{2} }\), where X̅ is the average over 1 million realizations and \(X(j)\) is an average over 1000 realizations.
3 Results
We implement our method for networks of various sizes \(N_{c}\), with two time-varying inputs. We choose F to be a sigmoidal: \(F_{j}(\cdot ) = 0.5(1+\tanh ((x-x_{\mathrm{rev},j})/x_{\mathrm{sp},j}))\in [0,1]\) (arbitrary units, \(x_{\mathrm{rev},j}\) and \(x_{\mathrm{sp},j}\) are parameters). To include heterogeneity, parameters were chosen randomly from the following distributions:
where \(\mathbb{U}\in [0,1]\) is a uniform random variable, and \(\mathbb{N}\) is a normal random variable. The input correlation matrix Cr was generated so to have approximately independent off-diagonal entries as follows: (i) create a matrix A with i.i.d. entries \(\mathbf{A}_{jk}\sim \mathbb{N}(0,0.8^{2})\); (ii) create a diagonal matrix \(\boldsymbol{\varLambda }_{\vec{d_{s}}}\) from the vector \(\vec{d_{s}}\) where \(\vec{d}_{s}(j)=1/ \sqrt{(\mathbf{A}^{T}{\mathbf{A}})_{jj}}\); (iii) set \(\mathbf{Cr} = ( \boldsymbol{\varLambda }_{\vec{d_{s}}}) \mathbf{A}^{T}{\mathbf{A}} ( \boldsymbol{\varLambda }_{\vec{d_{s}}})\). By construction, Cr is symmetric positive semidefinite with 1’s on the diagonal. Finally, the entries of the coupling matrix G are independently chosen: \(\mathbf{G}_{jk} \sim \mathbb{N}(0,v_{l})\) where \(v_{l}=(l/10)^{2}\) with \(l=1\) for Figs. 1–2, and \(l=1,2,3\), or 4 in Figs. 3–4. All entries of G are nonzero (i.e. coupling is all-to-all), with inhibitory, excitatory, and self-coupling cases.
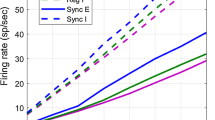
(A) Our method (solid) is very accurate in capturing the results of Monte Carlo (dashed) (cf. Fig. 1(B)) for all first and second order non-equilibrium statistics. (B) With fast sinusoidal input \(\mu(t)\) (left), the actual non-equilibrium statistics (dashed) are very different from QSS (gray curves), but again our method accurately captures the statistics
Applying our method to a larger network of \(N_{c}=50\) neurons. As coupling strength increases (red → green → cyan → purple), performance worsens. (A) The absolute value of the error of our method with the Monte Carlo simulations as a function of time. Each Average Absolute Error time point is averaged over the entire set of statistics (i.e., for the mean and variances the average is over all 50, for covariances the average is over \(1225=49*25\)). (A) Left: the average for the mean activity \(X_{j}\) (solid) and mean firing \(F(X_{j})=\nu_{j}\) (dot-dashed); with the progression of colors (red to purple) representing stronger (i.e., larger) coupling values \(G_{j,k}\). (A) Middle: Error of covariances (thinner lines, \(j\neq k\)) and variances (thicker lines, \(j=k\)) of activity \(X_{j}\). (A) Right: Error of covariances (thinner lines, \(j\neq k\)) and variances (thicker lines, \(j=k\)) of firing \(F(X_{j})=\nu_{j}\). (B) Representative comparisons of our method with the Monte Carlo simulations. (B) Left: although the average error increases with coupling magnitude, the discrepancies are not noticeable for mean activity and firing (not shown). (B) Middle: the method is visibly worse for the variance of activity as coupling magnitude increases. (B) Right: the method is visibly worse as coupling magnitude increases – note that the weakest coupling (red) is between green (second weakest) and purple (strongest)
Applying our method to a larger network of \(N_{c}=50\) neurons. Same format as Fig. 3 except with sinusoidal input (see Fig. 2(B)). (A) Again as coupling strength increases (red → green → cyan → purple), performance worsens. (B) Representative comparisons of our method with the Monte Carlo simulations. (B) Left: although the average error increases with coupling magnitude, the discrepancies are not noticeable for mean activity and firing (not shown). (B) Middle: the method is visibly worse for the variance of activity as coupling magnitude increases. (B) Right: the method is visibly worse as coupling magnitude increases for variance of firing – note that the weakest coupling (red) has largest variance of firing
Figure 1(B) shows that with relatively fast time-varying \(\mu (t)\), a network of \(N_{c}=3\) cells has complex non-equilibrium network statistics that cannot be approximated by the QSS approximation (i.e., assuming the system immediately equilibrates to the steady-state solution for each time point). This is true for the complete set of activity and response statistics, although for brevity only a subset are shown. All parameters are chosen as in Eq. (11) except for \(\mu (t)\), which is the same for all three cells.
Figure 2(A) shows that the time-varying method (Eq. (5), (8), and (9)), when applied to same network as in Fig. 1(B), gives accurate results for the complete set of first/second order statistics. Figure 2(B) shows a detailed comparison of another instance of the \(N_{c}=3\) cell network, but with a time-varying sinusoidal input. Again, the QSS method does not capture the actual network statistics, but our method does very well (colored solid curves). We only show a subset of statistics to illustrate our point; the others are qualitatively similar.
Thus far we have only consider small networks. In Figs. 3 and 4, our methods are applied to a large network of \(N_{c}=50\) coupled cells where the magnitude of the coupling strengths vary: \(\mathbf{G}_{jk}\sim \mathbb{N}(0,\frac{l^{2}}{100})\), for \(l=1,2,3,4\). Figure 3 shows the results with pulse input (Fig. 1(B) upper-left) applied to all 50 cells, while Fig. 4 shows results from applying the sinusoidal input (Fig. 2(B) left) to all 50 cells. Figure 3(A) (top row) shows the error between our method and the actual (Monte Carlo) statistics; we plot the absolute error averaged over all cells or pairs:
i.e., for mean and variance of activity and firing, \(M=50\); for covariance of activity and firing, averaging over all \(M=50*49/2\) distinct pairs. All six sets of statistics are shown in Fig. 3(A): the left panel shows the average absolute error for both mean activity (solid) and mean firing (dot-dashed), middle panel shows the variance (thick solid) and covariance of activity (thin solid), the right panel shows the variance (thick solid) and covariance (thin solid) of firing. In all cases, as the coupling magnitude increases (red → green → cyan → purple), the error increases. For reference, the bottom row (Fig. 3(B)) compares our method with the Monte Carlo simulations for a particular cell (or cell pair); the chosen cell or pair is the one that most closely matches the average absolute error. In Fig. 3(B), we only show three out of the six statistics (left is mean activity, middle is variance of activity, right is variance of firing) because these clearly show the performance of our method in relation to the size of the average absolute error. Figure 4 has exactly the same format as Fig. 3, but with sinusoidal input.
Finally, in Fig. 5, to assess the performance of our method, we plot the absolute value of the error averaged over all six statistics and over all cells/pairs (vertical axis) as a function of a measure of coupling strength l (Fig. 5(A) is with pulse input, (B) with sinusoidal input). Each curve shows a different network size, ranging from \(N_{c}=3, 5, 10, 25, 50\), with a particular instance of randomly chosen parameters for each curve.Footnote 1 The magnitude of the coupling strength, l, on the horizontal axis is from \(\mathbf{G}_{jk}\sim \mathbb{N}(0,\frac{l^{2}}{100})\), so that the average of all \(N_{c}^{2}\) values of \(\vert {\mathbf{G}}_{jk} \vert \) is \(\frac{l}{5\sqrt{2\pi }}\) in the infinite limit \(N_{c}\to \infty \). Not surprisingly, the average error increases as coupling strength increases for each curve. Assessing how much absolute error is acceptable depends on the purposes of the approximation, but for reference, the instances of networks from prior figures are denoted in gray. Figure 5 indicates that, as long as the average absolute error is below 0.01, our method likely performs very well, independent of network size (cf. with Figs. 2–4). Average absolute errors larger than 0.01 might indicate at least some of the statistics calculated by our method are likely to be inaccurate, although others may be accurate depending on cell or pair (cf. Figs. 3–4).
Our method implicitly assumes weak coupling, so as the average magnitude of the coupling strength increases, the performance decreases. We demonstrate this with several instances of coupling matrices and network sizes \(N_{c}=3, 5, 10, 25\), and \(N_{c}=50\) with the four coupling values in Figs. 3 and 4, using the same pulse (A) and sinusoidal (B) inputs. On vertical axis, we plot the average absolute error over all first and second order statistics, including all cells and pairs, while on the horizontal axis, we plot a measure of average magnitude of the coupling values l. Note that, since \(\mathbf{G}_{jk}\sim\mathbb{N}(0,\frac{l ^{2}}{100})\), the average of all \(\vert{\mathbf{G}}_{jk} \vert\) is \(\frac{l}{5\sqrt{2\pi}}\) in the infinite limit \(N_{c}\to\infty\). For reference, some of the points on these curves are from prior figures, denoted in gray text and arrows
4 Conclusion
The role of mathematical theory and computation in addressing neuroscience questions is as vital as ever despite tremendous advances in recording technologies. As detailed in the Introduction, the common assumption of equilibrium neural network responses is inaccurate in many neural systems. Here we derived and implemented a reduction method to calculate the complete set of first and second order non-equilibrium statistics in coupled heterogeneous networks of firing-rate models [10] receiving background correlated noise [30,31,32]. Importantly, our method captures the non-equilibrium statistics when they are vastly different from the quasi-steady-state, and works very well even with significant heterogeneity in all model parameters. As the overall magnitude of the coupling strengths increase, the performance of our method declines because the moment closure method assumes weak coupling.
Mathematical reductions that well approximate the statistics of firing-rate models [33], such as the one described here, are likely to be relevant for future theoretical studies of neural networks for several reasons. Wilson–Cowan type models [10] are commonly used because of their simplicity and history of successful application in neural systems. Analysis of spiking statistics using mean-field methods often results in similar firing-rate equations [34,35,36,37]. Finally, such methods might be useful for mechanistic investigations of neural function across multiple brain regions that commonly rely on larger models with more parameters and complexity [7, 11].
Notes
On each curve, the intrinsic parameters are randomly chosen and fixed as l varies. The same realization of \(\mathbf{G}_{jk}\) is used for each curve, and simply scaled by l to vary the coupling strength.
Abbreviations
- QSS:
-
Quasi-Steady-State
- RHS:
-
Right-hand side
- ODEs:
-
Ordinary differential equations
- PDEs:
-
Partial differential equations
- SDEs:
-
Stochastic differential equations
References
Ahrens MB, Orger MB, Robson DN, Li JM, Keller PJ. Whole-brain functional imaging at cellular resolution using light-sheet microscopy. Nat Methods. 2013;10(5):413–20.
Prevedel R, Yoon Y-G, Hoffmann M, Pak N, Wetzstein G, Kato S, Schrödel T, Raskar R, Zimmer M, Boyden ES, et al.. Simultaneous whole-animal 3d imaging of neuronal activity using light-field microscopy. Nat Methods. 2014;11(7):727–30.
Kandel ER, Markram H, Matthews PM, Yuste R, Koch C. Neuroscience thinks big (and collaboratively). Nat Rev Neurosci. 2013;14(9):659–64.
Lemon WC, Pulver SR, Höckendorf B, McDole K, Branson K, Freeman J, Keller PJ. Whole-central nervous system functional imaging in larval drosophila. Nat Commun. 2015;6:7924.
Marder E. Variability, compensation, and modulation in neurons and circuits. Proc Natl Acad Sci. 2011;108:15542–8.
Cohen MR, Kohn A. Measuring and interpreting neuronal correlations. Nat Neurosci. 2011;14:811–9.
Stringer C, Pachitariu M, Steinmetz NA, Okun M, Bartho P, Harris KD, Sahani M, Lesica NA. Inhibitory control of correlated intrinsic variability in cortical networks. eLife. 2016;5:19695.
Gerstner W, Kistler W. 5. Spiking Neuron Models. Cambridge: Cambridge University Press; 2002. p. 147–163.
Barreiro A, Ly C. Practical approximation method for firing-rate models of coupled neural networks with correlated inputs. Phys Rev E. 2017;96:022413. https://doi.org/10.1103/PhysRevE.96.022413.
Wilson HR, Cowan JD. Excitatory and inhibitory interactions in localized populations of model neurons. Biophys J. 1972;12:1–24.
Barreiro A, Gautam S, Shew W, Ly C. A theoretical framework for analyzing coupled neuronal networks: application to the olfactory system. PLoS Comput Biol. 2017;13:1005780.
Ritt JT, Andermann ML, Moore CI. Embodied information processing: vibrissa mechanics and texture features shape micromotions in actively sensing rats. Neuron. 2008;57:599–613.
Grothe B, Klump GM. Temporal processing in sensory systems. Curr Opin Neurobiol. 2000;10:467–73.
Köppl C. Phase locking to high frequencies in the auditory nerve and cochlear nucleus magnocellularis of the barn owl, Tyto alba. J Neurosci. 1997;17:3312–21.
Mason A, Oshinsky M, Hoy R. Hyperacute directional hearing in a microscale auditory system. Nature. 2001;410:686–90.
Benda J, Longtin A, Maler L. A synchronization–desynchronization code for natural communication signals. Neuron. 2006;52:347–58.
van Steveninck RRdR, Lewen GD, Strong SP, Koberle R, Bialek W. Reproducibility and variability in neural spike trains. Science. 1997;275(5307):1805–8.
Cury KM, Uchida N. Robust odor coding via inhalation-coupled transient activity in the mammalian olfactory bulb. Neuron. 2010;68(3):570–85.
Gschwend O, Beroud J, Carleton A. Encoding odorant identity by spiking packets of rate-invariant neurons in awake mice. PLoS ONE. 2012;7(1):30155.
Grabska-Barwińska A, Barthelmé S, Beck J, Mainen ZF, Pouget A, Latham PE. A probabilistic approach to demixing odors. Nat Neurosci. 2017;20:98–106.
Liu CY, Nykamp DQ. A kinetic theory approach to capturing interneuronal correlation: the feed-forward case. J Comput Neurosci. 2009;26(3):339–68.
Ly C, Doiron B. Divisive gain modulation with dynamic stimuli in integrate-and-fire neurons. PLoS Comput Biol. 2009;5(4):1000365. https://doi.org/10.1371/journal.pcbi.1000365.
Risken H. 1. The Fokker–Planck equation: methods of solutions and applications. New York: Springer; 1989.
Chapman SI, Cowling TG. The Mathematical Theory of Non-Uniform Gases. New York: Cambridge University Press; 1970.
Dreyer W, Junk M, Kunik M. On the approximation of the Fokker–Planck equation by moment systems. Nonlinearity. 2001;14:881–906.
Ly C, Tranchina D. Critical Analysis of Dimension Reduction by a Moment Closure Method in a Population Density Approach to Neural Network Modeling. Neural Comput. 2007;19:2032–92.
Williams GS, Huertas MA, Sobie EA, Jafri MS, Smith GD. Moment closure for local control models of calcium-induced calcium release in cardiac myocytes. Biophys J. 2008;95(4):1689–703.
Buice MA, Cowan JD, Chow CC. Systematic fluctuation expansion for neural network activity equations. Neural Comput. 2010;22:377–426.
Stinchcombe AR, Forger DB. An efficient method for simulation of noisy coupled multi-dimensional oscillators. J Comput Phys. 2016;321:932–46.
Doiron B, Litwin-Kumar A, Rosenbaum R, Ocker G, Josić K. The mechanics of state-dependent neural correlations. Nat Neurosci. 2016;19(3):383–93.
Barreiro AK, Ly C. When do correlations increase with firing rates in recurrent networks? PLoS Comput Biol. 2017;13:1005506. https://doi.org/10.1371/journal.pcbi.1005506.
Barreiro A, Ly C. Investigating the correlation-firing rate relationship in heterogeneous recurrent networks. J Math Neurosci. 2018;8:8. https://doi.org/10.1186/s13408-018-0063-y.
Bressloff PC. Path-integral methods for analyzing the effects of fluctuations in stochastic hybrid neural networks. J Math Neurosci. 2015;5:4.
Ermentrout B. Reduction of conductance-based models with slow synapses to neural nets. Neural Comput. 1994;6(4):679–95.
Faugeras O, Touboul J, Cessac B. A constructive mean-field analysis of multi-population neural networks with random synaptic weights and stochastic inputs. Front Comput Neurosci. 2009;3:1.
Rosenbaum R, Smith MA, Kohn A, Rubin JE, Doiron B. The spatial structure of correlated neuronal variability. Nat Neurosci. 2017;20(1):107–14.
Huang C, Ruff DA, Pyle R, Rosenbaum R, Cohen MR, Doiron B. Circuit models of low-dimensional shared variability in cortical networks. Neuron. 2019;101:1–12.
Acknowledgements
We thank the Shew Lab, in particular Shree Hari Gautam, for their expertise in the olfactory system that motivated some of this work. We thank the Southern Methodist University (SMU) Center for Research Computation for providing computational resources.
Availability of data and materials
Software used to generate the computational results shown here can be found at http://github.com/chengly70/nonequilibriumFR.
Funding
CL is supported by a grant from the Simons Foundation (# 355173). These funding bodies had no role in the design of the study; collection, analysis, and interpretation of computational results; or in writing the manuscript.
Author information
Authors and Affiliations
Contributions
CL, WLS, AKB designed the project. AKB and CL wrote the software. CL designed the figures. CL, WLS, AKB wrote the paper. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Ethics approval and consent to participate
Not applicable.
Competing interests
The authors declare that they have no competing interests.
Consent for publication
Not applicable.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Ly, C., Shew, W.L. & Barreiro, A.K. Efficient calculation of heterogeneous non-equilibrium statistics in coupled firing-rate models. J. Math. Neurosc. 9, 2 (2019). https://doi.org/10.1186/s13408-019-0070-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13408-019-0070-7