Abstract
In this paper, the robust finite-time filter design problem for uncertain systems subject to missing measurements is investigated. It is assumed that the system is subject to the norm-bounded uncertainties and the measurements of the output are intermittent. For the model of the missing measurements, the Bernoulli process is adopted. A full-order filter is proposed to estimate the signal which can track the signal to be estimated. By augmenting the system vector, a stochastic augmented system is obtained. Based on the analysis of the robust stochastic finite-time stability and the performance, the filter design method is obtained. The filter parameters can be calculated by solving a sequence of linear matrix inequalities. Finally, a numerical example is used to show the design procedure and the effectiveness of the proposed design approach.
Similar content being viewed by others
1 Introduction
In the modern control, a filter plays an important role since the filter can be used to estimate the unavailable state and filter the external noise. Therefore, the filter design has been a hot research topic since the original development of the modern control. It is well known that the Kalman filter is an effective way to estimate state. However, the Kalman filter requires the preliminary knowledge of the spectrum of the noise and the precise system model. However, in many practical cases, these requirements cannot be satisfied. In these cases, the filter is a great alternative. The filter, which was originally proposed in the late 1980s [1], has attracted a lot of attention due to the fact that the filter can be easily utilized to deal with the uncertainties and the attenuation effect from the external input to the estimated signal [2–5].
In the state-space model, it is always assumed that system matrices are precise. However, in the real world, these matrices are unavoidable to contain uncertainties which can result from the modeling error or variations of the system parameters. During the past 20 years, the norm-bounded uncertainties have been widely adopted in the system modeling for practical plants, such as the works in [6–10]. In [11], the norm-bounded uncertainties were used in the time-delay linear systems. While in [9], the norm-bounded uncertainties were used in the neutral systems.
In the literature, most of the works on the filtering were based on the Lyapunov asymptotic stability. However, in many practical applications, the asymptotic stability is not enough if large values of the state are not acceptable, see [4, 12–27] and the references therein. Although the finite-time stability was early proposed in 1960s [12], it was not a hot research topic in the following 40 years. Recently, as the development and the application of the linear matrix inequalities [28, 29], the finite-time stability has been devoted considerable efforts.
The missing measurements have been attracting a great number of attention due to the fact that the measurements are missing when sensors temporally fail [30–34]. If the phenomenon of missing measurements is not considered during the filter design, the actual missing measurements may deteriorate the designed filters. Although, there are many results on the filtering, uncertain systems, and finite-time stability, there are few results on the filtering for uncertain systems subject to missing measurements. This fact motivates me to do the research. In this paper, the contributions can be summarized as follows. The missing measurements are considered the finite-time framework. Due to the existence of the stochastic variable in the augmented system, the robust stochastic finite-time boundedness is studied for the uncertain stochastic system. Moreover, the filtering with the robust stochastic finite-time stability is investigated.
2 Problem formulation
In this paper, the following uncertain discrete-time linear system is considered:
where denotes the state vector, is the system output, is the signal to be estimated, and is the time-varying disturbance which satisfies
where is a given scalar.
The matrices A, B, C, D, and E are constant matrices with appropriate dimensions. ΔA, ΔB, ΔC, and ΔD are real time-varying matrix functions representing the time-varying parameter uncertainties. It is assumed that the uncertainties are norm-bounded and admissible, which can be modeled as
where , , , , , and are known real constant matrices and is an unknown time-varying matrix function satisfying
If the sampling of the output is perfect, the input of the filter is equal to the output of the system. However, if considering the intermittent sensor failures, the phenomenon of missing measurements occurs. This phenomenon was firstly proposed in [35]. Since the reliability of the system becomes more and more important, the filter and control design problem for systems subject to missing measurements has been a hot topic in recent years [31, 34, 36]. Inspired by the work in [35], the model of the missing measurement in this paper is expressed as follows:
where is the input of the filter to be designed. If a Bernoulli process is used to describe the phenomenon, the measured output is expressed as
where the stochastic variable is a Bernoulli distributed white sequence taking values in the set .
The main objective of this paper is to design a full-order filter for the system (1) in the following form:
where is the state of the filter, is an estimation of , and , and are filter parameters to be designed later.
Suppose that β is the probability of the available measuring. Defining the filtering error as , the following augmented system can be obtained:
where
Note that there is a stochastic variable and some norm-bounded uncertainties in the augmented system in (8). Therefore, the challenge now is how to design the filter such that the augmented system in (8) is robustly stochastically finite-time bounded and the effect of the disturbance input to the signal to be estimated is constrained to a prescribed level.
Before proceeding, the following definitions are introduced.
Definition 1 (Finite-time stable (FTS) [13])
For a class of discrete-time linear systems,
is said to be FTS with respect to , where R is a positive definite matrix, and , if , then for all .
Definition 2 (Robustly stochastically finite-time stable (RSFTS))
For a class of discrete-time linear uncertain systems,
is said to be RSFTS with respect to , where the system matrix has the uncertainty and the stochastic variable, R is a positive definite matrix, and , if for all admissible uncertainties ΔA, stochastic variable , , then for all .
Definition 3 (Robustly stochastically finite-time bounded (RSFTB))
For a class of discrete-time linear uncertain systems,
is said to be RSFTB with respect to , where the system matrix has the uncertainty and the stochastic variable, the input matrix contains the norm-bounded uncertainty, R is a positive definite matrix, and , if for all admissible uncertainties ΔA and ΔB, stochastic variable , , then for all .
With the above definitions, the main objectives in this paper can be summarized as follows. For the uncertainty in 1, design the full-order filter (7) such that for all the admissible uncertainties and the missing measurements,
-
the augmented system (8) is RSFTS;
-
under the zero-initial condition, the signal to be estimated satisfies
(12)
for all -bounded , where the prescribed value γ is the attenuation level.
In addition, some useful lemmas are also needed.
Lemma 1 (Schur complement [6])
Given a symmetric matrix , the following three conditions are equivalent to each other:
-
;
-
, ;
-
, .
Let , and be real matrices with compatible dimensions, and let be time-varying and satisfy (4). Then it can be concluded that the following condition:
holds if and only if there exists a positive scaler such that
is satisfied.
3 Main results
3.1 Finite-time stability and performance analysis
In this section, the finite-time stability, robust finite-time stability, and robust stochastic finite-time stability will be analyzed by assuming the parameters of the filter to be designed are given.
Theorem 1 The augmented system in (8) is RSFTB with respect to if there exist positive-definite matrices , and two scalars and such that the following conditions hold:
and
where
Proof Consider the following Lyapunov function:
where is a symmetric positive-definite matrix. For the augmented system in (8), the expectation of one step advance of the Lyapunov function can be derived as
where
Note that
where
By using the Schur complement, the condition in (15) implies that
since the condition in (15) can be rewritten as
where
With the condition (21), the following inequality can be obtained:
Taking the iterative operation with respect to the time instant k, the following inequality is derived:
It follows from the Lyapunov function that
Combing (24) and (25), one gets
It is inferred from the conditions (16) and (26) that
Therefore, if the conditions (15) and (16) hold, the augmented system (8) is RSFTB. The proof is completed. □
It is noticed that there is a positive-definite matrix in Theorem 2. The matrix can be randomly chosen. For considering the performance, other sufficient conditions are provided in the following theorem.
Theorem 2 The augmented system in (8) is RSFTB with respect to if there exist positive-definite matrix and three scalars , , and such that the following conditions hold:
and
where and .
Proof To prove the theorem, and in Theorem 1 can be replaced with P and , respectively. The proof is completed. □
The robust stochastic finite-time stability and the robust stochastic finite-time boundedness of the augmented system (8) have been offered. Now, we are going to consider the performance.
Theorem 3 The augmented system in (8) is RSFTB with respect to and with an attenuation level γ if there exist positive-definite matrix and three scalars , , and such that the following conditions hold:
and
where and .
Proof In the proof of performance, it is required that the initial value of the state is zero. Therefore, in Theorem 2 is set to be zero. Under the zero-initial condition, consider the following cost function:
The cost function can be revaluated with similar lines in Theorem 1. □
3.2 Filter design
The robust stochastic finite-time stability and the performance have been investigated in the above subsection. In this subsection, the filter design method will be proposed.
Theorem 4 Given a positive constant γ and two scalars σ and ρ, the closed-loop system in (8) is RSFTB with respect to and with a prescribed attenuation level γ if there exists a positive-definite matrices , matrices , two scalars , and such that the following conditions hold:
and
where
Moreover, the filter parameters can be calculated as and .
Proof It is assumed that the Lyapunov weighting matrix has the following structure:
where σ is a prescribed scalar. With this assumption, the coupled terms in Theorem 3 can be evaluated as follows:

Defining new variables as and , the condition in (30) is equivalent to (33). Supposing that
the conditions (34) and (35) can guarantee that the condition (31) is satisfied. □
The performance γ refers to the attenuation level from the external noise to the signal to be estimated. Therefore, it is desired that the performance γ should be as small as possible. For fixed θ and , the optimal γ can be obtained by
4 Numerical example
Consider the system in (1) with the following matrix:
In this example, the following values are chosen for the finite-time stability:
It is assumed that the probability of the available measurements is 0.95, that is, 5% of the output is randomly missing. With the proposed filter design problem in (39), the achieved minimum performance index is and the corresponding optimal filter is
In the simulation, assume that the external disturbance satisfies
and the time-varying parameter satisfies
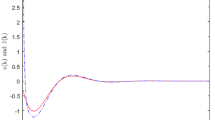
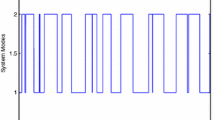
It is easy to check that the 2-norm of the external disturbance is less than d which is 0.1 and the time-varying parameter . It can be seen from Figure 1 that the estimated signal can track the signal to be estimated well. The intermittent measurements in the random simulation are shown in Figure 2.
5 Conclusion
In this paper, the robust finite-time filter design problem of discrete-time systems subject to missing measurements has been investigated. The uncertainties in the system matrices are assumed to be norm-bounded. The measurements of the system output are intermittent and a Bernoulli process is used to model the intermittent measurements. Based on the results of the robust stochastic finite-time stability and the performance, the filter design approach was proposed. Finally, an illustrative example was used to show the design procedure and the effectiveness of the proposed design approach.
References
Elsayed A, Grimble MJ:A new approach to the design of optimal digital linear filters. IMA J. Math. Control Inf. 1989, 6(2):233–251. 10.1093/imamci/6.2.233
Grigoriadis KM, Watson JT:Reduced-order and filtering via linear matrix inequalities. IEEE Trans. Aerosp. Electron. Syst. 1997, 33(4):1326–1338.
Wang Q, Lam J, Xu S, Gao H: Delay-dependent and delay-independent energy-to-peak model approximation for systems with time-varying delay. Int. J. Syst. Sci. 2005, 36(8):445–460. 10.1080/00207720500139773
Meng Q, Shen Y: Finite-time stabilization via dynamic output feedback. Commun. Nonlinear Sci. Numer. Simul. 2009, 14(4):1043–1049. 10.1016/j.cnsns.2008.03.010
Wu L, Wang Z, Gao H, Wang C: and filtering for two-dimensional linear parameter-varying systems. Int. J. Robust Nonlinear Control 2007, 17(12):1129–1154. 10.1002/rnc.1169
Han Q-L, Gu K: On robust stability of time-delay systems with norm-bounded uncertainty. IEEE Trans. Autom. Control 2001, 46(9):1426–1431. 10.1109/9.948471
Garcia G, Bernussou J, Arzelier D: Robust stabilization of discrete-time linear systems with norm-bounded time-varying uncertainty. Syst. Control Lett. 1994, 22(5):327–339. 10.1016/0167-6911(94)90030-2
Zhou K, Khargonekar PP: Robust stabilization of linear systems with norm-bounded time-varying uncertainty. Syst. Control Lett. 1988, 10(1):17–20. 10.1016/0167-6911(88)90034-5
Han Q-L: On robust stability of neutral systems with time-varying discrete delay and norm-bounded uncertainty. Automatica 2004, 40(6):1087–1092. 10.1016/j.automatica.2004.01.007
Yu L, Chu J, Su H:Robust memoryless controller design for linear time-delay systems with norm-bounded time-varying uncertainty. Automatica 1996, 32(12):1759–1762. 10.1016/S0005-1098(96)80016-1
Shi P, Agarwal RK, Boukas E-K, Shue S-P:Robust state feedback control of discrete time-delay linear systems with norm-bounded uncertainty. Int. J. Syst. Sci. 2000, 31(4):409–415. 10.1080/002077200290984
Weiss L, Infante EF: Finite time stability under perturbing forces and on product spaces. IEEE Trans. Autom. Control 1967, AC-12(1):54–59.
Amato F, Ariola M: Finite-time control of discrete-time linear systems. IEEE Trans. Autom. Control 2005, 50(5):724–729.
Liu H, Shen Y: finite-time control for switched linear systems with time-varying delay. Intell. Control Autom. 2011, 2(2):203–213.
Shen Y: Finite-time control of linear parameter-varying systems with norm-bounded exogenous disturbance. J. Control Theory Appl. 2008, 6(2):184–188. 10.1007/s11768-008-6176-1
Yin Y, Liu F, Shi P: Finite-time gain-scheduled control on stochastic bioreactor systems with partially known transition jump rates. Circuits Syst. Signal Process. 2011, 30(3):609–627. 10.1007/s00034-010-9236-y
Luan X, Liu F, Shi P: Robust finite-time control for a class of extended stochastic switching systems. Int. J. Syst. Sci. 2011, 42(7):1197–1205. 10.1080/00207720903428898
Zhao S, Sun J, Liu L: Finite-time stability of linear time-varying singular systems with impulsive effects. Int. J. Control 2008, 81(11):1824–1829. 10.1080/00207170801898893
Amato F, Ariola M, Dorato P: Finite-time control of linear systems subject to parametric uncertainties and disturbances. Automatica 2001, 37(9):1459–1463. 10.1016/S0005-1098(01)00087-5
Karafyllis I: Finite-time global stabilization using time-varying distributed delay feedback. SIAM J. Control Optim. 2006, 45(1):320–342. 10.1137/040616383
Bhat SP, Bernstein DS: Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38(3):751–766. 10.1137/S0363012997321358
Amatoa F, Ariolab M, Cosentino C: Finite-time stabilization via dynamic output feedback. Automatica 2006, 42(2):337–342. 10.1016/j.automatica.2005.09.007
Hong Y, Xu Y, Huang J: Finite-time control for robot manipulators. Syst. Control Lett. 2002, 46(4):243–263. 10.1016/S0167-6911(02)00130-5
Moulay E, Perruquetti W: Finite-time stability and stabilization of a class of continuous systems. J. Math. Anal. Appl. 2006, 323(2):1430–1443. 10.1016/j.jmaa.2005.11.046
Bhat SP, Bernstein DS: Geometric homogeneity with applications to finite-time stability. Math. Control Signals Syst. 2005, 17(1):101–127.
Bhat SP, Bernstein DS: Continuous finite-time stabilization of the translational and rotational double integrator. IEEE Trans. Autom. Control 1998, 43(5):678–682. 10.1109/9.668834
Moulay E, Dambrine M, Perruquetti NYW: Finite-time stability and stabilization of time-delay systems. Syst. Control Lett. 2008, 57(7):561–566. 10.1016/j.sysconle.2007.12.002
Rajchakit M, Rajchakit G: Mean square robust stability of stochastic switched discrete-time systems with convex polytopic uncertainties. J. Inequal. Appl. 2012., 2012: Article ID 135
Zhu E, Xu Y: Pathwise estimation of stochastic functional Kolmogorov-type systems with infinite delay. J. Inequal. Appl. 2012., 2012: Article ID 171
Hounkpevi FO, Yaz EE: Robust minimum variance linear state estimators for multiple sensors with different failure rates. Automatica 2007, 43(7):1274–1280. 10.1016/j.automatica.2006.12.025
Wang Z, Yang F, Ho DWC, Liu X:Robust control for networked systems with random packet losses. IEEE Trans. Syst. Man Cybern., Part B, Cybern. 2007, 37(4):916–924.
Huang M, Dey S: Stability of Kalman filtering with Markovian packet losses. Automatica 2007, 43(4):598–607. 10.1016/j.automatica.2006.10.023
Wei G, Wang Z, Shu H: Robust filtering with stochastic nonlinearities and multiple missing measurements. Automatica 2009, 45(3):836–841. 10.1016/j.automatica.2008.10.028
Wang Z, Ho DWC, Liu X: Variance-constrained filtering for uncertain stochastic systems with missing measurements. IEEE Trans. Autom. Control 2003, 48(7):1254–1258. 10.1109/TAC.2003.814272
Nahi NE: Optimal recursive estimation with uncertain observation. IEEE Trans. Inf. Theory 1969, 15(4):457–462. 10.1109/TIT.1969.1054329
Wang Z, Yang F, Ho DWC, Liu X: Robust finite-horizon filtering for stochastic systems with missing measurements. IEEE Signal Process. Lett. 2005, 12(6):437–440.
Shi P, Boukas E-K, Agarwal RK: Control of Markovian jump discrete-time systems with norm bounded uncertainty and unknown delay. IEEE Trans. Autom. Control 2005, 44(11):2139–2144.
Song S-H, Kim J-K: control of discrete-time linear systems with norm-bounded uncertainties and time delay in state. Automatica 1998, 34(1):137–139. 10.1016/S0005-1098(97)00182-9
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that they have no competing interests.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Deng, Z. Robust finite-time filtering for uncertain systems subject to missing measurements. J Inequal Appl 2013, 236 (2013). https://doi.org/10.1186/1029-242X-2013-236
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1029-242X-2013-236