The improved disc theorems for the Schur complements of diagonally dominant matrices

Abstract

The theory of Schur complement is very important in many fields such as control theory and computational mathematics. In this paper, applying the properties of Schur complement, utilizing some inequality techniques, some new estimates of diagonally dominant degree on the Schur complement of matrices are obtained, which improve some relative results. Further, as an application of these derived results, we present some distributions for the eigenvalues of the Schur complements. Finally, the numerical example is given to show the advantages of our derived results.

MSC:15A45, 15A48.

1 Introduction

The Schur complement has been proved to be a useful tool in many fields such as numerical algebra and control theory. [1, 2] proposed a kind of iteration called the Schur-based iteration. Applying this method, we can solve large scale linear systems though reducing the order by the Schur complement. In addition, when utilizing the conjugate gradient method to solve large scale linear systems, if the eigenvalues of the system matrix are more concentrated, the convergent speed of the iterative method is faster (see, e.g., [[3], pp.312-317]). From [1, 2], it can be seen that for large scale linear systems, after applying the Schur-based iteration to reduce the order, the corresponding system matrix of linear equations is the Schur complement of the system matrix of original large scale linear systems and its eigenvalues are more concentrated than those of the original system matrix, leading to the Schur-based conjugate gradient method computing faster than the ordinary conjugate gradient method.

Hence, it is always interesting to know whether some important properties of matrices are inherited by their Schur complements. Clearly, the Schur complements of positive semidefinite matrices are positive semidefinite, the same is true for M-matrices, H-matrices and inverse M-matrices (see [4, 5]). Carlson and Markham showed that the Schur complements of strictly diagonally dominant matrices are diagonally dominant (see [6]). Li, Tsatsomeros and Ikramov independently proved the Schur complement of a strictly doubly diagonally dominant matrix is strictly doubly diagonally dominant (see [7, 8]). These properties have been repeatedly used for the convergence of iterations in numerical analysis and for deriving matrix inequalities in matrix analysis (see [3, 9, 10]). More importantly, the distribution for the eigenvalues of the Schur complement is of great significance, as shown in [1, 2, 8, 11–17]. The aim of this paper is to study the distributions for the eigenvalues of the Schur complement of some diagonally dominant matrices.

Denote by ${\mathbb{C}}^{n\times n}$ the set of all $n\times n$ complex matrices. Let $N=\{1,2,\dots ,n\}$. For $A=(a_{ij})\in {\mathbb{C}}^{n\times n}$ ($n\ge 2$), assume

$$P_i(A)=\sum _{j\in N,j\ne i}|a_{ij}|,S_i(A)=\sum _{j\in N,j\ne i}|a_{ji}|,i=1,2,\dots ,n.$$

Set

$$N_r(A)=\{i|i\in N,|a_{ii}|>P_i(A)\};N_c(A)=\{j|j\in N,|a_{jj}|>S_j(A)\}.$$

Let us recall that A is a (row) diagonally dominant matrix ($D_n$) if

$$|a_{ii}|\ge P_i(A),\mathrm{\forall }i\in N;$$

(1.1)

A is a doubly diagonally dominant matrix (${\mathit{DD}}_n$) if

$$|a_{ii}||a_{jj}|\ge P_i(A)P_j(A),\mathrm{\forall }i\ne j,i,j\in N;$$

(1.2)

A is a γ-diagonally dominant matrix ($D_n^{\gamma }$) if there exists $\gamma \in [0,1]$ such that

$$|a_{ii}|\ge \gamma P_i(A)+(1-\gamma )Q_i(A),\mathrm{\forall }i\in N;$$

(1.3)

A is a product γ-diagonally dominant matrix (${\mathit{PD}}_n^{\gamma }$) if there exists $\gamma \in [0,1]$ such that

$$|a_{ii}|\ge {[P_i(A)]}^{\gamma }{[Q_i(A)]}^{1-\gamma },\mathrm{\forall }i\in N.$$

(1.4)

If all inequalities in (1.1)-(1.4) are strict, then A is said to be a strictly (row) diagonally dominant matrix (${\mathit{SD}}_n$), a strictly doubly diagonally dominant matrix (${\mathit{SDD}}_n$), a strictly γ-diagonally dominant matrix (${\mathit{SD}}_n^{\gamma }$) and a strictly product γ-diagonally dominant matrix (${\mathit{SPD}}_n^{\gamma }$), respectively.

Liu and Zhang in [14] have pointed out the fact as follows. If $A\in {\mathit{SDD}}_n$ but $A\notin {\mathit{SD}}_n$, then there exists a unique index $i_0$ such that

$$|a_{i_0{i}_0}|\le P_{i_0}(A).$$

(1.5)

As in [1, 2], for $1\le i\le n$ and $\gamma \in [0,1]$, we call $|a_{ii}|-P_i(A)$, $|a_{ii}|-\gamma P_i(A)-(1-\gamma )S_i(A)$ and $|a_{ii}|-{[P_i(A)]}^{\gamma }{[S_i(A)]}^{1-\gamma }$ the i th (row) dominant degree, γ-dominant degree and product γ-dominant degree of A, respectively.

The comparison matrix of A, denoted by $\mu (A)=(t_{ij})$, is defined to be

$$t_{ij}=\{\begin{array}{cc}|a_{ij}|,\hfill & \text{if }i=j,\hfill \\ -|a_{ij}|,\hfill & \text{if }i\ne j.\hfill \end{array}$$

A matrix A is an M-matrix if it can be written in the form of $A=mI-P$ with P being nonnegative and $m>\rho (P)$, where $\rho (P)$ denotes the spectral radius of P. A matrix A is a H-matrix if $\mu (A)$ is a M-matrix. We denote by ${\mathbb{H}}_n$ and ${\mathbb{M}}_n$ the sets of $n\times n$ H- and M-matrices, respectively.

For $\alpha \subseteq N$, denote by $|\alpha |$ the cardinality of α and ${\alpha }^{\prime }=N-\alpha$. If $\alpha ,\beta \subseteq N$, then $A(\alpha ,\beta )$ is the submatrix of A lying in the rows indicated by α and the columns indicated by β. In particular, $A(\alpha ,\alpha )$ is abbreviated to $A(\alpha )$. Assume that $A(\alpha )$ is nonsingular. Then

$$A/\alpha =A/A(\alpha )=A\left({\alpha }^{\prime }\right)-A({\alpha }^{\prime },\alpha ){[A(\alpha )]}^{-1}A(\alpha ,{\alpha }^{\prime }),$$

is called the Schur complement of A with respect to $A(\alpha )$.

The paper is organized as follows. In Section 2, we give several new estimates of diagonally dominant degree on the Schur complement of matrices, which improve some relative results. In Section 3, as an application of these derived results, the distributions for eigenvalues are obtained. In Section 4, we give a numerical example to show the advantages of our derived results.

2 The diagonally dominant degree for the Schur complement

In this section, we give several new estimates of diagonally dominant degree on the Schur complement of matrices, which improve some relative results.

Lemma 1 [4]

If A is an H-matrix, then ${[\mu (A)]}^{-1}\ge |A^{-1}|$.

Lemma 2 [4]

If $A\in {\mathit{SD}}_n$ or ${\mathit{SDD}}_n$, then $\mu (A)\in {\mathbb{M}}_n$, i.e., $A\in {\mathbb{H}}_n$.

Lemma 3 [11]

If $A\in {\mathit{SD}}_n$ or ${\mathit{SDD}}_n$ and $\alpha \subseteq N$, then the Schur complement of A is in ${\mathit{SD}}_{|{\alpha }^{\prime }|}$ or ${\mathit{SDD}}_{|{\alpha }^{\prime }|}$ , where ${\alpha }^{\prime }=N-\alpha$ is the Schur complement of α in N and $|{\alpha }^{\prime }|$ is the cardinality of ${\alpha }^{\prime }$.

Lemma 4 [1]

Let $a>b$, $c>b$, $b>0$ and $0\le r\le 1$. Then

$$a^r{c}^{1-r}\ge {(a-b)}^r{(c-b)}^{1-r}+b.$$

Theorem 1 Let $A\in {\mathbb{C}}^{n\times n}$, $\alpha =\{i_1,i_2,\dots ,i_k\}\subseteq N_r(A)$, ${\alpha }^{\prime }=N-\alpha =\{j_1,j_2,\dots ,j_l\}$, $|\alpha |<n$ and denote $A/\alpha =(a_{ts}^{\prime })$. Then for all $1\le t\le l$,

$$\left|a_{tt}^{\prime }\right|-P_t(A/\alpha )\ge |a_{j_t{j}_t}|-P_{j_t}(A)+w_{j_t}\ge |a_{j_t{j}_t}|-P_{j_t}(A)$$

(2.1)

and

$$\left|a_{tt}^{\prime }\right|+P_t(A/\alpha )\le |a_{j_t{j}_t}|+P_{j_t}(A)-w_{j_t}\le |a_{j_t{j}_t}|+P_{j_t}(A),$$

(2.2)

where

$$w_{j_t}=\underset{1\le \omega \le k}{min}\frac{|a_{i_{\omega }{i}_{\omega }}|-P_{i_{\omega }}(A)}{|a_{i_{\omega }{i}_{\omega }}|-{\sum }_{\underset{u\ne \omega }{u=1}}^k|a_{i_{\omega }{i}_u}|}\sum _{u=1}^k|a_{j_t{i}_u}|.$$

(2.3)

Proof According to Lemmas 1 and 2, we have ${\{\mu [A(\alpha )]\}}^{-1}\ge {[A(\alpha )]}^{-1}$. Thus, $\mathrm{\forall }\epsilon >0$ and $t=1,2,\dots ,l$,

(2.4)

Denote

$$B_t\equiv \left(\begin{array}{cc}x& \begin{array}{ccc}-|a_{j_t{i}_1}|& \cdots & -|a_{j_t{i}_k}|\end{array}\\ \begin{array}{c}-{\sum }_{u=1}^l|a_{i_1{j}_u}|\\ ⋮\\ -{\sum }_{u=1}^l|a_{i_k{j}_u}|\end{array}& \mu [A(\alpha )]\end{array}\right).$$

(2.5)

If

$$x>\underset{1\le \omega \le k}{max}\frac{{\sum }_{u=1}^l|a_{i_{\omega }{j}_u}|}{|a_{i_{\omega }{i}_{\omega }}|-{\sum }_{\underset{u\ne \omega }{u=1}}^k|a_{i_{\omega }{i}_u}|}\sum _{u=1}^k|a_{j_t{i}_u}|,$$

then

$$\frac{x}{{\sum }_{u=1}^k|a_{j_t{i}_u}|}>\underset{1\le \omega \le k}{max}\frac{{\sum }_{u=1}^l|a_{i_{\omega }{j}_u}|}{|a_{i_{\omega }{i}_{\omega }}|-{\sum }_{\underset{u\ne \omega }{u=1}}^k|a_{i_{\omega }{i}_u}|}.$$

Choose ${\epsilon }_t\in {\mathbb{R}}^{+}$ such that

$$\frac{x}{{\sum }_{u=1}^k|a_{j_t{i}_u}|}>{\epsilon }_t>\underset{1\le \omega \le k}{max}\frac{{\sum }_{u=1}^l|a_{i_{\omega }{j}_u}|}{|a_{i_{\omega }{i}_{\omega }}|-{\sum }_{\underset{u\ne \omega }{u=1}}^k|a_{i_{\omega }{i}_u}|},$$

where we denote $\frac{x}{{\sum }_{u=1}^k|a_{j_t{i}_u}|}=\mathrm{\infty }$ if ${\sum }_{u=1}^k|a_{j_t{i}_u}|=0$. Set $D=diag(y_1,y_2,\dots ,y_{k+1})$, where

$$y_i=\{\begin{array}{cc}1,\hfill & i=1,\hfill \\ {\epsilon }_t,\hfill & i=2,3,\dots ,k+1.\hfill \end{array}$$

Denote $C_t=B_{t}D=(c_{sv})$. If $s=1$, then

$$|c_{ss}|-\sum _{v\ne i}|c_{sv}|=|c_{11}|-\sum _{s=2}^{k+1}|c_{1v}|=x-\sum _{v=1}^k{\epsilon }_t|a_{j_t{i}_v}|=x-{\epsilon }_t\sum _{v=1}^k|a_{j_t{i}_v}|>0;$$

otherwise,

$$\begin{array}{rcl}|c_{ss}|-\sum _{s\ne v}^{k+1}|c_{sv}|& =& {\epsilon }_t|a_{i_{\omega }{i}_{\omega }}|-\sum _{v\ne \omega }^k{\epsilon }_t|a_{i_{\omega }{i}_v}|-\sum _{u=1}^l|a_{i_{\omega }{j}_u}|\\ =& {\epsilon }_t(|a_{i_{\omega }{i}_{\omega }}|-\sum _{v\ne \omega }^k|a_{i_{\omega }{i}_v}|)-\sum _{u=1}^l|a_{i_{\omega }{j}_u}|\\ >& \frac{{\sum }_{u=1}^l|a_{i_{\omega }{j}_u}|}{|a_{i_{\omega }{i}_{\omega }}|-{\sum }_{\underset{u\ne \omega }{u=1}}^k|a_{i_{\omega }{i}_u}|}(|a_{i_{\omega }{i}_{\omega }}|-\sum _{\underset{u\ne \omega }{u=1}}^k|a_{i_{\omega }{i}_u}|)-\sum _{u=1}^l|a_{i_{\omega }{j}_u}|=0.\end{array}$$

Therefore, we have $C_t\in {\mathit{SD}}_{k+1}$, and so $B_t\in {\mathbb{H}}_{k+1}$. Note that $B_t=\mu (B_t)$. So,

$$det{B}_t>0.$$

(2.6)

Take $x={\sum }_{u=1}^k|a_{j_t{i}_u}|-w_{j_t}+\epsilon$ in (2.5), then

Noting that $det\{\mu [A(\alpha )]\}>0$, by (2.4) and (2.6), we have

$$\left|a_{tt}^{\prime }\right|-P_t(A/\alpha )\ge |a_{j_t{j}_t}|-P_{j_t}(A)+{\omega }_{j_t}-\epsilon .$$

Let $\epsilon \to 0$, thus we easily get (2.1). Similarly, we obtain (2.2). □

Remark 1 Observe that

$$\frac{P_{i_w}(A)}{|a_{i_w{i}_w}|}\ge \frac{{\sum }_{u=1}^l|a_{i_{\omega }{j}_u}|}{|a_{i_{\omega }{i}_{\omega }}|-{\sum }_{\underset{u\ne \omega }{u=1}}^k|a_{i_{\omega }{i}_u}|}.$$

This means that Theorem 1 improves Theorem 1 of [14].

Theorem 2 Let $A\in {\mathit{SDD}}_n$, $\alpha =\{i_0,i_1,i_2,\dots ,i_k\}$ with the index $i_0$ satisfying (1.5), ${\alpha }^{\prime }=N-\alpha =\{j_1,j_2,\dots ,j_l\}$, $|\alpha |<n$ and denote $A/\alpha =(a_{ts}^{\prime })$. Then for all $1\le t\le l$,

$$\begin{array}{rcl}\left|a_{tt}^{\prime }\right|-P_t(A/\alpha )& \ge & |a_{j_t{j}_t}|-P_{j_t}(A)+(1-\frac{{\sum }_{u=1}^l|a_{i_0{j}_u}|}{|a_{i_0{i}_0}|-{\sum }_{j\ne i_0}^{j\in \alpha }|a_{i_{0}j}|})\sum _{v=1}^k|a_{j_t{i}_v}|\\ \ge & |a_{j_t{j}_t}|-\frac{{\sum }_{u=1}^l|a_{i_0{j}_u}|}{|a_{i_0{i}_0}|-{\sum }_{j\ne i_0}^{j\in \alpha }|a_{i_{0}j}|}{P}_{j_t}(A)\end{array}$$

(2.7)

and

$$\begin{array}{rcl}\left|a_{tt}^{\prime }\right|+P_t(A/\alpha )& \le & |a_{j_t{j}_t}|+P_{j_t}(A)-(1-\frac{{\sum }_{u=1}^l|a_{i_0{j}_u}|}{|a_{i_0{i}_0}|-{\sum }_{j\ne i_0}^{j\in \alpha }|a_{i_{0}j}|})\sum _{v=1}^k|a_{j_t{i}_v}|\\ \le & |a_{j_t{j}_t}|+\frac{{\sum }_{u=1}^l|a_{i_0{j}_u}|}{|a_{i_0{i}_0}|-{\sum }_{j\ne i_0}^{j\in \alpha }|a_{i_{0}j}|}{P}_{j_t}(A).\end{array}$$

(2.8)

Proof For all $1\le t\le l$, we have

$$\begin{array}{rcl}\left|a_{tt}^{\prime }\right|-P_t(A/\alpha )& =& \left|a_{tt}^{\prime }\right|-\underset{s\ne t}{\overset{l}{\sum _{s=1}}}\left|a_{ts}^{\prime }\right|\\ =& |a_{j_t{j}_t}-(a_{j_t{i}_1},\dots ,a_{j_t{i}_k}){[A(\alpha )]}^{-1}\left(\begin{array}{c}{a}_{i_1{j}_t}\\ ⋮\\ a_{i_k{j}_t}\end{array}\right)|\\ -\underset{s\ne t}{\overset{l}{\sum _{s=1}}}|a_{j_t{j}_s}-(a_{j_t{i}_1},\dots ,a_{j_t{i}_k}){[A(\alpha )]}^{-1}\left(\begin{array}{c}{a}_{i_1{j}_s}\\ ⋮\\ a_{i_k{j}_s}\end{array}\right)|\\ \ge & |a_{j_t{j}_t}|-P_{j_t}(A)+(1-\frac{{\sum }_{u=1}^l|a_{i_0{j}_u}|}{|a_{i_0{i}_0}|-{\sum }_{j\ne i_0}^{j\in \alpha }|a_{i_{0}j}|})\sum _{v=1}^k|a_{j_t{i}_v}|\\ +\frac{{\sum }_{u=1}^l|a_{i_0{j}_u}|}{|a_{i_0{i}_0}|-{\sum }_{j\ne i_0}^{j\in \alpha }|a_{i_{0}j}|}\sum _{v=1}^k|a_{j_t{i}_v}|\\ -\sum _{s=1}^l\left|(|a_{j_t{i}_1}|,\dots ,|a_{j_t{i}_k}|){\left\{\mu [A(\alpha )]\right\}}^{-1}\left(\begin{array}{c}|a_{i_1{j}_s}|\\ ⋮\\ |a_{i_k{j}_s}|\end{array}\right)\right|.\end{array}$$

Thus,

Take $x=\frac{{\sum }_{u=1}^l|a_{i_0{j}_u}|}{|a_{i_0{i}_0}|-{\sum }_{j\ne i_0}^{j\in \alpha }|a_{i_{0}j}|}{\sum }_{v=1}^k|a_{j_t{i}_v}|$ in (2.5). By (2.6), thus it is not difficult to get that (2.7) follows. Similarly, we obtain (2.8). □

It is known that the Schur complements of diagonally dominant matrices are diagonally dominant (see [12, 13]). However, this property is not always true for γ-diagonally dominant matrices and for product γ-diagonally dominant matrices, as shown in [1].

In the sequel, we obtain some disc separations for the γ-diagonally and product γ-diagonally dominant degree of the Schur complement, from which we provide that the Schur complement of the γ-diagonally and product γ-diagonally dominant matrices is also γ-diagonally dominant and product γ-diagonally under some restrictive conditions.

Theorem 3 Let $A\in {\mathbb{C}}^{n\times n}$, $\alpha =\{i_1,i_2,\dots ,i_k\}\subseteq N_r(A)\cap N_c(A)\ne \mathrm{\varnothing }$, ${\alpha }^{\prime }=N-\alpha =\{j_1,j_2,\dots ,j_l\}$, $|\alpha |<n$ and denote $A/\alpha =(a_{ts}^{\prime })$. Then for all $1\le t\le l$,

$$\begin{array}{rcl}\left|a_{tt}^{\prime }\right|-P_t^{\gamma }(A/\alpha )S_t^{(1-\gamma )}(A/\alpha )& >& |a_{j_t{j}_t}|-{(P_{j_t}(A)-w_t)}^{\gamma }{(S_{j_t}(A)-w_t^T)}^{1-\gamma }\\ >& |a_{j_t{j}_t}|-P_{j_t}^{\gamma }(A)S_{j_t}^{1-\gamma }(A)\end{array}$$

(2.9)

and

$$\begin{array}{rcl}\left|a_{tt}^{\prime }\right|+P_t^{\gamma }(A/\alpha )S_t^{(1-\gamma )}(A/\alpha )& <& |a_{j_t{j}_t}|+{(P_{j_t}(A)-w_t)}^{\gamma }{(S_{j_t}(A)-w_t^T)}^{1-\gamma }\\ <& |a_{j_t{j}_t}|+P_{j_t}^{\gamma }(A)S_{j_t}^{1-\gamma }(A),\end{array}$$

(2.10)

where

Proof For all $1\le t\le l$, we have

(2.11)

Similar as in the proof of Theorem 1, we easily obtain

(2.12)

Similarly,

(2.13)

Set

$$h=(|a_{j_t{i}_1}|,\dots ,|a_{j_t{i}_k}|){\left\{\mu [A(\alpha )]\right\}}^{-1}\left(\begin{array}{c}|a_{i_1{j}_t}|\\ ⋮\\ |a_{i_k{j}_t}|\end{array}\right).$$

From (2.11), (2.12), (2.13), using Lemma 4, we have

Thus we get (2.9). Similarly, we have (2.10). □

Remark 2 Observe that

This means that Theorem 3 improves Theorem 2 of [1].

In a similar way to the proof of Theorem 3, we get the following theorem immediately.

Theorem 4 Let $A\in {\mathbb{C}}^{n\times n}$, $\alpha =\{i_1,i_2,\dots ,i_k\}\subseteq N_r(A)\cap N_c(A)\ne \mathrm{\varnothing }$, ${\alpha }^{\prime }=N-\alpha =\{j_1,j_2,\dots ,j_l\}$, $|\alpha |<n$ and denote $A/\alpha =(a_{ts}^{\prime })$. Then for all $1\le t\le l$,

(2.14)

and

(2.15)

Corollary 1 Let $A\in D^{\gamma }$ and $N_r(A)\cap N_c(A)\ne \mathrm{\varnothing }$. Then for any $\alpha \subseteq N_r(A)\cap N_c(A)$ with $|\alpha |<n$,

$$A/\alpha \in {\mathit{SD}}_{n-|\alpha |}^{\gamma }.$$

Proof By (2.14), we have

$$\left|a_{tt}^{\prime }\right|-\gamma P_t(A/\alpha )-(1-\gamma )S_t(A/\alpha )>|a_{j_t{j}_t}|-\gamma P_{j_t}(A)-(1-\gamma )S_{j_t}(A)\ge 0.$$

 □

Corollary 2 Let $A\in {\mathit{PD}}_n^{\gamma }$ and $N_r(A)\cap N_c(A)\ne \mathrm{\varnothing }$. Then for any $\alpha \subseteq N_r(A)\cap N_c(A)$ with $|\alpha |<n$,

$$A/\alpha \in {\mathit{SPD}}_{n-|\alpha |}^{\gamma }.$$

3 Distribution for eigenvalues

In this section, as an application of our results in Section 2, we present some locations for the eigenvalues of the Schur complements.

Theorem 5 Let $A\in {\mathbb{C}}^{n\times n}$, $\alpha =\{i_1,i_2,\dots ,i_k\}\subset N_r\ne \mathrm{\varnothing }$, ${\alpha }^{\prime }=N-\alpha =\{j_1,j_2,\dots ,j_l\}$. Then for each eigenvalue λ of $A/\alpha$, there exists $1\le t\le l$ such that

$$|\lambda -a_{j_t{j}_t}|<P_{j_t}(A)-w_{j_t}.$$

(3.1)

Proof Set $A/\alpha =(a_{st}^{\prime })$. Using the Gerschgorin circle theorem, we know there exists $1\le t\le l$ such that

$$|\lambda -a_{tt}^{\prime }|\le P_t(A/\alpha ).$$

Thus

$$\begin{array}{rcl}0& \ge & |\lambda -a_{tt}^{\prime }|-P_t(A/\alpha )\\ =& |\lambda -a_{j_t{j}_t}+(a_{j_t{i}_1},\dots ,a_{j_t{i}_k}){[A(\alpha )]}^{-1}\left(\begin{array}{c}{a}_{i_1{j}_t}\\ ⋮\\ a_{i_k{j}_t}\end{array}\right)|\\ -\underset{s\ne t}{\overset{l}{\sum _{s=1}}}|a_{j_t{j}_s}-(a_{j_t{i}_1},\dots ,a_{j_t{i}_k}){[A(\alpha )]}^{-1}\left(\begin{array}{c}{a}_{i_1{j}_s}\\ ⋮\\ a_{i_k{j}_s}\end{array}\right)|\\ \ge & |\lambda -a_{j_t{j}_t}|-\underset{s\ne t}{\overset{l}{\sum _{s=1}}}|a_{j_t{j}_s}|-\sum _{s=1}^l|(a_{j_t{i}_1},\dots ,a_{j_t{i}_k}){[A(\alpha )]}^{-1}\left(\begin{array}{c}{a}_{i_1{j}_s}\\ ⋮\\ a_{i_k{j}_s}\end{array}\right)|\\ \ge & |\lambda -a_{j_t{j}_t}|-\underset{s\ne t}{\overset{l}{\sum _{s=1}}}|a_{j_t{j}_s}|-\sum _{s=1}^l(|a_{j_t{i}_1}|,\dots ,|a_{j_t{i}_k}|){\left\{\mu [A(\alpha )]\right\}}^{-1}\left(\begin{array}{c}|a_{i_1{j}_s}|\\ ⋮\\ |a_{i_k{j}_s}|\end{array}\right)\\ \text{(by Lemmas 1 and 2)}\\ =& |\lambda -a_{j_t{j}_t}|-P_{j_t}(A)+\sum _{u=1}^k|a_{j_t{i}_u}|+w_{j_t}-w_{j_t}\\ -\sum _{s=1}^l(|a_{j_t{i}_1}|,\dots ,|a_{j_t{i}_k}|){\left\{\mu [A(\alpha )]\right\}}^{-1}\left(\begin{array}{c}|a_{i_1{j}_s}|\\ ⋮\\ |a_{i_k{j}_s}|\end{array}\right)\\ =& |\lambda -a_{j_t{j}_t}|-P_{j_t}(A)+w_{j_t}\\ +\sum _{u=1}^k|a_{j_t{i}_u}|-w_{j_t}-(|a_{j_t{i}_1}|,\dots ,|a_{j_t{i}_k}|){\left\{\mu [A(\alpha )]\right\}}^{-1}\left(\begin{array}{c}{\sum }_{s=1}^l|a_{i_1{j}_s}|\\ ⋮\\ {\sum }_{s=1}^l|a_{i_k{j}_s}|\end{array}\right)\\ =& |\lambda -a_{j_t{j}_t}|-P_{j_t}(A)+w_{j_t}\\ +\frac{1}{det\{\mu [A(\alpha )]\}}det\left(\begin{array}{cc}{\sum }_{u=1}^k|a_{j_t{i}_u}|-w_{j_t}& \begin{array}{ccc}-|a_{j_t{i}_1}|& \cdots & -|a_{j_t{i}_k}|\end{array}\\ \begin{array}{c}-{\sum }_{s=1}^l|a_{i_1{j}_s}|\\ ⋮\\ -{\sum }_{s=1}^l|a_{i_k{j}_s}|\end{array}& \mu [A(\alpha )]\end{array}\right).\end{array}$$

Hence, it is not difficult to get by (2.6) that

$$0\ge |\lambda -a_{tt}^{\prime }|-P_t(A/\alpha )>|\lambda -a_{j_t{j}_t}|-P_{j_t}(A)+w_{j_t},$$

i.e.,

$$|\lambda -a_{j_t{j}_t}|<P_{j_t}(A)-w_{j_t}.$$

 □

Remark 3 By Remark 2, it is obvious that Theorem 5 improves Theorem 3 of [1].

Corollary 3 Let $A\in {\mathbb{C}}^{n\times n}$, $\alpha =\{i_1,i_2,\dots ,i_k\}\subset N_r\ne \mathrm{\varnothing }$, ${\alpha }^{\prime }=N-\alpha =\{j_1,j_2,\dots ,j_l\}$. Then for each eigenvalue λ of $A/\alpha$, there exists $1\le t\le l$ such that

$$|\lambda -a_{j_t{j}_t}|<P_{j_t}(A).$$

In a similar way to the proof of Theorem 5, we obtain the following theorem according to Theorem 2.

Theorem 6 Let $A\in {\mathit{SDD}}_n$, $\alpha =\{i_0,i_1,i_2,\dots ,i_k\}$ with the index $i_0$ satisfying (1.5), ${\alpha }^{\prime }=N-\alpha =\{j_1,j_2,\dots ,j_l\}$. Then for each eigenvalue λ of $A/\alpha$, there exists $1\le t\le l$ such that

$$|\lambda -a_{j_t{j}_t}|<P_{j_t}(A)-(1-\frac{{\sum }_{u=1}^l|a_{i_0{j}_u}|}{|a_{i_0{i}_0}|-{\sum }_{j\ne i_0}^{j\in \alpha }|a_{i_{0}j}|})\sum _{v=1}^k|a_{j_t{i}_v}|.$$

(3.2)

Next, we obtain some distributions for the eigenvalues of the Schur complements of matrices under the conditions such as ${\mathit{PD}}_n^{\gamma }$ degree.

Lemma 5 [1]

Let $A\in {\mathbb{C}}^{n\times n}$ and $0\le \gamma \le 1$. Then for every eigenvalue λ of A, there exists $1\le i\le n$ such that

$$|\lambda -a_{ii}|\le P_i^{\gamma }(A)S_i^{1-\gamma }(A).$$

(3.3)

Theorem 7 Let $A\in {\mathbb{C}}^{n\times n}$, $\alpha =\{i_1,i_2,\dots ,i_k\}\subseteq N_r(A)\cap N_c(A)\ne \mathrm{\varnothing }$, ${\alpha }^{\prime }=N-\alpha =\{j_1,j_2,\dots ,j_l\}$, $|\alpha |<n$ . Then for each eigenvalue λ of $A/\alpha$, there exists $1\le t\le l$ such that

$$|\lambda -a_{j_t{j}_t}|<{(P_{j_t}(A)-w_t)}^{\gamma }{(S_{j_t}(A)-w_t^T)}^{1-\gamma }.$$

(3.4)

Proof Set $A/\alpha =(a_{ts}^{\prime })$. From Lemma 5, we know that for each eigenvalue λ of $A/\alpha$, there exists $1\le t\le l$ such that

$$|\lambda -a_{tt}^{\prime }|\le P_t^{\gamma }(A/\alpha )S_t^{1-\gamma }(A/\alpha ).$$

(3.5)

Hence,

$$\begin{array}{rcl}0& \ge & |\lambda -a_{tt}^{\prime }|-P_t^{\gamma }(A/\alpha )S_t^{(1-\gamma )}(A/\alpha )\\ =& |\lambda -a_{tt}^{\prime }|-{\left(\underset{s\ne t}{\overset{l}{\sum _{s=1}}}\left|a_{ts}^{\prime }\right|\right)}^{\gamma }{\left(\underset{s\ne t}{\overset{l}{\sum _{s=1}}}\left|a_{st}^{\prime }\right|\right)}^{1-\gamma }\\ =& |\lambda -a_{j_t{j}_t}+(a_{j_t{i}_1},\dots ,a_{j_t{i}_k}){[A(\alpha )]}^{-1}\left(\begin{array}{c}{a}_{i_1{j}_t}\\ ⋮\\ a_{i_k{j}_t}\end{array}\right)|\\ -{\left[\underset{s\ne t}{\overset{l}{\sum _{s=1}}}|a_{j_t{j}_s}-(a_{j_t{i}_1},\dots ,a_{j_t{i}_k}){[A(\alpha )]}^{-1}\left(\begin{array}{c}{a}_{i_1{j}_s}\\ ⋮\\ a_{i_k{j}_s}\end{array}\right)|\right]}^{\gamma }\\ \times {\left[\underset{s\ne t}{\overset{l}{\sum _{s=1}}}|a_{j_s{j}_t}-(a_{j_s{i}_1},\dots ,a_{j_s{i}_k}){[A(\alpha )]}^{-1}\left(\begin{array}{c}{a}_{i_1{j}_t}\\ ⋮\\ a_{i_k{j}_t}\end{array}\right)|\right]}^{(1-\gamma )}\\ \ge & |\lambda -a_{j_t{j}_t}|-|(a_{j_t{i}_1},\dots ,a_{j_t{i}_k}){[A(\alpha )]}^{-1}\left(\begin{array}{c}{a}_{i_1{j}_t}\\ ⋮\\ a_{i_k{j}_t}\end{array}\right)|\\ -{\left(\underset{s\ne t}{\overset{l}{\sum _{s=1}}}[|a_{j_t{j}_s}|+|(a_{j_t{i}_1},\dots ,a_{j_t{i}_k}){[A(\alpha )]}^{-1}\left(\begin{array}{c}{a}_{i_1{j}_s}\\ ⋮\\ a_{i_k{j}_s}\end{array}\right)|]\right)}^{\gamma }\\ \times {\left(\underset{s\ne t}{\overset{l}{\sum _{s=1}}}[|a_{j_s{j}_t}|+|(a_{j_s{i}_1},\dots ,a_{j_s{i}_k}){[A(\alpha )]}^{-1}\left(\begin{array}{c}{a}_{i_1{j}_t}\\ ⋮\\ a_{i_k{j}_t}\end{array}\right)|]\right)}^{1-\gamma }.\end{array}$$

(3.6)

From the proof of Theorem 3, we know

Therefore, from (3.6) we obtain

$$\begin{array}{rcl}0& \ge & |\lambda -a_{tt}^{\prime }|-P_t^{\gamma }(A/\alpha )S_t^{1-\gamma }(A/\alpha )\\ >& |\lambda -a_{j_t{j}_t}|-{(P_{j_t}(A)-w_t)}^{\gamma }{(S_{j_t}(A)-w_t^T)}^{1-\gamma }.\end{array}$$

Thus (3.4) holds. □

Remark 4 By Remark 2, it is obvious that Theorem 7 improves Theorem 4 of [1].

Corollary 4 Let $A\in {\mathbb{C}}^{n\times n}$, $\alpha =\{i_1,i_2,\dots ,i_k\}\subseteq N_r(A)\cap N_c(A)\ne \mathrm{\varnothing }$, ${\alpha }^{\prime }=N-\alpha =\{j_1,j_2,\dots ,j_l\}$, $|\alpha |<n$. Then for each eigenvalue λ of $A/\alpha$, there exists $1\le t\le l$ such that

$$|\lambda -a_{j_t{j}_t}|<P_{j_t}^{\gamma }(A)S_{j_t}^{1-\gamma }\le \gamma P_{j_t}(A)+(1-\gamma )S_{j_t}(A).$$

4 A numerical example

In this section, we show how to estimate the bounds for eigenvalues of the Schur complement with the elements of the original matrix to show the advantages of our results.

Example Let

$$A=\left(\begin{array}{ccccc}330& 323& 2& 3& 1\\ 321& 328& 3& 1& 2\\ 3& 2& 6& 7& 2\\ 2& 1& 1& 2& 6\\ 2& 1& 2& 3& 4\end{array}\right),\alpha =\{1,2\}.$$

If we estimate the bounds for eigenvalues of $A/\alpha$ by the elements of $A/\alpha$, there would be great computations to do. However, as

Since $\alpha \in N_r(A)$, according to Theorem 5, the eigenvalue z of $A/\alpha$ satisfies

$$z\in \{z\mid |z-6|\le 13.29\}\cup \{z\mid |z-2|\le 9.58\}\cup \{z\mid |z-4|\le 7.58\}\equiv G_1.$$

(4.1)

According to Theorem 3 in [1], the eigenvalue z of $A/\alpha$ satisfies

$$z\in \{z\mid |z-6|\le 13.98\}\cup \{z\mid |z-2|\le 9.99\}\cup \{z\mid |z-4|\le 7.99\}\equiv G_1^{\prime }.$$

(4.2)

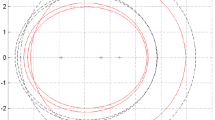
Further, we use Figure 1 to illustrate (4.1) and (4.2).

Figure 1

The red dotted line and blue dashed line denote the corresponding discs of ${\mathit{G}}_{\mathbf{1}}$ and ${\mathit{G}}_{\mathbf{1}}^{\mathbf{\prime }}$ , respectively.

It is clear that $G_1\subset G_1^{\prime }$ from both (4.1), (4.2) and Figure 1.

In addition, since $\alpha \in N_r(A)\cap N_c(A)$, by taking $\gamma =\frac{1}{2}$ in Theorem 7, the eigenvalue z of $A/\alpha$ satisfies

$$z\in \{z\mid |z-6|\le 9.64\}\cup \{z\mid |z-2|\le 11.24\}\cup \{z\mid |z-4|\le 8.87\}\equiv G_2.$$

(4.3)

According to Theorem 4 in [1], the eigenvalue z of $A/\alpha$ satisfies

$$z\in \{z\mid |z-6|\le 10.57\}\cup \{z\mid |z-2|\le 11.82\}\cup \{z\mid |z-4|\le 9.37\}\equiv G_2^{\prime }.$$

(4.4)

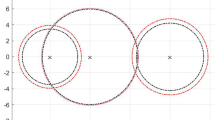
Further, we use Figure 2 to illustrate (4.3) and (4.4).

Figure 2

The red dotted line and blue dashed line denote the corresponding discs of ${\mathit{G}}_{\mathbf{2}}$ and ${\mathit{G}}_{\mathbf{2}}^{\mathbf{\prime }}$ , respectively.

It is clear that $G_2\subset G_2^{\prime }$ from both (4.3), (4.4) and Figure 2.