Dynamical system analysis of three-form field dark energy model with baryonic matter

Abstract

A cosmological model having matter field as (non) interacting dark energy (DE) and baryonic matter and minimally coupled to gravity is considered in the present work with flat FLRW space time. The DE is chosen in the form of a three-form field while radiation and dust (i.e; cold dark matter) are the baryonic part. The cosmic evolution is studied through dynamical system analysis of the autonomous system so formed from the evolution equations by suitable choice of the dimensionless variables. The stability of the non-hyperbolic critical points are examined by Center manifold theory and possible bifurcation scenarios have been examined.

1 Introduction

The cosmologists for the last 2 decades are tirelessly searching for a theory which shows the present accelerated expansion of the universe as predicted by a series of observational results [1]. Cosmologists are not unanimous over this issue rather they have two distinct opinions – one group is in favour of standard cosmology and they introduce some exotic matter (known as DE having large negative pressure) to explain this accelerated expansion while the other group prefers some modified gravity theory instead of Einstein gravity and they speculate that the extra geometric terms may responsible for this accelerated expansion [2].

In the context of the opinion of the first group the best candidate so far for DE is the cosmological constant which is simple in nature and observationally most favourable. But unfortunately, it has two severe drawbacks namely cosmological constant problem and cosmic coincidence problem [3]. As a result, several dynamic DE models in the form of perfect fluid with variable equation of state parameter (of various forms) come into picture (namely quintessence, tachyon, phantom [4] and chameleon [5, 6] etc). Also some complicated fields namely spinors [7], vectors [8], higher order spin field and three-form field [9, 10] are considered as DE (also one may refer [11,12,13,14] on the p-form and their stability properties, the three-form inflation and the center manifold). Also other positive aspects of the three-form fields in the context of cosmology are to obtain dynamically the late-time acceleration, to describe the phantom like behaviour [15] and to produce non-Gaussianities [16].

In the present work the three-form field is chosen as DE candidate. It has been shown that the dual of the three-form field is a scalar field which has an equivalence with K-inflation model [17] if the potential is non-quadratic in form. The present cosmological model contains this three-form field with (interacting, non-interacting) baryonic matter in the form of dust and radiation. Due to complicated form of the Einstein field Equations, the evolution equations are converted into an autonomous system by suitable choice of the dimensionless variables and non-hyperbolic equilibrium points are analyzed by Center manifold theory on the Hilbert space [18,19,20]. Bifurcation analysis [21] has been done to find the qualitative changes of global behavior due to different parameter values. The plan of the paper is as follows: Sect. 2 deals with basic equations for the three form field, Einstein field equations and energy conservation equations of both types of fluids. Autonomous system is formed and critical points are determined in Sect. 3. Also stability analysis and possible bifurcation scenarios have been examined in this section. Finally, the summary of the present work is proposed in Sect. 4.

2 The model and basic equations

For a three-form field $A_{\mu \nu \rho }$, the field strength tensor is given by

$$\begin{aligned} F_{\mu \nu \rho \sigma }= & {} 4\bigtriangledown _{_[\mu }A_{\nu \rho \sigma ]} \end{aligned}$$

(1)

where square bracket indicates anti-symmetrization of the indices. The action of this three-form field is given by

$$\begin{aligned} S_A= & {} \int d^4x \sqrt{-g}\left[ \frac{F^2}{48}+V(A^2)\right] \end{aligned}$$

(2)

where $V(A^2)$ is the potential of the field with $A^2=A^{\mu \nu \rho }A_{\mu \nu \rho }$. The energy–momentum tensor corresponding to this action is given by

$$\begin{aligned} T_{\mu \nu }= & {} \frac{1}{6}F_{\mu \alpha \beta \gamma }F^{\alpha \beta \gamma }_{\nu } +6V'(A^2)A_{\mu \alpha \beta }A^{\alpha \beta }_{\nu }\nonumber \\&-g_{\mu \nu } \left( \frac{1}{48}F_{\alpha \beta \gamma \rho } F^{\alpha \beta \gamma \rho }+V(A^2)\right) \end{aligned}$$

(3)

and the evolution equation of the three form field is obtained by varying the above action (2) with respect to $A^{\mu \nu \rho }$ as

$$\begin{aligned} \bigtriangledown ^{\alpha }F_{\alpha \mu \nu \rho }= & {} 12 V'(A^2)A_{\mu \nu \rho } \end{aligned}$$

(4)

where an over dash denotes differentiation with respect to the argument. The present cosmological model is considered in the background of homogeneous and isotropic flat Friedmann–Lemaître–Robertson–Walker (FLRW) space-time manifold having line element (choosing $c=1$)

$$\begin{aligned} ds^2=-dt^2+a^2(t)\left[ dr^2+r^2\left( d\theta ^2+sin^2\theta d\phi ^2\right) \right] . \end{aligned}$$

(5)

So the three form field has only time dependence and the above evolution Eq. (4) results $A_{0\mu \nu }=0$. Thus the spatial components of the three-form field can be written as

$$\begin{aligned} A_{ijk}= & {} a^3(t)\epsilon _{ijk}X(t), \end{aligned}$$

(6)

where $\epsilon _{ijk}$ is the three dimensional Levi-Civita symbol (with $\epsilon _{123}$=1). So the scalars $A^2$ and X are related as $A^2=6X^2$ and the equation of motion (4) of the three-form field gives the evolution of the scalar field X(t) as

$$\begin{aligned} {\ddot{X}}-3H{\dot{X}}-3{\dot{H}}X= & {} -V,_{X} \end{aligned}$$

(7)

where differentiation with respect to the cosmic time ‘t’ is denoted by over dot in the above equation. Now from the expression (3) of the energy–momentum tensor for the three-form field, the explicit form of the energy–density and the pressure of the scalar field X are given by

$$\begin{aligned} \rho _{_X}= & {} \frac{1}{2}\left( {\dot{X}}+3HX\right) ^2+V(X) \end{aligned}$$

(8)

$$\begin{aligned} p_{_X}= & {} -\frac{1}{2}\left( {\dot{X}}+3HX\right) ^2-V(X)+XV,_X \end{aligned}$$

(9)

having equation of state parameter

$$\begin{aligned} \omega _{_X}=\frac{ p_{_X}}{\rho _{_X}}=-1+\frac{XV,_X}{\rho _{_X}}. \end{aligned}$$

(10)

Thus if $V,_X(=\frac{dV}{dX})$ is positive then the three-form field behaves as DE (i.e; non-phantom) while the field behaves as phantom field if $V,_X<0$.

Now for the present cosmological model the action integral for the whole system (assuming the three-form field to be minimally coupled to gravity) is given by

$$\begin{aligned} S_T= & {} -\int d^4x \sqrt{-g}\left[ \frac{1}{2{\kappa }^2} R-\frac{F^2}{48}-V(A^2)\right] +S_{B}, \end{aligned}$$

(11)

where $\kappa ^2=8\pi G$, R is the usual Ricci scalar and $S_B$, the standard action integral for the baryonic matter (in the form of dust and radiation) is given by

$$\begin{aligned} S_B=-\int d^4x\sqrt{-g}~\rho _{_B}=\int d^4x\sqrt{-g}~p_{_B}. \end{aligned}$$

(12)

The last equality in the above expression for $S_B$ holds upto a total derivative [22]. Here $\rho _{_B}$ and $p_{_B}$ are the energy density and thermodynamic pressure of the baryonic matter respectively. Now varying the action with respect to the metric tensor gives the usual Friedmann equations as

$$\begin{aligned} 3H^2= & {} \kappa ^2\left( \rho _{A}+\rho _{_r}+\rho {_d}\right) , \end{aligned}$$

(13)

$$\begin{aligned} 2{\dot{H}}= & {} -\kappa ^2[\left( \rho _{_A}+p_{_A}\right) +\rho {_r}\left( 1+\omega {_r}\right) +\rho {_d}], \end{aligned}$$

(14)

where $\rho _r$, $\rho _d$ are respectively the energy density of radiation and dust part of the matter and $\omega _r=\frac{1}{3}$ is the equation of state parameter for radiation. Also the energy conservation equations are [assuming three form field interacts with dust, the cold dark matter (CDM)]

$$\begin{aligned}&\dot{\rho _{_A}}+3H(\rho _{A}+p_{A})=-Q, \end{aligned}$$

(15)

$$\begin{aligned}&\dot{\rho _{r}}+4H\rho _{r}=0, \end{aligned}$$

(16)

$$\begin{aligned}&\dot{\rho _{_d}}+3H\rho _{d}=Q. \end{aligned}$$

(17)

Now due to this interaction, the evolution of the scalar field X (i.e., Eq. (7)) modifies to

$$\begin{aligned} {\ddot{X}}+3H{\dot{X}}+3{\dot{H}}X+\frac{dV}{dX}= & {} -\frac{Q}{{\dot{X}}+3HX}. \end{aligned}$$

(18)

In the present work, two possible choices for Q are taken as (i) $Q=\alpha \rho _{_d}({\dot{X}}+3HX)$ and (ii) $Q=\alpha \rho _{_d} H$, where $\alpha$ is the coupling parameter. Note that the above choices of Q are purely phenomenological and the only motivation of choosing such Q is the formation of the autonomous system (in Sect. 3 below) with the choices of the dimensionless variables [in Eq. (20)]. Further, in order to derive the evolution Eqs. (15) and (17) for the three-form field and dust, the interaction Lagrangian is of the form [22]

$$\begin{aligned} {\mathcal {L}}_{int}=-\sqrt{-g}~f\left( X,{\dot{X}}, \rho _{_m}, H\right) , \end{aligned}$$

(19)

where ‘f’ is an arbitrary function which will specify the particular model. Also ‘f’ depends only on the dynamical degrees of freedom of the fluids.

3 Formation of autonomous system: critical point and stability analysis

We now define a set of dimensionless variables as [23]

$$\begin{aligned} x\equiv & {} \kappa X,\quad y\equiv \frac{\kappa }{\sqrt{6}}(X'+3X),\quad z^2\equiv \frac{\kappa ^2 V}{3H^2},\nonumber \\ u^2\equiv & {} \frac{\kappa ^2\rho _{_r}}{3H^2},\quad v^2\equiv \frac{\kappa ^2 \rho _{_d}}{3H^2},\quad \lambda (x)\equiv -\frac{1}{\kappa }\frac{V,_X}{V}, \end{aligned}$$

(20)

the equation of state parameter can be written in the form

$$\begin{aligned} \omega _{tot}= -y^2-z^2(1+\lambda (x) x) +u^2 \end{aligned}$$

(21)

and the cosmic evolution equations (in the last section) can be written in an autonomous system as

$$\begin{aligned} x'= & {} 3\left( \sqrt{\frac{2}{3}}y-x\right) , \end{aligned}$$

(22)

$$\begin{aligned} y'= & {} -\frac{3}{2}\lambda (x) z^2\left( xy-\sqrt{\frac{2}{3}}\right) +\frac{3}{2}\left( \frac{4}{3}u^2+v^2\right) y, \end{aligned}$$

(23)

$$\begin{aligned} v'= & {} -\frac{3}{2}v\left[ 1+\lambda (x) x z^2-\frac{4}{3}u^2-v^2\right] , \end{aligned}$$

(24)

$$\begin{aligned} u'= & {} -\frac{3}{2}u\left[ \frac{4}{3}+\lambda (x) x z^2-\frac{4}{3}u^2-v^2\right] , \end{aligned}$$

(25)

where ‘dash’ over a variable denotes differentiation with respect to $N=ln~a$. Note that all the above dimensionless variables are not independent, rather due to first Friedmann equation (i.e; Eq. (13)) they are constrained by the relation

$$\begin{aligned} y^2+z^2+u^2+v^2= & {} 1 \end{aligned}$$

(26)

and we have 4D phase space for the dynamical system.

In the present work for simplicity of calculation the potential of the scalar field X (i.e; V(X) ) is chosen as

$$\begin{aligned} V(X)=V_0 e^{-\mu x} \end{aligned}$$

(27)

where $V_0(>0)$ and $\mu$ are constant parameters, so that $\lambda (X)$ is a non-zero constant. Also $\mu$ can be interpreted as the rate of decrease of the logarithm of the potential function. The properties of the critical points of the above autonomous system (22–25) are represented in the following lemmas.

Lemma 1

Critical points can be located either on u-nullcline or on v-nullcline.

Proof

Let us prove this by contradiction. We assume that both v and u $\ne 0$. Then from Eqs. (24) and (25) we have

$$\begin{aligned} 1+R=0\quad \text {and} \quad \frac{4}{3} +R=0 \end{aligned}$$

where $R=\lambda (x) x z^2-\frac{4}{3}u^2-v^2$. But it is not possible to exist any such R. $\square$

Lemma 2

If $v=0$ and $u \ne 0$, then either $y=0$ or $\sqrt{\frac{2}{3}}\lambda (x) y \ne -2\sqrt{2}$ and $\lambda (x) y <0$.

Table 1 Table shows the set of critical points, existence of critical points and the value of cosmological parameters corresponding to autonomous system (22–25)

Proof

If $v=0$, then either $u=0$ or $\frac{4}{3}(1-u^2) + \lambda (x) x z^2 = 0$. From Eq. (22) we have $x=\sqrt{\frac{2}{3}}y$. This implies

$$\begin{aligned} \frac{4}{3}(1-u^2) + \sqrt{\frac{2}{3}}\lambda (x) y z^2=0. \end{aligned}$$

(28)

So either $y=0$ or $z^2=\frac{-2\sqrt{2}(1-u^2)}{\sqrt{3}\lambda (x) y}$. For $v=0$, we also have the condition $u^2+y^2+z^2 =1$. If $\sqrt{\frac{2}{3}}\lambda (x) y= -2\sqrt{2}$, then $z^2=1-u^2$ which implies $y=0$. This proves $\sqrt{\frac{2}{3}}\lambda (x) y \ne -2\sqrt{2}$ and $\lambda (x) y <0$. $\square$

Lemma 3

If $v= 0$, $u \ne 0$ and $y\ne 0$, then $(u^2-1)(y^2-1)=u^2y^2$.

Proof

From Eqs. (22) and (23) we have

$$\begin{aligned} -\frac{3}{2}\lambda (x) z^2 (y^2-1) + 2 u^2y=0 \end{aligned}$$

Multiplying both side by y and using Eq. (28) we get $(u^2-1)(y^2-1)=u^2y^2$. $\square$

Lemma 4

If $u=0$ and $v\ne 0$, then either $y=0$ or $y=-\sqrt{\frac{2}{3}}\lambda (x)z^2$.

Proof

From Eq. (23) we have

$$\begin{aligned} \sqrt{\frac{3}{2}}v^2y=\lambda (x) z^2(y^2-1). \end{aligned}$$

(29)

On the other hand, for $y\ne 0$, from Eq. (24) we have

$$\begin{aligned} v^2y=y+\sqrt{\frac{2}{3}}\lambda (x)y^2z^2 \end{aligned}$$

(30)

Equating $v^2y$ in Eqs. (29) and (30) we can derive $y=-\sqrt{\frac{2}{3}}\lambda (x)z^2$. $\square$

Theorem 1

• 1. $x=\pm \sqrt{\frac{2}{3}}$ are the critical points of the autonomous system (22–25).

• 2. There is no critical point for which $u\ne 0$ and $v\ne 0$.

• 3. If $v=0$ and $u \ne 0$, then $u= \pm 1$.

• 4. If $u=0$ and $v\ne 0$, then $v=\pm 1$.

Proof

• (1) Follows form Eqs. (22) and (23) when u and v are both 0.

• (2) Follows from Lemma 1.

• (3) If we consider the hypothesis of Lemma 3, then from Lemma 2 we can derive $\sqrt{\frac{2}{3}}\lambda (x) y = -2\sqrt{2}$ which is a contradiction to our hypothesis. So y must be 0. Then from the relation $u^2+y^2+z^2 =1$, we have $z=\pm \sqrt{1-u^2}$. But due to Eq. (23), $z=0$ which yields $u=\pm 1$.

• (4) If $y=0$, then $x=0$. And Eq. (23) implies $z=0$. Then the relation $y^2+z^2+v^2=1$ yields $v=\pm 1$.

If $y\ne 0$, then by Lemma 4 we have $v= \pm \sqrt{1-\frac{2}{3}\lambda ^2(x)z^4-z^2}$. But $y^2+z^2+v^2=1$ and Eq. (23) yield $z=0$. So $v= \pm 1$. $\square$

3.1 Non-interacting three-form field

The vector fields of the autonomous system (22–25) for non-interacting three-form field for exponential potential can be analyzed as follows. By taking exponential potential we will get $\lambda (x)=\mu$. The set of critical points, existence of critical points and the value of cosmological parameters are shown in Table 1 and the eigenvalues and the nature of critical points are shown in Table 2.

Table 2 Table shows the eigenvalues $(\lambda _1,~\lambda _2,~\lambda _3,~\lambda _4)$ of the Jacobian matrix corresponding to the critical points and the nature of all critical points for this non-interacting model:

The first two critical points (i.e., $C_0$, $C_1$) represent the evolution of the universe with barotropic matter and vanishing DE. In fact, the critical point $C_0$ describes the relativistic radiation era of evolution while $C_1$ represents the dust phase of evolution. The remaining three critical points namely $C_2 - C_4$ are fully dominated by DE and they correspond to de-Sitter phase.

4 Stability analysis

4.1 Critical point $C_0$

The Jacobian matrix at the critical point $C_0$ can be put as

$$\begin{aligned} J(C_0)=\begin{bmatrix} -3 &{} \sqrt{6} &{} 0 &{} 0\\ 0 &{} 2 &{} 0 &{} \mp \sqrt{6} \mu \\ 0 &{} 0 &{} \frac{1}{2} &{} 0 \\ 0 &{} 0 &{} 0 &{} 4\\ \end{bmatrix}. \end{aligned}$$

(31)

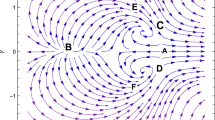
The eigenvalues of $J(C_0)$ are $-3$, 2, $\frac{1}{2}$ and 4 (hyperbolic in character) with eigenvectors $[1,0,0,0]^T$, $\left[ \frac{\sqrt{6}}{5}, 1, 0, 0\right] ^T$, $[0 , 0, 1, 0]^T$ and $\left[ \mp \frac{3\mu }{7}, \mp \sqrt{\frac{3}{2}}\mu , 0, 1\right] ^T$ respectively. So, we can use Hartman–Grobman theorem for analyzing the stability of this critical point. As three eigenvalues are positive and one is negative, so the critical point $C_0$ is a saddle node and unstable in nature. For $\mu >0$ the phase portrait in all possible 3D coordinate system near the origin are shown as in Fig. 1.

Fig. 1

All possible 3 dimensional phase plots corresponding to the critical point $C_0(0,0,0,1)$ for $\mu >0$; a represents phase plot in xyv-coordinate system (saddle node), b represents phase plot in yvu-coordinate system (unstable node), c represents phase plot in xyu-coordinate system (saddle node), d represents phase plot in xvu-coordinate system (saddle node). We refer the interested readers to Appendix A for corresponding Mathematica code

4.2 Critical point $C_1$

The Jacobian matrix at the critical point $C_1$ can be put as

$$\begin{aligned} J(C_1)=\begin{bmatrix} -3 &{} \sqrt{6} &{} 0 &{} 0\\ 0 &{} \frac{3}{2} &{} \mp \sqrt{6} \mu &{} 0\\ 0 &{} 0&{} 3 &{} 0 \\ 0 &{} 0 &{} 0 &{} -\frac{1}{2}\\ \end{bmatrix}. \end{aligned}$$

(32)

The eigenvalues of $J(C_1)$ are $-3$, $\frac{3}{2}$, 3 and $-\frac{1}{2}$ (hyperbolic in character) with eigenvectors $[1,0,0,0]^T$, $\left[ \frac{2}{3}\sqrt{\frac{2}{3}}, 1, 0, 0\right] ^T$, $\left[ \mp \frac{2\mu }{3} , \mp 2\sqrt{\frac{2}{3}}\mu , 1, 0\right] ^T$ and $[ 0, 0, 0, 1]^T$ respectively. So, we can use Hartman–Grobman theorem for analyzing the stability of this critical point. Since two eigenvalues are positive and another two eigenvalues are negative, hence the critical point $C_1$ is unstable due to its saddle nature.

4.3 Critical point $C_2$

The Jacobian matrix at the critical point $C_2$ can be put as

$$\begin{aligned} J(C_2)=\begin{bmatrix} -3 &{} \sqrt{6} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0&{} -\frac{3}{2} &{} 0 \\ 0 &{} 0 &{} 0 &{} -2\\ \end{bmatrix}. \end{aligned}$$

(33)

The eigenvalues of $J(C_2)$ are $-3$, 0, $-\frac{3}{2}$ and $-2$ (non-hyperbolic in character) with eigenvectors $[1, 0, 0, 0]^T$, $\left[ \sqrt{\frac{2}{3}}, 1, 0, 0\right] ^T$, $[0, 0, 1, 0]^T$, $[0, 0, 0, 1, 0]^T$ and $[0, 0, 0, 1]^T$ respectively. To apply Center Manifold Theory, we first transform the coordinate system $\left( x=X+\sqrt{\frac{2}{3}},~ y=Y+1, v=V,~ u=U\right)$ so that $C_2$ moves to the origin. As a result, the autonomous system (22–25) changes to

$$\begin{aligned} X'= & {} -3X+\sqrt{6}Y, \end{aligned}$$

(34)

$$\begin{aligned} Y'= & {} \sqrt{6}\mu Y^2+3\mu XY+\frac{3}{2}V^2+2U^2+\sqrt{\frac{3}{2}}\mu Y^3\nonumber \\&+\frac{9}{2}\mu XY^2+\frac{3}{2}\mu XU^2\nonumber \\&+\frac{3}{2}\mu XV^2+\frac{3}{2}\mu XY^3\nonumber \\&+\frac{3}{2}\mu XYU^2+\frac{3}{2}\mu XYV^2\nonumber \\&+\sqrt{\frac{3}{2}}\mu U^2Y +\sqrt{\frac{3}{2}}\mu V^2Y+2U^2Y+\frac{3}{2}V^2Y, \end{aligned}$$

(35)

$$\begin{aligned} V'= & {} -\frac{3}{2}V+\sqrt{6}\mu VY+3\mu VXY+\frac{3}{2}\mu VXU^2\nonumber \\&+\sqrt{\frac{3}{2}}\mu VU^2+\frac{3}{2}\mu XV^3+\sqrt{\frac{3}{2}}\mu V^3 +\frac{3}{2}\mu VXY^2\nonumber \\&+\sqrt{\frac{3}{2}}\mu VY^2 +2U^2V+\frac{3}{2}V^3, \end{aligned}$$

(36)

$$\begin{aligned} U'= & {} -2U+\sqrt{6}\mu UY+2U^3+\frac{3}{2}UV^2+3\mu UXY\nonumber \\&+\sqrt{\frac{3}{2}}\mu U^3+\frac{3}{2}\mu UXY^2+\sqrt{\frac{3}{2}}\mu UY^2+\frac{3}{2}\mu XU^3\nonumber \\&+\frac{3}{2}\mu UXV^2+\sqrt{\frac{3}{2}}\mu UV^2. \end{aligned}$$

(37)

Now, we can see that there is a linear term of Y in the R.H.S. of (34), so we have to introduce another set of new coordinates so that the Jacobian matrix (33) transforms into the diagonal form. By using the eigenvectors of the Jacobian matrix (33), we introduce the following coordinate system

$$\begin{aligned} \begin{bmatrix} X_T\\ Y_T\\ V_T \\ U_T \end{bmatrix}=\begin{bmatrix} 1 &{} -\sqrt{\frac{2}{3}} &{} 0 &{} 0 \\ 0 &{} 1 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \\ 0 &{} 0 &{} 0 &{} 1 &{} \end{bmatrix} \begin{bmatrix} X\\ Y\\ V\\ U \end{bmatrix} \end{aligned}$$

(38)

Fig. 2

Vector field near the origin for the critical point $C_2$ in ($X_TY_T$)-plane. L.H.S. is for $\mu <0$ and R.H.S. is for $\mu >0$

and in these new coordinates the equations are transformed into

$$\begin{aligned} \begin{bmatrix} X_T'\\ Y_T'\\ V_T'\\ U_T' \end{bmatrix}= \begin{bmatrix} -3 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} -\frac{3}{2} &{} 0 \\ 0 &{} 0 &{} 0 &{} -2 \end{bmatrix} \begin{bmatrix} X_T\\ Y_T\\ V_T\\ U_T \end{bmatrix}+ \begin{bmatrix} non\\ lin\\ ear\\ terms \end{bmatrix}. \end{aligned}$$

(39)

So by center manifold theory there exists a continuously differentiable function $h:\mathbb {R} \rightarrow \mathbb {R}^3$ such that

$$\begin{aligned} h(Y_T)=\begin{bmatrix} X_T \\ V_T \\ U_T \end{bmatrix} =\begin{bmatrix} a_1Y_T^2+a_2Y_T^3 + {\mathcal {O}}\left( Y_T^4\right) \\ b_1Y_T^2+b_2Y_T^3 + {\mathcal {O}}\left( Y_T^4\right) \\ c_1Y_T^2+c_2Y_T^3 + {\mathcal {O}}\left( Y_T^4\right) \end{bmatrix}. \end{aligned}$$

(40)

Differentiating both sides with respect to N, we get

$$\begin{aligned} X_T'= & {} (2a_1Y_T+3a_2Y_T^2)Y_T'+{\mathcal {O}}\left( Y_T^3\right) , \end{aligned}$$

(41)

$$\begin{aligned} V_T'= & {} (2b_1Y_T+3b_2Y_T^2)Y_T'+{\mathcal {O}}\left( Y_T^3\right) , \end{aligned}$$

(42)

$$\begin{aligned} U_T'= & {} (2c_1Y_T+3c_2Y_T^2)Y_T'+{\mathcal {O}}\left( Y_T^3\right) , \end{aligned}$$

(43)

where $a_i$, $b_i$, $c_i$ $\epsilon$ $\mathbb {R}$. We only concern about the non-zero coefficients of the lowest power terms in Center Manifold Theory as we analyze arbitrary small neighborhood of the origin. Comparing coefficients of the corresponding power of $Y_T$, we get the following center manifold

$$\begin{aligned} X_T= & {} -\frac{4\mu }{3}Y_T^2+\left( -\frac{4\mu }{3}+\frac{20}{3} \sqrt{\frac{2}{3}}\mu ^2\right) Y_T^3+{\mathcal {O}}\left( Y_T^4\right) , \end{aligned}$$

(44)

$$\begin{aligned} V_T= & {} 0, \end{aligned}$$

(45)

$$\begin{aligned} U_T= & {} 0. \end{aligned}$$

(46)

This implies that one dimensional center manifold lies on the $(X_TY_T)$-plane and tangent to the center subspace ($Y_T$ axis) at the origin. The flow on the center manifold near the origin is determined by

$$\begin{aligned} \frac{dY_T}{dN}= & {} 2\sqrt{6}\mu Y_T^2+(2\sqrt{6}\mu -4\mu ^2)Y_T^3+{\mathcal {O}}\left( Y_T^4\right) . \end{aligned}$$

(47)

The flow on the center manifold depends on the sign of $\mu$. For both the cases $\mu >0$ and $\mu <0$, the origin is a saddle node and unstable in nature (Fig. 2). As the new coordinate system $\left( X_T,~Y_T,~V_T,~U_T\right)$ is topologically equivalent to the old one, hence the origin in the new coordinate system, i.e., the critical point $C_2$ in the old coordinate system (x,  y,  u,  v) is a saddle node and unstable in nature.

4.4 Critical point $C_3$

The Jacobian matrix at the critical point $C_3$ and the corresponding eigenvalues and eigenvectors are same as for the critical point $C_2$. If we put forward similar argument as we have mentioned for the analysis of $C_2$ then we get the following center manifold

$$\begin{aligned} X_T= & {} -\frac{4\mu }{3}Y_T^2+\left( \frac{4\mu }{3}+\frac{20}{3} \sqrt{\frac{2}{3}}\mu ^2\right) Y_T^3, \end{aligned}$$

(48)

$$\begin{aligned} V_T= & {} 0, \end{aligned}$$

(49)

$$\begin{aligned} U_T= & {} 0 \end{aligned}$$

(50)

and the flow on the center manifold is determined by

$$\begin{aligned} \frac{dY_T}{dN}= & {} 2\sqrt{6}\mu Y_T^2-(2\sqrt{6}\mu +4\mu ^2)Y_T^3+{\mathcal {O}}\left( Y_T^4\right) . \end{aligned}$$

(51)

Since our interest only on the coefficient of the lowest power term of $Y_T$ in the expression of the center manifold and also the flow on the center manifold, so the vector field near the origin is same as for the critical point $C_2$ (Fig. 2). Hence, the critical point $C_3$ is unstable due to its saddle nature in the old coordinate system.

4.5 Critical point $C_4$

The critical point $C_4$ exists only for $\mu =0$. The Jacobian matrix at the critical point $C_4$ is same as (33), so the eigenvalues and corresponding eigenvectors are same as for (33). Since, the critical point $C_4$ is non-hyperbolic in nature so we can use center manifold theory. But here the center manifold is determined by

$$\begin{aligned} X_T= & {} 0, \end{aligned}$$

(52)

$$\begin{aligned} V_T= & {} 0, \end{aligned}$$

(53)

$$\begin{aligned} U_T= & {} 0 \end{aligned}$$

(54)

and the flow on the center manifold is determined by

$$\begin{aligned} \frac{dY_T}{dN}= & {} 0. \end{aligned}$$

(55)

Since, from this information we can not determine the nature of the vector field near the origin. So, we only try to define stability of the vector field near the origin on each plane. The stability of the vector field on each plane are shown in Table 3.

Table 3 Stability of the vector field on every coordinate plane for the critical point $C_4$

4.6 Coupling three-form field with dark matter

The existence of the coupling can be represented by the modified continuity equations (15) and (17), where $\rho _{_d}$ stands for energy density of dust, $\rho _{_A}$ is the energy density of three-form field and Q is the energy transfer between dark energy and dark matter.

Then the autonomous system changes due to Eqs. (15) and (17) as follows

$$\begin{aligned} x'= & {} 3\left( \sqrt{\frac{2}{3}}y-x\right) , \end{aligned}$$

(56)

$$\begin{aligned} y'= & {} I-\frac{3}{2}\lambda (x) z^2\left( xy-\sqrt{\frac{2}{3}}\right) +\frac{3}{2}\left( \frac{4}{3}u^2+v^2\right) y, \end{aligned}$$

(57)

$$\begin{aligned} v'= & {} -\frac{Iy}{v}-\frac{3}{2}v\left[ 1+\lambda (x) x z^2-\frac{4}{3}u^2-v^2\right] , \end{aligned}$$

(58)

$$\begin{aligned} u'= & {} -\frac{3}{2}u\left[ \frac{4}{3}+\lambda (x) x z^2-\frac{4}{3}u^2-v^2\right] , \end{aligned}$$

(59)

where $I=\frac{\kappa Q}{\sqrt{6}({\dot{X}}+3HX)H^2}$ and ‘prime’ denotes derivative w.r.t $N=ln~a$.

The properties of the critical points of the above autonomous system (depending on the choices of I) are presented in the form of lemmas as follows (we shall consider the relation $x=\sqrt{\frac{2}{3}}y$ due to Eq. (56)).

Lemma 5

If u, v and y are non-zero, then $z=0$ and the following relations must hold together

• 1. $I=\frac{v^2}{2y}$,

• 2. $y^2+ u^2 + v^2 =1$,

• 3. $4u^2+3v^2=4$.

Proof

• (1) From Eq. (59), it is to be noted that $R=-\frac{4}{3}$. Then from Eq. (58), we have $I=\frac{v^2}{2y}$.

• (2) The Eq. (57) and I yield

  $$\begin{aligned} \sqrt{6}\lambda (x)z^2(y^2-1)y= 4u^2y^2+3v^2y^2 + v^2. \end{aligned}$$

  (60)

  On the other hand, $R= -\frac{4}{3}$ yields

  $$\begin{aligned} \sqrt{6}\lambda (x) y z^2= 4u^2+3v^2 -4 \end{aligned}$$

  (61)

  So from Eqs. (60) and (61) we have $y^2+ u^2 + v^2 =1$.

• (3) The result of (2) implies $z=0$ due to relation (26). So from Eq. (61) we have $4u^2+3v^2=4$.

$\square$

Lemma 6

If only $u=0$, then the following conditions must hold together

• 1. $\lambda (x)=\sqrt{\frac{3}{2}}\frac{v^2}{z^2y}$,

• 2. $I=-\frac{3}{2}\frac{v^2}{y}$,

• 3. $y^2+v^2+z^2=1$.

Proof

• (1) From Eq. (58) , we have

  $$\begin{aligned} Iy=-\frac{3v^2}{2}\left[ 1+\sqrt{\frac{2}{3}}\lambda (x)yz^2-v^2\right] \end{aligned}$$

  (62)

  From Eq. (57), we have

  $$\begin{aligned} Iy=\sqrt{\frac{3}{2}}\lambda (x)yz^2(y^2-1)-\frac{3}{2}y^2. \end{aligned}$$

  (63)

  Eliminating Iy from (62) and (63) and using (26), we have $\lambda (x)=\sqrt{\frac{3}{2}}\frac{v^2}{z^2y}$.

• (2) Put the expression of $\lambda (x)$ in (58), we have $I=-\frac{3}{2}\frac{v^2}{y}$.

• (3) Due to relation (26), we get $y^2+v^2+z^2=1$.

$\square$

Corollary 1

If only $u=0$ and $I=\frac{v}{y}\alpha$, then $\alpha =-\frac{3v}{2}$ and critical points contain any real y,v and z with $y^2+v^2+z^2=1$.

Lemma 7

If only u and $z=0$, then $I=-\frac{3}{2}v^2y$ and critical points contain any real v and y with $v^2+y^2=1$.

Proof

From (57), we have

$$\begin{aligned} I=-\frac{3}{2}v^2y. \end{aligned}$$

(64)

From (58), we have

$$\begin{aligned} I=-\frac{3}{2}\frac{v^2(1-v^2)}{y}. \end{aligned}$$

(65)

From (64) and (65) we get $v^2+y^2=1$ which also satisfies (26). $\square$

Corollary 2

If only u, $z=0$ and $I=\frac{v}{y}\alpha$, then $\alpha =-\frac{3}{2}vy^2$ and critical points contain any real v and y with $v^2+y^2=1$.

Lemma 8

If $v=0$ and $I=v\alpha$, then y must be 0 and $u=\pm 1$.

Proof

From (58). we have $y=0$. Then from (59), we have $u= \pm 1$ which satisfies (57) due to (26). $\square$

Lemma 9

Consider $I=v^2 \alpha$. Then if $v=0$, then $z=0$ and critical points contain any real u and y with $u^2+y^2=1$.

Proof

We consider $y\ne 0$. So from (57), we have

$$\begin{aligned} \sqrt{6}\lambda (x)yz^2(y^2-1)=4u^2y^2. \end{aligned}$$

(66)

From (59), we have

$$\begin{aligned} \sqrt{6}\lambda (x)yz^2=4u^2-4. \end{aligned}$$

(67)

So eliminating $\sqrt{6}\lambda (x)yz^2$ from (66) and (67) we get $u^2+y^2=1$ and (26) yield $z=0$. $\square$

Corollary 3

Consider $I=v^2 \alpha$. If v, $u=0$ and $y\ne 0$, then $z=0$ which implies $y=\pm 1$. If v, $y=0$ and $u\ne 0$, then $z=0$ which implies $u=\pm 1$ and if v, u, $y=0$, then $z=\pm 1$.

Lemma 10

If $y=0$, then either $u=\pm 1$ or $v=\pm 1$ and $I=0$ at the critical points.

Proof

From (58) and (59) we get at least one of u and v is 0. If $u=0$ then $v=\pm 1$ and if $v=0$ then $u =\pm 1$. For the both cases, (26) yields $z=0$. The Eq. (57) implies $I=0$ at the critical points. $\square$

Remark 1

If y, u and v are 0, then $z=\pm 1$. In this case, $I=-\sqrt{\frac{3}{2}}\lambda (x)$.

Lemma 11

If $z\ne 0$ and $y\ne 0$, then $u=0$ and $v\ne 0$, so lemma 6 can be applied.

Proof

Let us assume v and $u\ne 0$. From (58), we have $I=\frac{v^2}{2y}$. From (59), we have $\sqrt{6}\lambda (x)yz^2=4u^2+3v^2-4$. Then from (57) we get $u^2+v^2+y^2=1$. So by (26), $z=0$ which contradicts to our hypothesis.

Now we consider only $v=0$. Then by Lemmas 8 and 9, $z=0$ which contradicts to our hypothesis. So $u=0$ and Lemma 6 can be applied. $\square$

Theorem 2

• 1. There is no critical point with all non-zero coordinates for any I and $\lambda (x)$.

• 2. Any critical point can not contain both u and v non-zero coordinates.

• 3. critical points on the u-nullcline satisfy $z^2\lambda (x)=-\sqrt{\frac{2}{3}}I$.

• 4. On the v-nullcline the critical points form a right cylinder of height $2\sqrt{\frac{2}{3}}$ with circular base for $I=v^n\alpha$, ($n>1$).

• 5. Origin is the only critical point on zy-plane.

Proof

• (1) If any critical point contains all non-zero coordinates then Lemma 5 contradicts.

• (2) If both u and v are non-zero, then y has to be non zero. Otherwise, Theorem 1 contradicts. Now by Lemma 5z turns out to be 0 and $I=\frac{v^2}{2y}$. On the other hand, if we put the expression of I and $4u^2+3v^2=4$ in (57) we derive that $v^2+4y^2=0$ which implies both v and y are 0. But this contradicts our hypothesis.

• (3) For u-nullcline, by Lemma 6, we have $\lambda (x)=\sqrt{\frac{3}{2}}\frac{v^2}{z^2y}$. So $z^2\lambda (x)=-\sqrt{\frac{2}{3}}I$.

• (4) For $n=1$, by Lemma 8, we have $u=\pm 1$. Now the result true for $n=2$ by Lemma 9. It is also should be note that the result is true for $n>2$ with exactly same argument as of $n=2$ in Lemma 9

• (5) Origin is a critical point. Now by Lemma 11 we can derive that both u and v cant not be 0 in this case.

$\square$

For two choices of Q, i.e., $(a)~ Q=\alpha \rho _{_d}({\dot{X}}+3HX)$, $(b)~ Q= \alpha \rho _{_d} H$; I becomes $\frac{\alpha }{2}v^2$, $\frac{\alpha v^2}{2y}$ respectively. Now for these two choices of Q we analyze the stability of the vector field near the origin for the autonomous system (56–59).

4.7 $Q=\alpha \rho _{_d}(\dot{X}+3HX)$

For this choice of interaction the autonomous system (56–59) changes to

$$\begin{aligned} x'= & {} 3\left( \sqrt{\frac{2}{3}}y-x\right) , \end{aligned}$$

(68)

$$\begin{aligned} y'= & {} \frac{\alpha }{2}v^2-\frac{3}{2}\mu z^2\left( xy-\sqrt{\frac{2}{3}}\right) +\frac{3}{2}\left( \frac{4}{3}u^2+v^2\right) y, \end{aligned}$$

(69)

$$\begin{aligned} v'= & {} -\frac{\alpha vy}{2}-\frac{3}{2}v\left[ 1+\mu x z^2-\frac{4}{3}u^2-v^2\right] , \end{aligned}$$

(70)

$$\begin{aligned} u'= & {} -\frac{3}{2}u\left[ \frac{4}{3}+\mu x z^2-\frac{4}{3}u^2-v^2\right] . \end{aligned}$$

(71)

The critical points, existence of critical points and the value of cosmological parameters are shown in Table 4 and the eigenvalues and the nature of critical points are shown in Table 5.

Table 4 Table shows the set of critical points, existence of critical points and the value of cosmological parameters corresponding to autonomous system (68–71)

Table 5 Table shows the eigenvalues $(\lambda _1,~\lambda _2,~\lambda _3,~\lambda _4)$ of the Jacobian matrix for the autonomous system (68–71) corresponding to the critical points ($P_0$–$P_4$) and the nature of the critical points ($P_0$–$P_4$)

In Table 4 there are six critical points of which the first four namely $P_0$–$P_3$ are equivalent to the critical points$C_0, C_2$–$C_4$ respectively in Table 1 from cosmological view point. The critical point $P_4$ describes the cosmic evolution due to interacting DE and CDM for $\alpha \ne \pm 3$. For $\alpha =\pm 3$; the matter is purely in the form of cosmological constant. So this critical point corresponds to scaling solution in cosmology. As long as the coupling parameter ‘$\alpha$’ is restricted as $\alpha ^2<3$ then CDM dominates over DE otherwise there is accelerated expansion. For critical point $P_5$ the DE in the form of a scalar field interacting with CDM. But here cosmic evolution is dominated by DE and is in the de-Sitter era of evolution.

5 Stability analysis

5.1 Critical point $P_0$

The Jacobian matrix at $P_0$ is same as (31). So the eigenvalues and the corresponding eigenvectors are also same. Since, the critical point is hyperbolic, we can analyze the stability of this critical point by Hartman–Grobman theorem. The stability of this critical point is same as the stability for $C_0$ (Fig. 1).

5.2 Critical point $P_1$

The Jacobian matrix at the critical point $P_1$ can be put as

$$\begin{aligned} J(P_1)=\begin{bmatrix} -3 &{} \sqrt{6} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0&{} -\frac{(3+\alpha )}{2} &{} 0 \\ 0 &{} 0 &{} 0 &{} -2\\ \end{bmatrix}. \end{aligned}$$

(72)

Here we will take four choices of $\alpha$ for analyzing the stability of this critical point :

• (i) $\alpha \ne -3, 1, 3$;

• (ii) $\alpha =-3$;

• (iii) $\alpha =1$;

• (iv) $\alpha =3$.

5.3 Case (i): $\alpha \ne -3, 1, 3$

For this case the eigenvalues of the above Jacobian matrix are $-3$, 0, $-\frac{(3+\alpha )}{2}$, $-2$ (non-hyperbolic in nature) and $[1, 0, 0, 0]^T$, $\left[ 1, \sqrt{\frac{3}{2}}, 0, 0\right] ^T$, $[0, 0, 1, 0]^T$, $[0, 0, 0, 1]^T$ are the corresponding eigenvectors. We put forward similar argument as we have mentioned for the analysis of $C_2$ then the center manifold is given by (44–46) and the flow on the center manifold is determined by (47). So, the origin is a saddle node and unstable in nature (Fig. 2). Hence, in this case the origin in the new coordinate system, i.e., the critical point $P_1$ in the old coordinate system is a saddle node and unstable in nature.

5.4 Case (ii): $\alpha =-3$

In this case the Jacobian matrix at the critical point $P_1$ can be put as

$$\begin{aligned} J(P_1)=\begin{bmatrix} -3 &{} \sqrt{6} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0&{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -2\\ \end{bmatrix}. \end{aligned}$$

(73)

The eigenvalues of the above Jacobian matrix are $-3$, 0, 0, $-2$ (non-hyperbolic in nature). $[1, 0, 0, 0]^T$ and $[0, 0, 0, 1]^T$ are the eigenvectors corresponding to the eigenvalues $-3$ and $-2$ respectively, $\left[ 1, \sqrt{\frac{3}{2}}, 0, 0\right] ^T$ and $[0, 0, 1, 0]^T$ are the eigenvectors corresponding to the eigenvalue 0. Since the algebraic multiplicity and the geometric multiplicity corresponding to each eigenvalues are equal so we can transform (73) to the diagonal form. Similarly as above we will take the same transformations so that $P_1$ moves to the origin and then introduce another transformation (38) (by using the eigenvectors of (73)) to make the Jacobian matrix (73) into the diagonal form. In these coordinates, our system of equations are transformed into

$$\begin{aligned} \begin{bmatrix} X_T'\\ Y_T'\\ V_T'\\ U_T' \end{bmatrix}= \begin{bmatrix} -3 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} -2 \end{bmatrix} \begin{bmatrix} X_T\\ Y_T\\ V_T\\ U_T \end{bmatrix}+ \begin{bmatrix} non\\ lin\\ ear\\ terms \end{bmatrix}. \end{aligned}$$

(74)

So by center manifold theory there exists two continuously differentiable functions $\chi$:$\mathbb {R}^2 \rightarrow \mathbb {R}$ and $\phi$:$\mathbb {R}^2 \rightarrow \mathbb {R}$ such that

$$\begin{aligned} X_T=&\chi (Y_T,V_T)=a_1Y_T^2+a_2Y_TV_T+a_3V_T^2\nonumber \\&+\,higher\, order\,terms, \end{aligned}$$

(75)

$$\begin{aligned} U_T=&\phi (Y_T,V_T)=b_1Y_T^2+b_2Y_TV_T+b_3V_T^2\nonumber \\&+\,higher\,order\,terms. \end{aligned}$$

(76)

Now differentiating both sides with respect to N, we get

$$\begin{aligned} \frac{dX_T}{dN}=\left[ 2a_1Y_T+a_2V_T ~ a_2U_T+2a_3V_T\right] \begin{bmatrix} \frac{dY_T}{dN}\\ ~\\ \frac{dV_T}{dN}\\ \end{bmatrix}, \end{aligned}$$

(77)

$$\begin{aligned} \frac{dU_T}{dN}=\left[ 2b_1Y_T+b_2V_T ~ b_2U_T+2b_3V_T\right] \begin{bmatrix} \frac{dY_T}{dN}\\ ~\\ \frac{dV_T}{dN}\\ \end{bmatrix}. \end{aligned}$$

(78)

Comparing L.H.S. and R.H.S. of (77) and (78), we get $a_1=-\frac{4\lambda }{3}, a_2=0, a_3=0$ and $b_i=0$ for all i. Then the center manifold is given by

$$\begin{aligned} X_T= & {} -\frac{4\mu }{3}Y_T^2 +higher \,order\,terms, \end{aligned}$$

(79)

$$\begin{aligned} U_T= & {} 0. \end{aligned}$$

(80)

The flow on the center manifold is determined by

$$\begin{aligned} \frac{dY_T}{dN}= & {} 2\sqrt{6}\mu Y_T^2+\left( 2\sqrt{6}\mu -4\mu ^2\right) Y_T^3\nonumber \\&+\left( \frac{3}{2}+\sqrt{6}\mu \right) V_T^2Y_T+higher\,order\,terms, \end{aligned}$$

(81)

$$\begin{aligned} \frac{dV_T}{dN}= & {} \left( \frac{3}{2}+\sqrt{6}\mu \right) V_TY_T+3\sqrt{\frac{3}{2}}\mu V_TY_T^2\nonumber \\&+\left( \frac{3}{2}+\sqrt{\frac{3}{2}}\mu \right) V_T^3+ higher\,order\,terms. \end{aligned}$$

(82)

Case (ii)(a): $\mu >0$

Then the coefficient of lowest power terms of (81) and (82) both are positive. Now divide both sides of (81) and (82) by $2\sqrt{6}$ and $(\frac{3}{2}+\sqrt{6}\mu )$ respectively and since by dividing both sides any positive number there will no effect on the flow of the vector field, we take $r^2=Y_T^2+V_T^2$, in arbitrary small neighborhood of the origin. Differentiating both sides with respect to N, we get $r'=Y_T r$. For $Y_T<0$ one has $r'<0$ while $r'>0$ for $Y_T>0$. So, for $\mu >0$ the origin is a saddle node and unstable in nature (vector field near the origin is same as Fig. 2b).

Case (ii)(b): $\mu <-\frac{1}{2}\sqrt{\frac{3}{2}}$

Then the coefficient of lowest power terms of (81) and (82) both are negative. We assume $2\sqrt{6}\mu$=-$\sigma ^2$ and $(\frac{3}{2}+\sqrt{6}\mu )=-\gamma ^2$ and divide (81) by $\sigma ^2$ and (82) by $\gamma ^2$ and we take $r^2=Y_T^2+V_T^2$, in arbitrary small neighborhood of the origin. Differentiating both sides with respect to N, we get $r'=-Y_T r$. For $Y_T<0$ one has $r'>0$ while $r'<0$ for $Y_T>0$. So, for $\mu <-\frac{1}{2}\sqrt{\frac{3}{2}}$ the origin is a saddle node and unstable in nature (vector field near the origin is same as Fig. 2a).

As for both of the subcases in this case the origin is unstable due to its saddle nature. Hence, in the old coordinate system (x,  y,  v,  u) the critical point $P_1$ is a saddle node, i.e., unstable in nature.

5.5 Case (iii): $\alpha = 1$

In this case the eigenvalues of the Jacobian matrix are $-3$, 0, $-2$, $-2$ and $[1, 0, 0, 0]^T$, $\left[ 1, \sqrt{\frac{3}{2}}, 0, 0\right] ^T$ are the eigenvectors corresponding to the eigenvalues $-3$ and 0 respectively, $[0, 0, 1, 0]^T$ and $[0, 0, 0, 1]^T$ are the eigenvectors corresponding to the eigenvalue $-2$. But for this case we will get the same vector field as Case-(i).

5.6 Case (iv): $\alpha = 3$

Then the eigenvalues of the Jacobian matrix are $-3$, 0, $-3$ and $-2$. $[1, 0, 0, 0]^T$ and $[0, 0, 1, 0]^T$ are the eigenvectors corresponding to the eigenvalue $-3$ and $\left[ 1, \sqrt{\frac{3}{2}}, 0, 0\right] ^T$ and$[0, 0, 0, 1]^T$ are the eigenvectors corresponding to the eigenvalues 0 and $-2$ respectively. But for this case also we will get the same vector field as Case (i).

5.7 Critical point $P_2$

The Jacobian matrix at the critical point $P_2$ can be put as

$$\begin{aligned} J(P_2)=\begin{bmatrix} -3 &{} \sqrt{6} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0&{} \frac{(\alpha -3)}{2} &{} 0 \\ 0 &{} 0 &{} 0 &{} -2\\ \end{bmatrix} \end{aligned}$$

(83)

For avoiding similar calculation, we only state the expression of the center manifold and the flow on the center manifold. Here we also take four choices of $\alpha$ for analyzing the stability of this critical point :

• (i) $\alpha \ne -3, -1, 3$;

• (ii) $\alpha =3$;

• (iii) $\alpha =-1$;

• (iv) $\alpha =-3$.

5.8 Case (i): $\alpha \ne -3,-1,3$

The eigenvalues of the Jacobian matrix are $-3$, 0, $\frac{(\alpha -3)}{2}$, $-2$ and $[1, 0, 0, 0]^T$, $\left[ 1, \sqrt{\frac{3}{2}}, 0, 0\right] ^T$, $[0, 0, 1, 0]^T$ and $[0, 0, 0, 1]^T$ are the corresponding eigenvectors. In this case the center manifold is same as (48–50) and the flow on the center manifold is determined by (51). So, the origin is a saddle node and unstable in nature (Fig. 2). Hence in the new coordinate system due to saddle nature of the origin, the critical point $P_2$ is a saddle node and unstable in nature.

5.9 Case (ii): $\alpha = 3$

In this case, the center manifold is given by

$$\begin{aligned} X_T= & {} -\frac{4\mu }{3}Y_T^2 +higher \,order\,terms, \end{aligned}$$

(84)

$$\begin{aligned} U_T= & {} 0. \end{aligned}$$

(85)

The flow on the center manifold is determined by

$$\begin{aligned} \frac{dY_T}{dN}= & {} 2\sqrt{6}\mu Y_T^2-\left( 2\sqrt{6}\mu +4\mu ^2\right) Y_T^3\nonumber \\&+\left( \frac{3}{2}-\sqrt{6}\mu \right) V_T^2Y_T+higher\,order\,terms, \end{aligned}$$

(86)

$$\begin{aligned} \frac{dV_T}{dN}= & {} \left( -\frac{3}{2}+\sqrt{6}\mu \right) V_TY_T-3\sqrt{\frac{3}{2}}\mu V_TY_T^2\nonumber \\&+\left( \frac{3}{2}-\sqrt{\frac{3}{2}}\mu \right) V_T^3+higher \,order\,terms. \end{aligned}$$

(87)

Case (ii)(a): $\mu >\frac{1}{2}\sqrt{\frac{3}{2}}$

In this case as above, divide both sides of (86) and (87) by $2\sqrt{6}\mu$ and $(-\frac{3}{2}+\sqrt{6}\mu )$ respectively and by taking $r^2=Y_T^2+V_T^2$ , we can get $r'=Y_Tr$. If $Y_T>0$ then $r'>0$ and $r'<0$ while $Y_T<0$. So, the origin is a saddle node and unstable in nature (same as Fig. 2b).

Case (ii)(b): $\mu <0$

In this case also by taking $r^2=Y_T^2+V_T^2$ , we can get $r'=-Y_Tr$ and as above we can determine that the origin is a saddle node and unstable in nature (same as Fig. 2a).

As for both of the subcases in this case also the origin is a saddle node, hence in the old coordinate system (x,  y,  v,  u) the critical point $P_2$ is a saddle node and unstable in nature.

5.10 Case (iii) $\alpha =-1$

In this case we will get the same eigenvalues and eigenvectors as in Case (iii) of the critical point $P_1$ and the center manifold is given by (48–50) and the flow on the vector field near the origin is determined by (51).

5.11 Case (iv) $\alpha =-3$

In this case we will get the same eigenvalues and eigenvectors as in Case (iv) of the critical point $P_1$ and the center manifold is given by (48–50) and the flow on the vector field near the origin is determined by (51).

5.12 Critical point $P_3$

The Jacobian matrix at the critical point $P_3$ can be put as

$$\begin{aligned} J(P_3)=\begin{bmatrix} -3 &{} \sqrt{6} &{} 0 &{} 0\\ 0 &{} 0 &{} 0 &{} 0\\ 0 &{} 0&{} -\frac{(3+\alpha y_c)}{2} &{} 0 \\ 0 &{} 0 &{} 0 &{} -2\\ \end{bmatrix}. \end{aligned}$$

(88)

and the center manifold is same as (52–54) and the flow on the center manifold is determined by (55). So, here we only define the stability near the origin on each coordinate plane which is shown in Table 6.

Table 6 Stability of the vector field on every coordinate plane for the critical point $P_3$

5.13 Critical point $P_4$

The Jacobian matrix at the critical point $P_4$ can be put as

$$\begin{aligned} J(P_4)=\begin{bmatrix} -3 &{} \sqrt{6} &{} 0 &{} 0\\ 0 &{} \left( 1-\frac{\alpha ^2}{9}\right) \left( \frac{3}{2}+\alpha \mu \sqrt{\frac{2}{3}}\right) &{} \mp \sqrt{6}\mu \left( 1-\frac{\alpha ^2}{9}\right) ^\frac{3}{2} &{} 0\\ 0 &{} \mp \sqrt{\left( 1-\frac{\alpha ^2}{9}\right) }\left( \frac{\alpha ^2\mu }{3}\sqrt{\frac{2}{3}}-\frac{\alpha }{2}\right) &{} 3\left( 1-\frac{\alpha ^2}{9}\right) \left( 1-\frac{\alpha \mu }{3}\sqrt{\frac{2}{3}}\right) &{} 0 \\ 0 &{} 0 &{} 0 &{} -\frac{1}{2}\left( 1+\frac{\alpha ^2}{3}\right) \\ \end{bmatrix}. \end{aligned}$$

(89)

Table 7 The set of critical points, existence of critical points and the value of cosmological parameters corresponding to the critical points for the autonomous system (90–93)

Table 8 Table shows the eigenvalues $(\lambda _1,~\lambda _2,~\lambda _3,~\lambda _4)$ of the Jacobian matrix for the autonomous system (90–93) corresponding to the above critical points and the nature of the critical points:

The eigenvalues of $J(P_4)$ are $-3$, $3\left( 1-\frac{\alpha ^2}{9}\right)$, $\frac{3}{2}\left( 1-\frac{\alpha ^2}{9}\right)$ and $-\frac{1}{2}\left( 1+\frac{\alpha ^2}{3}\right)$ and the corresponding eigenvectors are $[1, 0, 0, 0]^T$, $\left[ \pm \frac{\sqrt{6}(k-n+p)}{m(6+k+n+p)}, \pm \frac{k-n+p}{2m}, 1, 0\right] ^T$, $\left[ \pm \frac{\sqrt{6}(k-n-p)}{m(6+k+n-p)}, \pm \frac{k-n+p}{2m}, 1, 0\right] ^T$, $[0, 0, 0, 1]^T$ respectively; where $k=\left( 1-\frac{\alpha ^2}{9}\right) \left( \frac{3}{2}+\alpha \mu \sqrt{\frac{2}{3}}\right)$, $l=-\sqrt{6}\mu \left( 1-\frac{\alpha ^2}{9}\right) ^\frac{3}{2}$, $m=-\sqrt{\left( 1-\frac{\alpha ^2}{9}\right) }\left( \frac{\alpha ^2\mu }{3}\sqrt{\frac{2}{3}}-\frac{\alpha }{2}\right)$, $n=3\left( 1-\frac{\alpha ^2}{9}\right) \left( 1-\frac{\alpha \mu }{3}\sqrt{\frac{2}{3}}\right)$, $p=\frac{3}{2}\left( 1-\frac{\alpha ^2}{9}\right)$. The critical point $P_4$ is non-hyperbolic for $\alpha =\pm 3$ and for $\alpha =-3$ the critical point is same as $P_1$ and we have already analyzed the stability of this critical point and for $\alpha =3$ the critical point is same as $P_2$ and we have also analyzed the stability of this critical point. So we have to analyze the stability of the critical point $P_4$ only when this is hyperbolic in nature and by Hartman–Grobman theorem we shall analyze the stability of this critical point. All eigenvalues of the above Jacobian matrix are negative only when $\alpha >3$ or $\alpha <-3$ but this contradicts the existence of this critical point. So we have two positive and two negative eigenvalues and by Hartman–Grobman theorem we can say that the critical point $P_4$ is unstable due to its saddle nature.

If we try to analyze the stability of the critical point $P_5$ then we see that the values of $\frac{\partial f_1}{\partial x}$, $\frac{\partial f_1}{\partial y}$, $\frac{\partial f_2}{\partial x}$, $\frac{\partial f_2}{\partial y}$, $\frac{\partial f_2}{\partial v}$, $\frac{\partial f_3}{\partial x}$, $\frac{\partial f_3}{\partial y}$, $\frac{\partial f_3}{\partial v}$, $\frac{\partial f_4}{\partial u}$ are non-zero and without $\frac{\partial f_1}{\partial x}$, $\frac{\partial f_1}{\partial y}$ all other elements at this critical point contain complicated terms and this is very difficult to find the eigenvalues and corresponding eigenvectors of the Jacobian matrix. For this complicated calculation, we skip the stability analysis of this critical point.

5.14 $Q=\alpha \rho _{_d} H$

For this choice of interaction with exponential potential the autonomous system (56–59) changes to

$$\begin{aligned} x'= & {} 3\left( \sqrt{\frac{2}{3}}y-x\right) , \end{aligned}$$

(90)

$$\begin{aligned} y'= & {} \frac{\alpha }{2y}v^2-\frac{3}{2}\mu z^2\left( xy-\sqrt{\frac{2}{3}}\right) +\frac{3}{2}\left( \frac{4}{3}u^2+v^2\right) y, \end{aligned}$$

(91)

$$\begin{aligned} v'= & {} -\frac{\alpha v}{2}-\frac{3}{2}v\left[ 1+\mu x z^2-\frac{4}{3}u^2-v^2\right] , \end{aligned}$$

(92)

$$\begin{aligned} u'= & {} -\frac{3}{2}u\left[ \frac{4}{3}+\mu x z^2-\frac{4}{3}u^2-v^2\right] . \end{aligned}$$

(93)

The critical points, existence of critical points and the value of cosmological parameters are shown in Table 7 and the eigenvalues and the nature of critical points are shown in Table 8.

The first three critical points $B_1$–$B_3$ in Table 7 are cosmologically equivalent to the critical points $C_2$–$C_4$ in Table 1. The critical point $B_4$ represents a scaling cosmological solution where DE is interacting with CDM. The CDM dominates the evolution for $-1<\alpha <0$, otherwise there is accelerated expansion due to dominance of DE. For $\alpha =-3$ the matter is purely in the form of cosmological constant.

6 Stability analysis

6.1 Critical point $B_1$

The Jacobian matrix at the critical point $B_1$ is same as (72). So here we also take four choices of $\alpha$ (same as $P_1$) for analyzing the stability of this critical point.

6.2 Case (i): $\alpha \ne -3, 1, 3$

In this case we have the same eigenvalues and corresponding eigenvectors of the Jacobian matrix. We put forward similar argument as we have mentioned for the stability analysis of $P_1$ in case (i), then the center manifold is given by (44–46) and the flow on the vector field near the origin is determined by (47) (Fig. 2).

Table 9 Center manifold, flow on the CM and the stability near the origin corresponding to the critical point $B_2$

Table 10 Stability of the vector field on every coordinate plane for the critical point $B_3$

6.3 Case (ii): $\alpha =-3$

In this case we also get the same Jacobian matrix (73), so have the same eigenvalues and corresponding eigenvectors. We put forward similar argument as we have mentioned for the analysis of $P_1$ in case (ii), then we get the center manifold same as (79–80) and the flow on the center manifold is determined by

$$\begin{aligned} \frac{dY_T}{dN}= & {} 2\sqrt{6}\mu Y_T^2+\left( 2\sqrt{6}\mu -4\mu ^2\right) Y_T^3\nonumber \\&+\left( \frac{3}{2}+\sqrt{6}\mu \right) V_T^2Y_T+higher \,order\, terms, \end{aligned}$$

(94)

$$\begin{aligned} \frac{dV_T}{dN}= & {} \sqrt{6}\mu V_TY_T+3\sqrt{\frac{3}{2}}\mu V_TY_T^2\nonumber \\&+\left( \frac{3}{2}+\sqrt{\frac{3}{2}}\mu \right) V_T^3 +higher\, order\,terms. \end{aligned}$$

(95)

Case (ii)(a): $\mu >0$

Divide (94) and (95) by $2\sqrt{6}\mu$ and $\sqrt{6}\mu$ respectively and as the flow on the vector field is not changed due to divide by positive number on the flow equation, we take $r^2=Y_T^2+V_T^2$, then we get $r'=Y_T r$. If $Y_T>0$ then $r'>0$ and $r'<0$ while $Y_T<0$. So, the origin is a saddle node and unstable in nature (Fig. 2b).

Case (ii)(b): $\mu <0$

We put forward similar argument as we have mentioned above then we also obtain that the origin is a saddle node and unstable in nature (same as Fig. 2a).

As for both of the subcases in this case the origin is unstable due to its saddle nature. Hence, in the old coordinate system (x,  y,  v,  u) the critical point $B_1$ is a saddle node, i.e., unstable in nature.

6.4 Case (iii): $\alpha = 1$

In this case the eigenvalues of the Jacobian matrix are $-3$, 0, $-2$, $-2$ and $[1, 0, 0, 0]^T$, $\left[ 1, \sqrt{\frac{3}{2}}, 0, 0\right] ^T$ are the eigenvectors corresponding to the eigenvalues $-3$ and 0 respectively, $[0, 0, 1, 0]^T$ and $[0, 0, 0, 1]^T$ are the eigenvectors corresponding to the eigenvalue $-2$. But for this case we will get the same vector field as Case (i).

6.5 Case (iv): $\alpha = 3$

Then the eigenvalues of the Jacobian matrix are $-3$, 0, $-3$ and $-2$. $[1, 0, 0, 0]^T$ and $[0, 0, 1, 0]^T$ are the eigenvectors corresponding to the eigenvalues $-3$, $\left[ 1, \sqrt{\frac{3}{2}}, 0, 0\right] ^T$ and $[0, 0, 0, 1]^T$ are the eigenvectors corresponding to the eigenvalues 0 and $-2$ respectively. But for this case also we will get the same vector field as Case (i).

6.6 Critical point $B_2$

The Jacobian matrix at this critical points is also same as (72). Here also arises four cases. The center manifold and the flow on the center manifold are shown in the Table 9. As for all possible cases in the new coordinate system $\left( X_T,~Y_T,~V_T,~U_T\right)$ the origin is a saddle node, i.e., unstable in nature. Hence, in the old coordinate system (x,  y,  v,  u) the critical point $B_2$ is a saddle node and unstable in nature.

6.7 Critical point $B_3$

The Jacobian matrix at the critical point $B_3$ is same as (72). Here, we will get the center manifold same as (52–54) and the flow on the center manifold is same as (55). So, here we only define the stability of the vector field near the origin on each coordinate plane, shown in Table 10.

6.8 Critical point $B_4$

The Jacobian matrix at $B_4$ can be put as

$$\begin{aligned}&J(B_4)=\nonumber \\&\quad \begin{bmatrix} -3 &{} \sqrt{6} &{} 0 &{} 0\\ 0 &{} \left( 1+\frac{\alpha }{3}\right) (3\mp \sqrt{-2\alpha }\mu )&{} \mp \sqrt{6}\mu \left( 1+\frac{\alpha }{3}\right) ^\frac{3}{2} &{} 0\\ 0 &{} \mp \sqrt{\frac{2}{3}}\mu \alpha \sqrt{\left( 1+\frac{\alpha }{3}\right) }&{} \left( 1+\frac{\alpha }{3}\right) (3\pm \sqrt{-2\alpha }\mu ) &{} 0 \\ 0 &{} 0 &{} 0 &{} -\frac{1}{2}(1-\alpha ) \end{bmatrix}.\nonumber \\ \end{aligned}$$

(96)

The eigenvalues of the above Jacobian matrix are $-3$, $\alpha +3$, $\alpha +3$ and $-\frac{1}{2}(1-\alpha )$. $[1, 0, 0, 0]^T$, $[0,0,0,1]^T$ are the eigenvectors corresponding to the eigenvalues $-3$ and $-\frac{1}{2}(1-\alpha )$ respectively and $[\frac{\sqrt{6}(k-n)}{m(6+k+n)},\frac{k-n}{2m}, 1, 0]^T$ be the eigenvector corresponding to the eigenvalue $\alpha +3$; where $k=\left( 1+\frac{\alpha }{3}\right) (3\mp \sqrt{-2\alpha }\mu )$, $m=\mp \sqrt{\frac{2}{3}}\mu \alpha \sqrt{\left( 1+\frac{\alpha }{3}\right) }$ and $n=\left( 1+\frac{\alpha }{3}\right) (3\pm \sqrt{-2\alpha }\mu )$). We clearly see that this critical point is non-hyperbolic only when $\alpha =-3$ and the stability analysis for this case already studied for $B_1$. So here we analyze the stability of this critical point only when $\alpha \epsilon (-3,0)$. For this case the two eigenvalues are positive and another two are negative. So by Hartman–Grobman theorem we can say that the critical point $B_4$ is unstable due to its saddle nature.

7 Global behavior and bifurcation analysis

For non-interacting model with exponential potential, we have five critical points $(C_0$–$C_4)$ for various choices of $\mu$. It is to be noted from matrix (32), that $C_0$ is saddle with one stable and three unstable eigen-directions. On the other hand, $C_1$ is saddle with two stable and two unstable eigen-directions. The stability of $C_0$ and $C_1$ do not depend on the parameter $\mu$. At $C_2$ and $C_3$ the effective potential [10] reaches its extreme point in the dark energy dominated period. We can have global behavior of phase space and the main property of bifurcations on different nullclines. On the Y-nullcline, the vector field does not depend on $\mu$. But on the center manifold of $C_2$ and $C_3$ the flow reverses its direction when $\mu$ passes through the value $\mu =0$. But the vector fields remain topologically equivalent even after $\mu$ changes its sign. At $\mu =0$, the stability is classified by considering the flow of the remaining eigen-directions. At $\mu =0$, new non-isolated critical point $C_4$ appears to exist. $C_4$ is normally hyperbolic and stable in nature. It is to be noted that, for $\mu \ne 0$, $C_2$ and $C_3$ are saddle-node in nature. So there exists a non-generic de-Sitter evolution of the universe through only one trajectory (i.e; invariant manifold) from past ($C_2$ or $C_3$) to future ($C_3$ or $C_2$). For $\mu >0$, if the trajectory starts near $C_2$ and ends asymptotically to $C_3$, then the three form field transit from phantom field to non-phantom field and reverse transition happens for $\mu <0$. As $C_4$ is stable with de-Sitter phase, so there is a generic evolution near $C_2$ or $C_3$ towards $C_4$ at $\mu =0$.

Next, we have considered the interaction $Q=\alpha (\rho _{_d})({\dot{X}}+3HX)$. For exponential potential there exists three critical points $(P_0$–$P_5)$ for various choices to $\mu$. At $\alpha =\pm 3$, $P_1$ and $P_2$ change its stability. On the other hand, at $\mu =0$, new non-isolated critical point $P_3$ appears to exist. $P_3$ is normally hyperbolic and on the Y-nullcline $P_3$ becomes stable node to saddle node when $\alpha$ becomes smaller than $-\frac{3}{y_c}$, $(y_c\ne 0)$ for any fixed $y_c$ ($0<y_c\leqslant 1$). When $\alpha$ touches $\pm 3$ and lies in $[-3,0)\cup (0,3]$, a new critical point $P_4$ appears to exist. $P_1$ and $P_2$ are the special case of $P_4$ at $\alpha =\pm 3$.

For interaction $Q=\alpha (\rho _{_d})yH$, at $\alpha \ne 3,-3$, both $P_1$ and $P_2$ are saddle node in nature. So there exists a non-generic de-Sitter evolution of the universe through the invariant manifold (86) from past $P_2$ to future $P_3$.

For the interaction $\alpha \rho _{_d} H$, a new critical point $B_4$ appears to exist for $\alpha \in [-3,0)$. This critical point changes its stability at $-3$ and $\mu =0$. For $\mu \ne 0$, $B_4$ is saddle node in nature. So the evolution of the universe through the invariant manifold is performed as in the previous case.

Now, it is to be noted that at $\mu =0$, the system associated with non-interacting model becomes structurally unstable. On the other hand, two new bifurcation values appear for the interacting model, namely $\alpha =-3,~3$. Moreover, at $\mu =0$, the system associated with interacting model becomes structurally unstable. Also one may note that the potential becomes runaway to non-runaway through bifurcation value $\mu =0$ [23]. On the other hand, if we neglect the contribution of matter and radiation, the fixed points at the extremum point of the effective potential [10] are same as in our non-interacting dynamical equation i.e., $C_2$ and $C_3$ which trigger non-generic evolution of the universe.

8 Summary

The present work is an example where without making any attempt of solving the complicated coupled cosmic evolution equations (Einstein field equations), the cosmological interferences have been done using the technique of dynamical system analysis. The cosmic matter is chosen as three-form field (DE) interacting/non-interacting with baryonic matter (radiation with CDM). By suitable choice of the dimensionless variables the evolution equations are converted into an autonomous system for non-interacting case and for two suitable choices of the interaction. Out of total fifteen equilibrium points (presented in Tables 1, 4 and 7) the following sets of critical points $(C_0, P_0)$, $(C_2, P_1, B_1)$, $(C_3, P_2, B_2)$, $(C_4, P_3, B_3)$ are equivalent both cosmologically as well as from dynamical system analysis. It is to be noted that the set of critical points $(C_4, P_3. B_3)$ are essentially a line of critical points. The first set describes the radiation era of evolution while the remaining three sets correspond to accelerated expansion at the de-Sitter phase. The critical point $C_1$ describes the CDM dominated decelerated expansion. Although the critical point $P_5$ represents interacting DE and CDM but it also corresponds to de-Sitter phase. The most interesting critical points are $P_4$ and $B_4$ which are representing scaling cosmological solutions. Also the cosmic evolution representing these two critical points are observationally important as by choosing the coupling parameter $\alpha$ to be closed to $\pm 3$ (for critical point $P_4$) / $-3$ (for $B_4$) the equation of state parameter agrees (within confidence limit) with the latest plank data [24].

The stability of the critical points are analysed by studying the eigenvalues of the Jacobian matrix for hyperbolic critical points while center manifold theory has been employed for non-hyperbolic critical points. The two parameters $\mu$ (in the potential) and $\alpha$ (coupling) on the system are found to be important for bifurcation analysis. Usually, it is speculated that at the bifurcation point there may be a cosmic phase transition.

Finally, the general nature of the critical points both for non-interacting and interacting cases have been presented in the form of lemmas and theorems. Lastly, one may note that the present work does not depend effectively on the choice of V(X) .

Appendices

Appendix A: Mathematica code for Fig. 1 (choose $\mu =1$)

Mathematica code for Fig. 1a:

Fig. 3

Vector field near the origin in $Y_TV_T$-plane for $\alpha =-3$. After shifting and matrix transformation, the line of critical points $B_3$ (in the old coordinate system (x, y, v, u)) is completely lying on the $Y_T$ axis in the new coordinate system. For determining this vector field we have taken $y_c=\frac{1}{2}$. So, in the new coordinate system the origin in $Y_TV_T$-plane is corresponding to $\left( 0,\frac{1}{2},0,0\right)$ in old coordinate system. We refer the interested readers to Appendix B for corresponding Matlab code

${PhasePlot}[\{-3x+\sqrt{6} y,2y,\frac{1}{2} v\},\{x,-1,1\},\{y,-1,1\},\{v,-1,1\},\{-10,10\},{GridPoints}\rightarrow 5,PlotStyle\rightarrow RGBColor,Axes\rightarrow True]$

Mathematica code for Fig. 1b:

${PhasePlot}[\{2y-\sqrt{6}u,\frac{1}{2} v,4u\},\{y,-1,1\},\{v,-1,1\},\{u,-1,1\},\{-10,10\},{GridPoints}\rightarrow 5,PlotStyle\rightarrow RGBColor,Axes\rightarrow True]$

Mathematica code for Fig. 1c:

${PhasePlot}[\{-3x+\sqrt{6}y,2y-\sqrt{6}u,4u\},\{x,-1,1\}, \{y,-1,1\},\{u,-1,1\},\{-10,10\},{GridPoints}\rightarrow 5 ,PlotStyle\rightarrow RGBColor,Axes\rightarrow True]$

Mathematica code for Fig. 1d:

${PhasePlot}[\{-3x,\frac{1}{2} v,4u\},\{x,-1,1\},\{v,-1,1\},\{u,-1,1\}, \{-10,10\},{GridPoints}\rightarrow 5,PlotStyle\rightarrow RGBColor,Axes\rightarrow True]$

Appendix B: Matlab code for Fig. 3