1 Introduction

Observations through gravitational waves [1,2,3,4,5,6] and radio waves [7,8,9,10,11,12] have shown that black holes are widespread in the Universe. As the simplest celestial object predicted by Einstein’s general relativity (GR), a black hole has some distinguishing features, such as the event horizon and the central singularity, whereas these two characteristics bring serious problems as well, like the loss of information and breakdown of GR. Proposals to remove the singularity cover construction of a regular core [13,14,15,16], bounce by the quantum pressure [17,18,19] and formation of a quasi-black hole [20,21,22,23] (see Ref. [24] for a review).

Recently, a black-bounce/traversable wormhole spacetime has arisen [25] and it can interpolate between a regular black hole (a black bounce) and a traversable wormhole, reducing to the Ellis wormhole [26] in the massless case. Because of its interesting characters, a lot of attention has been paid on it. A time-dependent version [27] of such a spacetime was extended from its original static one and a spherically symmetric thin-shell traversable wormhole was established by it [28]. Its quasinormal modes [29], absorption of scalar waves [30] and gravitational lensing [31] were also investigated.

In the present work, we will focus on the bound geodesic orbits of timelike particles around the black-bounce/traversable wormhole, which were absent in the literature. Bound orbits can be further classified into precessing and periodic orbits. It is no doubt that the anomalous perihelion advance of Mercury belongs to the earliest observational evidences of GR [32] and its next-to-leading-order advance has been examined as well [33,34,35]. Nowadays, the periastron advances of the planets around the Sun [36,37,38,39,40,41,42,43] and other stars [44,45,46,47], of binary stars [48,49,50,51,52,53,54] and of stars around the supermassive black hole in the Galactic Center Sgr A* [55,56,57,58,59,60,61,62,63,64] have been widely adopted and discussed for probing and constraining modified theories of gravity and new physics. Especially, the Schwarzschild precession in the orbit of the star S2 orbiting Sgr A* predicted by GR was just detected by the interferometry GRAVITY [64], paving the way for testing the fundamental theories of gravity and investigating the properties of Sgr A* by making use of the precessing motion of geodesic orbits around various kinds of black holes and other spacetimes.

The small anomalous precessing motion of Mercury’s orbit is due to the small relativistic effects of the Sun on it. If a timelike particle in the vicinity of a black hole is considered, its geodesic motions can have zoom-whirl behaviors [65,66,67,68] which are unique features in the strong gravitational field. It was found that the zoom-whirl behavior can be quantified by a characteristic number q, specifying the ratio of the average angular frequency to the radial frequency per radial cycle [69]. When q is an irrational number, the timelike particle will follow a precessing and aperiodic orbit. However, if q is a rational number, the particle will trace out a perfect periodic orbit and will return to its initial conditions after a finite time span. Although generic orbits are aperiodic with irrational q, they can be approximated by a nearby periodic one because the rational numbers are dense on the real number domain. With the methodology of such a taxonomy [69], the periodic orbits around a Schwarzschild black hole [69] and a Kerr black hole [70,71,72,73,74] and those of black hole binaries [75, 76] were investigated, while the periodic geodesics around various kinds of black holes were also examined [77,78,79,80,81,82].

Inspired by these theoretical and observational works and in order to shed light on gravitational properties of the black-bounce/traversable wormhole, we will detailedly investigate the precessing and periodic motions of geodesic orbits around it, attempting to obtain a preliminary bound on the characteristic length scale of such a spacetime by the detected precession of S2 around Sgr A* [64] and to analyze the effects of the length scale on the periodic orbits.

In Sect. 2, we briefly review the spacetime of the black-bounce/traversable wormhole and examine bound geodesic orbits of a timelike particle around it. In Sect. 3, we investigate the precessing motion of the particle and infer a limit on the length scale of this spacetime. We study the periodic orbits around it and pay much attention to the transition of these orbits in Sect. 4. Finally, in Sect. 5, we conclude and discuss our results.

2 Spacetime and bound orbits

2.1 Spacetime

The spacetime of a static black-bounce/traversable wormhole spacetime with mass \(m_{\bullet }\) reads (\(G=c=1\)) [25]

$$\begin{aligned} \mathrm {d}s^2 = -A(r) \mathrm {d}t^2 + B(r)\mathrm {d}r^2 + C(r)(\mathrm {d}\theta ^2+\sin ^2{\theta }\mathrm {d}\phi ^2) \end{aligned}$$
(1)

where

$$\begin{aligned} A(r)= & {} [B(r)]^{-1} = 1-\frac{2m_{\bullet }}{\sqrt{r^2+\alpha _{\bullet }^2}}, \end{aligned}$$
(2)
$$\begin{aligned} C(r)= & {} r^2+\alpha _{\bullet }^2, \end{aligned}$$
(3)

and \(\alpha _{\bullet }\) is a parameter with the dimension of length. When \(\alpha _{\bullet }=0\), it is the Schwarzschild black hole; when \(0<\alpha _{\bullet }<2m_{\bullet }\) it is a regular black hole with a one-way spacelike throat and with an event horizon at

$$\begin{aligned} r_{\mathrm {H}} = \sqrt{4m_{\bullet }^2-\alpha _{\bullet }^2}, \end{aligned}$$
(4)

which also a describes a black-bounce into a future universe [25]; when \(\alpha _{\bullet }=2m_{\bullet }\), it is one–way wormhole with a null throat; and when \(\alpha _{\bullet }>2m_{\bullet }\), it is a traversable wormhole in the Morris–Thorne sense. When \(m_{\bullet }\) vanishes, the spacetime (1) returns to the Ellis wormhole whose gravitational lensing have been widely examined [83,84,85,86,87,88,89,90,91,92,93,94].

For later convenience, we define that

$$\begin{aligned} \alpha = \frac{\alpha _{\bullet }}{m_{\bullet }}\quad \mathrm {and} \quad x = \frac{r}{m_{\bullet }}. \end{aligned}$$
(5)

Figure 1 shows A(x) with respect to \(\alpha \). It is clear that, when \(\alpha \ne 0\), the spacetime (1) is regular at \(x=0\) and it is asymptotically flat as \(x\rightarrow +\infty \). For a given x, a bigger \(\alpha \) can arise A(x) higher.

Fig. 1
figure 1

A(x) against various \(\alpha \)

Full size image

2.2 Bound orbits

For a timelike test particle freely moving in the equatorial plane \(\theta =\pi /2\) of the spacetime (1), its Lagrangaian is

$$\begin{aligned} 2{\mathcal {L}}=-A(r){\dot{t}}^2+B(r){\dot{r}}^2+C(r){\dot{\phi }}^2=-1, \end{aligned}$$
(6)

where dot means taking derivative against the proper time. We can have two constants of motion as

$$\begin{aligned} E= & {} A(r){\dot{t}}, \end{aligned}$$
(7)
$$\begin{aligned} L= & {} C(r){\dot{\phi }}, \end{aligned}$$
(8)

and the equation of radial motion as

$$\begin{aligned} {\dot{r}}^2 = E^2 - V_{\mathrm {eff}} \end{aligned}$$
(9)

where the effective potential is

$$\begin{aligned} V_{\mathrm {eff}} = A(r) \bigg [ 1 + \frac{L^2}{C(r)} \bigg ], \end{aligned}$$
(10)

and the relation of \(A(r)B(r)=1\) is used. We define that

$$\begin{aligned} l = \frac{L}{m_{\bullet }} \quad \mathrm {and} \quad y = \sqrt{x^2+\alpha ^2}, \end{aligned}$$
(11)

so that we can have

$$\begin{aligned} V_{\mathrm {eff}} = \bigg (1-\frac{2}{y}\bigg ) \bigg ( 1 + \frac{l^2}{y^2} \bigg ). \end{aligned}$$
(12)

If there is a timelike particle, its geodesic orbit starts at rest at infinity with zero binding energy and has a specific amount of angular momentum so that it can eventually be trapped in an unstable circular orbit around the black-bounce/traversable wormhole. Such a marginally bound orbit, also called zero binding energy zoom-whirl orbit, physically requires that \({\dot{r}}\rightarrow 0\) as \(r\rightarrow \infty \) and \({\dot{r}}=\ddot{r}=0\) at \(r=r_{\mathrm {mb}}\) for its asymptotically circular orbit, which are mathematically equivalent to require the following conditions that

$$\begin{aligned} V_{\mathrm {eff}}(x)=1 \quad \mathrm {and}\quad V'_{\mathrm {eff}}(x)=0, \end{aligned}$$
(13)

where \('\) denotes a derivative against x. Since

$$\begin{aligned} V'_{\mathrm {eff}}(x) = \frac{2x}{y^5}(y^2-l^2y+3l^2), \end{aligned}$$
(14)

we can have

$$\begin{aligned} y_{\mathrm {mb}}= & {} 4, \end{aligned}$$
(15)
$$\begin{aligned} l_{\mathrm {mb}}= & {} 4, \end{aligned}$$
(16)

which lead to

$$\begin{aligned} x_{\mathrm {mb}} = \sqrt{16-\alpha ^2}, \end{aligned}$$
(17)

and

$$\begin{aligned} 0 \le \alpha \le 4. \end{aligned}$$
(18)

For a timelike particle, there exists a minimal radius permitting stable circular motions around the black-bounce/traversable wormhole. Such an innermost stable circular orbit plays an important role in astrophysics, such as setting the inner edge of an accretion disk and a transition region from inspiral to plunge for a binary coalescence. The innermost stable circular orbit is located at where the maximum and minimum points of the effective potential merge, requiring the conditions that

$$\begin{aligned} V_{\mathrm {eff}}(x)=E^2, \quad V'_{\mathrm {eff}}(x)=0 \quad \mathrm {and} \quad V''_{\mathrm {eff}}(x)=0. \end{aligned}$$
(19)

Since

$$\begin{aligned} V''_{\mathrm {eff}}(x)= & {} -2 y^{-7}[ 2 y^4 - 3 l^2 y^3 +3 ( 4 l^2 - \alpha ^2 ) y^2 \nonumber \\&+ 4 \alpha ^2 l^2 y -15 \alpha ^2 l^2 ], \end{aligned}$$
(20)

we can obtain

$$\begin{aligned} y_{\mathrm {isco}}= & {} 6, \end{aligned}$$
(21)
$$\begin{aligned} l_{\mathrm {isco}}= & {} 2\sqrt{3},\end{aligned}$$
(22)
$$\begin{aligned} E_{\mathrm {isco}}= & {} \frac{2\sqrt{2}}{3}, \end{aligned}$$
(23)

which yield

$$\begin{aligned} x_{\mathrm {isco}} = \sqrt{36-\alpha ^2}, \end{aligned}$$
(24)

and

$$\begin{aligned} 0 \le \alpha \le 6. \end{aligned}$$
(25)

Therefore, the marginally bound orbit and the innermost stable circular orbit impose bounds on \(\alpha \) and l for any bound orbit around the black-bounce/traversable wormhole as

$$\begin{aligned} {\mathcal {D}}\,' = \{(\alpha ,l)|0 \le \alpha \le 4,\ 2\sqrt{3} \le l \le 4\}. \end{aligned}$$
(26)

Figure 2 shows the radii, angular momentum and energy (if applicable) for the marginally bound orbit and the innermost stable circular orbit against \(\alpha \). It is distinctive that the existence of \(\alpha \) does not affect the values of \(l_{\mathrm {mb}}\), \(l_{\mathrm {isco}}\) and \(E_{\mathrm {isco}}\) for the black-bounce/traversable wormhole, all of which are identical with those for the Schwarzschild black hole. For a given \(\alpha \), \(x_{\mathrm {mb}}\) is always smaller than \(x_{\mathrm {isco}}\), while \(l_{\mathrm {mb}}\) is bigger than \(l_{\mathrm {isco}}\).

Fig. 2
figure 2

The radii, angular momentum and energy (if applicable) for the marginally bound orbit and the innermost stable circular orbit against \(\alpha \)

Full size image
Fig. 3
figure 3

\(V_{\mathrm {eff}}\) with various \(\alpha \) and l are shown in the left column and \(\dot{r}^2\) with various \(\alpha \) and E are shown in the right one

Full size image

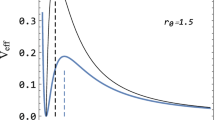
The \(V_{\mathrm {eff}}\) for several values of \(\alpha \) are shown in the left column of Fig. 3; in each panel (a)–(e), a curve with a specific color denotes \(V_{\mathrm {eff}}\) with a specific angular momentum l. The red curves correspond to the marginally bound orbits, each of which has two distinct extreme points. As l decreases, \(V_{\mathrm {eff}}\) becomes less, while its the maximum and minimum points are getting closer to each other and eventually merge into one at the innermost stable circular orbits demonstrated as the purple curves. With a comparison of the curves in the case of \(\alpha =0\), a bigger \(\alpha \) increases \(V_{\mathrm {eff}}\) more significantly near \(x\approx 0\). The right column of Fig. 3 shows \({\dot{r}}^2\) with \(l=(l_{\mathrm {mb}}+l_{\mathrm {isco}})/2\) for different \(\alpha \) from top to bottom; in each panel (f)–(j), a curve with a specific color denotes \({\dot{r}}^2\) with a specific energy E. Either a too big or a too small E makes the curves of \({\dot{r}}^2\) have only a root which will never allow bound orbits. As long as \({\dot{r}}^2\) has at least two roots, the bound orbits around the black-bounce/traversable wormhole will be allowable. Since \(V'_{\mathrm {eff}}(x)=0\) leads to

$$\begin{aligned} x_{E_{\pm }} = \bigg [\frac{l^2}{2} ( l^2 -6 \pm l \sqrt{l^2-12} ) -\alpha ^2 \bigg ]^{1/2}, \end{aligned}$$
(27)

and

$$\begin{aligned} {\dot{x}}^2|_{x=x_{E_{\pm }}} =0, \end{aligned}$$
(28)

we can obtain that, for a given l, the allowable energy for any bound motion is

$$\begin{aligned} E^2_{-} \le E^2 \le E^2_{+}, \end{aligned}$$
(29)

where

$$\begin{aligned} E^2_{\pm } = \frac{1}{54l} [ l^3 + 36 l \pm (l^2-12)\sqrt{l^2-12}]. \end{aligned}$$
(30)

Figure 4 shows the allowable range of energy for bound orbits around the black-bounce/traversable wormhole. For a given l, the upper-bound on E is \(E_+\) and the lower-bound is \(E_-\). After including the range of E, we can extend the bounds on \(\alpha \), the angular momentum and the energy for a bound orbit as

$$\begin{aligned} {\mathcal {D}} = \{(\alpha ,l,E)|0 \le \alpha \le 4,\ 2\sqrt{3} \le l \le 4, E_-\le E \le E_+ \}.\nonumber \\ \end{aligned}$$
(31)
Fig. 4
figure 4

The allowable range of E for bound orbits around the black-bounce/traversable wormhole with respect to l. Its upper-bound and lower-bound on E is respectively \(E_+\) and \(E_-\), see Eq. (30)

Full size image

For a bound orbit around the black-bounce/traversable wormhole, every orbit with given l and E can be described by a number q measuring the amount of orbital precession per radial cycle from one periastron to its succeeding periastron, \({\varDelta }\phi \), with a relation as [69]

$$\begin{aligned} {\varDelta }\phi =2 \pi (q+1). \end{aligned}$$
(32)

When q is an irrational number, it is a precessing orbit where the particle will never exactly return to one point in its worldline after any finite time span. For each revolution, the precession is

$$\begin{aligned} {\varDelta }\, \omega = {\varDelta }\phi -2\pi . \end{aligned}$$
(33)

When q is a rational number, it is a periodic orbit that can return to its initial conditions after a finite time. For a periodic orbit, the number q can be decomposed into three ingredients [69]

$$\begin{aligned} q = w+\frac{v}{z}, \end{aligned}$$
(34)

where z is the integer number of closed leaf in the orbit, w is the integer number of nearly circular whirls close to periastron per leaf and v indicates the order in which the z leaves are traced out. The total accumulated angle in one full orbital period is

$$\begin{aligned} {\varDelta }\phi = \oint \mathrm {d}\phi , \end{aligned}$$
(35)

and it can be rewritten as

$$\begin{aligned} {\varDelta }\phi = 2 \int _{r_-}^{r_+} \frac{\mathrm {d}\phi }{\mathrm {d}r} \mathrm {d}r = 2 \int _0^{\pi } \frac{\mathrm {d}\phi }{\mathrm {d}\chi } \mathrm {d}\chi \end{aligned}$$
(36)

where \(r_{\pm }\) are two turning points of the bound orbit and such an orbit is reparameterized as

$$\begin{aligned} r = \frac{a(1-e^2)}{1+e\cos \chi } \end{aligned}$$
(37)

with a and e being the semi-major axis and the eccentricity satisfying

$$\begin{aligned} r_- = a(1-e) \quad \mathrm {and} \quad r_+ = a(1+e). \end{aligned}$$
(38)

Therefore, we can have

$$\begin{aligned} \frac{\mathrm {d}\phi }{\mathrm {d}\chi }= & {} ae(1-e^2)L \bigg \{ E^2 - A(r) \bigg [ 1 + \frac{L^2}{C(r)} \bigg ] \bigg \}^{-1/2} \nonumber \\&\times [C(r)]^{-1} (1+e\cos \chi )^{-2} \sin \chi \end{aligned}$$
(39)

in which, based on \({\dot{r}}_{\pm }=0\), the energy and angular momentum can be found as

$$\begin{aligned} E^2= & {} \frac{A(r_-)A(r_+)[C(r_+)-C(r_-)]}{A(r_-)C(r_+)-A(r_+)C(r_-)}, \end{aligned}$$
(40)
$$\begin{aligned} L^2= & {} \frac{C(r_-)C(r_+)[A(r_+)-A(r_-)]}{A(r_-)C(r_+)-A(r_+)C(r_-)}. \end{aligned}$$
(41)

It is clear that (E, l) directly relate to \(r_{\pm }\) or (a, e).

Fig. 5
figure 5

Color-indexed q maps on \((\eta ,\varepsilon )\) for \(\alpha =\{0,\ 1,\ 2,\ 3,\ 4\}\) from top to bottom

Full size image

3 Precessing orbits

In this section, we will investigate the precessing motion around the black-bounce/traversable wormhole in three scenarios: its Newtonian limit, semi-classic periastron advance and relativistic advance. In addition, we will obtain a preliminary bound on \(\alpha _{\bullet }\) based on the detection of the precession of the star S2 around Sgr A* [64].

3.1 Newtonian limit

As a pedagogical example, we will calculate the precession of the orbit around the black-bounce/traversable wormhole in the Newtonian limit by using the formulae given in the last section. In such a trivial case, the metric (1) reduces to

$$\begin{aligned} A_{\mathrm {N}}(r)= & {} 1-\frac{2m_{\bullet }}{r} +{\mathcal {O}}\bigg (\frac{m_{\bullet }a^2_{\bullet }}{r^3}\bigg ), \end{aligned}$$
(42)
$$\begin{aligned} B_{\mathrm {N}}(r)= & {} 1+{\mathcal {O}}\bigg (\frac{m_{\bullet }}{r},\frac{m_{\bullet }a^2_{\bullet }}{r^3}\bigg ), \end{aligned}$$
(43)
$$\begin{aligned} C_{\mathrm {N}}(r)= & {} r^2\bigg [1+{\mathcal {O}}\bigg (\frac{a^2_{\bullet }}{r^2}\bigg )\bigg ]. \end{aligned}$$
(44)

Substituting them into Eq. (39), we can obtain

$$\begin{aligned} \frac{\mathrm {d}\phi }{\mathrm {d}\chi }\bigg |_{\mathrm {N}} = 1 + {\mathcal {O}}\bigg (\frac{m_{\bullet }}{r},\frac{a^2_{\bullet }}{r^2}\bigg ), \end{aligned}$$
(45)

so that, after integrating it and putting it into Eq. (33), we find the precession per orbit as

$$\begin{aligned} {\varDelta }\, \omega _{\mathrm {N}} = {\mathcal {O}}\bigg (\frac{m_{\bullet }}{r},\frac{a^2_{\bullet }}{r^2}\bigg ). \end{aligned}$$
(46)

It merely confirms the well-known result of the Keplerian two-body problem under Newton’s laws.

3.2 Semi-classic periastron advance

In the sufficiently weak field, the gravitational influence of the black-bounce/traversable wormhole on the timelike particle can be treated according to a modified Newtonian potential. This approach has been widely used in testing the inverse-square law of gravity [95], such as parameterizing deviation from the inverse-square law by a Yukawa-type correction. In the semi-classic approach, the metric (1) reduces to

$$\begin{aligned} A_{\mathrm {S}}(r)= & {} 1-\frac{2m_{\bullet }}{\sqrt{r^2+\alpha _{\bullet }^2}}, \end{aligned}$$
(47)
$$\begin{aligned} B_{\mathrm {S}}(r)= & {} 1+{\mathcal {O}}\bigg (\frac{m_{\bullet }}{r},\frac{m_{\bullet }a^2_{\bullet }}{r^3}\bigg ), \end{aligned}$$
(48)
$$\begin{aligned} C_{\mathrm {S}}(r)= & {} r^2\bigg [1+{\mathcal {O}}\bigg (\frac{a^2_{\bullet }}{r^2}\bigg )\bigg ], \end{aligned}$$
(49)

and the modified Newtonian potential is

$$\begin{aligned} U = \frac{1}{2}[1-A_{\mathrm {S}}(r)] = \frac{m_{\bullet }}{\sqrt{r^2+\alpha _{\bullet }^2}}. \end{aligned}$$
(50)

It is coincidently the same as the Plummer model for a spherical gravitational system [96], which was used to fit observations of globular clusters, and the parameter \(\alpha _{\bullet }\) in this case can also be interpreted as the Plummer scale length. For a small r, the potential U is proportional to \(r^2\) plus a constant; and for a large r, it is proportional to \(r^{-1}\). Substituting the semi-classic metric into Eq. (39), we can obtain

$$\begin{aligned} \frac{\mathrm {d}\phi }{\mathrm {d}\chi }\bigg |_{\mathrm {S}} = 1 -\frac{\alpha ^2_{\bullet }(3+e\cos \chi )}{2a^2(1-e^2)^2} + {\mathcal {O}}\Bigg (\frac{m_{\bullet }}{a},\frac{\alpha ^4_{\bullet }}{a^4}\Bigg ), \end{aligned}$$
(51)

which leads to

$$\begin{aligned} {\varDelta }\, \omega _{\mathrm {S}} = -\frac{3\pi \alpha ^2_{\bullet }}{a^2(1-e^2)^2} + {\mathcal {O}}\Bigg (\frac{m_{\bullet }}{a},\frac{\alpha ^4_{\bullet }}{a^4}\Bigg ). \end{aligned}$$
(52)

It is distinct that, in the semi-classic approach, \(\alpha _{\bullet }\) of the black-bounce/traversable wormhole can make the orbit of a timelike particle precess negatively, whose direction is opposite to the well-known post-Newtonian periastron advance in GR.

3.3 Relativistic periastron advance

In order to calculate the relativistic periastron advance of a timelike particle around the black-bounce/traversable wormhole, we have to take the full expression of metric (1) into account. After substituting it into Eq. (39), we can obtain

$$\begin{aligned} \frac{\mathrm {d}\phi }{\mathrm {d}\chi }\bigg |_{\mathrm {R}}= & {} 1 + \frac{m_{\bullet }(3+e\cos \chi )}{a(1-e^2)} \nonumber \\&+\frac{\alpha ^2_{\bullet }(1-e\cos \chi +e^2\sin ^2\chi )}{2a^2(1-e^2)^2} \nonumber \\&+ {\mathcal {O}}\bigg (\frac{m^2_{\bullet }}{a^2},\frac{m_{\bullet } \alpha ^2_{\bullet }}{a^3},\frac{\alpha ^4_{\bullet }}{a^4}\bigg ), \end{aligned}$$
(53)

which leads to

$$\begin{aligned} {\varDelta }\, \omega _{\mathrm {R}}= & {} \frac{6\pi m_{\bullet }}{a(1-e^2)}+\frac{\pi \alpha ^2_{\bullet }(e^2+2)}{2a^2(1-e^2)^2} \nonumber \\&+ {\mathcal {O}}\bigg (\frac{m^2_{\bullet }}{a^2},\frac{m_{\bullet } \alpha ^2_{\bullet }}{a^3},\frac{\alpha ^4_{\bullet }}{a^4}\bigg ). \end{aligned}$$
(54)

We can see that, when \(\alpha _{\bullet }=0\), \({\varDelta }\, \omega _{\mathrm {R}}\) returns the one of the Schwarzschild black hole in the first-order post-Newtonian approximation under GR, which will also be called the Schwarzschild precession and be denoted as

$$\begin{aligned} {\varDelta }\, \omega _{\mathrm {GR}} \equiv \frac{6\pi m_{\bullet }}{a(1-e^2)} . \end{aligned}$$
(55)

The full contributions of the spacetime of the black-bounce/traversable wormhole, i.e., the whole effects of A(r), B(r) and C(r), make the direction of the periastron advance caused by \(\alpha _{\bullet }\) (the second term in \({\varDelta }\, \omega _{\mathrm {R}}\)) have the same direction of the one caused by \(m_{\bullet }\) (the first term in \({\varDelta }\, \omega _{\mathrm {R}}\)), which is dramatically different the case of the semi-classic advance \({\varDelta }\, \omega _{\mathrm {S}}\) (52). It was also pointed out [61] that the fully relativistic description of the geodesic motion represents the better way for tests of theories of gravity than the semi-classical approach.

Fig. 6
figure 6

For \(\alpha =\{0,\ 1,\ 2,\ 3,\ 4\}\), the left panel shows variation of q with respect to E for specific l and the right panel shows variation of q with respect to l for specific E

Full size image
Fig. 7
figure 7

Some examples of bound orbits around black-bounce/traversable wormhole with \(l=3.8\) where \((X,\ Y)=(x\cos \phi ,\ x\sin \phi )\). Each column shares the same value of \(\alpha \) while each row has the same E. Periodic orbits with specific (z, w, v) are shown under the condition \(\alpha =0\) and q for all the bound orbits are also denoted

Full size image
Fig. 8
figure 8

This figure is similar to Fig. 7, except that \(l=3.9\) and periodic orbits are shown under the condition \(\alpha =2\)

Full size image

3.4 Example of Sgr A*

Recently, with combination of astrometric and spectroscopic measurements on the star S2 orbiting the supermassive black hole at the Galactic Center, Sgr A*, especially with the astrometry by the four-VLT-telescope interferometric beam combiner instrument GRAVITY, the first detection of the Schwarzschild precession in the orbit of S2 under GR was reported [64]. The consistency between the inferred precession and the predicted one is [64]

$$\begin{aligned} f_{\mathrm {SP}} = \frac{ {\varDelta }\, \omega _{\mathrm {S2}}}{ {\varDelta }\, \omega _{\mathrm {GR}}} = 1.10\pm 0.19. \end{aligned}$$
(56)

If we assume Sgr A* as a black-bounce/traversable wormhole, the precession of S2 could be modeled by Eq. (54) so that we can have

$$\begin{aligned} f_{\mathrm {SP}} = 1 + \frac{\alpha _{\bullet }^2(e^2+2)}{12am_{\bullet }(1-e^2)}. \end{aligned}$$
(57)

By taking the best-fit orbit parameters of S2 provided in Appendix E of Ref. [64], we can deduce that

$$\begin{aligned} \alpha _{\bullet } = (3.0\pm 2.9)\times 10^{11}\ \mathrm {m}, \end{aligned}$$
(58)

or

$$\begin{aligned} \alpha = \frac{\alpha _{\bullet }}{m_{\bullet }} = 47.9 \pm 45.5\ . \end{aligned}$$
(59)

Here, such a big value of \(\alpha >2\) does not mean that Sgr A* is a traversable wormhole and it is merely an outcome from the current stage of observational determination of \(f_{\mathrm {SP}}\). If \(f_{\mathrm {SP}}-1\) could be improved to be at the level of \(\lesssim 1.7\times 10^{-4}\), then \(\alpha \) would be constrained to be \(\lesssim 2\), consistent with a black hole. In the estimation of \(\alpha _{\bullet }\) and its uncertainty, we take the variances of all the variables in Eq. (57) into account, but leave their covariances alone, since the correlation coefficients of these variables are not directly available although the posterior distribution of the orbit fit can be found in Ref. [64]. Our result (58) or (59) is based on the statistics of the best-fit orbit parameters of S2, which are obtained under an assumption that Sgr A* is a Schwarzschild black hole instead of a black-bounce/traversable wormhole. However, the orbital parameters of S2, such as the semi-major axes a, eccentricity e and the mass of Sgr A* \(m_{\bullet }\), are all correlated to the parameter \(\alpha _{\bullet }\) of the black-bounce/traversable wormhole more or less. The modification of the precession of S2 star due to \(\alpha _{\bullet }\) (54) can be partially reabsorbed during the fit of parameters correlated with it. Therefore, our approach might overestimate the constraint on \(\alpha _{\bullet }\) of the black-bounce/traversable wormhole because of these correlations among the parameters. See Ref. [97] for a more detailed discussion about this issue. We suggest that our result (58) or (59) should be taken as a preliminary bound on \(\alpha _{\bullet }\) instead of a genuine constraint on the black-bounce/traversable wormhole based on a full statistical analysis with the whole observational data set.

4 Periodic orbits

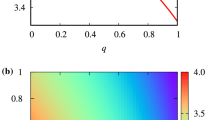
Periodic orbits are those bound orbits with rational q which can further characterized by three integers (z, w, v), see Eq. (34). Before detailedly investigating specific periodic orbits, it is necessary to survey possible values of q on the domain \({\mathcal {D}}\) for a global picture. Since the sub-space of allowable l and E in \({\mathcal {D}}\) is in a shape like a triangle, see Fig. 4, we map it to a neat one for convenience as

$$\begin{aligned} \{l,\ E\} \mapsto \{\varepsilon ,\ \eta \} \end{aligned}$$
(60)

where

$$\begin{aligned} \varepsilon = \frac{l-l_{\mathrm {isco}}}{l_{\mathrm {mb}}-l_{\mathrm {isco}}}\in [0,1], \quad \eta = \frac{E-E_{-}}{E_+-E_-}\in [0,1]. \end{aligned}$$
(61)

Figure 5 shows color-indexed q-maps on \(\{\varepsilon ,\ \eta \}\) for \(\alpha =\{0,\ 1,\ 2,\ 3,\ 4\}\) from top to bottom. When \(\varepsilon \approx 0\) in each map for all of \(\alpha \), q can increase to more than 3 indicated by the red color. The q-maps with \(\alpha =\{0,\ 1,\ 2\}\) are very similar, while the red areas become significantly larger for those with \(\alpha =\{3,\ 4\}\) covering the region with \(\varepsilon \approx 0\) and \(\eta \approx 1\). It suggests that a bigger \(\alpha \) can make q bigger. In order to more clearly demonstrate the variation of q on \({\mathcal {D}}\), the left panel of Fig. 6 shows q with respect to E for some specific values of l and \(\alpha \). It can be found that, for a given l, the increment of E can raise q, while a larger \(\alpha \) can cause q to grow more significantly and distinctly, corresponding to the increase of the red region in a q-map with a larger \(\alpha \) in Fig. 5. As l becomes bigger, the allowable range of E gets larger, which can also be seen from Fig. 4. The right panel of Fig. 6 shows q with respect to l for some specific values of E and \(\alpha \). It is clear that, for a given E, the increment of l can decrease q, while a larger \(\alpha \) can cause q to augment.

Figure 7 shows some examples of bound orbits around the black-bounce/traversable wormhole with \(l=3.8\) where \((X,\ Y)=(x\cos \phi ,\ x\sin \phi )\). Each column of it shares the same value of \(\alpha \), while each row has the same E. Periodic orbits with specific (z, w, v) are shown under the condition \(\alpha =0\) and q for all the bound orbits are also denoted. A distinct feature is that after finding (z, w, v) according q by Eq. (34), the number of the leaf in the orbit is directly indicated by the integer z. We can see that, in each row, q increases with the growth of \(\alpha \). While the periodic orbits are set at \(\alpha =0\), a bigger \(\alpha \) might generate a quasi-periodic orbit with the same l and E. For example, in the forth row, the bound orbit with \(\alpha =2\) has \(q\approx 1.66\) and its pattern is very close to the periodic orbit with \(q=5/3\) (see the fifth row). Another example is the bound orbit in the sixth row with \(\alpha =3\) and \(q\approx 2.65\). Such a quasi-periodic orbit is similar to the periodic orbit with \(q=8/3\) (see the last row).

Figure 8 also shows some bound orbits except that \(l=3.9\) and periodic orbits are shown under the condition \(\alpha =2\). With a bigger l, the eccentricity of the (quasi-)leaf in each orbit becomes larger than the one with the same value of q in Fig. 7. There are some cases of transition from a periodic orbit to a quasi-periodic one and vice versa. In the third row, the quasi-periodic orbit with \(q\approx 1.20\) under \(\alpha =0\) changes to a periodic orbit with \(q=4/3\) when \(\alpha \) increase to 2. In the forth row, the periodic orbit with \(q=3/2\) under \(\alpha =2\) becomes to a quasi-periodic orbit with \(q\approx 2.75\) by raising \(\alpha \) to 4. In the fifth row, a quasi-periodic orbit with \(q\approx 1.5\) and \(\alpha =0\) jumps to a periodic orbit with \(q=5/3\) after \(\alpha \) reaches 2 and then changes to a quasi-periodic orbit with \(q\approx 2.0\) when \(\alpha \) increases to 3. Meanwhile, in the last row, the periodic orbit with \(q=8/3\) under \(\alpha =2\) becomes to a quasi-periodic orbit with \(q\approx 2.66\) under \(\alpha =4\).

In a summary, for the periodic orbits with given l and E around the black-bounce/traversable wormhole, we find that (1) the increment of \(\alpha \) can make q larger and (2) the change of \(\alpha \) can allow transition from a periodic orbit to a quasi-periodic orbit and vice versa.

5 Conclusions and discussion

In order to gain more understanding about the black-bounce/traversable wormhole, we detailedly investigate the precessing and periodic geodesic motions of timelike particles around it. We obtain its semi-classic and relativistic periastron advance and find the latter is the proper one to account for the precessing motion. Based on the predicted relativistic advance and the detected precession of S2 around Sgr A* [64], we work out the preliminary bound on \(\alpha _{\bullet }\) of the black-bounce/traversable wormhole as \((3.0\pm 2.9)\times 10^{11}\) m, corresponding to \(\alpha = 47.9 \pm 45.5\). Although this value of \(\alpha \) seems to favor a traversable wormhole, we expect it will be improved with more precise measurements. We also study the periodic orbits and find that the increment of \(\alpha \) can make the characteristic number q of periodic orbits grow and can cause the transition from a periodic orbit to a quasi-periodic orbit and vice versa.

In this work, a static black-bounce/traversable wormhole without spinning was considered. However, in the real Universe, the black-bounce/traversable wormhole could rotate. Its spin might bring more complexity into the geodesic motions around it and give birth to some new features. The gravitational radiation of the particle and its back reaction on the worldlines were not taken into account neither. They might change the characteristic number q during the infall of the particle. More dedicated works in the future are required to have insights into these issues, helping to searching and distinguishing the black-bounce/traversable wormhole.