Probing a black-bounce-Reissner–Nordström spacetime with precessing and periodic motion

Abstract

We investigate the precessing and periodic orbits of a test timelike particle around the black-bounce-Reissner–Nordström spacetime which is characterized by its charge and bounce parameter. Its marginally bound orbit and innermost stable circular orbit are obtained in the exact forms. We pay closely attention to its precessing orbits and find the resulting relativistic periastron advance. We also study its periodic orbits and demonstrate that small variations of the charge and bounce parameter can make the motion jump among the periodic and precessing orbits. In these two kinds of orbits, we find a distinct degeneracy that some specific combinations of the charge and bounce parameters can generate exactly the same orbital motion in the black-bounce-Reissner–Nordström spacetime, which can also mimic those of the Schwarzschild black hole. In order to break such a degeneracy, we make use of the precession of S2 star around Sgr A* detected by GRAVITY together with the shadow diameter of Sgr A* measured by Event Horizon Telescope and find preliminary bounds on the charge and bounce parameter.

1 Introduction

The detection of gravitational waves [1,2,3,4,5,6] and the direct images of the supermassive black holes in the centers of galaxy M87 [7,8,9,10,11,12] and of the Galaxy [13,14,15,16,17,18] reveal that black holes, predicted by the Einstein’s general relativity more than one hundred years ago, are very common in the Universe. As an ideal laboratory for examining and testing the theories of gravity in the strong fields, a black hole might be poisoned by its event horizon that would cause the information-loss problem, and by its central singularity that would break the general relativity down. In order to erase the singularity, a number of ways have been proposed, such as bouncing by quantum pressure [19,20,21], building a regular core [22,23,24,25], and forming a quasi-black hole [26,27,28,29] (see Ref. [30] for a review).

In the past few years, the family of black-bounce spacetimes has been paid much attention (see Ref. [31] for a brief review). They are built under the general relativity, globally free from curvature singularities, and smoothly interpolate between regular black holes and traversable wormholes. The simplest black-bounce spacetime is the black-bounce-Schwarzschild spacetime [32], which can reduce to the Schwarzschild spacetime and the Ellis wormhole [33] as its bounce parameter and mass vanish, respectively. Its gravitational properties and astrophysical features have been intensively investigated [34,35,36,37,38,39,40,41], and it has been extended to several new classes [42,43,44].

In this work, we focus on the black-bounce-Reissner–Nordström spacetime [45], which is a charged extension of black-bounce-Schwarzschild spacetime and can be interpreted as standard Maxwell electromagnetism with an anisotropic fluid. It is well accepted that astrophysical objects must be without electric charges because of quickly neutralizing by environmental plasma. But the sounds that a black hole might be charged by some mechanisms, such as accumulating charged matter, induction through the rotation in the external magnetic field [46] and inheriting from its charged collapsed progenitor [47], can also be heard. It is likely that the supermassive black hole Sgr A* in the Galactic center might have transient and small positive charge [48], implying studies on the charged spacetimes may go beyond the territory of theoretical interests. Although we have investigated the gravitational-lensing properties of the black-bounce-Reissner–Nordström spacetime, it turns out that current observations might constrain its charge only but leave its bounce parameter untouched [49]. Therefore, in the present work, we will consider the bound orbits around the black-bounce-Reissner–Nordström spacetime, especially the precessing and periodic motion, hoping to provide more clues for testing such a spacetime.

Since the advance of the perihelion of Mercury becomes one of the earliest evidences of the general relativity [50], precessing orbits have been a promising tool for testing alternative theories of gravity. The precessing motion in various gravitational fields, such as those of the planets around the Sun [51,52,53,54,55,56,57,58,59,60,61,62,63,64], of the exoplanets around other stars [65,66,67,68], of the binary pulsars [69,70,71,72,73,74] and of the stars around Sgr A* [75,76,77,78,79,80,81,82,83,84], have also been investigated intensively. In particular, the detection of the Schwarzschild precession of S2 around Sgr A* by GRAVITY [84] lays the observational foundation for testing the theories of gravitation and detecting new physics in the surroundings of the supermassive black hole.

As another subclass of the bound orbits, the periodic orbits will emerge when a timelike particle is in the vicinity of a black hole, showing zoom-whirl patterns [85,86,87,88]. This strong-field feature can be indicated by the ratio of the average angular frequency to the radial frequency per radial cycle [89]. When the ratio is irrational, the particle will depict a precessing orbit; otherwise, it will go back to the initial location exactly in the finite time and trace out a perfectly periodic orbit. Since the rational numbers are dense on the real number domain, a generic precessing orbit with an irrational ratio can be sufficiently approximated by a close-by periodic one. Though the zoom-whirl pattern of a periodic orbits has yet been observed, the periodic orbits might be helpful for faster computation of adiabatic extreme mass-ratio inspirals [90] and for providing information about strong-field properties of the spacetime that is unavailable from the precessing orbits. Therefore, the periodic orbits around a Schwarzschild black hole [89], a Kerr black hole [90,91,92,93,94] and other black holes [95,96,97,98,99,100,101,102,103,104,105,106], as well as those in binary black holes [107, 108] have been intensively examined.

Triggered by these theoretical and observational progresses and in order to further explore the black-bounce-Reissner–Nordström spacetime, we will intensively investigate the precessing and periodic orbits around it in this work, providing more information about its signatures in the geodesic motion. The outline of this paper is as follows. In Sect. 2, we briefly review the black-bounce-Reissner–Nordström spacetime and investigate the bound orbits, including the marginally bound orbit and innermost stable circular orbit of a timelike particle around it. We focus on its precessing motion and estimate the bounds on the charge and bounce parameter based on the observations of GRAVITY and Event Horizon Telescope (EHT) in Sect. 3. In Sect. 4, we examine the periodic orbits around it and pay close attention to their transition with respect to small variations of the charge and the bounce parameter. Conclusions and discussion are presented in Sect. 5.

2 Spacetime and bound orbits

2.1 Metric

The black-bounce-Reissner–Nordström spacetime can be regarded as the solution to the electrovac Einstein field equations of the general relativity in the curvature coordinates $(t,r,\theta ,\varphi )$ with an interpretation as standard Maxwell electromagnetism with an anisotropic fluid [45]. It can be obtained with the Reissner–Nordström spacetime by keeping ${\mathrm {d}}r$ in the metric tensor unchanged and replacing the radial coordinate r with $\sqrt{r^2+\alpha _{\bullet }^2}$, where $\alpha _{\bullet }$ is the bounce parameter with the dimension of length. Thus, the metric of the black-bounce-Reissner–Nordström spacetime with mass $m_{\bullet }$ and the charge $Q_{\bullet }$ can be written as ($G=c=1$) [45]

$$\begin{aligned} {\mathrm {d}}s^2=-A(r){\mathrm {d}}t^2+B(r){\mathrm {d}}r^2+ C(r) ({\mathrm {d}}\theta ^2+\sin ^2\theta {\mathrm {d}}\varphi ^2 ), \end{aligned}$$

(1)

where

$$\begin{aligned} A(r)= & {} \left[ B(r)\right] ^{-1} = 1-\frac{2 m_{\bullet }}{\sqrt{r^2+\alpha _{\bullet }^2}} + \frac{Q_{\bullet }^2}{r^2+\alpha _{\bullet }^2}, \end{aligned}$$

(2)

$$\begin{aligned} C(r)= & {} r^2+\alpha _{\bullet }^2. \end{aligned}$$

(3)

It is asymptotically flat as $|r|\rightarrow \pm \infty$ and is globally regular due to the existence of the bounce parameter. The general relativity is thought to be valid at least sufficiently far away from its core region [45]. When $\alpha _{\bullet }=0$, the black-bounce-Reissner–Nordström spacetime goes back to the Reissner–Nordström spacetime. As the charge vanishes, i.e., $Q_{\bullet }=0$, one recovers the black-bounce-Schwarzschild spacetime [32]. When $m_{\bullet }=0$ and $Q_{\bullet }=0$, the spacetime (1) arrives at the Ellis wormhole [33]. As $Q_{\bullet }=0$ and $\alpha _{\bullet }=0$, one returns to the Schwarzschild black hole.

The radius of the outer and inner event horizons for the spacetime (1) are [45]

$$\begin{aligned} r_{\mathrm {H}}^{\pm }=\sqrt{\left( m_{\bullet }\pm \sqrt{m_{\bullet }^2-Q_{\bullet }^2}\right) ^2-\alpha _{\bullet }^2}, \end{aligned}$$

(4)

respectively, which requires

$$\begin{aligned} Q^2_{\bullet }\le m^2_{\bullet } \quad \text {and} \quad \alpha ^2_{\bullet } \le \left( m_{\bullet }\pm \sqrt{m_{\bullet }^2-Q_{\bullet }^2} \right) ^2 \end{aligned}$$

(5)

for the existence of real $r_{\mathrm {H}}^{\pm }$. For later convenience, we define the following dimensionless quantities as

$$\begin{aligned} x=\frac{r}{m_{\bullet }},\quad \alpha =\frac{\alpha _{\bullet }^2}{m_{\bullet }^2} \quad \text {and} \quad q=\frac{Q_{\bullet }^2}{m_{\bullet }^2}, \end{aligned}$$

(6)

and the rescaled bounce parameter as

$$\begin{aligned} \lambda = \frac{\alpha }{ (1 + \sqrt{1-q} )^2 }. \end{aligned}$$

(7)

The condition for the existence of the outer event horizon (5) can be rewritten as

$$\begin{aligned} {\mathcal {D}}_{\mathrm {H}} = \{(q,\lambda )\,|\ 0\le q \le 1, \ 0\le \lambda \le 1\}, \end{aligned}$$

(8)

and the dimensionless radius of the outer event horizon can be defined as

$$\begin{aligned} x_{\mathrm {H}}= \frac{r_{\mathrm {H}}^+}{m_{\bullet }} = \sqrt{1-\lambda } \left( 1+\sqrt{1-q} \right) . \end{aligned}$$

(9)

As our first step in the study of geodesic motions around the black-bounce-Reissner–Nordström spacetime, we focus on such a spacetime with its event horizon(s) in this work and adopt the domain (8) in the following sections. The geodesic motions around the horizonless one will be left in our next moves.

2.2 Bound orbits

For a timelike test particle moving freely around the black-bounce-Reissner–Nordström spacetime, its Lagrangian can be expressed as

$$\begin{aligned} 2{\mathcal {L}}=-A(r)\dot{t}^2+B(r)\dot{r}^2+C(r)\dot{\varphi }^2=-1, \end{aligned}$$

(10)

where the particle is assumed to be confined in the equatorial plane $\theta =\pi /2$ and a dot represents the differentiation with respect to the proper time. We can obtain two motion constants as

$$\begin{aligned} E= & {} A(r)\dot{t}, \end{aligned}$$

(11)

$$\begin{aligned} L= & {} C(r) \dot{\varphi }, \end{aligned}$$

(12)

and the equation of radial motion as

$$\begin{aligned} \dot{r}^{2} = E^2-V_{{\mathrm {eff}}}, \end{aligned}$$

(13)

with the effective potential defined as

$$\begin{aligned} V_{{\mathrm {eff}}} = A(r)\bigg [ 1 + \frac{L^2}{C(r)}\bigg ], \end{aligned}$$

(14)

where the relation $A(r)B(r)=1$ is used. Based on Eq. (6), the effective potential can be rewritten as

$$\begin{aligned} V_{{\mathrm {eff}}}=\left( 1-\frac{2}{\sqrt{x^2+\alpha }} + \frac{q}{x^2+\alpha }\right) \bigg (1 + \frac{l^2}{x^2+\alpha }\bigg ), \end{aligned}$$

(15)

with

$$\begin{aligned} l = \frac{L}{m_{\bullet }}. \end{aligned}$$

(16)

If a timelike particle falls to the black-bounce-Reissner–Nordström spacetime freely from $r=\infty$ and $\dot{r}=0$, it would be finally captured into an unstable circular orbit around the black hole with $\dot{r}=\ddot{r}=0$ at $r=r_{\mathrm {mb}}$ which is called marginally bound orbit, also known as zero binding energy zoom-whirl orbit. Such a marginally bound orbit satisfies that

$$\begin{aligned} V_{{\mathrm {eff}}}(r)=1 \quad \text {and} \quad V'_{{\mathrm {eff}}}(r)=0, \end{aligned}$$

(17)

where $'$ denotes the derivative against r. From Eq. (17), we can obtain the dimensionless angular momentum and the dimensionless radius of the marginally bound orbit as (see Appendix A for details)

$$\begin{aligned} l_{\mathrm {mb}}= & {} y_{\mathrm {mb}} \sqrt{\frac{2y_{\mathrm {mb}} -q}{y_{\mathrm {mb}}^2 -2y_{\mathrm {mb}} +q}}, \end{aligned}$$

(18)

$$\begin{aligned} x_{\mathrm {mb}}= & {} \sqrt{ y_{\mathrm {mb}}^2-\lambda \left( 1 + \sqrt{1-q}\right) ^2}, \end{aligned}$$

(19)

where

$$\begin{aligned} y_{\mathrm {mb}} = \frac{4}{3}\sqrt{4-3q}\cos {\theta _{\mathrm {mb}}}+\frac{4}{3} , \end{aligned}$$

(20)

with

$$\begin{aligned} \theta _{\mathrm {mb}} =\frac{1}{3} \arccos \left[ \frac{27q^2 -144q +128}{16\left( 4-3q\right) ^{\frac{3}{2}}}\right] . \end{aligned}$$

(21)

Due to the sole dependence of $y_{\mathrm {mb}}$ on the charge q, $l_{\mathrm {mb}}$ is unaffected by the dimensionless bounce parameter $\alpha$ and it decreases with the increment of q, as seen in Fig. 1a. Based on Fig. 1b, we find that $x_{\mathrm {mb}}$ decreases with the growth of q and $\lambda$. Thus, for a given $(q,\lambda )\in {\mathcal {D}}_{\mathrm {H}}$, the ranges of the marginally bound orbit are

$$\begin{aligned} {\mathcal {D}}_{\mathrm {mb}} =\bigg \{ (l_{\mathrm {mb}},x_{\mathrm {mb}})&\bigg | \frac{\sqrt{5}+1}{2}\sqrt{\sqrt{5}+2} \le l_{\mathrm {mb}} \le 4, \nonumber \\&\frac{1}{2}\sqrt{10+6\sqrt{5}} \le x_{\mathrm {mb}} \le 4 \bigg \}. \end{aligned}$$

(22)

It also suggests that the marginally bound orbit in the black-bounce-Reissner–Nordström spacetime could be closer to the central object than the one of the Schwarzschild spacetime and than the one of the Reissner–Nordström black hole for a given q. As the charge of the spacetime (1) vanishes, i.e., $q=0$, $l_{\mathrm {mb}}$ and $x_{\mathrm {mb}}$ go back to those of the black-bounce-Schwarzschild spacetime [37]. When both q and $\alpha$ disappear, they return to those of the Schwarzschild spacetime with $l_{\mathrm {mb,Sch}}=4$ and $x_{\mathrm {mb,Sch}}=4$.

Fig. 1

The dimensionless angular momentum $l_{\mathrm {mb}}$ and the dimensionless radius $x_{\mathrm {mb}}$ of the marginally bound orbit for the black-bounce-Reissner–Nordström spacetime are shown on the domain of ${\mathcal {D}}_{\mathrm {H}}$, where $l_{\mathrm {mb}}$ is independent on $\lambda$

Another special case for the geodesic motion of a timelike particle is the stable circular motion with a minimal radius around the black-bounce-Reissner–Nordström spacetime which is known as innermost stable circular orbit. It is important in astrophysics because it is usually regarded as the inner edge of an accretion disk around the black hole and plays as a transition from inspiral to plunge for a binary merger. The innermost stable circular orbit emerges when the maximum and minimum points of the effective potential coincide by demanding that

$$\begin{aligned} V_{{\mathrm {eff}}}(r)=E^2 ,\quad V'_{{\mathrm {eff}}}(r)=0 \quad \text {and}\quad V''_{{\mathrm {eff}}}(r)=0. \end{aligned}$$

(23)

After some calculations (see Appendix B for details), we have

$$\begin{aligned} E_{\mathrm {isco}}= & {} \frac{y_{\mathrm {isco}}^2-2y_{\mathrm {isco}}+q}{y_{\mathrm {isco}}\sqrt{y_{\mathrm {isco}}^2 -3y_{\mathrm {isco}} +2q}}, \end{aligned}$$

(24)

$$\begin{aligned} l_{\mathrm {isco}}= & {} y_{\mathrm {isco}}\sqrt{\frac{y_{\mathrm {isco}}-q}{y_{\mathrm {isco}}^2-3y_{\mathrm {isco}}+2q}} , \end{aligned}$$

(25)

$$\begin{aligned} x_{\mathrm {isco}}= & {} \sqrt{ y_{\mathrm {isco}}^2-\lambda \left( 1 + \sqrt{1-q}\right) ^2}, \end{aligned}$$

(26)

where

$$\begin{aligned} y_{\mathrm {isco}} = 2\sqrt{4-3q}\cos {\theta _{\mathrm {isco}}}+2 , \end{aligned}$$

(27)

with

$$\begin{aligned} \theta _{\mathrm {isco}} =\frac{1}{3} \arccos \left[ \frac{2q^2 -9q +8}{\left( 4-3q\right) ^{\frac{3}{2}}}\right] . \end{aligned}$$

(28)

Since $y_{\mathrm {isco}}$ only depends on the charge q, the bounce parameter $\alpha$ does not affect the $E_{\mathrm {isco}}$ and $l_{\mathrm {isco}}$. As seen in Fig. 2a and b, both of them decrease with the increment of q, while $x_{\mathrm {isco}}$ shrinks with the growth of q and $\lambda$, see Fig. 2c. Thus, the ranges of the innermost stable circular orbit on the domain ${D}_{\mathrm {H}}$ can be found as

$$\begin{aligned} {\mathcal {D}}_{\mathrm {isco}}= & {} \left\{ \left( E_{\mathrm {isco}}, l_{\mathrm {isco}}, x_{\mathrm {isco}}\right) \bigg | \ \frac{3\sqrt{6}}{8} \le E_{\mathrm {isco}} \le \frac{2}{3}\sqrt{2}, \right. \nonumber \\&\left. 2\sqrt{2} \le l_{\mathrm {isco}} \le 2\sqrt{3},\ \sqrt{15}\le x_{\mathrm {isco}} \le 6 \right\} . \end{aligned}$$

(29)

It shows that the innermost stable circular orbit in the black-bounce-Reissner–Nordström spacetime could be closer to the central object than the one of the Schwarzschild spacetime and than the one of the Reissner–Nordström black hole for a given q. The innermost stable circular orbit returns to the one of the black-bounce-Schwarzschild spacetime as $q=0$ [37]. When $q=\lambda =0$, it goes back to the one of the Schwarzschild spacetime with $E_{{\mathrm {isco,Sch}}}=2\sqrt{2}/3$, $l_{{\mathrm {isco,Sch}}}=2\sqrt{3}$ and $x_{{\mathrm {isco,Sch}}}=6$.

Fig. 2

The energy $E_{\mathrm {isco}}$, the dimensionless angular momentum $l_{\mathrm {isco}}$ and the dimensionless radius $x_{\mathrm {isco}}$ of the innermost stable circular orbit for the black-bounce-Reissner–Nordström spacetime are shown on the domain ${\mathcal {D}}_{\mathrm {H}}$ where $E_{\mathrm {isco}}$ and $l_{\mathrm {isco}}$ are independent on $\lambda$

For a timelike test particle with given E and l in the black-bounce-Reissner–Nordström spacetime, its bound orbit can be described by a unique number p as [89]

$$\begin{aligned} p=\frac{\Delta \varphi }{2\pi }-1. \end{aligned}$$

(30)

where ${\Delta } \varphi$ is the accumulated azimuth between successive periastron during a radial period and can be expressed as

$$\begin{aligned} {\Delta } \varphi = 2\int _{r_{-}}^{r_{+}}\frac{{\mathrm {d}} \varphi }{{\mathrm {d}} r}{\mathrm {d}}r = 2\int _{r_{-}}^{r_{+}}\frac{L}{C(r)\sqrt{E^2-V_{{\mathrm {eff}}}}}{\mathrm {d}}r, \end{aligned}$$

(31)

where Eqs. (12) and (13) have been used and $r_{\pm }$ are two turning points of the bound orbit, i.e., the roots of $\dot{r}^2=0$. When p is a rational number, the test particle will move in a periodic orbit and go back to its initial location exactly after a finite time. Otherwise, it runs a precessing orbit with an irrational number p. The precession per revolution of a timelike particle can be obtained as

$$\begin{aligned} {\Delta } \omega = {\Delta } \varphi -2\pi . \end{aligned}$$

(32)

After having these essentials about the bound motion of a timelike particle around the black-bounce-Reissner–Nordström spacetime, we will focus on the precessing and periodic orbits in the following sections.

3 Precessing orbits

When p is an irrational number, the timelike particle will run a precessing orbit. As a particular subclass of the bound orbits, precessing orbits are usually used to test the theories of gravitation. In order to evaluate the periastron advance of the particle around the black-bounce-Reissner–Nordström spacetime and given the relation between the standard coordinate $r_{\mathrm {s}}$ and the radial coordinate r that $r_{\mathrm {s}}^2=r^2+\alpha _{\bullet }^2$ , we parametrize its orbit as¹

$$\begin{aligned} r(\chi )=\sqrt{r_{\mathrm {s}}^2-\alpha _{\bullet }^2}, \end{aligned}$$

(33)

where the standard coordinate $r_{\mathrm {s}}$ has a well-known parametrization as

$$\begin{aligned} r_{\mathrm {s}} = \frac{a(1-e^2)}{1+e\cos \chi } \end{aligned}$$

(34)

with a being the semi-major axis, e being the eccentricity and $\chi$ being the relativistic true anomaly. Then, the periastron $r_-$ and apoastron $r_+$ can be obtained for $\chi =0$ and $\pi$, respectively, which are

$$\begin{aligned} r_{\pm } = \sqrt{a^2(1 \pm e)^2-\alpha _{\bullet }^2} . \end{aligned}$$

(35)

With the fact that the radial velocity at the turning points $r_{\pm }$ is zero, i.e. $\dot{r}^2_{\pm }=0$, the energy and angular momentum can be determined by Eq. (13) as

$$\begin{aligned} E^2= & {} \frac{A(r_{+})A(r_{-})[C(r_{+})-C(r_{-})]}{A(r_{-})C(r_{+})-A(r_{+})C(r_{-})}, \end{aligned}$$

(36)

$$\begin{aligned} L^2= & {} \frac{[A(r_{+})-A(r_{-})]C(r_{+})C(r_{-})}{A(r_{-})C(r_{+})-A(r_{+})C(r_{-})}. \end{aligned}$$

(37)

Thus, Eq. (31) can be rewritten as

$$\begin{aligned} {\Delta } \varphi = 2\int _{r_{-}}^{r_{+}}\frac{{\mathrm {d}} \varphi }{{\mathrm {d}} r}{\mathrm {d}}r =2 \int _0^\pi \frac{{\mathrm {d}} \varphi }{{\mathrm {d}} \chi }{\mathrm {d}}\chi , \end{aligned}$$

(38)

where

$$\begin{aligned} \frac{{\mathrm {d}}\varphi }{{\mathrm {d}}\chi } = La^2e(1-e^2)^2 \frac{r(\chi )^{-\frac{1}{2}} R(\chi )^{-\frac{1}{2}} \sin \chi }{C[r(\chi )](1+e \cos \chi )^3}, \end{aligned}$$

(39)

with

$$\begin{aligned} R(\chi )=E^2-A[r(\chi )]\bigg \{1+\frac{L^2}{C[r(\chi )]}\bigg \} . \end{aligned}$$

(40)

Although the precession of a timelike particle around the black-bounce-Reissner–Nordström spacetime can be calculated numerically based on Eq. (38) with the given E and L (or $r_{\pm }$), it would be helpful to obtain it analytic approximation, which might provide some intuitive information about how the charge and bounce parameter affect the orbital precession.

Treating the effects of the charge and the bounce parameter as perturbation and keeping their leading terms, we can obtain the precession of a timelike test particle around the black-bounce-Reissner–Nordström spacetime as

$$\begin{aligned} {\Delta } \omega = \frac{6\pi m_{\bullet }}{a(1-e^2)} -\frac{Q_{\bullet }^2\pi }{m_{\bullet }a(1-e^2)}+\frac{\pi \alpha _{\bullet }^2\left( e^2+2\right) }{2a^2\left( 1-e^2\right) ^2}. \end{aligned}$$

(41)

Here, the first term is the well-known post-Newtonian precession in the Schwarzschild spacetime, and the second and third ones are caused by the charge and the bounce parameter, respectively. When $\alpha _{\bullet }=0$, the precession ${\Delta } \omega$ returns to the one of the Reissner–Nordström spacetime [109,110,111,112]. As $Q_{\bullet }=0$, it goes back to the one of the black-bounce-Schwarzschild spacetime [37].

We can clearly see that the contributions of the charge $Q_{\bullet }$ and the bounce parameter $\alpha _{\bullet }$ in the precession ${\Delta } \omega$ have opposite signs, leading to opposite precessing directions. Therefore, even though both of them have some quite big values, they would cancel out in the precession as long as

$$\begin{aligned} Q^2_{\bullet } = \alpha ^2_{\bullet }\frac{m_{\bullet }\left( e^2+2\right) }{2a\left( 1-e^2\right) }, \end{aligned}$$

(42)

making the precession of the black-bounce-Reissner– Nordström spacetime indistinguishable from the one of the Schwarzschild spacetime. In general, there is a degeneracy of $Q_{\bullet }$ and $\alpha _{\bullet }$ in the precession, showing a hyperbola on the space of parameters. Given the detection of the Schwarzschild precession in the orbit of S2 around Sgr A* [84], we demonstrate the ratio $f_{\mathrm {SP}}$ of the precession ${\Delta } \omega$ to the Schwarzschild precession ${\Delta } \omega _{\mathrm {SP}}$ for S2 on the domain of $Q_{\bullet }$ and $\alpha _{\bullet }$ in Fig. 3 where

$$\begin{aligned} f_{\mathrm {SP}}= \frac{{\Delta } \omega }{{\Delta } \omega _{\mathrm {SP}}}, \end{aligned}$$

(43)

and

$$\begin{aligned} {\Delta } \omega _{\mathrm {SP}} = \frac{6\pi m_{\bullet }}{a(1-e^2)}. \end{aligned}$$

(44)

For S2 star, we adopt its eccentricity $e=0.885$ and semi-major axis $a=1031$ au and mark the inferred values of $f_{\mathrm {SP}}$ provided by GRAVITY’s observations on it as [84]

$$\begin{aligned} f_{\mathrm {SP}}=1.10\pm 0.19. \end{aligned}$$

(45)

The black, red and blue dashed lines represent the best-fit estimation of, the lower and the upper limits of $f_{\mathrm {SP}}$, respectively, while the dash-dotted line indicates the line of $f_{\mathrm {SP}}=1$. From Fig. 3, the measured S2’s precession might rule out two regions of the parameter space for the black-bounce-Reissner–Nordström spacetime: one with $\alpha _{\bullet } > rsim 100$ $m_{\bullet }$ and the other with $Q_{\bullet }\approx m_{\bullet }$. However, it is unable to separate $Q_{\bullet }$ and $\alpha _{\bullet }$ by the single measurement of S2 star. It demands measurements on the precession of more S stars or other kinds of observables to break the degeneracy of $Q_{\bullet }$ and $\alpha _{\bullet }$.

Recently, directly imaging Sgr A* by EHT [13,14,15,16,17,18] might provide such an independent observable. We showed in Ref. [49] that the size of the photon sphere for the black-bounce-Reissner–Nordström spacetime is determined by the charge $Q_{\bullet }$ and it is immune to the bounce parameter $\alpha _{\bullet }$. The size of the shadow cast by such a photon sphere also relies on the mass and distance of Sgr A*, which was adopted from GRAVITY’s measurement [113] for self-consistently joint analysis with the precession of S2 measured by GRAVITY [84]. Following the approach of the Ref. [18], we find the bound on $Q_{\bullet }$ according to the measured diameter of Sgr A*’s shadow and then obtain the range of $\alpha _{\bullet }$ based on the precession of S2. These results are

$$\begin{aligned} 0< \frac{Q_{\bullet }}{m_{\bullet }}<0.90 \quad \text {and} \quad 49.3< \frac{\alpha _{\bullet }}{m_{\bullet }} < 75.7, \end{aligned}$$

(46)

which are consistent with the one of the Reissner–Nordström spacetime ($\alpha _{\bullet }=0$) [112] and the one of the black-bounce-Schwarzschild spacetime ($Q_{\bullet }=0$) [37]. Such a big value of $\alpha _{\bullet }$ does not suggest that Sgr A* is a traversable wormhole, but indicates the insufficient precision of current measurements. In estimation of the range of $Q_{\bullet }$, we did not take the spin of the black-bounce-Reissner–Nordström spacetime into account, since it is well known that the shape and size of the shadow have a very weak dependence on the spin and its inclination [114]. We expect it is valid at least at the leading order and we will leave this subtle issue as our next move. In estimation of $\alpha _{\bullet }$, we used the best-fit values of a and e of S2 provided by GRAVITY [84], which were determined with assuming Sgr A* as a Schwarzschild black hole. It would make the range of $\alpha _{\bullet }$ be overestimated due to the lack of the correlations among the orbital parameters and the model parameters in our approach. Given these facts, we suggest that one should take our results (46) as preliminary bounds on $Q_{\bullet }$ and $\alpha _{\bullet }$ and they mainly manifest the potential of multiple kinds of observations to break the degeneracy of parameters in constraining the properties of a spacetime.

Fig. 3

The color-indexed $f_{\mathrm {SP}}$ for the black-bounce-Reissner–Nordström spacetime against the charge $Q_{\bullet }$ and bounce parameter $\alpha _{\bullet }$ is shown. The black, red and blue dashed lines represent the best-fit estimation of, the lower and the upper limit of S2 star’s $f_{\mathrm {SP}}$, respectively, while the dash-dotted line marks the line of $f_{\mathrm {SP}}=1$ for the Schwarzschild precession

4 Periodic orbits

Another specific subclass of the bound orbits is the periodic orbit which possesses a rational number p. Since the distribution of the rational numbers are dense on the real number domain, a generic orbit with an irrational p can be well approximated by a nearby periodic one. A periodic orbit can be specified by three integers (z, w, v) as [89]

$$\begin{aligned} p = w + \frac{v}{z}, \end{aligned}$$

(47)

where z is the zoom number representing the number of closed leaf in the orbit, w is the whirl number representing the number of nearly circular whirls close to periastron per leaf, and v is the vertex number indicating the order in which the z leaves are traced out.

Fig. 4

The number of p versus q and $\lambda$ with $E=0.966$ and $l=4$

Figure 4 shows an example of the variation of p with respect of q and $\lambda$ under the energy $E=0.966$ and the angular momentum $l=4$. We can see that p increases slowly with the growth of $\lambda$ and decreases very fast with q. Moreover, Fig. 4 clearly demonstrates the degeneracy of p between the charge q and the bounce parameter $\lambda$. It means that given E and l, two different sets of $(q,\ \lambda )$ can generate the same orbit with the same p. Similar behavior in the orbital precession was also discussed in Sect. 3.

Fig. 5

Some examples of bound orbits around the black-bounce-Reissner–Nordström spacetime with $l=3.98$, where (X, Y) is defined by Eq. (48) and the unique p is denoted in each panel. Each row shares the same E. The periodic orbits in the first, third and fifth columns have the same shape with the same p, although they have very different $(q, \lambda )$

In order to reveal the degeneracy for the periodic orbits, Fig. 5 shows some examples of the bound orbits around the black-bounce-Reissner–Nordström spacetime with various E but a fixed $l=3.98$ where (X, Y) are defined as²

$$\begin{aligned} (X, Y) = m_{\mathrm {\bullet }}^{-1} \left( \sqrt{r^2+\alpha _{\bullet }^2} \cos \varphi , \sqrt{r^2+\alpha _{\bullet }^2} \sin \varphi \right) \end{aligned}$$

(48)

and it is easy to compare our results with those for other metrics in the standard coordinates. In each row, all orbits share the same E, and both q and $\lambda$ for each panel increase from 0 to some specific values. The periodic orbits in the first, third and fifth columns have the same shape with the same p, although they have very different $(q, \lambda )$. It means that the periodic orbits in the third and fifth columns can mimic those around the Schwarzschild black hole in the first column ($q=\lambda =0$). For $(q,\lambda )$ between those of the columns with the periodic orbits, the orbits might either become precessing orbits in most cases, or transition to another periodic orbit with different p, such as the cases in panel Fig. 5(4a) and (4b) where p jumps from 5/6 to 4/5 after small changes of q and $\lambda$. Figure 6 also shows some examples of the bound orbits around the black-bounce-Reissner–Nordström spacetime. It is similar to Fig. 5 except that its each row shares the same l under the fixed energy $E=0.986$. Likewise, the periodic orbits in the first, third and fifth columns have the same p and shape but with different $(q, \lambda )$. It also demonstrates that, small variations of q and $\lambda$ might not only make bound motions change from the periodic orbits to the precessing ones, but also cause them to transition between the periodic ones with different p, such as those in the panels of (4a)$\rightarrow$(4b)$\rightarrow$(4c) and of (5a)$\rightarrow$(5b)$\rightarrow$(5c) in Fig. 6.

Fig. 6

Some examples of bound orbits around the black-bounce-Reissner–Nordström spacetime with $E=0.986$, where (X, Y) is defined by Eq. (48) and the unique p is denoted in each panel. Each row shares the same l. The periodic orbits in the first, third and fifth columns have the same p and shape but with different $(q, \lambda )$

In summary, there is a degeneracy of bound motion between q and $\lambda$, whose small changes can also make the motion jump among the periodic orbits and precessing ones.

5 Conclusions and discussion

In this work, we investigate the bound motion of a timelike test particle around the black-bounce-Reissner–Nordström spacetime. We obtain its marginally bound orbit and innermost stable circular orbit in the exact forms, whose energy and angular momentum depend on the charge $Q_{\bullet }$ only and whose radii are affected by both $Q_{\bullet }$ and the bounce parameter $\alpha _{\bullet }$. Then, we pay closely attention to its precessing orbits and find the resulting relativistic periastron advance. We also study its periodic orbits and demonstrate that small variations of $Q_{\bullet }$ and $\alpha _{\bullet }$ can make the motion jump among the periodic orbits and precessing ones. In both precessing and periodic orbits, we find a distinct degeneracy so that orbital motion with non-vanishing $Q_{\bullet }$ and $\alpha _{\bullet }$ can mimic those of the Schwarzschild black hole. In order to test the black-bounce-Reissner–Nordström spacetime and constrain its parameters, it requires other independent measurements to break such a degeneracy. Therefore, based on the precession of S2 star around Sgr A* detected by GRAVITY [84] together with the shadow diameter of Sgr A* measured by EHT [13,14,15,16,17,18], we find preliminary bounds on $Q_{\bullet }$ and $\alpha _{\bullet }$, see Eq. (46).

The black-bounce-Reissner–Nordström spacetime we considered is without rotation, while celestial objects are rotating in the real Universe. Although the nonrotational approximation might be adequate for bound motion sufficiently far from it or for very slowly rotating cases, one has to take its spin into account for those much close to its center, bringing more complicated and new features. As the spinning version of a charged black bounce spacetime, the black-bounce-Kerr–Newman spacetime is known, but such a solution requires non-trivial matter content [45]. Other effects, such as the gravitational radiation and its backreaction on the motion of the particle, will be interesting topics for testing this spacetime with gravitational waves in the future. These sophisticated studies might demand dedicated numerical methods [115,116,117,118,119,120] to investigate the dynamics of particles which would be necessary for extracting meaningful physical information from their motion.

Appendices

Appendix A: Determination of marginally bound orbit

With the dimensionless quantities $x=m_{\bullet }^{-1}\, r$ and $l=m_{\bullet }^{-1}\,L$, the conditions for the marginally bound orbit (17) can be rewritten as

$$\begin{aligned} V_{{\mathrm {eff}}}(x)= & {} 1, \end{aligned}$$

(A.1)

$$\begin{aligned} V_{{\mathrm {eff}},x}(x)= & {} 0. \end{aligned}$$

(A.2)

From Eq. (A.1), we can obtain $l^2$ as

$$\begin{aligned} l^2=\left[ \frac{1}{A(x)}-1\right] \left( x^2+\alpha \right) . \end{aligned}$$

(A.3)

Substituting Eq. (A.3) into Eq. (A.2), we have

$$\begin{aligned} \frac{2x P(y)}{(x^2+\alpha )^3 A(x)}=0, \end{aligned}$$

(A.4)

where

$$\begin{aligned} P(y) = y^3-4y^2+4qy-q^2 , \end{aligned}$$

(A.5)

with

$$\begin{aligned} y = \sqrt{x^2+\alpha }. \end{aligned}$$

(A.6)

Considering the timelike geodesics must stay outside the event horizon, i.e., $x > x_{\mathrm {H}}$ and $A(x) > 0$, we can find

$$\begin{aligned} y > \sqrt{x_{\mathrm {H}}^2+\alpha } = 1+\sqrt{1-q} \ge 1, \end{aligned}$$

(A.7)

where Eqs. (9) and (7) are used, and Eq. (A.4) is equivalent to

$$\begin{aligned} P(y)=0. \end{aligned}$$

(A.8)

Fig. 7

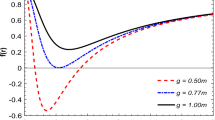
Curves of P(y) with various q against y and the shadowed region represents the unallowed range of y for the marginally bound orbit from the condition Eq. (A.7)

Figure 7 shows the curves of P(y) with various q against y and the shadowed region represents the unallowed range of y for the marginally bound orbit from the condition Eq. (A.7). Although P(y) has three roots on the domain ${\mathcal {D}}_{\mathrm {H}}$ (8), two of them fall into the shadowed region and must be excluded. Thus, the biggest root of P(y) is the solution for the marginally bound orbit of the black-bounce-Reissner–Nordström spacetime and it reads

$$\begin{aligned} y_{\mathrm {mb}} = \frac{4}{3}\sqrt{4-3q}\cos {\theta _{\mathrm {mb}}}+\frac{4}{3} , \end{aligned}$$

(A.9)

where

$$\begin{aligned} \theta _{\mathrm {mb}} =\frac{1}{3} \arccos \left[ \frac{27q^2 -144q +128}{16\left( 4-3q\right) ^{\frac{3}{2}}}\right] . \end{aligned}$$

(A.10)

It clearly shows that $y_{\mathrm {mb}}$ solely depends on the charge q. On ${\mathcal {D}}_{\mathrm {H}}$, it reaches the smallest and biggest values as $q=1$ and $q=0$, respectively, so that

$$\begin{aligned} y_{\mathrm {mb}} \in \left[ \frac{3}{2}+\frac{\sqrt{5}}{2},4\right] . \end{aligned}$$

(A.11)

Substituting Eqs. (A.6) and (A.9) into (A.3), we can determine the dimensionless angular momentum for the marginally bound orbit as

$$\begin{aligned} l_{\mathrm {mb}} = y_{\mathrm {mb}} \sqrt{\frac{2y_{\mathrm {mb}} -q}{y_{\mathrm {mb}}^2 -2y_{\mathrm {mb}} +q}}. \end{aligned}$$

(A.12)

Due to exclusive dependence of $y_{\mathrm {mb}}$ on q, Eq. (A.12) makes $l_{\mathrm {mb}}$ immune to the dimensionless bounce parameter $\alpha$. As $q=1$ and $q=0$ respectively, $l_{\mathrm {mb}}$ arrive at its smallest and biggest values that

$$\begin{aligned} l_{\mathrm {mb}} \in \left[ \frac{\sqrt{5}+1}{2}\sqrt{\sqrt{5}+2},4\right] , \end{aligned}$$

(A.13)

where Eq. (A.11) has been used.

Using the Eq. (A.6) and (A.9), we can find the dimensionless radius of the marginally bound orbit as

$$\begin{aligned} x_{\mathrm {mb}} = \sqrt{ y_{\mathrm {mb}}^2-\lambda \left( 1 + \sqrt{1-q}\right) ^2}, \end{aligned}$$

(A.14)

where $\alpha$ is replaced with the rescaled bounce parameter $\lambda$ by Eq. (7). On ${\mathcal {D}}_{\mathrm {H}}$, $x_{\mathrm {mb}}$ reaches its the biggest value at $q=0$ and $\lambda =0$ and its smallest one at $q=1$ and $\lambda =1$, respectively, that

$$\begin{aligned} x_{\mathrm {mb}} \in \left[ \frac{1}{2}\sqrt{10+6\sqrt{5}},4\right] . \end{aligned}$$

(A.15)

As $q=0$, $l_{\mathrm {mb}}$ and $x_{\mathrm {mb}}$ return to those of the black-bounce-Schwarzschild spacetime [37]. When both q and $\lambda$ disappear, they go back to those of the Schwarzschild spacetime with $l_{\mathrm {mb,Sch}}=4$ and $x_{\mathrm {mb,Sch}}=4$.

Appendix B: Determination of innermost stable circular orbit

With the dimensionless quantities $x=m_{\bullet }^{-1}\, r$ and $l=m_{\bullet }^{-1}\,L$, the conditions for the innermost stable circular orbit (23) can be rewritten as

$$\begin{aligned} V_{{\mathrm {eff}}}(x)= & {} E^2, \end{aligned}$$

(B.16)

$$\begin{aligned} V_{{\mathrm {eff}},x}= & {} 0 , \end{aligned}$$

(B.17)

$$\begin{aligned} V_{{\mathrm {eff}},xx}= & {} 0 . \end{aligned}$$

(B.18)

We can solve $l^2$ from Eq. (B.16) as

$$\begin{aligned} l^2=\left( x^2+\alpha \right) \bigg [\frac{E^2}{A(x)}-1\bigg ], \end{aligned}$$

(B.19)

and substitute it into Eq. (B.17) to obtain

$$\begin{aligned} \frac{2A(x)^2x -E^2[2A(x)x -A_{,x}(x)(x^2+\alpha )] }{A(x)\left( x^2+\alpha \right) }=0. \end{aligned}$$

(B.20)

Since A(x) is positive for any timelike particles outside the event horizon, we can find $E^2$ from Eq. (B.20) as

$$\begin{aligned} E^2=\frac{2A(x)^2x}{2A(x)x-A_{,x}(x)\left( x^2+\alpha \right) }. \end{aligned}$$

(B.21)

Substituting Eqs. (B.19) and (B.21) into Eq. (B.18), we can obtain

$$\begin{aligned} \frac{2x^2 E^2 N(y)}{\left( x^2+\alpha \right) ^4 A(x)^2}=0, \end{aligned}$$

(B.22)

where

$$\begin{aligned} N(y) = y^3 -6y^2 +9qy -4q^2, \end{aligned}$$

(B.23)

and y is defined in Eq. (A.6). Due to $A(x)>0$ for $x>x_{\mathrm {H}}$, Eq. (B.22) is equivalent to

$$\begin{aligned} N(y)=0. \end{aligned}$$

(B.24)

Fig. 8

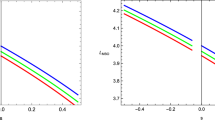
Curves of N(y) with various q against y and the shadowed region represents the unallowed range of y for the innermost stable circular orbit from the condition Eq. (A.7)

Figure 8 depicts the curves of N(y) with various q against y and the shadowed region represents the unallowed range of y for the innermost stable circular orbit based on the condition (A.7). It indicates that N(y) only has one solution to the innermost stable circular orbit of the black-bounce-Reissner–Nordström spacetime for any given $q\in {\mathcal {D}}_{\mathrm {H}}$, which is found as

$$\begin{aligned} y_{\mathrm {isco}} = 2\sqrt{4-3q}\cos {\theta _{\mathrm {isco}}}+2 , \end{aligned}$$

(B.25)

where

$$\begin{aligned} \theta _{\mathrm {isco}} =\frac{1}{3} \arccos \left[ \frac{2q^2 -9q +8}{\left( 4-3q\right) ^{\frac{3}{2}}}\right] . \end{aligned}$$

(B.26)

It clearly shows that $y_{\mathrm {isco}}$ is merely determined by the charge q. As $q=0$ and $q=1$, $y_{\mathrm {isco}}$ arrives at its biggest and smallest values, respectively, that

$$\begin{aligned} y_{\mathrm {isco}} \in \left[ 4,6\right] . \end{aligned}$$

(B.27)

Substituting Eqs. (A.6) and (B.25) into (B.21), we can obtain the energy for the innermost stable circular orbit as

$$\begin{aligned} E_{\mathrm {isco}}=\frac{y_{\mathrm {isco}}^2-2y_{\mathrm {isco}}+q}{y_{\mathrm {isco}}\sqrt{y_{\mathrm {isco}}^2 -3y_{\mathrm {isco}} +2q}}. \end{aligned}$$

(B.28)

Since $y_{\mathrm {isco}}$ only depends on q, Eq. (B.28) ensures that $E_{\mathrm {isco}}$ is unaffected by the dimensionless bounce parameter $\alpha$. $E_{\mathrm {isco}}$ reaches its biggest and smallest values as $q=0$ and $q=1$, respectively, that

$$\begin{aligned} E_{\mathrm {isco}} \in \left[ \frac{3\sqrt{6}}{8}, \frac{2\sqrt{2}}{3}\right] . \end{aligned}$$

(B.29)

where Eq. (B.27) has been used.

Making use of Eqs. (A.6), (B.25), (B.28) and (B.19), we can find the dimensionless angular momentum for the innermost stable circular orbit as

$$\begin{aligned} l_{\mathrm {isco}}=y_{\mathrm {isco}}\sqrt{\frac{y_{\mathrm {isco}}-q}{y_{\mathrm {isco}}^2-3y_{\mathrm {isco}}+2q}}, \end{aligned}$$

(B.30)

which is neither influenced by $\alpha$. As $q=0$ and $q=1$, it arrives at the biggest and smallest values, respectively, that

$$\begin{aligned} l_{\mathrm {isco}} \in \left[ 2\sqrt{2},2\sqrt{3}\right] . \end{aligned}$$

(B.31)

Finally, based on Eqs. (B.25) and (A.6), we can have the dimensionless radius of the innermost stable circular orbit as

$$\begin{aligned} x_{\mathrm {isco}} = \sqrt{ y_{\mathrm {isco}}^2-\lambda \left( 1 + \sqrt{1-q}\right) ^2}, \end{aligned}$$

(B.32)

where Eq. (7) has been used to replace $\alpha$ with the rescaled bounce parameter $\lambda$. On ${\mathcal {D}}_{\mathrm {H}}$, $x_{\mathrm {isco}}$ reaches its biggest value at $q=0$ and $\lambda =0$, and its smallest one at $q=1$ and $\lambda =1$, respectively, that

$$\begin{aligned} x_{\mathrm {isco}} \in \left[ \sqrt{15}, 6\right] . \end{aligned}$$

(B.33)

When $q=0$, $E_{\mathrm {isco}}$, $l_{\mathrm {isco}}$ and $x_{\mathrm {isco}}$ return to those of the black-bounce-Schwarzschild spacetime [37]. When both q and $\lambda$ disappear, they reduce to those of the Schwarzschild spacetime with $E_{{\mathrm {isco,Sch}}}=2\sqrt{2}/3$, $l_{{\mathrm {isco,Sch}}}=2\sqrt{3}$ and $x_{{\mathrm {isco,Sch}}}=6$.