Particle physics violating crypto-nonlocal realism

Abstract

It has been well established that quantum mechanics (QM) violates Bell inequalities (BI), which are consequences of local realism (LR). Remarkably QM also violates Leggett inequalities (LI), which are consequences of a class of nonlocal realism called crypto-nonlocal realism (CNR). Both LR and CNR assume that measurement outcomes are determined by preexisting objective properties, as well as hidden variables (HV) not considered in QM. We extend CNR and LI to include the case that the measurement settings are not externally fixed, but determined by HV. We derive a new version of LI, which is then shown to be violated by entangled $B_d$ mesons, if charge–conjugation–parity (CP) symmetry is indirectly violated, as indeed established. The experimental result is quantitatively estimated by using the indirect CP violation parameters, and the maximum of a suitably defined relative violation is about $2.7\%$. Our work implies that particle physics violates CNR. Our LI can also be tested in other systems such as photon polarizations.

1 Introduction

In 1935, Einstein, Podolsky and Rosen (EPR) questioned the completeness of QM, by applying a criterion of LR to a pair of particles in a quantum state which Schrödinger subsequently referred to as entangled [1, 2]. Locality means that two events cannot have any mutual physical influence if they are spacelike separated, that is, their spatial separation is larger than the distance the fastest physical signal, i.e. the light, can travel within the time difference between the two events. In 1964, Bell proposed the first BI satisfied by any local realistic theory while violated by QM [3]. A more experimentally suitable version of BI, called Clauser–Horne–Shimony–Holt inequality [4], was demonstrated to be violated in many experiments, including the ones closing the locality loophole [5, 6], the detection loophole [7, 8], and both [9,10,11]. To close yet another loophole called measuring setting or freedom of choice loophole, observations of Milky Way stars [12, 13] and human choices [14] have been employed. Great progress has been made in making use of quantum entanglement in quantum information science.

With the conflict between LR and QM well established, it is important to identify which aspects of LR are the sources of the conflict. For this purpose, Leggett in 2003 proposed the LI, which is satisfied by CNR and is violated by QM [15]. This means that even nonlocal realism, at least a subset, cannot avoid the conflict with QM, so the source of conflict seems to be more likely realism. In 2007, a version of LI was experimentally demonstrated to be violated by using polarizations of entangled photons generated in spontaneous parametric down conversion, first under an additional assumption of rotational invariance [16], then without this assumption [17, 18]. LI violation was also demonstrated by using polarizations of photons from fibre-based source [19], as well as the orbital angular momenta of photons [20]. Similar phenomena were observed in different degrees of freedom of single particles [21, 22]. Various extended discussions have also been made [23,24,25,26].

It is highly interesting to extend the investigations on BI and LI to particle physics, of which standard model (SM) is based on quantum field theory combining QM with special relativity, emphasizing causality and using local gauge principle to describe fundamental interactions. Massive and possibly unstable particles governed by strong and weak interactions and flying in relativistic velocities represent a new class beyond both photons and nonrelativistic particles governed merely by electromagnetism, and can still easily achieve spacelike separation. Besides, one might also wonder whether high energy particles, as excitations of quantum fields, may display nonlocal effects.

In particle physics, entanglement, more often called EPR correlation, has been noted in pseudoscalar meson pairs since 1960s [27,28,29,30]. Various discussions were made on its rigorous verification [31, 33,34,35,36,37], which was experimentally done in $K^0{\bar{K}}^0$ pairs produced in proton–antiproton annihilation [38], in $\phi$ resonance [39,40,41], as well as in $B^0_d{\bar{B}}^0_d$ pairs produced in $\Upsilon (4S)$ resonance [42,43,44]. Entanglement is routinely used to tag mesons by identifying their entangled partners [41, 44,45,46,47,48,49]. Moreover, entangled meson pairs are used in measuring various parameters [48,49,50,51,52,53], and studying violations of discrete symmetries [54,55,56,57,58,59,60], including CP [54, 55, 61,62,63,64,65,66], time reversal (T) [67,68,69,70,71], and CPT [72, 73]. A possible scheme of teleporting mesons was also proposed [74,75,76]. There exists similar entanglement in hyperon pairs generated from electron-positron annihilation, which was used recently to measure the phase between the amplitudes of the decays to different helicity states [77].

Many proposals had been made on BI test in entangled mesons [78, 80,81,82,83,84,85,86], and in the analogous spin-entangled particles [87,88,89,90,91,92]. There had been an early experiment using entangled protons to test BI under a few additional assumptions [93]. There was an experiment using entangled $B^0_d{\bar{B}}^0_d$ pairs to test BI, in which meson decay acts as effective measurement settings [42]. However, it was not regarded as a genuine Bell test, because of the lack of active measurement [44, 87, 94,95,96]. Basically this is a manifestation of the loophole of measurement settings, for the following reason. One can envisage a local HV (LHV) theory in which HVs in the source of the particle pairs determine the times, modes and even products of the decays, and the information is carried by the particles, consequently the two particles are secretely correlated no matter how far away they are separated, rendering the violation of BI. Other approaches to BI using entangled high energy particles are difficult to realize, as the alternative bases of measurement are physically limited.

In this paper, we extend CNR and LI to include the case that the measurement settings are not externally fixed, but determined by HV, therefore the above situation jeopardizing BI test in entangled mesons is allowed in CNR, and we propose LI test using entangled neutral $B_d$ mesons. From QM calculation of single particle decays, we identify the time-dependent effective measuring directions due to the decays, as counterparts of the directions of the polarizers measuring the photon polarizations. For different decay times, they all lie on a plane and a cone, respectively. For such effective measuring directions, whether it is externally fixed or emerge from averages of measurement outcomes over HV, we derive a new version of LI, which is violated by QM and entangled $B_d$ mesons. We calculate the measurable quantities characterizing the relative magnitude of the LI violation, and find their maxima to be about $2.7\%$. It turns out that the LI can only be violated when CP symmetry is violated indirectly, i.e. in the mass matrix. Our work establish the true randomness of particle decay, including its time, mode, and product. On the other hand, our new LI can also be tested in other systems such as photon polarizations.

2 Pseudoscalar neutral mesons

In QM, a neutral pseudoscalar meson M can be regarded as living in a two-dimensional Hilbert space, with basis states $|M^0\rangle$ and $|{\bar{M}}^0\rangle$, which are flavor eigenstates and mutual CP conjugates, i.e. $CP|M^0\rangle = |{\bar{M}}^0\rangle$, $CP |{\bar{M}}^0\rangle = |M^0\rangle$. In this basis, the mass matrix is

$$\begin{aligned} H\equiv \mathbf{M}-\frac{i}{2}{\Gamma } = \left( \begin{array}{cc} H_{00} &{} H_{0{\bar{0}}} \\ H_{{\bar{0}}0} &{} H_{{\bar{0}}{\bar{0}}} \end{array}\right) , \end{aligned}$$

(1)

where $H_{00}\equiv \langle M^0|H|M^0\rangle$, $H_{0{\bar{0}}}\equiv \langle M^0|H|{\bar{M}}^0\rangle$, and so on. The eigenstates of H are

$$\begin{aligned} \big |M_1\big \rangle&=\frac{1}{\sqrt{|p|^2+|q|^2}}\left[ p\big |M^0\big \rangle + q\big |{\bar{M}}^0\big \rangle \right] ,\nonumber \\ \big |M_2\big \rangle&=\frac{1}{\sqrt{|p|^2+|q|^2}}\left[ p\big |M^0\big \rangle - q|{\bar{M}}^0\big \rangle \right] , \end{aligned}$$

(2)

with $p/q \equiv \sqrt{H_{{\bar{0}}0}/H_{0{\bar{0}}} }$. The corresponding eigenvalues are

$$\begin{aligned} \lambda _{1}&= m_{1}-\frac{i}{2}\Gamma _{1}=H_{00} +\sqrt{ H_{0{\bar{0}}}H_{{\bar{0}}0} },\nonumber \\ \lambda _{2}&= m_{2}-\frac{i}{2}\Gamma _{2} =H_{00} - \sqrt{ H_{0{\bar{0}}}H_{{\bar{0}}0} }. \end{aligned}$$

(3)

H governs the evolution of the meson state

$$\begin{aligned} \big |\psi (t)\big \rangle = a(t) \big |M^0\big \rangle + b(t) \big |{\bar{M}}^0\big \rangle , \end{aligned}$$

(4)

with

$$\begin{aligned} \left( \begin{array}{c} a(t) \\ b(t) \\ \end{array}\right) =U(t) \left( \begin{array}{c} a(0)\\ b(0) \\ \end{array} \right) , \end{aligned}$$

(5)

where

$$\begin{aligned} U(t) = \exp (-iHt)= g_+(t)+g_-(t) \left( \begin{array}{cc} 0&{}p/q \\ q/p&{}0 \\ \end{array} \right) , \end{aligned}$$

(6)

with $g_{\pm }(t) \equiv \frac{e^{-i\lambda _2 t} \pm e^{-i\lambda _1 t}}{2}$. This leads to the mixing phenomena. Especially, $M^0$ and ${\bar{M}}^0$ at $t=0$ evolve respectively to

$$\begin{aligned} \big |M^0(t)\big \rangle&= g_+(t)\big |M^0\big \rangle +\frac{q}{p}g_-(t)\big |{\bar{M}}^0\big \rangle ,\nonumber \\ \big |{\bar{M}}^0(t)\big \rangle&= \frac{p}{q}g_-(t)\big |M^0\big \rangle +g_+(t)\big |{\bar{M}}^0\big \rangle . \end{aligned}$$

(7)

For a meson in an arbitrary state, its decay to some final state f indicates that there has been a projection or filtering to some basis state $|\phi \rangle$, which decays to f, $|\phi \rangle$ being [56, 57]

$$\begin{aligned} \big |\phi \big \rangle = \frac{1}{\sqrt{\big |A_f\big |^2+ \big |{\bar{A}}_f\big |^2} } \left( {\bar{A}}_f^*\big |M^0\Big \rangle + A_f^*\big |{\bar{M}}^0\big \rangle \right) , \end{aligned}$$

(8)

where $A_f=\langle f |W|M^0\rangle$ and ${\bar{A}}_f=\langle f |W|{\bar{M}}^0\rangle$ are, respectively, the amplitudes of the decays from $M^0$ and ${\bar{M}}^0$ to the final state f. $W = {\mathcal {U}}H_w$, where $H_w$ being the weak decay Hamiltonian while ${\mathcal {U}}$ being the strong evolution operator and reducing to the identity if final state interactions are neglected.

A pair of neutral mesons can be produced as $C=-1$ antisymmetric entangled state

$$\begin{aligned} \big |\Psi _- \big \rangle = \frac{1}{\sqrt{2}}\left( \big |M^0 \big \rangle \big |{\bar{M}}^0 \big \rangle - \big |{\bar{M}}^0 \big \rangle \big |M^0 \big \rangle \right) , \end{aligned}$$

(9)

where in each term, the first and second basis states are those of mesons a and b respectively.

Suppose this two-particle state evolves up to $t_a$, when meson a decays to some final state $f_a$, indicating that there is a projection or filtering of a to some basis state $|\phi \rangle _a$, which decays to $f_a$. $|\phi \rangle _a$ is $|\phi \rangle$ as given in (8) for meson a. The meson b continues to evolve till it decays to some final state $f_b$ at $t_b$, indicating that there is a projection or filtering of b to some basis state $|\phi \rangle _b$, which decays to $f_b$. $|\phi \rangle _b$ is $|\phi \rangle$ as given in (8) for meson b. The time evolution of the entangled state up to the projections can be described as $P_bU_b(t_b-t_a)P_aU_b(t_a)U_a(t_a)|\Psi _-\rangle = P_bP_aU(t_b)U(t_a)|\Psi _-\rangle = P_b P_a|\Psi _-(t_a,t_b) \rangle$, where $P_a =|\phi \rangle _{aa} \langle \phi |$ and $P_b=|\phi \rangle _{bb} \langle \phi |$ are projection operators, and the commutativity between operators on a and those on b have been used. This justifies the usual use of a state vector with two time variables

$$\begin{aligned} \big |\Psi _-(t_a,t_b)\big \rangle&\equiv U(t_b)U(t_a)\big |\Psi _-\big \rangle \nonumber \\&= \frac{1}{\sqrt{2}}\left( \big |M^0(t_a)\big \rangle \big |{\bar{M}}^0(t_b)\big \rangle \right. \nonumber \\&\left. - \big |{\bar{M}}^0(t_a)\big \rangle \big |M^0(t_b)\big \rangle \right) , \end{aligned}$$

(10)

which means that the two mesons decay at $t_a$ and $t_b$, respectively.

Specifically, we use neutral $B_d$ mesons, because of the advantage that $\Gamma _2 \approx \Gamma _1$, $q/p\approx e^{2i\beta }$, where $2\beta$ is a phase factor, $\beta$ is given as $\sin (2\beta )= 0.695$ [97]. Then $M^0=B^0$, ${\bar{M}}^0={\bar{B}}^0$, $M_1=B_L$, $M_2=B_H$, and U(t) is simplified to

$$\begin{aligned} U(t)&=e^{-iMt-\frac{\Gamma }{2} t}\nonumber \\&\quad \times \left( \cos \frac{x\Gamma t}{2}+i\sin \frac{x\Gamma t}{2} \Big [ \cos (2\beta )\sigma ^x+\sin (2\beta )\sigma ^y\Big ]\right) , \end{aligned}$$

(11)

where $\sigma ^{i}$, $(i=x,y,z)$, are Pauli operators, $x \equiv (m_H-m_L)/\Gamma$, $M \equiv ( m_H+m_L)/2$ and $\Gamma \equiv (\Gamma _L+\Gamma _H)/2$, the subscripts following those of $B_H$ and $B_L$.

In Bloch representation, $|B^0\rangle$, like the horizontally polarized state of a photon or the spin-up state of an electron, is represented as the vector (0, 0, 1), while $|{\bar{B}}^0_d\rangle$, like the vertically polarized state of a photon or the spin-down state of an electron, is represented as the vector $(0,0,-1)$. They can be chosen as the “measuring directions” or bases of measurement.

However, for a measurement following time evolution, it is more convenient to define an effective time-dependent basis or “measuring direction”. A state of a two-state system can be parameterized as

$$\begin{aligned} \big |\mathbf{u} \big \rangle =e^{i\zeta } \left( \cos \frac{\theta _\mathbf{u}}{2}\big |0\big \rangle + e^{i\rho _\mathbf{u}} \sin \frac{\theta _\mathbf{u}}{2} \big |1\big \rangle \right) , \end{aligned}$$

(12)

where $|0\rangle$ and $|1\rangle$ represent the basis states. We consider its time evolution that can be parameterized as

$$\begin{aligned} U(\theta _\mathbf{a},\rho _\mathbf{a}) =\left( \cos \frac{\theta _\mathbf{a}}{2}-i\sin \frac{\theta _\mathbf{a}}{2}\left( \cos (\rho _\mathbf{a})\sigma ^x+\sin (\rho _\mathbf{a})\sigma ^y\right) \right) , \end{aligned}$$

(13)

of which (11) is an example, multiplied by an additional decay factor $e^{-iMt-\frac{\Gamma }{2} t}$.

Suppose that following the evolution $U(\theta _\mathbf{a},\rho _\mathbf{a})$, a signal is recorded as ${\mathcal {A}}=+1$ if $|0\rangle$ is detected, while ${\mathcal {A}}=-1$ if $|1\rangle$ is detected. The QM expectation value of ${\mathcal {A}}$ is

$$\begin{aligned}&\bar{{\mathcal {A}}}(\mathbf{u})=\frac{|\langle 0|U|\mathbf{u}\rangle \big |^2-\big |\big \langle 1\big |U\big |\mathbf{u}\big \rangle \big |^2}{\big |\big \langle 0\big |U\big |\mathbf{u}\big \rangle \big |^2+\big |\big \langle 1\big |U\big |\mathbf{u}\big \rangle \big |^2}=\mathbf{u}\cdot \mathbf{a}, \end{aligned}$$

(14)

where

$$\begin{aligned} \mathbf{u} =\left( \sin \theta _\mathbf{u}\cos \rho _\mathbf{u}, \sin \theta _\mathbf{u} \sin \rho _\mathbf{u}, \cos \theta _\mathbf{u}\right) \end{aligned}$$

(15)

is the Bloch vector of $|\mathbf{u} \rangle$, while

$$\begin{aligned} \mathbf{a} = \left( -\sin \theta _{a}\sin \rho _{a}, \sin \theta _{a} \cos \rho _{a}, \cos \theta _{a}\right) \end{aligned}$$

(16)

is the Bloch vector of $U^\dagger (\theta _\mathbf{a},\rho _\mathbf{a}) |0\rangle$. This can be easily understood by regarding $\bar{{\mathcal {A}}}(\mathbf{u})$ as expectation value of the signal obtained by measuring the initial state $|\mathbf{u}\rangle$ in the rotated basis $\{U^\dagger |0\rangle , U^\dagger |1\rangle \}$. The rotation $U^\dagger$ of the basis is realized by evolution.

For a $B_d$ meson, the measurement in the flavor basis {$|B^0\rangle$, $|{\bar{B}}^0\rangle$}, corresponding to ${\mathcal {A}}_l=\pm 1$, can be made through the semileptonic decay channel, as the direct CP violation or wrong sign decay is negligible [97]. Thus $|\phi \rangle$ in (8) reduces to $|B^0\rangle$ or $|{\bar{B}}^0\rangle$, and one can define

$$\begin{aligned}&\bar{{\mathcal {A}}}_l(\mathbf{u})=\frac{\big |\big \langle B^0\big |U(t)\big |\mathbf{u} \big \rangle \big |^2-\big |\big \langle {\bar{B}}^0\big |U(t)\big |\mathbf{u}\big \rangle \big |^2}{\big |\big \langle B^0\big |U(t)\big |\mathbf{u}\big \rangle \big |^2+\big |\big \langle {\bar{B}}^0\big |U(t)\big |\mathbf{u}\big \rangle \big |^2}=\mathbf{u} \cdot \mathbf{a}^l(t), \end{aligned}$$

(17)

where

$$\begin{aligned} \mathbf{a}^l (t)=\left( \sin (2 \beta ) \sin ( x\Gamma t), -\cos (2 \beta ) \sin (x\Gamma t), \cos (x\Gamma t)\right) . \end{aligned}$$

Likewise, as the direct CP violation is negligible [97], if the decay products are CP eigenstates $S_{\pm }$, they signals the projection of the meson to CP basis states $|B_{\pm }\rangle \equiv \left( |B^0\rangle \pm |{\bar{B}}^0\rangle \right) /\sqrt{2}$. In this case, $|\phi \rangle$ in (8) reduces to $|B_\pm \rangle$.

With $B_{\pm }$ corresponding to ${\mathcal {A}}_s=\pm 1$, one can define

$$\begin{aligned} \bar{{\mathcal {A}}}_s(\mathbf{u})=\frac{\big |\big \langle B_+|U(t)|\mathbf{u}\Big \rangle \big |^2-\big |\big \langle B_-\big |U(t)\big |\mathbf{u}\Big \rangle \big |^2}{\big |\big \langle B_+\big |U(t)\big |\mathbf{u}\Big \rangle \big |^2+\big |\big \langle B_-\big |U(t)\big |\mathbf{u}\Big \rangle \big |^2}=\mathbf{u}\cdot \mathbf{a}^s(t), \nonumber \\ \end{aligned}$$

(18)

where

$$\begin{aligned} \mathbf{a}^s (t)&=\left( \sin ^2(2 \beta ) \cos (x\Gamma t)+\cos ^2(2 \beta ),\right. \\&\quad \left. \sin (4 \beta ) \sin ^2\left( x\Gamma t/2\right) ,-\sin (2 \beta ) \sin (x\Gamma t)\right) . \end{aligned}$$

Equations (17) and (18) are of the same form as the standard QM result (14) because the factor $e^{-\Gamma t}$ exists in all terms in both denominator and the numerator, and thus cancels.

Note that $|\langle B^0|U(t)|\mathbf{u} \rangle |^2$, $|\langle {\bar{B}}^0|U(t)|\mathbf{u}\rangle |^2$ and $|\langle B_\pm |U(t)|{} \mathbf{u}\rangle |^2$ do not depend on the specific decay channels signalling the projection, hence is not directly observed. In contrast CP asymmetries usually defined depend on which channels are observed.

However, under the assumption of no wrong sign decays and no direct CP violation, $|\langle B^0|U(t)|\mathbf{u} \rangle |^2$, $|\langle {\bar{B}}^0|U(t)|\mathbf{u}\rangle |^2$ and $|\langle B_\pm |U(t)|\mathbf{u}\rangle |^2$ and thus the asymmetries we define above are related to the rates of decays in specific channels. For flavor eigenstates $l^{\pm }$, as the final states of semileptonic decays,

$$\begin{aligned} \big \langle l^+\big |WU(t)\big |\mathbf{u} \big \rangle = \big \langle l^+\big |W \big |B^0\big \rangle \big \langle B^0\big |U(t)\big |\mathbf{u} \big \rangle =A_{l^+}\big \langle B^0\big |U(t)\big |\mathbf{u} \big \rangle ,\\ \big \langle l^-\big |WU(t)\big |\mathbf{u} \big \rangle =\big \langle l^-\big |W \big | {\bar{B}}^0\big \rangle \big \langle {\bar{B}}^0\big |U(t)\big |\mathbf{u}\big \rangle ={\bar{A}}_{l^-}\big \langle {\bar{B}}^0\big |U(t)\big |\mathbf{u}\big \rangle . \end{aligned}$$

For $|l^-\rangle =CP|l^+\rangle$, we have $A_{l^+}={\bar{A}}_{l^-}=A_l$. For CP eigenstates $S_\pm$ as the final states,

$$\begin{aligned} \big \langle S_+\big |WU(t)\big |\mathbf{u}\big \rangle= & {} \big \langle S_+\big |W\big |B_+\big \rangle \big \langle B_+\big |U(t)\big |\mathbf{u}\big \rangle ,\\ \big \langle S_-\big |WU(t)\big |\mathbf{u}\big \rangle= & {} \big \langle S_-\big |W\big |B_-\big \rangle \big \langle B_-\big |U(t)\big |\mathbf{u}\big \rangle . \end{aligned}$$

Note that here there is no special relation between $l^+$ and $l^-$, or between $S_+$ and $S_-$, as different decay channels may signal a same projection in the meson Hilbert space. The examples of flavor eigenstates $l^{\pm }$ as the final states include $M^-e^+\nu$, $M^+ e^-{\bar{\nu }}$, $M^-\mu ^+\nu$, $M^+ \mu ^-{\bar{\nu }}$, etc. The examples of CP eigenstates $S_\pm$ as the final states include $J/\psi K_S$, $J/\psi K_L$, KK, KKK, $\pi \pi$, $\pi \pi \pi$, DD, etc.

Therefore, the asymmetries ${\bar{A}}_{l}$ and ${\bar{A}}_{s}$, defined above in the meson Hilbert space, can be obtained from experimentally measurable quantities,

$$\begin{aligned} \bar{{\mathcal {A}}}_l(\mathbf{u})&=\frac{\frac{\big |\big \langle l^+\big |WU(t)\big |\mathbf{u} \big \rangle \big |^2}{\big |\big \langle l^+\big |W\big |B^0\big \rangle \big |^2}-\frac{\big |\big \langle l^-\big |WU(t)\big |\mathbf{u}\big \rangle \big |^2}{\big |\big \langle l^-\big |W\big |{\bar{B}}^0\big |^2}}{\frac{\big |\big \langle l^+\big |WU(t)\big |\mathbf{u} \big \rangle \big |^2}{\big |\big \langle l^+\big |W\big |B^0\big \rangle \big |^2}+\frac{\big |\big \langle l^-\big |WU(t)\big |\mathbf{u}\big \rangle \big |^2}{\big |\big \langle l^-\big |W\big |{\bar{B}}^0\big |^2}},\\ \bar{{\mathcal {A}}}_s(\mathbf{u})&=\frac{\frac{\big |\big \langle S_+\big |WU(t)\big |\mathbf{u}\big \rangle \big |^2}{\big |\big \langle S_+\big |W\big |B_+\big \rangle \big |^2}-\frac{\big |\big \langle S_-\big |WU(t)\big |\mathbf{u}\big \rangle \big |^2}{\big |\big \langle S_-\big |W\big |B_-\big \rangle \big |^2}}{\frac{\big |\big \langle S_+\big |WU(t)\big |\mathbf{u}\big \rangle \big |^2}{\big |\big \langle S_+\big |W\big |B_+\big \rangle \big |^2}+\frac{\big |\big \langle S_-\big |WU(t)\big |\mathbf{u}\big \rangle \big |^2}{\big |\big \langle S_-\big |W\big |B_-\big \rangle \big |^2}}. \end{aligned}$$

As shown in Fig. 1, with the time passing, $\mathbf{a}^l(t)$ rotates on a plane, while $\mathbf{a}^s(t)$ rotates on a cone whose axis is perpendicular to $\mathbf{a}^l$ plane. For convenience, we adopt a new coordinate system in which $\mathbf{a}^l$ plane is the xy plane, then

$$\begin{aligned} \mathbf{a}^l(\phi _l)&=\left( \cos \phi _l,\sin \phi _l,0\right) ,\nonumber \\ \mathbf{a}^s(\theta _s,\phi _s)&=\left( \sin \theta _s \cos \phi _s,\sin \theta _s\sin \phi _s,\cos \theta _s \right) , \end{aligned}$$

(19)

where $\phi _l= x\Gamma t$ and $\phi _s=x\Gamma t+\pi /2$ are the azimuthal angles of $\mathbf{a}^l$ and $\mathbf{a}^s$, respectively, $\theta _s=2\beta$ is the polar angle of $\mathbf{a}^s$, and it suffices to consider $0< \theta _s\le \pi /2$.

$\mathbf{a}^l(\phi _l)$ and $\mathbf{a}^s(\theta _s,\phi _s)$ are two effective measurement settings or “measuring directions”. For $B_d$ mesons, they are time-dependent. The rotation of basis or measuring direction realized by evolution explains the similarity between decay time and polarizer angle. But $\mathbf{a}^l(\phi _l)$ and $\mathbf{a}^s(\theta _s,\phi _s)$ can also be used, say, for photon polarization, by directly adjusting $\phi _l$ and $(\theta _s,\phi _s)$ in experiments.

Fig. 1

The effective measuring directions $\mathbf{a}^l$ and $\mathbf{a}^s$. In a certain coordinate system, $\mathbf{a}^l(\phi _l)$ is on xy plane, $\mathbf{a}^s(\theta _s,\phi _s)$ is on a cone. For $B_d$ mesons, $\phi _l = x\Gamma t$, $(\phi _s, \theta _s)=(x\Gamma t+\pi /2,2\beta )$, corresponding to flavor and CP measurements following evolution of time t, respectively. For photon polarizations, $\mathbf{a}^l$ and $\mathbf{a}^s$ are polarizer directions in Bloch representation, and can be adjusted directly

3 CNHV theories

$|\mathbf{u}\rangle$ is an eigenstate of the Pauli operator $\varvec{\sigma }\cdot {\mathbf {u}}$ in the direction of ${\mathbf {u}}$. A particle in this state has a definite ${\mathbf {u}}$. For a single particle, QM result can be reproduced by a realistic or HV theory, in which the measurement outcomes are determined by preexisting properties independent of the measurement, or “elements of reality” in the words of EPR. Thus ${\mathbf {u}}$ is identified as such an element of reality.

Consider a HV theory. Suppose a particle with property $\mathbf{u}$ is measured along direction $\mathbf{a}$, then the dichotomic measurement outcome $A=\pm 1$ is determined by the hidden variables $\lambda$ in addition to the property $\mathbf{u}$ and the local parameter $\mathbf{a}$. This is also called a local realistic theory, in which the parameter $\mathbf{a}$ is local. In a nonlocal realistic theory, A also depends on a non-local parameters, collectively denoted as $\eta$. In a crypto-nonlocal HV (CNHV) theory, the individual properties of each particle, after averaging over distribution $\rho _{{\mathbf {u}} }(\lambda )$ of the hidden variables $\lambda$, become local, as indicated in countless phenomena,

$$\begin{aligned} \int d \lambda \rho _{{\mathbf {u}} } \left( \lambda \right) A\left( {\mathbf {u}},{\mathbf {a}},\eta ,\lambda \right) ={\bar{A}}({\mathbf {u}}, {\mathbf {a}}). \end{aligned}$$

(20)

A concrete example of ${\bar{A}}({\mathbf {u}}, {\mathbf {a}})$ is the Malus’ law [16]

$$\begin{aligned} {\bar{A}}\left( {\mathbf {u}}, {\mathbf {a}}\right) ={\mathbf {u}} \cdot {\mathbf {a}}, \end{aligned}$$

(21)

which is consistent with QM results of photon polarizations. In the last section, we have just shown that it is also consistent with QM result of the meson decay following its evolution.

For a pair of particles from a common source, with respective properties ${\mathbf {u}}$ and ${\mathbf {v}}$, the measuring direction of the other particle can serve as the nonlocal parameter, and one can also assume nonlocal parameters $\eta _a$ and $\eta _a$, which are nonlocal with respect to a and b, respectively. The measurement outcomes along respective directions $\mathbf{a}$ and $\mathbf{b}$ are $A({\mathbf {u}},{\mathbf {v}},{\mathbf {a}},{\mathbf {b}}, \eta _a,\eta _b,\lambda )=\pm 1$ and $B({\mathbf {v}},{\mathbf {u}},{\mathbf {b}},{\mathbf {a}}, \eta _b,\eta _a,\lambda )=\pm 1$. The local measurement of each particle cannot detect its correlation with the other particle, hence the nonlocal dependence disappears after averaging over the hidden variables,

$$\begin{aligned} \int d \lambda \rho _{{\mathbf {u}},{\mathbf {v}}} (\lambda ) A({\mathbf {u}},{\mathbf {v}},{\mathbf {a}},{\mathbf {b}}, \eta _a,\eta _b,\lambda )= & {} {\bar{A}}({\mathbf {u}}, {\mathbf {a}}), \end{aligned}$$

(22)

$$\begin{aligned} \int d \lambda \rho _{{\mathbf {u}},{\mathbf {v}}} (\lambda ) B({\mathbf {v}},{\mathbf {u}},{\mathbf {b}},{\mathbf {a}}, \eta _b,\eta _a,\lambda )= & {} {\bar{B}}({\mathbf {v}}, {\mathbf {b}}). \end{aligned}$$

(23)

A general physical state is a statistical mixture of subensembles with definite $\mathbf{u}$ and $\mathbf{v}$. Hence the final expectation values, which is experimentally measured, are [15, 16]

$$\begin{aligned} \big \langle A \big \rangle&= \int d {\mathbf {u}} F({\mathbf {u}}) {\bar{A}}({\mathbf {u}}),\nonumber \\ \big \langle B \big \rangle&= \int d {\mathbf {v}} F({\mathbf {v}}) {\bar{B}}({\mathbf {u}}), \end{aligned}$$

(24)

where $F({\mathbf {u}})$ and $F({\mathbf {v}})$ are probability distribution of polarizations ${\mathbf {u}}$ and ${\mathbf {v}}$, respectively. In case of correlated particles, they are the reduced ones

$$\begin{aligned} \begin{array}{ll} F({\mathbf {u}})=&{}\int d\mathbf {v} F(\mathbf{u},\mathbf{v}), \\ F({\mathbf {v}})=&{}\int d\mathbf {u} F(\mathbf{u},\mathbf{v}). \end{array} \end{aligned}$$

(25)

The two-body quantities may indicate correlations. For definite $\mathbf{u}$ and $\mathbf{v}$,

$$\begin{aligned} {\overline{AB}}\left( \mathbf{u},\mathbf{v},\mathbf{a},\mathbf{b}\right)&= \int d\lambda \rho _{\mathbf{u},\mathbf{v}} (\lambda ) A \left( \mathbf{u},\mathbf{v},\mathbf{a},\mathbf{b},\lambda \right) \nonumber \\&\quad B(\mathbf{v},\mathbf{u},\mathbf{b},\mathbf{a},\lambda ). \end{aligned}$$

(26)

For a general state,

$$\begin{aligned} E\left( \mathbf{a},\mathbf{b}\right) =\int d\mathbf{u}d\mathbf{v}F \left( \mathbf{u}, \mathbf{v}\right) {\overline{AB}}\left( \mathbf{u},\mathbf{v},\mathbf{a},\mathbf{b}\right) , \end{aligned}$$

(27)

which is the main quantity to be investigated, as it may differ with the corresponding QM result when entanglement is present, in which case a probability distribution over subensembles with definite polarizations leads to inequalities violated by the entangled state in QM.

Here we extend CNHV theories to include the case that $\mathbf{a}$ and $\mathbf{b}$ are not externally fixed. In each measurement, the measurement settings $\tilde{\mathbf{a}}(\lambda )$ and $\tilde{\mathbf{b}}(\lambda )$ are determined by HV $\lambda$, thus the measurement outcomes are like $A({\mathbf {u}}, \tilde{\mathbf{a}}(\lambda ), \eta , \lambda )$. Nevertheless, for those measurements with $\tilde{\mathbf{a}}(\lambda )= \mathbf{a}$, we can obtain the average of the outcomes. In the case of a single particle, the average is

$$\begin{aligned}&\int d \lambda \rho '_{{\mathbf {u}},{\mathbf {a}} }(\lambda ) A({\mathbf {u}},\tilde{\mathbf{a}}(\lambda ),\eta ,\lambda )={\bar{A}}({\mathbf {u}}, {\mathbf {a}})={\mathbf {u}} \cdot {\mathbf {a}}, \end{aligned}$$

(28)

where $\rho '_{{\mathbf {u}},{\mathbf {a}} }(\lambda ) \equiv \rho _{{\mathbf {u}} }(\lambda )\delta (\tilde{\mathbf{a}}(\lambda )-{\mathbf {a}})$ is a shorthand.

Likewise, for two correlated particles, the outcomes of those measurements with $\tilde{\mathbf{a}}(\lambda )= \mathbf{a}$ and $\tilde{\mathbf{b}}(\lambda )= \mathbf{b}$ give rise to

$$\begin{aligned}&\int d \lambda \rho _{{\mathbf {u}},{\mathbf {v}}} (\lambda ) \delta (\tilde{\mathbf{a}}(\lambda )-{\mathbf {a}})\delta (\tilde{\mathbf{b}}(\lambda )-{\mathbf {b}}) \nonumber \\&\qquad \times A({\mathbf {u}},{\mathbf {v}},\tilde{\mathbf{a}}(\lambda ),\tilde{\mathbf{b}}(\lambda ),\eta _a,\eta _b,\lambda )\nonumber \\&\quad ={\bar{A}}({\mathbf {u}}, {\mathbf {a}})={\mathbf {u}}\cdot {\mathbf {a}}, \end{aligned}$$

(29)

$$\begin{aligned}&\int d \lambda \rho _{{\mathbf {u}},{\mathbf {v}}} (\lambda ) \delta (\tilde{\mathbf{a}}(\lambda )-{\mathbf {a}})\delta (\tilde{\mathbf{b}}(\lambda )-{\mathbf {b}}) \nonumber \\&\qquad \times B({\mathbf {v}},{\mathbf {u}},\tilde{\mathbf{b}}(\lambda ),\tilde{\mathbf{a}}(\lambda ),\eta _b,\eta _a,\lambda )\nonumber \\&\quad ={\bar{B}}({\mathbf {v}}, {\mathbf {b}})={\mathbf {v}}\cdot {\mathbf {b}}. \end{aligned}$$

(30)

$$\begin{aligned} {\overline{AB}}(\mathbf{u},\mathbf{v},\mathbf{a},\mathbf{b})&=\int d\lambda \rho _{{\mathbf {u}},{\mathbf {v}}} (\lambda ) \delta (\tilde{\mathbf{a}}(\lambda )-{\mathbf {a}})\delta (\tilde{\mathbf{b}}(\lambda )-{\mathbf {b}}) \nonumber \\&\quad \times A(\mathbf{u},\mathbf{v},\tilde{\mathbf{a}}(\lambda ),\tilde{\mathbf{b}}(\lambda ),\eta _a,\eta _b,\lambda ) \nonumber \\&\quad B(\mathbf{v},\mathbf{u},\tilde{\mathbf{b}}(\lambda ),\tilde{\mathbf{a}}(\lambda ),\eta _b,\eta _a,\lambda ). \end{aligned}$$

(31)

Clearly the original formalism is a special case of this extension, by externally fixing $\tilde{\mathbf{a}}(\lambda )$ to be always ${\mathbf {a}}$ and $\tilde{\mathbf{b}}(\lambda )$ to be always ${\mathbf {b}}$, independent of $\lambda$.

4 LI for measuring directions on a plane and a cone

We now consider a pair of particles a and b, with the measurement outcomes $A=\pm 1$ and $B=\pm 1$, respectively. The average of those outcomes A with a same measurement setting $\mathbf{a}$ satisfy the Malus’ Law (29). The average of those outcomes B with a same measurement setting $\mathbf{b}$ satisfy the Malus’ Law (30). The correlation function is defined in the way of (31). ${\mathbf {a}}$ and ${\mathbf {b}}$ are each given as $\mathbf{a}^l(\phi _i)$ or $\mathbf{a}^s(\theta _s,\phi _i)$, $(i=a,b)$, as in (19).

We first consider correlation functions of various combinations of $\mathbf{a}^l$ and $\mathbf{a}^s$ . Define ${\hat{E}}^\pm (\mathbf{a},\mathbf{b})\equiv E(\mathbf{a},\mathbf{b} )+ E(\mathbf{b},\pm \mathbf{b})$, and rewrite ${\hat{E}}^{\pm }(\mathbf{a}^s(\theta _s,\phi _a),\mathbf{a}^l(\phi _b))$ as ${\hat{E}}^{\pm }_{sl}(\theta _s,\xi ,\varphi )$, where $\xi \equiv (\phi _a+\phi _b)/2$, $\varphi \equiv \phi _a-\phi _b$. ${\hat{E}}^{\pm }_{ll}(\theta _s,\xi ,\varphi )$ and ${\hat{E}}^{+}_{ss}(\theta _s,\xi ,\varphi )$ are similarly defined. Furthermore, we consider the averages over $\xi$, ${\hat{E}}^{-}_{sl} (\theta _s,\varphi )\equiv \int \frac{d\xi }{2\pi } {\hat{E}}^{-}_{sl} (\theta _s,\xi ,\varphi )$ and so on.

In the Appendix, we prove the following LI. The upper bound is given by

$$\begin{aligned}&{\hat{E}}^{-}_{sl} (\theta _s,\varphi _1)+\frac{\pi \cos (\theta _{1}(\theta _s, \varphi _1)) L_1(\theta _s,\varphi _1) }{4\cos \left( \frac{\varphi _2}{2}\right) } {\hat{E}}^{-}_{ll}(\theta _s,\varphi _2) \nonumber \\&\quad \le 2 \left( 1+\frac{\pi \cos \left( \theta _{1}(\theta _s, \varphi _1)\right) L_1(\theta _s,\varphi _1) }{4\cos \left( \frac{\varphi _2}{2}\right) }\right) \nonumber \\&\qquad -\cos (\theta _{1}(\theta _s, \varphi _1)) L_1(\theta _s,\varphi _1), \end{aligned}$$

(32)

where

$$\begin{aligned} L_1\left( \theta _s,\varphi \right)&\equiv |\mathbf{a}^s+\mathbf{a}^l|=\sqrt{2+2\cos \left( \varphi \right) \sin \left( \theta _s\right) },\\ \theta _{1}\left( \theta _s,\varphi \right)&=\cos ^{-1}\frac{\cos \left( \theta _s\right) }{\sqrt{2+2\cos \left( \varphi \right) \sin \left( \theta _s\right) }}. \end{aligned}$$

With $0<\theta _s<\pi /2$, we have $\sin (\theta _{1})> 0$, $\cos (\theta _{1})> 0$.

We find two lower bounds. The first is given as

$$\begin{aligned}&{\hat{E}}^+_{sl}(\theta _s,\varphi _1)+\frac{\pi \cos (\theta _{2}(\theta _s,\varphi _1))L_2(\theta _s,\varphi _1)}{4\left| \sin \left( \frac{\varphi _2}{2}\right) \right| }{\hat{E}}^+_{ll}(\theta _s,\varphi _2) \nonumber \\&\quad \ge -2\left( 1+\frac{\pi \cos (\theta _{2}(\theta _s,\varphi _1)) L_2(\theta _s,\varphi _1)}{4\left| \sin \left( \frac{\varphi _2}{2}\right) \right| }\right) \nonumber \\&\qquad + \cos (\theta _{2}(\theta _s,\varphi _1)) L_2(\theta _s,\varphi _1). \end{aligned}$$

(33)

where

$$\begin{aligned} L_2(\theta _s,\varphi )&\equiv |\mathbf{a}^s-\mathbf{a}^l|=\sqrt{2-2\cos (\varphi )\sin (\theta _s)},\\ \theta _{2}(\theta _s,\varphi )&=\cos ^{-1}\frac{\cos (\theta _s)}{\sqrt{2-2\cos (\varphi )\sin (\theta _s)}}. \end{aligned}$$

The second lower bound is given as

$$\begin{aligned}&{\hat{E}}^+_{sl}(\theta _s,\varphi _1)+\frac{\pi \cos (\theta _2(\theta _s,\varphi _1)) L_2(\theta _s,\varphi _1)}{4\sin (\theta _s)\left| \sin \left( \frac{\varphi _2}{2}\right) \right| }{\hat{E}}^+_{ss}(\varphi _2) \nonumber \\&\quad \ge -2\left( 1+\frac{\pi \cos \left( \theta _2(\theta _s,\varphi _1)\right) L_2(\theta _s,\varphi _1)}{4\sin (\theta _s)\left| \sin \left( \frac{\varphi _2}{2}\right) \right| }\right) \nonumber \\&\qquad +\cos (\theta _2)L_2(\theta _s,\varphi _1). \end{aligned}$$

(34)

Equations (32), (33) and (34) comprise our LI.

The correlation functions averaged over $\xi$ are not directly observable, therefore rotational invariance or fair sampling of the averages needs to be assumed for measurements, in order that LI in terms of these average correlation functions can be experimentally examined [17, 18]. In the case of meson decays, the rotational invariance in Bloch representation is actually time translational invariance.

To drop this additional assumption, we can redefine each average in a discrete way,

$$\begin{aligned}&{\hat{E}}^{\pm }_{sl}(\theta _s,\varphi )\equiv \frac{1}{N}\sum _{n=1}^N {\hat{E}}^{\pm }_{sl}\left( \theta _s,\xi _n =\frac{2n\pi }{N},\varphi \right) , \end{aligned}$$

(35)

and ${\hat{E}}^{\pm }_{ll}(\theta _s,\varphi )$ and ${\hat{E}}^{+}_{ss}(\theta _s,\varphi )$ similarly. As derived in the Appendix, for these discrete average correlation functions, our LI can be obtained from Eqs. (32), (33) and (34) by simply replacing $\pi /4$ as $1/2u_N$, where $u_N\equiv \frac{1}{N}\cot \left( \frac{\pi }{2N}\right)$. $N\ge 2$ is required. As $N\rightarrow \infty$, $u_N\rightarrow 2/\pi$, then the discrete version approaches the continuous version.

Our LI can be tested using various systems, in which measurement directions $\mathbf{a}^l(\phi _l)$ and $\mathbf{a}^s(\theta _s,\phi _s)$ can be directly adjusted.

For meson decays, $\theta _s=2\beta$ is fixed, while $\phi _l=\phi _l(t) = x\Gamma t$, $\phi _s=\phi _s(t) = x\Gamma t+\frac{\pi }{2}$ are given by the decay time t. We mention that for the two particles a and b to be separated in spacelike distance, there is a constraint on the decay times $t_a$ and $t_b$. Suppose the particle pairs are generated from a particle at rest and each flies in velocity v to opposite directions. Then spacelike separation means $(1+w)t_a > (1-w) t_b$, where $w=(v/c)/\sqrt{1-v^2/c^2}$. Consequently there is a constraint on possible values of $\xi$, but it does not affect the averages over $\xi$, which is an angle mathematically, hence its functions are periodic.

5 Testing LI in entangled $B_d$ mesons

We now come back to the $C=-1$ $B^0{\bar{B}}^0$ entangled meson pairs, and we can write the correlation functions as

$$\begin{aligned} E(\mathbf{a}^X(t_a),\mathbf{a}^Y(t_b)), (X,Y=l,s). \end{aligned}$$

By definition,

$$\begin{aligned}&E\left( \mathbf{a}^X(t_a),\mathbf{a}^Y(t_b)\right) \nonumber \\&\quad =\big [\big (P(X+,Y+,t_a,t_b\big )+P\big (X-,Y-,t_a,t_b\big )\nonumber \\&\qquad - P\big (X+,Y-,t_a,t_b\big )-P\big (X-,Y+,t_a,t_b\big )\big ]/ \nonumber \\&\qquad \big [P\big (X+,Y+,t_a,t_b\big )+P\big (X-,Y-,t_a,t_b\big )\nonumber \\&\qquad + P\big (X+,Y-,t_a,t_b\big )+P\big (X-,Y+,t_a,t_b\big )\big ], \end{aligned}$$

(36)

where for convenience, we have invented the shorthand

$$\begin{aligned} l+ \equiv B^0, \,\, l-\equiv {\bar{B}}^0, \, \, s\pm \equiv B_\pm , \end{aligned}$$

(37)

which should not be confused with $l^{\pm }$ and $S_{\pm }$, with ± as the superscript or subscript, denoting the final states of decays.

$P(X\pm ,Y\pm ,t_a,t_b)$ is the probability that the measurement results of a and b are $X\pm$ and $Y\pm$ at $t_a$ and $t_b$, respectively, indicated by the final states of their respective decays. The measurement or filtering or projection in the flavor basis $\{ B^0, {\bar{B}}^0\}$ is made through a semileptonic decay to a flavor eigenstate $|l^\pm \rangle$. The measurement or filtering or projection in CP basis $\{ B_+, B_-\}$ is made through a decay into CP eigenstate $|S_\pm \rangle$. With direct CP violation negligible, we have $A_{l^-}={\bar{A}}_{l^+}=0$, $A_{S_{\pm }}=\pm {\bar{A}}_{S_{\pm }}$. Only if $|l^-\rangle =CP |l^+\rangle$, we have $A_{l^+}={\bar{A}}_{l^-}$. Note that the decay products of a and b may be different even though their flavor or CP eigenvalues are the same, and may not be CP conjugates even though their flavor eigenvalues are opposites.

The basis of measurement, namely flavor or CP basis, is not actively chosen by experiments, but is signalled by the decay products. Our extension of CNHV and LI addresses this issue, as the main achievement of this paper.

A key quantity is the joint decay rate for particle a decaying to $f _a$ at $t_a$ while particle b decaying to $f_b$ at $t_b$, $R(f _a,f _b, t_a, t_b) \propto \left| \langle f _a, f _b| W_a W_b | \Psi (t_a,t_b)\rangle \right| ^2$. The following joint decay amplitudes will be needed.

There are four amplitudes in the form of

$$\begin{aligned} \big \langle l^\pm _a, l^\pm _b\big | W_a W_b \big | \Psi (t_a,t_b)\big \rangle = A_{l^\pm _a} A_{l^\pm _b} \big \langle l \pm , l\pm \big | \Psi (t_a,t_b)\big \rangle , \end{aligned}$$

(38)

where, ± in $l^\pm _a$ corresponds to the first $l \pm$ on RHS, ± in $l^\pm _b$ corresponds to the second $l \pm$ on RHS.

There are four amplitudes of the form of

$$\begin{aligned}&\big \langle S_\pm ^a, S_\pm ^b\big | W_a W_b \big | \Psi (t_a,t_b)\big \rangle = 2 A_{S_\pm ^a} A_{S_\pm ^b} \big \langle s\pm , s\pm \big | \Psi (t_a,t_b)\big \rangle , \end{aligned}$$

(39)

where we have used $\langle S_\pm |W|B_\pm \rangle =(A_{S_\pm }\pm {\bar{A}}_{S_\pm })/\sqrt{2}=\sqrt{2} A_{S_\pm }$.

There are four other amplitudes of the form of

$$\begin{aligned}&\big \langle S_\pm ^a, l^\pm _b\big | W_a W_b \big | \Psi (t_a,t_b)\big \rangle = \sqrt{2} A_{S_\pm ^a} A_{l^\pm _b} \big \langle s\pm , l\pm \big | W_a W_b \big | \Psi (t_a,t_b)\big \rangle . \end{aligned}$$

(40)

The experimentally measured quantity is the number of the joint events $N(f_a,f_b,t_a,t_b) \propto \epsilon _{f_a,f_b}R(f_a,f_b,t_a,t_b)$, where $\epsilon _{f_a,f_b}$ is the detection efficiency for that channel [49], $R(f_a,f_b,t_a,t_b)$ is proportional to the modulo square of the joint decay amplitude, as given in Eqs. (38–40).

Therefore the correlation function (36) can be obtained from event numbers as

$$\begin{aligned}&E\left( \mathbf{a}^l(t_a),\mathbf{a}^l(t_b)\right) =\nonumber \\&\quad \left( \frac{N(l_a^+,l_b^+,t_a,t_b)}{\epsilon _{l_a^+,l_b^+}\big |A_{l_a^+}\big |^2\big |A_{l_b^+}\big |^2} +\frac{N(l_a^-,l_b^-,t_a,t_b)}{\epsilon _{l_a^-,l_b^-}\big |{\bar{A}}_{l_a^-}\big |^2\big |{\bar{A}}_{l_b^-}\big |^2}\right. \nonumber \\&\quad \left. -\frac{N(l_a^+,l_b^-,t_a,t_b)}{\epsilon _{l_a^+,l_b^-}\big |A_{l_a^+}\big |^2\big |{\bar{A}}_{l_b^-}\big |^2} -\frac{N(l_a^-,l_b^+,t_a,t_b)}{\epsilon _{l_a^-,l_b^+}\big |{\bar{A}}_{l_a^-}\big |^2\big |A_{l_b^+}\big |^2} \right) \nonumber \\&\quad \Big /\left( \frac{N(l_a^+,l_b^+,t_a,t_b)}{\epsilon _{l_a^+,l_b^+}\big |A_{l_a^+}\big |^2\big |A_{l_b^+}\big |^2} +\frac{N(l_a^-,l_b^-,t_a,t_b)}{\epsilon _{l_a^-,l_b^-}\big |{\bar{A}}_{l_a^-}\big |^2\big |{\bar{A}}_{l_b^-}\big |^2}\right. \nonumber \\&\quad \left. +\frac{N(l_a^+,l_b^-,t_a,t_b)}{\epsilon _{l_a^+,l_b^-}\big |A_{l_a^+}\big |^2\big |{\bar{A}}_{l_b^-}\big |^2} +\frac{N(l_a^-,l_b^+,t_a,t_b)}{\epsilon _{l_a^-,l_b^+}\big |{\bar{A}}_{l_a^-}\big |^2\big |A_{l_b^+}\big |^2} \right) , \end{aligned}$$

(41)

$$\begin{aligned}&E\left( \mathbf{a}^s(t_a),\mathbf{a}^l(t_b)\right) =\nonumber \\&\quad \left( \frac{N(S_a^+,l_b^+,t_a,t_b)}{\epsilon _{S_a^+,l_b^+}\big |A_{S_a^+}\big |^2 \big |A_{l_b^+}\big |^2 } +\frac{N(S_a^-,l_b^-,t_a,t_b)}{\epsilon _{S_a^-,l_b^-}\big |A_{S_a^-}\big |^2\big |{\bar{A}}_{l_b^-}\big |^2}\right. \nonumber \\&\quad \left. -\frac{N(S_a^+,l_b^-,t_a,t_b)}{\epsilon _{S_a^+,l_b^-}\big |A_{S_a^+}\big |^2 \big |{\bar{A}}_{l_b^-}\big |^2 } -\frac{N(S_a^-,l_b^+,t_a,t_b)}{\epsilon _{S_a^-,l_b^+}\big |A_{S_a^-}\big |^2 \big |A_{l_b^+}\big |^2 }\right) \nonumber \\&\quad \Big /\left( \frac{N(S_a^+,l_b^+,t_a,t_b)}{\epsilon _{S_a^+,l_b^+}\big |A_{S_a^+}\big |^2 \big |A_{l_b^+}\big |^2 } +\frac{N(S_a^-,l_b^-,t_a,t_b)}{\epsilon _{S_a^-,l_b^-}\big |A_{S_a^-}\big |^2\big |{\bar{A}}_{l_b^-}\big |^2}\right. \nonumber \\&\qquad \left. +\frac{N(S_a^+,l_b^-,t_a,t_b)}{\epsilon _{S_a^+,l_b^-}\big |A_{S_a^+}\big |^2 \big |{\bar{A}}_{l_b^-}\big |^2 } +\frac{N(S_a^-,l_b^+,t_a,t_b)}{\epsilon _{S_a^-,l_b^+}\big |A_{S_a^-}\big |^2 \big |A_{l_b^+}\big |^2 } \right) , \end{aligned}$$

(42)

$$\begin{aligned}&E\left( \mathbf{a}^s(t_a),\mathbf{a}^s(t_b)\right) =\nonumber \\&\quad \left( \frac{N(S_a^+,S_b^+,t_a,t_b)}{\epsilon _{S_a^+,S_b^+}\big |A_{S_a^+}\big |^2\big |A_{S_b^+}\big |^2} +\frac{N(S_a^-,S_b^-,t_a,t_b)}{\epsilon _{S_a^-,S_b^-}\big |A_{S_a^-}\big |^2 \big |A_{S_b^-}\big |^2 }\right. \nonumber \\&\quad \left. -\frac{N(S_a^+,S_b^-,t_a,t_b)}{\epsilon _{S_a^+,S_b^-}\big |A_{S_a^+}\big |^2\big |A_{S_b^-}\big |^2} -\frac{N(S_a^-,S_b^+,t_a,t_b)}{\epsilon _{S_a^-,S_b^+}\big |A_{S_a^+}\big |^2\big |A_{S_b^+}\big |^2}\right) \nonumber \\&\quad \Big /\left( \frac{N(S_a^+,S_b^+,t_a,t_b)}{\epsilon _{S_a^+,S_b^+}\big |A_{S_a^+}\big |^2\big |A_{S_b^+}\big |^2} +\frac{N(S_a^-,S_b^-,t_a,t_b)}{\epsilon _{S_a^-,S_b^-}\big |A_{S_a^-}\big |^2 \big |A_{S_b^-}\big |^2 }\right. \nonumber \\&\quad \left. +\frac{N(S_a^+,S_b^-,t_a,t_b)}{\epsilon _{S_a^+,S_b^-}\big |A_{S_a^+}\big |^2\big |A_{S_b^-}\big |^2} +\frac{N(S_a^-,S_b^+,t_a,t_b)}{\epsilon _{S_a^-,S_b^+}\big |A_{S_a^+}\big |^2\big |A_{S_b^+}\big |^2}\right) , \end{aligned}$$

(43)

where $\epsilon$’s are the detection efficiencies. In experiments, $|A_{l^{\pm }_{i}}|^2$ and $|A_{S_{i}^{\pm }}|^2$, $(i=a,b)$, can be absorbed to the redefinitions of detection efficiencies.

Furthermore, one obtains

$$\begin{aligned} {\hat{E}}^{ll\pm }(\phi _a,\phi _b)&\equiv E\left( \mathbf{a}^l(x\Gamma t_a),\mathbf{a}^l(x\Gamma t_b)\right) \nonumber \\&\quad +E\left( \mathbf{a}^l(x\Gamma t_b),\pm \mathbf{a}^l(x\Gamma t_b)\right) ,\nonumber \\ {\hat{E}}^{sl\pm }(\phi _a,\phi _b)&\equiv E\left( \mathbf{a}^s\left( x\Gamma t_a+\frac{\pi }{2}\right) ,\mathbf{a}^l(x\Gamma t_b)\right) \nonumber \\&\quad +E\left( \mathbf{a}^l(x\Gamma t_b),\pm \mathbf{a}^l(x\Gamma t_b)\right) ,\nonumber \\ {\hat{E}}^+_{ss}(\phi _a,\phi _b)&\equiv E\left( \mathbf{a}^s\left( x\Gamma t_a+\frac{\pi }{2}\right) ,\mathbf{a}^l(x\Gamma t_b)\right) \nonumber \\&\quad + E\left( \mathbf{a}^s\left( x\Gamma t_b+\frac{\pi }{2}\right) ,\mathbf{a}^s\left( x\Gamma t_b+\frac{\pi }{2}\right) \right) , \end{aligned}$$

(44)

from which the averages ${\hat{E}}^{ll\pm }(\varphi )$, ${\hat{E}}^{sl\pm }(\varphi )$, ${\hat{E}}^{ss+}(\varphi )$ can be obtained. Note that we did not define ${\hat{E}}^{ss-}$, which would not have physical meaning, as $-\mathbf{a}^s$ is not on the cone, where all possible $\mathbf{a}^s$’s lie. In SM, with $\Delta \Gamma = 0$, $R(f_b,f_b,t_a,t_b)$ can be obtained as

$$\begin{aligned} R\big (f _a,f _b,t_a, t_b\big )&=\frac{e^{-\Gamma \big (t_a+t_b\big )}}{4}\times \left\{ \big (\big |\xi _-\big |^2+\big |\zeta _-\big |^2\big )\right. \nonumber \\&\quad \left. -\big (\big |\xi _-\big |^2-\big |\zeta _-\big |^2\big )\cos \big (x\Gamma \big (t_a-t_b\big )\big )\right. \nonumber \\&\quad \left. -2Im\big (\zeta _-^*\xi _-\big )\sin \big (x \Gamma \big (t_a-t_b\big )\big )\right\} , \end{aligned}$$

(45)

where $\xi _- \equiv -\left( \frac{p}{q}A_{f_a}A_{f_b}- \frac{q}{p}{\bar{A}}_{f_a} {\bar{A}}_{f_b}\right)$, $\zeta _- \equiv \left( A_{f_a}{\bar{A}}_{f_b}\right.$ $\left. {\bar{A}}_{f_a}A_{f_b}\right)$.

In experiments, it is more convenient to use the time-integrated joint decay rate

$$\begin{aligned} R\left( f _a,f _b,\Delta t\right) =\int _0^{\infty }dt_aR_-\left( f _a,f _b, t_a, t_a+\Delta t\right) , \end{aligned}$$

(46)

which is obtained as

$$\begin{aligned} R\big (f _a,f _b,\Delta t\big )&= \frac{e^{-\Gamma |\Delta t|}}{8\Gamma }\times \left\{ \big (|\xi _-|^2+|\zeta _-|^2\big )\right. \nonumber \\&\quad \left. -\, \big (|\xi _-|^2-|\zeta _-|^2\big )\cos \big (x\Gamma \Delta t\big )\right. \nonumber \\&\quad \left. +\,2Im\big (\zeta _-^*\xi _-\big )\sin \big (x\Gamma \Delta t\big )\right\} , \end{aligned}$$

(47)

It is more rigorous to test LI of the discrete version of the average correlation functions, rather than that of the continuous version. However, it is experimentally much easier to measure $N(f_a,f_b,\Delta t)\propto \epsilon _{f_a,f_b}R(f_a,f_b,\Delta t)$ than $N_{f_a,f_b}(t_a,t_b)$, consequently it is much easier to test LI in terms of the continuous version of the average correlation functions.

From (45) and (47), it can be seen that in SM, $R(f_a,f_b,t_b+\Delta t,t_b)=2\Gamma e^{-\Gamma (t_a+t_b)} e^{\Gamma |\Delta t|} R(f_a,f_b, \Delta t)$. Consequently, ${\hat{E}}(\varphi )$, as an average of $E(\phi _a, \phi _b)$ over $\xi \equiv x\Gamma (t_a+t_b)/2+\pi /2$, can be directly related to $N(f_a,f_b,\Delta t)$ as

$$\begin{aligned}&{\hat{E}}^{ll}(\varphi = x\Gamma \Delta t) =\nonumber \\&\quad \left( \frac{N(l_a^+,l_b^+,\Delta t)}{\epsilon _{l_a^+,l_b^+}|A_{l_a^+}|^2|A_{l_b^+}|^2} +\frac{N(l_a^-,l_b^-,\Delta t)}{\epsilon _{l_a^-,l_b^-}|{\bar{A}}_{l_a^-}|^2|{\bar{A}}_{l_b^-}|^2}\right. \nonumber \\&\quad \left. -\frac{N(l_a^+,l_b^-,\Delta t)}{\epsilon _{l_a^+,l_b^-}|A_{l_a^+}|^2|{\bar{A}}_{l_b^-}|^2} -\frac{N(l_a^-,l_b^+,\Delta t)}{\epsilon _{l_a^-,l_b^+}|{\bar{A}}_{l_a^-}|^2|A_{l_b^+}|^2}\right) \nonumber \\&\quad \Big /\left( \frac{N(l_a^+,l_b^+,\Delta t)}{\epsilon _{l_a^+,l_b^+}|A_{l_a^+}|^2|A_{l_b^+}|^2} +\frac{N(l_a^-,l_b^-,\Delta t)}{\epsilon _{l_a^-,l_b^-}|{\bar{A}}_{l_a^-}|^2|{\bar{A}}_{l_b^-}|^2}\right. \nonumber \\&\quad \left. +\frac{N(l_a^+,l_b^-,\Delta t)}{\epsilon _{l_a^+,l_b^-}|A_{l_a^+}|^2|{\bar{A}}_{l_b^-}|^2} +\frac{N(l_a^-,l_b^+,\Delta t)}{\epsilon _{l_a^-,l_b^+}|{\bar{A}}_{l_a^-}|^2|A_{l_b^+}|^2} \right) , \end{aligned}$$

(48)

$$\begin{aligned}&{\hat{E}}^{sl}(\varphi = x\Gamma \Delta t+\frac{\pi }{2})=\nonumber \\&\quad \left( \frac{N(S_a^+,l_b^+,\Delta t)}{\epsilon _{S_a^+,l_b^+}|A_{S_a^+}|^2 |A_{l_b^+}|^2 } -\frac{N(S_a^-,l_b^-,\Delta t)}{\epsilon _{S_a^-,l_b^-}|A_{S_a^-}|^2|{\bar{A}}_{l_b^-}|^2}\right. \nonumber \\&\quad \left. +\frac{N(S_a^+,l_b^-,\Delta t)}{\epsilon _{S_a^+,l_b^-}|A_{S_a^+}|^2 |{\bar{A}}_{l_b^-}|^2 } -\frac{N(S_a^-,l_b^+,\Delta t)}{\epsilon _{S_a^-,l_b^+}|A_{S_a^-}|^2 |A_{l_b^+}|^2 } \right) \nonumber \\&\quad \Big /\left( \frac{N(S_a^+,l_b^+,\Delta t)}{\epsilon _{S_a^+,l_b^+}|A_{S_a^+}|^2 |A_{l_b^+}|^2 } +\frac{N(S_a^-,l_b^-,\Delta t)}{\epsilon _{S_a^-,l_b^-}|A_{S_a^-}|^2|{\bar{A}}_{l_b^-}|^2}\right. \nonumber \\&\quad \left. +\frac{N(S_a^+,l_b^-,\Delta t)}{\epsilon _{S_a^+,l_b^-}|A_{S_a^+}|^2 |{\bar{A}}_{l_b^-}|^2 } +\frac{N(S_a^-,l_b^+,\Delta t)}{\epsilon _{S_a^-,l_b^+}|A_{S_a^-}|^2 |A_{l_b^+}|^2 } \right) , \end{aligned}$$

(49)

$$\begin{aligned}&{\hat{E}}^{ss}(\varphi = x\Gamma \Delta t) =\nonumber \\&\quad \left( \frac{N(S_a^+,S_b^+,\Delta t)}{\epsilon _{S_a^+,S_b^+}|A_{S_a^+}|^2|A_{S_b^+}|^2} +\frac{N(S_a^-,S_b^-,\Delta t)}{\epsilon _{S_a^-,S_b^-}|A_{S_a^-}|^2 |A_{S_b^-}|^2 }\right. \nonumber \\&\quad \left. -\frac{N(S_a^+,S_b^-,\Delta t)}{\epsilon _{S_a^+,S_b^-}|A_{S_a^+}|^2|A_{S_b^-}|^2} -\frac{N(S_a^-,S_b^+,\Delta t)}{\epsilon _{S_a^-,S_b^+}|A_{S_a^+}|^2|A_{S_b^+}|^2}\right) \nonumber \\&\quad \Big /\left( \frac{N(S_a^+,S_b^+,\Delta t)}{\epsilon _{S_a^+,S_b^+}|A_{S_a^+}|^2|A_{S_b^+}|^2} +\frac{N(S_a^-,S_b^-,\Delta t)}{\epsilon _{S_a^-,S_b^-}|A_{S_a^-}|^2 |A_{S_b^-}|^2 }\right. \nonumber \\&\quad \left. +\frac{N(S_a^+,S_b^-,\Delta t)}{\epsilon _{S_a^+,S_b^-}|A_{S_a^+}|^2|A_{S_b^-}|^2} +\frac{N(S_a^-,S_b^+,\Delta t)}{\epsilon _{S_a^-,S_b^+}|A_{S_a^+}|^2|A_{S_b^+}|^2}\right) . \end{aligned}$$

(50)

Moreover, the integration over $\xi$ of ${\hat{E}}^{\pm }(\mathbf{a},\mathbf{b})=E(\mathbf{a},\mathbf{b})+E(\mathbf{b},\pm \mathbf{b})$ can be performed independently for the two terms on RHS, consequently,

$$\begin{aligned} {\hat{E}}^+_{ll}(\varphi )&={\hat{E}}^{ll}(\varphi )+{\hat{E}}^{ll}(0),\;\;{\hat{E}}^{-}_{ll}(\varphi )={\hat{E}}^{ll}(\varphi )+{\hat{E}}^{ll}(\pi )\nonumber \\ {\hat{E}}^+_{sl}(\varphi )&={\hat{E}}^{sl}(\varphi )+{\hat{E}}^{ll}(0),\;\; {\hat{E}}^{-}_{sl}(\varphi )={\hat{E}}^{sl}(\varphi )+{\bar{E}}^{ll}(\pi )\nonumber \\ {\hat{E}}^+_{ss}(\varphi )&={\hat{E}}^{ss}(\varphi )+{\hat{E}}^{ss}(0). \end{aligned}$$

(51)

Note that Eqs. (41–43) and (48–50) are mainly for the use in analyzing experimental data. QM result can be obtained simply from $\big \langle \mathbf{a}^X,\mathbf{a}^Y|\Psi _-\big \rangle =- \mathbf{a}^X\cdot \mathbf{a}^Y$, therefore

$$\begin{aligned} {\hat{E}}^{sl} (\varphi )&=-\sin (2\beta )\cos (\varphi ),\;\; {\hat{E}}^{ll} (\varphi )=-\cos (\varphi ), \nonumber \\ {\hat{E}}^{ss }(\varphi )&=-\cos ^2(2\beta )-\sin ^2(2\beta )\cos (\varphi ). \end{aligned}$$

(52)

It is interesting to test our LI using various systems, in which $\varphi _a$ and $\varphi _b$ are directly adjusted.

For $B_d$ mesons, QM result (52) can also be obtained from the definition (36) of correlation functions, with

$$\begin{aligned} P(X\pm ,Y\pm ,t_a,t_b) \propto \end{aligned}$$

$\left| \big \langle X\pm ,Y\pm | W_a W_b | \Psi (t_a,t_b)\big \rangle \right| ^2$ obtained by substituting LHS of $R(f _a,f _b, t_a, t_b) \propto$ $\left| \big \langle f _a, f _b| W_a W_b | \Psi (t_a,t_b)\big \rangle \right| ^2$ with the result (45) of $R(f _a,f _b, t_a, t_b)$, and RHS with the joint amplitudes (38–40), and then having $A_f$ and ${\bar{A}}_f$ cancelled. For $B_d$ mesons, the values of $\beta$ and x are given by $\sin (2\beta )=0.695$, $x=0.769$ [97].

The upper bound of a our LI violation can be quantified as

$$\begin{aligned} g^u(\varphi _1,\varphi _2) \equiv \frac{h^u_{L}(\varphi _1,\varphi _2)-h^u_{R}(\varphi _1,\varphi _2)}{\left| h^u_{L}(\varphi _1,\varphi _2)\right| }, \end{aligned}$$

(53)

where $h^u_{R}$ and $h^u_{L}(\varphi _1,\varphi _2)$ are RHS and LHS of (32), respectively. The first lower bound can be quantified as

$$\begin{aligned} g^{d1}(\varphi _1,\varphi _2)=\frac{h^{d1}_{R}\left( \varphi _1,\varphi _2\right) -h^{d1}_{L}\left( \varphi _1,\varphi _2\right) }{\left| h^{d1}_{L}\left( \varphi _1,\varphi _2\right) \right| }, \end{aligned}$$

(54)

where $h^{d1}_R$ and $h^{d1}_L$ are RHS and LHS of (33), respectively. The second lower bound can be quantified as

$$\begin{aligned} g^{d2}(\varphi _1,\varphi _2)=\frac{h^{d2}_{R}\left( \varphi _1,\varphi _2\right) -h^{d2}_{L}\left( \varphi _1,\varphi _2\right) }{\left| h^{d2}_{L}(\varphi _1,\varphi _2)\right| }, \end{aligned}$$

(55)

where $h^{d2}_R$ and $g^{h2}_L$ are RHS and LHS of (34), respectively. Each of these three quantities larger than 0 represents the violation of the corresponding bound of LI.

From $\partial _{\varphi _1}g^u(\varphi _1,\varphi _2)= \partial _{\varphi _1}g^{d1}(\varphi _1,\varphi _2)= \partial _{\varphi _1}g^{d2}(\varphi _1,\varphi _2)=0$, it is determined that the maximum of $g^{u}$ is on $\varphi _1=\pi$, while the maxima of $g^{d1}$ and $g^{d1}$ are both on $\varphi _1=0$. $L_1(\varphi _1=\pi )=L_2(\varphi _1=0)\approx 0.781$, $\theta _{1}(\varphi _1=\pi )=\theta _{ 2}( \varphi _1=0)\approx 0.401$.

Furthermore, solving $\partial _{\varphi _2}g^u(\pi ,\varphi _2)=0$ numerically, we find that $g^u(\pi , \varphi _2)$ reaches its maximum at $\varphi _2\approx \pm 2.81$. We also find numerically that $g^u(\pi ,\varphi _2)>0$ when $2.39<|\varphi _2|<\pi$. Similarly, solving $\partial _{\varphi _2}g^{d1}(0,\varphi _2)=0$ numerically, we find that $g^{d1}(0,\varphi _2)$ reaches the maximum at $\varphi _2\approx \pm 0.336$. We also find numerically that $g^{d1}(0,\varphi _2)>0$ when $0<|\varphi _2|<0.75$.

Solving $\partial _{\varphi _2}g^{d2}(0,\varphi _2)=0$ numerically, we find that $g^{d2}(0,\varphi _2)$ reaches its maximum at $\varphi _2\approx \pm 0.486$, and we find numerically that $g^{d_2}(0,\varphi _2)>0$ when $0<|\varphi _2|<1.11$. The $\varphi _2$ range of $g^{d2}>0$ is larger than that of $g^{d1}>0$. The maxima of $g^u$, $g^{d1}$ and $g^{d2}$ are all about $2.7\%$. The results are depicted in Fig. 2.

Fig. 2

LI violation of entangled $B_d$ mesons. $\theta _s$ is fixed to be $\sin ^{-1}{0.695}$. Our LI is violated when $g^u(\varphi _1,\varphi _2)>0$ or $g^{d1}(\varphi _1,\varphi _2)>0$ or $g^{d2}(\varphi _1,\varphi _2)>0$. $g^u>0$ when $\varphi _1=\pi$, $2.39<|\varphi _2|<\pi$, and the maximum is at $\varphi _1=\pm \pi , \varphi _2\approx \pm 2.81$. $g^{d1} >0$ when $\varphi _1=0$, $0<|\varphi _2|<0.75$, and the maximum is at $\varphi _1=0, \varphi _2\approx \pm 0.336$. $g^{d2} >0$ when $\varphi _1=0$, $0<|\varphi _2|<1.11$, and the maximum is at $\varphi _1=0, \varphi _2\approx \pm 0.486$. The maxima are all about $2.7\%$

A $B_d$ meson is unstable, and the time interval between the two decays is of the order of the lifetime $\tau _B$ [71]. So it is better to study the case in which $\Delta t$ is of the order of $\tau _B$, so that the number of events is large. Thus it is easier to test $g^{d2}$, because in its violation region, $\Delta t$ is closer to $\tau _B$.

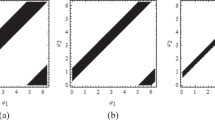
We now focus on how to make measurements to confirm the violation of the second lower bound. $g^{d2}(\varphi _1,\varphi _2)>0$ can be found in the regime $(\varphi _1=0$, $0<|\varphi _2|<1.11)$, as calculated above. The function $g^{d2}(\varphi _1,\varphi _2)$ contains ${\hat{E}}^+_{sl}(\varphi _1)={\hat{E}}^{sl}(\varphi _1)+ {\hat{E}}^{ll}(0)$ and ${\hat{E}}^+_{ss}(\varphi _2)={\hat{E}}^{ss}(\varphi )+ {\hat{E}}^{ss}(0)$. Hence one first measures ${\hat{E}}^{ll}(\Delta t_1=0)$ and ${\hat{E}}^{sl}(\varphi _1=0)= {\hat{E}}^{sl}(\Delta t_1 =-\pi / 2x \Gamma \approx -2.04\tau _B )$, as shown in Fig. 3. Thus ${\hat{E}}^+_{sl}(\varphi _1=0)= {\hat{E}}^{sl}(\varphi _1=0)+{\bar{E}}^{ll}(\varphi _1=0)$ is obtained. One also needs to measure ${\hat{E}}^{ss}(\Delta t_2 =0)$ and ${\hat{E}}^{ss}(\Delta t_2)$ with $0<|\Delta t_2|<1.11/x\Gamma \approx 1.44\tau _B$, such that ${\hat{E}}^+_{ss}(\varphi _2)$ with $0<|\varphi _2|<1.11$ is obtained. Thus one obtains $g^{d2}(\varphi _1,\varphi _2)>0$ in this regime. The violation is maximal when $\Delta t_2 \approx 0.486/x\Gamma \approx 0.633\tau _B$, then $g^{d2}(\varphi _1,\varphi _2)\approx 2.7\%$, as shown in Fig. 3. Typically, the resolution of the signal is proportional to the inverse of square of event numbers [71]. Therefore it can be estimated that the expected signal of LI violation can be observed when the event number is about $10^4$–$10^5$, which can be achieved in current experiments [64].

Fig. 3

The correlation functions to be measured. The left picture represents ${\hat{E}}^{sl}(\Delta t = \pi / 2x\Gamma \approx 2.04\tau _B)={\hat{E}}^{sl}(\varphi _1=0)$. The right picture represents ${\hat{E}}^{ss}(\Delta t = 0.486 / x\Gamma \approx 0.633\tau _B)={\hat{E}}^{ss}(\varphi _2\approx 0.486)$. They give rise to $g^{d1}( \varphi _1=0,\varphi _2\approx 0.486)$, which maximally violates the second lower bound of our LI

It is also possible to test LI in polarization-entangled baryon-antibaryon pairs produced in, say, $J/\Psi \rightarrow \Lambda {\bar{\Lambda }}$ decays, where the polarizations of $\Lambda$ and ${\bar{\Lambda }}$ can be measured through the angular distribution of the momenta of their decay products pions. However, the effective measuring directions satisfying the Malus’ law are yet to be found out.

Fig. 4

LI violation in case $\theta _s$ is a variable. The maxima of $g^u$, $g^{d1}$ and $g^{d2}$ are still at $\varphi _1= \pi ,0,0$, respectively. $g^u(\theta _s,\pi ,\varphi _2)$, $g^{d1}(\theta _s,0,\varphi _2)$ and $g^{d2}(\theta _s,0,\varphi _2)$ are functions of $\theta _s$ and $\varphi _2$

If using other systems such as photon polarizations to test our LI, $\theta _s$ may become a variable. The results of $\partial _{\varphi _1}g^u(\varphi _1,\varphi _2)= \partial _{\varphi _1}g^{d1}(\varphi _1,\varphi _2)= \partial _{\varphi _1}g^{d2}(\varphi _1,\varphi _2)=0$ do not depend on $\theta _s$, hence their maxima are still at $\varphi _1= \pi ,0,0$, respectively. $g^u(\theta _s,\pi ,\varphi _2)$, $g^{d1}(\theta _s,0,\varphi _2)$ and $g^{d2}(\theta _s,0,\varphi _2)$ as functions of $\theta _s$ and $\varphi _2$ are shown in Fig. 4. Interestingly, in a certain range of $\varphi _2$, for any value of $\theta _s$ except 0 and $\pi /2$, we always have $g^{d2}>0$, that is, the second lower bound is always violated.

Furthermore, we numerically found the maximal violations of the three bounds are all $3.87482\%$ when $\theta _s=1.18208$, i.e.

$$\begin{aligned} g^u(1.18208,\pm \pi , \pm 2.7373)&=g^{d1}(1.18208,0, \pm 0.404296)\nonumber \\&=g^{d2}(1.18208,0, \pm 0.437399)\nonumber \\&=3.87482\%. \end{aligned}$$

(56)

It is also found that

$$\begin{aligned} g^{d1}(1.18208,0,\varphi _2)>0,\,\text{ when }\,\, 0<|\varphi _2|<1.0734, \end{aligned}$$

(57)

$$\begin{aligned} g^{d2}(1.18208,0,\varphi _2)>0,\,\text{ when }\, \, 0<|\varphi _2|<1.17078. \end{aligned}$$

(58)

The latter is wider, as shown in Fig 5.

Fig. 5

The two lower bounds are maximally violated on $\theta _s=1.18208$, $\varphi _1=0$. Shown here are the dependence of $g^{d1}(\theta _s=1.18208,\varphi _1=0,\varphi _2)$ and $g^{d2}(\theta _s=1.18208,\varphi _1=0,\varphi _2)$ on $\varphi _2$. $g^{d1} >0$ when $0<|\varphi _2|<1.0734$, while $g^{d2} >0$ when $0<|\varphi _2|<1.17078$

6 Summary and discussions

To summarize, we have extended the CNHV theories to include the case that the measuring settings, together with the measurement outcomes, are not externally fixed, but determined by HVs. The outcomes of those measurements with the same settings give averages satisfying Malus’ Law and make up correlation functions. We show that such is the case of meson decays, which could be determined by HVs at the source of the meson pairs. This extension does not change the validity of LI. Therefore, entangled meson pairs can be used to test LI.

We find that for a $B_d$ meson, the effective measuring directions appearing in Malus’ Law are on a cone and a plane, corresponding to semileptonic decays and decays to CP eigenstates, respectively. For such effective measuring directions, we present a new LI. This can be tested in $C=-1$ entangled state of $B^0-{\bar{B}}^0$ pairs, within the present experimental capability. The expected violation is estimated quantitatively, using the indirect CP violation and other parameters. Our LI is violated if there is indirect CP violation. There may be profound reason for this surprising connection. Besides, our new LI can also be tested in other systems such as photon polarizations, where the measuring directions are simply directions externally fixed.

Appendices

Two inequalities

We derive a new LI, for $\mathbf{a}^l(\phi _l)$ on a plane and $\mathbf{a}^s(\theta _s,\phi _s)$ on a cone.

For each particle, each measurement yields an outcome $A=A(\mathbf{u},\mathbf{v},\tilde{\mathbf{a}}(\lambda ),\tilde{\mathbf{b}}(\lambda ),\lambda )=\pm 1$ or $B= B(\mathbf{v},\mathbf{u},\tilde{\mathbf{b}}(\lambda ),\tilde{\mathbf{a}}(\lambda ),\lambda )=\pm 1$. Using $-1+\int d\lambda \rho ' _{\mathbf{u},\mathbf{v},\mathbf{a},\mathbf{b}}(\lambda ) \left| A+B\right| =\int d\lambda \rho '_{\mathbf{u},\mathbf{v},\mathbf{a},\mathbf{b}}(\lambda )AB=1-\int d\lambda \rho ' _{\mathbf{u},\mathbf{v},\mathbf{a},\mathbf{b}}(\lambda )\left| A-B\right|$, where $\rho '_{{\mathbf {u}},{\mathbf {v}},{\mathbf {a}},{\mathbf {b}}}(\lambda ) \equiv \rho _{{\mathbf {u}},{\mathbf {v}},{\mathbf {v}}} (\lambda ) \delta (\tilde{\mathbf{a}}(\lambda )-{\mathbf {a}})\delta (\tilde{\mathbf{b}}(\lambda )-{\mathbf {b}})$, and ${\bar{A}}=\int d \lambda \rho '_{{\mathbf {u}},{\mathbf {v}},{\mathbf {a}},{\mathbf {b}} }(\lambda ) A({\mathbf {u}},{\mathbf {v}},\tilde{\mathbf{a}}(\lambda ),\tilde{\mathbf{b}}(\lambda ),\lambda ) ={\mathbf {u}}\cdot {\mathbf {a}}$, ${\bar{B}}=\rho '_{{\mathbf {u}},{\mathbf {v}},{\mathbf {a}},{\mathbf {b}} }(\lambda ) B({\mathbf {v}},{\mathbf {u}},\tilde{\mathbf{b}}(\lambda ),\tilde{\mathbf{a}}(\lambda ),\lambda ) ={\mathbf {v}}\cdot {\mathbf {b}}$, one finds $1-\int d\mathbf{u}d\mathbf{v}F(\mathbf{u},\mathbf{v})|\mathbf{u}\cdot \mathbf{a}-\mathbf{v}\cdot \mathbf{b}| \ge E(\mathbf{a},\mathbf{b}) \ge -1+\int d\mathbf{u}d\mathbf{v}F(\mathbf{u},\mathbf{v})|\mathbf{u}\cdot \mathbf{a}+\mathbf{v}\cdot \mathbf{b}|$ [15, 16].

Furthermore [23], considering $|\mathbf{u}\cdot \mathbf{a}+\mathbf{v}\cdot \mathbf{b}| +|\mathbf{u}\cdot \mathbf{b}+\mathbf{v}\cdot \mathbf{b}| \ge \left| \mathbf{u}\cdot \mathbf{a}+\mathbf{v}\cdot \mathbf{b}-\left( \mathbf{u}\cdot \mathbf{b}+\mathbf{v}\cdot \mathbf{b}\right) \right| =\left| \mathbf{u}\cdot \left( \mathbf{a}- \mathbf{b}\right) \right|$, and $|\mathbf{u}\cdot \mathbf{a}-\mathbf{v}\cdot \mathbf{b}|+ |\mathbf{u}\cdot \mathbf{b}+\mathbf{v}\cdot \mathbf{b}| \ge \left| \mathbf{u}\cdot \left( \mathbf{a} + \mathbf{b}\right) \right|$, one obtains

$$\begin{aligned} {\hat{E}}^+(\mathbf{a},\mathbf{b})\ge & {} -2+\int d\mathbf{u}F(\mathbf{u})|\mathbf{u}\cdot \left( \mathbf{a}-\mathbf{b}\right) |, \end{aligned}$$

(59a)

$$\begin{aligned} {\hat{E}}^-(\mathbf{a},\mathbf{b})\le & {} 2-\int d\mathbf{u}F(\mathbf{u})|\mathbf{u}\cdot \left( \mathbf{a}+ \mathbf{b}\right) |. \end{aligned}$$

(59b)

with ${\hat{E}}^+(\mathbf{a},\mathbf{b})\equiv E(\mathbf{a},\mathbf{b} )+ E(\mathbf{b},\mathbf{b})$ and ${\hat{E}}^-(\mathbf{a},\mathbf{b})\equiv E(\mathbf{a},\mathbf{b} )+ E(\mathbf{b},-\mathbf{b})$.

All the results remain valid in the special case that $\tilde{\mathbf{a}}(\lambda )$ and $\tilde{\mathbf{b}}(\lambda )$ are externally set to be always $\mathbf{a}$ and ${\mathbf {b}}$ respectively.

Upper bound

Suppose $\mathbf{a} = \mathbf{a}^s(\theta _s,\phi _a)$, $\mathbf{b}=\mathbf{a}^l(\phi _b)$. Then Eqs. (59b) reads

$$\begin{aligned} {\hat{E}}^{-}(\mathbf{a}^s(\theta _s,\phi _a),\mathbf{a}^l(\phi _b))&\le 2-\int _0^{\pi }\sin \theta _ud\theta _u \nonumber \\&\times \int _0^{2\pi } d\phi _uF(\theta _u,\phi _u)\nonumber \\&\quad \left| \mathbf{u}(\theta _u,\phi _u)\cdot (\mathbf{a}^s(\phi _a)+ \mathbf{a}^l(\phi _b))\right| . \end{aligned}$$

(60)

Fig. 6

Geometric relations among $\mathbf{a}^s$, $\mathbf{a}^l$, $\mathbf{a}^s+\mathbf{a}^l$ and $\mathbf{a}^s-\mathbf{a}^l$

As shown in Fig. 6,

$$\begin{aligned} \mathbf{a}^s(\theta _s,\phi _a)+\mathbf{a}^l(\phi _b)&= L_1(\theta _s,\varphi ) \left( \sin (\theta _{1})\cos (\xi +\alpha _1), \right. \nonumber \\&\quad \left. \sin (\theta _{1})\sin (\xi _1),\cos (\theta _{1})\right) , \end{aligned}$$

(61)

where

$$\begin{aligned} L_1(\theta _s,\varphi )&\equiv \big |\mathbf{a}^s+\mathbf{a}^l\big |=\sqrt{2+2\cos (\varphi )\sin (\theta _s)},\\ \theta _{1}(\theta _s,\varphi )&=\cos ^{-1}\frac{\cos (\theta _s)}{\sqrt{2+2\cos (\varphi )\sin (\theta _s)}}, \end{aligned}$$

$\varphi = \phi _a-\phi _b,$ $\xi =\frac{\phi _a+\phi _b}{2}$, $\alpha _1$ is an angle depending on $\varphi$ and $\theta _s$ while independent of $\xi$, as shown in Fig. 6. With $0<\theta _s<\pi /2$, we have $\sin (\theta _{1})> 0$, $\cos (\theta _{1})> 0$.

Rewriting ${\hat{E}}^{-}(\mathbf{a}^s(\theta _s,\phi _a),\mathbf{a}^l(\phi _b))$ as ${\hat{E}}^{-}_{sl}(\theta _s,\xi ,\varphi )$, then

$$\begin{aligned} {\hat{E}}^{-}_{sl} \left( \theta _s,\varphi \right)&\equiv \int \frac{d\xi }{2\pi } {\hat{E}}^{-}_{sl} \left( \theta _s,\xi ,\varphi \right) \nonumber \\&\quad \le 2 -L_1\left( \theta _s,\varphi \right) \int _0^{2\pi }\frac{d\xi }{2\pi }\int _0^{\pi }\sin \theta _ud\theta _u \int _0^{2\pi } d\phi _uF\left( \theta _u,\phi _u\right) \nonumber \\&\qquad \times \left| \sin \left( \theta _u\right) \sin \left( \theta _{1}\right) \cos \left( \phi _u-\xi -\alpha _1\right) +\cos \left( \theta _u\right) \cos \left( \theta _{1}\right) \right| \nonumber \\&\quad \le 2 -L_1\left( \theta _s,\varphi \right) \int _0^{\pi }\sin \theta _ud\theta _u F(\theta _u)\cos \left( \theta _{1}\right) \left| \cos (\theta _u)\right| , \end{aligned}$$

(62)

where $F(\theta _u)\equiv \int _0^{2\pi } d\phi _u F(\theta _u,\phi _u)$. In obtaining the second inequality, we have used

$$\begin{aligned}&\int _0^{2\pi }\frac{d\xi }{2\pi }\left| \sin \left( \theta _{1}\right) \cos \left( \phi _u-\xi -\alpha _1 \right) \sin \left( \theta _u\right) \right. \nonumber \\ {}&\qquad \left. +\cos \left( \theta _{1}\right) \cos \left( \theta _u\right) \right| \nonumber \\&\quad =\int _0^{2\pi }\frac{d\xi }{2\pi }\left| \sin \left( \theta _{1}\right) \cos \left( \xi \right) \sin \left( \theta _u\right) +\cos \left( \theta _{1}\right) \cos \left( \theta _u\right) \right| \nonumber \\&\quad \ge \cos \left( \theta _{1}\right) \left| \cos \left( \theta _u\right) \right| , \end{aligned}$$

(63)

as

$$\begin{aligned} \int _0^{2\pi }d\xi \left| \cos \left( \xi + \beta \right) +a\right|&=\int _0^{2\pi }d\xi \left| \cos \left( \xi \right) +a\right| \\&=4\text {Re}\left( \sqrt{1-a^2}+a\sin ^{-1}(a)\right) \\&\quad \ge 2\pi \left| a\right| , \end{aligned}$$

where a and $\beta$ are arbitrary real numbers.

The case that the two vectors are on a same plane is a special case of above with $\theta _s=\pi / 2$. In this special case, $L_1=2\cos \left( \varphi /2\right)$, $\theta _{1}=\pi / 2$. Hence

$$\begin{aligned} {\hat{E}}^{-}_{ll}\left( \theta _s,\varphi \right)&\equiv \int \frac{d\xi }{2\pi }E\left( \mathbf{a}^l\left( \xi + \frac{\varphi }{2}\right) ,\mathbf{a}^l\left( \xi -\frac{\varphi }{2}\right) \right) \nonumber \\&\le 2-2\cos \left( \frac{\varphi }{2}\right) \int _0^{2\pi }\frac{d\xi }{2\pi }\int _0^{\pi }\sin \theta _ud\theta _u F\left( \theta _u\right) \nonumber \\&\qquad \left| \cos (\xi )\sin \left( \theta _u\right) \right| \nonumber \\&=\, 2 {-}\frac{4}{\pi }\cos \left( \frac{\varphi '}{2}\right) \int _0^{\pi }\sin \theta _ud\theta _u F\left( \theta _u\right) \left| \sin \left( \theta _u\right) \right| {,} \end{aligned}$$

(64)

where $\int _0^{2\pi }d\xi |\cos (\xi )|=4$ is used.

Therefore one obtains

$$\begin{aligned}&{\hat{E}}^{-}_{sl}\left( \theta _s,\varphi _1\right) +\frac{\pi \cos \left( \theta _{1}\left( \theta _s, \varphi _1\right) \right) L_1\left( \theta _s,\varphi _1\right) }{4\cos \left( \frac{\varphi _2}{2}\right) }{{\hat{E}}^{ll-}}\left( \theta _s,\varphi _2\right) \nonumber \\&\quad \le 2\left( 1+\frac{\pi \cos \left( \theta _{1}\left( \theta _s, \varphi _1\right) \right) L_1\left( \theta _s,\varphi _1\right) }{4\cos \left( \frac{\varphi _2}{2}\right) }\right) \nonumber \\&\qquad -\cos \left( \theta _{1}\left( \theta _s, \varphi _1\right) \right) L_1\left( \theta _s,\varphi _1\right) \nonumber \\&\qquad \times \int _0^{\pi }\sin \theta _ud\theta _u F\left( \theta _u\right) \left( \big |\cos \left( \theta _u\right) \big |+\big |\sin \left( \theta _u\right) \big |\right) . \end{aligned}$$

(65)

Using $\int _0^{\pi }d\theta _u \sin (\theta _u) F(\theta _u)=1$ and $|\cos (\theta _u)|+|\sin (\theta _u)| \ge 1$, one obtains

$$\begin{aligned}&{\hat{E}}^{-}_{sl} (\theta _s,\varphi _1)+\frac{\pi \cos (\theta _{1}(\theta _s, \varphi _1)) L_1(\theta _s,\varphi _1) }{4\cos (\frac{\varphi _2}{2})} {\hat{E}}^{-}_{ll}(\theta _s,\varphi _2) \nonumber \\&\le 2 \left( 1+\frac{\pi \cos (\theta _{1}(\theta _s, \varphi _1)) L_1(\theta _s,\varphi _1) }{4\cos (\frac{\varphi _2}{2})}\right) \nonumber \\&\quad -\cos (\theta _{1}(\theta _s, \varphi _1)) L_1(\theta _s,\varphi _1). \end{aligned}$$

(66)

Lower bounds

From Eq. (59a), one obtains

$$\begin{aligned}&{\hat{E}}^{+} \left( \mathbf{a}^s\left( \theta _s,\phi _a\right) ,\mathbf{a}^l\left( \phi _b\right) \right) \ge -2+\int _0^{\pi }\sin \theta _ud\theta _u \int _0^{2\pi } d\phi _u\nonumber \\&\qquad \times F\left( \theta _u,\phi _u\right) \left| \mathbf{u}\left( \theta _u,\phi _u\right) \cdot \left( \mathbf{a}^s\left( \theta _s,\phi _a\right) -\mathbf{a}^l\left( \phi _b\right) \right) \right| . \end{aligned}$$

(67)

As shown in Fig. 6,

$$\begin{aligned} \mathbf{a}^s\left( \theta _s,\phi _a\right) -\mathbf{a}^l\left( \phi _b\right)&= L_2\left( \theta _s,\varphi \right) \left( \sin \left( \theta _{2}\right) \cos \left( \xi +\alpha _2\right) ,\right. \nonumber \\&\left. \quad \sin \left( \theta _{2}\right) \sin \left( \xi _2\right) ,\cos \left( \theta _{2}\right) \right) , \end{aligned}$$

(68)

where

$$\begin{aligned} L_2(\theta _s,\varphi )&\equiv \big |\mathbf{a}^s-\mathbf{a}^l\big |=\sqrt{2-2\cos (\varphi )\sin (\theta _s)}\\ \theta _{2}&=\cos ^{-1}\frac{\cos (\theta _s)}{\sqrt{2-2\cos (\varphi )\sin (\theta _s)}}, \end{aligned}$$

$\alpha _2$ is an angle depending on $\theta _s$ and $\varphi$ while independent of $\xi$.

Rewriting ${\hat{E}}^{+}(\mathbf{a}^s(\theta _s,\phi _a),\mathbf{a}^l(\phi _b))$ as ${\hat{E}}^{+}_{sl}(\theta _s,\xi ,\varphi )$,

$$\begin{aligned} {\hat{E}}^{+}_{sl} \left( \theta _s,\varphi \right)&\equiv \int \frac{d\xi }{2\pi } {\hat{E}}^{+}_{sl} \left( \theta _s,\xi ,\varphi \right) \nonumber \\&\ge -2+L_2\left( \theta _s,\varphi \right) \int _0^{2\pi }\frac{d\xi }{2\pi }\int _0^{\pi }\sin \theta _ud\theta _u\nonumber \\&\quad \times \int _0^{2\pi } d\phi _uF\left( \theta _u,\phi _u\right) \nonumber \\&\quad \times \left| \sin \left( \theta _u\right) \sin \left( \theta _{2}\right) \cos \left( \phi _u-\xi -\alpha _2\right) \right. \nonumber \\ {}&\left. +\cos \left( \theta _u\right) \cos \left( \theta _{2}\right) \right| . \end{aligned}$$

(69)

Considering the special case of $\theta _s=\pi / 2$, one obtains

$$\begin{aligned} {\hat{E}}^+_{ll}\left( \varphi \right)&\ge -2+2\left| \sin \left( \frac{\varphi }{2}\right) \right| \int _0^{2\pi }\frac{d\xi }{2\pi }\int _0^{\pi }\sin \theta _ud\theta _u \nonumber \\&\qquad \times F\left( \theta _u\right) \left| \cos (\xi )\sin \left( \theta _u\right) \right| . \end{aligned}$$

(70)

Therefore

$$\begin{aligned}&{\hat{E}}^+_{sl}\left( \theta _s,\varphi _1\right) +\frac{\pi \cos \left( \theta _{2}\left( \theta _s,\varphi _1\right) \right) L_2\left( \theta _s,\varphi _1\right) }{4\left| \sin \left( \frac{\varphi _2}{2}\right) \right| }{\hat{E}}^+_{ll}\left( \theta _s,\varphi _2\right) \nonumber \\&\ge -2\left( 1+\frac{\pi \cos \left( \theta _{2}\left( \theta _s,\varphi _1\right) \right) L_2\left( \theta _s,\varphi _1\right) }{4\left| \sin \left( \frac{\varphi _2}{2}\right) \right| }\right) \nonumber \\&\quad + \cos \left( \theta _{2}\left( \theta _s,\varphi _1\right) \right) L_2\left( \theta _s,\varphi _1\right) . \end{aligned}$$

(71)

We find the second lower bound, in terms of correlation function ${\hat{E}}^{ss+}(\theta _s,\phi _a,\phi _b)$ between $\mathbf{a}^s(\theta _s,\phi _a)$ and $\mathbf{a}^s(\theta _s,\phi _b)$, which are on a same plane, with $|\mathbf{a}^s(\theta _s,\phi _a)-\mathbf{a}^s(\theta _s,\phi _b)|=2\sin (\theta _s)\sin (\varphi / 2)$, as shown in Fig. 7. We find

$$\begin{aligned} {\hat{E}}^+_{ss} \left( \theta _s,\varphi \right)&\ge -2+2\sin \left( \theta _s\right) \left| \sin \left( \frac{\varphi }{2}\right) \right| \nonumber \\&\quad \times \int _0^{2\pi }\frac{d\xi }{2\pi }\int _0^{\pi }\sin \theta _ud\theta _u F\left( \theta _u\right) \left| \cos (\xi )\sin (\theta _u)\right| . \end{aligned}$$

(72)

Fig. 7

Geometric relations of $\mathbf{a}^s(\phi _a)$, $\mathbf{a}^s(\phi _b)$ and $\mathbf{a}^s(\phi _a)-\mathbf{a}^s(\phi _b)$

Therefore,

$$\begin{aligned}&{\hat{E}}^+_{sl}\left( \theta _s,\varphi _1\right) +\frac{\pi \cos \left( \theta _2\left( \theta _s,\varphi _1\right) \right) L_2\left( \theta _s,\varphi _1\right) }{4\sin \left( \theta _s\right) \left| \sin \left( \frac{\varphi _2}{2}\right) \right| }{\hat{E}}^+_{ss}(\varphi _2) \nonumber \\&\ge -2\left( 1+\frac{\pi \cos \left( \theta _2\left( \theta _s,\varphi _1\right) \right) L_2\left( \theta _s,\varphi _1\right) }{4\sin \left( \theta _s\right) \left| \sin \left( \frac{\varphi _2}{2}\right) \right| }\right) \nonumber \\&\qquad +\cos \left( \theta _2\right) L_2\left( \theta _s,\varphi _1\right) . \end{aligned}$$

(73)

Equations (66), (71) and (73) comprise our LI.

LI in terms of discrete versions of average correlation functions

In the discrete version, Eq. (64) is changed to

$$\begin{aligned} {\hat{E}}^{-}_{sl } \left( \theta _s,\varphi \right)&\equiv \frac{1}{N}\sum _{n=1}^N{{\hat{E}}^{-}_{sl}} \left( \theta _s,\frac{2n\pi }{N},\varphi \right) \nonumber \\&{\le }2{-}L_1\left( \theta _s{,}\varphi \right) \int _0^{\pi }\sin \theta _ud\theta _u \int _0^{2\pi } d\phi _uF\left( \theta _u{,}\phi _u\right) \nonumber \\&\qquad \times \frac{1}{N}\sum _{n=1}^N\left| \sin \left( \theta _u\right) \sin \left( \theta _{1} \left( \theta _s,\varphi \right) \right) \cos \left( \phi _u \right. \right. \nonumber \\&\qquad \left. \left. -\alpha _1-\frac{2n\pi }{N}\right) \right. \nonumber \\&\qquad \left. +\cos \left( \theta _u\right) \cos \left( \theta _{1} \left( \theta _s,\varphi \right) \right) \right| . \end{aligned}$$

(74)

Noting

$$\begin{aligned}&\frac{1}{N}\sum _{n=1}^N \left| \cos (\frac{2n\pi }{N} + \beta )+a\right| \ge |a| \end{aligned}$$

(75)

for arbitrary real numbers $\beta$ and a, we can change Eq. (63) to

$$\begin{aligned}&\frac{1}{N}\sum _{n=1}^N\left| \sin (\theta _{1} (\theta _s,\varphi )) \cos \left( \phi _u-\frac{2n\pi }{N}-\alpha _1 \right) \sin (\theta _u)\right. \nonumber \\&\quad \left. +\cos (\theta _{1})\cos (\theta _u)\right| \ge \cos (\theta _{1} (\theta _s,\varphi ))\left| \cos (\theta _u)\right| . \end{aligned}$$

(76)

which is then used in Eq. (74). One finds

$$\begin{aligned} {\hat{E}}^{-}_{sl } (\theta _s,\varphi )\le 2- L_1(\theta _s,\varphi )\int _0^{\pi }\sin \theta _ud\theta _u F(\theta _u) \cos (\theta _{1})\left| \cos (\theta _u) \right| . \end{aligned}$$

(77)

Similarly, one has

$$\begin{aligned} {\hat{E}}^+_{sl } \left( \theta _s,\varphi \right) \ge -2+ L_2\left( \theta _s,\varphi \right) \int _0^{\pi }\sin \theta _ud\theta _u F\left( \theta _u\right) \nonumber \\ \cos \left( \theta _{n_2}\right) \left| \cos (\theta _u) \right| . \end{aligned}$$

(78)

On the other hand, Eq. (64) can be changed to

$$\begin{aligned} {\hat{E}}^{-}_{ll }(\varphi ')&\equiv \frac{1}{N}\sum _{n=1}^NE \left( \mathbf{a}^l \left( \frac{2n\pi }{N} + \frac{\varphi '}{2}\right) ,\mathbf{a}^l \left( \frac{2n\pi }{N} -\frac{\varphi '}{2}\right) \right) \nonumber \\&\le 2-2\cos \left( \frac{\varphi '}{2}\right) \frac{1}{N}\sum _{n=1}^N\int _0^{\pi }\sin \theta _ud\theta _u\nonumber \\&\quad \times F\left( \theta _u\right) \left| \cos \left( \frac{2n\pi }{N}\right) \sin (\theta _u)\right| . \end{aligned}$$

(79)

Using $\frac{1}{N}\sum _{n=1}^N \left| \cos (\frac{2n\pi }{N} + \beta )\right| \ge \frac{1}{N}\cot \left( \frac{\pi }{2N}\right) \equiv u_N$ [18], one obtains

$$\begin{aligned}&{\hat{E}}^{-}_{ll }(\varphi )\le 2-2u_N\cos \left( \frac{\varphi }{2}\right) \int _0^{\pi }\sin \theta _ud\theta _u F(\theta _u) \left| \sin (\theta _u)\right| . \end{aligned}$$

(80)

Similarly, we have

$$\begin{aligned} {\hat{E}}^{+}_{ll }(\varphi )&\le -2+2u_N\cos (\frac{\varphi }{2})\int _0^{\pi }\sin \theta _ud\theta _u F(\theta _u) \left| \sin (\theta _u)\right| . \nonumber \\ {\hat{E}}^+_{ss }(\varphi )&\ge -2+2u_N\sin (\theta _s)\left| \sin (\frac{\varphi }{2})\right| \nonumber \\&\qquad \quad \times \int _0^{\pi }\sin \theta _ud\theta _u F(\theta _u) \left| \sin (\theta _u)\right| . \end{aligned}$$

(81)

With Eqs. (77), (78), (80) and (81), we establish LI in terms of the discrete version of average correlation functions,

$$\begin{aligned}&{\hat{E}}^{-}_{sl }(\varphi _1)+\frac{\cos (\theta _{1}) L_1(\theta _s,\varphi _1)}{2u_N\cos (\frac{\varphi _2}{2})}{\hat{E}}^{-}_{ll }(\varphi _2) \nonumber \\&\quad \le 2\left( 1+\frac{\cos (\theta _{1}) L_1(\theta _s,\varphi _1)}{2u_N\cos (\frac{\varphi _2}{2})}\right) -\cos (\theta _{1})L_1(\theta _s,\varphi _1), \nonumber \\&{\hat{E}}^+_{sl}(\varphi _1)+\frac{\cos (\theta _{2}) L_2(\theta _s,\varphi _1)}{2u_N\left| \sin (\frac{\varphi _2}{2})\right| }{\hat{E}}^+_{ll N}(\varphi _2) \nonumber \\&\quad \ge -2\left( 1+\frac{ \cos (\theta _{2}) L_2(\theta _s,\varphi _1)}{2u_N\left| \sin (\frac{\varphi _2}{2})\right| }\right) +\cos (\theta _2)L_2(\theta _s,\varphi _1). \nonumber \\&{\hat{E}}^+_{sl }(\varphi _1)+\frac{\cos (\theta _{2}) L_2(\theta _s,\varphi _1)}{2u_N\sin (\theta _s)\left| \sin (\frac{\varphi _2}{2})\right| }{\hat{E}}^+_{ss N}(\varphi _2) \nonumber \\&\quad \ge -2\left( 1+\frac{\cos (\theta _{2}) L_2(\theta _s,\varphi _1)}{2u_N\sin (\theta _s)\left| \sin (\frac{\varphi _2}{2})\right| }\right) +\cos (\theta _2)L_2(\theta _s,\varphi _1). \end{aligned}$$

(82)