1 Introduction

Ever since Hawking deduced the thermodynamics of black holes [1], thermodynamic approach to gravitating systems [2,3,4,5,6] provides good insights because it considers a relatively few thermodynamic variables rather than dealing complicated dynamic gravitational field equations. Getting thermodynamic quantities has thus been widely studied to understand gravitating systems. Examining self-gravitating systems has been one of those efforts for decades, which helps us to understand astrophysical systems. Especially, the entropy of a spherically symmetric self-gravitating radiation and its stability were calculated in a series of researches [7, 8].

Those studies have shown that requiring maximum entropy of self-gravitating radiation in a spherical box reproduces the Tolman–Oppenheimer–Volkoff (TOV) equation for hydrostatic equilibrium [9, 10]. This equivalence has been dubbed as ‘Maximum Entropy Principle’(MEP). The total entropy is regarded as an action functional of mass, m(r), the energy density \(\rho (r)\) and the radius r. Varying the total entropy, one gets the hydrostatic equation. Hence, having exact entropy of a system enables one to get a hydrostatic equation through MEP. Recently, there have been discussions on the MEP in more general perspectives [11,12,13]. In most of those studies, the gravitating matters were assumed to be perfect fluids of which pressure \(p(r) = w\rho (r)\) is locally isotropic. The entropy density for perfect fluids can be deduced from the continuity equation with series of thermodynamic equation combined [14]. It was given by a function of the energy density and w, that is, \(s_P\equiv s_P(\rho ,w)\).

When the energy distribution is smooth in a sufficiently small region of volume V, one can define energy density \(\rho \) from \(U(T,V)=\rho (T)V\) for the total energy U inside the volume. Using the first law of thermodynamics, \(TdS=dU+pdV\), we have

$$\begin{aligned} dS=\frac{V}{T}\frac{d\rho }{dT}dT+\frac{\rho +p}{T}dV, \end{aligned}$$
(1)

where T and S denote the temperature and the entropy of the system respectively. Since the entropy is a scalar quantity, the exactness condition of S determines \(\rho \) as a function of T:

$$\begin{aligned} \frac{\partial }{\partial T}\frac{\partial S}{\partial V}=\frac{\partial }{\partial V}\frac{\partial S}{\partial T} ~~\longrightarrow ~~\rho =\sigma (w) ~T^{\frac{1+w}{w}}, \end{aligned}$$
(2)

for a perfect fluid with \(p=w\rho \), where w is a constant. The entropy density of the fluid can be deduced by considering an isochoric process, for which \(dU = TdS\),Footnote 1

$$\begin{aligned} S&=(1+w)\sigma (w)~T^{\frac{1}{w}}V+\text{ constant } \, \nonumber \\&\rightarrow \, s_P\equiv \frac{S}{V}=\alpha _w \rho ^{\frac{1}{1+w}},~~~\alpha _w =(1+w)\sigma (w)^{\frac{w}{1+w}}, \end{aligned}$$
(3)

where the integral constant can be set to zero by using the third law of thermodynamics. The constant \(\alpha _w\) depends on the physical nature of matter consisting the fluid such as w. This entropy density was already given in Refs. [15, 16]. For radiation with \(w=1/3\), the density \(\rho _\mathrm{rad}=\sigma _\mathrm{rad} T^4\) and the constant \(\sigma _\mathrm{rad}\) is the Stefan–Boltzmann constant.Footnote 2

Although majority of researches have focused on the dynamics of perfect fluid [17,18,19], anisotropic matter in cosmological configuration has recently drawn interests [20,21,22,23,24,25,26,27,28]. For example, the authors in [29] obtained stable black holes with anisotropic matter. It is well known that, in general relativity, the throat of a traversable wormhole needs to be made of anisotropic matter [30, 31]. Thus studies on the dynamics of anisotropic matter including thermodynamics become more important than ever.

For an anisotropic matter satisfying the linear equation of state,

$$\begin{aligned} p_k=w_k\rho , \quad k=1,2,3, \end{aligned}$$
(4)

the entropy density \(s_A\) will depend on \(\rho ,\) and \(w_k\) where the subscript A denotes the ‘anisotropic’ nature. That is, \(s_A\equiv s_A(\rho ,w_1,w_2,w_3)\). When all w’s are equal, \(s_A\) goes to that of the perfect fluid. Since an entropy density is a scalar quantity, \(s_A\) can be written as a product of \(s_P\) in Eq. (3) and a scalar function \(\phi \) that describes the effect of anisotropy:

$$\begin{aligned}&s_A(\rho ,w_1,w_2,w_3) \nonumber \\&=\phi (w_1-w,w_2-w,w_3-w, \rho )\cdot s_P(\rho ,w) \end{aligned}$$
(5)

where \(\phi (w_k)\rightarrow 1\) in the isotropic limit. The function \(\phi \) may also contain matter information which is not described by the equation of state.

In the above discussion, the pressure \(\vec p\equiv (p_1,p_2,p_3)\) is divided into two parts. One is the isotropic part of pressure \(\vec p_\mathrm{iso} \equiv p_\mathrm{iso} (1,1,1)\) and the other is the deviation from it, \(\vec {p}_\mathrm{d} \equiv \vec p-\vec p_\mathrm{iso}\). However, there is an arbitrariness in the choice of the isotropic part. The first intuitive choice is \( p_\mathrm{iso}\equiv \bar{p},~\bar{p}=( p_1+p_2+ p_3)/3\). The other choice could be that \(p_\mathrm{iso}\equiv p_1\), and so on. The resulting entropy should be independent of this choice. This freedom will be gauged by a compensation vector later in this work.

We obtain the explicit form of the entropy density of self-gravitating anisotropic matter confined to a spherically symmetric box of radius R from thermodynamic consideration up to a constant multiplication factor, which depends on the individual characteristics of matter. With this entropy density, we perform the variation of total entropy of the anisotropic matter and show that the variational equation reproduces a modified TOV equation. The result of this article shows that MEP still holds. We also seek applications of this entropy to cosmological phenomena.

The order of the article is the following: We review properties of anisotropic matter in Sect. 2. In Sect. 3, the entropy of an anisotropic matter is obtained by comparing the continuity equation with thermodynamic relations. The MEP for a perfect fluid is briefly reviewed in Sect. 4. The MEP yields the exact dynamical equation (modified TOV) using the entropy density of the anisotropic matter obtained in Sect. 3. We obtain explicitly the total entropy of a ball of anisotropic matter and apply this calculation to discuss properties of objects such as wormhole and a compact star in Sect. 5. Finally, we summarize our work and discuss about future issues in Sect. 6.

2 Anisotropic matter

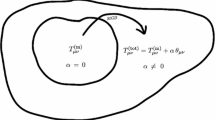
The stress-energy tensor \(T^{ab}\) of a relativistic matter can be divided into a thermostatic part \(T_0^{ab}\) and a dissipative part \(T_1^{ab}\) as

$$\begin{aligned} T^{ab}=T_0^{ab}+T_1^{ab}. \end{aligned}$$
(6)

The dissipative part is written as

$$\begin{aligned} T_1^{ab}=u^aq^b+u^bq^a+\pi ^{ab}, \quad u_aq^a=0, \end{aligned}$$
(7)

where \(u^a\) is a timelike unit normal vector field. The quantities q and \(\pi ^{ab}\) are interpreted as a heat flux vector and a viscous shear tensor, respectively. The viscous shear tensor satisfies \(\pi ^{ab}u_b=0\) or \(u_a\pi ^{ab}u_b=0\) for the Landau frame or the Eckart frame, respectively [14].

The thermostatic part of an isotropic perfect fluid has the form

$$\begin{aligned}&T_0^{ab}=\rho u^au^b+p h^{ab},\nonumber \\&h^{ab}=x^ax^b+y^ay^b+z^az^b=g^{ab}+u^au^b, \end{aligned}$$
(8)

where \(\rho \) and p are the rest frame energy density and the isotropic pressure, respectively. The set of four mutually orthogonal vector fields \(\{u^a,x^a,y^a,z^a\}\) conforms a frame of orthonormal vector fields. That is,

$$\begin{aligned}&g^{ab}=-u^au^b+x^ax^b+y^ay^b+z^az^b,\nonumber \\&u_au^a=-1,~~x_ax^a=y_ay^a=z_az^a=1. \end{aligned}$$
(9)

When matter is not perfect, more general tensor for anisotropic pressure replaces \(T_0\), for example, elastic solid has anisotropic stress tensor [32]. In the absence of sheer, off-diagonal components of \(\pi ^{ab}\) vanishes. The energy–momentum tensor of the anisotropic matter being considered in this article has the form:Footnote 3

$$\begin{aligned} T_A^{ab}\equiv (T_A)_0^{ab}=\rho u^au^b+p_1x^ax^b+p_2y^ay^b+p_3z^az^b,\nonumber \\ \end{aligned}$$
(11)

where \(\rho \) and \(p_k(k=1,2,3)\) denote the energy density and the pressure measured in locally orthogonal rest frame, respectively.

A static, spherically symmetric metric can be written as

$$\begin{aligned} ds^2=-e^{u(r)}dt^2+e^{v(r)}dr^2+r^2(d\theta ^2+\sin ^2{\theta }d\varphi ^2).\nonumber \\ \end{aligned}$$
(12)

Because of the spherical symmetry, we have \(p_\theta =p_\phi \). We denote \(p_1\equiv p_r\) and \(p_2\equiv p_\theta =p_\varphi \) from now on. The Einstein equations \(G^t_{~t}=8\pi T^t_{~t}\) and \(G^r_{~r}=8\pi T^r_{~r}\) read

$$\begin{aligned}&e^{-v}=1-\frac{2m(r)}{r}, \quad m(r)\equiv \int ^r dr'4\pi r^2\rho (r'),\nonumber \\&u'=\frac{2(m+4\pi r^3p_1)}{r^2\left( 1-\frac{2m}{r}\right) }. \end{aligned}$$
(13)

With these equations and \(G^\theta _{~\theta }=8\pi T^\theta _{~\theta }\) gives the modified TOV equation:

$$\begin{aligned} \frac{dp_1}{dr}=-\frac{\rho +p_1}{r(r-2m)} (m+4\pi r^3p_1)+\frac{2}{r}(p_2-p_1), \end{aligned}$$
(14)

which resembles the TOV equation of the isotropic fluid [9, 10] up to the last term:

$$\begin{aligned} \frac{dp}{dr}=-\frac{\rho +p}{r(r-2m)}\left( m+4\pi r^3p\right) . \end{aligned}$$
(15)

3 Entropy density of anisotropic matter

The temporal part of the continuity equation, \(\nabla _aT_A^{ab}=0\), can be interpreted as a thermal relation

$$\begin{aligned} -u_b\nabla _aT_A^{ab}=T\nabla _a(s_A u^a)+\mu _N\nabla _a(n u^a), \end{aligned}$$
(16)

here \(T, s_A, n\) and \(\mu _N\) denote the temperature, the entropy density, the number density and the chemical potential of the particles composing the anisotropic matter, respectively.

In the presence of the dissipative part, \(T_1^{ab}\ne 0\), the entropy vector \(s_A^a\) can be defined [14, 33]:

$$\begin{aligned} s_A^a=s_A u^a-\beta u_b(T_{1}^{ab}), \end{aligned}$$
(17)

where \(\beta \) is the inverse temperature (\(\beta \equiv T^{-1}\)). The net entropy production can be written as in Ref. [34],

$$\begin{aligned} \nabla _a s_A^a=-\nabla _{(a}\beta u_{b)}\cdot T_1^{ab}. \end{aligned}$$
(18)

There are two ways for the entropy to be conserved. First, there exists a timelike Killing vector field \(\xi ^a\equiv \beta u^a\). Second, the dissipation is absent, \(T_1=0\) or \(T^{ab}=T_A^{ab}\). In this work, both of the two requirements hold.

When the number of particles does not change, \(\nabla _a(nu^a)=0\), the continuity equation reads:

$$\begin{aligned} -u_b\nabla _a T_A^{ab}=T\nabla _a(s_Au^a)=0. \end{aligned}$$
(19)

Let us write the entropy density of anisotropic matter as \(s_A=\phi \cdot s_P\) as in Eq. (5). Here, \(s_P\propto \rho ^{\frac{1}{1+w}}u^a\) is the entropy density for a perfect fluid with an isotropic pressure \(p_\mathrm{iso}=w\rho \), and the function \(\phi \equiv \phi (w_1-w,w_2-w,w_3-w)\) describes how much the entropy deviates from that of the isotropic form. Hence, \(\phi = 1\) when \(w_1=w_2=w_3\), i.e., when isotropic.

The Eq. (19) becomes

$$\begin{aligned} \nabla _a s_A^a=0~\rightarrow ~\nabla _a(s_P^a)=-\nabla _a(\log \phi ) \cdot (s_P^a), \end{aligned}$$
(20)

where \(s_A^a\equiv s_Au^a\) and \(s_P^a\equiv \alpha _w\rho ^{\frac{1}{1+w}}u^a\). In general, the energy–momentum tensor (11) can be divided as:

$$\begin{aligned} T_A^{ab}= & {} T_p^{ab}+(p_1-p)x^ax^b\nonumber \\&+(p_2-p)y^ay^b+(p_3-p)z^az^b,\nonumber \\ T_p^{ab}\equiv & {} (\rho +p)u^au^b+pg^{ab}. \end{aligned}$$
(21)

The continuity equation reads

$$\begin{aligned}&-u_b\nabla _aT_A^{ab}=0 ~\rightarrow ~ u\cdot \nabla \rho +(\rho +p)\nabla \cdot u\nonumber \\&\quad = \sum _{k=1}^3(p_k-p)(x_k\cdot \nabla x_k)_a u^a. \end{aligned}$$
(22)

The above equation can be written as a divergence relation of the entropy density vector of a perfect fluid \(s_P\propto \rho ^{1/(1+w)}u^a\):

$$\begin{aligned} \nabla _a\left( \rho ^{\frac{1}{1+w}}u^a\right) = \sum _{k=1}^3\frac{w_k-w}{1+w}(x_k\cdot \nabla x_k)_a \left( \rho ^{\frac{1}{1+w_1}} u^a \right) .\nonumber \\ \end{aligned}$$
(23)

The case when \(w=-1 (\rho +p=0)\) will be treated separately. Comparing this equation with Eq. (20) gives

$$\begin{aligned}&\nabla _a(\log \phi )\nonumber \\&\quad = \left[ \frac{w_1-w}{1+w}x\cdot \nabla x_a+ \frac{w_2-w}{1+w}y\cdot \nabla y_a+ \frac{w_3-w}{1+w}z\cdot \nabla z_a \right] \nonumber \\&\qquad + \, \Phi _a(x), \end{aligned}$$
(24)

where \(\Phi _a(x)\) is the compensation vector mentioned in Sect. 1. It is a vector orthogonal to \(u^a\) (\(\Phi _au^a=0\)) and represents the anisotropic effect. In other words, \(\Phi _a=0\) when matter is isotropic.

For a spherically symmetric configuration, we can take \(x^a,y^a,z^a\) as unit radial, axial and azimuthal spacelike vectors, respectively. In this case, for the metric (12), a calculation in the orthonormal basis

$$\begin{aligned}&u^a=e^{-u/2}\left( \frac{\partial }{\partial t}\right) ^a, \quad x^a=e^{-v/2}\left( \frac{\partial }{\partial r}\right) ^a, \nonumber \\&y^a=\frac{1}{r}\left( \frac{\partial }{\partial \theta }\right) ^a, \quad z^a=\frac{1}{r\sin \theta }\left( \frac{\partial }{\partial \varphi }\right) ^a, \end{aligned}$$
(25)

gives

$$\begin{aligned}&x\cdot \nabla x_a=0, \quad y\cdot \nabla y_a=-\frac{1}{r}\delta _{ar}, \nonumber \\&\quad z\cdot \nabla z_a= -\frac{1}{r}\delta _{ar}-\cot \theta ~\delta _{a\theta }. \end{aligned}$$
(26)

With \(w_2=w_\theta =w_\phi \), one gets from (24) and (26),

$$\begin{aligned}&\partial _t(\log \phi )=\Phi _t,\nonumber \\&\partial _r(\log \phi )=\frac{2}{r}\frac{w_2-w}{1+w}+\Phi _r,\nonumber \\&\partial _\theta (\log \phi )=\cot \theta +\Phi _\theta ,\nonumber \\&\partial _\varphi (\log \phi )=\Phi _\varphi . \end{aligned}$$
(27)

Since the factor \(\phi \) depends only on the radial coordinate, one can determine the components of \(\Phi _a\) to be \(\Phi _t=0,\Phi _\theta =-\cot \theta ,\Phi _\varphi =0\) and \(\Phi _r=\Phi _r(r)\) without loss of generality. Therefore, one function \(\Phi _r\) is sufficient to gauge the difference between two isotropic pressures. Solving the equations gives

$$\begin{aligned} \phi =C(w_2-w)\Phi _w(r)~ r^{\frac{2(w_2-w)}{1+w}} , \end{aligned}$$
(28)

where C is an integral constant and \(\Phi _w(r)\equiv e^{\int \Phi _r}\) is a function to be determined. We call this function \(\Phi _w\) a compensation factor. Therefore, in general, the anisotropic entropy density has the form:

$$\begin{aligned} s_A=\alpha _w\Phi _{w}(r) \rho ^{\frac{1}{1+w}}r^{\frac{2(w_2-w)}{1+w}}. \end{aligned}$$
(29)

The entropy density is a function of energy density and other related parameters (w’s here). Because entropy density is an intensive quantity, the r dependence above seems awkward at first sight. Actually, the entropy density can be written as a function of energy density, \(s_A\equiv s_A(\rho )\). One can regard r as a function of \(\rho \) since \(\rho \) satisfies a first order differential equation

$$\begin{aligned} \frac{d\rho }{dr}=f(u(r),v(r),\rho ,r) \end{aligned}$$
(30)

for a given metric u, v in Eq. (12). Given a specific u(r) and v(r), the above equation solves r as a function of energy density, \(r=r(\rho )\).

If one knows a compensation factor \(\Phi _w(r)\) for a choice of isotropic pressure, \(p_\mathrm{iso}=w\rho \), the compensation factor \(\Phi _{w'}(r)\) for other choice \(p'_\mathrm{iso}=w'\rho \) can be calculated. By equating entropies \(s_A(w,w_2)=s_A(w',w_2)\),

$$\begin{aligned} \alpha _w\Phi _w(r)\rho ^{\frac{1}{1+w}}r^{\frac{2(w_2-w)}{1+w}} = \alpha _{w'}\Phi _{w'}(r)\rho ^{\frac{1}{1+w'}}r^{\frac{2(w_2-w')}{1+w'}}, \end{aligned}$$
(31)

one gets \(\Phi _{w'}\) in terms of \(\Phi _w\). Obtaining a compensation factor \(\Phi _w\) for a specific choice which gives a modified TOV in Eq. (14) is not always an easy task. However, if there is a choice \(w_0\) which makes \(\Phi _{w_0}\) be a constant, a general compensation factor will have the form:

$$\begin{aligned} \Phi _w(r)\propto \left[ \rho (r) r^{2(1+w_2)}\right] ^{\frac{w-w_0}{(1+w)(1+w_0)}} . \end{aligned}$$
(32)

We will show that, with a choice \(\vec p_\mathrm{iso}=\vec p_1\), i.e. \(w_0 = w_1\), the MEP with a constant \(\Phi \) produces the exact modified TOV equation. Consequently, one can write down the entropy density of anisotropic matter as:

$$\begin{aligned} s_A=\alpha _{(w_1,w_2)}~ \rho ^{\frac{1}{1+w_1}}r^{\frac{2(w_2-w_1)}{1+w_1}}, \end{aligned}$$
(33)

where \(\alpha _{(w_1,w_2)}\) is a constant that does not modify the equation of motion and is determined by the physical nature of anisotropic matter as we mentioned above in Ref. [16].

When \(\rho +p_1=0\) or \(w_1=-1\), it is obvious that one cannot use the formula (33) directly. Thankfully, one can use the freedom of choice for the isotropic part to solve this problem. As an example, we obtain an explicit form of the compensation factor for \(w_1=-1\) in the next section.

4 Requiring maximum entropy

The local maximum of entropy of relativistic matter coincides with a dynamically stable equilibrium configuration (MEP) [7, 8]. The premises in those papers about extrema of total entropy also work here. The system being considered in this article is static and spherically symmetric. The only difference is that the pressure of matter is anisotropic. Thus, all the arguments used in Ref. [8] about extrinsic curvature \(K_{ab}\) of a spacelike hyper-surface \(\Sigma \) holds here.

In this section, we briefly review the MEP for an isotropic matter (perfect fluid) and then generalize to the anisotropic matter case. Finally, for the exceptional case with \(w_1=-\,1\), we obtain the entropy density separately.

4.1 Isotropic matter case

The total entropy of the isotropic fluid in a spherical box of radius R is given by

$$\begin{aligned} S\equiv \int d\Sigma ~ s_P^an_a= & {} 4\pi \alpha _w\int _0^Rdr~\frac{r^2}{\sqrt{1-\frac{2m(r)}{r}}}\rho ^{\frac{1}{1+w}}\nonumber \\= & {} (4\pi )^{\frac{w}{1+w}}\alpha _w\int _0^Rdr~ m'^{\frac{1}{1+w_1}}r^{2\left( 1-\frac{1}{1+w_1}\right) }\nonumber \\&\times \,\left( 1-\frac{2m}{r}\right) ^{-\frac{1}{2}}. \end{aligned}$$
(34)

The total entropy can be regarded as an action integral \(I=\int _0^R dr~\mathcal {L}_0[m(r),m'(r);r]\) where the corresponding Lagrangian is

$$\begin{aligned} \mathcal {L}_0[m(r),m'(r);r]\equiv & {} (4\pi )^{\frac{w}{1+w}}\alpha _w m'^{\frac{1}{1+w_1}}r^{2\left( 1-\frac{1}{1+w_1}\right) }\nonumber \\&\times \,\left( 1-\frac{2m}{r}\right) ^{-\frac{1}{2}}. \end{aligned}$$
(35)

As expected, the Euler-Lagrange equation, \(\frac{d}{dr}\left( \frac{\partial \mathcal {L}_0}{\partial m'}\right) -\frac{\partial \mathcal {L}_0}{\partial m}=0,\) gives the original TOV equation (15).

4.2 Anisotropic matter when \(w_1\ne -1\)

For anisotropic matter with static, spherically symmetric distribution, in accordance with MEP, the variation of total entropy gives the exact modified TOV equation (14). The total entropy of the anisotropic matter in a box of radius R is given by

$$\begin{aligned} S_A= & {} \int d\Sigma ~s_A^an_a\nonumber \\= & {} 4\pi \alpha _{w}\int _0^Rdr \frac{r^2}{\sqrt{1-\frac{2m(r)}{r}}}r^{\frac{2(w_2-w_1)}{1+w_1}}\rho ^{\frac{1}{1+w_1}}, \end{aligned}$$
(36)

where we use the entropy density in Eq. (33) with \(\Phi _w=1\). In this case, the action to be extremized is given by

$$\begin{aligned} I= & {} \int _0^R dr~\mathcal {L}(m,m';r),~~~\nonumber \\ \mathcal {L}(m,m';r)\equiv & {} r^{\frac{2(w_2-w_1)}{1+w_1}}\mathcal {L}_0(m,m';r)\nonumber \\= & {} (4\pi )^{\frac{w}{1+w}}\alpha _{w}\left( m'\right) ^{\frac{1}{1+w_1}} r^{\frac{2w_2}{1+w_1}}\left( 1-\frac{2m}{r}\right) ^{-\frac{1}{2}} ,\nonumber \\ \end{aligned}$$
(37)

where \(\mathcal {L}_0\) is the Lagrangian for the isotropic part in Eq. (35). The Euler–Lagrange equation

$$\begin{aligned} \frac{d}{dr}\left( \frac{\partial \mathcal {L}}{\partial m'}\right) -\frac{\partial \mathcal {L}}{\partial m}=0, \end{aligned}$$
(38)

reproduces the modified TOV equation  (14) where we use the relation \(m'=4\pi r^2\rho \).

4.3 Anisotropic matter when \(w_1=-1\)

The entropy density for anisotropic matter depends on the energy density \(\rho (r)=4\pi r^2 m'(r)\). Thus the Lagrangian for perfect fluid (35) can be generalized to the form:

$$\begin{aligned} \mathcal {L}_{ab}=c(m')^a r^b \left( 1-\frac{2m}{r}\right) ^{-\frac{1}{2}}, \end{aligned}$$
(39)

where a, b, c are constants to be determined. The Euler equation,

$$\begin{aligned}&\frac{m'^2}{\mathcal {L}_{ab}}\times \left( \frac{d}{dr}\frac{\partial \mathcal {L}_{ab}}{\partial m'}-\frac{\partial \mathcal {L}_{ab}}{\partial m}\right) =0 ~\Rightarrow ~ a(a-1)m''\nonumber \\&\qquad + \, \frac{ab}{r}m'+\frac{(a-1)m'^2-a\frac{mm'}{r}}{r-2m}=0, \end{aligned}$$
(40)

can be rewritten as a form of modified TOV equation:

$$\begin{aligned} p_1'= & {} -\frac{\frac{w_1}{1-a}\rho }{r(r-2m)}\left( m+\frac{1-a}{a w_1}4\pi r^3 p_1\right) \nonumber \\&+\frac{\frac{b}{1-a}-2}{r}w_1\rho . \end{aligned}$$
(41)

Comparing this with the modified TOV equation (14) one obtains:

$$\begin{aligned} a=\frac{1}{1+w_1},~b=\frac{2w_2}{1+w_1}. \end{aligned}$$
(42)

For \(w_1\ne -1\), the Lagrangian exactly corresponds to the one for the entropy density (33) obtained in Sect. 3, hence confirms our result.

For \(w_1=-1\), the solution was explicitly obtained in Ref. [29]. It is sufficient that we use the results from the article:

$$\begin{aligned}&m(r)=M+\frac{K}{2r^{2w_2-1}}, \nonumber \\&\rho (r)=-p_1(r)=\frac{(1-2w_2)K}{8\pi r^{2+2w_2}}, \end{aligned}$$
(43)

where M and K are constants. Putting this information into Eq. (40) we get a and b:Footnote 4

$$\begin{aligned} a=1-\frac{1}{2w_2}, \quad b=2(a-1)w_2. \end{aligned}$$
(44)

Therefore, the entropy density for \(w_1=-1\) which satisfy the maximum entropy principle is

$$\begin{aligned} s=s_0 ~\rho ^{1-\frac{1}{2w_2}}r^{-\frac{1+w_2}{w_2}}, \end{aligned}$$
(45)

where \(s_0\) is a constant.

As we discussed in the previous section, one can determine ‘the compensation factor’ \(\Phi _w(r)\) for the above entropy density. When \(w_1=-1\), to avoid the denominator to vanish, one can choose the isotropic part of the pressure as \(p_\mathrm{iso}\equiv p_1-2p_2\) or \(w_\mathrm{iso}=w_1-2w_2(=-1-2w_2)\). The entropy density using the anisotropic factor (28) is obtained to be

$$\begin{aligned} s~\propto ~\Phi _{w}(r)\rho ^{-\frac{1}{2w_2}}r^{-\frac{(1+3w_2)}{w_2}}, \end{aligned}$$
(46)

by putting \(w=-1-2w_2\) to Eq. (29). After requiring MEP, one obtains the factor \(\Phi _w(r)=r^{-2w_2}\) up to a multiplicative constant. By using the relation \(\rho (r)\propto r^{-2(1+w_2)}\) in Eq. (43), one reproduces the entropy in Eq. (45).

5 Total entropy and applications

Total entropy of self-gravitating radiation confined to a box of radius R was obtained in Ref. [8]. By using the same method, we obtain a general form of total entropy of anisotropic matter confined to the box:

$$\begin{aligned} S= & {} \left. S_A(r)\right| ^{r=R}_{r=0}\nonumber \\= & {} \left. \frac{(4\pi )^{\frac{w_1}{1+w_1}}\alpha _{w}}{(1+w_1+2w_2)}\frac{\frac{m}{r}+w_1\frac{dm}{dr}}{\left( \frac{dm}{dr}\right) ^\frac{w_1}{1+w_1}\left( 1-\frac{2m}{r}\right) ^\frac{1}{2}}r^{\frac{1+w_1+2w_2}{1+w_1}}\right| ^{r=R}_{r=0}.\nonumber \\ \end{aligned}$$
(47)

One can verify that the derivative of the function on the right-hand side is the Lagrangian (37) by using the relation (40). We call the indefinite integral \(S_A(r)\) as ‘entropy function’. One can see that the above total entropy reproduces that in Ref. [8] when \(w_1=w_2=w_3=1/3\).

In a general case, solutions of the Einstein equation can be singular at the origin. In order for a solution to be regular at \(r=0\), \(m(r)\sim (4\pi r^3/3)\rho (0)\sim r^3\), and \(\rho (r)\sim r^\alpha \) with \(\alpha > 0\). Otherwise the solution will be singular at the center. To analyze the singularity more explicitly, one needs to have an exact solution. The properties of solutions with \(w_1=-1\) at \(r=0\) is extensively analyzed in Ref. [29] with the exact solutions in Eq. (43).

The entropy function above can be further simplified to

$$\begin{aligned} S_A(r)= & {} \frac{m+4\pi r^3p_1}{\left( 1-\frac{2m}{r}\right) ^\frac{1}{2}}\left( \frac{s_A(r)}{\rho +p_1+2p_2}\right) \end{aligned}$$
(48)

by using \(m'=4\pi r^2\rho \) and the relation (4) and (33).

Recently, in Ref. [35] the author suggested conditions to avoid naked singularities for a system with an anisotropic fluid. One of the conditions is \(\rho +p_1+2p_2<0\), which indicates a violation of the strong energy condition. Putting this into the relations (47) or (48), the entropy function takes a negative value. Since entropy is defined by a possible number of physical configurations of a system, negative value of entropy seems unreasonable. If we look into the derivation of total entropy carefully, the total entropy, \(\int _a^b\mathcal {L}_A=S_A(b)-S_A(a)\), is always non-negative since the entropy function \(S_A(r)\) is monotonically increasing function of r even if \(S_A(r)<0\). It is because the Lagrangian density, \(\mathcal {L}_A=S'_A(r)\), is positive. Therefore, even though \(\rho +p_1+2p_2<0\), the total entropy of the system is positive.

A wormhole is a solution of general relativity that has a throat and two sides of entrance and exit [36,37,38]. In general relativity, the throat of a traversable wormhole needs to be made of exotic, anisotropic material which violates energy conditions (especially null energy condition [39] along with weak, strong and dominant energy conditions). If anisotropic matter (that creates a wormhole) is bound (\(r<R\)) and the wormhole’s throat is located at \(r=B\), the entropy of the wormhole will be given by

$$\begin{aligned} S =2[S_A(R)-S_A(B)], \end{aligned}$$
(49)

provided that both sides of the wormhole have the same shape.

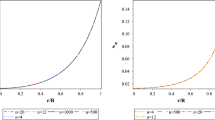
Morris and Thorne [30] suggested specific wormhole solutions which use exotic material minimally: (1) a zero-tidal force solutions, (2) a solution with a finite radial cutoff of the stress-energy and (3) a solution with exotic matter limited to the throat vicinity. The first and the second solutions satisfy the equation of state of type \(p_k=w_k\rho \) with \(1+w_1+2w_2=0\). Although the equation of state of the third solution does not have the linear form, the matter still satisfy \(\rho +p_1+2p_2=0\). Putting these conditions into the total entropy formula (47), (48), one immediately gets indefinite value for the entropy function. From the Einstein equation for the metric (12), one gets

$$\begin{aligned} 8\pi (\rho +p_1+2p_2)= & {} \left( 1-\frac{2m}{r}\right) \nonumber \\&\times \,\left( \frac{2}{r}u'-\frac{v'u'}{2}+\frac{u'^2}{2}+u''\right) . \end{aligned}$$
(50)

When \(u'=0\) throughout the region where exotic matter is used, \(\rho +p_1+2p_2=0\). The three examples in Ref. [30] is the case. For the same metric, the entropy function can be written as

$$\begin{aligned} S_A(r)= \frac{4\pi r^2 }{\left( 1-\frac{2m}{r}\right) ^\frac{1}{2}}\frac{s_A}{\left( \frac{2}{r}-\frac{v'}{2}+\frac{u'}{2}+\frac{u''}{u'}\right) }, \end{aligned}$$
(51)

where we use the relation (13). We may slightly perturb the above wormhole solutions to avoid the divergence of the entropy function. If we compare two configurations of \(S(u'=0)\) and \(S(|u'|\ne 0)\), one may tell which configuration is more favourable than the other. For a smooth function \(u'(r)~(|u'|\ll 1\) with dimension of inverse length) near the throat vicinity, the quantities \((u')^2,u''\) are much smaller than \(u'\). The denominator of the above equation reduces to

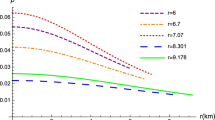
$$\begin{aligned} \text{ The } \text{ denominator }\propto ~~ e^{v}\frac{2r-3m-rm'}{r^2} +\frac{u'}{2}. \end{aligned}$$
(52)

The sign of the first term may switch from positive to negative and vice versa. For example, in the third wormhole in Ref. [30] the mass was given by \(m(r)=b[1-(r-b)/a]^2\), where \(u'=0\) in the region \(b\le r\le b+a\). Provided that perturbations around \(u'= 0\) is small and the solution of m(r) has the same quadratic form, occasional sign changes appear for various values of a and b. The entropy function becomes extremely large when the denominator approaches zero. When there is a sign change, the indefinite value makes comparison difficult.

As we discussed in Sect. 3, the freedom of choice in isotropic pressure part may help us to prevent from this pathology. When we set the isotropic pressure part as \(\mathcal {P}\equiv p_1+2p_2\), the process of getting the anisotropic factor \(\phi \) suffers the same pathology when \(\rho +p_1+2p_2=0\) or \(w_1+2w_2=-1\) as in the case when \(w_1=-1\). We expect that with proper ‘compensation factor’ \(\Phi _w\) one can obtain finite form of entropy density by using a similar process in Sect. 4.3.

The thermodynamic stability of the configuration \(u'=0\) can be estimated by the difference of the entropy functions, \(\Delta S=[S_A(r,u'=0)-S_A(r,u'\ne 0)]^b_a\). To this end, further analysis with wider range of exact solutions including \(u'\ne 0\) will be necessary.

Incidentally, we get another form of the entropy function

$$\begin{aligned} S_A(r)= -4\pi \frac{(m+4\pi r^3p_1)}{\sqrt{1-\frac{2m}{r}}~R^0_{~0}}s_A. \end{aligned}$$
(53)

using \(R^0_{~0}=-4\pi ( \rho +p_1+2p_2)\).

6 Summary and discussions

In this article we considered a system of self-gravitating, static and spherically symmetric matter of which pressure satisfies the linear equation of state \(p_1=w_1\rho \) and \(p_2=p_3=w_2\rho \). We obtained a form of entropy density for the anisotropic matter. To obtain the exact form of entropy density, we introduced a scalar function \(\phi (x)\), the anisotropic factor that contains the information of anisotropic deviation from an isotropic perfect fluid. The choice of an isotropic part of the pressure was shown to have an arbitrariness. A compensation vector was obtained to gauge this arbitrariness. This gauge freedom could be beneficial when we meet a problem. In the process, the maximum entropy principle (MEP) played a key role in obtaining the exact form of the entropy. We showed that the requirement of local maximum of total entropy gives the exact Einstein equation of the system composed of the anisotropic matter. This observation supports the correspondence between thermodynamics and gravity. By the guidance of this correspondence, the entropy density for \(p_1=- \, \rho \) or \(w_1=- \, 1\) was obtained separately.

The entropy density in this article has a multiplicative factor that describes the anisotropic effect. The quantity we obtained is a function of radius r and \(w_2-w_1\). This comes from the use of the spherical coordinate system and the simple form of anisotropy between the radial and the angular directions. In a more general situation, the entropy density is expected to have various forms as a function of energy density and pressure.

With the explicit form of the total entropy function (47), as an application, we tried to analyze a wormhole solution by estimating the entropy in the vicinity of a throat. Actually, most of the issues about wormholes come from the fact that matter composing wormholes are not ordinary but exotic. There are various ways to overcome or to go around this issue. For a modified gravity theory, one may find wormholes without exotic matter. There were many articles in which a throat of traversable wormholes is composed of ordinary matter in various modified gravity theories, e.g., Einstein–Gauss–Bonet theory [40] or Lovelock theory [41], f(R) gravity [42], etc. [43, 44]. Similar analysis on the entropy for the wormholes in those theories is worth trying. Especially, the method in this article can be applicable to an anisotropic matter in the context of f(R) gravity, because the MEP was proven for self-gravitating fluid in f(R) gravity [45]. On the other hand, if we stick to the Einstein gravity, our result shows that building materials or conditions should be chosen carefully.

There are many studies on astro-physical objects such as relativistic stars, neutron stars, etc. in which anisotropic pressure takes important roles [21, 24, 46]. We expect that the entropy obtained in this article can be used to estimate the state of a relativistic star by comparing the values of entropy for different configurations of the star. The self-gravitating solutions for the anisotropic matter were classified in Ref. [47]. For the case of matter with non-linear equation of states, the analysis will be quite difficult and deeper studies on the entropy formula will be required.