1 Introduction

It is necessary to solve the nonlinear Einstein field equations to describe physical systems in relativistic astrophysics. One approach to solve the field equations systematically is to utilize the underlying symmetries and group structure of the equations. The Lie symmetry generators that leave an equation invariant to generate a Lie algebra and facilitate finding an exact solution. Some recent examples of this approach in describing stellar systems are contained in the works of Govinder and Govender [1], Abebe et al. [2, 3] and Mohanlal et al. [4, 5]. Therefore, the group theoretic approach is useful in solving nonlinear equations for relativistic stars. A second approach in solving the field equations systematically is to utilize the presence of symmetries on the spacetime manifold. A practical example of a spacetime symmetry is a conformal symmetry. Conformal Killing vectors generate constants of the motion along null geodesics. The presence of a conformal symmetry restricts the metric functions and often leads to new exact solutions. Early examples of relativistic systems with a conformal Killing vector are the models of Herrera and Ponce de Leon [6] and Herrera et al. [7]. Esculpi and Aloma [8] and Rahaman et al. [9] constructed spheres with anisotropic pressures with a one-parameter group of conformal motions. Manjonjo et al. [10, 11] showed that the two metric functions in static spherically symmetric spacetimes are related if a conformal Killing vector exists. Mafa Takisa et al. [12] and Kileba Matondo et al. [13, 14] have shown that this relationship between the potentials may be exploited to model relativistic stars with anisotropy and electric charge. Therefore, the conformal symmetry approach is also useful in solving the nonlinear field equations for gravitating objects.

Solutions of the Einstein field equations may be categorised and classified using a number of approaches. A well-known approach is to use the Petrov classification which utilizes the algebraic symmetries of the Weyl tensor. Another approach is to utilize spacetime symmetries to classify and categorise exact solutions as emphasized by Stephani et al. [15]. The symmetry approach can lead to new exact solutions, e.g. in spherically symmetric spacetimes cosmological solutions have been found by Dyer et al. [16], Havas [17] and Sussman [18] with homothetic and conformal vectors. This symmetry approach will also be useful in describing gravitational phenomena in astrophysical situations. Only a few results have been found for compact objects, and only for the special case of a conformal Killing vector. Shee et al. [19], and Newton Singh et al. [20] analytically obtained new exact spherically symmetric solutions with conformal geometry for compact stars in strong gravitational fields. We expect that a comprehensive analysis of conformal symmetries will provide deeper insights into many other astrophysical situations. Other types of spacetime symmetries such as curvature collineations need to be considered in the study of compact stars.

We now make some comments relating to the physical features of local anisotropy and conformal symmetries. Firstly, local anisotropy has been discussed by several authors most notably in the comprehensive treatment of Herrera and Santos [21] and references therein. Some recent references for anisotropy are contained in the analysis of Kileba Matondo et al. [13] who regain observational parameters for astronomical objects such as PSR J1614-2230 and SAX J1808.4-3658. Possible sources for anisotropy include the variation of the magnetic field intensity in neutron stars in the period of post-main sequence development, the presence of a very high density region in the core, several condensate states (such as pion condensates, meson condensates, etc.), a type 3A superfluid, fluid mixtures of various types and rotational motion. The concept of cracking was introduced in [21] which is directly related to the presence of anisotropy. Cracking is essential to describe the stability of the matter distribution close to equilibrium. Secondly, the presence of conformal motions has been related to physical processes for stars. Important references in this regard are the pioneering treatments of Herrera and coworkers [6, 7]. Several stellar models with spherical symmetry in general relativity have been generated with a conformal Killing vector, see for example the recent paper of Kileba Matondo et al. [13]. Conformal motions are related to the property of self-similarity which was emphasized in the study of Herrera and Di Prisco [22] for static axially symmetric relativistic fluids. Self-similarity is important in systems with no characteristic length scale, and for systems close to the critical point with infinite correlation length. Density fluctuations then occur at all length scales as seen in critical opalescence arising in regions of continuous phase transitions. In particular conformal motions, extending the concept of geometric similarity, have applied to models of wormholes in general relativity. Most analyses of conformal motions have been restricted to spherically symmetric models. e.g. the stellar model in [12, 13]. Recently, Ivanov [23] has proposed a conformally flat realistic anisotropic compact star model by using only analytical approach. The study of Herrera and Di Prisco [22] is related to the important physically geometry system of static axial symmetry. Axial symmetry should be an area that is considered in future work using the approach of this paper; this should produce new results not present in models with spherical symmetry.

Finding an exact solution to the Einstein field equations do not always lead to a physically acceptable model for a relativistic star. Physical criteria such as causality and regularity at the centre should be satisfied. In addition, the predictions of the model should be consistent with observations relating to quantities much as the stellar radius, mass and redshift. This has become more important in recent times since there has been a substantial improvement in the observations for highly compact relativistic stars. In this paper, we impose a conformal symmetry in static spherical spacetimes and utilize the results of Manjonjo et al. [11]. The matter distribution is anisotropic. It is then possible to solve the Einstein field equations. A detailed and comprehensive analysis shows that the model is regular, well behaved and satisfies the criteria for physical acceptability. Our analysis in this paper shows that the conformal geometry produces a model consistent with observations. This is true for the obtained masses and radii of compact objects in particular. Our analysis shows that a conformal Killing vector may be associated with the real life astronomical objects.

The article starts with the introduction in Sect. 1. In Sect. 2, we present the appropriate Einstein field equations with an anisotropic fluid distribution for a spherically symmetric spacetime containing a conformal Killing vector. The exact solution for conformal anisotropic models by considering gravitational metric potential \(e^{\lambda }\) is presented in Sect. 3. In Sect. 4, We introduce the matching conditions and determine the constant parameters A, B and b with the total mass of star \(m_s\). We present all the physical conditions for well behaved anisotropic conformal models in Sect. 5. In Sect. 6, we performed a detailed physical analysis (analytical and graphical) of the spherical conformal model via. physical conditions as mentioned in Sect. 5. The Conclusion of the paper has been made in Sect. 7.

2 Metric and the Einstein field equations

Consider the line element for the spherically symmetric static fluid distributions which can be written as

$$\begin{aligned} ds^{2} = e^{\nu (r) } \, dt^{2}-e^{\lambda (r)} dr^{2} -r^{2}(d\theta ^{2} +\sin ^{2} \theta \, d\varphi ^{2}), \end{aligned}$$
(1)

in the coordinates \((x^b)=(t, r, \theta ,\varphi )\) where \(\nu = \nu (r)\) and \(\lambda = \lambda (r)\) are the two unknown gravitational potential functions of the radial coordinate r alone due to this being a static system. These gravitational potentials uniquely determine the surface redshift and gravitational mass function, respectively. The matter distribution is assumed to composed of an anisotropic fluid so that the associated energy momentum tensor can be written as

$$\begin{aligned} {T}_{a\,b} = (\rho , -p_r, -p_t, -p_t). \end{aligned}$$
(2)

The fluid 4-velocity \(u^a\) is comoving, unit and timelike vector which has the form \(u^b=e^{-\nu /2}\,\delta ^b_0\). The quantities \(\rho \), \(p_r\), \(p_t\) are the density, radial pressure and tangential pressure, respectively. We assume that the matter distribution is anisotropic which means \(p_r \ne p_t\). Consequently, \(\Delta \) = \(p_t - p_r\) is denoted as the anisotropy factor [24], and it determines the pressure anisotropy of the fluid. The anisotropy vanishes (\(\Delta =0\)) when the pressure is isotropic i.e. the radial pressure is equal to the tangential pressure (\(p_t = p_r\)). Using (1) and (2), we obtain the Einstein field equations and pressure anisotropy which are given by

$$\begin{aligned}&\kappa \, \rho (r) = \frac{1}{r^2} \,\left[ r\,(1-e^{-\lambda }) \right] ^{\prime }, \end{aligned}$$
(3)
$$\begin{aligned}&\kappa \, p_{r}(r) = \frac{\nu '}{r} e^{-\lambda } -\frac{(1-e^{-\lambda } )}{r^{2} }, \end{aligned}$$
(4)
$$\begin{aligned}&\kappa \, p_{t}(r) = \left[ 2\,\nu '' -\lambda ' \nu ' +{\nu '}^{2} +\frac{2\,\nu '}{r}-\frac{2\,\lambda '}{r} \right] \,\frac{e^{-\lambda }}{4} , \end{aligned}$$
(5)
$$\begin{aligned}&\Delta =\kappa \, (p_{t} -\, p_{r} ) \nonumber \\&= \frac{e^{-\lambda }}{4} \left[ 2\,\nu '' -\lambda ' \nu ' +{\nu '}^{2} -\frac{2\,\nu '}{r}-\frac{2\,\lambda '}{r} -\frac{4}{r^{2} } \right] \, +\frac{1}{r^{2} }, \nonumber \\ \end{aligned}$$
(6)

It should be noted here that the anisotropic force is represented by \(\Delta /r\), which is attractive if \(p_{t} < p_{r}\) and repulsive whenever \(p_{t} > p_{r}\) in the stellar model. We assume natural units \(\kappa =8\,\pi \) and \(G=c=1\) throughout our discussion.

The field equations (3)–(6) are highly nonlinear in general and it is difficult to find exact solutions. For determining the exact solution of the field equations, we assume that the spacetime admits a conformal symmetry. The line element (1) admits four linearly independent Killing vectors. The conformal symmetry places additional restrictions on the gravitational potentials; this takes the form of further differential equations which have to be solved in addition to the field equations. (In the case of the static line element (1) the conformal conditions lead to Eq. (12) given below). In the presence of a conformal Killing vector \(\mathbf X \), the Lie dragged metric tensor \(g_{ab}\) has to satisfy the following equation

$$\begin{aligned} {\pounds }_\mathbf{{X}}\,g_{ab}=-2\,\zeta \,g_{ab}, \end{aligned}$$
(7)

where \({\pounds }_\mathbf{{X}}\) is the Lie derivative operator and \(\zeta (x^b)\) is the conformal factor. For spherically symmetric spacetimes the investigation of conformal motions has been completed by Maharaj et al. [25], Maartens et al. [26, 27] and Manjonjo et al. [11]. It is feasible to produce the components of general conformal vector \(\mathbf{{X}} = (X^0, X^1, X^2, X^3)\) and conformal factor \(\zeta \) subject to integrability conditions which take place restrictions on the gravitational potential \(\nu (r)\) and \(\lambda (r)\). The complete study of the conformal structure of the static spherically symmetric spacetimes is provided by the

general solution of the (7). Some exact solutions are already known with particular choices of the conformal Killing vector \(\mathbf {X}\). Recently, Rahaman et al. [29] have obtained a conformally symmetric relativistic anisotropic star with a Tolman-like geometry. They assumed that all known conformally spherical symmetric solutions are connected with the particular case of the conformal Killing vector

$$\begin{aligned} \mathbf{{X}}= & {} \alpha (t, r)\,\frac{\partial }{\partial \,t} + \beta (t, r)\,\frac{\partial }{\partial \,r}, \end{aligned}$$
(8)
$$\begin{aligned} \zeta= & {} \zeta (t, r). \end{aligned}$$
(9)

If we consider the Weyl tensor \(C^h{}_{ijk}\) the existence of a conformal Killing vector is subjected to the condition

$$\begin{aligned} {\pounds }_\mathbf{{X}}\,C^h{}_{ijk} = 0 , \end{aligned}$$
(10)

which is conformally invariant. The nonzero components of Weyl tensor for the static spacetime (1) are:   \(C^0{}_{101}=-\frac{1}{3}\,\beta \),   \(C^0{}_{202}=\frac{1}{6}\,r^2\,e^{-2\,\lambda }\,\beta \),   \(C^0{}_{303}=\frac{1}{6}\,r^2\,\sin ^2\theta \,e^{-2\,\lambda }\,\beta \), \(C^1{}_{212}=C^0{}_{202}\),   \(C^1{}_{313}=C^0{}_{303}\),   \(C^2{}_{323}=-2\,C^0{}_{303}\). However the conformal spherical symmetric spacetime (1) provides a relation between two gravitational potential [25] given by

$$\begin{aligned} \frac{\nu ''}{2}+\frac{\nu '^2}{4}-\frac{\lambda '\,\nu '}{4}+\frac{(\lambda '-\nu ')}{2\,r}+\frac{(1-e^{\lambda })}{r^2}=\beta . \end{aligned}$$
(11)

The presence of quantity \(\beta \) helps in determining the conformal symmetry. The quantity \(\beta =0\) gives conformally flat spacetime while \(\beta \ne 0\) provides a nonconformally flat spacetime. From (10) we find \(\beta =\frac{e^{2\,\lambda }}{r^2}\,k\) where k is constant of integration. It is note that the constant \(k=0\) and \(k\ne 0\) determines corresponding conformally and nonconformally flat solutions which can be expressed by following theorem as given in [11]:

Theorem A static metric with a spherically symmetric conformal symmetry (8) and a nonstatic conformal factor (9) leads to the following relationship between the gravitational potentials \(e^{\nu (r)}\) and \(e^{\lambda (r)}\):

$$\begin{aligned} e^{\nu /2} = \left\{ \begin{array}{lcl} A\,r\,\exp {\left( \sqrt{\alpha \,(k+1)}\,\int {\frac{e^{\lambda /2}}{r} dr}\,\right) } + \\ ~B\,r\,\exp {\left( -\sqrt{\alpha \,(k+1)} \,\int {\frac{e^{\lambda /2}}{r} dr}\,\right) }, &{}\quad \text{ where } &{}\quad \alpha =\pm 1 ~~ \text {for} ~~ k+1 >0 ~~ \text {and} ~~k+1< 0, \\ A\, r\, \int {\frac{e^{\lambda /2}}{r}dr}+B\,r, &{}\quad \text{ where } &{} k+1=0 \end{array}\right. \end{aligned}$$
(12)

where A and B are constants. If \(k=0\) then the spherical symmetric spacetime is conformally flat while \(k\ne 0\) leads to the nonconformally flat model. Equation (11) for the case \(\beta = k=0\) was first derived and integrated by Herrera et al. [28]. We point out that the first solution in (12) (the only one compatible with \(k=0\)) is a particular case of the solution (40) of that reference.

In the present investigation we consider the case \(k+1>0\) and \(k+1<0\). Therefore, the relation (12) permits us to rewrite the Einstein field equations (3)–(6) in the form

$$\begin{aligned} 8\,\pi \,\rho= & {} \frac{\lambda ^{\prime }\,}{\,r^2~ e^{\lambda }}+\frac{e^{\lambda }-1}{r^2 ~ e^{\lambda }} ~~, \end{aligned}$$
(13)
$$\begin{aligned} 8\,\pi \,p_{r}(r)= & {} \frac{\left[ \,A\,\xi _{11}(r)-B \,\right] \, \sqrt{\alpha (k+1)} }{\left[ \,A\,\,\xi _{11}(r)+B \,\right] \,r^2} -\frac{(e^{\lambda }-2 )}{r^{2}~e^{\lambda } }, \end{aligned}$$
(14)
$$\begin{aligned} 8\,\pi \,p_t= & {} \frac{1}{e^{\lambda }}\,\left[ \,\frac{2\,e^{\lambda }\,\xi _{14}(r)-2\,\xi ^2_{12}(r)+\left[ \xi _{13}(r)\,e^{\lambda }+\xi _{12}(r)\right] ^2}{4\,\,r^2\,\xi ^2_{12}(r)}\right. \nonumber \\&\left. -\,\frac{\lambda ^{\prime }\,\left[ \xi _{13}(r)\,e^{\lambda }+\xi _{12}(r)\right] }{4\,r\,\xi _{12}(r)} +\frac{\left[ \xi _{13}(r)\,e^{\lambda }+\xi _{12}(r)\right] }{2\,r^2\,\xi _{12}(r)} -\frac{\lambda ^{\prime }}{2\,r}\,\right] , \end{aligned}$$
(15)
$$\begin{aligned} 8\,\pi \,\Delta= & {} \frac{1}{e^{\lambda }}\,\left[ \,\frac{\xi _{15}(r)}{4\,\,r^2\,\xi ^2_{12}(r)}-\frac{\lambda ^{\prime }\,\left[ \xi _{13}(r)\,e^{\lambda }+\xi _{12}(r)\right] }{4\,r\,\xi _{12}(r)}\right. \nonumber \\&\left. +\,\frac{\left[ \xi _{13}(r)\,e^{\lambda }+\xi _{12}(r)\right] }{2\,r^2\,\xi _{12}(r)} -\frac{\lambda ^{\prime }}{2\,r}\,\right] -\frac{\xi _{13}(r)\, \sqrt{\alpha (k+1)} }{r^2\,\xi _{12}(r)}\nonumber \\&+\,\frac{(e^{\lambda }-2 )}{r^{2}~e^{\lambda } }, \end{aligned}$$
(16)

where the coefficients used in above equations are as follows:

$$\begin{aligned} \xi _{11}(r)= & {} \exp \left( 2\,\sqrt{\alpha (k+1)}\, \int {\frac{e^{\lambda }}{r}dr}\,\right) ,\\ \xi _{12}(r)= & {} \left[ A\,\exp \left( 2\,\sqrt{\alpha (k+1)}\, \int {\frac{e^{\lambda }}{r}dr}\,\right) +B \right] ,\\ \xi _{13}(r)= & {} \left[ A\,\exp \left( 2\,\sqrt{\alpha (k+1)}\, \int {\frac{e^{\lambda }}{r}dr}\,\right) -B \right] ,\\ \xi _{14}(r)= & {} 2\,A\,e^{\lambda }\,\sqrt{\alpha (k+1)}\,\,\xi _{11}(r) \,[\,\xi _{12}(r)-\xi _{13}(r)\,]\\&+\,\xi _{12}(r)\,\xi _{13}(r)\,[\,r\,\lambda ^{\prime }-1\,], \\ \xi _{15}(r)= & {} 2\,e^{\lambda }\,\xi _{14}(r)-2\,\xi ^2_{12}(r)+\left[ \xi _{13}(r)\,e^{\lambda }+\xi _{12}(r)\right] ^2. \\ \end{aligned}$$

From (13)–(16) we observe that all the physical parameters such as the radial pressure, the tangential pressure, matter density and pressure anisotropy depend upon the gravitational metric potential \(e^{\lambda (r)}\). Therefore, the exact solution under the conformally spherical symmetry could be determined by a specific choice of the gravitational metric potential \(e^{\lambda (r)}\). The gravitational mass of a compact star of radius r for the relativistic anisotropic compact object is

$$\begin{aligned} m(r) = 4\,\pi \, \int ^r_0{\rho (x)\,x^2\,dx} \end{aligned}$$
(17)

3 Exact solution for conformal anisotropic models

We need to find matter variables associated with the pressures, density and anisotropy factor to discuss the complete structure of the conformal spherical symmetric anisotropic models. For this purpose, we need to choose a proper gravitational metric function \(e^{\lambda }\) which should provide a complete integration of relation (12) and generate the new exact solution of the Einstein field equations. However, the particular choice of metric potential \(e^{\lambda }\) should be singularity free at \(r=0\) and finite regular everywhere within the model. We consider the gravitational metric potential \(e^{\lambda }\) of the form

$$\begin{aligned} e^{\lambda /2}=\frac{1}{\sqrt{\alpha \,(k+1)}}\,\left[ \frac{ a\,r^2+\left( \sqrt{\alpha \,(k+1)}-b\,r^2\,\right) ^n}{\left( \sqrt{\alpha \,(k+1)}-b\,r^2\,\right) ^n} \right] , \end{aligned}$$
(18)

where \(\alpha =\pm \,1\),   \(k\ne -1\) and n is a positive constant with \(n\ne 1\).

By substituting the value of \(e^{\lambda }\) into relation (12), we find other metric potential   \(e^{\nu (r)}\) as

$$\begin{aligned} e^{\nu /2}= & {} A\,r^2\,\exp {\left[ \,\frac{a\,\left( \sqrt{\alpha \,(k+1)}-b\,r^2\,\right) ^{1-n}}{2\,b~(n-1)}\,\right] }\nonumber \\&+\,B\,\exp {\left[ -\,\frac{a\,\left( \sqrt{\alpha \,(k+1)}-b\,r^2\,\right) ^{1-n}}{2\,b~(n-1)}\,\right] } , \end{aligned}$$
(19)

Both potentials (18) and (19) are regular, finite and nonsingular at \(r=0\). By plugging the value of potential (18) into Einstein’s field equations (13)–(16), the expressions for matter variables density, pressures and anisotropy are given as

$$\begin{aligned}&\rho =\frac{1}{8\,\pi }\,\left[ \frac{4\,a\,\alpha \,(k+1) ~ {f}^{(2n-1)}\,\left[ \sqrt{\alpha \,(k+1)} +(n-1)\,b\,r^2\right] }{\left[ {f}^{n}+a\,r^2 \, \right] ^3} +\frac{[{f}^{n}+a\,r^2 ]^2-\alpha \,(k+1)\,f^{2n}}{[{f}^{n}+a\,r^2 ]^2}\right] , \end{aligned}$$
(20)
$$\begin{aligned}&p_r=\frac{-a^2 \,r^4 \, [\,B + A\, r^2\, \psi (r)\,] - 2 \, a\, r^2\, f^n\, \xi _{21}(r)+f^{2\, n}~ [\, B\, (-1 + \alpha + \alpha \, k) + A\, \psi (r) \, (-1 + 5 \, \alpha (1 + k)) r^2\,]}{8\,\pi \,r^2~\left[ A\,r^2\,\psi (r)+B\right] ~\,[a\,r^2+f^n]^2} , \end{aligned}$$
(21)
$$\begin{aligned}&p_t=\frac{4 \, A \, \psi (r)\, f^{3\, n } + a^3\, r^4 \, [\, B + A\,r^2\, \psi (r) \,] + a^2\, r^2 \, f^{n}\, (B + 5 \, A\, r^2\,)-4 \, a\, f^{2\, n-1}\, [B \, (f + n\, b\, r^2) + A\, r^2\, \psi (r) (-f + n\, b\, r^2)]}{8\,\pi \,\,[\alpha \,(1+k)]^{-1}\,\left[ A\,r^2\,\psi (r)+B\right] ~\,[ a\,r^2+f^n ]^3} , \end{aligned}$$
(22)
$$\begin{aligned}&\Delta =\frac{\alpha \,(1+k)[\,4 \, A \, \psi (r)\, f^{3\, n } + a^3\, r^4 \, (\, B + A\,r^2\, \psi (r) \,) + \xi _{22}(r)\,]+(a\,r^2+f^n)[\,a^2 \,r^4 \, (\,B + A\, r^2\, \psi (r)\,) + 2 \, a\, r^2\, f^n\, \xi _{21}(r)+f^{2\, n}~ \xi _{23}(r)\,]}{8\,\pi \,\,\,\left[ A\,r^2\,\psi (r)+B\right] ~\,[ a\,r^2+f^n ]^3}, \nonumber \\ \end{aligned}$$
(23)

where the coefficients used in above expressions are as follows:

$$\begin{aligned} \psi (r)= & {} \exp {\left[ \,\frac{a\,\left( \sqrt{\alpha \,(k+1)}-b\,r^2\right) ^{n-1}}{b\,(n-1)}\,\right] },\\ f= & {} (\sqrt{\alpha \,(k+1)}-b\,r^2\,), \\ \xi _{21}(r)= & {} B \, (1 + \alpha + \alpha \, k) - A\, \psi (r) \, (-1 + \alpha + \alpha \, k)\, r^2,\\ \xi _{22}(r)= & {} a^2\, r^2 \, f^{n}\, (B + 5 \, A\, r^2\,)-4 \, a\, f^{2\, n-1}\, [B \, (f + n\, b\, r^2) \\&+\, A\, r^2\, \psi (r) (-f + n\, b\, r^2)],\\ \xi _{23}(r)= & {} B\, (-1 + \alpha + \alpha \, k) + A\, \psi (r) \, (-1 + 5 \, \alpha (1 + k)) r^2\,. \\ \end{aligned}$$

Moreover, we have presented all possible solutions of Einstein field equations for a static spherically symmetric locally anisotropic fluids for conformally symmetric matter distribution in terms of two generating functions by using of solution generating technique of Herrera et al. [42] in Appendix-I.

4 Matching conditions

To construct the anisotropic models for conformal symmetry compact star, it is necessary that at the boundary of the star \(r = r_s\) the conformally symmetric interior solution should match smoothly to the exterior Schwarzschild solution

$$\begin{aligned} ds^2= & {} \left( 1-\frac{2\,m_s}{r_s} \right) dt^2 - \left( 1-\frac{2\,m_s}{r_s} \right) ^{-1} dr^2\nonumber \\&-\, r^2\,(d\theta ^2+ \sin ^2\theta \,d\varphi ^2), \end{aligned}$$
(24)

where \(m_s = m(r_s)\) defines the total mass of star. This matching conditions provides the line element at the surface as well as total mass \(m_s\) of the star of radius \(r_s\),

$$\begin{aligned} e^{\nu (r_s)}=e^{-\lambda (r_s)}=1-\frac{2\,m_s}{r_s}. \end{aligned}$$
(25)

The expression for total mass \(m_s\) for the star is determined by

$$\begin{aligned}&m_s=\frac{r_s}{2}\nonumber \\&\qquad \times \left( \frac{\left[ \left( \sqrt{\alpha (1 + k)} - b\,r_s^2\right) ^{n}+ a\,r_s^2\,\right] ^2{-}\alpha (1 + k)\,\left( \sqrt{\alpha (1 + k)} - b\,r_s^2\right) ^{2n}}{\left[ \left( \sqrt{\alpha (1 + k)} - b\,r_s^2\right) ^{n}+ a\,r_s^2\right] ^2}\right) . \nonumber \\ \end{aligned}$$
(26)

It is also necessary that the radial pressure should vanish at the surface, \(p_{rs}=0\) at \(r=r_s\). However the tangential pressure and energy density need not to be zero at the surface. This condition is also known as second fundamental form which requires the continuity of \(\frac{\partial \,g_{tt}}{\partial \,t}\) across the boundary \(r=r_s\). Using this fundamental forms together with Eq. (26) the value of arbitrary constants A, B and parameter b in terms of total mass \(m_s\) and radius \(r_s\) are

$$\begin{aligned} A= & {} \exp \left( {\frac{a\,(\xi _m(r_s))^{\frac{n-1}{n}}}{2\,b\,(1-n)}}\right) \nonumber \\&\times \left( \frac{\sqrt{1-2m_s/r_s}\,\left[ a\,(2\,m_s - r_s)\,(\xi _m(r_s))^{1/n}+b\,m_s\, n\,\xi _m(r_s)\right] }{2\,r_s^2\,(2m_s-r_s)\,\left[ a\,(\xi _m(r_s))^{1/n}-b\,n\,\xi _m(r_s)\right] }\right) \end{aligned}$$
(27)
$$\begin{aligned} B= & {} \exp \left( {\frac{a\,(\xi _m(r_s))^{\frac{n-1}{n}}}{2b(n-1)}}\right) \nonumber \\&\times \left( \frac{\sqrt{1-2m_s/r_s}\,\left[ a\,(2\, m_s - r_s)\,(\xi _m(r_s))^{1/n}-b\,n\,(5\,m_s - 2\,r_s)\,\xi _m(r_s)\right] }{2\,(2m_s-r_s)\,\left[ a\,(\xi _m(r_s))^{1/n}-b\,n\,\xi _m(r_s)\right] }\right) \end{aligned}$$
(28)
$$\begin{aligned} b= & {} \frac{\sqrt{\alpha (k+1)}\,\left[ \sqrt{\alpha (k+1)}-\sqrt{1-2\,m_s/r_s}\right] ^{1/n}-(a\,r_s^2)^{1/n}\,(1-2\,m_s/r_s)^{1/2n}}{r_s^2\,\left[ \sqrt{\alpha (k+1)}-\sqrt{1-2\,m_s/r_s}\right] ^{1/n}}.\nonumber \\ \end{aligned}$$
(29)

where the expression of coefficient \(\xi _m({r_s})\) is given as,

$$\begin{aligned} \xi _m(r_s)=(a\,r_s^2\sqrt{1 - 2\,m_s/r_s} )/(\sqrt{\alpha \,(1 + k)} - \sqrt{1-2\, m_s/r_s}) \end{aligned}$$

5 Physical conditions for anisotropic conformal models

Any realistic stellar model includes the following set of physical conditions:

A1. The gravitational metric potentials must be positive, finite and free from singularity inside the star. At the centre, it should satisfy    \(e^{\lambda (0)}=1\) and \(e^{\nu (0)}=positive~ constant\). On the other hand, these gravitational potentials \(e^{\nu }\) and \(e^{\lambda }\) provides the mass function m(r) and redshift Z of the self-gravitating star respectively. The relation between the potentials, mass and redshift function of the star can be expressed as

$$\begin{aligned} e^{-\lambda (r)} = 1-\frac{2\,m(r)}{r} ~~~~~~ \text {and}~~~~~~~ Z(r)= e^{-\nu (r)}-1. \end{aligned}$$
(30)

A2. The pressures (radial and tangential) and energy density should be nonnegative throughout within the star. Also, they should have finite values at the centre say \(p_r(0)=p_{r0}\),   \(p_t(0)=p_{t0}\) and \(\rho (0)=\rho _0\). At the centre the radial pressure is equal to tangential pressure i.e. \(p_{r0}=p_{t0}\). Moreover, the pressures and density should attain the maximum value at the centre and decrease monotonically towards the boundary of the star so that they should satisfy the conditions \(p^{\prime }_r(0)=p^{\prime }_t(0)=\rho ^{\prime }(0)=0\) and the inequalities \(p^{\prime }_r\le 0\),   \(p^{\prime }_t\le 0\),   \(\rho ^{\prime }\le 0\) for \(0 \le r \le r_s\), where \(r_s\) is the boundary of the star. The radial pressure (\(p_r\)) must have lesser value than the tangential pressure (\(p_t\)) throughout the star except at the centre.

A3. Causality condition: It is well known that the radial and tangential sound velocity should not be more than the light velocity in any medium. The radial and tangential velocities of sound are denoted as \(v^2_r=\frac{dp_r}{d\rho }\) and \(v^2_t=\frac{dp_t}{d\rho }\). Therefore both velocities should satisfy the inequality \(0<\frac{dp_r}{d\rho } \le 1\) and \(0<\frac{dp_t}{d\rho } \le 1\) everywhere inside the star.

A4. Energy conditions: The anisotropic conformal solution should satisfy the following energy conditions namely dominant energy condition (DEC)   \(\rho \ge p_r\) and \(\rho \ge p_t\). From (A2) it is obvious that the null energy condition (NEC) should be satisfied as well. furthermore the solution must hold for the strong energy condition (SEC)   \(\rho + p_r+2\,p_t \ge 0\) and trace energy condition (TEC) or strong dominant energy condition   \(\rho \ge p_r+2\,p_t\) (it is not necessary) at the interior of the star.

A5. The interior redshift of the star: The redshift of the model should decrease with increase of its radial coordinate r. The surface redshift function is defined as

$$\begin{aligned} Z_s =\left( 1-\frac{2\,m_s}{r_s}\right) ^{-1/2} -1=\left( 1-u_s\right) ^{-1/2} -1 . \end{aligned}$$
(31)

The surface redshift \(Z_s\) and mass-radius ratio \(m_s/r_s\) (which is also known as the compactness (\(u_s\))) satisfy universal upper bounds; therefore the surface redshift cannot be arbitrarily large. For isotropic fluid spheres, the surface redshift and compactness should less than 2 and 4 / 9 respectively [30]. For anisotropic case, the upper bounds of \(Z_s\) and \(u_s\) are 5.211 and 0.587 respectively for the dominant energy condition within the star. However, if the solution holds the trace energy condition then the bounds are 3.842 and 0.5785 [31].

A6. The Harrison–Zeldovich–Novikov stability criterion: The Harrison–Zeldovich–Novikov criterion for the stability of the self-gravitating compact star states that the mass of the star increases with the central density (\(\rho _0\)) which implies that \(dM_{\rho _0}/d \rho _0 > 0\) for the stable region where \(M_{\rho _0}\) is the mass function in terms of the central density.

A7. The stability criterion via. adiabatic index \(\Gamma \) : This adiabatic index \(\Gamma \) should be larger than 4 / 3 for any realistic stable model. For isotropic stars, Knutsen [32] has shown that if the pressure-density ratio is monotonically decreasing towards the boundary then adiabatic index \(\Gamma \) has value more than unity which implies that the temperature is decreasing away from centre. Later Herrera and his collaborators have given a criterion for analyzing the stability of the anisotropic fluid models which is given as [24, 33]

$$\begin{aligned} \Gamma > \frac{4}{3}+\dfrac{4}{3}\left[ \frac{4\pi ~\overline{\rho }_0 ~\overline{p}_{r0}~r^2+(\overline{p}_{t0}-\overline{p}_{r0})}{r\,|\overline{p}^\prime _{r0}|}\right] , \end{aligned}$$
(32)

where, \(\overline{p}_{t0}\), \(\overline{p}_{r0}\), and \(\overline{\rho }_0\) are the initial tangential pressure, radial pressure and energy density respectively in static equilibrium stage. This adiabatic index is the ratio of two particular heat which can be defined as

$$\begin{aligned} \Gamma = \left( \frac{p_r+\rho }{p_r}\right) \,\frac{dp_r}{d\rho }. \end{aligned}$$
(33)
Fig. 1
figure 1

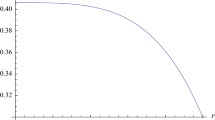
Variation of the gravitational potentials \(e^{\lambda (r)}\) (left) and \(e^{\nu (r)}\) (right) with respect to the radial coordinate (r / R). For purpose of plotting this figure , the numerical values of the constants for different parameters n are mentioned in Table 1

Full size image

A8. Stability against cracking: The concept of cracking was introduced by Herrera [24] which shows that the cracking appears in the self-gravitating star if the radial force is directed inward inside star and reverses its signature after some value of its radial coordinate or if the force is directed outward within the star and opposite its sign beyond some specific value of radial coordinate within the self-gravitating star. Later on Aberu et al. [34] again investigated this cracking concept and proposed a simpler restriction for avoiding this cracking situation to occur within the self-gravitating compact objects. This requirement is known as the stability region which is

$$\begin{aligned} 0 \le |v^2_t - v^2_r| \le 1. \end{aligned}$$
(34)

A9. Tolman–Oppenheimer–Volkoff (TOV) equation: Tolman–Oppenheimer–Volkoff (TOV) equation is the combination of different kind of forces namely hydrostatic force (\(F_h\)), gravitational force (\(F_g\)), anisotropic force (\(F_a\)) and electric force (\(F_e\)) which provides the equilibrium condition of the solution. The TOV equation was determined first for isotropic solution [13] and later on it was generalized by Bowers and Liang [35] for the anisotropic case. Here we are interested in only anisotropic version of TOV equation i.e. electric force component (\(F_e\)) is zero. Now using Eqs. (3), (4) and (30) we find that,

$$\begin{aligned}&\nu ^{\prime }=\frac{8\,\pi \,p_r+2m/r^2}{1-2m/r}, \end{aligned}$$
(35)
$$\begin{aligned}&\frac{\nu ^{\prime }}{2}\,(\rho + p_r) = -p^{\prime }_r+\frac{2 (p_t - p_r)}{r}. \end{aligned}$$
(36)

Combining Eqs. (35) and (36) together we get

$$\begin{aligned} \frac{(\rho + p_r)\,(8\,\pi \,p_r+2m/r^2)}{2\,(1-2m/r)}=-p^{\prime }_r+\frac{2\,(p_t - p_r)}{r}. \end{aligned}$$
(37)

The above Eq. (37) is the well known Tolman–Oppenheimer–Volkoff (TOV) equation for anisotropic matter distribution. The gravitational force (\(F_g\)) on the left is balanced by the joint action of the hydrostatic (\(F_h\)) and the anisotropic force (\(F_a\)) on the right.

6 physical analysis of the spherical conformal model

The physically realistic model should satisfy the conditions (A1)–(A9) which arise in Sect. 5. These conditions depend upon the choice of parameters k and \(\alpha \). We have to choose the values of these parameters so that the conformal symmetric anisotropic solution is well behaved and satisfies the conditions (A1)–(A9) everywhere within the star . Therefore we have chosen following set of values of the parameters: (i). \(k=0\) and \(\alpha =1\) (Conformally flat),    (ii). \(k=-2\)   and   \(\alpha =-1\) (Nonconformally flat). Then the values the physical parameters for conformally and nonconformally flat solution at the centre (\(r = 0\)) are given as:

B1. From (18) the potential \(e^{\lambda (r)}{=}\left[ 1+a\,r^2/(1{-}b\,r^2)^n \right] ^2\). Since the parameters a and b are positive then the factor \((1-b\,r^2)^n\) decreases with increase of r which implies that \(e^{\lambda (r)}\) is monotonically increasing away from centre and \(e^{(\lambda (0)}=1\) (Fig. 1). However from (19), the metric potential \(e^{\nu (0)}=B^2\,e^{\frac{a}{(b-n\,b)}}\). For a regular model the potential \(e^{\nu (0)}\) should be finite and positive which gives the condition that the constant B should be positive. Figure 1 shows that the potential \(e^{\nu (r)}\) is increasing monotonically away from the centre.

Fig. 2
figure 2

Variation of the radial pressure \(p_r\) (top left), tangential pressure \(p_t\) (top middle), energy density \(\rho \) (top right), anisotropy \(\Delta \) (bottom left), radial pressure-density ratio, \(\omega _r=p_r/\rho \) (bottom middle), and tangential pressure-density ratio \(\omega _r=p_r/\rho \) (bottom right) with respect to the radial coordinate (r / R). For purpose of plotting this figure , the numerical values of the constants for different parameters n are mentioned in Table 1

Full size image
Fig. 3
figure 3

Variation of the radial velocity \(v^2_r\) (left) and tangential velocity \(v^2_t\) (right) with respect to the radial coordinate (r / R). For purpose of plotting this figure , the numerical values of the constants for different parameters n are mentioned in Table 1

Full size image
Fig. 4
figure 4

Variation of the energy conditions with respect to the radial coordinate (r / R) for different values of n. For purpose of plotting this figure , the numerical values of the constants for different parameters n are mentioned in Table 1

Full size image
Fig. 5
figure 5

Variation of the compactification factor \(m_s/r_s\) (left) and redshift z (right) with respect to the radial coordinate (r / R). For purpose of plotting this figure , the numerical values of the constants for different parameters n are mentioned in Table 1

Full size image
Fig. 6
figure 6

Variation of the mass \(\hbox {M}{\odot }\) with respect to the central density (\(\rho _0\)) (left) and Variation of the adiabatic index (\(\Gamma \)) (right) with respect to the radial coordinate (r / R). For purpose of plotting this figure , the numerical values of the constants for different parameters n are mentioned in Table 1

Full size image

B2. Equation (20) gives \(\rho _{0}=\frac{3\,a}{4\,\pi }\). Since a is positive therefore the density profile is positive at the centre. Then (21) and (22) show that \(p_{r0}=p_{t0}=\frac{[\,A\,e^{a/{(n\,b - b)}}-a\,B\,]}{2\,\pi \,B}\). Then the positivity of pressures at centre (\(r=0\)) provides

$$\begin{aligned} \frac{A}{B} > \frac{a}{e^{a/(n\,b-b)}} \end{aligned}$$
(38)

From (38) the ratio A / B is positive and from (B1) the constant B is positive therefore the constant A will be also positive. The fluid model should also satisfy the Zeldovich condition at centre of the star which implies that \(\frac{p_{r0}}{\rho _0}\) and \(\frac{p_{t0}}{\rho _0}\) should not be more than unity at \(r=0\). This gives the following inequality

$$\begin{aligned} \frac{A}{B}~\le ~\frac{5\,a}{2\,e^{a/(n\,b-b)}}. \end{aligned}$$
(39)

From inequalities (38) and (39) we get

$$\begin{aligned} \frac{a}{e^{a/(b\,n-b)}}\,<\,\frac{A}{B}\,\le \, \frac{5\,a}{2\,e^{a/(n\,b-b)}}. \end{aligned}$$
(40)

Moreover, we have shown the trend of the density profile and pressure profiles within the stellar compact objects in Fig. 2. It can be observed that density and pressures are positive, finite and attains a maximum value at the centre and decreases outward. From this figure we also note that the ratio of radial pressure and density is decreasing while pressure anisotropy (\(\Delta \)) is increasing away from centre which shows that the temperature is decreasing towards the surface and force due to anisotropy is directed outward.

B3. Due to the causality condition the radial velocity \(v^2_{r0}\) and tangential velocity \(v^2_{t0}\) at the centre should satisfy

$$\begin{aligned}&0< v^2_{r0} \le 1~~ \Longrightarrow ~~ 0<\frac{1}{5\,a\,(3\,a-2\,b\,n)}\nonumber \\&\quad \left[ -7\,a^2+4\,a^2\,\frac{A^2\,e^{2a/(n\,b-b)}}{B^2} +4\,a\,b\,n \right] \le 1 , \end{aligned}$$
(41)
$$\begin{aligned}&0< v^2_{t0} \le 1~~ \Longrightarrow ~~ 0<\frac{1}{5\,a\,(3\,a-2\,b\,n)}\nonumber \\&\quad \left[ -13\,a^2+4\,a^2\,\frac{A^2\,e^{2a/(n\,b-b)}}{B^2} +8\,a\,b\,n \right] \le 1 . \end{aligned}$$
(42)

From (41) and (42) we obtain

$$\begin{aligned}&\left( \frac{A}{B}+\frac{\sqrt{7\,a^2-4\,a\,b\,n}}{2~e^{a/(b\,n-b)}\,}\right) \left( \frac{A}{B}-\frac{\sqrt{7\,a^2-4\,a\,b\,n}}{2~e^{a/(b\,n-b)}\,}\right) > 0 ~~~ \text {and}\nonumber \\&\quad ~~\left( \frac{A}{B}+\frac{\sqrt{11\,a^2-7\,a\,b\,n}}{\sqrt{2}~e^{a/(b\,n-b)}\,}\right) \nonumber \\&\quad \left( \frac{A}{B}-\frac{\sqrt{11\,a^2-7\,a\,b\,n}}{\sqrt{2}~e^{a/(b\,n-b)}\,}\right) \le 0, \end{aligned}$$
(43)
$$\begin{aligned}&\left( \frac{A}{B}+\frac{\sqrt{13\,a^2-8\,a\,b\,n}}{2~e^{a/(b\,n-b)}\,}\right) \nonumber \\&\quad \left( \frac{A}{B}-\frac{\sqrt{13\,a^2-8\,a\,b\,n}}{2~e^{a/(b\,n-b)}\,} \right) > 0 ~~~ \text {and}\nonumber \\&\quad ~~\left( \frac{A}{B}+\frac{\sqrt{14\,a^2-9\,a\,b\,n}}{\sqrt{2}~e^{a/(b\,n-b)}\,}\right) \nonumber \\&\quad \left( \frac{A}{B}-\frac{\sqrt{14\,a^2-9\,a\,b\,n}}{\sqrt{2}~e^{a/(b\,n-b)}\,} \right) \le 0. \end{aligned}$$
(44)

From the inequalities (40), (43) and (44) we find that

$$\begin{aligned}&\frac{A}{B} > \frac{\sqrt{7\,a^2-4\,a\,b\,n}}{2~e^{a/(b\,n-b)}\,} ~~\text {and}~~ \frac{\sqrt{13\,a^2-8\,a\,b\,n}}{2~e^{a/(b\,n-b)}} ~~~~ \text {and}\nonumber \\&\frac{A}{B} \le \frac{\sqrt{11\,a^2-7\,a\,b\,n}}{\sqrt{2}~e^{a/(b\,n-b)}}~~\text {and}~~\frac{\sqrt{14\,a^2-9\,a\,b\,n}}{\sqrt{2}~e^{a/(b\,n-b)}\,} \end{aligned}$$
(45)

and

$$\begin{aligned}&\frac{a}{e^{a/(b\,n-b)}\,}< \frac{\sqrt{7\,a^2-4\,a\,b\,n}}{2~e^{a/(b\,n-b)}\,}< \frac{\sqrt{13\,a^2-8\,a\,b\,n}}{2~e^{a/(b\,n-b)}} ~~~~ \text {and}~~~\nonumber \\&\frac{\sqrt{11\,a^2-7\,a\,b\,n}}{\sqrt{2}~e^{a/(b\,n-b)}}< \frac{\sqrt{14\,a^2-9\,a\,b\,n}}{\sqrt{2}~e^{a/(b\,n-b)}\,} <\,\frac{5\,a}{2\,e^{a/(n\,b-b)}}. \nonumber \\ \end{aligned}$$
(46)

Therefore the inequalities (45) and (46) restrict the ratio A / B and parameter b in the following range

$$\begin{aligned}&\frac{\sqrt{13\,a^2-8\,a\,b\,n}}{2~e^{a/(b\,n-b)}}\,<\,\frac{A}{B}\nonumber \\&\quad \le \,\frac{\sqrt{11\,a^2-7\,a\,b\,n}}{\sqrt{2}~e^{a/(b\,n-b)}}~~~~~\text {and}~~~b< \frac{3\,a}{4\,n}\, . \end{aligned}$$
(47)

We have obtained the numerical computation of the all inequalities (40), (43) and (44) which are shown in Fig. 9 (see in appendix II). Due to the complexity of the expression of velocities we plot the radial velocity (\(v^2_r\)) and tangential velocity \((v^2_t)\) in Fig. 3 and observe that \(v^2_r\) and \(v^2_t\) are less than unity throughout inside the model. It can be also seen that radial velocity attains its maximum value at an interior point in the compact model while the tangential velocity is increasing outward and reaches its maximum at the boundary of the star.

Fig. 7
figure 7

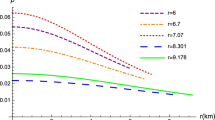
Variation of the velocity difference \((|v^2_t-v^2_r|)\) with respect to the radial coordinate (r / R). For purpose of plotting this figure , the numerical values of the constants for different parameters n are mentioned in Table 1

Full size image
Fig. 8
figure 8

Variation of the forces (\(F_i\)) with respect to the radial coordinate (r / R) for different values of n. For purpose of plotting this figure , the numerical values of the constants for different parameters n are mentioned in Table 1

Full size image

B4. Since the anisotropic fluid model satisfies the dominant and null energy conditions at \(r=0\) (as B2 holds) which implies that the strong energy condition is also satisfied. Now we calculate the trace energy at centre (\(r=0\)),

$$\begin{aligned}&\rho _{0}-p_{r0}-2\,p_{t0}= \frac{1}{4\,\pi }\,\left[ 9\,a\,-\frac{6\,A\,e^{a/{(n\,b - b)}}}{B} \right] \nonumber \\&\quad \ge \, \left[ 9\,a\,-\frac{6\,\sqrt{11\,a^2-7\,a\,b\,n}}{\sqrt{2}}\right] \,\text {is negative if }b \backsimeq \frac{3\,a}{4\,n}. \nonumber \\ \end{aligned}$$
(48)

The inequality (48) shows that the solution does not satisfy the trace energy condition (TEC) within the star . The variation of energy conditions is shown in Fig. 4 for each different n. From Fig. 4, we observe that \(\rho < (p_r +2p_t)\) for each value of n. This implies that the trace energy condition (TEC) is not satisfied inside the star.

Table 1 Physical parameters for different values of n for the star with mass = 2.01 (\(M_{\theta }\)) and predicted radius (R) = 7 km
Full size table

B5. Equation (31) together with (19) show that the redshift Z is decreasing monotonically throughout (in Fig. 5). However the surface redshift of the star can be determined as

$$\begin{aligned} Z_s= & {} \left( 1-\frac{2m_s}{r_s}\right) ^{-1/2}-1= e^{\lambda (r_s)/2}-1\nonumber \\= & {} \frac{a\,r^2_s}{(1-b\,r^2_s)^n}. \end{aligned}$$
(49)

From (49) we observe that the surface redshift function is zero at the centre and increases with radius \(r_s\). The value of \(Z_s\) and \(u_s=m_s/r_s\) are 1.5571 and 0.4235 respectively which can be found from Fig. 5. These values satisfy the upper bounds limits of a physical stellar model.

B6. In order to discuss the Harrison–Zeldovich–Novikov stability criterion we find the values of \(M_{\rho _0}\) and \(dM_{\rho _0}/d\rho _0\):

$$\begin{aligned}&M_{\rho _0}=\frac{8\,\pi \,\rho _0\,r^3_s\,[\,4\,\pi \,\rho _0\,r^2_s + 3\,(1 -b\, r^2_s)^n\,]}{[\,8\,\pi \,\rho _0\,r^2 + 3\,(1 - b\,r^2_s)^n\,]^2}~~~~ \text {and}\nonumber \\&\frac{dM_{\rho _0}}{d\rho _0}=\frac{72\,\pi \,r^3_s\,(1 - b\,r^2_s)^{2\,n}}{[\,8\,\pi \,\rho _0\,r^2 + 3\,(1 - b\,r^2_s)^n\,]^3} \end{aligned}$$
(50)

From (25) we observe that \(M_{\rho _0}\) and \(dM_{\rho _0}/d\rho _0\) are positive. From Fig. 6, we observe that the \(M_{\rho _0}\) is increasing with increase of its central density \((\rho _0)\) and after reaching its maximum value it becomes asymptotic. This indicates that the our model is stable.

B7. The behaviour of the adiabatic index \((\Gamma )\) is given by Fig. 6 which shows that it is greater than 4 / 3 throughout inside the star. On the other hand, the ratio of radial pressure and density is also decreasing outwards (see Fig. 2) which indicates that our model is stable and the temperature is decreasing away from the centre.

B8. From the Fig. 3 we observe that the causality condition should be satisfied within the star [24], i.e. the square of the radial  \(\left( v^2_{r}\right) \) and tangential  \(\left( v^2_{t}\right) \) sound velocity are lying within the interval [0, 1]. We also observe from Fig. 7 that the inequality \(0 \le |v^2_t - v^2_r| \le 1\) is satisfied throughout the stellar model which implies that our model is stable.

B9. Figure 8 shows the behaviour of the TOV equation which describes the equilibrium condition of the solution. From Fig. 8, we observe that the gravitational force is counter-balanced by the joint action of the hydrostatic force and anisotropic force. It is also noted that the hydrostatic force is more than the anisotropic force when \(r/r_s \in (0, 7.6)\) and has less value when \(r/r_s\in [7.6, 1)\).

For Table 1, we used the numerical values of the gravitational constant \(G=6.673\times 10^{-8} cm^3/gs^2\), velocity of light \(c=2.997\times 10^{10} cm/s\), solar mass \(M_{\theta }=1.475\) km while we have chosen the radius of the star at boundary \(r_r=R\) in the graphical representation. For plotting of the figures, the numerical values of physical parameters have been obtained for various values of n for the compact star which are presented in Table 1. We Note that the value of surface density for the compact star is approx. 6.63 times higher than nuclear saturation density (\(2.3 \times 10^{14}\)).

7 Conclusion

We have pursued the solution of the Einstein field equations with anisotropies by imposing a conformal Killing vector. A parallel treatment and associated methodology have been developed in anisotropic gravity and supergravity models using external fields. This has been pursued by Mateos and Trancanelli [36] for strong coupled anisotropic plasmas, by Jain et al. [37] for anisotropic fluids from dilaton driven holography, and Giataganas et al. [38] for Einstein-axion-dilaton systems. These results provide a path to obtain such gravity solutions which have been useful in explaining properties of strongly coupled plasmas in the papers of Giataganas [39] and Chernicoff et al. [40]. We similarly expect that this alternate approach may also lead to useful insights in studying stellar systems that have been analyzed in this paper with conformal motions.

Here we have presented a new class of exact solutions to the Einstein system of equations for an anisotropic fluid distribution in the presence of a conformal Killing vector. This new class of solutions is physically acceptable in an astrophysical scenario and can be used to model relativistic compact objects. We have achieved this by producing analytic expressions for the matter variables and the metric functions. A detailed graphical analysis of the matter variables was performed and we checked the criteria for physical acceptability. In particular, we demonstrated that the energy conditions were satisfied, causality is obeyed, and the star is stable in terms of cracking, the Harrison–Zeldovich–Novikov stability criterion, and the adiabatic index inequality. In this paper, we have highlighted the role of conformal symmetries in generating exact solutions of the Einstein field equations. We have shown the exact solution may be used to model a star with anisotropic distributions. In this sense, our solution extends the earlier treatments of Mafa Takisa et al. [12] and Kileba Matondo et al. [13, 14]. The advantage of this investigation is that we obtain a model which satisfies all physical criteria: regularity, casuality, stability and energy conditions for a realistic matter distribution. In advantage, we can characterise our model geometrically with a conformal Killing vector. This paper is part of our endeavour to extend the geometrical characterisation of cosmological solutions to astrophysical solutions for compact objects.

To present the numerical analysis of the achieved solution we consider the mass of the compact stellar object is \(2.01~M_{\odot }\) and the chosen parametric values of n are given as \(n=4, 12, 20, 500\) and 1000. In the left and right panel of Fig. 1 we have shown variation of metric potentials viz., \(e^\lambda \) and \(e^\nu \), respectively. The variation of \(p_t\), \(p_r\) and \(\rho \) are shown in the left, middle and right top panel of Fig. 2 which features that they all have finite value at the centre and they decrease monotonically to reach their minimum values at the surface. Further, we present the change of anisotropy (\(\Delta \)), radial (\(\omega _r\)) and tangential (\(\omega _t\)) equation of state parameter with respect to the fractional radial coordinate r / R in the left, middle and right bottom panel of Fig. 2. Based on the Figs. 1 and 2 it is worthwhile to mention that our system is free from any sort of singularity whether geometrical or physical. Interestingly, we find that the anisotropy in the present system is minimum, i.e., zero at the centre and increases throughout the interior of the stellar system to reach it’s maximum value at the surface as predicted by Deb et al. [41]. The profile of \(v^2_r\) and \(v^2_t\) are shown in the left and right panel of Fig. 3, respectively and the profile of the difference of the square of the sound velocities is shown in Fig. 7 which confirm the stability of the present model as it is consistent with both the causality condition and Herrera cracking condition by following the inequalities \(0<v^2_r, v^2_t<1\) and \(0<\mid v^2_t - v^2_r \mid < 1 \). Figure 4 features that as all the energy condition is valid for this model and confirms the physical validity of the achieved solution. In Fig. 5 we present the profile for compactification factor and redshift in the left and right panel, respectively. The variation of mass with respect to central density has been shown in the left panel of Fig. 6 which features that for our system \(dM/d{\rho _c}>1\) and indicates stability of the system by following the Harrison–Zeldovich–Novikov stability criterion. In the right panel of Fig. 6 we have shown the variation of the adiabatic index \(\Gamma \) and find that as in the present case \(\Gamma >4/3\) our system is dynamically stable against the infinitesimal radial pulsation. Finally, The Fig. 8 shows that the present system is stable under the hydrostatic equilibrium which represents the variation of the different forces viz., anisotropic (\(F_a\)), hydrostatic (\(F_h\)) and gravitational (\(F_g\)) with respect to the radial coordinate r / R. We find that the present system is in hydrostatic equilibrium as resultant of the forces is zero, ie., \(F_a+F_h+F_g=0\). In Table 1 we have predicted values of the different physical parameters and constants due to the chosen parametric values of n and assumed value of the gravitational mass of the stellar system. In a nutshell, in this article by imposing a conformal Killing vector we present a singularity free and physically acceptable model which is suitable to study anisotropic and spherically symmetric compact stars.

We believe that this geometrical approach may provide deeper insights into the spacetime geometry, and may, in fact, lead to new exact solutions which are not easily obtainable via other methods. In the future, we intend to consider other spacetime symmetries such as curvature collineations in the astrophysical context.