1 Introduction

Einstein–Dilaton gravity has attracted considerable attention since it arises in low energy string theory. It is well known that the presence of the dilaton field has important consequences on constructing exact black hole solutions, the asymptotic behavior and the causal structure of the spacetime, and the thermodynamic properties of black holes [1,2,3,4]. For example, the dilaton black holes are always neither asymptotically flat nor (A)dS (see [5,6,7,8,9] and references therein), due to its non-vanishing asymptotic behavior at infinity \(r\rightarrow \infty \). The discussion were also generalized into the gravity with multi-dilaton fields [10,11,12,13] and the coupling of dilaton field with other gauge fields [2, 5,6,7, 9, 12, 13], which both have a profound effects on the resulting solutions and other physical properties. Thus much interest has been focused on the study of the dilaton black holes in recent years.

On the other side, gravity in three dimensional spacetime has been a fascinating area of theoretical investigations, even it is locally trivial in the absence of matter source because of the lack of propagating degrees of freedom. The main reasons include the discovery of the famous BTZ black hole solutions [14] and the study of AdS/CFT duality [15, 17, 18], which always shed some light on the understanding of more complicated cases of four and higher dimensional gravity. Therefore it is worthwhile to see how the presence of the dilaton field would modify the spacetime in three dimensions. Actually, a lots of literatures focus on this subject, including the study on \((2+1)\) dimensional dilaton black hole solutions [19,20,21,22,23,24,25,26], black hole thermodynamics [27,28,29,30] and other interesting physical properties (see the books [31, 32] and references therein).

Motivated by the above, we consider three dimensional static charged dilaton black hole solutions and their formation in this paper. For the study of the formation of black holes due to gravitational collapse [33,34,35], it is the fundamental and important topic in general relativity, which always sheds light on the understanding of spacetime singularities, cosmic censorship, critical phenomenon and gravitational waves [36,37,38,39]. Hence one always pays much attention for this subject. Especially for the formation of scalar black holes due to the gravitational collapse of scalar field, there are only several literatures, including the time-dependent solutions describing the gravitational collapse to the static (un-)charged/accelerating scalar black holes in four [40,41,42] and higher dimensions [43,44,45] and a three dimensional static scalar black hole [46, 47].

In this paper, we present the static charged dilaton solutions and black hole formation in three dimensions. Firstly we will revisit the famous static charged black hole solution obtained by Chan and Mann [19] in three dimensional Einstein–Maxwell–Dilaton gravity. This solution with \(b=4a\) will lead to the three dimensional string solution. Then we give another class of charged dilaton black hole solution with \(b\ne 4a\). We discuss their geometrical properties, the horizon structure and the causal structure. It is shown that there exist (non-)extremal black holes and black holes with negative mass for Chan–Mann solution, while there exist only black holes with a single event horizon for another dilaton solution. Besides, the (un)charged black holes of this two families should both have a negative cosmological constant, which is consistent with the No–Go theorem in three dimensions [48]. The time-dependent solution is also presented, which can characterize the three dimensional charged black hole formation in Einstein–Dilaton gravity. We also have studied the global properties and the gravitational collapse of a dilaton field in the context of the Cosmic Censorship Conjecture. Especially, there is no exact time-dependent solution describing the gravitational collapse to the Chan–Mann charged dilaton black hole, which is a submanifold of \(3+1\) dimensional Einstein spacetime based on the viewpoint of the Kaluza–Klein theory [49, 50], therefore no extra matter source can drive an evolution of the spacetime. As a consequence, we believe that these static/time-dependent black hole solutions are of some interest.

The paper is organized as follows. We introduce three dimensional Einstein–Maxwell–Dilaton gravity in next section. In Sect. 3, we revisit the Chan–Mann charged dilaton black hole and discuss its physical properties. In Sect. 4, we obtain another charged dilaton black hole, and study its geometrical properties, the horizon structure and the causal structure in detailed. In Sect. 5, we present the time-dependent charged dilaton solution and the properties. Finally, some concluding remarks are given in Sect. 6.

2 Three dimensional Einstein–Maxwell–Dilaton gravity

In this section, we introduce three dimensional Einstein–Maxwell–Dilaton gravity with the action [19]

$$\begin{aligned}&I=\int \mathrm {d} x^3\sqrt{-g}\left[ R-\frac{\gamma }{2}g^{\mu \nu }\nabla _{\mu }\phi \nabla _{\nu }\phi \right. \nonumber \\&\qquad \left. -e^{-4a\phi }F_{\mu \nu }F^{\mu \nu }-2e^{b\phi }\Lambda \right] , \end{aligned}$$
(1)

where \(\phi \) is the dilaton field, \(V(\phi )=e^{b\phi }\Lambda \) is the dilaton potential and \(\gamma ,a, b\) are constant. Though the spacetime does not behave as (A)dS spacetime as the presence of a non-trivial dilaton, we still refer \(V(0)=\Lambda \) as the cosmological constant. When setting \(\gamma =8, a=1, b=4\) and taking the conformal transformation \(g_{\mu \nu }^{S}=e^{4\phi }g_{\mu \nu }\), one can turn to the string theory with the action [51]

$$\begin{aligned}&I^{S}=\int \mathrm {d} x^3\sqrt{-g^{S}}e^{-2\phi }\bigg [R[g^{S}]+4g^E_{\mu \nu }\nabla ^{\mu }\phi \nabla ^{\nu }\phi \\&\qquad -F_{\mu \nu }F^{\mu \nu }-2\Lambda \bigg ]. \end{aligned}$$

The equations of motion for gravity, Maxwell field and dilaton field read as

$$\begin{aligned}&E_{\mu \nu }\equiv \,G_{\mu \nu }-T^{A}_{\mu \nu }-T^{\phi }_{\mu \nu }+e^{b\phi }\Lambda \,g_{\mu \nu }=0, \end{aligned}$$
(2)
$$\begin{aligned}&\partial _{\mu }\bigg (\sqrt{-g}e^{-4a\phi }F^{\mu \nu }\bigg )=0, \end{aligned}$$
(3)
$$\begin{aligned}&\frac{\gamma }{2}\nabla ^{\rho }\nabla _{\rho }\phi +2ae^{-4a\phi }F_{\mu \nu }F^{\mu \nu }-\partial _{\phi }V(\phi )=0, \end{aligned}$$
(4)

respectively. Here the energy momentum for Maxwell field and dilaton field are

$$\begin{aligned}&T^{A}_{\mu \nu }=e^{-4a\phi }\bigg (2F_{\mu \rho }F_{\nu }{}^{\rho }-\frac{1}{2}g_{\mu \nu }F_{\lambda \sigma }F^{\lambda \sigma }\bigg ),\\&T^{\phi }_{\mu \nu }=\frac{\gamma }{2}\bigg (\nabla _{\mu }\phi \nabla _{\nu }\phi -\frac{1}{2}g_{\mu \nu }\nabla ^{\rho }\phi \nabla _{\rho }\phi \bigg ). \end{aligned}$$

Follow [19], we introduce the Schwarzschild-like metric ansatz

$$\begin{aligned} \mathrm {d}s^{2}=-f(r)\mathrm {d}t^{2} +\frac{1}{f(r)}\mathrm {d}r^2 +\lambda ^2r^{N}\mathrm {d}\psi ^2, \end{aligned}$$

where N is arbitrary constant and \(\lambda \) is an integration constant with dimension \([L]^{\frac{2-N}{2}}\). In \(2+1\) dimensions, one can never have \(g_{tt}=-\frac{1}{g_{rr}}\) and \(g_{\psi \psi }=r^2\) simultaneously when one considers a non-trivial solution with dilaton. Actually, when choosing \(N=2\), one can only get the BTZ black hole solution [14] with vanishing \(\gamma , a, b\) in the action. As we consider the solutions with dilaton, the case with \(N=2\) will be out of our discussion.

The dilaton field in three dimensions is chosen as [19]

$$\begin{aligned} \phi (r)=k\ln \left( \frac{r}{\beta }\right) , \end{aligned}$$
(5)

where k and \(\beta \) are constants. We assume that the Maxwell field depends only on the radial coordinate r, i.e.

$$\begin{aligned} A_{\mu }\mathrm {d}x^{\mu }=qA(r)\mathrm {d}t. \end{aligned}$$
(6)

Then the Maxwell equation gives

$$\begin{aligned} A(r)=\,{\frac{2{r}^{4\,a\,k+1-\frac{N}{2}}}{\lambda \left( 8\,a\,k-N+2 \right) {\beta }^{4\,a\,k} }},\quad \left( 4\,a\,k+1-\frac{N}{2}\ne 0\right) , \end{aligned}$$
(7)

When \(4\,a\,k+1-\frac{N}{2}=0\), the above one is singular. Actually, for this case the Maxwell field must be changed into

$$\begin{aligned} A(r)=\,{\frac{{\beta }^{1-\frac{N}{2}}}{\lambda }}\ln (r),\quad \left( 4\,a\,k+1-\frac{N}{2}=0\right) . \end{aligned}$$
(8)

which is the usual form in three dimensions. Inserting the dilaton field and Maxwell field, one can find that the component of Einstein equations \(E^{t}{}_{r}=0\) leads to

$$\begin{aligned} 2\gamma \,k^2+N^2-2N=0, \end{aligned}$$
(9)

or equivalently \(\gamma =\frac{N(2-N)}{2\,k^2}\). In this paper, we will only consider the system with \(\gamma >0\), which means physically the kinetic energy of the dilaton is positive. From the above equation, we can find \(0<N<2\).

Then another component of Einstein equations \(E^{r}{}_{r}\) becomes

$$\begin{aligned}&{\frac{N \left( N-2 \right) }{8{r}^{2}}}f \left( r \right) +\, {\frac{N}{4r}}\left( \frac{d}{dr}f(r)\right) + \left( {\frac{r}{\beta }} \right) ^{bk}\Lambda \\&\quad +\left( {\frac{r}{\beta }} \right) ^{4\,a\,k}\frac{{q}^{2}}{{\lambda }^{2}{r}^{N}}=0, \end{aligned}$$

which gives

$$\begin{aligned} f(r)=\,&\frac{8{q}^{2}\,{r}^{-N+2}}{{\lambda }^{2}\left( N-8\,a\,k-2 \right) {N}} \left( {\frac{r}{\beta }} \right) ^{4\,a\,k}\nonumber \\&-\frac{8\,\Lambda {r}^{2}}{\left( N+2\,bk+2\right) {N}}\, \left( {\frac{r}{\beta }} \right) ^{bk} +B{r}^{1-\frac{\,N}{2}}. \end{aligned}$$
(10)

where B is integration constant related to the mass of black holes. The other non-vanishing components of Einstein equations can be simplified as

$$\begin{aligned}&\frac{\,{\lambda }^{2}\Lambda }{{\beta }^{bk}} \left( N-bk-2\right) \nonumber \\&\quad +\frac{{q}^{2}}{{\beta }^{4ak}} \left( N-4\,a\,k-2 \right) \,{r}^{\left( 4\,a-b \right) k-N}=0. \end{aligned}$$
(11)

From this equation, one can find two families of static charged dilaton black hole solutions:

  • Chan–Mann charged dilaton black hole [19], i.e. \(b=4a=\frac{}{}\frac{N-2}{k}\), one can find that the constant term and \({r}^{\left( 4\,a-b \right) k-N}\) term in Eq. (11) both vanish. This is the famous one parameter family of static charged dilaton black hole obtained by Chan and Mann in [19].

  • Another charged dilaton black hole, i.e. \(4a-b=\frac{N}{k}\), one can find \(\left( 4\,a-b \right) k-N=0\). Then only constant term exists in Eq. (11), which is vanishing and will fix all constants of this solution.

We will first revisit the Chan–Mann charged dilaton black hole in next section and present another charged dilaton black hole in Sect. 4. Their geometrical property and the horizon structure are also studied respectively.

3 Chan–Mann charged dilaton black hole

In this section, we firstly revisit the Chan–Mann charged dilaton black hole and then discuss its horizon structure. Note that the horizon structure of black hole with \(\frac{2}{3}<N<2\) was analyzed in detailed in [19]. Hence we will give a general discussion about the case \(0<N<2\).

3.1 The solution and quasilocal charges

Consider Eq. (11), one can easily find one family of its solutions

$$\begin{aligned} 4ak=bk=N-2, \end{aligned}$$
(12)

for which both the constant term and \({r}^{\left( 4\,a-b \right) k-N}\) term are vanishing. Then one can find that the following solutions for the Maxwell field, dilaton field and metric:

  • When \(N\ne 2\) and \(N\ne \frac{2}{3}\),

    $$\begin{aligned}&A_{\mu }\mathrm {d}x^{\mu }=\,{\frac{2q{r}^{\frac{N}{2}-1}{\beta }^{2-N}}{\lambda \left( N-2\right) }}\mathrm {d}t,\quad \,\phi (r)=k\ln \left( \frac{r}{\beta }\right) ,\nonumber \\&f(r)={-}\frac{8{\beta }^{2-N}}{N}\bigg (\frac{{q}^{2}}{{\lambda }^{2}\left( N-2\right) }+\frac{\,\Lambda {r}^{N}}{\left( 3N{-}2\right) }\bigg ){+}B{r}^{1{-}\frac{\,N}{2}}, \end{aligned}$$
    (13)

    where Eqs. (9) and (12) give the constants

    $$\begin{aligned} N\ne \frac{2}{3},\quad \, k=-\,{\frac{4a}{\gamma +8a^{2}}},\quad \, N=\,{\frac{2\gamma }{\gamma {+}8a^{2}}},\quad \, b=4a, \end{aligned}$$
    (14)

    and \(\beta \) is arbitrary, B and q are related to the mass and charge respectively. This is the famous one parameter family of static charged dilaton black hole solution in three dimensions, which is obtained by Chan and Mann in [19]. When \(N=1\), the above solution reduces to the \((2+1)\) dimensional MSW charged black hole [52, 53]. As mentioned previously, the system is related to the string theory by a conformal transformation and choosing parameters \(\gamma =8, b=4a=4\) which forces \(N=1\).

  • Note that the metric function of the above solution with \(N=\frac{2}{3}\) is singular. For this case, one can find the dilaton solution taking the following form

    $$\begin{aligned}&A_{\mu }\mathrm {d}x^{\mu }=-\,{\frac{3q{\beta }^{\frac{4}{3}}}{2\lambda {r}^{\frac{2}{3}}}}\mathrm {d}t,\quad \,\phi (r)=k\ln \left( \frac{r}{\beta }\right) ,\nonumber \\&f(r)=3{\beta }^{\frac{4}{3}}\bigg (\,{\frac{3{q}^{2}}{{\lambda }^{2}}}-2\Lambda {r}^{\frac{2}{3}}\,\ln \left( r \right) \bigg )+B{r}^{\frac{2}{3}}, \end{aligned}$$
    (15)

    where the constants become

    $$\begin{aligned} N=\frac{2}{3},\quad \, k=-\,{\frac{1}{3a}},\quad \, \gamma =4a^2,\quad \, b=4a. \end{aligned}$$
    (16)

On the other hand, one can find that this dilaton solution fails to fulfill the falloff conditions for asymptotically AdS spacetime [54]. Meanwhile, as the parameter k characterizes the strength of dilaton field, one may expect that the solutions with constant dilaton field (i.e. vanishing k) reduce to the BTZ black hole solution with \(\ln (r)\) Maxwell field and modified cosmological constants (by the dilaton potential). However, this does not work as there is no dilaton solution with \(\ln (r)\) Maxwell field which corresponds to \(a=b=\gamma =k=0, N=2\) and is actually the BTZ black hole. Hence this kind of black hole solutions does not belong to the family of BTZ black holes, which can be continuously connected to BTZ black hole. For the same reason, there exists no limit of the charged scalar black hole solutions (i.e. \(a=0\) which gives \(b=\gamma =0, N=2\) as well) for this family of black holes. For \(q=0\), the solution reduces to the uncharged scalar black hole in Einstein–Scalar gravity with the Liouville potential.

Taking the coordinate transformation \(\mathrm {d}t=\mathrm {d}u-\frac{\mathrm {d}r}{f(r)}\), we can obtain the solution in Eddington–Finekelstein-like coordinates, i.e.

$$\begin{aligned} \mathrm {d}s^{2}=-f(r)\mathrm {d}u^{2} +2\mathrm {d}u\mathrm {d}r +\lambda ^2r^{N}\mathrm {d}\psi ^2, \end{aligned}$$
(17)

which will be useful to construct its time-dependent solution. Then performing the coordinate transformation \(\lambda ^2r^{N}\rightarrow \,r^2\), one can turn to the system with the usual radial co-ordinate r. Then the dilaton solution behaves as

$$\begin{aligned}&\mathrm {d}s^{2}=-f(r)\mathrm {d}u^{2} +\frac{4r^{\frac{2}{N}-1}}{N\lambda ^{\frac{2}{N}}}\mathrm {d}u\mathrm {d}r +r^2\mathrm {d}\psi ^2 \end{aligned}$$
(18)

with the horizon function

$$\begin{aligned} f(r)&=\frac{8Q^2}{(2-N)N}-\frac{8\Lambda \,r^2}{(3N-2)N}\nonumber \\&\quad -\frac{2M}{N}r^{\frac{2}{N}-1},\quad N\ne \frac{2}{3}\ \mathrm{and}\ N\ne 2; \end{aligned}$$
(19)
$$\begin{aligned}&f(r)=9{Q}^{2}-18\Lambda \,\ln \left( r \right) {r}^{2}-3M{r}^{2},\qquad \qquad \quad \,N=\frac{2}{3}, \end{aligned}$$
(20)

where one has absorbed \(\lambda ^{1-\frac{2}{N}}\) into the constant B and chosen \(\beta ^{2-N}=\lambda ^2\). Here the mass and electric charge of this black hole are [19]

$$\begin{aligned} M=-\frac{NB}{2},\quad \, Q=q \end{aligned}$$
(21)

by using the quasilocal charges method [55,56,57]. Note the constant \(\lambda ^{\frac{2}{N}}\) was absorbed into M for convenience (i.e. M has dimension \([L]^{\frac{N-2}{N}}\)).

3.2 The horizon structure

We firstly consider the geometric quantities of this solution, for example, the the Ricci scalar R and other higher order curvature invariants (\(R_{\mu \nu }R^{\mu \nu }\) and \(R_{\mu \nu \rho \sigma }R^{\mu \nu \rho \sigma }\)). One can easily find an essential singularity at \(r=0\) if either \(M\ne 0\) or \(Q\ne 0\). In order to avoid the naked singularity, the solution must contain an event horizon \(r_{+}\) and the static region of spacetime (i.e. \(f(r)>0\)) must stay at \(r>r_{+}\).

When \(\frac{2}{3}<N<2\), the horizon structure was analyzed in detailed in [19]. Here we give a general discussion about the case \(0<N<2\). We first consider the case \(0<N<2,N\ne \frac{2}{3}\). Note we always focus on the black hole with positive mass, i.e. \(M>0\). There are three extra parameters in the solutions \(Q,\Lambda ,N\), which are closely related to the horizon structure. Hence the discussion of black hole solution could be divided into the following cases:

  • When \(Q=0\), i.e. the uncharged solutions: the horizon function reduces to \(f(r)=\frac{2Mr^2}{N}(r_{+}^{\frac{2}{N}-3}-r^{\frac{2}{N}-3})\), where the zero is \(r_{+}=(\frac{4\Lambda }{M(2-3N)})^{\frac{N}{2-3N}}\). The existence of horizons leads to \((2-3N)\Lambda >0\). Besides, consider the static region \(f(r)>0\) (which must stay at \(r>r_{+}\)), one can get that \(N<0\) for the case with power \(\frac{2}{N}-3>0\), while \(N>0\) for the case with power \(\frac{2}{N}-3<0\). Hence when \(Q=0\), only the case with \(\Lambda <0\) and \(\frac{2}{3}<N<2\) corresponds to the AdS uncharged dilaton black hole with single horizon.

  • When \(Q\ne 0, \Lambda =0\), i.e. the charged flat solution: we get \(f(r)=\frac{2M}{N}(r_{+}^{\frac{2}{N}-1}-r^{\frac{2}{N}-1})\), where \(r_{+}=(\frac{4Q^2}{M(2-N)})^{\frac{N}{2-N}}\). As \(\frac{2}{N}-1>0\), we can similarly get \(N<0\) in order to observe the black hole horizon, namely equivalent \(\gamma <0\). The negative kinetic energy in the action indicates that the dilaton acts as a phantom field. Hence in flat spacetime, only when \(Q\ne 0, N<0\), one can find the charged flat phantom black hole, other than the dilaton black hole.

  • When \(Q\ne 0, M=0\), i.e. the “massless” charged solution: the horizon function takes the simplified form as \(f(r)=\frac{8(2-N)}{NQ^2}(1-\frac{r^2}{r_{+}^2})\), where \(r_{+}=\sqrt{\frac{(3N-2)}{(2-N)\Lambda }}Q\). Black hole solution is the one with conditions \((3N-2)(2-N)\Lambda >0\) and \((2-N)N<0\) holding, which give \(\Lambda <0\), \(N>2\) or \(N<0\) (i.e. \(\gamma <0\)). This is actually the AdS “massless” charged phantom black hole.

  • When \(Q\ne 0, \Lambda \ne 0, M\ne 0\), i.e. the general charged non-flat “massive” solution: the discussion is complicated. We introduce the first order derivative \(f'(r)=\frac{16\Lambda \,r}{(3N-2)N}((\frac{r}{r_{ex}})^{\frac{2}{N}-3}-1)\), with its single zero

    $$\begin{aligned} r_{ex}=\left( \frac{8\Lambda \,N}{(N-2)(3N-2)M}\right) ^{\frac{2}{2-3N}}. \end{aligned}$$
    (22)

    Hence f(0), \(f(+\infty )\) and the extremum \(f(r_{ex})\) determine the curve of f(r). Consider the leading terms of f(r) at \(r=0\) and \(r=+\infty \), they are both dependent of N. Then we can find two subcases:

    1. 1.

      For \(0<N<\frac{2}{3}\): we know \(\frac{2}{N}-1>2\). This case gives that \(f(0)=\frac{8Q^2}{(2-N)N}>0,\) \(f(+\infty )=-\frac{2M}{N}\times \infty <0\) and the maximum of f(r) is \(f(r_{ex})>0\). These indicate that the curve of f(r) across zero only once at \(r=r_{+}\), and the static region is \(r<r_{+}\), hence this corresponds to the naked singularity which is physically unacceptable.

    2. 2.

      For \(\frac{2}{3}<N<2\): we find \(0<\frac{2}{N}-1<2\). From the the leading terms, it is shown that \(f(0)=\frac{8Q^2}{(2-N)N}>0,f(+\infty )=-\frac{8\Lambda }{(3N-2)N}\times \infty =-\Lambda \times \infty \). When \(\Lambda >0\), there is no real \(r_{ex}\) and f(r) monotonically decrease from positive value to \(-\infty \). There is a horizon \(r=r_{+}\) and the static region is \(r<r_{+}\) in the spacetime, which corresponds to the naked singularity. When \(\Lambda <0\), it is shown that \(f(0)>0\), \(f(+\infty )=+\infty \) and the minimum is \(f(r_{ex})\). When \(f(r_{ex})=0\), it corresponds to the extremal black hole with the mass

      $$\begin{aligned} M_{ex}=\left( \frac{8N}{(3N-2)(2-N)}\right) Q^{\frac{3N-2}{N}}(-\Lambda )^{\frac{2-N}{2N}}. \end{aligned}$$
      (23)

      If \(f(r_{ex})<0\), one can find the non-extremal black hole with two horizons. Note condition \(f(r_{ex})<0\) leads to the mass bound \(M>\,M_{ex}\).

When \(N=\frac{2}{3}\), the horizon structure is more simpler. One can find that \(f(0)=9{Q}^{2}>0\) and \(f(+\infty )=-18\Lambda \times \infty \). Then consider the first order derivative \(f'(r)=-2r(9\,\Lambda +18\,\Lambda \,\ln \left( r \right) +3\,M)\). For dS spacetime, we get \(f'(r)<0\) which shows that f(r) monotonically decrease from positive value to \(-\infty \). Though there is a horizon, the solution can not avoid the naked singularity because the static region is \(r<r_{+}\). For the same reason, the special cases with vanishing M or \(\Lambda \) in (A)dS spacetime are also the naked singularity even they have a horizon. When \(\Lambda <0\), it is easy to find the extremal black hole with the mass

$$\begin{aligned} M_{ex}=-3\Lambda -6\Lambda \ln \left( \frac{Q}{\sqrt{-\Lambda }}\right) =-3\Lambda \ln \left( \frac{eQ^2}{-\Lambda }\right) , \end{aligned}$$
(24)

and the horizon

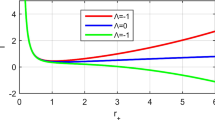
$$\begin{aligned} r_{ex}=\frac{Q}{\sqrt{-\Lambda }}. \end{aligned}$$
(25)

The non-extremal black hole corresponds to the solution with \(M>\,M_{ex}\). Note when \(\Lambda \le -eQ^2\), one can find that \(M_{ex}\le 0\) and there exist charged dilaton black hole solutions with negative mass. Especially for the case with \(Q=0\), i.e. \(M_{ex}=-\infty \), we conclude that AdS uncharged solutions with arbitrary mass correspond to the black holes. One can look at Fig. 1, where we have plotted the horizon function f(r) with \(\Lambda =-1, N=\frac{2}{3}\) and different values of parameters M, Q.

Fig. 1
figure 1

Horizon structure of Chan–Mann dilaton solution with \(\Lambda =-1, N=\frac{2}{3}\). In the left plot, \(\Lambda \le -eQ^2\) indicates that there exist charged dilaton black hole solutions with negative mass. In the right one, uncharged solutions with arbitrary mass correspond the black holes with single horizon

Full size image

Putting all cases together, we see that the physically acceptable bounds for parameters are \(\frac{2}{3}\le \,N<2\), \(\Lambda <0\) and \(M\ge \,M_{ex}\), which correspond to the AdS dilaton (charged/uncharged) black holes. Especially for charged solution, the one with \(M=\,M_{ex}\) is also physically acceptable and is the extremal black hole, while the one with \(M>\,M_{ex}\) corresponds to the non-extremal black hole and the one with \(\Lambda \le -eQ^2\) corresponds to charged dilaton black hole solutions with negative mass. For uncharged solution, we conclude that the AdS solutions with \(\frac{2}{3}<N<2,\ M>0\) or \(N=\frac{2}{3}\) always are the black hole with single horizon. Besides, the (un)charged black holes all have a negative cosmological constant, which is consisten with the No-Go theorem in three dimensions [48].

3.3 The causal structure

To end this section, we revisit the causal structure of Chan–Mann black hole, which is studied in [19]. We take the uncharged case \(Q=0\) as an example to introduce the method of obtaining the Penrose diagrams. Then in the metric Eq. (18), the horizon function of uncharged black hole reduces to

$$\begin{aligned}&f(r)=\bigg (-\frac{8\Lambda \,r^{3-\frac{2}{N}}}{(3N-2)N}-\frac{2M}{N}\bigg )r^{\frac{2}{N}-1},\nonumber \\&\qquad \quad \times \frac{2}{3}<N<2,\ M>0,\ \Lambda <0. \end{aligned}$$
(26)

One can find the tortoise coordinate \(r_{*}\)

$$\begin{aligned} r_{*}\equiv \int \sqrt{-\frac{g_{rr}}{g_{tt}}}\mathrm {d} r=\frac{(3N-2)N}{-8\Lambda }\int \frac{\mathrm {d}r}{(r^{3-\frac{2}{N}}-r_{+}^{3-\frac{2}{N}})}. \end{aligned}$$
(27)

It is clear that the tortoise coordinate depends on parameter N, which may lead to different causal structures.

We show the subcase with \(N=\frac{6}{5}\) firstly. The tortoise coordinate could be simplified as

$$\begin{aligned} r_{*}=\,&\frac{(3N-2)N}{-8\Lambda }\int \frac{\mathrm {d}r}{(r^{4/3}-r_{+}^{4/3})}\nonumber \\ =\,&\frac{3}{-10\Lambda \,r_{+}^{1/3}\lambda ^{5/3}}\left[ \ln \left( \frac{r^{1/3}-r_{+}^{1/3}}{r^{1/3}+r_{+}^{1/3}}\right) \right. \nonumber \\&\left. +2\arctan \left( \frac{r^{1/3}}{r_{+}^{1/3}}\right) \right] . \end{aligned}$$
(28)

After defining the advanced and retarded null coordinates

$$\begin{aligned} u=t-r_{*},\quad \,v=t+r_{*} \end{aligned}$$
(29)

and the Kruskal coordinates

$$\begin{aligned} U&=\frac{3}{5\Lambda \,r_{+}^{1/3}\lambda ^{5/3}}e^{\frac{5\Lambda \,r_{+}^{1/3}\lambda ^{5/3}}{3}u},\nonumber \\ V&=\frac{3}{-5\Lambda \,r_{+}^{1/3}\lambda ^{5/3}}e^{\frac{-5\Lambda \,r_{+}^{1/3}\lambda ^{5/3}}{3}v}, \end{aligned}$$
(30)

the metric can be re-written as

$$\begin{aligned} \mathrm {d} s^2=\,&-\left( \frac{5Mr^2}{3}\right) \left( \frac{1}{r_{+}^{4/3}}-\frac{1}{r^{4/3}}\right) \nonumber \\&\left( \frac{r^{1/3}+r_{+}^{1/3}}{r^{1/3}-r_{+}^{1/3}}\right) e^{-2\arctan \left( \frac{r^{1/3}}{r_{+}^{1/3}}\right) }\mathrm {d} U\mathrm {d} V, \end{aligned}$$
(31)

and a useful relationship is given

$$\begin{aligned} UV=-\left( \frac{3}{5\Lambda \,r_{+}^{1/3}\lambda ^{5/3}}\right) ^2\left( \frac{r^{1/3}-r_{+}^{1/3}}{r^{1/3}+r_{+}^{1/3}}\right) e^{2\arctan \left( \frac{r^{1/3}}{r_{+}^{1/3}}\right) }. \end{aligned}$$
(32)

As \(r\rightarrow +\infty \), \(UV\rightarrow -(\frac{3}{5\Lambda \,r_{+}^{1/3}\lambda ^{5/3}})^2e^\pi \), which is timelike and corresponds to a vertical line in the Penrose diagram. The horizon is located at \(r=r_{+}\), which indicates \(UV=0\). For \(r=0\), since the metric Eq. (31) changes sign and one should take the transformation \(U\rightarrow -U\), then one can obtain \(UV=-\left( \frac{3}{5\Lambda \,r_{+}^{1/3}\lambda ^{5/3}}\right) ^2\), implying that the singularity is timelike as well. These correspond to the various causal boundaries in the Penrose diagrams, which is depicted as in Fig. 2a. When the charge Q is added, there could exist two horizons: the event horizon \(r_{+}\) and the Cauchy horizon \(r_{-}\); hence the discussion becomes more complicated, and we only present the Penrose diagrams here. For the non-extremal black hole, the Penrose diagrams is given in Fig. 3a; for the extremal cases, it becomes Fig. 3b.

Fig. 2
figure 2

Penrose diagrams for uncharged Chan–Mann black hole: a, b respectively correspond to \(N=\frac{6}{5}\) and \(N=\frac{6}{7}\). The double line indicates the curvature singularity \(r=0\)

Full size image

We next consider the subcase with \(N=\frac{6}{7}\). The tortoise coordinate is given as

$$\begin{aligned} r_{*}&\propto \int \frac{\mathrm {d}r}{(r^{2/3}-r_{+}^{2/3})}\nonumber \\&=\frac{3r_{+}^{1/3}}{2}\left[ \ln \left( \frac{r^{1/3}-r_{+}^{1/3}}{r^{1/3}+r_{+}^{1/3}}\right) +2\left( \frac{r^{1/3}}{r_{+}^{1/3}}\right) \right] . \end{aligned}$$
(33)

Following the similar coordinate transformations (the advanced and retarded null coordinates and the Kruskal coordinates) outlined above, we can obtain the relationship

$$\begin{aligned} UV\propto -\left( \frac{r^{1/3}-r_{+}^{1/3}}{r^{1/3}+r_{+}^{1/3}}\right) e^{2\left( \frac{r^{1/3}}{r_{+}^{1/3}}\right) }. \end{aligned}$$
(34)

Then the causal boundaries in the Penrose diagrams are

$$\begin{aligned} \lim _{r\rightarrow 0}UV\propto -1,\quad \,\lim _{r\rightarrow \,r_{+}}UV=0,\quad \,\lim _{r\rightarrow +\infty }UV=-\infty . \end{aligned}$$
(35)

The corresponding Penrose diagrams is depicted in Fig. 2b. This is different from the subcase with \(N=\frac{6}{5}\), and it is similar to the one for an extremal Reissner–Nordstrom black hole in four dimensions. The causal structure of charged black hole with \(N=\frac{6}{7}\) could be obtained from the one for Reissner–Nordstrom black hole by a \(\frac{\pi }{2}\) rotation. Especially for the extremal charged black hole with \(N=\frac{6}{7}\), the corresponding Penrose diagrams could be simply obtained through a \(\frac{\pi }{2}\) rotation of Fig. 2b.

Fig. 3
figure 3

Penrose diagrams for charged Chan–Mann black hole with \(N=\frac{6}{5}\): a, b respectively correspond to the non-extremal and extremal cases. The double line indicates the curvature singularity \(r=0\)

Full size image

4 Another charged dilaton black hole

4.1 The solution and its properties

Back to Eq. (11), one can find another solution

$$\begin{aligned}&(4a-b)k-N=0, \end{aligned}$$
(36)
$$\begin{aligned}&{\lambda }^{2}\Lambda \left( N-bk-2\right) +\frac{{q}^{2}}{{\beta }^{N}} \left( N-4\,a\,k-2 \right) =0, \end{aligned}$$
(37)

where only constant term exists and vanishes in Eq. (11), and will fix all constants of this solution. Inserting these conditions, the solutions are divided into three cases as follows

  • When \(N+2\,bk+2\ne 0\) and \(bk+2\ne 0\), the solution is simplified as

    $$\begin{aligned}&A_{\mu }\mathrm {d}x^{\mu }\nonumber \\&\quad =\,{\frac{2q{r}^{b\,k+1+\frac{N}{2}}}{\lambda \left( N+2b\,k+2 \right) {\beta }^{b\,k+N} }}\mathrm {d}t,\quad \,\phi (r)=k\ln \left( \frac{r}{\beta }\right) ,\nonumber \\&f(r)=-\,{\frac{8{r}^{bk+2}\Lambda {\beta }^{-bk}}{\left( N+2\,bk+2 \right) \left( bk+2 \right) }}+B{r}^{-\frac{\,N}{2}+1}, \end{aligned}$$
    (38)

    with the constants

    $$\begin{aligned} \beta ^{N}=\,&{\frac{{q}^{2} \left( bk+2 \right) }{\Lambda \,{\lambda }^{2} \left( N- bk-2 \right) }},\quad k=-\,{\frac{2(b-4\,a)}{2\,\gamma +\left( b-4\,a\right) ^{2}}}, \nonumber \\ N=\,&\,{\frac{2 \left( b-4\,a\right) ^{2}}{2\,\gamma +\left( b-4\,a\right) ^{2}}}. \end{aligned}$$
    (39)

  • When \(N+2\,bk+2=0\), we get the following dilaton solutions with \(\ln (r)\) Maxwell field

    $$\begin{aligned}&A_{\mu }\mathrm {d}x^{\mu }={\frac{q{\beta }^{1-\frac{\,N}{2}}}{\lambda }}\ln \left( r\right) \mathrm {d}t,\quad \,\phi (r)=k\ln \left( \frac{r}{\beta }\right) ,\nonumber \\&f(r)={r}^{1-\frac{\,N}{2}}\bigg (\,{\frac{8{\beta }^{1+\frac{N}{2}} \Lambda }{N-2}}\ln \left( r \right) +B\bigg ), \end{aligned}$$
    (40)

    where the constants are

    $$\begin{aligned} \beta ^{N}=\,&{\frac{ \left( 1-\frac{N}{2}\right) {q}^{2}}{\Lambda \,{\lambda }^{2} \left( \frac{3N}{2}-1 \right) }},\quad k=-\,{\frac{8a}{\gamma +32\,{a}^{2}}}, \nonumber \\ N=\,&\,{\frac{2\gamma }{\gamma +32\,{a}^{2}}},\quad \, b=\,{\frac{\gamma +16\,{a}^{2}}{4a}}. \end{aligned}$$
    (41)

  • When \(bk+2=0\), the solution becomes

    $$\begin{aligned}&A_{\mu }\mathrm {d}x^{\mu }=\,{\frac{2q{\beta }^{2-N}{r}^{\frac{N}{2}-1}}{ \left( N-2 \right) \lambda }}\mathrm {d}t,\quad \,\phi (r)=k\ln \left( \frac{r}{\beta }\right) ,\nonumber \\&f(r)=-\,{\frac{8{\beta }^{2-N}{q}^{2}}{ \left( N-2 \right) N{\lambda }^{2}} }+B{r}^{1-\frac{N}{2}}, \end{aligned}$$
    (42)

    with the following constants

    $$\begin{aligned} \Lambda =\,&0,\quad N=\,{\frac{2(b-4\,a)}{b}},\quad k=-\frac{2}{\,{b}},\nonumber \\ \gamma =\,&2\, \left( b-4\,a\right) a. \end{aligned}$$
    (43)

One can find that only when \(N=0\) (i.e. \(b=4a\)), this solution can be seen as a reduced string solution of the Chan–Mann charged dilaton solution. Note in the former two cases, \(\beta \) is not arbitrary and is fixed by the strength constants \(\gamma ,a,b,\Lambda \) in the action and the electric charge parameter q, while \(\beta \) is arbitrary for the third case which could only exist in the flat spacetime. For the charged scalar solution, i.e. \(a=0\), the first case reduces to

$$\begin{aligned}&A_{\mu }\mathrm {d}x^{\mu }=\,{\frac{2q{r}^{1-\frac{N}{2}}}{\lambda \left( 2-N\right) }}\mathrm {d}t,\quad \,\phi (r)=k\ln \left( \frac{r}{\beta }\right) ,\nonumber \\&f(r)={r}^{1-\frac{\,N}{2}}\bigg (B-\,{\frac{8\Lambda {\beta }^{N}}{\left( 2-N \right) ^2}}{r}^{1-\frac{\,N}{2}}\bigg ),\nonumber \\&\beta ^{N}={\frac{{q}^{2} \left( 2-N\right) }{2\Lambda \,{\lambda }^{2} \left( N-1\right) }},\quad k=-\,{\frac{2b}{2\,\gamma +b^{2}}}, \quad N={\frac{2b^{2}}{2\,\gamma +b^{2}}}, \end{aligned}$$
(44)

while the latter two become the BTZ solution. Namely, there is no charged scalar black hole with \(\ln (r)\) Maxwell field.

To get the uncharged solution, one can directly choose the \(q=0\) limit of the above solutions. One should be careful of the choice of the parameters. When \(q=0\), Eq. (36) results in \(\Lambda =0\) or \(N=bk+2\), and the Maxwell field is vanishing. If \(\Lambda =0\), the horizon function of this uncharged solutions reduces to the vacuum solution \(f(r)=Br^{-\frac{N}{2}+1}\). Hence for the uncharged dilaton solution, we get the same form of the solution and additionally choose \(N=bk+2\) while parameter \(\beta \) is free.

4.2 The horizon structure

Firstly, we perform the coordinate transformation \(\lambda ^2r^{N}\rightarrow \,r^2\), in order to focus on the dilaton solution in the metric Eq. (18) with the usual radial co-ordinate r. We get

$$\begin{aligned}&f(r)={r}^{\frac{2-\,N}{N}}\bigg (\frac{-8\Lambda {r}^{\frac{N+2bk+2}{N}}{\beta }^{-bk}}{\left( N+2\,bk+2 \right) \left( bk+2 \right) }-\frac{2M}{N}\bigg ),\nonumber \\&\quad N+2\,bk+2\ne 0\ \mathrm{and}\ bk+2\ne 0; \end{aligned}$$
(45)
$$\begin{aligned}&f(r)=\frac{{r}^{\frac{2-N}{N}}}{N}\bigg (\,{\frac{-16\Lambda {\beta }^{1+\frac{N}{2}}}{(2-N)}}\ln \left( r \right) -2M\bigg ),\nonumber \\&\quad N+2\,bk+2=0; \end{aligned}$$
(46)
$$\begin{aligned}&f(r)=\frac{1}{N}\left( \,{\frac{8{Q}^{2}}{ \left( 2-N\right) }}-2M{r}^{\frac{2-N}{N}}\right) ,\quad bk+2=0, \end{aligned}$$
(47)

where we still choose \(M=-\frac{NB}{2}\) and \(Q=q\) as the quasilocal charges of the solution. We have also chosen \(\lambda =1\) in the former two and \({\beta }^{2-N}={\lambda }^{2}\) for the third one, for simplicity.

To consider the horizon structure, we begin with the geometrical properties. We focus on the dilaton solutions with positive kinetic energy, i.e. \(0<N<2\). Calculate the Ricci scalar for each case, we find

$$\begin{aligned} R&=\,{\frac{ 4\left( 4+6\,bk+2\,{b}^{2}{k}^{2}+2\,N+2\,Nbk+{N}^{2} \right) }{ \left( N-bk-2 \right) \left( N+2\,bk+2 \right) {\beta }^{bk+N}}}\frac{{Q}^{2}}{{r}^{-\frac{bk}{N}}}\nonumber \\&\quad +\,{\frac{M \left( N-2 \right) }{2\,{r}^{\frac{N+2}{N}}}},\; N+2\,bk+2\ne 0\ { and}\ bk+2\ne 0;\end{aligned}$$
(48)
$$\begin{aligned} R&=\frac{2\,{\beta }^{1-\frac{N}{2}} \left( 2\left( N-2 \right) \ln \left( {\frac{r}{\beta ^{N/2}}} \right) +4 \right) {Q}^{2}}{ \left( 3\,N-2 \right) \left( {r}^{\frac{N+2}{N}} \right) }\nonumber \\&\quad +\,{\frac{M \left( N-2 \right) }{2\,{r}^{\frac{N+2}{N}}}},\quad N+2\,bk+2=0;\end{aligned}$$
(49)
$$\begin{aligned} R&=\,{\frac{4{Q}^{2}}{{r}^{\frac{2}{N}}}}+\,{\frac{M \left( N-2 \right) }{2\,{r}^{\frac{N+2}{N}}}},\; bk+2=0, \end{aligned}$$
(50)

which always indicates an essential singularity at \(r=0\) if either \(M\ne 0\) or \((Q\ne 0,bk<0)\). Hence the solution must contain an event horizon \(r_{+}\) and the static region \(r>r_{+}\) to avoid the naked singularity. Especially for the first branch, the charged solution with \(bk\ge 0\) has two essential singularities located in \(r=0\) and \(r=+\infty \). This is also discussed in detailed in what follows. Besides, whenever \(M\ne 0\) or \(Q\ne 0\), one can easily find some non-vanishing components of the Cotton tensor which indicate that the solutions are non-conformally flat [58].

Then consider the charged black hole solutions. Note \(0<N<2\) and \(\beta \) is always positive. We can find the corresponding branches:

  • When \(bk+2=0\), the discussion is the simplest. The horizon function can be rewritten as \(f(r)=\frac{2M}{N}({r_{+}}^{\frac{2-N}{N}}-{r}^{\frac{2-N}{N}})\) with the real zero \(r_{+}=(\,{\frac{8{Q}^{2}}{2M ( 2-N)}})^{\frac{N}{2-N}}\). However, one can find \(f(r)>0\) leads to the static region \(r<r_{+}\) which does not correspond to the black hole solution. If we relax the positive mass and positive kinetic energy, one can find that the phantom solutions with \(N>2, M<0\) or \(N<0, M>0\) also have the physically unacceptable static region \(r<r_{+}\). Thus this case is always the naked singularity.

  • When \(N+2\,bk+2=0\), we get \(f(r)=\,{\frac{-16\Lambda }{(2-N)N}}{\beta }^{1+\frac{N}{2}}{r}^{\frac{2-N}{N}}(\ln ( r )-\ln (r_{+}))\). Thus the static region \(r>r_{+}\) indicates that \(\Lambda <0\), where the single root is \(r_{+}=\exp (\frac{2M(2-N)}{-16\Lambda {\beta }^{1+\frac{N}{2}}} )\) \((r_{+}>1)\). Besides, \(\beta ^{N}\) should be positive and results in \(0<N<\frac{2}{3}\), which gives an additional constraint \(-\frac{4}{3}<bk<-1\). Only in this condition, we can find the charged dilaton AdS black hole. Note when \(\Lambda >0\), \(N>2\) or \(N<0\), it corresponds to the charged phantom dS black hole. When Q is vanishing, one can find that we must choose \(bk=-\frac{4}{3}\) (i.e. \(N=bk+2=\frac{2}{3}\)). The event horizon \(r_{+}\) takes the same form with the charged one and can be simplified as \(r_{+}=\exp (\frac{M}{-6\Lambda {\beta }^{4/3}} )\), while the parameter \(\beta \) is free. The charged black hole reduces to the uncharged dilaton AdS and phantom dS black hole, respectively.

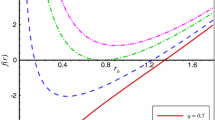
  • When \(N+2\,bk+2\ne 0\ \mathbf{and}\ bk+2\ne 0\), we rewrite the horizon function as \(f(r)=\frac{2M}{N}{r}^{\frac{2-\,N}{N}}((\frac{{r}}{{r_{+}}})^{\frac{N+2bk+2}{N}}-1)\), together with the single zero \({r_{+}}=(\frac{M( N+2\,bk+2 ) ( bk+2){\beta }^{bk} }{-4N\Lambda })^{\frac{N}{N+2bk+2}}\). Then we can find three conditions for the black hole solution with \(bk<0\): the parameter \(\beta \) is positive, thus the form of \(\beta ^{N}>0\) results in \(\Lambda (bk+2)(N-(bk+2))>0\); the solution has an event horizon indicating \(-\Lambda ( N+2\,bk+2 ) ( bk+2 )>0\); the single singularity is located in \(r=0\), hence the static region \(r>r_{+}\) leads to \(N+2bk+2>0\). Based on the above three constraints on the parameters and \(0<N<2\), we can finally obtain the physically acceptable solution: For \(\Lambda<0, -2<bk<0\) and \( max\{0,-2(bk+1)\}<N<bk+2\), this solution corresponds to the charged dilaton AdS black hole. For solutions with \(bk\ge 0\), there are two singularities located in \(r=0\) and \(r=+\infty \), which always make the solutions physically unacceptable. When \(Q=0\), we must choose \(N=bk+2\), while parameter \(\beta \) is free. There is always a singularity located in \(r=0\). Hence we only care about two constraints: the event horizon \(r_{+}\) is simplified as \({r_{+}}=(\frac{M\left( 3\,bk+4 \right) {\beta }^{bk} }{-4\Lambda })^{\frac{bk+2}{3bk+4}}\), indicating \(-\Lambda ( 3\,bk+4 )>0\); the static region \(r>r_{+}\) leads to \(3bk+4>0\). These together give \(\Lambda <0, bk>-\frac{4}{3}\) (i.e. \(N>\frac{2}{3}\)) corresponding to the uncharged dialton AdS black hole solutions.

Totally, one can obtain that this family of solutions only have black hole with negative cosmological constant, which is the same with that the Chan–Mann dilaton black hole and is also consistent with the No–Go theorem in three dimensions [48]. Besides,

  • In Einstein–Maxwell–Dilaton gravity, only solutions with either \(N+2\,bk+2=0,\ 0<N<\frac{2}{3}\) (i.e. \(-\frac{4}{3}<bk<-1\)), or \( max\{0,-2(bk+1)\}<N<bk+2,\ -2<bk<0\) corresponds to the charged dilaton AdS black hole with fixed parameter \(\beta \).

  • For uncharged dilaton AdS black hole, it has \(N=bk+2,\ \frac{2}{3}\le \,N<2\) (i.e. \(-\frac{4}{3}\le bk<0\)) and free parameter \(\beta \), which is consistent with the uncharged limit of the Chan–Mann dilaton black hole.

These black holes always have a single horizon (i.e. the event horizon) and do not contain an additional mass bound (but the usual \(M>0\)). Hence there is no physically acceptable (non-)extremal dilaton black hole for this family of dilaton solutions. For the charged phantom black hole, we have given some results in the above paragraphs and one can follow the same procedure to give a whole discussion of the horizon structure.

4.3 The causal structure

Since there always exists a single horizon for this family of charged dilaton black hole, the causal structure becomes simple and is similar to the uncharged case of the Chan–Mann dilaton black hole. Following the same procedure, we firstly introduce the tortoise coordinate \(r_{*}\)

$$\begin{aligned} r_*=\frac{1}{M\lambda ^{5/3}}\int \frac{\mathrm {d}r}{\bigg (\left( \frac{r}{r_{+}}\right) ^{\frac{(N+2bk+2)}{N}}{-}1\bigg )}, \quad N{+}2\,bk{+}2\ne 0, \end{aligned}$$
(51)

which is actually similar to the one of the uncharged case of the Chan–Mann dilaton black hole.

Then we take some examples to explore the causal structure of this family of charged dilaton black hole. When \(N=1,bk=-\frac{5}{6}\), the above tortoise coordinate could be simplified as

$$\begin{aligned} r_*&\propto \int \frac{\mathrm {d}r}{\bigg (\left( \frac{r}{r_{+}}\right) ^{4/3}-1\bigg )}, \nonumber \\&=\bigg [\ln \left( \frac{r^{1/3}-r_{+}^{1/3}}{r^{1/3}+r_{+}^{1/3}}\right) +2\arctan \left( \frac{r^{1/3}}{r_{+}^{1/3}}\right) \bigg ]. \end{aligned}$$
(52)

After takeing the similar the advanced and retarded null coordinates, and the Kruskal coordinates, we get the relationship

$$\begin{aligned} UV\propto -\left( \frac{r^{1/3}-r_{+}^{1/3}}{r^{1/3}+r_{+}^{1/3}}\right) e^{2\arctan \left( \frac{r^{1/3}}{r_{+}^{1/3}}\right) }. \end{aligned}$$
(53)

and the following causal boundaries

$$\begin{aligned} \lim _{r\rightarrow 0}UV\propto -1,\quad \,\lim _{r\rightarrow \,r_{+}}UV=0,\quad \,\lim _{r\rightarrow +\infty }UV=-1. \end{aligned}$$
(54)

This indicates that the corresponding Penrose diagram is the same with Fig. 2a. Here we show other similar subcases with \(N=\frac{6}{5},bk=-\frac{2}{5}\) or \(N=\frac{6}{7},bk=-\frac{4}{7}\). The tortoise coordinate becomes

$$\begin{aligned} r_*&\propto \int \frac{\mathrm {d}r}{\bigg (\left( \frac{r}{r_{+}}\right) ^{2}-1\bigg )}=\frac{r_{+}}{2}\ln \left( \frac{r-r_{+}}{r+r_{+}}\right) . \end{aligned}$$
(55)

After takeing the similar coordinates transformations, we get the relationship

$$\begin{aligned} UV\propto -\left( \frac{r-r_{+}}{r+r_{+}}\right) , \end{aligned}$$
(56)

which leads to the same causal boundaries Eq. (54), hence the the same Penrose diagram with Fig. 2a.

Considering the subcase with \(N=\frac{3}{4},bk=-\frac{9}{8}\), the tortoise coordinate \(r_{*}\) reduces to

$$\begin{aligned} r_*&\propto \int \frac{\mathrm {d}r}{\bigg (\left( \frac{r}{r_{+}}\right) ^{2/3}-1\bigg )}, \nonumber \\&=\bigg [\ln \left( \frac{r^{1/3}-r_{+}^{1/3}}{r^{1/3}+r_{+}^{1/3}}\right) +2\left( \frac{r^{1/3}}{r_{+}^{1/3}}\right) \bigg ]. \end{aligned}$$
(57)

Following the standard coordinates transformations, one will get

$$\begin{aligned} UV\propto -\left( \frac{r^{1/3}-r_{+}^{1/3}}{r^{1/3}+r_{+}^{1/3}}\right) e^{2\left( \frac{r^{1/3}}{r_{+}^{1/3}}\right) }. \end{aligned}$$
(58)

and the following causal boundaries

$$\begin{aligned} \lim _{r\rightarrow 0}UV\propto -1,\quad \,\lim _{r\rightarrow \,r_{+}}UV=0,\quad \,\lim _{r\rightarrow +\infty }UV=-\infty , \end{aligned}$$
(59)

for which, the Penrose diagram should be exactly the same with Fig. 2b.

Finally, we turn to the Penrose diagram of the special case with \(N+2bk+2=0\), for which the tortoise coordinate is

$$\begin{aligned} r_*&\propto \int \frac{\mathrm {d}r}{\bigg (\ln (r)-\ln (r_{+})\bigg )},\quad \,0<N<\frac{2}{3} \nonumber \\&=-r_{+} Ei\bigg (1,-\ln (r)+\ln (r_{+})\bigg ), \end{aligned}$$
(60)

where the function Ei is the exponential integrals. Following the same procedure, we can get a useful relationship of the Kruskal coordinates,

$$\begin{aligned} UV\propto -e^{-Ei\bigg (1,-\ln (r)+\ln (r_{+})\bigg )}. \end{aligned}$$
(61)

The corresponding causal boundaries take the form

$$\begin{aligned}&\lim _{r\rightarrow 0}UV\propto -e^{-Ei\bigg (1,+\infty \bigg )}=-1, \end{aligned}$$
(62)
$$\begin{aligned}&\lim _{r\rightarrow \,r_{+}}UV\propto -e^{-Ei\bigg (1,0\bigg )}=0,\end{aligned}$$
(63)
$$\begin{aligned}&\lim _{r\rightarrow +\infty }UV\propto -e^{-Ei\bigg (1,-\infty \bigg )}=-\infty . \end{aligned}$$
(64)

Thus the corresponding Penrose diagrams should be also the same with Fig. 2b.

5 The time-dependent system

In this section, we present the general time-dependent black hole solution and its properties in three dimensional Einstein–Maxwell–Dilaton gravity.

5.1 The dynamical solution

To find the exact time-dependent solution, we follow the static metric Eq. (18) and introduce the similar metric ansatz in Eddington–Finekelstein-like coordinates

$$\begin{aligned} \mathrm {d}s^{2}=-f(u,R)\mathrm {d}u^{2} +4g(u)R^{\ell }\mathrm {d}u\mathrm {d}R +R^2\mathrm {d}\psi ^2. \end{aligned}$$
(65)

As introduced in the static metric Eq. (18), one can find

$$\begin{aligned} \ell =\frac{2}{N}-1. \end{aligned}$$
(66)

Then the equation of motion for the Maxwell field

$$\begin{aligned} A_{\mu }\mathrm {d}x^{\mu }=QA(u,R)\mathrm {d}u \end{aligned}$$
(67)

leads to

$$\begin{aligned} \frac{\partial }{\partial R} A(u,R)={\mathrm{e}^{4\,a\,\phi \left( u,R \right) }}R^{\ell -1}g(u) . \end{aligned}$$
(68)

To get the static limit, we consider the following evolution of scalar field

$$\begin{aligned} \phi (u,R)=\ln \bigg (\phi _1(u)\phi _2(R)\bigg ) \end{aligned}$$
(69)

with

$$\begin{aligned}&\phi _1(u)=u^{p},\quad \,\phi _2(R)=R^{k}. \end{aligned}$$
(70)

Thus the scalar field could be simplified as

$$\begin{aligned} \phi (u,R)={k}\ln (R)+{p}\ln (u). \end{aligned}$$
(71)

Then the component of Einstein equations \(E^{u}{}_{R}=0\) is reduced into

$$\begin{aligned} \gamma - \frac{2 \ell }{k^2} =0. \end{aligned}$$
(72)

Taking the combination of the component of Einstein equations \(E^{u}{}_{u}=0\) and the equation of scalar field, one can obtain a equation of function g(u),

$$\begin{aligned}&\bigg (4(\gamma \,k+b)\Lambda \,R^{\gamma \,k^2+b k+2}\phi _1(u)^{b+1}\nonumber \\&\qquad +(\gamma \,k+4a)Q^2R^{\gamma \,k^2+4ak}\phi _1(u)^{4a+1}\bigg )g(u)\nonumber \\&\quad =\gamma \,R^{\frac{\gamma \,k^2}{2}+1}\partial _{u}\phi _1(u), \end{aligned}$$
(73)

where the function f(u, R) is disappeared. For time-dependent solution, the variable R in above Eq. (73) requires the following relations

$$\begin{aligned} {\gamma \,k^2+bk+2}={\gamma \,k^2+4ak}={\frac{\gamma \,k^2}{2}+1}. \end{aligned}$$
(74)

After considering the relation Eq. (72), we can obtain the constants in action

$$\begin{aligned} a = -\frac{(\ell -1)}{4k} ,\quad b =4a-\frac{2}{k}= -\frac{(\ell +1)}{k},\quad \gamma = \frac{2\ell }{k^2}. \end{aligned}$$
(75)

One can also choose the parameters in the form of a and b as

$$\begin{aligned} \ell =\frac{b+4a}{b-4a},\quad k=\frac{2}{4a-b},\quad \gamma =\frac{b^2-16a^2}{2}. \end{aligned}$$
(76)

or equivalently

$$\begin{aligned} N=\frac{b-4a}{b},\quad k=\frac{2}{4a-b},\quad \gamma =\frac{b^2-16a^2}{2}. \end{aligned}$$
(77)

For there parameters in action and metric, as \(a>0,b>0,\gamma >0\), one can find some additional constraints on the parameters

$$\begin{aligned} b>4a,\quad \,\ell >1,\quad \,k<0. \end{aligned}$$
(78)

Then Eq. (73) could be simplified as

$$\begin{aligned}&\bigg (4(\gamma \,k+b)\Lambda \phi _1(u)^{b+1}\nonumber \\&\quad +(\gamma \,k+4a)Q^2\phi _1(u)^{4a+1}\bigg )g(u)=\gamma \partial _{u}\phi _1(u), \end{aligned}$$
(79)

which leads to

$$\begin{aligned} g(u)=\,{\frac{2 \,{u}^{-1+\frac{p}{k}(\ell +1)}p\ell }{k\bigg ({u}^{\frac{2p}{k}}{Q}^{2} \left( {\ell }+1 \right) +4\,\Lambda \, \left( {\ell }-1 \right) \bigg )}}. \end{aligned}$$
(80)

Finally, considering the other components of component of Einstein equations, one can easily obtain the horizon function

$$\begin{aligned} f(u,R)={\frac{ \bigg ( -8\, \left( {u}^{\frac{2p}{k}}{Q}^{2}{+}4\,\Lambda \right) p^2\ell ^2R{u}^{\frac{p}{k}(\ell -1)}-M(\ell +1)\bigg ) {R}^\ell { u}^{\frac{2p}{k} -2}}{k^2 \bigg ( {u}^{\frac{2p}{k} }{Q}^{2} \left( \ell +1 \right) + 4\,\Lambda \, \left( \ell -1 \right) \bigg ) ^{2}}}, \end{aligned}$$
(81)

where M is the mass of static black hole. The Maxwell field is

$$\begin{aligned} A(u,R)=\frac{2p\ell \,Ru^{\frac{2p}{k}-1}}{k\bigg (u^{\frac{2p}{k}}Q^2(\ell +1)+4\Lambda (\ell -1)\bigg )}. \end{aligned}$$
(82)

There is still an arbitrary parameter p, which characterizes the evolution of dilaton field. For every time \(u=u_0\), the time-dependent solution with fixed p is actually reduced to the static charged dilaton black hole. Besides, one should note that the dynamical solution is obtained only for special case with \(\gamma =\frac{b^2-16a^2}{2}\) (\(b\ne 4a\)).

5.2 Solution in other coordinate system

One can take the transformation \(u=u(U)\), and then observe other evolution ways of matter field and the spacetime. For example, after choosing \(u=u_0\tanh (\kappa \,U)\), one can obtain an exact time-dependent solution describing the gravitational collapse to a charged dilaton black hole at the infinite time \(U\rightarrow +\infty \).

Here we introduce the solution in following coordinate system to study the related properties. After considering the transformation

$$\begin{aligned} \frac{u^{\frac{2p}{k}-1}}{k\bigg (u^{\frac{2p}{k}}Q^2(\ell +1)+4\Lambda (\ell -1)\bigg )}\mathrm {d}u\rightarrow \mathrm {d}U, \end{aligned}$$
(83)

one can find that the Maxwell field is not time-dependent, i.e

$$\begin{aligned} A_{\mu }\mathrm {d}x^{\mu }=2p\ell \,QR\mathrm {d}U. \end{aligned}$$
(84)

The above transformation takes the form

$$\begin{aligned} U=\frac{\ln \bigg (u^{2p/k}Q^2(\ell +1)+4\Lambda (\ell -1)\bigg )}{2pQ^2(\ell +1)}. \end{aligned}$$
(85)

or equivalently

$$\begin{aligned} u=u(U)=\bigg (\frac{e^{2pQ^2(\ell +1)U}}{Q^2(\ell +1)}\bigg )^{k/2p}. \end{aligned}$$
(86)

Then this solution can be simplified as

$$\begin{aligned} \mathrm {d}s^{2}=\,&-f(U,R)\mathrm {d}U^{2} +4g(U)R^{\ell }\mathrm {d}U\mathrm {d}R +R^2\mathrm {d}\psi ^2, \end{aligned}$$
(87)
$$\begin{aligned} f(U,R)=\,&\bigg ( -8\, \left( {u}^{\frac{2p}{k}}{Q}^{2}+4\,\Lambda \right) p^2\ell ^2R{u}^{\frac{p}{k}(\ell -1)}\nonumber \\&-M(\ell +1)\bigg ) {R}^\ell {u}^{-\frac{2p}{k}}, \end{aligned}$$
(88)
$$\begin{aligned} \phi (U,R)=\,&{k}\ln (R)+{p}\ln (u),\quad g(U)=\,{2 \,{u}^{\frac{p}{k}(\ell -1)}p\ell }. \end{aligned}$$
(89)

For the extra matter source, only the dilaton field is time-dependent. This means that the dilaton field drives the evolution of spacetime. The parameter p is also arbitrary, which characterizes the evolution of dilaton field and spacetime.

5.3 Global properties of dynamical solution

We firstly calculate some geometrical quantities to understand the geometrical features of the time-dependent solution Eqs. (87, 88, 89). Noting that the conditions Eq. (78) are always used in the following discussion. Considering the Cotton tensor, there exist some non-vanishing components. For example,

$$\begin{aligned} C_{RuR}=\,&\frac{MQ^{(\ell +1)}(\ell -2)(\ell +1)^{(\ell +3)/2}}{16pR^3}\nonumber \\&\exp {\bigg (-p(\ell +1)^2Q^2U\bigg )} \end{aligned}$$
(90)

is not vanishing when \((M\ne 0,Q\ne 0,\ell \ne 2)\). This indicating that the metric is non-conformally flat [58].

On the other hand, one can calculate the polynomial curvature invariants to study the singularities. Here we focus on the Ricci scalar, while other higher order curvature invariants have similar properties and more complicated forms hence are not listed here. From the Ricci scalar

$$\begin{aligned} R\equiv&R_{\mu \nu }g^{\mu \nu }\nonumber \\ =\,&-\frac{MQ^{2\ell }(\ell +1)^{(\ell +1)}}{16p^2\ell \,R^{(\ell +2)}}\exp {\bigg (-2p\ell (\ell +1)Q^2U\bigg )}\nonumber \\&+\bigg (\frac{Q}{R}\bigg )^{(\ell +1)}(\ell +1)^{(\ell -1)/2} \nonumber \\&\times \bigg [4(\ell +1)\Lambda \exp {\bigg (-p(\ell +1)^2Q^2U\bigg )}\nonumber \\&+\exp {\bigg (-p(\ell ^2-1)Q^2U\bigg )}\bigg ], \end{aligned}$$
(91)

it is easy to find that when \(U\rightarrow 0\), the spacetime has a singularity at \(R=0\) when \((M\ne 0,Q\ne 0)\). Then from the metric function f(u, R) Eq. (81), one can find that only when \(\Lambda <0\), there exist black hole horizons. As u is finite, the dilaton field is finite for \(U=0\), which indicates that the system is a dynamical AdS black hole at the beginning. The global structure at \(U=+\infty \) (i.e. \(u\rightarrow 0\)) is more subtle. If \(p<0\), the Ricci scalar is singular at \(U=+\infty \) (i.e. \(u\rightarrow 0\)), which can not be protected by a radial horizon, and hence the cases are not physically acceptable. This indicates that the parameter p should be positive.

Besides, from the metric function f(U, R) Eq. (88), we can get the effective time-dependent “Vaidya mass” measured at infinity as

$$\begin{aligned} M(U)=M{u}^{-\frac{2p}{k}}=M\frac{Q^2(\ell +1)}{e^{2pQ^2(\ell +1)U}}. \end{aligned}$$
(92)

When \(u\rightarrow \,1\), i.e. \(U\rightarrow \,U_0,U_0=\frac{\ln (Q^2(\ell +1))}{2pQ^2(\ell +1)}\), one can get \(M(u)\rightarrow \,M\), hence the system actually takes finite time \(U=U_0\) to reach the static dilaton AdS black hole with \(\gamma =\frac{b^2-16a^2}{2}\) and the mass M. When \(U=0,\Lambda <0\), the system is a dynamical AdS black hole with mass \(MQ^2(\ell +1)\) at the beginning. Actually, when the time U increases, the mass of black hole decreases, and when \(U\rightarrow +\infty \) (with \(p>0\)) i.e. \(u=0\), the black hole mass is vanishing. Equivalently, when the time u increases, the mass of black hole increases, and the black hole mass is vanishing at the beginning \(u=0\) (with \(p>0\)).

To sum, for time \(u=u_0\), the time-dependent solution with \((\gamma =\frac{b^2-16a^2}{2},b>4a,\ell>1,k<0,p>0)\) characterizes the charged black hole formation in three dimensions (while the charged black hole perishes when time \(U=U_0\) increases.). Moreover, The dynamical system should be an AdS black hole, which is consistent with the static cases in lase two sections.

5.4 No dynamical Chan–Mann solution under the collapse of dilaton field

One may be interested in the case \(b=4a\), in order to find the time-dependent solution of Chan–Mann charged dilaton black hole Eq. (18). For this case, the equation Eq. (73) reduces to

$$\begin{aligned}&(4\Lambda \,R^{2}+Q^2)(\gamma \,k+4a)R^{\gamma \,k^2+4a k}\phi _1(u)^{4a+1}g(u)\nonumber \\&\quad =\gamma \,R^{\frac{\gamma \,k^2}{2}+1}\partial _{u}\phi _1(u), \end{aligned}$$
(93)

which only has the solution

$$\begin{aligned} (\gamma \,k+4a)=0,\quad \,\partial _{u}\phi _1(u)=0, \end{aligned}$$
(94)

i.e.

$$\begin{aligned}&\gamma =-\frac{4a}{k}, \end{aligned}$$
(95)
$$\begin{aligned}&\phi _1(u)=\phi _0, \end{aligned}$$
(96)

where \(\phi _0\) is a constant. After choosing \(p,\ell ,\phi _0\) properly, one will find that this is just the static Chan–Mann charged dilaton solution. However, this means that there is no time-dependent solution of Chan–Mann charged dilaton black hole.

Now we try to understand this. As the Einstein–Maxwell–Dilaton action Eq. (1) with \(b=4a\) is equivalent to string action Eq. (2) via taking a conformal transformation [51], while the later one can be lift to \((3+1)\) dimensions Einstein action with cosmological constant by the Kaluza–Klein theory [49, 50] (see [59] for a review). The \((2+1)\) dimensional metric is accordingly a sub-manifold of \((3+1)\) dimensional spactime. Actually, for static solutions, one could always obtain dilaton solutions arising from \((3+1)\) dimensional gravity [60,61,62], achieved by a compactification of solutions with cylindrical symmetry in \((3+1)\) dimensions; Also, embedding the \((2+1)\) dimensional solutions in \((3+1)\) dimensions leads to new rotating solutions with cylindrical symmetry. If the \((2+1)\) dimensional submanifold takes an evolution, the \((3+1)\) dimensional spacetime will become time-dependent. However, there is no extra matter source in \((3+1)\) dimensions driving an evolution of the Einstein spacetime. Hence one can not expect the existence of time-dependent solution of Chan–Mann charged dilaton black hole. Actually, one can consider the Vaidya-like solution [33] describing the formation of Chan–Mann charged dilaton black hole. For the charged dilaton solutions with \(b\ne 4a\), they could not be lift to \((3+1)\) dimensions, hence characterize the properties of Einstein–Dilaton theory; for the time-dependent solution in this case, the dilaton field could drive the evolution of the spacetime.

5.5 The gravitational collapse of a dilaton field and the Cosmic Censorship Conjecture

In three dimensions, the gravitational collapse of a scalar field is studied in [47], where the causal structure and the Penrose diagram of uncharged dynamical black hole with scalar are given. When studying the causal structure of the charged case in this paper, the discussion becomes too complicated. The difficulty is palpable. Actually, one may hope to follow a similar procedure obtaining the Penrose diagram of the static charged black hole to study the dynamical case. Namely after takeing a coordinate transformation \((u,R)\rightarrow (u,v)\) such that

$$\begin{aligned} \mathrm {d}v=\mathrm {d}u+2\epsilon \frac{A(u,R)}{B(u,R)}\mathrm {d}R, \end{aligned}$$
(97)

the line element may be brought to the Kruskal form \(\mathrm {d}s^2=-B(u,R(u))\mathrm {d}u\mathrm {d}v+R(u,v)^2\mathrm {d}\psi ^2\). Unfortunately, the condition Eq. (97) does not have an integral in closed form, so an explicit expression for \(R=R(u,v)\) is out of reach.

In order to obtain a some pictures about the spacetime of the charged dynamical dilaton black hole solution, we are interested in studying the gravitational collapse of a dilaton field in the context of the Cosmic Censorship Conjecture (CCC [63]) in this paper. We will follow the discussion about the gravitational collapse of matter fields in the generalized Vaidya spacetime [64, 65], where a general mathematical framework is developed to study the conditions on the mass function of matter fields so that future directed non-spacelike geodesics can terminate at the singularity in the past. The nature (a locally naked singularity or a black hole) of the collapsing solutions can be characterized by the existence of radial null geodesics coming out of the singularity [66, 67]. When approaching the singularity \((R=0,u=0)\) along the radial null geodesic, if the slope of radial null geodesics \(X_0=\lim _{R=0,u=0}\frac{u}{R}=\lim _{R=0,u=0}\frac{\mathrm {d}u}{\mathrm {d}R}\) is positive, the singularity will be observed in the interior of black hole, which corresponds to the case that the strong Cosmic Censorship Conjecture (sCCC) fails [64, 65]. The existence of the apparent horizon, which is the boundary of the trapped surface region in the spacetime also determines the nature of the singularity. If at least one value of the limiting positive values \(X_0\) is less than the slope of the apparent horizon at the central singularity \((R=0,u=0)\), then the singularity is locally naked with the outgoing radial null geodesics escaping from the past to the future. This breaks the weak Cosmic Censorship Conjecture (wCCC) [64, 65].

As we are interested in the collapse of a dilaton field, we firstly introduce a coordinate system with an arbitrary evolution ways of dilaton field \(\phi ={k}\ln (R)+\Phi (T)\) by taking the transformation \(p\ln (u)\rightarrow \Phi (T)\). Then the solution becomes

$$\begin{aligned} \mathrm {d}s^{2}=-f(u,R)\frac{u^2\dot{\Phi }^2}{p^2}\mathrm {d}T^{2} {+}4g(u)R^{\ell }\frac{u\dot{\Phi }}{p}\mathrm {d}T\mathrm {d}R +R^2\mathrm {d}\psi ^2, \end{aligned}$$
(98)

where \(u=u(T)=e^{\Phi (T)/p},\dot{\Phi }=\frac{\mathrm {d}\Phi (T)}{\mathrm {d}T}\).

It is easy to calculate the equation for outgoing radial null geodesics

$$\begin{aligned}&\frac{\mathrm {d}T}{\mathrm {d}R}=\frac{4pg(u)R^{\ell }}{u\dot{\Phi }f(u,R)}=8k\ell \frac{A}{\dot{\Phi }B}, \end{aligned}$$
(99)
$$\begin{aligned}&A=e^{\Phi (\ell -1)/k}\bigg [e^{2\Phi /k}Q^2(\ell +1)+4\Lambda (\ell -1)\bigg ],\end{aligned}$$
(100)
$$\begin{aligned}&B=\bigg [-8\ell ^2R^2(e^{2\Phi /k}Q^2+4\Lambda )e^{\Phi (\ell -1)/k}-M(\ell +1)\bigg ]. \end{aligned}$$
(101)

One should note that there exist the conditions

$$\begin{aligned} k<0,\ell >1 \end{aligned}$$
(102)

for the dynamical solution, which is very important in the following discussions. Then the slope of radial null geodesics approaching the singularity \((R=0,T=0)\) along the radial null geodesic should be

$$\begin{aligned} X_0=\lim _{R=0,T=0}\frac{T}{R}=\lim _{R=0,T=0}\frac{\mathrm {d}T}{\mathrm {d}R}=8k\ell \lim _{R=0,T=0}\frac{A}{\dot{\Phi }B}. \end{aligned}$$
(103)

Considering the different evolution of the dilaton field: (1) \(\lim _{R=0,T=0}\Phi (T)=const.\); (2) \(\lim _{R=0,T=0}\Phi (T)=-\infty \); (3) \(\lim _{R=0,T=0}\Phi (T)=+\infty \), the discussion about sCCC could be divided into several cases:

  • (1) For the case with \(\lim _{R=0,T=0}\Phi (T)=\Phi _0\): \(X_0\) could be simplified as

    $$\begin{aligned} X_0=\frac{8k\ell }{[-8M(\ell +1)]}\lim _{R=0,T=0}\frac{\,A(\Phi _0)}{\dot{\Phi }}, \end{aligned}$$
    (104)

    where \(A(\Phi _0)=A|_{\Phi =\Phi _0}\). There exist three subcases:

    • If \(\Phi (T)=\Phi _0+\zeta T\), we get \(X_0=\frac{8k\ell \,A(\Phi _0)}{[-8M\zeta (\ell +1)]}\). When \(\zeta \,A(\Phi _0)>0\), \(X_0>0\) hence the sCCC fails; while the sCCC of the subcase with \(\zeta \,A(\Phi _0)<0\) always holds.

    • If \(\Phi (T)=\Phi _0+\zeta T^\eta ,\eta >1\), i.e. \(\dot{\Phi }=0\), it leads to \(X_0\rightarrow +\infty \), which corresponds to the case that the sCCC breaks.

    • If \(\Phi (T)=\Phi _0+\zeta T^\eta ,0<\eta <1\), we find \(\dot{\Phi }\rightarrow \infty \) and \(X_0=0\), thus the sCCC holds.

  • (2) For the case with \(\lim _{R=0,T=0}\Phi (T)=-\infty \): one can directly get \(\dot{\Phi }\rightarrow +\infty ,A(\Phi _0)\rightarrow +\infty \). After applying the L ’Hospital’s rule, \(X_0\) takes the limit as \(+\infty \), which indicates that the sCCC breaks.

  • (3) For the case with \(\lim _{R=0,T=0}\Phi (T)=+\infty \): i.e. \(\dot{\Phi }\rightarrow -\infty \), as \(A(\Phi _0)\rightarrow 0\), one can find \(X_0=0\) implying that the sCCC holds.

Then we consider the wCCC. The apparent horizon of the dynamical spacetime is defined by \(f(u,R)=0\). Thus we can calculate the slope of the apparent horizon at the central singularity \((R=0,T=0)\) as

$$\begin{aligned}&X_{AH}=\left( \frac{\mathrm {d}T}{\mathrm {d}R}\right) _{AH}=\frac{8k\ell ^2}{M(\ell +1)}\lim _{R=0,T=0}\frac{C}{\dot{\Phi }D}, \end{aligned}$$
(105)
$$\begin{aligned}&C=e^{2\Phi (\ell -1)/k}\bigg (e^{2\Phi /k}Q^2+4\Lambda \bigg )^2,\end{aligned}$$
(106)
$$\begin{aligned}&D=\bigg [Q^2(\ell +1)e^{\Phi (\ell +1)/k}+4\Lambda (\ell -1) e^{\Phi (\ell -1)/k}\bigg ]. \end{aligned}$$
(107)

The conditions destroying the wCCC is \(0<X_0<X_{AH}\). Similarly, we can find the following cases:

  • (1) For the case with \(\lim _{R=0,T=0}\Phi (T)=\Phi _0\): \(X_{AH}\) reduces to

    $$\begin{aligned} X_{AH}=\frac{8k\ell ^2}{M(\ell +1)}\lim _{R=0,T=0}\frac{C(\Phi _0)}{\dot{\Phi }D(\Phi _0)}, \end{aligned}$$
    (108)

    where \(C(\Phi _0)=C|_{\Phi =\Phi _0},D(\Phi _0)=D|_{\Phi =\Phi _0}\). Hence it still contains three subcases. For simplicity, here we only discuss the cases that the wCCC breaks. The results are as follow:

    • When \(\Phi (T)=\Phi _0+\zeta T\), we get \(X_{AH}=\frac{8k\ell ^2C(\Phi _0)}{M(\ell +1)\zeta D(\Phi _0)}\). As \(C(\Phi _0)>0\), The condition \(0<X_{0}<X_{AH}\) for a failed wCCC leads to \(0<\frac{\,A(\Phi _0)}{8\zeta }<-\frac{\ell \,C(\Phi _0)}{\zeta D(\Phi _0)}\).

    • If \(\Phi (T)=\Phi _0+\zeta T^\eta ,\eta >1\), i.e. \(\dot{\Phi }=0\), it leads to \(X_{AH}\rightarrow -\infty \times \,D(\Phi _0)\). If \(D(\Phi _0)\ge 0\), we obtain \(X_{AH}=-\infty <X_0\), for which the wCCC does not breaks.

    • If \(\Phi (T)=\Phi _0+\zeta T^\eta ,0<\eta <1\), we get \(\dot{\Phi }\rightarrow \infty \) and \(X_{AH}=0=X_{0}\), thus the wCCC does not breaks as well.

  • (2) For the case with \(\lim _{R=0,T=0}\Phi (T)=-\infty \): one can derive that \(X_{AH}=-\infty <X_{0}\), which corresponds to the subcase that the wCCC does not breaks.

  • (3) For the case with \(\lim _{R=0,T=0}\Phi (T)=+\infty \): it corresponds to \(X_{AH}=0=X_0\), implying that the sCCC does not fail.

From the discussion above, it is obvious that the evolution of dilaton field does affect the nature of the dynamical spacetime.

Table 1 The parameters for solutions
Full size table

6 Conclusion

In this paper, we present the static charged dilaton solutions and black hole formation in three dimensions. There are always two families of solutions of physical interest: the famous Chan–Mann charged dilaton solution with \(b=4a\) and another charged dilaton solution with \(b\ne 4a\) (One can look at Table 1 for different parameter choices of solutions). We discuss their geometrical properties, the horizon structure and the causal structure. The parameter bounds for the existence of static black holes are summarized in Table 2. Besides, we find:

  • There exist (non-)extremal black holes and black holes with negative mass for Chan–Mann solution, while there exist only black holes with a single event horizon for another dilaton solution.

  • The (un)charged black holes of this two families both have a negative cosmological constant, which is consistent with the No-Go theorem in three dimensions [48].

The time-dependent solution is also presented (See Table 1), which can characterize the three dimensional charged black hole formation in Einstein–Dilaton gravity. Especially, there is no exact time-dependent solution describing the gravitational collapse to the Chan–Mann charged dilaton black hole, which is a submanifold of \(3+1\) dimensional Einstein spactime based on the viewpoint of the Kaluza–Klein theory, therefore no extra matter source can drive an evolution of the spacetime. Finally, we discuss the gravitational collapse of a dilaton field in the context of the CCC, and summarize the conditions for breaking the CCC in Table 3. It is clear that the evolution of dilaton field does affect the properties of the dynamical spacetime.

Table 2 The parameter bounds for the existence of static black holes. There only exist black holes with \(\Lambda <0\)
Full size table

For the future tasks, one can apply T-duality to the static charged dilaton black holes, in order to obtain rotating charged black hole solutions in Einstein–Maxwell–Dilaton gravity. Considering the Einstein–Maxwell–Dilaton gravity with the fluid source, one can construct the Vaidya-like solution describing the formation of Chan–Mann charged dilaton black hole. Besides, we will consider the effect of dilaton field on the physical properties of black holes, including the causal structure and black hole thermodynamics. Based on the AdS/CFT correspondence, it is also interesting to use the charged time-dependent AdS black hole solutions to study non-equilibrium thermalization of certain strongly-coupled field theory.

Table 3 The conditions for breaking the Cosmic Censorship Conjecture. These conditions are all related close to the evolution of a dilaton field
Full size table