1 Introduction

Standard quantum mechanics and general relativity, in spite of their wonderful successes, are not capable of addressing separately the physical phenomena near the Planck scale. A unified theory of quantum mechanics and general relativity, quantum gravity, is the ultimate theory governing such an extreme scale. Despite many attempts and efforts, we were unable to formulate the ultimate quantum gravity theory so far. Nevertheless, there are some elegant approaches to quantum gravity proposal capable of realizing some phenomenological aspects of the final theory. A phenomenological, and in the same time mathematical, outcome of known approaches to quantum gravity is the realization of a minimal length scale of the order of the Planck length. Albeit, such a cutoff can be implemented in the framework of an effective field theory approach. This natural cutoff that regularizes quantum field theory in a fascinating manner, comes out nontrivially from marriage of gravity with quantum mechanics for instance, in Heisenberg’s Electron Microscope Gedanken Experiment, by approving the existence of a minimal uncertainty in position measurement. Therefore, as a nontrivial assumption one can quantum theoretically describe the minimal length as a nonzero uncertainty in position measurement. The existence of such a minimal measurable length restricts the resolution of spacetime adjacent points. While in the standard quantum mechanics there is essentially no limit on the complete resolution of spacetime points, in a gravitational quantum mechanics this resolution is finite, resulting a discrete structure for spacetime manifold at the Planck scale [1,2,3,4,5,6,7].

Incorporation of such a minimal length cutoff in standard quantum mechanical problems imposes several important corrections on the basics of these problems. A vast number of research papers in recent years are devoted to this issue and some lights are shed on phenomenological aspects of the final quantum gravity proposal, see for instance [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25]. For some more recent references see for instance [26,27,28,29,30,31]. Recently in the context of the DSR theories (for review see [32,33,34,35,36]), it is shown that as a result of the existence of a minimal measurable length, there should be a maximum measurable momentum, of the order of the Planck momentum, to the measurement precision of the particles’ momentum [37,38,39,40]. That is, there is an upper bound for a test particles’ momentum. Adopting a GUP that admits the presence of both a minimal length and a maximal momentum [41,42,43,44] provides some novel and interesting features which ordinary quantum mechanics is unable to explain them in essence [44, 45]. It seems that the outcomes of all these attempts could be considered essentially as the foundation of a so-called gravitational quantum mechanics which may be a road toward the ultimate quantum theory of spacetime/quantum gravity. With a minimal length cutoff in spacetime structure, which mathematically can be attributed to the compactness of symplectic manifolds [46], the Hilbert space representation of the standard quantum mechanics fails to be consistent since the notion of locality and also position space representation needs to be reconsidered [11, 47,48,49,50]. In this case one can proceed either in momentum space representation (in the absence of a minimal momentum) or construct a set of maximally localized states (a generalization of the standard quantum mechanics’ Hilbert space based on the maximally localized states). It is possible also to work in quasi-space representation [11]. When one considers both a minimal length and a maximal momentum, some shortcomings of the seminal reference [11] can be addressed properly [44]. This issue gets even more complication if one considers another cutoff, that is, a minimal measurable momentum which provides an infra-red cutoff [48, 51,52,53,54].

With these preliminaries, in the present work our main goal is to study the modifications of kernel functions and then the Feynman path integrals in the presence of both a minimal length and a maximal momentum. This is an important issue since it potentially sheds some light on quantum field theory (its regularity and renormalizability) and also statistical physics (through the connection between the path integral and partition function) in the presence of these cutoffs. We start by an overview on GUP and some of its implications in the realm of quantum mechanics. We show that these modifications result in a generalized form of the kernel functions in the context of quantum mechanics. Then we look at the Feynman path integral formalism in the presence of these cutoffs. Incorporation of these natural cutoffs makes the path integrals and scattering amplitudes to be naturally ultra-violet regularized. We show that unlike the ordinary quantum mechanics, here we would have the wave-like approach towards this formulation as well as the particle-like approach. Finally, as an important application of modified path integrals, we use the connection between the path integrals and statistical mechanics to obtain a modified partition function in the presence of natural cutoffs and then we study modifications of some thermodynamical properties of an ideal gas in this context. A brief summary and conclusion closes this work.

2 Generalized (gravitational) uncertainty principle

Heisenberg uncertainty principle is described by the relation

$$\begin{aligned} \Delta x \approx \frac{\hbar }{\Delta p}. \end{aligned}$$
(1)

To achieve such a relation one can follow the Heisenberg’s Electron Microscope Gedanken Experiment. However, in deriving such a relation Heisenberg had disregarded the gravitational interaction of the light beams (photons) with electron. Since gravity is coupled to everything, one has to consider such a gravitational interaction between photon and electron. Specially, when one tries to probe electron position more carefully with more energetic photons, incorporation of such a gravitational interaction is inevitable. The situation becomes even more serious when one approaches the high energy regime towards the Planck scale. In such a scales (\(\approx 10^{19}~\hbox {GeV}\)), the Schwarzschild radius becomes comparable with the Compton wavelength. When one includes the gravitational effects of very high energy beams (photons), a gravitational contribution to the position uncertainty emerges as [7]

$$\begin{aligned} {\Delta x}_{g} \approx \frac{G\hbar }{\lambda c^3}, \end{aligned}$$

where \(\lambda \) is the photon’s wavelength. So, taking this effects into account, one must add the new source of uncertainty (the gravitational contribution) to the HUP and thus the ordinary HUP turns into the Gravitational (Generalized) Uncertainty Principle or GUP as

$$\begin{aligned} \Delta x \approx \frac{\hbar }{\Delta p} + \ell _{Pl}^2 \frac{\Delta p}{\hbar }, \end{aligned}$$
(2)

where \(\ell _{Pl}=\sqrt{\frac{G\hbar }{c^3}}\) is the Planck length. In the framework of HUP, it is possible in principle to determine the position of a test particle accurately, i.e. \(\Delta x\rightarrow 0\). This is possible since uncertainty in momentum can be large towards \(\Delta p\rightarrow \infty \). However, with GUP as (2), it is impossible to reach \(\Delta x\rightarrow 0\) even for \(\Delta p\rightarrow \infty \). In fact, in this case there exists a minimal uncertainty in the test particle’s position measurement which is of the order of the Planck length, \(\Delta x_{min}\sim \ell _{Pl}\). From a string theory viewpoint, this minimal uncertainty could be of the order of the string length, \(\Delta x_{min}\sim \ell _{S}\) [1, 2]. From this result, one can nontrivially conclude that there must be a minimum, physically meaningful distance [7]; a minimal length, which cannot be probed in essence. This means that one faces with a finite and limited resolution of adjacent spacetime points. As a result, the size of a test particle, \(\ell _{tp}\), cannot be smaller than such a minimal measurable length, \(\ell _{tp}\ge (\Delta x)_{min}\). Existence of such a minimal length makes quantum field theory to be UV-regularized [25]. It gives also a discrete structure of the very spacetime [42]. In another perspective, spacetime attains a fuzzy [55] or even granular structure [56]. Point-particles are no longer definable, instead a particle smears in a finite region of space [57]. This minimum distance is because of the fluctuations of the background spacetime metric due to the very powerful gravitational effects.

It is shown that one of the common form of GUP in the presence of minimal length would be represented as [21, 22]

$$\begin{aligned} \Delta x_{i} \Delta p_{i} \ge \frac{\hbar }{2}\bigg [1 + \beta \Big ((\Delta p)^2 + \langle p\rangle ^2\Big ) + 2\beta \Big ((\Delta p_{i})^2 + \langle p_{i}\rangle ^2\Big )\bigg ],\nonumber \\ \end{aligned}$$
(3)

where \(\beta \) is the GUP parameter and would be defined as

$$\begin{aligned} \beta = \frac{\beta _0}{(M_{pl}c)^2}=\beta _0\frac{\ell _{pl}^2}{\hbar ^2}, \end{aligned}$$

so that \([\beta ]=(momentum)^{-2}\) and \(\beta _0\) is a dimensionless quantity. It is normally assumed that \(\beta _0\) is of the order of unity, \(\beta _0\approx 1\). One can find that the inequality (3) follows the modified Heisenberg algebra as

$$\begin{aligned}{}[x_{i},p_{j}] = i\hbar \Big [\delta _{ij} + \beta (p^2 \delta _{ij} + 2 p_{i}p_{j})\Big ], \end{aligned}$$
(4)

which ensures the Jacobi identity, \([[x_i,x_j],p_k]+[[x_j,p_k],x_i]+[[p_k,x_i],x_j]=0\), with respect to the canonical commutation relations \([x_i,p_j]=i\hbar \delta _{ij}\) and \([x_i,x_j]=0=[p_i,p_j]\).

In the framework of DSR theories one encounters another type of the modified Heisenberg algebra as [40]

$$\begin{aligned}{}[x_{i},p_{j}] = i\hbar \Big [(1-\ell _{pl}|{\vec {p}}|)\delta _{ij}+ \ell _{pl}^2\,p_{i}p_{j}\Big ]. \end{aligned}$$
(5)

This type of GUP, in addition to a minimum distance \((\Delta x)_{min}\), refers to a maximum physically meaningful momentum of the order of the Planck momentum, \((\Delta p)_{max}\approx P_{pl}\). This means that we can never measure a test particle’s momenta larger than a maximal momenta, i.e. \(P_{tp}\le (\Delta p)_{max}\). As the latter case, via the Jacobi identity and also the canonical commutation relations the following more common form would be obtained for (5) [41, 43]

$$\begin{aligned}{}[x_{i},p_{j}] = i\hbar \bigg [\delta _{ij} - \alpha \Big (p\delta _{ij} + \frac{p_{i}p_{j}}{p}\Big ) + \alpha ^2\Big (p^2 \delta _{ij} + 3p_{i}p_{j}\Big )\bigg ],\nonumber \\ \end{aligned}$$
(6)

where \(\alpha =\frac{\alpha _{0}}{M_{pl}c}\) and \(\alpha _{0}\approx 1\). Dimensionally \(\alpha \) is related to \(\beta \) with \([{\alpha }^2]=[\beta ]\). In one dimension, from Eq. (6) up to \({\mathcal {O}}({\alpha }^{2})\) we obtain

$$\begin{aligned} \Delta x \Delta p\ge & {} \frac{\hbar }{2}\ \Big (\ 1 - 2\alpha \langle p\rangle +\ 4\alpha ^2 \langle p^2\rangle \ \Big )\nonumber \\\ge & {} \frac{\hbar }{2}\left[ 1 + \left( 4\alpha ^{2} + \frac{\alpha }{\sqrt{\langle p^2\rangle }}\right) (\Delta p)^2 \right. \nonumber \\&\left. + 4\alpha ^2 \langle p\rangle ^2 - 2\alpha \sqrt{\langle p^2\rangle }\phantom {\ge \frac{\hbar }{2}\left[ 1 + \left( 4\alpha ^{2} + \frac{\alpha }{\sqrt{\langle p^2\rangle }}\right) (\Delta p)^2 \right. }\right] \end{aligned}$$
(7)

whence we can conclude the corresponding Heisenberg algebra for this type of GUP as [44]

$$\begin{aligned}{}[x,p] = i\hbar \Big (1 - \alpha p + 2\alpha ^2 p^2\Big ). \end{aligned}$$
(8)

All these preliminaries reveal that in order to study the very high energy physics towards the Planck scale, like the very early universe, one should adopt some generalization in quantum mechanics due to gravitational effects. That is, foundations of the standard quantum mechanics need a thorough reconsideration in the presence of gravitational effects. Now, by using the mentioned GUPs and modified Heisenberg algebra we can proceed to introduce some basic notions of a gravitational quantum mechanics.

3 Some fundamental features of a gravitational quantum mechanics

In this section, we are going to study some basic features of a quantum mechanics where gravitational effects are taken into account via a phenomenologically generalized uncertainty principle. We start by defining the operators \(\mathcal P\) and \(\mathcal X\) in the following forms

$$\begin{aligned} {\mathcal P}= & {} p\nonumber \\ {\mathcal X}= & {} (1-\alpha p+2{\alpha }^2 p^2)x \end{aligned}$$
(9)

where x and p satisfy the canonical commutation relation \([x,p]=i\hbar \), and \(\mathcal P\), \(\mathcal X\) satisfy the relation (8). One can interpret x as the position operator at low energies that is the realm of ordinary quantum mechanics, and \(\mathcal X\) as the position operator at the high energies near the Planck scale; the realm of Quantum Gravity.

In this situation, the generalized identity operator would be represented as [44]

$$\begin{aligned} \mathbf 1 =\int _{-P_{pl}}^{+P_{pl}}|p\rangle \langle p| \frac{dp}{1-\alpha p+2\alpha ^2 p^2}, \end{aligned}$$
(10)

and the generalization of the scalar product of momentum eigenstates would be obtained as

$$\begin{aligned} \langle p|p'\rangle =\Big (1-\alpha p+2\alpha ^2 p^2\Big )\delta (p-p'). \end{aligned}$$
(11)

Now our proposed playground is no longer the standard quantum mechanics, but we are studying a gravitational quantum mechanics which includes a minimal length and also a maximal momentum as natural cutoffs. With a maximal momentum cutoff, the bounds of integrals over p change from \((-\infty ,+\infty )\) to \([-P_{pl}, +P_{pl}]\). Also, because of the presence of a minimal length cutoff, the notion of a point in the language of mathematical analysis breaks down and therefore position space representation should be reconsidered and modified. Hence, one needs to reconstruct a new quantum mechanical framework (Hilbert space) based on a modified position space representation. We refer to Refs. [11, 44, 47] for early works on the issue of Hilbert space representation in the presence of cutoffs. To proceed, we choose to work in the quasi-position space which is a redefinition of the usual position space representation [11, 44, 49]. In the standard quantum mechanics we deal with the concept of absolute localization for particles and the commutation relation

$$\begin{aligned}{}[x_i,x_j]=0, \end{aligned}$$
(12)

holds. This is because there is, in principle, no restriction on the position measurements and one can have the absolute accuracy (complete resolution) in the position measurements, i.e. \((\Delta x)_{min}=0\). So, space has a commutative geometry. But by considering the natural effects of gravity in the ultraviolet regime, there appears a nonzero minimum uncertainty in position measurements, \((\Delta x)_{min}\ne 0\), which prevents absolute accuracy in our measurements of the position. This minimal uncertainty in position measurement means that a test particle, at best, can be localized in a finite length, i.e. it can only be maximally localized up to a minimal measurable length. In this regard, a complete resolution of adjacent points of spacetime is impossible. Also, in GUP framework, because of the minimum measurable length, we have no longer a commutative structure of spacetime, that is, (see Ref. [44])

$$\begin{aligned}{}[{\mathcal {X}}_i,{\mathcal {X}}_j]=i\alpha \hbar \left( 4\alpha -\frac{1}{p}\right) ({\mathcal {P}}_i{\mathcal {X}}_j-{\mathcal {P}}_j{\mathcal {X}}_i)\ne 0. \end{aligned}$$
(13)

On the other hand, we cannot build a Hilbert space on the position space wave functions \(\psi _{\alpha }(x)=\big <x|\alpha \big>\), because there is no longer a zero uncertainty in position measurement

$$\begin{aligned} (\Delta x)^2 _{|\psi>}=\big<\psi |(X-\big <\psi |X|\psi \big>)^2|\psi \big >\ge (\Delta x)_{min}, \end{aligned}$$
(14)

and thus there can not be any physical state as a position eigenstate [11, 44, 47]. Therefore, the ordinary position space representation is no longer applicable. The appropriate choice is the quasi-position representation [11]. In this representation we have the maximal localization states \(|\varphi ^{Ml}_{x}\big>\) with given position expectation value x

$$\begin{aligned} \langle \varphi ^{Ml}_x|X|\varphi ^{Ml}_x\rangle =x. \end{aligned}$$
(15)

In the quasi-position representation, the notion of point, strictly speaking localizability, would be modified from zero to the minimum measurable distance, and one has

$$\begin{aligned} (\Delta x)_{|\varphi ^{Ml}_x\rangle }=(\Delta x)_{min}\simeq \ell _{Pl}. \end{aligned}$$
(16)

In this framework, one can find the momentum space wave functions \(\varphi ^{Ml}_x (p)\) of the states that are maximally localized [in the language of Eq. (15)] around a position x as in Ref. [44])

$$\begin{aligned} \varphi ^{Ml}_x(p)= & {} \frac{\sqrt{6\alpha }\left[ \sqrt{8}e^{\eta \tan ^{-1}(\eta )}-e^{-\eta \tan ^{-1}\left( \frac{\eta }{3}\right) }\right] ^{-\frac{1}{2}}}{(1-\alpha p+2\alpha ^2 p^2)^{\frac{3}{4}}}\nonumber \\&\times e^{-\frac{\eta }{2}\tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) } e^{-i\frac{2x}{\alpha \hbar \sqrt{7}}\left( \tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) +\tan ^{-1}\left( \frac{\eta }{3}\right) \right) }\nonumber \\ \end{aligned}$$
(17)

in which \(\eta =\frac{4\alpha P_{{Pl}}+1}{\sqrt{7}}\simeq \frac{3}{\sqrt{7}}\). Note that these states are calculated for \(\big <p\big >=0\), i.e. the absolutely, maximally localized states, and \(\Delta p\simeq \frac{1}{2\alpha }\), i.e. the states of critical momentum uncertainty which are obtained at the boundary of the allowed region where the minimal position uncertainty \((\Delta x)_{min}\simeq 2\alpha \hbar \) is achieved (for details see [44]). By projecting arbitrary states \(|\phi \rangle \) on maximally localized states \(|\varphi ^{Ml}_x\rangle \), we can define the state’s quasi-position wave function as the probability amplitude for the particle being maximally localized around the position x

$$\begin{aligned} \phi (x):=\langle \varphi ^{Ml}_x|\phi \rangle . \end{aligned}$$
(18)

Now we are in the position to present the quasi-position wave function which is counterpart of the standard position space wave function in the presence of quantum gravitational effects encoded in cutoffs. The transformation of a momentum space wave function into a quasi-position space (qps) wave function, \(\psi ^{qps}(x)\), is given by

$$\begin{aligned} \psi ^{qps}(x)= & {} \sqrt{6\alpha }\left[ \sqrt{8}e^{\eta \tan ^{-1}(\eta )}-e^{-\eta \tan ^{-1}\left( \frac{\eta }{3}\right) }\right] ^{-\frac{1}{2}}\nonumber \\&\times \int _{-P_{pl}}^{+P_{pl}}(1-\alpha p+2\alpha ^2 p^2)^{-\frac{3}{4}}\nonumber \\&\times e^{-\frac{\eta }{2}\tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) }\ e^{i\frac{2x}{\alpha \hbar \sqrt{7}}\left( \tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) +\tan ^{-1}\left( \frac{\eta }{3}\right) \right) }\nonumber \\&\times \psi (p)\frac{dp}{1-\alpha p+2\alpha ^2 p^2}, \end{aligned}$$
(19)

which is a generalization of the Fourier transformation. Then, by inverse Fourier transform we obtain the transformation of a quasi-position space wave function to a momentum space wave function as [44]

$$\begin{aligned} \psi (p)= & {} \left[ \frac{\sqrt{8}e^{\eta \tan ^{-1}(\eta )}-e^{-\eta \tan ^{-1}\left( \frac{\eta }{3}\right) }}{24\pi ^2\hbar ^2\alpha }\right] ^{\frac{1}{2}}\nonumber \\&\times \int _{-\infty }^{+\infty }(1-\alpha p+2\alpha ^2 p^2)^{\frac{3}{4}}\nonumber \\&\times e^{\frac{\eta }{2}\tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) } e^{-i\frac{2x}{\alpha \hbar \sqrt{7}}\left( \tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) +\tan ^{-1}\left( \frac{\eta }{3}\right) \right) }\nonumber \\&\times \psi ^{qps}(x)dx. \end{aligned}$$
(20)

In analogy with ordinary quantum mechanics one can derive the modified wave number in quasi-position space as

$$\begin{aligned} e^{ix\frac{2}{\alpha \hbar \sqrt{7}}\left( \tan ^{-1}(\frac{4\alpha p-1}{\sqrt{7}})+\tan ^{-1}\left( \frac{\eta }{3}\right) \right) } \equiv e^{ix{\mathcal {K}}_{qps}}, \end{aligned}$$
(21)

and therefore the modified wavelength is given by

$$\begin{aligned} \lambda _{qps}(p)=\frac{\pi \alpha \hbar \sqrt{7}}{\tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) +\tan ^{-1}\left( \frac{\eta }{3}\right) }. \end{aligned}$$
(22)

This means interestingly that, by using the de Broglie relation \(p=\frac{h}{\lambda }\), one can define a quasi-momentum \({\mathcal {P}}_{qps}(p)\equiv \frac{h}{\lambda _{qps}(p)}\) in quasi-position representation which has the following form

$$\begin{aligned} {\mathcal {P}}_{qps}(p)=\frac{2}{\alpha \sqrt{7}}\left( \tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) +\tan ^{-1}\left( \frac{\eta }{3}\right) \right) . \end{aligned}$$
(23)

By using the Eqs. (22) and (23), there would be a modified form of the particle’s energy (we call it “quasi-energy”) which is responsible for the time evolution of quasi-position wave functions. In standard quantum mechanics, time evolution of a state vector \(|\psi (t)\rangle \) of a system is given by \(i\hbar \, \partial _{t}|\psi (t)\rangle = H|\psi (t)\rangle \), whence it follows the time evolution operator \(U(t,t_0)\) as

$$\begin{aligned} |\psi (t)\rangle = U(t,t_{0})|\psi (t_0)\rangle ,\quad \quad \quad U(t,t_{0})\equiv e^{-i\frac{H(t-t_0)}{\hbar }}. \end{aligned}$$
(24)

So, the time-dependent wave function in quasi-position space, \(\psi ^{Ml}(x,t)\), evolves as follows

$$\begin{aligned} \psi ^{Ml}(x,t)= & {} \langle \varphi ^{Ml}_x|\psi (t)\rangle =\left\langle \varphi ^{Ml}_x|e^{-i\frac{H(t-t_0)}{\hbar }}|\psi (t_0)\right\rangle . \end{aligned}$$
(25)

Now, with these preliminaries we study two important issues, propagators and Feynman path integrals, in the context of gravitational quantum mechanics.

4 Kernel functions

In this section we focus on the modifications of kernel functions K which generally are defined as

$$\begin{aligned} (T\psi )(x,t)=\int _{-\infty }^{+\infty } K(x,t;x',t')\ \psi (x',t')\ dx'. \end{aligned}$$
(26)

In standard quantum mechanics, using the Heisenberg picture one defines a propagator

$$\begin{aligned} K(x_f, t_f; x_i, t_i)=\langle x_f,t_f|x_i,t_i\rangle _{Heisenberg} \end{aligned}$$
(27)

as the probability amplitude to find a point particle in the position \(x_{f}\) at the time \(t_{f}\), while initially it was in the position \(x_{i}\) at the time \(t_{i}\). Based on what was explained in the previous section, in the quasi-position formalism we can write

$$\begin{aligned} K_{qps}(x_f, t_f; x_i, t_i)=\langle \varphi ^{Ml}_{x_f},t_f|\varphi ^{Ml}_{x_i},t_i\rangle _{Heisenberg}. \end{aligned}$$
(28)

This is a generalized form of propagator in the so-called gravitational quantum mechanics, where we displaced the localized states \(|x\rangle \) with the maximally localized states \(|\varphi ^{Ml}_x\rangle \). Using Eq. (10) we can expand \(K_{qps}\) in the momentum space bases as

$$\begin{aligned}&K_{qps}(x_f, t_f; x_i, t_i)\nonumber \\&\quad =\int _{-P_{pl}}^{+P_{pl}}\langle \varphi ^{Ml}_{x_{{f}}},t_{f}|p\rangle \langle p|\varphi ^{Ml}_{x_{{i}}},t_{i}\rangle \frac{dp}{1-\alpha p+2\alpha ^2 p^2}. \end{aligned}$$
(29)

Then, from Eqs. (19) and (20) and also the formal relation \(e^{i H}|p\rangle =e^{i E_{p}}|p\rangle \) we find

$$\begin{aligned}&K_{qps}(x_f, t_f; x_i, t_i)\nonumber \\&\quad =\frac{1}{2\pi \hbar }\int _{-P_{pl}}^{+P_{pl}}e^{-i\frac{E_{p}(t_{f}-t_{i})}{\hbar }}e^{i\frac{2(x_{f}-x_{i})}{\alpha \hbar \sqrt{7}} \left( \tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) +\tan ^{-1}\left( \frac{\eta }{3}\right) \right) }\nonumber \\&\qquad \times \frac{dp}{1-\alpha p+2\alpha ^2 p^2}. \end{aligned}$$
(30)

Mathematically one can easily explore the differences between this result and the corresponding one in ordinary quantum mechanics since in the limit of \(\alpha \rightarrow 0\) (or \(P_{pl}\longrightarrow \infty \)) one recovers the ordinary quantum mechanics’ Kernel function as

$$\begin{aligned}&\lim _{\alpha \rightarrow 0}K_{qps}(x_f, t_f; x_i, t_i)\nonumber \\&\quad =\frac{1}{2\pi \hbar }\int _{-\infty }^{+\infty }e^{-i\frac{E_{p}(t_{f}-t_{i})}{\hbar }}e^{i\frac{p(x_{f} -x_{i})}{\hbar }}dp. \end{aligned}$$
(31)

But physically the main difference with the standard case comes from the modification of the standard dispersion relation, since now one faces with, in essence, the replacement of p with \(p\big (1 - \alpha p + 2\alpha ^2 p^2\big )\). The outcome of such a modified dispersion relation is, in addition to regularization of underlying quantum field theory, a possible violation of the Lorentz symmetry at the high energy regime. The form of dispersion relation is fixed by the Lorentz symmetry, but in the presence of minimal length and maximal momentum the dispersion relation gets modified leading to Lorentz symmetry breaking. While Lorentz symmetry is one of the most important symmetry in the nature, it can be potentially broken in the ultraviolet regime. So, we can attribute the conceptual difference of our result with the corresponding standard results to the modification of the standard dispersion relation. This modification can be originated from spacetime foam, spacetime discreteness, spacetime fuzziness or spacetime noncommutativity. All these notions are related conceptually. We note that generalization of the issue of modified dispersion relation to a curved spacetime leads to the idea of gravity’s rainbow.

Note that the modified Kernel function (30) depends on the form of energy \(E_{p}\). For this reason, we proceed in two approaches: particle-like and wave-like approaches where energy is given as \(E=\frac{1}{2m}p^2\) and \(E=h\nu \) respectively.

4.1 Particle-like approach

In this case we consider a free particle. But, according to what was mentioned in the previous section, we should now put the modified form of the energy inspired by the quasi-momentum, \({\mathcal {P}}_{qps}(p)=\hbar {\mathcal {K}}_{qps}(p)\). So, the related kernel function in quasi-position formalism would be

$$\begin{aligned}&K_{qps}(x_f, t_f; x_i, t_i)\nonumber \\&\quad =\frac{1}{2\pi \hbar }\int _{-P_{pl}}^{+P_{pl}}e^{-i\frac{{\mathcal {P}}_{qps}^2(t_{f}-t_{i})}{2m\hbar }}e^{i\frac{2(x_{f}-x_{i})}{\alpha \hbar \sqrt{7}} \left( \tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) +\tan ^{-1}\left( \frac{\eta }{3}\right) \right) }\nonumber \\&\qquad \times \frac{dp}{1-\alpha p+2\alpha ^2 p^2} \end{aligned}$$
(32)

and from Eq. (23) we would have

$$\begin{aligned}&K_{qps}(x_f, t_f; x_i, t_i)\nonumber \\&\quad =\frac{1}{2\pi \hbar }\int _{-P_{pl}}^{+P_{pl}}e^{-i\frac{2(t_{f}-t_{i})}{7m\alpha ^{2}\hbar }\left( \tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) +\tan ^{-1}\left( \frac{\eta }{3}\right) \right) ^2}\nonumber \\&\qquad \times e^{i\frac{2(x_{f}-x_{i})}{\alpha \hbar \sqrt{7}}\left( \tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) +\tan ^{-1}\left( \frac{\eta }{3}\right) \right) }\frac{d p}{1-\alpha p+2\alpha ^2 p^2}.\nonumber \\ \end{aligned}$$
(33)

Then by some calculations one can solve this integral to obtain

$$\begin{aligned}&K_{qps}(x_f, t_f; x_i, t_i)\nonumber \\&\quad =\sqrt{\frac{m}{i2\pi \hbar (t_f-t_i)}}e^{i\frac{m(x_f-x_i)^2}{2\hbar (t_f-t_i)}}\nonumber \\&\qquad \times \left[ \frac{1}{2}erf\left( \sqrt{i\frac{2(t_f-t_i)}{7\alpha ^2m\hbar } }\left( 2\tan ^{-1}\left( \frac{\eta }{3}\right) \right. \right. \right. \nonumber \\&\qquad \left. \left. -\frac{\alpha m\sqrt{7}(x_f-x_i)}{2(t_f-t_i)}\right) \right) \nonumber \\&\qquad -\frac{1}{2}erf\left( \sqrt{i\frac{2(t_f-t_i)}{7\alpha ^2m\hbar }}\left( \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta )\right. \right. \nonumber \\&\qquad \left. \left. \left. -\frac{\alpha m\sqrt{7}(x_f-x_i)}{2(t_f-t_i) }\right) \right) \right] , \end{aligned}$$
(34)

where erf(x) is the error function. This is the modified kernel function for a free particle in the quasi-position representation with maximally localized states and modified energy spectrum. In the limit \(\alpha \rightarrow 0\) one can check that

$$\begin{aligned} \lim _{\alpha \rightarrow 0}K_{qps}(x_f, t_f; x_i, t_i)=\sqrt{\frac{m}{i2\pi \hbar (t_f-t_i)}}e^{i\frac{m(x_f-x_i)^2}{2\hbar (t_f-t_i)}} \end{aligned}$$
(35)

which is the standard (non-deformed) free particle’s kernel function as is expected from the correspondence principle. Using the error function’s expansion series as

$$\begin{aligned} erf(x)=\sum _{n=0}^{\infty }{\frac{2(-1)^{n}{x}^{2n+1}}{\sqrt{\pi }n!(2\,n+1)}}, \end{aligned}$$

we can expand Eq. (34) to find

$$\begin{aligned}&K_{qps}(x_f, t_f; x_i, t_i)\nonumber \\&\quad =\sqrt{\frac{m}{i2\pi \hbar (t_f-t_i)}}e^{i\frac{m(x_f-x_i)^2}{2\hbar (t_f-t_i)}}\nonumber \\&\qquad \times \left\{ \left( i\frac{2(t_f-t_i)}{7\pi m\alpha ^2\hbar }\right) ^{\frac{1}{2}}\tan ^{-1}\left( \frac{1}{\sqrt{7}}\right) \right. \nonumber \\&\qquad +\frac{1}{3\sqrt{\pi }}\left( i\frac{2(t_f-t_i)}{7\pi m\alpha ^2\hbar }\right) ^{\frac{3}{2}}\tan ^{-1}\left( \frac{1}{\sqrt{7}}\right) \nonumber \\&\qquad \times \left[ -\frac{21\alpha ^2m^2(x_f-x_i)^2}{4(t_f-t_i)^2}-\frac{3\sqrt{7}\alpha m(x_f-x_i)}{2(t_f-t_i)}\right. \nonumber \\&\qquad \times \left( \tan ^{-1}\left( \frac{3}{\sqrt{7}}\right) \right) ^{2}-7\left( \tan ^{-1}\left( \frac{1}{\sqrt{7}}\right) \right) ^2\nonumber \\&\qquad -3\tan ^{-1}\left( \frac{3}{\sqrt{7}}\right) \left[ \tan ^{-1}\left( \frac{1}{\sqrt{7}}\right) \right. \nonumber \\&\qquad \left. \left. \left. +\tan ^{-1}\left( \frac{3}{\sqrt{7}}\right) +\cdots \right] +\cdots \phantom {\times \left\{ \left( i\frac{2(t_f-t_i)}{7\pi m\alpha ^2\hbar }\right) ^{\frac{1}{2}}\tan ^{-1}\left( \frac{1}{\sqrt{7}}\right) \right. }\right] +\cdots \right\} . \end{aligned}$$
(36)

It is important to note that the role of a maximal momentum in this setup is that it solves some shortcomings of the theory without such a cutoff such as divergence of a free particle’s energy. In another words, a kernel obtained in the presence of just a minimal length results in a divergent particle’s energy that can be resolved by taking the maximal momentum into account.

4.2 Wave-like approach

In the wave-like approach, by respect to the modified form of the frequency in the quasi-position space representation as

$$\begin{aligned} \nu _{qps}=\frac{c}{\pi \alpha \hbar \sqrt{7}}\left( \tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) +\tan ^{-1}\left( \frac{\eta }{3}\right) \right) , \end{aligned}$$
(37)

we obtain the modified Planck relation as

$$\begin{aligned} E=\frac{2c}{\alpha \sqrt{7}}\left( \tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) +\tan ^{-1}\left( \frac{\eta }{3}\right) \right) . \end{aligned}$$
(38)

Thus, by putting this modified relation of energy into Eq. (30), the corresponding kernel function would be represented as

$$\begin{aligned}&K_{qps}(x_f, t_f; x_i, t_i)\nonumber \\&\quad =\frac{1}{2\pi \hbar }\int _{-P_{pl}}^{+P_{pl}}e^{-i\frac{2c(t_f-t_i)}{\alpha \hbar \sqrt{7}}\left( \tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) +\tan ^{-1}\left( \frac{\eta }{3}\right) \right) }\nonumber \\&\qquad \times e^{i\frac{2(x_f-x_i)}{\alpha \hbar \sqrt{7}}\left( \tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) +\tan ^{-1}\left( \frac{\eta }{3}\right) \right) }\frac{dp}{1-\alpha p+2\alpha ^2 p^2}.\nonumber \\ \end{aligned}$$
(39)

Solving this integral, we obtain the modified kernel function in the wave-like approach as

$$\begin{aligned}&K_{qps}(x_f, t_f; x_i, t_i)\nonumber \\&\quad =\frac{i}{2\pi [c(t_f-t_i)-(x_f-x_i)]}\left[ e^{-i\frac{4[c(t_f-t_i)-(x_f-x_i)]}{\alpha \hbar \sqrt{7}}\left( \tan ^{-1}\left( \frac{\eta }{3}\right) \right) }\right. \nonumber \\&\qquad \left. -e^{-i\frac{2[c(t_f-t_i)-(x_f-x_i)]}{\alpha \hbar \sqrt{7}}\left( \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta )\right) }\right] . \end{aligned}$$
(40)

Then, using Euler’s formula this can be written as

$$\begin{aligned}&K_{qps}(x_f, t_f; x_i, t_i)\\&\quad =K_{qps}^{(Re)}(x_f, t_f; x_i, t_i)+iK_{qps}^{(Im)}(x_f, t_f; x_i, t_i), \end{aligned}$$

so that

$$\begin{aligned}&K_{qps}^{Re}(x_f, t_f; x_i, t_i)\nonumber \\&\quad =\frac{1}{2\pi [c(t_f-t_i)-(x_f-x_i)]}\nonumber \\&\qquad \times \left\{ \sin \left( \frac{4[c(t_f-t_i)-(x_f-x_i)]}{\alpha \hbar \sqrt{7}}\left[ \tan ^{-1}\left( \frac{\eta }{3}\right) \right] \right) \right. \nonumber \\&\qquad +\sin \left( \frac{2[c(t_f-t_i)-(x_f-x_i)]}{\alpha \hbar \sqrt{7}}\right. \nonumber \\&\qquad \times \left. \left. \left[ \tan ^{-1}(\eta )-\tan ^{-1}\left( \frac{\eta }{3}\right) \right] \phantom {\times \left\{ \sin \left( \frac{4[c(t_f-t_i)-(x_f-x_i)]}{\alpha \hbar \sqrt{7}}\left[ \tan ^{-1}\left( \frac{\eta }{3}\right) \right] \right) \right. }\right) \right\} , \end{aligned}$$
(41)

and

$$\begin{aligned}&K_{qps}^{Im}(x_f, t_f; x_i, t_i)\nonumber \\&\quad =\frac{1}{2\pi [c(t_f-t_i)-(x_f-x_i)]}\nonumber \\&\qquad \times \left\{ \cos \left( \frac{4[c(t_f-t_i)-(x_f-x_i)]}{\alpha \hbar \sqrt{7}}\left[ \tan ^{-1}\left( \frac{\eta }{3}\right) \right] \right) \right. \nonumber \\&\qquad -\cos \left( \frac{2[c(t_f-t_i)-(x_f-x_i)]}{\alpha \hbar \sqrt{7}}\right. \nonumber \\&\qquad \times \left. \left. \left[ \tan ^{-1}(\eta )-\tan ^{-1}\left( \frac{\eta }{3}\right) \right] \phantom {\times \left\{ \cos \left( \frac{4[c(t_f-t_i)-(x_f-x_i)]}{\alpha \hbar \sqrt{7}}\left[ \tan ^{-1}\left( \frac{\eta }{3}\right) \right] \right) \right. }\right) \right\} . \end{aligned}$$
(42)

By comparison with ordinary quantum mechanics we find that, while in ordinary quantum mechanics the kernel function for the wave-like case is ambiguous in general, here we have an explicit relation for this kernel function due to existence of cutoffs. This is another new result derived from the presence of minimal length and maximal momentum in the context of gravitational quantum mechanics. Once again, the physical origin of the difference with the standard case is the modification of the standard dispersion relation as Eq. (38). In fact, a finite resolution of spacetime is the source of modified dispersion relation and makes the theory to be UV-regularized.

Now, based on the obtained results, we investigate the Feynman path integrals in the language of gravitational quantum mechanics.

5 Generalized Feynman path integrals

In quantum mechanics and within a different perspective, the kernel function K can provide a new formulation which was presented by Feynman; the so-called path integral formalism. Here, we are going to probe the Feynman path integral modifications in the high energy physics, near the Planck scale \(E_{Pl}\simeq 10^{19}\) GeV, which is characterized by the presence of a minimal measurable length and a maximal test particles’ momentum. We begin by splitting up the time interval \(t_N-t_0\) into N equal parts \(\Delta t\), i.e. \(t_N-t_0=N\Delta t\). Then by using the maximally localized states, from Eq. (28) we have

$$\begin{aligned}&\langle \varphi ^{Ml}_{x_N},t_N|\varphi ^{Ml}_{x_0},t_0\rangle _{_{Heisenberg}}\nonumber \\&\quad =\prod _{j=1}^{N-1}\int \left\langle \varphi ^{Ml}_{x_N}\left| e^{-i\frac{H\Delta t}{\hbar }} \right| \varphi ^{Ml}_{x_{N-1}}\right\rangle \nonumber \\&\qquad \left\langle \varphi ^{Ml}_{x_N-1}\left| e^{-i\frac{H\Delta t}{\hbar }}\right| \varphi ^{Ml}_{x_N-2}\right\rangle \langle \varphi ^{Ml}_{x_N-2}|\ \cdots \nonumber \\&\qquad \quad \cdots \ |\varphi ^{Ml}_{x_1}\rangle \left\langle \varphi ^{Ml}_{x_1}\left| e^{-i\frac{H\Delta t}{\hbar }}\right| \varphi ^{Ml}_{x_0}\right\rangle \ dx_j, \end{aligned}$$
(43)

where we used the complete set of states \(\int |\varphi ^{Ml}_{x_{\kappa }}\rangle \langle \varphi ^{Ml}_{x_{\kappa }}|dx_{\kappa }=1\). As is demonstrated in Eq. (30), these expressions would be in the form of

$$\begin{aligned}&\left\langle \varphi ^{Ml}_{x_j}\left| e^{-i\frac{H\Delta t}{\hbar }}\right| \varphi ^{Ml}_{x_{j-1}}\right\rangle =K_{qps}(x_j, x_{j-1}, \Delta t)\nonumber \\&\quad =\frac{1}{2\pi \hbar }\int _{-P_{pl}}^{+P_{pl}}e^{-i\frac{E_{p}\Delta t}{\hbar }}e^{i\frac{2(x_j-x_{j-1})}{\alpha \hbar \sqrt{7}}\left( \tan ^{-1}\left( \frac{4\alpha p-1}{\sqrt{7}}\right) +\tan ^{-1}\left( \frac{\eta }{3}\right) \right) }\nonumber \\&\qquad \times \frac{dp}{1-\alpha p+2\alpha ^2 p^2}, \end{aligned}$$
(44)

in which the solution of the integral depends on the form of energy relation \(E_{p}\). Similar to the previous section we investigate this issue for particle-like and wave-like approaches separately.

5.1 Particle-like approach

Considering a free particle, and also the quasi-momentum \({\mathcal {P}}_{qps}\), we have the generalized energy relation \(E=\frac{1}{2m} {\mathcal {P}}_{qps}^2\). So, from Eq. (34) we would have

$$\begin{aligned}&K_{qps}(x_j, x_{j-1}, \Delta t)\nonumber \\&\quad =\sqrt{\frac{m}{i2\pi \hbar \Delta t}}e^{i\frac{m(x_j-x_{j-1})^2}{2\hbar \Delta t}}\nonumber \\&\qquad \times \left[ \frac{1}{2}erf\left( \sqrt{i\frac{2\Delta t}{7\alpha ^2m\hbar }}\left( 2\tan ^{-1}\left( \frac{\eta }{3}\right) -\frac{\alpha m\sqrt{7}(x_j-x_{j-1})}{2\Delta t}\right) \right) \right. \nonumber \\&\qquad -\frac{1}{2}erf\left( \sqrt{i\frac{2\Delta t}{7\alpha ^2m\hbar }}\left( \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta )\right. \right. \nonumber \\&\qquad \left. \left. \left. -\frac{\alpha m\sqrt{7}(x_j-x_{j-1})}{2\Delta t }\right) \right) \right] . \end{aligned}$$
(45)

Then, defining \(Erf(x_j, x_{j-1}, \Delta t)\) as

$$\begin{aligned}&Erf(x_j, x_{j-1}, \Delta t)\nonumber \\&\quad \equiv \frac{1}{2}erf\left( \sqrt{i\frac{2\Delta t}{7\alpha ^2m\hbar }}\left( 2\tan ^{-1}\left( \frac{\eta }{3}\right) -\frac{\alpha m\sqrt{7}(x_j-x_{j-1})}{2\Delta t}\right) \right) \nonumber \\&\qquad -\frac{1}{2}erf\left( \sqrt{i\frac{2\Delta t}{7\alpha ^2m\hbar }}\left( \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta )\right. \right. \nonumber \\&\qquad \left. \left. -\frac{\alpha m\sqrt{7}(x_j-x_{j-1})}{2\Delta t }\right) \right) , \end{aligned}$$
(46)

Eq. (43) can be written as

$$\begin{aligned}&\langle \varphi ^{Ml}_{x_N},t_N|\varphi ^{Ml}_{x_0},t_0\rangle _{Heisenberg}\nonumber \\&\quad =\left( \frac{m}{i2\pi \hbar \Delta t}\right) ^{\frac{N}{2}}\prod _{j=1}^{N-1}\int e^{i\frac{m\Delta t}{2\hbar }\sum _{j=1}^{N} \left( \frac{x_j-x_{j-1}}{\Delta t}\right) ^2}\nonumber \\&\qquad \times \left( \prod _{j=1}^{N}erf(x_j, x_{j-1}, \Delta t)\right) \ dx_j. \end{aligned}$$
(47)

This is the path integral in the presence of natural cutoffs as a minimal measurable length and a maximal momentum within the particle-like approach. An important point should be stressed here: In the so-called gravitational quantum mechanics framework, owing to the appearance of a minimal measurable distance \(\Delta x_{min}=\ell _{min}\), due to the relation between displacement \(\Delta x\) and time interval \(\Delta t\), i.e. \(\Delta x=v\Delta t\), there would be a minimum time interval \(\Delta t_{min}\) too

$$\begin{aligned} (\Delta t)_{min}=\frac{\ell _{min}}{v} \end{aligned}$$

whence we obtain the notable consequence

$$\begin{aligned} N_{max}=\frac{t_N-t_0}{\Delta t_{min}}=\frac{v(t_N-t_0)}{\ell _{min}}. \end{aligned}$$

This result means that in gravitational quantum mechanics there is an upper bound for N, say, \(N_{max}\), and in contrast to ordinary quantum mechanics where one can set essentially \(N\rightarrow \infty \) and so \(\Delta t\rightarrow 0\), here one can no longer propel N toward infinity. Therefore, the gravitationally modified ultimate limit of Eq. (47) would be

$$\begin{aligned}&\langle \varphi ^{Ml}_{x_{N_{max}}},t_{N_{max}}|\varphi ^{Ml}_{x_0},t_0\rangle _{_{Heisenberg}}\nonumber \\&\quad =\int {\mathcal {D}}x\ e^{i\sum _{j=1}^{N_{max}}\frac{m\Delta t_{min}}{2\hbar }\left( \frac{x_j-x_{j-1}}{\Delta t_{min}}\right) ^2}\nonumber \\&\qquad \times \left( \prod _{j=1}^{N_{max}}erf(x_j, x_{j-1}, \Delta t_{min})\right) \end{aligned}$$
(48)

where \({\mathcal {D}}x\) is defined as

$$\begin{aligned} \int {\mathcal {D}}x\equiv \left( \frac{m}{i2\pi \hbar \Delta t_{min}}\right) ^{\frac{N_{max}}{2}}\prod _{j=1}^{N_{max}-1}\int dx_j. \end{aligned}$$
(49)

This is the generalized form of the Feynman path integral in the presence of a minimal length and a maximal momentum in a gravitational quantum mechanics setup. Comparing Eq. (48) with the ordinary quantum mechanics result, we find the presence of the additional term \(\prod _{j=1}^{N_{max}}erf(x_j, x_{j-1}, \Delta t_{min})\) as the correction of the Feynman path integral in the presence of quantum gravitational effects. The origin of this extra ingredient, that regularizes the path integral at the UV regime, comes back to the modification of the dispersion relation due to discreteness of spacetime at the Planck scale. One can check that in the limit \(\alpha \rightarrow 0\) which is equivalent to \(N\rightarrow \infty \) and \(\Delta t\rightarrow 0\), the usual Feynman path integral formulation would be recovered.

5.2 Wave-like approach

Now we use the modified Planck relation (37) that takes into account the generalized form of the frequency in the quasi-position space \(\nu _{qps}\). Putting this relation into Eq. (44) and solving the integral, we obtain

$$\begin{aligned}&K_{qps}(x_j, x_{j-1}, \Delta t)\nonumber \\&\quad =\frac{i}{2\pi [c\Delta t-(x_j-x_{j-1})]}\left\{ e^{-i\frac{4[c\Delta t-(x_j-x_{j-1})]}{\alpha \hbar \sqrt{7}}\left[ \tan ^{-1}\left( \frac{\eta }{3}\right) \right] }\right. \nonumber \\&\qquad \left. -e^{-i\frac{2[c\Delta t-(x_j-x_{j-1})]}{\alpha \hbar \sqrt{7}}\left[ \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta ))\right] }\right\} . \end{aligned}$$
(50)

Then, the path integral relation in Eq. (43) follows that

$$\begin{aligned}&\langle \varphi ^{Ml}_{x_N},t_N|\varphi ^{Ml}_{x_0},t_0\rangle _{Heisenberg}\nonumber \\&\quad =\prod _{j=1}^{N-1}\int \left( \prod _{j=1}^{N}\frac{i}{2\pi [c\Delta t-(x_j-x_{j-1})]}\right. \nonumber \\&\qquad \times \left\{ e^{-i\frac{4[c\Delta t-(x_j-x_{j-1})]}{\alpha \hbar \sqrt{7}}\left[ \tan ^{-1}\left( \frac{\eta }{3}\right) \right] }\right. \nonumber \\&\qquad -\left. \left. e^{-i\frac{2[c\Delta t-(x_j-x_{j-1})]}{\alpha \hbar \sqrt{7}}\left[ \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta ))\right] }\right\} \phantom {=\prod _{j=1}^{N-1}\int \left( \prod _{j=1}^{N}\frac{i}{2\pi [c\Delta t-(x_j-x_{j-1})]}\right. }\right) dx_j. \end{aligned}$$
(51)

Finally, by using \(N_{max}\) and \(\Delta t_{min}\) as defined above, Eq. (51) takes the following form

$$\begin{aligned}&\langle \varphi ^{Ml}_{x_{N_{max}}},t_{N_{max}}|\varphi ^{Ml}_{x_0},t_0\rangle _{Heisenberg}\nonumber \\&\quad =\int {\mathcal {D'}}x\left( \prod _{j=1}^{N_{max}}\frac{1}{c-\frac{x_j-x_{j-1}}{\Delta t_{min}}}\right. \nonumber \\&\qquad \times \left[ e^{-i\frac{4\Delta t_{min}\left( c-\frac{x_j-x_{j-1}}{\Delta t_{min}}\right) }{\alpha \hbar \sqrt{7}}\left( \tan ^{-1}\left( \frac{\eta }{3}\right) \right) }\right. \nonumber \\&\qquad \left. \left. - e^{-i\frac{2\Delta t_{min}\left( c-\frac{x_j-x_{j-1}}{\Delta t_{min}}\right) }{\alpha \hbar \sqrt{7}}\left( \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta )\right) }\right] \right) , \end{aligned}$$
(52)

where \({\mathcal {D'}}x\) is defined as

$$\begin{aligned} \int {\mathcal {D'}}x\equiv \frac{i}{2\pi \Delta t_{min}}\prod _{j=1}^{N_{max}-1}\int dx_j. \end{aligned}$$
(53)

The relation as given by Eq. (52) is the Feynman path integral of a free particle in the wave-like approach where quantum gravitational effects, encoded in a minimal length and a maximal momentum, are taken into account. So, unlike the ordinary quantum mechanics, we were able to construct a path integral in the wave-like approach thanks to the presence of natural cutoffs. This is another new result due to the presence of natural cutoffs. We note that the path integral (52) is UV-regularized due to the modified dispersion relation encoded in the definition of \(\nu _{qps}\) as \(\nu _{qps}=\frac{c}{\pi \alpha \hbar \sqrt{7}}\Big (\tan ^{-1}(\frac{4\alpha p-1}{\sqrt{7}})+\tan ^{-1}(\frac{\eta }{3})\Big )\) which is a result of the spacetime fuzziness at the Planck scale.

6 Generalized Feynmam path integral and some thermodynamical properties of an ideal gas

In this section, via the connection between the Euclidean path integral and statistical mechanics, we briefly explore some thermodynamical properties of an ideal gas in the presence of the mentioned natural cutoffs. We consider an ensemble system at thermodynamical equilibrium with energy spectrum of microstates as \(\{E_n\}\) with \(n=1,2,\ldots \). The partition function Z of statistical mechanics in position space reads as,

$$\begin{aligned} Z=\sum _{n=1}^{\infty }e^{-\beta E_n}, \end{aligned}$$
(54)

where \(\beta = \frac{1}{K_{B}T}\) is the inverse temperature of the system at a given temperature T with Boltzmann’s constant \(K_{B}\). This form of the partition function resembles the time-dependent wave function in quasi-space representation in the presence of natural cutoffs, Eq. (25). It is important to look for partition function through a path integral formalism. For this end, one can proceed by replacing the time variable t with the Euclidean time \(\tau \) by an analytical continuation \(t\rightarrow -i\tau \). In this manner one can derive a modified partition function from a modified path integral. For this goal we rewrite the imaginary time propagator between the maximally localized states \(\varphi _{x_f}^{Ml}\) and \(\varphi _{x_i}^{Ml}\) by decomposing the bra and ket into a basis of eigenstates and then apply time-evolution to each one as

$$\begin{aligned}&K_{qps}(x_f,\tau ;x_i)\nonumber \\&\quad =\int _{-P_{Pl}}^{+P_{Pl}}\frac{d p}{1-\alpha p+2\alpha ^{2}p^{2}}<\varphi _{x_f}^{Ml}|p>e^{\frac{-iE_{p}(-i\tau )}{\hbar }}\langle p|\varphi _{x_i}^{Ml}\rangle \nonumber \\&\quad =\int _{-P_{Pl}}^{+P_{Pl}}\frac{d p}{1-\alpha p+2\alpha ^{2}p^{2}}\langle p|\varphi _{x_i}^{Ml}\rangle e^{\frac{-iE_{p} (-i\tau )}{\hbar }}\langle \varphi _{x_f}^{Ml}|p\rangle .\nonumber \\ \end{aligned}$$
(55)

Setting \(x_f = x_i\equiv x\) and \(\tau = \beta \hbar \) along with integrating over all x we find

$$\begin{aligned}&\int dx K_{qps}(x,\beta \hbar ;x)\nonumber \\&\quad =\int _{-P_{Pl}}^{+P_{Pl}}\frac{d p}{1-\alpha p+2\alpha ^{2}p^{2}}\left\langle p|\int _{x} dx e^{-\beta E_p}|\varphi _{x}^{Ml}\right\rangle \langle \varphi _{x}^{Ml}|p\rangle \nonumber \\&\quad =\int _{-P_{Pl}}^{+P_{Pl}}\frac{d p}{1-\alpha p+2\alpha ^{2}p^{2}}e^{-\beta E_p}=Z. \end{aligned}$$
(56)

In this manner, the modified partition function for a bosonic ideal gas can be deduced by integrating (34) over \(d^{3}x\) (that is, for three space dimensions) and then extending the result to N particles. The result is as follows

$$\begin{aligned}&{Z}_N(\beta ,V)\nonumber \\&\quad =\frac{1}{N!}\left[ V\left( \frac{m}{2\pi \beta \hbar ^{2}}\right) ^{\frac{3}{2}}\right] ^{N} \left\{ \frac{1}{2}erf\left( \sqrt{\frac{8\beta }{7\alpha ^2m}}\tan ^{-1}\left( \frac{\eta }{3}\right) \right) \right. \nonumber \\&\qquad \left. -\frac{1}{2}erf\left( \sqrt{\frac{2\beta }{7\alpha ^2m}}[\tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta )] \right) \right\} ^{3N}. \end{aligned}$$
(57)

In what follows we use this modified partition function, which includes the effects of natural cutoffs, to study thermostatistics of a bosonic ideal gas. Note that the basis of our calculations in this section is a path integral that is UV-regularized due to the discrete nature of spacetime at the Planck scale. So the corresponding thermodynamics is also free of irregularities at the UV regime.

6.1 Helmholtz free energy

The Helmholtz free energy, A, of a system is defined as

$$\begin{aligned} {A}=-\frac{1}{\beta }\ln [{Z}_N(\beta ,V)]. \end{aligned}$$
(58)

By applying the Stirling formula, \(\ln N!\approx N\ln N-N\), in expression for the partition function (57), we arrive at the result

$$\begin{aligned} {A}= & {} \frac{N}{\beta }\left\{ \ln \left[ \frac{N}{V}\left( \frac{2\pi \beta \hbar ^{2}}{m}\right) ^{\frac{3}{2}}\right] \right. \nonumber \\&-1-\ln \left[ \frac{1}{2}erf\left( \sqrt{\frac{8\beta }{7\alpha ^2m}}\tan ^{-1}\left( \frac{\eta }{3}\right) \right) \right. \nonumber \\&\left. \left. -\frac{1}{2}erf\left( \sqrt{\frac{2\beta }{7\alpha ^2m}}\left[ \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta )\right] \right) \right] ^{3}\right\} \nonumber \\ \end{aligned}$$
(59)

In the limit \(\alpha \rightarrow 0\) one recovers the non-deformed result.

6.2 Chemical potential

Having the functional form of the Helmholtz free energy, we can compute the chemical potential of the system \(\mu \) defined as

$$\begin{aligned} \mu =\Big (\frac{\partial A}{\partial N}\Big )_{V,T}, \end{aligned}$$
(60)

to fined

$$\begin{aligned} \mu= & {} \frac{1}{\beta }\left\{ \ln \left[ \frac{N}{V}\left( \frac{2\pi \beta \hbar ^{2}}{m}\right) ^{\frac{3}{2}}\right] -\ln \left[ \frac{1}{2}erf\left( \sqrt{\frac{8\beta }{7\alpha ^2m}}\tan ^{-1}\left( \frac{\eta }{3}\right) \right) \right. \right. \nonumber \\&\left. \left. -\frac{1}{2}erf\left( \sqrt{\frac{2\beta }{7\alpha ^2m}}\left[ \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta )\right] \right) \right] ^{3}\right\} \, \end{aligned}$$
(61)

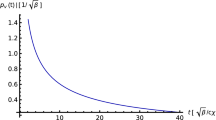
for the chemical potential of a classical system of ideal gas modified in the presence of natural cutoffs. In the limit \(\alpha \rightarrow 0\) one recovers the standard non-deformed result. Figure 1 shows the variation of \(\mu \) versus \(\beta \). As this figure shows, at the high temperatures, deviation from the classical result is significant which reflects the effect of natural cutoffs through modified dispersion relation. Note also that the classical, non-deformed chemical potential is negative at sufficiently high temperature. In the presence of natural cutoffs this is not the case and chemical potential is always positive. Positivity of the chemical potential means that the change in Helmholtz free energy when a particle is added to the system (here the ideal gas) is positive.

Fig. 1
figure 1

Behavior of the chemical potential of an ideal gas, \(\mu \), versus \(\beta \) for both the classical and deformed theory. The solid thick curve represents the chemical potential in the classical theory. The other curves are corresponding results in the deformed theory with natural cutoffs for different values of the parameter \(\alpha = 0.2,\, 0.3,\, 0.4, \,0.5\), from bottom to top, respectively. In this plot and other ones in this paper we have set \(N=10{,}000\) and \(V,\,\hbar ,\, K_{B},\, m\) are set equal to unity for the sake of simplicity in numerical study

Full size image

6.3 Entropy

Using the expression for the free energy (59) and the derivative identity

$$\begin{aligned} S=-\Big (\frac{\partial A}{\partial T}\Big )_{N,V}=K_{_{B}}\beta ^{2} \frac{\partial A}{\partial \beta }, \end{aligned}$$
(62)

we arrive at the following expression for entropy of an ideal gas in the presence of natural cutoffs

$$\begin{aligned} S= & {} N K_{_{B}}\phantom {\left. \left. -\frac{1}{2}erf\left( \sqrt{\frac{2\beta }{7\alpha ^2m}}\left[ \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta )\right] \right) \right] ^{3}-f_1\right\} ;}\left\{ \ln \left[ \frac{V}{N}\left( \frac{m}{2\pi \beta \hbar ^{2}}\right) ^{\frac{3}{2}}\right] +\frac{5}{2}\right. \nonumber \\&+\ln \left[ \frac{1}{2}erf\left( \sqrt{\frac{8\beta }{7\alpha ^2m}}\tan ^{-1}\left( \frac{\eta }{3}\right) \right) \right. \nonumber \\&\left. \left. -\frac{1}{2}erf\left( \sqrt{\frac{2\beta }{7\alpha ^2m}}\left[ \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta )\right] \right) \right] ^{3}-f_1\right\} ;\nonumber \\ \end{aligned}$$
(63)

where by definition

$$\begin{aligned} f_1\equiv 3\frac{\tan ^{-1}\left( \frac{\eta }{3}\right) \sqrt{\frac{2\beta }{7\pi m\alpha ^2}}\left[ e^{-\frac{8\beta \left[ \tan ^{-1} \left( \frac{\eta }{3}\right) \right] ^2}{7m\alpha ^2}}-\frac{1}{2}\left( 1-\frac{\tan ^{-1}(\eta )}{\tan ^{-1}\left( \frac{\eta }{3}\right) }\right) e^{-\frac{2\beta }{7m\alpha ^2}\left( \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta )\right) ^2}\right] }{\frac{1}{2}erf\left( \sqrt{\frac{8\beta }{7\alpha ^2m}}\tan ^{-1}\left( \frac{\eta }{3}\right) \right) -\frac{1}{2}erf\left( \sqrt{\frac{2\beta }{7\alpha ^2m}} \left[ \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta )\right] \right) }. \end{aligned}$$
(64)

It is easy to show that in the limit \(\alpha \rightarrow 0\), the logarithm term containing \(\alpha \) and also \(f_1\) tend to zero and one recovers the standard, non-deformed entropy.

Fig. 2
figure 2

Behavior of the specific heat of an ideal gas \(C_{V}\) versus \(\beta \) for both the classical and deformed theory. The colored thick curve represents the result of the classical theory while other curves correspond to results in the presence of natural cutoffs for different values of \(\alpha = 0.1,\, 0.12,\, 0.14, \,0.16\), from solid to the dashed-dot curve respectively

Full size image

6.4 Specific heat

Specific heat in a constant volume \(C_V\) is another important thermodynamic parameter, through which we can see the modifications in the expression for THE entropy by the following relations

$$\begin{aligned} {C}_V=T\Big (\frac{\partial {S}}{\partial T}\Big )_{N,V}=-\beta \Big (\frac{\partial {S}}{\partial \beta }\Big ). \end{aligned}$$
(65)

Now by using Eq. (63), we get from Eq. (65)

$$\begin{aligned} {C}_V=N K_{B}\Big [\frac{3}{2}-f_{1}\Big (\frac{1}{2}+\frac{f_{1}}{3}\Big )-f_2\Big ], \end{aligned}$$
(66)

where

$$\begin{aligned} f_2\equiv & {} \frac{12\pi \left( \tan ^{-1}\left( \frac{\eta }{3}\right) \right) ^{3}\left( \frac{2\beta }{7\pi \alpha ^2m}\right) ^{\frac{3}{2}}}{{\frac{1}{2}erf\left( \sqrt{\frac{8\beta }{7\alpha ^2m}}\tan ^{-1}\left( \frac{\eta }{3}\right) \right) -\frac{1}{2} erf\left( \sqrt{\frac{2\beta }{7\alpha ^2m}}\left[ \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta )\right] \right) }} \nonumber \\&\times \left[ e^{-\frac{8\beta }{7\alpha ^2m}\left( \tan ^{-1}\left( \frac{\eta }{3}\right) \right) ^2}\right. \nonumber \\&\left. -\left[ \frac{1}{2} \left( 1-\frac{\tan ^{-1}(\eta )}{\tan ^{-1}\left( \frac{\eta }{3}\right) }\right) \right] ^{3}e^{-\frac{2\beta }{7\alpha ^2m}\left( \tan ^{-1}\left( \frac{\eta }{3}\right) -\tan ^{-1}(\eta )\right) ^2}\right] . \end{aligned}$$
(67)

As usual, in the absence of the natural cutoffs (that is, \(\alpha \rightarrow 0\)) the classical result is recovered since \(\lim _{_{\alpha \rightarrow 0 }}f_{1,~2}=0\). As Fig. 2 shows, in the presence of natural cutoffs and for small values of \(\beta \), the specific heat is not constant, rather asymptotically increases to predicted value of the classical model in low temperature.

6.5 Internal energy

Internal energy U is the last thermodynamic parameter we calculate here. Having the expressions for the free energy and entropy and by using the relation

$$\begin{aligned} {U}={A}+T{S}, \end{aligned}$$
(68)

the internal energy U in the presence of natural cutoffs takes the following form

$$\begin{aligned} {U}=\frac{N}{\beta }\Big (\frac{3}{2}-f_{1}\Big )~. \end{aligned}$$
(69)

In the absence of natural cutoffs this relation recovers the standard result. Unlike one’s expectation from the classical theory, in the presence of the natural cutoffs the value of internal energy of an ideal gas is not divergent, rather it is finite as \(\beta \) approaches zero. This is another consequence of the modified dispersion relation in the presence of natural cutoffs.

7 Summary and conclusion

A minimal measurable length (of the order of the Planck length) and a maximal momentum (of the order of Planck momentum) are two high energy cutoffs appearing in alternative approaches to quantum gravity. Existence of these cutoffs naturally regularizes the quantum field theory at the ultra-violet regime. These cutoffs are a consequence of very nature of spacetime at the high energy regime towards the Planck scale. At this scale, spacetime has a noncommutative, discrete and fuzzy nature in the sense that there is a finite resolution of spacetime points. One cannot probe spacetime in length scales shorter than the Planck length. As a result, the standard dispersion relation gets modified, leading to modified dispersion relations which reflect possible violation of the Lorentz symmetry at the Planck scale. It is so important to see the role of these natural cutoffs in the path integral formalism of quantum mechanics. This issue, with just a minimal measurable length, has been studied firstly in Ref. [58]. But since existence of a minimal measurable length inevitably requires existence of a maximal energy (momentum), it is necessary to incorporate the maximal momentum in calculating the kernels and path integrals. In fact, if one ignores existence of a maximal momentum, then some shortcomings such as divergence of free particle’s energy would be inevitable (see [11, 44]. By focusing on the path integral formalism of quantum mechanics, in this paper we obtained the modified kernels and the path integrals in the presence of a minimal length and a maximal momentum. These are naturally UV-regularized and well-behavior in our setup. To achieve these goals, we used the quasi-position representation of the Hilbert space by adopting maximally localized states in position space. We have done our analysis for both the particle-like and wave-like scenarios. In this manner, unlike the ordinary quantum mechanics, we were able to construct a path integral in the wave-like approach, thanks to the presence of natural cutoffs. Then via the connection between path integrals and statistical physics partition function, we studied as an example the thermodynamics of an ideal gas in some details.