1 Introduction

The thermodynamics of black hole is one of the most exciting and challenging topics in theoretical physics. Due to AdS/CFT [1,2,3], the AdS black holes attract more and more attention. Especially in recent years, the research for the space-time properties of the AdS black holes showed that there is a deeply connection between the black hole and thermodynamics. It was first noted that in AdS space, there exists a phase transition between the Schwarzschild anti-de-Sitter black hole and the thermal anti-de-Sitter space by Hawking and Page [4], which is called the Hawking-Page phase transition. This phenomenon can be explained as the confinement/deconfinement phase transition in QCD [3, 5].

Recently, it is found that the charged AdS black hole has the first order phase transition between a large black hole and a small black hole [6,7,8,9]. With the temperature increasing, the coexistence curve terminates at the critical point and the first order phase transition becomes the second order one. The behavior of the phase transition is quite similar to the van der Waals phase transition.

Subsequently, the AdS black hole thermodynamics can be generally promoted to the extended phase space. It has been found that when the cosmological constant is considered as a thermodynamic variable, the more abundant phase structure of the AdS black hole can be obtained [10,11,12]. Therefore, the first law of thermodynamics is modified to the form including the VdP term, where \(P=-\frac{\varLambda }{8 \pi }\) [13, 14]. In this context, the mass of black hole M is considered as the enthalpy rather than the internal energy. In 2012, Kubiznak et al. [15] restudied the thermodynamic properties of charged AdS black holes in the extended phase space. They found that the black hole and the van der Waals system share the same \(P-V\) oscillatory behavior, critical exponents and equal area law. Therefore, the AdS black hole and the van der Waals system can be identified in the extended phase space. Since then, many works have studied the thermodynamic properties of different AdS black holes [16,17,18,19,20,21,22].

On the other hand, the pioneering efforts by Weinhold [23, 24] and Ruppeiner [25, 26] have shown that the equilibrium space of a thermodynamic system can be considered as the Riemannian geometry and the metric derives from the Gaussian fluctuation moments. Thermodynamic geometry is a powerful tool for studying thermodynamic systems, which constructs an intimate connection between the description of thermodynamics and the description of statistics. In other words, the thermodynamic geometry can construct an intimate connection between the macrostate and the microstate. The Riemann scalar curvature can be calculated when the equilibrium space is established. The scalar curvature is proportional to the correlation volume of the thermodynamic system [26]. Therefore, the magnitude of scalar curvature can reflect the interaction strength of microscopic particles in the system. Meanwhile, the sign of the scalar curvature represents the attraction or exclusion of the microscopic particles in the system [26]. The method of the thermodynamic geometry can be applied to the black hole, to construct an intimate connection between the macroscopic state and the microscopic state of the black hole. Although the method of thermodynamic geometry has been applied to investigate phase transition of a black hole, the Ruppeiner scalar curvature can only expect the second-order phase transitions for some special black holes [27,28,29,30]. However, for an arbitrary black hole, the scalar curvature in both the Weinhold and Ruppeiner geometry cannot completely locate the second-order critical point. Subsequent studies have found that the Weinhold geometry is associated with the Ruppeiner geometry by conformal transformation [31, 32]. In order to avoid this disadvantage, another geometric formulation of thermodynamics was proposed by Quevedo [33, 34]. Quevedo’s geometry incorporates Legendre invariance in a natural way, and it allows us to derive Legendre invariant metrics in the space of equilibrium states. Some drawbacks in Weinhold and Ruppeiner’s geometry can be avoided by Quevedo’s geometry. However, the scalar curvature of Quevedo’s geometry also cannot completely locate the second-order critical points in an arbitrary black hole yet.

Afterwards, Mansoori et al. [35] investigated the extrinsic curvature of hypersurface at constant Q in the Ruppeiner geometry. They gave a general expression of the extrinsic curvature of the hypersurface. It was shown that the extrinsic curvature of the hypersurface can completely locate the second-order critical point and determinate the stability of the black hole. This shows that the extrinsic curvature can obtain more information than the method of scalar curvature. Therefore, we will use the method of extrinsic curvature to study the thermodynamic geometry of the three-dimensional Einstein–Maxwell-dilaton black hole.

In this paper, based on the first law of thermodynamics and the definition of thermodynamic geometry, the two-dimensional Ruppeiner and Quevedo geometry are constructed. Afterwards, the scalar curvature and the extrinsic curvature of hypersurfaces at constant Q are calculated respectively. The difference between the heat capacity and both the scalar and the extrinsic curvature is shown. Subsequently, we take the fluctuation of AdS radius into account and modify the first law of thermodynamics. According to the modified first law and the definition of the Quevedo geometry, the new three-dimensional Quevedo geometry of the black hole is reconstructed. And then the scalar curvature and the extrinsic curvature are calculated, respectively.

The organization of the paper is as follows. In Sect. 2, we will review the solution of the three-dimensional Einstein–Maxwell-dilaton black hole and the first law of thermodynamics for the black hole. In Sect. 3, we combine the first law of thermodynamics with the thermodynamic metric to construct the Ruppeiner and Quevedo geometry, and then calculate both the scalar curvature and the extrinsic curvature of hypersurface at constant Q of two types of geometries. Furthermore, we compare the two types of curvatures with the heat capacity. In Sect. 4, we consider the fluctuation of AdS radius and modify the first law of thermodynamics. Combining the modified first law with the definition of the Quevedo metric, we reconstruct the new Quevedo geometry and calculate the scalar curvature and the extrinsic curvature of hypersurface at constant Q. The paper ends with conclusions in Sect. 5.

2 A three dimensional Einstein–Maxwell-dilaton black hole and the first law of thermodynamics

In this section, we will review the three-dimensional Einstein–Maxwell-dilaton black hole [36]. The scalar-tensor theory has two equivalent formulations, which are Jordan and Einstein frames related by conformal transformation. In the Jordan frame, the action is written in the way that the Ricci scalar is multiplied by some functions of the scalar field. The general form of the three-dimensional action of the scalar-tensor modified gravity theory in the Jordan frame can be expressed as [37]

$$\begin{aligned} I^{(ST)}= & {} -\frac{1}{16 \pi } \int \sqrt{-\tilde{g}} d^3 x [F(\psi ) \tilde{\mathcal {R}}-2U(\psi )\nonumber \\&+\,G(\psi ) \tilde{g}^{\mu \nu } \tilde{\nabla }_{\mu } \psi \tilde{\nabla }_{\nu } \psi -L(\mathcal {\tilde{F}})]. \end{aligned}$$
(1)

In which, \(\tilde{g}^{\mu \nu }\) is the space-time metric, \(\tilde{\mathcal {R}}=\tilde{g}^{\mu \nu } \mathcal {\tilde{R}}_{\mu \nu }\) is the Ricci scalar, \(\psi \) is the scalar field, \(F(\psi )\), \(U(\psi )\) and \(G(\psi )\) are arbitrary functions of the scalar field. The covariant derivative is denoted by \(\tilde{\nabla }\) in the Jordan frame. The electromagnetic Lagrangian \(L(\mathcal {\tilde{F}})=-\mathcal {\tilde{F}}\) and \(\mathcal {\tilde{F}}=\mathcal {\tilde{F}}^{\alpha \beta } \mathcal {\tilde{F}}_{\alpha \beta }\) is the Maxwell invariant with \(\tilde{F}_{\alpha \beta }=\partial _\alpha A_\beta - \partial _\beta A_\alpha \) and \(\tilde{F}^{\rho \lambda } = \tilde{g}^{\rho \alpha } \tilde{g}^{\lambda \beta } \tilde{F}_{\alpha \beta }\).

Because of the strong coupling between the scalar and the gravitational fields, the equation of motions for the action (1) is very difficult to solve. Therefore, we must translate it into the Einstein-dilaton action in the Einstein frame to simplify the calculation. According to the conformal transformation [38,39,40]

$$\begin{aligned} \tilde{g}_{\mu \nu } \rightarrow \tilde{g}_{\mu \nu } =(\varOmega (\psi ))^2 g_{\mu \nu }, \end{aligned}$$
(2)

the metric \(\tilde{g}_{\mu \nu }\) in the Jordan frame can be transformed into the metric \(g_{\mu \nu }\) in the Einstein frame. By conformal transformation, the expression of the action can be changed as

$$\begin{aligned} I=-\frac{1}{16 \pi } \int \sqrt{-g} d^3 x [\mathcal {R}-V(\phi )-2g^{\mu \nu } \nabla _\mu \phi \nabla _\nu \phi + L({\mathcal {F}}, \phi )]. \end{aligned}$$
(3)

In which, \(\phi \) is a new scalar field in the Einstein frame which is coupled to itself via the functional form \(V(\phi )\) with \({\mathcal {F}}=F^{\mu \nu }F_{\mu \nu }\) being the Maxwell invariant with \(F_{\mu \nu }=\partial _\mu A_\nu - \partial _\nu A_{\mu }\), and \(A_\mu \) is the electromagnetic potential. The three-dimensional Einstein–Maxwell-dilaton gravity theory can choose the electromagnetic Lagrangian \(L({\mathcal {F}}, \phi )\) as [41,42,43,44]

$$\begin{aligned} L({\mathcal {F}}, \phi )=-{\mathcal {F}}e^{-2\alpha \phi }, \end{aligned}$$
(4)

where the parameter \(\alpha \) is known as the scalar electromagnetic coupling constant.

From Eq. (3), the field equations can be derived and the three-dimensional spherically symmetry solution of the field equations is

$$\begin{aligned} ds^2=-f(r)dt^2+\frac{1}{f(r)}dr^2+r^2R^2(r)d\theta ^2, \end{aligned}$$
(5)

where \(R(r)=r^\nu \) and the metric function f(r) is given by

$$\begin{aligned} f(r)= {\left\{ \begin{array}{ll} -mr^{\frac{2}{3}}-3(r b^2)^{\frac{2}{3}} \left[ 2\varLambda ln\left( \frac{r}{L} \right) -\frac{3q^2}{(\alpha -1)^2} b^{-\frac{2}{3}(2\alpha +1)} \left( \frac{b}{r} \right) ^{\frac{2}{3}(\alpha -1)} \right] , &{}\quad \nu =-\frac{2}{3}, \alpha> 1, \\ -\frac{m}{r^{\nu }}-\frac{2r^2}{\nu +1} \left[ \frac{\varLambda }{2+3\nu } \left( \frac{b}{r} \right) ^{-2\nu } - \frac{q^2 \varGamma }{B b^{2(1+B)}} \left( \frac{b}{r} \right) ^{2(1+\alpha \gamma +\nu )} \right] , &{}\quad \nu \ne -\frac{2}{3}, -1<\nu <0, B>0. \end{array}\right. } \end{aligned}$$
(6)

In which, b is a positive constant, L is a dimensional constant and \(\nu \) must be in the range of \(-1<\nu <0\). Other parameters in the metric function can be expressed as

$$\begin{aligned} \varGamma =\frac{\nu +1}{1+\alpha \gamma +2\nu }, \, B=\nu +2 \alpha \gamma , \,\gamma =\sqrt{-\frac{\nu (\nu +1)}{2}}. \end{aligned}$$
(7)

Subsequently, the first law of a three-dimensional

Einstein–Maxwell-dilaton black hole has been investigated in Ref. [36]. In order to study the first law of the black hole, the relevant thermodynamic quantities must be introduced. Firstly, the entropy of the black hole can be calculated using the Bekenstein–Hawking entropy \(S=\frac{A}{4}\), where A is the area of the event horizon. In this context, the entropy of the black hole can be expressed as

$$\begin{aligned} S=\frac{\pi }{2} r_{+}^{\nu +1}, \end{aligned}$$
(8)

where \(r_{+}\) is the radius of the horizon which is the real root of the relation \(f(r_{+})=0\). Secondly, the total mass of the black hole can be obtained as [45, 46]

$$\begin{aligned} M=\frac{\nu +1}{8}m. \end{aligned}$$
(9)

Thirdly, the black hole electric charge Q, which is a conserved quantity, can be found through the flux of the electromagnetic field at infinity [47, 48]. Utilizing the Gauss’s electric law, we have

$$\begin{aligned} Q=\frac{1}{4\pi } \int \sqrt{-g} e^{-2 \alpha \phi } F_{tr} d\varOmega . \end{aligned}$$
(10)

Thinking of the equation \(F_{t r}=q r^{-(B+1)}\), we obtain

$$\begin{aligned} q=2Qb^{2 \alpha \gamma }. \end{aligned}$$
(11)

Finally, the black hole’s electric potential \(\varPhi \) can be obtained by utilizing the following standard relation [49, 50]

$$\begin{aligned} \varPhi =A_\mu \chi ^\mu |_{reference}-A_\mu \chi ^{\mu }|_{r=r_{+}}, \end{aligned}$$
(12)

where \(A_t\) is the only nonvanishing component of the electromagnetic potential, \(\chi ^\mu =C \delta _t^\mu \) is the null generator of the horizon, and C is an arbitrary constant [51, 52]. Therefore, the electric potential of the black hole can be expressed as

$$\begin{aligned} \varPhi =C\frac{q}{B}r^{-B}. \end{aligned}$$
(13)

With the above physical quantities, the first law of thermodynamics of a three-dimensional Einstein–Maxwell-dilaton black hole is presented as [36]

$$\begin{aligned} dM(S,Q)=TdS+\varPhi dQ. \end{aligned}$$
(14)

3 Thermodynamic geometry and phase transition

In this section, we will use the method of thermodynamic geometry proposed by Ruppeiner and Quevedo to study the phase transition of the three-dimensional Einstein–Maxwell-dilaton black hole. In order to calculate the metric of thermodynamic geometry in the mass representation, the relation between the mass of the black hole and the conserved quantity must be obtained. It can be derived from Eq. (6) by imposing the condition \(f(r_{+})=0\). The mass of the black hole as the function of thermodynamic extensive parameters S and Q is written as

$$\begin{aligned}&M(S,Q)\nonumber \\&\quad ={\left\{ \begin{array}{ll} \frac{b^{\frac{2}{3}}}{4} \left[ \frac{6Q^2}{(\alpha -1)^2} \left( \frac{b}{r_{+}} \right) ^{\frac{2}{3} (\alpha -1)} +\frac{b^{\frac{2}{3}}}{l^2} ln\left( \frac{r_{+}}{L} \right) \right] , &{}\quad \text {for}\; \nu =-\frac{2}{3}, \\ \frac{r_{+}^\nu }{4} \left( \frac{b}{r_{+}} \right) ^{-2\nu } \left[ -\frac{\varLambda r_{+}^2}{2+3\nu } + \frac{4 Q^2 \varGamma }{B b^{2B}} \left( \frac{b}{r_{+}} \right) ^{2(\alpha \gamma +2 \nu )} \right] , &{}\quad \text {for} \; \nu \ne -\frac{2}{3}. \end{array}\right. }\nonumber \\ \end{aligned}$$
(15)

Combining the definition of Ruppeiner and Quevedo metric and the expression of the black hole mass, the thermodynamic geometry of the Einstein–Maxwell-dilaton black hole can be constructed. In the following subsection, the scalar curvature and extrinsic curvature of two different types of thermodynamic geometry are discussed, respectively.

3.1 Ruppeiner geometry

From the first law of thermodynamics, the Hawking temperature and the heat capacity are defined as follows

$$\begin{aligned} T=\left( \frac{\partial M}{\partial S} \right) _{Q}, \, C_{Q}=T \left( \frac{\partial S}{\partial T} \right) _{Q}. \end{aligned}$$
(16)

The Ruppeiner metric in the mass representation can be defined as [25, 26]

$$\begin{aligned} g_{ij}=\frac{H_{i,j}M}{T}, \end{aligned}$$
(17)

where \(H_{i,j}M=\left( \frac{\partial ^2 M}{\partial X^i \partial X^j} \right) \) is called the Hessian matrix and \(X^i=(S,Q)\) are extensive parameters. Based on the definition of the Ruppeiner metric, the scalar curvature of the equilibrium space can be calculated. Comparing the scalar curvature with the heat capacity, we want verify that whether the scalar curvature can play the role of heat capacity to locate the second-order critical point and determinate the stability of the black hole or not.

Recently, Mansoori et al. [35] have found that the extrinsic curvature of the hypersurface at constant Q in the equilibrium space of the Ruppeiner geometry is better than the scalar curvature to locate the second-order critical points and determinate the stability of the black hole near the critical point. According to the definition of extrinsic curvature

$$\begin{aligned} K=\nabla _\mu n^\mu =\frac{1}{\sqrt{-g}} \partial _\mu (\sqrt{-g} n^\mu ), \end{aligned}$$
(18)

where g is the determinant of the spacetime metric and \(n^\mu \) is the normal vector of an arbitrary hypersurface in the spacetime. The extrinsic curvature of hypersurface at constant Q in the Ruppeiner geometry can be written as

$$\begin{aligned} K=\frac{T C_Q C_S}{2} \left[ \sqrt{|T C_S|} \, \partial _Q \left( \frac{1}{T C_Q C_S} \right) \right] + \partial _Q \sqrt{|T C_S|}, \end{aligned}$$
(19)

where T and \(C_Q\) have been defined by Eq. (16), \(C_S\) can be defined as \(C_S=\left( \frac{\partial Q}{\partial \varPhi } \right) _S\) using the first law of thermodynamics. The metric function f(r) of a three-dimensional Einstein–Maxwell-dilaton black hole contains two cases, so we will discuss both the scalar curvature and extrinsic curvature in these two cases.

3.1.1 \(\nu =-\frac{2}{3}\)

Combining the first case of Eq. (15) with Eq. (17), we can obtain the Ruppeiner metric for \(\nu =-\frac{2}{3}\) case. According to the first law of thermodynamics and the Ruppeiner metric, the scalar curvature of the two-dimensional equilibrium state space can be expressed as

$$\begin{aligned} R=\frac{A}{2 l^2 S^{31}A_1 A_2 A_3 A_4 A_5}, \end{aligned}$$
(20)

in which

$$\begin{aligned} A_1= & {} \left[ \pi ^2 4^{\alpha } (\alpha -1) b^{\frac{2}{3}} \left( \frac{b}{S^3}\right) ^{\frac{2}{3}}-64 \pi ^{2 \alpha } Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\right] ^5, \nonumber \\ A_2= & {} \left[ \pi ^2 4^{\alpha } (\alpha -1) b^{\frac{2}{3}} \left( \frac{b}{S^3}\right) ^{\frac{2}{3}}-16 \pi ^{2 \alpha } Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\right] ^5, \nonumber \\ A_3= & {} \left[ \pi ^2 4^{\alpha } (\alpha -1) b^{\frac{2}{3}} \left( \frac{b}{S^3}\right) ^{\frac{2}{3}}+16 \pi ^{2 \alpha } (2 \alpha -3) Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\right] ^2,\nonumber \\ A_4= & {} \left[ \pi ^2 4^{\alpha } (\alpha -1) b^{\frac{2}{3}} \left( \frac{b}{S^3}\right) ^{\frac{2}{3}}+64 \pi ^{2 \alpha } (2 \alpha -3) Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\right] ^2, \nonumber \\ A_5= & {} \pi ^2 4^{\alpha } (\alpha -1) b^{\frac{2}{3}} \left( \frac{b}{S^3}\right) ^{\frac{2}{3}}+16 \pi ^{2 \alpha } (2 \alpha -3) l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}.\nonumber \\ \end{aligned}$$
(21)

Because the expression of coefficient A is too long and we only focus on the singularity of the scalar curvature, we can ignore the concrete form of coefficient A.

According to the expression of extrinsic curvature (19), the extrinsic curvature of hypersurface at constant Q in Ruppeiner geometry can be written as

$$\begin{aligned} K=\frac{A_1}{S \sqrt{B_1} B_2 }, \end{aligned}$$
(22)

where

$$\begin{aligned} A_1= & {} \pi ^2 2^{2 \alpha +3} (\alpha -1)^2 Q b^{\frac{1}{3} (-2) (\alpha -2)} \left( S^3\right) ^{\frac{2 (\alpha -1)}{3}} \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}},\nonumber \\ B_1= & {} \frac{\pi ^{-2 \alpha } b^{-\frac{2 \alpha }{3}-\frac{1}{3}} S^{2 \alpha +1} \left[ \pi ^2 4^{\alpha } (\alpha -1) b^{\frac{5}{3}}-16 \pi ^{2 \alpha } b l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 (\alpha -1)}{3}}\right] }{l^2 S^4},\nonumber \\ B_2= & {} 16 \pi ^{2 \alpha } (2 \alpha -1) l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}-\pi ^2 4^{\alpha } (\alpha -1) b^{\frac{2}{3}} \left( \frac{b}{S^3}\right) ^{\frac{2}{3}}. \end{aligned}$$
(23)

Next, according to the definition of heat capacity Eq. (16), we have

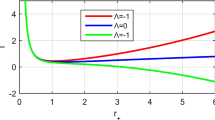
$$\begin{aligned} C_Q=\frac{S \left[ 16 \pi ^{2 \alpha } l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}-\pi ^2 4^{\alpha } (\alpha -1) b^{\frac{2}{3}} \left( \frac{b}{S^3}\right) ^{\frac{2}{3}}\right] }{\pi ^2 4^{\alpha } (\alpha -1) b^{\frac{2}{3}} \left( \frac{b}{S^3}\right) ^{\frac{2}{3}}-16 \pi ^{2 \alpha } (2 \alpha -1) l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}}. \end{aligned}$$
(24)

Finally, we compare the heat capacity of the black hole with the scalar curvature and the extrinsic curvature of hypersurface at constant Q, respectively. The results are shown in Fig. 1.

Fig. 1
figure 1

a The the scalar curvature R and the heat capacity \(C_Q\) as a function of entropy S when \(b=3,l=1,\alpha =2.477,Q=1\). b The extrinsic curvature K and the heat capacity\(C_Q\) as a function of entropy S when \(b= 3,l=1,\alpha =2.477,Q=1\)

Full size image

Figure 1a shows that the scalar curvature cannot locate the second-order critical point of the heat capacity, since there is an extra divergent point in the curve of the scalar curvature. The curve of the heat capacity does not have the critical point near the extra divergent point in scalar curvature curve. It means that the extra divergent point in the curve of the scalar curvature does not refer to the second-order critical point. As well as the signs of both sides near the divergent point of the scalar curvature are not the same as the curve of the heat capacity near the critical point. For a thermodynamic system, the sign of the heat capacity reflects the local stability of the system. If the value of the heat capacity is positive, the system is locally stable. In this context, if the sign of scalar curvature can be the same as the heat capacity curve, it means that the curve of scalar curvature can replace the heat capacity to determinate the local stability of the system. Therefore, according to above statement, the scalar curvature of Ruppeiner metric cannot locate the second-order critical point and determinate the stability of the black hole.

If we choose the hypersurface at constant Q in the equilibrium space and calculate the extrinsic curvature for the hypersurface, the result can be seen in Fig. 1b. The extrinsic curvature can locate the second-order critical point, as well as the signs of both sides near the divergent point are the same as the heat capacity near the critical point. Therefore, the extrinsic curvature can play the role of heat capacity to locate the second-order critical point and determinate the stability of the black hole. Thus, it can be considered that the method of extrinsic curvature in Ruppeiner geometry is much better than the method of scalar curvature to judge the critical point and the stability of the black hole. However, for values of the entropy below that for which the specific heat diverges, the extrinsic curvature diverges somewhere. The extra divergent point does not refer to a critical point, and this is exactly the defect of the extrinsic curvature expression. Although we only consider the properties of interior and extrinsic curvature near the second-order critical point of the heat capacity, the extra divergent point still influence the accuracy of the extrinsic curvature method. Therefore, the extra divergent point should be canceled.

3.1.2 \(\nu \ne -\frac{2}{3}\)

Combining the second case of Eq. (15) with Eq.(16), the heat capacity can be obtained as

$$\begin{aligned} C_Q=\frac{(\nu +1) S(A_1-A_2)}{B_1-B_2}, \end{aligned}$$
(25)

where

$$\begin{aligned} A_1= & {} 8 \pi ^{\frac{2}{\nu +1}} (\nu +1) Q^2 \left[ \sqrt{2} \alpha \sqrt{-\nu (\nu +1)}+\nu \right] \nonumber \\&\times \,\left[ b \left( \frac{\pi }{2}\right) ^{\frac{1}{\nu +1}} S^{-\frac{1}{\nu +1}}\right] ^{\sqrt{2} \alpha \sqrt{-\nu (\nu +1)}+4 \nu },\nonumber \\ A_2= & {} \varLambda 4^{\frac{1}{\nu +1}} \left[ 2 \left( \alpha ^2-2\right) \nu ^2\right. \nonumber \\&\left. -\nu \left( -2 \alpha ^2+5 \sqrt{2} \alpha \sqrt{-\nu (\nu +1)}+2\right) \right. \nonumber \\&\left. -2 \sqrt{2} \alpha \sqrt{-\nu (\nu +1)}\right] b^{2 \nu } S^{\frac{2}{\nu +1}},\nonumber \\ B_1= & {} 8 \pi ^{\frac{2}{\nu +1}} (\nu +1) Q^2 \left[ 2 \left( \alpha ^2-1\right) \nu ^2 \right. \nonumber \\&\left. -\nu \left( -2 \alpha ^2+3 \sqrt{2} \alpha \sqrt{-\nu (\nu +1)}+1\right) \right. \nonumber \\&\left. -\sqrt{2} \alpha \sqrt{-\nu (\nu +1)}\right] \left[ b \left( \frac{\pi }{2}\right) ^{\frac{1}{\nu +1}} S^{-\frac{1}{\nu +1}}\right] ^{\sqrt{2} \alpha \sqrt{-\nu (\nu +1)}+4 \nu },\nonumber \\ B_2= & {} \varLambda 4^{\frac{1}{\nu +1}} (2 \nu +1) \left[ 2 \left( \alpha ^2-2\right) \nu ^2\right. \nonumber \\&\left. -\nu \left( -2 \alpha ^2+5 \sqrt{2} \alpha \sqrt{-\nu (\nu +1)}+2\right) \right. \nonumber \\&\left. -2 \sqrt{2} \alpha \sqrt{-\nu (\nu +1)}\right] b^{2 \nu } S^{\frac{2}{\nu +1}}. \end{aligned}$$
(26)

According to Ref. [36], if we take \(-1<\nu <-0.492\), there is no horizon with the naked singularity. According to the cosmic censorship hypothesis, this situation is meaningless. In order to obtain the physical result, we must assign \(-0.492<\nu <0\). Based on the above analysis, the heat capacity of black hole in the second case is plotted in Fig. 2.

Fig. 2
figure 2

The heat capacity \(C_Q\) as a function of entropy S when \(\nu = -0.34,b= 0.2,\varLambda = -1,\alpha = 2.5,Q= 0.5,c= 1\)

Full size image

Figure 2 shows that there is only first order phase transition in the second case, which is the change of value for heat capacity from negative to positive. Based on above statements, thermodynamic geometry can only be used to analyze second-order phase transitions, then the method cannot be used in this context.

From above discussions, we can see the extrinsic curvature in Ruppeiner geometry can locate the critical point and determinate the stability of the black hole except it has an extra divergent point. However, for other thermodynamic geometries, does the extrinsic curvature have such good properties?

3.2 Quevedo geometry

In this section, we will use the Quevedo metric to investigate the thermodynamic properties of the three-dimensional Einstein–Maxwell-dilaton black hole.

Firstly, we briefly review the Quevedo geometry. According to Refs. [33, 34], the phase space of thermodynamics can be considered as a Riemannian contact manifold \(({\mathcal {T}}, \varTheta , G)\), where \({\mathcal {T}}\) is a \((2n+1)\)-dimensional manifold, \(\varTheta \) is a linear differential 1-form satisfying the condition \(\varTheta \wedge (d \varTheta )^n = 0\). The manifold \({\mathcal {E}}\) is a submanifold of \({\mathcal {T}}\) which is defined by the embedding mapping \(\phi : {\mathcal {E}} \rightarrow {\mathcal {T}}\). Thus, the submanifold \({\mathcal {E}}\) is called the space of thermodynamic equilibrium states that must satisfy the pullback condition \(\phi ^*(\varTheta )=0\). Therefore, the geometric properties of thermodynamic equilibrium states space can reflect the physical properties of the thermodynamic equilibrium system. In the phase space \({\mathcal {T}}\), the coordinates on the space can be written as \(Z^A=(\varPhi , E^a,I^a)\), where \(\varPhi \) is corresponding to the thermodynamic potential, \(E^a\) and \(I^a\) are corresponding to the extensive and intensive variables, respectively. The 1-form \(\varTheta \) can be expressed as \(\varTheta =d\varPhi -\delta _{ab} I^a dE^b\), where \(\delta _{ab}\) is the Euclidean metric. If we choose \(E^a\) as the coordinates of the submanifold \({\mathcal {E}}\), the embedding mapping \(\phi : {\mathcal {E}} \rightarrow {\mathcal {T}}\) can be expressed as

$$\begin{aligned} \phi : \{ E^a \} \rightarrow Z^A \{ \varPhi (E^a),E^a,I^a(E^a) \}. \end{aligned}$$
(27)

Therefore, the condition \(\phi ^*(\varTheta )=0\) can be written as

$$\begin{aligned} d\varPhi =\delta _{ab} I^a dE^b, \, \, \frac{\partial \varPhi }{\partial E^a}=\delta _{ab} I^b. \end{aligned}$$
(28)

Equation (28) represents the first law of thermodynamics and the condition of the thermodynamic equilibrium, respectively. To make the metric Legendre invariant in the manifold \({\mathcal {T}}\) as

$$\begin{aligned} G=(d\varPhi -\delta _{ab} I^a dE^b)^2 +(\delta _{ab} E^a I^b)(\eta _{cd} dE^c dI^d), \end{aligned}$$
(29)

where \(\eta _{ab}=(-1,1,\ldots ,1)\) is a pseudo-Euclidean metric in submanifold \({\mathcal {E}}\). It is easy to see that the metric G is invariant under the Legendre transformation

$$\begin{aligned}&\{ \varPhi , E^a, I^a \} \mapsto \{\tilde{\varPhi }, \tilde{E}^a, \tilde{I}^a \}, \end{aligned}$$
(30)
$$\begin{aligned}&\varPhi =\tilde{\varPhi }-\delta _{ab} \tilde{E}^a \tilde{I}^b, \, E^a=-\tilde{I}^a, \, I^a=\tilde{E}^a. \end{aligned}$$
(31)

When the metric pullbacks on \({\mathcal {E}}\), \(g=\phi ^*(G)\), the general expression of the metric is

$$\begin{aligned} g=\left( E^c \frac{\partial \varPhi }{\partial E^c} \right) \left( \eta _{ab} \delta ^{bc} \frac{\partial ^2 \varPhi }{\partial E^c \partial E^d} dE^a dE^d \right) . \end{aligned}$$
(32)

According to the first law of thermodynamics Eq. (14), the space of thermodynamic equilibrium states is two-dimensional, so the Quevedo metric can be written as

$$\begin{aligned} ds^2=\varOmega (-M_{SS}dS^2+M_{QQ}dQ^2), \end{aligned}$$
(33)

where \(M_{SS}\) and \(M_{QQ}\) are the second order derivative of mass with respect to entropy and charge, \(\varOmega \) is the conformal factor as [53]

$$\begin{aligned} \varOmega ={\left\{ \begin{array}{ll} SM_S+QM_Q, &{}\quad \text {case I} \\ SM_S, &{}\quad \text {case II} \end{array}\right. } \end{aligned}$$
(34)

where \(M_{S}\) and \(M_{Q}\) are the first order derivative of mass with respect to entropy and charge.

3.2.1 Case I

According to the Quevedo metric Eqs. (33) and (34), the scalar curvature of the thermodynamic space can be given as

$$\begin{aligned} R=\frac{A}{9 S^{18} A_1 A_2 A_3 A_4 A_5 A_6}, \end{aligned}$$
(35)

where

$$\begin{aligned} A_1= & {} \left[ \pi ^2 4^{\alpha } (\alpha -1)^2 b^{2/3} \left( \frac{b}{S^3}\right) ^{2/3}-64 \pi ^{2 \alpha } (\alpha -2) Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\right] ^2,\nonumber \\ A_2= & {} \left[ \pi ^2 4^{\alpha } (\alpha -1)^2 b^{2/3} \left( \frac{b}{S^3}\right) ^{2/3}-16 \pi ^{2 \alpha } (\alpha -2) Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\right] ^2, \nonumber \\ A_3= & {} \pi ^2 4^{\alpha } (\alpha -1)^2 b^{2/3} \left( \frac{b}{S^3}\right) ^{2/3}-16 \pi ^{2 \alpha } (\alpha -2) l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}, \nonumber \\ A_4= & {} \left[ \pi ^2 4^{\alpha } (\alpha -1) b^{2/3} \left( \frac{b}{S^3}\right) ^{2/3}-64 \pi ^{2 \alpha } (2 \alpha -1) Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\right] ^2, \nonumber \\ A_5= & {} \pi ^2 4^{\alpha } (\alpha -1) b^{2/3} \left( \frac{b}{S^3}\right) ^{2/3}-16 \pi ^{2 \alpha } (2 \alpha -1) Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}},\nonumber \\ A_6= & {} \pi ^2 4^{\alpha } (\alpha -1) b^{2/3} \left( \frac{b}{S^3}\right) ^{2/3}-16 \pi ^{2 \alpha } (2 \alpha -1) l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}.\nonumber \\ \end{aligned}$$
(36)

Because the expression of coefficient A is too long and we only focus on the singularity of the scalar curvature, we can ignore the concrete form of coefficient A.

Meanwhile, the extrinsic curvature of hypersurface at constant Q is

$$\begin{aligned} K=\frac{16 \pi ^{4 \alpha } b l^2 Q \left( \frac{b}{S^3}\right) ^{\frac{2 (\alpha -1)}{3}} A_1 A_2}{B_1 B_2}, \end{aligned}$$
(37)

where

$$\begin{aligned} A_1= & {} \left[ \frac{16^{\alpha } \pi ^{4-2 \alpha } (\alpha -1)^4 l^2 \left( \frac{b}{S^3}\right) ^{\frac{1}{3}-\frac{2 \alpha }{3}}}{9 \pi ^2 4^{\alpha } (\alpha -1)^2 S^6 \left( \frac{b}{S^3}\right) ^{5/3}-144 \pi ^{2 \alpha } (\alpha -2) \root 3 \of {b} l^2 Q^2 S^3 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}} \right] ^{\frac{1}{2}}, \nonumber \\ A_2= & {} -4^{\alpha +4} \pi ^{4 \alpha +2} (\alpha -2)^2 \left( 10 \alpha ^3-24 \alpha ^2+17 \alpha -3\right) b^{5/3} l^4 Q^4 S^3 \left( \frac{b}{S^3}\right) ^{\frac{4 \alpha }{3}}\nonumber \\&+\,2^{4 \alpha +5} \pi ^{2 \alpha +4} (\alpha -1)^3 \alpha \left( 4 \alpha ^2-13 \alpha +10\right) b^{7/3} l^2 Q^2 S^3 \left( \frac{b}{S^3}\right) ^{\frac{2 (\alpha +1)}{3}} \nonumber \\&+\,\pi ^6 \left( -64^{\alpha }\right) (\alpha -1)^5 \left( 2 \alpha ^2-2 \alpha -1\right) b^4 \root 3 \of {\frac{b}{S^3}}\nonumber \\&+\,8192 \pi ^{6 \alpha } (\alpha -2)^3 (2 \alpha -1) l^6 Q^6 S^6 \left( \frac{b}{S^3}\right) ^{2 \alpha +\frac{1}{3}}, \nonumber \\ B_1= & {} 16 \pi ^{2 \alpha } (\alpha -2) b l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 (\alpha -1)}{3}}-\pi ^2 4^{\alpha } (\alpha -1)^2 b^{5/3},\nonumber \\ B_2= & {} -4^{\alpha +4} \pi ^{6 \alpha +2} \alpha \left( 4 \alpha ^3-17 \alpha ^2+23 \alpha -10\right) b^{5/3} l^4 Q^4 S^3 \left( \frac{b}{S^3}\right) ^{\frac{4 \alpha }{3}} \nonumber \\&+\,(2 \pi )^{4 (\alpha +1)} (\alpha -1)^3 \left( 2 \alpha ^2-\alpha -3\right) b^{7/3} l^2 Q^2 S^3 \left( \frac{b}{S^3}\right) ^{\frac{2 (\alpha +1)}{3}} \nonumber \\&-\,64^{\alpha } \pi ^{2 \alpha +6} (\alpha -1)^5 b^4 \root 3 \of {\frac{b}{S^3}}+4096 \pi ^{8 \alpha } \nonumber \\&(\alpha -2)^2 (2 \alpha -1) l^6 Q^6 S^6 \left( \frac{b}{S^3}\right) ^{2 \alpha +\frac{1}{3}}. \end{aligned}$$
(38)

From the expression of heat capacity Eq. (24), we can compare the scalar curvature and the extrinsic curvature with the heat capacity in Quevedo geometry. The result is shown in Fig. 3.

Fig. 3
figure 3

a The scalar curvature R and the heat capacity \(C_Q\) as a function of entropy S when \(b=3,l=1,\alpha =2.477,Q=1\). b The extrinsic curvature K and the heat capacity \(C_Q\) as a function of entropy S when \(b= 3,l=1,\alpha =2.477,Q=1\)

Full size image

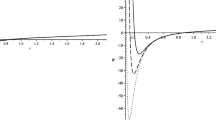
Figure 3a shows that the scalar curvature in Quevedo geometry cannot locate the second-order critical point of the heat capacity, since there are three extra divergent points in the curve of scalar curvature. And the scalar curvature also does not determinate the stability of the black hole, because the signs of both sides near the divergent point does not correspond to the sign of heat capacity near the critical point. Figure 3b shows that one of these divergent points corresponds to the second-order critical point and the signs of both sides near the divergent point are the same as the heat capacity near the critical point. Therefore, the curve of extrinsic curvature can locate the second-order critical point and determinate the stability near the critical point. Thus, in the first case of Quevedo geometry, the method of extrinsic curvature which can be used to judge the critical point and the stability of the black hole is still much better than the method of scalar curvature. However, the curve of extrinsic curvature also has an extra divergent point somewhere as the entropy is smaller than the critical point. Although this divergent point is not second-order critical point, it can still influence the accuracy of the extrinsic curvature method.

3.2.2 Case II

The scalar curvature can be given as

$$\begin{aligned} R=\frac{A}{9 S^{18} A_1 A_2 A_3 A_4 A_5 A_6}, \end{aligned}$$
(39)

where

$$\begin{aligned} A_1= & {} \left[ \pi ^2 4^{\alpha } (\alpha -1) b^{2/3} \left( \frac{b}{S^3}\right) ^{\frac{2}{3}}-64 \pi ^{2 \alpha } Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\right] ^2, \nonumber \\ A_2= & {} \left[ \pi ^2 4^{\alpha } (\alpha -1) b^{\frac{2}{3}} \left( \frac{b}{S^3}\right) ^{\frac{2}{3}}-16 \pi ^{2 \alpha } Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\right] ^2, \nonumber \\ A_3= & {} \pi ^2 4^{\alpha } (\alpha -1) b^{\frac{2}{3}} \left( \frac{b}{S^3}\right) ^{\frac{2}{3}}-16 \pi ^{2 \alpha } l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}, \nonumber \\ A_4= & {} \pi ^2 4^{\alpha } (\alpha -1) b^{\frac{2}{3}} \left( \frac{b}{S^3}\right) ^{\frac{2}{3}}-16 \pi ^{2 \alpha } (2 \alpha -1) Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}},\nonumber \\ A_5= & {} \pi ^2 4^{\alpha } (\alpha -1) b^{\frac{2}{3}} \left( \frac{b}{S^3}\right) ^{\frac{2}{3}}-16 \pi ^{2 \alpha } (2 \alpha -1) l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}, \nonumber \\ A_6= & {} \left[ \pi ^2 4^{\alpha } (\alpha -1) b^{\frac{2}{3}} \left( \frac{b}{S^3}\right) ^{\frac{2}{3}}-64 \pi ^{2 \alpha } (2 \alpha -1) Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\right] ^2.\nonumber \\ \end{aligned}$$
(40)

Because the expression of coefficient A is too long and we only focus on the singularity of the scalar curvature, we can also ignore the concrete form of coefficient A. Meanwhile, the extrinsic curvature of hypersurface at constant Q is

$$\begin{aligned} K=\frac{A_1 A_2}{3S^3 B_1 B_2 B_3 B_4}, \end{aligned}$$
(41)

where

$$\begin{aligned} A_1= & {} 2^{4 \alpha +5} \pi ^{2 \alpha +4} (\alpha -1)^3 b^{2/3} l^4 Q,\nonumber \\ A_2= & {} -4^{\alpha +6} \pi ^{6 \alpha +2} \left( 7 \alpha ^2-10 \alpha +3\right) b^{2/3} l^6 Q^6 S^6 \left( \frac{b}{S^3}\right) ^{2 \alpha +\frac{2}{3}} \nonumber \\&+\,3 \times 16^{\alpha +2} \pi ^{4 \alpha +4} (\alpha -1)^2 (3 \alpha -1) b^{10/3} l^4 Q^4 \left( \frac{b}{S^3}\right) ^{\frac{4 \alpha }{3}-\frac{2}{3}} \nonumber \\&+\,\pi ^8 256^{\alpha } (\alpha -1)^4 \alpha b^{14/3} \left( \frac{b}{S^3}\right) ^{2/3} \nonumber \\&-\,4^{3 \alpha +2} \pi ^{2 \alpha +6} (\alpha -1)^3 (5 \alpha -1) b^4 l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\nonumber \\&+\,65536 \pi ^{8 \alpha } (2 \alpha -1) l^8 Q^8 S^6 \left( \frac{b}{S^3}\right) ^{\frac{8 \alpha }{3}}, \nonumber \\ B_1= & {} -16 \pi ^{2 \alpha } b l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 (\alpha -1)}{3}}+\pi ^2 4^{\alpha } (\alpha -1) b^{5/3}, \nonumber \\ B_2= & {} \left[ \pi ^2 4^{\alpha } (\alpha -1) b^{2/3} \left( \frac{b}{S^3}\right) ^{2/3}-16 \pi ^{2 \alpha } l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\right] ^2, \nonumber \\ B_3= & {} \left[ -\frac{16^{\alpha } \pi ^{4-2 \alpha } (\alpha -1)^3 l^2 \left( \frac{b}{S^3}\right) ^{\frac{1}{3} (-2) (\alpha -1)}}{16 \pi ^{2 \alpha } b^{4/3} l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 (\alpha -1)}{3}}-\pi ^2 4^{\alpha } (\alpha -1) b^2} \right] ^{\frac{1}{2}}, \nonumber \\ B_4= & {} -4^{\alpha +4} \pi ^{6 \alpha +2} \left( 4 \alpha ^2-5 \alpha +1\right) b^{5/3} l^4 Q^4 S^3 \left( \frac{b}{S^3}\right) ^{\frac{4 \alpha }{3}} \nonumber \\&+\,(2 \pi )^{4 (\alpha +1)} (\alpha -1)^2 (2 \alpha +1) b^{7/3} l^2 Q^2 S^3 \left( \frac{b}{S^3}\right) ^{\frac{2 (\alpha +1)}{3}} \nonumber \\&-\,64^{\alpha } \pi ^{2 \alpha +6} (\alpha -1)^3 b^4 \root 3 \of {\frac{b}{S^3}}+4096 \pi ^{8 \alpha } \nonumber \\&(2 \alpha -1) l^6 Q^6 S^6 \left( \frac{b}{S^3}\right) ^{2 \alpha +\frac{1}{3}}. \end{aligned}$$
(42)

From Eq. (24), we also compare the scalar curvature and the extrinsic curvature with the heat capacity in Quevedo geometry. The result is shown in Fig. 4.

Fig. 4
figure 4

a The the scalar curvature R and the heat capacity \(C_Q\) as a function of entropy S when \(b=3,l=1,\alpha =2.477,Q=1\). b The extrinsic curvature K and the heat capacity \(C_Q\) as a function of entropy S when \(b= 3,l=1,\alpha =2.477,Q=1\)

Full size image

From Fig. 4a, we can see that the second case of Quevedo geometry is almost identical to the first case. The curve of scalar curvature has two more divergent points than the curve of heat capacity, and that the signs of both sides near the divergent point of the scalar curvature do not correspond to the curve of heat capacity near the critical point. From Fig. 4b, one of these divergent points in the curve of extrinsic curvature corresponds to the second-order critical point of heat capacity, and the signs of both sides near the divergent point are the same as the heat capacity near the critical point. Thus, in the second case of Quevedo geometry, the method of extrinsic curvature which can be used to judge the critical point and the stability of the system is still much better than the method of scalar curvature. However, the curve of extrinsic curvature also has an extra divergent point somewhere as the entropy is smaller than the critical value.

According to above statement, the extrinsic curvature is much better than the scalar curvature in the Ruppeiner and the Quevedo geometry. This method can not only locate the second-order critical point, but also accurately determinate the stability of the black hole near the critical point. However, the curve of extrinsic curvature has an extra divergency when the value of entropy is smaller than the critical point. Although we only care about the properties of the interior and extrinsic curvature near the second-order critical point, the extra divergent point can influence the accuracy of the thermodynamic geometry method. Therefore, we want to cancel the extra divergent point in the following discussion.

4 The fluctuation of AdS radius

Any constant in the physics theory, such as Yukawa couplings, gauge coupling constants and Newton’s constant G, are not fixed a priori [11]. The renormalization group theory points out that the value of the coupling constant for the Yukawa and the gauge theory depends on the energy scale, which can increase or decrease with the change of the energy scale. The Newton’s constant G can also change with the expansion of the universe. Therefore, we cannot assume that the cosmological constant \(\varLambda \) is a constant. In fact, there has been a lot of work to discuss the variation of cosmological constant. The idea that the cosmological constant is considered as a dynamical variable or a fluctuating thermodynamic parameter was proposed by Teitelboim and Brown [54]. Subsequently, Kubiznak et al. [15] considered that a negative cosmological constant induces a vacuum pressure, so they identified the cosmological constant as the thermodynamic pressure. The first law of thermodynamics for the black hole can be modified as \(dM=TdS+\varPhi dQ+VdP\) and the phase space constructed by these thermodynamic quantities is called the extended phase space. In this space, more abundant phase structures of the black hole can be shown.

Thermodynamic geometry is constructed by the fluctuation of thermodynamic quantities in the system. If the cosmological constant is considered as a variable, the fluctuation of the cosmological constant must be considered when we construct the thermodynamic metric. If we construct the space of the thermodynamics using all variables, we may obtain the result much more closer to the reality. Especially, considering the extrinsic curvature of hypersurface at constant Q in the space of thermodynamic, adding the extra one-dimensional fluctuation will have a certain effect on the result. In the three-dimensional Einstein–Maxwell-dilaton black hole, there is a relationship between the cosmological constant and the AdS radius, as \(\varLambda =-l^{-2}\). Based on this condition, if the fluctuation of cosmological constant was considered, the fluctuation of AdS radius should also be considered. In the following, we will consider the fluctuation of AdS radius and discuss how the fluctuation influences thermodynamic geometry.

Considering the fluctuation of AdS radius, the first law of thermodynamics for the black hole must be modified as

$$\begin{aligned} dM=TdS+\varPhi dQ + \varTheta dl, \end{aligned}$$
(43)

where \(\varTheta \) is the conjugate thermodynamic variable with l. We will use the Quevedo metric to discuss the thermodynamic properties of the black hole and compare the result with the previous results.

Combining Quevedo metric Eq. (32) with the modified first law of thermodynamics Eq. (43),we have

$$\begin{aligned} ds^2= & {} (SM_S+QM_Q+lM_l)(-M_{SS}dS^2+M_{QQ}dQ^2 \nonumber \\&+\,M_{ll}dl^2+2M_{Ql}dQdl). \end{aligned}$$
(44)

The scalar curvature of the metric can be obtained as

$$\begin{aligned} R=\frac{A}{3 b^{\frac{4}{3}} \ln ^2\left( \frac{8 S^3}{\pi ^3 L}\right) S^6 A_1 A_2}, \end{aligned}$$
(45)

where

$$\begin{aligned} A_1= & {} \left[ \pi ^2 4^{\alpha } (\alpha -1) b^{2/3} \left( \frac{b}{S^3}\right) ^{2/3}-16 \pi ^{2 \alpha } (2 \alpha -1) l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\right] ^2, \nonumber \\ A_2= & {} \left[ \pi ^2 2^{2 \alpha +1} (\alpha -1)^2 b^{2/3} \left( \frac{b}{S^3}\right) ^{2/3} \ln \left( \frac{8 S^3}{\pi ^3 L}\right) \right. \nonumber \\&\left. -3 \pi ^2 4^{\alpha } (\alpha -1)^2 b^{2/3} \left( \frac{b}{S^3}\right) ^{2/3} +\,48 \pi ^{2 \alpha } (\alpha -2) l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\right] ^3.\nonumber \\ \end{aligned}$$
(46)

Because the expression of coefficient A is too long and we only focus on the singularity of the scalar curvature, we can ignore the concrete form of coefficient A. The extrinsic curvature of hypersurface at constant Q can be given as

$$\begin{aligned} K=\frac{\pi ^4 16^{\alpha +1} (\alpha -1)^4 l^4 Q A_1}{\sqrt{3} \root 3 \of {b} S^6 B_1 B_2 B_3}, \end{aligned}$$
(47)

where

$$\begin{aligned} A_1= & {} -3 \pi ^2 4^{\alpha } \left( 2 \alpha ^3-3 \alpha ^2-2 \alpha +3\right) b^{5/3}\nonumber \\&+\,\pi ^2 2^{2 \alpha +1} (\alpha -1)^2 (2 \alpha -1) b^{5/3} \ln \left( \frac{8 S^3}{\pi ^3 L}\right) \nonumber \\&+\,144 \pi ^{2 \alpha } \left( 2 \alpha ^2-5 \alpha +2\right) b l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 (\alpha -1)}{3}}, \nonumber \\ B_1= & {} \pi ^2 4^{\alpha } (\alpha -1) b^{2/3} \left( \frac{b}{S^3}\right) ^{2/3}-16 \pi ^{2 \alpha } (2 \alpha -1) l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}, \nonumber \\ B_2= & {} \left[ \frac{2^{2 \alpha -2} \pi ^{2-2 \alpha } (\alpha -1)^2 \left( \frac{b}{S^3}\right) ^{\frac{1}{3} (-2) (\alpha -1)}}{b^{2/3} \left[ -\frac{b^{4/3} \ln \left( \frac{8 S^3}{\pi ^3 L}\right) }{2 l^2}+\frac{3 b^{4/3}}{4 l^2}-\frac{3\ 4^{1-\alpha } \pi ^{2 \alpha -2} (\alpha -2) b^{2/3} Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 (\alpha -1)}{3}}}{(\alpha -1)^2}\right] } \right] ^{\frac{1}{2}}, \nonumber \\ B_3= & {} \left[ \pi ^2 2^{2 \alpha +1} (\alpha -1)^2 b^{2/3} \left( \frac{b}{S^3}\right) ^{2/3} \ln \left( \frac{8 S^3}{\pi ^3 L}\right) \right. \nonumber \\&\left. -3 \pi ^2 4^{\alpha } (\alpha -1)^2 b^{2/3} \left( \frac{b}{S^3}\right) ^{2/3} +\,48 \pi ^{2 \alpha } (\alpha -2) l^2 Q^2 \left( \frac{b}{S^3}\right) ^{\frac{2 \alpha }{3}}\right] ^2.\nonumber \\ \end{aligned}$$
(48)

From Eq. (24), we can compare the scalar curvature and the extrinsic curvature with the heat capacity in new Quevedo geometry. The result is shown in Fig. 5.

Fig. 5
figure 5

a The the scalar curvature R and the heat capacity \(C_{Q \, l}\) as a function of entropy S when \(b=3,l=1,\alpha =2.5,Q=1,L=1\). b The extrinsic curvature K and the heat capacity \(C_{Q \, l}\) as a function of entropy S when \(b=3,l=1,\alpha =2.5,Q=1,L=1\)

Full size image

Comparing both Figs. 3a and 4a with Fig. 5a, we can clearly find that the difference in the two type of Quevedo geometries. Considering the fluctuation of AdS radius, the curve of scalar curvature in Quevedo geometry is only one more divergent point than the curve of heat capacity. It means that the curve of the scalar curvature is obviously better locate the second-order critical point than the previous results. However, the scalar curvature still has an extra divergent point and the signs of both sides near the divergent point of the scalar curvature are different from the curve of heat capacity near the critical point. From Fig. 5b, we can find the intriguing result that the extra divergent point in the curve of extrinsic curvature is canceled and the curve has only one divergent point which corresponds to the second-order critical point of the heat capacity. In addition, the signs of both sides near the divergent point are the same as the curve of the heat capacity near the critical point. Therefore, the extrinsic curvature can completely locate the second-order phase transition and determinate the stability of the black hole near the critical point. From above statement, we can see that the extrinsic curvature of the hypersurface at constant Q is much better than the scalar curvature to locate the second-order critical point and determinate the stability while considering the fluctuation of AdS radius. Therefore, the cosmological constant or the AdS radius should be considered as a variable, when the thermodynamics of an AdS black hole is investigated.

5 Conclusions

We have investigated the thermodynamic properties of three-dimensional Einstein–Maxwell-dilaton black hole using the method of thermodynamic geometry. We calculated the scalar curvature and the extrinsic curvature in Ruppeiner and Quevedo geometry. Comparing both the scalar curvature and the extrinsic curvature with the heat capacity, we found that the scalar curvature has more divergence points than the curve of heat capacity. The signs of both sides near the divergent point of the scalar curvature curve are not the same as the curve of the heat capacity near the critical point, so it cannot locate the second-order critical point and determinate the stability of the black hole. Nonetheless, one of these divergent points in the curve of extrinsic curvature corresponds to the critical points of heat capacity and its signs of both sides near the divergent point are the same as the heat capacity near the critical point. Hence, the extrinsic curvature can locate the second-order critical point and determinate the stability of the black hole. However, there is an extra divergent point when the value of entropy is smaller than the critical point. Although the divergent point is not a critical point, it should be eliminated to avoid influencing the accuracy of the extrinsic curvature. When the AdS radius is considered as a variable, we reconstruct the Quevedo geometry, and calculate the scalar curvature and the extrinsic curvature of hypersurface at constant Q. From the results, we can see that the scalar curvature is better than the previous results, but it also cannot locate the second-order critical point and determinate the stability of the black hole. Since the curve has an extra divergent point and the signs of both sides near the divergent point are not same as the heat capacity. Nevertheless, the extrinsic curvature can completely locate the second-order critical point and determinate the stability of the black hole near the critical point. Meanwhile, the extra divergent point of the curve is canceled. Hence, if the AdS radius is considered as a variable, the curve of extrinsic curvature only has one divergent point which can locate the critical point of the heat capacity, and its sign can also corresponds to the sign of the heat capacity near the critical points. Therefore, when the fluctuation of AdS radius is considered, the extrinsic curvature of hypersurface at constant Q can be closer to the real physics. Therefore, the AdS radius or cosmological constant should be considered as a variable, when the thermodynamics of AdS black holes is investigated.