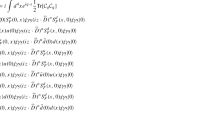The ratio $\mathcal {R}(D)$ and the D-meson distribution amplitude

Abstract

In this paper, we calculate the $B\rightarrow D$ transition form factors (TFFs) within the light-cone sum rules (LCSRs) and predict the ratio $\mathcal {R}(D)$. More accurate D-meson distribution amplitudes (DAs) are essential to get a more accurate theoretical prediction. We construct a new model for the twist-3 DAs $\phi ^p_{3;D}$ and $\phi ^\sigma _{3;D}$ based on the QCD sum rules under the background field theory for their moments as we have done for constructing the leading-twist DA $\phi _{2;D}$. As an application, we observe that the twist-3 contributions are sizable in whole $q^2$-region. Taking the twist-2 and twist-3 DAs into consideration, we obtain $f^{B\rightarrow D}_{+,0}(0) = 0.659^{+0.029}_{-0.032}$. As a combination of the Lattice QCD and the QCD LCSR predictions on the TFFs $f^{B\rightarrow D}_{+,0}(q^2)$, we predict $\mathcal {R}(D) = 0.320^{+0.018}_{-0.021}$, which is about $1.5\sigma$ deviation from the HFAG average of the Belle and BABAR data. At present the data still have large errors, and we need further accurate measurements of the experiment to confirm whether there is a signal of new physics from the ratio $\mathcal {R}(D)$.

1 Introduction

The B-meson physics provides a good platform for accurately testing the standard model (SM) and for finding the possible signal of new physics (NP), which has received much attention from physicists. In particular, the ratio $\mathcal {R}(D)$ in the semileptonic decay $B\rightarrow Dl\bar{\nu }_l$ has aroused great interests in recent years, since there appears to be a considerable difference between the experimental data and the SM theoretical predictions.

In 2012, the BaBar Collaboration reported a first measurement of the ratio $\mathcal {R}(D)$, which is defined as

$$\begin{aligned} \mathcal {R}(D) = \frac{\mathcal {B}(B\rightarrow D\tau \bar{\nu }_\tau )}{\mathcal {B}(B\rightarrow Dl^\prime \bar{\nu }_{l^\prime })} \end{aligned}$$

(1)

with $l^\prime$ standing for the light lepton e or $\mu$. The BaBar Collaboration gives $\mathcal {R}^\mathrm{exp}(D)=0.440\pm 0.058 \pm 0.042$ [1, 2]. The Belle Collaboration gives a slightly smaller value, $\mathcal {R}^\mathrm{exp}(D)=0.375 \pm 0.064 \pm 0.026$ [3]. The weighted average of those experimental measurements (HFAG average) gives $\mathcal {R}^\mathrm{exp}(D)=0.407\pm 0.039 \pm 0.024$ [4]. Many approaches have been tried to explain the data. Based on heavy quark effective theory (HQET), Refs. [5, 6] predict $\mathcal {R}(D)=0.302\pm 0.015$. By using the lattice QCD (LQCD), the FNAL/MILC Collaboration gives $\mathcal {R}(D)=0.299\pm 0.011$ [7] and the HPQCD Collaboration gives $\mathcal {R}(D)=0.300\pm 0.008$ [8], whose average gives $\mathcal {R}(D)=0.300\pm 0.008$ [9]. By using a global fit of the available LQCD predictions and experimental data, Ref. [10] predicts $\mathcal {R}(D)=0.299\pm 0.003$. Those SM predictions are consistent with each other within errors, however, all of them are lower than its measured value, e.g. the LQCD prediction has about $2.1\sigma$ deviation from the HFAG average. This inconsistency has motivated various speculations on the possible NP beyond the SM [11,12,13].

The theoretical prediction of $\mathcal {R}(D)$ strongly depends on the $B\rightarrow D$ transition form factors (TFFs) $f_{+,0}^{B\rightarrow D}(q^2)$, which are mainly non-perturbative and can only be perturbatively calculated for large recoil region with $q^2\sim 0$. Thus before drawing any definite conclusion, we have to know those TFFs better. The TFFs $f_{+,0}^{B\rightarrow D}(q^2)$ have been studied within the LQCD approach [7, 8], the pQCD factorization approach [14, 15], and the light-cone sum rule (LCSR) approach [16,17,18,19,20]. The pQCD approach is applicable for large recoil region and the LQCD approach is applicable for soft regions with large $q^2$. The LCSR approach involves both the hard and the soft contributions below $\sim 8 \mathrm{GeV}^{2}$. In the paper, we shall first adopt the LCSR approach to recalculating the TFFs and then combine the LQCD prediction to obtain a reliable prediction of the TFFs within the whole $q^2$-region.

The LCSRs for the TFFs $f_{+,0}^{B\rightarrow D}(q^2)$ can be expanded as a series over various D-meson light-cone distribution amplitudes (DAs). The high-twist DAs are generally power suppressed but could be sizable and helpful for a precise prediction. Several models for the leading-twist DA $\phi _{2;D}$ have been proposed in the literature [21,22,23,24,25,26,27]. In Ref. [19], we have studied the DA $\phi _{2;D}$ by recalculating its moments within the frame work of QCD SVZ sum rules [28] in the framework of background field theory (BFT) [29,30,31]. However, at present, there is little research on the D-meson twist-3 DAs $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$. According to our experience, it is reasonable to assume that the twist-3 DAs shall have sizable contributions to the TFFs $f_{+,0}^{B\rightarrow D}(q^2)$. In a previous pQCD treatment, the twist-3 DA $\phi _{3;D}^p$ is usually approximated by the leading-twist DA $\phi _{2;D}$ due to the difference between the moments of $\phi _{3;D}^p$ and $\phi _{2;D}$ is power suppressed by $\sim \mathcal {O}(\bar{\Lambda }/m_D)$ (where $\bar{\Lambda }=m_D-m_c$ with the c-quark mass $m_c$ and the D-meson mass), and the contribution from $\phi _{3;D}^\sigma$ is usually neglected, which is suppressed by $\mathcal {O}(\bar{\Lambda }/m_D)$ compared to those of $\phi _{2;D}$ and $\phi _{3;D}^p$ [21]. Thus more accurate twist-3 DAs shall also be helpful for achieving a precise prediction under pQCD factorization approach. In the paper, we will construct a new model for the D-meson twist-3 DAs $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$, whose moments will be determined by using the QCD SVZ sum rules under the BFT.

The remaining parts of the paper are organized as follows. The LCSRs for the TFFs $f_{+,0}^{B\rightarrow D}(q^2)$ with the next-to-leading order (NLO) corrections to the D-meson leading-twist DA contributions are given in Sect. 2. The models for the D-meson DAs are discussed in Sect. 3. A brief review of our previous model for the D-meson leading-twist DA $\phi _{2;D}$ is presented in Sect. 3.1, which shall be improved by including the spin-space part into the wavefunctions. A new model for the twist-3 DAs $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$ is given in Sect. 3.2. Numerical analysis and discussions are presented in Sect. 4. Section 5 is reserved for a summary.

2 The Ratio $\mathcal {R}(D)$ and the $B\rightarrow D$ TFFs $f^{B\rightarrow D}_{+,0}(q^2)$ in the Light-Cone Sum Rules

The ratio $\mathcal {R}(D)$ is determined by the branching ratio $\mathcal {B}(B\rightarrow D l\bar{\nu }_l)$, which can be calculated with

$$\begin{aligned} \mathcal {B}(B\rightarrow Dl\bar{\nu }_l) = \tau _B \int ^{(m_B - m_D)^2}_{m_l^2} dq^2 \frac{d\Gamma (B\rightarrow Dl\bar{\nu }_l)}{dq^2} \end{aligned}$$

(2)

and

$$\begin{aligned}&\frac{d}{dq^2} \Gamma (B\rightarrow Dl\bar{\nu }_l) \nonumber \\&\quad = \frac{G_F^2 |V_\mathrm{cb}|^2}{192\pi ^3 m_B^3} \left( 1 - \frac{m_l^2}{q^2} \right) ^2\nonumber \\&\qquad \times \left[ \left( 1 + \frac{m_l^2}{2q^2} \right) \lambda ^{3/2}(q^2) |f_+^{B\rightarrow D}(q^2)|^2 \right. \nonumber \\&\qquad + \left. \frac{3m_l^2}{2q^2} \left( m_B^2 - m_D^2 \right) ^2 \lambda ^{1/2}(q^2) |f_0^{B\rightarrow D}(q^2)|^2 \right] , \end{aligned}$$

(3)

where we have the phase-space factor $\lambda (q^2) = (m_B^2 + m_D^2 - q^2)^2 - 4m_B^2 m_D^2$, $\tau _B$ is for the B-meson lifetime, $m_{B}$ stands for the B-meson mass, $G_F$ is the Fermi constant, $|V_\mathrm{cb}|$ is the CKM matrix element, and $m_l$ is the lepton mass.

The TFFs $f^{B\rightarrow D}_{+,0}(q^2)$ are important components of the ratio $\mathcal {R}(D)$, which are defined as

$$\begin{aligned} \left\langle D(p)\left| \bar{c}\gamma _\mu b\right| B(p+q)\right\rangle= & {} 2f_{+}^{B\rightarrow D}(q^2) p_\mu + \left[ f_{+}^{B\rightarrow D}(q^2) \right. \nonumber \\&\left. +f_{-}^{B\rightarrow D}(q^2) \right] q_\mu \end{aligned}$$

(4)

and

$$\begin{aligned} f_{0}^{B\rightarrow D}(q^2) = f_{+}^{B\rightarrow D}(q^2) + \frac{q^2}{m_B^2 - m_D^2} f_{-}^{B\rightarrow D}(q^2), \end{aligned}$$

(5)

where p is the D-meson momentum and q is the transition momentum. To determine the TFFs $f_{+,0}^{B\rightarrow D}(q^2)$, we adopt the LCSR method and take the correlator as

$$\begin{aligned} \Pi _\mu (p,q)= & {} i \int d^4x e^{iq\cdot x} \nonumber \\&\times \left\langle D(p)\left| \bar{c}(x)\gamma _\mu b(x), m_b \bar{b}(0)i\gamma _5 q(0) \right| 0\right\rangle . \end{aligned}$$

(6)

Following the standard LCSR procedures, we obtain

$$\begin{aligned}&f^{B\rightarrow D}_+(q^2) \nonumber \\&\quad = \frac{e^{m_B^2/M^2}}{2m_B^2 f_B} \left[ F_0(q^2,M^2,s_0^B) + \frac{\alpha _s C_F}{4\pi } F_1(q^2,M^2,s_0^B) \right] \nonumber \\ \end{aligned}$$

(7)

and

$$\begin{aligned}&f^{B\rightarrow D}_+(q^2) + f^{B\rightarrow D}_-(q^2) \nonumber \\&\quad = \frac{e^{m_B^2/M^2}}{m_B^2 f_B} \left[ \widetilde{F}_0(q^2,M^2,s_0^B) + \frac{\alpha _s C_F}{4\pi } \widetilde{F}_1(q^2,M^2,s_0^B) \right] , \nonumber \\ \end{aligned}$$

(8)

where

$$\begin{aligned}&F_0(q^2,M^2,s_0^B) \nonumber \\&\quad = m_b^2 f_D \int ^1_\Delta du \exp \left[ -\frac{m_b^2 - \bar{u}q^2 + u\bar{u}m_D^2}{uM^2} \right] \nonumber \\&\qquad \times \left\{ \phantom {\left. \left. \frac{m_b^2 + q^2 - u^2 m_D^2}{m_b^2 - q^2 + u^2 m_D^2} \frac{d}{du} \right) \phi _{3;D}^\sigma (u) \right] } \frac{\phi _{2;D}(u)}{u} + \frac{1}{m_b} \left[ \phantom {\left. \left. \frac{m_b^2 + q^2 - u^2 m_D^2}{m_b^2 - q^2 + u^2 m_D^2} \frac{d}{du} \right) \phi _{3;D}^\sigma (u) \right] } \mu _D^p \phi _{3;D}^p(u) \right. \right. \nonumber \\&\qquad + \frac{\mu _D^\sigma }{6} \left( 1 - \frac{m_c^2}{m_D^2} \right) \left( \frac{2}{u} + \frac{4u m_b^2 m_D^2}{\left( m_b^2 - q^2 + u^2 m_D^2 \right) ^2} \right. \nonumber \\&\qquad - \left. \left. \left. \frac{m_b^2 + q^2 - u^2 m_D^2}{m_b^2 - q^2 + u^2 m_D^2} \frac{d}{du} \right) \phi _{3;D}^\sigma (u) \right] \right\} , \end{aligned}$$

(9)

$$\begin{aligned}&\widetilde{F}_0(q^2,M^2,s_0^B) \nonumber \\&\quad = m_b f_D \int ^1_\Delta du \exp \left[ -\frac{m_b^2 - \bar{u}q^2 + u\bar{u}m_D^2}{uM^2} \right] \nonumber \\&\qquad \times \left[ \mu _D^p \phi _{3;D}^p(u) + \frac{\mu _D^\sigma }{6u} \left( 1 - \frac{m_c^2}{m_D^2} \right) \frac{d\phi _{3;D}^\sigma (u)}{du} \right] , \end{aligned}$$

(10)

with

$$\begin{aligned} \Delta= & {} \left[ \sqrt{(s_0^B - q^2 - m_D^2)^2 + 4m_D^2 (m_b^2 - q^2)} \right. \\&\left. \phantom {\left[ \sqrt{(s_0^B - q^2 - m_D^2)^2 + 4m_D^2 (m_b^2 - q^2)} \right. } -(s_0^B - q^2 - m_D^2) \right] /\left( 2m_D^2 \right) . \end{aligned}$$

The first terms in Eqs. (7) and (8) are leading-order (LO) contributions for $f^{B\rightarrow D}_+(q^2)$ and $f^{B\rightarrow D}_+(q^2) + f^{B\rightarrow D}_-(q^2)$, respectively. $f_{B(D)}$ is the B(D)-meson decay constant, $m_{b}$ is the b-quark mass, $s_0^B$ is the threshold parameter, M is the Borel parameter, and finally $\mu _D^{p(\sigma )}$ is the normalization parameter of the DA $\phi _{3;D}^{p(\sigma )}$. The second terms in Eqs. (7) and (8) are NLO corrections. Those LCSRs show that up to twist-3 accuracy, we have to know the twist-2 DA $\phi _{2;D}$ and twist-3 DAs $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$ well. There are also three-particle twist-3 terms, whose contributions are rather small and can be safely neglected. The $\bar{\Lambda }/m_D$ power-suppression and the $\alpha _s$-suppression are quantitatively at the same order level, thus in the paper, we shall consider the NLO corrections to the twist-2 terms and keep the twist-3 terms at the LO level. As an estimation, we neglect the charm-quark current-mass effect to the twist-2 NLO terms of the $B\rightarrow D$ TFFs and take them to be the same as the ones of the $B\rightarrow \pi$ TFFs [32].

3 The D-meson leading-twist and twist-3 DAs

3.1 An improved model for the D-meson leading-twist DA $\phi _{2;D}$

In Ref. [19] we have suggested a new light-cone harmonic oscillator model for the D-meson leading-twist wavefunction, which is based on the Brodsky–Huang–Lepage (BHL)-prescription [33,34,35], e.g.,

$$\begin{aligned} \psi _{2:D}(x,\mathbf {k}_\perp ) = \chi _{2:D}(x,\mathbf {k}_\perp ) \psi ^R_{2:D}(x,\mathbf {k}_\perp ). \end{aligned}$$

(11)

In Eq. (11), $\chi _{2:D}(x,\mathbf {k}_\perp ) = \tilde{m}/\sqrt{\mathbf {k}^2_\perp + \tilde{m}^2}$ with $\tilde{m} = \hat{m}_c x + \hat{m}_q(1-x)$ stands for the spin-space wavefunction. $\psi ^R_{2:D}(x,\mathbf {k}_\perp )$ indicates the spatial wavefunction and which can be divided into two parts, i.e., the x-dependent part and the $\mathbf {k}_\perp$-dependent part. The x-dependent part dominates the longitudinal distribution broadness of the wavefunction and can be expanded in terms of the Gegenbauer polynomials. We only keep the first few terms and take

$$\begin{aligned} \varphi _D(x) = 1 + \sum ^4_{n=1} B_n^D C_n^{3/2}(2x-1). \end{aligned}$$

For the $\mathbf {k}_\perp$-dependent part, according to the suggestion of BHL, i.e., there is a possible connection between the rest frame wavefunction and the light-cone wavefunction, and considering the approximate bound-state solution in the quark model for D-meson in the rest frame, we have

$$\begin{aligned} \Psi ^R_{2;D}(x,\mathbf {k}_\perp ) \propto \exp \left[ -\frac{1}{\beta _D^2} \left( \frac{\mathbf {k}_\perp ^2 + \hat{m}_c^2}{1-x} + \frac{\mathbf {k}_\perp ^2 + \hat{m}_q^2}{x} \right) \right] . \end{aligned}$$

As a combination, one can obtain the explicit form of the spatial wavefunction

$$\begin{aligned} \Psi ^R_{2;D}(x,\mathbf {k}_\perp )= & {} A_D \varphi _D(x) \nonumber \\&\times \exp \left[ -\frac{1}{\beta _D^2} \left( \frac{\mathbf {k}_\perp ^2 + \hat{m}_c^2}{1-x} + \frac{\mathbf {k}_\perp ^2 + \hat{m}_q^2}{x} \right) \right] , \nonumber \\ \end{aligned}$$

(12)

where $\mathbf {k}_\perp$ is the transverse momentum, $\hat{m}_c$ and $\hat{m}_q$ are the constituent charm-quark and light-quark masses, and we adopt $\hat{m}_c = 1.5 \mathrm GeV$ and $\hat{m}_q = 0.3 \mathrm GeV$. This model is applicable for both $\overline{D}^0$ and $D^-$ leading-twist wavefunctions since the mass difference between u and d is negligible. One can obtain the leading-twist wavefunction of $D^0$ or $D^+$ by replacing x with $1-x$ in Eq. (11).

After integrating out the transverse momentum $\mathbf {k}_\perp$ component in the wavefunction $\Psi _{2;D}(x,\mathbf {k}_\perp )$, the D-meson leading-twist DA $\phi _{2;D}$ can be obtained. We have approximately taken $\chi _{2;D}\rightarrow 1$ in our previous treatment [19]; at present, we keep the $\chi _{2;D}$-terms to obtain a more accurate behavior for $\phi _{2;D}$, i.e.

$$\begin{aligned}&\quad \phi _{2;D}(x,\mu _0) \nonumber \\&\quad = \frac{\sqrt{3} A_D \tilde{m} \beta _D}{2 \pi ^{3/2} f_D} \sqrt{x(1-x)} \varphi _D(x) \nonumber \\&\qquad \times \exp \left[ - \frac{\hat{m}_c^2x + \hat{m}_q^2(1-x) - \tilde{m}^2}{8\beta _D^2 x(1-x)} \right] \nonumber \\&\qquad \times \left\{ \mathrm{Erf} \left[ \sqrt{\frac{\tilde{m}^2 + \mu _0^2}{8\beta _D^2 x(1-x)}} \right] - \mathrm{Erf} \left[ \sqrt{\frac{\tilde{m}^2}{8\beta _D^2 x(1-x)}} \right] \right\} ,\nonumber \\ \end{aligned}$$

(13)

where $\mu _0$ is the factorization scale; $\mathrm{Erf}(x)$ is the error function. The input parameters $A_D$, $B_n^D$ and $\beta _D$ can be fixed by the normalization condition of $\phi _{2;D}$, the probability of finding the leading Fock-state $\left| \bar{c}q\right\rangle$ in the D-meson Fock-state expansion which can be taken as $P_D \simeq 0.8~$[25], and the known moments $\left\langle \xi ^n\right\rangle _D$ [or the known Gegenbauer moments $a^D_n$] of $\phi _{2;D}$. Furthermore, the average value of the squared D-meson transverse momentum $\left\langle \mathbf {k}_\perp ^2\right\rangle _D$ can be calculated in the following way:

$$\begin{aligned} \left\langle \mathbf {k}_\perp ^2\right\rangle _D= & {} \frac{1}{P_D} \int ^1_0 dx \int \frac{d^2\mathbf {k}_\perp }{16\pi ^3} \mathbf {k}_\perp ^2 \left| \Psi ^R_{2;D}(x,\mathbf {k}_\perp ) \right| ^2 \nonumber \\= & {} \frac{A_D^2 \beta _D^4}{\pi ^2 P_D} \int ^1_0 dx x^2(1-x)^2 (\varphi _D(x))^2 \nonumber \\&\times \exp \left[ -\frac{\hat{m}_c^2x + \hat{m}_q^2(1-x)}{4\beta _D^2 x(1-x)} \right] , \end{aligned}$$

(14)

which can be used to constrain the behaviors of the D-meson twist-3 DAs $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$.

3.2 A new model for the D-meson twist-3 DAs

Following the above idea of constructing the D-meson leading-twist DA, we suggest the following model for the twist-3 DA $\phi _{3;D}^p$:

$$\begin{aligned} \phi _{3;D}^p(x,\mu _0)= & {} \frac{\sqrt{3} A_D^p \tilde{m} \beta _D^p}{2 \pi ^{3/2} f_D} \sqrt{x(1-x)} \varphi _D^p(x) \nonumber \\&\times \exp \left[ - \frac{\hat{m}_c^2x + \hat{m}_q^2(1-x) - \tilde{m}^2}{8(\beta _D^p)^2 x(1-x)} \right] \nonumber \\&\times \left\{ \mathrm{Erf} \left[ \sqrt{\frac{\tilde{m}^2 + \mu _0^2}{8(\beta _D^p)^2 x(1-x)}} \right] \right. \nonumber \\&- \left. \mathrm{Erf} \left[ \sqrt{\frac{\tilde{m}^2}{8(\beta _D^p)^2 x(1-x)}} \right] \right\} , \end{aligned}$$

(15)

with

$$\begin{aligned} \varphi _D^p(x) = 1 + \sum _{n=1}^4 B_n^{D,p} \times C_n^{1/2}(2x-1). \end{aligned}$$

(16)

The model parameters $A_D^p$, $B_n^{D,p}$ and $\beta _D^p$ are determined by the following constraints:

• The normalization condition of $\phi _{3;D}^p$,

  $$\begin{aligned} \int ^1_0 dx \phi _{3;D}^p(x,\mu _0) = 1. \end{aligned}$$

  (17)

• The average value of the squared D transverse momentum $\left\langle \mathbf {k}_\perp ^2\right\rangle _D$, i.e.

  $$\begin{aligned} \left\langle \mathbf {k}_\perp ^2\right\rangle _D= & {} \frac{(A_D^p)^2 (\beta _D^p)^4}{\pi ^2 P_D} \int ^1_0 dx x^2(1-x)^2 (\varphi _D^p(x))^2 \nonumber \\&\times \exp \left[ -\frac{\hat{m}_c^2x + \hat{m}_q^2(1-x)}{4(\beta _D^p)^2 x(1-x)} \right] . \end{aligned}$$

  (18)

• The moments $\left\langle \xi ^n_p\right\rangle _D$ of the D-meson twist-3 DA $\phi _{3;D}^p$ are defined as

  $$\begin{aligned} \left\langle \xi ^n_p\right\rangle _D |_{\mu _0} = \int ^1_0 dx (2x-1)^n \phi _{3;D}^p(x,\mu _0), \end{aligned}$$

  (19)

  which can be calculated by using the QCD sum rules in the framework of BFT.

The twist-3 DA $\phi _{3;D}^\sigma$ can be constructed in the same way. By replacing the upper index ‘p’ with ‘$\sigma$’ in Eq. (15) and taking the expansion

$$\begin{aligned} \varphi _D^\sigma (x) = 1 + \sum _{n=1}^4 B_n^{D,\sigma } \times C_n^{3/2}(2x-1), \end{aligned}$$

(20)

we obtain the model for $\phi _{3;D}^\sigma$.

In the above equations, the factorization scale is taken as $\mu _0\sim 1$ GeV, and the DAs at any other scale can be obtained via the conventional evolution equation [36].

In addition to the known parameters, our task left is to determine the moments of the twist-3 DAs $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$. We adopt the following correlators to obtain the sum rules for the moments $\left\langle \xi ^n_p\right\rangle _D$ and $\left\langle \xi ^n_\sigma \right\rangle _D$:

$$\begin{aligned} \Pi ^{p}_D(q)= & {} i\int d^4x e^{iq\cdot x} \left\langle 0\left| T\left\{ J^\mathrm{PS}_n(x) J^\mathrm{PS \dagger }_0 \right\} \right| 0\right\rangle \nonumber \\= & {} (z\cdot q)^n I^{p}_D(q^2) \end{aligned}$$

(21)

and

$$\begin{aligned} \Pi ^{\sigma }_D(q)= & {} i\int d^4x e^{iq\cdot x} \left\langle 0\left| T\left\{ J^\mathrm{PT}_n(x) J^\mathrm{PS \dagger }_0 \right\} \right| 0\right\rangle \nonumber \\= & {} -i(q_\mu z_\nu - q_\nu z_\mu ) (z\cdot q)^n I^{\sigma }_D(q^2), \end{aligned}$$

(22)

where $z^2 = 0$, $J^\mathrm{PS}_n(x)$ and $J^\mathrm{PT}_n(x)$ are pseudo-scalar and pseudo-tensor currents

$$\begin{aligned} J^\mathrm{PS}_n(x)= & {} \bar{c}(x)\gamma _5(iz\cdot \overset{\leftrightarrow }{D})^n q(x), \end{aligned}$$

(23)

$$\begin{aligned} J^\mathrm{PT}_n(x)= & {} \bar{c}(x)\sigma _{\mu \nu }\gamma _5(iz\cdot \overset{\leftrightarrow }{D})^{n+1} q(x) \end{aligned}$$

(24)

with $\sigma _{\mu \nu } = \frac{i}{2}(\gamma _\mu \gamma _\nu -\gamma _\nu \gamma _\mu )$.

Following the standard procedures of the SVZ QCD sum rules under the BFT [19, 31] with the help of the relations between the hadronic transition matrix elements and the moments

$$\begin{aligned} \left\langle 0\left| J^\mathrm{PS}_n(0) \right| D(q)\right\rangle= & {} -i\mu _D^p f_D \left\langle \xi ^n_p\right\rangle _D (z\cdot q)^n , \end{aligned}$$

(25)

$$\begin{aligned} \left\langle 0\left| J^\mathrm{PT}_n(0) \right| D(q)\right\rangle= & {} -\frac{n+1}{3} \mu _D^\sigma f_D \left( 1 - \frac{m_c^2}{m_D^2} \right) \left\langle \xi ^n_\sigma \right\rangle _D \nonumber \\&\times (q_\mu z_\nu - q_\nu z_\mu ) (z\cdot q)^n, \end{aligned}$$

(26)

one can obtain the required sum rules, i.e.

$$\begin{aligned} \left\langle \xi ^n_p\right\rangle _D= & {} \frac{M^2 e^{\frac{m_D^2}{M^2}}}{\left( \mu _D^p\right) ^2 f_D^2} \left\{ \frac{1}{\pi } \frac{1}{M^2} \int ^{s^D_0}_{m_c^2} ds e^{-\frac{s}{M^2}} \mathrm{Im} I^{p}_{D,\mathrm pert.} \right. \nonumber \\&+ \hat{L}_M I^{p}_{D,\left\langle \bar{q}q\right\rangle } + \hat{L}_M I^{p}_{D,\left\langle G^2\right\rangle } + \hat{L}_M I^{p}_{D,\left\langle \bar{q}Gq\right\rangle } \nonumber \\&+ \left. \phantom {\left\{ \frac{1}{\pi } \frac{1}{M^2} \int ^{s^D_0}_{m_c^2} ds e^{-\frac{s}{M^2}} \mathrm{Im} I^{p}_{D,\mathrm pert.} \right. } \hat{L}_M I^{p}_{D,\left\langle \bar{q}q\right\rangle ^2} + \hat{L}_M I^{p}_{D,\left\langle G^3\right\rangle } \right\} , \end{aligned}$$

(27)

$$\begin{aligned} \left\langle \xi ^n_\sigma \right\rangle _D= & {} \frac{3M^2 e^{\frac{m_D^2}{M^2}}}{(n+1)\mu _D^p \mu _D^\sigma f_D^2} \frac{m_D^2}{m_D^2-m_c^2} \nonumber \\&\times \left\{ \frac{1}{\pi } \frac{1}{M^2} \int ^{s^D_0}_{m_c^2} ds e^{-\frac{s}{M^2}} \mathrm{Im} I^{\sigma }_{D,\mathrm pert.} \right. \nonumber \\&+ \hat{L}_M I^{\sigma }_{D,\left\langle \bar{q}q\right\rangle } + \hat{L}_M I^{\sigma }_{D,\left\langle G^2\right\rangle } + \hat{L}_M I^{\sigma }_{D,\left\langle \bar{q}Gq\right\rangle } \nonumber \\&+ \left. \phantom {\left\{ \frac{1}{\pi } \frac{1}{M^2} \int ^{s^D_0}_{m_c^2} ds e^{-\frac{s}{M^2}} \mathrm{Im} I^{\sigma }_{D,\mathrm pert.} \right. } \hat{L}_M I^{\sigma }_{D,\left\langle \bar{q}q\right\rangle ^2} + \hat{L}_M I^{\sigma }_{D,\left\langle G^3\right\rangle } \right\} , \end{aligned}$$

(28)

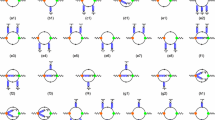
where $\hat{L}_M$ is the Borel transformation operator. The explicit expressions for the short notations like $\mathrm{Im} I^{p}_{D,\mathrm pert.}$, $\hat{L}_M I^{p}_{D,\left\langle \bar{q}q\right\rangle }$ etc. are presented in the appendix. In doing the calculation, we have used the quark propagator formula listed in Ref. [31], in which the quark mass terms are preserved, and thus the effect of the c-quark mass in the sum rules (27) and (28) is included completely.

4 Numerical analysis

4.1 Input parameters

To determine the moments of the D-meson twist-3 DAs, we take [37]

$$\begin{aligned} m_{D^-}= & {} 1869.59 \pm 0.09 \;\mathrm{MeV}, \nonumber \\ f_D= & {} 203.7 \pm 4.7 \pm 0.6\; \mathrm{MeV}, \nonumber \\ \bar{m}_{c}(\bar{m}_c)= & {} 1.28 \pm 0.03 \;\mathrm{GeV}, \nonumber \\ \bar{m}_d(2\mathrm{GeV})= & {} 4.7^{+0.5}_{-0.4} \;\mathrm{MeV}. \end{aligned}$$

(29)

For the condensates up to dimension six, we take [38]

$$\begin{aligned} \left\langle \bar{q}q\right\rangle (1 \mathrm{GeV})= & {} -(240 \pm 10 \;\mathrm{MeV})^3, \nonumber \\ \left\langle g_s\bar{q}\sigma TGq\right\rangle (1 \;\mathrm{GeV})= & {} 0.8 \left\langle \bar{q}q\right\rangle (1 \;\mathrm{GeV}), \nonumber \\ \left\langle \alpha _sG^2\right\rangle= & {} 0.038 \pm 0.011 \;\mathrm{GeV}^4, \nonumber \\ \left\langle g_s^3fG^3\right\rangle= & {} 0.045\; \mathrm{GeV}^6, \nonumber \\ \left\langle g_s\bar{q}q\right\rangle ^2= & {} 1.8 \times 10^{-3}\; \mathrm{GeV}^6. \end{aligned}$$

(30)

The scale-dependent parameters at any other scales can be obtained by using the renormalization group equation [39, 40]. As exceptions, the gluon condensates $\left\langle \alpha _sG^2\right\rangle$ and $\left\langle g_s^3fG^3\right\rangle$ are scale-independent, and we ignore the scale-dependence of the four-quark condensate $\left\langle g_s\bar{q}q\right\rangle ^2$, whose contribution to the twist-3 DA moment is small. In doing the calculation, we take the renormalization scale $\mu =M$, since the Borel parameter M characterizes the typical momentum flow of the process. For the continuous threshold $s_0^{D}$, as discussed in Ref. [19], we take $s_0^D \simeq 6.5 \text {GeV}^2$.

4.2 Update for the D-meson twist-2 DA $\phi _{2;D}$

Table 1 Criteria for determining the Borel windows of the moments $\left\langle \xi ^{n=1,\ldots ,4}\right\rangle _D$

Table 2 The Borel windows and the allowable regions for the moments $\left\langle \xi ^{n=1,\ldots ,4}\right\rangle _D$. All other input parameters are set to be their central values

Here, we adopt the value of $\left\langle g_s^3fG^3\right\rangle$ being the commonly used one suggested by Ref. [38], instead of the one adopted in our previous paper [19]. Then the corresponding results as regards the moments of the D-meson leading-twist DA $\phi _{2;D}$ should be updated. The criteria for determining the Borel windows of $\left\langle \xi ^{n=1,\ldots ,4}\right\rangle _D$ is exhibited in Table 1; the Borel windows and the allowable regions for $\left\langle \xi ^{n=1,\ldots ,4}\right\rangle _D$ are displayed in Table 2. Then the values of those moments are updated as

$$\begin{aligned} \left\langle \xi ^1\right\rangle _D|_{2\; \mathrm{GeV}}= & {} -0.421^{+0.025}_{-0.026}, \nonumber \\ \left\langle \xi ^2\right\rangle _D|_{2\; \mathrm{GeV}}= & {} 0.316^{+0.023}_{-0.021}, \nonumber \\ \left\langle \xi ^3\right\rangle _D|_{2\; \mathrm{GeV}}= & {} -0.186^{+0.015}_{-0.015}, \nonumber \\ \left\langle \xi ^4\right\rangle _D|_{2\; \mathrm{GeV}}= & {} 0.153^{+0.011}_{-0.010}. \end{aligned}$$

(31)

Table 3 Typical values for the model parameters of the D-meson leading-twist DAs at the scale $\mu =2\mathrm{GeV}$

Fig. 1

The D-meson leading-twist DA $\phi _{2;D}$ corresponds to the input parameter values listed in Table 3

With the values of $\left\langle \xi ^{n=1,\cdots ,4}\right\rangle _D$ shown in Eq. (19), the input parameters of the model (13) for the D-meson leading-twist DA $\phi _{2;D}$ can be obtained, and their typical values at the scale $\mu = 2\mathrm{GeV}$ are shown in Table 3. The corresponding curves of $\phi _{2;D}$ are shown in Fig. 1. Comparing with the old simplified model suggested in Ref. [19], the improved model (13) has a more obvious double-humped behavior and is narrower, but both have a peak around $x \sim 0.2$. Substituting the model parameters exhibited in Table 3 into Eq. (14), one can obtain $\left\langle \mathbf {k}_\perp ^2\right\rangle _D^{1/2} \simeq (651 - 1038) \mathrm{MeV}$ (the central value is $755\mathrm{MeV}$). The behavior of the twist-3 DAs is insensitive to the average value of the squared transverse momentum [31]. We will take the central values of $\left\langle \xi ^{n=1,\cdots ,4}\right\rangle _D$, corresponding to $\left\langle \mathbf {k}_\perp ^2\right\rangle _D^{1/2} = 755 \mathrm{MeV}$, to constrain the behaviors of $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$ in later subsections.

4.3 Moments of the D-meson twist-3 DAs

Table 4 Criteria for determining the Borel windows of $\mu _D^{p}$ and $\mu _D^{\sigma }$, $\left\langle \xi ^{n=1,\cdots ,4}_p\right\rangle _D$ and $\left\langle \xi ^{n=1,\cdots ,4}_\sigma \right\rangle _D$

Table 5 The Borel windows and the allowable regions for $\mu _D^{p}$, $\mu _D^{\sigma }$, $\left\langle \xi ^n_p\right\rangle _D$ and $\left\langle \xi ^n_\sigma \right\rangle _D$. All other input parameters are set to their central values

As suggested by Refs. [41, 42], the quarks inside the bound state are not exactly on shell, and a more reasonable prediction for $\mu _\pi ^{p}$ or $\mu _\pi ^{\sigma }$ could be obtained by using the sum rules derived from the zeroth moment of the pion twist-3 DA. More explicitly, by taking $n=0$ in the sum rules (27) and (28) and using the normalization conditions $\left\langle \xi _p^0\right\rangle _D = \left\langle \xi _\sigma ^0\right\rangle _D = 1$, we obtain the sum rules for $\mu _\pi ^{p}$ or $\mu _\pi ^{\sigma }$. We present the criteria for determining the Borel window in Table 4, where for convenience we have also presented the criteria for the moments $\left\langle \xi ^{n=1,\ldots ,4}_p\right\rangle _D$ and $\left\langle \xi ^{n=1,\ldots ,4}_\sigma \right\rangle _D$. The determined Borel windows together with the determined values of $\mu _D^p$ and $\mu _D^\sigma$ are presented in Table 5. Table 5 shows

$$\begin{aligned} \mu _D^p= & {} 2.535^{+0.136}_{-0.131}\; \mathrm{GeV}, \end{aligned}$$

(32)

$$\begin{aligned} \mu _D^\sigma= & {} 2.534^{+0.267}_{-0.246}\; \mathrm{GeV}, \end{aligned}$$

(33)

where the errors are squared average of those from the errors of the parameters such as the Borel parameter, the condensates and the bound-state parameters. As a comparison, if roughly using the equation of motion for the on-shell particles [43,44,45], we obtain $\mu _D^{p}=\mu _D^{\sigma }\simeq m_D^2/m_c \sim 3.04$ GeV, which are about $20\%$ larger than the sum rule predictions.

Fig. 2

The D-meson twist-3 DAs moments $\left\langle \xi _p^n\right\rangle _D$ and $\left\langle \xi _\sigma ^n\right\rangle _D$ $(n=1,2,3,4)$ versus the Borel parameter $M^2$, where all input parameters are set to be their central values. The solid, the dashed, the dotted and the dash-dotted lines are for the first, the second, the third and the fourth moments, respectively

We present the criteria for determining the Borel windows of the moments $\left\langle \xi _p^n\right\rangle _D$ and $\left\langle \xi _\sigma ^n\right\rangle _D\ (n=1,2,3,4)$ in Table 4. The determined Borel windows and the corresponding moments are displayed in Table 5. Figure 2 shows the stabilities of the D-meson twist-3 DAs moments $\left\langle \xi _p^n\right\rangle _D$ and $\left\langle \xi _\sigma ^n\right\rangle _D$ $(n=1,2,3,4)$ within the allowable Borel windows.

Table 6 The impact of various inputs on the moments $\left\langle \xi _p^n\right\rangle _D$ and $\left\langle \xi _\sigma ^n\right\rangle _D$. The Borel parameter M is fixed to its central value. The labels “$|_{\mathrm{up}}$” and “$|_{\mathrm{low}}$” stand for the upper and lower bounds of the inputs, and the symbols “$+$” and “−” represent the positive and negative errors brought about by the corresponding input, respectively. The $\left\langle G^2\right\rangle$, $\left\langle \bar{q}Gq\right\rangle$ and $\left\langle G^3\right\rangle$ are abbreviations of the vacuum condensates $\left\langle \alpha _sG^2\right\rangle$, $\left\langle g_s\bar{q}\sigma TGq\right\rangle$ and $\left\langle g_s^3fG^3\right\rangle$, respectively

Following the same idea as suggested by Ref. [19], we analyze the impact of various inputs on the moments $\left\langle \xi _p^n\right\rangle _D$ and $\left\langle \xi _\sigma ^n\right\rangle _D$; the results are put in Table 6. Table 6 shows that the effects of the input parameters on $\left\langle \xi _p^n\right\rangle _D$ and $\left\langle \xi _\sigma ^n\right\rangle _D$ are similar to those of the leading-twist moments $\left\langle \xi ^n\right\rangle _D$ [19]. By varying the mentioned error sources within allowable regions, we obtain

$$\begin{aligned} \left\langle \xi _p^1\right\rangle _D|_{2 \mathrm{GeV}}= & {} -0.484^{+0.075}_{-0.080}, \nonumber \\ \left\langle \xi _p^2\right\rangle _D|_{2 \mathrm{GeV}}= & {} 0.400^{+0.057}_{-0.052}, \nonumber \\ \left\langle \xi _p^3\right\rangle _D|_{2 \mathrm{GeV}}= & {} -0.277^{+0.037}_{-0.041}, \nonumber \\ \left\langle \xi _p^4\right\rangle _D|_{2 \mathrm{GeV}}= & {} 0.242^{+0.035}_{-0.033}, \end{aligned}$$

(34)

and

$$\begin{aligned} \left\langle \xi _\sigma ^1\right\rangle _D|_{2 \mathrm{GeV}}= & {} -0.381^{+0.068}_{-0.071}, \nonumber \\ \left\langle \xi _\sigma ^2\right\rangle _D|_{2 \mathrm{GeV}}= & {} 0.296^{+0.037}_{-0.033}, \nonumber \\ \left\langle \xi _\sigma ^3\right\rangle _D|_{2 \mathrm{GeV}}= & {} -0.190^{+0.043}_{-0.044}, \nonumber \\ \left\langle \xi _\sigma ^4\right\rangle _D|_{2 \mathrm{GeV}}= & {} 0.156^{+0.024}_{-0.022}, \end{aligned}$$

(35)

where the errors are squared averages of the errors from all the mentioned error sources. The errors are dominated by the parameters $\mu _D^{p,\sigma }$, $f_D$, $m_c$, and the condensates $\left\langle \bar{q}q\right\rangle$ and $\left\langle g_s\bar{q}\sigma TGq\right\rangle$.

Table 7 Typical values for the input parameters of the D-meson twist-3 DAs at the scale $\mu =2\;\mathrm{GeV}$

Fig. 3

The D-meson twist-3 DAs $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$ with the parameter values given in Table 7

4.4 Properties of the twist-3 DAs $\phi ^p_{3;D}$ and $\phi ^\sigma _{3;D}$

Similar to the leading-twist DA [19], the twist-3 DA moments cannot be varied independently. For example, if $\left\langle \xi _p^1\right\rangle _D$ and $\left\langle \xi _p^3\right\rangle _D$ take the upper bound, $\left\langle \xi _p^2\right\rangle _D$ and $\left\langle \xi _p^4\right\rangle _D$ should take the lower bound so as to obtain a self-consistent estimation of $\phi _{3;D}^p$ uncertainty. The error band of $\phi _{3;D}^p$ can be determined by two sets of $\left\langle \xi _p^n\right\rangle _D$, namely, (i) $\left\langle \xi _p^1\right\rangle _D|_{2\mathrm{GeV}} = -0.484^{+0.075}$, $\left\langle \xi _p^2\right\rangle _D|_{2\mathrm{GeV}} = 0.400_{-0.052}$, $\left\langle \xi _p^3\right\rangle _D|_{2\mathrm{GeV}} = -0.277^{+0.037}$, $\left\langle \xi _p^4\right\rangle _D|_{2\mathrm{GeV}} = 0.242_{-0.033}$; (ii) $\left\langle \xi _p^1\right\rangle _D|_{2\mathrm{GeV}} = -0.484_{-0.080}$, $\left\langle \xi _p^2\right\rangle _D|_{2\mathrm{GeV}} = 0.400^{+0.057}$, $\left\langle \xi _p^3\right\rangle _D|_{2\mathrm{GeV}} = -0.277_{-0.041}$, $\left\langle \xi _p^4\right\rangle _D|_{2\mathrm{GeV}} = 0.242^{+0.035}$. The twist-3 DA $\phi _{3;D}^\sigma$ can be treated in the same way. We present the determined values for the parameters of the twist-3 DAs $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$ at the scale $\mu =2\mathrm{GeV}$ in Table 7, and the corresponding curves are displayed in Fig.  3.

Comparing Eqs. (34) and (31), one can find that the differences among the moments of $\phi _{3;D}^p$ and $\phi _{2;D}$ are about 13–$37\%$, and these increase with the increase of the moment order. Figures 1 and 3 show that there is a large difference between the behaviors of $\phi _{2;D}$ and $\phi _{3;D}^p$. It is then reasonable to assume that a large discrepancy on the predictions involving them could be obtained by taking the rough approximation $\phi _{3;D}^p \simeq \phi _{2;D}$.

Fig. 4

The D-meson twist-3 DAs $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$ at different scales, where the solid, the dashed, the dotted and the dash-dotted lines are for the scales $\mu = 2$, 3, 10, 100 GeV, respectively

The D-meson twist-3 DAs $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$ at any other scales can be obtained by using the evolution equation. We present the twist-3 DAs $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$ with several typical scales, such as $\mu = 2$ ,3, 10 and 100 GeV, in Fig. 4. With the increment of $\mu$, $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$ become more symmetric with the peak around $x=0.5$, both of which tend to the asymptotic form $6x(1-x)$. This situation in $\phi _{3;D}^p$ is different from that of the heavy pseudo-scalar meson, which shows a humped behavior near the end-point region $x\rightarrow 0,1$ for high scales [46]. Unlike the asymptotic form of $\phi _{3;D}^p$, i.e. $\phi _{3;D}^p(x,\mu \rightarrow \infty ) \equiv 1$, the model (15) for $\mu \rightarrow \infty$ still equals zero as $x\rightarrow 0$ or $x\rightarrow 1$, which is due to an exponential suppression from the BHL-prescription. It has already been observed that more reasonable twist-3 contributions to the pion form factor [47] and the $B\rightarrow \pi$ TFFs [48] can be achieved by using the pion twist-3 DAs with similar end-point behaviors. Thus the D-meson DAs with suitable end-point singularity behavior shall be helpful for obtaining more reliable twist-3 predictions within the pQCD approach.

4.5 The $B\rightarrow D$ TFFs

Substituting the D-meson twist-2 and twist-3 DAs into the LCSRs (7) and (8), we can obtain the $B\rightarrow D$ TFFs $f^{B\rightarrow D}_{+,0}(q^2)$ with the help of Eq. (5). To do the numerical calculation, we take the B-meson mass $m_{\overline{B}^0} = 5279.63 \pm \mathrm{MeV}$, the decay constant $f_B = 188 \pm 17 \pm 18 \mathrm{MeV}$, and the b-quark mass $\bar{m}_b(\bar{m}_b) = 4.18^{+0.04}_{-0.03} \mathrm{GeV}$ [37]. For the continuous threshold parameter $s_0^B$, we take it to be $s_0^B = 36 \pm 1\; \mathrm{GeV^2}$; we take the Borel parameter $M^2 = (20 \sim 30) \mathrm{GeV^2}$, the factorization scale $\mu \simeq 3 \mathrm{GeV}$. We need to run the model parameters of the D-meson twist-2, 3 DAs exhibited in Table 3 and 7 up to the scale $\mu = 3\mathrm GeV$ via the QCD evolution equation, which are presented in Table 8. It is found that the differences caused by different bound-state masses are less than $10^{-4}$ of the total contributions, thus TFFs $f^{B\rightarrow D}_{+,0}(q^2)$ obtained with the above parameters can be applied for both the decays $B^- \rightarrow D^0 l\bar{\nu }_{l}$ and $\overline{B}^0 \rightarrow D^+ l \bar{\nu }_l$.

Table 8 Typical values for the input parameters of the D-meson twist-2 and twist-3 DAs at the scale $\mu =3\;\mathrm{GeV}$

At the maximum recoil point $q^2 = 0$, we have

$$\begin{aligned} f^{B\rightarrow D}_{+,0}(0) = 0.570\ ^{+0.029}_{-0.032}|_\mathrm{LO} + 0.089|_\mathrm{NLO}, \end{aligned}$$

(36)

where the error is obtained by adding all the errors in quadrature, whose error sources contain the choices of $\phi _{2;D}$, $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$, the Borel parameter $M^2$, the continuum threshold $s_0^B$, the B(D)-meson decay constant $f_{B(D)}$, the b-quark mass $m_b$ and the normalization parameter $\mu _D^{p(\sigma )}$. For the LO contributions, we have found that different choices of the D-meson DAs $\phi _{2;D}$, $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$ shall bring about $(0.1\sim 0.5)\%$, $(1.5\sim 2.1)\%$ and $(0.1\sim 0.2)\%$ errors to $f^{B\rightarrow D}_{+,0}(0)$, respectively. Thus the more precise twist-2 DA $\phi _{2;D}$ and the twist-3 DA $\phi _{3;D}^p$ are important for a precise prediction on the $B\rightarrow D$ TFFs.

Fig. 5

The LO LCSR prediction on the TFF $f^{B\rightarrow D}_{+}(q^2)$, where the solid line is for the total LO TFF $f^{B\rightarrow D}_{+}(q^2)$; the dashed, the dash-dot and the dotted lines are for the separate contributions from $\phi _{2;D}$, $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$, respectively

To show how various D-meson DAs contribute to the TFF, we present the LO contributions to the TFF $f^{B\rightarrow D}_{+}(q^2)$ separately from $\phi _{2;D}$, $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$ in Fig. 5, in which all input parameters are set to their central values. In the whole $q^2$-region, the twist-3 contributions are sizable but smaller than the twist-2 contribution. For example, at $q^2=0$, we have $f^{B\rightarrow D}_{+}(0)|_{\phi _{2;D}} = 0.347$, $f^{B\rightarrow D}_{+}(0)|_{\phi _{3;D}^p} = 0.138$ and $f^{B\rightarrow D}_{+}(0)|_{\phi _{3;D}^\sigma } = 0.085$, which lead to $61\%$, $24\%$ and $15\%$ contributions to the LO TFF $f^{B\rightarrow D}_{+}(0)$, respectively.

Fig. 6

The LCSR prediction on the TFF $f^{B\rightarrow D}_{+}(q^2)$ by using four different twist-3 DA $\phi _{3;D}^p$, where the solid, the dashed, the dash-dot, and the dotted lines are for $\phi _{3;D}^{p, I}$, $\phi _{3;D}^{p, II}$, $\phi _{3;D}^{p, III}$ and $\phi _{3;D}^{p, IV}$, respectively

To show how various twist-3 DA $\phi _{3;D}^p$ models affect the LO TFF, we take four models for the twist-3 DA $\phi _{3;D}^p$, e.g. I) $\phi _{3;D}^{p, I}$, which equals our present model (15); II) $\phi _{3;D}^{p, II}= \phi _{2;D}$ with $\phi _{2;D}$ from Eq. (13); III) $\phi _{3;D}^{p, III}= \phi _{2;D}$ with $\phi _{2;D}$ equal to the KLS-model [22]; IV) $\phi _{3;D}^{p, IV}\equiv 1$. We present a comparison in Fig. 6, in which all other parameters are set to their central values. Figure 6 shows that the TFF is sensitive to the behavior of $\phi _{3;D}^p$. For example, at the large recoil point, by taking $\phi _{3;D}^p=\phi _{3;D}^{p, II}$, we obtain $f^{B\rightarrow D}_{+}(0) = 0.598$, which is $4.9\%$ larger than the value derived by taking $\phi _{3;D}^p=\phi _{3;D}^{p, I}$; by taking $\phi _{3;D}^p=\phi _{3;D}^{p, IV}$, we obtain $f^{B\rightarrow D}_{+}(0) = 0.546$, which is $4.2\%$ smaller than the value derived by taking $\phi _{3;D}^p=\phi _{3;D}^{p, I}$. Moreover, by taking $\phi _{3;D}^p=\phi _{3;D}^{p, III}$, we obtain $f^{B\rightarrow D}_{+}(0) = 0.563$, which is close to the value derived by taking $\phi _{3;D}^p=\phi _{3;D}^{p, I}$; the reason is that the behavior of $\phi _{3;D}^{p, I}$ at $\mu = 3\mathrm GeV$ is coincidentally close to $\phi _{3;D}^{p, III}$.

Fig. 7

The LCSR predictions on the TFF $f^{B\rightarrow D}_{+}(q^2)$ for various models of the D-meson twist-2 DA $\phi _{2;D}$. The thick-solid line is for our model (13), and the dashed, the dash-dot, the solid, and the dotted lines are for the GH-model [25], the KLS-model [21, 22], the LLZ-model [23], and the LM-model [24], respectively

Figure 7 shows the model dependence of the TFF $f^{B\rightarrow D}_{+}(q^2)$ for different choices of the D-meson leading-twist DA $\phi _{2;D}$, where the dashed, the dash-dot, the solid, and the dotted lines are for the GH-model [25], the KLS-model [21, 22], the LLZ-model [23], and the LM-model [24], respectively. In drawing the figure, the NLO correction to the twist-2 DA is considered. Compared with the predictions of our model (13) and the LM-model, the predictions for the GH-model, the KLS-model and the LLZ-model give smaller values for $f^{B\rightarrow D}_{+}(q^2)$ in the low $q^2$-region, which, however, grow faster with the increment of $q^2$.

Table 9 The fitted parameters $a_{+(0)}$ and $b_{+(0)}$ for the extrapolation of the TFFs $f^{B\rightarrow D}_{+(0)}(q^2)$

4.6 The ratio $\mathcal {R}(D)$

The LCSRs for the TFFs $f^{B\rightarrow D}_{+,0}(q^2)$ are reliable in low and intermediate regions such as $q^2\in [0,8]\;\mathrm{GeV}^2$, and to make it applicable in all $q^2$-region, one usually extrapolates it by using the following parametrization [49]:

$$\begin{aligned} f^{B\rightarrow D}_{+(0)}(q^2) = \frac{f^{B\rightarrow D}_{+(0)}(0)}{1 - a_{+(0)}\left( q^2/m_B^2\right) + b_{+(0)}\left( q^2/m_B^2\right) ^2}. \nonumber \\ \end{aligned}$$

(37)

On the other hand, the LQCD results for the TFFs $f^{B\rightarrow D}_{+,0}(q^2)$ are available for the high energy region [7, 8]; thus one may combine the LCSR and LQCD predictions to have an accurate reliable prediction within the whole $q^2$-region. In making the combination, we adopt the extrapolation formulas (37) to fit our LCSR predictions for the TFFs with $\phi _{3;D}^{p, I}$ and the LQCD predictions by the HPQCD Collaboration [8]. The fitted parameters $a_{+(0)}$ and $b_{+(0)}$ are presented in Table 9.

Fig. 8

The fitted LCSR and LQCD predictions on the TFFs $f^{B\rightarrow D}_{+,0}(q^2)$. The solid lines are central values of the TFFs $f^{B\rightarrow D}_{+,0}(q^2)$, and the shaded bands are their corresponding uncertainties. The extrapolated LCSR predictions with the vacuum-to-B-meson correlator [20], and the LQCD predictions by the HPQCD Collaboration [8] or by the FNAL/MILC Collaboration [7], and the data from the Belle Collaboration [50] and the BaBar Collaboration [51] are presented as a comparison

We present the fitting TFFs $f^{B\rightarrow D}_{+,0}(q^2)$ and their uncertainties in Fig. 8. The solid lines are the central values of the TFFs $f^{B\rightarrow D}_{+}(q^2)$ and $f^{B\rightarrow D}_{0}(q^2)$ and the shaded hands are their uncertainties. The extrapolated LCSR predictions with the vacuum-to-B-meson correlator [20], and the LQCD predictions by the HPQCD Collaboration [8] or by the FNAL/MILC Collaboration [7], and the data from the Belle and BaBar Collaborations [50, 51] are presented as a comparison. Figure 8 shows that our predictions on the TFFs $f^{B\rightarrow D}_{+}(q^2)$ agree with the Belle and BaBar measurements within errors.

Fig. 9

Differential decay rates for the decay $\overline{B}^0 \rightarrow D^+l\bar{\nu }_{l}$. The solid lines are for $\overline{B}^0 \rightarrow D^+l^\prime \bar{\nu }_{l^\prime }$ and $\overline{B^0} \rightarrow D^+\tau \bar{\nu }_{\tau }$, respectively. The shaded hands are their uncertainties. The extrapolated LCSR prediction with the vacuum-to-B-meson correlation [20], the LQCD prediction by the HPQCD Collaboration [8] and the FNAL/MILC Collaboration [7] are presented as a comparison. The experimental data are from the Belle Collaboration [50]

To proceed, we present the differential decay rates for the decay $\overline{B}^0 \rightarrow D^+l\bar{\nu }_{l}$ in Fig. 9, where the solid lines are for $\overline{B}^0 \rightarrow D^+l^\prime \bar{\nu }_{l^\prime }$ and $\overline{B}^0 \rightarrow D^+\tau \bar{\nu }_{\tau }$, respectively. The shaded bands are their uncertainties. The extrapolated LCSR prediction with the vacuum-to-B-meson correlation [20], the LQCD prediction by the HPQCD Collaboration [8] and the FNAL/MILC Collaboration [7] are presented as a comparison.

Table 10 Theoretical predictions for the branching ratios (in units of $10^{-2}$) of the $B\rightarrow D l\bar{\nu }_l$ decays. As a comparison, the PDG values [37], the BaBar predictions [1, 2, 52], the HQET predictions [5] are also presented

Fig. 10

The ratio $\mathcal {R}(D)$ of the semileptonic decays $B\rightarrow D l\bar{\nu }_l$. The dashed line stands for the central value and the shaded band is its uncertainty

We present the branching ratios for the decay $B\rightarrow D l\bar{\nu }_l$ in Table 10, where the PDG values [37], the BaBar data [1, 2, 52], and the HQET predictions [5] are presented as a comparison. To do the numerical calculation, we adopt $G_F = 1.1663787(6)\times 10^{-5} \mathrm{GeV}^{-2}$, $|V_{cb}| = (40.5 \pm 1.5) \times 10^{-3}$, $m_\tau = 1776.86 \pm 0.12 \mathrm{MeV}$, $m_{B^-} = 5279.32 \pm 0.14 \mathrm{MeV}$, $m_{D^0} = 1864.83 \pm 0.05 \mathrm{MeV}$, $\tau _{\overline{B}^0} = (1.520 \pm 0.004) \times 10^{-12}s$ and $\tau _{B^-} = (1.638 \pm 0.004) \times 10^{-12} s$[37]. Table 10 shows our predictions on the branching ratios $\mathcal {B}(\overline{B}^0 \rightarrow D^+ l^\prime \bar{\nu }_{l^\prime })$, $\mathcal {B}(B^- \rightarrow D^0 l^\prime \bar{\nu }_{l^\prime })$ and $\mathcal {B}(B^- \rightarrow D^0 \tau \bar{\nu }_\tau )$ are in agreement with the HQET prediction, PDG values and the BaBar data within the errors; our prediction of $\mathcal {B}(\overline{B}^0 \rightarrow D^+\tau \bar{\nu }_\tau )$ agrees with the HQET prediction, but it is smaller than the value given by the BaBar Collaboration and the PDG average value. We finally get

$$\begin{aligned} \mathcal {R}(D) = 0.320^{+0.018}_{-0.021}. \end{aligned}$$

(38)

This value is shown in Fig. 10, where the central value and its uncertainty are indicated by the dashed line and the shaded band, respectively. As a comparison, the experimental data reported by the BaBar Collaboration [1, 2], the Belle Collaboration [3] and the weighted average of those experimental measurements (HFAG average) [4] are presented. The HQET prediction [5, 6], the LQCD prediction [9] and the LCSR prediction [20] are presented as a comparison.

5 Summary

In the paper, we have adopted the LCSR approach to calculating the key components of the $B\rightarrow D$ semileptonic decays, i.e. the $B\rightarrow D$ TFFs. The LCSR predictions on the $B\rightarrow D$ TFFs depend heavily on the D-meson DAs. At present, we have little knowledge of the D-meson twist-3 DAs, and the rough approximation $\phi _{3;D}^{p} \simeq \phi _{2;D}$ is usually adopted. In the paper, we have constructed a new model for the twist-3 DAs $\phi _{3;D}^p$ and $\phi _{3;D}^\sigma$. The input parameters of the twist-3 DAs have been fixed by using the normalization condition, the average value of the D-meson transverse momentum and the moments $\left\langle \xi _p^n\right\rangle _D$ and $\left\langle \xi _\sigma ^n\right\rangle _D$, which have been calculated by using the QCD SVZ sum rules within the framework of BFT up to NLO level.

Taking $n=0$ in sum rules (27) and (28) and using the normalization conditions $\left\langle \xi _p^0\right\rangle _D = \left\langle \xi _\sigma ^0\right\rangle _D = 1$, we obtain the sum rules for $\mu _\pi ^{p}$ and $\mu _\pi ^{\sigma }$, leading to $\mu _D^p = 2.535^{+0.136}_{-0.131} \mathrm{GeV}$ and $\mu _D^\sigma = 2.534^{+0.267}_{-0.246} \mathrm{GeV}$ at the scale $\mu = 2 \mathrm GeV$. The twist-3 DA moments up to fourth order, at the scale $\mu = 2 \mathrm GeV$, are

$$\begin{aligned} \left\langle \xi _p^1\right\rangle _D= & {} -0.484^{+0.075}_{-0.080},\; \left\langle \xi _\sigma ^1\right\rangle _D = -0.381^{+0.068}_{-0.071}, \end{aligned}$$

(39)

$$\begin{aligned} \left\langle \xi _p^2\right\rangle _D= & {} +0.400^{+0.057}_{-0.052}, \; \left\langle \xi _\sigma ^2\right\rangle _D = +0.296^{+0.037}_{-0.033}, \end{aligned}$$

(40)

$$\begin{aligned} \left\langle \xi _p^3\right\rangle _D= & {} -0.277^{+0.037}_{-0.041}, \; \left\langle \xi _\sigma ^3\right\rangle _D = -0.190^{+0.043}_{-0.044}, \end{aligned}$$

(41)

$$\begin{aligned} \left\langle \xi _p^4\right\rangle _D= & {} +0.242^{+0.035}_{-0.033}, \; \left\langle \xi _\sigma ^4\right\rangle _D = +0.156^{+0.024}_{-0.022}. \end{aligned}$$

(42)

Using the determined D-meson twist-3 DAs, we have found that the contributions from the twist-3 DAs are large, which are added up to $39\%$ for LO $f^{B\rightarrow D}_+(0)$. We have also shown how various models of the twist-3 DA $\phi _{3;D}^p$ affect the $B\rightarrow D$ TFF $f^{B\rightarrow D}_{+}(q^2)$. Figure 6 shows that the models $\phi _{3;D}^{p,II,IV}$ bring about a (4–$5)\%$ error for the LO $f^{B\rightarrow D}_{+}(q^2)$; thus, a proper $\phi _{3;D}^{p}$ shall be important for a precise prediction. Figures 8 and 9 show that the TFF $f^{B\rightarrow D}_{+}(q^2)$ and the differential decay rates for the decay $\overline{B}^0 \rightarrow D^+l\bar{\nu }_{l}$ are in agreement with the experimental measurements within errors.

Previous SM theoretical predictions for the ratio $\mathcal {R}(D)$ are always lower than the experimental measurements; some people thus think this inconsistency could indicate a signal of NP. In combination with the LQCD predictions with the LCSR predictions for the TFFs $f^{B\rightarrow D}_{+,0}(q^2)$, we achieve a more reliable prediction of the TFFs in the whole physical region; and we further predict $\mathcal {R}(D) = 0.320^{+0.018}_{-0.021}$, whose central value is slightly larger than previous SM predictions and is within $1\sigma$ deviation from the 2015 Belle data. At present the data still contain large errors, and our prediction is still about $1.5\sigma$ deviation from the HFAG average of the Belle and BABAR data. We need further accurate measurements of the experiment to confirm whether there is a signal of NP from the ratio $\mathcal {R}(D)$.

Appendix: Expressions for the terms in the sum rules (27) and (28)

We present the expressions for the terms in the sum rules (27) and (28) in the following:

$$\begin{aligned}&\mathrm{Im} I_{D,\mathrm pert.}^p\nonumber \\&\quad = \frac{3s}{16\pi (n+1)(n+2)} \left\{ \phantom {\left. \left( 1 - 2\frac{m_c^2}{2} \right) ^{n+2} \left[ (n+2) - (n+1)\frac{m_c^2}{s} \right] \right\} } (-1)^n \left[ (n+2) - (n+3)\frac{m_c^2}{s} \right] \right. \nonumber \\&\qquad +\left. \left( 1 - 2\frac{m_c^2}{2} \right) ^{n+2} \left[ (n+2) - (n+1)\frac{m_c^2}{s} \right] \right\} \nonumber \\&\qquad + \frac{3m_c^2}{16\pi (n+1)(n+2)} \left\{ \phantom {\left. \left( 1 - 2\frac{m_c^2}{s} \right) ^{n+1} + (-1)^n \right\} } \left[ (2n+3) - 2(n+1)\frac{m_c^2}{s} \right] \right. \nonumber \\&\qquad \times \left. \left( 1 - 2\frac{m_c^2}{s} \right) ^{n+1} + (-1)^n \right\} , \end{aligned}$$

(A1)

$$\begin{aligned}&\hat{L}_M I_{D,\left\langle \bar{q}q\right\rangle }^p\nonumber \\&\quad = \frac{\left\langle \bar{q}q\right\rangle }{M^2} \frac{(-1)^n}{2} \exp \left[ -\frac{m_c^2}{M^2}\right] \left( m_q \frac{m_c^2}{M^2} - 2m_c + m_q(n+1) \right) , \nonumber \\&\hat{L}_M I_{D,\left\langle G^2\right\rangle }^p\nonumber \\&\quad = \frac{\left\langle \alpha _sG^2\right\rangle }{24\pi } \left[ 3(n+1)\mathcal {H}(n,0,1,1) + 2n(n^2-1)\right. \nonumber \\&\qquad \times \mathcal {H}(n-2,1,2,1) - m_c^2 n \mathcal {H}(n,1,0,2) + 3m_c^2 \mathcal {H}(n,0,1,2) \nonumber \\&\qquad + \left. 2m_c^2n(n-1)\mathcal {H}(n-1,1,2,2) - 2m_c^4\mathcal {H}(n,1,0,3) \right] , \end{aligned}$$

(A2)

$$\begin{aligned}&\hat{L}_M I_{D,\left\langle \bar{q}Gq\right\rangle }^p \nonumber \\&\quad = \frac{\left\langle g_s\bar{q}\sigma TGq\right\rangle }{(M^2)^2} \frac{(-1)^n}{36} \exp \left[ -\frac{m_c^2}{M^2}\right] \left\{ -4m_q\left( \frac{m_c^2}{M^2}\right) ^2 \right. \nonumber \\&\qquad + 3\left[ 3m_c + m_q(3-4n)\right] \frac{m_c^2}{M^2} + 18(n-1)m_c \nonumber \\&\qquad - \left. n(8n-5)m_q \right\} , \nonumber \\&\hat{L}_M I_{D,\left\langle \bar{q}q\right\rangle ^2}^p \nonumber \\&\quad = \frac{\left\langle g_s\bar{q}q\right\rangle ^2}{(M^2)^2} \frac{(-1)^n}{81} \exp \left[ -\frac{m_c^2}{M^2}\right] \left[ 3\frac{m_c^2}{M^2} + (2n^2+7n-12) \right] , \nonumber \\&\hat{L}_M I_{D,\left\langle G^3\right\rangle }^p \nonumber \\&\quad = \frac{\left\langle g_s^3fG^3\right\rangle }{2880\pi ^2} \left[ \phantom {\left. 6(17n-52)\frac{m_c^2}{M^2} - 222n - 32 \right] } -280\mathcal {F}(n,-1,0,2) - 110m_c^2\mathcal {F}(n,-1,0,3)\right. \nonumber \\&\qquad + 200\mathcal {F}(n,-1,1,2) + 140m_c^2\mathcal {F}(n,-1,1,3) \nonumber \\&\qquad - 45n\mathcal {F}(n,-1,2,2) - 45m_c^2\mathcal {F}(n,-1,2,3)\nonumber \\&\qquad + 210\mathcal {F}(n,-2,0,2) - 280\mathcal {F}(n,-2,1,2) \nonumber \\&\qquad + 70\mathcal {F}(n,-2,2,2) - 255n\mathcal {F}(n,-2,3,2)\nonumber \\&\qquad - 255m_c^2\mathcal {F}(n,-2,3,3) - 10n(n-1)\mathcal {F}(n-2,-1,3,2) \nonumber \\&\qquad - 70\left( 3\frac{m_c^2}{M^2} - 2 \right) \widetilde{\mathcal {F}}(n,0,0,2) - 110m_c^2 \widetilde{\mathcal {F}}(n,0,0,3)\nonumber \\&\qquad + 40 \left( 7\frac{m_c^2}{M^2} - 9 \right) \widetilde{\mathcal {F}}(n,0,1,2) \nonumber \\&\qquad + 140m_c^2 \widetilde{\mathcal {F}}(n,0,1,3) - \left( 70\frac{m_c^2}{M^2} + 45n -140 \right) \nonumber \\&\qquad \times \widetilde{\mathcal {F}}(n,0,2,2) - 45m_c^2 \widetilde{\mathcal {F}}(n,0,2,3) \nonumber \\&\qquad + 255n \left( \frac{m_c^2}{M^2} - 2 \right) \widetilde{\mathcal {F}}(n,0,3,2) + 255m_c^2 \left( \frac{m_c^2}{M^2} - 3 \right) \nonumber \\&\qquad \times \widetilde{\mathcal {F}}(n,0,3,3) - 10n(n-1) \widetilde{\mathcal {F}}(n-2,0,3,2) \nonumber \\&\qquad + 210 \widetilde{\mathcal {F}}(n,1,0,2) - 180 \widetilde{\mathcal {F}}(n,1,1,2) + 70 \widetilde{\mathcal {F}}(n,1,2,2)\nonumber \\&\qquad - 255n \widetilde{\mathcal {F}}(n,1,3,2) - 255m_c^2 \widetilde{\mathcal {F}}(n,1,3,3) \nonumber \\&\qquad + 70\mathcal {H}(n,0,0,2) + 80m_c^2\mathcal {H}(n,0,0,3) + 210m_c^4\mathcal {H}(n,0,0,4) \nonumber \\&\qquad - 45n\mathcal {H}(n,0,1,2) - 30(4n-1)m_c^2 \mathcal {H}(n,0,1,3) \nonumber \\&\qquad - 360m_c^4\mathcal {H}(n,0,1,4) - 255n\mathcal {H}(n,1,0,2)\nonumber \\&\qquad - 30m_c^2(n+16)\mathcal {H}(n,1,0,3) + 18m_c^4(2n-9)\mathcal {H}(n,1,0,4) \nonumber \\&\qquad + 144m_c^6\mathcal {H}(n,1,0,5) - 30n(n-1)\mathcal {H}(n-2,0,2,2) \nonumber \\&\qquad - 10n(n-1)\mathcal {H}(n-2,1,1,2) \nonumber \\&\qquad - 20m_c^2n(n-1)\mathcal {H}(n-2,1,1,3) - 20n^2(n^2-1)\nonumber \\&\qquad \times \mathcal {H}(n-2,1,3,2) - 80m_c^2n^2(n-1)\mathcal {H}(n-2,1,3,3) \nonumber \\&\qquad - 120m_c^4n(n-1)\mathcal {H}(n-2,1,3,4) + \frac{5(-1)^n}{2(M^2)^2}\nonumber \\&\qquad \times \exp \left[ -\frac{m_c^2}{M^2}\right] \left\{ \phantom {\left. + 187\left( \frac{m_c^2}{M^2}\right) ^2 + 9(17n-52)\frac{m_c^2}{M^2} - 222n - 32 \right\} } \left( \ln \frac{M^2}{\mu ^2} - \gamma _E \right) \right. \nonumber \\&\qquad \times \left[ \phantom {\left. \left. + 187\left( \frac{m_c^2}{M^2}\right) ^2 + 9(17n-52)\frac{m_c^2}{M^2} - 222n - 32 \right\} \right] } \left( 306\frac{m_c^2}{M^2} + 306n + 56 \right) \delta ^{n0} \right. \nonumber \\&\qquad - 4n(n-1)\theta (n-2) + \left( 102(2n+3) \frac{m_c^2}{M^2} + 204n^2\right. \nonumber \\&\qquad \left. + 306n + 56 \right) \theta (n-1) + 102 \left( \frac{m_c^2}{M^2}\right) ^2 \nonumber \\&\qquad + \left. 6(17n-52)\frac{m_c^2}{M^2} - 222n - 32 \right] \nonumber \\&\qquad + \left( 459\frac{m_c^2}{M^2} + 306n - 28 \right) \delta ^{n0} - 4n(n-1) \theta (n-2)\nonumber \\&\qquad + \left( 153(2n+3)\frac{m_c^2}{M^2} + 204n^2 + 306n + 56 \right) \theta (n-1) \nonumber \\&\qquad \left. \left. + 187\left( \frac{m_c^2}{M^2}\right) ^2 + 9(17n-52)\frac{m_c^2}{M^2} - 222n - 32 \right\} \right] , \end{aligned}$$

(A3)

$$\begin{aligned}&\mathrm{Im} I^\sigma _{D,\mathrm pert.}\nonumber \\&\quad = \frac{3s}{16\pi (n+2)(n+3)} \left\{ \phantom {\left. + \left( 1 - 2\frac{m_c^2}{2} \right) ^{n+2} \left[ (n+2) - (n+1)\frac{m_c^2}{s} \right] \right\} } (-1)^n \left[ (n+2) - (n+3)\frac{m_c^2}{s} \right] \right. \nonumber \\&\qquad \left. + \left( 1 - 2\frac{m_c^2}{2} \right) ^{n+2} \left[ (n+2) - (n+1)\frac{m_c^2}{s} \right] \right\} , \end{aligned}$$

(A4)

$$\begin{aligned}&\hat{L}_M I_{D,\left\langle \bar{q}q\right\rangle }^\sigma \nonumber \\&\quad = \frac{\left\langle \bar{q}q\right\rangle }{M^2} (n+1) \frac{(-1)^n}{2} \exp \left[ -\frac{m_c^2}{M^2}\right] m_q, \nonumber \\&\hat{L}_M I_{D,\left\langle G^2\right\rangle }^\sigma \nonumber \\&\quad = \frac{\left\langle \alpha _sG^2\right\rangle }{24\pi }(n+1 ) \left[ \phantom {\left. + 2n(n-1)\mathcal {H}(n-2,1,2,1) - m_c^2\mathcal {H}(n,1,0,2) \right] } \mathcal {H}(n,0,1,1) \right. \nonumber \\&\qquad \left. + 2n(n-1)\mathcal {H}(n-2,1,2,1) - m_c^2\mathcal {H}(n,1,0,2) \right] , \end{aligned}$$

(A5)

$$\begin{aligned}&\hat{L}_M I_{D,\left\langle \bar{q}Gq\right\rangle }^\sigma \nonumber \\&\quad = \frac{\left\langle g_s\bar{q}\sigma TGq\right\rangle }{(M^2)^2} (n+1) \frac{(-1)^n}{36} \exp \left[ -\frac{m_c^2}{M^2}\right] \nonumber \\&\qquad \times \left[ -4m_q\frac{m_c^2}{M^2} - \left[ 6m_c+(8n+1)m_q\right] \right] , \nonumber \\&\hat{L}_M I_{D,\left\langle \bar{q}q\right\rangle ^2}^\sigma \nonumber \\&\quad = \frac{\left\langle g_s\bar{q}q\right\rangle ^2}{(M^2)^2} (n+1) \frac{(-1)^n}{81} \exp \left[ -\frac{m_c^2}{M^2}\right] \left( 2n-5 - 2\frac{m_c^2}{M^2} \right) , \nonumber \\&\hat{L}_M I_{D,\left\langle G^3\right\rangle }^\sigma \nonumber \\&\quad = \frac{\left\langle g_s^3fG^3\right\rangle }{2880\pi ^2}(n+1) \left[ 15\mathcal {F}(n,-1,2,2) \right. \nonumber \\&\qquad - 10(n+1)(3n-1)\mathcal {F}(n,-1,3,2) - 10m_c^2(3n-1)\nonumber \\&\mathcal {F}(n,-1,3,3) \nonumber \\&\qquad - 255\mathcal {F}(n,-2,3,2) - 5n(3n+5)\mathcal {F}(n-1,-1,3,2)\nonumber \\&\qquad - 30n m_c^2\mathcal {F}(n-1,-1,3,3) \nonumber \\&\qquad + 15n(n-1)\mathcal {F}(n-2,-1,3,2) + 15 \widetilde{\mathcal {F}}(n,0,2,2)\nonumber \\&\qquad + 5\left( 51\frac{m_c^2}{M^2} - 2(3n^2+2n+50) \right) \widetilde{\mathcal {F}}(n,0,3,2) \nonumber \\&\qquad - 10(3n-1) m_c^2 \widetilde{\mathcal {F}}(n,0,3,3) - 5n(3n+5) \widetilde{\mathcal {F}}(n-1,0,3,2) \nonumber \\&\qquad - 30n m_c^2 \widetilde{\mathcal {F}}(n-1,0,3,3) \nonumber \\&\qquad + 15n(n-1) \widetilde{\mathcal {F}}(n-2,0,3,2) - 255 \widetilde{\mathcal {F}}(n,1,3,2) \nonumber \\&\qquad + 15 \mathcal {H}(n,0,1,2) + 20m_c^2\mathcal {H}(n,0,1,3) \nonumber \\&\qquad - 20(n+1)\mathcal {H}(n,0,2,2) - 40m_c^2\mathcal {H}(n,0,2,3) \nonumber \\&\qquad - 255\mathcal {H}(n,1,0,2) - 30m_c^2\mathcal {H}(n,1,0,3) + 36m_c^4\mathcal {H}(n,1,0,4) \nonumber \\&\qquad + 90(n+1)\mathcal {H}(n,1,1,2) - 20m_c^2(n-9)\mathcal {H}(n,1,1,3) \nonumber \\&\qquad - 180m_c^4\mathcal {H}(n,1,1,4) + 240m_c^4\mathcal {H}(n,1,2,4) \nonumber \\&\qquad - 40(n+1)(n+2)\mathcal {H}(n,2,1,2) - 160(n+1)m_c^2\mathcal {H}(n,2,1,3)\nonumber \\&\qquad + 60n(n+1)\mathcal {H}(n-1,0,3,2) \nonumber \\&\qquad + 120n m_c^2\mathcal {H}(n-1,0,3,3) + 5n(7n+5)\mathcal {H}(n-1,1,1,2)\nonumber \\&\qquad + 80n m_c^2\mathcal {H}(n-1,1,1,3) \nonumber \\&\qquad - 60n(n+1)\mathcal {H}(n-1,1,2,2) - 160n m_c^2\mathcal {H}(n-1,1,2,3)\nonumber \\&\qquad + 40n m_c^2\mathcal {H}(n-1,2,1,3) \nonumber \\&\qquad - 30n(n-1)\mathcal {H}(n-2,0,3,2) + 5n(n-1)\mathcal {H}(n-2,1,1,2) \nonumber \\&\qquad - 30n(n-1)\mathcal {H}(n-2,1,2,2) \nonumber \\&\qquad - 20n(n^2-1)\mathcal {H}(n-2,1,3,2) - 40n(n-1)m_c^2\nonumber \\&\qquad \times \mathcal {H}(n-2,1,3,3) + \frac{5(-1)^n}{2(M^2)^2} \exp \left[ -\frac{m_c^2}{M^2}\right] \nonumber \\&\qquad \times \left\{ \left( \ln \frac{M^2}{\mu ^2} - \gamma _E + 1 \right) \left[ 306 \delta ^{n0} + 6n(n-1) \theta (n-2)\right. \right. \nonumber \\&\qquad + \left( 12n \frac{m_c^2}{M^2} + 6n^2 + 214n + 306 \right) \theta (n-1) \nonumber \\&\qquad - \left. 2(6n-53)\frac{m_c^2}{M^2} - 2(6n^2+4n+97) \right] \nonumber \\&\qquad \left. \left. + 6n\frac{m_c^2}{M^2} \theta (n-1) - (6n-53)\frac{m_c^2}{M^2} \right\} \right] , \end{aligned}$$

(A6)

where

$$\begin{aligned}&\mathcal {F}(n,a,b,c) \\&\quad = \frac{1}{\left( M^2\right) ^c} \exp \left[ -\frac{m_c^2}{M^2} \right] \sum ^n_{k=0} \frac{(-1)^k n! \Gamma (k+b+1)}{k! (n-k)!}\\&\qquad \times \sum ^\infty _{l=-a} \frac{\Gamma (l+c) \Gamma (n-k+l+a+1)}{\Gamma (n+l+a+b+2)} \\&\qquad \times \sum ^l_{i=0} \frac{1}{i! (l-i)! (l-i+c-1)!} \left( -\frac{m_c^2}{M^2} \right) ^{l-i}, \\&\widetilde{\mathcal {F}}(n,i,b,c) \\&\quad = \frac{1}{\left( M^2\right) ^c} \exp \left[ -\frac{m_c^2}{M^2}\right] \sum ^{n-1-i}_{k=0}\\&\qquad \times \frac{(-1)^k n! \Gamma (k+b+1) \Gamma (n+b+i) \Gamma (n-k-i)}{k! (n-k)! \Gamma (n+b) \Gamma (n+b+1)} ,\\&\mathcal {H}(n,a,b,c) \\&\quad = \frac{1}{(c-1)!} \frac{1}{(M^2)^c} \int ^1_0 dx (2x-1)^n \\&\qquad \times x^a (1-x)^{b-c} \exp \left[ -\frac{m_c^2}{M^2(1-x)} \right] . \end{aligned}$$